Abstract
Let D be an open set in \(\mathbb {R}^d\) and \(u:D\to \mathbb {R}\) be a (non-negative) local minimizer of \(\mathcal F_\Lambda \) in D
You have full access to this open access chapter, Download chapter PDF
Let D be an open set in \(\mathbb {R}^d\) and \(u:D\to \mathbb {R}\) be a (non-negative) local minimizer of \(\mathcal F_\Lambda \) in D. Recall that, by Theorem 3.1, we have that u is locally Lipschitz continuous in D. Let x 0 ∈ ∂ Ωu ∩ D be a given point on the free boundary. For every r > 0, we define the rescaled function
Let (r n)n≥1 be a vanishing sequence of positive numbers. We say that the sequence of functions \(u_{x_0,r_n}\) is a blow-up sequence. We notice that \(u_{x_0,r_n}\) is not defined on the entire \(\mathbb {R}^d\) (since a priori we might have that \(D\neq \mathbb {R}^d\)), its domain of definition being the set
On the other hand, since r n converges to zero, for every fixed R > 0, there exists m > 0 such that, for every n ≥ m, \(u_{x_0,r_n}\) is defined on B R, that is,
Now since,
we have that
Since u is locally Lipschitz continuous and u(x 0) = 0, we get that the sequence \(u_{x_0,r_n}\) is uniformly bounded and equicontinuous on B R. Thus, by the Theorem of Ascoli-Arzelà, we obtain that there is a subsequence of \(u_{x_0,r_n}\) that converges uniformly in the ball B R. Repeating this argument for every (natural number) R > 0 and extracting a diagonal sequence, we get that there exists a function \(u_0:\mathbb {R}^d\to \mathbb {R}\) such that, for every R > 0, the sequence \(u_{x_0,r_n}\) converges uniformly to u 0 in B R,
We will say that the function \(u_0:\mathbb {R}^d\to \mathbb {R}\) is a blow-up limit of u at x 0 if (6.1) does hold.
We notice that every blow-up limit u 0 of a local minimizer u of \(\mathcal F_\Lambda \) is non-negative, Lipschitz continuous (in \(\mathbb {R}^d\)) and vanishes in zero. We also stress that there might be numerous blow-up limits, each one depending on the choice of the (sub-)sequence \(u_{x_0,r_n}\). If this is the case, then we simply say that the blow-up limit is not unique. For instance, the function \(\phi :B_1\to \mathbb {R}\) defined in polar coordinates as (see Fig. 6.1)
has infinitely many blow-up limits in zero (but it is not a local minimizer of the functional \(\mathcal F_\Lambda \)). We will denote the family of all blow-up limits of u at x 0 by \(\mathcal {B}\mathcal {U}_{u}(x_0)\). The classification of all the possible blow-up limits and the uniqueness of the blow-up limit at a given point x 0 ∈ ∂ Ωu are both central questions in the free boundary regularity theory, which do not have a complete answer yet.
In this chapter we will decompose the free boundary into a regular and singular parts according to the structure of the space of blow-up limits at the points of ∂ Ωu. The Sects. 6.1, 6.2, and 6.3 are dedicated to the proof of the following result.
Let D be an open subset of \(\mathbb {R}^d\) and let \(u:D\to \mathbb {R}\) be non-negative, \(u\in H^1_{loc}(D)\) and a local minimizer of \(\mathcal F_\Lambda \) in D. Let x 0 ∈ ∂ Ω u ∩ D and let r n → 0 be a vanishing sequence of positive real numbers such that the blow-up sequence \(u_{x_0,r_n}\) converges locally uniformly to the blow-up limit \(u_0:\mathbb {R}^d\to \mathbb {R}\) in the sense of (6.1). Then, there is a subsequence such that, for every R > 0, we have:
-
(i)
the sequence \(u_{x_0,r_n}\) converges to u 0 strongly in H 1(B R);
-
(ii)
the sequence of characteristic functions
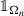 converges to
converges to
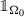 in L
1(B
R), where
$$\displaystyle \begin{aligned} \Omega_n:=\{u_{x_0,r_n}>0\}\qquad \mathit{\text{and}}\qquad \Omega_0:=\{u_0>0\}\,; \end{aligned}$$
in L
1(B
R), where
$$\displaystyle \begin{aligned} \Omega_n:=\{u_{x_0,r_n}>0\}\qquad \mathit{\text{and}}\qquad \Omega_0:=\{u_0>0\}\,; \end{aligned}$$ -
(iii)
the sequence of sets \(\overline \Omega _n\) converges locally Hausdorff in B R to \(\overline \Omega _0\);
-
(iv)
u 0 is a non-trivial local minimizer of \(\mathcal F_\Lambda \) in \(\mathbb {R}^d\).
In particular, Sect. 6.1 is dedicated to the strong convergence of the blow-up sequences (claims (i) and (ii)) and the optimality of the blow-up limits (claim (iv)); the main result of this section (Lemma 6.3) is more general and will also be used in the proof of Theorem 1.9. Section 6.2 is dedicated to the local Hausdorff convergence of the free boundaries (claim (iii)); the results of this section apply both to Theorem 1.2 and Theorem 1.9. In Sect. 6.3, we conclude the proof of Proposition 6.2.
In Sect. 6.4, we define the regular part Reg(∂ Ωu) and the singular part Sing(∂ Ωu) of the free boundary. Moreover, we prove that the singular set Sing(∂ Ωu) has zero (d − 1)-dimensional Hausdorff measure (Proposition 6.12). We notice that this result applies to Theorems 1.2, 1.4, and 1.9, but is interesting only for Theorem 1.2, in which we do not make use of monotonicity formulas. In fact, in Sect. 10, we will obtain better estimates on the dimension of the singular set by means of the Weiss’ monotonicity formula, which we will apply to both Theorem 1.4 and Theorem 1.9.
6.1 Convergence of Local Minimizers
In this section we prove the strong convergence of the blow-up sequences and the minimality of the blow-up limits at every point of the free boundary of a local minimizer. Our result (Lemma 6.3) is more general and applies also to other free boundary problems; for instance, we will use it in the proof of Theorem 1.9.
Lemma 6.3
Let Λ > 0 be a given constant, \(B_R\subset \mathbb {R}^d\) and u n ∈ H 1(B R) be a sequence of non-negative functions such that:
-
(a)
every u n is a local minimizer of \(\mathcal F_\Lambda \) in B R or, more generally, satisfies
$$\displaystyle \begin{aligned} \mathcal F_\Lambda(u_n,B_R)\le \mathcal F_\Lambda(u_n+\varphi,B_R)+{\varepsilon}_n\quad \mathit{\text{for every}}\quad \varphi\in H^1_0(B_r)\quad \mathit{\text{and every}}\quad r<R\ , \end{aligned}$$where ε n is a vanishing sequence of positive constants.
-
(b)
the sequence u n is uniformly bounded in H 1(B R), that is, for some constant C > 0,
$$\displaystyle \begin{aligned} \|u_n\|{}_{H^1(B_R)}^2=\mathcal F_0(u_n,B_R)+\int_{B_R}u_n^2\,dx\le C\qquad \mathit{\text{for every}}\qquad n\ge 1. \end{aligned}$$
Then, there is a function u ∞∈ H 1(B R) such that, up to a subsequence, we have
-
(i)
u n converges to u ∞ strongly in H 1(B r), for every 0 < r < R;
-
(ii)
the sequence of characteristic functions
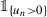 converges to
converges to
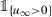 strongly in L
1(B
r) and pointwise almost-everywhere in B
r
, for every 0 < r < R;
strongly in L
1(B
r) and pointwise almost-everywhere in B
r
, for every 0 < r < R;
-
(iii)
u ∞ is a local minimizer of \(\mathcal F_\Lambda \) in B R.
Proof
The idea of the proof is very similar to the one in Lemma 3.14, but is more involved due to the presence of the measure term. Up to extracting a subsequence, we can suppose that the sequence u n converges to a function u ∞∈ H 1(B R) weakly in H 1(B R), strongly in L 2(B R) and pointwise (Lebesgue) almost-everywhere in B R. We set for simplicity
The weak H 1-convergence implies that for every 0 < r ≤ R
with an equality, if and only if, (up to a subsequence) the convergence is strong in B r. On the other hand, the pointwise convergence of u n implies that for almost-every x ∈ B R
In particular, this implies that

and so, by the Fatou Lemma, for every 0 < r ≤ R, we have
with an equality, if and only if, (again, up to a subsequence)  converges strongly to
converges strongly to  in L
1(B
r). Notice that, up to extracting a subsequence we may assume that the limits in the right-hand sides of (6.3) and (6.2) do exist.
in L
1(B
r). Notice that, up to extracting a subsequence we may assume that the limits in the right-hand sides of (6.3) and (6.2) do exist.
In order to prove (i) and (ii), it is sufficient to prove that, for fixed 0 < r < R, we have
Let \(\eta :B_R\to \mathbb {R}\) be a function such that
Consider the test function \(\tilde u_n=\eta u_{n}+(1-\eta )u_\infty \). Since u n is a local minimizer for \(\mathcal F_\Lambda \) in B R, and since \(u_n=\tilde u_n\) on ∂B R, we have \(\mathcal F_\Lambda (u_n,B_R)\le \mathcal F_\Lambda (\tilde u_n,B_R)+{\varepsilon }_n\), that is,
where we have set \(\tilde \Omega _n:=\{\tilde u_n>0\}\). We first estimate
By the Fatou Lemma on the set  , we have that
, we have that

and so, we get
We next calculate
Now since u n → u ∞ strongly in L 2(B R), we have that

By the weak H
1 convergence of u
n to u
∞ on the set  , we have
, we have
This estimate, together with (6.6) and the minimality of u n, gives
Since η is arbitrary, we finally obtain
which implies (6.4) and, as a consequence, the claims (i) and (ii).
We now prove (iii). Let 0 < r < R and \(\varphi \in H^1_0(B_r)\). We will show that
In order to prove(6.7), we will use the optimality of u n and we will pass to the limit. We notice that, for a fixed n ≥ 1, the natural competitor is simply u n + φ. Unfortunately, we cannot follow this strategy since we do NOT a priori know that
Thus, we consider a function \(\eta :B_R\to \mathbb {R}\) that satisfies (6.5) and is such that the set \(\mathcal N:=\{\eta <1\}\) is a ball strictly contained in B R. Precisely, we have that the following inclusions do hold:
the last two inclusions being strict. We define the competitor
and we set for simplicity v
∞ := u
∞ + φ. Now, since φ = 0 on  , we have that v
n = v
∞ on the set {η = 0} and (6.7) is equivalent to
, we have that v
n = v
∞ on the set {η = 0} and (6.7) is equivalent to
By the points (i) and (ii), we have that
The optimality of u n and the strong H 1 convergence of u n to u ∞ in \(\mathcal N\) give
Moreover, since
we have
which, together with (6.9) and (6.8), gives
Now, since the set {0 < η < 1} is arbitratry, we get (6.8) and so, the claim (iii). □
6.2 Convergence of the Free Boundary
This section is dedicated to the proof of Proposition 6.2 (iii). In particular, we define the notion of local Hausdorff convergence (see Definition 6.4 below) and we prove several results, which are general and can be used in the context of different free boundary problems.
Definition 6.4 (Local Hausdorff Convergence)
Suppose that X n is a sequence of closed sets in \(\mathbb {R}^d\) and Ω is an open subset of \(\mathbb {R}^d\). We say that X n converges locally Hausdorff in Ω to (the closed set) X, if for every compact set \(\mathcal K\subset \Omega \) and every open set \(\mathcal U\), such that \(\mathcal K\subset \mathcal U\subset \Omega \), we have
where, for any pair of closed subset X, Y of Ω, we define
Lemma 6.5 (Hausdorff Convergence of the Supports)
Let B R be the ball of radius R in \(\mathbb {R}^d\) . Let \(u_n:B_{2R}\to \mathbb {R}\) be a sequence of continuous non-negative functions such that:
-
(a)
u n converges uniformly in B 2R to the continuous non-negative function \(u_0:B_{2R}\to \mathbb {R}\);
-
(b)
u n is uniformly non-degenerate, that is, there is a strictly increasing function
$$\displaystyle \begin{aligned} \underline\omega:[0,+\infty)\to[0,+\infty), \end{aligned}$$such that \( \underline \omega (0)=0\) and
$$\displaystyle \begin{aligned} \|u_n\|{}_{L^\infty(B_r(x_0))}\ge \underline\omega(r)\quad \mathit{\text{for every}}\quad x_0\in \overline\Omega_{u_n}\cap B_{\frac{3R}2}\ ,\quad r\in(0,\frac{R}2)\quad \mathit{\text{and}}\quad n\in\mathbb{N}\,. \end{aligned}$$
Then the sequence of closed sets \(\overline \Omega _{u_n}\) converges locally Hausdorff in B R to \(\overline \Omega _{u_0}\).
Proof
We first prove the non-degeneracy of u 0. Suppose that \(x\in \overline \Omega _{u_0}\cap \overline B_{R}\) and r ≤ R∕2. Then, there is y ∈ B r∕2(x) such that u 0(y) > 0 and so, for n large enough we have that u n(y) > 0. By the non-degeneracy of u n, there is a point z n ∈ B r∕2(y) such that \(u_n(z_n)\ge \underline \omega (\frac {r}2)\). Up to a subsequence z n converges to some \(z\in \overline B_{\frac {r}2}(y)\). By the uniform convergence of u n we have
which proves that
We can now prove the local Hausdorff convergence of \(\overline \Omega _{u_n}\) to \(\overline \Omega _{u_0}\). Let \(\mathcal K\subset B_R\) be a given compact set and \(\mathcal U\subset B_R\) be an open set containing \(\mathcal K\). Let δ > 0 be the distance from \(\mathcal K\) to the boundary of \(\mathcal U\). We reason by contradiction. Indeed, suppose that there is ε > 0 such that \(\displaystyle \text{dist}_{\,\mathcal K, \mathcal U}\big (\overline \Omega _{u_n},\overline \Omega _{u_0}\big )>{\varepsilon }.\) Then, up to extracting a subsequence, we can assume that one of the following does hold:
-
(1)
There is a sequence (x n)n such that
$$\displaystyle \begin{aligned} x_n\in \overline\Omega_{u_n}\cap\mathcal K\quad \text{and}\quad \mathrm{dist}\,(x_n,\overline\Omega_{u_0}\cap\mathcal U)\ge{\varepsilon}. \end{aligned}$$ -
(2)
There is a sequence (x n)n such that
$$\displaystyle \begin{aligned} x_n\in \overline\Omega_{u_0}\cap\mathcal K\quad \text{and}\quad \mathrm{dist}\,(x_n,\overline\Omega_{u_n}\cap\mathcal U)\ge{\varepsilon}. \end{aligned}$$
Moreover, we can assume that 0 < ε ≤ δ.
Suppose that (1) holds. Since \(x_n\in \overline \Omega _{u_n}\) we have that there is \(y_n\in B_{\frac {\varepsilon }2}(x_n)\subset \mathcal U\) such that \(u_n(y_n)> \underline \omega (\frac {{\varepsilon }}2)\). On the other hand, (1) implies that u 0(y n) = 0, in contradiction with the uniform convergence of u n to u 0.
Suppose that (2) holds. By the non-degeneracy of u 0 we have that there is \(y_n\in B_{\frac {\varepsilon }2}(x_n)\subset \mathcal U\) such that \(u_0(y_n)\ge \underline \omega (\frac {{\varepsilon }}4)\). On the other hand u n(y n) = 0, in contradiction with the uniform convergence of u n to u 0. □
Lemma 6.6 (Hausdorff Convergence of the Zero Level Sets)
Let B R be the ball of radius R in \(\mathbb {R}^d\) . Let \(u_n:B_{2R}\to \mathbb {R}\) be a sequence of continuous non-negative functions such that:
-
(a)
u n converges uniformly in B 2R to the continuous non-negative function \(u_0:B_{2R}\to \mathbb {R}\);
-
(b)
u n(0) = 0 and u n satisfies the following uniform growth condition:
$$\displaystyle \begin{aligned} u_n(x)\ge \underline\omega\big(\mathrm{dist}\,(x,\{u_n=0\}\cap \overline B_{2R})\big)\quad \mathit{\text{for every}}\quad x\cap \overline B_R\quad \mathit{\text{and every}}\quad n\in\mathbb{N}\,, \end{aligned}$$where \( \underline \omega :[0,+\infty )\to [0,+\infty )\) is a strictly increasing function such that \( \underline \omega (0)=0\).
Then the sequence of closed sets {u n = 0} converges locally Hausdorff in B R to {u 0 = 0}.
Proof
Let \(\mathcal K\subset B_R\) be a compact set and let \(\mathcal U\subset B_R\) be an open set containing \(\mathcal K\). Let δ > 0 be the distance from \(\mathcal K\) to the boundary \(\partial \mathcal U\). We reason by contradiction and we suppose that there is ε ∈ (0, δ) such that
Then, up to a subsequence, we have one of the following possibilities:
-
(1)
There is a sequence (x n)n such that
$$\displaystyle \begin{aligned} x_n\in \{u_n=0\}\cap\mathcal K\quad \text{and}\quad \text{dist}(x_n,\{u_0=0\}\cap\mathcal U)\ge {\varepsilon}. \end{aligned}$$ -
(2)
There is a sequence (x n)n such that
$$\displaystyle \begin{aligned} x_n\in \{u_0=0\}\cap\mathcal K\quad \text{and}\quad \text{dist}(x_n,\{u_n=0\}\cap\mathcal U)\ge {\varepsilon}. \end{aligned}$$
Suppose first that (1) holds. Up to extracting a subsequence, we can suppose that x n converges to \(x_0\in \mathcal K\). By the uniform convergence of u n and the continuity of u 0, we have
Passing to the limit as n →∞, we get that u 0(x 0) = 0, which is a contradiction since
Suppose now that (2) holds. Now, let y n be the point in B 2R ∩{u n = 0} that realizes the distance from x n to this set. There are two possibilities:
-
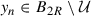 . In this case, we have |x
n − y
n|≥ δ.
. In this case, we have |x
n − y
n|≥ δ. -
\(y_n\in \mathcal U\). Then, we have \(\text{dist}(x_n,\{u_n=0\}\cap \mathcal U)=|x_n-y_n|\ge {\varepsilon }\).
In both cases, we have that |x n − y n|≥ ε. By the uniform growth condition (b), we have
which is a contradiction with the uniform convergence of u n to u 0. □
Lemma 6.7 (Hausdorff Convergence of the Free Boundaries)
Let B R be the ball of radius R in \(\mathbb {R}^d\) . Let \(u_n:B_{2R}\to \mathbb {R}\) be a sequence of continuous non-negative functions and \(u_0:B_{2R}\to \mathbb {R}\) be a continuous non-negative function such that:
-
(a)
the sequence \(\overline \Omega _{u_n}\) converges locally Hausdorff in B R to \(\overline \Omega _{u_0}\);
-
(b)
the sequence {u n = 0} converges locally Hausdorff in B R to {u 0 = 0}.
Then, \(\partial \Omega _{u_n}\) converges locally Hausdorff in B R to \(\partial \Omega _{u_0}\).
Proof
Let \(\mathcal K\subset B_R\) be a fixed compact set and \(\mathcal U\subset B_R\) be a given open set. Let δ > 0 be the distance between \(\mathcal K\) and \(\partial \mathcal U\). Let ε ∈ (0, δ) be fixed.
Let \(x_0\in \partial \Omega _{u_0}\cap \mathcal K\). By the Hausdorff convergence of \(\overline \Omega _{u_n}\) and {u n = 0}, we get that, for n large enough, there are points
such that
Since u n is continuous, there is a point w n on the segment [y n, z n] such that \(w_n\in \partial \Omega _{w_n}\). Moreover, by construction \(w_n\in B_{\varepsilon }(x_0)\subset \mathcal U\). Since x 0 is arbitrary, we get that
Conversely, let \(x_n\in \partial \Omega _{u_n}\cap \mathcal K\) be fixed. Using again the Hausdorff convergence of \(\overline \Omega _{u_n}\) and {u n = 0}, we get that, for n large enough, there are points
such that
Now, by the continuity of u 0, we get that there is a point w 0 on the segment [y 0, z 0] such that \(w_0\in \partial \Omega _{w_0}\cap B_{\varepsilon }(x_n)\). Since x n is arbitrary, we get
which concludes the proof. □
6.3 Proof of Proposition 6.2
By the local Lipschitz continuity of u, we have that for any fixed R > 0, the sequence \(u_n=u_{x_0,r_n}\) is uniformly bounded in H 1(B R). Thus, applying Lemma 6.3, we get at once the claims (i), (ii) and (iv) of Proposition 6.2. We notice that the fact that the blow-up limit is non-trivial (u 0 ≡ 0) follows by the non-degeneracy of u, which assures that for every n ≥ N and every R > 0, there is a point \(x_n\in \overline B_R\) such that \(u_{x_0,r_n}(x_n)\ge \kappa \), where κ is a constant that depends only on Λ and the dimension d. The Hausdorff convergence of the free boundary (Proposition 6.2 (iii)) follows by Lemma 6.5; Lemma 6.6 and finally, by Lemma 6.7. Notice that the non-degeneracy condition of Lemma 6.5 follows by Proposition 4.1, while the uniform growth condition of Lemma 6.6 is a consequence of the following lemma (Lemma 6.8).
Lemma 6.8
Let \(u:B_{2R}\to \mathbb {R}\) be a continuous non-negative function such that:
-
(1)
u(0) = 0;
-
(2)
u satisfies the following non-degeneracy condition:
$$\displaystyle \begin{aligned} \|u\|{}_{L^\infty(B_r(x))}\ge \kappa r\quad \mathit{\text{for every}}\quad x\in \overline\Omega_u\cap B_R\quad \mathit{\text{and every}}\quad r\in(0,R), \end{aligned}$$for some given constant κ > 0;
-
(3)
u is harmonic in Ω u ∩ B 2R.
Then, u satisfies the following growth condition:
Proof
Suppose that x 0 ∈ Ωu ∩ B R and let y 0 ∈ ∂ Ωu ∩ B 2R be such that
Then, the non-degeneracy of u implies that there is a point z 0 ∈ B r∕2(x 0) at which
Now, since u is harmonic in Ωu, we get
Since u is non-negative and harmonic in B r(x 0) , we have that
which concludes the proof. □
As an immediate corollary, we obtain the following well-known result (see for instance [3]), which we give here for the sake of completeness.
Corollary 6.9
Suppose that u is a (non-negative) minimizer of \(\mathcal F_\Lambda \) in the ball \(B_{2R}\subset \mathbb {R}^d\) such that u(0) = 0. Then, there are constants C 1 and C 2 , depending only on Λ and d, such that the following inequality does hold:
Proof
The first inequality follows by Lemma 6.8, while the second one is due to the Lipschitz continuity of u (see Theorem 3.1). □
6.4 Regular and Singular Parts of the Free Boundary
In this section, we define the regular and the singular parts of the free boundary.
Let D be a bounded open set in \(\mathbb {R}^d\) and let \(u:D\to \mathbb {R}\) be a non-negative continuous function (in particular, one can take u to be a minimizer of \(\mathcal F_\Lambda \) in D). Let x 0 be a fixed point on the free boundary ∂ Ωu ∩ D, where Ωu = {u > 0}.
Definition 6.10 (Decomposition of the Free Boundary)
We say that x 0 is a regular point if there exists a blow-up limit u 0 of u at x 0 (see Definition 6.1) of the form
for some unit vector \(\nu \in \mathbb {R}^d\). We will denote the set of all regular points x 0 ∈ ∂ Ωu ∩ D by Reg(∂ Ωu), and we define the singular part of the free boundary as

In Chap. 8, we will prove that Reg(∂ Ωu) is an open subset of ∂ Ωu and is a C 1, α-regular surface in \(\mathbb {R}^d\). In this section, we will prove that the reduced boundary ∂ ∗ Ωu is actually a subset of the regular part Reg(∂ Ωu) and (as a consequence) that the singular set is small. Precisely, we will show that
We start with the following lemma.
Lemma 6.11
Let D be a bounded open set in \(\mathbb {R}^d\) and u be a minimizer of \(\mathcal F_\Lambda \) in D. Let x 0 ∈ ∂ Ω u ∩ D be a free boundary point, for which there exists a unit vector \(\nu \in \mathbb {R}^d\) and a vanishing sequence r n → 0 such that

where \(\Omega _n:=\frac 1{r_n}(-x_0+\Omega _u)\) and \(H_\nu :=\{x\in \mathbb {R}^d\ :\ x\cdot \nu >0\}\) . Then, x 0 ∈ Reg(∂ Ω u).
Proof
Let u n be the blow-up sequence
Notice that Ωn = {u
n > 0}. By Proposition 6.2, we have that, up to a subsequence and for every R > 0, u
n converges locally uniformly in B
R and strongly in H
1 to a function u
0, which is a non-negative Lipschitz continuous global minimizer of \(\mathcal F_\Lambda \) in \(\mathbb {R}^d\). Moreover, we have that the sequence of characteristic functions  converges in L
1(B
R) to
converges in L
1(B
R) to  . In particular, this implies that \(\Omega _{u_0}=H_\nu \) almost everywhere. Now, the minimality of u
0 and the fact that |{u
0 = 0}∩ H
ν| = 0 implies that u
0 is harmonic in H
ν. By the maximum principle, we get that \(\Omega _{u_0}=H_\nu \). Thus, u
0 is C
∞ smooth up to the boundary ∂H
ν (where it vanishes).
. In particular, this implies that \(\Omega _{u_0}=H_\nu \) almost everywhere. Now, the minimality of u
0 and the fact that |{u
0 = 0}∩ H
ν| = 0 implies that u
0 is harmonic in H
ν. By the maximum principle, we get that \(\Omega _{u_0}=H_\nu \). Thus, u
0 is C
∞ smooth up to the boundary ∂H
ν (where it vanishes).
We will next prove that
Indeed, suppose that this is not the case. Then, there are two possibilities:
-
(1)
there is a point y ∈ ∂H ν such that ∇u 0 = Aν for some \(A>\sqrt {\Lambda }\);
-
(2)
there is a point y ∈ ∂H ν such that ∇u 0 = Bν for some \(0<B<\sqrt {\Lambda }\).
Suppose that (1) holds. Let h r,R be the radial solution from Proposition 2.15, where r is large enough and R = R(r) is uniquely determined by r. Recall that:

Moreover, the function \(\sqrt {\Lambda }\,h_{r,R}\) is a local minimizer of \(\mathcal F_\Lambda \) in  . Let \(y_r\in \mathbb {R}^d\) be such that the ball B
R(y
r) is contained in H
ν and is tangent to ∂H
ν at y. Let r > 0 be fixed and such that
. Let \(y_r\in \mathbb {R}^d\) be such that the ball B
R(y
r) is contained in H
ν and is tangent to ∂H
ν at y. Let r > 0 be fixed and such that
Then, there is ε > 0 small enough, for which the function
satisfies the following conditions:
-
the support of \(\tilde h\) is not entirely contained in H ν, that is, \(\{\tilde h>0\}\cap \{u_0=0\}\neq \emptyset \);
-
\(\tilde h>u_0\) only in a small neighborhood of y, precisely, \(\{\tilde h>u_0\}\subset B_{{1}/{2}}(y)\).
Next, we notice that both \(\tilde h\) and u 0 are minimizers of \(\mathcal F_\Lambda \) in B := B 1∕2(y). Since, by construction u 0 ≥ h on ∂B, we get that
On the other hand,
which means that both the inequalities in (6.11) are equalities and that both the functions \(\tilde h\wedge u_0\) and \(\tilde h\vee u_0\) are minimizers of \(\mathcal F_\Lambda \) in B. For instance, this means that \(\tilde h\vee u_0\) is harmonic in the set \(\{\tilde h>0\}\cap B\), which is impossible since by construction \(\tilde h\vee u_0\) is not C 1 (for instance, the gradient is not continuous on the segment [y, y r]). Thus, (1) cannot happen. By the same argument, also (2) cannot happen, which means that
Now, by the unique continuation principle we have that \(u_0(x)=\sqrt {\Lambda }\,(x\cdot \nu )\) on H ν. Indeed, the function \(\tilde u_0\), defined as

is harmonic in the entire space \(\mathbb {R}^d\) and so, it should coincide everywhere with the function \(x\mapsto \sqrt {\Lambda }\, (x\cdot \nu )\). This concludes the proof. □
Proposition 6.12 (The Singular Set Is Negligible)
Let D be a bounded open set in \(\mathbb {R}^d\) and u ∈ H 1(D) be a minimizer of \(\mathcal F_\Lambda \) in D. Then, \(\mathcal {H}^{d-1}\big (Sing(\partial \Omega _u)\big )=0.\)
Proof
By Proposition 5.3, Ωu has locally finite perimeter in D. Let ∂ ∗ Ωu be the reduced boundary of Ωu. It is well-known (see for instance [43, Theorem 5.15]) that, for every x 0 ∈ ∂ ∗ Ωu, there is a unit vector \(\nu \in \mathbb {R}^d\) such that the property (6.10) does hold. Thus, by Lemma 6.11, we have that ∂ ∗ Ωu ⊂ Reg(∂ Ωu). On the other hand, by the Second Theorem of Federer (see [43]), we have that

Recall that, by Lemma 5.1, there are no points of density 1 and 0 on the free boundary, that is,
Thus, by (6.12)

Now, by the definition of the singular part, we have

which concludes the proof. □
References
H.W. Alt, L.A. Caffarelli, Existence and regularity for a minimum problem with free boundary. J. Reine Angew. Math. 325, 105–144 (1981)
F. Maggi, Sets of Finite Perimeter and Geometric Variational Problems: An Introduction to Geometric Measure Theory, vol. 135 (Cambridge University Press, Cambridge, 2012)
Author information
Authors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2023 The Author(s)
About this chapter
Cite this chapter
Velichkov, B. (2023). Blow-Up Sequences and Blow-Up Limits. In: Regularity of the One-phase Free Boundaries. Lecture Notes of the Unione Matematica Italiana, vol 28. Springer, Cham. https://doi.org/10.1007/978-3-031-13238-4_6
Download citation
DOI: https://doi.org/10.1007/978-3-031-13238-4_6
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-13237-7
Online ISBN: 978-3-031-13238-4
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)



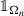 converges to
converges to
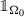 in L
1(B
R), where
in L
1(B
R), where
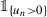 converges to
converges to
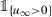 strongly in L
1(B
r) and pointwise almost-everywhere in B
r
, for every 0 < r < R;
strongly in L
1(B
r) and pointwise almost-everywhere in B
r
, for every 0 < r < R;
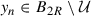 . In this case, we have |x
n − y
n|≥ δ.
. In this case, we have |x
n − y
n|≥ δ.