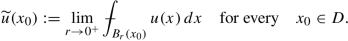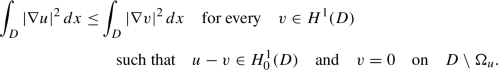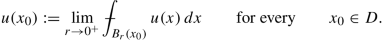Existence of Solutions, Qualitative Properties and Examples

Abstract

In this section, we prove that local minimizers of the functional $\mathcal F_\Lambda$ do exist (Proposition 2.1) and we give several important examples of local minimizers that can be computed explicitly (Proposition 2.10, Lemmas 2.15 and 2.16).

In this section, we prove that local minimizers of the functional $\mathcal F_\Lambda$ do exist (Proposition 2.1) and we give several important examples of local minimizers that can be computed explicitly (Proposition 2.10, Lemmas 2.15 and 2.16).

FormalPara Proposition 2.1

Let Λ > 0, $D \subset \mathbb {R}^d$ be a bounded open set and the function g ∈ H ¹(D) be fixed and such that g ≥ 0 in D. Then, there exists a solution to the variational problem

$$\displaystyle \begin{aligned} \min\big\{\mathcal F_\Lambda(u,D)\ :\ u\in H^1(D),\ u-g\in H^1_0(D)\big\}. \end{aligned} $$

(2.1)

Moreover, every solution u of (2.1) has the following properties:

• (i) u is non-negative in D;

• (ii) u is locally bounded in D;

• (iii) there is a function $\tilde u:D\to \mathbb {R}$ such that $\tilde u\ge 0$ and $\tilde u=u$ almost everywhere in D and

  $$\displaystyle \begin{aligned} \tilde u(x_0)=\lim_{r\to 0}\frac 1{|B_r|}\int_{B_r(x_0)}\tilde u(x)\,dx\qquad \mathit{\text{for every}}\qquad x_0\in D. \end{aligned}$$

FormalPara Remark 2.2

From now on, we will identify any solution u of (2.1) with its representative $\tilde u$; for the sake of simplicity, we will always write u instead of $\tilde u$.

The rest of the section is organized as follows. In Sect. 2.1 we discuss some of the properties (scaling and truncation) of the function $\mathcal F_\Lambda$. Section 2.2 is dedicated to the proof of Proposition 2.1. In Sects. 2.3 and 2.4, we discuss several examples of local minimizers, which we will find application in the next sections.

2.1 Properties of the Functional $\mathcal F$

In this section, we discuss several basic properties of the functional

$$\displaystyle \begin{aligned} (\Lambda,t,D)\mapsto \mathcal F_\Lambda(u,D). \end{aligned}$$

We give the precise statements in Lemmas 2.3, 2.4 and 2.5.

Lemma 2.3 (Scaling)

Let $\Omega \subset \mathbb {R}^d$ be an open set and u ∈ H ¹( Ω).

• (a) Let $x_0\in \mathbb {R}$ , r > 0 and

  $$\displaystyle \begin{aligned} u_{x_0,r}(x):=\frac 1ru(x_0+rx)\qquad \mathit{\text{and}}\qquad \Omega_{x_0,r}=\left\{x=\frac{y-x_0}{r}\in\mathbb{R} :\ y\in \Omega\right\}. \end{aligned}$$

  Then $u_{x_0,r}\in H^1(\Omega _{x_0,r})$ and

  $$\displaystyle \begin{aligned} \mathcal F_\Lambda(u_{x_0,r},\Omega_{x_0,r})=r^{-d}\,\mathcal F_\Lambda(u,\Omega). \end{aligned}$$

  In particular, if u is a minimizer of $\mathcal F_\Lambda$ in Ω, then $u_{x_0,r}$ is a minimizer of $\mathcal F_\Lambda$ in $\Omega _{x_0,r}$.

• (b) For every t > 0, we have

  $$\displaystyle \begin{aligned} \mathcal F_{t^{2}\Lambda}(tu,\Omega)=t^2\,\mathcal F_\Lambda(u,\Omega). \end{aligned}$$

  In particular, if u is a minimizer of $\mathcal F_\Lambda$ in Ω, then tu is a minimizer of $\mathcal F_{t^{2}\Lambda }$ in Ω.

Proof

The proof is a straightforward computation. □

Lemma 2.4 (Truncation)

Let $\Omega \subset \mathbb {R}^d$ be an open set and u ∈ H ¹( Ω). Then,

$$\displaystyle \begin{aligned} \mathcal F_\Lambda(u,\Omega)-\mathcal F_\Lambda(0\vee u,\Omega)=\int_{\{u<0\}\cap\Omega}|\nabla u|{}^2\,dx. \end{aligned}$$

Moreover, for every t ≥ 0, we have

$$\displaystyle \begin{aligned} \mathcal F_\Lambda(u,\Omega)-\mathcal F_\Lambda(u\wedge t,\Omega)=\int_{\{u>t\}\cap\Omega}|\nabla u|{}^2\,dx. \end{aligned}$$

Proof

The proof follows by the definition of $\mathcal F$ and the identities

□

Lemma 2.5 (Comparison)

Let $\Omega \subset \mathbb {R}^d$ be an open set and u, v ∈ H ¹( Ω) be two given functions. Then we have

$$\displaystyle \begin{aligned} \mathcal F_\Lambda(u\vee v,\Omega)+\mathcal F_\Lambda(u\wedge v,\Omega)=\mathcal F_\Lambda(u,\Omega)+\mathcal F_\Lambda(v,\Omega). \end{aligned}$$

Proof

The proof is a straightforward computation. In fact, we have

$$\displaystyle \begin{aligned} \mathcal F_\Lambda & (u\vee v,\Omega)+\mathcal F_\Lambda(u\wedge v,\Omega)\\ & =\int_\Omega|\nabla (u\vee v)|{}^2\,dx+\Lambda|\{u\vee v>0\}\cap\Omega|\\ & \qquad +\int_\Omega|\nabla (u\wedge v)|{}^2\,dx+\Lambda|\{u\wedge v>0\}\cap\Omega|\\ & =\int_{\Omega\cap\{u\ge v\}}|\nabla u|{}^2\,dx+\int_{\Omega\cap\{u< v\}}|\nabla v|{}^2\,dx+\Lambda\big|\big(\{u>0\}\cup\{v>0\}\big)\cap\Omega\big|\\ & \qquad +\int_{\Omega\cap\{u\ge v\}}|\nabla v|{}^2\,dx+\int_{\Omega\cap\{u< v\}}|\nabla u|{}^2\,dx+\Lambda\big|\{u>0\}\cap\{v>0\}\cap\Omega\big|\\ & =\int_\Omega|\nabla u|{}^2\,dx+\Lambda|\{u>0\}\cap\Omega|+\int_\Omega|\nabla v|{}^2\,dx+\Lambda|\{v>0\}\cap\Omega|\\ & =\mathcal F_\Lambda(u,\Omega)+\mathcal F_\Lambda(v,\Omega)\,, \end{aligned} $$

which concludes the proof. □

2.2 Proof of Proposition 2.1

In this section we prove Proposition 2.1. We will first show that the minimizers of $\mathcal F_\Lambda$ are subharmonic functions (Lemmas 2.6 and 2.7) and then we will deduce the claim (iii) of Proposition 2.1 (see Remark 2.2). At the end of this section, we will complete the proof of Proposition 2.1 by proving that there is a solution to the variational problem (2.1). Finally, in Lemma 2.9, we discuss the definition of the free boundary, which can be (equivalently) defined both as the topological boundary of the representative $\tilde u$ (of the function u ∈ H ¹(D)) defined in Proposition 2.1 and as the measure-theoretic boundary of Ω_u, which does not depend on the representative of u and is defined as the set of points x ₀ ∈ D for which

Lemma 2.6 (The Minimizers of $\mathcal F_\Lambda$ Are Subharmonic Functions)

Let $D\subset \mathbb {R}^d$ be a bounded open set and the non-negative function u ∈ H ¹(D) be a minimizer of $\mathcal F_\Lambda$ in D. Then u is subharmonic, Δu ≥ 0, on D in sense of distributions:

$$\displaystyle \begin{aligned} \int_{D}\nabla u\cdot\nabla\varphi\,dx\le 0\quad \mathit{\text{for every}}\quad \varphi\in C^\infty_c(D)\quad \mathit{\text{such that}}\quad \varphi\ge 0 \quad \mathit{\text{on}}\quad D. \end{aligned}$$

Proof

Let $\varphi \in C^\infty _c(D)$ be a given non-negative function. Suppose that t ≥ 0 and v = u − tφ. Then we have that v ₊ ≤ u. In particular, integrating on the support of φ we have

$$\displaystyle \begin{aligned} \mathcal F_\Lambda(u,D) & =\int_D |\nabla u|{}^2\,dx+\Lambda|\{u>0\}\cap D|\\ & \le \int_D |\nabla v_+|{}^2\,dx\!+\!\Lambda|\{v_+>0\}\cap D|\le \int_D |\nabla v|{}^2\,dx\!+\!\Lambda|\{u>0\}\cap D|. \end{aligned} $$

This implies that

$$\displaystyle \begin{aligned} \int_D |\nabla u|{}^2\,dx\!\le\! \int_D |\nabla (u-t\varphi)|{}^2\,dx\!=\!\int_D |\nabla u|{}^2\,dx\!-\!2t\int_D \nabla u\cdot\nabla\varphi\,dx\!+\!t^2\int_D |\nabla \varphi|{}^2\,dx, \end{aligned} $$

and the claim follows by taking the (right) derivative at t = 0. □

There is also a more general result, which applies not only to minimizers, but also to generic non-negative functions, which are harmonic where they are strictly positive. The proof can also be found in the book of Henrot and Pierre [36].

Lemma 2.7 (The Minimizers of $\mathcal F_\Lambda$ Are Subharmonic Functions II)

Let $D\subset \mathbb {R}^d$ be a bounded open set and the non-negative function u ∈ H ¹(D) be harmonic in the set Ω _u := {u > 0}, that is

Then u is subharmonic, Δu ≥ 0, on D in sense of distributions.

Proof

Let $\phi \in C^\infty _c(D)$ be a given non-negative function and let $p_{\varepsilon }:\mathbb {R}\to \mathbb {R}$ be given by

$$\displaystyle \begin{aligned} p_{\varepsilon}(x)=\begin{cases}\begin{array}{cl}\displaystyle 0 & \ \text{ if }x\le {\varepsilon}/2,\\ \displaystyle \frac{1}{{\varepsilon}}(2x-{\varepsilon}) & \ \text{ if }x\in[{\varepsilon}/2,{\varepsilon}],\\ 1 & \ \text{ if }x\ge {\varepsilon}\,. \end{array}\end{cases}\end{aligned}$$

Since u _t := u + t p _ε(u)ϕ is a competitor for u and for $t\in \mathbb {R}$ small enough

$$\displaystyle \begin{aligned} \{u>0\}=\{u_t>0\}, \end{aligned}$$

we have that for t small enough

$$\displaystyle \begin{aligned} \int_{D} |\nabla u|{}^2\,dx\le \int_{D} |\nabla u_t|{}^2\,dx, \end{aligned}$$

which gives

$$\displaystyle \begin{aligned} \int_D p_{\varepsilon}(u)\nabla u\cdot\nabla \phi\,dx& \le \int_D p^{\prime}_{\varepsilon}(u)|\nabla u|{}^2\phi\,dx+\int_D p_{\varepsilon}(u)\nabla u\cdot\nabla \phi\,dx\\ & =\int_D \nabla u\cdot\nabla (p_{\varepsilon}(u)\phi)\,dx=0\,, \end{aligned} $$

where the last inequality is due to the fact that p _ε is increasing. Now since p _ε(u) converges to , as ε → 0, we get that

$$\displaystyle \begin{aligned} \int_D \nabla u\cdot\nabla \phi\,dx\le 0, \end{aligned}$$

which concludes the proof. □

Remark 2.8 (Pointwise Definition of a Subharmonic Function)

Let D be an open set and u ∈ H ¹(D) be a subharmonic function. Then, for every x ₀ ∈ D, we have that

(2.2)

As a consequence of (2.2), we obtain that:

• u is locally bounded, $u\in L^\infty _{loc}(D)$;

• we define $\tilde u:D\to \mathbb {R}$ as

  

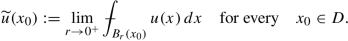
Proof of Proposition 2.1

We first prove that a solution exists. Let u _n ∈ H ¹(D) be a minimizing sequence such that $u_n-g\in H^1_0(D)$ and

$$\displaystyle \begin{aligned} \mathcal F_\Lambda(u_n,D)\le \mathcal F_\Lambda(g,D)\qquad \text{for every}\qquad n\ge 1. \end{aligned}$$

By Lemma 2.4 we may assume that, for every n ≥ 1, u _n ≥ 0 on D. For simplicity, we assume that d > 2 (the case d = 2 is analogous) and we set $\displaystyle 2^*=\frac {2d}{d-2}$. Then, we have

$$\displaystyle \begin{aligned} \|u_n-g\|{}_{L^{2^\ast}(D)}^2& \le C_d\int_{D}|\nabla(u_n-g)|{}^2\,dx\le 2C_d\left(\int_{D}|\nabla u_n|{}^2\,dx+\int_{D}|\nabla g|{}^2\,dx\right)\\ & \le 2C_d\big(\mathcal F_\Lambda(u_n,D)+\mathcal F_\Lambda(g,D)\big)\le 4C_d\mathcal F_\Lambda(g,D). \end{aligned} $$

Now, we estimate,

$$\displaystyle \begin{aligned} \|u_n-g\|{}_{L^{2}(D)}^2& \le |\{u_n-g\neq0\}|{}^{2/d}\,\|u_n-g\|{}_{L^{2^\ast}(D)}^2\\ & \!\le\! \big(|\{u_n>0\}\cap D|+|\{g>0\}\cap D|\big)^{2/d}4C_d\mathcal F_\Lambda(g,D)\!\le\! 8C_d\Lambda^{-\frac 2d}\mathcal F_\Lambda(g,D)^{\frac{2+d}{d}}, \end{aligned} $$

which implies that the sequence u _n is uniformly bounded in H ¹(D). Then, up to a subsequence, we may assume that u _n converges weakly in H ¹(D) and strongly in L ²(D) to a function u ∈ H ¹(D). Now, the semi-continuity of the H ¹ norm (with respect to the weak H ¹ convergence) gives that

$$\displaystyle \begin{aligned} \int_D|\nabla u|{}^2\,dx\le \liminf_{n\to\infty} \int_D|\nabla u_n|{}^2\,dx. \end{aligned}$$

On the other hand, passing again to a subsequence, we get that u _n converges pointwise almost everywhere to u. This implies that

and so,

$$\displaystyle \begin{aligned} |\{u>0\}\cap D|\le \liminf_{n\to\infty}|\{u_n>0\}\cap D|, \end{aligned}$$

which finally gives that

$$\displaystyle \begin{aligned} \mathcal F_\Lambda(u,D)\le \liminf_{n\to\infty}\mathcal F_\Lambda(u_n,D), \end{aligned}$$

and so, u is a solution to (2.1). Now, we notice that Lemma 2.4 implies that u ≥ 0 on D. Lemma 2.6 and Remark 2.8 give the claims (ii) and (iii). □

We conclude this subsection with the following lemma, where we show that the set Ω_u has a topological boundary that coincides with the measure theoretic one.

Lemma 2.9 (Topological and Measure Theoretic Free Boundaries)

Let $D\subset \mathbb {R}^d$ be a bounded open set and u be a local minimizer of $\mathcal F_\Lambda$ in the open set $D\subset \mathbb {R}^d$ or, more generally, let $u:D\to \mathbb {R}$ , u ∈ H ¹(D), be a non-negative function satisfying

• (a) u is harmonic in Ω _u = {u > 0} in the sense that

  

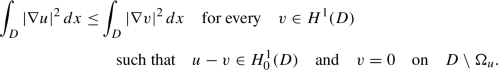
• (b) u is defined everywhere in D and

  

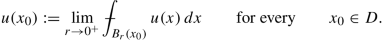
Then, the topological boundary of Ω _u coincides with the measure-theoretic one:

$$\displaystyle \begin{aligned} \partial\Omega_u\cap D=\Big\{x\in D\ :\ |B_r(x)\cap\Omega_u|>0\quad \mathit{\text{and}}\quad |B_r(x)\cap\{u=0\}|>0,\ \forall r>0\Big\}. \end{aligned}$$

Proof

We first notice that the following inclusion holds :

$$\displaystyle \begin{aligned} \partial\Omega_u\cap D\supset\Big\{x\in D\ :\ |B_r(x)\cap\Omega_u|>0\quad \text{and}\quad |B_r(x)\cap\{u=0\}|>0,\ \forall r>0\Big\}. \end{aligned}$$

In order to prove the opposite inclusion we show that

• (i) if |B _r ∩{u = 0}| = 0, then u is harmonic in B _r and B _r ∩{u = 0} = ∅.

• (ii) if |B _r ∩{u > 0}| = 0, then u = 0 in B _r, i.e. B _r ∩{u > 0} = ∅.

In order to prove (i) we notice that u is necessarily harmonic in B _r, since otherwise we can contradict the minimality of u by replacing it with the harmonic function with the same boundary values. By the strong maximum principle, u is strictly positive in B _r. The proof of (ii) follows directly from (b). □

2.3 Half-Plane Solutions

The so-called half-plane solutions (see Fig. 2.1)

$$\displaystyle \begin{aligned} h_\nu(x)=\sqrt{\Lambda}\,(x\cdot\nu)_+ \end{aligned}$$

play a fundamental role in the free boundary regularity theory. In fact, in the next sections we will show that if a local minimizer u is close to a half-plane solution (at some, possibly very small, scale), then the free boundary is C ^{1, α} regular; then, we will also prove that at almost-every free boundary point the solution u coincides with a half-plane solution at order 1.

Fig. 2.1

A half-plane solution

In this subsection, we make a first step in this direction and we prove that the half-plane solutions are global minimizers. This result is usually omitted in the literature since it is implicitly contained in the fact that the blow-up limits at the points of the reduced free boundary (of any local minimizer) are indeed half-plane solutions (we will prove this fact later, in Lemma 6.11). The main result of this subsection is the following.

Proposition 2.10 (The Half-Plane Solutions Are Local Minimizers)

Let $\nu \in \mathbb {R}^d$ be a unit vector. Then the function $H_\nu (x)=\sqrt {\Lambda }\,(\nu \cdot x)_+$ is a global minimizer of $\mathcal F_\Lambda$.

Definition 2.11 (Local Minimizers)

Let D be an open set in $\mathbb {R}^d$. We say that the function $u:D\to \mathbb {R}$ is a local minimizer of $\mathcal F_\Lambda$ in D, if $u\in H^1_{loc}(D)$, u ≥ 0, and for any bounded open set Ω such that $\overline \Omega \subset D$, we have

$$\displaystyle \begin{aligned} \mathcal F_\Lambda(u,\Omega)\le \mathcal F_\Lambda(v,\Omega)\qquad \text{for every}\qquad v\in H^1_{loc}(D) \quad \text{such that}\quad u-v\in H^1_0(\Omega). \end{aligned}$$

Definition 2.12 (Global Minimizers)

We say that the function $u:\mathbb {R}^d\to \mathbb {R}$ is a global minimizer of $\mathcal F_\Lambda$, if u is non-negative on $\mathbb {R}^d$, $u\in H^1_{loc}(\mathbb {R}^d)$ and u is a local minimizer of $\mathcal F_\Lambda$ in $\mathbb {R}^d$.

In order to prove the minimality of the half-plane solutions, we will need the following lemma. We notice that it is useful also in other contexts. For instance, it allows to prove that the solutions of (2.1) are bounded.

Lemma 2.13

Let $D\subset \mathbb {R}^d$ be a bounded smooth open set or $D=\mathbb {R}^d$ . Let $x_0\in \mathbb {R}^d$ be a given point, $\nu \in \mathbb {R}^d$ be a unit vector and let

$$\displaystyle \begin{aligned} v(x)=h_\nu(x-x_0)=\sqrt{\Lambda} \,\sup\{0,(x-x_0)\cdot\nu\}. \end{aligned}$$

Suppose that u ∈ H ¹(D) is a non-negative function such that

$$\displaystyle \begin{aligned} u=0 \quad \mathit{\mbox{on}}\quad \partial D\cap \{v=0\}. \end{aligned}$$

Then

$$\displaystyle \begin{aligned} \mathcal F_\Lambda(u\wedge v,D)\le \mathcal F_\Lambda(u,D), \end{aligned}$$

with an equality if and only if u = u ∧ v.

In particular, if u is a solution to (2.1), then u has bounded support. Precisely, u = 0 outside the set conv(D) + B ₁ , where conv(D) is the convex hull of D.

Proof

Without loss of generality we can suppose that ν = e _d and x ₀ = 0. For the sake of simplicity, we set H ₊ = {x _d > 0} and H ₋ = {x _d < 0}. Then

$$\displaystyle \begin{aligned} \mathcal F_\Lambda(u,D)-\mathcal F_\Lambda(u\wedge v,D) & =\int_{H_-}|\nabla u|{}^2\,dx+\Lambda\big|H_-\cap\{u>0\}\big|\\ & \qquad \qquad +\int_{H_+\cap \{u>\sqrt{\Lambda}\, x_d\}}\big(|\nabla u|{}^2-|\nabla v|{}^2\big)\,dx, \end{aligned} $$

where (in the case when D is bounded) we assume that u is extended by zero on . By the fact that $v(x)=\Lambda x_d^+$ is harmonic on {x _d > 0}, we get that

$$\displaystyle \begin{aligned} \int_{H_+\cap \{u>\sqrt{\Lambda}\, x_d\}}\big(|\nabla u|{}^2-|\nabla v|{}^2\big)\,dx & =\int_{H_+\cap \{u>\sqrt{\Lambda}\,x_d\}}\big(|\nabla (u-v)|{}^2+2\nabla v\cdot\nabla (u-v)_+\big)\,dx\\ & =\int_{H_+\cap \{u>\sqrt{\Lambda}\, x_d\}}|\nabla (u-v)|{}^2\,dx-2\sqrt{\Lambda}\int_{\{x_d=0\}}u\,d\mathcal{H}^{d-1}. \end{aligned} $$

We recall that for every u ∈ H ¹({x _d < 0}) we have the inequality¹

$$\displaystyle \begin{aligned} \int_{\{x_d<0\}}|\nabla u|{}^2\,dx+\Lambda\big|\{u>0\}\cap \{x_d<0\}\big|\ge 2\sqrt{\Lambda}\int_{\{x_d=0\}}u\,d\mathcal{H}^{d-1}, \end{aligned}$$

where the equality holds, if and only if, u ≡ 0 on {x _d < 0}. Thus, we obtain

$$\displaystyle \begin{aligned} \mathcal F_\Lambda(u,\Omega)-\mathcal F_\Lambda(u\wedge v,\Omega)\ge \int_{H_+\cap \{u>\sqrt{\Lambda}\,x_d\}}|\nabla (u-v)|{}^2\,dx\ge 0, \end{aligned} $$

where the last inequality is an equality if and only if u ≤ v on $\mathbb {R}^d$. □

Proof of Proposition 2.10

Without loss of generality we may suppose that ν = e _d and set

$$\displaystyle \begin{aligned} h(x)=\sqrt {\Lambda}\, x_d^+. \end{aligned}$$

Suppose that R > 0 and $u\in H^1_{loc}(\mathbb {R}^d)$ is a non-negative function such that $u-h\in H^1_0(B_R)$. It is sufficient to prove that $\mathcal F_\Lambda (h,B_R)\le \mathcal F_\Lambda (u,B_R)$. By Lemma 2.13 we have that

$$\displaystyle \begin{aligned} \mathcal F_\Lambda(u\wedge h, B_R)\le \mathcal F_\Lambda(u,B_R). \end{aligned}$$

Thus, we may suppose that u ≤ h. Since h is harmonic in {x _d > 0} we get that

$$\displaystyle \begin{aligned} \mathcal F_\Lambda(u,B_R)-\mathcal F_\Lambda(h,B_R) & =\int_{\{x_d>0\}}\big|\nabla (u-h)\big|{}^2\,dx-\Lambda\big|\{x_d>0\}\cap\{u=0\}\big|\\ & =\int_{\{x_d>0\}\cap\{u>0\}}\big|\nabla (u-h)\big|{}^2\,dx, \end{aligned} $$

where the last equality is due to the fact that

$$\displaystyle \begin{aligned} |\nabla(u-h)|=|\nabla h|=\sqrt{\Lambda}\qquad \text{on the set}\qquad \{u=0\}. \end{aligned}$$

This concludes the proof. □

2.4 Radial Solutions

In this subsection, we give two examples of local minimizers, which are radial functions. Despite of being ones of the few non-trivial examples of local minimizers, they will also be useful in the proof (to be precise, in one of the two proofs that we will give) of the fact that the local minimizers satisfy an overdetermined condition on the free boundary in viscosity sense (see Definition 7.6 and Proposition 7.1).

Let D be a bounded open set in $\mathbb {R}^d$ with smooth boundary. We consider the following variational minimization problem in the exterior domain .

$$\displaystyle \begin{aligned} \min\left\{\int_{\mathbb{R}^d}|\nabla u|{}^2\,dx+\big|\{u>0\}\big|\ :\ u\in H^1(\mathbb{R}^d),\ u=1\ \text{in}\ D\right\}. \end{aligned} $$

(2.3)

The “interior” version of this problem reads as

$$\displaystyle \begin{aligned} \min\left\{\int_{D}|\nabla u|{}^2\,dx+\big|\{u>0\}\cap D\big|\ :\ u\in H^1(D),\ u=1\ \text{on}\ \partial D\right\}. \end{aligned} $$

(2.4)

We first prove that the problems (2.3) and (2.4) admit solutions.

Lemma 2.14 (Existence of a Solution)

Suppose that D is a bounded open set in $\mathbb {R}^d$ with smooth boundary. Then the variational problems (2.3) and (2.4) admit solutions.

Proof

We give the proof for (2.3), the case (2.4) being analogous (and easier as it does not require the use of Lemma 2.13). Let u _n be a minimizing sequence in $H^1(\mathbb {R}^d)$. By Lemmas 2.4 and 2.13 we can suppose that 0 ≤ u _n ≤ 1 and supp (u _n) ⊂ conv(D) + B ₁. Now, up to a subsequence, we may suppose that u _n converges in $L^2(\mathbb {R}^d)$ and pointwise almost everywhere to a function $u\in H^1(\mathbb {R}^d)$. The claim follows by the semicontinuity of $\mathcal F_\Lambda$. □

In Propositions 2.15 and 2.16, we will prove that, in the special case when the domains D in (2.3) and (2.4) are balls, the solution is unique and can be computed explicitly.

Proposition 2.15 (Optimal Exterior Domains)

Let the domain D in $\mathbb {R}^d$ be the ball B _r . Then, there is a unique solution u _r of (2.3). Moreover, for every r, there is a radius R > r, uniquely determined by r and d, such that u _r is given by

where h _r is a radial harmonic function (as on Fig. 2.2). Precisely, h _r is given by

$$\displaystyle \begin{aligned} h_r(x)= \frac{|x|{}^{2-d}-R^{2-d}}{r^{2-d}-R^{2-d}}\quad \mathit{\text{if}}\quad d\ge 3\ ,\qquad h_r(x)= \frac{\ln |x|-\ln R}{\ln r-\ln R}\quad \mathit{\text{if}}\quad d=2\ .\end{aligned}$$

Fig. 2.2

An exterior radial solution

Moreover, the radius R and the function u _r satisfy the following properties:

• (i) The radius R = R(r) is a continuous function of r such that

  $$\displaystyle \begin{gathered} r<R<r+1\\ \mathit{and}\\ \displaystyle\lim_{r\to+\infty}|R(r)-(r+1)|=0. \end{gathered} $$

• (ii) The gradient of h _r is given by

  $$\displaystyle \begin{aligned} |\nabla h_r|(x)=\left(|x|/R\right)^{1-d}. \end{aligned}$$

Proof

We first notice that taking the Schwartz symmetrization u ^∗ of any function u we get that $\mathcal F_1(u^\ast ,\mathbb {R}^d)\le \mathcal F_1(u,\mathbb {R}^d)$. Thus, there is a minimizer of $\mathcal F_1$ which is a radial function. We first show that there is a unique radial function that minimizes of $\mathcal F_1$ in the class of radial functions.

Let d ≥ 3. For every 0 < r < R, consider the function

$$\displaystyle \begin{aligned} u_{r,R}(x)=\begin{cases} 1,\quad \text{if}\quad |x|\le r,\\ \displaystyle \frac{|x|{}^{2-d}-R^{2-d}}{r^{2-d}-R^{2-d}},\quad \text{if}\quad r<|x|<R,\\ 0,\quad \text{if}\quad |x|\ge R. \end{cases}\end{aligned}$$

Since u _r,R is the unique harmonic function in , we get that the minimizer of $\mathcal F_1$ among the radial functions is necessarily given by a function of the form u _r,R. We calculate the energy

We notice that the function $f(R):=\displaystyle \frac {d(d-2)}{r^{2-d}-R^{2-d}}+ R^d$ is strictly convex and

$$\displaystyle \begin{aligned} \displaystyle\lim_{R\to r^+}f(R)=\lim_{R\to+\infty}f(R)=+\infty. \end{aligned}$$

Thus, there is a unique radius R > r that minimizes f. We denote this radius by R _∗. Notice that, since f′(R _∗) = 0, we have

$$\displaystyle \begin{aligned} R_{\ast}^{d-1}\big(r^{2-d}-R_\ast^{2-d}\big)=d-2. \end{aligned} $$

(2.5)

Let d = 2. For every 0 < r < R, consider the function

$$\displaystyle \begin{aligned} u_{r,R}(x)=\begin{cases} 1,\quad \text{if}\quad |x|\le r,\\ \displaystyle \frac{\ln\left(R/|x|\right)}{\ln\left(R/r\right)},\quad \text{if}\quad r<|x|<R,\\ 0,\quad \text{if}\quad |x|\ge R. \end{cases}\end{aligned}$$

As in the case d ≥ 3, we calculate the energy

As in the case d > 2, there is a unique R _∗ > r that minimizes the function $R\mapsto \mathcal F(u_{r,R})$. Moreover, R _∗ is such that

$$\displaystyle \begin{aligned} R_{\ast}\big(\ln{R_\ast}-\ln r\big)=1. \end{aligned} $$

(2.6)

We notice that the claims (i) and (ii) follow by (2.5) and (2.6).

We now prove that the functions $u_{r,R_\ast }$ are the unique minimizers of $\mathcal F_1$ among all admissible functions. Indeed, consider any minimizer u of $\mathcal F_1$ and suppose that it is not radial. We notice that the symmetrized function u ^∗ is also a solution. Since it is radial, we get that $u^\ast =u_{r,R^\ast _d}$ and in particular $|\{u>0\}|=|B_{R_\ast }|$. By Lemma 2.5, the functions v = u ∧ u ^∗ and V = u ∨ u ^∗ are also minimizers of $\mathcal F$. If u is not radial, then we have $|\{v>0\}|\neq |B_{R_\ast }|$ or $|\{v>0\}|\neq |B_{R_\ast }|$. On the other hand the symmetrized function v ^∗ and V ^∗ are also solutions and so, we must have v ^∗ = V ^∗ = u ^∗ and in particular $|\{v>0\}|=|\{V>0\}|=|B_{R_\ast }|$, which is in contradiction with the assumption that u is not radially symmetric. □

Proposition 2.16 (Optimal Interior Domains)

Let the domain D in $\mathbb {R}^d$ be the ball B _R . Then, there is a dimensional constant C _d > 0 such that, for every R > C _d , there is a unique solution u _R of (2.4). Moreover, u _R is radially symmetric and has the following properties:

(2.7)

where h _R is a radially symmetric harmonic function (see Fig. 2.3). Precisely,

$$\displaystyle \begin{aligned} {} h_R(x)= \frac{|x|{}^{2-d}-r^{2-d}}{R^{2-d}-r^{2-d}}\quad \mathit{\text{if}}\quad d\ge 3\ ,\qquad h_R(x)= \frac{\ln |x|-\ln r}{\ln R-\ln r}\quad \mathit{\text{if}}\quad d=2\ , \end{aligned}$$

Fig. 2.3

An interior radial solution

where the radius r depends on R and d and has the following properties:

• (i) The radius r = r(R) is a continuous function of R such that

  $$\displaystyle \begin{aligned} \displaystyle\lim_{R\to+\infty}|r(R)-(R-1)|=0. \end{aligned}$$

• (ii) The gradient of h _R is given by

  $$\displaystyle \begin{aligned} |\nabla h_R|(x)=\left({|x|/r}\right)^{1-d}. \end{aligned}$$

Proof

As in the proof of Lemma 2.15, we start by noticing that for every function u, there is a radially symmetric function u ^∗ with lower energy. In fact, it is sufficient to consider the function v = 1 − u and its Schwartz symmetrization v ^∗. We define u ^∗ as u ^∗ := 1 − v ^∗ and we notice that

$$\displaystyle \begin{aligned} \mathcal F_1(u^\ast,B_R) & =\int_{B_R}|\nabla u^\ast|{}^2\,dx+|\{u^\ast>0\}\cap B_R|=\int_{B_R}|\nabla v^\ast|{}^2\,dx+|\{v^\ast<1\}\cap B_R|\\ & \le\int_{B_R}|\nabla v|{}^2\,dx+|\{v<1\}\cap B_R|=\int_{B_R}|\nabla u|{}^2\,dx+|\{u>0\}\cap B_R|=\mathcal F_1(u, B_R). \end{aligned} $$

Thus, there exists a radially symmetric minimizer u ^∗ of $\mathcal F$. Now, since u ^∗ is harmonic in {u ^∗ > 0}, it should be of the form u ^∗ = u _r,R, where u _r,R is given by (2.7) for some radius r < R. Now, for any r ∈ (0, R), the energy of u _r,R is given by

Consider the function

$$\displaystyle \begin{aligned} f(r):=\displaystyle\frac{d(d-2)}{r^{2-d}-R^{2-d}}-r^d. \end{aligned}$$

It is easy to check that,

$$\displaystyle \begin{aligned} \displaystyle\lim_{r\to 0}f(r)=0\qquad \text{and}\qquad \lim_{r\to R}f(r)=+\infty. \end{aligned}$$

Moreover, for R large enough, f(R∕2) < 0. We now calculate

$$\displaystyle \begin{aligned} f'(r)=\frac{d(d-2)^2r^{1-d}}{\big(r^{2-d}-R^{2-d}\big)^2}-dr^{d-1}. \end{aligned}$$

Thus, f′(r) = 0 if and only if

$$\displaystyle \begin{aligned} g(r):=(d-2)-r+r^{d-1}R^{2-d}=0. \end{aligned}$$

Now, the equation g(r) = 0 has at most two solutions and we have that

$$\displaystyle \begin{aligned} g(0)=g(R)=d-2>0. \end{aligned}$$

On the other hand, for R large enough, we have

$$\displaystyle \begin{aligned} g(d-1)<0\qquad \text{and}\qquad g(R-2)<0. \end{aligned}$$

Thus, the equation g(r) = 0 has exactly two solutions:

$$\displaystyle \begin{aligned} r_-\in (0,d-1)\qquad \text{and}\qquad r_+\in(R-2,R). \end{aligned}$$

Now, let M _d be the minimum of f in the interval [0, d − 1]. For R large enough, we have

$$\displaystyle \begin{aligned} f(R-2)=(R-2)^{d-2}\left(\frac{d(d-2)}{1-(1-{2/R})^{d-2}}-(R-2)^2\right)<M_d. \end{aligned}$$

Thus, there is a unique r ∈ (0, R) that minimizes f in (0, R). Moreover, R − 2 < r < R. Moreover, the claim (i) follows from the fact that, for every ε > 0, there is R _ε > 0 such that if R > R _ε, then

$$\displaystyle \begin{aligned} g(R-(1-{\varepsilon}))<0\qquad \text{and}\qquad g(R-(1+{\varepsilon}))>0. \end{aligned}$$

This implies that R − (1 + ε) ≤ r(R) ≤ R − (1 − ε), which is precisely (i).

Let now d = 2. For every r ∈ (0, R), consider the function u _r,R given by (2.7) for some r > 0. We calculate the energy

Next, we define

$$\displaystyle \begin{aligned} f(r):=\frac{2}{\ln R-\ln r}-r^2, \end{aligned}$$

we calculate

$$\displaystyle \begin{aligned} f'(r)=\frac{2}{r(\ln R-\ln r)^2}-2r, \end{aligned}$$

and we set

$$\displaystyle \begin{aligned} g(r):=1-r(\ln R-\ln r). \end{aligned}$$

As above, g can have at most two zeros in the interval (0, R). Moreover, g(0) = g(R) = 1 and for R large enough, we have

$$\displaystyle \begin{aligned} g(1)=1-\ln R<0\qquad \text{and}\qquad g(R-2)=1-(R-2)\ln\left(1-\frac{2}{R-2}\right)<0. \end{aligned}$$

Thus, the two zeros of g are in the intervals (0, 1) and (R − 2, R), respectively. Now, for R large enough, we have

$$\displaystyle \begin{aligned} f(R-2)=\frac{2}{\ln\left(1+\frac{2}{R-2}\right)}-(R-2)^2<-1<f(1). \end{aligned}$$

Thus, for large enough R, there is a unique r that minimizes f in (0, R) and R − 2 < r < R. The claim (i) follows as in the case d > 2. The claim (ii) is immediate and follows from the equation g(r) = 0. The uniqueness of the solution now follows as in Lemma 2.15. □