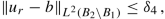Abstract
Throughout this section, we will use the notation
where B 1 is the unit ball in \(\mathbb {R}^d\), d ≥ 2 and u ∈ H 1(B 1).
You have full access to this open access chapter, Download chapter PDF
Throughout this chapter, we will use the notation
where B 1 is the unit ball in \(\mathbb {R}^d\), d ≥ 2 and u ∈ H 1(B 1).
The aim of this chapter is to prove an epiperimetric inequality for the energy W in dimension two. As a consequence, we will obtain the C 1, α regularity of the one-phase free boundaries in dimension two (see Proposition 12.13). Our main result is the following.
There are constants δ 0 > 0 and ε > 0 such that: if c ∈ H 1(∂B 1) is a non-negative function on the boundary of the disk \(B_1\subset \mathbb {R}^2\) and
then, there exists a (non-negative) function h ∈ H 1(B 1) such that h = c on ∂B 1 and
z ∈ H 1(B 1) being the one-homogeneous extension of c in B 1 , that is,

On the figures in this section, we will use the following convention:
-
 is the support Ωh = {h > 0} of the competitor h;
is the support Ωh = {h > 0} of the competitor h; -
 is the support Ωz = {z > 0} of the one-homogeneous function z;
is the support Ωz = {z > 0} of the one-homogeneous function z; -
 is the boundary ∂ Ωh;
is the boundary ∂ Ωh; -
 is the boundary ∂ Ωz;
is the boundary ∂ Ωz; -
 is the common boundary ∂ Ωh ∩ ∂ Ωz.
is the common boundary ∂ Ωh ∩ ∂ Ωz.
In Theorem 12.1 the main assumption on the trace c is that the set Ωc ⊂ ∂B 1 is close to the half-sphere. In [49, Theorem 1] the epiperimetric inequality was proved under the different assumption that the trace is non-degenerate. In fact, the epiperimetric inequality (12.1) holds without any assumption on the trace \(c:\partial B_1\to \mathbb {R}\) or its free boundary ∂ Ωc ⊂ ∂B 1. Indeed, in the Appendix, we will prove the following result, which covers both Theorem 12.1 and [49, Theorem 1].
There is a constant ε > 0 such that: If c ∈ H 1(∂B 1) is a non-negative function on the boundary of the disk \(B_1\subset \mathbb {R}^2\) then, there exists a (non-negative) function h ∈ H 1(B 1) such that (12.1) holds and h = c on ∂B 1.
FormalPara Remark 12.4 (The Epiperimetric Inequality in Dimension d ≥ 2)In higher dimension, the epiperimetric inequality for the one-phase energy is still an open problem. We expect that it will still be true under the assumption that the spherical set Ωc is close to the half-sphere with respect to the Hausdorff distance. Indeed, it is an immediate consequence from the results in [29] that the epiperimetric inequality holds when the free boundary Ωc is a C 2, α regular graph (in the sphere) over the equator.
We stress that in higher dimension the epiperimetric inequality can hold only under some additional assumption on the distance from the trace to the half-plane solution. Indeed, if this was not the case (and so, the epiperimetric inequality was true in dimension d without any assumption on the trace), then the singular set would be empty in any dimension. This is due to the following remark.
We claim that if u is a local minimizer of \(\mathcal F_\Lambda \) in a neighborhood of x 0 and
holds, for every r > 0, then x 0 is a regular point. This is due to the following facts:
-
A point x 0 ∈ ∂ Ωu is regular, of and only if, the Lebesgue density of Ωu at x 0 is precisely equal to
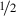 (see Lemma 9.22).
(see Lemma 9.22). -
There are no points of Lebesgue density smaller than
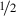 (Lemma 9.22).
(Lemma 9.22). -
The function \(r\mapsto W(u_{r,x_0})\) is non-decreasing and the limit
$$\displaystyle \begin{aligned} \displaystyle\lim_{r\to0}W(u_{r,x_0}) \end{aligned}$$is precisely the Lebesgue density of Ωu at x 0 (see Lemma 9.20); in particular

-
Suppose that the epiperimetric inequality (12.2) holds for every r > 0. Then, by the Weiss formula (Lemma 9.2) we obtain the following bound on the energy
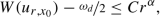
for some α > 0 depending on ε (this was proved in (12.28), which is the first step of the proof of Lemma 12.14). Since \(W(u_{r,x_0})-\frac {\omega _d}{2}\) is non-negative, we get that
$$\displaystyle \begin{aligned} \displaystyle\lim_{r\to0}W(u_{r,x_0})=\frac{\omega_d}2. \end{aligned}$$In particular, x 0 is a point of Lebesgue density
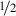 and so, it should be a regular point, as mentioned in the first bullet above.
and so, it should be a regular point, as mentioned in the first bullet above.
As a consequence of Remark 12.5 at the singular points of the free boundary (12.2) cannot hold, which means that in higher dimension the epiperimetric inequality can only be true under the additional assumption that the trace on ∂B 1 is close (in some sense) to a half-plane solution.
In this chapter, we will prove Theorem 12.1 and we will show that it implies the regularity of the free boundary (Proposition 12.13). The proof of Theorem 12.1 will be a consequence of the following two lemmas. The first one (Lemma 12.6) is based on a PDE argument which does not depend on the geometry of the free boundary; this lemma is proved in Sect. 12.5 and holds in any dimension d ≥ 2. The second lemma (Lemma 12.7) reflects the interaction of the free boundary with the Dirichlet energy; we prove it in Sect. 12.3.3 and the proof strongly uses the fact that we work in dimension two, even if the main idea can be used also in dimension d ≥ 2. Precisely, we use the Slicing Lemma (Lemma 12.10) to write the total energy as an integral of an energy defined on the spheres ∂B r. Then, we prove the epiperimetric inequality by writing the second order expansion of the spherical energy for sets which are graphs over the equator (that is, arcs of length close to π).
Let ∂B 1 be the unit sphere in dimension d ≥ 2. For every κ > 0, there are constants ρ ∈ (0, 1), ε ∈ (0, 1) and α > 1, depending only on κ and d such that:
If ψ ∈ H 1(∂B 1) satisfies the inequality
then, we have
where in polar coordinates the functions \(z,\,h_\rho \,:\,B_1\to \mathbb {R}\) are given by
Precisely, we can take
Let B 1 be the unit ball in \(\mathbb {R}^2\) . There are constants δ 0 > 0 and ε > 0 such that the following holds.
If the continuous non-negative function \(c:\partial B_1\to \mathbb {R}\) , c ∈ H 1(∂B 1), is a multiple of the first eigenfunction on {c > 0}⊂ ∂B 1 and
then, there exists a (non-negative) function h ∈ H 1(B 1) such that h = c on ∂B 1 and
z ∈ H 1(B 1) being the one-homogeneous extension of c in B 1 . Moreover, if we assume that the function c is of the form

then the one-homogeneous extension is given by z(r, θ) = r c(θ) and the competitor h can be chosen as (the support of h is illustrated on Fig. 12.1)

12.1 Preliminary Results
In this section we prove several preliminary results that we will use in the proof of Theorem 12.1 (and also in the proof of Theorem 12.3).
This section is organized as follows:
-
In Lemmas 12.8 and 12.9 we discuss the scale-invariance and the decomposition of the energy in orthogonal directions; both these results are implicitly contained in [49].
-
The Slicing Lemma (Lemma 12.10) shows how to disintegrate the energy along the different spheres ∂B r, 0 < r < 1. This result appeared for the first time in [29] and was crucial for the analysis of the free boundary around isolated singularities. We will use it in the proof of Lemma 12.7 (Sect. 12.3) and also in Sect. 12.2.
We start with the following result, which states that once we have a competitor for z in B 1, then we can rescale it and use it in any ball B ρ (ρ ≤ 1) by attaching it to z at ∂B ρ.
Lemma 12.8 (Scaling)
Suppose that \(z:B_1\to \mathbb {R}\) , z(r, θ) = rc(θ) is a one-homogeneous function and that h ∈ H 1(B 1) is such that h = c = z on ∂B 1 . For every ρ ∈ (0, 1), we set

then, we have
Proof
We first compute
On the other hand, for the measure term, we have
which concludes the proof. □
Lemma 12.9 (Decomposition of the Energy)
Suppose that the functions h 1, h 2 ∈ H 1(B 1) are such that, for every r ∈ (0, 1], we have
Then
Proof
The claim follows directly from the definition of W 0 and the formula
which holds for any h ∈ H 1(B 1). □
Lemma 12.10 (Slicing Lemma)
Let B 1 be the unit ball in \(\mathbb {R}^2\) . Let \(\phi :(0,1]\times \mathbb S^1\to \mathbb {R}\) be a function such that \(\phi \in H^1((0,1]\times \mathbb S^1)\) . Then, setting ϕ(r, θ) = ϕ r(θ), we have
and
where, for any \(\phi \in H^1(\mathbb S^1)\) , we set
Proof
Let \(\phi :]0,1]\times \partial B_1\to \mathbb {R}\). Then,
Integrating by parts, we get that
which implies that
In order to prove (12.4), it is sufficient to notice that
where h(r, θ) = rϕ r(θ). □
Remark 12.11 (The Energy of a One-Homogeneous Function)
As an immediate consequence of Lemma 12.10, we get that if c ∈ H 1(∂B 1) and \(z:B_1\to \mathbb {R}\) is the one homogeneous extension of c in B 1, that is, z(r, θ) = rc(θ), then
12.2 Homogeneity Improvement of the Higher Modes: Proof of Lemma 12.6
Let ρ ∈ (0, 1) be fixed. We will first compute the energy of h ρ. For this purpose, we will use the Slicing Lemma; for every r ∈ [ρ, 1], we set
and we compute
Integrating in r, we obtain
We now compute
Integrating in r ∈ [ρ, 1] and using that α ≥ 1 and d ≥ 2, we get
Together with the inequality
which we have by hypothesis, this implies
Furthermore, it is immediate to check that for every α ≤ 2 and \(\rho \le \frac 12\) we have
In particular,
which, together with (12.5) implies:
Analogously, from (12.6), we deduce
We are now in position to estimate the difference W 0(h ρ) − W 0(z). First of all, we set
Using the identity (see Remark 12.11)
and the inequalities (12.7) and (12.8), we estimate
We now choose

Substituting in (12.9), we obtain

In particular, the first inequality in (12.3) holds for any  . In order to prove the second inequality in (12.3), we notice that, by the definition of h
ρ, we have
. In order to prove the second inequality in (12.3), we notice that, by the definition of h
ρ, we have
Thus,
Choosing

we have that  and so, we obtain
and so, we obtain
which concludes the proof of (12.3). □
12.3 Epiperimetric Inequality for the Principal Modes: Proof of Lemma 12.7
We suppose that the spherical set {c > 0} is the arc (0, π + δ), where \(\delta \in \mathbb {R}\) (and it might change sign). We recall that in Lemma 12.7 we assume that |δ| < δ 0. Then, we can write the trace c in the following form
Next, for every \(t\in \mathbb {R}\), we define the function \(\phi _t:\mathbb S^1\to \mathbb {R}\) as
Then set
and
We consider the function
and define the competitor h δ as
which we will use in both Lemmas 12.7 and A.2.
We will show that for ε > 0 and δ > 0 small enough, we have
where z δ is the one-homogeneous extension of ϕ δ in B 1
12.3.1 Reduction to the Case c 1 = 1
Let h δ and z δ be defined by (12.10) and (12.12). We claim that if, for some δ > 0 and ε > 0, we have
then (12.11) does hold for every c 1 > 0.
Indeed, using the homogeneity of W 0, we get that
On the other hand, we have that
for every (continuous) function \(u:B_1\to \mathbb {R}\). Thus,
The analogous computation for the competitor h δ gives
Putting together these computations, we obtain
where we used that the function t(r) is chosen in such a way that, for any δ and ε, we have
The rest of Sect. 12.3 is dedicated to the proof of (12.13).
12.3.2 An Estimate on the Energy Gain
The Slicing Lemma (Lemma 12.10) implies that
We first notice that the error term \(\displaystyle \int _0^1|t^{\prime }(r)|{ }^2 g(t(r))\,r^3dr\) is lower order. Precisely, we have
where C is a universal numerical constant. Thus, we get
where we have set
We will show that F is always negative in a neighborhoods of t = 0. First of all, we notice that the function f can be explicitly computed.
12.3.3 Computation of f
We now compute

where we set for simplicity  . In particular, this implies that
. In particular, this implies that
Moreover, we have that

12.3.4 Conclusion of the Proof of Lemma 12.7
Notice that, by using (12.16) and taking the derivative under the sign of the integral, we get that
Moreover, for the second derivative, we obtain
where we have set
Thus, the second order Taylor expansion of F in zero is given by
We will next show that

Indeed, using (12.17) we can compute
which gives (12.18).
Now, using (12.14), we estimate
where C is the numerical constant from (12.14) and we recall that, by hypothesis, |δ|≤ δ 0.
We now choose ε and δ 0.
We set ε = 16πδ 0. In particular, if \(\displaystyle 0<\delta _0\le \frac {1}{48\pi }\), then \(\displaystyle 1-\frac {3{\varepsilon }}{2}\ge \frac 12,\) and so
which is negative, whenever \(\displaystyle \delta _0\le \frac {1}{256\pi ^2C}\). This means that in the end, choosing
(12.13) holds for every δ such that |δ|≤ δ 0. This concludes the proof of Lemma 12.7. □
12.4 Proof of Theorem 12.1
Since c ∈ H 1(∂B 1), we have that c is continuous and so, the set {c > 0} is a countable union of disjoint intervals (arcs), that is,
where, by hypothesis, we have
where \(|\mathcal I_j|=\mathcal {H}^1(\mathcal I_j)\) denotes the length of the interval \(\mathcal I_j\). Now, we consider two cases:
-
Case 1. There is one interval, say \(\mathcal I_1\), of length \(|\mathcal I_1|\ge \pi -\delta _0\). See Fig. 12.2.
-
Case 2. All the intervals are shorter than π − δ 0, that is, \(|\mathcal I_j|\le \pi -\delta _0\), for every j ≥ 1. See Fig. 12.3.
We first notice that if \(\phi \in H^1_0(\mathcal I_j)\), then
In particular, if \(|\mathcal I_j|\le \pi -\delta _0\), then
Thus, if we are in Case 2, then the epiperimetric inequality is an immediate consequence of Lemma 12.6 with  .
.
Suppose that we are in Case 1. Let {ϕ j}j≥1 be a complete orthonormal system of eigenfunctions on the interval \(\mathcal I_1\). For every j ≥ 1, we set c j to be the Fourier coefficient
Then, we can decompose the trace c as
where
and ψ 2 is the restriction of c on the set \(\displaystyle \bigcup _{j\ge 2}\mathcal I_j\). We first claim that, for i = 1, 2, we have
where κ > 0 is a constant depending only on δ 0. Indeed, since ψ 2 is supported on \(\displaystyle \bigcup _{j\ge 2}\mathcal I_j\) and since \(|\mathcal I_j|\le 2\delta _0\), for j ≥ 2, we have that
On the other hand, ψ 1 contains only higher modes on the interval \(\mathcal I_1\). Thus,
Now, choosing δ
0 small enough (for instance,  ), (12.20) and (12.21) imply (12.19). Let now ρ > 0 and ε
ψ > 0 be the constants from Lemma 12.6 corresponding to the constant κ from (12.19). Let \(h_{\psi _1}\) and \(h_{\psi _2}\) be the competitors from Lemma 12.6 associated to the traces ψ
1 and ψ
2, respectively. Thus, we have
), (12.20) and (12.21) imply (12.19). Let now ρ > 0 and ε
ψ > 0 be the constants from Lemma 12.6 corresponding to the constant κ from (12.19). Let \(h_{\psi _1}\) and \(h_{\psi _2}\) be the competitors from Lemma 12.6 associated to the traces ψ
1 and ψ
2, respectively. Thus, we have
where \(z_{\psi _i}(r,\theta ):=z\psi _i(\theta )\).
Let \(\tilde h\) be the competitor from Lemma 12.7, associated to the trace c 1 ϕ 1, and let
We set

Thus, Lemmas 12.7 and 2.3 imply that
\(\tilde {\varepsilon }\) being the constant from Lemma 12.7. We now define the competitor \(h:B_1\to \mathbb {R}\) as:
-
h = z if
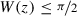 , where \(z=\tilde z+z_{\psi _1}+z_{\psi _2}\) is the 1-homogeneous extension of c;
, where \(z=\tilde z+z_{\psi _1}+z_{\psi _2}\) is the 1-homogeneous extension of c; -
\(h=\tilde z+h_{\psi _1}+h_{\psi _2}\) if
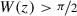 , but
, but 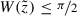 ;
; -
\(h=\tilde h+h_{\psi _1}+h_{\psi _2}\) if
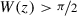 and
and 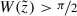 .
.
The first case is trivial and the second one follows directly by (12.22). We will prove the epiperimetric inequality in the most interesting third case. We first notice that the decomposition lemma (Lemma 12.9) implies that
and
where in the second decomposition, we use the fact that \(h_{\psi _1}=h_{\psi _2}=0\) in B ρ and that \(\tilde h=\tilde z\) outside B ρ. Now, setting
the epiperimetric inequality (12.1) follows by (12.22) and (12.23). □
12.5 Epiperimetric Inequality and Regularity of the Free Boundary
In this section we will show how the epiperimetric inequality (12.1) implies the C 1, α regularity of the free boundary. The main result of this section is Proposition 12.13, which we prove under the following assumption.
Condition 12.12 (Epiperimetric Inequality in Dimension d ≥ 2)
We say that the epiperimetric inequality holds in dimension d if there are constants δ d > 0 and ε d > 0 such that, for every non-negative one-homogeneous function z ∈ H 1(B 1), which is δ d -flat in the ball B 1 in some direction ν ∈ ∂B 1 , that is
there exists a non-negative function \(h:B_1\to \mathbb {R}\) such that z = h on ∂B 1 and
Proposition 12.13 (ε-Regularity via Epiperimetric Inequality)
Suppose that the epiperimetric inequality holds in dimension d (that is, Condition 12.12 holds). Then, there is a constant ε > 0 such that if \(u:B_1\to \mathbb {R}\) is a non-negative minimizer of \(\mathcal F_1\) in B 1 and is ε-flat in B 1 in some direction ν ∈ ∂B 1
then the free boundary ∂ Ω
u
is C
1, α
regular in
 .
.
Proof
The claim is a consequence of Lemma 12.18, Lemma 12.14 and the results of the previous sections. By Condition 12.12 and Lemma 12.18, we have that the epiperimetric inequality (12.24) holds whenever

is small enough for some half-plane solution h ν.
Using this, together with the Weiss’ monotonicity formula (Lemma 9.2), we get that the energy
satisfies the hypotheses of Lemma 12.14. Thus, we obtain the uniqueness of the blow-up limit and the decay of the blow-up sequences at every point of the free boundary in  , that is, for every
, that is, for every  , there is a function \(u_{x_0}:\mathbb {R}^d\to \mathbb {R}\) such that
, there is a function \(u_{x_0}:\mathbb {R}^d\to \mathbb {R}\) such that
Moreover, \(u_{x_0}\) is a global minimizer of \(\mathcal F_1\) in \(\mathbb {R}^d\) (Proposition 6.2) and is one-homogeneous (Proposition 9.12). Using again Lemma 12.14 (see the energy-decay estimate (12.28) in the first step of the proof), we get that
Thus, the strong convergence of the blow-up sequence \(u_{r,x_0}\) (Proposition 6.2) implies that
By Lemma 9.22, we get that \(u_{x_0}\) is a half-plane solution. Thus, by Proposition 8.6, we get that the free boundary is a C
1, α regular in  . □
. □
The idea that a purely variational inequality as (12.1) encodes the local behavior of the free boundary goes back to Reifenberg [45] who proved the regularity of the area-minimizing surfaces via an epiperimetric inequality for the area functional. Weiss was the first to prove an epiperimetric inequality in the context of a free boundary problem; in [53] he proved such an inequality for the obstacle problem and recovered the C 1, α regularity of the (regular part of the) free boundary in any dimension, which was first proved by Caffarelli [11]. In [49], together with Luca Spolaor, we proved for the first time an epiperimetric inequality for the one-phase problem; in this case the interaction between the geometry of the free boundary and the Dirichlet energy functional is very strong and induced us to introduce the different constructive approach, which was the core of the previous section. In all these different contexts, once we have the epiperimetric inequality, we can obtain the regularity of the free boundary essentially by the same argument that we will describe in this section. The key result of this subsection is Lemma 12.14, which we attribute to Reifenberg, who was also the first to relate the variational epiperimetric inequality to the regularity of the local behavior of the free boundary (or area-minimizing surface).
Vocabulary and Notations
We recall that, for any \(u:B_1\to \mathbb {R}\) and r ≤ 1, we use the notation u r to indicate the one-homogeneous rescaling of u
Then, if \(\mathcal E:H^1(B_1)\to \mathbb {R}\) is a given energy (for instance, \(\displaystyle \mathcal E(u)=W_1(u)-\frac {\omega _d}2\)), we will use the following terminology:
-
By variation of the energy we mean the variation, with respect to r, of the energy \(\mathcal E\) of the rescaling u r. In other words, the variation of the energy is simply
$$\displaystyle \begin{aligned} \frac{\partial}{\partial r}\mathcal E(u_r). \end{aligned}$$ -
The energy deficit of a function \(v:B_1\to \mathbb {R}\) is the difference
$$\displaystyle \begin{aligned} \mathcal E(v)-\mathcal E(u), \end{aligned}$$where \(u:B_1\to \mathbb {R}\) is a minimizer of \(\mathcal E\) among all functions such that u = v on ∂B 1.
-
The deviation of a function \(u:B_1\to \mathbb {R}\) (from being one-homogeneous) is
$$\displaystyle \begin{aligned} \mathcal D(u):=\int_{\partial B_1}|x\cdot\nabla u(x)-u(x)|{}^2\,d\mathcal{H}^{d-1}(x). \end{aligned}$$We notice that a function
$$\displaystyle \begin{aligned} \begin{array}{rcl} & u\in H^1(B_1)\quad \text{is one-homogeneous}\quad \\ & \Leftrightarrow\quad \mathcal D(u_r)=0\quad \text{for}\ \text{almost-every}\quad r\in(0,1). \end{array} \end{aligned} $$
Lemma 12.14 (Reifenberg [45])
Suppose that the function u ∈ H 1(B 1) and the energy functional \(\mathcal E:H^1(B_1)\to \mathbb {R}\) are such that:
-
(i)
Minimality. u r ∈ H 1(B 1) minimizes \(\mathcal E\) in B 1 , for every 0 < r ≤ 1, that is,
$$\displaystyle \begin{aligned} \mathcal E(u_r)\le \mathcal E(v)\quad \mathit{\text{for every}}\quad v\in H^1(B_1),\quad v=u_r\quad \mathit{\text{on}}\quad \partial B_1. \end{aligned}$$ -
(ii)
The variation of the energy controls the deviation. The function \(r\mapsto \mathcal E(u_r)\) is non-negative, differentiable and there is a constant C 2 > 0 such that
$$\displaystyle \begin{aligned} \frac{\partial }{\partial r}\mathcal E(u_r)\ge \frac{C_2}{r} \mathcal D(u_r)\qquad \mathit{\text{for every}}\qquad 0<r<1, \end{aligned}$$where \(\mathcal D\) is given by
$$\displaystyle \begin{aligned} \mathcal D(u):=\int_{\partial B_1}|x\cdot\nabla u(x)-u(x)|{}^2\,d\mathcal{H}^{d-1}(x). \end{aligned}$$ -
(iii)
The variation of the energy controls the energy deficit of the homogeneous extension. There is a constant C 3 > 0 such that
$$\displaystyle \begin{aligned} \frac{\partial }{\partial r}\mathcal E(u_r)\ge \frac{C_3}{r}\big(\mathcal E(z_r)-\mathcal E(u_r)\big)\qquad \mathit{\text{for every}}\qquad 0<r<1, \end{aligned}$$where \(z_r:B_1\to \mathbb {R}\) is the one-homogeneous extension of the trace \(u_r|{ }_{\partial B_1}\) , that is,
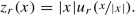
-
(iv)
Epiperimetric inequality. There is a one-homogeneous function \(b:\mathbb {R}^d\to \mathbb {R}\) such that, if u r is close to b in , then an epiperimetric inequality holds in B 1 . Precisely, there are constants ε > 0 and δ 4 > 0 such that:
For every
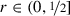 satisfying
satisfying
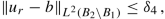 (12.25)
(12.25)there is a function h r ∈ H 1(B 1) such that h r = u r = z r on ∂B 1 and
$$\displaystyle \begin{aligned} \mathcal E(h_r)\le \big(1-{\varepsilon}\big)\mathcal E(z_r).\end{aligned} $$(12.26)
Under the hypotheses (i) , (ii) , (iii) and (iv) , there is δ > 0 such that, if u satisfies

then there is a unique u 0 ∈ H 1(B 1) such that

where the constants γ and C can be chosen as
Remark 12.15
If the epiperimetric inequality (12.26) holds without the closeness assumption (12.25), then the Step 4 of the proof of Lemma 12.14 can be omitted.
Remark 12.16
The energy to which we will apply Lemma 12.14 is the Weiss’ boundary adjusted energy
In this case, both (ii) and (iii) are implied by the Weiss’ formula (Lemma 9.2).
Remark 12.17
In our case, the function b from assumption (iv) is the half-plane solution b(x) = (x ⋅ ν)+ for some ν ∈ ∂B 1. Notice, that this does not mean that the blow-up limit u 0 of u r is equal to b. In fact, it may happen that the blow-up limit is another half-plane solution \(b(x)=(x\cdot \tilde \nu )_+\), with \(\tilde \nu \), which is close to ν. More generally, this lemma can be applied to situations in which u 0 is not just a rotation of b, but is a completely different function. This happens for instance at isolated singularities in higher dimension (see [29]).
Proof of Lemma 12.14
Let now  be the smallest non-negative number such that
be the smallest non-negative number such that

and so, we can apply the epiperimetric inequality (12.26) for every u
r with  . Notice that, since b is 1-homogeneous, a simple change of variables gives that
. Notice that, since b is 1-homogeneous, a simple change of variables gives that

Thus, by choosing δ < 4d+2 δ 4, we get that

for every  . Thus,
. Thus,  .
.
We divide the proof in several steps.
Step 1: The Epiperimetric Inequality Implies the Decay of the Energy
Let  . By (iii), (iv) and the minimality of u
r (assumption (i)), we have
. By (iii), (iv) and the minimality of u
r (assumption (i)), we have
Setting \(\displaystyle \gamma =\frac 12{\varepsilon } C_3\), we get that
and so,

Step 2: The Energy Controls the Deviation
We set
By (ii), we get that

which implies that for every  , we have the estimate
, we have the estimate

Step 3: The Deviation Controls the Oscillation of the Blow-up Sequence ur
Let x ∈ ∂B 1 be fixed. Then, we have
Integrating in r, we get that, for every 0 < r 1 < r 2 ≤ 1,
Integrating in x ∈ ∂B
1, and taking  , we obtain
, we obtain

Step 4: The Blow-up Sequence Remains Close to b
Taking  and r
1 = r ∈ (ρ, r
2) in (12.29), we get
and r
1 = r ∈ (ρ, r
2) in (12.29), we get

Now, since

we can choose  such that
such that

On the other hand, taking  , we obtain
, we obtain

This implies that if u = u 1 is such that

then ρ = 0, that is, the epiperimetric inequality (12.26) can be applied to every r ∈ (0, 1].
Step 5: Conclusion
As a consequence of the previous step, the decay estimate (12.29) holds on the whole interval (0, 1]:

Thus, there is u 0 ∈ L 2(∂B 1), which is the strong L 2(∂B 1)-limit of the blow-up sequence u r
Finally, taking r 2 = r ∈ (0, 1) and passing to the limit as r 1 → 0 in (12.30), we obtain (12.27). This concludes the proof.
□
In order to prove Proposition 12.13 under the Condition 12.12 we will need the following lemma.
Lemma 12.18
For every ε > 0 there is δ > 0 such that the following holds.
If \(u:B_2\to \mathbb {R}\) is a (non-negative) minimizer of \(\mathcal F_1\) in B 2 satisfying

where h ν is the half-plane solution h ν(x) = (x ⋅ ν)+,
then u is ε-flat in the direction ν in the ball B 1 , that is,
Proof
We will first prove that there is ε > 0 such that u is ε-flat on  , that is,
, that is,

From this, we will deduce that u is ε-flat in B 1.
In order to prove (12.32), we start by noticing that that, since u minimizes \(\mathcal F_1\) in B
2, it is L-Lipschitz continuous in  , for some L ≥ 1 depending only on the dimension (see Theorem 3.1). Then, also the function
, for some L ≥ 1 depending only on the dimension (see Theorem 3.1). Then, also the function

is (2L)-Lipschitz continuous. Thus, there is a dimensional constant C d such that

We now choose δ > 0 such that

Thus,

Now, using (12.34), we obtain the estimate from below

while from above we only have

Indeed, if  , then
, then

Thus, in order to prove that (12.32) it is sufficient to show that

On the other hand, u is also non-degenerate in the annulus , that is, there is a dimensional constant 0 < κ < 1 such that (see Proposition 4.1)
Suppose by absurd that there is a point
Then, taking  we get that there is
we get that there is

such that
If we choose δ such that
then we reach a contradiction. Notice that, since κ < 1, (12.36) implies (12.33).
This concludes the proof of (12.32). The conclusion now follows by Proposition 12.19. □
12.6 Comparison with Half-Plane Solutions
In this subsection, we prove the following result, which we use in the proof of Lemma 12.18; but is also of general interest.
Proposition 12.19
Let \(D\subset \mathbb {R}^d\) be a bounded open set and let \(u:\overline D\to \mathbb {R}\) be a non-negative continuous function and a minimizer of the functional \(\mathcal F_\Lambda \) in D. Let \(c\in \mathbb {R}\) be a constant, \(\nu \in \mathbb {R}^d\) be a unit vector and
be a half-plane solution. Then, the following claims do hold.
-
(i)
If u ≤ h on ∂D, then u ≤ h in D.
-
(ii)
If u ≥ h on ∂D, then u ≥ h in D.
Remark 12.20
Up to replacing u and h by  and
and  (which are minimizers of \(\mathcal F_1\) in D), we may assume that Λ = 1.
(which are minimizers of \(\mathcal F_1\) in D), we may assume that Λ = 1.
We will give two different proofs to Proposition 12.19. The first one is more natural, but is based on the notion of viscosity solution and so it requires the results from Sect. 7.1. The second proof is direct and is based on a purely variational argument in the spirit of Lemma 2.13.
Proof I of Proposition 12.19
By Proposition 7.1, u is a viscosity solution (see Definition 7.6) of
The conclusion now follows by Lemma 12.21 bellow. □
Proof II of Proposition 12.19
We only prove the first claim, the proof of the second one being analogous. For every t > 0, consider the half-plane solution
Then, for every x ∈ ∂D ∩ Ωu, we have that h(x) ≥ u(x) > 0 and so,
Thus, we can apply Lemma 12.22 to u and h t, obtaining that u ≤ h t in D. Since t is arbitrary, we obtain claim (i). □
Lemma 12.21 (Comparison of a Viscosity and a Half-Plane Solution)
Let D be a bounded open set in \(\mathbb {R}^d\) and let \(u:D\to \mathbb {R}\) be a non-negative continuous function and a viscosity solution (see Definition 7.6 ) to
Let \(c\in \mathbb {R}\) be a constant, \(\nu \in \mathbb {R}^d\) be a unit vector and h(x) = (x ⋅ ν + c) + be a half-plane solution. Then, the following claims do hold.
-
(i)
If u ≥ h on ∂D, then u ≥ h in D.
-
(ii)
If u ≤ h on ∂D, then u ≤ h in D.
Proof
We first prove (i). Let \(M=\|h\|{ }_{L^\infty (D)}\).
For any t > 0, we define the real function \(f_t:\mathbb {R}\to \mathbb {R}\) as
for every \(s\in \mathbb {R}\). Then, it is immediate to check that the function
satisfies the following conditions:
-
(1)
Δv t > 0 in the set {v t > 0};
-
(2)
|∇v t| > 1 on \(\overline {\{v_{t}>0\}}\);
-
(3)
v t(x) ≤ h(x) ≤ u(x) for every x ∈ ∂D.
Indeed, the first two conditions are immediate, since h is the positive part of an affine function. In order to prove (3), we notice that the inequality is trivial whenever x ⋅ ν + c − M(M + 1)t ≤ 0. The case x ⋅ ν + c − M(M + 1)t > 0 is a consequence of the following estimate, which holds for any S := x ⋅ ν + c > M(M + 1)t.
We next claim that v t ≤ u on D. Indeed, suppose that this is not the case and let T > 0 be the smallest real number such that (v t − T)+ ≤ u on \(\overline D\). Then, there is \(x_0\in \overline \Omega _u\) such that v t(x 0) − T = u(x 0) and (v t(x) − T)+ ≤ u(x), for every other \(x\in \overline D\), that is, the test function (v t − T)+ touches from below u at x 0. Since u is a viscosity solution (see Definition 7.6 and Proposition 7.1) of
we have that  and x
0∉ Ωu. Then, the only possibility is that x
0 ∈ ∂D, but this is also impossible since (v
t − T)+ < v
t ≤ u on ∂D. This proves that v
t ≤ u on D. Now, letting t → 0, we get that
and x
0∉ Ωu. Then, the only possibility is that x
0 ∈ ∂D, but this is also impossible since (v
t − T)+ < v
t ≤ u on ∂D. This proves that v
t ≤ u on D. Now, letting t → 0, we get that
which concludes the proof of (i).
The proof of claim (ii) is analogous. We give the proof for the sake of completeness. For any t > 0, we define the real function
where ε > 0 will be chosen below. We set
The test function
satisfies the following conditions:
-
1.
w t ≥ 0 for every 0 < t ≤ M u and every s ≤ M h;
-
2.
Δw t < 0 in the open set {w t > 0};
-
3.
|∇w t| < 1 on the closed set \(\overline {\{w_{t}>0\}}\);
-
4.
w t(x) ≥ h(x) ≥ u(x) for every x ∈ ∂D and every t ≤ M u.
We start with (1w). We notice that
Thus, in order to have (1w), we choose
Again (2w) and (3w) are trivial, while for (4w) we will need the following estimate, which holds for every S > 0 and t > 0.
In order to have (4w), we choose
We next complete the proof of (4w). First, notice that the second inequality is always true by hypothesis. Since w t ≥ 0, the first inequality is trivial whenever x ⋅ ν + c ≤ 0. Thus, we only need to prove that w t(x) ≥ h(x), whenever x ⋅ ν + c > 0. This follows by (12.37) and the second bound on ε (12.38). This concludes the proof of (1w) − (4w).
We now consider the set
We notice that I t is non-empty since M u ∈ I t. Let
If T > 0, then there is a point \(x_0\in \overline \Omega _u\) such that w T touches u from above in x 0. But this contradicts (2w) − (4w). Indeed, (2w) implies that x 0∉ Ωu ∩ D, (3w) gives that x 0∉∂ Ωu ∩ D and (4w) gives that x 0∉∂D. Thus, T = 0, which concludes the proof. □
Lemma 12.22 (Comparison of Minimizers)
Let D be a bounded open set in \(\mathbb {R}^d\) and \(u,v:\overline D\to \mathbb {R}\) be continuous non-negative functions and minimizers of \(\mathcal F_\Lambda \) in D. Suppose that:
-
(a)
u ≤ v on ∂D;
-
(b)
the above inequality is strict on the set \(\overline \Omega _u\cap \partial D\) , that is, \(\displaystyle \min _{\overline \Omega _u\cap \partial D}(v-u)=m>0.\)
Then, u ≤ v in D.
Proof
Let Ω := {x ∈ D : u(x) > v(x)}. We will prove that Ω = ∅. We first claim that Ω is strictly contained in D, that is
Suppose that this is not the case. Then, there is a sequence x n ∈ Ω converging to some x 0 ∈ ∂D. Since u and v are continuous, we get that
On the other hand, for every \(n\in \mathbb {N}\), we have
which gives that x n ∈ Ωu. Then, x n ∈ Ωu and thus, x 0 ∈ ∂ Ωu. This is a contradiction with the assumption (b).
We will next prove that
We consider the competitors
Since
the minimality of u and v implies that
On the other hand, we have
Thus, both inequalities in (12.39) are in fact equalities and so u ∧ v is a minimizer of \(\mathcal F_\Lambda \) in D. Suppose that
Then, u(x 0) = v(x 0) > 0 and by the continuity of u and v, there is a ball B r(x 0) such that
Thus, both the functions u and u ∧ v are positive and harmonic in B r(x 0). Thus, the strong maximum principle implies that u = u ∧ v in B r(x 0). This is contradiction with the assumption that x 0 ∈ ∂{u > v}.
We are now in position to prove that Ω = ∅. Indeed, suppose that this is not the case. Then, for every x 0 ∈ ∂ Ωu, we have that u(x 0) = 0. Thus, we consider the function

Then, \(\widetilde u=u\) on ∂D and \(\widetilde u\in H^1(D)\) (this follows, from instance from the facts that u is Lipschitz continuous on the compact subsets of D and that \(\overline \Omega \subset D\)). Thus, \(\widetilde u\) is an admissible competitor for u and we have
In particular,
and so, Ω = ∅, which concludes the proof. □
References
L. Caffarelli, The regularity of free boundaries in higher dimensions. Acta Math. 139 (1977)
M. Engelstein, L. Spolaor, B. Velichkov, Uniqueness of the blow-up at isolated singularities for the Alt-Caffarelli functional. Duke Math. J. 169(8), 1541–1601 (2020)
E.R. Reifenberg, An epiperimetric inequality related to the analyticity of minimal surfaces. Ann. Math. 80, 1–14 (1964)
L. Spolaor, B. Velichkov, An epiperimetric inequality for the regularity of some free boundary problems: the 2-dimensional case. Commun. Pure Appl. Math. 72(2), 375–421 (2019)
G.S. Weiss, A homogeneity improvement approach to the obstacle problem. Invent. Math. 138(1), 23–50 (1999)
Author information
Authors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2023 The Author(s)
About this chapter
Cite this chapter
Velichkov, B. (2023). An Epiperimetric Inequality Approach to the Regularity of the One-Phase Free Boundaries. In: Regularity of the One-phase Free Boundaries. Lecture Notes of the Unione Matematica Italiana, vol 28. Springer, Cham. https://doi.org/10.1007/978-3-031-13238-4_12
Download citation
DOI: https://doi.org/10.1007/978-3-031-13238-4_12
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-13237-7
Online ISBN: 978-3-031-13238-4
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)


 is the support Ωh = {h > 0} of the competitor h;
is the support Ωh = {h > 0} of the competitor h; is the support Ωz = {z > 0} of the one-homogeneous function z;
is the support Ωz = {z > 0} of the one-homogeneous function z; is the boundary ∂ Ωh;
is the boundary ∂ Ωh; is the boundary ∂ Ωz;
is the boundary ∂ Ωz; is the common boundary ∂ Ωh ∩ ∂ Ωz.
is the common boundary ∂ Ωh ∩ ∂ Ωz.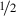 (see Lemma
(see Lemma 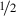 (Lemma
(Lemma 
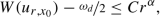
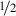 and so, it should be a regular point, as mentioned in the first bullet above.
and so, it should be a regular point, as mentioned in the first bullet above.


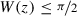 , where
, where 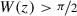 , but
, but 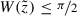 ;
;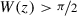 and
and 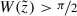 .
.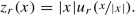
 satisfying
satisfying