Abstract
Let D be a connected bounded open set in \(\mathbb {R}^d\) and let v ∈ H 1(D) be a given non-negative function. This chapter is dedicated to the problem
where m ∈ (0, |D|) is a fixed constant and we recall that
In this chapter, we give the main steps of the proof of Theorem 1.9.
You have full access to this open access chapter, Download chapter PDF
Let D be a connected bounded open set in \(\mathbb {R}^d\) and let v ∈ H 1(D) be a given non-negative function. This chapter is dedicated to the problem
where m ∈ (0, |D|) is a fixed constant and we recall that
In this chapter, we give the main steps of the proof of Theorem 1.9.
-
Section 11.1. Existence of minimizers.
In this section, we prove that (11.1) admits a solution and that every solution is a non-negative subharmonic function (see Proposition 11.1).
-
Section 11.2. Euler-Lagrange equations.
In this section, we prove that if u is a solution to (11.1), then there exists a Lagrange multiplier Λ ≥ 0 such that the first variation of \(\mathcal F_\Lambda \) vanishes, that is,
$$\displaystyle \begin{aligned} \delta \mathcal F_\Lambda(u,D)[\xi]=0\quad \text{for every}\quad \xi\in C^\infty_c(D;\mathbb{R}^d). \end{aligned}$$ -
Section 11.3. Strict positivity of the Lagrange multiplier.
In this section we prove that Λ > 0.
-
Section 11.4. Convergence of the Lagrange multipliers.
In this section, we prove a technical lemma, that we will use several times in the next section. Roughly speaing, we show that if u n is a sequence of solutions converging to a solution u, then also the sequence of Lagrange multipliers converge to the Lagrange multipliers of u.
-
Section 11.5. Almost optimality of u at small scales.
In this section, we show that if u is a solution to (11.1), then it minimizes \(\mathcal F_\Lambda \) in every ball B r, up to an error that depends on the radius r and vanishes as r → 0. At this point, the regularity of the free boundary (Theorem 1.9) follows by the same arguments that we used for Theorem 1.2 and Theorem 1.4, the necessary modifications being pointed out in the sketch of the proof given in the introduction.
11.1 Existence of Minimizers
In this section we prove that there is a solution to the problem (11.1). This follows by a standard argument which can be divided in two steps. We will first show that there is a solution u to the auxiliary problem
where for simplicity we set
Then we will prove that the constraint is saturated, that is, every solution u of (11.2) is such that \(|\Omega _u|=|\Omega _u^+|=m\). We give the details in the following proposition.
Proposition 11.1 (Existence of Minimizers)
Let D be a connected bounded open set in \(\mathbb {R}^d\) , v ∈ H 1(D) be a non-negative function and 0 < m < |D|. Then,
-
(i)
there is a solution to the variational problem (11.1);
-
(ii)
the function u ∈ H 1(D) is a solution to (11.1) if and only if it is a solution to (11.2);
-
(iii)
every solution (to (11.1) and (11.2)) is a non-negative subharmonic function in D and, in particular, is defined at every point of D.
Proof
We will proceed in several steps.
Step 1. There is a solution to the auxiliary problem(11.2). This follows by a direct argument. Indeed, let u n be a minimizing sequence for (11.2), that is, \(u_n-v\in H^1_0(D)\), \(|\Omega _u^+\cap D|\le m\) and
Then, up to a subsequence, u n converges weakly in H 1(D), strongly in L 2(D) and pointwise a.e. in D to a function u ∞∈ H 1(D) such that \(u_\infty -v\in H^1_0(D)\). Then, we have
and, by the pointwise convergence of u n to u ∞,

which means that u ∞ is a solution to (11.2).
Step 2. Every solution u to(11.2) is non-negative. Indeed, this follows simply by the fact that if u = u + − u − is a solution to (11.2), then the function u + still satisfies the constraints \(u_+-v\in H^1_0(\Omega )\) and \(|\Omega _{u_+}|\le m\), and we have
with an equality if and only if u −≡ 0.
Step 3. Every solution u to(11.2) is subharmonic. This follows by the fact that
for every φ ≤ u with the same boundary values as u. In particular, this means that u is defined pointwise. In fact, we simply consider the representative of u defined as

Step 4. Every solution u to(11.2) satisfies the condition | Ωu| = m. Indeed, suppose that this is not the case. Let r 0 > 0 be such that \(|B_{r_0}|\le m-|\Omega _u|\). Take x 0 ∈ D and \(r<\min \big \{r_0,\text{dist}(x_0,\partial D)\big \}\). Let h be the harmonic extension of u in B r(x 0), that is, h is a solution of the PDE
Then, let \(\widetilde u\) be the competitor defined as

Then, \(|\Omega _{\widetilde u}|\le m\) and so, the optimality of u gives
which means that h = u in B
r(x
0). In particular, we get that the set {u > 0} is open: if u(x
0) > 0, then  for some r small enough, but then u > 0 in B
r(x
0) because it coincides with its (non-zero) harmonic extension. On the other hand {u > 0} is also closed. Indeed, if there is a sequence of points x
n converging to x
0 such that u(x
n) > 0, then the harmonic extension of u in B
r(x
0) is non-zero, so it is strictly positive, and so, u(x
0) > 0. Since D is connected, this means that {u > 0} = D, which is a contradiction with the fact that | Ωu|≤ m < |D|.
for some r small enough, but then u > 0 in B
r(x
0) because it coincides with its (non-zero) harmonic extension. On the other hand {u > 0} is also closed. Indeed, if there is a sequence of points x
n converging to x
0 such that u(x
n) > 0, then the harmonic extension of u in B
r(x
0) is non-zero, so it is strictly positive, and so, u(x
0) > 0. Since D is connected, this means that {u > 0} = D, which is a contradiction with the fact that | Ωu|≤ m < |D|.
Step 5. u ∈ H 1(D) is a solution to(11.2) if and only if it is a solution to(11.1). This is a trivial consequence of Step 4. □
In the rest of this section, without loss of generality, we will only consider functions u ∈ H 1(D), which are non-negative and satisfy the following optimality condition:
11.2 Euler-Lagrange Equation
In this section, we will prove the existence of a Lagrange multiplier for functions satisfying (11.3). We will follow step-by-step the proof from [46]. Our main result is the following.
Proposition 11.2 (Euler-Lagrange Equation)
Let \(D\subset \mathbb {R}^d\) be a connected bounded open set and let the non-negative function \(u:D\to \mathbb {R}\) be a solution of (11.3). Then, there is a constant Λ u > 0 such that
We start with the following lemma.
Lemma 11.3 (Variation of the Measure)
Let D be a connected open set in \(\mathbb {R}^d\) and let Ω ⊂ D be a Lebesgue measurable set such that 0 < | Ω| < |D|. Then, there is a smooth vector field \(\xi \in C^\infty _c(D;\mathbb {R}^d)\) such that
Proof
Assume, by contradiction, that we have
In particular, for every ball B ρ(x 0) ⊂ D, we may choose ξ to be the vector field
where
By (11.5), we have
Passing to the limit as ε → 0, we obtain
In particular, we get that
which means that the function ρ↦ρ
−d| Ω∩ B
ρ(x
0)| is constant. In particular, if x
0 ∈ B
r is a point of zero Lebesgue density for Ω, then Ω has zero Lebesgue measure in a neighborhood of x
0. Precisely, setting  we have that
we have that
Now, notice that (11.6) is both an open and a closed subset of D. Since, by hypothesis, D is connected, we have that Ω(0) = D or Ω(0) = ∅, which concludes the proof. □
Proof of Proposition 11.2
Let \(\xi \in C^\infty _c(D;\mathbb {R}^d)\). Using the notations from Lemma 9.5, for any (small enough) \(t\in \mathbb {R}\), we set
By Lemma 9.5, we have that
Now, let the vector field \(\xi _0\in C^\infty _c(D;\mathbb {R}^d)\) be such that
We are now going to prove that (11.4) holds with
We fix \(\xi \in C^\infty _c(D;\mathbb {R}^d)\) and we consider two cases.
Case 1. \(\displaystyle \int _{\Omega _u} \text{div}\,{\xi }\,dx = 0.\)
Let ξ 1 := ξ − ηξ 0 , where η > 0 is a real constant. Then, we have
Setting u t = u ∘ Φt, where Φt := (Id + tξ 1)−1, we have that, for t > 0 small enough,
By Proposition 11.1 (see Step 5 of the proof), we have that
Taking the derivative at t = 0, we obtain
which can be re-written as
Since η is arbitrary, we can deduce that
Finally, repeating the same argument for − ξ instead of ξ, we obtain that
which concludes the proof of (11.4) in this case.
Case 2. \(\displaystyle \int _{\Omega _u} \text{div}\,{\xi }\,dx \neq 0\).
Let \(\displaystyle \xi _2 := \xi - \xi _0 \int _{\Omega _u} \text{div}\,{\xi }\,dx\). Then \(\displaystyle \int _{\Omega _u} \text{div}\,{\xi _2}\,dx = 0\) and, by Case 1, we obtain
which concludes the proof of (11.4).
It only remains to prove that Λu ≥ 0. Indeed, let u t = u ∘ Φt, where Φt = (Id − tξ 0)−1. For t > 0 small enough, we have that \(|\Omega _{u_t}|\le |\Omega _u|\). We reason as in Case 1. By Proposition 11.1, we get that \(\mathcal F_0(u,D)\le \mathcal F_0(u_t,D)\). Then, taking the derivative at t = 0, we deduce
The strict positivity of Λu is more involved and follows by Proposition 11.4, which we prove in the next subsection. □
11.3 Strict Positivity of the Lagrange Multiplier
In this section we prove that the Lagrange multiplier from Proposition 11.2 is strictly positive. Precisely, we will show that a function, which is critical for the functional \(\mathcal F_0\) has a monotone Almgren frequency function N(r). Now, the monotonicity of the frequency function implies that u cannot decay too fast around the free boundary points. On the other hand, if u is harmonic in Ωu, then we can use a Caccioppoli inequality to show that if the Lebesgue density of Ωu is too small, then the decay of u on the balls of radius r should be very fast. The combination of these two estimates implies that the Lebesgue density of Ωu should be bounded from below at every point of D. In particular, there cannot be points of zero Lebesgue density for Ωu in D. The results from this subsection come directly from [46], but this unique-continuation argument goes back to the work of Garofalo and Lin [34]. The main result of this subsection is the following.
Proposition 11.4
Let D be a connected open set in \(\mathbb {R}^d\) . Suppose that u ∈ H 1(D) is a non-identically-zero function such that
-
(a)
u is a solution of the equation
$$\displaystyle \begin{aligned} {} \Delta u=0\quad \mathit{\text{in}}\quad \Omega_u=\{u\neq 0\}; \end{aligned}$$ -
(b)
u satisfies the extremality condition
$$\displaystyle \begin{aligned} \delta \mathcal F_0(u)[\xi]=0\quad \mathit{\text{for every}}\quad \xi\in C^\infty_c(D;\mathbb{R}^d), \end{aligned}$$where \(\delta \mathcal F_0(u)[\xi ]\) is the first variation of \(\mathcal F_0\) in the direction ξ and is given by
$$\displaystyle \begin{aligned} \delta \mathcal F_0(u)[\xi] := \int_D \Big[2\nabla u\cdot D\xi(\nabla u) -|\nabla u|{}^2\mathit{\text{div}}\, \xi\Big]\,dx. \end{aligned} $$(11.7)
Then,
 .
.
Remark 11.5
It is sufficient to prove Proposition 11.4 in the case u ≥ 0. In fact, if \(u:D\to \mathbb {R}\) satisfies the hypotheses (a) and (b) above, then the function \(|u|:D\to \mathbb {R}\) satisfies the same hypotheses.
In the proof of Proposition 11.4 we will use the following Faber-Krahn-type inequality, which was first proved in [10] (we report here the original proof).
Lemma 11.6 (A Faber-Krahn Inequality, [10])
There is a dimensional constant C d > 0 such that for every ball \(B_r\subset \mathbb {R}^d\) and every function v ∈ H 1(B r) satisfying
we have the inequality
where we recall that Ω v = {v ≠ 0}.
Proof
We first notice that:
-
We can assume that v is non-negative in B r. In fact, for every v ∈ H 1(B r), we have that |v|∈ H 1(B r) and the following identities do hold:
$$\displaystyle \begin{aligned} \Omega_v=\Omega_{|v|}\,,\qquad v^2=|v|{}^2\qquad \text{and}\qquad |\nabla v|{}^2=|\nabla |v||{}^2. \end{aligned}$$ -
We can assume that r = 1. Indeed, setting v r(x) = v(rx), we have that
$$\displaystyle \begin{aligned} |\Omega_v\cap B_r|=r^d|\Omega_{v_r}\cap B_1|\ ,\qquad \int_{B_r}v^2\,dx={r^d}\int_{B_1}v_r^2\,dx\,, \end{aligned}$$$$\displaystyle \begin{aligned} \int_{B_r}|\nabla v|{}^2\,dx={r^{d-2}}\int_{B_1}|\nabla v_r|{}^2\,dx\,. \end{aligned}$$
We now proceed with the proof of (11.8) in the case r = 1 and v ≥ 0 on B 1.
Step 1. We claim that there is a dimensional constant C iso > 0 such that
where Per( Ω;B r) is the relative perimeter in the sense of De Giorgi. The claim follows by a standard compactness argument.
Step 2. Let \(n\in \mathbb {N}\) and let D n = {x ⋅ ν 1 > 0}∩{x ⋅ ν 2 > 0} be the unbounded domain formed by the intersection of the two hyperplanes {x ⋅ ν 1 = 0} and {x ⋅ ν 2 = 0} forming (an interior) angle 2π∕n. We claim that, for every Ω ⊂ B 1 satisfying \(|\Omega |\le \frac {\omega _d}{2}\), there is a radius ρ > 0 such that
Indeed, for every Ω, there is a unique ρ > 0 such that |B ρ ∩ D n| = | Ω|. We set Ω∗ := B ρ ∩ D n. Then, we have
Now, the isoperimetric inequality (11.9) implies
Taking n large enough, such that \(n^{\frac 1d} \ge C_{iso}\, d\omega _d^{\frac 1d}\), we get P( Ω;D) ≥ Per( Ω∗;D n), which proves (11.10).
Step 3. For every non-negative function v ∈ H 1(B 1) we define the symmetrized function v ∗∈ H 1(D n) obtained through the symmetrization of each level of v, that is,
We claim that
The first part of (11.11) follows by the area formula
while for the second part we will use the co-area formula. Indeed, setting
we have
where the first inequality follows by Cauchy-Schwartz and the second one is a consequence of (11.10).
Step 4. We claim that there is a constant C d,n > 0, depending only on d and n, such that
Let \(\tilde v_\ast :\mathbb {R}^d\to \mathbb {R}\) be the radially decreasing function defined by
where y ∈ D n is any point such that |x| = |y|. By the classical Faber-Krahn inequality in \(\mathbb {R}^d\), there is a dimensional constant C d such that
which gives that
which is precisely (11.12). This, together with (11.11), concludes the proof. □
In the next lemma, we prove that the Almgren frequency function is monotone. This is a classical result, which was first proved by Almgren [2].
Lemma 11.7 (Almgren Monotonicity Formula)
Let u ∈ H 1(B R). For r ∈ (0, R], we define
and, if H(r) ≠ 0, we define the Almgren frequency function
Suppose that u is a solution of the equation
and satisfies the extremality condition
where \(\delta \mathcal F_0(u)[\xi ]\) is given by (11.7). If, moreover, H > 0 on the interval (a, b) ⊂ (0, R), then the frequency function N is non-decreasing on (a, b).
Proof
We first calculate the derivative of H
which we rewrite as
Next, we notice that the extremality condition \(\delta \mathcal F_0(u)=0\) gives that the following equipartition of the energy does hold:
which can be rewritten as
We now compute the derivative of N.
Notice that, since u is harmonic in Ωu, we have
and so, by the Cauchy-Schwarz inequality and (11.14) we obtain N ′(r) ≥ 0. □
Remark 11.8 (The Derivative of \(\ln H\))
Notice that, by (11.13), we get that
We are now in position to prove Proposition 11.4.
Proof of Proposition 11.4
Let x 0 = 0 ∈ D. We set H(r), D(r) and N(r) to be as in Lemma 11.7 and Remark 11.8. Let r 0 > 0 be such that \(B_{r_0}(x_0)\subset D\) and H(r 0) > 0. Since u ∈ H 1(D), there is some ε > 0 such that H > 0 on the interval (r 0 − ε, r 0). Then, the function r↦N(r) is non-decreasing in r and so
By (11.15), we have
and integrating we get
This means that, for every ε > 0, H is bounded from below by a positive constant on the interval [r 0 − ε, r 0]. In particular, H > 0 on (0, r 0]. Thus, we can take ε = r 0.
Let now, r ∈ (0, r 0∕2]. Integrating the inequality (11.16) from r to 2r, we get
This implies that
Integrating once more in r we get
We next prove a Caccioppoli inequality for u in the ball B 2r. Indeed, let \(\phi \in C^\infty _c(\mathbb {R}^d)\) be a cut-off function such that

Since, u is harmonic in Ωu, the following Caccioppoli inequality does hold:
On the other hand, by Lemma 11.6, there is a dimensional constant C d > 0 such that:
This, together with the Caccioppoli and the doubling inequality (11.17), gives that
Since, \(\displaystyle \int _{B_r}u^2\,dx>0\), we get that there is a dimensional constant C d such that
In particular, we have a lower density bound for Ωu at every point of D, which implies that  and concludes the proof. □
and concludes the proof. □
11.4 Convergence of the Lagrange Multipliers
In this section we prove that the Lagrange multipliers, associated to the solutions of variational problems with measure constraint in a fixed connected open set \(D\subset \mathbb {R}^d\), are continuous with respect to variations of the constraint. This fact will be used several times in the proof of the optimality of the blow-up limits. In the next Lemma, which comes directly from [46], we will use the notation
for every Lebesgue measurable set \(\Omega \subset \mathbb {R}^d\) and every vector field \(\xi \in C^\infty _c(\mathbb {R}^d;\mathbb {R}^d)\).
Lemma 11.9 (Convergence of the Lagrange Multipliers)
Let D be a connected bounded open set in \(\mathbb {R}^d\) and let \(u\in H^1_0(D)\) be a non-negative function for which (11.3) does hold. Let Λ u be the Lagrange multiplier from (11.4) in D.
Let B ⊂ D be a connected bounded open set such that 0 < m := | Ω u ∩ B| < |B|.
Let \( \left (m_n\right )_{n\geq 1}\) be a sequence such that limn→∞ m n = m and let u n ∈ H 1(B) be a solution (which exists due to Proposition 11.1) to the problem
Then, we have:
-
(i)
for every n, there is a Lagrange multiplier \(\Lambda _{u_n}>0\) for which
$$\displaystyle \begin{aligned} \delta \mathcal F_0(u_n,B)[\xi] + \Lambda_{u_n}\delta{\mathrm{Vol}}\,(\Omega_{u_n})[\xi]=0\qquad \mathit{\text{for every}}\qquad \xi\in C^\infty_c(B;\mathbb{R}^d), \end{aligned} $$(11.19) -
(ii)
for every n, there is a vector field \(\xi _n\in C^\infty _c(B;\mathbb {R}^d)\) such that
$$\displaystyle \begin{aligned} \delta\mathcal F_0(u_n,B)[\xi_n]+\Lambda_{u_n}=0\qquad \mathit{\text{and}}\qquad \delta{\mathrm{Vol}}\,(\Omega_{u_n})[\xi_n]=1\,. \end{aligned} $$(11.20) -
(iii)
u n converges strongly in \(H^1_0(D)\) and pointwise almost everywhere to a function u ∞ , which is a solution to the problem
$$\displaystyle \begin{aligned} \min\Big\{\mathcal F_0(v,B)\, :\ v\in H^1(B),\ v-u\in H^1_0(B),\ |\Omega_v| = m\Big\}; \end{aligned} $$(11.21) -
(iv)
the sequence of characteristic functions
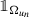 converges to
converges to
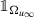 pointwise almost everywhere and strongly in L
2(D);
pointwise almost everywhere and strongly in L
2(D); -
(v)
\(\displaystyle \lim _{n\to \infty }\Lambda _{u_n}=\Lambda _{u_\infty }\) , where \(\Lambda _{u_\infty }>0\) is the Lagrange multiplier of u ∞ in B, that is,
$$\displaystyle \begin{aligned} \delta \mathcal F_0(u_\infty,B)[\xi] + \Lambda_{u_\infty}\delta{\mathrm{Vol}}\,(\Omega_{u_\infty})[\xi]=0\qquad \mathit{\text{for every}}\qquad \xi\in C^\infty_c(B;\mathbb{R}^d), \end{aligned} $$(11.22) -
(vi)
Suppose that B ≠ D and that there is a connected component \(\mathcal C\) of
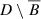 such that
$$\displaystyle \begin{aligned} 0<|\Omega_u\cap \mathcal C|< |\mathcal C|, \end{aligned}$$
such that
$$\displaystyle \begin{aligned} 0<|\Omega_u\cap \mathcal C|< |\mathcal C|, \end{aligned}$$then \(\Lambda _{u_\infty }=\Lambda _u\).
Proof
The existence of a solution u n follows from Proposition 11.1. The existence of a Lagrange multiplier \(\Lambda _{u_n}\) and a vector field \(\xi _n\in C^\infty _c(B;\mathbb {R}^d)\) with the properties (11.20) follows by Proposition 11.2. Let \(\xi _0\in C^\infty _c(B;\mathbb {R}^d)\) be a vector field such that
Setting u t := u ∘ (Id + tξ 0)−1, we get that, for t small enough, \(u_t-u\in H^1_0(D)\). Moreover, to every n large enough, we can associate a unique \(t_n\in \mathbb {R}\) such that
Thus, we can use \(u_{t_n}\) as a test function in (11.18). Thus, there is a constant C depending only on u and ξ 0 such that, for every n large enough (say n ≥ n 0 for some \(n_0\in \mathbb {N}\)), we have
Then the sequence \(\left (u_n\right )_{n\geq 1}\) is uniformly bounded in H 1(B) and so, up to a subsequence, u n converges weakly in H 1, strongly in L 2 and pointwise almost everywhere to a function u ∞∈ H 1(B) such that \(u_\infty -u\in H^1_0(B)\). In particular, the pointwise convergence of u n to u ∞ implies that

Thus, we get that
and so, the minimality of u implies that
On the other hand, the weak H 1 convergence of u n gives that
so, we get \(\mathcal F_0(u_\infty ,B)=\mathcal F_0(u,B)\). Thus, u ∞ is a solution to (11.21) and \(|\Omega _{u_\infty }|=m\). Moreover, using again the optimality of u n and the fact that \(u_{t_n}\) converges to u, we obtain
which gives that
Since u n converges strongly in L 2(B) and weakly in H 1(B) to u ∞, we get that the convergence of u n to u ∞ is strong in H 1(B).
We next prove (iv). We will first show that  convergence strongly in L
2(B) to
convergence strongly in L
2(B) to  .
.
Indeed, we first notice that, up to a subsequence, there is h ∈ L
2(B) such that  weakly in L
2(B). On the other hand, the pointwise convergence of u
n to u
∞ implies that
weakly in L
2(B). On the other hand, the pointwise convergence of u
n to u
∞ implies that

Thus, for any non-negative function φ ∈ L 2(B), the Fatou Lemma implies that

which yields  . In particular,
. In particular,
On the other hand, the weak L
2 convergence of  to h gives that
to h gives that

As a consequence,

which implies that  converges to h strongly in L
2(B). Now, since
converges to h strongly in L
2(B). Now, since

we get that  , from which we conclude that
, from which we conclude that  converges to
converges to  strongly in L
2(B), and so, up to a subsequence
strongly in L
2(B), and so, up to a subsequence  converges to
converges to  pointwise almost everywhere.
pointwise almost everywhere.
We now prove (v). We first notice that u and u ∞ are both solutions of (11.21). By Proposition 11.2, there is a Lagrange multiplier \(\Lambda _\infty :=\Lambda _{u_\infty }>0\) such that (11.22) does hold. Moreover, by (iii) and (iv), we get that, for every fixed \(\xi \in C^\infty _c(B;\mathbb {R}^d)\),
Now, choosing any \(\xi \in C^\infty _c(B;\mathbb {R}^d)\) such that
and using (11.22) and (11.19) we get that \(\Lambda _{u_n}\) converges to Λ∞.
We prove the last claim (vi). Indeed, since
we get that the function

is in H 1(D) and is a solution to the problem
In particular, \(\widetilde u\) is a critical point of \(\mathcal F_{\Lambda _\infty }\) in the entire D, that is,
On the other hand, in the connected component \(\mathcal C\), we have that \(\widetilde u =u\) and so, there is a vector field \(\xi ^{\prime }_0\in C^\infty _c(\mathcal C;\mathbb {R}^d)\) such that \(\delta \text{Vol}\,(\Omega _{u})[\xi _0^{\prime }]=\delta \text{Vol}\,(\Omega _{\widetilde u})[\xi _0^{\prime }]=1\). This implies that
which concludes the proof. □
11.5 Almost Optimality of u at Small Scales
Let \(D\subset \mathbb {R}^d\) be a connected bounded open set and \(u:D\to \mathbb {R}\) be a non-negative function satisfying (11.3). In this section, we will prove the following result, which is analogous to the results of Briançon [5], Briançon-Lamboley [6], and the more recent [46], which are all dedicated to different (and technically more involved) free boundary problems arising in Shape Optimization.
Proposition 11.10
Let D be a connected bounded open set in \(\mathbb {R}^d\) and let u ∈ H 1(D) be a non-negative function satisfying (11.3). Let Λ > 0 be the corresponding Lagrange multiplier, that is, Λ is such that \(\delta \mathcal F_\Lambda (u,D)=0\) . Let B ⊂ D be a ball such that:
-
0 < | Ω u ∩ B| < |B|;
-
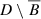 is connected:
is connected:
-
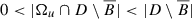 .
.
Then, for every ε > 0, there exists r > 0 such that u satisfies the following optimality conditions in every B r(x 0) ⊂ B:
Remark 11.11
An immediate consequence of the inwards (11.24) and the outwards (11.23) optimality is that u satisfies the following almost-minimality condition:
In order to prove Proposition 11.10 we will use the contradiction argument of Briançon [5]. The proof presented here follows step-by-step the exposition from [46] and uses only the existence of a Lagrange multiplier, variations with respect to smooth vector fields and elementary variational arguments. Roughly speaking, the main idea is to replace the localization condition \(u-v\in H^1_0(B_r)\) in (11.24) and (11.23) by a bound on the measure of Ωv, | Ωv|≤| Ωu| + δ, for which the passages to the limit are somehow easier. Proposition 11.10 is a direct consequence of Proposition 11.16
Remark 11.12
We notice that we work in the ball B ⊂ D only because of the fact that we will use several times the convergence of the Lagrange multipliers associated to solutions of auxiliary problems. Indeed, in order to assure the convergence of these Lagrange multipliers to Λ (the Lagrange multiplier of the solution u), we need to work strictly inside the domain D (see Lemma 11.9, claim (vi)).
Definition 11.13 (Upper and Lower Lagrange Multipliers)
We fix u, D and B to be as in Proposition 11.10. We set m := | Ωu ∩ B|. For any constant δ > 0, we define the upper Lagrange multiplier μ +(δ) as follows:
Analogously, we define the lower Lagrange multiplier μ −(δ):
Lemma 11.14
Suppose that D is a connected bounded open set in \(\mathbb {R}^d\) and that u ∈ H 1(D) is a given non-negative function such that:
-
(a)
u ≠ 0 and
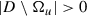 ;
; -
(b)
u is stationary for \(\mathcal F_\Lambda \) , that is,
$$\displaystyle \begin{aligned} \delta\mathcal F_\Lambda(u,D)[\xi]=0\qquad \mathit{\text{for every}}\qquad \xi\in C^\infty_c(D;\mathbb{R}^d). \end{aligned}$$
Then, we have the following claims:
-
(i)
Suppose that there are δ > 0 and μ > 0 such that u satisfies (11.25). Then, Λ ≤ μ.
-
(ii)
Suppose that there are δ > 0 and μ > 0 such that u satisfies (11.26). Then, Λ ≥ μ.
Proof
Let us first prove claim (i). By Lemma 11.3 and the hypothesis (a), we get that there is a vector field \(\xi \in C^\infty _c(D;\mathbb {R}^d)\) such that
where u t = u ∘ (Id + tξ)−1. Since for t small enough, we have that \(|\Omega _u|\le |\Omega _{u_t}|\le |\Omega _{u}|+\delta \), the minimality of u gives that
Thus, taking the derivative at t = 0, we get that
which proves (i). The proof of (ii) is analogous. □
As an immediate corollary, we obtain the following lemma.
Lemma 11.15 (μ −≤ Λu ≤ μ +)
Let D be a connected bounded open set in \(\mathbb {R}^d\) and u ∈ H 1(D) be a non-negative function such that (11.3) holds. Let m = | Ω u| and Λ u > 0 be the Lagrange multiplier of u in D, that is,
Let B, μ +(δ) and μ −(δ) be as in Definition 11.13 . Then, for every δ > 0, we have
Notice that we still might have μ −(δ) = 0 and μ +(δ) = +∞. In Proposition 11.16 below we will prove that this cannot occur.
Proposition 11.16 (Convergence of the Upper and the Lower Lagrange Multipliers)
Let D be a connected bounded open set in \(\mathbb {R}^d\) . Let u ∈ H 1(D) be a non-negative function satisfying the minimality condition (11.3) in D and let Λ u > 0 be the Lagrange multiplier of u in D, given by Proposition 11.2 . Let B ⊂ D be as in Proposition 11.10 . Then, we have
Proof
We will work only in the ball B. The presence of the larger domain D is only necessary to assure the convergence of the Lagrange multipliers (see Lemma 11.9) for the different auxiliary problems that we will use below. We will proceed in three steps.
Step 1 We will first prove that μ +(δ) < +∞, for every δ > 0. This is equivalent to prove that there is some μ > 0, for which the minimality condition (11.25) is satisfied. Assume, by contradiction, that for every n > 0, there exists some function u n ∈ H 1(B) such that
Thus, if v n is a solution of the auxiliary problem
then, we have that
Thus, by Proposition 11.1 (Step 5 of the proof), we obtain \(|\Omega _{v_n}|>m.\) Thus, we may assume
Using again (11.28), we obtain
which, in particular, implies that
Now, notice that, setting \(m_n:=|\Omega _{v_n}|\), we have that v n is a solution of
In particular, there is a Lagrange multiplier \(\Lambda _{v_n}\) such that
and a vector field \(\xi _n\in C^\infty _c(B;\mathbb {R}^d)\) such that
We set \(v_n^t = v_n\circ (Id+t\xi _n)^{-1}\). Choosing t > 0 small enough and \(n\in \mathbb {N}\) big enough, we get
Then, by (11.27), we have
which implies \(n \leq \Lambda _{v_n}\). On the other hand, Lemma 11.9 implies that
which is a contradiction. This concludes the proof of Step 1.
Step 2 In this step, we prove that limδ→0 μ +(δ) = Λu.
Let δ n be an infinitesimal decreasing sequence. We will prove that limn→∞ μ +(δ n) = Λu.
Fix ε ∈ (0, Λu) and set α n to be
We will show that, for n big enough, α n ≤ Λu. Let u n ∈ H 1(B) be solution to the auxiliary problem
We consider two cases:
Case 1 (of Step 2). Suppose that \(|\Omega _{u_n}|\le m\). Then, the optimality of u gives
On the other hand, the optimality of u n gives
for every v ∈ H 1(B) such that \(u-v\in H^1_0(B)\) and m ≤| Ωv|≤ m + δ n, which contradicts the definition of μ +(δ n).
Case 2 (of Step 2). Suppose that \(m<|\Omega _{u_n}|\le m+\delta _n.\) Notice that, setting \(m_n:=|\Omega _{u_n}|\), the solution u n to (11.29) is also a solution to the problem
By Proposition 11.2, there is a Lagrange multiplier \(\Lambda _{u_n}\geq 0\) such that
and a vector field \(\xi _n\in C^\infty _c(B_r;\mathbb {R}^d)\) such that \(\delta \text{Vol}\,(\Omega _{u_n})[\xi _n]=1.\)
We set \(u_n^t:=u_n\circ (Id+t\xi _n)^{-1}\). By the minimality of u n, for t < 0 small enough, we have
from which we deduce that \(\Lambda _{u_n}\geq \alpha _n\). Now, by Lemma 11.9 we get that
Since Λu ≤ μ +(δ n) and ε > 0 is arbitrary, we get the claim of Step 2.
Step 3 In this last step we will prove that limδ→0 μ −(δ) = Λu.
It is sufficient to show that, for aby decreasing infinitesimal sequence δ n → 0, we have
Precisely, we will show that for any fixed constant ε > 0, we have Λu − ε ≤limn→∞ μ −(δ n).
Let β n := μ −(δ n) + ε and u n be a solution of the problem
We consider three cases:
Case 1 (of Step 3). Suppose that \(|\Omega _{u_n}|=m.\)
By the minimality of u, we have that \(\mathcal F_0(u,B)\le \mathcal F_0(u_n,B)\). Now, the minimality of u n, gives that, for every v ∈ H 1(B) such that \(v-u\in H^1_0(B)\) and m − δ n ≤| Ωv|≤ m, we have
which contradicts the definition of μ −(δ n).
Case 2 (of Step 3). Suppose that \(|\Omega _{u_n}|<m-\delta _n.\)
Then we have
for every \(\varphi \in C^\infty _c(B)\) with sufficiently small compact support. This implies that u n is harmonic in B. By the strong maximum principle, we obtain that either u n ≡ 0 or u n > 0 in B, which is impossible for n large enough.
Case 3 (of Step 3). Suppose that \(m-\delta _n\le |\Omega _{u_n}|<m\).
We set \(m_n:=|\Omega _{u_n}|\). Then, u n is a solution to the problem
By Proposition 11.2, there is a Lagrange multiplier \(\Lambda _{u_n}\geq 0\) such that
and a vector field \(\xi _n\in C^\infty _c(B;\mathbb {R}^d)\) such that \(\delta \text{Vol}\,(\Omega _{u_n})[\xi _n]=1.\)
We set \(u_n^t:=u_n\circ (Id+t\xi _n)^{-1}\). Let t > 0 be small enough. Then \(u_n^t\) is such that
Thus, by the minimality of u n, we get
which implies that
Finally, by Lemma 11.9, we get
which concludes the proof. □
References
F.J. Almgren Jr., Dirichlet’s problem for multiple valued functions and the regularity of mass minimizing integral currents. Minimal Submanifolds and Geodesics (Kaigai, Tokyo, 1979), pp. 1–6
T. Briançon, Regularity of optimal shapes for the Dirichlet’s energy with volume constraint. ESAIM, Control Optim. Calc. Var. 10, 99–122 (2004)
T. Briançon, J. Lamboley, Regularity of the optimal shape for the first eigenvalue of the Laplacian with volume and inclusion constraints. Ann. Inst. H. Poincaré Anal. Non Linéaire 26(4), 1149–1163 (2009)
G. Buttazzo, B. Velichkov, A shape optimal control problem with changing sign data. SIAM J. Math. Anal. 50(3), 2608–2627 (2018)
N. Garofalo, F.-H. Lin, Monotonicity properties of variational integrals, A p weights and unique continuation. Indiana Univ. Math. J. 35, 245–268 (1986)
E. Russ, B. Trey, B. Velichkov, Existence and regularity of optimal shapes for elliptic operator with drift. Calc. Var. PDE 58(6), 199 (2019)
Author information
Authors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2023 The Author(s)
About this chapter
Cite this chapter
Velichkov, B. (2023). Regularity of the Free Boundary for Measure Constrained Minimizers. In: Regularity of the One-phase Free Boundaries. Lecture Notes of the Unione Matematica Italiana, vol 28. Springer, Cham. https://doi.org/10.1007/978-3-031-13238-4_11
Download citation
DOI: https://doi.org/10.1007/978-3-031-13238-4_11
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-13237-7
Online ISBN: 978-3-031-13238-4
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)


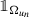 converges to
converges to
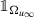 pointwise almost everywhere and strongly in L
2(D);
pointwise almost everywhere and strongly in L
2(D);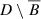 such that
such that
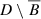 is connected:
is connected:
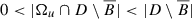 .
.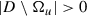 ;
;