Playing Against Fair Adversaries in Stochastic Games with Total Rewards

Abstract

We investigate zero-sum turn-based two-player stochastic games in which the objective of one player is to maximize the amount of rewards obtained during a play, while the other aims at minimizing it. We focus on games in which the minimizer plays in a fair way. We believe that these kinds of games enjoy interesting applications in software verification, where the maximizer plays the role of a system intending to maximize the number of “milestones” achieved, and the minimizer represents the behavior of some uncooperative but yet fair environment. Normally, to study total reward properties, games are requested to be stopping (i.e., they reach a terminal state with probability 1). We relax the property to request that the game is stopping only under a fair minimizing player. We prove that these games are determined, i.e., each state of the game has a value defined. Furthermore, we show that both players have memoryless and deterministic optimal strategies, and the game value can be computed by approximating the greatest-fixed point of a set of functional equations. We implemented our approach in a prototype tool, and evaluated it on an illustrating example and an Unmanned Aerial Vehicle case study.

This work was supported by ANPCyT PICT-2017-3894 (RAFTSys), ANPCyT PICT 2019-03134, SeCyT-UNC 33620180100354CB (ARES), and EU Grant agreement ID: 101008233 (MISSION).

1 Introduction

Game theory [25] admits an elegant and profound mathematical theory. In the last decades, it has received widespread attention from computer scientists because it has important applications to software synthesis and verification. The analogy is appealing, the operation of a system under an uncooperative environment (faulty hardware, malicious agents, unreliable communication channels, etc.) can be modeled as a game between two players (the system and the environment), in which the system tries to fulfill certain goals, whereas the environment tries to prevent this from happening. This view is particularly useful for controller synthesis, i.e., to automatically generate decision-making policies from high-level specifications. Thus, synthesizing a controller consists of computing optimal strategies for a given game.

In this paper we focus on zero-sum, perfect-information, two-player, turn-based stochastic games with (non-negative) rewards [18]. Intuitively, these games are played in a graph by two players who move a token in turns. Some vertices are probabilistic, in the sense that, if a token is in a probabilistic vertex, then the next vertex is randomly selected. Furthermore, the players select their moves using strategies. Associated with each vertex there is a reward (which, in this paper, is taken to be non-negative). The goal of Player 1 is to maximize the expected amount of collected rewards during the game, whereas Player 2 aims at minimizing this value. This is what [28] calls total reward objective. These kinds of games have been shown useful to reason about several classes of systems such as autonomous vehicles, fault-tolerant systems, communication protocols, energy production plants, etc. Particularly, in this paper we consider those games in which one of the players employs fair strategies.

Fairness restrictions, understood as fair resolutions of non-determinism of actions, play an important role in software verification and controller synthesis. Especially, fairness assumptions over environments make possible the verification of liveness properties on open systems. Several authors have indicated the need for fairness assumptions over the environment in the controller synthesis approach, e.g., [2, 16]. As a simple example consider an autonomous vehicle that needs to traverse a field where moving objects may interfere in its path. Though the precise behavior of the objects may be unknown, it is reasonable to assume that they will not continuously obstruct the vehicle attempts to avoid them. In this sense, while stochastic behavior may be a consequence of the vehicle faults, we can only assume a fair behavior of the surrounding moving objects. In this work, we consider stochastic games in which one of the players (the one playing the environment) is assumed to play only with strong fair strategies.

In order to guarantee that the expected value of accumulated rewards is well defined in (perhaps infinite) plays, some kind of stopping criteria is needed. A common way to do this is to force the strategies to decide to stop with some positive probability in every decision. This corresponds to the so-called discounted stochastic games [18, 27], and has the implications that the collected rewards become less important as the game progresses (the “importance reduction” is given by the discount factor). Alternatively, one may be interested in knowing the expected total reward, that is, the expected accumulated reward without any loss of it as time progresses. For this value to be well defined, the game itself needs to be stopping. That is, no matter the strategies played by the players, the probability of reaching a terminal state needs to be 1 [13, 18]. We focus on this last type of game. However, we study here games that may not be stopping in general (i.e., for every strategy), but instead, require that they become stopping only when the minimizer plays in a fair way. We use a notion of (almost-sure) strong fairness, mostly following the ideas introduced in [7] for Markov decision processes. We show that these kinds of games are determined, i.e., each state of the game has a value defined. Furthermore, we show that memoryless and deterministic optimal strategies exist for both players. Moreover, the value of the game can be calculated via the greatest fixed point of the corresponding functionals. It is important to remark that most of the properties discussed in this paper hold when the fairness assumptions are made over the minimizer. Similar properties may not hold if the role of players is changed. However, these conditions encompass a large class of scenarios, where the system intends to maximize the total collected reward and the environment has the opposite objective.

In summary, the contributions of this paper are the following: (1) we introduce the notion of stopping under fairness stochastic game, a generalization of stopping game that takes into account fair environments; (2) we prove that it can be decided in polynomial time whether a game is stopping under fairness; (3) we show that these kinds of games are determined and both players possess optimal stationary strategies, which can be computed using Bellman equations; and (4) we implemented these ideas in a prototype tool embedded in the PRISM-games toolset [22], which we used to evaluate the viability of our approach through illustrative case studies.

The paper is structured as follows. Section 2 introduces an illustrating example to motivate the use of having fairness restrictions over the minimizer. Section 3 fixes terminology and introduces background concepts. In Sect. 4 we describe a polynomial procedure to check whether a game stops under fairness assumptions, we also prove that determinacy is preserved in these games as well as the existence of (memoryless and deterministic) optimal strategies. Experimental results are described in Sect. 5. Finally, Sects. 6 and 7 discuss related work and draw some conclusions, respectively.

2 Roborta vs. the Fair Light (A Motivating Example)

Consider the following scenario. Roborta the robot is navigating a grid of $4 \times 4$ cells. Roborta ’s moves respond to a traffic light: if the light is yellow, she must move sideways (at a border cell, Roborta is allowed to wrap around to the other side); if the light is green she ought to move forward; if the light is red, she cannot perform any movement; finally, if the light is off, Roborta is free to move either sideways or forward. The light and Roborta change their states in turns. In addition, a (non-negative) reward is associated with each cell of the grid. Also, some cells restrict the sideway movement to only one direction. Moreover, we consider possible failures on the behavior of the robot and the light. If Roborta fails, she loses her turn to move. If the light fails, it turns itself off. The failures occur with a given probability and are not permanent (they only affect the current play). The goal of Roborta is to collect as many rewards as possible. In opposition, the light aims at minimizing this value.

The specification of this game is captured in Fig. 1 (using PRISM-like notation [23]). In this model, WIDTH and LENGTH are constants defining the dimension of the grid. MOVES is a two-dimensional array modeling the possible sideways movements in the grid (0 allows the robot to move only to the left, 1, to either side, and 2, only to the right). The light plays when it is red (light=0) and it can choose whether to turn on the yellow light (transition labelled with l_y) or green (transition labelled l_g). Notice that with any choice, the light may fail with probability Q, in which case it turns itself off (light’=3). If the light is not red, then it is Roborta ’s turn to play. If the light is yellow (light=1) or off (light=3), Roborta can chose whether to move left (r_l) or right (r_r), provided the grid allows the movements. If the light is green (light=2) or off (light=3), she can choose to move forward (notice that if light=2 this is the only possible move). Like the light, each of Roborta ’s choices has a failure probability of P, in which case, she does not move and only passes the turn to the light (by setting light’=0). For completeness, we mention that the rewards are stored in a secondary matrix which is not shown in Fig. 1.

Fig. 1.

Model for the Game

Figure 2 shows the assignment of rewards to each cell of the $4 \times 4$ grid as well as the sideway movement restrictions (shown on the bottom-right of each cell with white arrows). The game starts at the cell (0, 0) and it stops when Roborta escapes through the end of the grid (i.e., $\texttt {row}=\texttt {LENGTH}$).

A possible scenario in this game is as follows. Roborta starts in cell (0, 0) and, in an attempt to minimize the rewards accumulated by the robot, the environment switches the yellow light on. For the sake of simplicity, we assume no failures on the light, i.e., $\texttt {Q}=0$. Notice that, if the environment plays always in this way (signaling a yellow light), then Roborta does not collect rewards (since all rewards in the first row are 0) but also she will never reach the goal and the game never stops. This scenario occurs when the light plays in an unfair way, i.e., an action (the one that turns the green light on) is enabled infinitely often, but it is not executed infinitely often. Assuming fairness over the environment, we can ensure that a green light will be eventually switched on, allowing the robot to move forward.

For the case in which $\texttt {Q}=0$, the best strategy for Roborta when the light is yellow is shown in black arrows on the top-right of each cells with no movement restrictions (restricting cells provide only one choice). As a result, when both players play their optimal strategies, the path taken by Roborta to achieve the goal can be observed in the yellow-highlighted portion of the grid in Fig. 2. In Sect. 5, we evaluate this problem experimentally with different configurations of the game.

Fig. 2.

A robot on a $4 \times 4$ grid

3 Preliminaries

We introduce some basic definitions and results on stochastic games that will be necessary across the paper.

A (discrete) probability distribution $\mu$ over a denumerable set S is a function $\mu : S \rightarrow [0, 1]$ such that $\mu (S) = \sum _{s \in S} \mu (s) = 1$. Let $\mathcal {D}(S)$ denote the set of all probability distributions on S. $\varDelta _s \in \mathcal {D}(S)$ denotes the Dirac distribution for $s \in S$, i.e., $\varDelta _s(s) =1$ and $\varDelta _s(s') = 0$ for all $s' \in S$ such that $s'\ne s$. The support set of $\mu$ is defined by $Supp (\mu ) = \{s |~\mu (s) > 0\}$.

Given a set V, $V^*$ (resp. $V^\infty$) denotes the set of all finite sequences (resp. infinite sequences) of elements of V. Concatenation is represented using juxtaposition. We use variables $\omega , \omega ', \dots \in V^\infty$ as ranging over infinite sequences, and variables $\hat{\omega }, \hat{\omega }', \dots \in V^*$ as ranging over finite sequences. The i-th element of a finite (resp. infinite) sequence $\hat{\omega }$ (resp. $\omega$) is denoted $\hat{\omega }_i$ (resp. $\omega _i$). Furthermore, for any finite sequence $\hat{\omega }$, $|\hat{\omega }|$ denotes its length. For $\omega \in V^\infty$, $\inf (\omega )$ denotes the set of items appearing infinitely often in $\omega$. Given $S \subseteq V^*$, $S^k$ is the set obtained by concatenating k times the sequences in S.

A stochastic game [11, 28] is a tuple $\mathcal {G}= ( V, (V_1, V_2, V_\mathsf {P}), \delta )$, where V is a finite set of vertices (or states) with $V_1, V_2, V_\mathsf {P}\subseteq V$ being a partition of V, and $\delta : V \times V \rightarrow [0,1]$ is a probabilistic transition function, such that for every $v \in V_1\cup V_2$, $\delta (v,v') \in \{0,1\}$, for any $v' \in V$; and $\delta (v,\cdot ) \in \mathcal {D}(V)$ for $v \in V_\mathsf {P}$. If $V_\mathsf {P}= \emptyset$, then $\mathcal {G}$ is called a two-player game graph. Moreover, if $V_1 = \emptyset$ or $V_2 = \emptyset$, then $\mathcal {G}$ is a Markov decision process (or MDP). Finally, in case that $V_1= \emptyset$ and $V_2 = \emptyset$, $\mathcal {G}$ is a Markov chain (or MC). For all states $v \in V$ we define $post ^\delta (v) = \{v' \in V \mid \delta (v,v')>0 \}$, the set of successors of v. Similarly, $pre ^\delta (v') = \{v \in V \mid \delta (v,v')>0 \}$ as the set of predecessors of $v'$, we omit the index $\delta$ when it is clear from context. Also, when useful, we fix an initial state for a game, in such a case we use the notation $\mathcal {G}_v$ to indicate that the game starts from v. Furthermore, we assume that $post (v) \ne \emptyset$ for every $v \in V$. A vertex $v \in V$ is said to be terminal if $\delta (v,v) = 1$, and $\delta (v,v')=0$ for all $v \ne v'$. Most results on MDPs rely on the notion of end component [5], we straightforwardly extend this notion to two-player games: an end component of $\mathcal {G}$ is a pair $(V',\delta ')$ such that (a) $V' \subseteq V$; (b) $\delta '(v) = \delta (v)$ for $v \in V_\mathsf {P}$; (c) $\emptyset \ne post ^{\delta '}(v) \subseteq post ^\delta (v)$ for $v \in V_1 \cup V_2$; (d) $post ^{\delta '}(v) \subseteq V'$ for all $v \in V'$; (e) the underlying graph of $(V',\delta ')$ is strongly connected. Note that an end component can also be considered as being a game. The set of end components of $\mathcal {G}$ is denoted $EC (\mathcal {G})$.

A path in the game $\mathcal {G}$ is an infinite sequence of vertices $v_0 v_1 \dots$ such that $\delta (v_k, v_{k+1})>0$ for every $k \in \mathbb {N}$. $Paths _{\mathcal {G}}$ denotes the set of all paths, and $FPaths _{\mathcal {G}}$ denotes the set of finite prefixes of paths. Similarly, $Paths _{\mathcal {G},v}$ and $FPaths _{\mathcal {G},v}$ denote the set of paths and the set of finite paths starting at vertex v.

A strategy for Player i (for $i\in \{1,2\}$) in a game $\mathcal {G}$ is a function $\pi _{i}: V^* V_i \rightarrow \mathcal {D}(V)$ that assigns a probabilistic distribution to each finite sequence of states such that $\pi _{i}(\hat{\omega }v)(v') > 0$ only if $v' \in post (v)$. The set of all the strategies for Player i is named $\varPi _{i}$. A strategy $\pi _{i}$ is said to be pure or deterministic if, for every $\hat{\omega } v \in V^*V_i$, $\pi _{i}(\hat{\omega } v)$ is a Dirac distribution, and it is called memoryless if $\pi _{i}(\hat{\omega } v) = \pi _{i}(v)$, for every $\hat{\omega } \in V^*$. Let $\varPi ^{\textit{M}}_{i}$ and $\varPi ^{\textit{D}}_{i}$ be respectively the set of all memoryless strategies and the set of all deterministic strategies for Player i. $\varPi ^{\textit{MD}}_{i} = \varPi ^{\textit{M}}_{i} \cap \varPi ^{\textit{D}}_{i}$ is the set of all its deterministic and memoryless strategies.

Given two strategies $\pi _{1} \in \varPi _{1}$, $\pi _{2} \in \varPi _{2}$ and an initial vertex v, the result of the game is a Markov chain [11], denoted $\mathcal {G}^{\pi _{1}, \pi _{2}}_v$. An event $\mathcal {A}$ is a measurable set in the Borel $\sigma$-algebra generated by the cones of $Paths _{\mathcal {G}}$. The cone or cylinder spanned by the finite path $\hat{\omega } \in FPaths _{\mathcal {G}}$ is the set $cyl (\hat{\omega })=\{\omega \in Paths _\mathcal {G}\mid \forall 0 \le i < |\hat{\omega }|: \omega _i = \hat{\omega }_i \}$. $Prob ^{\pi _{1}, \pi _{2}}_{\mathcal {G},v}$ is the associated probability measure obtained when fixing strategies $\pi _{1}$, $\pi _{2}$, and an initial vertex v [11]. Intuitively, $Prob ^{\pi _{1}, \pi _{2}}_{\mathcal {G},v}(\mathcal {A})$ is the probability that strategies $\pi _{1}$ and $\pi _{2}$ generates a path belonging to the set $\mathcal {A}$ when the game $\mathcal {G}$ starts in v. When no confusion is possible, we just write $Prob ^{\pi _{1}, \pi _{2}}_{\mathcal {G},v}(\hat{\omega })$ instead of $Prob ^{\pi _{1}, \pi _{2}}_{\mathcal {G},v}( cyl (\hat{\omega }))$. Similar notations are used for MDPs and MCs. A stochastic game (defined as above) is said to be stopping [14] if for all pair of strategies $\pi _{1}, \pi _{2}$ the probability of reaching a terminal state is 1. We use LTL notation to represent specific set of paths, e.g., $\Diamond T = \{\omega \in Paths _{\mathcal {G}} \mid \exists i \ge 0 : \omega _i \in T \}$ is the set of all the plays in the game that reach vertices in T.

A quantitative objective or payoff function is a measurable function $f: V^{\infty } \rightarrow \mathbb {R}$. Let $\mathbb {E}^{\pi _{1}, \pi _{2}}_{\mathcal {G},v}[f]$ be the expectation of measurable function f under probability $Prob ^{\pi _{1}, \pi _{2}}_{\mathcal {G},v}$. The goal of Player 1 is to maximize this value whereas the goal of Player 2 is to minimize it. Sometimes quantitative objective functions can be defined via rewards. These are assigned by a reward function $r :V \rightarrow \mathbb {R}^+$. We usually consider stochastic games augmented with a reward function. Moreover, we assume that for every terminal vertex v, $r (v) = 0$.

The value of the game for Player 1 at vertex v under strategy $\pi _{1}$ is defined as the infimum over all the values resulting from Player 2 strategies in that vertex, i.e., $\inf _{\pi _{2} \in \varPi _{2}} \mathbb {E}^{\pi _{1}, \pi _{2}}_{\mathcal {G},v}[f]$. The value of the game for Player 1 is defined as the supremum of the values of all Player 1 strategies, i.e., $\sup _{\pi _{1} \in \varPi _{1}} \inf _{\pi _{2} \in \varPi _{2}} \mathbb {E}^{\pi _{1}, \pi _{2}}_{\mathcal {G},v}[f]$. Similarly, the value of the game for a Player 2 under strategy $\pi _{2}$ and the value of the game for Player 2 are defined as $\sup _{\pi _{1} \in \varPi _{1}} \mathbb {E}^{\pi _{1}, \pi _{2}}_{\mathcal {G},v}[f]$ and $\inf _{\pi _{2} \in \varPi _{2}} \sup _{\pi _{1} \in \varPi _{1}} \mathbb {E}^{\pi _{1}, \pi _{2}}_{\mathcal {G},v}[f]$, respectively. We say that a game is determined if both values are the same, that is, $\sup _{\pi _{1} \in \varPi _{1}} \inf _{\pi _{2} \in \varPi _{2}} \mathbb {E}^{\pi _{1}, \pi _{2}}_{\mathcal {G},v}[f] = \inf _{\pi _{2} \in \varPi _{2}} \sup _{\pi _{1} \in \varPi _{1}} \mathbb {E}^{\pi _{1}, \pi _{2}}_{\mathcal {G},v}[f]$. Martin [24] proved the determinacy of stochastic games for Borel and bounded objective functions.

In this paper we focus on the total accumulated reward payoff function, i.e., $\textit{rew}(\omega ) = \sum ^\infty _{i=0} r (\omega _i)$. Since $\textit{rew}$ is unbounded, the results of Martin [24] do not apply to this function. In this paper we restrict ourselves to non-negative rewards, as shown in the next sections, non-negative rewards are enough to deal with interesting case studies, we briefly discuss in Sect. 7 the possible extension of the results presented here to games having negative rewards.

4 Stopping Games and Fair Strategies

We begin this section by introducing the notions of (almost sure) fair strategy and stopping games under fairness. From now on, we assume that Player 2 represents the environment, which tries to minimize the amount of rewards obtained by the system, thus fairness restrictions will be applied to this player.

Definition 1

Given a stochastic game $\mathcal {G}= (V, (V_1, V_2, V_\mathsf {P}), \delta )$. The set of fair plays for Player 2 (denoted $FP ^2$) is defined as follows:

$$ FP ^2 = \{ \omega \in Paths _{\mathcal {G}} \mid \forall v' \in V_2: v' \in \inf (\omega ) \Rightarrow post (v') \subseteq \inf (\omega ) \} $$

Alternatively, if we consider each vertex as a proposition, $FP ^2$ can be written using LTL notation as: $\bigwedge _{v \in V_2} \bigwedge _{v' \in post (v)}(\Box \Diamond v \Rightarrow \Box \Diamond v')$. This property is $\omega$-regular, thus it is measurable in the $\sigma$-algebra generated by the cones of $Paths _{\mathcal {G}}$ (see e.g., [5, p.804]). This is a state-based notion of fairness, but it can be straightforwardly extended to settings where transitions are considered. For the sake of simplicity we do not do so in this paper.

Next, we introduce the notion of (almost-sure) fair strategies for Player 2.

Definition 2

Given a stochastic game $\mathcal {G}= (V, (V_1, V_2, V_\mathsf {P}), \delta )$, a strategy $\pi _{2} \in \varPi _{2}$ is said to be almost-sure fair (or simply fair) iff it holds that: $Prob ^{\pi _{1}, \pi _{2}}_{\mathcal {G},v}( FP ^2) = 1$, for every $\pi _{1} \in \varPi _{1}$ and $v \in V$.

The set of all the fair strategies for Player 2 is denoted by $\varPi ^{\mathcal {F}}_{2}$. We combine this notation with the notation introduced in Sect. 3, e.g., $\varPi ^{\textit{M}\mathcal {F}}_{2}$ refers to the set of all memoryless and fair strategies for Player 2. The previous definition is based on the notion of fair scheduler as introduced for Markov decision processes [5, 7].

Note that for stopping games, every strategy is fair, because the probability of visiting a vertex infinitely often is 0. Also notice that there are games which are not stopping, but they become stopping if Player 2 uses only fair strategies. This is the main idea behind the notion of stopping under fairness as introduced in the following definition.

Definition 3

A stochastic game $\mathcal {G}= (V, (V_1, V_2, V_\mathsf {P}), \delta )$ is said to be stopping under fairness iff for all strategies $\pi _{1} \in \varPi _{1}, \pi _{2} \in \varPi ^{\mathcal {F}}_{2}$ and vertex $v \in V$, it holds that $Prob ^{\pi _{1}, \pi _{2}}_{\mathcal {G},v}(\Diamond T)=1$, where T is the set of terminal vertices of $\mathcal {G}$.

Checking stopping criteria. This section is devoted to the effective characterization of games that are stopping under fairness. The following lemma states that, for every game that is not stopping under fairness, there is a memoryless deterministic strategy for Player 1 and a fair strategy for Player 2 that witnesses it.

Lemma 1

Let $\mathcal {G}= (V, (V_1, V_2, V_\mathsf {P}), \delta )$ be a stochastic game, $v \in V$, and T the set of terminal states of $\mathcal {G}$. If $Prob ^{\pi _{1}, \pi _{2}}_{\mathcal {G}, v}(\Diamond T) < 1$ for some $\pi _{1} \in \varPi _{1}$ and $\pi _{2} \in \varPi ^{\mathcal {F}}_{2}$, then, for some memoryless and deterministic strategy $\pi _{1}' \in \varPi ^{\textit{MD}}_{1}$ and fair strategy $\pi _{2}' \in \varPi ^{\mathcal {F}}_{2}$, $Prob ^{\pi _{1}', \pi _{2}'}_{\mathcal {G}, v}(\Diamond T) < 1$.

The proof of this lemma follows by noticing that, if $Prob ^{\pi _{1}, \pi _{2}}_{\mathcal {G}, v}(\Diamond T) < 1$, there must be a finite path that leads with some probability to an end component not containing a terminal state and which is a trap for the fair strategy $\pi _{2}$. This part of the game enables the construction of a memoryless deterministic strategy for Player 1 by ensuring that it follows the same finite path (but skipping loops) and that it traps Player 2 in the same end component.

The next theorem states that checking stopping under fairness in a stochastic game $\mathcal {G}$ can be reduced to check the stopping criteria in a MDP, which is obtained from $\mathcal {G}$ by fixing a strategy in Player 2 that selects among the output transitions according to a uniform distribution. Thus, this theorem enables a graph solution to determine stopping under fairness.

Theorem 1

Let $\mathcal {G}= (V, (V_1, V_2, V_\mathsf {P}), \delta )$ be a stochastic game and T its set of terminal states. Consider the Player 2 (memoryless) strategy $\pi ^{\mathrm {u}}_{2} : V_2 \rightarrow \mathcal {D}(V)$ defined by $\pi ^{\mathrm {u}}_{2}(v)(v') = \frac{1}{\# post (v)}$, for all $v \in V_2$ and $v' \in post(v)$. Then, $\mathcal {G}$ is stopping under fairness iff $Prob ^{\pi _{1}, \pi ^{\mathrm {u}}_{2}}_{\mathcal {G},v}(\Diamond T)=1$ for every $v\in V$ and $\pi _{1} \in \varPi _{1}$.

While the “only if” part of the theorem is direct, the “if” part is proved by contraposition using Lemma 1.

Theorem 1 introduces an algorithm to check if the stochastic game $\mathcal {G}$ is stopping under fairness: transform $\mathcal {G}$ into the MDP $\mathcal {G}^{\pi ^{\mathrm {u}}_{2}}$ by fixing $\pi ^{\mathrm {u}}_{2}$ in $\mathcal {G}$ and check whether $Prob ^{\pi _{1}}_{\mathcal {G}^{\pi ^{\mathrm {u}}_{2}},v}(\Diamond T)=1$ for all $v\in V$. As a consequence, we have the following theorem.

Theorem 2

Checking whether the stochastic game $\mathcal {G}$ is stopping under fairness or not is in $O( poly ( size (\mathcal {G})))$.

Alternatively, we can use Theorem 1 to provide a direct algorithm on $\mathcal {G}$ and avoiding the construction of the intermediate MDP. The main idea is to use a modification of the standard $pre$ operator, as shown in the following definition:

$$\begin{aligned} \exists Pre _f(C) = {}&\{ v \in V \mid \delta (v,C)> 0\} \\ \forall Pre _f(C) = {}&\{ v \in V_2{\cup } V_\mathsf {P}\mid \delta (v,C)>0\} \cup \{ v \in V_1 \mid \forall v' {\in } V : \delta (v,v') > 0 \Rightarrow v' {\in } C \} \end{aligned}$$

As usual we consider the transitive closures of these operators denoted $\exists Pre _f^*$ and $\forall Pre _f^*$, respectively.

Theorem 3

Let $\mathcal {G}= (V, (V_1, V_2, V_\mathsf {P}), \delta )$, be a stochastic game and let T be the set of its terminal states. Then, (1) $Prob ^{\pi _{1}, \pi _{2}}_{\mathcal {G},v}(\Diamond T) = 1$ for every $\pi _{1} \in \varPi _{1}$ and $\pi _{2} \in \varPi ^{\mathcal {F}}_{2}$ iff $v \in V\setminus \exists Pre _f^*(V \setminus \forall Pre _f^*(T))$, and (2) $\mathcal {G}$ is stopping under fairness iff $\exists Pre _f^*(V \setminus \forall Pre _f^*(T)) = \emptyset$.

Determinacy of Stopping Games under Fairness. The determinacy of stochastic games with Borel and bounded payoff functions follows from Martin’s results [24]. The function $\textit{rew}$ is unbounded, so Martin’s theorems do not apply to it. In [18], the determinacy of a general class of stopping stochastic games (called transient) with total rewards is proven. However, note that we restrict Player 2 to only play with fair strategies and hence, the last result does not apply either. In [26] the authors classify Player 2’s strategies into proper (those ensuring termination) and improper (those prolonging the game indefinitely). For proving determinacy, the authors assume that the value of the game for Player 2’s improper strategies is $\infty$. It is worth noting that, for proving the results below, we do not make any assumption about unfair strategies. In the following we prove that the restriction to fair plays does not affect the determinacy of the games.

Fig. 3.

A roadmap to proving Theorems 4 and 5

Figure 3 shows the dependencies of the lemmas that eventually lead to our main results, namely, Theorem 4, which states that the general problem can be limited to only memoryless and deterministic strategies, and Theorem 5, which establishes determinacy and the correctness of the algorithmic solution through the Bellman equations. To prove Theorem 4 we use the intermidiate notion of semi-Markov strategies [18] and a first step to this reduction is presented in Lemma  2. Lemmas 3 and 4 ensure the transient carachteristics of stopping under fairness problems. They are essential to prove that every possible total reward play yields a solution (Lemma 5). Already approaching Theorem 4, Lemma 6 states that there is always a minimizing fair strategy that is memoryless and deterministic, and Lemma 7 helps to reduce the problem from the domain of semi-Markov strategies to the domain of memoryless deterministic strategies. Using Theorem 4 and Proposition 1, which states that the Bellman equations are well behaved in the lattice of solutions, Theorem 5 is finally proved.

Intuitively, a semi-Markov strategy only takes into account the length of a play, the initial state, and the current state to select the next step in the play.

Definition 4

Let $\mathcal {G}= (V, (V_1, V_2, V_\mathsf {P}), \delta )$ be a stochastic game. A strategy $\pi _{i} \in \varPi _{i}$ is called semi-Markov if: $\pi _{i}(v \hat{\omega }v') = \pi _{i}(v \hat{\omega }'v')$, for every $v \in V$ and $\hat{\omega }, \hat{\omega }' \in V^*$ such that $|\hat{\omega }|=|\hat{\omega }'|$.

Notice that, by fixing an initial state v, a semi-Markov strategy $\pi _{i}$ can be thought of as a sequence of memoryless strategies $\pi _{i}^{0,v}\pi _{i}^{1,v}\pi _{i}^{2,v}\ldots$ where $\pi _{i}(v)=\pi _{i}^{0,v}(v)$ and $\pi _{i}(v\hat{\omega }v')=\pi _{i}^{|\hat{\omega }|+1,v}(v')$. The set of all semi-Markov (resp. semi-Markov fair) strategies for player i is denoted $\varPi ^{\textit{S}}_{i}$ (resp. $\varPi ^{\textit{S}\mathcal {F}}_{i}$).

The importance of semi-Markov strategies lies in the fact that, when Player 2 plays a semi-Markov strategy, any Player 1’s strategy can be mimicked by a semi-Markov strategy as stated in the following lemma.

Lemma 2

Let $\mathcal {G}$ be a stopping under fairness stochastic game, and let $\pi _{2} \in \varPi ^{\textit{S}\mathcal {F}}_{2}$ be a fair and semi-Markov strategy. Then, for any $\pi _{1} \in \varPi _{1}$, there is a semi-Markov strategy $\pi ^*_{1} \in \varPi ^{\textit{S}}_{1}$ such that $\mathbb {E}^{\pi _{1}, \pi _{2}}_{\mathcal {G}, v}[\textit{rew}] = \mathbb {E}^{\pi ^*_{1}, \pi _{2}}_{\mathcal {G}, v}[\textit{rew}]$.

Proof (Sketch)

The proof follows the arguments of Theorem 4.2.7 in [18] adapted to our setting.

Consider the event $\Diamond ^{k} v' = \{ \omega \in Paths _\mathcal {G}\mid \omega _k = v'\}$, for $k\ge 0$. That is, the set of runs in which $v'$ is reached after exactly k steps. We define $\pi ^*_{1}$ as follows. For $v'$ with $Prob ^{\pi _{1}, \pi _{2}}_{\mathcal {G},v}(\Diamond ^k v') > 0$ and $|\hat{\omega }v'| = k$,

$$ \pi ^*_{1}(\hat{\omega }v')(v'') = Prob ^{\pi _{1}, \pi _{2}}_{\mathcal {G},v}(\Diamond ^{k+1} v'' \mid \Diamond ^k v'). $$

For $v'$ with $Prob ^{\pi _{1}, \pi _{2}}_{\mathcal {G},v}(\Diamond ^k v') = 0$ and $|\hat{\omega }v'| = k$ we define $\pi ^*_{1}(\hat{\omega }v')$ to be the uniform distribution on $post (v')$. Notice that $\pi ^*_{1}$ is a semi-Markov strategy. We prove that $\pi ^*_{1}$ is the strategy that satisfies the conclusion of the lemma. For this, we first show that $Prob ^{\pi _{1}, \pi _{2}}_{\mathcal {G},v}(\Diamond ^{k} v') = Prob ^{\pi ^*_{1}, \pi _{2}}_{\mathcal {G},v}(\Diamond ^{k} v')$ by induction on k, and use it to conclude the following.

In a stopping game, all non-terminal states are transient (a state is transient if the expected time that both players spend in it is finite). In fact, [18] defines a stopping game with terminal states in T as a transient game, i.e., a game in which $\sum ^\infty _{N=1} \sum _{\hat{\omega } \in (V \setminus T)^{N}} Prob ^{\pi _{1}, \pi _{2}}_{\mathcal {G},v}(\hat{\omega }) < \infty$ for all strategies $\pi _{1}\in \varPi _{1}$ and $\pi _{2}\in \varPi _{2}$. Obviously, this generality does not hold in our case since unfair strategies make the game dwell infinitely on a set of non-terminal states. Therefore, we prove a weaker property in our setting. Roughly speaking, the next lemma states that, in games that stop under fairness, non-terminal states are transient, provided that the two players play memoryless strategies, and in particular, that Player 2 plays only fair.

Lemma 3

Let $\mathcal {G}= (V, (V_1, V_2, V_\mathsf {P}), \delta )$ be a stochastic game that is stopping under fairness with T being the set of terminal states. Let $\pi _{1} \in \varPi ^{\textit{M}}_{1}$ be a memoryless strategy for Player 1 and $\pi _{2} \in \varPi ^{\textit{M}\mathcal {F}}_{2}$ a memoryless fair strategy for Player 2. Then $\sum ^\infty _{N=1} \sum _{\hat{\omega } \in (V \setminus T)^{N}} Prob ^{\pi _{1}, \pi _{2}}_{\mathcal {G},v}(\hat{\omega }) < \infty$.

This result can be extended to all the strategies of Player 1. The main idea behind the proof is to fix a stationary fair strategy for Player 2 (e.g., a uniform distributed strategy). This yields an MDP that stops for every strategy of Player 1, and furthermore, it can be seen as a one-player transient game (as defined in [18]). Hence, the result follows from Lemma 3 and Theorem 4.2.12 in [18].

Lemma 4

Let $\mathcal {G}$ be a stochastic game that is stopping under fairness and let T be the set of terminal states. In addition, let $\pi _{1} \in \varPi _{1}$ be a strategy for Player 1 and $\pi _{2} \in \varPi ^{\textit{M}\mathcal {F}}_{2}$ be a fair and memoryless strategy for Player 2. Then $\sum ^\infty _{N=0} \sum _{\hat{\omega } \in v(V \setminus T)^N} Prob ^{\pi _{1}, \pi _{2}}_{\mathcal {G},v}(\hat{\omega }) < \infty$.

Using the previous lemma, some fairly simple calculations lead to the fact that the value of the total accumulated reward payoff game is well-defined for any strategy of the players. As a consequence, the value of the game is bounded from above for any Player 1’s strategy. This is stated in the next lemma.

Lemma 5

Let $\mathcal {G}= (V, (V_1, V_2, V_\mathsf {P}), \delta , r )$ be a stochastic game that is stopping under fairness, $\pi _{1} \in \varPi _{1}$ a strategy for Player 1. Then, for all memoryless fair strategy $\pi _{2} \in \varPi ^{\textit{M}\mathcal {F}}_{2}$ for Player 2 and all $v \in V$, $\mathbb {E}^{\pi _{1}, \pi _{2}}_{\mathcal {G},v}[\textit{rew}] < \infty$. Moreover, for every vertex $v \in V$, $\inf _{\pi _{2} \in \varPi ^{\mathcal {F}}_{2}} \mathbb {E}^{\pi _{1}, \pi _{2}}_{\mathcal {G},v}[\textit{rew}] < \infty$.

The following lemma is crucial and plays an important role in the rest of the paper. Intuitively, it states that, when Player 1 plays with a memoryless strategy, Player 2 has an optimal deterministic memoryless fair strategy. This lemma is the guarantee of the eventual existence of a minimizing memoryless deterministic fair strategy for Player 2 in general.

Lemma 6

Let $\mathcal {G}= (V, (V_1, V_2, V_\mathsf {P}), \delta , r )$ be a stochastic game that is stopping under fairness and let $\pi _{1} \in \varPi ^{\textit{M}}_{1}$ be a memoryless strategy for Player 1. There exists a deterministic memoryless fair strategy $\pi ^*_{2}\in \varPi ^{\textit{MD}\mathcal {F}}_{2}$ such that $\inf _{\pi _{2} \in \varPi ^{\mathcal {F}}_{2}} \mathbb {E}^{\pi _{1}, \pi _{2}}_{\mathcal {G},v}[\textit{rew}] = \mathbb {E}^{\pi _{1}, \pi ^*_{2}}_{\mathcal {G},v}[\textit{rew}]$, for every $v \in V$.

Proof (Sketch)

Though it differs in the details, the proof strategy is inspired by the proof of Lemma 10.102 in [5]. We first construct a reduced MDP $\mathcal {G}^{\pi _{1}}_{\min }$ which preserves exactly the optimizing part of the MDP $\mathcal {G}^{\pi _{1}}$. Thus $\delta ^{\pi _{1}}_{\min }(v,v')=\delta ^{\pi _{1}}(v,v')$ if $v\in V_1\cup V_\mathsf {P}$, or $v\in V_2$ and $x_v= r (v)+x_{v'}$, where, for every $v\in V$, $x_v = \inf _{\pi _{2} \in \varPi ^{\mathcal {F}}_{2}} \mathbb {E}^{\pi _{1}, \pi _{2}}_{\mathcal {G},v}[\textit{rew}]$ (which exists due to Lemma 5). Otherwise, $\delta ^{\pi _{1}}_{\min }(v,v')=0$. $\mathcal {G}^{\pi _{1}}_{\min }$ can be proved to be stopping under fairness.

Then, the strategy $\pi ^*_{2}$ for $\mathcal {G}^{\pi _{1}}_{\min }$ is constructed as follows. For every $v\in V$, let ${\Vert {v}\Vert }$ be the length of the shortest path fragment to some terminal vertex in T in the MDP $\mathcal {G}^{\pi _{1}}_{\min }$. Define $\pi ^*_{2}(v)(v')=1$ for some $v'$ such that $\delta ^{\pi _{1}}_{\min }(v,v')=1$ and ${\Vert {v}\Vert }={\Vert {v'}\Vert }+1$. By definition, $\pi ^*_{2}$ is memoryless. We prove first that $\pi ^*_{2}$ yields the optimal solution of $\mathcal {G}^{\pi _{1}}$ by showing that the vector $(x_v)_{v\in V}$ (i.e., the optimal values of $\mathcal {G}^{\pi _{1}}$) is a solution to the set of equations for expected rewards of the Markov chain $\mathcal {G}^{\pi _{1},\pi ^*_{2}}$. Being the solution unique, we have that $x_v=\mathbb {E}^{}_{\mathcal {G}^{\pi _{1},\pi ^*_{2}},v}[\textit{rew}]$ for all $v\in V$ and hence the optimality of $\pi ^*_{2}$. To conclude the proof we show by contradiction that $\pi ^*_{2}$ is fair.    $\square$

As already noted, semi-Markov strategies can be thought of as sequences of memoryless strategies. The next lemma uses this fact to show that, when Player 2 plays a memoryless and fair strategy, semi-Markov strategies do not improve the value that Player 1 can obtain via memoryless deterministic strategies. The proof of the following lemma adapts the ideas of Theorem 4.2.9 in [18] to our games.

Lemma 7

For any stochastic game $\mathcal {G}$ that is stopping under fairness, and vertex v, it holds that:

$$\sup _{\pi _{1} \in \varPi ^{\textit{S}}_{1}} \inf _{\pi _{2} \in \varPi ^{\textit{MD}\mathcal {F}}_{2}} \mathbb {E}^{\pi _{1}, \pi _{2}}_{\mathcal {G},v}[\textit{rew}] = \sup _{\pi _{1} \in \varPi ^{\textit{MD}}_{1}} \inf _{\pi _{2} \in \varPi ^{\textit{MD}\mathcal {F}}_{2}} \mathbb {E}^{\pi _{1}, \pi _{2}}_{\mathcal {G},v}[\textit{rew}] $$

Using the previous lemma, we can conclude that the problem of finding $\sup _{\pi _{1} \in \varPi _{1}} \inf _{\pi _{2} \in \varPi ^{\mathcal {F}}_{2}} \mathbb {E}^{\pi _{1}, \pi _{2}}[\textit{rew}]$, for any vertex v, can be solve by only focusing on deterministic memoryless strategies as stated and proved in the following theorem.

Theorem 4

For any stochastic game $\mathcal {G}$ that is stopping under fairness we have:

$$ \sup _{\pi _{1} \in \varPi _{1}} \inf _{\pi _{2} \in \varPi ^{\mathcal {F}}_{2}} \mathbb {E}^{\pi _{1}, \pi _{2}}_{\mathcal {G},v}[\textit{rew}] = \sup _{\pi _{1} \in \varPi ^{\textit{MD}}_{1}} \inf _{\pi _{2} \in \varPi ^{\textit{MD}\mathcal {F}}_{2}} \mathbb {E}^{\pi _{1}, \pi _{2}}_{\mathcal {G},v}[\textit{rew}] $$

Proof

First, we prove that the left-hand term is less than or equal to the right-hand one:

$$\begin{aligned} \sup _{\pi _{1} \in \varPi _{1}} \inf _{\pi _{2} \in \varPi ^{\mathcal {F}}_{2}} \mathbb {E}^{\pi _{1}, \pi _{2}}_{\mathcal {G},v}[\textit{rew}]&{} \le \sup _{\pi _{1} \in \varPi _{1}} \inf _{\pi _{2} \in \varPi ^{\textit{MD}\mathcal {F}}_{2}} \mathbb {E}^{\pi _{1}, \pi _{2}}_{\mathcal {G},v}[\textit{rew}]\\&{} \le \sup _{\pi _{1} \in \varPi ^{\textit{S}}_{1}} \inf _{\pi _{2} \in \varPi ^{\textit{MD}\mathcal {F}}_{2}} \mathbb {E}^{\pi _{1}, \pi _{2}}_{\mathcal {G},v}[\textit{rew}]\\&{}\le \sup _{\pi _{1} \in \varPi ^{\textit{MD}}_{1}} \inf _{\pi _{2} \in \varPi ^{\textit{MD}\mathcal {F}}_{2}} \mathbb {E}^{\pi _{1}, \pi _{2}}_{\mathcal {G},v}[\textit{rew}]. \end{aligned}$$

The first inequality follows from $\varPi ^{\textit{MD}\mathcal {F}}_{2} \subseteq \varPi ^{\mathcal {F}}_{2}$, the second inequality is due to Lemma 2 and the fact that memoryless strategies are semi-Markov, and the last inequality is obtained by applying Lemma 7.

To prove the other inequality, we calculate:

$$\begin{aligned} \sup _{\pi _{1} \in \varPi ^{\textit{MD}}_{1}} \inf _{\pi _{2} \in \varPi ^{\textit{MD}\mathcal {F}}_{2}} \mathbb {E}^{\pi _{1}, \pi _{2}}_{\mathcal {G},v}[\textit{rew}]&{} = \sup _{\pi _{1} \in \varPi ^{\textit{MD}}_{1}} \inf _{\pi _{2} \in \varPi ^{\mathcal {F}}_{2}} \mathbb {E}^{\pi _{1}, \pi _{2}}_{\mathcal {G},v}[\textit{rew}] \\&{} \le \sup _{\pi _{1} \in \varPi _{1}} \inf _{\pi _{2} \in \varPi ^{\mathcal {F}}_{2}} \mathbb {E}^{\pi _{1}, \pi _{2}}_{\mathcal {G},v}[\textit{rew}]. \end{aligned}$$

The first equality is a consequence of Lemma 6 and the second inequality is due to properties of suprema.    $\square$

The standard technique to prove the determinacy of stopping games is by showing that the Bellman operator

$$ \varGamma (f)(v) = {\left\{ \begin{array}{ll} r (v) + \mathop {\sum }\nolimits _{v' \in post (v)} \delta (v,v') f(v') &{} \text { if } v \in V_\mathsf {P}\setminus T \\ \max \{ r (v) + f(v') \mid v' \in post (v) \}&{} \text { if } v \in V_1 \setminus T, \\ \min \{ r (v) + f(v') \mid v' \in post (v) \} &{} \text { if } v \in V_2 \setminus T, \\ 0 &{} \text { if } v \in T. \end{array}\right. } $$

has a unique fixpoint. However, in the case of games stopping under fairness, $\varGamma$ has several fixpoints as shown by the next example.

Fig. 4.

A game with infinite fixpoints

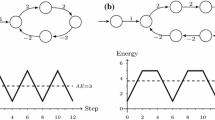
Example 1. Consider the (one-player) game in Fig. 4, where Player 1’s vertices are drawn as boxes, Player 2’s vertices are drawn as diamonds, and probabilistic vertices are depicted as circles. Note that, in that game, the greatest fixpoint is (1, 1, 1, 0). Yet, (0.5, 0.5, 1, 0) is also a fixpoint as $\varGamma (0.5,0.5,1,0) = (0.5,0.5,1,0)$. In fact, the Bellman operator for this game has infinite fixpoints: any f of the form (x, x, 1, 0) with $x\in [0,1]$.

Thus, the standard approach cannot be used here. Instead, we use the greatest fixpoint for proving determinacy, but this cannot be done directly on $\varGamma$. A main difficulty is that the Knaster-Tarski theorem does not apply for $\varGamma$ since $(\mathbb {R}^V, \le )$ is not a complete lattice. Using instead the extended reals ($(\mathbb {R} \cup \{\infty \})^V$) is not a solution, as in some cases the greatest fixpoint will assign $\infty$ to some vertices (e.g., $(\infty ,\infty ,0)$ would be the greatest fixpoint in the Markov chain of Fig. 5). One possible approach is to approximate the greatest fixpoint from an estimated upper bound via value iteration. Unfortunately, there may not be an order relation between f and $\varGamma (f)$ and it may turn out that for some vertex v, $\varGamma (f)(v)>f(v)$ before converging to the fixpoint. This is shown in the next example.

Example 2. Consider the game depicted in Fig. 5. The (unique) fixpoint in this case is (100, 90, 0). Observe that, we have that $\varGamma (120,100,0) = (110, 108, 0)$, thus the value at $v_1$ increases after one iteration. Several iterations are needed then to reach the greatest fixpoint. Thus, in general, starting value iteration from an estimated upper bound does not guarantee a monotone convergence to the greatest fixpoint.

Fig. 5.

A game where value iteration may go up

We overcome the aforementioned issues by using a modified version of $\varGamma$. Roughly speaking, we modify the Bellman operator in such a way that it operates over a complete lattice.

Notice that, by Lemma 5, the value $\mathbb {E}^{\pi _{1}, \pi _{2}}_{\mathcal {G},v}[\textit{rew}]$ is finite for every stopping game under fairness $\mathcal {G}$ and strategies $\pi _{1} \in \varPi ^{\textit{MD}}_{1}$, $\pi _{2} \in \varPi ^{\textit{MD}\mathcal {F}}_{2}$. Furthermore, because the number of deterministic memoryless strategies is finite, we also have that the number $\max \{ \inf _{\pi _{2} \in \varPi ^{\textit{MD}\mathcal {F}}_{2}} \sup _{\pi _{1} \in \varPi ^{\textit{MD}}_{1}} \mathbb {E}^{\pi _{1}, \pi _{2}}_{\mathcal {G},v}[\textit{rew}] \mid v \in V \}$ is well defined. From now on, fix a number $\mathbf {U}\ge \max \{ \inf _{\pi _{2} \in \varPi ^{\textit{MD}\mathcal {F}}_{2}} \sup _{\pi _{1} \in \varPi ^{\textit{MD}}_{1}} \mathbb {E}^{\pi _{1}, \pi _{2}}_{\mathcal {G},v}[\textit{rew}] \mid v \in V \}$. We define a modified Bellman operator $\varGamma ^*: [0,\mathbf {U}]^V \rightarrow [0,\mathbf {U}]^V$ as follows.

$$ \varGamma ^*(f)(v) = {\left\{ \begin{array}{ll} \min \big ( r (v) + \mathop {\sum }\nolimits _{v' \in post (v)} \delta (v,v') f(v'), \ \mathbf {U}\ \big ) &{} \text { if } v \in V_\mathsf {P}\setminus T \\ \min \big ( \max \{ r (v) + f(v') \mid v' \in post (v) \}, \ \mathbf {U}\ \big )&{} \text { if } v \in V_1 \setminus T, \\ \min \big ( \min \{ r (v) + f(v') \mid v' \in post (v) \}, \ \mathbf {U}\ \big ) &{} \text { if } v \in V_2 \setminus T, \\ 0 &{} \text { if } v \in T. \end{array}\right. } $$

Note that $\varGamma ^*$ is monotone, which can be proven by observing that maxima, minima and convex combinations are all monotone operators. Furthermore, $\varGamma ^*$ is also Scott continuous (it preserves suprema of directed sets), this can be proven similarly as in [10]. The following proposition formalizes these properties.

Proposition 1

$\varGamma ^*$ is monotone and Scott-continuous.

Note that $([0,\mathbf {U}]^V, \le )$ is a complete lattice. Thus by Proposition 1 and the Knaster-Tarski theorem [15], the (non-empty) set of fixed points of $\varGamma ^*$ forms a complete lattice, and the greatest fixpoint of the operator can be approximated by successive applications of $\varGamma ^*$ to the top element (i.e., $\mathbf {U}$) [15]. In the following we denote by $\nu \varGamma ^*$ the greatest fixed point of $\varGamma ^*$.

The following theorem states that games restricted to fair strategies on Player 2 are determinate. Furthermore, the value of the game is given by the greatest fixpoint of $\varGamma ^*$.

Theorem 5

Let $\mathcal {G}$ be a stochastic game that is stopping under fairness. It holds that:

$$\inf _{\pi _{2} \in \varPi ^{\mathcal {F}}_{2}} \sup _{\pi _{1} \in \varPi _{1}} \mathbb {E}^{\pi _{1}, \pi _{2}}_{\mathcal {G},v}[\textit{rew}] = \sup _{\pi _{1} \in \varPi _{1}} \inf _{\pi _{2} \in \varPi ^{\mathcal {F}}_{2}} \mathbb {E}^{\pi _{1}, \pi _{2}}_{\mathcal {G},v}[\textit{rew}] = \nu \varGamma ^*(v) $$

Proof

First, note that $\inf _{\pi _{2} \in \varPi ^{\textit{MD}\mathcal {F}}_{2}} \sup _{\pi _{1} \in \varPi ^{\textit{MD}}_{1}} \mathbb {E}^{\pi _{1}, \pi _{2}}_{\mathcal {G},v}[\textit{rew}]$ is a fixed point of $\varGamma ^*$. Thus we have:

$$\begin{aligned} \sup _{\pi _{1} \in \varPi _{1}} \inf _{\pi _{2} \in \varPi ^{\mathcal {F}}_{2}} \mathbb {E}^{\pi _{1}, \pi _{2}}_{\mathcal {G},v}[\textit{rew}]&\le \inf _{\pi _{2} \in \varPi ^{\mathcal {F}}_{2}} \sup _{\pi _{1} \in \varPi _{1}} \mathbb {E}^{\pi _{1}, \pi _{2}}_{\mathcal {G},v}[\textit{rew}] \\&\le \inf _{\pi _{2} \in \varPi ^{\textit{MD}\mathcal {F}}_{2}} \sup _{\pi _{1} \in \varPi ^{\textit{MD}}_{1}} \mathbb {E}^{\pi _{1}, \pi _{2}}_{\mathcal {G},v}[\textit{rew}] \le \nu \varGamma ^*(v) \end{aligned}$$

for any v. The first inequality is a standard property of suprema and infima [21], the second inequality holds because $\varPi ^{\textit{MD}\mathcal {F}}_{2} \subseteq \varPi ^{\mathcal {F}}_{2}$ and standard properties of MDPs: by fixing a deterministic memoryless fair strategy for Player 2 we obtain a transient MDP, the optimal strategy for Player 1 in this MDP is obtained via a deterministic memoryless strategy [20]. The last inequality holds because $\inf _{\pi _{2} \in \varPi ^{\textit{MD}\mathcal {F}}_{2}} \sup _{\pi _{1} \in \varPi ^{\textit{MD}}_{1}} \mathbb {E}^{\pi _{1}, \pi _{2}}_{\mathcal {G},v}[\textit{rew}]$ is a fixpoint of $\varGamma ^*$.

Rest to prove that $\sup _{\pi _{1} \in \varPi _{1}} \inf _{\pi _{2} \in \varPi ^{\mathcal {F}}_{2}} \mathbb {E}^{\pi _{1}, \pi _{2}}_{\mathcal {G},v}[\textit{rew}] \ge \nu \varGamma ^*(v)$. Note that, if there is $\pi _{1} \in \varPi _{1}$ such that $\inf _{\pi _{2} \in \varPi ^{\mathcal {F}}_{2}} \mathbb {E}^{\pi _{1}, \pi _{2}}_{\mathcal {G},v}[\textit{rew}] \ge \nu \varGamma ^*(v)$ the property above follows by properties of supremum. Consider the strategy $\pi ^*_{1}$ defined as follows: $\pi ^*_{1}(v) \in \mathop {\mathrm {argmax}}\limits \{\nu \varGamma ^*(v') + r (v) \mid v' \in post (v) \}$. Note that $\pi ^*_{1}$ is a memoryless and deterministic strategy. For any memoryless, deterministic and fair strategy $\pi _{2} \in \varPi ^{\textit{MD}\mathcal {F}}_{2}$ we have $\nu \varGamma ^*(v) \le \mathbb {E}^{\pi ^*_{1}, \pi _{2}}_{\mathcal {G},v}[\textit{rew}]$ (by definition of $\varGamma ^*$). Thus, $\nu \varGamma ^*(v) \le \inf _{\pi _{2} \in \varPi ^{\textit{MD}\mathcal {F}}_{2}} \mathbb {E}^{\pi ^*_{1}, \pi _{2}}_{\mathcal {G},v}[\textit{rew}]$ and then: $\nu \varGamma ^*(v) \le \sup _{\pi _{1} \in \varPi ^{\textit{MD}}_{1}} \inf _{\pi _{2} \in \varPi ^{\textit{MD}\mathcal {F}}_{1}} \mathbb {E}^{\pi _{1}, \pi _{2}}_{\mathcal {G},v}[\textit{rew}]$. Finally, by Theorem 4 we get: $\nu \varGamma ^*(v) \le \sup _{\pi _{1} \in \varPi _{1}} \inf _{\pi _{2} \in \varPi ^{\mathcal {F}}_{2}} \mathbb {E}^{\pi _{1}, \pi _{2}}_{\mathcal {G},v}[\textit{rew}]$.    $\square$

Considerations for an algorithmic solution. Value iteration [9] has been used to compute maximum/minimum expected accumulated reward in MDPs, e.g., in the PRISM model checker. Usually, the value is computed by approximating the least fixpoint from below using the Bellman equations [9]. In [6], the authors propose to approach these values from both a lower and an upper bound (known as interval iteration [19]). To do so, [6] shows a technique for computing upper bounds for the expected total rewards for MDPs. This approach is based on the fact that, given a stopping MDP $\mathcal {G}$, $\mathbb {E}^{\pi _{1}}_{\mathcal {G},v}[\textit{rew}] = \sum _{v' \in R(v)} \zeta _v^{\pi _{1}}(v')* r (v')$, where R(v) denotes the set of reachable states from v, and $\zeta _v^{\pi _{1}}(v')$ denotes the expected number of times to visit $v'$ in the Markov chain induced by $\pi _{1}$ when starting at v. [6] describes how to compute a value $\zeta _{v}^*(v')$, such that $\zeta _v^*(v') \ge \sup _{\pi _{1} \in \varPi _{1}} \zeta _v^{\pi _{1}}(v')$. Thus, $\sum _{v' \in R(v)} \zeta _v^{*}(v')* r (v')$ gives an upper bound for $\sup _{\pi _{1}} \mathbb {E}^{\pi _{1}}_{\mathcal {G},v}[\textit{rew}]$. Our algorithm uses these ideas to provide an upper bound for two-player games. Roughly speaking, the above defined functional $\varGamma ^*$ presents a form of Bellman equations that enables a value iteration algorithm to solve these games. We need to start with some value vector larger than such a fixpoint. Given a stopping under fairness game, we fix a (memoryless) fair strategy for the environment, thus obtaining an MDP. We then use the techniques described above to find an

upper bound for this MDP, which in turn is an upper bound in the original game. The obvious fair strategy to use is the one based on the uniform distribution (as in Theorem 1). This idea is described in Algorithm 1. It is worth noting that, instead of using a unique upper bound for every vertex (as in the definition of $\varGamma ^*$), the algorithm may use a different upper bound for each component of the value vector, this improves the number of iterations performed by the algorithm. We have implemented Algorithm 1 as a prototype embedded in the PRISM-games toolset [22], as described in the next section.

5 Experimental Validation

In order to evaluate the viability of our approach we have extended the model checker PRISM [22, 23] with an operator to compute the expected rewards for stochastic games that stop under fairness. The prototype also allows one to check whether a game is stopping under fairness. The tool takes as input a model describing the game in PRISM notation and returns as output the optimal expected total reward for a given initial state as well as the synthesized optimal controller strategy (under fairness assumptions). The experimental evaluation shows that our approach can cope with non-trivial case studies. For computing these values we set a relative error of at most $\varepsilon = 10^{-6}$.

Roborta vs. the Fair Light. Table 1 shows the results of the example introduced in Sect. 2 for multiple configurations. We considered three variants of the case study: version A (the light does not fail), version B (the light can only fail when trying to signal a green light), and version C (the light can fail when trying to signal any kind of light). We assumed that, when Roborta fails, she cannot move (this is beneficial to Roborta since she can re-collect the reward); when the light fails, the robot can freely move into any allowed direction. The grid configuration (movement restrictions and rewards) are randomly generated. For each setting, Table 1 describes the results for three different scenarios generated starting at different seeds. For the grid configuration shown in Sect. 2 with parameters $P=0.1$ and $Q=0$, the tool derived the optimal strategy depicted in Fig. 2 and reports an expected total reward of 5.55.

Fig. 6.

UAV Network for ISR missions adapted from [17]

Autonomous UAV vs. Human Operator. We adapted the case study analyzed in [17]. A remotely controlled Unmanned Aerial Vehicle (UAV) is used to perform intelligence, surveillance, and reconnaissance (ISR) missions over a road network. The UAV performs piloting functions autonomously (selecting a path to fly between waypoints). The human operator (environment) controls the onboard sensor to capture imagery at a waypoint as well as the piloting functions on certain waypoints (called checkpoints). Note that an operator can continuously try to get a better image by making the UAV loiter around a certain waypoint, this may lead to an unfair behavior. Each successful capture from an unvisited waypoint grants a reward. Figure 6 shows an example of road network consisting of six surveillance waypoints labeled $w_0,w_2,...,w_5$, the edges represent connecting paths, a red-dashed line means that the path is dangerous enough to make the UAV stop working with probability 1, while on any other path, this probability is S. Checkpoints are depicted as pink nodes, therein the operator can still delegate the piloting task to the UAV with probability D. Each node is annotated with three possible rewards. For instance, for $S=0.3$ and $D=0.5$ and the leftmost reward values in each triple, the synthesized strategy for the UAV tries to follow the optimal circuit $w_0,w_1,w_2,w_3,w_4,w_5$. While for the middle and rightmost reward values, the optimal circuits to follow are $w_0,w_5,w_0,w_1,w_2,w_3,w_4$ and $w_0,w_5,w_4,w_1,w_2,w_3$, respectively. Table 2 shows the results obtained for this game for several randomly generated road networks.

Tables 1 and 2 do not report the time taken to compute the results, but in all cases the output was computed in less than 400 s.All the experiments were run on a MacBook Air with Intel Core i5 at 1.3 GHz and 4 Gb of RAM.

Table 1. Results for Roborta vs. Light Game. First column describes the grid size. Second column indicates the fault probability for the robot (P) and light (Q). The other columns describe the size of the model, the expected total reward for the optimal strategy, and the number of iterations performed, respectively, for three different randomly generated grid configurations.

Table 2. Results for the UAV vs. Operator Game. First column describes the number of waypoints used. Second column indicates probability of delegation (D), and the probability that the UAV stops working (S). The other columns show the size of the model, the expected total reward for the optimal strategy, and the number of iterations performed, respectively, for three different randomly generated roadmap configurations.

6 Related Work

Stochastic games with payoff functions have been extensively investigated in the literature. In [18], several results are presented about transient games, a generalized version of stopping stochastic games with total reward payoff. In transient games, both players possess optimal (memoryless and deterministic) strategies. Most importantly, the games are determined and their value can be computed as the least fixed point of a set of equations. Most of these results are based on the fact that the $\varGamma$ functional (see Sect. 4) for transient games has a unique fixed point. Notice that in this paper we have dealt with games that are stopping only under fairness assumptions. Thus, the corresponding functional may have several fixed points. Hence, the main results presented in [18] do not apply to our setting.

[12] and [28] present logical frameworks for the verification and synthesis of systems. While [12] provides a solution for a probabilistic branching temporal logic extended with expected total, discounted, and average reward objective functions, [28] does the same in a similar extension of a probabilistic linear temporal logic. Both frameworks were implemented in the tool PRISM [22, 23]. Although a vast class of properties can be expressed in these frameworks, none of them are presented under fair environments. In fact, these works are on stochastic multiplayer games in which each player is treated equally.

However, of all the operators in [12, 22, 28], $\langle \langle p_1 \rangle \rangle \ \textsf {R}_{\text {max}{=}?}[\textsf {F}^{\infty } T]$ is the closest to our proposal and it deserves a deeper comparison. $\langle \langle p_1 \rangle \rangle \ \textsf {R}_{\text {max}{=}?}[\textsf {F}^{\infty } T]$ returns the expected accumulated reward until reaching T in which infinite plays receive an infinite value [12, 22]. PRISM approximates this value by computing a greatest fixpoint. It uses a two-phase algorithm to do so: (i) it first replaces zero rewards with a small positive value and applies value iteration on this modification to get an estimated upper bound, and (ii) this upper bound is used to start another value iteration process aimed to compute the greatest fixpoint. This heuristic could return erroneous approximations of the greatest fixpoint. We illustrate this with a simple example. Consider the game depicted in Fig. 7, For any $\textsf {p}$, the value of the greatest fixpoint in vertex $v_0$ is 2. However, by taking $\textsf {p}=0.99$ and tolerance $\epsilon =10^{-6}$, PRISM returns a value close to 39608. This occurs because PRISM changes 0 to the value 0.02, which results in an extremely large upper bound. Obviously, it also returns an incorrect strategy for vertex $v_0$. We have checked this example with our tool, and it returned the correct value for vertex $v_0$ in 2 iterations, regardless of the value of $\textsf {p}$. We have chosen a large value for $\textsf {p}$ to make the difference noticeable. Small values also may produce different values in, e.g., $\textsf {v}_1$ only that it could be blamed on approximation errors. We have also run this operator on our case studies and observed small differences in many of them (particularly on Roborta) that get larger when the fault probabilities get larger as well.

Fig. 7.

A simple two-player game: only probability less than 1 are shown

Stochastic shortest path games [26] are two-player stochastic games with (negative or positive) rewards in which the minimizer’s strategies are classified into proper and improper, proper strategies are those ensuring termination. As proven in [26], these games are determined, and both players posses memoryless optimal strategies. To prove these results, the authors assume that the expected game value for improper strategies is $\infty$, this ensures that the corresponding functional is a contraction and thus it has a unique fixpoint. In contrast, we restrict ourselves to non-negative rewards but we do not make any assumptions over unfair strategies, as mentioned above the corresponding functional for our games may have several fixpoints. Furthermore, we proved that the value of the game is given by the greatest fixpoint of $\varGamma$. In recent years, several authors have investigated stochastic shortest path problems for MDPs (i.e., one-player games), where the assumption over improper strategies is relaxed (e.g., [3]); to the best of our knowledge, these results have not be extended to two-player games.

In [4] the authors tackle the problem of synthesizing a controller that maximizes the probability of satisfying an LTL property. Fairness strategies are used to reduce this problem to the synthesis of a controller maximizing a PCTL property over a product game. However, this article does not address expected rewards and game determinacy under fairness assumptions.

Interestingly, in [2] the authors consider the problem of winning a (non-stochastic) two-player games with fairness assumptions over the environment. The objective of the system is to guarantee an $\omega$-regular property. The authors show that winning in these games is equivalent to almost-sure winning in a Markov decision process. It must be noted that this work only considers non-stochastic games. Furthermore, payoff functions are not considered therein.

Finally, we remark that in qualitative $\omega$-regular stochastic games [1] strong fairness can easily be consider by properly transforming the original $\omega$-regular objective. Notably, in this setting, [8] shows that qualitative Rabin conditions on stochastic games can be solved by translating this problem into a two-player (non-stochastic) game with the same Rabin condition under extreme fairness following a somewhat inverse direction to that we used to prove Theorem 2.

7 Concluding Remarks

In this paper, we have investigated the properties of stochastic games with total reward payoff under the assumption that the minimizer (i.e., the environment) plays only with fair strategies. We have shown that, in this scenario, determinacy is preserved and both players have optimal memoryless and deterministic strategies; furthermore, the value of the game can be calculated by approximating a greatest fixed point of a Bellman operator. We have only considered non-negative rewards in this paper. A possible way of extending the results presented here to games with negative rewards is to adapt the techniques presented in [3] for MDPs with negative costs, we leave this as a further work.

In order to show the applicability of our technique, we have presented two examples of applications and an experimental validation over diverse instances of these case studies using our prototype tool. We believe that fairness assumptions allow one to consider more realistic behavior of the environment.

We have not investigated other common payoff functions such as discounted payoff or limiting-average payoff. A benefit of these classes of functions is that the value of games are well-defined even when the games are not stopping. At first sight, the notion of fairness is little relevant for games with discounted payoff, since these kinds of payoff functions take most of their value from the initial parts of runs. For limiting-average the situation is different, and fairness assumptions may be relevant as they could change the value of games, we leave this as further work.