Abstract
Workflow nets are a well-established mathematical formalism for the analysis of business processes arising from either modeling tools or process mining. The central decision problems for workflow nets are k-soundness, generalised soundness and structural soundness. Most existing tools focus on k-soundness. In this work, we propose novel scalable semi-procedures for generalised and structural soundness. This is achieved via integral and continuous Petri net reachability relaxations. We show that our approach is competitive against state-of-the-art tools.
An extended version of this paper with an appendix containing the missing proofs can be obtained from https://arxiv.org/abs/2206.02606.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others


1 Introduction
Workflow nets are a well-established mathematical formalism for the description of business processes arising from software modelers and process mining (e.g., see [2, 3]), and further notations such as UML activity diagrams [4]. More precisely, a workflow net consists of places that contain resources, and transitions that can consume, create and move resources concurrently. Two designated places, denoted \(\mathsf {i} \) and \(\mathsf {f} \), respectively model the initialization and completion of a process. Workflow nets, which form a subclass of Petri nets, enable the automatic formal verification of business processes. For example, 1-soundness states that from the initial configuration \(\{\mathsf {i} :1\}\), every reachable configuration can reach the final configuration \(\{\mathsf {f} :1\}\). Informally, this means that given any partial execution of a business process, it is possible to complete it properly.
Soundness. The main decision problems concerning workflow nets revolve around soundness properties. The generalisation of 1-soundness to several resources is k-soundness. It asks whether from \(\{\mathsf {i} :k\}\), every reachable configuration can reach \(\{\mathsf {f} :k\}\) (here, \(\{p :k\}\) indicates that place p contains k resources). Intuitively, 1-soundness guarantees that every initialised process terminates, and k-soundness guarantees that k initialised processes working in parallel will all terminate (see e.g. [1, 2]). Generalised soundness asks whether k-soundness holds for all \(k \ge 1\). Unlike k-soundness, generalised soundness preserves desirable properties like composition and has other desirable properties for business applications [20]. Structural soundness is the existential counterpart of generalised soundness, i.e. it asks whether k-soundness holds for some \(k \ge 1\). Structural soundness gives information on how many processes can be controlled in parallel [31], moreover, by applying results about structural soundness, one can compute the set of all k for which the workflow net is k-sound [9, Section 7].
These problems are all decidable [1, 21, 31], but with high complexity: either PSPACE- or EXPSPACE-complete [9]. Most of the (software) tools focus on k-soundness, with an emphasis on \(k = 1\). Existing algorithms for generalised and structural soundness rely on Petri net reachability [19, 21, 31], which was recently shown Ackermann-complete [13, 24], so not primitive recursive. In this work, we describe novel scalable semi-procedures for generalised and structural soundness.
We focus on “negative instances”, i.e. where soundness does not hold. Let us motivate this. It is known that given a workflow net \(\mathcal {N}\), one can iteratively apply simple reduction rules to \(\mathcal {N}\). The resulting workflow net \(\mathcal {N}'\) is sound iff \(\mathcal {N}\) is as well [10, 22]. In practice, one infers that \(\mathcal {N}\) is sound from the fact that \(\mathcal {N}'\) has been reduced to a trivial workflow net where only \(\mathsf {i} \) and \(\mathsf {f} \) remain. However, if \(\mathcal {N}\) is not sound, one obtains some nontrivial \(\mathcal {N}'\) that must be verified via some other approach such as model checking. In this work, we provide algorithmic building blocks for this case, where state-space exploration is prohibitive.
Relaxations. This is achieved by considering two reachability relaxations, namely integer reachability and continuous reachability. As their name suggests, these two notions relax some forbidden behaviour of workflow nets. Informally, integer reachability allows for the amount of resources to become temporarily negative, while continuous reachability allows the fragmentation of resources into pieces. Such relaxations possibly introduce spurious behaviour, but enjoy significantly better algorithmic properties (e.g., see [7]). For example, they have been successfully employed for the verification of multi-threaded program skeletons [5, 8, 15].
Generalised Soundness. Based on these relaxations, we provide two necessary conditions for generalised soundness: integer boundedness and continuous soundness. The former states that the state-space of a given workflow net is bounded (from above) even under integer reachability. The latter states that a given workflow net is 1-sound under continuous reachability. We show the following for integer boundedness and continuous soundness:
-
Well-established classical reduction rules preserve both properties;
-
Integer boundedness is testable in polynomial time, and continuous soundness is coNP-complete;
-
From a practical viewpoint, they are respectively translatable into instances of linear programming and linear arithmetic (which can be solved efficiently by dedicated tools such as SMT solvers);
-
Under a mild computational assumption, continuous soundness implies integer boundedness.
Thus, altogether, in order to check whether a workflow net \(\mathcal {N}\) is generalised unsound, one may first use classical reduction rules to obtain a smaller workflow net \(\mathcal {N}'\); test integer unboundedness in polynomial time; and, if needed, move onto testing continuous unsoundness.
The fact that continuous reachability can be used to semi-decide generalised soundness is arguably surprising. Using the notation of computation temporal logic (CTL), k-soundness can be rephrased as \(\{\mathsf {i} :k\} \models \forall \mathsf {G}\, \exists \mathsf {F}\, \{\mathsf {f} :k\}\). Some other well-studied properties have a similar structure, e.g. liveness and home-stateness amount to “\(\mathbf {m}_\text {init} \models \bigwedge _{t \in T} \forall \mathsf {G}\, \exists \mathsf {F}\, (t~\text {is enabled})\)” and “\(\mathbf {m}_\text {init} \models \forall \mathsf {G}\, \exists \mathsf {F}\, \mathbf {m}_\text {home}\)”. It is known that liveness, home-stateness, and other properties such as boundedness and inclusion, cannot be approximated continuously [8, Sect. 4]. Yet, generalised soundness quantifies k-soundness universally, and this enables a continuous over-approximation. Consequently, we provide a novel application of continuous relaxations for the efficient verification of properties beyond reachability.
Structural Soundness. The authors of [31] have observed that a property called structural quasi-soundness is a necessary condition for structural soundness. The former states that \(\{\mathsf {i} :k\}\) can reach \(\{\mathsf {f} :k\}\) for some \(k \ge 1\). In [31], structural quasi-soundness is reduced to Petri net reachability, which has non primitive recursive complexity. In this work, we show that structural quasi-soundness can be rephrased as continuous reachability. Since the latter can be tested in polynomial time [18], or alternatively via SMT solving [8], this vastly improves the practicability of structural quasi-soundness. We further show that this approach can be adapted so that it provides a lower bound on the first k such that \(\{\mathsf {i} :k\}\) can reach \(\{\mathsf {i} :f\}\). From a practical point of view, this is useful as it can vastly reduce the number of reachability queries to decide structural soundness.
Free-Choice Nets. Many real-world workflow nets have a specific structure where concurrency is restricted. Such nets are known as free-choice workflow nets (e.g., see [14] for a book). In particular, free-choice workflow nets allow for the modeling of many features present in common workflow management systems [2]. Generalised soundness is equivalent to 1-soundness for free-choice workflow nets [28]. In this work, we prove that continuous soundness is equivalent to generalised soundness. As a byproduct of our proof, we show that structural soundness is also equivalent to continuous soundness. Altogether, the notions of \(\{\)1-\(, \text {generalised}, \text {structural}, \text {continuous}\}\) soundness all coincide for free-choice nets. In particular, this means that the continuous relaxation is exact and can serve as an efficient addition to the existing algorithmic toolkit.
Experimental Results. To demonstrate the viability of our approach, we have implemented and experimentally evaluated a prototype. As part of our evaluation, we propose several new synthetic instances for generalised and structural soundness, which are hard to decide with naive approaches. Some of these instances involve the composition of workflow nets arising from the modeling of business processes in the IBM WebSphere Business Modeler. Our prototype is competitive against both a state-of-the-art Petri net model checker, and a workflow net analyzer. In particular, our approach exhibits better signs of scalability.
Organization. The paper follows the structure of this introduction. Section 2 introduces notation, workflow nets and some properties. Section 3 defines integer and continuous relaxations, and further shows that they are preserved under reduction rules. Sections 4, 5, 6 present the aforementioned results on generalised soundness, structural soundness and free-choice nets. Section 7 provides experimental results. Section 8 concludes. Some proofs are deferred to an appendix.
2 Preliminaries
We use \(\mathbb {Z}\), \(\mathbb {N}\), \(\mathbb {Q}\) and \(\mathbb {Q}_{\ge 0}\) to respectively denote the integers, the naturals (including 0), the rationals and the nonnegative rationals (including 0). Let \(\mathbf {x}, \mathbf {y} \in \mathbb {Q}^S\) be vectors over a finite set S. We write \(\mathbf {x} \le \mathbf {y}\) if \(\mathbf {x}[s] \le \mathbf {y}[s]\) for all \(s \in S\). We write \(\mathbf {x} < \mathbf {y}\) if \(\mathbf {x} \le \mathbf {y}\) and \(\mathbf {x}[s] < \mathbf {y}[s]\) for some \(s \in S\). We extend addition and subtraction to vectors, i.e. \((\mathbf {x} + \mathbf {y})[s] {:}{=}\mathbf {x}[s] + \mathbf {y}[s]\) and \((\mathbf {x} - \mathbf {y})[s] {:}{=}\mathbf {x}[s] - \mathbf {y}[s]\) for all \(s \in S\). We define \(\mathrm {supp}(\mathbf {x}) = \{s \in S \mid \mathbf {x}[s] \ne 0\}\). Given \(c \in \mathbb {Q}\), \(\mathbf {c} \in \mathbb {Q}^S\) denotes the vector such that \(\mathbf {c}[s] = c\) for all \(s \in S\).
2.1 Petri Nets
A Petri net \(\mathcal {N}\) is a triple (P, T, F), where P is a finite set of places; T is a finite set of transitions, such that \(T \cap P = \emptyset \); and \(F :((P \times T) \cup (T \times P)) \rightarrow \{0, 1\}\) is a set of arcs. For readers familiar with Petri nets, note that arc weights are not allowed, i.e. the weights are always 1. A marking is a vector \(\mathbf {m}\in \mathbb {N}^P\) such that \(\mathbf {m}[p]\) denotes the number of tokens in place p. We denote markings listing nonzero values, e.g. \(\mathbf {m}= \{p_1 :1\}\) means \(\mathbf {m}[p_1] = 1\) and \(\mathbf {m}[p] = 0\) for \(p \ne p_1\).
Let \(t \in T\). We define the pre-vector of t as \({^\bullet t} \in \mathbb {N}^P\), where \({^\bullet t}[p] {:}{=}F(p,t)\). We define its post-vector symmetrically with \({t^\bullet }[p] {:}{=}F(t, p)\). The effect of t is denoted as \(\varDelta (t) {:}{=}{t^\bullet } - {^\bullet t}\). We say that a transition t is enabled at a marking \(\mathbf {m}\) if \(\mathbf {m}\ge {^\bullet t}\). If this is the case, then t can be fired at \(\mathbf {m}\), which results in a marking \(\mathbf {m}'\) such that \(\mathbf {m}' {:}{=}\mathbf {m}+ \varDelta (t)\). We write \(\mathbf {m}\xrightarrow {}^{t}\) to denote that t is enabled at \(\mathbf {m}\), and we write \(\mathbf {m}\xrightarrow {}^{t} \mathbf {m}'\) whenever we care about the marking \(\mathbf {m}'\) resulting from the firing. We further write \(\mathbf {m}\xrightarrow {}^{} \mathbf {m}'\) to denote that \(\mathbf {m}\xrightarrow {}^{t} \mathbf {m}'\) for some \(t \in T\).
We say that a sequence of transitions \(\pi = t_1 \cdots t_n\) is a run. We extend the notion of effect, enabledness and firing from transitions to runs in a straightforward way. The effect of a run is defined as the sum of the effects of its transitions, that is, \(\varDelta (\pi ) {:}{=}\varDelta (t_1) + \ldots + \varDelta (t_n)\). The run \(\pi \) is enabled at \(\mathbf {m}\), denoted as \(\mathbf {m}\xrightarrow {}^{\pi }\), if \(\mathbf {m}\xrightarrow {}^{t_1} \mathbf {m}_1 \xrightarrow {}^{t_2} \mathbf {m}_2 \cdots \xrightarrow {}^{t_{n-1}} \mathbf {m}_{n-1} \xrightarrow {}^{t_{n}}\) for some markings \(\mathbf {m}_1, \mathbf {m}_2, \dots , \mathbf {m}_{n-1}\). Furthermore, firing \(\pi \) from \(\mathbf {m}\) leads to \(\mathbf {m}'\), denoted as \(\mathbf {m}\xrightarrow {}^{\pi } \mathbf {m}'\), if \(\mathbf {m}\xrightarrow {}^{\pi }\) and \(\mathbf {m}' = \mathbf {m}+ \varDelta (\pi )\). We denote the reflexive and transitive closure of \({\xrightarrow {}^{}}\) by \({\xrightarrow {}^{*}}\).
A pair \((\mathcal {N}, \mathbf {m})\), where \(\mathcal {N}\) is a Petri net and \(\mathbf {m}\) is a marking of \(\mathcal {N}\), is called a marked Petri net. We write \(\text {Reach}(\mathcal {N}, \mathbf {m}) {:}{=}\{\mathbf {m}' \mid \mathbf {m}\xrightarrow {}^{*}\mathbf {m}'\}\) to denote the set of markings reachable from \(\mathbf {m}\) in \(\mathcal {N}\).
A marked Petri net \((\mathcal {N}, \mathbf {m})\) is bounded if there exists \(b \in \mathbb {N}\) such that \(\mathbf {m}' \in \text {Reach}(\mathcal {N}, \mathbf {m})\) implies \(\mathbf {m}'[p] \le b\) for all \(p \in P\). It is further safe if \(b = 1\). We say unbounded and unsafe for “not bounded” and “not safe”.
Sometimes, we argue about transformations on Petri nets which take as an input a Petri net \(\mathcal {N}\) and output a Petri net \(\mathcal {N}'\). We say that such a transformation preserves some property if \(\mathcal {N}\) satisfies that property iff \(\mathcal {N}'\) satisfies it.
Example 1
The left-hand side of Fig. 1 illustrates a Petri net \(\mathcal {N}_\text {left} = (P, T, F)\) where \(P {:}{=}\{\mathsf {i}, p_1, p_2, q_1, q_2, \mathsf {f} \}\), \(T {:}{=}\{s, t_1, t_2, u\}\), and F is depicted by arcs, e.g. \(F[\mathsf {i}, s] = 1\) and \(F[s, \mathsf {i} ] = 0\). The Petri net is marked by \(\{\mathsf {i} :1\}\), i.e. with one token in place \(\mathsf {i} \). We have \(\{\mathsf {i} :1\} \xrightarrow {}^{s} \{p_1 :1, p_2 :1\} \xrightarrow {}^{t_1 t_2} \{q_1 :1, q_2 :1\} \xrightarrow {}^{u} \{\mathsf {f} :1\}\).\(\lhd \)
2.2 Workflow Nets
A workflow net \(\mathcal {N}\) is a Petri net [1] such that:
-
there is a designated initial place \(\mathsf {i} \) such that \({t^\bullet }[\mathsf {i} ] = 0\) for all \(t \in T\);
-
there is a designated final place \(\mathsf {f} \ne \mathsf {i} \) such that \({^\bullet t}[\mathsf {f} ] = 0\) for all \(t \in T\); and
-
each place and transition lies on at least one path from \(\mathsf {i} \) to \(\mathsf {f} \) in the underlying graph of \(\mathcal {N}\), i.e. (V, E) where \(V {:}{=}P \cup T\) and \((u, v) \in E\) iff \(F(u, v) \ne 0\).
We say that \(\mathcal {N}\) is:
-
k-sound if for all \(\mathbf {m}\in \text {Reach}(\mathcal {N}, \{\mathsf {i} :k\})\) it is the case that \(\mathbf {m}\xrightarrow {}^{*}\{\mathsf {f} :k\}\) [1];
-
generalised sound if \(\mathcal {N}\) is k-sound for all \(k \in \mathbb {N}_{\ge 1}\) [20, Def. 3],
-
structurally sound if \(\mathcal {N}\) is k-sound for some \(k \in \mathbb {N}_{\ge 1}\) [6].
Example 2
Figure 1 depicts two workflow nets: \(\mathcal {N}_\text {left}\) and \(\mathcal {N}_\text {right}\). The former is generalised sound, but the latter is not. Indeed, from \(\{\mathsf {i} :1\}\), transition t cannot be enabled (as transitions preserve the sum of all tokens). Both workflow nets are structurally sound. Indeed, \(\mathcal {N}_\text {right}\) is 2-sound as it is always possible to redistribute the two tokens so that t can be fired in order to reach \(\{\mathsf {f} :2\}\). \(\lhd \)
3 Reachability Relaxations
Fix a Petri net \(\mathcal {N}= (P, T, F)\). We describe the two aforementioned relaxations.
Integer Reachability. An integral marking is a vector \(\mathbf {m}\in \mathbb {Z}^P\). Any transition \(t \in T\) is enabled in \(\mathbf {m}\in \mathbb {Z}^P\), and firing t leads to \(\mathbf {m}' {:}{=}\mathbf {m}+ \varDelta (t)\), denoted \(\mathbf {m}\xrightarrow {}_{\mathbb {Z}}^{t} \mathbf {m}'\). We define \(\mathbf {m}\xrightarrow {}_{\mathbb {Z}}^{} \mathbf {m}'\) and \(\mathbf {m}\xrightarrow {}_{\mathbb {Z}}^{*}\mathbf {m}'\) analogously to the standard setting but w.r.t. \(\xrightarrow {}_{\mathbb {Z}}^{t}\) rather than \(\xrightarrow {}^{t}\). Similarly, \(\mathbb {Z}\text {-Reach}(\mathcal {N}, \mathbf {m}) {:}{=}\{\mathbf {m}' \in \mathbb {Z}^P \mid \mathbf {m}\xrightarrow {}_{\mathbb {Z}}^{*}\mathbf {m}'\}\). As transitions are always enabled, the order of a firing sequence is irrelevant. In particular, \(\mathbf {m}\xrightarrow {}_{\mathbb {Z}}^{*}\mathbf {m}'\) iff there exists \(\mathbf {x} \in \mathbb {N}^T\) such that \(\mathbf {m}' = \mathbf {m}+ \sum _{t \in T} \mathbf {x}[t] \cdot \varDelta (t)\). Thus, integer reachability amounts to integer linear programming. Moreover, it is NP-complete [12].
Continuous Reachability. A continuous marking is a vector \(\mathbf {m}\in \mathbb {Q}_{\ge 0}^P\). Let \(\lambda \in (0,1]\). We say that \(\lambda t\) is enabled in \(\mathbf {m}\), denoted \(\mathbf {m}\xrightarrow {}_{\mathbb {Q}_{\ge 0}}^{\lambda t}\), if \(\mathbf {m}\ge \lambda \cdot {^\bullet t}\). In this context, \(\lambda \) is called the scaling factor. Furthermore, we denote by \(\mathbf {m}\xrightarrow {}_{\mathbb {Q}_{\ge 0}}^{\lambda t} \mathbf {m}'\) that \(\lambda t\) is enabled in \(\mathbf {m}\), and that its firing results in \(\mathbf {m}' {:}{=}\mathbf {m}+ \lambda \cdot \varDelta (t)\). A sequence of pairs of scaling factors and transitions is called a continuous run.
The notations \(\mathbf {m}\xrightarrow {}_{\mathbb {Q}_{\ge 0}}^{} \mathbf {m}'\) and \(\mathbf {m}\xrightarrow {}_{\mathbb {Q}_{\ge 0}}^{*}\mathbf {m}'\) are defined analogously to the discrete case but with respect to \(\xrightarrow {}_{\mathbb {Q}_{\ge 0}}^{\lambda t}\) rather than \(\xrightarrow {}^{t}\) (the internal factors \(\lambda \) can differ). Similarly, \(\mathbb {Q}_{\ge 0}\text {-Reach}(\mathcal {N}, \mathbf {m}) {:}{=}\{\mathbf {m}' \mid \mathbf {m}\xrightarrow {}_{\mathbb {Q}_{\ge 0}}^{*}\mathbf {m}'\}\) denotes the markings continuously reachable from \(\mathbf {m}\). For example, for \(\mathcal {N}_\text {left}\) from Fig. 1 and \(\pi {:}{=}\frac{1}{2} s\, \frac{1}{4} t_1\), we have \(\{\mathsf {i} :1\} \xrightarrow {}_{\mathbb {Q}_{\ge 0}}^{\pi } \{\mathsf {i} :1/2, p_1 :1/4, p_2 :1/2, q_1 :1/4\}\). It is known that continuous reachability, namely determining whether \(\mathbf {m}\xrightarrow {}_{\mathbb {Q}_{\ge 0}}^{*}\mathbf {m}'\), given \(\mathbf {m}, \mathbf {m}' \in \mathbb {Q}_{\ge 0}^P\), can be checked in polynomial time [18].
Let us establish the following helpful lemma similar to [18, Lemma 12(1)].
Lemma 1
Let \(\mathbf {m}\), \(\mathbf {m}'\) be continuous markings. It is the case that \(\mathbf {m}\xrightarrow {}_{\mathbb {Q}_{\ge 0}}^{*}\mathbf {m}'\) iff there exists \(b \in \mathbb {N}_{\ge 1}\) such that \(b \cdot \mathbf {m}\xrightarrow {}^{*}b \cdot \mathbf {m}'\).
3.1 Preservation Under Reduction Rules
In [10], the authors present six reduction rules, denoted \(R_1, \ldots , R_6\), that generalize the existing reduction rules of [27]. In the following, we show that these reduction rules preserve natural properties for the two reachability relaxations. This means we will be able to check these properties on a reduced workflow net and get the same results as on the original one.
Formally, the rules simplify a given workflow net \(\mathcal {N}= (P, T, F)\). In particular, the places of the resulting workflow net \(\mathcal {N}' = (P', T, F')\) form a subset of P. Let us fix a domain \(\mathbb {D}\in \{\mathbb {N}, \mathbb {Z}, \mathbb {Q}_{\ge 0}\}\) and let \(P' \subseteq P\). For ease of notation, we write \(P'' = P \setminus P'\) to denote the (possibly empty) set of removed places. Rules never remove the initial and output places, i.e. \(\mathsf {i}, \mathsf {f} \in P'\). We denote by \(\pi :\mathbb {D}^{P} \rightarrow \mathbb {D}^{P'}\) the obvious projection function, and by \(\pi _0 :\mathbb {D}^{P'} \rightarrow \mathbb {D}^{P}\) the “reverse projection” which fills new places with 0. Formally, \(\pi _0(\mathbf {m})[p'] {:}{=}\mathbf {m}[p']\) for all \(p' \in P'\) and \(\pi _0(\mathbf {m})[p''] {:}{=}0\) for all \(p'' \in P''\).
In [10], the authors prove that the rules preserve generalised soundness. This of course implies that they preserve k-soundness for all k. The technical proposition below will be helpful in the forthcoming sections to show the preservation of useful properties based on reachability relaxations.
Proposition 1
Let \(\mathcal {N}= (P, T, F)\) be a workflow net, and let \(\mathbb {D}\in \{\mathbb {N}, \mathbb {Z}, \mathbb {Q}_{\ge 0}\}\). Let \(\mathcal {N}' = (P', T', F')\) be a workflow net obtained by applying a reduction rule \(R_i\) to \(\mathcal {N}\), where \(P = P' \cup P''\). The following holds.
-
Rule \(R_1\). We have \(P'' = \{p\}\). There exists a nonempty set \(R' \subseteq P'\) such that if \(\{\mathsf {i} :1\} \xrightarrow {}_{\mathbb {D}}^{*}\mathbf {m}\) in \(\mathcal {N}\), then \(\mathbf {m}[p] = \sum _{r \in R'} \mathbf {m}[r']\). Moreover, \(\mathbf {m}\xrightarrow {}_{\mathbb {D}}^{*}\mathbf {n}\) in \(\mathcal {N}\) iff \(\pi (\mathbf {m}) \xrightarrow {}_{\mathbb {D}}^{*}\pi (\mathbf {n})\) in \(\mathcal {N}'\).
-
Rules \(R_2\) and \(R_3\). We have \(P'' = \emptyset \) and \(\mathbf {m}\xrightarrow {}_{\mathbb {D}}^{*}\mathbf {n}\) in \(\mathcal {N}\) iff \(\mathbf {m}\xrightarrow {}_{\mathbb {D}}^{*}\mathbf {n}\) in \(\mathcal {N}'\).
-
Rules \(R_4\) and \(R_5\). We have \(P'' = \{p\}\). For all \(\mathbf {m}'\) and \(\mathbf {n}'\), \(\mathbf {m}' \xrightarrow {}_{\mathbb {D}}^{*}\mathbf {n}'\) in \(\mathcal {N}'\) iff \(\pi _0(\mathbf {m}') \xrightarrow {}_{\mathbb {D}}^{*}\pi _0(\mathbf {n}')\) in \(\mathcal {N}\). Further, for all \(t \in T\) and \(p' \in P'\): either \({^\bullet t}[p] = 1\) implies \({^\bullet t}[p'] = 0\); or \({t^\bullet }[p] = 1\) implies \({t^\bullet }[p'] = 0\). Also, for \(\mathbb {D}\ne \mathbb {Z}\), if
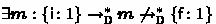 holds in \(\mathcal {N}\), then
holds in \(\mathcal {N}\), then  holds in \(\mathcal {N}'\).
holds in \(\mathcal {N}'\). -
Rule \(R_6\). We have \(P'' = \{p_2, \ldots , p_k\}\). There exists \(p_1 \in P'\) such that for all \(\mathbf {n}\in P^{\mathbb {D}}\), if \(\sum _{i = 1}^k \mathbf {m}[p_i] = \sum _{i=1}^k\mathbf {n}[p_i]\) and \(\mathbf {n}[p'] = \mathbf {m}[p']\) for \(p' \in P' \setminus \{p_1\}\), then \(\mathbf {m}\xrightarrow {}_{\mathbb {D}}^{*}\mathbf {n}\). Moreover, if \(\mathbf {m}[p_i] = \mathbf {n}[p_i] = 0\) for \(i > 1\), then \(\mathbf {m}\xrightarrow {}_{\mathbb {D}}^{*}\mathbf {n}\) in \(\mathcal {N}\) iff \(\pi (\mathbf {m}) \xrightarrow {}_{\mathbb {D}}^{*}\pi (\mathbf {n})\) in \(\mathcal {N}'\).
4 Using Relaxations For Generalised Soundness
In this section, we explain how reachability relaxations can be leveraged in order to semi-decide generalised soundness of workflow nets. More precisely, we state two necessary conditions for a workflow net to be generalised sound: one phrased in terms of integer reachability, and one in terms of continuous reachability. Furthermore, for each condition we: (1) show that it is preserved under reduction rules, and (2) establish its computational complexity. Overall, this means that to conclude that a given workflow net \(\mathcal {N}\) is not generalised sound, one may first reduce \(\mathcal {N}\), and then efficiently test for one of these two necessary conditions.
For integer boundedness, we need the mild assumption of nonredundancy. Let \(\mathcal {N}= (P, T, F)\) be a workflow net. We say that a place \(p \in P\) is nonredundantFootnote 1 if there exist \(k \in \mathbb {N}_{\ge 1}\) and \(\mathbf {m}\in \mathbb {N}^P\) such that \(\{\mathsf {i} :k\} \xrightarrow {}^{*}\mathbf {m}\) and \(\mathbf {m}[p] \ge 1\). It is known (and simple to see) that redundant places can be removed from a workflow net without changing whether it is generalised sound. Moreover, testing whether a place is nonredundant can be done in polynomial time. Indeed, by Lemma 1, it amounts to testing for the existence of some \(\mathbf {m}\in \mathbb {Q}_{\ge 0}^P\) such that \(\{\mathsf {i} :1\} \xrightarrow {}_{\mathbb {Q}_{\ge 0}}^{*}\mathbf {m}\) and \(\mathbf {m}[p] > 0\). The latter is known as a coverability query and it can be checked in polynomial time [18]. Thus, in order to test whether a given workflow net is generalised sound, one can first remove its redundant places. We call a workflow net without redundant places a nonredundant workflow net.
4.1 Integer Unboundedness
Recall that a marked Petri net \((\mathcal {N}, \mathbf {m})\) is bounded if there exists \(b \in \mathbb {N}\) such that \(\mathbf {m}' \in \text {Reach}(\mathcal {N}, \mathbf {m})\) implies \(\mathbf {m}' \le \mathbf {b}\). It is well-known that any 1-sound workflow net must be bounded from \(\{\mathsf {i} :1\}\) [1]. In particular, this means that boundedness is a necessary condition for generalised soundness. However, testing boundedness has extensive computational cost as it is EXPSPACE-complete [11, 29]. Consider the relaxed property of integer boundedness. It is defined as boundedness, but where “\(\mathbf {m}' \in \text {Reach}(\mathcal {N},\mathbf {m})\)” is replaced with “\(\mathbf {m}' \in \mathbb {Z}\text {-Reach}(\mathcal {N}, \mathbf {m}) \cap \mathbb {N}^P\)”.
Proposition 2
([9, Lemma 5.9]). Let \(\mathcal {N}\) be a nonredundant workflow net. If \((\mathcal {N}, \{\mathsf {i} :1\})\) is integer unbounded, then \(\mathcal {N}\) is not generalised sound.
Proposition 3
The reduction rules from [10] preserve integer unboundedness.
Next, we establish the complexity of integer unboundedness in two steps. The first step, in the next proposition, shows that testing integer boundedness amounts to a simple condition, independent of the initial marking. The second step shows the condition can be translated into a linear program over \(\mathbb {Q}\), rather than \(\mathbb {N}\). As a corollary, integer unboundedness is testable in polynomial time.
Proposition 4
A marked Petri net \((\mathcal {N}, \mathbf {m})\) is integer unbounded iff there exists a marking \(\mathbf {m}' > \mathbf {0}\) such that \(\mathbf {0} \xrightarrow {}_{\mathbb {Z}}^{*}\mathbf {m}'\) (independent of \(\mathbf {m}\)).
Proof
Let \(\mathcal {N}= (P, F, T)\) be a Petri net and let \(\mathbf {m}\in \mathbb {N}^P\).
\(\Rightarrow \)) By assumption, there exist \(\mathbf {m}_0, \mathbf {m}_1, \ldots \in \mathbb {Z}\text {-Reach}(\mathcal {N}, \mathbf {m}) \cap \mathbb {N}^P\) such that, for every \(i \in \mathbb {N}\), it is the case that \(m_i \not \le \mathbf {i}\). Since \((\mathbb {N}^P, \le )\) is well-quasi-ordered, there exist indices \(i_0, i_1, \ldots \) such that \(\mathbf {m}_{i_j} \le \mathbf {m}_{i_k}\) for all \(j < k\). Without loss of generality, we can assume that \(\mathbf {m}_{i_j} < \mathbf {m}_{i_k}\) for all \(j < k\), as we could otherwise extract such a subsequence. Recall that each \(\mathbf {m}_{i_\ell } \in \mathbb {Z}\text {-Reach}(\mathcal {N}, \mathbf {m})\). Let \(\pi _\ell \in T^*\) be such that \(\mathbf {m}\xrightarrow {}_{\mathbb {Z}}^{\pi _\ell } \mathbf {m}_{i_\ell }\). Let \(\mathbf {x}_\ell \in \mathbb {N}^T\) be the vector such that \(\mathbf {x}_\ell (t)\) indicates the number of occurrences of transition t in \(\pi _\ell \). Since \((\mathbb {N}^T, \le )\) is well-quasi-ordered, there exist \(j < k\) such that \(\mathbf {x}_j \le \mathbf {x}_k\). Let \(\mathbf {m}' {:}{=}\mathbf {m}_{i_k} - \mathbf {m}_{i_j}\) and \(\pi {:}{=}\prod _{t \in T} t^{(\mathbf {x}_k[t] - \mathbf {x}_\ell [t])}\). We have \(\mathbf {0} \xrightarrow {}_{\mathbb {Z}}^{\pi } \mathbf {m}' > \mathbf {0}\) as desired since:
\(\Leftarrow \)) By assumption \(\mathbf {0} \xrightarrow {}_{\mathbb {Z}}^{\pi } \mathbf {m}' > \mathbf {0}\). In particular, this means that \(\mathbf {m}\xrightarrow {}_{\mathbb {Z}}^{\pi } \mathbf {m}+ \mathbf {m}' \xrightarrow {}_{\mathbb {Z}}^{\pi } \mathbf {m}+ 2\mathbf {m}' \xrightarrow {}_{\mathbb {Z}}^{} \cdots \). Therefore, \((\mathcal {N}, \mathbf {m})\) is not integer bounded. \(\square \)
Proposition 5
A marked Petri net \((\mathcal {N}, \mathbf {m})\), where \(\mathcal {N}= (P, T, F)\), is integer unbounded iff this system has a solution: \(\exists \mathbf {x} \in \mathbb {Q}_{\ge 0}^T : \sum _{t \in T} \mathbf {x}[t] \cdot \varDelta (t) > \mathbf {0}\). In particular, given a workflow net \(\mathcal {N}\), testing integer boundedness of \((\mathcal {N}, \{\mathsf {i} :1\})\) can be done in polynomial time.
4.2 Continuous Soundness
Let us now introduce a continuous variant of 1-soundness based on continuous reachability. We prove that this variant, which we call continuous soundness, is a necessary condition for generalised soundness, and preserved by reduction rules. Moreover, we show that continuous soundness is coNP-complete, and relates to integer boundedness.
We say that a workflow net \(\mathcal {N}\) is continuously sound if for all continuous markings \(\mathbf {m}\in \mathbb {Q}_{\ge 0}\text {-Reach}(\mathcal {N}, \{\mathsf {i} :1\})\) it is the case that \(\mathbf {m}\xrightarrow {}_{\mathbb {Q}_{\ge 0}}^{*}\{\mathsf {f} :1\}\).
Theorem 1
Continuous unsoundness implies generalised unsoundness.
Proof
Let \(\mathcal {N}= (P, T, F)\) be a workflow net that is not continuously sound. By definition of continuous soundness, there exists some continuous marking \(\mathbf {m}\in \mathbb {Q}_{\ge 0}^P\) such that  and
and  . By Lemma 1, there exists \(b \in \mathbb {N}_{\ge 1}\) such that \(\{\mathsf {i} :b\} \xrightarrow {}^{*}b \cdot \mathbf {m}\). Furthermore, by Lemma 1,
. By Lemma 1, there exists \(b \in \mathbb {N}_{\ge 1}\) such that \(\{\mathsf {i} :b\} \xrightarrow {}^{*}b \cdot \mathbf {m}\). Furthermore, by Lemma 1,  . This means that \(\mathcal {N}\) is not b-sound, and consequently not generalised sound. \(\square \)
. This means that \(\mathcal {N}\) is not b-sound, and consequently not generalised sound. \(\square \)
Proposition 6
The reduction rules from [10] preserve continuous soundness.
Theorem 2
Continuous soundness is coNP-complete. Moreover, coNP-hardness holds even if the underlying graph of the given workflow net is acyclic.
Proof (of membership in coNP)
The inclusion problem consists in determining whether, given Petri nets \(\mathcal {N}\) and \(\mathcal {N}'\) over a common set of places, and markings \(\mathbf {m}\) and \(\mathbf {m}'\), it is the case that \(\mathbb {Q}_{\ge 0}\text {-Reach}(\mathcal {N}, \mathbf {m}) \subseteq \mathbb {Q}_{\ge 0}\text {-Reach}(\mathcal {N}', \mathbf {m}')\). The inclusion problem is known to be coNP-complete [8, Prop. 4.6].
Let \(\mathcal {N}= (P, T)\) be a workflow net. Let \(\mathcal {N}^{-1} = (P, T^{-1})\) be defined as \(\mathcal {N}\) but with its transitions reversed, i.e. where \(T^{-1} {:}{=}\{t^{-1} \mid t \in T\}\) with \({^\bullet (t^{-1})} {:}{=}{t^\bullet }\) and \({(t^{-1})^\bullet } {:}{=}{^\bullet t}\). It is the case that \(\mathbf {m}\xrightarrow {}_{\mathbb {Q}_{\ge 0}}^{*}\mathbf {m}'\) in \(\mathcal {N}\) iff \(\mathbf {m}' \xrightarrow {}_{\mathbb {Q}_{\ge 0}}^{*}\mathbf {m}\) in \(\mathcal {N}^{-1}\). Observe that \(\mathcal {N}\) is continuously sound iff the following holds for all \(\mathbf {m}\):
So, as \(\{\mathsf {f} :1\} \in \mathbb {Q}_{\ge 0}\text {-Reach}(\mathcal {N}, \mathbf {m})\) is equivalent to \(\mathbf {m}\in \mathbb {Q}_{\ge 0}\text {-Reach}(\mathcal {N}^{-1}, \{\mathsf {f} :1\})\), continuous soundness holds iff \( \mathbb {Q}_{\ge 0}\text {-Reach}(\mathcal {N}, \{\mathsf {i} :1\}) \subseteq \mathbb {Q}_{\ge 0}\text {-Reach}(\mathcal {N}^{-1}, \{\mathsf {f} :1\}) \). As inclusion can be tested in coNP, membership follows.
\(\square \)
A workflow net \(\mathcal {N}_\varphi \) such that \(\mathcal {N}_\varphi \) is continuously sound iff \(\varphi = (x_1 \wedge x_2 \wedge \lnot x_4) \vee (x_1 \wedge x_3 \wedge x_4)\) is a tautology. Places and transitions contain their names (not values). Arcs corresponding to the first and second clauses are respectively dotted and dashed.
Proof (of coNP-hardness)
We give a reduction from the problem of determining whether a Boolean formula in disjunctive normal form (DNF) is a tautology. We adapt a construction from [30] used to show that soundness in acyclic workflow nets is coNP-hard. The proof is more challenging under the continuous semantics as several variable valuations and clauses can be simultaneously used.
The reduction is depicted in Fig. 2 for \(\varphi = (x_1 \wedge x_2 \wedge \lnot x_4) \vee (\lnot x_1 \wedge x_3 \wedge x_4)\). In general, let \(\varphi = \bigvee _{j \in [1..k]} C_j\) be a Boolean formula in DNF with k clauses over variables \(x_1, \ldots , x_m\). We define a workflow net \(\mathcal {N}_\varphi = (P, T, F)\).
Definition. The places are defined as \(P {:}{=}\{\mathsf {i}, p_\text {cl}, \mathsf {f} \} \cup P_\text {var} \cup P_\text {clean}\), where \( P_\text {var} {:}{=}\bigcup _{i \in [1..m]} \{p_{i,?}, p_{i,1}, p_{i,0}\} \text { and } P_\text {clean} {:}{=}\bigcup _{i \in [1..m]} \{q_i, r_i\} \). The transitions are defined as \(T {:}{=}\{t_\text {init}, t_\text {fin}\} \cup T_\text {var} \cup T_\text {clauses} \cup T_{\overline{\text {var}}}\), where

Let us explain how \(\mathcal {N}_\varphi \) is intended to work. Transition \(t_\text {init}\) enables the initialization of variables and the selection of a clause that satisfies \(\varphi \), i.e. \({^\bullet t_\text {init}} {:}{=}\{\mathsf {i} :1\}\) and \({t_\text {init}^\bullet } {:}{=}\{p_{i,?} :1 \mid i \in [1..m]\} + \{p_\text {cl} :1\}\). A token in place \(p_{i,b}\) indicates that variable \(x_i\) has been assigned value b (where “?” indicates “none”). Consequently, we have \({^\bullet v_{i,b}} {:}{=}p_{i,?}\) and \({v_{i,b}^\bullet } {:}{=}p_{i,b}\) for each \(i \in [1..m]\) and \(b \in \{0, 1\}\).
Transition \(c_j\) consumes a token associated to each literal of clause \(C_j\), i.e. \({^\bullet c_j} {:}{=}\{v_{i,1} \mid x_i \in C_j\} + \{v_{i,0} \mid \lnot x_i \in C_j\}\). A token in place \(q_i\) indicates that variable \(x_i\) is not needed anymore (due to some satisfied clause). A token in place \(r_i\) indicates that variable \(x_i\) has been discarded. Therefore, transition \(c_j\) produces these tokens: \( {c_j^\bullet } {:}{=}\{q_i \mid x_i \notin C_j \wedge \lnot x_i \notin C_j\} + \{r_i \mid x_i \in C_j \vee \lnot x_i \in C_j\} \).
Transition \(\overline{v}_{i,b}\) discards variable \(x_i\), i.e. \({^\bullet \overline{v}_{i,b}} {:}{=}\{p_{i,b}, q_i\}\) and \({^\bullet \overline{v}_{i,b}} {:}{=}\{q_i\}\). Once each variable is discarded, transition \(t_\text {fin}\) terminates the execution, i.e. \({^\bullet t_\text {fin}} {:}{=}\{r_i \mid i \in [1..m]\}\) and \({t_\text {fin}^\bullet } {:}{=}\{\mathsf {f} :1\}\).
Correctness. Note that under \(\xrightarrow {}_{\mathbb {Q}_{\ge 0}}^{*}\), the workflow net needs not to proceed as described. Indeed, it could, e.g., assign half a token to \(p_{i,0}\) and half a token to \(p_{i,1}\). Similarly, several clauses can be used, with distinct scaling factors. Nonetheless, \(\mathcal {N}_{\varphi }\) is continuously sound iff \(\varphi \) is a tautology.
\(\Rightarrow \)) Let \(b_1, \ldots , b_m \in \{0, 1\}\). Let \(\pi {:}{=}t_\text {init} v_{1, b_1} \cdots v_{m, b_m}\). We have: \( \{\mathsf {i} :1\} \xrightarrow {}_{\mathbb {Q}_{\ge 0}}^{\pi } \{v_{i, b_i} :1 \mid i \in [1..m]\} + \{p_\text {cl} :1\} \). Since \(\mathcal {N}_\varphi \) is continuously sound by assumption, there must exists some \(j \in [1..k]\) such that \(c_j\) is enabled. This implies that clause \(C_j\) is satisfied by the assignment. Hence, \(\varphi \) is a tautology.
\(\Leftarrow \)) The proof is technical and involves several invariants (see appendix). \(\square \)
We may now prove that any nonredundant workflow net that is integer unbounded is also continuously unsound (the reverse is not necessarily true). Therefore, integer unboundedness relates to continuous soundness much like continuous unsoundness relates to generalised soundness.
Proposition 7
Let \(\mathcal {N}\) be a nonredundant workflow net and \(\mathbf {m}\in \mathbb {N}^P\). If \((\mathcal {N}, \mathbf {m})\) is integer unbounded, then \(\mathcal {N}\) is not continuously sound.
Proof
Let \(\mathcal {N}= (P, T, F)\) and \(\mathbf {m}\in \mathbb {N}^P\) be such that \((\mathcal {N}, \mathbf {m})\) is not integer bounded. By Proposition 4, there exists \(\mathbf {m}' > \mathbf {0}\) such that \(\mathbf {0} \xrightarrow {}_{\mathbb {Z}}^{*}\mathbf {m}'\). By nonredundancy, there exist \(\lambda \in \mathbb {N}_{\ge 1}\) and \(\mathbf {m}'' \in \mathbb {N}^P\) such that \(\{\mathsf {i} :\lambda \} \xrightarrow {}^{*}\{\mathsf {f} :1\} + \mathbf {m}''\).
In [21, Lemma 12], it is shown that \(\{\mathsf {i} :k\} \xrightarrow {}_{\mathbb {Z}}^{*}\mathbf {n}\) implies the existence of some \(\ell \in \mathbb {N}\) such that \(\{\mathsf {i} :k + \ell \} \xrightarrow {}^{*}\{\mathsf {f} :\ell \} + \mathbf {n}\). By invoking this lemma with \(k {:}{=}0\) and \(\mathbf {n}{:}{=}\mathbf {m}'\), we obtain \(\{\mathsf {i} :\ell \} \xrightarrow {}^{*}\{\mathsf {f} :\ell \} + \mathbf {m}'\) for some \(\ell \in \mathbb {N}\).
Altogether, \(\{\mathsf {i} :\lambda + \ell \} \xrightarrow {}^{*}\{\mathsf {f} :\lambda + \ell \} + \mathbf {m}' + \mathbf {m}''\). Since \(\lambda + \ell \ge 1\), Lemma 1 yields \(\{\mathsf {i} :1\} \xrightarrow {}_{\mathbb {Q}_{\ge 0}}^{*}\{\mathsf {f} :1\} + \mathbf {m}'''\) where \(\mathbf {m}''' {:}{=}(1 / (\lambda + \ell )) \mathbf {m}'\). As every transition of a workflow net produces at least one token, this contradicts the fact that \(\mathcal {N}\) is continuously sound. Indeed, it is impossible to fully get rid of \(\mathbf {m}''' > \mathbf {0}\). \(\square \)
5 Using Relaxations For Structural Soundness
A workflow net \(\mathcal {N}\) is k-quasi-sound if \(\{\mathsf {i} :k\} \xrightarrow {}^{*}\{\mathsf {f} :k\}\). Furthermore, \(\mathcal {N}\) is structurally quasi-sound if it is k-quasi-sound for some \(k \in \mathbb {N}_{\ge 1}\).
As observed in [31], structural quasi-soundness is a necessary condition for structural soundness. The notion of structural quasi-soundness is naturally generalised to an arbitrary Petri net \(\mathcal {N}= (P, T, F)\). Given markings \(\mathbf {m}, \mathbf {m}' \in \mathbb {N}^P\), we say that \(\mathbf {m}\) structurally reaches \(\mathbf {m}'\) in \(\mathcal {N}\) if \(k \cdot \mathbf {m}\xrightarrow {}^{*}k \cdot \mathbf {m}'\) for some \(k \in \mathbb {N}_{\ge 1}\). A workflow net is structurally quasi-sound iff \(\mathbf {m} {:}{=}\{\mathsf {i} :1\}\) structurally reaches \(\mathbf {m}' {:}{=}\{\mathsf {f} :1\}\). So, the observation of [31] can be rephrased as follows.
Proposition 8
Let \(\mathcal {N}\) be a workflow net. If \(\{\mathsf {i} :1\}\) does not structurally reach \(\{\mathsf {f} :1\}\) in \(\mathcal {N}\), then \(\mathcal {N}\) is not structurally sound.
The problem of structural quasi-soundness can be reduced to an instance of the Petri net reachability problem [31, Lemma 2.1]. Intuitively, the reduction produces a Petri net that nondeterministically chooses multiples of \(\{\mathsf {i} :1\}\) and \(\{\mathsf {f} :1\}\) for which to check reachability. Such an approach has a prohibitive computational cost as Petri net reachability is Ackermann-complete. However, we observe that structural reachability, and hence structural quasi-soundness, is equivalent to continuous reachability by Lemma 1.
Proposition 9
Let \(\mathcal {N}= (P, T, F)\) be a Petri net, and let \(\mathbf {m}, \mathbf {m}' \in \mathbb {N}^P\) be markings. It is the case that \(\mathbf {m}\) structurally reaches \(\mathbf {m}'\) iff \(\mathbf {m}\xrightarrow {}_{\mathbb {Q}_{\ge 0}}^{*}\mathbf {m}'\).
For a workflow net \(\mathcal {N}= (P, T, F)\), let \(k_{\mathcal {N}} \in \mathbb {N}_{\ge 1}\cup \{\infty \}\) be the smallest number for which \(\mathcal {N}\) is \(k_{\mathcal {N}}\)-quasi-sound. Then \(\mathcal {N}\) is structurally sound iff \(k_{\mathcal {N}} \ne \infty \) and \(\mathcal {N}\) is \(k_{\mathcal {N}}\)-sound [31, Thm 2.1]. By Proposition 9, \(k_{\mathcal {N}} \ne \infty \) can be checked in polynomial time via a continuous reachability query. Moreover, a lower bound on \(k_{\mathcal {N}}\) can be obtained by computing \(k_{\mathcal {N},\mathbb {Z}} \in \mathbb {N}_{\ge 1}\cup \{\infty \}\), defined as the smallest value such that \(\{\mathsf {i} :k\} \xrightarrow {}_{\mathbb {Z}}^{*}\{\mathsf {f} :k\}\). We obtain a better bound by defining \(k_{\mathcal {N}, \mathbb {Q}_{\ge 0}} \in \mathbb {N}_{\ge 1}\cup \{\infty \}\) as the smallest value for which there is a continuous run \(\pi = \lambda _1 t_1 \cdots \lambda _n t_n\) such that \(\{\mathsf {i} :k\} \xrightarrow {}_{\mathbb {Q}_{\ge 0}}^{\pi } \{\mathsf {f} :k\}\) and \(\mathbf {\pi } \in \mathbb {N}^T\), where \(\mathbf {\pi }[t] {:}{=}\sum _{i \in [1..n] : t_i = t} \lambda _i\). Values \(k_{\mathcal {N},\mathbb {Z}}\) and \(k_{\mathcal {N},\mathbb {Q}_{\ge 0}}\) can respectively be computed by a translation to integer linear programming, and a decidable optimization modulo theory.
Proposition 10
Let \(\mathcal {N}\) be a workflow net. It is the case that \(k_{\mathcal {N},\mathbb {Z}} \le k_{\mathcal {N},\mathbb {Q}_{\ge 0}} \le k_{\mathcal {N}}\). Moreover, \(k_{\mathcal {N},\mathbb {Z}}\) can be computed from an integer linear program \(\mathcal {P}\); \(k_{\mathcal {N},\mathbb {Q}_{\ge 0}}\) can be obtained by computing \(\min k \in \mathbb {N}_{\ge 1}: \varphi (k)\) where \(\varphi \) is a formula from the existential fragment of mixed linear arithmetic \(\varphi \), i.e. \(\exists \mathsf {FO}(\mathbb {Q}, \mathbb {Z}, <, +)\); and both \(\mathcal {P}\) and \(\varphi \) are constructible in polynomial time from \(\mathcal {N}\).
6 Free-Choice Workflow Nets
Let \(\mathcal {N}= (P, T, F)\) be a Petri net. We say that \(\mathcal {N}\) is free-choice if for any \(s, t \in T\), it is the case that either \(\mathrm {supp}({^\bullet s}) \cap \mathrm {supp}({^\bullet t}) = \emptyset \) or \({^\bullet s} = {^\bullet t}\). For example, the nets \(\mathcal {N}_\text {left}\) and \(\mathcal {N}_\text {right}\) from Fig. 1 are respectively free-choice and not free-choice.
It is known that generalised soundness is equivalent to 1-soundness in free-choice workflow nets [28]. We will show that the same holds for structural soundness, and that, surprisingly, for continuous soundness as well. This means that notions of soundness collapse for free-choice nets. This is proven in the forthcoming Lemma 2 and Theorem 3, which form one of the main theoretical contributions of this work.
Let \((\mathcal {N}, \mathbf {m})\) be a marked Petri net. We say that a transition t is quasi-live in \((\mathcal {N}, \mathbf {m})\) if there exists \(\mathbf {m}'\) such that \(\mathbf {m}\xrightarrow {}^{*}\mathbf {m}' \xrightarrow {}^{t}\). Similarly, we say that a transition t is live in \((\mathcal {N}, \mathbf {m})\) if for all \(\mathbf {m}'\) such that \(\mathbf {m}\xrightarrow {}^{*}\mathbf {m}'\), t is quasi-live in \((\mathcal {N},\mathbf {m}')\). In words, quasi-liveness states that there is at least one way to enable t, and liveness states that t can always be re-enabled. The set of quasi-live and live transitions of \((\mathcal {N}, \mathbf {m})\) are defined respectively as \(F(m) {:}{=}\{t \in T \mid t~\text {is quasi-live in}~(\mathcal {N}, \mathbf {m})\}\) and \(L(m) {:}{=}\{t \in T \mid t~\text {is live in}~(\mathcal {N}, \mathbf {m})\}\).
Lemma 2
Let \(\mathcal {N}= (P, T, F)\) be a free-choice Petri net, let \(c \in \mathbb {N}_{\ge 1}\), and let \(\mathbf {m}\in \mathbb {N}^P\). The following statements hold.
-
1.
There exists a marking \(\mathbf {m}'\) such that \(\mathbf {m}\xrightarrow {}^{*}\mathbf {m}'\) and \(L(\mathbf {m}') = F(\mathbf {m}')\).
-
2.
If \(L(\mathbf {m}) = F(\mathbf {m})\), then \(L(c \cdot \mathbf {m}) = F(c \cdot \mathbf {m}) = F(\mathbf {m})\).
-
3.
If \(L(c \cdot \mathbf {m}) = F(c \cdot \mathbf {m})\), \(c \cdot \mathbf {m}\xrightarrow {}^{*}\{\mathsf {f} :c\}\) and \((\mathcal {N}, c \cdot \mathbf {m})\) is bounded, then \(\mathbf {m}= \{\mathsf {f} :1\}\).
Lemma 3
Let \(\mathcal {N}\) be a workflow net. If \(\mathcal {N}\) is continuously sound, then \((\mathcal {N}, \{\mathsf {i} :k\})\) is bounded for all \(k \in \mathbb {N}_{\ge 1}\).
Theorem 3
Let \(\mathcal {N}\) be a free-choice workflow net. These statements are equivalent: (1) \(\mathcal {N}\) is 1-sound, (2) \(\mathcal {N}\) is generalised sound, (3) \(\mathcal {N}\) is structurally sound, and (4) \(\mathcal {N}\) is continuously sound.
Proof
(1) \(\Rightarrow \) (2). This was shown in [28].
(2) \(\Rightarrow \) (3). By definition, if \(\mathcal {N}\) is k-sound for all k, then it is for some k.
(2) \(\Rightarrow \) (4). By Theorem 1.
(3) \(\Rightarrow \) (1). Let \(k \in \mathbb {N}_{\ge 1}\) be such that \(\mathcal {N}\) is k-sound. Let \(\mathbf {m}\in \mathbb {N}^P\) be such that \(\{\mathsf {i} :1\} \xrightarrow {}^{*}\mathbf {m}\). By Lemma 2(1), there is a marking \(\mathbf {m}' \in \mathbb {N}^P\) such that \(\mathbf {m}\xrightarrow {}^{*}\mathbf {m}'\) and \(F(\mathbf {m}') = L(\mathbf {m}')\). By Lemma 2(2), we have \(L(k \cdot \mathbf {m}') = F(k \cdot \mathbf {m}') = F(\mathbf {m}')\).
By k-soundness, \((\mathcal {N}, \{\mathsf {i} :k\})\) must be bounded [9, Proposition 3.2 and Lemma 3.6]. Thus, since \(\{\mathsf {i} :k\} \xrightarrow {}^{*}k \cdot \mathbf {m}\xrightarrow {}^{*}k \cdot \mathbf {m}'\), it is also the case that \((\mathcal {N}, k \cdot \mathbf {m}')\) is bounded. By k-soundness, \(k \cdot \mathbf {m}' \xrightarrow {}^{*}\{\mathsf {f} :k\}\). By invoking Lemma 2(3) with \(c {:}{=}k\), we conclude that \(\mathbf {m}' = \{\mathsf {f} :1\}\). So, \(\mathcal {N}\) is 1-sound as \(\{\mathsf {i} :1\} \xrightarrow {}^{*}\mathbf {m}\xrightarrow {}^{*}\mathbf {m}' = \{\mathsf {f} :1\}\).
(4) \(\Rightarrow \) (1). Assume that \(\mathcal {N}\) is continuously sound. Let \(\mathbf {m}\in \mathbb {N}^P\) be a marking such that \(\{\mathsf {i} :1\} \xrightarrow {}^{*}\mathbf {m}\). By Lemma 2(1), there exists \(\mathbf {m}' \in \mathbb {N}^P\) such that \(\mathbf {m}\xrightarrow {}^{*}\mathbf {m}'\) and \(L(m') = F(m')\). Clearly, \(\{\mathsf {i} :1\} \xrightarrow {}_{\mathbb {Q}_{\ge 0}}^{*}\mathbf {m}'\) and by continuous soundness \(\mathbf {m}' \xrightarrow {}_{\mathbb {Q}_{\ge 0}}^{*}\{\mathsf {f} :1\}\). By Lemma 1, there exists \(b \in \mathbb {N}_{\ge 1}\) such that \(b \cdot \mathbf {m}' \xrightarrow {}^{*}\{\mathsf {f} :b\}\).
By Lemma 3, continuous soundness of \(\mathcal {N}\) implies that \((\mathcal {N}, b \cdot \mathbf {m}')\) is bounded, as \(\{\mathsf {i} :b\} \xrightarrow {}^{*}b \cdot \mathbf {m}'\). Since \(L(m') = F(m')\), it follows from Lemma 2(2) that \(L(b \cdot \mathbf {m}') = F(b \cdot \mathbf {m}')\). By invoking Lemma 2(3) with \(c {:}{=}b\), we derive \(\mathbf {m}' = \{\mathsf {f} :1\}\). Therefore, \(\mathcal {N}\) is 1-sound as \(\{\mathsf {i} :1\} \xrightarrow {}^{*}\mathbf {m}\xrightarrow {}^{*}\mathbf {m}' = \{\mathsf {f} :1\}\). \(\square \)
7 Experimental Evaluation
We implemented our approaches for generalised and structural soundness in C#.Footnote 2 We test continuous soundness via SMT solving. More precisely, we use an existential \(\psi _{\mathcal {N}}\) formula of linear arithmetic, i.e. \(\mathsf {FO}(\mathbb {Q}, <, +)\), from [8]. This formula is such that \(\psi (\mathbf {m}, \mathbf {m}')\) holds iff \(\mathbf {m}\xrightarrow {}_{\mathbb {Q}_{\ge 0}}^{*}\mathbf {m}'\) in \(\mathcal {N}\). Continuous soundness amounts to the \(\exists \forall \)-formula \(\psi _{\mathcal {N}}(\{\mathsf {i} :1\}, \mathbf {m}) \wedge \lnot \psi _{\mathcal {N}}(\mathbf {m}, \{\mathsf {f} :1\})\). To solve such formulas, we use Z3 [26]. We further use Z3 to decide structural quasi-soundness and compute \(k_{\mathcal {N},\mathbb {Q}_{\ge 0}}\) (see Proposition 10), again via the formulas of [8].
We evaluated our prototype implementation on a standard benchmark suite used regularly in the literature, and a novel suite of synthetic instances where generalised or structural soundness are hard to decide with a naive approach.
We compared with two established tools for soundness: LoLA (v2.0) [35], and Woflan [33].Footnote 3 The latter can only decide classical soundness (1-soundness + quasi-liveness). Nonetheless, we use quasi-live instances, so for which 1-soundness and classical soundness are equivalent. We further use a transformation to reduce the verification of k-soundness to the one of 1-soundness [9, Lemma 3.6]. On the other hand, LoLA can directly decide k-soundness. To do so, we start from \(\{\mathsf {i} :k\}\) and check a CTL formula of the form \(\forall \mathsf {G}\, \exists \mathsf {F}\, ((\mathbf {m}[\mathsf {f} ] = k) \wedge \bigwedge _{p \ne \mathsf {f}} \mathbf {m}[p] = 0)\).
Experiments were run on an 8-Core Intel® Core™ i7-7700 CPU @ 3.60 GHz with Ubuntu 18.04. We limited memory to \(\sim \)8 GB, and time to 120 s for each instance. Tools were called from a Python script. For LoLA and our implementation, we used the time module to measure time. Running Woflan involves some overhead, so we instead take the total verification time reported by Woflan itself.
7.1 Free-Choice Benchmark Suite
The benchmark suite encompasses 1386 free-choice Petri nets that represent business processes modeled in the IBM WebSphere Business Modeler. It was originally presented in [16], and has been studied frequently in the literature [10, 17]. These nets are not workflow nets by our definition, but can be transformed using a known procedure [23]. Intuitively, the nets are workflow nets with multiple final places, and the procedure adds a dedicated output place and ensures that the resulting workflow net represents the desired behaviour. However, roughly \(1\%\) of the nets are not workflow nets by our definition even after the procedure, as they contain nodes that are not on a path from \(\mathsf {i} \) to \(\mathsf {f} \). We removed these nets.
We further checked each net for safety using LoLA and dropped unsafe nets. Recall that \((\mathcal {N}, \{\mathsf {i} :1\})\) is sound if each reachable marking has at most one token per place. Unsafe instances can be dropped as unsafety implies 1-unsoundness in free-choice nets [34, Thm. 4.2 and 4.4], and as existing methods for checking safety, e.g. via state-space exploration with partial order reductions, are very efficient (here needing a mean of 3 ms). Thus, we considered safe instances only. Among the 1386 instances, 1382 are workflow nets, and 977 are further safe.
We also invoked an implementation of the reduction rules of [10] to reduce the size of all instances.Footnote 4 As discussed in the introduction, the rules can reduce some instances to trivially sound nets. However, even the size of nontrivial reduced instances tends to be small, with an average number of places and transitions of roughly 14, while three quarters of nets have at most 18 places and transitions. This is small enough that a complete state-splace enumeration is often feasible, in particular as the nets are safe and especially LoLA utilizes powerful partial order reductions for such nets. As we want to focus on scalability, we chained instances to produce challenging synthetic nets based on real-world instances. This is a natural way of constructing workflow nets, intuitively, the final process can be composed of many subtasks. It can be seen as a special case of refinement operations, studied in the context of generalised soundness [20].
The chaining procedure merges two workflow nets \(\mathcal {N}= (P, T, F)\) and \(\mathcal {N}' = (P', T', F')\) into \(\mathcal {N}'' {:}{=}(P'', T'', F'')\) where \(P'' {:}{=}P \cup P'\), \(T'' {:}{=}T \cup T' \cup \{t_{aux}\}\) with \(F''\) as \(F' + F''\) extended with \({^\bullet t_{\mathrm {aux}}}[\mathsf {f} ] {:}{=}1\), \({t_{\mathrm {aux}}^\bullet }[\mathsf {i} '] {:}{=}1\), and \({^\bullet t_{\mathrm {aux}}}[p] = {t_{\mathrm {aux}}^\bullet }[p'] {:}{=}0\) for other entries. It is readily seen that this construction (1) produces a free-choice net if both \(\mathcal {N}\) and \(\mathcal {N}'\) are free-choice; and (2) preserves safety.
This way, we generated large instances by using \(\ell \in \{1, 21, 41, \dots , 401\}\) randomly chosen unreduced safe instances from the benchmark suite as inputs to be chained into one instance, then reduced that instance. For each number \(\ell \), we produced 20 combined nets, with a fresh random choice each time, in order to have a more representative collection of nets for \(\ell \). This resulted in 420 instances, of which 405 are nontrivial after applying reduction rules.
A caveat is that such large nets may seem unlikely to arise in practice. It seems a human designer would avoid designing highly complex processes corresponding to Petri nets with thousands of places. However, process models are not only explicitly written by humans, but also machine-generated, e.g. by mining event logs (see [32] for a book on the topic). In particular, being free-choice is preserved by chaining, so a large free-choice net may “hide” and combine several less complex processes, which might necessitate analyzing large workflow nets.
Results. We checked the safe free-choice instances obtained as explained above for 1-soundness using LoLA, Woflan and our implementation of continuous soundness. The results are shown on the left of Fig. 3. The right-hand side of the figure provides an overview over the sizes of the nets. In each case, N refers to the number of original instances that were chained to create each instance.
Experiments on chained free-choice instances. The x-value denotes the number N of chained nets. Dark thick lines denote the mean, and light thin lines of the same color denote the minimum and maximum, respectively. For Woflan, the minimum line is slightly below the line of this work. For this work, the minimum and maximum lines are very close to the mean. Left: The y-value denotes time for checking soundness of the 20 nets for each N. Marks on the gray line at 120 s denote timeouts. Right: The y-value denotes the size of generated nets. (Color figure online)
The results show that state-space exploration via LoLA is very fast for moderate sizes, but does not scale as well. Continuous soundness is in fact outperformed by LoLA for \(N \le 100\), but scales much better, showing essentially linear growth in the given data range. For instance, continuous soundness takes a mean of 0.25 s for \(N = 1\), a mean of 1.07 s for \(N = 201\), and a mean of 2.28 s for \(N = 401\).
Woflan performs very well on the original instances, but times out frequently for larger instances. Woflan checks so-called S-coverability [34]. This is fast on many instances, even large ones, but starts running into the exponential-time worst case when instances get larger. For \(N = 1\) and \(N = 21\), Woflan does not ever time out, while it times out for roughly half of the instances in the range from \(N = 201\) to \(N = 401\). Overall, we infer that for large free-choice workflow nets, deciding soundness by checking continuous soundness can outperform existing techniques, while the procedure is still competitive on moderate instances.
7.2 Synthetic Instances
In the previously discussed benchmark suite, nets are free-choice. So structural and generalised soundness are equivalent by Theorem 3. We considered including a second suite of 590 non-free-choice Petri nets that represent processes of the SAP reference model [25]. However them turn out to be 1-quasi-sound but not 1-sound, so they represent trivial cases for generalised and structural soundness: simply checking 1-soundness, or 1-quasi-soundness and then 1-soundness, decides all instances. It’s also worth mentioning that none of the 590 SAP instances are continuously sound, so all of them can be shown to not be generalised sound by checking continuous soundness, without having to check 1-soundness.
In order to have a wider variety of challenging instances, we introduce several families of synthetic workflow nets. The nets are simple to understand, but have large numbers of reachable marking, so are challenging for approaches relying on state-space exploration, e.g. model checking.
Encoding Arc Weights. To simplify the presentation, we describe synthetic instances utilizing arcs with weights. For benchmarking, we removed the arc weights and instead input equivalent weightless nets. To do so, we used an encoding that simulates exponentially large weights by polynomially many transitions and places (the encoding is explained in ??). It preserves (quasi-)soundness, but significantly increases the number of reachable markings. Indeed, our synthetic instances are mostly trivial to solve by enumerating reachable markings when arcs have weights, but become much harder to decide when the encoding is used.Footnote 5 While much of the literature on workflow nets does not consider nets with arc weights, implicit structural encodings can occur in practice.
Generalised Soundness
Benchmark Instances. We introduce a synthetic family of nets where generalised soundness appears to be challenging. The family \(\{\mathcal {N}_c\}_{c \in \mathbb {N}_{\ge 1}}\) is defined at the top of Fig. 4. Parameter \(c \in \mathbb {N}_{\ge 1}\) is the smallest value for which \(\mathcal {N}_c\) is c-unsound. From \(\{\mathsf {i} :c\}\), the sequence \(t_\mathsf {i} ^{c} t_r^{c+1}\) can be fired, which leads to the deadlock \(\{r :c+1\}\). Yet, when starting with \(k < c\) tokens in \(\mathsf {i} \), and firing \(t_\mathsf {i} ^k\), transitions \(t_r\) and \(t_\mathsf {f} \) can only be fired exactly k times, and \(\{\mathsf {f} :k\}\) will be reached.
Top: A workflow net \(\mathcal {N}_c\) that is c-unsound and k-sound for all \(k \in [1..c-1]\). Bottom: Three families of instances. Bottom left: \(\mathcal {N}_{\text {sound-}c}\) is quasi-sound and \(\ell c\)-sound for all \(\ell \in \mathbb {N}_{\ge 1}\). Bottom center: \(\mathcal {N}_{\lnot \text {quasi-}c}\) is not structurally quasi-sound. Bottom right: \(\mathcal {N}_{\lnot \text {sound-}c}\) is \(\ell c\)-quasi-sound for all \(\ell \in \mathbb {N}_{\ge 1}\), but not structurally sound.
The naive approach to decide generalised soundness is to check k-soundness for all k until a counterexample is found or a bound is exceeded. It is known that if a counterexample exists, then there also is one of size at most exponential [9, Lemma 5.6 and 5.8]. The approach we chose for semi-deciding generalised soundness is to check continuous soundness. Recall that continuous soundness is a necessary (albeit not sufficient) condition, as shown in Theorem 1.
In our evaluation, we used Woflan and LoLA to check generalised soundness of the family for different c by checking 1-sound, ..., c-soundness, and compared the result to the time needed for testing continuous soundness. Our main goal is to evaluate whether checking continuous soundness is efficient enough to serve as an inexpensive way to witness generalised unsoundness for nontrivial instances.
Results. Figure 5 depicts the results. Woflan and LoLA show good performance for small values of c, but do not scale well to larger values. They respectively time out for \(c \ge 5\) and \(c \ge 8\). The instances are not free-choice, so LoLA and Woflan need to explore the state-space for each \(k \le c\), which becomes infeasible. For \(c \ge 14,\) Woflan cannot even check 1-soundness within the time limit. LoLA can check 1- and 2-soundness for \(c \le 28\), but cannot handle 2-soundness for larger c. Continuous soundness is efficiently verifiable even for \(c = 40\). In particular, we need less than 5 s on all instances. The greatest time is at \(c = 33\). Further, at most 1 s is needed on 34 out of 40 instances (mean of 0.6 s).
Structural Soundness
Benchmark Instances. For structural soundness, recall that our decision procedure is based on checking structural quasi-soundness and obtaining some lower bound for the smallest number for which the net is quasi-sound. Thus, we want to test on both benchmark instances that are structurally quasi-sound and those that are not. We introduce three families of non-free-choice nets for which structural soundness appears challenging. These instances are defined at the bottom of Fig. 4. We respectively denote them \(\mathcal {N}_{\text {sound-}c}\) (left), \(\mathcal {N}_{\lnot \text {quasi-}c}\) (center) and \(\mathcal {N}_{\lnot \text {sound-}c}\) (right). We claim that: \(\mathcal {N}_{\text {sound-}c}\) is \(\ell c\)-sound for all \(\ell \in \mathbb {N}_{\ge 1}\); \(\mathcal {N}_{\lnot \text {quasi-}c}\) is not structurally quasi-sound; \(\mathcal {N}_{\lnot \text {sound-}c}\) is \(\ell c\)-quasi-sound for all \(\ell \in \mathbb {N}_{\ge 1}\), not k-quasi-sound for any other number \(k \in \mathbb {N}_{\ge 1}\), and not structurally sound.
For the experiments, our goal is twofold. First, we want to evaluate whether utilizing continuous reachability to decide structural quasi-soundness is more efficient than using the known reduction to reachability described in [31, Lemma 2.1]. Woflan does not directly support checking reachability, so we only compare with LoLA. Second, we want to evaluate whether the lower bound for the smallest number for which the net is quasi-sound, which we dubbed \(k_{\mathcal {N},\mathbb {Q}_{\ge 0}}\) towards the end of Sect. 5, is close to the actual smallest number, dubbed \(k_{\mathcal {N}}\).
A caveat of this evaluation is that we evaluate only on our synthetic instances, and that computing \(k_{\mathcal {N},\mathbb {Q}_{\ge 0}}\) is only one step in deciding structural soundness. However, we think that the evaluation on these hard synthetic instances can give insights into the applicability on nontrivial real-world instances.
Results. Figure 6 compares the time needed to verify structural reachability for LoLA and our prototype. For small instances, LoLA sometimes performs very well, but we scale better for large values. Of particular note is that in the absence of quasi-soundness, LoLA will generate an infinite state-space, so will generally run out of time or memory. In particular, LoLA times out for all c on \(\mathbb {N}_{\lnot \text {quasi-}c}\). It also times out for \(c \ge 32\) on \(\mathbb {N}_{\lnot \text {sound-}c}\). On the other hand, continuous soundness never times out for the given values of c. In fact, when we tested continuous soundness for much larger values of c, we found that our implementation of continuous reachability decides structural quasi-soundness for \(N_{\lnot \text {quasi-}c}\) in under 2s for \(c = 20~000~000\).
We further found that for all instances, \(k_{\mathcal {N},\mathbb {Q}_{\ge 0}} = k_\mathcal {N}\), that is, our lower bound exactly matches the smallest number for which the net is quasi-sound. Thus, it only remains to decide \(k_{\mathcal {N},\mathbb {Q}_{\ge 0}}\)-quasi-soundness and \(k_{\mathcal {N},\mathbb {Q}_{\ge 0}}\)-soundness in order to decide structural soundness. This is in contrast to the naive approach, which starts at \(k=1\) and checks k-quasi-soundness for each value up to \(k_{\mathcal {N},\mathbb {Q}_{\ge 0}}\).
Time taken vs parameter c for checking structural quasi-soundness using the reduction to reachability, and utilizing our approach to compute \(k_{\mathcal {N},\mathbb {Q}_{\ge 0}}\), for each of the three families at the bottom of Fig. 4: \(\mathcal {N}_{\text {sound-}c}\) (left),\(\mathcal {N}_{\lnot \text {quasi-}c}\) (center), \(\mathcal {N}_{\lnot \text {sound-}c}\) (right). Note that the axis ranges differ. Marks on the gray line at 120 s denote timeouts. (Color figure online)
8 Conclusion
In this work, we have shown how reachability relaxations allow to efficiently semi-decide generalised and structural soundness. Our approach combines nicely with reduction rules, as they all preserve relaxations. In particular, we have introduced continuous soundness as an approximation of generalised soundness, and shown that it coincides with other types of soundness for free-choice nets.
As part of future work, we plan to migrate our prototype into the process mining framework ProM, to make the algorithms available to practitioners.
Notes
- 1.
This notion is adapted from batch workflow nets considered in [21].
- 2.
The implementation can be obtained from https://doi.org/10.6084/m9.figshare.19721674.v2.
- 3.
A version of Woflan suitable for running without user interaction was provided, via personal communication, by its maintainer.
- 4.
At time of writing, an implementation is available at https://github.com/LoW12/Hadara-AdSimul.
- 5.
It is deliberately used to make instances challenging, not to ensure compatibility with LoLA or Woflan, as both support arc weights.
References
van der Aalst, W.M.P., et al.: Verification of workflow nets. In: Azéma, P., Balbo, G. (eds.) ICATPN 1997. LNCS, vol. 1248, pp. 407–426. Springer, Heidelberg (1997). https://doi.org/10.1007/3-540-63139-9_48
van der Aalst, W.M.P.: The application of Petri nets to workflow management. J. Circuits Syst. Comput. 8(1), 21–66 (1998). https://doi.org/10.1142/S0218126698000043
van der Aalst, W.M.P., et al.: Workflow verification: finding control-flow errors using Petri-net-based techniques. In: van der Aalst, W., Desel, J., Oberweis, A. (eds.) Business Process Management. LNCS, vol. 1806, pp. 161–183. Springer, Heidelberg (2000). https://doi.org/10.1007/3-540-45594-9_11
van der Aalst, W.M.P., van Hee, K.M.: Workflow Management: Models, Methods, and Systems. Cooperative Information Systems. MIT Press, Cambridge (2002)
Athanasiou, K., Liu, P., Wahl, T.: Unbounded-thread program verification using thread-state equations. In: Olivetti, N., Tiwari, A. (eds.) IJCAR 2016. LNCS (LNAI), vol. 9706, pp. 516–531. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-40229-1_35
Barkaoui, K., Petrucci, L.: Structural analysis of workflow nets with shared resources. In: Proceedings of Workflow Management: Net-Based Concepts, Models, Techniques and Tools (WFM), vol. 98/7, pp. 82–95 (1998)
Blondin, M.: The ABCs of Petri net reachability relaxations. ACM SIGLOG News 7(3) (2020). https://doi.org/10.1145/3436980.3436984
Blondin, M., Finkel, A., Haase, C., Haddad, S.: The logical view on continuous Petri nets. ACM Trans. Comput. Log. (TOCL) 18(3), 24:1–24:28 (2017). https://doi.org/10.1145/3105908
Blondin, M., Mazowiecki, F., Offtermatt, P.: The complexity of soundness in workflow nets. In: Proceedings of 37th Symposium on Logic in Computer Science (LICS) (2022)
Bride, H., Kouchnarenko, O., Peureux, F.: Reduction of workflow nets for generalised soundness verification. In: Bouajjani, A., Monniaux, D. (eds.) VMCAI 2017. LNCS, vol. 10145, pp. 91–111. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-52234-0_6
Cardoza, E., Lipton, R.J., Meyer, A.R.: Exponential space complete problems for Petri nets and commutative semigroups: preliminary report. In: Proceedings of 8th Annual ACM Symposium on Theory of Computing (STOC), pp. 50–54 (1976). https://doi.org/10.1145/800113.803630
Chistikov, D., Haase, C., Halfon, S.: Context-free commutative grammars with integer counters and resets. Theor. Comput. Sci. 735, 147–161 (2018). https://doi.org/10.1016/j.tcs.2016.06.017
Czerwinski, W., Orlikowski, L.: Reachability in vector addition systems is Ackermann-complete. In: Proceedings of 62nd Annual IEEE Symposium on Foundations of Computer Science (FOCS) (2021, to appear)
Desel, J., Esparza, J.: Free Choice Petri Nets. Cambridge University Press, Cambridge (1995). https://doi.org/10.1017/CBO9780511526558
Esparza, J., Ledesma-Garza, R., Majumdar, R., Meyer, P., Niksic, F.: An SMT-based approach to coverability analysis. In: Biere, A., Bloem, R. (eds.) CAV 2014. LNCS, vol. 8559, pp. 603–619. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-08867-9_40
Fahland, D., et al.: Instantaneous soundness checking of industrial business process models. In: Dayal, U., Eder, J., Koehler, J., Reijers, H.A. (eds.) BPM 2009. LNCS, vol. 5701, pp. 278–293. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-03848-8_19
Favre, C., Völzer, H., Müller, P.: Diagnostic information for control-flow analysis of workflow graphs (a.k.a. free-choice workflow nets). In: Chechik, M., Raskin, J.-F. (eds.) TACAS 2016. LNCS, vol. 9636, pp. 463–479. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49674-9_27
Fraca, E., Haddad, S.: Complexity analysis of continuous Petri nets. Fundamenta Informaticae 137(1), 1–28 (2015). https://doi.org/10.3233/FI-2015-1168
van Hee, K., Oanea, O., Sidorova, N., Voorhoeve, M.: Verifying generalized soundness of workflow nets. In: Virbitskaite, I., Voronkov, A. (eds.) PSI 2006. LNCS, vol. 4378, pp. 235–247. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-70881-0_21
van Hee, K., Sidorova, N., Voorhoeve, M.: Soundness and separability of workflow nets in the stepwise refinement approach. In: van der Aalst, W.M.P., Best, E. (eds.) ICATPN 2003. LNCS, vol. 2679, pp. 337–356. Springer, Heidelberg (2003). https://doi.org/10.1007/3-540-44919-1_22
van Hee, K., Sidorova, N., Voorhoeve, M.: Generalised soundness of workflow nets is decidable. In: Cortadella, J., Reisig, W. (eds.) ICATPN 2004. LNCS, vol. 3099, pp. 197–215. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-27793-4_12
Hoffmann, P.E.: Workflow nets: reduction rules and games. Ph.D. thesis, Technische Universität München (2017)
Kiepuszewski, B., ter Hofstede, A.H.M., van der Aalst, W.M.P.: Fundamentals of control flow in workflows. Acta Informatica 39(3), 143–209 (2003). https://doi.org/10.1007/s00236-002-0105-4
Leroux, J.: The reachability problem for Petri nets is not primitive recursive. In: Proceedings of 62nd Annual IEEE Symposium on Foundations of Computer Science (FOCS) (2021, to appear)
Mendling, J., et al.: Faulty EPCs in the SAP reference model. In: Dustdar, S., Fiadeiro, J.L., Sheth, A.P. (eds.) BPM 2006. LNCS, vol. 4102, pp. 451–457. Springer, Heidelberg (2006). https://doi.org/10.1007/11841760_38
de Moura, L., Bjørner, N.: Z3: an efficient SMT solver. In: Ramakrishnan, C.R., Rehof, J. (eds.) TACAS 2008. LNCS, vol. 4963, pp. 337–340. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-78800-3_24https://github.com/Z3Prover/z3
Murata, T.: Petri nets: properties, analysis and applications. Proc. IEEE 77(4), 541–580 (1989). https://doi.org/10.1109/5.24143
Ping, L., Hao, H., Jian, L.: On 1-soundness and soundness of workflow nets. In: Third Workshop on Modelling of Objects, Components, and Agents, p. 21 (2004)
Rackoff, C.: The covering and boundedness problems for vector addition systems. Theor. Comput. Sci. 6, 223–231 (1978). https://doi.org/10.1016/0304-3975(78)90036-1
Ţiplea, F.L., Bocăneală, C., Chiroşcă, R.: On the complexity of deciding soundness of acyclic workflow nets. IEEE Trans. Syst. Man Cybern. Syst. 45(9), 1292–1298 (2015). https://doi.org/10.1109/TSMC.2015.2394735
Ţiplea, F.L., Marinescu, D.C.: Structural soundness of workflow nets is decidable. Inf. Process. Lett. 96(2), 54–58 (2005). https://doi.org/10.1016/j.ipl.2005.06.002
van der Aalst, W.: Data science in action. In: Process Mining, pp. 3–23. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49851-4_1
Verbeek, E., van der Aalst, W.M.P.: Woflan 2.0 a Petri-net-based workflow diagnosis tool. In: Nielsen, M., Simpson, D. (eds.) ICATPN 2000. LNCS, vol. 1825, pp. 475–484. Springer, Heidelberg (2000). https://doi.org/10.1007/3-540-44988-4_28
Verbeek, H.M.W., Basten, T., van der Aalst, W.M.P.: Diagnosing workflow processes using Woflan. Comput. J. 44(4), 246–279 (2001). https://doi.org/10.1093/comjnl/44.4.246
Wolf, K.: Petri Net model checking with LoLA 2. In: Khomenko, V., Roux, O.H. (eds.) PETRI NETS 2018. LNCS, vol. 10877, pp. 351–362. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-91268-4_18
Acknowledgements
We thank Dirk Fahland and Eric Verbeek for their help with Woflan. Michael Blondin was supported by a Discovery Grant from the Natural Sciences and Engineering Research Council of Canada (NSERC), and by the Fonds de recherche du Québec - Nature et technologies (FRQNT).
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2022 The Author(s)
About this paper
Cite this paper
Blondin, M., Mazowiecki, F., Offtermatt, P. (2022). Verifying Generalised and Structural Soundness of Workflow Nets via Relaxations. In: Shoham, S., Vizel, Y. (eds) Computer Aided Verification. CAV 2022. Lecture Notes in Computer Science, vol 13372. Springer, Cham. https://doi.org/10.1007/978-3-031-13188-2_23
Download citation
DOI: https://doi.org/10.1007/978-3-031-13188-2_23
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-13187-5
Online ISBN: 978-3-031-13188-2
eBook Packages: Computer ScienceComputer Science (R0)






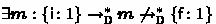 holds in
holds in  holds in
holds in 



