Abstract
We present the tool Ranker for complementing Büchi automata (BAs). Ranker builds on our previous optimizations of rank-based BA complementation and pushes them even further using numerous heuristics to produce even smaller automata. Moreover, it contains novel optimizations of specialized constructions for complementing (i) inherently weak automata and (ii) semi-deterministic automata, all delivered in a robust tool. The optimizations significantly improve the usability of Ranker, as shown in an extensive experimental evaluation with real-world benchmarks, where Ranker produced in the majority of cases a strictly smaller complement than other state-of-the-art tools.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others


1 Introduction
Büchi automata (BA) complementation is an essential operation in the toolbox of automata theory, logic, and formal methods. It has many applications, e.g., implementing negation in decision procedures of some logics (such as the monadic second-order logic S1S [1, 2], the temporal logics EPTL and QPTL [3], or the first-order logic over Sturmian words [4]), proving termination of programs [5,6,7], or model checking of temporal properties [8]. BA complementation also serves as the foundation stone of algorithms for checking inclusion and equivalence of \(\omega \)-regular languages. In all applications of BAs, the number of states of a BA affects the overall performance. The many uses of BA complementation, as well as the challenging theoretical nature of the problem, has incited researchers to develop a number of different approaches, e.g., determinization-based [9,10,11], rank-based [12,13,14], or Ramsey-based [1, 15], some of them [14, 16] producing BAs with the number of states asymptotically matching the lower bound \((0.76n)^n\) of Yan [17]. Despite their theoretical optimality, for many real-world cases the constructions create BAs with a lot of unnecessary states, so optimizations making the algorithms efficient in practice are needed.
We present Ranker, a robust tool for complementing (transition-based) BAs. Ranker uses several complementation approaches based on properties of the input BA: it combines an optimization of the rank-based procedure developed in [18,19,20] with specialized (and further optimized) procedures for complementing semi-deterministic BAs [21], inherently weak BAs [22, 23], and elevator BAs [19]. An extensive experimental evaluation on a wide range of automata occurring in practice shows that Ranker can obtain a smaller complement in the majority of cases compared to the other state-of-the-art tools.
Contribution. We describe a major improvement of Ranker [18, 19], turning it from a prototype into a robust tool. We list the particular optimizations below.
-
We extended the original BA complementation procedure with improved deelevation (cf. [19]) and advanced automata reductions.
-
We also equipped Ranker with specialized constructions tailored for widely-used semi-deterministic and inherently weak automata.
-
On top of that, we propose novel optimizations of the original NCSB construction for semi-deterministic BAs and a simulation-based optimization of the Miyano-Hayashi algorithm for complementing inherently weak automata.
All of these improvements are pushing the capabilities of Ranker, and also of practical BA complementation itself, much further.
2 Büchi Automata
Words, Functions. We fix a finite nonempty alphabet \(\Sigma \) and the first infinite ordinal \(\omega = \{0, 1, \ldots \}\). An (infinite) word \(\alpha \) is a function \(\alpha :\omega \rightarrow \Sigma \) where the i-th symbol is denoted as \(\alpha _{i}\). We abuse notation and sometimes represent \(\alpha \) as an infinite sequence \(\alpha = \alpha _{0} \alpha _{1} \dots \) \(\Sigma ^\omega \) denotes the set of all infinite words over \(\Sigma \).
Büchi Automata. A (nondeterministic transition/state-based) Büchi automaton (BA) over \(\Sigma \) is a quintuple \(\mathcal {A}= (Q, \delta , I, Q_F, \delta _F)\) where Q is a finite set of states, \(\delta :Q \times \Sigma \rightarrow 2^Q\) is a transition function, \(I \subseteq Q\) is the sets of initial states, and \(Q_F\subseteq Q\) and \(\delta _F\subseteq \delta \) are the sets of accepting states and accepting transitions respectively. \(\mathcal {A}\) is called deterministic if \(|I|\le 1\) and \(|\delta (q,a)|\le 1\) for each \(q\in Q\) and \(a \in \Sigma \). We sometimes treat \(\delta \) as a set of transitions \(p \overset{a}{\rightarrow } q\), for instance, we use \(p \overset{a}{\rightarrow } q \in \delta \) to denote that \(q \in \delta (p, a)\). Moreover, we extend \(\delta \) to sets of states \(P \subseteq Q\) as \(\delta (P, a) = \bigcup _{p \in P} \delta (p,a)\). The notation  for \(S \subseteq Q\) is used to denote the restriction of the transition function \(\delta \cap (S \times \Sigma \times S)\). Moreover, for \(q \in Q\), we use \(\mathcal {A}[q]\) to denote the automaton \((Q, \delta , \{q\}, Q_F, \delta _F)\).
for \(S \subseteq Q\) is used to denote the restriction of the transition function \(\delta \cap (S \times \Sigma \times S)\). Moreover, for \(q \in Q\), we use \(\mathcal {A}[q]\) to denote the automaton \((Q, \delta , \{q\}, Q_F, \delta _F)\).
A run of \(\mathcal {A}\) from \(q \in Q\) on an input word \(\alpha \) is an infinite sequence \(\rho :\omega \rightarrow Q\) that starts in q and respects \(\delta \), i.e., \(\rho _0 = q\) and \(\forall i \ge 0:\rho _i \overset{\alpha _{i}}{\rightarrow }\rho _{i+1} \in \delta \). Let \(\inf _{Q,\delta }(\rho )\subseteq Q \cup \delta \) denote the set of states and transitions occurring in \(\rho \) infinitely often. The run \(\rho \) is called accepting iff \(\inf _{Q,\delta }(\rho )\cap (Q_F\cup \delta _F) \ne \emptyset \). A word \(\alpha \) is accepted by \(\mathcal {A}\) from a state \(q \in Q\) if \(\mathcal {A}\) has an accepting run \(\rho \) on \(\alpha \) from q, i.e., \(\rho _0 = q\). The set \(\mathcal {L}_{\mathcal {A}}(q) = \{\alpha \in \Sigma ^\omega \mid \mathcal {A}\text { accepts } \alpha \text { from } q\}\) is called the language of q (in \(\mathcal {A}\)). Given a set of states \(R \subseteq Q\), we define the language of R as \(\mathcal {L}_{\mathcal {A}}(R) = \bigcup _{q \in R} \mathcal {L}_{\mathcal {A}}(q)\) and the language of \(\mathcal {A}\) as \(\mathcal {L}(\mathcal {A})= \mathcal {L}_{\mathcal {A}}(I)\). If \(\delta _F= \emptyset \), we call \(\mathcal {A}\) state-based and if \(Q_F= \emptyset \), we call \(\mathcal {A}\) transition-based.
A co-Büchi automaton (co-BA) \(\mathcal {C}\) is the same as a BA except the definition of when a run is accepting: a run \(\rho \) of \(\mathcal {C}\) is accepting iff \(\inf _{Q,\delta }(\rho )\cap (Q_F\cup \delta _F) = \emptyset \).
Automata Types. Let \(\mathcal {A}= (Q, \delta , I, Q_F, \delta _F)\) be a BA. \(C \subseteq Q\) is a strongly connected component (SCC) of \(\mathcal {A}\) if for any pair of states \(q, q' \in C\) it holds that q is reachable from \(q'\) and \(q'\) is reachable from q. C is maximal (MSCC) if it is not a proper subset of another SCC. An MSCC is non-accepting if it contains no accepting state and no accepting transition. We say that an SCC C is inherently weak accepting (IWA) iff every cycle in the transition diagram of \(\mathcal {A}\) restricted to C contains an accepting state or an accepting transition. We say that an SCC C is deterministic iff  is deterministic. \(\mathcal {A}\) is inherently weak (IW) if all its MSCCs are inherently weak accepting or non-accepting, and weak if for states \(q, q'\) that belong to the same SCC, \(q \in Q_F\) iff \(q' \in Q_F\). \(\mathcal {A}\) is semi-deterministic (SDBA) if \(\mathcal {A}[q]\) is deterministic for every \(q \in Q_F\cup \{p \in Q \mid s \overset{a}{\rightarrow } p \in \delta _F, s \in Q, a \in \Sigma \}\). Finally, \(\mathcal {A}\) is called elevator if all its MSCCs are inherently weak accepting, deterministic, or non-accepting.
is deterministic. \(\mathcal {A}\) is inherently weak (IW) if all its MSCCs are inherently weak accepting or non-accepting, and weak if for states \(q, q'\) that belong to the same SCC, \(q \in Q_F\) iff \(q' \in Q_F\). \(\mathcal {A}\) is semi-deterministic (SDBA) if \(\mathcal {A}[q]\) is deterministic for every \(q \in Q_F\cup \{p \in Q \mid s \overset{a}{\rightarrow } p \in \delta _F, s \in Q, a \in \Sigma \}\). Finally, \(\mathcal {A}\) is called elevator if all its MSCCs are inherently weak accepting, deterministic, or non-accepting.
3 Architecture
Ranker [24] is a publicly available command line tool, written in C++, implementing several approaches for complementation of (transition/state-based) Büchi automata. As an input, Ranker accepts BAs in the HOA [25] or the simpler ba [26] format. The architecture overview is shown in Fig. 1. An input automaton is first adjusted by various structural preprocessing steps to an intermediate equivalent automaton with a form suitable for a complementation procedure. Based on the intermediate automaton type, a concrete complementation procedure is used. The result of the complementation is subsequently polished by postprocessing steps, yielding an automaton on the output. In the following text, we provide details about the internal blocks of Ranker ’s architecture.
3.1 Preprocessing and Postprocessing
Before an input BA is sent to the complementation block itself, it is first transformed into a form most suitable for a concrete complementation technique. On top of that as a part of preprocessing, we identify structural features that are further used to enabling/disabling certain optimizations during the complementation. After the complementation, the resulting automaton is optionally reduced in a postprocessing step. Ranker provides several options of preprocessing/postprocessing that are discussed below.
Preprocessing. The following are the most important settings for preprocessing:
-
Reduction: In order to obtain a smaller automaton, reduction using direct simulation [27] can be applied (--preprocess=red). Moreover, if the input automaton is IW or SDBA, we transform it into a transition-based BA, which might be smaller (we only do local modifications and merge two states if they have the same successors while moving the acceptance condition from states to transitions entering accepting states). We, however, do not use this strategy for other BAs, because despite their possibly more compact representation, this reduction limits the effect of some optimizations used in the rank-based complementation procedure (the presence of accepting states allows to decrease the rank bound, cf. [19]).
-
Deelevation [19]: For elevator automata, Ranker supports a couple of deelevation strategies (extending a basic version introduced in [19]). Roughly speaking, deelevation makes a copy of MSCCs such that each copied MSCC becomes a terminal component (i.e., no run can leave it) and accepting states/transitions are removed from the original component (we call this the deelevation of the component). Deelevation increases the number of states but decreases the rank bounds for rank-based complementation. Ranker offers several strategies that differ on which components are deelevated:
-
--preprocess=copyall: Every component is deelevated.
-
--preprocess=copyiwa: Only IWA components are deelevated.
-
--preprocess=copyheur: This option combines two modifications applied in sequence: (i) If the input BA is not IW and the rank bound estimation [19] of the BA is at least 5, then all MSCCs with an accepting state/transition are deelevated (the higher rank bound indicates a longer sequence of components, for which deelevation is likely to be benefical). (ii) If on all paths from all initial states of the intermediate BA, the first non-trivial MSCC is non-accepting, then we partially determinize the initial part of the BA (up to the first non-trivial MSCCs); this reduces sizes of macrostates obtained in rank-based complementation.
-
-
Saturation of accepting states/transitions: Since a higher number of accepting states and transitions can help the rank-based complementation procedure, Ranker can (using --preprocess=accsat) saturate accepting states/transitions in the input BA (while preserving the language). This is, however, not always beneficial; for instance, saturation can break the structure for elevator rank estimation (cf. [19]).
-
Feature extraction: During preprocessing, we extract features of the BA that can help the complementation procedure in the second step. The features are, e.g., the type of the BA, rank bounds for individual states [19], or settings of particular optimizations from [18] (e.g., for deterministic automata with a smaller rank bound, it is counter-productive to use techniques reducing the rank bound based on reasoning about the waiting part).
Postprocessing. After the complementation procedure finishes, Ranker removes useless states and optionally applies simulation reduction (--postprocess=red).
3.2 Complementation Approaches
Based on the automaton type, Ranker uses several approaches for complementation (cf. Fig. 2). These are, ordered by decreasing priority, the following:
-
Inherently weak BAs: For the complementation of inherently weak automata, both the Miyano-Hayashi construction [22] and its optimization of adjusting macrostates (described in Sect. 4.1), are implemented. The construction converts an input automaton into an intermediate equivalent co-Büchi automaton, which is then complemented. The implemented optimizations adjust macrostates of the Miyano-Hayashi construction according to a direct simulation relation. By default (--best), the Miyano-Hayashi construction and the optimization of pruning simulation-smaller states from macrostates are used and the smaller result is output. For the option --light, only the optimized construction is used.
-
Semi-deterministic BA: For SDBAs, Ranker by default (--best) uses both an NCSB-based [21] procedure and an optimized rank-based construction with advanced rank estimation [18, 19]; the smaller result is picked. The particular NCSB-based procedure used is NCSB-MaxRank from Sect. 4.2 (Ranker also contains an implementation of NCSB-Lazy from [7], which can be turned on using --ncsb-lazy, but usually gives worse results). For the option --light, only NCSB-MaxRank is used.
-
Otherwise: For BAs with no special structure, Ranker uses the optimized rank-based complementation algorithm from [18, 19] with Spot as the backoff [18] (i.e., Ranker can determine when the input has a structure that is bad for the rank-based procedure and use another approach). Particular optimizations are selected according to the features of the input BA (e.g., the number of states or the structure of the automaton).
4 Optimizations of the Constructions
In this section, we provide details about new optimizations of complementation of inherently weak and semi-deterministic automata implemented in Ranker. Proofs of their correctness can be found in the technical report [28].
4.1 Macrostates Adjustment for Inherently Weak Automata
For complementing IW automata, Ranker uses a method based on the Miyano-Hayashi construction (denoted as MiHay) [22]: In the first step, accepting states of an input IW BA \(\mathcal {A}\) are saturated to obtain a language-equivalent weak automaton \(\mathcal {W}= (Q, \delta , I, Q_F, \emptyset )\) (we remove accepting transitions because they do not provide any advantage for IW automata). In the second step, \(\mathcal {W}\) is converted to the equivalent co-Büchi automaton \(\mathcal {C}= (Q, \delta , I, Q_F' = Q\setminus Q_F, \emptyset )\) by swapping accepting and non-accepting states. Finally, the Miyano-Hayashi construction is used to obtain the complement (state-based) BA.
Our optimizations of the MiHay procedure are inspired by optimizations of the determinization algorithm for automata over finite words [29] and by saturation of macrostates in rank-based BA complementation procedure [20], where simulation relations are used to adjust macrostates in order to obtain a smaller automaton. We modify the original construction by introducing an adjustment function that modifies obtained macrostates, either to obtain smaller macrostates (for pruning strategy) or larger macrostates (for saturating strategy; the hope is that more original macrostates map to the same saturated macrostate). Formally, given a co-BA \(\mathcal {C}\) and an adjustment function \(\theta :2^Q \rightarrow 2^Q\), the construction \(\textsc {MiHay} _\theta \) gives the (deterministic, state-based) BA \(\textsc {MiHay} _\theta (\mathcal {C}) = (Q', \delta ', I', Q_F', \emptyset )\), whose components are defined as follows:
-
\(Q' = 2^Q \times 2^Q\),
-
\(I' = \{(\theta (I), \theta (I) \setminus Q_F')\}\),
-
\(\delta '((S, B), a) = (S', B')\) where
-
\(S' = \theta (\delta (S, a))\),
-
and
-
\(*\) \(B' = S' \setminus Q_F'\) if \(B = \emptyset \) or
-
\(*\) \(B' = (\delta (B, a) \cap S') \setminus Q_F'\) if \(B \ne \emptyset \), and
-
-
-
\(F' = 2^Q \times \{\emptyset \}\).
Intuitively, the construction tracks in the S-component all runs over a word and uses the B-component to check that each of the runs sees infinitely many accepting states from \(Q_F'\) (by a cut-point construction). The original MiHay procedure can be obtained by using identity for the adjustment function, \(\theta = \mathrm {id}\).
In the following, we use \(\mathrel {\preceq _{ di }^{\mathcal {W}}}\) and \(\mathrel {\preceq _{f}^{\mathcal {C}}}\) to denote a direct simulation on \(\mathcal {W}\) and a fair simulation on \(\mathcal {C}\) respectively (see, e.g., [30] for more details; in particular, \(p \mathrel {\preceq _{f}^{\mathcal {C}}}q\) iff for every trace of \(\mathcal {C}\) from state p over \(\alpha \) with finitely many accepting states, there exists a trace from q with finitely many accepting states over \(\alpha \)).
Let \({\sqsubseteq }\subseteq Q\times Q\) be a relation on the states of \(\mathcal {C}\) defined as follows: \(p \sqsubseteq q\) iff (i) \(p \mathrel {\preceq _{f}^{\mathcal {C}}}q\), (ii) q is reachable from p in \(\mathcal {C}\), and (iii) either p is not reachable from q in \(\mathcal {C}\) or \(p=q\). The two adjustment functions \( pr , sat :2^Q \rightarrow 2^Q\) are then defined for each \(S \subseteq Q\) as follows:
-
pruning: \( pr (S) =S'\) where \(S'\subseteq S\) is the lexicographically smallest set (given a fixed ordering on Q) such that \(\forall q \in S \exists q'\in S' :q\sqsubseteq q'\) and
-
saturating: \( sat (S) = \{ p\in Q \mid \exists q \in Q:p \mathrel {\preceq _{f}^{\mathcal {C}}}q \}\).
Informally, \( pr \) removes simulation-smaller states and \( sat \) saturates a macrostate with all simulation-smaller states.Footnote 1 The correctness of the constructions is summarized by the following theorem:
Theorem 1
For a co-BA \(\mathcal {C}\), \(\mathcal {L}(\textsc {MiHay} _ sat (\mathcal {C})) = \mathcal {L}(\textsc {MiHay} _ pr (\mathcal {C})) = \Sigma ^\omega \setminus \mathcal {L}(\mathcal {C})\).
In Ranker, we approximate a fair simulation \(\mathrel {\preceq _{f}^{\mathcal {C}}}\) by a direct simulation \(\mathrel {\preceq _{ di }^{\mathcal {W}}}\) (which is easier to compute); the correctness holds due to the following lemma:
Lemma 2
Let \(\mathcal {W}= (Q, \delta , I, Q_F, \emptyset )\) be a weak BA and \(\mathcal {C}= (Q, \delta , I, Q_F' = Q\setminus Q_F, \emptyset )\) be a co-BA. Then \(\mathrel {\preceq _{ di }^{\mathcal {W}}}{\subseteq } \mathrel {\preceq _{f}^{\mathcal {C}}}\).
4.2 NCSB-MaxRank Construction
The structure of semi-deterministic BAs allows to use more efficient complementation techniques. From the point of view of rank-based complementation, the maximum rank of semi-deterministic automata can be bounded by 3. If a rank-based complementation procedure based on tight rankings (such as [18, 19]) is used to complement an SDBA, it can suffer from having too many states due to the presence of the waiting part (intuitively, runs wait in the waiting part of the complement until they can see only tight rankings, then they jump to the tight part where they can accept, cf. [13, 14, 18] for more details). Furthermore, the information about ranks of individual runs may sometimes be more precise than necessary, which disables merging some runs. The NCSB construction [21] overcomes these issues by not considering the waiting part and keeping only rough information about the ranks. As a matter of fact, NCSB and the rank-based approach are not comparable due to tight-rankings and additional techniques restricting the ranking functions [18, 19], taking into account structural properties of the automaton, which is why Ranker in the default setting tries both rank-based and NCSB-based procedures for complementing SDBAs.
An issue of the NCSB algorithm is a high degree of nondeterminism of the constructed BA (and therefore also a higher number of states). The NCSB-Lazy construction [7] improves the original algorithm with postponing the nondeterministic choices, which usually produces smaller results. Even the NCSB-Lazy construction may, however, suffer in some cases from generating too many successors. We propose an improvement of the original NCSB algorithm, inspired by the MaxRank construction in rank-based complementation from [18] (which is inspired by [14, Section 4]), hence called the NCSB-MaxRank construction, reducing the number of successors of any macrostate and symbol to at most two.
Formally, for a given SDBA  where
where  are the states reachable from an accepting state or transition and
are the states reachable from an accepting state or transition and  is the rest,
is the rest,  ,
,  , and
, and  is the transition function between
is the transition function between  and
and  , we define \(\text {NCSB-}\textsc {MaxRank} (\mathcal {A}) = (Q',I',\delta ',Q_F', \emptyset )\) to be the (state-based) BA whose components are the following:
, we define \(\text {NCSB-}\textsc {MaxRank} (\mathcal {A}) = (Q',I',\delta ',Q_F', \emptyset )\) to be the (state-based) BA whose components are the following:
-
 ,
, -
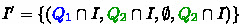 ,
, -
\(\delta ' = \gamma _1 \cup \gamma _2\) where the successors of a macrostate (N, C, S, B) over \(a \in \Sigma \) are defined such that if \(\delta _F(S,a) \ne \emptyset \) then \(\delta '((N, C, S, B), a) = \emptyset \), else
-
\(\gamma _1((N, C, S, B), a) = \{(N', C', S', B')\}\) where
-
\(*\)
 ,
, -
\(*\)
 ,
, -
\(*\)
 , and
, and -
\(*\) \(B' = C'\) if \(B = \emptyset \), otherwise
 .
.
-
-
If \(B' \cap Q_F= \emptyset \), we also set \(\gamma _2((N, C, S, B), a) = \{(N', C^\bullet , S^\bullet , B^\bullet )\}\) with
-
\(*\) \(B^\bullet = \emptyset \),
-
\(*\) \(S^\bullet = S' \cup B'\), and
-
\(*\) \(C^\bullet = C' \setminus S^\bullet \),
else \(\gamma _2((N, C, S, B), a) = \emptyset \).
-
-
-
\(Q_F' = \{(N,C,S,B) \in Q' \mid B = \emptyset \}\).
Intuitively, NCSB-MaxRank provides at most two choices for each macrostate: either keep all states in B or move all states from B to S (if B contains no accepting state). If a word is not accepted by \(\mathcal {A}\), it will be safe to put all states from B to S at some point. The construction is in fact incomparable to the original NCSB algorithm [21] (in particular due to the condition  , which need not hold in NCSB-MaxRank). Correctness of the construction is given by the following theorem.
, which need not hold in NCSB-MaxRank). Correctness of the construction is given by the following theorem.
Theorem 3
Let \(\mathcal {A}\) be an SDBA. Then \(\mathcal {L}(\text {NCSB-}\textsc {MaxRank} (\mathcal {A})) = \Sigma ^\omega \setminus \mathcal {L}(\mathcal {A})\).
5 Experimental Evaluation
We compared the improved version of Ranker presented in this paper with other state-of-the-art tools, namely, Goal [33] (implementing Piterman [10], Safra [9], and Fribourg [16]), Spot 2.9.3 [31] (implementing Redziejowski’s algorithm [11]), Seminator 2 [34], LTL2dstar 0.5.4 [35], Roll [36], and the previous version of Ranker from [19], denoted as \(\textsc {Ranker}_{\textsc {Old}} \). All tools were set to the mode where they output a state-based BA. The correctness of our implementation was tested using Spot’s autcross on all of BAs from our benchmarks. The experimental evaluation was performed on a 64-bit GNU/Linux Debian workstation with an Intel(R) Xeon(R) CPU E5-2620 running at 2.40 GHz with 32 GiB of RAM, using a 5-minute timeout. Axes in plots are logarithmic. An artifact that allows reproduction of the results is available as [37].
Datasets. We use automata from the following three datasets: (i) random containing 11,000 BAs over a two letter alphabet used in [38], which were randomly generated via the Tabakov-Vardi approach [39], starting from 15 states and with various parameter settings; (ii) LTL with 1,721 BAs over larger alphabets (up to 128 symbols) used in [34], obtained from LTL formulae from literature (221) or randomly generated (1,500), (iii) Automizer containing 906 BAs over larger alphabets (up to \(2^{35}\) symbols) used in [7], which were obtained from the Ultimate Automizer tool (all benchmarks are available at [40]). Note that we included random in order to simulate applications that cannot easily generate BAs of one of the easier fragments (unlike, e.g., Ultimate Automizer, which generates in most cases SDBAs) and have thus, so far, not been seriously considered by the community due to the lack of practically efficient BA complementation approaches (e.g., the automata-based S1S decision procedure [1]). All automata were preprocessed using Spot’s autfilt (using the {-}{-}high simplification level), and converted to the HOA format [25]. We also removed trivial one-state BAs. In the end, we were left with 4,533 (random,  data points), 1,716 (LTL,
data points), 1,716 (LTL,  data points), and 906 (Automizer,
data points), and 906 (Automizer,  data points) automata. We use all to denote their union (7,155 BAs).
data points) automata. We use all to denote their union (7,155 BAs).
5.1 Effect of the Proposed Optimizations
In the first part of the experimental evaluation, we measured the effect of the proposed optimizations from Sect. 4 on the size of the generated state space, i.e., sizes of output automata without any postprocessing. This use case is motivated by language inclusion and equivalence checking, where the size of the generated state space directly affects the performance of the algorithm. We carried out the evaluation on LTL and Automizer benchmarks (we use both to denote their union) since most of the automata there are either IW or SDBAs.
The first experiment compares the number of states generated by the original MiHay and by the macrostates-pruning optimization \(\textsc {MiHay} _ pr \) from Sect. 4.1 on inherently weak BAs (948 BAs from LTL and 360 BAs from Automizer = 1,308 BAs). Note that we omit \(\textsc {MiHay} _ sat \) as it is overall worse than \(\textsc {MiHay} _ pr \). The scatter plot is shown in Fig. 3a and statistics are in the top part of Table 1. We can clearly see that the optimization works well, substantially decreasing both the mean and the median size of the output BAs.
The second experiment compares the size of the state space generated by NCSB-Lazy [7] and NCSB-MaxRank from Sect. 4.2 on 735 SDBAs (that are not IW) from LTL (328 BAs) and Automizer (407 BAs). We omit a comparison with the original NCSB [21] procedure, since NCSB-Lazy behaves overall better [7]. The results are in Fig. 3b and the bottom part of Table 1. Again, both the mean and the median are lower for NCSB-MaxRank. The scatter plot shows that the effect of the optimization is stronger when the generated state space is larger (for BAs where the output had \(\ge \) 150 states, our optimization was never worse).
5.2 Comparison with Other Tools
In the second part of the experimental evaluation, we compared Ranker with other state-of-the-art tools for BA complementation. We measured how small output BAs we can obtain, therefore, we compared the number of states after reduction using autfilt (with the simplification level --high). The scatter plots in Fig. 4 compare the numbers of states of automata generated by \(\textsc {Ranker} \), \(\textsc {Ranker}_{\textsc {Old}} \), and \(\textsc {Spot} \). Summarizing statistics are given in Table 2. The backoff strategy in Ranker was applied in 278 (264:1:13) cases.
 .
.First, observe that Ranker significantly outperforms \(\textsc {Ranker}_{\textsc {Old}} \), especially in the much lower number of timeouts, which decreased by 65 % (moreover, 66 of the 158 timeouts were due to the timeout of autfilt in postprocessing). The higher mean of \(\textsc {Ranker} \) compared to \(\textsc {Ranker}_{\textsc {Old}} \) is also caused by less timeouts). From Table 2, we can also see that Ranker has the smallest mean and median (except Roll and \(\textsc {Ranker}_{\textsc {Old}} \), but they have a much higher number of timeouts). Ranker has also the second lowest number of timeouts (Spot has the lowest). If we look at the number of wins and loses, we can see that Ranker in majority of cases produces a strictly smaller automaton compared to other tools. In Table 3, see that the run time of Ranker is comparable to the run times of other tools (much better than Goal and Roll, comparable with Seminator 2, and a bit worse than Spot and LTL2dstar).
References
Büchi, J.R.: On a decision method in restricted second order arithmetic. In: Proceedings of the International Congress on Logic, Method, and Philosophy of Science 1960. Stanford University Press, Stanford (1962)
Havlena, V., Lengál, O., Šmahlíková, B.: Deciding S1S: down the rabbit hole and through the looking glass. In: Echihabi, K., Meyer, R. (eds.) NETYS 2021. LNCS, vol. 12754, pp. 215–222. Springer, Cham (2021). https://doi.org/10.1007/978-3-030-91014-3_15
Sistla, A.P., Vardi, M.Y., Wolper, P.: The complementation problem for Büchi automata with applications to temporal logic. Theor. Comput. Sci. 49(2–3), 217–237 (1987)
Oei, R., Ma, D., Schulz, C., Hieronymi, P.: Pecan: an automated theorem prover for automatic sequences using Büchi automata. arXiv preprint arXiv:2102.01727 (2021)
Fogarty, S., Vardi, M.Y.: Büchi complementation and size-change termination. In: Kowalewski, S., Philippou, A. (eds.) TACAS 2009. LNCS, vol. 5505, pp. 16–30. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-00768-2_2
Heizmann, M., Hoenicke, J., Podelski, A.: Termination analysis by learning terminating programs. In: Biere, A., Bloem, R. (eds.) CAV 2014. LNCS, vol. 8559, pp. 797–813. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-08867-9_53
Chen, Y., et al.: Advanced automata-based algorithms for program termination checking. In: Proceedings of PLDI’18, pp. 135–150. ACM (2018)
Vardi, M.Y., Wolper, P.: An automata-theoretic approach to automatic program verification (preliminary report). In: Proceedings of LICS’86, pp. 332–344. IEEE (1986)
Safra, S.: On the complexity of \(\omega \)-automata. In: Proceedings of FOCS’88, pp. 319–327. IEEE (1988)
Piterman, N.: From nondeterministic Büchi and Streett automata to deterministic parity automata. In: Proceedings of LICS’06, pp. 255–264. IEEE (2006)
Redziejowski, R.R.: An improved construction of deterministic omega-automaton using derivatives. Fundam. Informat. 119(3–4), 393–406 (2012)
Kupferman, O., Vardi, M.Y.: Weak alternating automata are not that weak. ACM Trans. Comput. Log. 2(3), 408–429 (2001)
Friedgut, E., Kupferman, O., Vardi, M.: Büchi complementation made tighter. Int. J. Found. Comput. Sci. 17, 851–868 (2006)
Schewe, S.: Büchi complementation made tight. In: Albers, S., Marion, J., (eds.) Proceedings of STACS’09. Volume 3 of LIPIcs, Schloss Dagstuhl - Leibniz-Zentrum fuer Informatik, Germany, pp. 661–672 (2009)
Breuers, S., Löding, C., Olschewski, J.: Improved Ramsey-based Büchi complementation. In: Birkedal, L. (ed.) FoSSaCS 2012. LNCS, vol. 7213, pp. 150–164. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-28729-9_10
Allred, J.D., Ultes-Nitsche, U.: A simple and optimal complementation algorithm for Büchi automata. In: Proceedings of LICS’18, pp. 46–55. IEEE (2018)
Yan, Q.: Lower bounds for complementation of \(\omega \)-automata via the full automata technique. In: Proceedings of ICALP’06, pp. 589–600. Springer, Heidelberg (2006)
Havlena, V., Lengál, O.: Reducing (to) the ranks: efficient rank-based Büchi automata complementation. In: Proceedings of CONCUR’21. Volume 203 of LIPIcs, pp. 2:1–2:19. Schloss Dagstuhl - Leibniz-Zentrum für Informatik (2021)
Havlena, V., Lengál, O., Šmahlíková, B.: Sky is not the limit: tighter rank bounds for elevator automata in Büchi automata complementation. In: Proceedings of TACAS’22, vol. 13244, LNCS, pp. 118–136. Springer, Cham (2022). https://doi.org/10.1007/978-3-030-99527-0_7
Chen, Y.-F., Havlena, V., Lengál, O.: Simulations in Rank-Based Büchi Automata Complementation. In: Lin, A.W. (ed.) APLAS 2019. LNCS, vol. 11893, pp. 447–467. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-34175-6_23
Blahoudek, F., Heizmann, M., Schewe, S., Strejček, J., Tsai, M.-H.: Complementing Semi-deterministic Büchi Automata. In: Chechik, M., Raskin, J.-F. (eds.) TACAS 2016. LNCS, vol. 9636, pp. 770–787. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49674-9_49
Miyano, S., Hayashi, T.: Alternating finite automata on \(\omega \)-words. Theor. Comput. Sci. 32(3), 321–330 (1984)
Boigelot, B., Jodogne, S., Wolper, P.: On the use of weak automata for deciding linear arithmetic with integer and real variables. In: Goré, R., Leitsch, A., Nipkow, T. (eds.) IJCAR 2001. LNCS, vol. 2083, pp. 611–625. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-45744-5_50
Havlena, V., Lengál, O., Šmahlíková, B.: Ranker (2022). https://github.com/vhavlena/ranker
Babiak, T., et al.: The Hanoi omega-automata format. In: Kroening, D., Păsăreanu, C.S. (eds.) CAV 2015. LNCS, vol. 9206, pp. 479–486. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-21690-4_31
Abdulla, P.A., et al.: Simulation subsumption in Ramsey-based Büchi automata Universality and inclusion testing. In: Touili, T., Cook, B., Jackson, P. (eds.) CAV 2010. LNCS, vol. 6174, pp. 132–147. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-14295-6_14
Mayr, R., Clemente, L.: Advanced automata minimization. In: Proceedings of POPL’13, pp. 63–74 (2013)
Havlena, V., Lengál, O., Šmahlíková, B.: Complementing Büchi automata with Ranker (technical report). arXiv preprint arXiv:2206.01946 (2021)
van Glabbeek, R., Ploeger, B.: Five determinisation algorithms. In: Ibarra, O.H., Ravikumar, B. (eds.) CIAA 2008. LNCS, vol. 5148, pp. 161–170. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-70844-5_17
Etessami, K.: A hierarchy of polynomial-time computable simulations for automata. In: Brim, L., Křetínský, M., Kučera, A., Jančar, P. (eds.) CONCUR 2002. LNCS, vol. 2421, pp. 131–144. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-45694-5_10
Duret-Lutz, A., Lewkowicz, A., Fauchille, A., Michaud, T., Renault, É., Xu, L.: Spot 2.0 — A framework for LTL and \(\omega \)-automata manipulation. In: Artho, C., Legay, A., Peled, D. (eds.) ATVA 2016. LNCS, vol. 9938, pp. 122–129. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-46520-3_8
Löding, C., Pirogov, A.: New optimizations and heuristics for determinization of Büchi automata. In: Chen, Y.-F., Cheng, C.-H., Esparza, J. (eds.) ATVA 2019. LNCS, vol. 11781, pp. 317–333. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-31784-3_18
Tsai, M.-H., Tsay, Y.-K., Hwang, Y.-S.: GOAL for games, omega-automata, and logics. In: Sharygina, N., Veith, H. (eds.) CAV 2013. LNCS, vol. 8044, pp. 883–889. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-39799-8_62
Blahoudek, F., Duret-Lutz, A., Strejček, J.: Seminator 2 can complement generalized Büchi automata via improved semi-determinization. In: Lahiri, S.K., Wang, C. (eds.) CAV 2020. LNCS, vol. 12225, pp. 15–27. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-53291-8_2
Klein, J., Baier, C.: On-the-fly stuttering in the construction of deterministic \(\omega \)-automata. In: Proceedings of CIAA’07, vol. 4783, LNCS, pp. 51–61. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-76336-9_7
Li, Y., Sun, X., Turrini, A., Chen, Y.-F., Xu, J.: ROLL 1.0: \(\omega \)-regular language learning library. In: Vojnar, T., Zhang, L. (eds.) TACAS 2019. LNCS, vol. 11427, pp. 365–371. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-17462-0_23
Havlena, V., Lengál, O., Šmahlíková, B.: Artifact for the CAV’22 submission “Complementing Büchi Automata with Ranker” (2022). https://doi.org/10.5281/zenodo.6558229
Tsai, M.-H., Fogarty, S., Vardi, M.Y., Tsay, Y.-K.: State of Büchi complementation. In: Domaratzki, M., Salomaa, K. (eds.) CIAA 2010. LNCS, vol. 6482, pp. 261–271. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-18098-9_28
Tabakov, D., Vardi, M.Y.: Experimental evaluation of classical automata constructions. In: Sutcliffe, G., Voronkov, A. (eds.) LPAR 2005. LNCS (LNAI), vol. 3835, pp. 396–411. Springer, Heidelberg (2005). https://doi.org/10.1007/11591191_28
Lengál, O.: Automata Benchmarks Repository (2022). https://github.com/ondrik/automata-benchmarks/tree/master/omega
Acknowledgements
We thank the anonymous reviewers for their useful remarks that helped us improve the quality of the paper, the artifact evaluation committee for their thorough testing of the artifact, and Alexandre Duret-Lutz for useful feedback on an earlier version of the paper. This work was supported by the Czech Ministry of Education, Youth and Sports project LL1908 of the ERC.CZ programme, the Czech Science Foundation project 20-07487S, and the FIT BUT internal project FIT-S-20-6427.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2022 The Author(s)
About this paper
Cite this paper
Havlena, V., Lengál, O., Šmahlíková, B. (2022). Complementing Büchi Automata with Ranker. In: Shoham, S., Vizel, Y. (eds) Computer Aided Verification. CAV 2022. Lecture Notes in Computer Science, vol 13372. Springer, Cham. https://doi.org/10.1007/978-3-031-13188-2_10
Download citation
DOI: https://doi.org/10.1007/978-3-031-13188-2_10
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-13187-5
Online ISBN: 978-3-031-13188-2
eBook Packages: Computer ScienceComputer Science (R0)







 ,
,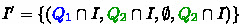 ,
, ,
, ,
, , and
, and .
.
