Abstract
We consider the quantitative problem of obtaining lower-bounds on the probability of termination of a given non-deterministic probabilistic program. Specifically, given a non-termination threshold \(p \in [0, 1],\) we aim for certificates proving that the program terminates with probability at least \(1-p\). The basic idea of our approach is to find a terminating stochastic invariant, i.e. a subset \( SI \) of program states such that (i) the probability of the program ever leaving \( SI \) is no more than p, and (ii) almost-surely, the program either leaves \( SI \) or terminates.
While stochastic invariants are already well-known, we provide the first proof that the idea above is not only sound, but also complete for quantitative termination analysis. We then introduce a novel sound and complete characterization of stochastic invariants that enables template-based approaches for easy synthesis of quantitative termination certificates, especially in affine or polynomial forms. Finally, by combining this idea with the existing martingale-based methods that are relatively complete for qualitative termination analysis, we obtain the first automated, sound, and relatively complete algorithm for quantitative termination analysis. Notably, our completeness guarantees for quantitative termination analysis are as strong as the best-known methods for the qualitative variant.
Our prototype implementation demonstrates the effectiveness of our approach on various probabilistic programs. We also demonstrate that our algorithm certifies lower bounds on termination probability for probabilistic programs that are beyond the reach of previous methods.
A longer version, including appendices, is available at [12].
Authors are ordered alphabetically.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
Probabilistic Programs. Probabilistic programs extend classical imperative programs with randomization. They provide an expressive framework for specifying probabilistic models and have been used in machine learning [22, 39], network analysis [20], robotics [41] and security [4]. Recent years have seen the development of many probabilistic programming languages such as Church [23] and Pyro [6], and their formal analysis is an active topic of research. Probabilistic programs are often extended with non-determinism to allow for either unknown user inputs and interactions with environment or abstraction of parts that are too complex for formal analysis [31].
Termination. Termination has attracted the most attention in the literature on formal analysis of probabilistic programs. In non-probabilistic programs, it is a purely qualitative property. In probabilistic programs, it has various extensions:
-
1.
Qualitative: The almost-sure (a.s.) termination problem asks if the program terminates with probability 1, whereas the finite termination problems asks if the expected number of steps until termination is finite.
-
2.
Quantitative: The quantitative probabilistic termination problem asks for a tight lower bound on the termination probability. More specifically, given a constant \(p \in [0, 1],\) it asks whether the program will terminate with probability at least \(1-p\) over all possible resolutions of non-determinism.
Previous Qualitative Works. There are many approaches to prove a.s. termination based on weakest pre-expectation calculus [27, 31, 37], abstract interpretation [34], type systems [5] and martingales [7, 9, 11, 14, 25, 26, 32, 35]. This work is closest in spirit to martingale-based approaches. The central concept in these approaches is that of a ranking supermartingale (RSM) [7], which is a probabilistic extension of ranking functions. RSMs are a sound and complete proof rule for finite termination [21], which is a stricter notion than a.s. termination. The work of [32] proposed a variant of RSMs that can prove a.s. termination even for programs whose expected runtime is infinite, and lexicographic RSMs were studied in [1, 13]. A main advantage of martingale-based approaches is that they can be fully automated for programs with affine/polynomial arithmetic [9, 11].
Previous Quantitative Works. Quantitative analyses of probabilistic programs are often more challenging. There are only a few works that study the quantitative termination problem: [5, 14, 40]. The works [14, 40] propose martingale-based proof rules for computing lower-bounds on termination probability, while [5] considers functional probabilistic programs and proposes a type system that allows incrementally searching for type derivations to accumulate a lower-bound on termination probability. See Sect. 8 for a detailed comparison.
Lack of Completeness. While [5, 14, 40] all propose sound methods to compute lower-bounds on termination probability, none of them are theoretically complete nor do their algorithms provide relative completeness guarantees. This naturally leaves open whether one can define a complete certificate for proving termination with probability at least \(1-p\in [0,1]\), i.e. a certificate that a probabilistic program admits if and only if it terminates with probability at least \(1-p\), which allows for automated synthesis. Ideally, such a certificate should also be synthesized automatically by an algorithm with relative completeness guarantees, i.e. an algorithm which is guaranteed to compute such a certificate for a sufficiently general subclass of programs. Note, since the problem of deciding whether a probabilistic program terminates with probability at least \(1-p\) is undecidable, one cannot hope for a general complete algorithm so the best one can hope for is relative completeness.
Our Approach. We present the first method for the probabilistic termination problem that is complete. Our approach builds on that of [14] and uses stochastic invariants in combination with a.s. reachability certificates in order to compute lower-bounds on the termination probability. A stochastic invariant [14] is a tuple \(( SI ,p)\) consisting of a set \( SI \) of program states and an upper-bound p on the probability of a random program run ever leaving \( SI \). If one computes a stochastic invariant \(( SI ,p)\) with the additional property that a random program run would, with probability 1, either terminate or leave \( SI \), then since \( SI \) is left with probability at most p the program must terminate with probability at least \(1-p\). Hence, the combination of stochastic invariants and a.s. reachability certificates provides a sound approach to the probabilistic termination problem.
While this idea was originally proposed in [14], our method for computing stochastic invariants is fundamentally different and leads to completeness. In [14], a stochastic invariant is computed indirectly by computing the set \( SI \) together with a repulsing supermartingale (RepSM), which can then be used to compute a probability threshold p for which \(( SI ,p)\) is a stochastic invariant. It was shown in [40, Section 3] that RepSMs are incomplete for computing stochastic invariants. Moreover, even if a RepSM exists, the resulting probability bound need not be tight and the method of [14] does not allow optimizing the computed bound or guiding computation towards a bound that exceeds some specified probability threshold.
In this work, we propose a novel and orthogonal approach that computes the stochastic invariant and the a.s. termination certificate at the same time and is provably complete for certifying a specified lower bound on termination probability. First, we show that stochastic invariants can be characterized through the novel notion of stochastic invariant indicators (SI-indicators). The characterization is both sound and complete. Furthermore, it allows fully automated computation of stochastic invariants for programs using affine or polynomial arithmetic via a template-based approach that reduces quantitative termination analysis to constraint solving. Second, we prove that stochastic invariants together with an a.s. reachability certificate, when synthesized in tandem, are not only sound for probabilistic termination, but also complete. Finally, we present the first relatively complete algorithm for probabilistic termination. Our algorithm considers polynomial probabilistic programs and simultaneously computes a stochastic invariant and an a.s. reachability certificate in the form of an RSM using a template-based approach. Our algorithmic approach is relatively complete.
While we focus on the probabilistic termination problem in which the goal is to verify a given lower bound \(1-p\) on the termination probability, we note that our method may be straightforwardly adapted to compute a lower bound on the termination probability. In particular, we may perform a binary-search on p and search for the smallest value of p for which \(1-p\) can be verified to be a lower bound on the termination probability.
Contributions. Our specific contributions in this work are as follows:
-
1.
We present a sound and complete characterization of stochastic invariants through the novel notion of stochastic invariant indicators (Sect. 4).
-
2.
We prove that stochastic invariants together with an a.s. reachability certificate are sound and complete for proving that a probabilistic program terminates with at least a given probability threshold (Sect. 5).
-
3.
We present a relatively complete algorithm for computing SI-indicators, and hence stochastic invariants over programs with affine or polynomial arithmetic. By combining it with the existing relatively complete algorithms for RSM computation, we obtain the first algorithm for probabilistic termination that provides completeness guarantees (Sect. 6).
-
4.
We implement a prototype of our approach and demonstrate its effectiveness over various benchmarks (Sect. 7). We also show that our approach can handle programs that were beyond the reach of previous methods.
2 Overview
Before presenting general theorems and algorithms, we first illustrate our method on the probabilistic program in Fig. 1. The program models a 1-dimensional discrete-time random walk over the real line that starts at \(x=0\) and terminates once a point with \(x<0\) is reached. In every time step, x is incremented by a random value sampled according to the uniform distribution \( Uniform ([-1,0.5])\). However, if the stochastic process is in a point with \(x\ge 100\), then the value of x might also be incremented by a random value independently sampled from \( Uniform ([-1,2])\). The choice on whether the second increment happens is non-deterministic. By a standard random walk argument, the program does not terminate almost-surely.
Outline of Our Method. Let \(p=0.01.\) To prove this program terminates with probability at least \(1-p=0.99\), our method computes the following two objects:
-
1.
Stochastic invariant. A stochastic invariant is a tuple \(( SI ,p)\) s.t. \( SI \) is a set of program states that a random program run leaves with probability at most p.
-
2.
Termination proof for the stochastic invariant. A ranking supermartingale (RSM) [7] is computed in order to prove that the program will, with probability 1, either terminate or leave the set \( SI \). Since \( SI \) is left with probability at most p, the program must terminate with probability at least \(1-p\).
Synthesizing SI. To find a stochastic invariant, our method computes a state function f which assigns a non-negative real value to each reachable program state. We call this function a stochastic invariant indicator (SI-indicator), and it serves the following two purposes: First, exactly those states which are assigned a value strictly less than 1 are considered a part of the stochastic invariant \( SI \). Second, the value assigned to each state is an upper-bound on the probability of leaving \( SI \) if the program starts from that state. Finally, by requiring that the value of the SI-indicator at the initial state of the program is at most p, we ensure a random program run leaves the stochastic invariant with probability at most p.
In Sect. 4, we will define SI-indicators in terms of conditions that ensure the properties above and facilitate automated computation. We also show that SI-indicators serve as a sound and complete characterization of stochastic invariants, which is one of the core contributions of this work. The significance of completeness of the characterization is that, in order to search for a stochastic invariant with a given probability threshold p, one may equivalently search for an SI-indicator with the same probability threshold whose computation can be automated. As we will discuss in Sect. 8, previous approaches to the synthesis of stochastic invariants were neither complete nor provided tight probability bounds. For Fig. 1, we have the following set \( SI \) which will be left with probability at most \(p = 0.01:\)
An SI-indicator for this stochastic invariant is:
It is easy to check that \(( SI , 0.01)\) is a stochastic invariant and that for every state \(s=(\ell , x, r_1, r_2),\) the value f(s) is an upper-bound on the probability of eventually leaving \( SI \) if program execution starts at s. Also, \(s \in SI \Leftrightarrow f(s) < 1.\)
Synthesizing a Termination Proof. To prove that a probabilistic program terminates with probability at least \(1-p\), our method searches for a stochastic invariant \(( SI ,p)\) for which, additionally, a random program run with probability 1 either leaves \( SI \) or terminates. This idea is formalized in Theorem 2, which shows that stochastic invariants provide a sound and complete certificate for proving that a given probabilistic program terminates with probability at least \(1-p\). In order to impose this additional condition, our method simultaneously computes an RSM for the set of states \(\lnot SI \cup State _{ term },\) where \( State _{ term }\) is the set of all terminal states. RSMs are a classical certificate for proving almost-sure termination or reachability in probabilistic programs. A state function \(\eta \) is said to be an RSM for \(\lnot SI \cup State _{ term }\) if it satisfies the following two conditions:
-
Non-negativity. \(\eta (\ell ,x,r_1,r_2)\ge 0\) for any reachable state \((\ell ,x,r_1,r_2) \in SI \);
-
\(\varepsilon \)-decrease in expectation. There exists \(\varepsilon >0\) such that, for any reachable non-terminal state \((\ell ,x,r_1,r_2) \in SI \), the value of \(\eta \) decreases in expectation by at least \(\varepsilon \) after a one-step execution of the program from \((\ell ,x,r_1,r_2)\).
The existence of an RSM for \(\lnot SI \cup State _{ term }\) implies that the program will, with probability 1, either terminate or leave \( SI \). As \(( SI ,p)\) is a stochastic invariant, we can readily conclude that the program terminates with probability at least \(1-p=0.99\). An example RSM with \(\varepsilon = 0.05\) for our example above is:
Simultaneous Synthesis. Our method employs a template-based approach and synthesizes the SI and the RSM simultaneously. We assume that our method is provided with an affine/polynomial invariant I which over-approximates the set of all reachable states in the program, which is necessary since the defining conditions of SI-indicators and RSMs are required to hold at all reachable program states. Note that invariant generation is an orthogonal and well-studied problem and can be automated using [10]. For both the SI-indicator and the RSM, our method first fixes a symbolic template affine/polynomial expression for each location in the program. Then, all the defining conditions of SI-indicators and RSMs are encoded as a system of constraints over the symbolic template variables, where reachability of program states is encoded using the invariant I, and the synthesis proceeds by solving this system of constraints. We describe our algorithm in Sect. 6, and show that it is relatively complete with respect to the provided invariant I and the probability threshold \(1-p\). On the other hand, we note that our algorithm can also be adapted to compute lower bounds on the termination probability by combining it with a binary search on p.
Completeness vs Relative Completeness. Our characterization of stochastic invariants using indicator functions is complete. So is our reduction from quantitative termination analysis to the problem of synthesizing an SI-indicator function and a certificate for almost-sure reachability. These are our core theoretical contributions in this work. Nevertheless, as mentioned above, RSMs are complete only for finite termination, not a.s. termination. Moreover, template-based approaches lead to completeness guarantees only for solutions that match the template, e.g. polynomial termination certificates of a bounded degree. Therefore, our end-to-end approach is only relatively complete. These losses of completeness are due to Rice’s undecidability theorem and inevitable even in qualitative termination analysis. In this work, we successfully provide approaches for quantitative termination analysis that are as complete as the best known methods for the qualitative case.
3 Preliminaries
We consider imperative arithmetic probabilistic programs with non-determinism. Our programs allow standard programming constructs such as conditional branching, while-loops and variable assignments. They also allow two probabilistic constructs – probabilistic branching which is indicated in the syntax by a command ‘if prob(p) then \(\dots \)’ with \(p\in [0,1]\) a real constant, and sampling instructions of the form \(x:=d\) where d is a probability distribution. Sampling instructions may contain both discrete (e.g. Bernoulli, geometric or Poisson) and continuous (e.g. uniform, normal or exponential) distributions. We also allow constructs for (demonic) non-determinism. We have non-deterministic branching which is indicated in the syntax by ‘\({{\textbf {if}} \star {\textbf {then}}\dots }\)’, and non-deterministic assignments represented by an instruction of the form \(x := {\textbf {ndet}}([a,b]\)), where \(a, b \in \mathbb {R} \cup \{\pm \infty \}\) and [a, b] is a (possibly unbounded) real interval from which the new variable value is chosen non-deterministically. We also allow one or both sides of the interval to be open. The complete syntax of our programs is presented in [12, Appendix A].
Notation. We use boldface symbols to denote vectors. For a vector \(\mathbf {x}\) of dimension n and \(1\le i\le n\), \(\mathbf {x}[i]\) denotes the i-th component of \(\mathbf {x}\). We write \(\mathbf {x}[i\leftarrow a]\) to denote an n-dimensional vector \(\mathbf {y}\) with \(\mathbf {y}[i]=a\) and \(\mathbf {y}[j]=\mathbf {x}[j]\) for \(j\ne i\).
Program Variables. Variables in our programs are real-valued. Given a finite set of variables V, a variable valuation of V is a vector \(\mathbf {x}\in \mathbb {R}^{|V|}.\)
Probabilistic Control-Flow Graphs (pCFGs). We model our programs via probabilistic control-flow graphs (pCFGs) [11, 14]. A probabilistic control-flow graph (pCFG) is a tuple \(\mathcal {C}=( L ,V,\ell _{ init },\mathbf {x}_{ init },\mapsto ,G, Pr , Up )\), where:
-
\( L \) is a finite set of locations, partitioned into locations of conditional branching \(L_C\), probabilistic branching \(L_P\), non-det branching \(L_N\) and assignment \(L_A\).
-
\(V=\{x_1,\dots ,x_{|V|}\}\) is a finite set of program variables;
-
\(\ell _{ init }\) is the initial program location;
-
\(\mathbf {x}_{ init }\in \mathbb {R}^{|V|}\) is the initial variable valuation;
-
\(\mapsto \subseteq L \times L \) is a finite set of transitions. For each transition \(\tau =(\ell ,\ell ')\), we say that \(\ell \) is its source location and \(\ell '\) its target location;
-
\(G\) is a map assigning to each transition \(\tau =(\ell ,\ell ')\in \,\mapsto \) with \(\ell \in L_C\) a guard \(G(\tau )\), which is a logical formula over V specifying whether \(\tau \) can be executed;
-
\( Pr \) is a map assigning to each transition \(\tau =(\ell ,\ell ')\in \,\mapsto \) with \(\ell \in L_P\) a probability \( Pr (\tau )\in [0,1]\). We require \(\sum _{\tau =(\ell ,\_)} Pr (\tau )=1\) for each \(\ell \in L _P\);
-
\( Up \) is a map assigning to each transition \(\tau =(\ell ,\ell ')\in \,\mapsto \) with \(\ell \in L_A\) an update \( Up (\tau )=(j,u)\) where \(j\in \{1,\dots ,|V|\}\) is a target variable index and u is an update element which can be:
-
the bottom element \(u=\bot \), denoting no update;
-
a Borel-measurable expression \(u:\mathbb {R}^{|V|}\rightarrow \mathbb {R}\), denoting a deterministic variable assignment;
-
a probability distribution \(u=d\), denoting that the new variable value is sampled according to d;
-
an interval \(u=[a,b]\subseteq \mathbb {R}\cup \{\pm \infty \}\), denoting a non-deterministic update. We also allow one or both sides of the interval to be open.
-
We assume the existence of the special terminal location denoted by \(\ell _ out \). We also require that each location has at least one outgoing transition, and that each \(\ell \in L _A\) has a unique outgoing transition. For each location \(\ell \in L_C\), we assume that the disjunction of guards of all transitions outgoing from \(\ell \) is equivalent to \( true \), i.e. \(\bigvee _{\tau =(l,\_)}G(\tau )\equiv true \). Translation of probabilistic programs to pCFGs that model them is standard, so we omit the details and refer the reader to [11]. The pCFG for the program in Fig. 1 is provided in [12, Appendix B].
States, Paths and Runs. A state in a pCFG \(\mathcal {C}\) is a tuple \((\ell ,\mathbf {x})\), where \(\ell \) is a location in \(\mathcal {C}\) and \(\mathbf {x}\in \mathbb {R}^{|V|}\) is a variable valuation of V. We say that a transition \(\tau =(\ell ,\ell ')\) is enabled at a state \((\ell ,\mathbf {x})\) if \(\ell \not \in L_C\) or if \(\ell \in L_C\) and \(\mathbf {x}\models G(\tau )\). We say that a state \((\ell ',\mathbf {x}')\) is a successor of \((\ell ,\mathbf {x})\), if there exists an enabled transition \(\tau =(\ell ,\ell ')\) in \(\mathcal {C}\) such that \((\ell ',\mathbf {x}')\) can be reached from \((\ell ,\mathbf {x})\) by executing \(\tau \), i.e. we can obtain \(\mathbf {x}'\) by applying the updates of \(\tau \) to \(\mathbf {x}\), if any. A finite path in \(\mathcal {C}\) is a sequence \((\ell _0,\mathbf {x}_0),(\ell _1,\mathbf {x}_1),\dots ,(\ell _k,\mathbf {x}_k)\) of states with \((\ell _0,\mathbf {x}_0)=(\ell _{ init },\mathbf {x}_{ init })\) and with \((\ell _{i+1},\mathbf {x}_{i+1})\) being a successor of \((\ell _i,\mathbf {x}_i)\) for each \(0\le i\le k-1\). A state \((\ell ,\mathbf {x})\) is reachable in \(\mathcal {C}\) if there exists a finite path in \(\mathcal {C}\) that ends in \((\ell ,\mathbf {x})\). A run (or execution) in \(\mathcal {C}\) is an infinite sequence of states where each finite prefix is a finite path. We use \( State _\mathcal {C}\), \( Fpath _\mathcal {C}\), \( Run _\mathcal {C}\), \( Reach _\mathcal {C}\) to denote the set of all states, finite paths, runs and reachable states in \(\mathcal {C}\), respectively. Finally, we use \( State _{ term }\) to denote the set \(\{(\ell _ out ,\mathbf {x})\mid \mathbf {x}\in \mathbb {R}^{|V|}\}\) of terminal states.
Schedulers. The behavior of a pCFG may be captured by defining a probability space over the set of all runs in the pCFG. For this to be done, however, we need to resolve non-determinism and this is achieved via the standard notion of a scheduler. A scheduler in a pCFG \(\mathcal {C}\) is a map \(\sigma \) which to each finite path \(\rho \in Fpath _\mathcal {C}\) assigns a probability distribution \(\sigma (\rho )\) over successor states of the last state in \(\rho \). Since we deal with programs operating over real-valued variables, the set \( Fpath _{\mathcal {C}}\) may be uncountable. To that end, we impose an additional measurability assumption on schedulers, in order to ensure that the semantics of probabilistc programs with non-determinism is defined in a mathematically sound way. The restriction to measurable schedulers is standard. Hence, we omit the formal definition.
Semantics of pCFGs. A pCFG \(\mathcal {C}\) with a scheduler \(\sigma \) define a stochastic process taking values in the set of states of \(\mathcal {C}\), whose trajectories correspond to runs in \(\mathcal {C}\). The process starts in the initial state \( (\ell _{ init },\mathbf {x}_{ init }) \) and inductively extends the run, where the next state along the run is chosen either deterministically or is sampled from the probability distribution defined by the current location along the run and by the scheduler \(\sigma \). These are the classical operational semantics of Markov decision processes (MDPs), see e.g. [1, 27]. A pCFG \(\mathcal {C}\) and a scheduler \(\sigma \) together determine a probability space \(( Run _\mathcal {C},\mathcal {F}_{\mathcal {C}},\mathbb {P}^{\sigma })\) over the set of all runs in \(\mathcal {C}\). For details, see [12, Appendix C]. We denote by \(\mathbb {E}^\sigma \) the expectation operator on \(( Run _\mathcal {C},\mathcal {F}_{\mathcal {C}},\mathbb {P}^{\sigma })\). We may analogously define a probability space \(( Run _{\mathcal {C}(\ell ,\mathbf {x})},\mathcal {F}_{\mathcal {C}(\ell ,\mathbf {x})},\mathbb {P}^{\sigma }_{\mathcal {C}(\ell ,\mathbf {x})})\) over the set of all runs in \(\mathcal {C}\) that start in some specified state \((\ell ,\mathbf {x})\).
Probabilistic Termination Problem. We now define the termination problem for probabilistic programs considered in this work. A state \((\ell ,\mathbf {x})\) in a pCFG \(\mathcal {C}\) is said to be a terminal state if \(\ell =\ell _ out \). A run \(\rho \in Run _{\mathcal {C}}\) is said to be terminating if it reaches some terminal state in \(\mathcal {C}\). We use \( Term \subseteq Run _{\mathcal {C}}\) to denote the set of all terminating runs in \( Run _{\mathcal {C}}\). The termination probability of a pCFG \(\mathcal {C}\) is defined as \(\inf _\sigma \mathbb {P}^{\sigma }[ Term ]\), i.e. the smallest probability of the set of terminating runs in \(\mathcal {C}\) with respect to any scheduler in \(\mathcal {C}\) (for the proof that \( Term \) is measurable, see [40]). We say that \(\mathcal {C}\) terminates almost-surely (a.s.) if its termination probability is 1. In this work, we consider the Lower Bound on the Probability of Termination (LBPT) problem that, given \(p \in [0, 1],\) asks whether \(1-p\) is a lower bound for the termination probability of the given probabilistic program, i.e. whether \(\inf _\sigma \mathbb {P}^{\sigma }[ Term ] \ge 1-p.\)
4 A Sound and Complete Characterization of SIs
In this section, we recall the notion of stochastic invariants and present our characterization of stochastic invariants through stochastic indicator functions. We fix a pCFG \(\mathcal {C}=( L ,V,\ell _{ init },\mathbf {x}_{ init },\mapsto ,G, Pr , Up )\). A predicate function in \(\mathcal {C}\) is a map F that to every location \(\ell \in L \) assigns a logical formula \(F(\ell )\) over program variables. It naturally induces a set of states, which we require to be Borel-measurable for the semantics to be well-defined. By a slight abuse of notation, we identify a predicate function F with this set of states. Furthermore, we use \(\lnot F\) to denote the negation of a predicate function, i.e. \((\lnot F)(\ell ) = \lnot F(\ell )\). An invariant in \(\mathcal {C}\) is a predicate function I which additionally over-approximates the set of reachable states in \(\mathcal {C}\), i.e. for every \((\ell ,\mathbf {x})\in Reach _\mathcal {C}\) we have \(\mathbf {x}\models I(\ell )\). Stochastic invariants can be viewed as a probabilistic extension of invariants, which a random program run leaves only with a certain probability. See Sect. 2 for an example.
Definition 1
(Stochastic invariant [14]). Let \( SI \) a predicate function in \(\mathcal {C}\) and \(p \in [0,1]\) a probability. The tuple \(( SI , p)\) is a stochastic invariant (SI) if the probability of a run in \(\mathcal {C}\) leaving the set of states defined by \( SI \) is at most p under any scheduler. Formally, we require that
Key Challenge. If we find a stochastic invariant \(( SI , p)\) for which termination happens almost-surely on runs that do not leave \( SI \), we can immediately conclude that the program terminates with probability at least \(1 - p\) (this idea is formalized in Sect. 5). The key challenge in designing an efficient termination analysis based on this idea is the computation of appropriate stochastic invariants. We present a sound and complete characterization of stochastic invariants which allows for their effective automated synthesis through template-based methods.
We characterize stochastic invariants through the novel notion of stochastic invariant indicators (SI-indicators). An SI-indicator is a function that to each state assigns an upper-bound on the probability of violating the stochastic invariant if we start the program in that state. Since the definition of an SI-indicator imposes conditions on its value at reachable states and since computing the exact set of reachable states is in general infeasible, we define SI-indicators with respect to a supporting invariant with the later automation in mind. In order to understand the ideas of this section, one may assume for simplicity that the invariant exactly equals the set of reachable states. A state-function in \(\mathcal {C}\) is a function f that to each location \(\ell \in L \) assigns a Borel-measurable real-valued function over program variables \(f(\ell ) : \mathbb {R}^{|V|} \rightarrow \mathbb {R}\). We use \(f(\ell , \mathbf {x})\) and \(f(\ell )(\mathbf {x})\) interchangeably.
Definition 2 (Stochastic invariant indicator)
A tuple \((f_{ SI },p)\) comprising a state function \(f_{ SI }\) and probability \(p \in [0,1]\) is a stochastic invariant indicator (SI-indicator) with respect to an invariant I, if it satisfies the following conditions:
- (\(C_1\)):
-
Non-negativity. For every location \(\ell \in L \), we have \(\mathbf {x}\models I(\ell )\Rightarrow f_{ SI }(\ell ,\mathbf {x})\ge ~0\).
- (\(C_2\)):
-
Non-increasing expected value. For every location \(\ell \in L \), we have:
- (\(C_2^1\)):
-
If \(\ell \in L_C\), then for any transition \(\tau =(\ell ,\ell ')\) we have \(\mathbf {x}\models I(\ell )\wedge G(\tau )\Rightarrow f_ SI (\ell ,\mathbf {x})\ge f_ SI (\ell ',\mathbf {x})\).
- (\(C_2^2\)):
-
If \(\ell \in L_P\), then \(\mathbf {x}\models I(\ell )\Rightarrow f_ SI (\ell ,\mathbf {x})\ge \sum _{\tau =(\ell ,\ell ')\in \,\mapsto }\Pr (\tau )\cdot f_ SI (\ell ',\mathbf {x})\).
- (\(C_2^3\)):
-
If \(\ell \in L_N\), then \(\mathbf {x}\models I(\ell )\Rightarrow f_ SI (\ell ,\mathbf {x})\ge \max _{\tau =(\ell ,\ell ')\in \,\mapsto }f_ SI (\ell ',\mathbf {x})\).
- (\(C_2^4\)):
-
If \(\ell \in L_A\) with \(\tau =(\ell ,\ell ')\) the unique outgoing transition from \(\ell \), then:
- –:
-
If \( Up (\tau )=(j,\bot )\), \(\mathbf {x}\models I(\ell ) \Rightarrow f(\ell ,\mathbf {x}) \ge f(\ell ',\mathbf {x}).\)
- –:
-
If \( Up (\tau )=(j,u)\) with \(u:\mathbb {R}^{|V|}\rightarrow \mathbb {R}\) an expression, we have \(\mathbf {x}\models I(\ell ) \Rightarrow f(\ell ,\mathbf {x}) \ge f(\ell ',\mathbf {x}[x_j\leftarrow u(\mathbf {x}_i)]).\)
- –:
-
If \( Up (\tau )=(j,u)\) with \(u=d\) a distribution, we have \(\mathbf {x}\models I(\ell ) \Rightarrow f(\ell ,\mathbf {x}) \ge \mathbb {E}_{X\sim d}[f(\ell ',\mathbf {x}[x_j\leftarrow X])].\)
- –:
-
If \( Up (\tau )=(j,u)\) with \(u=[a,b]\) an interval, we have \(\mathbf {x}\models I(\ell ) \Rightarrow f(\ell ,\mathbf {x}) \ge \sup _{X\in [a,b]}\{f(\ell ',\mathbf {x}[x_j\leftarrow X])\}.\)
- (\(C_3\)):
-
Initial condition. We have \(f(\ell _{ init },\mathbf {x}_{ init })\le p\).
Intuition. \((C_1)\) imposes that f is nonnegative at any state contained in the invariant I. Next, for any state in I, \((C_2)\) imposes that the value of f does not increase in expectation upon a one-step execution of the pCFG under any scheduler. Finally, the condition \((C_3)\) imposes that the initial value of f in \(\mathcal {C}\) is at most p. Together, the indicator thus intuitively over-approximates the probability of violating \( SI \). An example of an SI-indicator for our running example in Fig. 1 is given in (2). The following theorem formalizes the above intuition and is our main result of this section. In essence, we prove that \(( SI ,p)\) is a stochastic invariant in \(\mathcal {C}\) iff there exists an SI-indicator \((f_ SI ,p)\) such that \( SI \) contains all states at which \(f_ SI \) is strictly smaller than 1. This implies that, for every stochastic invariant \(( SI ,p)\), there exists an SI-indicator such that \(( SI ',p)\) defined via \( SI '(\ell )=(\mathbf {x}\models I(\ell ) \wedge f_ SI (\ell ,\mathbf {x}) < 1)\) is a stochastic invariant that is at least as tight as \(( SI ,p)\).
Theorem 1 (Soundness and Completeness of SI-indicators)
Let \(\mathcal {C}\) be a pCFG, I an invariant in \(\mathcal {C}\) and \(p \in [0,1]\). For any SI-indicator \((f_ SI , p)\) with respect to I, the predicate map \( SI \) defined as \( SI (\ell )=(\mathbf {x}\models I(\ell ) \wedge f_ SI (\ell ,\mathbf {x}) < 1)\) yields a stochastic invariant \(( SI ,p)\) in \(\mathcal {C}\). Conversely, for every stochastic invariant \(( SI ,p)\) in \(\mathcal {C}\), there exist an invariant \(I_ SI \) and a state function \(f_ SI \) such that \((f_ SI ,p)\) is an SI-indicator with respect to \(I_ SI \) and for each \(\ell \in L \) we have \( SI (\ell )\supseteq (\mathbf {x}\models I_ SI (\ell ) \wedge f_ SI (\ell ,\mathbf {x}) < 1)\).
Proof Sketch. Since the proof is technically involved, we present the main ideas here and defer the details to [12, Appendix E]. First, suppose that I is an invariant in \(\mathcal {C}\) and that \((f_ SI ,p)\) is an SI-indicator with respect to I, and let \( SI (\ell )=(\mathbf {x}\models I(\ell ) \wedge f_ SI (\ell ,\mathbf {x}) < 1)\) for each \(\ell \in L \). We need to show that \(( SI ,p)\) is a stochastic invariant in \(\mathcal {C}\). Let \(\sup _{\sigma }\mathbb {P}_{(\ell ,\mathbf {x})}^\sigma [ Reach (\lnot SI )]\) be a state function that maps each state \((\ell ,\mathbf {x})\) to the probability of reaching \(\lnot SI \) from \((\ell ,\mathbf {x})\). We consider a lattice of non-negative semi-analytic state-functions \((\mathcal {L},\sqsubseteq )\) with the partial order defined via \(f\sqsubseteq f'\) if \(f(\ell ,\mathbf {x})\le f'(\ell ,\mathbf {x})\) holds for each state \((\ell ,\mathbf {x})\) in I. See [12, Appendix D] for a review of lattice theory. It follows from a result in [40] that the probability of reaching \(\lnot SI \) can be characterized as the least fixed point of the next-time operator \(\mathbb {X}_{\lnot SI }:\mathcal {L}\rightarrow \mathcal {L}\). Away from \(\lnot SI \), the operator \(\mathbb {X}_{\lnot SI }\) simulates a one-step execution of \(\mathcal {C}\) and maps \(f\in \mathcal {L}\) to its maximal expected value upon one-step execution of \(\mathcal {C}\) where the maximum is taken over all schedulers, and at states contained in \(\lnot SI \) the operator \(\mathbb {X}_{\lnot SI }\) is equal to 1. It was also shown in [40] that, if a state function \(f\in \mathcal {L}\) is a pre-fixed point of \(\mathbb {X}_{\lnot SI }\), then it satisfies \(\sup _{\sigma }\mathbb {P}_{(\ell ,\mathbf {x})}^\sigma [ Reach (\lnot SI )]\le f(\ell ,\mathbf {x})\) for each \((\ell ,\mathbf {x})\) in I. Now, by checking the defining properties of pre-fixed points and recalling that \(f_{ SI }\) satisfies Non-negativity condition \((C_1)\) and Non-increasing expected value condition \((C_2)\) in Definition 2, we can show that \(f_{ SI }\) is contained in the lattice \(\mathcal {L}\) and is a pre-fixed point of \(\mathbb {X}_{\lnot SI }\). It follows that \(\sup _{\sigma }\mathbb {P}_{(\ell _{ init },\mathbf {x}_{ init })}^\sigma [ Reach (\lnot SI )]\le f_ SI (\ell _{ init },\mathbf {x}_{ init })\). On the other hand, by initial condition \((C_3)\) in Definition 2 we know that \(f_ SI (\ell _{ init },\mathbf {x}_{ init })\le p\). Hence, we have \(\sup _{\sigma }\mathbb {P}_{(\ell _{ init },\mathbf {x}_{ init })}^\sigma [ Reach (\lnot SI )]\le p\) so \(( SI ,p)\) is a stochastic invariant.
Conversely, suppose that \(( SI ,p)\) is a stochastic invariant in \(\mathcal {C}\). We show in [12, Appendix E] that, if we define \(I_ SI \) to be the trivial true invariant and define \(f_ SI (\ell ,\mathbf {x}) = \sup _{\sigma }\mathbb {P}_{(\ell ,\mathbf {x})}^\sigma [ Reach (\lnot SI )]\), then \((f_ SI ,p)\) forms an SI-indicator with respect to \(I_ SI \). The claim follows by again using the fact that \(f_ SI \) is the least fixed point of the operator \(\mathbb {X}_{\lnot SI }\), from which we can conclude that \((f_ SI ,p)\) satisfies conditions \((C_1)\) and \((C_2)\) in Definition 2. On the other hand, the fact that \(( SI ,p)\) is a stochastic invariant and our choice of \(f_{ SI }\) imply that \((f_ SI ,p)\) satisfies the initial condition \((C_3)\) in Definition 2. Hence, \((f_ SI ,p)\) forms an SI-indicator with respect to \(I_ SI \). Furthermore, \( SI (\ell ) \supseteq (\mathbf {x}\models I_ SI (\ell ) \wedge f_ SI (\ell ,\mathbf {x}) < 1)\) follows since \(1>f_ SI (\ell ,\mathbf {x}) = \sup _{\sigma }\mathbb {P}_{(\ell ,\mathbf {x})}^\sigma [ Reach (\lnot SI )]\) implies that \((\ell ,\mathbf {x})\) cannot be contained in \(\lnot SI \) so \(\mathbf {x}\models SI (\ell )\). This concludes the proof. \(\square \)
Based on the theorem above, in order to compute a stochastic invariant in \(\mathcal {C}\) for a given probability threshold p, it suffices to synthesize a state function \(f_ SI \) that together with p satisfies all the defining conditions in Definition 2 with respect to some supporting invariant I, and then consider a predicate function \( SI \) defined via \( SI (\ell )=(\mathbf {x}\models I(\ell ) \wedge f_ SI (\ell ,\mathbf {x}) < 1)\) for each \(\ell \in L \). This will be the guiding principle of our algorithmic approach in Sect. 6.
Intuition on Characterization. Stochastic invariants can essentially be thought of as quantitative safety specifications in probabilistic programs – \(( SI ,p)\) is a stochastic invariant if and only if a random probabilistic program run leaves \( SI \) with probability at most p. However, what makes their computation hard is that they do not consider probabilities of staying within a specified safe set. Rather, the computation of stochastic invariants requires computing both the safe set and the certificate that it is left with at most the given probability. Nevertheless, in order to reason about them, we may consider \( SI \) as an implicitly defined safe set. Hence, if we impose conditions on a state function \(f_ SI \) to be an upper bound on the reachability probability for the target set of states \((\mathbf {x}\models I(\ell ) \wedge f_ SI (\ell ,\mathbf {x}) < 1)\), and in addition impose that \(f_ SI (\ell _{ init },\mathbf {x}_{ init })\le p\), then these together will entail that p is an upper bound on the probability of ever leaving \( SI \) when starting in the initial state. This is the intuitive idea behind our construction of SI-indicators, as well as our soundness and completeness proof. In the proof, we show that conditions \((C_1)\) and \((C_2)\) in Definition 2 indeed entail the necessary conditions to be an upper bound on the reachability probability of the set \((\mathbf {x}\models I(\ell ) \wedge f_ SI (\ell ,\mathbf {x}) < 1).\)
5 Stochastic Invariants for LBPT
In the previous section, we paved the way for automated synthesis of stochastic invariants by providing a sound and complete characterization in terms of SI-indicators. We now show how stochastic invariants in combination with any a.s. termination certificate for probabilistic programs can be used to compute lower-bounds on the probability of termination. Theorem 2 below states a general result about termination probabilities that is agnostic to the termination certificate, and shows that stochastic invaraints provide a sound and complete approach to quantitative termination analysis.
Theorem 2 (Soundness and Completeness of SIs for Quantitative Termination)
Let \(\mathcal {C}=( L ,V,\ell _{ init },\mathbf {x}_{ init },\mapsto ,G, Pr , Up )\) be a pCFG and \(( SI ,p)\) a stochastic invariant in \(\mathcal {C}\). Suppose that, with respect to every scheduler, a run in \(\mathcal {C}\) almost-surely either terminates or reaches a state in \(\lnot SI \), i.e.
Then \(\mathcal {C}\) terminates with probability at least \(1-p\). Conversely, if \(\mathcal {C}\) terminates with probability at least \(1-p\), then there exists a stochastic invariant \(( SI ,p)\) in \(\mathcal {C}\) such that, with respect to every scheduler, a run in \(\mathcal {C}\) almost-surely either terminates or reaches a state in \(\lnot SI \).
Proof Sketch. The first part (soundness) follows directly from the definition of \( SI \) and (4). The completeness proof is conceptually and technically involved and presented in [12, Appendix H]. In short, the central idea is to construct, for every n greater than a specific threshold \(n_0\), a stochastic invariant \(( SI _n, p+\frac{1}{n})\) such that a run almost-surely either terminates or exists \( SI _n.\) Then, we show that \(\cap _{n=n_0}^\infty SI _n\) is our desired \( SI .\) To construct each \( SI _n,\) we consider the infimum termination probability at every state \((\ell , \mathbf {x})\) and call it \(r(\ell , \mathbf {x}).\) The infimum is taken over all schedulers. We then let \( SI _n\) be the set of states \((\ell , \mathbf {x})\) for whom \(r(\ell , \mathbf {x})\) is greater than a specific threshold \(\alpha .\) Intuitively, our stochastic invariant is the set of program states from which the probability of termination is at least \(\alpha ,\) no matter how the non-determinism is resolved. Let us call these states likely-terminating. The intuition is that a random run of the program will terminate or eventually leave the likely-terminating states with high probability. \(\square \)
Quantitative to Qualitative Termination. Theorem 2 provides us with a recipe for computing lower bounds on the probability of termination once we are able to compute stochastic invariants: if \(( SI ,p)\) is a stochastic invariant in a pCFG \(\mathcal {C}\), it suffices to prove that the set of states \( State _{ term } \cup \lnot SI \) is reached almost-surely with respect to any scheduler in \(\mathcal {C}\), i.e. the program terminates or violates SI. Note that this is simply a qualitative a.s. termination problem, except that the set of terminal states is now augmented with \(\lnot SI .\) Then, since \(( SI , p)\) is a stochastic invariant, it would follow that a terminal state is reached with probability at least \(1 - p\). Moreover, the theorem shows that this approach is both sound and complete. In other words, proving quantitative termination, i.e. that we reach \( State _{ term }\) with probability at least \(1-p\) is now reduced to (i) finding a stochastic invariant \(( SI , p)\) and (ii) proving that the program \(\mathcal {C}'\) obtained by adding \(\lnot SI \) to the set of terminal states of \(\mathcal {C}\) is a.s. terminating. Note that, to preserve completeness, (i) and (ii) should be achieved in tandem, i.e. an approach that first synthesizes and fixes \( SI \) and then tries to prove a.s. termination for \(\lnot SI \) is not complete.
Ranking Supermartingales. While our reduction above is agnostic to the type of proof/certificate that is used to establish a.s. termination, in this work we use Ranking Supermartingales (RSMs) [7], which are a standard and classical certificate for proving a.s. termination and reachability. Let \(\mathcal {C}=( L ,V,\ell _{ init },\mathbf {x}_{ init },\mapsto ,G, Pr , Up )\) be a pCFG and I an invariant in \(\mathcal {C}\). Note that as in Definition 2, the main purpose of the invariant is to allow for automated synthesis and one can again simply assume it to equal the set of reachable states. An \(\varepsilon \)-RSM for a subset T of states is a state function that is non-negative in each state in I, and whose expected value decreases by at least \(\varepsilon >0\) upon a one-step execution of \(\mathcal {C}\) in any state that is not contained in the target set T. Thus, intuitively, a program run has an expected tendency to approach the target set T where the distance to T is given by the value of the RSM which is required to be non-negative in all states in I. The \(\varepsilon \)-ranked expected value condition is formally captured via the next-time operator \(\mathbb {X}\) (See [12, Appendix E]). An example of an RSM for our running example in Fig. 1 and the target set of states \(\lnot SI \cup State _{ term }\) with \( SI \) the stochastic invariant in Eq. (1) is given in Eq. (3).
Definition 3 (Ranking supermartingales)
Let T be a predicate function defining a set of target states in \(\mathcal {C}\), and let \(\varepsilon >0\). A state function \(\eta \) is said to be an \(\varepsilon \)-ranking supermartingale (\(\varepsilon \)-RSM) for T with respect to the invariant I if it satisfies the following conditions:
-
1.
Non-negativity. For each location \(\ell \in L \) and \(\mathbf {x}\in I(\ell )\), we have \(\eta (\ell ,\mathbf {x})\ge 0\).
-
2.
\(\varepsilon \)-ranked expected value. For each location \(\ell \in L \) and \(\mathbf {x}\models I(\ell )\cap \lnot T(\ell )\), we have \(\eta (\ell ,\mathbf {x})\ge \mathbb {X}(\eta )(\ell ,\mathbf {x})+\varepsilon \).
Note that the second condition can be expanded according to location types in the exact same manner as in condition \(C_2\) of Definition 2. The only difference is that in Definition 2, the expected value had to be non-increasing, whereas here it has to decrease by \(\varepsilon .\) It is well-known that the two conditions above entail that T is reached with probability 1 with respect to any scheduler [7, 11].
Theorem 3
(Proof in [12, Appendix I]). Let \(\mathcal {C}\) be a pCFG, I an invariant in \(\mathcal {C}\) and T a predicate function defining a target set of states. If there exist \(\varepsilon >0\) and an \(\varepsilon \)-RSM for T with respect to I, then T is a.s. reached under any scheduler, i.e.
The following theorem is an immediate corollary of Theorems 2 and 3.
Theorem 4
Let \(\mathcal {C}\) be a pCFG and I be an invariant in \(\mathcal {C}\). Suppose that there exist a stochastic invariant \(( SI ,p)\), an \(\varepsilon >0\) and an \(\varepsilon \)-RSM \(\eta \) for \( State _{ term }\cup \lnot SI \) with respect to I. Then \(\mathcal {C}\) terminates with probability at least \(1-p\).
Therefore, in order to prove that \(\mathcal {C}\) terminates with probability at least \(1-p\), it suffices to find (i) a stochastic invariant \(( SI ,p)\) in \(\mathcal {C}\), and (ii) an \(\varepsilon \)-RSM \(\eta \) for \( State _{ term }\cup \lnot SI \) with respect to I and some \(\varepsilon >0\). Note that these two tasks are interdependent. We cannot simply choose any stochastic invariant. For instance, the trivial predicate function defined via \( SI = \text {true}\) always yields a valid stochastic invariant for any \(p\in [0,1]\), but it does not help termination analysis. Instead, we need to compute a stochastic invariant and an RSM for it simultaneously.
Power of Completeness. We end this section by showing that our approach certifies a tight lower-bound on termination probability for a program that was proven in [40] not to admit any of the previously-existing certificates for lower bounds on termination probability. This shows that our completeness pays off in practice and our approach is able to handle programs that were beyond the reach of previous methods. Consider the program in Fig. 2 annotated by an invariant I. We show that our approach certifies that this program terminates with probability at least 0.5. Indeed, consider a stochastic invariant \(( SI ,0.5)\) with \( SI (\ell )=\text {true}\) if \(\ell \ne \ell _3\), and \( SI (\ell _3)=\text {false}\), and a state function defined via \(\eta (\ell _{ init }, x)=-\log (x)+\log (2)+3\), \(\eta (\ell _1, x)=-\log (x)+\log (2)+2\), \(\eta (\ell _2, x) = 1\) and \(\eta (\ell _3,x)=\eta (\ell _ out ,x)=0\) for each x. Then one can easily check by inspection that \(( SI ,0.5)\) is a stochastic invariant and that \(\eta \) is a \((\log (2)-1)\)-RSM for \( State _{ term }\cup \lnot SI \) with respect to I. Therefore, it follows by Theorem 4 that the program in Fig. 2 terminates with probability at least 0.5.
6 Automated Template-Based Synthesis Algorithm
We now provide template-based relatively complete algorithms for simultaneous and automated synthesis of SI-indicators and RSMs, in order to solve the quantitative termination problem over pCFGs with affine/polynomial arithmetic. Our approach builds upon the ideas of [2, 9] for qualitative and non-probabilistic cases.
Input and Assumptions. The input to our algorithms consists of a pCFG \(\mathcal {C}\) together with a probability \(p \in [0, 1],\) an invariant I, Footnote 1 and technical variables \(\delta \) and M, which specify polynomial template sizes used by the algorithm and which will be discussed later. In this section, we limit our focus to affine/polynomial pCFGs, i.e. we assume that all guards \(G(\tau )\) in \(\mathcal {C}\) and all invariants \(I(\ell )\) are conjunctions of affine/polynomial inequalities over program variables. Similarly, we assume that every update function \(u: \mathbb {R}^{|V|} \rightarrow \mathbb {R}\) used in deterministic variable assignments is an affine/polynomial expression in \(\mathbb {R}[V].\)
Output. The goal of our algorithms is to synthesize a tuple \((f, \eta , \varepsilon )\) where f is an SI-indicator function, \(\eta \) is a corresponding RSM, and \(\varepsilon > 0,\) such that:
-
At every location \(\ell \) of \(\mathcal {C}\), both \(f(\ell )\) and \(\eta (\ell )\) are affine/polynomial expressions of fixed degree \(\delta \) over the program variables V.
-
Having \( SI (\ell ) := \{ \mathbf {x}~\vert ~ f(\ell , \mathbf {x}) < 1\},\) the pair \(( SI , p)\) is a valid stochastic invariant and \(\eta \) is an \(\varepsilon \)-RSM for \( State _{ term }\cup \lnot SI \) with respect to I.
As shown in Sects. 4 and 5, such a tuple \(w = (f, \eta , \varepsilon )\) serves as a certificate that the probabilistic program modeled by \(\mathcal {C}\) terminates with probability at least \(1-p.\) We call w a quantitative termination certificate.
Overview. Our algorithm is a standard template-based approach similar to [2, 9]. We encode the requirements of Definitions 2 and 3 as entailments between affine/polynomial inequalities with unknown coefficients and then apply the classical Farkas’ Lemma [17] or Putinar’s Positivstellensatz [38] to reduce the synthesis problem to Quadratic Programming (QP). Finally, we solve the resulting QP using a numerical optimizer or an SMT-solver. Our approach consists of the four steps below. Step 3 follows [2] exactly. Hence, we refer to [2] for more details on this step.
Step 1. Setting Up Templates. The algorithm sets up symbolic templates with unknown coefficients for \(f, \eta \) and \(\varepsilon .\)
-
First, for each location \(\ell \) of \(\mathcal {C},\) the algorithm sets up a template for \(f(\ell )\) which is a polynomial consisting of all possible monomials of degree at most \(\delta \) over program variables, each appearing with an unknown coefficient. For example, consider the program in Fig. 1 of Sect. 2. This program has three variables: \(x, r_1\) and \(r_2\). If \(\delta =1,\) i.e. if the goal is to find an affine SI-indicator, at every location \(\ell _i\) of the program, the algorithm sets
 Similarly, if the desired degree is \(\delta = 2,\) the algorithm symbolically computes:
Similarly, if the desired degree is \(\delta = 2,\) the algorithm symbolically computes: Note that every monomial of degree at most 2 appears in this expression. The goal is to synthesize suitable real values for each unknown coefficient
Note that every monomial of degree at most 2 appears in this expression. The goal is to synthesize suitable real values for each unknown coefficient 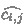 such that f becomes an SI-indicator. Throughout this section, we use the
such that f becomes an SI-indicator. Throughout this section, we use the  notation to denote an unknown coefficient whose value will be synthesized by our algorithm.
notation to denote an unknown coefficient whose value will be synthesized by our algorithm. -
The algorithm creates an unknown variable
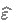 whose final value will serve as \(\varepsilon .\)
whose final value will serve as \(\varepsilon .\) -
Finally, at each location \(\ell \) of \(\mathcal {C},\) the algorithm sets up a template for \(\eta (\ell )\) in the exact same manner as the template for \(f(\ell )\). The goal is to synthesize values for
 and the
and the  variables in this template such that \(\eta \) becomes a valid
variables in this template such that \(\eta \) becomes a valid  -RSM for \( State _{ term }\cup \lnot SI \) with respect to I.
-RSM for \( State _{ term }\cup \lnot SI \) with respect to I.
Step 2. Generating Entailment Constraints. In this step, the algorithm symbolically computes the requirements of Definition 2, i.e. \(C_1\)–\(C_3\), and their analogues in Definition 3 using the templates generated in the previous step. Note that all of these requirements are entailments between affine/polynomial inequalities over program variables whose coefficients are unknown. In other words, they are of the form \( \forall \mathbf {x} ~~ A(\mathbf {x}) \Rightarrow b(\mathbf {x}) \) where A is a set of affine/polynomial inequalities over program variables whose coefficients contain the unknown variables  and
and  generated in the previous step and b is a single such inequality. For example, for the program of Fig. 1, the algorithm symbolically computes condition \(C_1\) at line \(\ell _1\) as follows: \( \textstyle \forall \mathbf {x} ~~ I(\ell _1, \mathbf {x}) \Rightarrow f(\ell _1, \mathbf {x}) \ge 0. \) Assuming that the given invariant is \(I(\ell _1, \mathbf {x}) := (x \le 1)\) and an affine (degree 1) template was generated in the previous step, the algorithm expands this to:
generated in the previous step and b is a single such inequality. For example, for the program of Fig. 1, the algorithm symbolically computes condition \(C_1\) at line \(\ell _1\) as follows: \( \textstyle \forall \mathbf {x} ~~ I(\ell _1, \mathbf {x}) \Rightarrow f(\ell _1, \mathbf {x}) \ge 0. \) Assuming that the given invariant is \(I(\ell _1, \mathbf {x}) := (x \le 1)\) and an affine (degree 1) template was generated in the previous step, the algorithm expands this to:

The algorithm generates similar entailment constraints for every location and every requirement in Definitions 2 and 3.
Step 3. Quantifier Elimination. At the end of the previous step, we have a system of constraints of the form \(\bigwedge _i \left( \forall \mathbf {x} ~~ A_i(\mathbf {x}) \Rightarrow b_i(\mathbf {x}) \right) .\) In this step, the algorithm sets off to eliminate the universal quantification over \(\mathbf {x}\) in every constraint. First, consider the affine case. If \(A_i\) is a set of linear inequalities over program variables and \(b_i\) is one such linear inequality, then the algorithm attempts to write \(b_i\) as a linear combination with non-negative coefficients of the inequalities in \(A_i\) and the trivial inequality \(1 \ge 0.\) For example, it rewrites (5) as  where
where  ’s are new non-negative unknown variables for which we need to synthesize non-negative real values. This inequality should hold for all valuations of program variables. Thus, we can equate the corresponding coefficients on both sides and obtain this equivalent system:
’s are new non-negative unknown variables for which we need to synthesize non-negative real values. This inequality should hold for all valuations of program variables. Thus, we can equate the corresponding coefficients on both sides and obtain this equivalent system:

This transformation is clearly sound, but it is also complete due to the well-known Farkas’ lemma [17]. Now consider the polynomial case. Again, we write \(b_i\) as a combination of the polynomials in \(A_i.\) The only difference is that instead of having non-negative real coefficients, we use sum-of-square polynomials as our multiplicands. For example, suppose our constraint is
where the \(g_i\)’s are polynomials with unknown coefficients. The algorithm writes
where each \(h_i\) is a sum-of-square polynomial of degree at most M. The algorithm sets up a template of degree M for each \(h_i\) and adds well-known quadratic constraints that enforce it to be a sum of squares. See [2, Page 22] for details. It then expands (7) and equates the corresponding coefficients of the LHS and RHS as in the linear case. The soundness of this transformation is trivial since each \(h_i\) is a sum-of-squares and hence always non-negative. Completeness follows from Putinar’s Positivstellensatz [38]. Since the arguments for completeness of this method are exactly the same as the method in [2], we refer the reader to [2] for more details and an extension to entailments between strict polynomial inequalities.
Step 4. Quadratic Programming. All of our constraints are converted to Quadratic Programming (QP) over template variables, e.g. see (6). Our algorithm passes this QP instance to an SMT solver or a numerical optimizer. If a solution is found, it plugs in the values obtained for the  and
and  variables back into the template of Step 1 and outputs the resulting termination witness \((f, \eta , \varepsilon ).\)
variables back into the template of Step 1 and outputs the resulting termination witness \((f, \eta , \varepsilon ).\)
We end this section by noting that our algorithm is sound and relatively complete for synthesizing affine/polynomial quantitative termination certificates.
Theorem 5
(Soundness and Completeness in the Affine Case). Given an affine pCFG \(\mathcal {C}\), an affine invariant I, and a non-termination upper-bound \(p \in [0, 1],\) if \(\mathcal {C}\) admits a quantitative termination certificate \(w = (f, \eta , \varepsilon )\) in which both f and \(\eta \) are affine expressions at every location, then w corresponds to a solution of the QP instance solved in Step 4 of the algorithm above. Conversely, every such solution, when plugged back into the template of Step 1, leads to an affine quantitative termination certificate showing that \(\mathcal {C}\) terminates with probability at least \(1-p\) over every scheduler.
Theorem 6
(Soundness and Relative Completeness in the Polynomial Case). Given a polynomial pCFG \(\mathcal {C}\), a polynomial invariant I which is a compact subset of \(\mathbb {R}^{|V|}\) at every location \(\ell \), and a non-termination upper-bound \(p \in [0, 1],\) if \(\mathcal {C}\) admits a quantitative termination certificate \(w = (f, \eta , \varepsilon )\) in which both f and \(\eta \) are polynomial expressions of degree at most \(\delta \) at every location, then there exists an \(M \in \mathbb {N},\) for which w corresponds to a solution of the QP instance solved in Step 4 of the algorithm above. Conversely, every such solution, when plugged back into the template of Step 1, leads to a polynomial quantitative termination certificate of degree at most \(\delta \) showing that \(\mathcal {C}\) terminates with probability at least \(1-p\) over every scheduler.
Proof
Step 2 encodes the conditions of an SI-indicator (Definition 2) and RSM (Definition 3). Theorem 4 shows that an SI-indicator together with an RSM is a valid quantitative termination certificate. The transformation in Step 3 is sound and complete as argued in [2, Theorems 4 and 10]Footnote 2. The affine version relies on Farkas’ lemma [17] and is complete with no additional constraints. The polynomial version is based on Putinar’s Positivstellensatz [38] and is only complete for large enough M, i.e. a high-enough degree for sum-of-square multiplicands. This is why we call our algorithm relatively complete. In practice, small values of M are enough to synthesize w and we use \(M=2\) in all of our experiments. \(\square \)
7 Experimental Results
Implementation. We implemented a prototype of our approach in Python and used SymPy [33] for symbolic computations and the MathSAT5 SMT Solver [15] for solving the final QP instances. We also applied basic optimizations, e.g. checking the validity of each entailment and thus removing tautological constraints.
Machine and Parameters. All results were obtained on an Intel Core i9-10885H machine (8 cores, 2.4 GHz, 16 MB Cache) with 32 GB of RAM running Ubuntu 20.04. We always synthesized quadratic termination certificates and set \(\delta = M = 2.\)
Benchmarks. We generated a variety of random walks with complicated behavior, including nested combinations of probabilistic and non-deterministic branching and loops. We also took a number of benchmarks from [14]. Due to space limitations, in Table 1 we only present experimental results on a subset of our benchmark set, together with short descriptions of these benchmarks. Complete evaluation as well as details on all benchmarks are provided in [12, Appendix J].
Results and Discussion. Our experimental results are summarized in Table 1, with complete results provided in [12, Appendix J]. In every case, our approach was able to synthesize a certificate that the program terminates with probability at least \(1-p\) under any scheduler. Moreover, our runtimes are consistently small and less than 6 s per benchmark. Our approach was able to handle programs that are beyond the reach of previous methods, including those with unbounded differences and unbounded non-deterministic assignments to which approaches such as [14] and [40] are not applicable, as was demonstrated in [40]. This adds experimental confirmation to our theoretical power-of-completeness result at the end of Sect. 5, which showed the wider applicability of our method. Finally, it is noteworthy that the termination probability lower-bounds reported in Table 1 are not tight. There are two reasons for this. First, while our theoretical approach is sound and complete, our algorithm can only synthesize affine/polynomial certificates for quantitative termination, and the best polynomial certificate of a certain degree might not be tight. Second, we rely on an SMT-solver to solve our QP instances. The QP instances often become harder as we decrease p, leading to the solver’s failure even though the constraints are satisfiable.
8 Related Works
Supermartingale-Based Approaches. In addition to qualitative and quantitative termination analyses, supermartingales were also used for the formal analysis of other properties in probabilistic programs, such as, liveness and safety properties [3, 8, 14, 42], cost analysis of probabilistic programs [36, 43]. While all these works demonstrate the effectiveness of supermartingale-based techniques, below we present a more detailed comparison with other works that consider automated computation of lower bounds on termination probability.
Comparison to [14]. The work of [14] introduces stochastic invariants and demonstrates their effectiveness for computing lower bounds on termination probability. However, their approach to computing stochastic invariants is based on repulsing supermartingales (RepSMs), and is orthogonal to ours. RepSMs were shown to be incomplete for computing stochastic invariants [40, Section 3]. Also, a RepSM is required to have bounded differences, i.e. the absolute difference of its value is any two successor states needs to be bounded from above by some positive constant. Given that the algorithmic approach of [14] computes linear RepSMs, this implies that the applicability of RepSMs is compromised in practice as well, and is mostly suited to programs in which the quantity that behaves like a RepSM depends only on variables with bounded increments and sampling instructions defined by distributions of bounded support. Our approach does not impose such a restriction, and is the first to provide completeness guarantees.
Comparison to [40]. The work of [40] introduces \(\gamma \)-scaled submartingales and proves their effectiveness for computing lower bounds on termination probability. Intuitively, for \(\gamma \in (0,1)\), a state function f is a \(\gamma \)-scaled submartingale if it is a bounded nonnegative function whose value in each non-terminal state decreases in expected value at least by a factor of \(\gamma \) upon a one-step execution of the pCFG. One may think of the second condition as a multiplicative decrease in expected value. However, this condition is too strict and \(\gamma \)-scaled submartingales are not complete for lower bounds on termination probability [40, Example 6.6].
Comparison to [5]. The work of [5] proposes a type system for functional probabilistic programs that allows incrementally searching for type derivations and accumulating a lower bound on termination probability. In the limit, it finds arbitrarily tight lower bounds on termination probability, however it does not provide any completeness or precision guarantees in finite time.
Other Approaches. Logical calculi for reasoning about properties of probabilistic programs (including termination) were studied in [18, 19, 29] and extended to programs with non-determinism in [27, 28, 31, 37]. These works consider proof systems for probabilistic programs based on the weakest pre-expectation calculus. The expressiveness of this calculus allows reasoning about very complex programs, but the proofs typically require human input. In contrast, we aim for a fully automated approach for probabilistic programs with polynomial arithmetic. Connections between martingales and the weakest pre-expectation calculus were studied in [24]. A sound approach for proving almost-sure termination based on abstract interpretation is presented in [34].
Cores in MDPs. Cores are a conceptually equivalent notion to stochastic invariants introduced in [30] for finite MDPs. [30] presents a sampling-based algorithm for their computation.
9 Conclusion
We study the quantitative probabilistic termination problem in probabilistic programs with non-determinism and propose the first relatively complete algorithm for proving termination with at least a given threshold probability. Our approach is based on a sound and complete characterization of stochastic invariants via the novel notion of stochastic invariant indicators, which allows for an effective and relatively complete algorithm for their computation. We then show that stochastic invariants are sound and complete certificates for proving that a program terminates with at least a given threshold probability. Hence, by combining our relatively complete algorithm for stochastic invariant computation with the existing relatively complete algorithm for computing ranking supermartingales, we present the first relatively complete algorithm for probabilistic termination. We have implemented a prototype of our algorithm and demonstrate its effectiveness on a number of probabilistic programs collected from the literature.
References
Agrawal, S., Chatterjee, K., Novotný, P.: Lexicographic ranking supermartingales: an efficient approach to termination of probabilistic programs. In: POPL (2018). https://doi.org/10.1145/3158122
Asadi, A., Chatterjee, K., Fu, H., Goharshady, A.K., Mahdavi, M.: Polynomial reachability witnesses via Stellensätze. In: PLDI (2021). https://doi.org/10.1145/3453483.3454076
Barthe, G., Espitau, T., Ferrer Fioriti, L.M., Hsu, J.: Synthesizing probabilistic invariants via Doob’s decomposition. In: Chaudhuri, S., Farzan, A. (eds.) CAV 2016. LNCS, vol. 9779, pp. 43–61. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-41528-4_3
Barthe, G., Gaboardi, M., Grégoire, B., Hsu, J., Strub, P.Y.: Proving differential privacy via probabilistic couplings. In: LICS (2016). http://doi.acm.org/10.1145/2933575.2934554
Beutner, R., Ong, L.: On probabilistic termination of functional programs with continuous distributions. In: PLDI (2021). https://doi.org/10.1145/3453483.3454111
Bingham, E., et al.: Pyro: Deep universal probabilistic programming. J. Mach. Learn. Res. (2019). http://jmlr.org/papers/v20/18-403.html
Chakarov, A., Sankaranarayanan, S.: Probabilistic program analysis with martingales. In: Sharygina, N., Veith, H. (eds.) CAV 2013. LNCS, vol. 8044, pp. 511–526. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-39799-8_34
Chakarov, A., Voronin, Y.-L., Sankaranarayanan, S.: Deductive proofs of almost sure persistence and recurrence properties. In: Chechik, M., Raskin, J.-F. (eds.) TACAS 2016. LNCS, vol. 9636, pp. 260–279. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49674-9_15
Chatterjee, K., Fu, H., Goharshady, A.K.: Termination analysis of probabilistic programs through Positivstellensatz’s. In: Chaudhuri, S., Farzan, A. (eds.) CAV 2016. LNCS, vol. 9779, pp. 3–22. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-41528-4_1
Chatterjee, K., Fu, H., Goharshady, A.K., Goharshady, E.K.: Polynomial invariant generation for non-deterministic recursive programs. In: PLDI (2020). https://doi.org/10.1145/3385412.3385969
Chatterjee, K., Fu, H., Novotný, P., Hasheminezhad, R.: Algorithmic analysis of qualitative and quantitative termination problems for affine probabilistic programs. TOPLAS 40(2), 7:1–7:45 (2018). https://doi.org/10.1145/3174800
Chatterjee, K., Goharshady, A., Meggendorfer, T., Žikelić, Đ.: Sound and complete certificates for quantitative termination analysis of probabilistic programs (2022). https://hal.archives-ouvertes.fr/hal-03675086
Chatterjee, K., Goharshady, E.K., Novotný, P., Zárevúcky, J., Žikelić, Đ: On lexicographic proof rules for probabilistic termination. In: Huisman, M., Păsăreanu, C., Zhan, N. (eds.) FM 2021. LNCS, vol. 13047, pp. 619–639. Springer, Cham (2021). https://doi.org/10.1007/978-3-030-90870-6_33
Chatterjee, K., Novotný, P., Žikelić, Đ.: Stochastic invariants for probabilistic termination. In: POPL (2017). https://doi.org/10.1145/3009837.3009873
Cimatti, A., Griggio, A., Schaafsma, B.J., Sebastiani, R.: The MathSAT5 SMT solver. In: Piterman, N., Smolka, S.A. (eds.) TACAS 2013. LNCS, vol. 7795, pp. 93–107. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-36742-7_7
Colón, M.A., Sankaranarayanan, S., Sipma, H.B.: Linear invariant generation using non-linear constraint solving. In: Hunt, W.A., Somenzi, F. (eds.) CAV 2003. LNCS, vol. 2725, pp. 420–432. Springer, Heidelberg (2003). https://doi.org/10.1007/978-3-540-45069-6_39
Farkas, J.: Theorie der einfachen ungleichungen. J. für die reine und angewandte Mathematik 1902(124), 1–27 (1902)
Feldman, Y.A.: A decidable propositional dynamic logic with explicit probabilities. Inf. Control 63(1), 11–38 (1984)
Feldman, Y.A., Harel, D.: A probabilistic dynamic logic. In: STOC (1982). https://doi.org/10.1145/800070.802191
Foster, N., Kozen, D., Mamouras, K., Reitblatt, M., Silva, A.: Probabilistic NetKAT. In: Thiemann, P. (ed.) ESOP 2016. LNCS, vol. 9632, pp. 282–309. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49498-1_12
Fu, H., Chatterjee, K.: Termination of nondeterministic probabilistic programs. In: Enea, C., Piskac, R. (eds.) VMCAI 2019. LNCS, vol. 11388, pp. 468–490. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-11245-5_22
Ghahramani, Z.: Probabilistic machine learning and artificial intelligence. Nature 521(7553), 452–459 (2015). https://doi.org/10.1038/nature14541
Goodman, N.D., et al.: Church: a language for generative models. In: UAI (2008)
Hark, M., Kaminski, B.L., Giesl, J., Katoen, J.: Aiming low is harder: induction for lower bounds in probabilistic program verification. In: POPL (2020). https://doi.org/10.1145/3371105
Huang, M., Fu, H., Chatterjee, K.: New approaches for almost-sure termination of probabilistic programs. In: Ryu, S. (ed.) APLAS 2018. LNCS, vol. 11275, pp. 181–201. Springer, Cham (2018). https://doi.org/10.1007/978-3-030-02768-1_11
Huang, M., Fu, H., Chatterjee, K., Goharshady, A.K.: Modular verification for almost-sure termination of probabilistic programs. In: OOPSLA (2019). https://doi.org/10.1145/3360555
Kaminski, B.L., Katoen, J., Matheja, C., Olmedo, F.: Weakest precondition reasoning for expected runtimes of randomized algorithms. J. ACM 65(5), 30:1–30:68 (2018). https://doi.org/10.1145/3208102
Katoen, J.-P., McIver, A.K., Meinicke, L.A., Morgan, C.C.: Linear-invariant generation for probabilistic programs: automated support for proof-based methods. In: Cousot, R., Martel, M. (eds.) SAS 2010. LNCS, vol. 6337, pp. 390–406. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-15769-1_24
Kozen, D.: Semantics of probabilistic programs. J. Comput. Syst. Sci. 22(3), 328–350 (1981). https://doi.org/10.1016/0022-0000(81)90036-2
Křetínský, J., Meggendorfer, T.: Of cores: a partial-exploration framework for Markov decision processes. LMCS (2020). https://doi.org/10.23638/LMCS-16(4:3)2020
McIver, A., Morgan, C.: Abstraction, Refinement and Proof for Probabilistic Systems. Monographs in Computer Science. Springer, New York (2005). https://doi.org/10.1007/b138392
McIver, A., Morgan, C., Kaminski, B.L., Katoen, J.: A new proof rule for almost-sure termination. In: POPL (2018). https://doi.org/10.1145/3158121
Meurer, A., et al.: SymPy: symbolic computing in Python. PeerJ Comput. Sci. (2017). https://doi.org/10.7717/peerj-cs.103
Monniaux, D.: An abstract analysis of the probabilistic termination of programs. In: Cousot, P. (ed.) SAS 2001. LNCS, vol. 2126, pp. 111–126. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-47764-0_7
Moosbrugger, M., Bartocci, E., Katoen, J., Kovács, L.: Automated termination analysis of polynomial probabilistic programs. In: ESOP (2021). https://doi.org/10.1007/978-3-030-72019-3_18
Ngo, V.C., Carbonneaux, Q., Hoffmann, J.: Bounded expectations: resource analysis for probabilistic programs. In: PLDI (2018). https://doi.org/10.1145/3192366.3192394
Olmedo, F., Kaminski, B.L., Katoen, J.P., Matheja, C.: Reasoning about recursive probabilistic programs. In: LICS (2016). https://doi.org/10.1145/2933575.2935317
Putinar, M.: Positive polynomials on compact semi-algebraic sets. Indiana Univ. Math. J. 42(3), 969–984 (1993)
Roy, D., Mansinghka, V., Goodman, N., Tenenbaum, J.: A stochastic programming perspective on nonparametric Bayes. In: ICML (2008)
Takisaka, T., Oyabu, Y., Urabe, N., Hasuo, I.: Ranking and repulsing supermartingales for reachability in randomized programs. ACM Trans. Program. Lang. Syst. 43(2), 5:1–5:46 (2021). https://doi.org/10.1145/3450967
Thrun, S.: Probabilistic algorithms in robotics. AI Mag. 21(4), 93–109 (2000). https://doi.org/10.1609/aimag.v21i4.1534
Wang, J., Sun, Y., Fu, H., Chatterjee, K., Goharshady, A.K.: Quantitative analysis of assertion violations in probabilistic programs. In: PLDI (2021). https://doi.org/10.1145/3453483.3454102
Wang, P., Fu, H., Goharshady, A.K., Chatterjee, K., Qin, X., Shi, W.: Cost analysis of nondeterministic probabilistic programs. In: PLDI (2019). https://doi.org/10.1145/3314221.3314581
Acknowledgements
This research was partially supported by the ERC CoG 863818 (ForM-SMArt), the HKUST-Kaisa Joint Research Institute Project Grant HKJRI3A-055, the HKUST Startup Grant R9272 and the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie Grant Agreement No. 665385.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2022 The Author(s)
About this paper
Cite this paper
Chatterjee, K., Goharshady, A.K., Meggendorfer, T., Žikelić, Đ. (2022). Sound and Complete Certificates for Quantitative Termination Analysis of Probabilistic Programs. In: Shoham, S., Vizel, Y. (eds) Computer Aided Verification. CAV 2022. Lecture Notes in Computer Science, vol 13371. Springer, Cham. https://doi.org/10.1007/978-3-031-13185-1_4
Download citation
DOI: https://doi.org/10.1007/978-3-031-13185-1_4
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-13184-4
Online ISBN: 978-3-031-13185-1
eBook Packages: Computer ScienceComputer Science (R0)







 Similarly, if the desired degree is
Similarly, if the desired degree is  Note that every monomial of degree at most 2 appears in this expression. The goal is to synthesize suitable real values for each unknown coefficient
Note that every monomial of degree at most 2 appears in this expression. The goal is to synthesize suitable real values for each unknown coefficient 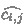 such that f becomes an SI-indicator. Throughout this section, we use the
such that f becomes an SI-indicator. Throughout this section, we use the  notation to denote an unknown coefficient whose value will be synthesized by our algorithm.
notation to denote an unknown coefficient whose value will be synthesized by our algorithm.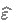 whose final value will serve as
whose final value will serve as  and the
and the  variables in this template such that
variables in this template such that  -RSM for
-RSM for