Abstract
This chapter introduces and discusses the exponential family (EF) and the exponential dispersion family (EDF). The EF and the EDF are by far the most important classes of distribution functions for regression modeling. They include, among others, the Gaussian, the binomial, the Poisson, the gamma, the inverse Gaussian distributions, as well as Tweedie’s models. We introduce these families of distribution functions, discuss their properties and provide several examples. Moreover, we introduce the Kullback–Leibler (KL) divergence and the Bregman divergence, which are important tools in model evaluation and model selection.
You have full access to this open access chapter, Download chapter PDF
We introduce the exponential family (EF) and the exponential dispersion family (EDF) in this chapter. The single-parameter EF has been introduced in 1934 by the British statistician Sir Fisher [128], and it has been extended to vector-valued parameters by Darmois [88], Koopman [223] and Pitman [306] between 1935 and 1936. It is the most commonly used family of distribution functions in statistical modeling; among others, it contains the Gaussian distribution, the gamma distribution, the binomial distribution and the Poisson distribution. Its parametrization is taken in a special form that is convenient for statistical modeling. The EF can be introduced in a constructive way providing the main properties of this family of distribution functions. In this chapter we follow Jørgensen [201,202,203] and Barndorff-Nielsen [23], and we state the most important results based on this constructive introduction. This gives us a unified notation which is going to be useful for our purposes.
2.1 Exponential Family
2.1.1 Definition and Properties
We define the EF w.r.t. a σ-finite measure ν on \({\mathbb R}\). The results in this section can be generalized to σ-finite measures on \({\mathbb R}^m\), but such an extension is not necessary for our purposes. Select an integer \(k\in {\mathbb N}\), and choose measurable functions \(a:{\mathbb R} \to {\mathbb R}\) and \(T:{\mathbb R} \to {\mathbb R}^k\).Footnote 1 Consider for a canonical parameter \(\boldsymbol {\theta } \in {\mathbb R}^k\) the Laplace transform

Assume that this Laplace transform is not identically equal to + ∞. The effective domain is defined by
Lemma 2.1. The effective domain \(\boldsymbol {\Theta } \subseteq {\mathbb R}^k\) is a convex set.
The effective domain Θ is not necessarily an open set, but in many applications it is open. Counterexamples are given in Problem 4.1 of Chapter 1 in Lehmann [244], and in the inverse Gaussian example in Sect. 2.1.3, below.
Proof of Lemma 2.1. Choose \(\boldsymbol {\theta }_i \in {\mathbb R}^k\), i = 1, 2, with \({\mathfrak L}(\boldsymbol {\theta }_i)<\infty \). Set θ = c θ 1 + (1 − c)θ 2 for c ∈ (0, 1). We use Hölder’s inequality, applied to the norms p = 1∕c and q = 1∕(1 − c),

This implies θ ∈ Θ and proves the claim. □
We define the cumulant function on the effective domain Θ
Definition 2.2. The EF with σ-finite measure ν on \({\mathbb R}\) and cumulant function \(\kappa :\boldsymbol {\Theta } \to {\mathbb R}\) is given by the distribution functions F on \({\mathbb R}\) with

for canonical parameters \(\boldsymbol {\theta } \in \boldsymbol {\Theta } \subseteq {\mathbb R}^k\).
Remarks 2.3.
-
The definition of the EF (2.2) assumes that the effective domain \(\boldsymbol {\Theta }\subseteq {\mathbb R}^k\) has been constructed from the choices \(a:{\mathbb R}\to {\mathbb R}\) and \(T:{\mathbb R}\to {\mathbb R}^k\) as described in (2.1). This is not explicitly stated in the surrounding text of (2.2).
-
The support of any random variable Y ∼ F(⋅;θ) of this EF does not depend on the explicit choice of the canonical parameter θ ∈ Θ, but solely on the choice of the σ-finite measure ν on \({\mathbb R}\), and the distribution functions F(⋅;θ) are mutually absolutely continuous (equivalent) w.r.t. ν.
-
In statistics, the main object of interest is the canonical parameter θ. Importantly for parameter estimation, the function a(⋅) does not involve the canonical parameter. Therefore, it is irrelevant for parameter estimation and (only) serves as a normalization so that F in (2.2) is a proper distribution function. In fact, this is the way how the EF is often introduced in the statistical and actuarial literature, but in this latter introduction we lose the deeper interpretation of the cumulant function κ, nor is it immediately clear what properties it possesses.
-
The case k ≥ 2 gives a vector-valued canonical parameter θ. The case k = 1 gives a single-parameter EF, and, if additionally T(y) = y, it is called a single-parameter linear EF.
Theorem 2.4. Assume the effective domain Θ has a non-empty interior  . Choose Y ∼ F(⋅;θ) for fixed
. Choose Y ∼ F(⋅;θ) for fixed  . The moment generating function of T(Y ) for sufficiently small \(\boldsymbol {r}\in {\mathbb R}^k\) is given by
. The moment generating function of T(Y ) for sufficiently small \(\boldsymbol {r}\in {\mathbb R}^k\) is given by

where the expectation operator \({\mathbb E}_{\boldsymbol {\theta }}\) illustrates the selected canonical parameter θ for Y .
Proof. Choose  and \(\boldsymbol {r} \in {\mathbb R}^k\) so small that
and \(\boldsymbol {r} \in {\mathbb R}^k\) so small that  . We receive
. We receive

where the last identity follows from the fact that the support of the EF does not depend on the explicit choice of the canonical parameter. □
Theorem 2.4 has a couple of immediate implications. First, in any interior point  both the moment generating function r↦M
T(Y )(r) (in the neighborhood of the origin) and the cumulant function θ↦κ(θ) have derivatives of all orders, and, similarly to Sect. 1.2, moments of all orders of T(Y ) exist, see also (1.1). Existence of moments of all orders implies that the distribution function of T(Y ) cannot have a regularly varying tails.
both the moment generating function r↦M
T(Y )(r) (in the neighborhood of the origin) and the cumulant function θ↦κ(θ) have derivatives of all orders, and, similarly to Sect. 1.2, moments of all orders of T(Y ) exist, see also (1.1). Existence of moments of all orders implies that the distribution function of T(Y ) cannot have a regularly varying tails.
Corollary 2.5. Assume  is non-empty. The cumulant function θ↦κ(θ) is convex, and for Y ∼ F(⋅;θ) with
is non-empty. The cumulant function θ↦κ(θ) is convex, and for Y ∼ F(⋅;θ) with 
where ∇θ is the gradient and \(\nabla ^2_{\boldsymbol {\theta }}\) the Hessian w.r.t. vector θ.
Similarly to \(T:{\mathbb R} \to {\mathbb R}^k\), we will not use boldface notation for the (multi-dimensional) mean because later on we will understand the mean \(\mu =\mu (\boldsymbol {\theta }) \in {\mathbb R}^k\) as a function of the canonical parameter θ; see Footnote 1 on page 1 on boldface notation.
Proof. Existence of the moment generating function for all sufficiently small \(\boldsymbol {r} \in {\mathbb R}^k\) (around the origin) implies that we have first and second moments. For the first moment we receive
Denote component j of \(T(Y) \in {\mathbb R}^k\) by T j(Y ). We have for 1 ≤ j, l ≤ k
This implies for the covariance
The convexity of κ follows because \(\nabla ^2_{\boldsymbol {\theta }} \kappa (\boldsymbol {\theta })\) is the positive semi-definite covariance matrix of T(Y ), for all  . This finishes the proof. □
. This finishes the proof. □
Assumption 2.6 (Minimal Representation). We assume that the interior  of the effective domain Θ is non-empty and that the cumulant function κ is strictly convex on this interior
of the effective domain Θ is non-empty and that the cumulant function κ is strictly convex on this interior  .
.
Remarks 2.7.
-
Throughout these notes we will work under Assumption 2.6 without making explicit reference. This assumption strengthens the properties of the cumulant function κ from being convex, see Corollary 2.5, to being strictly convex. This strengthening implies that the mean function θ↦μ = μ(θ) = ∇θ κ(θ) can be inverted; this is needed for the canonical link, see Definition 2.8, below.
-
The strict convexity of κ means that the covariance matrix \(\nabla ^2_{\boldsymbol {\theta }} \kappa (\boldsymbol {\theta })\) of T(Y ) is positive definite and has full rank k for all
 , see Corollary 2.5. This property is important, otherwise we do not have identifiability in the canonical parameter θ because we have a linear dependence between the components of T(Y ).
, see Corollary 2.5. This property is important, otherwise we do not have identifiability in the canonical parameter θ because we have a linear dependence between the components of T(Y ). -
Mathematically, this strict convexity is not a restriction because it can be obtained by working under a so-called minimal representation. If the covariance matrix \(\nabla ^2_{\boldsymbol {\theta }} \kappa (\boldsymbol {\theta })\) does not have full rank k, the choice k is “non-optimal” because the problem lives in a smaller dimension. Thus, w.l.o.g., we may and will assume to work in this smaller dimension, called minimal representation; for a rigorous derivation of a minimal representation we refer to Section 8.1 in Barndorff-Nielsen [23].
Definition 2.8. The canonical link is defined by h = (∇θ κ)−1.
The application of the canonical link h to the mean implies under Assumption 2.6
for mean \(\mu = {\mathbb E}_{\boldsymbol {\theta }}[T(Y)]\) of Y ∼ F(⋅;θ) with  .
.
Remarks 2.9 (Dual Parameter Space). Assumption 2.6 provides that the canonical link h is well-defined, and we can either work with the canonical parameter representation  or with its dual (mean) parameter representation \(\mu ={\mathbb E}_{\boldsymbol {\theta }}\left [T(Y)\right ] \in \mathcal {M}\) with
or with its dual (mean) parameter representation \(\mu ={\mathbb E}_{\boldsymbol {\theta }}\left [T(Y)\right ] \in \mathcal {M}\) with

Strict convexity of κ implies that there is a one-to-one correspondence between these two parametrizations. Θ is called the effective domain and \(\mathcal {M}\) is called the dual parameter space or the mean parameter space.
In Sect. 2.2.4, below, we introduce one more property called steepness that the cumulant function κ should satisfy. This additional property gives a relationship between the support \({\mathfrak T}\) of the random variables T(Y ) of the given EF and the boundary of the dual parameter space \(\mathcal {M}\). This steepness property is important for parameter estimation.
2.1.2 Single-Parameter Linear EF: Count Variable Examples
We start by giving single-parameter discrete linear EF examples based on counting measures on \({\mathbb N}_0\). Since we work in one dimension k = 1, we replace boldface θ by scalar \(\theta \in \boldsymbol {\Theta } \subseteq {\mathbb R}\) in this section.
2.1.2.1 Bernoulli Distribution as a Single-Parameter Linear EF
For the Bernoulli distribution with parameter p ∈ (0, 1) we choose as ν the counting measure on {0, 1}. We make the following choices: T(y) = y,
for effective domain \(\boldsymbol {\Theta }= {\mathbb R}\), dual parameter space \(\mathcal {M}=(0,1)\) and support \({\mathfrak T}=\{0,1\}\) of Y = T(Y ). With these choices we have
θ↦κ′(θ) is the logistic or sigmoid function, and the canonical link p↦h(p) is the logit function. Mean and variance are given by
and the probability weights satisfy for \(y\in {\mathfrak T}=\{0,1\}\)
2.1.2.2 Binomial Distribution as a Single-Parameter Linear EF
For the binomial distribution with parameters \(n\in {\mathbb N}\) and p ∈ (0, 1) we choose as ν the counting measure on {0, …, n}. We make the following choices: T(y) = y,
for effective domain \(\boldsymbol {\Theta }= {\mathbb R}\), dual parameter space \(\mathcal {M}=(0,n)\) and support \({\mathfrak T}=\{0,\ldots , n\}\) of Y = T(Y ). With these choices we have
Mean and variance are given by
where we set p = e θ∕(1 + e θ). The probability weights satisfy for \(y\in {\mathfrak T}=\{0,\ldots , n\}\)
2.1.2.3 Poisson Distribution as a Single-Parameter Linear EF
For the Poisson distribution with parameter λ > 0 we choose as ν the counting measure on \({\mathbb N}_0\). We make the following choices: T(y) = y,
for effective domain \(\boldsymbol {\Theta }= {\mathbb R}\), dual parameter space \(\mathcal {M}=(0,\infty )\) and support \({\mathfrak T}={\mathbb N}_0\) of Y = T(Y ). With these choices we have
The canonical link μ↦h(μ) is the log-link. Mean and variance are given by
where we set λ = e θ. The probability weights in the Poisson case satisfy for \(y\in {\mathfrak T}={\mathbb N}_0\)
2.1.2.4 Negative-Binomial (Pólya) Distribution as a Single-Parameter Linear EF
For the negative-binomial distribution with α > 0 and p ∈ (0, 1) we choose as ν the counting measure on \({\mathbb N}_0\); α plays the role of a nuisance parameter or hyper-parameter. We make the following choices: T(y) = y,
for effective domain Θ = (−∞, 0), dual parameter space \(\mathcal {M}=(0,\infty )\) and support \({\mathfrak T}={\mathbb N}_0\) of Y = T(Y ). With these choices we have
with p = e θ. Parameter α > 0 is treated as nuisance parameter, otherwise we drop out of the EF framework. We have first the two moments
This model allows us to model over-dispersion, in contrast to the Poisson model. In fact, the negative-binomial model is a mixed Poisson model with a gamma mixing distribution, for details see Sect. 5.3.5, below. Typically, one uses a different parametrization. Set e θ = λ∕(α + λ), for λ > 0. This implies
For \(\alpha \in {\mathbb N}\) this model can also be interpreted as the waiting time until we observe α successful trials among i.i.d. trials, for instance, for α = 1 we have the geometric distribution (with a small reparametrization).
The probability weights of the negative-binomial model satisfy for \(y\in {\mathfrak T}={\mathbb N}_0\)
2.1.3 Vector-Valued Parameter EF: Absolutely Continuous Examples
We give vector-valued parameter absolutely continuous EF examples with k = 2, and being based on the Lebesgue measure on (subsets of) \({\mathbb R}\), in this section.
2.1.3.1 Gaussian Distribution as a Vector-Valued Parameter EF
For the Gaussian distribution with parameters \(\mu \in {\mathbb R}\) and σ
2 > 0 we choose as ν the Lebesgue measure on \({\mathbb R}\), and we make the following choices:  ,
,

for effective domain \(\boldsymbol {\Theta }= {\mathbb R} \times (-\infty , 0)\), dual parameter space \(\mathcal {M}={\mathbb R} \times (0,\infty )\) and support \({\mathfrak T}={\mathbb R} \times [0,\infty )\) of  . With these choices we have
. With these choices we have

This is the Gaussian model with mean μ = θ 1∕(−2θ 2) and variance σ 2 = (−2θ 2)−1.
If we treat σ > 0 as a nuisance parameter, we obtain the Gaussian model as a single-parameter EF. This is the most common example of an EF. Set T(y) = y∕σ and
for effective domain \(\boldsymbol {\Theta }= {\mathbb R}\), dual parameter space \(\mathcal {M}={\mathbb R}\) and support \({\mathfrak T}={\mathbb R}\) of T(Y ) = Y∕σ. With these choices we have

and, in particular, the canonical link is the identity link μ↦θ = h(μ) = μ in this single-parameter EF example.
2.1.3.2 Gamma Distribution as a Vector-Valued Parameter EF
For the gamma distribution with parameters α, β > 0 we choose as ν the Lebesgue measure on \({\mathbb R}_+\). Then we make the following choices:  ,
,

for effective domain Θ = (−∞, 0) × (0, ∞), and setting β = −θ
1 > 0 and α = θ
2 > 0. The dual parameter space is \(\mathcal {M}=(0,\infty )\times {\mathbb R}\), and we have support \({\mathfrak T}=(0,\infty )\times {\mathbb R}\) of  . With these choices we obtain
. With these choices we obtain

This is a vector-valued parameter EF with k = 2, and the first moment is given by

Parameter α is called shape parameter and parameter β is called scale parameter.Footnote 2
If we treat the shape parameter α > 0 as a nuisance parameter we can turn the gamma distribution into a single-parameter linear EF. Set T(y) = y and
for effective domain Θ = (−∞, 0), dual parameter space \(\mathcal {M}=(0,\infty )\) and support \({\mathfrak T}=(0,\infty )\). With these choices we have for β = −θ > 0
This provides us with mean and variance
For parameter estimation one often needs to invert these identities which gives us
Remarks 2.10.
-
The gamma distribution contains as special cases the exponential distribution for α = θ 2 = 1 and β = −θ 1 > 0, and the \(\chi _r^2\)-distribution with r degrees of freedom for α = θ 2 = r∕2 and β = −θ 1 = 1∕2.
-
The distributions of the EF are all light-tailed in the sense that all moments of T(Y ) exist. Therefore, the EF does not allow for regularly varying survival functions, see (1.3). If Y is gamma distributed, then \(Z=\exp \{Y\}\) is log-gamma distributed (with the special case of the Pareto distribution for the exponential case α = θ 2 = 1). For an example we refer to Sect. 2.2.5. However, this log-transformation is not always recommended because it may provide accurate models on the transformed log-scale, but back-transformation to the original scale may not necessarily provide a good predictive model on that original scale.
-
The gamma density (2.6) may be a bit tricky in applications because the effective domain Θ = (−∞, 0) is one-sided bounded (we come back to this below). For this reason, in practice, one often uses links different from the canonical link h(μ) = −α∕μ. For instance, a parametrization \(\theta = -\exp \{-\vartheta \}\) for \(\vartheta \in {\mathbb R}\), see Ohlsson–Johansson [290], leads to the following model
$$\displaystyle \begin{aligned} dF(y;\vartheta) = \frac{y^{\alpha-1}}{\Gamma(\alpha)} \exp \left\{-e^{-\vartheta} y - \alpha \vartheta \right\} d\nu(y). \end{aligned} $$(2.7)We will study the gamma model in more depth below, and parametrization (2.7) will correspond to the log-link choice, see Example 5.5, below.
Figure 2.1 gives examples of gamma densities for shape parameters α ∈{1∕2, 1, 3∕2, 2} and scale parameters β ∈{1∕2, 1, 3∕2, 2} with α = β all providing the same mean \(\mu ={\mathbb E}_\theta [Y]=\alpha /\beta =1\). The crucial observation is that these gamma densities can have two different shapes, for α ≤ 1 we have a strictly decreasing shape and for α > 1 we have a unimodal density with mode in (α − 1)∕β.
2.1.3.3 Inverse Gaussian Distribution as a Vector-Valued Parameter EF
For the inverse Gaussian distribution with parameters α, β > 0 we choose as ν the Lebesgue measure on \({\mathbb R}_+\). Then we make the following choices:  ,
,

for  , and setting β = (−2θ
1)1∕2 and α = (−2θ
2)1∕2. The dual parameter space is \(\mathcal {M}=(0,\infty )^2\), and we have support \({\mathfrak T}=(0,\infty )^2\) of
, and setting β = (−2θ
1)1∕2 and α = (−2θ
2)1∕2. The dual parameter space is \(\mathcal {M}=(0,\infty )^2\), and we have support \({\mathfrak T}=(0,\infty )^2\) of  . With these choices we obtain
. With these choices we obtain

This is a vector-valued parameter EF with k = 2 and with first moment

For receiving (2.8) we have chosen canonical parameter  . Interestingly, we can close this parameter space for θ
1 = 0, i.e., the effective domain Θ is not open in this example. The choice θ
1 = 0 gives us cumulant function \(\kappa (\boldsymbol {\theta })=-\frac {1}{2} {\mbox{log}}(-2\theta _2)\) and boundary case
. Interestingly, we can close this parameter space for θ
1 = 0, i.e., the effective domain Θ is not open in this example. The choice θ
1 = 0 gives us cumulant function \(\kappa (\boldsymbol {\theta })=-\frac {1}{2} {\mbox{log}}(-2\theta _2)\) and boundary case

This is the distribution of the first-passage time of level α > 0 of a standard Brownian motion, see Bachelier [20]; this distribution is also known as Lévy distribution.
If we treat α > 0 as a nuisance parameter, we can turn the inverse Gaussian distribution into a single-parameter linear EF by setting T(y) = y,
for θ ∈ (−∞, 0), dual parameter space \(\mathcal {M}=(0,\infty )\) and support \({\mathfrak T}=(0,\infty )\). With these choices we have the inverse Gaussian model for β = (−2θ)1∕2 > 0
This provides us with mean and variance
For parameter estimation one often needs to invert these identities, which gives us
Figure 2.2 gives examples of inverse Gaussian densities for parameter choices α = β ∈{1∕2, 1, 3∕2, 2} all providing the same mean \(\mu ={\mathbb E}_\theta [Y]=\alpha /\beta =1\).
2.1.3.4 Generalized Inverse Gaussian Distribution as a Vector-Valued Parameter EF
For the generalized inverse Gaussian distribution with parameters α, β > 0 and \(\gamma \in {\mathbb R}\) we choose as ν the Lebesgue measure on \({\mathbb R}_+\). We combine the terms of the gamma and the inverse Gaussian models to the vector-valued choice:  with k = 3. Moreover, we choose a(y) = −logy and cumulant function
with k = 3. Moreover, we choose a(y) = −logy and cumulant function

for  , and where \(K_{\theta _2}\) denotes the modified Bessel function of the second kind with index \(\gamma =\theta _2 \in {\mathbb R}\). With these choices we obtain generalized inverse Gaussian density
, and where \(K_{\theta _2}\) denotes the modified Bessel function of the second kind with index \(\gamma =\theta _2 \in {\mathbb R}\). With these choices we obtain generalized inverse Gaussian density

setting α = −2θ 1 and β = −2θ 3. This is a vector-valued parameter EF with k = 3, and the first moment is given by

The effective domain Θ is a bit complicated because the possible choices of (θ 1, θ 3) depend on \(\theta _2 \in {\mathbb R}\), namely, for θ 2 < 0 the negative half-line (−∞, 0] can be closed at the origin for θ 1, and for θ 2 > 0 it can be closed at the origin for θ 3. The inverse Gaussian model is obtained for θ 2 = −1∕2 and the gamma model is obtained for θ 3 = 0. For further properties of the generalized inverse Gaussian distribution we refer to the textbook of Jørgensen [200].
2.1.4 Vector-Valued Parameter EF: Count Variable Example
We close our EF examples by giving a discrete example with a vector-valued parameter.
2.1.4.1 Categorical Distribution as a Vector-Valued Parameter EF
For the categorical distribution with \(k\in {\mathbb N}\) and p ∈ (0, 1)k such that \(\sum _{i=1}^k p_i<1\), we choose as ν the counting measure on the finite set {1, …, k + 1}. Then we make the following choices:  ,
,  ,
,  and
and
for effective domain \(\boldsymbol {\Theta }= {\mathbb R}^{k}\), dual parameter space \(\mathcal {M}=(0,1)^k\), and the support \({\mathfrak T}\) of T(Y ) are the k + 1 corners of the unit simplex in \({\mathbb R}^k\). This representation is minimal, see Assumption 2.6. With these choices we have (set θ k+1 = 0)

This is a vector-valued parameter EF with \(k\in {\mathbb N}\). The canonical link is slightly more complicated. Set vectors \(\boldsymbol {v}= \exp \{\boldsymbol {\theta }\} \in {\mathbb R}^{k}\) and  . This provides
. This provides  . Set matrix
. Set matrix  , the latter gives us p = A
p
v, and since A
p has full rank k, we obtain canonical link
, the latter gives us p = A
p
v, and since A
p has full rank k, we obtain canonical link

The last identity can be verified by explicit calculation

Remarks 2.11.
-
There are many more examples that belong to the EF. From Theorem 2.4, we know that all examples of the EF are light-tailed in the sense that all moments of T(Y ) exist. If we want to model heavy-tailed distributions within the EF, we first need to apply a suitable transformation. We could model the Pareto distribution using transformation T(y) = logy, and assuming that the transformed random variable has an exponential distribution. Different light-tailed examples are obtained by, e.g., using transformation T(y) = y τ for the Weibull distribution or
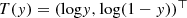 for the beta distribution. We refrain from giving explicit formulas for these or other examples.
for the beta distribution. We refrain from giving explicit formulas for these or other examples. -
Observe that in all examples above we have \({\mathfrak T}\subset \overline {\mathcal {M}}\), i.e., the support of T(Y ) is contained in the closure of the dual parameter space \(\mathcal {M}\), we come back to this observation in Sect. 2.2.4, below.
2.2 Exponential Dispersion Family
In the previous section we have introduced the EF, and we have explicitly studied the vector-valued parameter EF examples of the Gaussian, the gamma and the inverse Gaussian models. We have highlighted that these three vector-valued parameter EFs can be turned into single-parameter EFs by declaring one parameter to be a nuisance parameter that is not modeled (and acts as a hyper-parameter). This changes these three models into single-parameter EFs. These three single-parameter EFs with nuisance parameter can also be interpreted as EDF models. In this section we discuss the single-parameter EDF; this is sufficient for our purposes, and vector-valued parameter extensions can be obtained in a canonical way.
2.2.1 Definition and Properties
The EFs of Sect. 2.1 can be extended to EDFs. In the single-parameter case this is achieved by a transformation Y = X∕ω, where ω > 0 is a scaling and where X belongs to a single-parameter linear EF, i.e., with T(x) = x. We restrict ourselves to the single-parameter case k = 1 throughout this section. Choose a σ-finite measure ν 1 on \({\mathbb R}\) and a measurable function \(a_1:{\mathbb R} \to {\mathbb R}\). These choices give a single-parameter linear EF, directly modeling a real-valued random variable T(X) = X. By (2.2) we have distribution for the single-parameter linear EF random variable X
on the effective domain
and with cumulant function
Throughout, we assume that the effective domain Θ has a non-empty interior  . Thus, since Θ is convex, we assume that
. Thus, since Θ is convex, we assume that  is a non-empty (possibly infinite) open interval in \({\mathbb R}\).
is a non-empty (possibly infinite) open interval in \({\mathbb R}\).
Following Jørgensen [201, 202], we extend this linear EF to an EDF as follows. Choose a family of σ-finite measures ν ω on \({\mathbb R}\) and measurable functions \(a_\omega :{\mathbb R} \to {\mathbb R}\) for a given index set \(\mathcal {W}\ni \omega \) with \(\{1\}\subset \mathcal {W} \subset {\mathbb R}_+\). Assume that we have an ω-independent scaled cumulant function κ on this index set \(\mathcal {W}\), that is,
with effective domain Θ defined by (2.11), i.e., for ω = 1. This allows us to consider the distribution functions
in the third identity we did a change of variable x↦y = x∕ω. By re-parametrizing the function a ω(ω ⋅) and the σ-finite measures ν ω(ω ⋅) slightly differently, depending on the particular structure of the chosen σ-finite measures, we arrive at the following single-parameter EDF.
Definition 2.12. The (single-parameter) EDF is given by densities of the form
with
Remarks 2.13.
-
Exposure v > 0 and dispersion parameter φ > 0 provide the parametrization usually used for \(\omega =v/\varphi \in \mathcal {W}\). Their meaning and interpretation will become clear below, and they will always appear as a ratio ω = v∕φ.
-
The support of these EDF distributions does not depend on the explicit choice of the canonical parameter θ ∈ Θ, but it may depend on \(\omega =v/\varphi \in \mathcal {W}\) through the choices of the σ-finite measures ν ω, for \(\omega \in \mathcal {W}\). Consequently, a(y;ω) is a normalization such that f(y;θ, ω) integrates to 1 w.r.t. the chosen σ-finite measure ν ω to receive a proper distributional model.
-
The transformation x↦y = x∕ω in (2.13) is called duality transformation, see Section 3.1 in Jørgensen [203]. It provides the duality between the additive form (in variable x in (2.13)) and the reproductive form (in variable y in (2.13)) of the EDF; Definition 2.12 is the reproductive form.
-
Lemma 2.1 tells us that Θ is convex, thus, it is a possibly infinite interval in \({\mathbb R}\). To exclude trivial cases we will always assume that the σ-finite measure ν 1 is not concentrated in one single point (this relates to the minimal representation for k = 1 in the linear EF case, see Assumption 2.6), and that the interior
 of the effective domain Θ is non-empty.
of the effective domain Θ is non-empty.
Corollary 2.14. Assume  is non-empty and that ν
1 is not concentrated in one single point. Choose Y ∼ F(⋅;θ, v∕φ) for fixed
is non-empty and that ν
1 is not concentrated in one single point. Choose Y ∼ F(⋅;θ, v∕φ) for fixed  . The moment generating function of Y for small \(r\in {\mathbb R}\) satisfies
. The moment generating function of Y for small \(r\in {\mathbb R}\) satisfies
The first two moments of Y are given by
The cumulant function κ is smooth and strictly convex on  with canonical link h = (κ′)−1. The variance function is defined by μ↦V (μ) = (κ″ ∘ h)(μ) and, consequently, for the variance of Y we have \(\mbox{Var}_\mu \left (Y\right ) = \frac {\varphi }{v}V(\mu )\) for \(\mu \in \mathcal {M}\).
with canonical link h = (κ′)−1. The variance function is defined by μ↦V (μ) = (κ″ ∘ h)(μ) and, consequently, for the variance of Y we have \(\mbox{Var}_\mu \left (Y\right ) = \frac {\varphi }{v}V(\mu )\) for \(\mu \in \mathcal {M}\).
Proof. This follows analogously to Theorem 2.4. The linear case T(y) = y with ν 1 not being concentrated in one single point guarantees that the minimal dimension is k = 1, providing a minimal representation in this dimension, see Assumption 2.6. □
Before giving explicit examples we state the so-called convolution formula. Corollary 2.15 (Convolution Formula). Assume  is non-empty and that ν
1 is not concentrated in one single point. Assume that Y
i ∼ F(⋅;θ, v
i∕φ) are independent, for 1 ≤ i ≤ n, with fixed
is non-empty and that ν
1 is not concentrated in one single point. Assume that Y
i ∼ F(⋅;θ, v
i∕φ) are independent, for 1 ≤ i ≤ n, with fixed  . Set \(v_+=\sum _{i=1}^n v_i\). Then
. Set \(v_+=\sum _{i=1}^n v_i\). Then
Proof. The proof immediately follows from calculating the moment generating function \(M_{Y_+}(r)\) and from using the independence between the Y i’s. □
2.2.2 Exponential Dispersion Family Examples
The single-parameter linear EF examples introduced above can be reformulated as EDF examples.
2.2.2.1 Binomial Distribution as a Single-Parameter EDF
For the binomial distribution with parameters p ∈ (0, 1) and \(n\in {\mathbb N}\) we choose the counting measure on {0, 1∕n, …, 1} with ω = n. Then we make the following choices
for effective domain \(\boldsymbol {\Theta }= {\mathbb R}\) and dual parameter space \(\mathcal {M}=(0,1)\). With these choices we have
This is a single-parameter EDF. The canonical link p↦h(p) gives the logit function. Mean and variance are given by
and the variance function is given by V (μ) = μ(1 − μ). The binomial random variable is obtained by setting X = nY ∼Binom(n, p).
2.2.2.2 Poisson Distribution as a Single-Parameter EDF
For the Poisson distribution with parameters λ > 0 and v > 0 we choose the counting measure on \({\mathbb N}_0/v\) for exposure ω = v. Then we make the following choices
for effective domain \(\boldsymbol {\Theta }= {\mathbb R}\) and dual parameter space \(\mathcal {M}=(0,\infty )\). With these choices we have
This is a single-parameter EDF. The canonical link λ↦h(λ) is the log-link. Mean and variance are given by
and the variance function is given by V (λ) = λ, that is, the variance function is linear in the mean parameter λ. The Poisson random variable is obtained by setting X = vY ∼Poi(vλ). We choose φ = 1, here, meaning that we have neither under- nor over-dispersion. Thus, the choices v and φ in ω = v∕φ have the interpretation of an exposure and a dispersion parameter, respectively. This interpretation is going to be important in claim counts modeling, below.
2.2.2.3 Gamma Distribution as a Single-Parameter EDF
For the gamma distribution with parameters α, β > 0 we choose the Lebesgue measure on \({\mathbb R}_+\) and shape parameter ω = v∕φ = α. We make the following choices
for effective domain Θ = (−∞, 0) and dual parameter space \(\mathcal {M}=(0,\infty )\). With these choices we have
This is analogous to (2.6) with shape parameter α > 0 and scale parameter β = −θ > 0. Mean and variance are given by
and the variance function is given by V (μ) = μ 2, that is, the variance function is quadratic in the mean parameter μ. The gamma random variable is obtained by setting X = αY ∼ Γ(α, β). This gives us for the first two moments of X
Suppose v = 1, for shape parameter α > 1, we have under-dispersion φ = 1∕α < 1 and the gamma density is unimodal; for shape parameter α < 1, we have over-dispersion φ = 1∕α > 1 and the gamma density is strictly decreasing, we refer to Fig. 2.1.
2.2.2.4 Inverse Gaussian Distribution as a Single-Parameter EDF
For the inverse Gaussian distribution with parameters α, β > 0 we choose the Lebesgue measure on \({\mathbb R}_+\) and we set ω = v∕φ = α. We make the following choices
for θ ∈ (−∞, 0) and dual parameter space \(\mathcal {M}=(0,\infty )\). With these choices we have
where in the last step we did a change of variable y↦x = αy. This is exactly (2.8). Mean and variance are given by
and the variance function is given by V (μ) = μ 3, that is, the variance function is cubic in the mean parameter μ. The inverse Gaussian random variable is obtained by setting X = αY . The mean and variance of X are given by, set β = (−2θ)1∕2 > 0,
This inverse Gaussian density is illustrated in Fig. 2.2.
Similarly to (2.9), we can extend the inverse Gaussian model to the boundary case θ = 0, i.e., the effective domain Θ = (−∞, 0] is not open. This provides us with density
using, as above, the change of variable y↦x = αy. An additional transformation x↦1∕x gives a gamma distribution with shape parameter 1/2 and scale parameter α 2∕2.
Remark 2.16. The inverse Gaussian case gives an example of a non-open effective domain Θ = (−∞, 0]. It is worth noting that for the boundary parameter θ = 0, the first moment does not exist, i.e., Corollary 2.14 only makes statements in the interior  of the effective domain Θ. This also relates to Remarks 2.9 on the dual parameter space \(\mathcal {M}\).
of the effective domain Θ. This also relates to Remarks 2.9 on the dual parameter space \(\mathcal {M}\).
2.2.3 Tweedie’s Distributions
Tweedie’s compound Poisson (CP) model was introduced in 1984 by Tweedie [358], and it has been studied in detail in Jørgensen [202], Jørgensen–de Souza [204], Smyth–Jørgensen [342] and in the review paper of Delong et al. [94]. Tweedie’s CP model belongs to the EDF. We spend more time on explaining Tweedie’s CP model because it plays an important role in actuarial modeling.
Tweedie’s CP model is received by choosing as σ-finite measure ν 1 a mixture of the Lebesgue measure on (0, ∞) and a point measure in 0. Furthermore, we choose power variance parameter p ∈ (1, 2) and cumulant function
on the effective domain θ ∈ Θ = (−∞, 0). This provides us with Tweedie’s CP model
with exposure v > 0 and dispersion parameter φ > 0; the normalizing function a(⋅;v∕φ) does not have any simple closed form, we refer to Section 2.1 in Jørgensen–de Souza [204] and Section 4.2 in Jørgensen [203].
The first two moments of Tweedie’s CP random variable Y are given by
The parameter p ∈ (1, 2) determines the power variance functions V (μ) = μ p between the Poisson p = 1 and the gamma p = 2 cases, see Sect. 2.2.2.
The moment generating function of Tweedie’s CP random variable X = vY∕φ = ωY in its additive form is given by, we use Corollary 2.14,
Some readers will notice that this is the moment generating function of a CP distribution having i.i.d. gamma claim sizes. This is exactly the statement of the next proposition which is found, e.g., in Smyth–Jørgensen [342].
Proposition 2.17. Assume \(S=\sum _{i=1}^N Z_i\) is CP distributed with Poisson claim counts N ∼Poi(λv) and i.i.d. gamma claim sizes Z
i ∼ Γ(α, β) being independent of N. We have  by identifying the parameters as follows
by identifying the parameters as follows
Proof of Proposition 2.17. Assume S is CP distributed with i.i.d. gamma claim sizes. From Proposition 2.11 and Section 3.2.1 in Wüthrich [387] we receive that the moment generating function of S is given by
Using the proposed parameter identification, the claim immediately follows. □
Proposition 2.17 gives us a second interpretation of Tweedie’s CP model which was introduced in an EDF fashion, above. This second interpretation explains the name of this EDF model, it explains the mixture of the Lebesgue measure and the point measure in 0, and it also highlights why the Poisson model and the gamma model are the boundary cases in terms of power variance functions.
An interesting question is whether the EDF can be extended beyond power variance functions V (μ) = μ p with p ∈ [1, 2]. The answer to this question is yes, and the full answer is provided in Theorem 2 of Jørgensen [202]:
Theorem 2.18 (Jørgensen [202], Without Proof). Only power variance parameters p ∈ (0, 1) do not allow for EDF models.
Table 2.1 gives the EDF distributions that have a power variance function. These distributions are called Tweedie’s distributions, with the special case of Tweedie’s CP distributions for p ∈ (1, 2). The densities for p ∈{0, 1, 2, 3} have a closed form, but the other Tweedie’s distributions do not have a closed-form density. Thus, they cannot explicitly be constructed as suggested in Sect. 2.2.1. Besides the constructive approach presented above, there is a uniqueness theorem saying that the variance function V (⋅) on the domain \(\mathcal {M}\) characterizes the single-parameter linear EF, see Theorem 2.11 in Jørgensen [203]. This uniqueness theorem is the basis of the proof of Theorem 2.18. Tweedie’s distributions for p∉[0, 1] ∪{2, 3} involve infinite sums for the normalization \(\exp \{a(\cdot , \cdot )\}\), we refer to formulas (4.19), (4.20) and (4.31) in Jørgensen [203], this is the reason that one has to go via the uniqueness theorem to prove Theorem 2.18. Dunn–Smyth [112] provide methods of fast calculation of some of these infinite sums; in Sect. 5.5.2, below, we present an approximation (saddlepoint approximation). The uniqueness theorem is also useful to construct new examples within the EF, see, e.g., Section 2 of Awad et al. [15].
2.2.4 Steepness of the Cumulant Function
Assume we have a fixed EF satisfying Assumption 2.6. All random variables T(Y ) belonging to this EF have the same support, not depending on the particular choice of the canonical parameter θ ∈ Θ. We denote this support of T(Y ) by \({\mathfrak T}\).
Below, we are going to estimate the canonical parameter θ ∈ Θ from data using maximum likelihood estimation. For this it is advantageous to have the property \({\mathfrak T} \subset \mathcal {M}\), because, intuitively, this allows us to directly select \(\widehat {\mu }=T(Y)\) as the parameter estimate in the dual parameter space \(\mathcal {M}\), for a given observation \(T(Y) \in {\mathfrak T}\). This then translates to a canonical parameter \(\widehat {\boldsymbol {\theta }}=h(\widehat {\mu })=h(T(Y)) \in \boldsymbol {\Theta }\), using the canonical link h; this estimation approach will be better motivated in Chap. 3, below. Unfortunately, many examples of the EF do not satisfy this property \({\mathfrak T} \subset \mathcal {M}\). For instance, in the Poisson model the observation T(Y ) = Y = 0 is not included in \(\mathcal {M}\), see Table 2.1. This poses some challenges in parameter estimation, and the purpose of this small discussion is to be prepared for these challenges.
A cumulant function κ is called steep if for all  and all \(\widetilde {\boldsymbol {\theta }}\) in the boundary of Θ
and all \(\widetilde {\boldsymbol {\theta }}\) in the boundary of Θ

we refer to Formula (20) in Section 8.1 of Barndorff-Nielsen [23]. Define the convex closure of the support \({\mathfrak T}\) by \({\mathfrak C}=\overline {\mbox{conv}}({\mathfrak T})\).
Theorem 2.19 (Theorem 9.2 in Barndorff-Nielsen [23], Without Proof). Assume we have a fixed EF satisfying Assumption 2.6. The cumulant function κ is steep if and only if  .
.
Theorem 2.19 tells us that for a steep cumulant function we have  . In this case parameter estimation can be extended to observations \(T(Y)\not \in \mathcal {M}\) such that we may obtain a degenerate model at the boundary of \(\mathcal {M}\). Coming back to our Poisson example from above, in this case we set \(\widehat {\mu }=0\), which gives a degenerate Poisson model.
. In this case parameter estimation can be extended to observations \(T(Y)\not \in \mathcal {M}\) such that we may obtain a degenerate model at the boundary of \(\mathcal {M}\). Coming back to our Poisson example from above, in this case we set \(\widehat {\mu }=0\), which gives a degenerate Poisson model.
Throughout this book we will work under the assumption that κ is steep. The classical examples satisfy this assumption: the examples with power variance parameter p in {0}∪ [1, ∞) satisfy Theorem 2.19; this includes the Gaussian, the Poisson, the gamma, the inverse Gaussian and Tweedie’s CP models, see Table 2.1. Moreover, the examples we have met in Sect. 2.1 fulfill this assumption; these are the single-parameter linear EF models of the Bernoulli, the binomial and the negative binomial distributions, as well as the vector-valued parameter examples of the Gaussian, the gamma and the inverse Gaussian models and of the categorical distribution. The only models we have seen that do not have a steep cumulant function are the power variance models with p < 0, see Table 2.1.
Remark 2.20. Working within the EDF needs some additional thoughts because the support \({\mathfrak T}={\mathfrak T}_\omega \) of the single-parameter linear EDF random variable Y = T(Y ) may depend on the specific choice of the dispersion parameter \(\omega \in \mathcal {W} \supset \{1\}\) through the σ-finite measure dν ω(ω ⋅), see (2.13). For instance, in the binomial case the support of Y is given by \({\mathfrak T}_\omega =\{0,1/n,\ldots , 1\}\) with ω = n, see Sect. 2.2.2.
Assume that the cumulant function κ is steep for the single-parameter linear EF that corresponds to the single-parameter EDF with ω = 1. Theorem 2.19 then implies that for this choice we have  with convex closure \({\mathfrak C}_{\omega =1}=\overline {\mbox{conv}}({\mathfrak T}_{\omega =1})\).
with convex closure \({\mathfrak C}_{\omega =1}=\overline {\mbox{conv}}({\mathfrak T}_{\omega =1})\).
Consider \(\omega \in \mathcal {W}\setminus \{1\}\) which corresponds to the choice ν
ω of the σ-finite measure on \({\mathbb R}\). This choice belongs to the cumulant function θ↦ωκ(θ) in the additive form (x-parametrization in (2.13)). Since steepness (2.20) holds for any ω > 0 we receive that the convex closure of the support of this distribution in the x-parametrization in (2.13) is given by  . The duality transformation x↦y = x∕ω leads to the change of measure dν
ω(x)↦dν
ω(ωy) and to the corresponding change of support, see (2.13). The latter implies that in the reproductive form (y-parametrization) the convex closure of the support does not depend on the specific choice of \(\omega \in \mathcal {W}\). Since the EDF representation given in (2.14) corresponds to the y-parametrization (reproductive form), we can use Theorem 2.19 without limitation also for the single-parameter linear EDF given by (2.14), and \({\mathfrak C}\) does not depend on \(\omega \in \mathcal {W}\).
. The duality transformation x↦y = x∕ω leads to the change of measure dν
ω(x)↦dν
ω(ωy) and to the corresponding change of support, see (2.13). The latter implies that in the reproductive form (y-parametrization) the convex closure of the support does not depend on the specific choice of \(\omega \in \mathcal {W}\). Since the EDF representation given in (2.14) corresponds to the y-parametrization (reproductive form), we can use Theorem 2.19 without limitation also for the single-parameter linear EDF given by (2.14), and \({\mathfrak C}\) does not depend on \(\omega \in \mathcal {W}\).
2.2.5 Lab: Large Claims Modeling
From Corollary 2.14 we know that the moment generating function exists around the origin for all examples belonging to the EDF. This implies that the moments of all orders exist, and that we have an exponentially decaying survival function \({\mathbb P}_{\theta }[Y>y]=1-F(y;\theta ,\omega ) \sim \exp \{-\varrho y\}\) for some ϱ > 0 as y →∞, see (1.2). In many applied situations the data is more heavy-tailed and, thus, cannot be modeled by such an exponentially decaying survival function. In such cases one often chooses a distribution function with a regularly varying survival function; regular variation with tail index β > 0 has been introduced in (1.3). A popular choice is a log-gamma distribution which can be obtained from the gamma distribution (belonging to the EDF). We briefly explain how this is done and how it relates to the Pareto and the Lomax [256] distributions.
We start from the gamma density (2.6). The random variable Z has a log-gamma distribution with shape parameter α > 0 and scale parameter β = −θ > 0 if log(Z) = Y has a gamma distribution with these parameters. Thus, the gamma density of Y = log(Z) is given by
We do a change of variable \(y \mapsto z=\exp \{y\}\) to receive the density of the log-gamma distributed random variable \(Z=\exp \{Y\}\)
This log-gamma density has support (1, ∞). The distribution function of this log-gamma distributed random variable needs to be calculated numerically, and its survival function is regularly varying with tail index β > 0.
A special case of the log-gamma distribution is the Pareto distribution. The Pareto distribution is more tractable and it is obtained by setting shape parameter α = 1 in the log-gamma density. This gives us the Pareto density
The distribution function in this Pareto case is for z ≥ 1 given by
Obviously, this provides a regularly varying survival function with tail index β > 0; in fact, in this case we do not need to go over to the limit in (1.3) because we have an exact identity. The Pareto distribution has the nice property that it is closed under thresholding (lower-truncation) with M, that is, we remain within the family of Pareto distributions with the same tail index β by considering lower-truncated claims: for 1 ≤ M ≤ z we have
This is the classical definition of the Pareto distribution, and it allows to preserve full flexibility in the choice of the threshold M > 0.
The disadvantage of the Pareto distribution is that it does not provide a continuous density on \({\mathbb R}_+\) as there is a discontinuity in threshold M. For this reason, one sometimes explores another change of variable Z↦X = Z − M for a Pareto distributed random variable Z ∼ F(⋅;β, M). This provides the Lomax distribution, also called Pareto Type II distribution. X has the following distribution function on (0, ∞)
This distribution has again a regularly varying survival function with tail index β > 0. Moreover, we have
This says that we should choose the same threshold M > 0 for both the Pareto and the Lomax distribution to receive the same asymptotic tail behavior, and this also quantifies the rate of convergence between the two survival functions. Figure 2.3 illustrates this convergence in a log-log plot choosing tail index β = 2 and threshold M = 1′000′000.
For completeness we provide the density of the Pareto distribution
and of the Lomax distribution
2.3 Information Geometry in Exponential Families
We do a short excursion to information geometry. This excursion may look a bit disconnected from what we have done so far, but it provides us with important background information for the chapter on forecast evaluation, see Chap. 4, below.
2.3.1 Kullback–Leibler Divergence
There is literature in information geometry which uses techniques from differential geometry to study EFs as Riemannian manifolds with points corresponding to EF densities parametrized by their canonical parameters θ ∈ Θ, we refer to Amari [10], Ay et al. [16] and Nielsen [285] for an extended treatment of these mathematical concepts.
Choose a fixed EF (2.2) with cumulant function κ on the effective domain \(\boldsymbol {\Theta } \subseteq {\mathbb R}^k\) and with σ-finite measure ν on \({\mathbb R}\). We define the Kullback–Leibler (KL) divergence (relative entropy) from model θ 1 ∈ Θ to model θ 0 ∈ Θ within this EF by
Recall that the support of the EF does not depend on the specific choice of the canonical parameter θ in Θ, see Remarks 2.3; this implies that the KL divergence is well-defined, here. The positivity of the KL divergence is obtained from Jensen’s inequality; this is proved in Lemma 2.21, below.
The KL divergence has the interpretation of having a data model that is characterized by the distribution f(⋅;θ 0), and we would like to measure how close another model f(⋅;θ 1) is to the data model. Note that the KL divergence is not a distance function because it is neither symmetric nor does it satisfy the triangle inequality.
We calculate the KL divergence within the chosen EF

where we have used Corollary 2.5, and the positivity of the KL divergence can be seen from the convexity of κ. This allows us to consider the following (Taylor) expansion

This illustrates that the KL divergence corresponds to second and higher order differences between the cumulant value κ(θ 0) and another cumulant value κ(θ 1). The gradients of the KL divergence w.r.t. θ 1 in θ 1 = θ 0 and w.r.t. θ 0 in θ 0 = θ 1 are given by

This emphasizes that the KL divergence reflects second and higher-order terms in cumulant function κ; and that the data model θ 0 forms the minimum of this KL divergence (as a function of θ 1) as we will just see. We calculate the Hessian (second order term) w.r.t. θ 1 in θ 1 = θ 0

The positive definite matrix \(\mathcal {I}(\boldsymbol {\theta }_0)\) (in a minimal representation) is called Fisher’s information. Fisher’s information is an important tool in statistics that we will meet in Theorem 3.13 of Sect. 3.3, below. A function satisfying (2.21) (with being zero if and only if θ 0 = θ 1), fulfilling (2.23) and having positive definite Fisher’s information is called divergence, see Definition 5 in Nielsen [285]. Fisher’s information \(\mathcal {I}(\boldsymbol {\theta }_0)\) measures the curvature of the KL divergence in θ 0 and we have the second order Taylor approximation

Next-order terms are obtained from the so-called Amari–Chentsov tensor, see Amari [10] and Section 4.2 in Ay et al. [16]. In information geometry one studies the (possibly degenerate) Riemannian metric on the effective domain Θ induced by Fisher’s information; we refer to Section 3.7 in Nielsen [285].
Lemma 2.21. Consider two densities p and q w.r.t. a given σ-finite measure ν. We have D KL(p||q) ≥ 0, and D KL(p||q) = 0 if and only if p = q, ν-a.s.
Proof. Assume Y ∼ pdν, then we can rewrite the KL divergence, using Jensen’s inequality,
Equality holds if and only if p = q, ν-a.s. The last inequality of (2.24) considers that q does not necessarily need to be a density w.r.t. ν, i.e., we can also have \(\int q(y) d\nu (y) <1\). □
2.3.2 Unit Deviance and Bregman Divergence
In the next chapter we are going to introduce maximum likelihood estimation for parameters, see Definition 3.4, below. Maximum likelihood estimators are obtained by maximizing likelihood functions (evaluated in the observations). Maximizing likelihood functions within the EDF is equivalent to minimizing deviance loss functions. Deviance loss functions are based on unit deviances, which, in turn, correspond to KL divergences. The purpose of this small section is to discuss this relation. This should be viewed as a preparation for Chap. 4.
Assume we work within a single-parameter linear EDF, i.e., T(y) = y. Using the canonical link h we obtain the canonical parameter \(\theta = h(\mu ) \in \boldsymbol {\Theta } \subseteq {\mathbb R}\) from the mean parameter \(\mu \in \mathcal {M}\). If we replace the (typically unknown) mean parameter μ by an observation Y , supposed \(Y\in \mathcal {M}\), we get the specific model that is exactly calibrated to this observation. This provides us with the canonical parameter estimate \(\widehat {\theta }_Y = h(Y)\) for θ. We can now measure the KL divergence from any model represented by θ to the observation calibrated model \(\widehat {\theta }_Y = h(Y)\). This KL divergence is given by (we use (2.21) and we set ω = v∕φ = 1)
This latter object is the unit deviance (up to factor 2) of the chosen EDF. It plays a crucial role in predictive modeling.
We define the unit deviance under the assumption that κ is steep as follows:

where \({\mathfrak C}\) is the convex closure of the support \({\mathfrak T}\) of Y and \(\mathcal {M}\) is the dual parameter space of the chosen EDF. Steepness of κ implies  , see Theorem 2.19.
, see Theorem 2.19.
This unit deviance \({\mathfrak d}\) is received from the KL divergence, and it is (twice) the difference of two log-likelihood functions, one using canonical parameter h(y) and the other one having any canonical parameter  . That is, for μ = κ′(θ),
. That is, for μ = κ′(θ),
for general \(\omega =v/\varphi \in \mathcal {W}\). The latter can be rewritten as
This looks like a generalization of the Gaussian distribution, where the square difference (y − μ)2 in the exponent is replaced by the unit deviance \({\mathfrak d}(y,\mu )\) with μ = κ′(θ). This interpretation gets further support by the following lemma.
Lemma 2.22. Under Assumption 2.6 and the assumption that the cumulant function κ is steep, the unit deviance \({\mathfrak d}\left (y, \mu \right )\ge 0\) of the chosen EDF is zero if and only if y = μ. Moreover, the unit deviance \({\mathfrak d}\left (y, \mu \right )\) is twice continuously differentiable w.r.t. (y, μ) in  , and
, and
Proof. The positivity and the if and only if statement follows from Lemma 2.21 and the strict convexity of κ. Continuous differentiability follows from the smoothness of κ in the interior of Θ. Moreover we have
where V (μ) is the variance function of the chosen EDF introduced in Corollary 2.14. The remaining second derivatives are received by similar (straightforward) calculations. □
Remarks 2.23.
-
Lemma 2.22 shows that the unit deviance definition of \({\mathfrak d}(y, \mu )\) provides a so-called regular unit deviance according to Definition 1.1 in Jørgensen [203]. Moreover, any model that can be brought into the form (2.27) for a (regular) unit deviance is called (regular) reproductive dispersion model, see Definition 1.2 of Jørgensen [203].
-
In general the unit deviance \({\mathfrak d}(y, \mu )\) is not symmetric in its two arguments y and μ, we come back to this in Fig. 11.1, below.
More generally, the KL divergence and the unit deviance can be embedded into the framework of Bregman loss functions [50]. We restrict to the single-parameter EDF case. Assume that  is a strictly convex function. The Bregman divergence w.r.t. ψ between y and μ is defined by
is a strictly convex function. The Bregman divergence w.r.t. ψ between y and μ is defined by
where ψ′ is a (sub-)gradient of ψ. The lower bound holds because of convexity of ψ. Consider the specific choice ψ(μ) = μh(μ) − κ(h(μ)) for the chosen EDF. Similar to Lemma 2.22 we have ψ″(μ) = h′(μ) = 1∕V (μ) > 0, which says that this choice is strictly convex. Using this choice for ψ gives us unit deviance (up to factor 1∕2)
Thus, the unit deviance \(\mathfrak {d}\) can be understood as a difference of log-likelihoods (2.26), as a KL divergence D KL and as a Bregman divergence D ψ.
Example 2.24 (Poisson Model). We start with a single-parameter EF example. Consider cumulant function \(\kappa (\theta )=\exp \{\theta \}\) for canonical parameter \(\theta \in \boldsymbol {\Theta } = {\mathbb R}\), this gives us the Poisson model. For the KL divergence from model θ 1 to model θ 0 we receive
which is zero if and only if θ 0 = θ 1. Fisher’s information is given by
If we have observation Y > 0 we receive a model described by canonical parameter \(\widehat {\theta }_Y=h(Y)={\mbox{log}}(Y)\). This gives us unit deviance, see (2.26),
with \(\mu = \kappa '(\theta )= \exp \{\theta \}\). This Poisson unit deviance will commonly be used for model fitting and forecast evaluation, see, e.g., (5.28). \(\blacksquare \)
Example 2.25 (Gamma Model). The second example considers a vector-valued parameter EF example. We consider the cumulant function κ(θ) = log Γ(θ
2) − θ
2log(−θ
1) for  ; this gives us the gamma model, see Sect. 2.1.3. For the KL divergence from model θ
1 to model θ
0 we receive
; this gives us the gamma model, see Sect. 2.1.3. For the KL divergence from model θ
1 to model θ
0 we receive
Fisher’s information matrix is given by
The off-diagonal terms in Fisher’s information matrix \(\mathcal {I}(\boldsymbol {\theta })\) are non-zero which means that the two components of the canonical parameter θ interact. Choosing a different parametrization μ = θ 2∕(−θ 1) (dual mean parametrization) and α = θ 2 we receive diagonal Fisher’s information in (μ, α)
where Ψ is the digamma function, see Footnote 2 on page 10. This transformation is obtained by using the corresponding Jacobian matrix for variable transformation; more details are provided in (3.16) below. In this new representation, the parameters μ and α are orthogonal; the term \(\Psi '(\alpha ) -\frac {1}{\alpha }\) is further discussed in Remarks 5.26 and Remarks 5.28, below.
Using this second parametrization based on mean μ and dispersion 1∕α, we arrive at the EDF representation of the gamma model. This allows us to calculate the corresponding unit deviance (within the EDF), which in the gamma case is given by
\(\blacksquare \)
Example 2.26 (Inverse Gaussian Model). Our final example considers the inverse Gaussian vector-valued parameter EF case. We consider the cumulant function \(\kappa (\boldsymbol {\theta }) = -2(\theta _1\theta _2)^{1/2}-\frac {1}{2} {\mbox{log}}(-2\theta _2)\) for  , see Sect. 2.1.3. For the KL divergence from model θ
1 to model θ
0 we receive
, see Sect. 2.1.3. For the KL divergence from model θ
1 to model θ
0 we receive

Fisher’s information matrix is given by
Again the off-diagonal terms in Fisher’s information matrix \(\mathcal {I}(\boldsymbol {\theta })\) are non-zero in the canonical parametrization. We switch to the mean parametrization by setting μ = (−2θ 2∕(−2θ 1))1∕2 and α = −2θ 2. This provides us with diagonal Fisher’s information
This transformation is again obtained by using the corresponding Jacobian matrix for variable transformation, see (3.16), below. We compare the lower-right entries of (2.30) and (2.31). Remark that we have first order approximation of the digamma function
and taking derivatives says that these entries of Fisher’s information are first order equivalent; this is also used in the saddlepoint approximation in Sect. 5.5.2, below. Using this second parametrization based on mean μ and dispersion 1∕α, we arrive at the EDF representation of the inverse Gaussian model with unit deviance
\(\blacksquare \)
More examples will be given in Chap. 4, below.
Notes
- 1.
We could also use boldface notation for T because \(T(y)\in {\mathbb R}^k\) is vector-valued, but we prefer to not use boldface notation for (vector-valued) functions.
- 2.
The function \(\Psi (x) = \frac {d}{dx} {\mbox{log}} \Gamma (x) = \Gamma '(x)/\Gamma (x)\) is called digamma function.
References
Amari, S. (2016). Information geometry and its applications. New York: Springer.
Awad, Y., Bar-Lev, S. K., & Makov, U. (2022). A new class of counting distributions embedded in the Lee–Carter model of mortality projections: A Bayesian approach. Risks, 10/6. Article 111.
Ay, N., Jost, J., Lê, H. V., & Schwachhöfer, L. (2017). Information geometry. New York: Springer.
Bachelier, L. (1900). The theory of speculation. English translation by May, D. R. (2011). Annales Scientifiques de l’École Normale Supérieure, 3/17, 21–89.
Barndorff-Nielsen, O. (2014). Information and exponential families: In statistical theory. New York: Wiley.
Bregman, L. M. (1967). The relaxation method of finding the common point of convex sets and its application to the solution of problems in convex programming. USSR Computational Mathematics and Mathematical Physics, 7/3, 200–217.
Darmois, G., (1935). Sur les lois de probabilité à estimation exhaustive. Comptes Rendus de l’Académie des Sciences Paris, 260, 1265–1266.
Delong, Ł., Lindholm, M., & Wüthrich, M. V. (2021). Making Tweedie’s compound Poisson model more accessible. European Actuarial Journal, 11/1, 185–226.
Dunn, P. K., & Smyth, G. K. (2005). Series evaluation of Tweedie exponential dispersion model densities. Statistics and Computing, 15, 267–280.
Fisher, R. A. (1934). Two new properties of mathematical likelihood. Proceeding of the Royal Society A, 144/852, 285–307.
Jørgensen, B. (1981). Statistical properties of the generalized inverse Gaussian distribution. Lecture notes in statistics. New York: Springer.
Jørgensen, B. (1986). Some properties of exponential dispersion models. Scandinavian Journal of Statistics, 13/3, 187–197.
Jørgensen, B. (1987). Exponential dispersion models. Journal of the Royal Statistical Society, Series B, 49/2, 127–145.
Jørgensen, B. (1997). The theory of dispersion models. Boca Raton: Chapman & Hall.
Jørgensen, B., & de Souza, M. C. P. (1994). Fitting Tweedie’s compound Poisson model to insurance claims data. Scandinavian Actuarial Journal, 1994/1, 69–93.
Koopman, B. O. (1936). On distributions admitting a sufficient statistics. Transactions of the American Mathematical Society, 39, 399–409.
Lehmann, E. L. (1983). Theory of point estimation. New York: Wiley.
Lomax, K. S. (1954). Business failures: Another example of the analysis of failure data. Journal of the American Statistical Association, 49/268, 847–852.
Nielsen, F. (2020). An elementary introduction to information geometry. Entropy, 22/10, 1100.
Ohlsson, E., & Johansson, B. (2010). Non-life insurance pricing with generalized linear models. New York: Springer.
Pitman, E. J. G. (1936). Sufficient statistics and intrinsic accuracy. Proceedings of the Cambridge Philosophical Society, 32/4, 567–579.
Smyth, G. K., & Jørgensen, B. (2002). Fitting Tweedie’s compound Poisson model to insurance claims data: dispersion modeling. ASTIN Bulletin, 32/1, 143–157.
Tweedie, M. C. K. (1984). An index which distinguishes between some important exponential families. In J. K. Ghosh, & J. Roy (Eds.) Statistics: Applications and new directions. Proceeding of the Indian Statistical Golden Jubilee International Conference (pp. 579–604). Calcutta: Indian Statistical Institute.
Wüthrich, M. V. (2013). Non-life insurance: Mathematics & statistics. SSRN Manuscript ID 2319328. Version February 7, 2022.
Author information
Authors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2023 The Author(s)
About this chapter
Cite this chapter
Wüthrich, M.V., Merz, M. (2023). Exponential Dispersion Family. In: Statistical Foundations of Actuarial Learning and its Applications. Springer Actuarial. Springer, Cham. https://doi.org/10.1007/978-3-031-12409-9_2
Download citation
DOI: https://doi.org/10.1007/978-3-031-12409-9_2
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-12408-2
Online ISBN: 978-3-031-12409-9
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)


 , see Corollary 2.5. This property is important, otherwise we do not have identifiability in the canonical parameter θ because we have a linear dependence between the components of T(Y ).
, see Corollary 2.5. This property is important, otherwise we do not have identifiability in the canonical parameter θ because we have a linear dependence between the components of T(Y ).

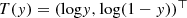 for the beta distribution. We refrain from giving explicit formulas for these or other examples.
for the beta distribution. We refrain from giving explicit formulas for these or other examples. of the effective domain Θ is non-empty.
of the effective domain Θ is non-empty.