Abstract
This chapter presents a selection of different topics. We discuss forecasting under model uncertainty, deep quantile regression, deep composite regression and the LocalGLMnet which is an interpretable FN network architecture. Moreover, we provide a bootstrap example to assess prediction uncertainty, we discuss mixture density networks, and we give an outlook to studying variational inference.
You have full access to this open access chapter, Download chapter PDF
11.1 Deep Learning Under Model Uncertainty
We revisit claim size modeling in this section. Claim size modeling is challenging because often there is no (simple) off-the-shelf distribution that allows one to appropriately describe all claim size observations. E.g., the main body of the claim size data may look like gamma distributed, and, at the same time, large claims seem to be more heavy-tailed (contradicting a gamma model assumption). Moreover, different product and claim types may lead to multi-modality in the claim size densities. In Sects. 5.3.7 and 5.3.8 we have explored a gamma and an inverse Gaussian GLM to model a motorcycle claims data set. In that example, the results have been satisfactory because this motorcycle data is neither multi-modal nor does it have heavy tails. These two GLM approaches have been based on the EDF (2.14), modeling the mean x↦μ(x) with a regression function and assuming a constant dispersion parameter φ > 0. There are two natural ways to extend this approach. One considers a double GLM with a dispersion submodel x↦φ(x), see Sect. 5.5, the other explores multi-parameter extensions like the generalized inverse Gaussian model, which is a k = 3 vector-valued EF, see (2.10), or the GB2 family that involves 4 parameters, see (5.79). These extensions provide more complexity, also in MLE. In this section, we are not going to consider multi-parameter extensions, but in a first step we aim at robustifying (mean) parameter estimation within the EDF. In a second step we are going to analyze the resulting dispersion φ(x). For these steps, we perform representation learning and parameter estimation under model uncertainty by simultaneously considering multiple models from Tweedie’s family. These considerations are closely related to Tweedie’s forecast dominance given in Definition 4.22.
We emphasize that we remain within a single distribution function choice in this section, i.e., we neither consider mixture distributions nor composite models in this section. Mixture density networks are going to be considered in Sect. 11.6, below, and a composite model approach is studied in Sect. 11.3, below. These mixture density networks and composite models allow us to model the body and the tail of the data with different distribution functions by either mixing or concatenating suitable distributions.
11.1.1 Recap: Tweedie’s Family
Tweedie’s family with power variance function V (μ) = μ p, p ≥ 2, provides us with a rich model class for claim size modeling if the claim sizes are strictly positive, a.s., and extending to p ∈ (1, 2) allows us to model claims with a positive point mass in 0. This class of distribution functions contains the gamma case (p = 2) and the inverse Gaussian case (p = 3). In general, p > 2 provides us with positive stable generated distributions and p ∈ (1, 2) gives Tweedie’s CP models, see Table 2.1. Tweedie’s family has cumulant function for p > 1
on the effective domain θ ∈ Θ∈ (−∞, 0) for p ∈ (1, 2], and θ ∈ Θ∈ (−∞, 0] for p > 2. The mean and the power variance function are for p > 1 given by
The unit deviance takes the following form for p > 1 and p ≠ 2, see (4.18),
and in the gamma case p = 2 we have, see Table 4.1,
Figure 11.1 (lhs) shows the unit deviances \(y\mapsto {\mathfrak d}_p(y,\mu )\) for fixed mean parameter μ = 2 and power variance parameters p ∈{0, 2, 2.5, 3, 3.5}; the case p = 0 corresponds to the symmetric Gaussian case \({\mathfrak d}_0(y, \mu )=(y-\mu )^2\). We observe that with an increasing power variance parameter p large claims Y = y receive a smaller loss punishment (if we interpret the unit deviance as a loss function). This is the situation where we have a fixed mean μ and where we assess claim sizes Y = y relative to this mean. For estimation purposes we have fixed observations Y = y and we study the sensitivities in μ. Note that, in general, the unit deviances \({\mathfrak d}_p(y,\mu )\) are not symmetric in y and μ. This second case is shown in Fig. 11.1 (rhs), and the general behavior in p is similar. As a result, by selecting different hyper-parameters p > 1, we can control the influence of large (and small) claims on parameter estimation, because the unit deviances \({\mathfrak d}_p(y, \cdot )\) have different slopes for different p’s. Basically, the choice of the loss function (unit deviance) determines the choice of the underlying distributional model, which then assesses the claim observations Y = y according to their sizes and how these sizes match the model assumptions made.
In Lemma 2.22 we have seen that the unit deviances \({\mathfrak d}_p\left (y, \mu \right )\ge 0\) are zero if and only if y = μ. The second derivatives given in Lemma 2.22 allow us to consider a second order Taylor expansion around a minimum μ 0 = y 0
Thus, locally around the minimum the unit deviances behave symmetric and like Gaussian squares, but this is only a local approximation around a minimum μ 0 = y 0 as can be seen from Fig. 11.1. I.e., in general, model fitting turns out to be rather different from the Gaussian square loss if we have small and large claim sizes under choices p > 1.
Remarks 11.1
-
Since unit deviances are Bregman divergences, we know that every unit deviance gives us a strictly consistent scoring function for the mean functional, see Theorem 4.19. Therefore, the specific choice of the power variance parameter p seems less relevant. However, strict consistency is an asymptotic statement, and choosing a unit deviance that matches the property of the data has better finite sample properties, i.e., a smaller variance in asymptotic normality; we come back to this in Sect. 11.1.4, below.
-
A function (y, μ)↦ψ(y, μ) is called b-homogeneous if there exists \(b\in {\mathbb R}\) such that for all (y, μ) and all λ > 0 we have ψ(λy, λμ) = λ b ψ(y, μ). Unit deviances \({\mathfrak d}_p\) are b-homogeneous with b = 2 − p. This b-homogeneity has the nice consequence that the decisions taken are independent of the scale, i.e., we have an invariance under changes of currencies. On the other hand, such a scaling influences the estimation of the dispersion parameter, i.e., if we scale the observation and the mean with λ we have unit deviance
$$\displaystyle \begin{aligned} {\mathfrak d}_p (\lambda y,\lambda \mu)=\lambda^{2-p}\,{\mathfrak d}_p(y,\mu). \end{aligned} $$(11.4)This influences the dispersion estimation for the cases different from the gamma case p = 2, see, e.g., saddlepoint approximation (5.60)–(5.62). This also relates to the different parametrizations in Sect. 5.3.8 where we study the inverse Gaussian model p = 3, which has a dispersion φ i = 1∕α i in the reproductive form and \(\varphi _i=1/\alpha ^2_i\) in parametrization (5.51).
-
We only consider power variance parameters p > 1 in this section for non-negative claim size modeling. Technically, this analysis could be extended to p ∈{0, 1}. We do not consider the Gaussian case p = 0 to exclude negative claims, and we do not consider the Poisson case p = 1 because this is used for claim counts modeling.
We recall that unit deviances of the EDF are equal to twice the corresponding KL divergences, which in turn are special cases of Bregman divergences. From Theorem 4.19 we know that Bregman divergences D ψ are the only strictly consistent loss/scoring functions for mean estimation.
Lemma 11.2
Choose p > 1. The scaled unit deviance \({\mathfrak d}_p(y,\mu )/2\) is a Bregman divergence \(D_{\psi _p}(y,\mu )\) on \({\mathbb R}_+\times {\mathbb R}_+\) with strictly decreasing and strictly convex function on \({\mathbb R}_+\)
for canonical link \(h_p(y)=(\kappa ^{\prime }_p)^{-1}(y)=y^{1-p}/(1-p)\).
Proof of Lemma 11.2
The Bregman divergence property follows from (2.29). For p > 1 and y > 0 we have the strictly decreasing property
The second derivative is \(\psi ^{\prime \prime }_p(y) =h^{\prime }_p(y)=y^{-p}=1/V(y)>0\) which provides the strict convexity. □
In the Gaussian case we have ψ 0(y) = y 2∕2, and \(\psi _0^{\prime }(y)>0\) on \({\mathbb R}_+\) implies that this is a strictly increasing convex function for positive claims y > 0. This is different to Lemma 11.2.
Assume we have independent observations (Y i, x i) following the same Tweedie’s distribution, and with means given by μ 𝜗(x i) for some parameter 𝜗. The M-estimator of 𝜗 using this Bregman divergence is given by

If we turn this M-estimator into a Z-estimator (supposed we have differentiability), the parameter estimate \(\widehat {\boldsymbol {\vartheta }}\) is found as a solution of the score equations

In the GLM case this exactly corresponds to (5.9). To determine the Z-estimator from (11.5), we scale the residuals Y i − μ i inversely proportional to the variances \(V(\mu _i)=\mu _i^p\) of the chosen Tweedie’s distribution. It is a well-known result that if we scale individual unbiased estimators inversely proportional to their variances, we receive the unbiased estimator with minimal variance, we come back to this in (11.16), below. This gives us the intuition behind a specific choice of the power variance parameter for mean estimation, as the sizes of the variances \(\mu _i^p\) scale (weight) the observed residuals Y i − μ i, and balance potential outliers in the observations correspondingly.
11.1.2 Lab: Claim Size Modeling Under Model Uncertainty
We present a proposal for deep learning under model uncertainty in this section. We explain this on an explicit example within Tweedie’s distributions. We emphasize that this methodology can be applied in more generality, but it is beneficial here to have an explicit example in mind to illustrate the different phenomena.
11.1.2.1 Generalized Linear Models
We analyze a Swiss accident insurance claims data set. This data is illustrated in Sect. 13.4, and an excerpt of the data is given in Listing 13.7. In total we have 339’500 claims with positive payments. We choose this data set because it ranges from very small claims of 1 CHF to very large claims, the biggest one exceeding 1’300’000 CHF. These claims are supported by feature information such as the labor sector, the injury type or the injured body part, see Listing 13.7 and Fig. 13.25. For our analysis, we partition the data into a learning data set \(\mathcal {L}\) and a test data set \(\mathcal {T}\). We do this partition stratified w.r.t. the claim sizes and in a ratio of 9 : 1. This results in a learning data set \(\mathcal {L}\) of size n = 305′550 and in a test data set \(\mathcal {T}\) of size T = 33′950.
We consider three Tweedie’s distributions with power variance parameters p ∈{2, 2.5, 3}, the first one is the gamma model, the last one the inverse Gaussian model, and the power variance parameter p = 2.5 gives a model in between. In a first step we consider GLMs, this requires feature engineering. We have three categorical features, one binary feature and two continuous ones. For the categorical and binary features we use dummy coding, and the continuous features Age and AccQuart are just included in its raw form. As link function g we choose the log-link which respects the positivity of the dual mean parameter space \(\mathcal {M}\), see Table 2.1, but this is not the canonical link of the selected models. In the gamma GLM this leads to a convex minimization problem, but in Tweedie’s GLM with p = 2.5 and in the inverse Gaussian GLM we have non-convex minimization problems, see Example 5.6. Therefore, we initialize Fisher’s scoring method (5.12) in the latter two GLMs with the solution of the gamma GLM. The gamma and the inverse Gaussian cases can directly be fitted with the R command glm [307], for the power variance parameter case p = 2.5 we have coded our own MLE routine using Fisher’s scoring method.
Table 11.1 shows the in-sample losses on the learning data \(\mathcal {L}\) and the corresponding out-of-sample losses on the test data \(\mathcal {T}\). The fitted GLMs (gamma, power variance parameter p = 2.5 and inverse Gaussian) are always evaluated on all three unit deviances \({\mathfrak d}_{p=2}(y,\mu )\), \({\mathfrak d}_{p=2.5}(y,\mu )\) and \({\mathfrak d}_{p=3}(y,\mu )\), respectively. We give some remarks. First, we observe that the in-sample loss is always minimized for the GLM with the same power variance parameter p as the loss \({\mathfrak d}_{p}\) studied (2.0695, 7.6971 and 3.9398 in bold face). This result simply states that the parameter estimates are obtained by minimizing the in-sample loss (or maximizing the corresponding in-sample log-likelihood). Second, the minimal out-of-sample losses are also highlighted in bold face. From these results we cannot give any preference to a single model w.r.t. Tweedie’s forecast dominance, see Definition 4.20. Third, we calculate the AIC values for all models. The gamma and the inverse Gaussian cases have a closed-form solution for the normalizing term a(y;v∕φ) in the EDF density, and we can directly calculate AIC. The case p = 2.5 is more difficult and we use the saddlepoint approximation of Sect. 5.5.2. Considering AIC we give preference to Tweedie’s GLM with p = 2.5. Note that the AIC values use the MLE for φ which is obtained from a general purpose optimizer, and which uses the saddlepoint approximation in the power variance case p = 2.5. Fourth, under a constant dispersion parameter φ, the mean estimation \(\widehat {\mu }_i\) can be done without explicitly specifying φ because it cancels in the score equations. In fact, we perform this mean estimation in the additive form and not in the reproductive form, see (2.13) and the discussions in Sects. 5.3.7–5.3.8.
Figure 11.2 plots the deviance residuals (for unit dispersion) against the logged fitted means \(\widehat {\mu }(\boldsymbol {x}_i)\) for p ∈{2, 2.5, 3} for 2’000 randomly selected claims; this is the Tukey–Anscombe plot. The green line has been obtained by a spline fit to the deviance residuals as a function of the fitted means \(\widehat {\mu }(\boldsymbol {x}_i)\), and the cyan lines give twice the estimated standard deviation of the deviance residuals as a function of the fitted means (also obtained from spline fits). This estimated standard deviation corresponds to the square-rooted deviance dispersion estimate \(\widehat {\varphi }^{\mathrm {D}}\), see (5.30), however, in the additive form because we work with unscaled claim size observations. A constant dispersion assumption is supported by cyan lines of roughly constant size. In the gamma case the dispersion seems increasing in the mean estimate, and in the inverse Gaussian case it is decreasing, thus, the power variance parameters p = 2 and p = 3 do not support a constant dispersion in this example. Only the choice p = 2.5 may support a constant dispersion assumption (because it does not have an obvious trend). This says that the variance should scale as V (μ) = μ 2.5 as a function of the mean μ, see also (11.5).
Tukey–Anscombe plots showing the deviance residuals against the logged GLM fitted means \(\widehat {\mu }(\boldsymbol {x}_i)\): (lhs) gamma GLM p = 2, (middle) power variance case p = 2.5, (rhs) inverse Gaussian GLM p = 3; the cyan lines show twice the estimated standard deviation of the deviance residuals as a function of the size of the logged estimated means \(\widehat {\mu }\)
11.1.2.2 Deep FN Networks
We compare the above GLMs to FN networks of depth d = 3 with (q 1, q 2, q 3) = (20, 15, 10) neurons. The categorical features are modeled with embedding layers of dimension b = 2. We fit this network architecture with Tweedie’s deviances losses having power variance parameters p ∈{2, 2.5, 3}. Moreover, we use 20% of the learning data \(\mathcal {L}\) as validation data \(\mathcal {V}\) to explore the early stopping rule.Footnote 1 To reduce the randomness coming from early stopping with different seeds, we average the deviance losses over 20 runs (this is not the nagging predictor: we only average the deviance losses to have stable conclusions concerning forecast dominance). The results are presented in Table 11.2.
First, we observe that the networks outperform the GLMs, saying that the feature engineering has not been done optimally for GLMs. Second, in-sample we no longer receive the lowest deviance loss in the model with the same p. This comes from the fact that we exercise early stopping, and, for instance, the gamma in-sample loss of the gamma network (p = 2) 1.9738 is bigger than the corresponding gamma loss of 1.9712 from the network with p = 2.5. Third, considering forecast dominance, preference is given either to the gamma network or to the power variance parameter p = 2.5. In general, it seems that fitting with higher power variance parameters leads to less stable results, but this statement needs more analysis. The disadvantage of this fitting approach is that we independently fit the models with the different power variance parameters to the observations, and, thus, the learned representations z (d:1)(x i) are rather different for different p’s. This makes it difficult to compare these models. This is exactly the point that we address next.
11.1.2.3 Robustified Representation Learning
To deal with the drawback of missing comparability of the network approaches with different power variance parameters, we can try to learn a representation that simultaneously fits different models. The implementation of this idea is rather straightforward in network modeling. We choose the above network of depth d = 3, which gives us the new (learned) representation z i = z (d:1)(x i) in the last FN layer. The general idea now is that we design multiple outputs for this learned representation to fit the different distributional models. That is, in the case of three Tweedie’s loss functions with power variance parameters p ∈{2, 2.5, 3} we consider a three-dimensional output mapping

for different output parameters \(\boldsymbol {\beta }_{2}, \boldsymbol {\beta }_{2.5}, \boldsymbol {\beta }_{3} \in {\mathbb R}^{q_d+1}\). These three expected responses (11.6) share the network parameters \(\boldsymbol {w}=(\boldsymbol {w}_1^{(1)}, \ldots ,\boldsymbol {w}_{q_d}^{(d)})\) in the FN layers, and the network fitting should learn these parameters such that z i = z (d:1)(x i) gives a good representation for all considered loss functions. Choose positive weights η p > 0, and define the combined deviance loss function
for the given observations (Y i, x i, v i), 1 ≤ i ≤ n. Note that the unit deviances \({\mathfrak d}_p\) live on different scales for different p’s. We use the (constant) weights η p > 0 to balance these scales so that all power variance parameters p roughly equally contribute to the total loss, while setting φ p ≡ 1 (which can be done for a constant dispersion). This approach is now fitted to the available learning data \(\mathcal {L}\). The corresponding R code is given in Listing 11.1. Note that the fitting also requires that we triplicate the observations (Y i, Y i, Y i) so that we can simultaneously evaluate the three chosen power variance deviance losses, see lines 18–21 of Listing 11.1. We fit this model to the Swiss accident insurance data, and the results are presented in Table 11.3 on the lines called ‘multi-out’.
Listing 11.1 FN network with multiple output

This simultaneous representation learning across different loss functions leads to more stability in the results between the different loss function choices, i.e., there is less variability between the losses of the different outputs compared to fitting the three different models independently. The predictive performance seems slightly better in this robustified vs. the independent case (see bold face out-of-sample figures). The similarity of the results across the different loss functions (using the jointly learned representation z i) allows us to directly compare the corresponding predictors \(\widehat {\mu }_p(\boldsymbol {x}_i)\) for the different p’s.
Figure 11.3 compares the three predictors by considering the ratios \(\widehat {\mu }_{p=2}(\boldsymbol {x}_i)/\widehat {\mu }_{p=2.5}(\boldsymbol {x}_i)\) in black color and \(\widehat {\mu }_{p=3}(\boldsymbol {x}_i)/\widehat {\mu }_{p=2.5}(\boldsymbol {x}_i)\) in blue color, i.e., we divide by the (middle) predictor with power variance parameter p = 2.5. The figure on the left-hand side shows these ratios in-sample and ordered on the x-axis w.r.t. the observed claim sizes Y i, and the darkgray and cyan lines give spline fits to these ratios. The figure on the right-hand side shows these ratios out-of-sample and ordered on the x-axis w.r.t. the average predictors \(\bar {\mu }_i=(\widehat {\mu }_{p=2}(\boldsymbol {x}_i)+\widehat {\mu }_{p=2.5}(\boldsymbol {x}_i)+\widehat {\mu }_{p=3}(\boldsymbol {x}_i))/3\). In view of (11.5) we expect that the models with a smaller power variance parameter p over-fit more to large claims. From Fig. 11.3 (lhs) we can observe that, indeed, this is the case (see gray and cyan spline fits which bifurcate for large claims). That is, models with a smaller power variance parameter react more sensitively to large observations Y i. The ratios in Fig. 11.3 provide differences of up to 7% for large claims.
Ratios \(\widehat {\mu }_{p=2}(\boldsymbol {x}_i)/\widehat {\mu }_{p=2.5}(\boldsymbol {x}_i)\) (black color) and \(\widehat {\mu }_{p=3}(\boldsymbol {x}_i)/\widehat {\mu }_{p=2.5}(\boldsymbol {x}_i)\) (blue color) of the three predictors (lhs) in-sample figures ordered on the x-axis w.r.t. the logged observed claims Y i, darkgray and cyan lines give spline fits, (rhs) out-of-sample figures ordered on the x-axis w.r.t. the logged average size of the three predictors
Remark 11.3
The loss function (11.7) can also be interpreted as regularization. For instance, if we choose η 2 = 1, and if we assume that this is our preferred model, then we can regularize this model with further models, and their weights η p > 0 determine the degree of regularization. Thus, in contrast to ridge and LASSO regularization of Sect. 6.2, regularization does not directly act on the model parameters, here, but rather on what we learn in terms of the representation z i = z (d:1)(x i).
11.1.2.4 Using Forecast Dominance to Deal with Model Uncertainty
In GLMs, the power variance parameter p typically acts as a hyper-parameter, i.e., one fits different GLMs for different choices of p. Model selection is then done, e.g., by analyzing the Tukey–Anscombe plot, AIC, cross-validation or by studying out-of-sample forecast dominance. In networks we should not use AIC as we neither have a parsimonious network parameter nor do we use the MLE. Here, we focus on forecast dominance for the network predictors (based on the different chosen power variance parameters). If we are mainly interested in receiving a model that provides optimal forecast dominance, we should not consider three different outputs as in (11.7), but rather fit the same output to different loss functions; the required changes are minimal, see Listing 11.2. Namely, consider one FN network with one output μ(x i), but evaluate this output simultaneously on the different chosen loss functions
In contrast to (11.7), we only have one FN network regression function x i↦μ(x i), here.
Listing 11.2 FN network with a single output for multiple losses

We present the results on the last line of Table 11.3, called ‘multi-loss’. In our case, this approach is slightly less competitive (out-of-sample), however, it is less sensitive to outliers since we need to have a good regression function simultaneously for multiple loss functions. Of course, this multiple loss fitting approach is not restricted to different power variance parameters. As stated in Theorem 4.19, Bregman divergences are the only consistent loss functions for mean estimation, and the unit deviances are examples of Bregman divergences. Forecast dominance now suggests that we may choose any Bregman divergence as a loss function in Listing 11.2 as long as it reflects the expected properties of the model (and of the observed data), otherwise we will receive bad convergence properties, see also Sect. 11.1.4, below. For instance, we can robustify the Poisson claim counts model by additionally considering the deviance loss of the negative binomial model that also assesses over-dispersion.
11.1.2.5 Nagging Predictor
The loss figures in Table 11.3 are averaged deviance losses over 20 different runs of the gradient descent algorithm with different seeds (to receive stable results). Rather than averaging over the losses, we should improve the models by averaging over the predictors and, then, calculate the losses on these averaged predictors; this is exactly the proposal of the nagging predictor (7.44). We calculate the nagging predictor of the models that are simultaneously fit to the different loss functions (lines ‘multi-output’ and ‘multi-loss’ of Table 11.3). The resulting nagging predictors are reported in Table 11.4. This table shows that we give a clear preference to the nagging predictors. The simultaneous loss fitting (11.8) gives the best out-of-sample results for the nagging predictor, see the last line of Table 11.4.
Figure 11.4 shows the Tukey–Anscombe plot of the multi-loss nagging predictor for the different deviance losses (for unit dispersion). Again, the case p = 2.5 is closest to having a constant dispersion, and the other cases will require dispersion modeling φ(x).
Tukey–Anscombe plots giving the deviance residuals of the multi-loss nagging predictor of Table 11.4 for different power variance parameters: (lhs) gamma deviances p = 2, (middle) power variance deviances p = 2.5, (rhs) inverse Gaussian deviances p = 3; the cyan lines show twice the estimated standard deviation of the deviance residuals as a function of the size of the logged estimated means \(\widehat {\mu }\)
Figure 11.5 shows the empirical auto-calibration property of the multi-loss nagging predictor. This auto-calibration property is calculated as in Listing 7.8. We observe that the auto-calibration property holds rather accurately. Only for claim predictors \(\widehat {\mu }(\boldsymbol {x}_i)\) above 10’000 CHF (vertical dotted line in Fig. 11.5) the fitted means under-estimate the observed average claim sizes. This affects (only) 1.7% of all claims and it could be corrected as described in Example 7.19.
11.1.3 Lab: Deep Dispersion Modeling
From the Tukey–Anscombe plots in Fig. 11.4 we conclude that the dispersion requires regression modeling, too, as the dispersion does not seem to be constant over the whole range of the expected claim sizes. We therefore explore a double FN network model, in spirit this is similar to the double GLM of Sect. 5.5. We therefore assume to work within Tweedie’s family with power variance parameters p ≥ 2, and with unit deviances given by (11.2)–(11.3). The saddlepoint approximation (5.59) gives us
with power variance function V (y) = y p. This saddlepoint approximation is formulated in the reproductive form for Y = X∕ω = Xφ∕v. This requires scaling of the observations X with the unknown φ to receive Y . In Sect. 5.5.4 we have shown how this problem can be solved. In this section we give a different proposal which is more robust in network fitting, and which benefits from the b-homogeneity of \({\mathfrak d}_p\), see (11.4).
We consider the variable transformation y↦x = yω = yv∕φ. In the absolutely continuous case p ≥ 2 this gives us the approximation
with mean μ p = μv∕φ of X = Y v∕φ. We set ϕ = −1∕φ p−1 < 0. This gives us the approximation
For given mean μ p we again have a gamma approximation on the right-hand side, but we scale the dispersion differently. This gives us the approximate first moment

The remainder of this modeling is similar to the residual MLE approach in Section 5.5.3. Namely, we set up two FN network regression functions
Parameter fitting is achieved by alternating the network parameter fitting of μ p(x) and φ p(x) see also Section 5.5.4. We start the iteration by setting the dispersion constant to \(\widehat {\varphi }_p^{(0)}(\boldsymbol {x})\equiv \mathrm {const}\). In this case, the dispersion cancels in the score equations and the mean \(\widehat {\mu }_p^{(1)}(\boldsymbol {x})\) can be estimated without the explicit knowledge of the (constant) dispersion parameter \(\widehat {\varphi }^{(0)}_p\); this exactly provides the results of the previous Sect. 11.1.2. Then, we iterate this procedure for t ≥ 1. For given mean estimate \(\widehat {\mu }_p^{(t)}(\boldsymbol {x})\) we receive deviances \(v^{p-1}{\mathfrak d}_p(X, \widehat {\mu }_p^{(t)}(\boldsymbol {x}))\), and this allows us to estimate \(\widehat {\varphi }_p^{(t)}(\boldsymbol {x})\) from the approximate gamma model (11.9), and for given dispersion parameters \(\widehat {\varphi }_p^{(t)}(\boldsymbol {x})\) we estimate \(\widehat {\mu }_p^{(t+1)}(\boldsymbol {x})\) from the corresponding Tweedie’s model for the observation X.
Example 11.4
We revisit the Swiss accident insurance data example of Sect. 11.1.2, and we use the robustified representation learning approach (11.7) that simultaneously fits Tweedie’s models for the power variance parameters p = 2, 2.5, 3. The initial calibration step is done for constant dispersions \(\widehat {\varphi }_p^{(0)}(\boldsymbol {x})\equiv \mathrm {const}\), and it provides us with the estimated means \(\widehat {\mu }_p^{(1)}(\boldsymbol {x})\) as illustrated in Fig. 11.3. For stability reasons we choose the nagging predictor averaging over 20 different SGD runs with 20 different seeds. These estimated means \(\widehat {\mu }_p^{(1)}(\boldsymbol {x})\) give us the deviances \(v^{p-1}{\mathfrak d}_p(X, \widehat {\mu }_p^{(1)}(\boldsymbol {x}))\).
Using these deviances allows us to alternate the dispersion and mean estimation for t ≥ 1. For given means \(\widehat {\mu }_p^{(t)}(\boldsymbol {x})\), p = 2, 2.5, 3, we set up a deep FN network x↦z (d:1)(x) that allows for a robustified deep dispersion learning φ p(x), for p = 2, 2.5, 3. Under the log-link choice we consider the regression function with multiple outputs

for different output parameters \(\boldsymbol {\alpha }_{2}, \boldsymbol {\alpha }_{2.5}, \boldsymbol {\alpha }_{3} \in {\mathbb R}^{q_d+1}\). These three dispersion responses (11.10) share the common network parameter \(\widetilde {\boldsymbol {w}}=(\widetilde {\boldsymbol {w}}_1^{(1)}, \ldots ,\widetilde {\boldsymbol {w}}_{q_d}^{(d)})\) in the FN layers of z (d:1). The network fitting learns these parameters simultaneously for the different power variance parameters. Choose positive weights \(\widetilde {\eta }_p>0\), and define the combined deviance loss function (based on the gamma model κ 2 and having dispersion parameter 2)
where X = (X 1, …, X n) collects the unscaled observations X i = Y i v i∕φ i. Thus, for all power variance parameters p = 2, 2.5, 3 we fit a gamma model \({\mathfrak d}_2(\cdot ,\cdot )/2\) to the observed deviances (observations) \(v^{p-1}_i{\mathfrak d}_p(X_i, \widehat {\mu }_p^{(t)}(\boldsymbol {x}_i))\) providing us with the estimated dispersions \(\widehat {\varphi }_p^{(t)}(\boldsymbol {x}_i)\). This fitting step is received by the R code of Listing 11.1, where the losses on line 20 are all given by gamma deviance losses (11.11) and the deviances \(v_i^{p-1}{\mathfrak d}_p(X_i, \widehat {\mu }_p^{(t)}(\boldsymbol {x}_i))\) play the role of the responses (observations).
In the next step we update the mean estimates \(\widehat {\mu }_p^{(t+1)}(\boldsymbol {x}_i)\), given the estimated dispersions \(\widehat {\varphi }_p^{(t)}(\boldsymbol {x}_i)\) from the previous step. This requires that we optimize the expected responses (11.6) for given heterogeneous dispersion parameters. We therefore consider the loss function for positive weights η p > 0, see (11.7),
We fit this model by iterating this approach for t ≥ 1: we start from the predictors of Sect. 11.1.2 providing us with the first mean estimates \(\widehat {\mu }_p^{(1)}(\boldsymbol {x}_i)\). Based on these mean estimates we iterate this robustified estimation of \(\widehat {\varphi }_p^{(t)}(\boldsymbol {x}_i)\) and \(\widehat {\mu }_p^{(t)}(\boldsymbol {x}_i)\). We give some remarks:
-
1.
We use the robustified versions (11.11) and (11.12), respectively, where we simultaneously fit all power variance parameters p = 2, 2.5, 3 on the commonly learned representations z i = z (d:1)(x i) in the last FN layer of the mean and the dispersion network, respectively.
-
2.
For both FN networks of mean μ and dispersion φ modeling we use the same network architecture of depth d = 3 having (q 1, q 2, q 3) = (20, 15, 10) neurons in the FN layers, the hyperbolic tangent activation function, and the log-link for the output. These two networks only differ in their network parameters (w, β 2, β 2.5, β 3) and \((\widetilde {\boldsymbol {w}}, \boldsymbol {\alpha }_{2}, \boldsymbol {\alpha }_{2.5}, \boldsymbol {\alpha }_{3})\), respectively.
-
3.
For fitting we use the nadam version of SGD. For the early stopping we use a training data \(\mathcal {U}\) to validation data \(\mathcal {V}\) split of 8 : 2.
-
4.
To ensure consistency within the individual SGD runs across t ≥ 1, we use the learned network parameter of loop t as initial value for loop t + 1. This ensures monotonicity across the iterations in the log-likelihood and the loss function, respectively, up to the fact that the random mini-batches in SGD may distort this monotonicity.
-
5.
To reduce the elements of randomness in SGD fitting we run this iteration procedure 20 times with different seeds, and we output the nagging predictors for \(\widehat {\mu }_p^{(t)}(\boldsymbol {x}_i)\) and \(\widehat {\varphi }_p^{(t)}(\boldsymbol {x}_i)\) averaged over the 20 runs for every t in Table 11.5.
Table 11.5 Iteration of mean \(\widehat {\mu }_p^{(t)}\) and dispersion \(\widehat {\varphi }_p^{(t)}\) estimation for the gamma model p = 2, the power variance parameter p = 2.5 model and the inverse Gaussian model p = 3: the numbers correspond to \(-2 \ell _{\boldsymbol {X}}(\widehat {\mu }_p^{(t)}, \widehat {\varphi }_p^{(t)})\); the last line corrects \(-2 \ell _{\boldsymbol {X}}(\widehat {\mu }_p^{(t)}, \widehat {\varphi }_p^{(t)})\) by 2 ⋅ 2 ⋅ 812 = 3′248 (twice the number of parameters used in the mean and dispersion FN networks)
We iterate this algorithm over two loops, and the results are presented in Table 11.5. We observe a decrease of \(-2 \ell _{\boldsymbol {X}}(\widehat {\mu }_p^{(t)}, \widehat {\varphi }_p^{(t)})\) by iterating the fitting algorithm for t ≥ 1. For AIC, we would have to correct twice the negative log-likelihood by twice the number of MLE estimated parameters. We also adjust here correspondingly, though the correction is not justified by any theory, because we do not work with the MLE nor do we have a parsimonious model for mean and dispersion estimation. Nevertheless, we receive smaller values than in Table 11.1 which supports the use of this more complex double FN network model.
Comparing the three power variance parameter models, we now give preference to the inverse Gaussian model, as it has the biggest log-likelihood. Note that we directly compare all power variance models as the complexity is equal in all models (they only differ in the chosen power variance parameter) and the joint robustified fitting applies the same stopping rule to all power variance parameter models. The same result is obtained by comparing the out-of-sample log-likelihoods. Note that we do not compare the deviance losses, here, because the unit deviances are not designed to estimate parameters in vector-valued parameter families; we model dispersion as a second parameter.
Next, we study the estimated dispersions \(\widehat {\varphi }_p(\boldsymbol {x}_i)\) as a function of the estimated means \(\widehat {\mu }_p(\boldsymbol {x}_i)\). We fit a spline to \(\widehat {\varphi }_p(\boldsymbol {x}_i)\) as a function of \(\widehat {\mu }_p(\boldsymbol {x}_i)\), and we receive estimates that almost perfectly match the cyan lines in Fig. 11.4. This provides a proof of concept that the dispersion regression model finds the right level of dispersion as a function of the expected means.
Using the mean and dispersion estimates, we can calculate the dispersion scaled deviance residuals

This then allows us to give the Tukey–Anscombe plots for the three considered power variance parameters.
The corresponding plots are given in Fig. 11.6; the difference to Fig. 11.4 is that the latter considers unit dispersion whereas the former scales the residuals with the rooted dispersion  ; note that v
i ≡ 1 in this example. By scaling with the rooted dispersion the resulting deviance residuals \(r_i^{\mathrm {D}}\) should roughly have unit standard deviation. From Fig. 11.6 we observe that indeed this is the case, the cyan line shows a spline fit of twice the standard deviation of the deviance residuals \(r_i^{\mathrm {D}}\). These splines are of magnitude 2 which verifies the unit standard deviation property. Moreover, the cyan lines are roughly horizontal which indicates that the dispersion estimation and the scaling works across all expected claim sizes \(\widehat {\mu }_p(\boldsymbol {x}_i)\). The three different power variance parameters p = 2, 2.5, 3 show different behaviors in the lower and upper tails in the residuals (centering around the orange horizontal zero line in Fig. 11.6) which corresponds to the different distributional properties of the chosen models.
; note that v
i ≡ 1 in this example. By scaling with the rooted dispersion the resulting deviance residuals \(r_i^{\mathrm {D}}\) should roughly have unit standard deviation. From Fig. 11.6 we observe that indeed this is the case, the cyan line shows a spline fit of twice the standard deviation of the deviance residuals \(r_i^{\mathrm {D}}\). These splines are of magnitude 2 which verifies the unit standard deviation property. Moreover, the cyan lines are roughly horizontal which indicates that the dispersion estimation and the scaling works across all expected claim sizes \(\widehat {\mu }_p(\boldsymbol {x}_i)\). The three different power variance parameters p = 2, 2.5, 3 show different behaviors in the lower and upper tails in the residuals (centering around the orange horizontal zero line in Fig. 11.6) which corresponds to the different distributional properties of the chosen models.
Tukey–Anscombe plots giving the dispersion scaled deviance residuals \(r_i^{\mathrm {D}}\) (11.13) of the models jointly fitting the mean parameters \(\widehat {\mu }_p(\boldsymbol {x}_i)\) and the dispersion parameters \(\widehat {\varphi }_p(\boldsymbol {x}_i)\): (lhs) gamma model, (middle) power variance parameter p = 2.5 model, and (rhs) inverse Gaussian models; the cyan lines correspond to 2 standard deviations
We further analyze the gamma and the inverse Gaussian models. Note that the analysis of the power variance models for general power variance parameters p ≠ 0, 1, 2, 3 is more difficult because neither the EDF density nor the EDF distribution function have a closed form. To analyze the gamma and the inverse Gaussian models we simulate observations \(X^{\mathrm {sim}}_t\), t = 1, …, T, from the estimated models (using the out-of-sample features \(\boldsymbol {x}^\dagger _t\) of the test data \(\mathcal {T}\)), and we compare them against the true out-of-sample observations \(X^\dagger _t\). Figure 11.7 shows the results for the gamma model (lhs) and the inverse Gaussian model (rhs) on the log-scale. A good fit has been achieved if the black dots lie on the red diagonal line (in the colored version), because then the simulated data shares similar features as the observed data. The fit of the inverse Gaussian model seems reasonably good.
On the other hand, we see that the gamma model gives a poor fit, especially in the lower tail. This supports the AIC values of Table 11.5. The problem with the gamma model is that the data is more heavy-tailed than the gamma model can accomplish. As a consequence, the dispersion parameter estimates \(\widehat {\varphi }_2(\boldsymbol {x}^\dagger _t)\) in the gamma model are compensating for this by taking values bigger than 1. A dispersion parameter bigger than 1 implies a shape parameter in the gamma model of \(\widehat {\alpha }^\dagger _t=1/\widehat {\varphi }_2(\boldsymbol {x}^\dagger _t)<1\), and the resulting gamma density is strictly decreasing, see Fig. 2.1. If we simulate from this model we receive many observations \(X^{\mathrm {sim}}_t\) close to zero (from the strictly decreasing density). This can be seen from the lower-left part of the graph in Fig. 11.7 (lhs), suggesting that we have many observations with \(X^\dagger _t \in (0,1)\), or on the log-scale \(\mathrm {log}(X^\dagger _t)<0\). However, the graph shows that this is not the case in the real data. Figure 11.7 (middle) shows the boxplot of the estimated shape parameters \(\widehat {\alpha }^\dagger _t\) on the test data, 1 ≤ t ≤ T, verifying that most insurance policies of the test data \(\mathcal {T}\) receive a shape parameter \(\widehat {\alpha }^\dagger _t\) less than 1.
We conclude that the inverse Gaussian double FN network model seems to work well for this data, and we give preference to this model. \(\blacksquare \)
11.1.4 Pseudo Maximum Likelihood Estimator
This short section gives a mathematical foundation to parameter estimation under model uncertainty and model misspecification. We summarize the results of Gourieroux et al. [168], and we refrain from giving any proofs in this section. Assume that the real-valued observations Y i, 1 ≤ i ≤ n, have been generated by the model
with (true) parameter \(\zeta _0 \in \Lambda \subset {\mathbb R}^r\), feature \(\boldsymbol {x}_i \in \mathcal {X} \subseteq \{1\}\times {\mathbb R}^q\), and where the conditional distribution of the noise random variables (ε i)1≤i≤n satisfies the conditional independence property \(p_\varepsilon (\varepsilon _1,\ldots , \varepsilon _n|\boldsymbol {x}_1,\ldots , \boldsymbol {x}_n) = \prod _{i=1}^n p_\varepsilon (\varepsilon _i|\boldsymbol {x}_i)\). Denote by p x(x) the portfolio distribution of the features x. Thus, under (11.14), the claim Y of a randomly selected policy is generated by the joint probability measure p 𝜖,x(ε, x) = p ε(ε|x)p x(x). The technical assumptions under which the following statements hold are given in Assumption 11.9 at the end of this section.
Let F 0(⋅|x i) denote the true conditional distribution of Y i, given x i. Typically, this (true) conditional distribution is unknown. It is assumed to provide the first two conditional moments
Thus, \(\varepsilon _i|{ }_{\boldsymbol {x}_i}\) is assumed to be centered with conditional variance \(\sigma ^2_0(\boldsymbol {x}_i)\), see (11.14). Our goal is to estimate the (true) parameter ζ 0 ∈ Λ, based on the fact that the conditional distribution F 0(⋅|x) of the observations is unknown. Throughout we assume parameter identifiability, i.e., if \(\mu _{\zeta _1}(\boldsymbol {x})=\mu _{\zeta _2}(\boldsymbol {x})\), p x-a.s., then ζ 1 = ζ 2. The following estimator is called pseudo maximum likelihood estimator (PMLE)

where \({\mathfrak d}(y,\mu )\) is the unit deviance of a (pre-chosen) single-parameter linear EDF being parametrized by the same parameter space \(\Lambda \subset {\mathbb R}^r\) as the original random variables (11.14); note that Λ is not the effective domain Θ of the chosen EDF. \(\widehat {\zeta }^{\mathrm {PMLE}}_n\) is called PMLE because it is a MLE for ζ 0 ∈ Λ, but not in the right model, because the pre-chosen EDF in (11.15) typically differs from the (unknown) true conditional distribution F 0(⋅|x). Nevertheless, we may hope to find the true parameter ζ 0, but possibly at a slower asymptotic rate. This is exactly what is going to be stated in the next theorems.
Theorem 11.5 (Theorem 1 of Gourieroux et al. [168])
Denote by
 the dual mean parameter space of the pre-chosen EDF (having cumulant function κ), and assume that
\(\mu _{\zeta }(\boldsymbol {x})\in \mathcal {M}\)
for all
\(\boldsymbol {x} \in \mathcal {X}\)
and ζ ∈ Λ. Let Assumption
11.9
, below, hold. The PMLE
\(\widehat {\zeta }^{\mathrm {PMLE}}_n\)
is strongly consistent for ζ
0
, i.e., it converges a.s. as n →∞.
the dual mean parameter space of the pre-chosen EDF (having cumulant function κ), and assume that
\(\mu _{\zeta }(\boldsymbol {x})\in \mathcal {M}\)
for all
\(\boldsymbol {x} \in \mathcal {X}\)
and ζ ∈ Λ. Let Assumption
11.9
, below, hold. The PMLE
\(\widehat {\zeta }^{\mathrm {PMLE}}_n\)
is strongly consistent for ζ
0
, i.e., it converges a.s. as n →∞.
This theorem tells us that we can perform MLE in a pre-chosen EDF (which may differ from the true data model), and asymptotically we find the true parameter ζ 0 of the data model F 0(⋅|x). Of course, this uses the fact that any unit deviance \({\mathfrak d}\) is a strictly consistent loss function for mean estimation, see Theorem 4.19. We do not only receive consistency, but the following theorem also gives us the rate of convergence.
Theorem 11.6 (Theorem 3 of Gourieroux et al. [168])
Set the same assumptions as in Theorem 11.5 . The PMLE \(\widehat {\zeta }^{\mathrm {PMLE}}_n\) has the following asymptotic behavior

with the following matrices evaluated in ζ = ζ 0

where h = (κ′)−1 is the canonical link of the pre-chosen EDF, and with the change of variable ζ↦θ = θ(ζ) = h(μ ζ(x)) ∈ Θ , for given feature x , having Jacobian

Remark that \(\mathcal {I}^\ast (\zeta )\) averages Fisher’s information \(\mathcal {I}^\ast (\zeta ;\boldsymbol {x})\) (of the chosen EDF) over the feature distribution p x. This theorem can be seen as a modification of (3.36) to the regression case. Theorem 11.6 gives us the asymptotic normality of the PMLE, and the resulting asymptotic variance depends on how well the pre-chosen EDF matches the true data distribution F 0(⋅|x). The following lemma corresponds to Property 5 in Gourieroux et al. [168].
Lemma 11.7
The asymptotic variance in Theorem 11.6 has the lower bound, set ζ = ζ 0 and \(\sigma ^2(\boldsymbol {x})=\sigma _0^2(\boldsymbol {x})\),

Proof
We set τ
2(x) = κ″(h(μ
ζ(x))). We have  . The following matrix is positive semi-definite and it satisfies
. The following matrix is positive semi-definite and it satisfies

This proves the claim. □
Theorem 11.6 and Lemma 11.7 tell us that if we estimate the parameter ζ 0 of the unknown model F 0(⋅|x) with PMLE based on a single-parameter linear EDF, we receive minimal asymptotic variance if we can match the variance \(V(\mu _{\zeta _0}(\boldsymbol {x}))=\kappa ''(h(\mu _{\zeta _0}(\boldsymbol {x})))\) of the chosen EDF with the variance \(\sigma ^2_0(\boldsymbol {x})\) of the true data model. E.g., if we know that the variance in the true model behaves as \(\sigma ^2_0(\boldsymbol {x}) = \mu ^3_{\zeta _0}(\boldsymbol {x})\) we should select the inverse Gaussian model with variance function V (μ) = μ 3 for PMLE.
If the members of the single-parameter linear EDF do not fully match the variance structure of the true data, we can turn our attention to a dispersion submodel as in Sect. 5.5.1. Assume for the variance structure of the true data
for a regression function \(\boldsymbol {x} \mapsto s^2_{\alpha _0}(\boldsymbol {x})\) involving the (true) regression parameter α 0 and exposures v i > 0. If we choose a fixed EDF, we have the log-likelihood function
Equating the variance structure of the true data model with the variance in this pre-specified EDF, we obtain feature-dependent dispersion parameter
with variance function V (μ) = (κ″ ∘ h)(μ). The following theorem proposes a two-step procedure for this estimation problem.
Theorem 11.8 (Theorem 4 of Gourieroux et al. [168])
Assume
\(\widetilde {\zeta }_n\)
and
\(\widetilde {\alpha }_n\)
are strongly consistent estimators for ζ
0
and α
0
, as n →∞, such that
 and
and
 are bounded in probability. The quasi-generalized pseudo maximum likelihood estimator (QPMLE) of ζ
0
is obtained by
are bounded in probability. The quasi-generalized pseudo maximum likelihood estimator (QPMLE) of ζ
0
is obtained by

Under Assumption 11.9 , below, \(\widehat {\zeta }^{\mathrm {QPMLE}}_n\) is strongly consistent and best asymptotically normal, i.e.,

This justifies the approach(es) in the previous chapters and sections, though, not fully, because we neither work with the MLE in FN networks nor do we care about identifiability in parameters. Nevertheless, this short section suggests to find strongly consistent estimators \(\widetilde {\zeta }_n\) and \(\widetilde {\alpha }_n\) for ζ 0 and α 0. This gives us a first model calibration step that allows us to specify the dispersion structure x↦φ(x) via (11.16). Using this dispersion structure and the deviance loss function (4.9) for a variable dispersion parameter φ(x), the QPMLE is obtained in the second step by, we replace the likelihood maximization by the deviance loss minimization,

This QPMLE is best asymptotically normal, thus, asymptotically optimal within the EDF. There might still be better estimators for ζ 0, but these are outside the EDF.
If we turn M-estimation into Z-estimation we have the requirement for ζ, see also (11.5),

Thus, it all boils down to find the right variance structure to receive the optimal asymptotic behavior.
The previous statements hold true under the following technical assumptions. These are taken from Appendix 1 of Gourieroux et al. [167], and they are an adapted version of the ones in Burguete et al. [61].
Assumption 11.9
-
(i)
μ ζ(x) and \({\mathfrak d}(y,\mu _{\zeta }(\boldsymbol {x}))\) are continuous w.r.t. all variables and twice continuously differentiable in ζ;
-
(ii)
\(\Lambda \subset {\mathbb R}^r\) is a compact set and the true parameter ζ 0 is in the interior of Λ;
-
(iii)
almost every realization of (ε i, x i) is a Cesàro sum generator w.r.t. the probability measure p 𝜖,x(ε, x) = p ε(ε|x)p x(x) and to a dominating function b(ε, x);
-
(iv)
the sequence (x i)i is a Cesàro sum generator w.r.t. p x and \(b(\boldsymbol {x})=\int _{{\mathbb R}} b(\varepsilon , \boldsymbol {x}) dp_{\varepsilon }(\varepsilon |\boldsymbol {x})\);
-
(v)
for each \(\boldsymbol {x} \in \{1\}\times {\mathbb R}^q\) , there exists a neighborhood \(N_{\boldsymbol {x}} \subset \{1\}\times {\mathbb R}^q\) such that
$$\displaystyle \begin{aligned} \int_{{\mathbb R}} \sup_{\boldsymbol{x}' \in N_{\boldsymbol{x}}} b(\varepsilon, \boldsymbol{x}')\, dp_\varepsilon(\varepsilon|\boldsymbol{x})<\infty; \end{aligned}$$ -
(vi)
the functions \({\mathfrak d}(Y,\mu _{\zeta }(\boldsymbol {x}))\), \(\partial {\mathfrak d}(Y,\mu _{\zeta }(\boldsymbol {x}))/\partial \zeta _k\), \(\partial ^2{\mathfrak d}(Y,\mu _{\zeta }(\boldsymbol {x}))/\partial \zeta _k \partial \zeta _l\) are dominated by b(ε, x).
11.2 Deep Quantile Regression
So far, in network regression modeling, we have not addressed the question of prediction uncertainty. As mentioned in Remarks 4.2 on forecast evaluation, there are different sources that contribute to prediction uncertainty. There is the model and parameter estimation uncertainty, which may result in an inappropriate model choice, and there is the irreducible risk which comes from the fact that we forecast random variables which inherit a natural randomness that cannot be controlled.
We have discussed methods of evaluating model and parameter estimation error, such as the asymptotic normality of MLEs within GLMs, and we have discussed forecast dominance, the bootstrap method or the nagging predictor that allow one to assess the different sources of prediction uncertainty. However, we have not explicitly quantified these sources of uncertainty within the class of network regression models. We do an attempt in Sect. 11.4, below, by considering the fluctuations generated by bootstrap simulations. The irreducible risk can be assessed once we have a suitable statistical model; in Example 11.4 we have studied a gamma and an inverse Gaussian model on an explicit data set, and these models can be used, e.g., to calculate quantiles. In this section we consider a distribution-free approach that directly estimates these quantiles. Recall from Section 5.8.3 that quantiles are elicitable with the pinball loss as a strictly consistent loss function, see Theorem 5.33. This allows us to directly estimate the quantiles from the data.
11.2.1 Deep Quantile Regression: Single Quantile
In this section we present a way of assessing the irreducible risk which does not require a sophisticated model evaluation of distributional assumptions. Quantile regression is increasingly used in the machine learning community because it is a robust way of quantifying the irreducible risk, we refer to Meinshausen [270], Takeuchi et al. [350] and Richman [314]. We recall that quantiles are elicitable having the pinball loss as a strictly consistent loss function, see Theorem 5.33. We define a FN network regression model that allows us to directly estimate the quantiles based on the pinball loss. We therefore use an adapted version of the R code of Listing 9 in Richman [314], this adapted version has been proposed in Fissler et al. [130] to ensure that different quantiles respect monotonicity. For any two quantile levels 0 < τ 1 < τ 2 < 1 we have
where F −1 denotes the generalized inverse of distribution function F, see (5.80). If we simultaneously learn these quantiles for different quantile levels τ 1 < τ 2, we need to enforce the network to respect this monotonicity (11.17). This can be achieved by exploring a special network architecture in the output layer, and this is going to be presented in the next section.
We start by considering a single deep τ-quantile regression for a quantile level τ ∈ (0, 1). For datum (Y, x) we consider the regression function
for a strictly monotone and smooth link function g, output parameter \(\boldsymbol {\beta }_\tau \in {\mathbb R}^{q_d+1}\), and where x↦z
(d:1)(x) is a deep network. We add a lower index Y |x to the generalized inverse \(F_{Y|\boldsymbol {x}}^{-1}\) to highlight that we consider the conditional distribution of Y , given feature \(\boldsymbol {x} \in \mathcal {X}\). In the case of a deep FN network, (11.18) involves a network parameter  that needs to be estimated. Of course, the deep network architecture x↦z
(d:1)(x) could also involve any other feature, such as CN or LSTM layers, embedding layers or a NLP text recognition feature. This would change the network architecture, but it would not change anything from a methodological viewpoint.
that needs to be estimated. Of course, the deep network architecture x↦z
(d:1)(x) could also involve any other feature, such as CN or LSTM layers, embedding layers or a NLP text recognition feature. This would change the network architecture, but it would not change anything from a methodological viewpoint.
To estimate this regression parameter 𝜗 from independent data (Y i, x i), 1 ≤ i ≤ n, we consider the objective function
with the strictly consistent pinball loss function L τ for the τ-quantile. Alternatively, we could choose any other loss function satisfying Theorem 5.33, and we may try to find the asymptotically optimal one (similarly to Theorem 11.8). We refrain from doing so, but we mention Komunjer–Vuong [222]. Fitting the network parameter 𝜗 is then done in complete analogy to finding an optimal network parameter for network mean modeling. The only change is that we replace the deviance loss function by the pinball loss, e.g., in Listing 7.3 we have to exchange the loss function on line 5 correspondingly.
11.2.2 Deep Quantile Regression: Multiple Quantiles
We now turn our attention to the multiple quantile case that should satisfy the monotonicity requirement (11.17) for any quantile levels 0 < τ 1 < τ 2 < 1. A separate deep quantile estimation for both quantile levels, as described in the previous section, may violate the monotonicity property, at least, in some part of the feature space \(\mathcal {X}\), especially if the two quantile levels are close. Therefore, we enforce the monotonicity by a special choice of the network architecture.
For simplicity, in the remainder of this section, we assume that the response Y is positive, a.s. This implies for the quantiles \(\tau \mapsto F_{Y|\boldsymbol {x}}^{-1}(\tau ) \ge 0\), and we should choose a link function with g −1 ≥ 0 in (11.18). To ensure the monotonicity (11.17) for the quantile levels 0 < τ 1 < τ 2 < 1, we choose a second positive link function with \(g^{-1}_+\ge 0\), and we set for multi-task forecasting

for a regression parameter  . The positivity \(g_+^{-1}\ge 0\) enforces the monotonicity in the two quantiles. We call (11.19) an additive approach as we start from a base level characterized by the smaller quantile \(F_{Y|\boldsymbol {x}}^{-1}(\tau _1)\), and any bigger quantile is modeled by an additive increment. To ensure monotonicity for multiple quantiles we proceed recursively by choosing the lowest quantile as the initial base level.
. The positivity \(g_+^{-1}\ge 0\) enforces the monotonicity in the two quantiles. We call (11.19) an additive approach as we start from a base level characterized by the smaller quantile \(F_{Y|\boldsymbol {x}}^{-1}(\tau _1)\), and any bigger quantile is modeled by an additive increment. To ensure monotonicity for multiple quantiles we proceed recursively by choosing the lowest quantile as the initial base level.
We can also consider the upper quantile as the base level by multiplicatively lowering this upper quantile. Choose the (sigmoid) function \(g_\sigma ^{-1} \in (0,1)\) and set for the multiplicative approach

Remark 11.10
In (11.19) and (11.20) we directly enforce the monotonicty by a corresponding regression function choice. Alternatively, we can also design a (plain-vanilla) multi-output network

If we just use a classical SGD fitting algorithm, we will likely result in a situation where the monotonicity will be violated in some part of the feature space. Kellner et al. [211] consider this problem. They add a penalization (regularization term) that punishes during SGD training network parameters that violate the monotonicity. Such a penalization can be constructed, e.g., with the ReLU function.
11.2.3 Lab: Deep Quantile Regression
We revisit the Swiss accident insurance data of Sect. 11.1.2, and we provide an example of a deep quantile regression using both the additive approach (11.19) and the multiplicative approach (11.20).
Listing 11.3 Multiple FN quantile regression: additive approach

We select 5 different quantile levels \(\mathcal {Q}=(\tau _1,\tau _2,\tau _3,\tau _4,\tau _5)=(10\%, 25\%, 50\%, 75\%, 90\%)\). We start with the additive approach (11.19). It requires to set τ 1 = 10% as the base level, and the remaining quantile levels are modeled additively in a recursive way for τ j < τ j+1, 1 ≤ j ≤ 4. The corresponding R code is given on lines 8–20 of Listing 11.3, and this compiles to the 5-dimensional output on line 22.
Listing 11.4 Multiple FN quantile regression: multiplicative approach

For the multiplicative approach (11.20) we set τ 5 = 90% as the base level, and the remaining quantile levels are received multiplicatively in a recursive way for τ j+1 > τ j, 4 ≥ j ≥ 1, see Listing 11.4. The additive and the multiplicative approaches take the extreme quantiles as initialization. One may also be interested in initializing the model in the median τ 3 = 50%, the smaller quantiles can then be received by the multiplicative approach and the bigger quantiles by the additive approach. We also explore this case and we call it the mixed approach.
Listing 11.5 Fitting a multiple FN quantile regression

These network architectures are fitted to the data using the pinball loss (5.81) for the quantile levels of \(\mathcal {Q}\); note that the pinball loss requires the assumption of having a finite first moment. Listing 11.5 shows the choice of the pinball loss functions. We then fit the three architectures (additive, multiplicative and mixed) to our learning data \(\mathcal {L}\), and we apply early stopping to prevent from over-fitting. Moreover, we consider the nagging predictor over 20 runs with different seeds to reduce the randomness coming from SGD fitting.
In Table 11.6 we give the out-of-sample pinball losses on the test data \(\mathcal {T}\) of the three considered approaches, and illustrating the 5 quantile levels of \(\mathcal {Q}\). The losses of the three approaches are rather close, giving a slight preference to the mixed approach, but the other two approaches seem to be competitive, too. We further analyze these quantile regression models by considering the empirical coverage ratios defined by

where \(\widehat {F}_{Y|\boldsymbol {x}^\dagger _t}^{-1}(\tau _j)\) is the estimated quantile for level τ j and feature \(\boldsymbol {x}_t^\dagger \). Remark that the coverage ratios (11.22) correspond to the identification functions that are essentially the derivatives of the pinball losses, we refer to Dimitriadis et al. [106]. Table 11.7 reports these out-of-sample coverage ratios on the test data \(\mathcal {T}\). From these results we conclude that on the portfolio level the quantiles are matched rather well.
In Fig. 11.8 we illustrate the estimated out-of-sample quantiles \(\widehat {F}_{Y|\boldsymbol {x}^\dagger _t}^{-1}(\tau _j)\) for individual claims on the quantile levels τ j ∈{10%, 25%, 50%, 75%, 90%} (cyan, blue, black, blue, cyan colors) using the mixed approach. The x-axis considers the logged estimated medians \(\widehat {F}_{Y|\boldsymbol {x}^\dagger _t}^{-1}(50\%)\). We observe heteroskedasticity resulting in quantiles that are not ordered w.r.t. the median (black line). This supports the multiple deep quantile regression model because we cannot (simply) extrapolate the median to receive the other quantiles.
Estimated out-of-sample quantiles \(\widehat {F}_{Y|\boldsymbol {x}^\dagger _t}^{-1}(\tau _j)\) of 2’000 randomly selected individual claims on the quantile levels τ j ∈{10%, 25%, 50%, 75%, 90%} (cyan, blue, black, blue, cyan colors) using the mixed approach, the red dots are the out-of-sample observations \(Y^\dagger _t\); the x-axis gives \(\mathrm {log} \widehat {F}_{Y|\boldsymbol {x}^\dagger _t}^{-1}(50\%)\) (also corresponding to the black diagonal line)
In the final step we compare the estimated quantiles \(\widehat {F}_{Y|\boldsymbol {x}}^{-1}(\tau _j)\) from the mixed deep quantile regression approach to the ones that can be calculated from the fitted inverse Gaussian model using the double FN network approach of Example 11.4. In the latter model we estimate the mean \(\widehat {\mu }(\boldsymbol {x})\) and the dispersion \(\widehat {\varphi }(\boldsymbol {x})\) with two FN networks, which then allow us to calculate the quantiles using the inverse Gaussian distributional assumption. Note that we cannot calculate the quantiles in Tweedie’s family with power variance parameter p = 2.5 because there is no closed form of the distribution function. Figure 11.9 compares the two approaches on the quantile levels of \(\mathcal {Q}\). Overall we observe a reasonably good match though it is not perfect. The small quantiles for level τ 1 = 10% seem slightly under-estimated by the inverse Gaussian approach (see Fig. 11.9 (top-left)), whereas big quantiles τ 4 = 75% and τ 5 = 90% seem more conservative in the inverse Gaussian approach (see Fig. 11.9 (bottom)). This may indicate that the inverse Gaussian distribution does not fully fit the data, i.e., that one cannot fully recover the true quantiles from the mean \(\widehat {\mu }(\boldsymbol {x})\), the dispersion \(\widehat {\varphi }(\boldsymbol {x})\) and an inverse Gaussian assumption. There are two ways to further explore these issues. One can either choose other distributional assumptions which may better match the properties of the data, this further explores the distributional approach. Alternatively, Theorem 5.33 allows us to choose loss functions different from the pinball loss, i.e., one could consider different increasing functions G in that theorem to further explore the distribution-free approach. In general, any increasing choice of the function G leads to a strictly consistent quantile estimation (this is an asymptotic statement), but these choices may have different finite sample properties. Following Komunjer–Vuong [222], we can determine asymptotically efficient choices for G. This would require feature dependent choices \(G_{\boldsymbol {x}_i}(y)=F_{Y|\boldsymbol {x}_i}(y)\), where \(F_{Y|\boldsymbol {x}_i}\) is the (true) distribution of Y i, conditionally given x i. This requires the knowledge of the true distribution, and Komunjer–Vuong [222] derive asymptotic efficiency when replacing this true distribution by a non-parametric estimator, this is in spirit similar to Theorem 11.8. We refrain from giving more details but refer to the corresponding paper.
11.3 Deep Composite Model Regression
We have established a deep quantile regression in the previous section. Next we jointly estimate quantiles and conditional tail expectations (CTEs), leading to a composite regression model that has a splicing point determined by a quantile level; for composite models we refer to Sect. 6.4.4. This is exactly the proposal of Fissler et al. [130] which we are going to present in this section. Note that having a composite model allows us to have different distributions and regression structures below and above the splicing point, e.g., we can have a more heavy-tailed model in the upper tail using a different feature engineering from the main body of the data.
11.3.1 Joint Elicitability of Quantiles and Expected Shortfalls
In the previous examples we have seen that the distributional models may misestimate the true tail of the data because model fitting often pays more attention to an accurate model fit in the main body of the data. An idea is to directly estimate this tail in a distribution-free way by considering the (upper) CTE
for a given quantile level τ ∈ (0, 1). The problem with (11.23) is that this is not an elicitable quantity, i.e., there is no loss/scoring function that is strictly consistent for the CTE functional.
If the distribution function F Y |x is continuous, we can rewrite the upper CTE as follows, see Lemma 2.16 in McNeil et al. [268] and (11.35) below,
This second object \(\mathrm {ES}^+_{\tau }(Y|\boldsymbol {x})\) is called the upper expected shortfall (ES) of Y , given x, on the security level τ. Fissler–Ziegel [131] and Fissler et al. [132] have proved that \(\mathrm {ES}^+_\tau (Y|\boldsymbol {x})\) is jointly elicitable with the τ-quantile \({F}_{Y|\boldsymbol {x}}^{-1}(\tau )\). That is, there is a strictly consistent bivariate loss function that allows one to jointly estimate the τ-quantile and the corresponding ES. In fact, Corollary 5.5 of Fissler–Ziegel [131] give the full characterization of the strictly consistent bivariate loss functions for the joint elicitability of the τ-quantile and the ES; note that Fissler–Ziegel [131] use a different sign convention. This result is used in Guillén et al. [175] for the joint estimation of the quantile and the ES within a GLM. Guillén et al. [175] use a two-step approach to fit the quantile and the ES.
Fissler et al. [130] extend the results of Fissler–Ziegel [131], allowing for the joint estimation of the composite triplet consisting of the lower ES, the τ-quantile and the upper ES. This gives us a composite model that has the τ-quantile as splicing point. The beauty of this approach is that we can fit (in one step) a deep learning model to the upper and the lower ES, and perform a (potentially different) regression in both parts of the distribution. The lower CTE and the lower ES are defined by, respectively,
and
Again, in case of a continuous distribution function F Y |x we have the following identity \(\mathrm {CTE}^-_{\tau }(Y|\boldsymbol {x})=\mathrm {ES}^-_{\tau }(Y|\boldsymbol {x})\). From the lower and upper CTEs we receive the mean of Y , given x, by
We introduce the auxiliary scoring functions

for \(y,a\in {\mathbb R}\) and for τ ∈ (0, 1). These auxiliary functions consider only the part of the pinball loss (5.81) that depends on action a, and we get the pinball loss as follows
Therefore, all three functions provide strictly consistent scoring functions for the τ-quantile, but only the pinball loss satisfies the calibration property (L0) on page 92.
For the following theorem we recall the general definition of the τ-quantile Q τ(F Y |x) of a distribution function F Y |x, see (5.82).
Theorem 11.11 (Theorem 2.8 of Fissler et al. [130], Without Proof)
Choose τ ∈ (0, 1) and let \(\mathcal F\) contain only distributions with a finite first moment, and being supported in the interval \({\mathfrak C} \subseteq {\mathbb R}\) . The loss function \(L: {\mathfrak C}\times {\mathfrak C}^3\to {\mathbb R}_+\) of the form

is strictly consistent for the composite triplet \((\mathrm {ES}^-_\tau , Q_\tau , \mathrm {ES}^+_\tau )\) relative to the class \(\mathcal {F}\) , if Ψ is strictly convex with (sub-)gradient ∇ Ψ such that for all \((e^-,e^+)\in {\mathfrak C}^2\) the function
is strictly increasing, and if \({\mathbb E}_F[|G(Y)|]<\infty \), \({\mathbb E}_F[|\Psi (Y,Y)|]<\infty \) for all \(Y\sim F\in \mathcal {F}\).
This opens the door for regression modeling of CTEs for continuous distribution functions F Y |x, \(\boldsymbol {x} \in \mathcal {X}\). Namely, we can choose a regression function ξ 𝜗 with a three-dimensional output
depending on a regression parameter 𝜗. This regression function is now used to describe the composite triplet \((\mathrm {ES}^-_{\tau }(Y|\boldsymbol {x}),F^{-1}_{Y|\boldsymbol {x}}(\tau ),\mathrm {ES}^+_{\tau }(Y|\boldsymbol {x}))\). Having i.i.d. data (Y i, x i), 1 ≤ i ≤ n, it can be fitted by solving

with loss function L given by (11.26). This then provides us with the estimates for the composite triplet
There remains the choice of the functions G and Ψ, such that Ψ is strictly convex and \(G_{e^-, e^+}\), defined in (11.27), is strictly increasing. Section 2.3 in Fissler et al. [130] discusses possible choices. A simple choice is to select the identity function G(y) = y (which gives the pinball loss on the first line of (11.26)) and
with ψ 1 and ψ 2 strictly convex and with (sub-)gradients \(\psi ^{\prime }_1>0\) and \(\psi ^{\prime }_2<0\). Inserting this choice into (11.26) provides the loss function
where L τ(y, q) is the pinball loss (5.81) and \(D_{\psi _1}\) and \(D_{\psi _2}\) are Bregman divergences (2.28). There remains the choices of ψ 1 and ψ 2 which should be strictly convex, the first one being strictly increasing and the second one being strictly decreasing.
We restrict ourselves to strictly convex functions ψ on the positive real line \({\mathbb R}_+\), i.e., for positive claims Y > 0, a.s. For \(b \in {\mathbb R}\), we consider the following functions on \({\mathbb R}_+\)
We compute the first and second derivatives. These are for y > 0 given by
Thus, for any \(b \in {\mathbb R}\) we have a convex function, and this convex function is decreasing on \({\mathbb R}_+\) for b < 1 and increasing for b > 1. Therefore, we have to select b > 1 for ψ 1 and b < 1 for ψ 2 to get suitable choices in (11.29). Interestingly, these choices correspond to Lemma 11.2 with power variance parameters p = 2 − b, i.e., they provide us with Bregman divergences from Tweedie’s distributions. However, (11.30) is more general, because it allows us to select any \(b \in {\mathbb R}\), whereas for power variance parameters p ∈ (0, 1) there do not exist any Tweedie’s distributions, see Theorem 2.18.
In view of Lemma 11.2 and using the fact that unit deviances \({\mathfrak d}_p\) are Bregman divergences, we select a power variance parameter p = 2 − b > 1 for ψ 2 and we select the Gaussian model p = 2 − b = 0 for ψ 1. This gives us the special choice for the loss function (11.29) for strictly positive claims Y > 0, a.s.,
with the Gaussian unit deviance \({\mathfrak d}_0(y,e^-)=(y-e^-)^2\) and Tweedie’s unit deviance \({\mathfrak d}_p\) with power variance parameter p > 1, see Sect. 11.1.1. The additional constants η 1, η 2 > 0 are used to balance the contributions of the individual terms to the total loss. Typically, we choose p ≥ 2 for the upper ES reflecting claim size models. This choice for ψ 2 implies that the residuals are weighted inversely proportional to the corresponding variances μ p within Tweedie’s family, see (11.5). Using this loss function (11.31) in (11.28) allows us to estimate the composite triplet \((\mathrm {ES}^-_{\tau }(Y|\boldsymbol {x}),F^{-1}_{Y|\boldsymbol {x}}(\tau ),\mathrm {ES}^+_{\tau }(Y|\boldsymbol {x}))\) with a strictly consistent loss function.
11.3.2 Lab: Deep Composite Model Regression
The joint elicitability of Theorem 11.11 allows us to directly estimate these functionals for a fixed quantile level τ ∈ (0, 1). In a similar way to quantile regression we set up a FN network that respects the monotonicity \(\mathrm {ES}^-_{\tau }(Y|\boldsymbol {x})\le F^{-1}_{Y|\boldsymbol {x}}(\tau )\le \mathrm {ES}^+_{\tau }(Y|\boldsymbol {x})\). We set for the regression function in the additive approach for multi-task learning

for link functions g and g + with \(g_+^{-1}\ge 0\), deep FN network \(\boldsymbol {z}^{(d:1)}:{\mathbb R}^{q_0+1} \to {\mathbb R}^{q_d+1}\), regression parameters \(\boldsymbol {\beta }_1,\boldsymbol {\beta }_2,\boldsymbol {\beta }_3 \in {\mathbb R}^{q_d+1}\), and with the action space \({\mathbb A}=\{(e^-,q,e^+)\in {\mathbb R}_+^3;e^-\le q \le e^+\}\) for positive claims. We also remind of Remark 11.10 for a different way of modeling the monotonicity.
Fitting this model is similar to the multiple deep quantile regression presented in Listings 11.3 and 11.5. There is one important difference though. Namely, we do not have multiple outputs and multiple loss functions, but we have a three-dimensional output with a single loss function (11.31) simultaneously evaluating all three components of the output (11.32). Listing 11.6 gives this loss for the inverse Gaussian case p = 3 in (11.31).
Listing 11.6 Loss function (11.31) for p = 3

We revisit the Swiss accident insurance data of Sect. 11.2.3. We again use a FN network of depth d = 3 with (q 1, q 2, q 3) = (20, 15, 10) neurons, hyperbolic tangent activation, two-dimensional embedding layers for the categorical features, exponential output activations for g −1 and \(g_+^{-1}\), and the additive structure (11.32). We implement the loss function (11.31) for quantile level τ = 90% and with power variance parameter p = 3, see Listing 11.6. This implies that for the upper ES estimation we scale residuals with V (μ) = μ 3, see (11.5). We then run an initial calibration of this FN network. Based on this initial calibration we can calculate the three loss contributions in (11.31) coming from the composite triplet. Based on these figures we choose the constants η 1, η 2 > 0 in (11.31) so that all three terms of the composite triplet contribute equally to the total loss. For the remainder of our calibration we hold on to these choices of η 1 and η 2.
We calibrate this deep FN architecture to the learning data \(\mathcal {L}\), using the strictly consistent loss function (11.31) for the composite triplet \((\mathrm {ES}^-_{90\%}(Y|\boldsymbol {x}), F_{Y|\boldsymbol {x}}^{-1}(90\%), \mathrm { ES}^+_{90\%}(Y|\boldsymbol {x}))\), and to reduce the randomness in prediction we average over 20 early stopped SGD calibrations with different seeds (nagging predictor).
Figure 11.10 shows the estimated lower and upper ES against the corresponding 90%-quantile estimates for 2’000 randomly selected insurance claims \(\boldsymbol {x}^\dagger _t\). The diagonal orange line shows the estimated 90%-quantiles \(\widehat {F}^{-1}_{Y|\boldsymbol {x}^\dagger _t}(90\%)\), and the cyan lines give spline fits to the estimated lower and upper ES. It is clearly visible that these respect the ordering
Comparison of the estimated lower \(\widehat {\mathrm {ES}}^{-}_{90\%}(Y|\boldsymbol {x}^\dagger _t)\) and the estimated upper \(\widehat {\mathrm {ES}}^{+}_{90\%}(Y|\boldsymbol {x}^\dagger _t)\) against the estimated 90%-quantile \(\widehat {F}^{-1}_{Y|\boldsymbol {x}^\dagger _t}(90\%)\) in the deep composite regression
for fixed features \(\boldsymbol {x}^\dagger _t \in \mathcal {X}\).
The deep quantile regression has been back-tested using the coverage ratios (11.22). Back-testing the ES is more difficult, the standalone ES is not elicitable, and the ES can only be back-tested jointly with the corresponding quantile. The part of the joint identification function that corresponds to the ES is given by, see (4.2)–(4.3) in Fissler et al. [130],

and

These (empirical) identifications should be close too zero if the model fits the data.
Remark that the latter terms in (11.33)–(11.34) describe the lower and upper ES also in the case of non-continuous distribution functions because we have the identity

the second term being zero for a continuous distribution F Y |x, but it is needed for non-continuous distribution functions.
We compare the deep composite regression results of this section to the deep gamma and inverse Gaussian models using a double FN network for dispersion modeling, see Sect. 11.1.3. This requires to calculate the ES in the gamma and the inverse Gaussian models. This can be done within the EDF, see Landsman–Valdez [233]. The upper ES in the gamma model Y ∼ Γ(α, β) is given by, see (6.47),
where \(\mathcal {G}\) is the scaled incomplete gamma function (6.48) and \(F^{-1}_{Y}(\tau )\) is the τ-quantile of Γ(α, β).
Example 4.3 of Landsman–Valdez [233] gives the inverse Gaussian case (2.8) with α, β > 0

where φ and Φ are the standard Gaussian density and distribution, respectively, \(F^{-1}_{Y}(\tau )\) is the τ-quantile of the inverse Gaussian distribution and

This now allows us to calculate the identifications (11.33)–(11.34) in the fitted deep double networks using the gamma and the inverse Gaussian distributions of Sect. 11.1.3.
Table 11.8 shows the out-of-sample coverage ratios and the identifications of the deep composite regression and the two distributional approaches. These figures suggest that the gamma model is not competitive; the deep composite model has the most precise coverage ratio. In terms of the ES identification terms, the deep composite model and the double network with inverse Gaussian claim sizes are comparably accurate (out-of-sample) determining the lower and upper 90% ES.
Finally, we paste the lower and upper ES from the deep composite regression model according to (11.25). This gives us an estimated mean (under a continuous distribution function)
Figure 11.11 compares these estimates of the deep composite regression model to the deep double inverse Gaussian model estimates. The black dots show 2’000 randomly selected claims \(\boldsymbol {x}^\dagger _t\), and the cyan line gives a spline fit to all out-of-sample claims in \(\mathcal {T}\). The body of the estimates is rather similar in both approaches but the deep composite approach provides more large estimates, the dotted orange lines show the maximum estimate from the deep double inverse Gaussian model.
Comparison of the estimated means from the deep double inverse Gaussian model and the deep composite model (11.25)
We conclude that in the case where no member of the EDF reflects the properties of the data in the tail, the deep composite regression approach presented in this section provides an alternative method for mean estimation that allows for separate models in the main body and the tail of the data. Fixing the quantile level allows for a straightforward fitting in one step, this is in contrast to the composite models where we fix the splicing point. The latter approaches are more difficult in fitting, e.g., using the EM algorithm.
11.4 Model Uncertainty: A Bootstrap Approach
As described in Sect. 4, there are different sources of prediction uncertainty when forecasting random variables. There is the irreducible risk that comes from the fact that we try to predict random variables. This source of uncertainty is always present, even if we know the true data generating mechanism, i.e., it is irreducible. In most applied situations we do not know the true data generating mechanism which results in additional prediction uncertainty. Within GLMs this source of uncertainty has mainly been allocated to parameter estimation uncertainty deriving from the fact that we estimate the parameters from a finite sample, we refer to Sects. 3.4 and 11.1.4 on asymptotic results. In network modeling, the situation is more complicated. Firstly, we have seen that there is no best network regression model even if the architecture and the hyper-parameters are fully specified. In Fig. 7.18 we have seen that in a claim frequency context the different solutions from an early stopped SGD fitting can have a coefficient of variation of up to 40% on the individual policy level, on average these coefficients of variation were around 10%. This has led to the consideration of network ensembling and the nagging predictor in Sect. 7.4.4. These considerations have been based on a fixed learning data set \(\mathcal {L}\). In this section, we assume that also the learning data set \(\mathcal {L}\) may look differently by considering different realizations of the (randomly generated) observations Y i. To reflect this source of randomness in outcomes we bootstrap new data from \(\mathcal {L}\) by exploring a non-parametric bootstrap with random drawings with replacements from \(\mathcal {L}\), see Sect. 4.3.1. This will allow us to study the volatility implied in estimation by considering a different set of observations, i.e., a different sample.
Ideally we would like to generate new observations from the true data generating mechanism, but, since this mechanism is not known, we can at best generate data from an estimated model. If we rely on a distributional model, we may suffer from model error, e.g., in Sect. 11.3 we have seen that it is rather difficult to specify a distributional regression model that has the right tail behavior. Therefore, we may give preference to a distribution-free approach. Non-parametric bootstrapping is such a distribution-free approach, the disadvantage being that we cannot enrich the existing observations by new observations, but we can only rearrange the available observations.
We revisit the robust representation learning approach of Sect. 11.1.2 on the same Swiss accident insurance data as explored in that section. In particular, we reconsider the deep multi-output models introduced in (11.6) and studied in Table 11.3 for power variance parameters p = 2, 2.5, 3 (and constant dispersion parameter). We perform exactly the same analysis, here, however we consider for this analysis bootstrapped data \(\mathcal {L}^\ast \) for model fitting.
First, we fit 100 times the same deep FN network architecture as in (11.6) with different seeds (on identical learning data \(\mathcal {L}\)). From this we calculate the nagging predictor. Second, we generate 100 different bootstrap samples \(\mathcal {L}^\ast =\mathcal {L}^{\ast (s)}\), 1 ≤ s ≤ 100, from \(\mathcal {L}\) (having an identical sample size) with random drawings with replacements, and we fit the same network architecture to these 100 bootstrap samples. We then also average over these 100 predictors obtained from the different bootstrap samples. Table 11.9 provides the resulting out-of-sample deviance losses on the test data \(\mathcal {T}\). We always hold on to the same test data \(\mathcal {T}\) which is disjoint/independent from the learning data \(\mathcal {L}\) and the bootstrap samples \(\mathcal {L}^\ast =\mathcal {L}^{\ast (s)}\), 1 ≤ s ≤ 100.
The nagging predictors over 100 seeds are roughly the same as over 20 seeds (see Table 11.3), which indicates that 20 different network fits suffice, here. Interestingly, the average bootstrapped version generally improves the nagging predictors. Thus, here the average bootstrap predictor provides a better balance among the observations to receive superior predictive power on the test data \(\mathcal {T}\), compare lines ‘nagging 100’ vs. ’bootstrap 100’ of Table 11.9.
The main purpose of this analysis is to understand the volatility involved in nagging and bootstrap predictors. We therefore consider the coefficients of variation Vcot introduced in (7.43) on individual policies 1 ≤ t ≤ T. Figure 11.12 shows these coefficients of variation on the individual predictors, i.e., for the individual claims \(\boldsymbol {x}_t^\dagger \) and the individual network calibrations with different seeds. The left-hand side gives the coefficients of variation based on 100 bootstrap samples, the right-hand side gives the coefficients of variation of 100 predictors fitted on the same data \(\mathcal {L}\) but with different seeds for the SGD algorithm; the y-scale is identical in both plots. We observe that the coefficients of variation are clearly higher under the bootstrap approach compared to holding on to the same data \(\mathcal {L}\) for SGD fitting with different seeds. Thus, the nagging predictor averages over the randomness in different seeds for network calibrations, whereas bootstrapping additionally considers possible different samples \(\mathcal {L}^\ast \) for model learning. We analyze the difference in magnitudes in more detail.
Figure 11.13 compares the two coefficients of variation for different claim sizes. The average coefficient of variation for fixed observations \(\mathcal {L}\) is 15.9% (cyan columns). This average coefficient of variation is increased to 24.8% under bootstrapping (orange columns). The blue line shows the average relative increase for the different claim sizes (right axis), and the blue dotted line is at a relative increase of 40%. From Fig. 11.13 we observe that this spread (relative increase) is rather constant across all claim predictions; we remark that 93.5% of all claim predictions are below 5’000. Thus, most claims are at the left end of Fig. 11.13.
From this small analysis we conclude that there is substantial model and estimation uncertainty involved, recall that we fit the deep network architecture to 305’550 individual claims having 7 feature components, this is a comparably large portfolio. On average, we have a coefficient of variation of 15% implied by SGD fitting with different seeds, and this coefficient of variation is increased to roughly 25% under additionally bootstrapping the observations. This is considerable, and it requires that we ensemble these predictors to receive more robust predictions. The results of Table 11.9 support this re-sampling and ensembling approach as we receive a better out-of-sample performance.
11.5 LocalGLMnet: An Interpretable Network Architecture
Network architectures are often criticized for not being (sufficiently) explainable. Of course, this is not fully true as we have gained a lot of insight about the data examples studied in this book. This criticism of non-explainability has led to the development of the post-hoc model-agnostic tools studied in Sect. 7.6. This approach has been questioned at many places, and it is not clear whether one should try to explain black box models, or whether one should rather try to make the models interpretable in the first place, see, e.g., Rudin [322]. In this section we take this different approach by working with a network architecture that is (more) interpretable. We present the LocalGLMnet proposal of Richman–Wüthrich [317, 318]. This approach allows for interpreting the results, and it allows for variable selection either using an empirical Wald test or LASSO regularization.
There are different other proposals that try to achieve similar explainability in specific network architectures. There is the explainable neural network of Vaughan et al. [367] and the neural additive model of Agarwal et al. [3]. These proposals rely on parallel networks considering one single variable at a time. Of course, this limits their performance because of a missing interaction potential. This has been improved in the Combined Actuarial eXplainable Neural Network (CAXNN) approach of Richman [314], which requires a manual specification of parallel networks for potential interactions. The LocalGLMnet, proposed in this section, does not require any manual engineering, and it still possesses the universal approximation property.
11.5.1 Definition of the LocalGLMnet
Starting point of the LocalGLMnet is a classical GLM. Choose a strictly monotone and smooth link function g. A GLM is received by considering the regression function
for features \(\boldsymbol {x} \in \mathcal {X} \subset {\mathbb R}^q\), intercept \(\beta _0 \in {\mathbb R}\) and regression parameter \(\boldsymbol {\beta } \in {\mathbb R}^q\). Compared to (5.5) we change the notation in this section by excluding the intercept component from the feature  , because this will be more convenient for the LocalGLMnet proposal. The beauty of this GLM regression function is that we obtain a linear function after applying the link function g. This linear function is considered to be explainable as we can precisely quantify how much the expected response will change by slightly changing one of the feature components x
j. In particular, this holds true for the log-link which leads to a multiplicative structure in the expected response.
, because this will be more convenient for the LocalGLMnet proposal. The beauty of this GLM regression function is that we obtain a linear function after applying the link function g. This linear function is considered to be explainable as we can precisely quantify how much the expected response will change by slightly changing one of the feature components x
j. In particular, this holds true for the log-link which leads to a multiplicative structure in the expected response.
The idea is to hold on to this additive structure (11.36) as far as possible, still trying to benefit from the universal approximation property of network architectures. Richman–Wüthrich [317] propose the following regression structure.
Definition 11.12 (LocalGLMnet)
Choose a FN network architecture \(\boldsymbol {z}^{(d:1)}:{\mathbb R}^q\to {\mathbb R}^q\) of depth \(d\in {\mathbb N}\) with equal input and output dimensions to model the regression attention

The LocalGLMnet is defined by the generalized additive decomposition
for a strictly monotone and smooth link function g.
This architecture is called LocalGLMnet because locally, around a given feature value x, it can be understood as a GLM, supposed that β(x) does not change too much in the environment of x. In the GLM context β is called regression parameter, and in the LocalGLMnet context β(x) is called regression attention because the components β j(x) determine how much attention there should be given to a specific value x j. We highlight this in the following discussion. Select one component 1 ≤ j ≤ q and study the individual term
-
(1)
If β j(x) ≡ 0, we should drop the term β j(x)x j from the regression function.
-
(2)
If β j(x) ≡ β j ( ≠ 0) is not feature dependent (and different from zero), we receive a GLM term in x j with regression parameter β j.
-
(3)
Property β j(x) = β j(x j) implies that we have a term β j(x j)x j that does not interact with any other term \(x_{j^{\prime }}\), j′≠ j.
-
(4)
Sensitivities of β j(x) in the components of x can be obtained by the gradient
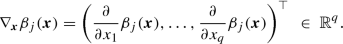 (11.38)
(11.38)The j-th component of ∇x β j(x) determines the (non-)linearity in term x j, the components different from j describe the interactions of term x j with the other components.
-
(5)
These interpretations need some care because we do not have identifiability. For the special regression attention \(\beta _j(\boldsymbol {x})=x_{j^{\prime }}/x_{j}\) we have
$$\displaystyle \begin{aligned} \beta_j(\boldsymbol{x}) x_j = x_{j^{\prime}}. \end{aligned} $$(11.39)Therefore, we talk about terms in items (1)–(4), e.g., item (1) means that the term β j(x)x j can be dropped, however, the feature component x j may still play a significant role in some of the regression attentions \(\beta _{j^{\prime }}(\boldsymbol {x})\), j′≠ j.
In practical applications we have not experienced identifiability issue (11.39). Having already the linear terms in the LocalGLMnet regression structure and starting the SGD fitting in the GLM gives already quite pre-determined regression functions, and the LocalGLMnet is built around this initialization, hardly falling into a completely different model (11.39).
-
(6)
The LocalGLMnet architecture has the universal approximation property discussed in Sect. 7.2.2, because networks can approximate any continuous function arbitrarily well on a compact support for sufficiently large networks. We can then select one component, say, x 1 and let \(\beta _1(\boldsymbol {x})=z_1^{(d:1)}(\boldsymbol {x})\) approximate a given continuous function f(x)∕x 1, i.e., f(x) ≈ β 1(x)x 1 arbitrarily well on the compact support.
11.5.2 Variable Selection in LocalGLMnets
The LocalGLMnet allows for variable selection through the regression attentions β j(x). Roughly speaking, if the estimated regression attentions \(\widehat {\beta }_j(\boldsymbol {x}) \approx 0\), then the term β j(x)x j can be dropped. We can also explore whether the entire variable x j should be dropped (not only the corresponding term β j(x)x j). For this, we have to refit the LocalGLMnet excluding the feature component x j. If the out-of-sample performance on validation data does not change, then x j also does not play an important role in any other regression attention \(\beta _{j^{\prime }}(\boldsymbol {x})\), j′≠ j, and it should be completely dropped from the model.
In GLMs we can either use the Wald test or the LRT to test a null hypothesis H 0 : β j = 0, see Sect. 5.3. We explore a similar idea in this section, however, empirically. We therefore first need to ensure that all feature components live on the same scale. We consider standardization with the empirical mean and the empirical standard deviation, see (7.30), and from now on we assume that all feature components are centered and have unit variance. Then, the main problem is to determine whether an estimated regression attention \(\widehat {\beta }_j(\boldsymbol {x})\) is significantly different from 0 or not.
We therefore extend the features  by an additional independent and purely random component x
q+1 that is also standardized. Since this additional component is independent of all other components it cannot have any predictive power for the response under consideration, thus, fitting this extended model should result in a regression attention \(\widehat {\beta }_{q+1}(\boldsymbol {x}^+) \approx 0\). The estimate will not be exactly zero, because there is noise involved, and the magnitude of this fluctuation will determine the rejection/acceptance region of the null hypothesis of not being significant.
by an additional independent and purely random component x
q+1 that is also standardized. Since this additional component is independent of all other components it cannot have any predictive power for the response under consideration, thus, fitting this extended model should result in a regression attention \(\widehat {\beta }_{q+1}(\boldsymbol {x}^+) \approx 0\). The estimate will not be exactly zero, because there is noise involved, and the magnitude of this fluctuation will determine the rejection/acceptance region of the null hypothesis of not being significant.
We fit the LocalGLMnet to the learning data \(\mathcal {L}\) with features \(\boldsymbol {x}_i^+\in {\mathbb R}^{q+1}\) extended by the standardized i.i.d. component x i,q+1 being independent of (Y i, x i). This gives us the estimated regression attentions \(\widehat {\beta }_1(\boldsymbol {x}^+_i), \ldots , \widehat {\beta }_{q}(\boldsymbol {x}^+_i), \widehat {\beta }_{q+1}(\boldsymbol {x}^+_i)\). We compute the empirical mean and standard deviation of the attention weight of the additional component x q+1

We expect approximate centering \(\bar { b}_{q+1} \approx 0\) because this additional component x q+1 does not enter the true regression function, and the empirical standard deviation \(\widehat {s}_{q+1}\) quantifies the expected fluctuation around zero of insignificant components.
We can now test the null hypothesis H 0 : β j(x) = 0 of component j on significance level α ∈ (0, 1∕2). We define centered interval
where Φ−1(p) denotes the standard Gaussian quantile for p ∈ (0, 1). H 0 should be rejected if the coverage ratio of this centered interval I α is substantially smaller than 1 − α, i.e.,

This proposal is designed for continuous feature components, and categorical variables are discussed in Sect. 11.5.4, below. For x q+1 we can choose a standard Gaussian distribution, a normalized uniform distribution or we can randomly permute one of the feature components x i,j across the entire portfolio 1 ≤ i ≤ n. Usually, the resulting empirical standard deviations \(\widehat {s}_{q+1}\) are rather similar.
11.5.3 Lab: LocalGLMnet for Claim Frequency Modeling
We revisit the French MTPL data example. We compare the LocalGLMnet approach to the deep FN network considered in Sect. 7.3.2, and we benchmark with the results of Table 7.3; we benchmark with the crudest FN network from above because, at the current stage, we need one-hot encoding for the LocalGLMnet approach. The analysis in this section is the same as in Richman–Wüthrich [317].
The French MTPL data has 6 continuous feature components (we treat Area as a continuous variable), 1 binary component and 2 categorical components. We pre-process the continuous and binary variables to centering and unit variance using standardization (7.30). This will allow us to do variable selection as presented in (11.41). The categorical variables with more than two levels are more difficult. In a first attempt we use one-hot encoding for the categorical variables. We prefer one-hot encoding over dummy coding because this ensures that for all levels there is a component x j with x j ≠ 0. This is important because the terms β j(x)x j are equal to zero for the reference level in dummy coding (since x j = 0). This does not allow us to study interactions with other variables for the term corresponding to the reference level. Remark that one-hot encoding and dummy coding do not lead to centering and unit variance.
This feature pre-processing gives us a feature vector \(\boldsymbol {x} \in {\mathbb R}^{q}\) of dimension q = 40. For variable selection of the continuous and binary components we extend the feature x by two additional independent components x q+1 and x q+2. We select two components to explore whether the particular distributional choice has some influence on the choice of the acceptance/rejection interval I α in (11.41). We choose for policies 1 ≤ i ≤ n

these two sets of variables being mutually independent, and being independent from all other variables. We define the extended features  with q
0 = q + 2, and we consider the LocalGLMnet regression function
with q
0 = q + 2, and we consider the LocalGLMnet regression function
We choose the log-link for Poisson claim frequency modeling. The time exposure v > 0 can either be integrated as a weight to the EDF or as an offset on the canonical scale resulting in the same Poisson model, see Sect. 5.2.3.
Listing 11.7 LocalGLMnet architecture

We are now ready to define the LocalGLMnet architecture. We choose a network \(\boldsymbol {z}^{(d:1)}:{\mathbb R}^{q_0}\to {\mathbb R}^{q_0}\) of depth d = 4 with (q 1, q 2, q 3, q 4) = (20, 15, 10, 42) neurons. The R code is given in Listing 11.7. We note that this is not much more involved than a plain-vanilla FN network. Slightly special in this implementation is the integration of the intercept β 0 on line 11. Naturally, we would like to add this intercept, however, there is no simple code for doing this. For that reason, we model the additive decomposition by
with real-valued parameters α 0 and α 1 being estimated on line 11 of Listing 11.7. Thus, in this implementation the regression attentions are obtained by α 1 β j(x +). Of course, there are also other ways of implementing this. This LocalGLMnet architecture has 1’799 network weights to be fitted.
We fit this LocalGLMnet using a training to validation data split of 8 : 2 and a batch size of 5’000. We initialize the gradient descent algorithm such that we exactly start in the GLM with \(\beta _j(\boldsymbol {x}^+)\equiv \widehat {\beta }^{\mathrm {MLE}}_j\). For this we set all weights in the last layer on line 8 of Listing 11.7 to zero, \(w_{l,j}^{(d)}=0\), and the corresponding intercepts to the MLEs of the GLM, i.e., \(w_{0,j}^{(d)}=\widehat {\beta }^{\mathrm {MLE}}_j\). This gives us the GLM initialization \(\sum _{j=1}^{q_0} \widehat {\beta }^{\mathrm {MLE}}_jx_j\) on line 10 of Listing 11.7. Moreover, on line 11 of that listing, we initialize α 1 = 1 and \(\alpha _0 = \widehat {\beta }^{\mathrm {MLE}}_0\). This implies that the gradient descent algorithm starts in the MLE estimated GLM. The SGD fitting turns out to be faster than in the plain-vanilla FN case, probably, because we start in the GLM having already the reasonable linear terms x j in the model, and we only need to find the regression attentions β j(x +) around these linear terms. The results are presented on the second last line of Table 11.10. The out-of-sample results are slightly worse than in the plain-vanilla FN case. There are many reasons for that, for instance, many levels in one-hot encoding may lead to more potential for over-fitting, and hence to an earlier stopping, here. The same applies if we add too many purely random components x q+l, l ≥ 1. Since the balance property will not hold, in general, we apply the bias regularization step (7.33) to adjust α 0 and α 1, the results are presented on the last line of Table 11.10; in Remark 3.1 of Richman–Wüthrich [317] a more sophisticated balance property correction is presented. Our goal now is to analyze this solution.
Listing 11.8 Extracting the regression attentions from the LocalGLMnet architecture

We start by analyzing the two additional components x i,q+1 and x i,q+2 being uniformly and Gaussian distributed, respectively. Listing 11.8 shows how to extract the estimated regression attentions \(\widehat {\boldsymbol {\beta }}(\boldsymbol {x}^+_i)\). We calculate the means and standard deviations of the estimated regression attentions of the two additional components
and
From these numbers we see that the regression attentions \(\widehat {\beta }_{q+2}(\boldsymbol {x}_i)\) are slightly biased, whereas \(\widehat {\beta }_{q+1}(\boldsymbol {x}_i)\) are fairly centered compared to the magnitudes of the standard deviations. If we select a significance level of α = 0.1%, we receive a two-sided standard normal quantile of | Φ−1(α∕2)| = 3.29. This provides us for interval (11.41) with
Figure 11.14 shows the estimated regression attentions \(\widehat {\beta }_j(\boldsymbol {x}^+_i)\) of the continuous and binary feature components for 2’000 randomly selected policies \(\boldsymbol {x}^+_i\), and the orange area shows the acceptance region I α on significance level α = 0.1%. Focusing on the figures of the two additional variables x i,q+1 and x i,q+2, Fig. 11.14 (bottom, middle and right), we observe that the estimated regression attentions are mostly within the confidence bounds of I α. This says that we should drop these two terms (of course, this is clear since we have set the bounds according to these regression attentions). Focusing on the other variables, we question the inclusion of the term VehPower as it seems concentrated within I α, and hence we cannot reject the null hypothesis H 0 : β VehPower(x) = 0. Moreover, the inclusion of the term Area needs further exploration.
Estimated regression attentions \(\widehat {\beta }_j(\boldsymbol {x}^+_i)\) of the continuous and binary feature components Area, BonusMalus, log-Density, DrivAge, VehAge, VehGas, VehPower and the two random features x i,q+1 and x i,q+2 of 2’000 randomly selected policies \(\boldsymbol {x}^+_i\); the orange area shows the interval I α for dropping term β j(x)x j on significance level α = 0.1%
We remind that dropping a term β j(x)x j does not necessarily imply that we have to completely drop x j because it may still play an important role in one of the other regression attentions \(\beta _{j^{\prime }}(\boldsymbol {x})\), j′≠ j. Therefore, we re-run the whole fitting procedure, but we drop the purely random feature components x i,q+1 and x i,q+2, and we also drop VehPower and Area to see whether we receive a model with a similar predictive power. This then would imply that we can drop these variables, in the sense of variable selection similar to the LRT and the Wald test of Sect. 5.3. We denote the feature where we drop these components by \(\boldsymbol {x}^{-} \in {\mathbb R}^{q-2}\).
We re-fit the LocalGLMnet on the reduced features \(\boldsymbol {x}_i^-\), and the results are presented in Table 11.11. We observe that the loss figures decrease. Indeed, this supports the null hypothesis of dropping VehPower and Area. The reason for being able to drop VehPower is that it does not contribute (sufficiently) to explain the systematic effects in the responses. The reason for being able to drop Area is slightly different: we have seen that Area and log-Density are highly correlated, see Fig. 13.12 (rhs), and it turns out that it is sufficient to only keep the Density variable (on the log-scale) in the model.
In a next step, we should analyze the robustness of these results by exploring the nagging predictor and/or bootstrapping as described in Sect. 11.4. We refrain from doing so, but we illustrate the LocalGLMnet solution of Table 11.11 in more detail.
Figure 11.15 shows the feature contributions \(\widehat {\beta }_j(\boldsymbol {x}_i^-)x_{i,j}\) of 2’000 randomly selected policies on the significant continuous and binary feature components. The magenta line gives a spline fit, and the more the black dots spread around these splines, the more interactions we have; for instance, higher bonus-malus levels interact with the age of driver which explains the scattering of the black dots. On average, frequencies are increasing in bonus-malus levels and density, decreasing in vehicle age, and for the driver’s age variable it is important to understand the interactions. We observe that the spline fit for the log-Density is close to a linear function, this reflects that the regression attentions \(\widehat {\beta }_{\mathtt {Density}}(\boldsymbol {x}_i)\) in Fig. 11.14 (top-right) are more or less constant. This is also confirmed by the marginal plot in Fig. 5.4 (bottom-rhs) which has motivated the choice of a linear term for the log-Density in model Poisson GLM1 of Table 5.3.
Using the regression attentions we define an importance measure. We consider the extended features x + in the following numerical analysis. We set
for 1 ≤ j ≤ q + 2, and where we aggregate over all policies 1 ≤ i ≤ n.
Figure 11.16 shows the importance measures IMj of the continuous and binary variables j. The bars are ordered w.r.t. these importance measures. The graph confirms our previous conclusion, the least important variables are the two additional purely random components x i,q+1 and x i,q+2, followed by Area and VehPower. These are exactly the components that have been dropped going from the full model x + to the reduced model x −.
Next, we analyze the interactions by studying the gradients (11.38). Figure 11.17 illustrates spline fits to the components \(\partial \widehat {\beta }_j(\boldsymbol {x}^-_i)/\partial {x_k}\) w.r.t. x j of the continuous variables BonusMalus, log-Density, DrivAge and VehAge over all policies i = 1, …, n. The components \(\partial \widehat {\beta }_j(\boldsymbol {x}^-_i)/\partial {x_j}\) show the non-linearity in x j. We conclude that BonusMalus, DrivAge and VehAge should be non-linear, and log-Density is linear because \(\partial \widehat {\beta }_j(\boldsymbol {x}^-_i)/\partial {x_j}\approx 0\). The components \(\partial \widehat {\beta }_j(\boldsymbol {x}^-_i)/\partial {x_k}\), k ≠ j, determine the interactions. We have the strongest interactions between BonusMalus and DrivAge, and BonusMalus has interactions with all variables. On the other hand, the log-Density only interacts with BonusMalus.
The reader will have noticed that we have excluded the categorical components VehBrand and Region from all model discussions. Firstly, these components are not standardized to zero mean and unit variance, and, secondly, we cannot study one level in isolation to be able to decide to keep or drop that variable. I.e., similar to group LASSO we need to study all levels simultaneously of each categorical feature component. We do this in the next section, and we conclude with the regression attentions \(\widehat {\beta }_j(\boldsymbol {x})\) of the categorical feature components in Fig. 11.18, which seem to be significantly different from zero (VehBrands B10, B11, and Regions R22, R43, R82, R93), but which do not allow for variable selection as just described.
Boxplot of the regression attentions \(\widehat {\beta }_j(\boldsymbol {x})\) of the categorical feature components VehBrand and Region; the y-scale is the same as in Fig. 11.15
Remark 11.13
The bias regularization in Table 11.11 has simply been obtained by applying an additional MLE step to α
0 and α
1. Alternatively, we can also define the new features  , and then apply a proper GLM step to these newly (learned) features \(\widehat {\boldsymbol {z}}_1,\ldots , \widehat {\boldsymbol {z}}_n\). Working with the canonical link will give us the balance property. This is discussed in more detail in Remark 3.1 of Richman–Wüthrich [317].
, and then apply a proper GLM step to these newly (learned) features \(\widehat {\boldsymbol {z}}_1,\ldots , \widehat {\boldsymbol {z}}_n\). Working with the canonical link will give us the balance property. This is discussed in more detail in Remark 3.1 of Richman–Wüthrich [317].
11.5.4 Variable Selection Through Regularization of the LocalGLMnet
A natural next step is to introduce regularization on the regression attentions β(x); this is the proposal suggested in Richman–Wüthrich [318]. We choose the LocalGLMnet architecture x↦μ(x) of Definition 11.12 having an intercept parameter \(\beta _0 \in {\mathbb R}\) and the network weights w. For fitting, we consider a loss function L and we add a regularization term to this loss function penalizing large regression attentions. That is, we aim at minimizing

with a penalty term (regularizer) \({\mathfrak R}(\cdot ) \ge 0\). For the penalty term \({\mathfrak R}\) we can choose different forms, e.g., the elastic net regularizer of Zou–Hastie [409] is obtained by, see Remark 6.3,

for a regularization parameter η ≥ 0 and weight α ∈ [0, 1]. For α = 0 we receive ridge regularization, and for α = 1 we get LASSO regularization of β(⋅).
For variable selection of categorical feature components we should rather use the group LASSO penalization of Yuan–Lin [398], see also (6.5). Assume the features x have a natural group structure  . We consider the optimization
. We consider the optimization

for regularization parameters η
k ≥ 0, and where β
k(x) collects all components β
j(x) of β(x) that belong to the k-th group x
k of x. Yuan–Lin [398] propose to scale the regularization parameters as  , where q
k is the size of group k. Remark that if every group has size one we exactly obtain LASSO regularization.
, where q
k is the size of group k. Remark that if every group has size one we exactly obtain LASSO regularization.
Solving the optimization problem (11.44) poses some challenges because the regularizer is not differentiable in zero. In Sect. 6.2.5 we have presented the generalized projection operator (using the soft-thresholding operator) to solve the group LASSO regularization within GLMs. However, this proposal will not work here: the generalized projection operator may help to project the regression attentions β(x i) back to the constraint set \(\mathcal {C}\). However, this does not tell us anything about how to choose the network parameters w and, therefore, will not work here. In a different setting, Oelker–Tutz [288] propose to use a differentiable 𝜖-approximation to the terms in (11.44). Choose 𝜖 > 0 and define for \(\boldsymbol {\beta }_k \in {\mathbb R}^{q_k}\)

This motivates to study the optimization problem for a fixed (small) 𝜖 > 0

In Fig. 11.19 we plot these 𝜖-approximations for 𝜖 ∈{10−1, 10−2, 10−3, 10−4, 10−5}. The plot on the left-hand side gives  for 𝜖 ↓ 0, and the plot on the right-hand side gives the unit ball
for 𝜖 ↓ 0, and the plot on the right-hand side gives the unit ball

For the last two 𝜖 choices there is no visible difference to the ℓ 1-norm.
The main disadvantage of the 𝜖-approximation is that it does not shrink unimportant components β j(x) exactly to zero. But it allows us to identify unimportant (small) components, which can then be removed manually. As mentioned in Lee et al. [237], LASSO regularization needs a second model calibration step only fitting the model on the selected components (and without regularization) to receive an optimal predictive power and a minimal bias. Thus, we need a second calibration step after the removal of the unimportant components anyway.
11.5.5 Lab: LASSO Regularization of LocalGLMnet
We revisit the LocalGLMnet architecture applied to the French MTPL claim frequency data, see Sect. 11.5.3. The goal is to perform a group LASSO regularization so that we can also study the importance of the terms coming from the categorical feature components VehBrand and Region. We first pre-process all feature components as follows. We apply dummy coding to the categorical variables, and then we standardize all components to centering and unit variance, this includes the dummy coded components.
Listing 11.9 Group LASSO regularization design

In a next step we need to define the natural groups  . We have 7 continuous and binary components which give us dimensions q
k = 1 for 1 ≤ k ≤ 7. VehBrand provides us with a group of size q
8 = 10, and Region gives us a group of size q
9 = 21. We set K = 9 and \(q=\sum _{k=1}^9q_k=38\). We code a (sort of) regularization design matrix to encode the K groups and weights
. We have 7 continuous and binary components which give us dimensions q
k = 1 for 1 ≤ k ≤ 7. VehBrand provides us with a group of size q
8 = 10, and Region gives us a group of size q
9 = 21. We set K = 9 and \(q=\sum _{k=1}^9q_k=38\). We code a (sort of) regularization design matrix to encode the K groups and weights  for the q components of x. This is done in Listing 11.9 providing us with a matrix of size 38 × 9 and the weights
for the q components of x. This is done in Listing 11.9 providing us with a matrix of size 38 × 9 and the weights  . This regularization design matrix enters the penalty term on lines 13 and 16 of Listing 11.10 which weights the penalizations ∥⋅∥2,𝜖.
. This regularization design matrix enters the penalty term on lines 13 and 16 of Listing 11.10 which weights the penalizations ∥⋅∥2,𝜖.
Listing 11.10 LocalGLMnet with group LASSO regularization

The entire group LASSO regularized LocalGLMnet is depicted in Listing 11.10, showing the regression attentions on lines 5–8, the regularization on lines 10–16, and the output on line 26 returns the expected response v i μ(x i) and the regularizer \(\sum _{k=1}^K \eta _k\| \boldsymbol {\beta }_k(\boldsymbol {x}_i) \|{ }_{2,\epsilon }\), we choose 𝜖 = 10−5 for our example.
Listing 11.11 Group LASSO regularized Poisson deviance loss

Finally, we need to code the loss function (11.42). This is done in Listing 11.11. We combine the Poisson deviance loss function with the group LASSO 𝜖-approximation \(\sum _{k=1}^K \eta _k\| \boldsymbol {\beta }_k(\boldsymbol {x}_i) \|{ }_{2,\epsilon }\), the latter being outputted by Listing 11.10. We fit this network to the French MTPL data (as above) for regularization parameters η ∈{0, 0.0025, 0.005}. Firstly, we note that the resulting networks are not fully competitive, this is probably due to the fact that the high-dimensional dummy coding leads to too much over-fitting potential which leads to a very early stopping in gradient descent fitting. Thus, this approach may not be useful to directly receive a good predictive model, but it may be helpful to select the right feature components to design a good predictive model.
Figure 11.20 gives the importance measures of the estimated regression attentions
of all components 1 ≤ j ≤ q = 38. The red color corresponds to regularization parameter η = 0.005, red + yellow colors to η = 0.0025, and red + yellow + green colors to η = 0 (no regularization). Figure 11.20 (lhs) shows the results on the original (standardized) features x. By far the smallest red + yellow column among the continuous features is observed for VehPower which confirms the variable selection of Sect. 11.5.3. Among the categorical variables Region seems more important (on average) than VehBrand because the red and yellow columns are generally bigger for Region. All these red and yellow columns of VehBrand and Region are bigger than the ones of VehPower which supports the inclusion of the two categorical variables.
Figure 11.20 (rhs) verifies this decision of keeping the categorical variables. For this latter graph we randomly permute Region across the entire portfolio, and we run the same group LASSO regularized fitting procedure again on this modified data. The vertical black line shows the average importance of the permuted Region variable for η = 0.0025. We see that only VehPower has a smaller importance measure, and all other variables dominate the permuted Region variable. This confirms our conclusions above.
We conclude that the LocalGLMnet architecture with a group LASSO regularization is helpful for variable selection, and, more generally, the LocalGLMnet architecture is useful for model interpretation, finding interactions and functional forms of the features entering the regression function. In examples that have categorical variables with many levels, the LocalGLMnet approach may not lead to a regression model that is fully competitive. In this case, the LocalGLMnet can be used for variable selection, and an other network architecture should then be fitted on the selected variables. Alternatively, we can embed the categorical variables in a preparatory network step, and then work with these embeddings of the categorical variables (kept fixed within the LocalGLMnet).
11.6 Selected Applications
11.6.1 Mixture Density Networks
In Sect. 6.3 we have introduced mixture distributions and we have presented the EM algorithm for fitting these mixture distributions. The EM algorithm considers two steps, an expectation step (E-step) and a maximization step (M-step). The E-step is motivated by (6.34). In this step the posterior distribution of the latent variable Z is determined, given the observation Y and the parameter estimates for the model parameters θ and p. The M-step (6.35) determines the optimal model parameters θ and p, based on the observation Y and the posterior distribution of Z. Typically, we explore MLE in the M-step. However, for the EM algorithm to function it is not important that we really work with the maximum in the M-step, but monotonicity in (6.38) is sufficient. Thus, if at algorithmic time t − 1 we have a parameter estimate \((\widehat {\boldsymbol {\theta }}^{(t-1)}, \widehat {\boldsymbol {p}}^{(t-1)})\), it suffices that the next estimate \((\widehat {\boldsymbol {\theta }}^{(t)}, \widehat {\boldsymbol {p}}^{(t)})\) increases the log-likelihood, without necessarily being the MLE; this latter approach is called generalized EM (GEM) algorithm. Exactly this point makes it feasible to also use the EM algorithm in cases where we model the parameters through networks which are fit using gradient descent (ascent) algorithms. These methods go under the name of mixture density networks (MDNs).
MDNs have been introduced by Bishop [35], who explores MDNs on Gaussian mixtures, and using SGD and quasi-Newton methods for model fitting. MDNs have also started to gain more popularity within the actuarial community, recent papers include Delong et al. [95], Kuo [230] and Al-Mudafer et al. [6], the latter two considering MDNs for claims reserving.
We recall the mixture density for a selected member of the EDF. The incomplete log-likelihood of the data (Y i, x i, v i)1≤i≤n is given by, see (6.24),
for canonical parameter  , dispersion parameter
, dispersion parameter  , mixture probability p ∈ ΔK, and K denotes the number of mixture components. MDNs model these parameters with networks. Choose a FN network \(\boldsymbol {z}^{(d:1)}: {\mathbb R}^{q+1} \to \{1\}\times {\mathbb R}^{q_d}\) of depth d, with input dimension q being equal to the dimension of the features \(\boldsymbol {x} \in \mathcal {X} \subseteq \{1\}\times {\mathbb R}^q\) and output dimension q
d + 1. This gives us the learned representations z
i = z
(d:1)(x
i). These learned representations are used to model the parameters. For the mixture probability p we build a logistic categorical GLM, based on z
i. For the (canonical) link h, we set linear predictor, see (5.72),
, mixture probability p ∈ ΔK, and K denotes the number of mixture components. MDNs model these parameters with networks. Choose a FN network \(\boldsymbol {z}^{(d:1)}: {\mathbb R}^{q+1} \to \{1\}\times {\mathbb R}^{q_d}\) of depth d, with input dimension q being equal to the dimension of the features \(\boldsymbol {x} \in \mathcal {X} \subseteq \{1\}\times {\mathbb R}^q\) and output dimension q
d + 1. This gives us the learned representations z
i = z
(d:1)(x
i). These learned representations are used to model the parameters. For the mixture probability p we build a logistic categorical GLM, based on z
i. For the (canonical) link h, we set linear predictor, see (5.72),

with regression parameter  . For the canonical parameter θ, the mean parameter μ, respectively, and the dispersion parameter φ we proceed analogously. Choose strictly monotone and smooth link functions g
μ and g
φ, and consider the double GLMs, for 1 ≤ k ≤ K, on the learned representations z
i
. For the canonical parameter θ, the mean parameter μ, respectively, and the dispersion parameter φ we proceed analogously. Choose strictly monotone and smooth link functions g
μ and g
φ, and consider the double GLMs, for 1 ≤ k ≤ K, on the learned representations z
i
with regression parameters  for the mean parameters and
for the mean parameters and  for the dispersion parameters. Thus, altogether this gives us a network parameter of dimension, set q
0 = q,
for the dispersion parameters. Thus, altogether this gives us a network parameter of dimension, set q
0 = q,
Remarks 11.14
-
The regression functions (11.47)–(11.48) use a slight abuse of notation, because, strictly speaking, these should be functions w.r.t. the features \(\boldsymbol {x}_i \in \mathcal {X}\), i.e., we should understand the learned representations z i as a short form for x i↦z (d:1)(x i).
-
It is not fully correct to say that (11.47) is the logistic categorical GLM of formula (5.72), because (11.47) does not lead to identifiable regression parameters. In fact, we should reduce the dimension of the categorical GLM to K − 1, by setting \(\boldsymbol {\beta }^{\boldsymbol {p}}_K=0\), see (5.70), because the probability of the last label K is fully determined if we know the probabilities of all other labels; this would also justify to say that h is the canonical link. Since in FN network modeling we do not have identifiability anyway, we neglect this normalization (redundancy), see line 16 of Listing 11.12, below.
-
The above proposal (11.47)–(11.48) suggests to use the same network z (d:1) for all mixture parameters involved. This requires that the chosen network is sufficiently large, so that it can comply simultaneously with these different tasks. Alternatively, we could choose three separate (parallel) networks for p, μ and φ, respectively. This second proposal does not (easily) allow for (non-trivial) interactions between the parameters, and it may also suffer from less robustness in fitting.
-
Proposal (11.48) defines double GLMs for the mixture components f k, 1 ≤ k ≤ K. If we decide to not model the dispersion parameters feature dependent, i.e., if we set \(\varphi _k(\boldsymbol {z})\equiv \varphi _k \in {\mathbb R}_+\), then the mixture components are modeled with GLMs on the learned representations z i = z (d:1)(x i). Nevertheless, this latter approach still requires that the dispersion parameters φ k are set to reasonable values, as they enter the score equations, this can be seen from (6.29) adapted to MDNs. Thus, in MDNs, the dispersion parameters do not cancel in the score equations, which is different from the single distribution case. The dispersion parameter can either be estimated (updated) during the M-step of the EM algorithm (supposed we use the EM algorithm), or it can be pre-specified as a given hyper-parameter.
-
As mentioned in Sect. 6.3, mixture density fitting can be challenging because, in general, mixture density log-likelihoods are unbounded. Therefore, a suitable initialization of the EM algorithm is important for a successful model fitting. This problem is less pronounced in MDNs as we use early stopping in SGD fitting that prevents the fitted parameters to depend on a small set of observations. For instance, Example 6.13 cannot occur because an individual observation Y 1 enters at most one (mini-)batch of SGD, and the SGD algorithm will provide a good balance across all batches. Moreover, early stopping will imply that the selected parameters must also be good on the validation data being disjoint (and independent) from the training data.
-
Delong et al. [95] present two different ways of fitting such MDNs. The crucial property in EM fitting is to preserve the monotonicity in the M-step. For MDNs this can either be achieved by using the parameters as offsets for the next EM iteration (this is called ‘EM network boosting’ in Delong et al. [95]) or to forward the network weights from one to the next loop (called ‘EM forward network’ in Delong et al. [95]). We are going to present the second option in the next example.
Example 11.15 (Gamma Claim Size Modeling and MDNs)
We revisit Example 6.14 which models the claim sizes of the French MTPL data. For the modeling of these claim sizes we choose the mixture distribution (6.39) which has four gamma components f 1, …, f 4 and one Lomax component f 5. In a first step we again model these five mixture components independent of the feature information x, and the feature information only enters the mixture probabilities p(x) ∈ Δ5. This modeling approach has been motivated by Fig. 13.17 which suggests that the features mainly result in systematic effects on the mixture probabilities. We choose the same model and feature information as in Example 6.14. We only replace the logistic categorical GLM part (6.40) for modeling p(x) by a depth d = 2 FN network with (q 1, q 2) = (20, 10) neurons. Area, VehAge, DrivAge and BonusMalus are modeled as continuous variables, and for the categorical variables VehBrand and Region we choose two-dimensional embedding layers.
Listing 11.12 R code of the MDN for modeling the mixture probability p(x)

Listing 11.12 shows the chosen network. Lines 13–16 model the mixture probability p(x). We also integrate the modeling of the (homogeneous) parameters of the mixture densities f 1, …, f 5. Lines 18 and 24 of Listing 11.12 consider the mean and shape parameter of the gamma components, and line 21 the tail parameter 1∕β 5 of the Lomax component. Note that we use the sigmoid activation for this Lomax parameter. This implies 1∕β 5 ∈ (0, 1) and, thus, β 5 > 1, which enforces a finite mean model. The exponential activations on lines 18 and 24 ensure positivity of these parameters. The input Bias to these variables is simply the constant 1, which is the homogeneous case not differentiating w.r.t. the features.
Listing 11.13 Mixture density negative incomplete log-likelihood

Observe that in most of the networks so far, the output of the network was equal to an expected response of a random variable that we try to predict. In this MDN we output the parameters of a distribution function, see line 27 of Listing 11.12. In our case this output has dimension 14, which then enters the score in Listing 11.13. In a first attempt we fit this MDN brute-force by just implementing the incomplete log-likelihood received from (6.39). Since the gamma function Γ(⋅) is not easily available in keras [77], we replace the gamma density by its saddlepoint approximation, see Sect. 5.5.2. Listing 11.13 shows the negative log-likelihood of the mixture density that is used to perform the brute-force SGD fitting. Lines 2–9 give the saddlepoint approximations to the four gamma components, and line 10 the Lomax component for the scale parameter M. Note that this brute-force approach is based only on the incomplete observation Y encoded in true[,1], see Listing 11.13.
We fit this logistic categorical FN network of Listing 11.12 under the score function of Listing 11.13 using the nadam version of SGD. Moreover, we use a stratified training-validation split, otherwise we did not obtain a competitive model. The results are presented in Table 11.12 on line ‘logistic FN network: brute-force fitting’. We observe a slightly worse performance (in-sample) than in the logistic GLM. This does not justify the use of the more complex network architecture. Or in other words, feature pre-processing seems to been done suitably in Example 6.14.
In a next step, we fit this MDN with the (generalized) EM algorithm. The E-step is exactly the same as in Example 6.14. For the M-step, having knowledge of the (latent mixture component) variables \(\widehat {\boldsymbol {Z}}_i\), 1 ≤ i ≤ n, implies that the mixture probability estimation and the mixture density estimation completely decouples. As a consequence, the parameters of the density components f 1, …, f 5 can directly be estimated using univariate MLEs, this is the same as in Example 6.14. The only part that needs further explanation is the estimation of the logistic categorical FN network for p(x). In each loop of the EM iteration we would like to find the optimal network parameter for p(x), and at the same time we have to ensure the monotonicity (6.38). Following the ‘EM forward network’ approach of Delong et al. [95], this is most easily achieved by just initializing the FN network in loop t of the algorithm with the optimal network parameter of the previous loop t − 1. Thus, the starting parameter of SGD reflects the optimal parameter from the previous step, and since SGD generally decreases losses, the monotonicity (6.38) holds. The latter statement is not strictly true, SGD introduces additional randomness through the building of (mini-)batches, therefore, monotonicity should be traced explicitly (which also ensures that the early stopping rule is chosen suitably). We have implemented such an EM-SGD algorithm, essentially, we just have to drop lines 17–28 of Listing 11.12 and lines 13–16 provide the entire response. As loss function we choose the categorical (multi-class) cross-entropy loss, see (4.19). The results in Table 11.12 on line ‘logistic FN network: EM fitting’ indicate a superior fitting behavior compared to the brute-force fitting. Nevertheless, this network approach is still not outperforming the GLM approach, saying that we should stay with the simpler GLM.
In a final step, we also model the mean parameters μ k(x), 1 ≤ k ≤ 4, of the gamma components feature dependent, to see whether we can gain predictive power from this additional flexibility or whether our initial model choice is sufficient. For robustness reasons we neither model the shape parameters β k , 1 ≤ k ≤ 4, of the gamma components feature dependent nor the tail parameter β 5 of the Lomax component. The implementation only requires small changes to Listing 11.12, see Listing 11.14.
Listing 11.14 R code of the MDN for modeling the mixture probability p(x) and the gamma means μ k(x)

A brute-force fitting of the MDN architecture of Listing 11.14 can directly be based on the score function (negative incomplete log-likelihood) of Listing 11.13. In the case of the EM algorithm we need to change the score function to the complete log-likelihood accounting for the variables \(\widehat {\boldsymbol {Z}}_i \in \Delta _5\). This is done in Listing 11.15 where \(\widehat {\boldsymbol {Z}}_i\) is encoded in the variables true[,2] to true[,6].
Listing 11.15 Mixture density negative complete log-likelihood

We fit this MDN using the two different fitting approaches, and the results are given on the last two lines of Table 11.12. Again the performance of the EM fitting is slightly better than the brute-force fitting, and the bigger log-likelihoods indicate that we can gain predictive power by also modeling the means of the gamma components feature dependent.
Figure 11.21 compares the QQ plot of the resulting MDN with EM fitting to the one received from the logistic categorical GLM of Example 6.14. These graphs are very similar. We conclude that in this particular example it seems that the simpler proposal of Example 6.14 is sufficient. \(\blacksquare \)
In a next step, we try to understand which feature components influence the mixture probabilities  most. Similarly to Examples 6.14 and 11.15, we therefore use a MDN where we only fit the mixture probability p(x) with a network and the mixture components f
1, …, f
K are assumed to be homogeneous.
most. Similarly to Examples 6.14 and 11.15, we therefore use a MDN where we only fit the mixture probability p(x) with a network and the mixture components f
1, …, f
K are assumed to be homogeneous.
Example 11.16 (MDN with LocalGLMnet)
We revisit Example 11.15. We choose the mixture distribution (6.39) which has four gamma components f 1, …, f 4 and a Lomax component f 5. We select their parameters independent of the features. The feature information x should only enter the mixture probability p(x) ∈ Δ5, similarly to the first part of Example 11.15. We replace the logistic FN network of Example 11.15 for modeling p(x) by a LocalGLMnet such that we can analyze the importance of the variables, see Sect. 11.5.
For the feature information we choose the continuous variables Area, VehPower, VehAge, DrivAge and BonusMalus, the binary variable VehGas and the categorical variables VehBrand and Region, thus, we extend by VehPower and VehGas compared to Example 11.15. These latter two variables have not been included previously, because they did not seem to be important w.r.t. Fig. 13.17. The continuous and binary variables are centered and normalized to unit variance. For the categorical variables we use two-dimensional embedding layers, and afterwards they are concatenated with the continuous variables with a subsequent normalization layer (to ensure that all components live on the same scale). This provides us with a 10-dimensional feature vector. This feature vector is complemented with an i.i.d. standard Gaussian component, called Random, to perform an empirical Wald type test. We call this pre-processed feature (after embedding and normalization of the categorical variables) \(\boldsymbol {x} \in {\mathbb R}^{q_0}\) with q 0 = 11.
We design a LocalGLMnet that acts on this feature \(\boldsymbol {x} \in {\mathbb R}^{q_0}\) for modeling a categorical multi-class output with K = 5 levels. Therefore, we choose the regression attentions
where z (d:1) is a network of depth d having a matrix-valued output of dimension q 0 × K. For the (canonical) link h, this gives us the predictor, see (5.72),

with intercepts \(\beta _{k,0} \in {\mathbb R}\), and where \(\boldsymbol {\beta }_k(\boldsymbol {x}) \in {\mathbb R}^{q_0}\) is the k-th column of regression attention \(\boldsymbol {\beta }(\boldsymbol {x})=\boldsymbol {z}^{(d:1)}(\boldsymbol {x}) \in {\mathbb R}^{q_0 \times K}\). We also refer to the second item of Remarks 11.14 concerning a possible dimension reduction in (11.49), i.e., in fact we apply the softmax activation function to the right-hand side of (11.49), neglecting the identifiability issue. Moreover, as in the introduction of the LocalGLMnet, we separate the intercept components from the remaining features in (11.49).
We fit this LocalGLMnet-MDN with the EM version presented in Example 11.15. We apply early stopping based on the same stratified training-validation split as in the aforementioned example, and this provides us with a log-likelihood of -198’290, thus, slightly bigger than the corresponding numbers in Table 11.12.
More interestingly, our goal is to understand the regression attentions given by \(\boldsymbol {\beta }(\boldsymbol {x}_i)=(\boldsymbol {\beta }_1(\boldsymbol {x}_i), \ldots , \boldsymbol {\beta }_5(\boldsymbol {x}_i)) \in {\mathbb R}^{11\times 5}\) over all claims 1 ≤ i ≤ n. Figure 11.22 shows the resulting boxplots, where each of the five graphs corresponds to one mixture component 1 ≤ k ≤ 5, and the different colors illustrate the 11 feature components providing the attention weights β k,j(x i), 1 ≤ j ≤ 11. The red boxplots show the purely random component Random for 1 ≤ k ≤ 5, which provides the acceptance region of an empirical Wald test for the null hypothesis that the corresponding term should be dropped. This is highlighted by the orange shaded area (at a significance level of 0.1%). Thus, whenever a boxplot lies within this orange shaded area we may consider dropping this term, e.g., for k = 2 (top-right), this is the case for Area, VehPower and Region2 (being the second component of the two-dimensional region embedding). Note that this interpretation needs some care because we do not have identifiability in the class probabilities.
The first observation is that, indeed, VehPower is mostly in the orange confidence area and, thus, may be dropped. This does not apply to the other feature components, and, thus, we should keep them in the model. The three gamma mixture components f 1, f 2 and f 3 correspond to the three modes at 75, 600 and 1’175 in Fig. 13.17. Component f 4 is a gamma component covering the whole range of claims, and f 5 is the Lomax component modeling the regular variation in the tail. Interestingly, DrivAge and BonusMalus seem very important for mixture components k = 1, k = 3 and k = 4 (with different signs), this is supported by Fig. 13.17. The Lomax component seems mostly impacted by DrivAge, VehBrand and Region. Only mixture component k = 2 is more difficult to interpret. This component seems influenced by most the feature components, in particular, the combination of VehAge, VehGas and VehBrand seems important. This could mean that mixture component k = 2 belongs to a certain type of vehicle.
In a next step we could study interactions and their impact on the mixture components, and LASSO regularization would provide us with another method of variable selection, see Sect. 11.5.4. We refrain from doing so and close the example.
\(\blacksquare \)
11.6.2 Estimation of Conditional Expectations
FN networks have also found their way into solving risk management problems. We briefly introduce a valuation problem and then describe a way of solving this problem. Assume we have a liability cash flow Y 1:T = (Y 1, …, Y T) with (random) payments Y t at time points t = 1, …, T. We assume that this liability cash flow Y 1:T is adapted to a filtration \((\mathcal {A}_t)_{1\le t \le T}\) on the underlying probability space \((\Omega , \mathcal {A}, {\mathbb P})\). Moreover, we assume to have a pricing kernel (state price deflator) ψ 1:T = (ψ 1, …, ψ T) on that probability space which is an \((\mathcal {A}_t)_{1\le t \le T}\)-adapted random vector with strictly positive components ψ t > 0, a.s., for all 1 ≤ t ≤ T. A no-arbitrage value of the outstanding liability cash flow at time 1 ≤ τ < T can be defined by (we assume existence of all second moments)
For the mathematical background on no-arbitrage pricing using state price deflators we refer to Wüthrich–Merz [393]. The \(\mathcal {A}_\tau \)-measurable quantity \(\mathcal {R}_\tau \) is called reserves of the outstanding liabilities at time τ. From a risk management and solvency point of view we would like to understand the volatility in the reserves \(\mathcal {R}_\tau \) seen from time 0, i.e., we try to model the random variable \(\mathcal {R}_\tau \) seen from time 0 (based on the trivial σ-algebra \(\mathcal {A}_0 =\{\emptyset , \Omega \}\)). In applied problems, the difficulty often is that the conditional expectations under the summation in (11.50) cannot be computed in closed form. Therefore the law of \(\mathcal {R}_\tau \) cannot be determined explicitly.
We provide a numerical solution to the calculation of the conditional expectations in (11.50). Assume that the information set \(\mathcal {A}_\tau \) can be described by a random vector X τ, i.e., \(\mathcal {A}_\tau =\sigma (\boldsymbol {X}_\tau )\). In that case we rewrite (11.50) as follows
The latter now indicates that we can determine the conditional expectations in (11.51) as regression functions in features X τ, and we try to understand for s > τ
The random variable \(\mathcal {R}_\tau \) can then be determined empirically by simulation. This requires two steps: (1) We have to be able to simulate ψ s Y s∕ψ τ, conditionally given X τ = x τ. This allows us to estimate the conditional expectation (11.52) with a regression function. (2) We need to be able to simulate X τ. This provides us with the empirical occurrence probabilities of specific choices X τ = x τ in (11.52) which then gives an empirical version of \(\mathcal {R}_\tau \).
In theory, this problem can be approached by nested simulations which is a two-stage procedure that first performs step (2), and then calculates step (1) empirically with Monte Carlo simulations for every realization of step (2), see, e.g., Lee [242] and Glynn–Lee [161]. The disadvantage of this two-stage nested simulation procedure is that it is computationally demanding. Building upon the work on valuation of American options by Carriere [65], Tsitsiklis–Van Roy [356] and Longstaff–Schwartz [257], the papers of Broadie et al. [55] and Ha–Bauer [177] propose to regress future cash flows on finitely many basis functions depending on the state variable X τ. More recently, machine learning tools such as FN networks have been proposed to determine these basis and regression functions, see, e.g., Cheridito et al. [74] or Krah et al. [224].
In the following, we assume that all random variables considered are square-integrable and, thus, we can work in a Hilbert space with the scalar product \(\langle X, Z \rangle = {\mathbb E}[XZ]\) for \(X, Z \in \mathcal {L}^2(\Omega , \mathcal {A}, {\mathbb P})\). Moreover, for simplicity, we drop the time indices and we also drop the stochastic discounting in (11.52) by assuming ψ s∕ψ τ ≡ 1. These simplifications are not essential technically and simplify our outline. The conditional expectation \(\mu (\boldsymbol {X})={\mathbb E}[Y | \boldsymbol {X}]\) can then be found by the orthogonal projection of Y onto the sub-space σ(X), generated by X, in the Hilbert space \(\mathcal {L}^2(\Omega , \mathcal {A}, {\mathbb P})\). That is, the conditional expectation is the measurable function \(\mu :{\mathbb R}^q \to {\mathbb R}\), X↦μ(X), that minimizes the mean squared error

among all measurable functions on X. In Example 3.7, we have seen that μ(⋅) is the minimizer of this problem if and only if

for p x-a.e. \(\boldsymbol {x} \in {\mathbb R}^q\), where p x is the distribution of X, and where F Y |x is the conditional distribution of Y , given feature X = x; we also refer to (3.6).
Under the assumption that we can simulate observations (Y, X) under \({\mathbb P}\), we can solve (11.53)–(11.54) approximately by restricting to a sufficiently rich family of regression functions. Choose a FN network \(\boldsymbol {z}^{(d:1)}:{\mathbb R}^q \to {\mathbb R}^{q_d}\) of depth d and the identity link g(x) = x. An optimal network parameter \(\widehat {\boldsymbol {\vartheta }}\) is found by minimizing

where (Y i, X i), 1 ≤ i ≤ n, are i.i.d. copies of (Y, X). This provides us with the fitted FN network \(\widehat {\boldsymbol {z}}^{(d:1)}(\cdot )\) and the fitted output parameter \(\widehat {\boldsymbol {\beta }}\). These can be used to receive an approximation to the conditional expectation, solution of (11.54),
This then allows us to approximate the random variable in (11.51) empirically by simulating features X and inserting them into left-hand side of (11.56).
Remarks 11.17
-
There are different types of errors involved. First, there is an irreducible approximation error if the chosen family of FN networks is not sufficiently rich to approximate the conditional expectation well. For example, if we choose the hyperbolic tangent activation function, then, naturally, z (d:1)(⋅) is uniformly bounded for a fixed network parameter 𝜗. This does not necessarily apply to the conditional expectation \({\mathbb E}[Y | \boldsymbol {X}=\cdot ]\) and, thus, the approximation in the tail may be poor. Second, we consider an approximation based on a finite sample in (11.55). However, this error can be made arbitrarily small by letting n →∞. In-sample over-fitting should not be an issue as we may generate samples of arbitrary large sample sizes. Third, having the approximation (11.56), we still need to simulate i.i.d. samples X k, k ≥ 1, having the same distribution as X to empirically approximate the distribution of the random variable \(\mathcal {R}_\tau \) in (11.51). Also in this step we benefit from the fact that we can simulate infinitely many samples to mitigate this approximation error.
-
To fit the network parameter 𝜗 in (11.55) we use i.i.d. copies (Y i, X i), 1 ≤ i ≤ n, that have the same distribution as (Y, X) under \({\mathbb P}\). However, to receive a good approximation to regression function x↦μ(x) we only need to simulate \(Y_i |{ }_{\{\boldsymbol {X}_i=\boldsymbol {x}_i\}}\) from \(F_{Y|\boldsymbol {x}_i}(\cdot )={\mathbb P}[\cdot | \boldsymbol {X}_i=\boldsymbol {x}_i]\), and X i can be simulated from an arbitrary equivalent distribution to p x, and we still get the right conditional expectation in (11.54). This is worth mentioning because if we need a higher precision in some part of the feature space of X, we can apply a sort of importance sampling by choosing a distribution for X that generates more samples in the corresponding part of the feature space compared to the original (true) distribution p x of X; this proposal has been emphasized in Cheridito et al. [74].
We study the example presented in Ha–Bauer [177] and Cheridito et al. [74]. This example considers a variable annuity (VA) with a guaranteed minimum income benefit (GMIB), and we revisit the network approach of Cheridito et al. [74].
Example 11.18 (Approximation of Conditional Expectations)
We consider the VA example with a GMIB introduced and studied in Ha–Bauer [177]. This example involves a 3-dimensional stochastic process, for t ≥ 0,
with q t being the log-value of the VA account at time t, r t is the short rate at time t, and m x+t is the force of mortality at time t of a person aged x at time 0. The payoff at fixed maturity date T > 1 of this insurance contract is given by
where \(e^{q_T}\) is the VA account value at time T, and b a x+T(r T, m x+T) is the GMIB at time T consisting of a face value b > 0 and with a x+T(r T, m x+T) being the value of an immediate annuity at time T of a person aged x + T. Our goal is to model the conditional expectation
for a fixed valuation time point 0 < τ < T, and where D(τ, T) = D(τ, T;X τ) is a σ(X τ)-measurable discount factor. This requires the explicit specification of the GMIB term as a function of (r T, m x+T), the modeling of the stochastic process (X t)0≤t≤T, and the specification of the discount factor D(τ, T;X τ). In financial and actuarial valuation the regression function μ(⋅) in (11.57) should reflect a no-arbitrage price. Therefore, \({\mathbb P}\) in (11.57) should be an equivalent martingale measure w.r.t. the selected numéraire. In our case, we choose a force of mortality (m x+t)t-adjusted zero-coupon bond price as numéraire. This implies that \({\mathbb P}\) is a mortality-adjusted forward measure; for details and its explicit derivation we refer to Sect. 5.1 of Ha–Bauer [177]. In particular, Ha–Bauer [177] introduce a three-dimensional Brownian motion based model for (X t)t from which they deduce all relevant terms explicitly. We skip these calculations here, because, once the GMIB term and the discount factor are determined, everything boils down to knowing the distribution of the random vector (X τ, X T) under the corresponding probability measure \({\mathbb P}\). We choose initial age x = 55, maturity T = 15 and (solvency) time horizon τ = 1. Under the model and parametrization of Ha–Bauer [177] we receive a multivariate Gaussian distribution under \({\mathbb P}\) given by

Under the model specification of Ha–Bauer [177], one can furthermore work out the discount factor and the annuity. Define for t ≥ 0 and k > 0 the affine term structure
with deterministic functions
with parameters for the short rate process α = 25%, σ r = 1%, for the force of mortality κ = 7%, ψ = 0.12%, the correlation between the short rate and the force of mortality ϱ 2,3 = −4%, and with market-price of the risk-adjusted mean reversion level \(\bar {\gamma }=1.92\%\) of the short rate process. These formulas can be retrieved because we work under an affine Gaussian structure. The discount factor is then given by
and the annuity is determined by (we cap at age 55 + 50 = 105)
Moreover, we set for the face value b = 10.79205. This parametrization implies that the VA account value \(e^{q_T}\) exceeds the GMIB b a x+T(r T, m x+T) with a probability of roughly 40%, i.e., in roughly 60% of the cases we exercise the GMIB option. Figure 11.23 shows the marginal densities of these two variables, moreover, their correlation is close to 0.
The model is now fully specified so that we can estimate the conditional expectation in (11.57) as a function of X τ. We therefore simulate n = 3′000′000 i.i.d. Gaussian observations \((\boldsymbol {X}^{(i)}_\tau , \boldsymbol {X}^{(i)}_T)\), 1 ≤ i ≤ n, from (11.58). This provides us with the observations
The resulting data \((Y_i, \boldsymbol {X}_\tau ^{(i)})_{1\le i \le n}\) is used for determining the regression function μ(⋅) in (11.57). We choose n = 3′000′000 samples in line with the least squares Monte Carlo approximation of Ha–Bauer [177].
We choose a FN network of depth d = 3 for approximating μ(⋅). For the three FN layers we choose (q 1, q 2, q 3) = (20, 15, 10) neurons with the hyperbolic tangent activation function, and as output activation we choose the identity function; we choose a more complex network compared to Cheridito et al. [74] because it seems that this gives us more accurate results. We fit this FN network using the square loss function. The square loss is motivated by (11.55). Furthermore, we average over 20 runs with different seeds. Thus, we receive 20 fitted FN networks \(\widehat {\mu }_k(\cdot )\) for the 20 different seeds 1 ≤ k ≤ 20 and the nagging predictor is obtained by averaging
We then generate new i.i.d. samples \(\boldsymbol {X}_\tau ^{(l)}\), 1 ≤ l ≤ L, from the multivariate Gaussian distribution (11.58), where this time we only need the first 3 components. This gives us the empirical samples
providing an empirical distribution \(\widehat {F}_{\mu (\boldsymbol {X}_\tau )}\) that approximates the distribution of μ(X τ), given in (11.57). In risk management and solvency analysis, this empirical distribution can be used to estimate the Value-at-Risk (VaR) and the (upper) conditional tail expectation (CTE) in valuation μ(X τ), seen from time 0, on different safety levels p ∈ (0, 1)
and
We also refer to Sect. 11.3. The VaR and the CTE are two commonly used risk measures in insurance practice that determine the necessary risk bearing capital to run the corresponding insurance business. Typically, the VaR is evaluated on p = 99.5%, i.e., we allow for a default probability of 0.5% of not being able to cover the changes in valuation over a τ = 1 year time horizon. Alternatively, the CTE is considered on p = 99% which means that we need sufficient capital to cover on average the 1% worst changes in valuation over a 1 year time horizon.
Figure 11.24 shows our FN network approximations. The boxplots shows the individual results of the estimates \(\widehat {\mu }_k(\cdot )\) with 20 different seeds, and the horizontal lines show the results of the nagging predictor (11.59). The red line at 140.97 gives the estimated VaR for p = 99.5%, this value is slightly bigger than the best estimate of 139.47 (orange line) in Ha–Bauer [177] which is based on a functional approximation involving 37 monomials and 40’000’000 simulated samples. CTEs on p = 99.5% and p = 99% are given by 145.09 and 141.49. We conclude that in the present example \(\widehat {\mathrm {VaR}}_{99.5\%}\) (used in Europe) and \(\widehat {\mathrm {CTE}}_{99\%}\) (used in Switzerland) are approximately of the same size for this VA with a GMIB.
Resulting \(\widehat {\mathrm {VaR}}_{99.5\%}\) (red), \(\widehat {\mathrm {CTE}}_{99.5\%}\) (green) and \(\widehat {\mathrm {CTE}}_{99\%}\) (blue); the orange line gives the result of Ha–Bauer [177] for the 99.5% VaR
This example shows how problems can be solved that require the computation of a conditional expectation. Alternatively, we could explore the LocalGLMnet architecture, which would allow us to explain the conditional expectation more explicitly in terms of the information X τ available at time τ. This may also be relevant in practice because it allows to determine the main risk drivers of the underlying insurance business.
Figure 11.25 shows the marginal densities of the components of X τ = (q τ, r τ, m x+τ) in blue color. In red color we show the corresponding conditional densities of X τ, conditioned on \(\widehat {\mu }(\boldsymbol {X}_\tau )>\widehat {\mathrm {VaR}}_{99.5\%}\), thus, these are the feature values X τ that lead to a shortfall beyond the 99.5% VaR of \(\widehat {\mu }(\boldsymbol {X}_\tau )\). From this figure we conclude that the main driver of VaR is the VA account variable q τ, whereas the short rate r τ and the force of mortality m x+τ are slightly lower beyond the VaR compared to their unconditioned counterparts. The explanation for these smaller values is that they lead to less discounting and, henceforth, to bigger GMIB values. This is useful information for exploring importance sampling as mentioned in Remarks 11.17. This closes the example. \(\blacksquare \)
Feature values X τ triggering VaR on the 99.5% level: (lhs) VA account log-value q τ, (middle) short rate r τ, and (rhs) force of mortality m x+τ, blue color shows the full density and red color shows the conditional density conditioned on being above the 99.5% VaR of \(\widehat {\mu }(\boldsymbol {X}_\tau )\)
11.6.3 Bayesian Networks: An Outlook
This section provides a short introduction to Bayesian networks and to variational inference. We see this section as a motivation for doing more research in that direction. In Sect. 11.4 we have assessed model uncertainty through bootstrapping. Alternatively, we could take a Bayesian viewpoint. We start from a fixed network architecture that involves a network parameter 𝜗. The Bayesian approach considered in Section 6.1 selects a prior density π(𝜗) on the space of network parameters (w.r.t. a measure ν). For given data (Y, x) we can then calculate the posterior density of 𝜗 by
A new data point Y † with feature x † has conditional density, given observation (Y, x),
supposed that (Y, x) and (Y †, x †) are conditionally independent, given 𝜗. Thus, there only remains to determine the posterior density (11.60) of the network parameter 𝜗. Unfortunately, this is a rather challenging problem because of the curse of dimensionality, and even advanced MCMC methods, such as HMC, often do not lead to satisfactory results (convergence), for MCMC we refer to Section 6.1. For this reason one often explores approximate inference methods, see, e.g., Chapter 10 of Bishop [36] or the tutorial of Jospin et al. [205]. A scalable version is to approximate the posterior density using the so-called method of variational inference. This is presented in the following.
Choose a family \(\mathcal {F}=\{q(\cdot ;\theta );\theta \in \boldsymbol {\Theta }\}\) of (more tractable) densities that have the same support as the prior π(⋅), and being parametrized by \(\theta \in \boldsymbol {\Theta } \subset {\mathbb R}^K\). This family \(\mathcal {F}\) is called the set of variational distributions, and the goal is to find the variational density \(q(\cdot ;\theta ) \in \mathcal {F}\) that is closest to the posterior density (11.60).
To evaluate the similarity between two densities, we use the KL divergence which analyzes the divergence from \(\pi \left (\left . \cdot \right | Y,\boldsymbol {x}\right )\) to q(⋅;θ) given by
The optimal approximation within \(\mathcal {F}\), for given data (Y, x), is found by solving

for the moment we neglect existence and uniqueness questions. A main difficulty is the computation of this KL divergence because it involves the intractable posterior density of 𝜗, given (Y, x). We modify the optimization problem such that we can circumvent the explicit calculation of this KL divergence.
Lemma 11.19
We have the following identity
for the (unconditional) density f(y|x) =∫𝜗 f(y|𝜗, x)π(𝜗)dν(𝜗) and the so-called evidence lower bound (ELBO)
Observe that the left-hand side in the statement of Lemma 11.19 is independent of θ ∈ Θ. Therefore, minimizing the KL divergence in θ is equivalent to maximizing the ELBO in θ. This follows exactly the same philosophy as the EM algorithm, see (6.32), in fact, the ELBO \(\mathcal {E}\) plays the role of functional \(\mathcal {Q}\) defined in (6.33).
Proof of Lemma 11.19
We start from the left-hand side of the statement
This proves the claim. □
The ELBO provides the lower bound (also called variational lower bound)
Interestingly, the ELBO does not include the posterior density, but only the joint density of Y and 𝜗, given x, which is assumed to be known (available). It can be rewritten as
the first term being the expected joint log-likelihood of (Y, 𝜗) under the variational density 𝜗 ∼ q(⋅;θ), and the second term being the entropy of the variational density.
The optimal approximation within \(\mathcal {F}\) for given data (Y, x) is then found by solving

That is we try to simultaneously maximize the expected joint log-likelihood of (Y, 𝜗) and the entropy over all variational densities q(⋅;θ) in \(\mathcal {F}\).
If we have multiple observations \(\mathcal {D}=\{(Y_i,\boldsymbol {x}_i); 1\le i \le n\}\), that are conditionally i.i.d., given 𝜗, we have to solve (we use conditional independence)

Typically, one solves this problem with gradient ascent methods which requires calculation of the gradient ∇θ of the objective function on the right-hand side. This is more difficult than plain vanilla gradient descent in network fitting because θ enters the expectation operator \({\mathbb E}_{q(\cdot ;\theta )}\).
Kingma–Welling [217] propose to use the following reparametrization trick. Assume that we can receive the random variable 𝜗 ∼ q(⋅;θ) by a reparametrization  for some smooth function t and where 𝜖 ∼ p does not depend on θ. E.g., if 𝜗 is multivariate Gaussian with mean μ and covariance matrix
for some smooth function t and where 𝜖 ∼ p does not depend on θ. E.g., if 𝜗 is multivariate Gaussian with mean μ and covariance matrix  , then
, then  for 𝜖 being standard multivariate Gaussian. Under the assumption that the reparametrization trick works for the family \(\mathcal {F}=\{q(\cdot ;\theta );\theta \in \boldsymbol {\Theta }\}\) we arrive at, for 𝜖 ∼ p,
for 𝜖 being standard multivariate Gaussian. Under the assumption that the reparametrization trick works for the family \(\mathcal {F}=\{q(\cdot ;\theta );\theta \in \boldsymbol {\Theta }\}\) we arrive at, for 𝜖 ∼ p,

The gradient of the ELBO is then given by (supposed we can exchange \({\mathbb E}_p\) and ∇θ)
These expected gradients are calculated empirically using Monte Carlo methods. Sample i.i.d. observations 𝜖 (i, j) ∼ p, 1 ≤ i ≤ n and 1 ≤ j ≤ m, and consider the empirical approximation
Using this empirical approximation we can use gradient ascent methods to estimate θ, known as stochastic gradient variational Bayes (SGVB) estimator, see Sect. 2.4.3 of Kingma–Welling [217], or as Bayes by Backprop, see Blundell et al. [41] and Jospin et al. [205].
Example 11.20
We consider the gradient (11.62) for an example from the EDF. First, if n is sufficiently large, it often suffices to set m = 1, and we still receive an accurate estimate. In that case we drop index j giving 𝜖 (i). Assume that the (conditionally independent) observations Y i belong to the same member of the EDF having cumulant function κ. Moreover, assume that the (conditional) mean of Y i, given x i, can be described by a FN network and a link function g such that, see (7.8),
for network parameter \(\boldsymbol {\vartheta } =(\boldsymbol {\beta }, \boldsymbol {w})\in {\mathbb R}^r\). In a Bayesian FN network this network parameter is not fixed but rather acts as a latent variable. In (11.62) this latent variable is for realization i given by (and using the reparametrization trick) \(\boldsymbol {\vartheta }=t(\epsilon ^{(i)};\theta ) \in {\mathbb R}^r\); θ is not the canonical parameter, here. Thus, we receive conditional mean of Y i, given 𝜖 (i) and x i,
with network parameter \(\boldsymbol {\vartheta }(\epsilon ^{(i)};\theta )=(\boldsymbol {\beta }(\epsilon ^{(i)};\theta ), \boldsymbol {w}(\epsilon ^{(i)};\theta ))=t(\epsilon ^{(i)},\theta ) \in {\mathbb R}^r\). Maximizing the ELBO implies that we need to calculate the gradients w.r.t. θ. First, we calculate the gradient w.r.t. the network parameter 𝜗 of the data log-likelihood
This gradient is calculated with back-propagation, we refer to (7.16) and Proposition 7.5. There remains the chain rule for evaluating the inner derivative coming from the reparametrization trick \(\theta \in \boldsymbol {\Theta } \subset {\mathbb R}^K \mapsto \boldsymbol {\vartheta }= t(\epsilon ^{(i)};\theta ) \in {\mathbb R}^r\). Consider the Jacobian matrix
This gives us the gradient w.r.t. θ

The prior distribution is often taken to be the multivariate Gaussian with prior mean \(\tau \in {\mathbb R}^r\) and (symmetric and positive definite) prior covariance matrix \(T \in {\mathbb R}^{r\times r}\), thus,

This implies for the gradient w.r.t. θ for the prior

There remains the choice of the family \(\mathcal {F}=\{q(\cdot ;\theta );\theta \in \boldsymbol {\Theta }\}\) of variational densities such that the reparametrization trick works. This is discussed in the remainder. \(\blacksquare \)
We briefly discuss the most popular and simplest family chosen for the variational distributions \(\mathcal {F}\). This family is the so-called mean field Gaussian variational family, meaning that all components of \(\boldsymbol {\vartheta } \in {\mathbb R}^r\) are assumed to be independent Gaussian, that is,

for  with K = 2r and with σ
j > 0 for all 1 ≤ j ≤ r. This allows us to apply the reparametrization trick
with K = 2r and with σ
j > 0 for all 1 ≤ j ≤ r. This allows us to apply the reparametrization trick

with r-dimensional standard Gaussian variable  . The Jacobian matrix is
. The Jacobian matrix is

The mean field Gaussian case provides the entropy of the variational distribution

This mean field Gaussian variational inference can be implemented with the R package tfprobability of Keydana et al. [212] and an explicit example is given in Kuo [230].
Example 11.20, Revisited
Working under the assumptions of Example 11.20 and additionally assuming that the family of variational distributions \(\mathcal {F}\) is multivariate Gaussian  leads us after some calculation to (the well-known formula)
leads us after some calculation to (the well-known formula)

This further simplifies if T and Σ are diagonal, the latter being the mean field Gaussian case. The remaining terms of the ELBO are treated empirically as in (11.63). \(\blacksquare \)
This section has provided a short introduction to uncertainty estimation in networks using Bayesian methods. We believe that this gives a promising outlook that certainly needs more theoretical and practical work to become useful in practical applications.
Notes
- 1.
In the standard implementation of SGD with early stopping, the learning and validation data partition is done non-stratified. If necessary, this can be changed manually.
References
Agarwal, R., Melnick, L., Frosst, N., Zhang, X., Lengerich, B., Caruana, R., & Hinton, G. E. (2021). Neural additive models: Interpretable machine learning with neural nets. arXiv:2004.13912v2.
Al-Mudafer, M. T., Avanzi, B., Taylor, G., & Wong, B. (2022). Stochastic loss reserving with mixture density neural networks. Insurance: Mathematics & Economics, 105, 144–147.
Bishop, C. M. (1994). Mixture Density Networks. Technical Report. Aston University, Birmingham.
Bishop, C. M. (2006). Pattern recognition and machine learning. New York: Springer.
Blundell, C., Cornebise, J., Kavukcuoglu, K., & Wiersta, D. (2015). Weight uncertainty in neural network. Proceedings of Machine Learning Research, 37, 1613–1622.
Broadie, M., Du, Y., & Moallemi, C. (2011). Efficient risk estimation via nested sequential estimation. Management Science, 57/6, 1171–1194.
Burguete, J., Gallant, R., & Souza, G. (1982). On unification of the asymptotic theory of nonlinear econometric models. Economic Review, 1/2, 151–190.
Carriere, J. F. (1996). Valuation of the early-exercise price for options using simulations and nonparametric regression. Insurance: Mathematics & Economics, 19/1, 19–30.
Cheridito, P., Ery, J., & Wüthrich, M. V. (2020). Assessing asset-liability risk with neural networks. Risks, 8/1. Article 16.
Chollet, F., Allaire, J. J., et al. (2017). R interface to Keras. https://github.com/rstudio/keras
Delong, Ł., Lindholm, M., & Wüthrich, M. V. (2021). Gamma mixture density networks and their application to modeling insurance claim amounts. Insurance: Mathematics & Economics, 101/B, 240–261.
Dimitriadis, T., Fissler, T., & Ziegel, J. F. (2020). The efficiency gap. arXiv:2010.14146.
Fissler, T., Merz, M., & Wüthrich, M. V. (2021). Deep quantile and deep composite model regression. arXiv:2112.03075.
Fissler, T., & Ziegel, J. F. (2016). Higher order elicitability and Osband’s principle. The Annals of Statistics, 4474, 1680–1707.
Fissler, T., Ziegel, J. F., & Gneiting, T. (2015). Expected shortfall is jointly elicitable with value at risk - Implications for backtesting. arXiv:1507.00244v2.
Glynn, P., & Lee, S. H. (2003). Computing the distribution function of a conditional expectation via Monte Carlo: Discrete conditioning spaces. ACM Transactions on Modeling and Computer Simulation, 13/3, 238–258.
Gourieroux, C., Laurent, J. P., & Scaillet, O. (2000). Sensitivity analysis of values at risk. Journal of Empirical Finance, 7/3–4, 225–245.
Gourieroux, C., Montfort, A., & Trognon, A. (1984). Pseudo maximum likelihood methods: Theory. Econometrica, 52/3, 681–700.
Guillén, M., Bermúdez, L., & Pitarque, A. (2021). Joint generalized quantile and conditional tail expectation for insurance risk analysis. Insurance: Mathematics & Economics, 99, 1–8.
Ha, H., & Bauer, D. (2022). A least-squares Monte Carlo approach to the estimation of enterprise risk. Finance and Stochastics, 26, 417–459.
Jospin, L. V., Buntine, W., Boussaid, F., Laga, H., & Bennamoun, M. (2020). Hands-on Bayesian neural networks - A tutorial for deep learning users. arXiv: 2007.06823.
Kellner, R., Nagl, M., & Rösch, D. (2022). Opening the black box - Quantile neural networks for loss given default prediction. Journal of Banking & Finance, 134, 1–20.
Keydana, S., Falbel, D., & Kuo, K. (2021). R package ‘tfprobability’: Interface to ‘TensorFlow Probability’. Version 0.12.0.0, May 20, 2021.
Kingma, D. P., & Welling, M. (2019). An introduction to variational autoencoders. Foundations and Trends in Machine Learning, 12/4, 307–392.
Komunjer, I., & Vuong, Q. (2010). Efficient estimation in dynamic conditional quantile models. Journal of Econometrics, 157, 272–285.
Krah, A.-S., Nikolić, Z., & Korn, R. (2020). Least-squares Monte Carlo for proxy modeling in life insurance: neural networks. Risks, 8/4. Article 116.
Kuo, K. (2020). Individual claims forecasting with Bayesian mixture density networks. arXiv:2003.02453.
Landsman, Z., & Valdez, E. A. (2005). Tail conditional expectation for exponential dispersion models. ASTIN Bulletin, 35/1, 189–209.
Lee, J. D., Sun, D. L., Sun, Y., & Taylor, J. E. (2016). Exact post-selection inference, with application to the lasso. Annals of Statistics, 44/3, 907–927.
Lee, S. H. (1998). Monte Carlo Computation of Conditional Expectation Quantiles. PhD Thesis, Stanford University.
Longstaff, F., & Schwartz, E. (2001). Valuing American options by simulation: A simple least-squares approach. The Review of Financial Studies, 14/1, 113–147.
McNeil, A. J., Frey, R., & Embrechts, P. (2015). Quantitative risk management: Concepts, techniques and tools (revised edition). Princeton: Princeton University Press.
Meinshausen, N. (2006). Quantile regression forests. Journal of Machine Learning Research, 7, 983–999.
Oelker, M.-R., & Tutz, G. (2017). A uniform framework for the combination of penalties in generalized structured models. Advances in Data Analysis and Classification, 11, 97–120.
R Core Team (2021). R: a language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. https://www.R-project.org/
Richman, R. (2021). Mind the gap - Safely incorporating deep learning models into the actuarial toolkit. SSRN Manuscript ID 3857693. Version April 2, 2021.
Richman, R., & Wüthrich, M. V. (2022). LocalGLMnet: Interpretable deep learning for tabular data. Scandinavian Actuarial Journal (in press).
Richman, R., & Wüthrich, M. V. (2021). LASSO regularization within the LocalGLMnet architecture. SSRN Manuscript ID 3927187. Version June 1, 2022.
Rudin, C. (2019). Stop explaining black box machine learning models for high stakes decisions and use interpretable models instead. Nature Machine Intelligence, 1, 206–215.
Takeuchi, I., Le, Q. V., Sears, T. D., & Smola, A. J. (2006). Nonparametric quantile estimation. Journal of Machine Learning Research, 7, 1231–1264.
Tsitsiklis, J., & Van Roy, B. (2001). Regression methods for pricing complex American-style options. IEEE Transactions on Neural Networks, 12/4, 694–703.
Vaughan, J., Sudjianto, A., Brahimi, E., Chen, J., & Nair, V. N. (2018). Explainable neural networks based on additive index models. arXiv:1806.01933v1.
Wüthrich, M. V., & Merz, M. (2013). Financial modeling, actuarial valuation and solvency in insurance. New York: Springer.
Yuan, X. T., & Lin, Y. (2007). Model selection and estimation in regression with grouped variables. Journal of the Royal Statistical Society, Series B, 68/1, 49–67.
Zou, H., & Hastie, T. (2005). Regularization and variable selection via the elastic net. Journal of the Royal Statistical Society, Series B, 67/2, 301–320.
Author information
Authors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2023 The Author(s)
About this chapter
Cite this chapter
Wüthrich, M.V., Merz, M. (2023). Selected Topics in Deep Learning. In: Statistical Foundations of Actuarial Learning and its Applications. Springer Actuarial. Springer, Cham. https://doi.org/10.1007/978-3-031-12409-9_11
Download citation
DOI: https://doi.org/10.1007/978-3-031-12409-9_11
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-12408-2
Online ISBN: 978-3-031-12409-9
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)















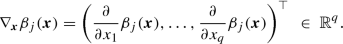






 for
for 




