Abstract
The analysis of complex dynamic systems is a core research topic in formal methods and AI, and combined modelling of systems with data has gained increasing importance in applications such as business process management. In addition, process mining techniques are nowadays used to automatically mine process models from event data, often without correctness guarantees. Thus verification techniques for linear and branching time properties are needed to ensure desired behavior.
Here we consider data-aware dynamic systems with arithmetic (DDSAs), which constitute a concise but expressive formalism of transition systems with linear arithmetic guards. We present a CTL\(^*\) model checking procedure for DDSAs that addresses a generalization of the classical verification problem, namely to compute conditions on the initial state, called witness maps, under which the desired property holds. Linear-time verification was shown to be decidable for specific classes of DDSAs where the constraint language or the control flow are suitably confined. We investigate several of these restrictions for the case of CTL\(^*\), with both positive and negative results: witness maps can always be found for monotonicity and integer periodicity constraint systems, but verification of bounded lookback systems is undecidable. To demonstrate the feasibility of our approach, we implemented it in an SMT-based prototype, showing that many practical business process models can be effectively analyzed.
This work is partially supported by the UNIBZ projects DaCoMan, QUEST, SMART-APP, VERBA, and WineId.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
The study of complex dynamic systems is a core research topic in AI, with a long tradition in formal methods. It finds application in a variety of domains, such as notably business process management (BPM), where studying the interplay between control-flow and data has gained momentum [9, 10, 24, 46]. Processes are increasingly mined by automatic techniques [1, 3] that lack any correctness guarantees, making verification even more important to ensure the desired behavior. However, the presence of data pushes verification to the verge of undecidability due to an infinite state space. This is aggravated by the use of arithmetic, in spite of its importance for practical applications [24]. Indeed, model checking of transition systems operating on numeric data variables with arithmetic constraints is known to be undecidable, as it is easy to model a two-counter machine.
In this work, we focus on the concise but expressive framework of data-aware dynamic systems with arithmetic (DDSAs) [28, 38], also known as counter systems [13, 20, 34]. Several classes of DDSAs have been isolated where specific verification tasks are decidable, notably reachability [6, 13, 29, 34] and linear-time model checking [14, 20, 22, 28, 38]. Fewer results are known about the case of branching time, except for flat counter systems [21], gap-order systems where constraints are restricted to the form \(x\,{-}\,y\,{\ge }\,2\) [8, 42], and systems with a nice symbolic valuation abstraction [31]. However, many processes in BPM and beyond fall into neither of these classes, as illustrated by the next example.
Example 1
The following DDSA \(\mathcal {B}\) models a management process for road fines by the Italian police [41]. It maintains seven so-called case data variables (i.e., variables local to each process instance, called “case” in the BPM literature): a (amount), t (total amount), d (dismissal code), p (points deducted), e (expenses), and time durations \( ds \), \( dp \), \( dj \). The process starts by creating a case, upon which the offender is notified within 90 days, i.e., 2160h (send fine). If the offender pays a sufficient amount t, the process terminates via silent actions \(\tau _1\), \(\tau _2\), or \(\tau _3\). For the less happy paths, the credit collection action is triggered if the payment was insufficient; while appeal to judge and appeal to prefecture reflect filed protests by the offender, which again need to respect certain time constraints.

This model was generated from real-life logs by automatic process mining techniques paired with domain knowledge [41], but without any correctness guarantee. For instance, data-aware soundness [4, 25] requires that the process can always reach a final state from any reachable configuration, expressed by the branching-time property \(\mathsf {A}\,\mathsf {G}\,\mathsf {E}\,\mathsf {F}\,\mathsf {end}\). This property is false here, as \(\mathcal {B}\) can get stuck in state \(\mathsf {p}_7\) if \(d\,{>}\,1\). In addition, process-specific linear-time properties are needed, e.g., that a send fine event is always followed by a sufficient payment (i.e., \(\langle \mathsf {send\,fine}\rangle \top \rightarrow \mathsf {F}\,\langle \mathsf {payment}\rangle (t \ge a)\), where \(\langle \alpha \rangle \) is the next operator via action \(\alpha \)).
This example highlights how both linear-time and branching-time verification are needed. In this paper, we present a CTL\(^*\) model checking algorithm for DDSAs, adopting a finite-trace semantics (CTL\(^*_f\)) [44] to reflect the nature of processes as in Example 1. More precisely, our approach can synthesize conditions on the initial variable assignment such that a given property \(\chi \) holds, called witness maps. If such a witness map can be found, it is in particular decidable what is more commonly called the verification problem, namely whether \(\chi \) is satisfied in a designated initial configuration. We derive an abstract criterion on the computability of witness maps, which is satisfied by two practical DDSA classes that restrict the constraint language to (a) monotonicity constraints [20, 25], i.e., variable-to-variable or variable-to-constant comparisons over \(\mathbb Q\) or \(\mathbb R\), and (b) integer periodicity constraints [18, 22], i.e., variable-to-constant and restricted variable-to-variable comparisons with modulo operators. On the other hand, we show that the verification problem is undecidable for bounded lookback systems [28], a control flow restriction that generalizes feedback freedom [14].
In summary, we make the following contributions:
-
1.
We present a model checking algorithm to generate a witness map for a given DDSA and CTL\(^*_f\) property;
-
2.
We prove an abstract termination criterion for this algorithm (Corollary 1);
-
3.
This result is used to show that witness maps can be effectively computed for monotonicity constraint and integer periodicity constraint systems;
-
4.
CTL\(^*_f\) verification is shown undecidable for bounded-lookback systems;
-
5.
We implemented our approach in the prototype ada using SMT solvers as backends and tested it on a range of business processes from the literature.
The paper is structured as follows: The rest of this section recapitulates related work. Section 2 compiles preliminaries about DDSAs and CTL\(^*_f\). Section 3 is dedicated to LTL with configuration maps, which is used by our model checking procedure in Sect. 4. Based on an abstract termination criterion, (un)decidability results for concrete DDSA classes are given in Sect. 5. We describe our implementation in Sect. 6. Complete proofs and further examples can be found in [27].
Related work. Verification of transition systems with arithmetic constraints, also called counter systems, has been studied in many areas including formal methods, database theory, and BPM. Reachability was proven decidable for a variety of classes, e.g., reversal-bounded counter machines [34], finite linear [29], flat [13], and gap-order constraint (GC) systems [6]. Considerable work has also been dedicated to linear-time verification: LTL model checking is decidable for monotonicity constraint (MC) systems [20]. LTL verification is also decidable for integer periodicity constraint (IPC) systems, even with past-time operators [18, 22]; and feedback-free systems, for an enriched constraint language referring to a read-only database [14]. DDSAs with MCs are also considered in [25] from the perspective of LTL with a finite-run semantics (LTL\(_f\)), giving a procedure to compute finite, faithful abstractions. LTL\(_f\) is moreover decidable for systems with the abstract finite summary property [28], which includes MC, GC, and systems with bounded lookback, where the latter generalizes feedback freedom.
Branching-time verification was less studied: Decidability of CTL\(^*\) was proven for flat counter systems with Presburger-definable loop iteration [21], even in NP [19]. Moreover, it was shown that CTL\(^*\) verification is decidable for pushdown systems, which can model counter systems with a single integer variable [30]. For integer relational automata (IRA), i.e., systems with constraints \(x\,{\ge }\,y\) or \(x\,{>}\,y\) and domain \(\mathbb Z\), CTL model checking is undecidable while the existential and universal fragments of CTL\(^*\) remain decidable [12]. For GC systems, which extend IRAs to constraints of the form \(x-y \ge k\), the existential fragment of CTL\(^*\) is decidable while the universal one is not [8]. A similar dichotomy holds for the EF and EG fragments of CTL [42]. A subclass of IRAs was considered in [7, 11], allowing only periodicity and monotonicity constraints. While satisfiability of CTL\(^*\) was proven decidable, model checking is not (as already shown in [12]), though it is decidable for CEF\(^+\) properties, an extension of the EF fragment [7]. In contrast, rather than restricting temporal operators, we show decidability of model checking under an abstract property of the DDSA and the verified property, which can be guaranteed by suitably constraining the constraint class or the control flow. More closely related is work by Gascon [31], who shows decidability of CTL\(^*\) model checking for DDSAs that admit a nice symbolic valuation abstraction, an abstract property which includes MC and IPC systems. The relationship between our decidability criterion and the property defined by Gascon will need further investigation. Another difference is that we here adopt a finite-path semantics for CTL\(^*\) as e.g. considered in [47], since for the analysis of real-world processes such as business processes it is sufficient to consider finite traces. On a high level, our method follows a common approach to CTL\(^*\): the verification property is processed bottom-up, computing solutions for each subproperty. These are then used to solve an equivalent linear-time problem [2, p. 429]. For the latter, we partially rely on earlier work [28].
2 Background
We start by defining the set of constraints over expressions of sort \( int \), \( rat \), or \( real \), with associated domains \(dom( int ) = \mathbb Z\), \(dom( rat ) = \mathbb Q\), and \(dom( real ) = \mathbb R\).
Definition 1
For a given set of sorted variables V, expressions \(e_s\) of sort s and atoms a are defined as follows:
where \(k_s\,{\in }\,dom(s)\), \(v_s\,{\in }\,V\) has sort s, and \(\equiv _n\) denotes equality modulo some \(n\,{\in }\,\mathbb N\). A constraint is then a quantifier-free boolean expression over atoms a.
The set of all constraints built from atoms over variables V is denoted by \(\mathcal {C}(V)\). For instance, \(x \ne 1\), \(x < y\,{-}\,z\), and \(x\,{-}\,y = 2 \wedge y \ne 1\) are valid constraints independent of the sort of \(\{x, y, z\}\), while \(u \equiv _3 v + 1\) is a constraint for integer variables u and v. We write \(\mathcal Var(\varphi )\) for the set of variables in a formula \(\varphi \). For an assignment \(\alpha \) with domain V that maps variables to values in their domain, and a formula \(\varphi \) we write \(\alpha \models \varphi \) if \(\alpha \) satisfies \(\varphi \).
We are thus in the realm of SMT with linear arithmetic, which is decidable and admits quantifier elimination [45]: if \(\varphi \) is a formula in \(\mathcal {C}(X \cup \{y\})\), thus having free variables \(X \cup \{y\}\), there is a quantifier-free \(\varphi '\) with free variables X that is equivalent to \(\exists y. \varphi \), i.e., \(\varphi '\,{\equiv }\,\exists y. \varphi \), where \(\equiv \) denotes logical equivalence.
2.1 Data-Aware Dynamic Systems with Arithmetic
From now on, V is a fixed, finite set of variables. We consider two disjoint, marked copies of V, denoted \(V^r = \{v^r \mid v\,{\in }\,V\}\) and \(V^w = \{v^w \mid v\,{\in }\,V\}\), called the read and write variables. They will refer to variable values before and after a transition, respectively. We also write \(\overline{V}\) for a vector that orders V in an arbitrary but fixed way, and \(\overline{V}^r\) and \(\overline{V}^w\) for vectors ordering \(V^r\) and \(V^w\) in the same way.
Definition 2
A DDSA \(\mathcal {B}=\langle B, b_{ I }, \mathcal {A}, T, B_F, V, \alpha _{ I }, guard \rangle \) is a labeled transition system where (i) B is a finite set of control states, with \(b_{ I }\,{\in }\,B\) the initial one; (ii) \(\mathcal {A}\) is a set of actions; (iii) \(T \subseteq B{\times }\mathcal {A}{\times }B\) is a transition relation; (iv) \(B_F \subseteq B\) are final states; (v) V is the set of process variables; (vi) \(\alpha _{ I }\) the initial variable assignment; (vii) \( guard :\mathcal {A}\mapsto \mathcal {C}(V^r \cup V^w)\) specifies executability constraints for actions over variables \(V^r\,{\cup }\,V^w\).
Example 2
We consider the following DDSAs \(\mathcal {B}\), \(\mathcal {B}_{ bl }\), and \(\mathcal {B}_{ ipc }\), where x, y have domain \(\mathbb Q\) and u, v, s have domain \(\mathbb Z\). Initial and final states have incoming arrows and double borders, respectively; \(\alpha _{ I }\) is not fixed for now.

Also the system in Example 1 represents a DDSA. If state b admits a transition to \(b'\) via action a, namely \((b, a, b')\in \varDelta \), this is denoted by  . A configuration of \(\mathcal {B}\) is a pair \((b, \alpha )\) where \(b\,{\in }\,B\) and \(\alpha \) is an assignment with domain V. A guard assignment is an assignment \(\beta \) with domain \(V^r \cup V^w\). For an action a, let \(write(a) = \mathcal Var( guard (a)) \cap V^w\). As defined next, an action a transforms a configuration \((b, \alpha )\) into a new configuration \((b', \alpha ')\) by updating the assignment \(\alpha \) according to the action guard, which can at the same time evaluate conditions on the current values of variables and write new values:
. A configuration of \(\mathcal {B}\) is a pair \((b, \alpha )\) where \(b\,{\in }\,B\) and \(\alpha \) is an assignment with domain V. A guard assignment is an assignment \(\beta \) with domain \(V^r \cup V^w\). For an action a, let \(write(a) = \mathcal Var( guard (a)) \cap V^w\). As defined next, an action a transforms a configuration \((b, \alpha )\) into a new configuration \((b', \alpha ')\) by updating the assignment \(\alpha \) according to the action guard, which can at the same time evaluate conditions on the current values of variables and write new values:
Definition 3
A DDSA \(\mathcal {B}\,{=}\,\langle B, b_{ I }, \mathcal {A}, T, B_F, V, \alpha _{ I }, guard \rangle \) admits a step from configuration \((b, \alpha )\) to \((b', \alpha ')\) via action a, denoted  , if
, if  , \(\alpha '(v) = \alpha (v)\) for all \(v \in V\setminus write(a)\), and the guard assignment \(\beta \) given by \(\beta (v^r) = \alpha (v)\) and \(\beta (v^w) = \alpha '(v)\) for all \(v \in V\), satisfies \(\beta \models guard (a)\).
, \(\alpha '(v) = \alpha (v)\) for all \(v \in V\setminus write(a)\), and the guard assignment \(\beta \) given by \(\beta (v^r) = \alpha (v)\) and \(\beta (v^w) = \alpha '(v)\) for all \(v \in V\), satisfies \(\beta \models guard (a)\).
For instance, for \(\mathcal {B}\) in Example 2 and initial assignment \(\alpha _{ I }(x) = \alpha _{ I }(y) = 0\), the initial configuration admits a step  with \(\beta (x^r) = \beta (x^w) = \beta (y^r) = 0\) and \(\beta (y^w) = 3\).
with \(\beta (x^r) = \beta (x^w) = \beta (y^r) = 0\) and \(\beta (y^w) = 3\).
A run \(\rho \) of a DDSA \(\mathcal {B}\) of length n from configuration \((b, \alpha )\) is a sequence of steps  . We also associate with \(\rho \) the symbolic run
. We also associate with \(\rho \) the symbolic run  where state and action sequences are recorded without assignments, and say that \(\sigma \) is the abstraction of \(\rho \) (or, \(\sigma \) abstracts \(\rho \)). For some \(m<n\), \(\sigma |_{m}\) denotes the prefix of \(\sigma \) that has m steps.
where state and action sequences are recorded without assignments, and say that \(\sigma \) is the abstraction of \(\rho \) (or, \(\sigma \) abstracts \(\rho \)). For some \(m<n\), \(\sigma |_{m}\) denotes the prefix of \(\sigma \) that has m steps.
2.2 History Constraints
In this section, we fix a DDSA \(\mathcal {B}= \langle B, b_{ I }, \mathcal {A}, T, B_F, V, \alpha _{ I }, guard\rangle \). We aim to build an abstraction of \(\mathcal {B}\) that covers the (potentially infinite) set of configurations by finitely many nodes of the form \((b,\varphi )\), where \(b \,{\in }\,B\) is a control state and \(\varphi \) a formula that expresses conditions on the variables V. A state \((b,\varphi )\) thus represents all configurations \((b,\alpha )\) s.t. \(\alpha \models \varphi \). To express how such a formula \(\varphi \) is modified by executing an action, let the transition formula of action a be \(\varDelta _{a}(\overline{V}^r, \overline{V}^w)\,{=}\, guard (a) \wedge \bigwedge _{v\in V\setminus write (a)} v^{w}\,{=}\,v^{r}\). This states conditions on variables before and after executing a: \( guard (a)\) must hold and the values of all variables that are not written are propagated by inertia. We write \(\varDelta _{a}(\overline{X}, \overline{Y})\) for the formula obtained from \(\varDelta _{a}\) by replacing \(\overline{V}^r\) by \(\overline{X}\) and \(\overline{V}^w\) by \(\overline{Y}\). Let a variable vector \(\overline{U}\) be a fresh copy of \(\overline{V}\) if it has the same length as \(|\overline{V}|\) and \(U\cap V = \emptyset \). To mimic steps on the abstract level, we define the following \( update \) function:
Definition 4
For a formula \(\varphi \) with free variables V and action a, \( update (\varphi , a) = \exists \overline{U}. \varphi (\overline{U}) \wedge \varDelta _a(\overline{U}, \overline{V})\), where \(\overline{U}\) is a fresh copy of \(\overline{V}\).
Our approach will generate formulas of a special shape called history constraints [28], obtained by iterated \( update \) operations in combination with a sequence of verification constraints \(\overline{\vartheta }\). Intuitively, the latter depends on the verification property. For now it suffices to consider \(\overline{\vartheta }\) an arbitrary sequence of constraints with free variables V. Its prefix of length k is denoted by \(\overline{\vartheta }|_k\). We need a fixed set of placeholder variables \(V_0\) disjoint from V, and assume an injective variable renaming \(\nu :V\,{\mapsto }\,V_0\). Let \(\varphi _\nu \) be the formula \(\varphi _\nu = \bigwedge _{v\in V} v \,{=}\,\nu (v)\).
Definition 5
For a symbolic run  , and verification constraint sequence \(\overline{\vartheta }= \langle \vartheta _0,\dots , \vartheta _n\rangle \), the history constraint \(h(\sigma , \overline{\vartheta })\) is given by \(h(\sigma , \overline{\vartheta }) \,{=}\,\varphi _\nu \wedge \vartheta _0\) if \(n\,{=}\,0\), and \(h(\sigma , \overline{\vartheta }) \,{=}\, update (h(\sigma |_{n-1}, \overline{\vartheta }|_{n-1}), a_{n}) \wedge \vartheta _n\) if \(n\,{>}\,0\).
, and verification constraint sequence \(\overline{\vartheta }= \langle \vartheta _0,\dots , \vartheta _n\rangle \), the history constraint \(h(\sigma , \overline{\vartheta })\) is given by \(h(\sigma , \overline{\vartheta }) \,{=}\,\varphi _\nu \wedge \vartheta _0\) if \(n\,{=}\,0\), and \(h(\sigma , \overline{\vartheta }) \,{=}\, update (h(\sigma |_{n-1}, \overline{\vartheta }|_{n-1}), a_{n}) \wedge \vartheta _n\) if \(n\,{>}\,0\).
Thus, history constraints are formulas with free variables \(V \cup V_0\). Satisfying assignments for history constraints are closely related to assignments in runs:Footnote 1
Lemma 1
For a symbolic run  and \(\overline{\vartheta }= \langle \vartheta _0,\dots , \vartheta _n\rangle \), \(\smash [t]{h(\sigma ,\overline{\vartheta })}\) is satisfied by assignment \(\alpha \) with domain \(V\,{\cup }\,V_0\) iff \(\sigma \) abstracts a run
and \(\overline{\vartheta }= \langle \vartheta _0,\dots , \vartheta _n\rangle \), \(\smash [t]{h(\sigma ,\overline{\vartheta })}\) is satisfied by assignment \(\alpha \) with domain \(V\,{\cup }\,V_0\) iff \(\sigma \) abstracts a run  such that (i) \(\alpha _0(v) = \alpha (\nu (v))\), and (ii) \(\alpha _n(v) = \alpha (v)\) for all \(v\in V\), and (iii) \(\alpha _i \models \vartheta _i\) for all i, \(0\le i \le n\).
such that (i) \(\alpha _0(v) = \alpha (\nu (v))\), and (ii) \(\alpha _n(v) = \alpha (v)\) for all \(v\in V\), and (iii) \(\alpha _i \models \vartheta _i\) for all i, \(0\le i \le n\).
2.3 CTL\(_f^*\)
For a DDSA \(\mathcal {B}\) as above, we consider the following verification properties:
Definition 6
CTL\(^*_f\) state formulas \(\chi \) and path formulas \(\psi \) are defined by the following grammar, for constraints \(c \,{\in }\,\mathcal {C}(V)\) and control states \(b\,{\in }\,B\):
We use the usual abbreviations \(\mathsf {F}\,\psi = \top \mathrel {\mathsf {U}}\psi \), \(\chi _1 \vee \chi _2 = \lnot (\lnot \chi _1 \wedge \lnot \chi _2)\), and \(\mathsf {A}\,\psi = \lnot \mathsf {E}\,\lnot \psi \). To simplify the presentation, we do not explicitly treat next state operators \(\langle a\rangle \) via a specific action a, as used in Example 1, though this would be possible (cf. [28]). However, such an operator can be encoded by adding a fresh data variable x to V, the conjunct \(x^w\,{=}\,1\) to \( guard (a)\), and \(x^w\,{=}\,0\) to all other guards, and replacing \(\langle a\rangle \psi \) in the verification property by \(\mathsf {X}\,(\psi \wedge x=1)\).
The maximal number of nested path quantifiers in a formula \(\psi \) is called the quantifier depth of \(\psi \), denoted by \( qd (\psi )\). We adopt a finite path semantics for CTL\(^*\) [44]: For a control state \(b\in B\) and a state assignment \(\alpha \), let \( FRuns (b,\alpha )\) be the set of final runs  such that \(b_n \in F\) is a final state. The i-th configuration \((b_i, \alpha _i)\) in \(\rho \) is denoted by \(\rho _i\).
such that \(b_n \in F\) is a final state. The i-th configuration \((b_i, \alpha _i)\) in \(\rho \) is denoted by \(\rho _i\).
Definition 7
The semantics of CTL\(^*_f\) is inductively defined as follows. For a DDSA \(\mathcal {B}\) with configuration \((b,\alpha )\), state formulas \(\chi \), \(\chi '\), and path formulas \(\psi \), \(\psi '\):
where \(\rho \models \psi \) iff \(\rho ,0 \models \psi \) holds, and for a run \(\rho \) of length n and all i, \(0\,{\le }\,i\,{\le }\,n\):
Instead of simply checking whether the initial configuration of a DDSA \(\mathcal {B}\) satisfies a CTL\(^*_f\) property \(\chi \), we try to determine, for every state \(b \in B\), which constraints on variables need to hold in order to satisfy \(\chi \). As the number of configurations \((b,\alpha )\) of a DDSA \(\mathcal {B}\) is usually infinite, configuration sets cannot be enumerated explicitly. Instead, we represent a set of configurations as a configuration map \(K:B \mapsto {\mathcal {C}(V)}\) that associates with every control state \(b \in B\) a formula \(K(b) \in \mathcal {C}(V)\), representing all configurations \((b,\alpha )\) such that \(\alpha \models K(b)\).
We now define when a configuration captures the maximal set of configurations in which a formula \(\chi \) holds. We call these witness maps.
Definition 8
For a DDSA \(\mathcal {B}\) and state formula \(\chi \), a configuration map K is a witness map if it holds that \((b,\alpha ) \models \chi \) iff \(\alpha \models K(b)\), for all \(b\,{\in }\,B\) and all \(\alpha \).
For instance, for \(\mathcal {B}\) from Example 2 and \(\chi _1 = \mathsf {A}\,\mathsf {G}\,(x\,{\ge }\,2)\), a witness map is given by \(K = \{ \mathsf {b}_1 \mapsto \bot ,\ \mathsf {b}_2 \mapsto x\,{\ge }\,2\wedge y\,{\ge }\,2,\ \mathsf {b}_3 \mapsto x \ge 2\}\). For \(\chi _2 \models \mathsf {E}\,\mathsf {X}\,(\mathsf {A}\,\mathsf {G}\,(x \ge 2))\), a solution is \(K' = \{ \mathsf {b}_1 \mapsto x\,{\ge }\,2,\ \mathsf {b}_2 \mapsto y\,{\ge }\,2 ,\ \mathsf {b}_3 \mapsto \bot \}\). As \(\mathsf {b}_1\) is the initial state, \(\mathcal {B}\) satisfies \(\chi _2\) with every initial assignment that sets \(\alpha _{ I }(x) \ge 2\).
In this paper we address the problem of finding a witness map for \(\mathcal {B}\) and \(\chi \). Note that a witness map in particular allows to decide what is commonly called the verification problem, namely to check whether \((b_{ I },\alpha _{ I }) \models \chi \) holds, by testing \(\alpha _{ I }\models K(b_{ I })\). It remains to investigate whether there exist a DDSA \(\mathcal {B}\) and \(\chi \) for which no witness map exists, as the configuration set satisfying \(\chi \) is not finitely representable. Even if it exists, finding it is in general undecidable. However, in this paper we identify DDSA classes where a witness map can always be found.
3 LTL with Configuration Maps
Following a common approach to CTL\(^*\) verification, our technique processes the property \(\chi \) bottom-up, computing solutions for each subformula \(\mathsf {E}\,\psi \), before solving a linear-time model checking problem \(\chi '\) in which the solutions to subformulas appear as atoms. Given our representation of sets of configurations, we use LTL formulas where atoms are configuration maps, and denote this specification language by \(\smash {LTL _f^\mathcal {B}} \). For a given DDSA \(\mathcal {B}\), it is formally defined as follows:
where \(K\in \mathcal {K}_\mathcal {B}\), for \(\mathcal {K}_\mathcal {B}\) is the set of configuration maps for \(\mathcal {B}\).
Definition 9
A run \(\rho \) of length n satisfies an \(\smash {LTL _f^\mathcal {B}} \) formula \(\psi \), denoted \(\rho \models _{\mathcal {K}}\psi \), iff \(\rho ,0 \models _{\mathcal {K}}\psi \) holds, where for all i, \(0 \le i \le n\):
Our approach to \(\smash {LTL _f^\mathcal {B}} \) verification proceeds along the lines of the LTL\(_f\) procedure from [28], with the difference that simple constraint atoms are replaced by configuration maps. In order to express the requirements on a run of a DDSA \(\mathcal {B}\) to satisfy an \(\smash {LTL _f^\mathcal {B}} \) formula \(\chi \), we use a nondeterministic automaton (NFA) \({\mathcal {N}}_{\psi }= (Q, \varSigma , \varrho , q_0, Q_F)\), where the states Q are a set of subformulas of \(\psi \), \(\varSigma \,{=}\, 2^{\mathcal {K}_\mathcal {B}}\) is the alphabet, \(\varrho \) is the transition relation, \(q_0 \in Q\) is the initial state, and \(Q_F\subseteq Q\) is the set of final states. The construction of \({\mathcal {N}}_{\psi }\) is standard [15, 28], treating configuration maps for the time being as propositions; but for completeness it is described in [27, Appendix C]. For instance, for a configuration map K, \(\psi = \mathsf {F}\,K\) corresponds to the NFA
 and \(\psi ' = \mathsf {X}\,K\) to
and \(\psi ' = \mathsf {X}\,K\) to
 . (For simplicity, edges labels \(\{K\}\) are shown as K, and edge labels \(\emptyset \) are omitted.)
. (For simplicity, edges labels \(\{K\}\) are shown as K, and edge labels \(\emptyset \) are omitted.)
For \(w_i\in \varSigma \), i.e., \(w_i\) is a set of configuration maps, \(w_i(b)\) denotes the formula \(\bigwedge _{K\in w}K(b)\). Moreover, for \(w = {w_0},\dots ,{w_{n}}\in \varSigma ^*\) and a symbolic run  , let \(w\otimes \sigma \) denote the sequence of formulas \(\langle w_0(b_0), \dots , w_{n}(b_n)\rangle \), i.e., the component-wise application of w to the control states of \(\sigma \). A word \({w_0},\dots ,{w_{n}}\in \varSigma ^*\) is consistent with a run
, let \(w\otimes \sigma \) denote the sequence of formulas \(\langle w_0(b_0), \dots , w_{n}(b_n)\rangle \), i.e., the component-wise application of w to the control states of \(\sigma \). A word \({w_0},\dots ,{w_{n}}\in \varSigma ^*\) is consistent with a run  if \(\alpha _i \models w_i(b_i)\) for all i, \(0\,{\le }\,i\,{\le }\,n\). The key correctness property of \({\mathcal {N}}_{\psi }\) is the following (cf. [28, Lemma 4.4], and see [27] for the proof adapted to \(\smash {LTL _f^\mathcal {B}} \)):
if \(\alpha _i \models w_i(b_i)\) for all i, \(0\,{\le }\,i\,{\le }\,n\). The key correctness property of \({\mathcal {N}}_{\psi }\) is the following (cf. [28, Lemma 4.4], and see [27] for the proof adapted to \(\smash {LTL _f^\mathcal {B}} \)):
Lemma 2
\({\mathcal {N}}_{\psi }\) accepts a word that is consistent with a run \(\rho \) iff \(\rho \models _{\mathcal {K}}\psi \).
Product Construction. As a next step in our verification procedure, given a control state b of \(\mathcal {B}\), we aim to find (a symbolic representation of) all configurations \((b,\alpha )\) that satisfy an \(\smash {LTL _f^\mathcal {B}} \) formula \(\psi \). To that end, we combine \({\mathcal {N}}_{\psi }\) with \(\mathcal {B}\) to a cross-product automaton \(\smash {\mathcal {N}^\psi _{\mathcal {B},b}}\). For technical reasons, when performing the product construction, the steps in \(\mathcal {B}\) need to be shifted by one with respect to the steps in \({\mathcal {N}}_{\psi }\). Hence, given \(b\,{\in }\,B\), let \(\mathcal {B}_b\) be the DDSA obtained from \(\mathcal {B}\) by adding a dummy initial state \(\smash {\underline{b}}\), so that \(\mathcal {B}_b\) has state set \(\smash {B' = B\cup \{\underline{b}\}}\) and transition relation \(\smash {T' = T \cup \{(\underline{b}, a_0, b)\}}\) for a fresh action \(a_0\) with \( guard (a_0) = \top \).
Definition 10
The product automaton \(\smash {\mathcal {N}^\psi _{\mathcal {B},b}}\) is defined for an \(\smash {LTL _f^\mathcal {B}} \) formula \(\psi \), a DDSA \(\mathcal {B}\), and a control state \(b\in B\). Let \(\mathcal {B}_b = \langle B', \underline{b}, \mathcal {A}, T', B_F, V, \alpha _{ I }, guard \rangle \) and \({\mathcal {N}}_{\psi }\) as above. Then \(\smash {\mathcal {N}^\psi _{\mathcal {B},b}=(P, R, p_0, P_F)}\) is as follows:
-
\(P \subseteq B' \times Q \times \mathcal {C}(V\cup V_0)\), i.e., states in P are triples \((b, q, \varphi )\) such that
-
the initial state is \(p_0=(\underline{b}, q_0, \varphi _\nu )\);
-
if
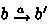 in \(T'\),
in \(T'\),  in \({\mathcal {N}}_{\psi }\), and \( update (\varphi , a) \wedge w(b')\) is satisfiable, there is a transition
in \({\mathcal {N}}_{\psi }\), and \( update (\varphi , a) \wedge w(b')\) is satisfiable, there is a transition  in R such that \(\varphi ' \equiv update (\varphi , a) \wedge w(b')\);
in R such that \(\varphi ' \equiv update (\varphi , a) \wedge w(b')\); -
\((b',q', \varphi ')\) is in the set of final states \(P_F \subseteq P\) iff \(b'\in B_F\), and \(q'\in Q_F\).
Example 3
Consider the DDSA \(\mathcal {B}\) from Example 2, and let \(K = \{ \mathsf {b}_1 \mapsto \bot ,\ \mathsf {b}_2 \mapsto x\,{\ge }\,2 \wedge y\,{\ge }\,2,\ \mathsf {b}_3 \mapsto x\,{\ge }\,2\}\). The property \(\psi = \mathsf {X}\,K\) is captured by the NFA
 . The product automata \(\smash {\mathcal {N}^\psi _{\mathcal {B},\mathsf {b}_1}}\) and \(\smash {\mathcal {N}^\psi _{\mathcal {B},\mathsf {b}_2}}\) are as follows:
. The product automata \(\smash {\mathcal {N}^\psi _{\mathcal {B},\mathsf {b}_1}}\) and \(\smash {\mathcal {N}^\psi _{\mathcal {B},\mathsf {b}_2}}\) are as follows:

where the shaded nodes are final. The formulas in nodes were obtained by applying quantifier elimination to the formulas built using \( update \) according to Definition 10. \(\smash {\mathcal {N}^\psi _{\mathcal {B},\mathsf {b}_3}}\) consists only of the dummy transition and has no final states.
Definition 10 need not terminate if infinitely many non-equivalent formulas occur in the construction. In Sect. 4 we will identify a criterion that guarantees termination. First, we state the key correctness property, which lifts [28, Theorem 4.7] to LTL with configuration maps. Its proof is similar to the respective result in [28], and can be found in [27].
Theorem 1
Let \(\psi \,{\in }\,\smash {LTL _f^\mathcal {B}} \) and \(b\,{\in }\,B\) such that there is a finite product automaton \(\smash {\mathcal {N}_{\mathcal {B},b}^\psi }\). Then there is a final run \(\rho :(b,\alpha _0) \rightarrow ^* (b_F, \alpha _F)\) of \(\mathcal {B}\) such that \(\rho \models _{\mathcal {K}}\psi \), iff \(\smash {\mathcal {N}_{\mathcal {B},b}^\psi }\) has a final state \((b_F, q_F, \varphi )\) for some \(q_F\) and \(\varphi \) such that \(\varphi \) is satisfied by assignment \(\gamma \) with \(\gamma (\overline{V_0}) \,{=}\,\alpha _0(\overline{V})\) and \(\gamma (\overline{V}) \,{=}\,\alpha _F(\overline{V})\).
Thus, witnesses for \(\psi \) correspond to paths to final states in the product automaton: e.g., in \(\smash {\mathcal {N}^\psi _{\mathcal {B},\mathsf {b}_1}}\) in Example 3 the formula in the left final node is satisfied by \(\gamma (x_0) = \gamma (x) = \gamma (y) = 3\) and \(\gamma (y_0) = 0\). For \(\alpha _0\) and \(\alpha _2\) such that \(\alpha _0(\overline{V}) = \gamma (\overline{V}_0) = \{x\mapsto 3, y\mapsto 0\}\) and \(\alpha _2(\overline{V}) = \gamma (\overline{V})= \{x\mapsto 3, y\mapsto 3\}\) there is a witness run for \(\psi \) from \((\mathsf {b}_1, \alpha _0)\) to \((\mathsf {b}_1, \alpha _2)\), e.g.,  .
.
4 Model Checking Procedure
Using the results of Sect. 3, we define a model checking procedure, shown in Fig. 1. First, we explain the tasks achieved by the three mutually recursive functions:
\(\bullet ~\) \( checkState (\chi )\) returns a configuration map representing the set of configurations that satisfy a state formula \(\chi \). In the base cases, it returns a function that checks the respective condition, for boolean operators we recurse on the arguments, and for a formula \(\mathsf {E}\,\psi \) we proceed to the \( checkPath \) procedure.
\(\bullet ~\) \( checkPath (\psi )\) returns a configuration map K that represents all configurations from which a path satisfying \(\psi \) exists. First, \( toLTL _\mathcal {K}\) is used to obtain an equivalent \(\smash {LTL _f^\mathcal {B}} \) formula \(\psi '\) (which entails the computation of solutions for all subproperties \(\mathsf {E}\,\eta \)). Then solution K is constructed as follows: For every control state b, we build the product automaton \(\smash {\mathcal {N}^{\psi '}_{\mathcal {B},b}}\), and collect the set \(\varPhi _F\) of formulas in final states. Every \(\varphi \in \varPhi _F\) encodes runs from b to a final state of \(\mathcal {B}\) that satisfy \(\psi '\). The variables \(\overline{V_0}\) and \(\overline{V}\) in \(\varphi \) act as placeholders for the initial and the final values of the runs, respectively. We rename variables in \(\varphi \) to use \(\overline{V}\) at the start and \(\overline{U}\) at the end, we quantify existentially over \(\overline{U}\) (as the final valuation is irrelevant), and take the disjunction over all \(\varphi \in \varPhi _F\). The resulting formula \(\varphi '\) encodes all final runs from b that satisfy \(\psi '\), so we set \(K(b):=\varphi '\).
\(\bullet ~\) \( toLTL _\mathcal {K}(\psi )\) computes an \(\smash {LTL _f^\mathcal {B}} \) formula equivalent to a path formula \(\psi \). To this end, it performs two kinds of replacements in \(\psi \): (a) \(\top \), \(b\,{\in }\,B\), and constraints c are represented as configuration maps; and (b) subformulas \(\mathsf {E}\,\eta \) are replaced by their solutions \(K_{\mathsf {E}\eta }\), which are computed by a recursive call to \( checkPath \).
To represent the base cases of formulas as configuration maps in Fig. 1, we define \(K_\top :=(\lambda \_.\,\top )\), \(K_b := (\lambda b'.\,b \,{=}\,b'\,?\,\top : \bot )\) for all \(b\,{\in }\,B\), and \(K_c := (\lambda \_.\,c)\) for constraints c. We also write \(\lnot K\) for \((\lambda b. \lnot K(b))\) and \(K \wedge K'\) for \((\lambda b. K(b) \wedge K'(b))\). The next example illustrates the approach.
Example 4
Consider \(\chi \,{=}\,\mathsf {E}\,\mathsf {X}\,(\mathsf {A}\,\mathsf {G}\,(x\,{\ge }\,2))\) and the DDSA \(\mathcal {B}\) in Example 2. To get a solution \(K_1\) to \( checkState (\chi ) = checkPath (\psi _1)\) for \(\psi _1 = \mathsf {X}\,(\mathsf {A}\,\mathsf {G}\,(x\,{\ge }\,2))\), we first compute an equivalent \(\smash {LTL _f^\mathcal {B}} \) formula \(\psi _1' = \mathsf {X}\,K_2\), where \(K_2\) is a solution to \(\mathsf {A}\,\mathsf {G}\,(x\,{\ge }\,2) \equiv \lnot \mathsf {E}\,\mathsf {F}\,(x\,{<}\,2)\). To this end, we run \( checkPath (\psi _2)\) for \(\psi _2 = \mathsf {F}\,(x\,{<}\,2)\), which is represented in \(\smash {LTL _f^\mathcal {B}} \) as \(\psi _2' = \mathsf {F}\,(K_{x<2})\) with NFA
 . Next, \( checkPath \) builds \(\smash {\mathcal {N}^{\psi _2'}_{\mathcal {B},b}}\) for all states b. For instance, for \(\mathsf {b}_2\) we get:
. Next, \( checkPath \) builds \(\smash {\mathcal {N}^{\psi _2'}_{\mathcal {B},b}}\) for all states b. For instance, for \(\mathsf {b}_2\) we get:

where dashed arrows indicate transitions to non-final sink states. For \(\overline{U} = \langle \hat{x}, \hat{y}\rangle \), and the formulas \(\varphi _1\), \(\varphi _2\), and \(\varphi _3\) in final nodes, we compute
so that \(K_3:= checkPath (\psi _2)\) sets \(K_3(\mathsf {b}_2) = \bigvee _{i=1}^3 \exists \overline{U}.\, \varphi _i(\overline{V}, \overline{U}) \equiv x\,{<}\,2 \vee y\,{<}\,2\). For reasons of space, the constructions for \(\mathsf {b}_1\) and \(\mathsf {b}_3\) are shown in [27, Appendix B]; we obtain \(K_3(\mathsf {b}_1) = \top \) and \(K_3(\mathsf {b}_3) = x < 2\). By negation, the solution \(K_2\) to \(\mathsf {A}\,\mathsf {G}\,(x \ge 2)\) is \(K_2 = \lnot K_3 = \{ \mathsf {b}_1 \mapsto \bot ,\ \mathsf {b}_2 \mapsto x \ge 2 \wedge y \ge 2,\ \mathsf {b}_3 \mapsto x \ge 2\}\). Now we can proceed with \( checkPath (\psi _1)\). The NFA and product automata for \(\psi _1' = \mathsf {X}\,K_2\) are as shown in Example 3 and in a similar way as above we obtain the solution \(K_1\) for \(\mathsf {E}\,\mathsf {X}\,\mathsf {A}\,\mathsf {G}\,(x \ge 2)\) as \(K_1 = \{ \mathsf {b}_1 \mapsto x\,{\ge }\,2,\ \mathsf {b}_2 \mapsto y\,{\ge }\,2 ,\ \mathsf {b}_3 \mapsto \bot \}\). Thus, \(\mathcal {B}\) satisfies the property for any initial assignment \(\alpha _{ I }\) with \(\alpha _{ I }(x) \ge 2\).
Next we prove correctness of \( checkState (\chi )\) under the condition that it is defined, i.e., all required product automata are finite. First we state our main result, but before giving its proof we show helpful properties of \( toLTL _\mathcal {K}\) and \( checkPath \).
Theorem 2
For every configuration \((b,\alpha )\) of the DDSA \(\mathcal {B}\) and every state property \(\chi \), if \( checkState (\chi )\) is defined then \((b,\alpha ) \models \chi \) iff \(\alpha \models checkState (\chi )(b)\).
Lemma 3
Let \(\psi \) be a path formula with \( qd (\psi ) \,{=}\,k\). Suppose that for all configurations \((b,\alpha )\) and path formulas \(\psi '\) with \( qd (\psi ')\,{<}\,k\), there is a \(\rho ' \in FRuns (b,\alpha )\) with \(\rho ' \models \psi '\) iff \(\alpha \models checkPath (\psi ')(b)\). Then \(\rho \models \psi \) iff \(\rho \models _{\mathcal {K}} toLTL _\mathcal {K}(\psi )\).
Proof
(sketch). By induction on \(\psi \). The base cases are by the definitions of \(K_\top \), \(K_b\), and \(K_c\). In the induction step, if \(\psi \,{=}\,\mathsf {E}\,\psi '\) then \(\rho \models \psi \) iff \(\exists \rho ' \,{\in }\, FRuns (b_0, \alpha _0)\) with \(\rho ' \models \psi '\), for \(\rho _0 \,{=}\,(b_0, \alpha _0)\). As \( qd (\psi ')\,{<}\, qd (\psi )\), this holds by assumption iff \(\alpha _0 \models checkPath (\psi ')(b_0)\). This is equivalent to \(\rho \models _{\mathcal {K}} toLTL _\mathcal {K}(\psi ) = checkPath (\psi ')\). All other cases are by the induction hypothesis and Definitions 7 and 9.
Lemma 4
If \(\psi ' = toLTL _\mathcal {K}(\psi )\) such that for all runs \(\rho \) it is \(\rho \models \psi \) iff \(\rho \models _{\mathcal {K}}\psi '\), there is a run \(\rho \,{\in }\, FRuns (b,\alpha )\) with \(\rho \models \psi \) iff \(\alpha \models checkPath (\psi )(b)\).
Proof
(\(\Longrightarrow \)) Suppose there is a run \(\rho \,{\in }\, FRuns (b,\alpha )\) with \(\rho \models \psi \), so \(\rho \) is of the form \((b,\alpha )\rightarrow ^* (b_F,\alpha _F)\) for some \(b_F \in B_F\). By assumption, this implies \(\rho \models _{\mathcal {K}}\psi '\), so that by Theorem 1, \(\smash {\mathcal {N}_{\mathcal {B},b}^{\psi '}}\) has a final state \((b_F, q_F, \varphi )\) where \(\varphi \) is satisfied by an assignment \(\gamma \) with domain \(V\cup V_0\) such that \(\gamma (\overline{V_0}) \,{=}\,\alpha (\overline{V})\) and \(\gamma (\overline{V}) \,{=}\,\alpha _F(\overline{V})\). By definition, \( checkPath (\psi )(b)\) contains a disjunct \(\exists \overline{U}.\,\varphi (\overline{V}, \overline{U})\). As \(\gamma \) satisfies \(\varphi \) and \(\gamma (\overline{V_0}) \,{=}\,\alpha (\overline{V})\), \(\alpha \models checkPath (\psi )(b)\). (\(\Longleftarrow \)) If \(\alpha \models checkPath (\psi )(b)\), by definition of \( checkPath \) there is a formula \(\varphi \) such that \(\alpha \models \exists \overline{U}.\,\varphi (\overline{V}, \overline{U})\) and \(\varphi \) occurs in a final state \((b_F, q_F, \varphi )\) of \(\smash {\mathcal {N}_{\mathcal {B},b}^{\psi '}}\). Hence there is an assignment \(\gamma \) with domain \(V\cup V_0\) and \(\gamma (\overline{V_0}) \,{=}\,\alpha (\overline{V})\) such that \(\gamma \models \varphi \). By Theorem 1, there is a run \(\rho :(b, \alpha ) \rightarrow ^* (b_F, \alpha _F)\) such that \(\rho \models _{\mathcal {K}}\psi '\). By the assumption, we have \(\rho \models \psi \). \(\square \)
At this point the main theorem can be proven:
Proof
(of Theorem 2). We first show (\(\star \)): for any path formula \(\psi \), there is a run \(\rho \in FRuns (b,\alpha )\) with \(\rho \models \psi \) iff \(\alpha \models checkPath (\psi )(b)\). The proof is by induction on \( qd (\psi )\). If \(\psi \) contains no path quantifiers, Lemma 3 implies that \(\rho \models \psi \) iff \(\rho \models _{\mathcal {K}} toLTL _\mathcal {K}(\psi )\) for all runs \(\rho \), so (\(\star \)) follows from Lemma 4. In the induction step, we conclude from Lemma 3, using the induction hypothesis of (\(\star \)) as assumption, that \(\rho \models \psi \) iff \(\rho \models _{\mathcal {K}} toLTL _\mathcal {K}(\psi )\) for all runs \(\rho \). Again, (\(\star \)) follows from Lemma 4.
The theorem is then shown by induction on \(\chi \): The base cases \(\top \), \(b'\,{\in }\,B\), \(c\,{\in }\,\mathcal {C}\) are easy to check, and for properties of the form \(\lnot \chi '\) and \(\chi _1 \wedge \chi _2\) the claim follows from the induction hypothesis and the definitions. Finally, for \(\chi = \mathsf {E}\,\psi \), \((b,\alpha ) \models \chi \) iff there is a run \(\rho \in FRuns (b,\alpha )\) such that \(\rho \models \psi \). By (\(\star \)) this is the case iff \(\alpha \models checkPath (\psi )(b) = checkState (\chi )(b)\). \(\square \)
Termination. We next show that the formulas generated in our procedure all have a particular shape, to obtain an abstract termination result. For a set of formulas \(\varPhi \subseteq {\mathcal {C}(V)}\) and a symbolic run \(\sigma \), let a history constraint \(h(\sigma ,\overline{\vartheta })\) be over basis \(\varPhi \) if \(\overline{\vartheta }= \langle \vartheta _0,\dots , \vartheta _n\rangle \) and for all i, \(1\,{\le }\,i\,{\le }\,n\), there is a subset \(T_i \subseteq \varPhi \) s.t. \(\vartheta _i = \bigwedge T_i\). Moreover, for a set of formulas \(\varPhi \), let \(\varPhi ^\pm = \varPhi \cup \{ \lnot \varphi \mid \varphi \in \varPhi \}\).
Definition 11
For a DDSA \(\mathcal {B}\), a constraint set \(\mathcal {C}\) over free variables V, and \(k\,{\ge }\, 0\), the formula sets \(\varPhi _k\) are inductively defined by \(\varPhi _0 = \mathcal {C}\cup \{\top , \bot \}\) and
where \(\mathcal {H}_k\) is the set of all history constraints of \(\mathcal {B}\) with basis \(\bigcup _{i\le k}\varPhi _{i}^\pm \).
Note that formulas in \(\varPhi _{k}\) have free variables V, while those in \(\mathcal {H}_k\) have free variables \(V_0 \cup V\). We next show that these sets correspond to the formulas generated by our procedure, if all constraints in the verification property are in \(\mathcal {C}\).
Lemma 5
Let \(\mathsf {E}\,\psi \) have quantifier depth k, \(\psi ' = toLTL _\mathcal {K}(\psi )\), and \(\smash {\mathcal {N}_{\mathcal {B},b}^{\psi '}}\) be a constraint graph constructed in \( checkPath (\psi )\) for some \(b\in B\). Then,
-
(1)
for all nodes \((b', q, \varphi )\) in \(\smash {\mathcal {N}_{\mathcal {B},b}^{\psi '}}\) there is some \(\varphi ' \in \mathcal {H}_k\) such that \(\varphi \equiv \varphi '\),
-
(2)
\( checkPath (\psi )(b)\) is equivalent to a formula in \(\varPhi _{k+1}\).
The statements are proven by induction on k, using the results on the product construction ([27, Lemma 6]). From part (1) of this lemma and Theorem 2 we thus obtain an abstract criterion for decidability that will be useful in the next section:
Corollary 1
For a DDSA \(\mathcal {B}\) as above and a state formula \(\chi \), if \(\mathcal {H}_j(b)\) is finite up to equivalence for all \(j\,{<}\, qd (\chi )\) and \(b\,{\in }\,B\), a witness map can always be computed.
Proof
By the assumption about the sets \(\mathcal {H}_j(b)\) for \(j\,{<}\, qd (\chi )\), all product automata constructions in recursive calls \( checkPath (\psi )\) of \( checkState (\chi )\) terminate if logical equivalence of formulas is checked eagerly. Thus \( checkState (\chi )\) is defined, and by Theorem 2 the result is a witness map. \(\square \)
The property that all sets \(\mathcal {H}_j(b)\), \(j\,{<}\, qd (\chi )\), are finite might not be decidable itself. However, in the next section we will show means to guarantee this property. Moreover, we remark that finiteness of all \(\mathcal {H}_j(b)\) implies a finite history set, a decidability criterion identified for the linear-time case [28, Definition 3.6]; but Example 5 below illustrates that the requirement on the \(\mathcal {H}_j(b)\)’s is strictly stronger.
5 Decidability of DDSA Classes
We here illustrate restrictions on DDSAs, either on the control flow or on the constraint language, that render our approach a decision procedure for CTL\(^*_f\).
Monotonicity constraints (MCs) restrict constraints (Definition 1) as follows: MCs over variables V and domain D have the form \(p \odot q\) where \(p,q\in {D\,{\cup }\,V}\) and \(\odot \) is one of \(=, \ne , \le , <, \ge \), or >. The domain D may be \(\mathbb R\) or \(\mathbb Q\). We call a boolean formula whose atoms are MCs an MC formula, a DDSA where all atoms in guards are MCs an MC-DDSA, and a CTL\(^*_f\) property whose constraint atoms are MCs an MC property. For instance, \(\mathcal {B}\) in Example 2 is an MC-DDSA.
We exploit a useful quantifier elimination property: If \(\varphi \) is an MC formula over a set of constants \(L\) and variables \(V \cup \{x\}\), there is some \(\varphi ' \equiv \exists x.\, \varphi \) such that \(\varphi '\) is a quantifier-free MC formula over V and \(L\). Such a \(\varphi '\) can be obtained by writing \(\varphi \) in disjunctive normal form and applying a Fourier-Motzkin procedure [36, Sect. 5.4] to each disjunct, which guarantees that all constants in \(\varphi '\) also occur in \(\varphi \).
Theorem 3
For any DDSA \(\mathcal {B}\) and property \(\chi \) over monotonicity constraints, a witness map is computable.
Proof
Let \(\chi \) be an MC property, and \(L\) the finite set of constants in constraints in \(\chi \), \({\alpha _0}\), and guards of \(\mathcal {B}\). Let moreover \(MC _{\!L}\) be the set of quantifier-free formulas whose atoms are MCs over \(V \cup V_0\) and \(L\), so \(MC _{\!L}\) is finite up to equivalence.
We show the following property (\(\star \)): all history constraints \(h(\sigma ,\overline{\vartheta })\) over basis \(MC _{\!L}\) are equivalent to a formula in \(MC _{\!L}\). For a symbolic run  and a sequence \(\overline{\vartheta }= \langle \vartheta _0,\dots , \vartheta _n\rangle \) over \(MC _{\!L}\), the proof is by induction on n. In the base case, \(h(\sigma , \overline{\vartheta }) \,{=}\,\varphi _\nu \wedge \vartheta _0\) is in \(MC _{\!L}\) because \(\varphi _\nu \) is a conjunction of equalities between \(V\cup V_0\), and \(\vartheta _0 \in MC _{\!L}\) by assumption. In the induction step, \(h(\sigma , \overline{\vartheta }) \,{=}\, update (h(\sigma |_{n-1}, \overline{\vartheta }|_{n-1}), a_{n}) \wedge \vartheta _n\). By induction hypothesis, \(h(\sigma |_{n-1}, \overline{\vartheta }|_{n-1})\equiv \varphi \) for some \(\varphi \) in \(MC _{\!L}\). Thus \(h(\sigma , \overline{\vartheta }) \equiv \exists \overline{U}. \varphi (\overline{U}) \wedge \varDelta _a(\overline{U}, \overline{V}) \wedge \vartheta _n\). As \(\mathcal {B}\) is an \(MC \)-DDSA, \(\varDelta _a(\overline{U}, \overline{V})\) is a conjunction of MCs over \(V\cup U\) and constants \(L\), and \(\vartheta _n \in MC _{\!L}\) by assumption. By the quantifier elimination property, there exists a quantifier-free MC-formula \(\varphi '\) over variables \(V_0\cup V\) that is equivalent to \(\exists \overline{U}. \varphi (\overline{U}) \wedge \varDelta _a(\overline{U}, \overline{V}) \wedge \vartheta _n\), and mentions only constants in \(L\), so \(\varphi ' \in MC _{\!L}\).
and a sequence \(\overline{\vartheta }= \langle \vartheta _0,\dots , \vartheta _n\rangle \) over \(MC _{\!L}\), the proof is by induction on n. In the base case, \(h(\sigma , \overline{\vartheta }) \,{=}\,\varphi _\nu \wedge \vartheta _0\) is in \(MC _{\!L}\) because \(\varphi _\nu \) is a conjunction of equalities between \(V\cup V_0\), and \(\vartheta _0 \in MC _{\!L}\) by assumption. In the induction step, \(h(\sigma , \overline{\vartheta }) \,{=}\, update (h(\sigma |_{n-1}, \overline{\vartheta }|_{n-1}), a_{n}) \wedge \vartheta _n\). By induction hypothesis, \(h(\sigma |_{n-1}, \overline{\vartheta }|_{n-1})\equiv \varphi \) for some \(\varphi \) in \(MC _{\!L}\). Thus \(h(\sigma , \overline{\vartheta }) \equiv \exists \overline{U}. \varphi (\overline{U}) \wedge \varDelta _a(\overline{U}, \overline{V}) \wedge \vartheta _n\). As \(\mathcal {B}\) is an \(MC \)-DDSA, \(\varDelta _a(\overline{U}, \overline{V})\) is a conjunction of MCs over \(V\cup U\) and constants \(L\), and \(\vartheta _n \in MC _{\!L}\) by assumption. By the quantifier elimination property, there exists a quantifier-free MC-formula \(\varphi '\) over variables \(V_0\cup V\) that is equivalent to \(\exists \overline{U}. \varphi (\overline{U}) \wedge \varDelta _a(\overline{U}, \overline{V}) \wedge \vartheta _n\), and mentions only constants in \(L\), so \(\varphi ' \in MC _{\!L}\).
For \(\mathcal {C}\) the set of constraints in \(\chi ,\) we now show that \(\mathcal {H}_j \subseteq MC _{\!L}\) for all \(j\ge 0\), by induction on j. In the base case (\(j\,{=}\,0\)), the claim follows from (\(\star \)), as all constraints in \(\varPhi _0\), i.e., in \(\chi \), are in \(MC _{\!L}\). For \(j\,{>}\,0\), consider first a formula \(\widehat{\varphi }\in \varPhi _{j}\) for some \(b\,{\in }\,B\). Then \(\widehat{\varphi }\) is of the form \(\widehat{\varphi }= \bigvee _{\varphi \in H} \exists \overline{U}.\ \varphi (\overline{V}, \overline{U})\) for some \(H\,{\subseteq }\, \mathcal {H}_{j-1}\). By the induction hypothesis, \(H\subseteq MC _{\!L}\), so by the quantifier elimination property of MC formulas, \(\widehat{\varphi }\) is equivalent to an MC-formula over V and \(L\) in \(MC _{\!L}\). As \(\mathcal {H}_j\) s built over basis \(\varPhi _{j}\), the claim follows from \((\star )\). \(\square \)
Notably, the above quantifier elimination property fails for MCs over integer variables; indeed, CTL model checking is undecidable in this case [42, Theorem 4.1].
Integer periodicity constraint systems confine the constraint language to variable-to-constant comparisons and restricted forms of variable-to-variable comparisons, and are for instance used in calendar formalisms [18, 22]. More precisely, integer periodicity constraint (IPC) atoms have the form \(x = y\), \(x \odot d\) for \(\odot \in \{=,\ne , <, >\}\), \(x \equiv _k y + d\), or \(x \equiv _k d\), for variables x, y with domain \(\mathbb Z\) and \(k,d\in \mathbb N\). A boolean formula whose atoms are IPCs is an IPC formula, a DDSA whose guards are conjunctions of IPCs an IPC-DDSA, and a CTL\(^*_f\) formula whose constraint atoms are IPCs an IPC property. For instance, \(\mathcal {B}_{ ipc }\) in Example 2 is an IPC-DDSA.
Using Corollary 1 and a known quantifier elimination property for IPCs [18, Theorem 2], one can show that witness maps are also computable for IPC-DDSAs, in a proof that resembles the one of Theorem 3 (see [27, Theorem 4]).
Theorem 4
For any DDSA \(\mathcal {B}\) and property \(\chi \) over integer periodicity constraints, a witness map is computable.
The proofs of both Theorems 3 and 4 rely on the fact that all transition guards and constraints in the verification property are in a finite set of constraints C that is closed under quantifier elimination, so that for all \(\varphi \in C\) and actions a, \( update (\varphi ,a)\) is again equivalent to a formula in C. However, this is not the only way to ensure the requirements of Corollary 1: For a simple example, these requirements are satisfied by a loop-free DDSA, where the number of runs is finite. Interestingly, while the cases of MC and IPC systems are also captured by the abstract decidability criterion by Gascon [31], this need not apply to loop-free DDSAs. A clarification of the relationship between the criteria in Corollary 1 and [31, Thm 4.5] requires further investigation.
Bounded lookback [28] restricts the control flow of a DDSA rather than the constraint language, and is a generalization of the earlier feedback-freedom property [14]. Intuitively, k-bounded lookback demands that the behavior of a DDSA at any point in time depends only on k events from the past. We refer to [28, Definition 5.9] for the formal definition. Systems that enjoy bounded lookback allow for decidable linear-time verification [28, Theorem 5.10]. However, we next show that this result does not extend to branching time.
Example 5
We reduce control state reachability of two-counter machines (2CM) to the verification problem of CTL\(^*_f\) formulas in bounded lookback systems, inspired by [42, Theorem 4.1]. 2CMs have a finite control structure and two counters \(x_1\), and \(x_2\) that can be incremented, decremented, and tested for 0. It is undecidable whether a 2CM will ever reach a designated control state f [43]. For a 2CM \(\mathcal {M}\), we build a feedback-free DDSA \(\mathcal {B}\,{=}\,\langle B, b_{ I }, \mathcal {A}, T, B_F, V, \alpha _{ I }, guard \rangle \) and a CTL\(^*_f\) property \(\chi \) such that \(\mathcal {B}\) satisfies \(\chi \) iff f is reachable in \(\mathcal {M}\). The set B consists of the control states of \(\mathcal {M}\), together with an error state \( e \) and auxiliary states \(b_t\) for transitions t of \(\mathcal {M}\), and \(B_F = \{f, e\}\). The set V consists of \(x_1\), \(x_2\) and auxiliary variables \(p_1\), \(p_2\), \(m_1\), \(m_2\). Zero-test transitions of \(\mathcal {M}\) are directly modeled in \(\mathcal {B}\), whereas a step \(q \rightarrow q'\) that increments \(x_i\) by one is modeled as:

The step \(q \rightarrow b_t\) writes \(x_i\), storing its previous value in \(p_i\), but if the write was not an increment by exactly 1, a step to state e is enabled. Decrements are modeled similarly. Intuitively, bounded lookback holds because variable dependencies are limited: in a run of \(\mathcal {M}\), a variable dependency that is not an equality extends over at most two time points. (More formally, non-equality paths in the computation graph have at most length 1.) As increments are not exact, \(\mathcal {B}\) overapproximates \(\mathcal {M}\). However, \(\chi = \mathsf {E}\,\mathsf {G}\,(\lnot \mathsf {E}\,\mathsf {X}\,e)\) asserts existence of a path that never allows for a step to e (i.e., it properly simulates \(\mathcal {M}\)) but reaches the final state f. Thus, \(\mathcal {B}\) satisfies \(\chi \) iff f is reachable in \(\mathcal {M}\).
6 Implementation
We implemented our approach in the prototype ada (arithmetic DDS analyzer) in Python; source code, benchmarks, and a web interface are available (https://ctlstar.adatool.dev). As input, the tool takes a CTL\(^*\) property \(\chi \) together with a DDSA in JSON format; alternatively, a given (bounded) Petri net with data (DPN) in PNML format [5] can be transformed into a DDSA. The tool then applies the algorithm in Fig. 1. If successful, it outputs the configuration map returned by \( checkState (\chi )\), and it can visualize the product constructions. For SMT checks and quantifier elimination, ada interfaces CVC5 [23] and Z3 [17]. Besides numeric variables, ada also supports variables of type boolean and string; for the latter, only equality comparison is supported, so different constants can be represented by distinct integers. In addition to the operations in Definition 6, ada allows next operators \(\langle a\rangle \) via an action a, which are useful for verification.
We tested ada on a set of business process models presented as Data Petri nets (DPNs) in the literature. As these nets are bounded, they can be transformed into DDSAs. The results are reported in the table below. We indicate whether the system belongs to a decidable class, the verified property and whether it is satisfied by the initial configuration, the verification time, the number of SMT checks, and the number of nodes in the DDSA \(\mathcal {B}\) and the sum of all product constructions, respectively. We used CVC5 as SMT solver; times are without visualization, which tends to be time-consuming for large graphs. All tests were run on an Intel Core i7 with \(4{\times }2.60\) GHz and 19 GB RAM.
process | property | sat | time | checks | \(|\mathcal {B}|\) | \(|\mathcal {N}^\psi _{\mathcal {B},b}|\) |
|---|---|---|---|---|---|---|
(a) road fines | No deadlock |
| 7.0s | 8161 | 9 | 2052 |
\(\mathsf {A}\,\!\mathsf {G}\,(\mathsf {p}_{7} \rightarrow \mathsf {E}\,\mathsf {F}\,\mathsf {end})\) |
| 7.6s | 7655 | 1987 | ||
\(\mathsf {A}\,\!\mathsf {G}\,(\mathsf {end} \rightarrow total \,{\le }\, amount )\) |
| 1m12s | 111139 | 3622 | ||
(b) road fines | No deadlock |
| 15m27s | 247563 | 9 | 4927 |
\(\mathsf {A}\,\!\mathsf {G}\,(\mathsf {p}_{7} \rightarrow \mathsf {E}\,\mathsf {F}\,\mathsf {end})\) |
| 16m7s | 246813 | 4927 | ||
(c) road fines | No deadlock |
| 9s | 9179 | 9 | 1985 |
\(\mathsf {A}\,\!\mathsf {G}\,(\mathsf {p}_{7} \rightarrow \mathsf {E}\,\mathsf {F}\,\mathsf {end})\) |
| 6.6s | 6382 | 1597 | ||
\(\psi _{c1} = \mathsf {E}\,\!\mathsf {F}\,( dS \,{\ge }\, 2160)\) |
| 11.5s | 17680 | 1280 | ||
\(\psi _{c2} = \mathsf {E}\,\!\mathsf {F}\,( dP \,{\ge }\, 1440)\) |
| 10.0s | 15187 | 1280 | ||
\(\psi _{c3} = \mathsf {E}\,\!\mathsf {F}\,( dJ \,{\ge }\, 1440)\) |
| 10.5 | 16000 | 1280 | ||
(d) hospital billing | No deadlock |
| 20m59s | 1234928 | 17 | 23147 |
\(\psi _{d1} = \mathsf {E}\,\!\mathsf {F}\,(\mathsf {p16} \wedge \lnot closed )\) |
| 10m20s | 669379 | 10654 | ||
(e) sepsis | No deadlock |
| 1m36s | 139 | 301 | 44939 |
\(\psi _{e1} =\mathsf {A}\,\!\mathsf {G}\,(\mathsf {sink} \rightarrow t_{ tr } < t_{ ab })\) |
| 30.1s | 170 | 22724 | ||
\(\psi _{e2} =\mathsf {A}\,\!\mathsf {G}\,(\mathsf {sink} \rightarrow t_{ tr }{+}60 \ge t_{ ab })\) |
| 32s | 153 | 22538 | ||
(f) sepsis | No deadlock |
| 7m24 | 4524 | 301 | 161242 |
\(\psi _{f1} =\mathsf {A}\,(\lnot lacticAcid \mathrel {\mathsf {U}}\langle \mathsf {diagnostic}\rangle \top )\) |
| 3m53s | 5734 | 74984 | ||
(g) board: register | No deadlock |
| 1.4s | 12 | 7 | 27 |
(h) board: transfer | No deadlock |
| 1.4s | 27 | 7 | 51 |
(i) board: discharge | No deadlock |
| 1.5s | 25 | 6 | 67 |
\(\psi _{i1} = \mathsf {A}\,\!\mathsf {G}\,( \mathsf {p_2} \wedge o _1{=}207 \rightarrow \mathsf {A}\,\!\mathsf {G}\, o _1{=}207)\) |
| 1.5s | 94 | 91 | ||
\(\psi _{i2} = \mathsf {A}\,( \mathsf {E}\,\!\mathsf {F}\,\langle \mathsf {tra}\rangle \top \wedge \mathsf {E}\,\!\mathsf {F}\,\langle \mathsf {his}\rangle \top )\) |
| 1.5s | 27 | 98 | ||
\(\psi _{i3} = \lnot \mathsf {E}\,(\mathsf {F}\,\langle \mathsf {tra}\rangle \top \wedge \mathsf {F}\,\langle \mathsf {his}\rangle \top )\) |
| 1.4s | 56 | 43 | ||
(j) credit approval | No deadlock |
| 1.7s | 470 | 6 | 230 |
\(\psi _{j1} = \mathsf {A}\,\!\mathsf {G}\,(\langle \mathsf {openLoan}\rangle \top \rightarrow ver \,{\wedge }\, dec )\) |
| 13.2s | 14156 | 645 | ||
\(\psi _{j2} = \mathsf {A}\,(\mathsf {F}\,( ver \,{\wedge }\, dec ) \rightarrow \mathsf {F}\,\langle \mathsf {openLoan}\rangle \top )\) |
| 3.7s | 3128 | 316 | ||
\(\psi _{j3} = \mathsf {A}\,(\mathsf {F}\,( ver \,{\wedge }\, dec ) \rightarrow \mathsf {E}\,\!\mathsf {F}\,\langle \mathsf {openLoan}\rangle \top )\) |
| 5.6s | 4748 | 548 | ||
(k) package handling | No deadlock |
| 2.7ss | 1025 | 16 | 693 |
No deadlock (\(\tau _1\)) |
| 2.5s | 1079 | 398 | ||
\(\psi _{k1} = \mathsf {E}\,\!\mathsf {F}\,\langle \mathsf {fetch}\rangle \top \) |
| 2.6s | 850 | 343 | ||
\(\psi _{k2} = \mathsf {E}\,\!\mathsf {F}\,\langle \tau _6 \rangle \top \) |
| 2.4s | 875 | 336 | ||
(l) auction | No deadlock |
| 10.8s | 1683 | 5 | 186 |
\(\mathsf {E}\,\!\mathsf {F}\,(\mathsf {sold} \wedge d\,{>}\,0 \wedge o\,{\le }\,t)\) |
| 6.4s | 1180 | 79 | ||
\(\mathsf {E}\,\!\mathsf {F}\,(b\,{=}\,1 \wedge o\,{>}\,t \wedge \mathsf {F}\,(\mathsf {sold} \wedge b\,{>}\,1))\) |
| 26.5s | 4000 | 263 |
We briefly comment on the benchmarks and some properties: For all examples we checked no deadlock, which abbreviates \(\mathsf {A}\,\!\mathsf {G}\,\mathsf {E}\,\!\mathsf {F}\,\chi _f\) where \(\chi _f\) is a disjunction of all final states. This is one of the two requirements of the crucial soundness property (cf. Example 1). Weak soundness [4] relaxes this requirement to demand only that if a transition is reachable, it does not lead to deadlocks; this is called here no deadlock(a), expressed by \(\mathsf {E}\,\!\mathsf {F}\,(\langle a\rangle \top ) \rightarrow \mathsf {A}\,\!\mathsf {G}\,(\langle a\rangle \top \rightarrow \mathsf {F}\,\chi _f)\). One can also check whether a specific state p is deadlock-free, via \(\mathsf {A}\,\!\mathsf {G}\,(p \rightarrow \mathsf {E}\,\!\mathsf {F}\,\chi _f)\).
-
(a)-(c) are versions of the road fine management process (cf. Example 1); (a) [40, Fig. 12.7] and (b) [37, Fig. 13] were mined automatically from logs, while (c) is the normative version [41, Fig. 7] shown in Example 1. While in (a) and (c) no deadlock is violated, this issue was fixed in version (b). The fact that \(\psi _{c1}\), \(\psi _{c2}\), and \(\psi _{c3}\) hold confirm that the time constraints are never violated.
-
(d) models a billing process in a hospital [40, Fig. 15.3], which is deadlock-free.
-
(e) is a normative model for a sepsis triage process in a hospital [40, Fig. 13.3], and (f) is a variation that was mined purely automatically from logs [40, Fig. 13.6]. According to [40, Sect. 13], triage should happen before antibiotics are administered, expressed by \(\psi _{e1}\), which is actually not satisfied. However, the desired time constraint expressed by \(\psi _{e2}\) holds.
-
(g)–(i) reflect activities in patient logistics of a hospital, based on logs of real-life processes [40, Fig. 14.3]. While the no deadlock property is satisfied by all initial configurations, the output of ada reveals that for (h) this need not hold for other initial assignments.
-
(j) is a credit approval process [16, Fig. 3]. It is deadlock-free; \(\psi _{j1}\) and \(\psi _{j2}\) verify desirable conditions under which a loan is granted to a client.
-
(k) is a package handling routine [26, Fig. 5]. The fact that the properties \(\psi _{k1}\) and \(\psi _{k2}\) are not satisfied shows that the transitions \(\tau _6\) and \(\mathsf {fetch}\) are dead.
-
(l) models an auction process [28, Example 1.1], for which ada reveals a deadlock. Results for two further properties from [28, Example 1.1] are listed as well.
Seven systems are in a decidable class wrt. the listed properties: (a), (b), (d), (f), (h), (i), (k) are MC, while (d), (h), (i), (k) are IPC. This is due to the fact that automatic mining techniques often produce monotonicity constraints [39].
7 Conclusion
This paper presents a technique to compute witness maps for a given DDSA and CTL\(^*_f\) property, where a witness map specifies conditions on the initial variable assignment such that the property holds. The addressed problem is thus a slight generalization of the common verification problem. While our model checking procedure need not terminate in general, we show that it does if an abstract property on history constraints holds. Moreover, witness maps always exist for monotonicity and integer periodicity constraint systems. However, this result does not extend to bounded lookback systems. We implemented our approach in the tool ada and showed its usefulness on a range of business process models.
We see various opportunities to extend this work. A richer verification language could support past time operators [18] and future variable values [20]. Further decidable fragments could be sought using covers [33], or aiming for compatibility with locally finite theories [32]. Moreover, a restricted version of the bounded lookback property could guarantee decidability of CTL\(^*_f\), similarly to the way feedback freedom was strengthened in [35]. The implementation could be improved to avoid the computation of many similar formulas, thus gaining efficiency. Finally, the complexity class that our approach implies for CTL\(^*_f\) in the decidable classes is yet to be clarified.
References
van der Aalst, W.M.P.: Process Mining: Data Science in Action. Springer (2016). https://doi.org/10.1007/978-3-662-49851-4
Baier, C., Katoen, J.: Principles of Model Checking. MIT Press (2008)
Baral, C., De Giacomo, G.: Knowledge representation and reasoning: what’s hot. In: Proceedings of the 29th AAAI, pp. 4316–4317 (2015)
Batoulis, K., Haarmann, S., Weske, M.: Various notions of soundness for decision-aware business processes. In: Mayr, H.C., Guizzardi, G., Ma, H., Pastor, O. (eds.) ER 2017. LNCS, vol. 10650, pp. 403–418. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-69904-2_31
Billington, J., et al.: The petri net markup language: concepts, technology, and tools. In: van der Aalst, W.M.P., Best, E. (eds.) ICATPN 2003. LNCS, vol. 2679, pp. 483–505. Springer, Heidelberg (2003). https://doi.org/10.1007/3-540-44919-1_31
Bozga, M., Gîrlea, C., Iosif, R.: Iterating octagons. In: Kowalewski, S., Philippou, A. (eds.) TACAS 2009. LNCS, vol. 5505, pp. 337–351. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-00768-2_29
Bozzelli, L., Gascon, R.: Branching-time temporal logic extended with qualitative Presburger constraints. In: Hermann, M., Voronkov, A. (eds.) LPAR 2006. LNCS (LNAI), vol. 4246, pp. 197–211. Springer, Heidelberg (2006). https://doi.org/10.1007/11916277_14
Bozzelli, L., Pinchinat, S.: Verification of gap-order constraint abstractions of counter systems. Theor. Comput. Sci. 523, 1–36 (2014). https://doi.org/10.1016/j.tcs.2013.12.002
Calvanese, D., De Giacomo, G., Montali, M.: Foundations of data-aware process analysis: a database theory perspective. In: Proceedings of the 32nd PODS, pp. 1–12 (2013). https://doi.org/10.1145/2463664.2467796
Calvanese, D., De Giacomo, G., Montali, M., Patrizi, F.: First-order \(\mu \)-calculus over generic transition systems and applications to the situation calculus. Inf. Comput. 259(3), 328–347 (2018). https://doi.org/10.1016/j.ic.2017.08.007
Carapelle, C., Kartzow, A., Lohrey, M.: Satisfiability of ECTL\(^*\) with constraints. J. Comput. Syst. Sci. 82(5), 826–855 (2016). https://doi.org/10.1016/j.jcss.2016.02.002
Čerāns, K.: Deciding properties of integral relational automata. In: Abiteboul, S., Shamir, E. (eds.) ICALP 1994. LNCS, vol. 820, pp. 35–46. Springer, Heidelberg (1994). https://doi.org/10.1007/3-540-58201-0_56
Comon, H., Jurski, Y.: Multiple counters automata, safety analysis and Presburger arithmetic. In: Hu, A.J., Vardi, M.Y. (eds.) CAV 1998. LNCS, vol. 1427, pp. 268–279. Springer, Heidelberg (1998). https://doi.org/10.1007/BFb0028751
Damaggio, E., Deutsch, A., Vianu, V.: Artifact systems with data dependencies and arithmetic. ACM Trans. Database Syst. 37(3), 22:1–22:36 (2012). https://doi.org/10.1145/2338626.2338628
de Giacomo, G., De Masellis, R., Montali, M.: Reasoning on LTL on finite traces: insensitivity to infiniteness. In: Proceedings of the 28th AAAI, pp. 1027–1033 (2014)
de Leoni, M., Mannhardt, F.: Decision discovery in business processes. In: Encyclopedia of Big Data Technologies, pp. 1–12. Springer (2018). https://doi.org/10.1007/978-3-319-63962-8_96-1
de Moura, L., Bjørner, N.: Z3: an efficient SMT solver. In: Ramakrishnan, C.R., Rehof, J. (eds.) TACAS 2008. LNCS, vol. 4963, pp. 337–340. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-78800-3_24
Demri, S.: LTL over integer periodicity constraints. Theor. Comput. Sci. 360(1–3), 96–123 (2006). https://doi.org/10.1016/j.tcs.2006.02.019
Demri, S., Dhar, A.K., Sangnier, A.: Equivalence between model-checking flat counter systems and Presburger arithmetic. Theor. Comput. Sci. 735, 2–23 (2018). https://doi.org/10.1016/j.tcs.2017.07.007
Demri, S., D’Souza, D.: An automata-theoretic approach to constraint LTL. Inform. Comput. 205(3), 380–415 (2007). https://doi.org/10.1016/j.ic.2006.09.006
Demri, S., Finkel, A., Goranko, V., van Drimmelen, G.: Model-checking CTL* over flat Presburger counter systems. J. Appl. Non Class. Logics 20(4), 313–344 (2010). https://doi.org/10.3166/jancl.20.313-344
Demri, S., Gascon, R.: Verification of qualitative Z constraints. Theor. Comput. Sci. 409(1), 24–40 (2008). https://doi.org/10.1016/j.tcs.2008.07.023
Deters, M., Reynolds, A., King, T., Barrett, C.W., Tinelli, C.: A tour of CVC4: how it works, and how to use it. In: Proceedings of the 14th FMCAD, p. 7 (2014). https://doi.org/10.1109/FMCAD.2014.6987586
Deutsch, A., Hull, R., Li, Y., Vianu, V.: Automatic verification of database-centric systems. ACM SIGLOG News 5(2), 37–56 (2018). https://doi.org/10.1145/3212019.3212025
Felli, P., de Leoni, M., Montali, M.: Soundness verification of decision-aware process models with variable-to-variable conditions. In: Proceedings of the 19th ACSD, pp. 82–91. IEEE (2019). https://doi.org/10.1109/ACSD.2019.00013
Felli, P., de Leoni, M., Montali, M.: Soundness verification of data-aware process models with variable-to-variable conditions. Fund. Inform. 182(1), 1–29 (2021). https://doi.org/10.3233/FI-2021-2064
Felli, P., Montali, M., Winkler, S.: CTL\(^*\) model checking for data-aware dynamic systems with arithmetic (extended version) (2022). https://doi.org/10.48550/arXiv.2205.08976
Felli, P., Montali, M., Winkler, S.: Linear-time verification of data-aware dynamic systems with arithmetic. In: Proceedings of the 36th AAAI (2022). https://doi.org/10.48550/arXiv.2203.07982
Finkel, A., Leroux, J.: How to compose Presburger-accelerations: applications to broadcast protocols. In: Agrawal, M., Seth, A. (eds.) FSTTCS 2002. LNCS, vol. 2556, pp. 145–156. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-36206-1_14
Finkel, A., Willems, B., Wolper, P.: A direct symbolic approach to model checking pushdown systems. In: Proc. 2nd INFINITY. ENTCS, vol. 9, pp. 27–37 (1997). https://doi.org/10.1016/S1571-0661(05)80426-8
Gascon, R.: An automata-based approach for CTL\(^*\) with constraints. In: Proceedings of the INFINITY 2006, 2007 and 2008. ENTCS, vol. 239, pp. 193–211 (2009). https://doi.org/10.1016/j.entcs.2009.05.040
Ghilardi, S., Nicolini, E., Ranise, S., Zucchelli, D.: Combination methods for satisfiability and model-checking of infinite-state systems. In: Pfenning, F. (ed.) CADE 2007. LNCS (LNAI), vol. 4603, pp. 362–378. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-73595-3_25
Gulwani, S., Musuvathi, M.: Cover algorithms and their combination. In: Drossopoulou, S. (ed.) ESOP 2008. LNCS, vol. 4960, pp. 193–207. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-78739-6_16
Ibarra, O.H., Su, J.: Counter machines: decision problems and applications. In: Jewels are Forever: Contributions on Theoretical Computer Science in Honor of Arto Salomaa, pp. 84–96 (1999)
Koutsos, A., Vianu, V.: Process-centric views of data-driven business artifacts. J. Comput. Syst. Sci. 86, 82–107 (2017). https://doi.org/10.1016/j.jcss.2016.11.012
Kroening, D., Strichman, O.: Decision Procedures - An Algorithmic Point of View. Second Edition. Springer (2016). https://doi.org/10.1007/978-3-662-50497-0
de Leoni, M., Felli, P., Montali, M.: A holistic approach for soundness verification of decision-aware process models. In: Trujillo, J.C., Davis, K.C., Du, X., Li, Z., Ling, T.W., Li, G., Lee, M.L. (eds.) ER 2018. LNCS, vol. 11157, pp. 219–235. Springer, Cham (2018). https://doi.org/10.1007/978-3-030-00847-5_17
de Leoni, M., Felli, P., Montali, M.: Strategy synthesis for data-aware dynamic systems with multiple actors. In: Proceedings of the 17th KR, pp. 315–325 (2020). https://doi.org/10.24963/kr.2020/32
de Leoni, M., Felli, P., Montali, M.: Integrating BPMN and DMN: modeling and analysis. J. Data Semant. 10(1), 165–188 (2021). https://doi.org/10.1007/s13740-021-00132-z
Mannhardt, F.: Multi-perspective process mining. Ph.D. thesis, Technical University of Eindhoven (2018)
Mannhardt, F., de Leoni, M., Reijers, H.A., van der Aalst, W.M.P.: Balanced multi-perspective checking of process conformance. Computing 98(4), 407–437 (2015). https://doi.org/10.1007/s00607-015-0441-1
Mayr, R., Totzke, P.: Branching-time model checking gap-order constraint systems. Fundam. Informaticae 143(3–4), 339–353 (2016). https://doi.org/10.3233/FI-2016-1317
Minsky, M.: Computation: Finite and Infinite Machines. Prentice-Hall (1967)
Murano, A., Parente, M., Rubin, S., Sorrentino, L.: Model-checking graded computation-tree logic with finite path semantics. Theor. Comput. Sci. 806, 577–586 (2020). https://doi.org/10.1016/j.tcs.2019.09.021
Presburger, M.: Über die Vollständigkeit eines gewissen Systems der Arithmetik ganzer Zahlen, in welchem die Addition als einzige Operation hervortritt. In: Comptes Rendus du I congres de Mathem. des Pays Slaves, pp. 92–101 (1929)
Reichert, M.: Process and data: two sides of the same coin? In: Meersman, R., Panetto, H., Dillon, T., Rinderle-Ma, S., Dadam, P., Zhou, X., Pearson, S., Ferscha, A., Bergamaschi, S., Cruz, I.F. (eds.) OTM 2012. LNCS, vol. 7565, pp. 2–19. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-33606-5_2
Sorrentino, L., Rubin, S., Murano, A.: Graded CTL* over finite paths. In: Proceedings of the 19th ICTCS. CEUR Workshop Proceedings, vol. 2243, pp. 152–161. CEUR-WS.org (2018)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2022 The Author(s)
About this paper
Cite this paper
Felli, P., Montali, M., Winkler, S. (2022). CTL\(^*\) Model Checking for Data-Aware Dynamic Systems with Arithmetic. In: Blanchette, J., Kovács, L., Pattinson, D. (eds) Automated Reasoning. IJCAR 2022. Lecture Notes in Computer Science(), vol 13385. Springer, Cham. https://doi.org/10.1007/978-3-031-10769-6_4
Download citation
DOI: https://doi.org/10.1007/978-3-031-10769-6_4
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-10768-9
Online ISBN: 978-3-031-10769-6
eBook Packages: Computer ScienceComputer Science (R0)




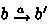 in
in  in
in  in R such that
in R such that 

































