Abstract
In the previous chapter, we saw how classical first-order logic can be enriched with questions, resulting in the system \(\textsf {InqBQ}\) of inquisitive first-order logic.
You have full access to this open access chapter, Download chapter PDF
In the previous chapter, we saw how classical first-order logic can be enriched with questions, resulting in the system \(\textsf {InqBQ}\) of inquisitive first-order logic. We now turn to the task of designing a proof system for \(\textsf {InqBQ}\). As discussed in the previous chapter, it is not currently known whether \(\textsf {InqBQ}\) in fact admits a complete proof system, since it is not known whether \(\textsf {InqBQ}\) is compact and whether its validities are recursively enumerable. However, in Sect. 6.1 we will describe a natural deduction system which is sound for \(\textsf {InqBQ}\) and which, as demonstrated in Sect. 6.2, is powerful enough to prove many \(\textsf {InqBQ}\)-entailments, including all the examples discussed in the previous chapter. In fact, for all we know this system might be complete, although this seems unlikely.Footnote 1 Moreover, we are going to show in Sect. 6.3 that this system is indeed complete for the classical antecedent fragment of \(\textsf {InqBQ}\), which is in itself a rich extension of first-order logic with questions.
6.1 Natural Deduction System for InqBQ
A natural deduction system for \(\textsf {InqBQ}\) is described in Fig. 6.1. The notational conventions are the usual ones: we write \(\Phi \vdash \psi \) to mean that there is a proof in this system whose conclusion is \(\psi \) and whose set of undischarged assumptions is included in \(\Phi \); we write \(\varphi _1,\dots ,\varphi _n\vdash \psi \) instead of \(\{\varphi _1,\dots ,\varphi _n\}\vdash \psi \), and write \(\varphi \dashv \vdash \psi \) to mean that both \(\varphi \vdash \psi \) and \(\psi \vdash \varphi \) hold. Before illustrating the system with some examples, let us comment briefly on the various inference rules.
A sound, but possibly incomplete, natural deduction system for InqBQ. As usual, we denote the introduction and elimination rules for an operator \(\circ \) as \((\circ \textsf {i})\) and \((\circ \textsf {e})\). In these rules, the variable \(\alpha \) ranges over classical formulas, while \(\varphi \) and \(\psi \) range over arbitrary formulas of InqBQ; \(\textsf {t}\) denotes a rigid term, while \(t,t'\) denote arbitrary terms, which may but need not be rigid. In either case, these terms must be free for x in the relevant formula. In the rule \((\forall \textsf {i})\), y must not occur free in any undischarged assumption. In \((\exists \textsf {e})\), y must not occur free in \(\psi \) or in any undischarged assumption
Connectives and quantifiers. As in the propositional system for InqB, each of the connectives \(\wedge ,\rightarrow ,\bot \) and  is handled by its standard introduction and elimination rules. The rules for the quantifiers are also standard—with one caveat: as we discussed in Sect. 5.5.4, in general it is only sound to instantiate \(\forall \) to, and to introduce \(\mathord {\exists \!\!\!\exists }\) from, a term which is rigid. As we saw in that section, it is also sound to instantiate a universal to a non-rigid term, but only when the relevant formula is classical. This is given as a second elimination rule for \(\forall \).
is handled by its standard introduction and elimination rules. The rules for the quantifiers are also standard—with one caveat: as we discussed in Sect. 5.5.4, in general it is only sound to instantiate \(\forall \) to, and to introduce \(\mathord {\exists \!\!\!\exists }\) from, a term which is rigid. As we saw in that section, it is also sound to instantiate a universal to a non-rigid term, but only when the relevant formula is classical. This is given as a second elimination rule for \(\forall \).
The rules for \(\lnot \) are obtained as special cases of the rules for implication. As for classical disjunction and classical existential, the rules shown in Fig. 6.2 are implicitly available in the system: whatever can be derived using these rules can in fact be derived from the rules in Fig. 6.1. Note that a classical existential can be introduced from an arbitrary term (not only from a rigid term, as in the case of \(\mathord {\exists \!\!\!\exists }\)); however, as in the case of classical disjunction, it can be eliminated only towards a classical conclusion. Without the restriction to classical conclusions, the elimination rule would not be sound; it would allow us, for instance, to infer the inquisitive existential \(\mathord {\exists \!\!\!\exists }xPx\) from the classical existential \(\exists xPx\).
Admissible rules for \(\vee \) and \(\exists \). Here, \(\alpha \) ranges over classical formulas, and \(\varphi ,\psi \) over arbitrary formulas; t is an arbitrary term (possibly non-rigid) free for x in \(\varphi \). The variable y should not occur free in \(\alpha \) or any undischarged assumption above the rule
Identity predicate. Standard introduction and elimination rules also take care of the identity predicate. The introduction rule is given by the fact that \(t=t\) is valid for any t. The elimination rule is backed by Proposition 5.4.3, which ensures the substitutability of terms whose identity is established in the state. Other features of identity, such as symmetry and transitivity, are provable.
Connection with intuitionistic logic. What we have described so far—at least in restriction to formulas containing only rigid terms—is simply a natural deduction system for intuitionistic first-order logic, with  and \(\mathord {\exists \!\!\!\exists }\) in the role of intuitionistic disjunction and existential quantifier respectively. The soundness of these rules implies that anything that is intuitionistically valid is also valid in \(\textsf {InqBQ}\). This observation is worth stating as a proposition.
and \(\mathord {\exists \!\!\!\exists }\) in the role of intuitionistic disjunction and existential quantifier respectively. The soundness of these rules implies that anything that is intuitionistically valid is also valid in \(\textsf {InqBQ}\). This observation is worth stating as a proposition.
Proposition 6.1.1
(InqBQ includes intuitionistic logic) Let \(\Phi \cup \{\psi \}\subseteq \mathcal {L}^{\textsf {Q}=}\) consist of formulas containing only rigid terms. If \(\Phi \) entails \(\psi \) in intuitionistic logic when  and \(\mathord {\exists \!\!\!\exists }\) are identified with intuitionistic disjunction and inquisitive existential respectively, then \(\Phi \models \psi \).
and \(\mathord {\exists \!\!\!\exists }\) are identified with intuitionistic disjunction and inquisitive existential respectively, then \(\Phi \models \psi \).
On top of this intuitionistic skeleton, \(\textsf {InqBQ}\) validates some further principles.
Classical double negation elimination. We saw that the classical fragment of \(\textsf {InqBQ}\) coincides with classical first-order logic. To capture this, we endow our system with a rule of double negation elimination restricted to classical formulas. In this way, our proof system includes a complete natural deduction system for classical first-order logic in restriction to classical formulas.
Split rules. In the propositional case, our system contains the  -split rule, which allows us to distribute a classical antecedent over an inquisitive-disjunctive consequent. In the first-order case, we have this rule as well as the analogous rule for the inquisitive existential quantifier. The soundness of these rules is given by Proposition 5.5.12. These rules reflect the specificity of statements (Proposition 5.5.10), that is, the crucial fact that statements denote specific pieces of information, and that to suppose a statement is to extend the available information in one particular way.
-split rule, which allows us to distribute a classical antecedent over an inquisitive-disjunctive consequent. In the first-order case, we have this rule as well as the analogous rule for the inquisitive existential quantifier. The soundness of these rules is given by Proposition 5.5.12. These rules reflect the specificity of statements (Proposition 5.5.10), that is, the crucial fact that statements denote specific pieces of information, and that to suppose a statement is to extend the available information in one particular way.
Constant domains. As is known from work on intuitionistic logic (see [2, 3]), assuming a constant domain of quantification has repercussions on the logic, rendering valid the schema

where \(x\not \in \text {FV}(\psi )\). By taking this principle on board as an inference rule, we make our proof system track the assumption that the domain of quantification is fixed and does not vary from world to world.
Classicality of negations. Recall that Proposition 5.3.8 ensures that a negation \(\lnot \varphi \) is always truth-conditional, and thus equivalent to a classical formula. The KF rule, which allows us to infer \(\lnot \lnot \forall x\varphi \) from \(\forall x\lnot \lnot \varphi \), is precisely what we need in order for our proof system to vindicate this fact. To see this, first recall that Proposition 5.3.9 tells us that the double negation \(\lnot \lnot \varphi \) of a formula is always equivalent with the classical variant, \(\varphi ^{cl}\). Using KF, we can prove this equivalence for every \(\varphi \)Footnote 2.
Proposition 6.1.2
For any \(\varphi \in \mathcal {L}^{\textsf {Q}}\), \(\lnot \lnot \varphi \dashv \vdash \varphi ^{cl}\).
Proof
We can show this by induction on the complexity of \(\varphi \). We focus on the most interesting case, namely, the inductive step for \(\forall \). The other cases are left as an exercise (Exercise 6.4.5). So, consider a formula \(\forall x\varphi \). Assume the claim holds for all formulas of lower complexity, which include all substitution instances of \(\varphi \) of the form \(\varphi [y/x]\). We want to show that \(\lnot \lnot \forall x\varphi \dashv \vdash (\forall x\varphi )^{cl}\).
The two proofs are given below. In these proofs, y is a fresh variable. Observe that by definition of classical variant, \((\forall x\varphi )^{cl}\) coincides with \(\forall x\varphi ^{cl}\) and \((\varphi [y/x])^{cl}\) coincides with \(\varphi ^{cl}[y/x]\). The label (IH) marks sub-proofs which exist by the induction hypothesis.

Note the crucial role of the KF rule in the first proof.\(\Box \)
Using this fact, we can then prove that all negations in \(\textsf {InqBQ}\) are classical.
Corollary 6.1.3
For all \(\varphi \in \mathcal {L}^{\textsf {Q}=}\), \(\,\lnot \varphi \dashv \vdash \lnot \varphi ^{cl}\).
Proof
We leave it to the reader to check that using the rules for implication we have \(\lnot \varphi \dashv \vdash \lnot \lnot \lnot \varphi \) for any \(\varphi \in \mathcal {L}^{\textsf {Q}=}\). Putting this together with the previous proposition we have \(\lnot \varphi \dashv \vdash \lnot \lnot \lnot \varphi \dashv \vdash (\lnot \varphi )^{cl}=\lnot \varphi ^{cl}\).\(\Box \)
We can also show that from a formula \(\varphi \in \mathcal {L}^{\textsf {Q}=}\) we can always infer its classical variant, \(\varphi ^{cl}\).
Corollary 6.1.4
For all \(\varphi \in \mathcal {L}^{\textsf {Q}=}\), \(\,\varphi \vdash \varphi ^{cl}\).
Proof
It is easy to see that for any \(\varphi \) we have \(\varphi \vdash \lnot \lnot \varphi \), and we know that \(\lnot \lnot \varphi \vdash \varphi ^{cl}\) by Proposition 6.1.2.\(\Box \)
This result can be used to give an easy proof of the fact that our system is complete for entailments whose conclusion is a classical formula.Footnote 3
Theorem 6.1.5
(Completeness for classical conclusions) Let \(\Phi \subseteq \mathcal {L}^{\textsf {Q}=}\), \(\alpha \in \mathcal {L}^{\textsf {Q}=}_c\). If \(\Phi \models \alpha \), then \(\Phi \vdash \alpha \).
Proof
Suppose \(\Phi \models \alpha \). As classical formulas are truth-conditional, it follows from Proposition 5.5.7 that \(\Phi ^{cl}\models \alpha \). Since entailment among classical formulas coincides with entailment in classical first-order logic, and since our proof system includes a complete proof system for classical first-order logic, it follows that \(\Phi ^{cl}\vdash \alpha \). This means that there must be \(\varphi _1,\dots ,\varphi _n\in \Phi \) such that \(\varphi _1^{cl},\dots ,\varphi _n^{cl}\vdash \alpha \). The previous corollary ensures that \(\varphi _i\vdash \varphi _i^{cl}\) for each \(i\le n\). Hence, \(\varphi _1,\dots ,\varphi _n\vdash \alpha \), which implies \(\Phi \vdash \alpha \).\(\Box \)
Before proceeding to show a more interesting completeness result, let us illustrate the deduction system with some examples.
6.2 Illustration
In order to illustrate our proof system, we show how we can use it to prove the examples of logical dependencies that we discussed in Sect. 5.5.1.
Example 6.2.1
Start with the entailment we discussed in Example 5.5.1:
Here is a proof of this entailment. Recall that ?Px and ?Qy abbreviate, respectively, the inquisitive disjunctions  and
and  .
.

Note how intuitive and familiar the reasoning is. Even though we manipulate questions, we do so by relatively standard and recognizable logical principles, such as the usual rules for disjunction and the universal quantifier.
Example 6.2.2
Next, consider the entailment of Example 5.5.2:
As we discussed above, this entailment depends crucially on the assumption that the domain of quantification is fixed. It is thus not too surprising that a proof of it makes crucial use of the constant domain rule CD. The last step, marked by (Def), is not a real inference step, but merely a rewriting of the conclusion according to our notational conventions.

Example 6.2.3
For a more complex example, involving both mention-all and mention-some questions, recall the entailment we discussed in Example 5.5.3:
This captures the fact that given the assumption that the extension of P is non-empty, from the information about what the extension of P is we can extract a witness for P. The proof of this fact makes again use of the constant domain rule, CD. Using this rule, we can show that if we are given a specification of the extension of P, from this information we can get either a witness for P, or the information that no object satisfies P. Here is the proof:

Call this proof \(\textsf {P}_1\). We can then use the conclusion of \(\textsf {P}_1\) in an (inquisitive) disjunctive syllogism: since our assumption \(\exists xP(x)\) allows us to rule out \(\forall x\lnot P(x)\), we can infer the other disjunct, \(\mathord {\exists \!\!\!\exists }xP(x)\). Here is the proof in detail (again, the step marked by (Def) is merely a re-writing of the assumption, spelling out the classical existential according to its definition).

Example 6.2.4
Finally, consider the entailment of Example 5.5.4, namely
where f is a rigid function symbol and a, b, c non-rigid constant symbols. Spelling out the definition of the identification questions, this entailment amounts to:
Here is a proof of this entailment. The premises \(\mathord {\exists \!\!\!\exists }x(x= b)\) and \(\mathord {\exists \!\!\!\exists }x(x= c)\) allow us to replace the constants b and c in the premise \(\textsf {f}(b,c)\) by variables, obtaining the term \(\textsf {f}(y,z)\); since this term is rigid, the inquisitive existential can be introduced from it.

Notice once more how intuitive and familiar the proof looks. In this case, reasoning with identification questions involves using familiar rules for identity and the existential quantifier, with the only subtlety of paying attention to rigidity.
6.3 Completeness for the Classical Antecedent Fragment
In this section we show, following Grilletti [6], that the system described in the previous section is complete for the classical antecedent fragment of \(\textsf {InqBQ}\) introduced in Sect. 5.7.2. In fact, we will prove something slightly stronger: if \(\Phi \cup \{\psi \}\) is a set of clant formulas and \(\Phi \models \psi \), then there is a proof of this entailment which involves only clant formulas and which moreover does not make use of the KF rule. This completeness result is especially significant as the clant fragment is very rich, including all examples of first-order questions discussed in the previous chapter (though not implications of such questions).
A sound and complete natural deduction system for the classical antecedent fragment of InqBQ. In the rules, \(\textsf {t}\) denotes a rigid term, while \(t,t'\) denote arbitrary terms, which may or may not be rigid. In both cases, the terms must be free for x in the relevant formula. The variable \(\alpha \) ranges over classical formulas, while \(\varphi \) and \(\psi \) range over clant formulas. The restrictions on variables are the same as in Fig. 6.1. The differences with respect to the general proof system of Fig. 6.1 are the restriction of all rules to clant formulas and the omission of the KF rule
6.3.1 Proof System for the Classical Antecedent Fragment
A sub-system of our natural deduction system for \(\textsf {InqBQ}\) is given in Fig. 6.3. This system differs from the general system in that it manipulates only clant formulas and in that the KF rule is not present. Throughout this section, we will use the notation \(\vdash \) for derivability in this weaker system. A priori, even in restriction to clant formulas, this could be a weaker derivability relation than the one given by the full system in Fig. 6.1; however, it will follow from the completeness result that, for clant formulas, the two relations in fact coincide with each other and with the semantic entailment relation.
The remainder of this section is devoted to the proof of the following theorem, due to Grilletti [6].
Theorem 6.3.1
(Completeness for the clant fragment) Suppose \(\Phi \cup \{\psi \}\subseteq \mathcal {L}_{\text {Clant}}\). Then \(\Phi \models \psi \iff \Phi \vdash \psi \).
As usual, the interesting direction is completeness, since soundness follows from the soundness of each inference rule.
6.3.2 Clant-Saturated Theories
Throughout this section, fix a signature \(\Sigma \). For simplicity, we suppose \(\Sigma \) to be countable, though this is not strictly required. Let \(A=\{\textsf {a}_0,\textsf {a}_1,\dots \}\) be a a countably infinite set of rigid constants not included in \(\Sigma \). Throughout this section we denote by \(\mathcal {L}\) and \(\mathcal {L}^A\) the set of clant sentences (thus excluding open formulas) in the signatures \(\Sigma \) and \(\Sigma \cup \{A\}\). We denote by \(\mathcal {L}_c\) and \(\mathcal {L}^A_c\) the restrictions of these sets to classical sentences, not containing  or \(\mathord {\exists \!\!\!\exists }\) .
or \(\mathord {\exists \!\!\!\exists }\) .
A crucial notion for our completeness proof is the notion of a clant-saturated theory. A clant-saturated theory is a set of clant sentences that has the right features to be the set of sentences supported by a non-empty information state, in a model where the constants in A name the individuals in the domain.
Definition 6.3.2
(Clant saturated theories) A set of clant sentences \(\Delta \subseteq \mathcal {L}^A\) is called a clant-saturated theory over A if it has the following properties:
-
Consistency: \(\bot \not \in \Delta \);
-
Deductive closure: for all \(\varphi \in \mathcal {L}^A\), if \(\Delta \vdash \varphi \) then \(\varphi \in \Delta \);
-
Inquisitive disjunction property: if
 then \(\varphi \in \Delta \) or \(\psi \in \Delta \);
then \(\varphi \in \Delta \) or \(\psi \in \Delta \); -
Inquisitive existence property: if \(\mathord {\exists \!\!\!\exists }x\varphi \in \Delta \) then \(\varphi [\textsf {a}/x]\in \Delta \) for some \(\textsf {a}\in A\);
-
Normality: if \(\forall x\varphi \not \in \Delta \) then \(\varphi [\textsf {a}/x]\not \in \Delta \) for some \(\textsf {a}\in A\).
An important fact about clant-saturated theories is that extending a clant-saturated theory consistently with a classical sentence leads to a new clant-saturated theory.
Lemma 6.3.3
Let \(\Delta \) be a clant-saturated theory over A and \(\alpha \) a classical sentence such that \(\Delta \not \vdash \lnot \alpha \). Then the deductive closure
is itself a clant-saturated theory.
Proof
Obviously, \(\Delta +\alpha \) is deductively closed. Let us consider the other requirements in turn.
-
Consistency. Suppose towards a contradiction that \(\bot \in (\Delta +\alpha )\). This means that \(\Delta \cup \{\alpha \}\vdash \bot \), and so by the rules for implication \(\Delta \vdash \lnot \alpha \), contrary to assumption.
-
Inquisitive disjunction property. Suppose
 . This means that
. This means that  , so by the rules for implication
, so by the rules for implication  . By the
. By the  -split rule,
-split rule,  . By the deductive closure and the disjunction property of \(\Delta \), it follows that \((\alpha \rightarrow \varphi )\in \Delta \) or \((\alpha \rightarrow \psi )\in \Delta \). In the former case we have \(\varphi \in (\Delta +\alpha )\), in the latter case \(\psi \in (\Delta +\alpha )\).
. By the deductive closure and the disjunction property of \(\Delta \), it follows that \((\alpha \rightarrow \varphi )\in \Delta \) or \((\alpha \rightarrow \psi )\in \Delta \). In the former case we have \(\varphi \in (\Delta +\alpha )\), in the latter case \(\psi \in (\Delta +\alpha )\). -
Inquisitive existence property. Similar to the previous item, using the \(\mathord {\exists \!\!\!\exists }\)-split rule and the inquisitive existence property.
-
Normality condition. Suppose \(\forall x\varphi \not \in (\Delta +\alpha )\). This means that \(\Delta \cup \{\alpha \}\not \vdash \forall x\varphi \), and thus by the rules for implication \(\Delta \not \vdash \alpha \rightarrow \forall x\varphi \). Now, since \(\alpha \) is a sentence, \(\alpha \rightarrow \forall x\varphi \) is provably equivalent in our system to \(\forall x(\alpha \rightarrow \varphi )\), and so also \(\Delta \not \vdash \forall x(\alpha \rightarrow \varphi )\). By the normality condition on \(\Delta \), for some \(\textsf {a}\in A\) we have \(\Delta \not \vdash (\alpha \rightarrow \varphi )[\textsf {a}/x]\). Since \(\alpha \) is a sentence, \((\alpha \rightarrow \varphi )[\textsf {a}/x]\) amounts to \(\alpha \rightarrow \varphi [\textsf {a}/x]\). So we have \(\Delta \not \vdash \alpha \rightarrow \varphi [\textsf {a}/x]\) which by the rules for implication gives \(\Delta \cup \{\alpha \}\not \vdash \varphi [\textsf {a}/x]\), that is, \(\varphi [\textsf {a}/x]\not \in (\Delta +\alpha )\).\(\Box \)
It is interesting to point out that this is the only place in the completeness proof where the two split rules play a role. We saw that the validity of these rules captures the fact that, semantically, there is always a single minimal way of strengthening a state s to support a classical formula \(\alpha \). Now we saw that these rules enforce the same property on the syntactic side: there is always a single minimal way to extend a clant-saturated theory to one that contains \(\alpha \).
Using the previous lemma, we can establish a very significant fact: a clant-saturated theory is completely determined by its classical part, i.e., by the set of classical formulas it contains.
Definition 6.3.4
Let \(\Delta \) be a clant-saturated theory. The classical part of \(\Delta \), \(\Delta _{cl}\), is the set of classical formulas in \(\Delta \).
Lemma 6.3.5
If \(\Delta ,\Delta '\) are clant-saturated theories over A with \(\Delta _{cl}=\Delta '_{cl}\), then \(\Delta =\Delta '\).
Proof
We prove the following claim by induction on \(\varphi \): for any clant sentence \(\varphi \), and for any two clant-saturated theories \(\Delta ,\Delta '\), if \(\Delta _{cl}=\Delta '_{cl}\) then \(\varphi \in \Delta \iff \varphi \in \Delta '\).
-
Atoms. If \(\varphi \) is an atom or \(\bot \) then \(\varphi \) is a classical formula. So if two clant-saturated theories have the same classical fragment, obviously they agree on \(\varphi \).
-
Conjunction. Suppose \(\varphi \) is a conjunction \(\psi \wedge \chi \) and take any clant-saturated theories \(\Delta ,\Delta '\) with the same classical fragment. By deductive closure of these theories and the induction hypothesis we have:
$$\begin{aligned} (\psi \wedge \chi )\in \Delta\iff & {} \psi \in \Delta \text { and }\chi \in \Delta \\\iff & {} \psi \in \Delta '\text { and }\chi \in \Delta '\\\iff & {} \psi \wedge \chi \in \Delta '. \end{aligned}$$ -
Inquisitive disjunction: this case is similar to the previous one, using the fact that for a clant-saturated theory \(\Delta \) we have
 , by deductive closure and the inquisitive disjunction property.
, by deductive closure and the inquisitive disjunction property. -
Implication. Suppose \(\varphi \) is an implication \(\alpha \rightarrow \psi \) (note that since \(\varphi \) is a clant sentence, the antecedent must be classical). Take any clant-saturated theories \(\Delta ,\Delta '\) with the same classical fragment. Note that by deductive closure and the rules for implication we have:
$$\begin{aligned} (\alpha \rightarrow \psi )\in \Delta\iff & {} \Delta \vdash \alpha \rightarrow \psi \\\iff & {} \Delta \cup \{\alpha \}\vdash \psi \\\iff & {} \psi \in (\Delta +\alpha ). \end{aligned}$$and similarly for \(\Delta '\). By the previous lemma, \(\Delta +\alpha \) and \(\Delta '+\alpha \) are clant-saturated theories. Moreover, these theories have the same classical fragment. To see this, take any classical sentence \(\beta \). Using the rules for implication and the fact that \(\Delta \) and \(\Delta '\) have the same classical fragment, we have:
$$\begin{aligned} \beta \in (\Delta +\alpha )\iff & {} \Delta \vdash \alpha \rightarrow \beta \\\iff & {} (\alpha \rightarrow \beta )\in \Delta \\\iff & {} (\alpha \rightarrow \beta )\in \Delta '\\\iff & {} \Delta '\vdash \alpha \rightarrow \beta \\\iff & {} \beta \in (\Delta '+\alpha ). \end{aligned}$$Since \(\Delta +\alpha \) and \(\Delta '+\alpha \) are clant-saturated theories with the same classical fragment, we can then use the induction hypothesis on \(\psi \) to conclude that \(\psi \in (\Delta +\alpha )\iff \psi \in (\Delta '+\alpha )\), which by what we have seen above implies \((\alpha \rightarrow \psi )\in \Delta \iff (\alpha \rightarrow \psi )\in \Delta '\).
-
Universal quantifier. Suppose \(\varphi \) has the form \(\forall x\psi \). Take any clant-saturated theories \(\Delta ,\Delta '\) with \(\Delta _{cl}=\Delta '_{cl}\). By deductive closure and normality we have \(\forall x\psi \in \Delta \iff (\psi [\textsf {a}/x]\in \Delta \) for all \(\textsf {a}\in A\)), and similarly for \(\Delta '\). Then using the inductive hypothesis we have:
$$\begin{aligned} \forall x\psi \in \Delta\iff & {} \psi [\textsf {a}/x]\in \Delta \text { for all }\textsf {a}\in A\\\iff & {} \psi [\textsf {a}/x]\in \Delta '\text { for all }\textsf {a}\in A\\\iff & {} \forall x\psi \in \Delta '. \end{aligned}$$ -
Inquisitive existential quantifer: this case is similar to the previous one, using deductive closure and the inquisitive existence property.\(\Box \)
It is an interesting open question whether an analogous result holds for the full language of \(\textsf {InqBQ}\).
Open Problem 6.3.6
Consider a notion of saturated theory for the full language, defined as in Definition 6.3.2 but without the restriction to clant sentences. Are there two saturated theories \(\Delta ,\Delta '\) such that \(\Delta _{cl}=\Delta '_{cl}\) but \(\Delta \ne \Delta '\)?
6.3.3 Canonical Model Construction
We are now going to show that any clant-saturated theory \(\Delta \) is the set of clant formulas supported by an information state in some model. To make this claim more precise, let us define the clant-theory of an information state.
Definition 6.3.7
(Clant theory of a state) Let M be a relational information model and s a state in M. The clant theory of s is the set of clant sentences supported by s:
Our next goal in this section is to show that for any clant-saturated theory\(\Delta \) there is a model M and a state s such that \(\Delta =\text {Th}_{\text {clant}}(M,s)\).
To this end, we will now show how to construct a canonical model based on the clant-saturated theory \(\Delta \). As in the propositional case, the worlds in this model will be complete theories of classical formulas. However, in our setting we need complete theories \(\Gamma \) with the extra property that every existential sentence in \(\Gamma \) is witnessed by a constant \(\textsf {a}\in \Gamma \). The idea will be familiar to the reader from the completeness proof for classical first-order logic. We call such theories classical saturated theories.
Definition 6.3.8
(Classical saturated theories) A classical saturated theory over A is a set \(\Gamma \subseteq \mathcal {L}^A_c\) of classical sentences in the signature \(\Sigma \cup \{A\}\) satisfying:
-
Consistency: \(\bot \not \in \Gamma \);
-
Deductive closure: for all \(\alpha \in \mathcal {L}^A_c\), if \(\Gamma \vdash \alpha \) then \(\alpha \in \Gamma \);
-
Classical disjunction property: if \(\alpha \vee \beta \in \Gamma \) then \(\alpha \in \Gamma \) or \(\beta \in \Gamma \);
-
Classical existence property: if \(\exists x\alpha \in \Gamma \) then \(\alpha [\textsf {a}/x]\in \Gamma \) for some \(\textsf {a}\in A\).
Lemma 6.3.9
(Classical saturated theories are complete) If \(\Gamma \) is a classical saturated theory, then for any classical sentence \(\alpha \in \mathcal {L}^A_c\), exactly one of \(\alpha \) and \(\lnot \alpha \) belongs to \(\Gamma \).
Proof
Take \(\alpha \in \mathcal {L}^A_c\). It is easy to check that the law of excluded middle \(\alpha \vee \lnot \alpha \) is provable in our system, and so by deductive closure it is in \(\Gamma \). By the classical disjunction property, one among \(\alpha \) and \(\lnot \alpha \) must be in \(\Gamma \). Moreover, \(\alpha \) and \(\lnot \alpha \) cannot both be in \(\Gamma \), since \(\alpha ,\lnot \alpha \vdash \bot \) and then \(\bot \) would have to be in \(\Gamma \) as well by deductive closure, violating consistency.\(\Box \)
We now need a standard saturation lemma showing that every consistent set of classical formulas with an extra property can be extended to a classical saturated theory.
Lemma 6.3.10
(Classical saturation lemma) Let \(\Theta \subseteq \mathcal {L}^A_c\) be a set of classical sentences satisfying:
-
Consistency: \(\Theta \not \vdash \bot \);
-
Normality: for all \(\alpha \in \mathcal {L}^A_c\), if \(\Theta \not \vdash \forall x\alpha \) then \(\Theta \not \vdash \alpha [\textsf {a}/x]\) for some \(\textsf {a}\in A\).
Then \(\Theta \) can be extended to a classical saturated theory \(\Gamma \).
Proof
Starting with \(\Gamma _0:=\Theta \), we will define a sequence \(\Gamma _0\subseteq \Gamma _1\subseteq \Gamma _2\subseteq \dots \) of sets, each of which satisfies consistency and normality. To define this sequence, fix an enumeration \(\{\alpha _0,\alpha _1,\alpha _2,\dots \}\) of the set \(\mathcal {L}^A_c\) of classical sentences. In order to define \(\Gamma _{n+1}\) inductively, we consider sentence \(\alpha _n\) and distinguish three cases:
-
Case 1: \(\Gamma _{n}\vdash \lnot \alpha _n\). In this case \(\Gamma _{n+1}:=\Gamma _n\). Consistency and normality are obviously preserved.
-
Case 2: \(\Gamma _n\not \vdash \lnot \alpha _n\) and \(\alpha _n\) is not of the form \(\exists x\gamma \). Then we let \(\Gamma _{n+1}:=\Gamma _n\cup \{\alpha _n\}\).
Note that \(\Gamma _{n+1}\) is consistent, otherwise by the rules for negation we would have \(\Gamma _n\vdash \lnot \alpha _n\). Moreover, \(\Gamma _{n+1}\) satisfies normality. For suppose \(\Gamma _{n+1}\not \vdash \forall x\beta \). By the rules for implication, it follows that \(\Gamma _n\not \vdash \alpha _n\rightarrow \forall x\beta \). Since \(\alpha _n\) is a sentence, \(\alpha _n\rightarrow \forall x\beta \) is provably equivalent to \(\forall x(\alpha _n\rightarrow \beta )\), so we have \(\Gamma _n\not \vdash \forall x(\alpha _n\rightarrow \beta )\). By the induction hypothesis, \(\Gamma _n\not \vdash (\alpha _n\rightarrow \beta )[\textsf {a}/x]\) for some \(\textsf {a}\in A\). Since \(\alpha _n\) is a sentence, and thus does not contain free occurrences of x, this amounts to \(\Gamma _n\not \vdash \alpha _n\rightarrow \beta [\textsf {a}/x]\). And again by the rules for implication, it follows that \(\Gamma _{n+1}\not \vdash \beta [\textsf {a}/x]\).
-
Case 3: \(\Gamma _n\not \vdash \lnot \alpha _n\) and \(\alpha _n\) is of the form \(\exists x\gamma \). Since in our system \(\lnot \exists x\gamma \) is inter-derivable with \(\forall x\lnot \gamma \), it follows that \(\Gamma _n\not \vdash \forall x\lnot \gamma \), and so by normality, \(\Gamma _n\not \vdash \lnot \gamma [\textsf {a}_i/x]\) for some i. We can then let \(\Gamma _{n+1}:=\Gamma _n\cup \{\alpha _n,\gamma [\textsf {a}_i/x]\}\) where i is the least number such that \(\Gamma _n\).
Note that \(\Gamma _{n+1}\) is consistent, because if we had \(\Gamma _{n}\cup \{\alpha _n,\gamma [\textsf {a}_i/x]\}\vdash \bot \), then since \(\gamma [\textsf {a}_i/x]\vdash \alpha _n\) we would have \(\Gamma _{n}\cup \{\gamma [\textsf {a}_i/x]\}\vdash \bot \), and then by the rules for negation also \(\Gamma _{n}\vdash \lnot \gamma [\textsf {a}_i/x]\), contrary to assumption. Moreover, with a reasoning analogous to the one given for Case 2 we can argue that \(\Gamma _{n+1}\) satisfies normality.
We can then let \(\Gamma :=\bigcup _{n\in \mathbb {N}}\Gamma _n\). We just need to check that \(\Gamma \) is a classical saturated theory.
Clearly, as a limit of a sequence of consistent sets, \(\Gamma \) is consistent. To see that \(\Gamma \) is deductively closed, suppose \(\Gamma \vdash \alpha _n\). Since \(\Gamma \) is consistent, this implies \(\Gamma \not \vdash \lnot \alpha _n\). Since \(\Gamma _n\subseteq \Gamma \), this implies \(\Gamma _n\not \vdash \lnot \alpha _n\). But then by construction \(\alpha _n\in \Gamma _{n+1}\) and thus also \(\alpha _n\in \Gamma \).
To see that \(\Gamma \) has the classical disjunction property, we reason by contraposition: suppose that \(\alpha _n,\alpha _m\not \in \Gamma \). By construction, this is only possible if \(\Gamma _n\vdash \lnot \alpha _n\) and \(\Gamma _m\vdash \lnot \alpha _m\), which implies \(\Gamma \vdash \lnot \alpha _n\) and \(\Gamma \vdash \lnot \alpha _m\). Since in our proof system we have \(\lnot \alpha _n,\lnot \alpha _m\vdash \lnot (\alpha _n\vee \alpha _m)\), by deductive closure we have \(\lnot (\alpha _n\vee \alpha _m)\in \Gamma \), which implies \(\alpha _n\vee \alpha _m\not \in \Gamma \).
Finally, to see that \(\Gamma \) has the existence property, suppose \(\exists x\gamma \in \Gamma \) and suppose \(\exists x\gamma =\alpha _n\). Then by consistency \(\Gamma \not \vdash \lnot \alpha _n\) and thus also \(\Gamma _n\not \vdash \lnot \alpha _n\). Therefore by construction we have \(\gamma [\textsf {a}/x]\in \Gamma _{n+1}\subseteq \Gamma \) for some \(\textsf {a}\in A\).\(\Box \)
We are now ready to define a canonical model for the clant-saturated theory \(\Delta \).
Definition 6.3.11
(Canonical model) Let \(\Delta \) be a clant saturated theory. We define the canonical model \(M^c_\Delta \) for \(\Delta \) as follows:
-
The set of worlds \(W_\Delta ^c\) is the set of classical saturated theories \(\Gamma \) over A such that \(\Delta _{cl}\subseteq \Gamma \).
-
The domain is A.
-
Given a relation symbol R and a world \(\Gamma \in W_\Delta ^c\), \(\langle \textsf {a}_{i_1},\dots ,\textsf {a}_{i_n}\rangle \in R_\Gamma \iff R(\textsf {a}_{i_1},\dots ,\textsf {a}_{i_n})\in \Gamma \).
-
The identity relation at world \(\Gamma \) is given by \(\textsf {a}_i\sim _\Gamma \textsf {a}_j\iff (\textsf {a}_i=\textsf {a}_j)\in \Gamma \).
-
For a non-rigid function symbol f and a world \(\Gamma \), we let \(f_\Gamma (\textsf {a}_{i_1},\dots ,\textsf {a}_{i_n})=\textsf {a}_{j}\) where j is the least number such that \(\Gamma \) contains the identity formula \(f(\textsf {a}_{i_1},\dots ,\textsf {a}_{i_n})=\textsf {a}_{j}\).
Notice that this j exists: the formula \(\exists x(f(\textsf {a}_{i_1},\dots ,\textsf {a}_{i_n})=x)\) is provable in our proof system (Exercise 6.4.2), and since it is a classical formula, by deductive closure it belongs to \(\Gamma \). Then by the classical existence property \(\Gamma \) must contain \(f(\textsf {a}_{i_1},\dots ,\textsf {a}_{i_n})=\textsf {a}_j\) for some \(\textsf {a}_j\in A\).
As a special case, for a non-rigid constant symbol c we let \(c_\Gamma =\textsf {a}_j\) where j is the least number such that \((c=\textsf {a}_j)\in \Gamma \).
-
For a rigid function symbol \(\textsf {f}\) and a world \(\Gamma \), we let \(\textsf {f}_\Gamma (\textsf {a}_{i_1},\dots ,\textsf {a}_{i_n})=\textsf {a}_{j}\) where j is the least number such that \(\Delta \) (rather than \(\Gamma \), as in the previous case) contains the identity formula \(\textsf {f}(\textsf {a}_{i_1},\dots ,\textsf {a}_{i_n})=\textsf {a}_{j}\).
Again, such a j exists: for \(\textsf {f}\) rigid, the formula \(\mathord {\exists \!\!\!\exists }x(\textsf {f}(\textsf {a}_{i_1},\dots ,\textsf {a}_{i_n})=x)\) is provable in our proof system (Exercise 6.4.2; note that this time the existential is an inquisitive one), and since it is a clant formula, by deductive closure it belongs to \(\Delta \), which is clant saturated. Then by the inquisitive existence property \(\Delta \) must contain \(\textsf {f}(\textsf {a}_{i_1},\dots ,\textsf {a}_{i_n})=\textsf {a}_j\) for some \(\textsf {a}_j\in A\).
Note that the interpretation of \(\textsf {f}\) does not depend on the specific world \(\Gamma \), but only on \(\Delta \), and thus the interpretation of \(\textsf {f}\) is indeed rigid.
As a special case, for a rigid constant symbol \(\textsf {c}\) we let \(\textsf {c}_\Gamma =\textsf {a}_j\) where j is the least number such that \((c=\textsf {a}_j)\in \Delta \).
Lemma 6.3.12
For any closed term t of the signature \(\Sigma \cup \{A\}\) and point \(\Gamma \in W^c_\Delta \), if \([t]_\Gamma =\textsf {a}\) then the formula \((t=\textsf {a})\) is in \(\Gamma \).
Proof
By induction on t.
-
If t is atomic, then since t is a closed term it must be a constant c. Then by definition we have \([c]_\Gamma =\textsf {a}_j\) for some constant \(\textsf {a}_j\) such that \((c=\textsf {a}_j)\in \Gamma \) (this holds also for the case in which c is rigid, since in that case \((c=\textsf {a}_j)\in \Delta _{cl}\subseteq \Gamma \)).
-
Suppose t is a complex term \(t=f(t_1,\dots ,t_n)\) and suppose the claim holds for \(t_1,\dots ,t_n\). Suppose \([t_i]_\Gamma =\textsf {a}_{k_i}\) for each i. By induction hypothesis, \(\Gamma \) contains the formula \(t_i=\textsf {a}_{k_i}\) By definition we have \([f(t_1,\dots ,t_n)]_\Gamma =f_\Gamma ([t_1]_\Gamma ,\dots ,[t_n]_\Gamma )=f_\Gamma (\textsf {a}_{k_1},\dots ,\textsf {a}_{k_1})=\textsf {a}_{j}\) for a constant \(\textsf {a}_j\) such that the formula \(f(\textsf {a}_{k_1},\dots ,\textsf {a}_{k_1})=\textsf {a}_{j}\) is in \(\Gamma \). By using the rule \((=\!\!\textsf {e})\), i.e., the replacement of identicals, we have:
$$(t_1=\textsf {a}_{k_1}),\dots ,(t_n=\textsf {a}_{k_n}),f(\textsf {a}_{k_1},\dots ,\textsf {a}_{k_1})=\textsf {a}_{j}\vdash f(t_1,\dots ,t_t)=\textsf {a}_{j}.$$Since \(\Gamma \) contains the premises and is closed under deduction of classical formulas, \(\Gamma \) contains the conclusion, which is exactly the formula \(t=\textsf {a}_j\) where \(\textsf {a}_j=[t]_\Gamma \).\(\Box \)
We are now in a position to show the truth lemma: for every classical formula, truth at a world \(\Gamma \) in the canonical model coincides with membership to \(\Gamma \).
Lemma 6.3.13
(Truth lemma) For any point \(\Gamma \in W^c_\Delta \) and any classical sentence \(\alpha \in \mathcal {L}^A_c\) we have:
Proof
By induction on \(\alpha \).
-
\(\alpha \) is an atomic formula \(R(t_1,\dots ,t_n)\). Suppose \([t_i]_\Gamma =\textsf {a}_{k_i}\). By the previous lemma, \(\Gamma \) contains the formula \(t_i=\textsf {a}_{k_i}\). We have
$$\begin{aligned} M^c_\Delta ,\Gamma \models R(t_1,\dots ,t_n)\iff & {} \langle \textsf {a}_{k_1},\dots ,\textsf {a}_{k_n}\rangle \in R_\Gamma \\\iff & {} R(\textsf {a}_{k_1},\dots ,\textsf {a}_{k_n})\in \Gamma \\\iff & {} R(t_1,\dots ,t_n)\in \Gamma \end{aligned}$$where the second biconditional uses the definition of \(R_\Gamma \), and the last uses the rule \((=\!\!\textsf {e})\) of replacement of identicals and the closure of \(\Gamma \) under classical deduction.
-
\(\alpha \) is an atomic formula \((t=t')\). Analogous to the previous case.
-
\(\alpha =\bot \). The claim is obvious, since \(\bot \) is not true at \(\Gamma \), and not contained in \(\Gamma \) by the consistency requirement.
-
\(\alpha =(\beta \wedge \gamma )\). We have:
$$\begin{aligned} M^c_\Delta ,\Gamma \models \beta \wedge \gamma\iff & {} M^c_\Delta ,\Gamma \models \beta \text { and }M^c_\Delta \models \gamma \\\iff & {} \beta \in \Gamma \text { and }\gamma \in \Gamma \\\iff & {} \beta \wedge \gamma \in \Gamma , \end{aligned}$$where the second step uses the induction hypothesis and the last step the closure of \(\Gamma \) under classical deduction.
-
\(\alpha =(\beta \rightarrow \gamma )\). We have:
$$\begin{aligned} M^c_\Delta ,\Gamma \models \beta \rightarrow \gamma\iff & {} M^c_\Delta ,\Gamma \not \models \beta \text { or }M^c_\Delta \models \gamma \\\iff & {} \beta \not \in \Gamma \text { or }\gamma \in \Gamma \\\iff & {} \lnot \beta \in \Gamma \text { or }\gamma \in \Gamma \\\iff & {} (\lnot \beta \vee \gamma )\in \Gamma \\\iff & {} (\beta \rightarrow \gamma )\in \Gamma . \end{aligned}$$Here, the second step uses the induction hypothesis. The third step uses Lemma 6.3.9. The fourth step uses the closure of \(\Gamma \) under classical deduction as well as the disjunction property of \(\Gamma \). And the last step uses again the closure of \(\Gamma \) under classical deduction, since in our system the formulas \(\lnot \beta \vee \gamma \) and \(\beta \rightarrow \gamma \) are inter-derivable.
-
\(\alpha =\forall x\beta \). We have:
$$\begin{aligned} M^c_\Delta ,\Gamma \models \forall x\beta\iff & {} M^c_\Delta ,\Gamma \models _{x\mapsto \textsf {a}_i} \beta \text { for all }\textsf {a}_i\in A\\\iff & {} M^c_\Delta ,\Gamma \models \beta [\textsf {a}_i/x]\text { for all }\textsf {a}_i\in A\\\iff & {} \beta [\textsf {a}_i/x]\in \Gamma \text { for all }\textsf {a}_i\in A\\\iff & {} \forall x\beta \in \Gamma . \end{aligned}$$Here, the second step uses the fact that \(M^c_\Delta ,\Gamma \models _{x\mapsto \textsf {a}_i}(x=\textsf {a}_i)\), which justifies the substitution of \(\textsf {a}_i\) for x in \(\beta \) and the dropping of referent to the assignment, since the result is a sentence. The third step uses the induction hypothesis. For the left-to-right direction of the last step, suppose towards a contradiction that \(\forall x\beta \not \in \Gamma \). Then by Lemma 6.3.9, \(\lnot \forall x\beta \in \Gamma \). Since in our system \(\lnot \forall x\beta \) is inter-derivable with \(\exists x\lnot \beta \), by closure under classical deduction we have \(\exists x\lnot \beta \in \Gamma \). By the classical existence property of \(\Gamma \), it follows that for some \(\textsf {a}_i\in A\), \(\lnot \beta [\textsf {a}_i/x]\in \Gamma \), and therefore by Lemma 6.3.9 \(\beta [\textsf {a}_i/x]\not \in \Gamma \). Hence, it is not the case that \(\beta [\textsf {a}_i/x]\in \Gamma \) for all \(\textsf {a}_i\in A\). The converse direction follows simply by closure under classical deduction, since \(\forall x\beta \vdash \beta [\textsf {a}_i/x]\).\(\Box \)
The next step in the proof is to show that the set of classical formulas supported by the entire universe \(W^c_\Delta \) of the canonical model \(M^c_\Delta \) is precisely the classical part of \(\Delta \).
Lemma 6.3.14
For any classical sentence \(\alpha \in \mathcal {L}^A_c\) we have
Proof
Suppose \(\alpha \in \Delta _{cl}\). Then \(\alpha \in \Gamma \) for every \(\Gamma \in W^c_\Delta \). By the previous lemma, this implies \(M^c_\Delta ,\Gamma \models \alpha \) for every \(\Gamma \in W^c_\Delta \). Since \(\alpha \) is classical and thus truth-conditional, this implies \(M^c_\Delta ,W^c_\Delta \models \alpha \).
For the converse, suppose \(\alpha \not \in \Delta _{cl}\). We claim that \(\Delta _{cl}\cup \{\lnot \alpha \}\not \vdash \bot \). For suppose towards a contradiction that \(\Delta _{cl}\cup \{\lnot \alpha \}\vdash \bot \). Then by the rules for implication we would have \(\Delta _{cl}\vdash \lnot \lnot \alpha \), and by classical double negation elimination also \(\Delta _{cl}\vdash \alpha \), whence \(\alpha \in \Delta _{cl}\) by the deductive closure of \(\Delta \), which contradicts our assumption.
Moreover, \(\Delta _{cl}\cup \{\lnot \alpha \}\) satisfies the normality condition. To see this, suppose \(\Delta _{cl}\cup \{\lnot \alpha \}\not \vdash \forall x\beta \). This means that \(\Delta _{cl}\not \vdash \lnot \alpha \rightarrow \forall x\beta \), and since \(\lnot \alpha \) is a sentence also \(\Delta _{cl}\not \vdash \forall x(\lnot \alpha \rightarrow \beta )\). This implies \(\forall x(\lnot \alpha \rightarrow \beta )\not \in \Delta _{cl}\), and so \(\forall x(\lnot \alpha \rightarrow \beta )\not \in \Delta \) (since \(\forall x(\lnot \alpha \rightarrow \beta )\) is a classical formula). By the normality of \(\Delta \), it follows that \(\Delta \not \vdash \lnot \alpha \rightarrow \beta [\textsf {a}/x]\) for some \(\textsf {a}\in A\), which implies \(\Delta \cup \{\lnot \alpha \}\not \vdash \beta [\textsf {a}/x]\). A fortiori also \(\Delta _{cl}\cup \{\lnot \alpha \}\not \vdash \beta [\textsf {a}/x]\).
So, we have shown that \(\Delta _{cl}\cup \{\lnot \alpha \}\) satisfies consistency and normality, By Lemma 6.3.10, this set can be extended to a classical saturated theory \(\Gamma \). Since \(\lnot \alpha \in \Gamma \) we have \(\alpha \not \in \Gamma \), and thus by the previous lemma \(M^c_\Delta ,\Gamma \not \models \alpha \). Finally, since \(\Gamma \in W^c_\Delta \) this implies \(M^c_\Delta ,W^c_\Delta \not \models \alpha \).\(\Box \)
The last step is to establish that the clant theory of the state \(W^c_\Delta \) is precisely \(\Delta \). For this, we first note that the clant theory of this state is a clant-saturated theory.
Lemma 6.3.15
For any non-empty state s, \(\text {Th}_{\text {clant}}(M^c_{\Delta },s)\) is a clant-saturated theory.
Proof
We have consistency since \(s\ne \emptyset \). Deductive closure follows since the rules of our proof system are sound and thus anything provable is also a semantic entailment. The remaining properties hold simply by the semantics and the fact that the domain of the model is A. As an illustration, consider normality. If \(\forall x\varphi \not \in \text {Th}_{\text {clant}}(M^c_{\Delta },s)\) this means that \(M^c_{\Delta },s\not \models \forall x\varphi \). Thus, for some \(\textsf {a}\in A\) we have \(M^c_{\Delta },s\not \models _{[x\mapsto \textsf {a}]}\varphi \). By definition of the canonical model we have \(M^c_{\Delta },s\models _{[x\mapsto \textsf {a}]}(x=\textsf {a})\), and therefore by Proposition 5.4.3 \(M^c_{\Delta },s\not \models \varphi [\textsf {a}/x]\), where we can drop reference to the assignment because \(\varphi [\textsf {a}/x]\) is a sentence. This means that \(\varphi [\textsf {a}/x]\not \in \text {Th}_{\text {clant}}(M^c_{\Delta },s)\). \(\Box \)
We can now prove the desired result.
Lemma 6.3.16
For any clant-saturated theory \(\Delta \), \(\text {Th}_{\text {clant}}(M^c_{\Delta },W^c_{\Delta })=\Delta \).
Proof
By the previous lemma, \(\text {Th}_{\text {clant}}(M^c_{\Delta },W^c_{\Delta })\) is a clant saturated theory. By Lemma 6.3.14, \(\text {Th}_{\text {clant}}(M^c_{\Delta },W^c_{\Delta })\) and \(\Delta \) have the same classical part. Therefore by Lemma 6.3.5, these theories coincide. \(\Box \)
6.3.4 Completeness
In the previous section, we have seen how given a clant-saturated theory\(\Delta \) we can find an information state that, among the clant sentences, satisfies all and only the sentences in \(\Delta \). In order to show completeness, what remains to be shown is the following saturation lemma.
Lemma 6.3.17
Let \(\Phi \cup \{\psi \}\subseteq \mathcal {L}\) be a set of clant sentences such that \(\Phi \not \vdash \psi \). Then there exists clant-saturated theory \(\Delta \subseteq \mathcal {L}^A\) over A such that \(\Phi \subseteq \Delta \) but \(\psi \not \in \Delta \).
In order to show this lemma, it is useful to introduce some new notation. If \(\Delta ,\Lambda \) are sets of clant formulas with \(\Lambda \ne \emptyset \), we write
to mean that there are formulas \(\lambda _1,\dots ,\lambda _m\in \Lambda \) such that  .Footnote 4
.Footnote 4
We have the following fact, which amounts to the admissibility of a cut rule for this relation. The proof involves only the rules for inquisitive disjunction, and is left as an exercise (Exercise 6.4.6).
Lemma 6.3.18
(Cut admissibility) If \(\Delta \cup \{\chi \}\vdash \Lambda \) and \(\Delta \vdash \Lambda \cup \{\chi \}\) then \(\Delta \vdash \Lambda \).
We are now ready to prove our saturation lemma.
Proof of Lemma 6.3.17. The proof adapts a construction by Dov Gabbay (see [3], Sect. 3.3, Theorem 2). Take \(\Phi \cup \{\psi \}\subseteq \mathcal {L}\) with \(\Phi \not \vdash \psi \). Fix an enumeration \(\varphi _0,\varphi _1,\varphi _2,\dots \) of all clant sentences in the extended language \(\mathcal {L}^A\). We will define inductively two sequences \(\Delta _0\subseteq \Delta _1\subseteq \dots \) and \(\Lambda _0\subseteq \Lambda _1\subseteq \dots \) making sure that for every n the following conditions are satisfied:
-
1.
\(\Delta _n\not \vdash \Lambda _n\);
-
2.
\(\Delta _n\cup \Lambda _n\) contains only finitely many constants \(\textsf {a}\in A\).
We start out by setting \(\Delta _0=\Phi \) and \(\Lambda _0=\{\psi \}\). The first condition amounts to \(\Phi \not \vdash \psi \), which is true by assumption. The second condition is true since \(\Phi \cup \{\psi \}\) is a set in the signature \(\Sigma \), and so contains no constants from A.
Now inductively, in order to define the \(n+1\)-th elements of the sequence, we consider the sentence \(\varphi _n\). Now we distinguish two cases.
-
Case 1: \(\Delta _n\cup \{\varphi _n\}\not \vdash \Lambda _n\). In this case, we distinguish two sub-cases.
-
*
Sub-case 1: \(\varphi _n\) is not of the form \(\mathord {\exists \!\!\!\exists }x\psi \). In this case we let \(\Delta _{n+1}=\Delta _n\cup \{\varphi _n\}\) and \(\Lambda _{n+1}=\Lambda _n\). Obviously conditions 1 and 2 are satisfied for the pair \(\Delta _{n+1},\Lambda _{n+1}\).
-
*
Sub-case 2: \(\varphi _n\) is of the form \(\mathord {\exists \!\!\!\exists }x\psi \). In this case, take the first fresh constant \(\textsf {a}_i\in A\) not occurring in \(\Delta _n\cup \{\varphi _n\}\cup \Lambda _n\), which exists because by induction hypothesis \(\Delta _n\cup \Lambda _n\) contains only finitely many constants from A. We let \(\Delta _{n+1}=\Delta _n\cup \{\varphi _n,\psi [\textsf {a}_i/x]\}\) and \(\Lambda _{n+1}=\Lambda _n\).
Obviously condition 2 is satisfied. To see that condition 1 is satisfied as well, suppose towards a contradiction that \(\Delta _{n+1}\vdash \Lambda _{n+1}\), i.e., \(\Delta _n\cup \{\varphi _n,\psi [\textsf {a}_i/x]\}\vdash \Lambda _n\). This means that there are \(\lambda _1,\dots ,\lambda _m\in \Lambda _n\) such that there is a proof
 . Now let y be a variable not occurring in this proof. If we replace every occurrence of \(\textsf {a}_i\) in the proof by y, we get a new proof \(P^\prime \). This replacement has no effect on any assumption besides \(\psi [\textsf {a}_i/x]\),
nor on the conclusion, since we chose \(\textsf {a}_i\) to be such that it does not occur in these
formulas. So we have
. Now let y be a variable not occurring in this proof. If we replace every occurrence of \(\textsf {a}_i\) in the proof by y, we get a new proof \(P^\prime \). This replacement has no effect on any assumption besides \(\psi [\textsf {a}_i/x]\),
nor on the conclusion, since we chose \(\textsf {a}_i\) to be such that it does not occur in these
formulas. So we have  . Now since y does not occur free in any assumption besides \(\psi [y/x]\) nor in the conclusion, and given that we have the premise \(\mathord {\exists \!\!\!\exists }x\psi \) available (which is \(\varphi _n\)), we can use the rule \((\mathord {\exists \!\!\!\exists }\textsf {e})\) to discharge the assumption \(\psi [y/x]\) and obtain
. Now since y does not occur free in any assumption besides \(\psi [y/x]\) nor in the conclusion, and given that we have the premise \(\mathord {\exists \!\!\!\exists }x\psi \) available (which is \(\varphi _n\)), we can use the rule \((\mathord {\exists \!\!\!\exists }\textsf {e})\) to discharge the assumption \(\psi [y/x]\) and obtain  . But this means that \(\Delta _n\cup \{\varphi _n\}\vdash \Lambda _n\), contrary to assumption.
. But this means that \(\Delta _n\cup \{\varphi _n\}\vdash \Lambda _n\), contrary to assumption.
-
Case 2: \(\Delta _n\cup \{\varphi _n\}\vdash \Lambda _n\). In this case, we must have \(\Delta _n\not \vdash \Lambda _n\cup \{\varphi _n\}\), otherwise by the previous lemma we would have \(\Delta _n\vdash \Lambda _n\), contrary to the induction hypothesis. Once again, we distinguish two sub-cases.
-
*
Sub-case 1: \(\varphi _n\) is not of the form \(\forall x\psi \). In this case we let \(\Delta _{n+1}=\Delta _n\) and \(\Lambda _{n+1}=\Lambda _n\cup \{\varphi _n\}\). Obviously conditions 1 and 2 are satisfied for the pair \(\Delta _{n+1},\Lambda _{n+1}\).
-
*
Sub-case 2: \(\varphi _n\) is of the form \(\forall x\psi \). In this case, take the first fresh constant \(\textsf {a}_i\in A\) not occurring in \(\Delta _n\cup \Lambda _n\cup \{\varphi _n\}\), which exists since by induction hypothesis \(\Delta _n\cup \Lambda _n\) contains only finitely many constants from A. We let \(\Delta _{n+1}=\Delta _n\) and \(\Lambda _{n+1}=\Lambda _n\cup \{\varphi _n,\psi [\textsf {a}_i/x]\}\).
Obviously condition 2 is satisfied by the resulting pair. To see that condition 1 is satisfied as well, suppose towards a contradiction that \(\Gamma _{n+1}\vdash \Lambda _{n+1}\), that is, \(\Gamma _{n}\vdash \Lambda _{n}\cup \{\forall x\psi ,\psi [\textsf {a}_i/x]\}\). Then there must be sentences \(\lambda _1,\dots ,\lambda _m\in \Lambda _n\) such that there is a proof
 . Let y be a variable not occurring in this proof. Replacing \(\textsf {a}_i\) by y throughout P we get a new proof \(P'\). Note that the substitution does not affect the premises of the proof, nor any of the formulas \(\lambda _i\) or \(\forall x\psi \), since \(\textsf {a}_i\) was chosen in such a way as not to occur in these sentences. So we have
. Let y be a variable not occurring in this proof. Replacing \(\textsf {a}_i\) by y throughout P we get a new proof \(P'\). Note that the substitution does not affect the premises of the proof, nor any of the formulas \(\lambda _i\) or \(\forall x\psi \), since \(\textsf {a}_i\) was chosen in such a way as not to occur in these sentences. So we have  . Since the variable y does not occur in the assumptions of the proof, we can use the rule \((\forall \textsf {i})\) and get
. Since the variable y does not occur in the assumptions of the proof, we can use the rule \((\forall \textsf {i})\) and get  . Since x does not occur free in any disjunct except \(\psi \) (as the other disjuncts are sentences), by the (CD) rule we get a proof
. Since x does not occur free in any disjunct except \(\psi \) (as the other disjuncts are sentences), by the (CD) rule we get a proof  . (Note that this is the only point in the completeness proof where the rule (CD) is used.) Recalling that \(\forall x\psi \) is simply \(\varphi _n\), this means that we have \(\Gamma _n\vdash \Lambda _n\cup \{\varphi _n\}\), contrary to assumption.
. (Note that this is the only point in the completeness proof where the rule (CD) is used.) Recalling that \(\forall x\psi \) is simply \(\varphi _n\), this means that we have \(\Gamma _n\vdash \Lambda _n\cup \{\varphi _n\}\), contrary to assumption.
Finally, let \(\Delta =\bigcup _{n\in \mathbb {N}}\Delta _n\) and \(\Lambda =\bigcup _{n\in \mathbb {N}}\Lambda _n\). Notice that we have \(\Delta \not \vdash \Lambda \), otherwise we should also have \(\Delta _n\vdash \Lambda _n\) for some n, which is not the case by construction. This implies, in particular, that \(\Delta \) and \(\Lambda \) are disjoint.
Moreover, \(\Delta \) and \(\Lambda \) partition the set of all clant sentences. For given a clant sentence \(\varphi _n\), by construction this is going to be included either in \(\Delta _{n+1}\) (and thus in \(\Delta \)) or in \(\Lambda _{n+1}\) (and thus in \(\Lambda \)).
We are going to show that \(\Delta \) is the clant-saturated theory that we need. First, we have \(\Phi \subseteq \Delta \) (since \(\Phi =\Delta _0\)) and \(\psi \not \in \Delta \) (since \(\psi \) is in \(\Lambda _0\), and so also in \(\Lambda \), which is disjoint from \(\Delta \)). It remains to be seen that \(\Delta \) is clant-saturated.
-
Consistency. We have \(\bot \not \in \Delta \), for if we had \(\bot \in \Delta \), then since \(\Lambda \) is non-empty, by the ex-falso rule we would have \(\Delta \vdash \Lambda \).
-
Deductive closure. If \(\Delta \vdash \varphi \) for a clant sentence \(\varphi \), then \(\varphi \) must be in \(\Delta \). Otherwise, \(\varphi \) would have to be in \(\Lambda \), and then we would have \(\Delta \vdash \Lambda \).
-
Inquisitive disjunction property. Suppose
 . Then at least one of \(\varphi \) and \(\psi \) must be in \(\Delta \). For otherwise, both \(\varphi \) and \(\psi \) would be in \(\Lambda \), and then since
. Then at least one of \(\varphi \) and \(\psi \) must be in \(\Delta \). For otherwise, both \(\varphi \) and \(\psi \) would be in \(\Lambda \), and then since  with \(\varphi ,\psi \in \Lambda \) we would have \(\Delta \vdash \Lambda \).
with \(\varphi ,\psi \in \Lambda \) we would have \(\Delta \vdash \Lambda \). -
Inquisitive existence property. Suppose \(\mathord {\exists \!\!\!\exists }x\psi \in \Delta \). Then \(\Delta \cup \{\mathord {\exists \!\!\!\exists }x\psi \}\not \vdash \Lambda \). Now suppose \(\mathord {\exists \!\!\!\exists }x\psi \) is enumerated as \(\varphi _n\). A fortiori, since \(\Delta _n\subseteq \Delta \) and \(\Lambda _n\subseteq \Lambda \), we have \(\Delta _n\cup \{\varphi _n\}\not \vdash \Lambda _n\). In this case, by construction \(\psi [\textsf {a}/x]\in \Delta _{n+1}\subseteq \Delta \) for some constant \(\textsf {a}\in A\).
-
Normality. Suppose \(\forall x\psi \not \in \Delta \), and suppose \(\forall x\psi \) is enumerated as \(\varphi _n\). Then \(\varphi _n\not \in \Delta _{n+1}\), and by construction this is only the case if we had \(\Delta _n\cup \{\varphi _n\}\vdash \Gamma _n\), i.e., if Case 2 applied to \(\varphi _n\). In this case, by construction we have \(\psi [\textsf {a}/x]\in \Lambda _{n+1}\subseteq \Lambda \) for some constant \(\textsf {a}\in A\). And since \(\Lambda \) is disjoint from \(\Delta \), \(\psi [\textsf {a}/x]\not \in \Delta \).\(\Box \)
With this saturation lemma in place, we are finally in a position to prove completeness. We first do so for the case of sentences.
Theorem 6.3.19
Let \(\Phi \cup \{\psi \}\subseteq \mathcal {L}\) be a set of clant sentences. If \(\Phi \models \psi \), then \(\Phi \vdash \psi \).
Proof
By contraposition, suppose \(\Phi \not \vdash \psi \). Then by the previous lemma we can find a clant saturated theory \(\Delta \) in the extended language \(\mathcal {L}^A\) with \(\Phi \subseteq \Delta \) and \(\psi \not \in \Delta \). By Lemma 6.3.16 there is a model M and an information state s in M such that \(\Delta \) is exactly the set of clant sentences supported at s. In particular, s supports all formulas in \(\Phi \) but not \(\psi \), which shows that \(\Phi \not \models \psi \).\(\Box \)
Finally, we can extend this result easily to open clant formulas.
Proof of Theorem 6.3.1. Suppose \(\Phi \cup \{\psi \}\) is a set of clant formulas in a signature \(\Sigma \) such that \(\Phi \not \vdash \psi \). Let \(\Sigma ^*\) be a larger signature obtained by adding a rigid constant \(\textsf {c}_x\) for each variable x occurring free in \(\Phi \cup \{\psi \}\). Let \(\Phi ^*\cup \{\psi ^*\}\) be the set of sentences obtained from \(\Phi \cup \{\psi \}\) by replacing each free occurrence of x by \(\textsf {c}_x\). We have that \(\Phi ^*\not \vdash \psi ^*\). For if we had \(\Phi ^*\vdash \psi ^*\), then it would be easy to turn a proof of this into a proof of \(\Phi \vdash \psi \). Thus by the previous Theorem, we have a model M and a state s such that \(M,s\models \Phi ^*\) but \(M,s\not \models \psi ^*\). Then, defining an assignment g such that \(g(x)=[\textsf {c}_x]\) for all variables x we have \(M,s\models _g\Phi \) and \(M,s\not \models _g\psi \), which shows that \(\Phi \not \models \psi \). \(\Box \)
A graphical illustration of the strategy of our completeness proof is given in Fig. 6.4. Note that the completeness theorem gives us an alternative route to two key meta-theoretic properties of the clant fragment, which we had obtained in Sect. 5.7.2 via a translation to classical first-order logic. First, entailment among clant formulas is compact (Theorem 5.7.9): if \(\Phi \cup \{\psi \}\subseteq \mathcal {L}_{\text {Clant}}\) and \(\Phi \models \psi \), the entailment is witnessed by a proof, in which only a finite set \(\Phi _0\) of assumptions from \(\Phi \) can appear; thus, \(\Phi _0\models \psi \) for some finite \(\Phi _0\subseteq \Phi \). Second, since there is a procedure to systematically generate all possibly proofs, it is possible to recursively enumerate the valid finitary entailments among clant formulas (Theorem 5.7.10).
As a further corollary, we also get a completeness theorem for the relation of id-entailment among clant formulas, obtained by restricting to id-models. Indeed, recall that by Proposition 5.5.31 we have \(\Phi \models _{\textsf {id}}\psi \iff \Phi ,\forall x\forall y?(x=y)\models \psi \). Notice that the formula \(\forall x\forall y?(x=y)\) is a clant formula. Therefore, by our completeness theorem we have \(\Phi \models _{\textsf {id}}\psi \) iff in our proof system for clant, \(\psi \) can be derived from \(\Phi \) with the additional premise \(\forall x\forall y?(x=y)\). Thus, if we extend our proof system by taking \(\forall x\forall y?(x=y)\) as an axiom, we get a system which is sound and complete for id-entailment.
Corollary 6.3.20
(Completeness for id-entailment) Let \(\Phi \cup \{\psi \}\subseteq \mathcal {L}_{\text {Clant}}\). We have \(\Phi \models _{\textsf {id}}\psi \iff \psi \) is derivable from \(\Phi \) in the proof system of Fig. 6.3 augmented with the axiom \(\forall x\forall y?(x=y)\).
We can also use our results above to show that every non-entailment among clant formulas can be refuted in a countable model, i.e., to establish the following theorem.
Theorem 6.3.21
(Existence of countable countermodels) Suppose \(\Phi \cup \{\psi \}\subseteq \mathcal {L}_{\text {Clant}}(\Sigma )\) for \(\Sigma \) a countable signature. If \(\Phi \not \models \psi \) then there is a model \(M=\langle W,D,I,\sim \rangle \) with \(\# W\le \aleph _0\) and \(\# D\le \aleph _0\), and an assignment g, such that \(M,W\models _g\Phi \) and \(M,W\not \models _g\psi \).
Note that the theorem does not follow directly from our canonical model construction, since the canonical models we constructed above are based on a countable domain D but have an uncountable universe W. To establish our result, we first prove a lemma: in a model with infinite domain D, every formula that can be refuted at all can in fact be refuted on state of size at most \(\# D\).
Lemma 6.3.22
Suppose \(M=\langle W,D,I,\sim \rangle \) is a relational information model with D infinite, s a state in M, and g an assignment. For all formulas \(\varphi \in \mathcal {L}^{\textsf {Q}=}\), if \(M,s\not \models _g\varphi \), there is a state \(t\subseteq s\) with \(\# t\le \# D\) such that \(M,t\not \models _g\varphi \).
Proof
By induction on \(\varphi \). If \(\varphi \) is an atomic sentence or \(\bot \), by truth-conditionality \(M,s\not \models _g\varphi \) implies \(M,t\not \models _g\varphi \) for some singleton state t, so the claim holds. We only spell out the most interesting case of the inductive step, namely, the one for \(\varphi =\mathord {\exists \!\!\!\exists }x\psi \) (for the case of  the idea is the same as in the proof of Proposition 5.6.3; for the remaining cases, see Exercise 5.9.6).
the idea is the same as in the proof of Proposition 5.6.3; for the remaining cases, see Exercise 5.9.6).
So, let \(\kappa =\# D\) and suppose \(M,s\not \models _g\mathord {\exists \!\!\!\exists }x\psi \). This means that for every \(d\in D\) we have \(M,s\not \models _{g[x\mapsto d]}\psi \). By the induction hypothesis, we thus have a substate \(t_d\subseteq s\) with \(\# t_d\le \# D\) such that \(M,t_d\not \models _{g[x\mapsto d]}\psi \). Now let \(t=\bigcup _{d\in D}t_d\). Since t is the union of \(\kappa \) sets each of which has cardinality at most \(\kappa \), we have \(\# t\le \kappa \cdot \kappa \), which is equal to \(\kappa \) since \(\kappa \) is infinite. For any given d, we have \(t_d\subseteq t\) and so by persistency \(M,t\not \models _{g[x\mapsto d]}\psi \). Therefore, \(M,t\not \models _g\mathord {\exists \!\!\!\exists }x\psi \), which completes the inductive step for \(\mathord {\exists \!\!\!\exists }\) .\(\Box \)
With this lemma at hand, we are now able to prove Theorem 6.3.21.
Proof of Theorem 6.3.21. Suppose \(\Phi \cup \{\psi \}\subseteq \mathcal {L}_{\text {Clant}}(\Sigma )\) where \(\Sigma \) is countable, and suppose \(\Phi \not \models \psi \). It follows from our canonical model construction above that there is a model \(M=\langle W,D,I,\sim \rangle \) with a countable domain D, and an assignment g, such that \(M,W\models _g\Phi \) but \(M,W\not \models _g\psi \). By Lemma 6.3.22, there is a countable substate \(t\subseteq W\) with \(M,t\not \models _g\psi \). Moreover, by persistency we have \(M,t\models _g\Phi \). Now the restriction of M to t, \(M_{|t}\), is a model with countable universe t and countable domain D, and by locality we have \(M_{|t},t\models _g\Phi \) and \(M_{|t},t\not \models _g\psi \).\(\Box \)
6.4 Exercises
Exercise 6.4.1
(Natural deduction for \(\textsf {InqBQ}\)) Consider again the (non)entailments in Exercise 5.9.4. For those entailments that are valid in \(\textsf {InqBQ}\), give natural deduction proofs.
Exercise 6.4.2
(Identity) Using the rules given in Fig. 6.1, prove the following facts:
-
Symmetry: if \(t,t'\) are any terms, \((t=t')\vdash (t'=t)\).
-
Transitivity: if \(t,t',t''\) are any terms, \((t=t'),(t'=t'')\vdash (t=t'')\).
-
Existence of referent: if t is a term not containing x, \(\vdash \exists x(t=x)\).
-
Identifiability of referent: if \(\textsf {t}\) is a rigid term not containing x, \(\vdash \mathord {\exists \!\!\!\exists }x(t=x)\).
Exercise 6.4.3
(Rigidity) We saw in Sect. 5.5.4 that, if t is not rigid, then the entailments \(\varphi (t)\models \mathord {\exists \!\!\!\exists }x\varphi (x)\) and \(\forall x\varphi (x)\models \varphi (t)\) are not generally valid. However these entailments become generally valid if we add the premise \(\lambda t\) stating that we can identify the referent of t (recall that \(\lambda t:=\mathord {\exists \!\!\!\exists }x(x=t)\) for some x not occurring in t). That is, we have:
-
\(\varphi (t),\lambda t\models \mathord {\exists \!\!\!\exists }x\varphi (x)\);
-
\(\forall x\varphi (x),\lambda t\models \varphi (t)\).
Show that these entailments are indeed valid by giving natural deduction proofs.
Exercise 6.4.4
(Classical existential) Show that the rules for classical existential given in Fig. 6.2 are implicitly available in the proof system of Fig. 6.1. That is, show that if \(\vdash \) denotes derivability in our system of Fig. 6.1, we have:
-
if \(\psi \in \mathcal {L}^{\textsf {Q}=}\) and t is a term free for x in \(\psi \), \(\psi [t/x]\vdash \exists x\psi \);
-
if \(\Phi \cup \{\psi \}\subseteq \mathcal {L}^{\textsf {Q}=},\alpha \in \mathcal {L}^{\textsf {Q}=}_c\), and y is a variable free for x in \(\psi \) which does not occur free in \(\Phi \cup \{\alpha \}\), then if \(\Phi ,\psi [y/x]\vdash \alpha \), also \(\Phi ,\exists x\psi \vdash \alpha \).
Exercise 6.4.5
(Provable classicality of negations) Complete the inductive proof of Proposition 6.1.2.
Exercise 6.4.6
(Admissibility of cut) Recall that, given two sets \(\Phi ,\Psi \) of \(\textsf {InqBQ}\) formulas, we write \(\Phi \vdash \Psi \) if for some \(n\ge 0\) there are \(\psi _1,\dots ,\psi _n\in \Psi \) such that  (such that \(\Phi \vdash \bot \), in case \(n=0\)). Prove that for any sets \(\Phi ,\Psi \) and any formula \(\chi \):
(such that \(\Phi \vdash \bot \), in case \(n=0\)). Prove that for any sets \(\Phi ,\Psi \) and any formula \(\chi \):
Notes
- 1.
See the conclusion section of Ciardelli and Grilletti [1] for an example of a valid \(\textsf {InqBQ}\)-entailment that is conjectured not to be provable in the system.
- 2.
For those readers who are familiar with intuitionistic logic, the following proposition is related to Glivenko’s theorem, which states that \(\lnot \lnot \varphi \) is intuitionistically valid iff \(\varphi \) is classically valid. Glivenko’s theorem holds in the setting of propositional logic, but not in the setting of predicate logic, essentially due to the fact that in intuitionistic logic, \(\forall x\lnot \lnot \varphi \not \models \lnot \lnot \forall x\varphi \). The validity of the entailment \(\forall x\lnot \lnot \varphi \models \lnot \lnot \forall x\varphi \), captured by the KF rule, is exactly what it takes in order for a super-intuitionistic first-order logic to validate Glivenko’s theorem (cf. Proposition 2.12.1 in [4]).
- 3.
This result is an analogue in our setting of a result by Kontinen and Väänänen [5], who axiomatized the classical consequences of first-order dependence logic.
- 4.
Note that the same relation can also be formulated more symmetrically as follows: \(\Delta \vdash \Lambda \) if there are \(\delta _1,\dots ,\delta _n\in \Delta \) and \(\lambda _1,\dots ,\lambda _m\in \Lambda \) such that
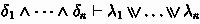 .
.
References
Ciardelli, I., & Grilletti, G. (2022). Coherence in inquisitive first-order logic. Annals of Pure and Applied Logic, 173(9). https://doi.org/10.1016/j.apal.2022.103155
Görnemann, S. (1971). A logic stronger than intuitionism. The Journal of Symbolic Logic, 36(02), 249–261.
Gabbay, D. (1981). Semantical investigations in Heyting’s intuitionistic logic (Vol. 148). Springer Science & Business Media.
Gabbay, D., Skvortsov, D., & Shehtman, V. (2009). Quantification in nonclassical logic. Elsevier
Kontinen, J., & Väänänen, J. (2013). Axiomatizing first-order consequences in dependence logic. Annals of Pure and Applied logic, 164(11), 1101–1117.
Grilletti, G. (2021). Completeness for the classical antecedent fragment of inquisitive first-order logic. Journal of Logic, Language, and Information, 30, 725–751.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2022 The Author(s)
About this chapter
Cite this chapter
Ciardelli, I. (2022). Inferences with First-Order Questions. In: Inquisitive Logic. Trends in Logic, vol 60. Springer, Cham. https://doi.org/10.1007/978-3-031-09706-5_6
Download citation
DOI: https://doi.org/10.1007/978-3-031-09706-5_6
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-09705-8
Online ISBN: 978-3-031-09706-5
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)





 then
then  . This means that
. This means that  , so by the rules for implication
, so by the rules for implication  . By the
. By the  -split rule,
-split rule,  . By the deductive closure and the disjunction property of
. By the deductive closure and the disjunction property of  , by deductive closure and the inquisitive disjunction property.
, by deductive closure and the inquisitive disjunction property. . Now let y be a variable not occurring in this proof. If we replace every occurrence of
. Now let y be a variable not occurring in this proof. If we replace every occurrence of  . Now since y does not occur free in any assumption besides
. Now since y does not occur free in any assumption besides  . But this means that
. But this means that  . Let y be a variable not occurring in this proof. Replacing
. Let y be a variable not occurring in this proof. Replacing  . Since the variable y does not occur in the assumptions of the proof, we can use the rule
. Since the variable y does not occur in the assumptions of the proof, we can use the rule  . Since x does not occur free in any disjunct except
. Since x does not occur free in any disjunct except  . (Note that this is the only point in the completeness proof where the rule (CD) is used.) Recalling that
. (Note that this is the only point in the completeness proof where the rule (CD) is used.) Recalling that  . Then at least one of
. Then at least one of  with
with 
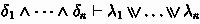 .
.