Keywords

1 Introduction

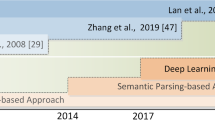
Designing an automatic solver for mathematical word problems (MWPs) has a long history dating back to the 1960s and continues to attract intensive attention as a frontier research topic. The problem is challenging because there remains a wide semantic gap to parse the human-readable words into machine-understandable logics to conduct quantitative reasoning. Various attempts have been made to bridge the gap, from rule-based pattern matching to semantic parsing with statistical machine learning, and to the recent end-to-end deep learning models that are considered as the state-of-the-art performers. To a certain extent, the problem has been recognized as a good test bed to evaluate the intelligence level of agents, as it requires semantic understanding of natural languages and capabilities of automatic reasoning. Hence, the successful solving of MWPs would constitute a milestone toward general AI.

A large body of research works start from solving arithmetic word problems for elementary school students. Its input is the text description for the math problem, represented in the form of a sequence of tokens. There are multiple quantities mentioned in the text and an unknown variable in the question whose value is to be resolved. The problem solver’s objective is to extract the relevant quantities and map this problem into an arithmetic expression whose evaluation value provides the solution to the problem. For simplicity, there are only four types of fundamental operators \(\mathcal {O}=\{+,-,\times ,\div \}\) involved in the math expression.

An example of an arithmetic word problem is illustrated in Fig. 1. The relevant quantities to be extracted from the text include 17, 7, and 80. The number of hours spent on the bike is the unknown variable x. To solve the problem, we need to identify the correct operators between the quantities and their operation order such that we can obtain the final equation 17 + 7x = 80 or expression x = (80 − 17) ÷ 7 and return 9 as the solution to this problem.

Fig. 1
figure 1

An example of an arithmetic word problem

Full size image

The early approaches mainly relied on rule-based reasoning. They heavily count upon human interventions to manually craft rules and schemas for pattern matching. Each rule consists of a set of conditions that must be satisfied and the actions to be carried out. For example, as a system published in 1985, WORDPRO, predefines a collection of rules to handle simple math problems. If the problem text matches the “HAVE-MORE-THAN” proposition, the agent will identify the two operands and use the “−” operator to derive the answer. It is evident that the usefulness of these rule-based solvers is doubtful because they can only resolve a limited number of scenarios that are defined in advance.

To improve the generality, subsequent efforts have been devoted to making use of semantic parsing to map the sentences from problem statements into structured logic representations so as to facilitate quantitative reasoning. It has regained considerable interests from the academic community, and a booming number of methods have been proposed in the past years. These methods leverage various strategies of feature engineering and statistical learning for performance boosting. For instance, if two quantities have the same dependent verbs, as in a problem like “in the first round she scored 40 points and in the second round she scored 50 points,” it is likely that “+ ” would be the operator for these two numbers. Despite the promising results claimed in some small datasets, these approaches are not completely automatic and still require human knowledge to help extract semantic features.

To further reduce human intervention and enable the automatic extraction of discriminative features, applying deep learning (DL) models in MWPs has become a promising research direction. In 2017, Wang et al. proposed DNS as the first end-to-end DL-based framework that directly converts the input of question text into the output of math expression. It is then a natural idea to apply an existing sequence-to-sequence (seq2seq) learning model to encode the text input and decode the hidden features into a math expression. The drawback is that the seq2seq model is a black box that lacks interpretability, and it cannot guarantee the output is in valid math format and normally requires a post-processing step. Nonetheless, this work still occupies an important position in the literature of MWP solving because it opened up a new research direction to apply end-to-end DL models to solve MWPs and attracted a good number of followers to contribute to this research area.

Following the research line of seq2seq models, various optimization techniques have been proposed to further improve accuracy. A recent breakthrough is that since the resulting math expression can be naturally represented as a tree structure, this finding allows us to leverage more informative context for decoding. For example, a math expression 2 + 3 can be converted to a tree structure in which the root is operator + , and there are two child nodes with operands 2 and 3. The decoder can recursively generate an expression tree in a top-down manner and take into account the encodings of parent node and sibling nodes as the more informative context. Following the idea, we have witnessed the success of seq2tree models which have exhibited clear superiority over seq2seq models. There have also emerged several incremental works on top of seq2tree models. The general idea is to replace the encoder or decoder with more effective graph-based embedding since sequences and trees can be viewed as two special cases of graphs.

At the end of the chapter, we will cover geometry problem solvers that require both textual and visual understanding. The problem is even more challenging because the input needs to be mapped into a logical representation that is compatible with both the problem text and the accompanying diagram. Common strategies to solve geometry word problems constitute three key components, including diagram understanding to capture visual clues, text parsing to capture semantic information, and deductive reasoning via a knowledge base with geometry axioms and theorems. We will introduce representative systems such as GEOS and Inter-GPS. They parse the problem text and geometry diagram into formal language and then perform symbolic reasoning step by step to derive the solution. The readers can try the demos of GEOS published by the University of Washington.Footnote 1

2 Methodology and Analysis

In the following, we present the general design principles of rule-based methods, statistic-based methods, tree-based methods, as well as recent advances with deep learning models.

2.1 Rule-Based Methods

The early approaches to math word problems are rule-based systems based on hand engineering. Published in 1985, WORDPRO (Fletcher 1985) can solve three types of simple one-step arithmetic problems, including value change, combine, and compare. A collection of rules is predefined for pattern matching. For example, given a problem text “Dan has six books. Jill has two books. How many books does Dan have more than Jill?,” it matches the predefined “HAVE-MORE-THAN” proposition. The agent will identify the two operands and use the “−” operator to derive the answer. Another system ROBUST, developed by (Bakman 2007), expanded the rule base and could better understand free-format multistep arithmetic word problems. It further extends the change schema of WORDPRO into six distinct categories. The multistep problem is solved by splitting the problem text into sentences and each sentence is mapped to a proposition. Yun et al. also proposed to use schema for multistep math problem solving (Yun et al. 2010). However, their implementation details were not explicitly revealed. Since these systems are out of date, we only provide such a brief overview for representativeness. The readers can refer to Mukherjee and Garain (2008) for a comprehensive survey of early rule-driven systems for automatic understanding of natural language math problems. Since these systems heavily rely upon human interventions to manually craft rules and schemas for pattern matching, it is evidently that the usefulness of these rule-based solvers is doubtful because they can only resolve a limited number of scenarios defined in advance.

2.2 Statistic-Based Methods

The statistic-based methods leverage traditional machine learning models to identify the entities, quantities, and operators from the problem text and yield the numeric answer with simple logic inference procedure. The scheme of quantity entailment proposed in (Roy et al. 2015) can be used to solve one-step arithmetic problems. It involves three types of classifiers to detect different properties of the word problem. The quantity pair classifier is trained to determine which pair of quantities would be used to derive the answer. The operator classifier picks the operator op ∈{+, −, ×, ÷} with the highest probability. The order classifier is relevant only for problems involving subtraction or division because the order of operands matters for these two types of operators. With the inferred expression, it is straightforward to calculate the numeric answer for the simple math problem.

To solve math problems with multistep arithmetic expression, the statistic-based methods require more advanced logic templates. This usually incurs additional preparatory overhead to annotate the text problems and associate them with the introduced template. As an early attempt, ARIS (Hosseini et al. 2014) defined a logic template named state that consists of a set of entities, their containers, attributes, quantities, and relations. For example, “Liz has 9 black kittens” initializes the number of kitten (referring to an entity) with black color (referring to an attribute) and belonging to Liz (referring to a container). The solution splits the problem text into fragments and tracks the update of the states by verb categorization. More specifically, the verbs are classified into seven categories: observation, positive, negative, positive transfer, negative transfer, construct, and destroy. To train such a classifier, we need to annotate each split fragment in the training dataset with the associated verb category. Another drawback of ARIS is that it only supports addition and subtraction. Sundaram and Khemani (2015) followed a similar processing logic to ARIS. They predefined a corpus of logic representation named schema, inspired by Bakman (2007). The sentences in the text problem are examined sequentially until the sentence matches a schema, triggering an update operation to modify the number associated with the entities.

Mitra and Baral (2016) proposed a new logic template named formula. Three types of formulas are defined, including part whole, change, and comparison, to solve problems with addition and subtraction operators. For example, the text problem “Dan grew 42 turnips and 38 cantelopes. Jessica grew 47 turnips. How many turnips did they grow in total?” is annotated with the part-whole template: 〈whole : x, parts : {42, 47}〉. To solve a math problem, the first step connects the assertions to the formulas. In the second step, the most probable formula is identified using the log-linear model with learned parameters and converted into an algebraic equation. Another type of annotation is introduced by Liang and colleagues (Liang et al. 2016a,b) to facilitate solving a math word problem. A group of logic forms is predefined and the problem text is converted into the logic form representation by certain mapping rules. For instance, the sentence “Fred picks 36 limes” will be transformed into verb(v 1, pick) & nsubj(v 1, Fred) & dobj(v 1, n 1) & head(n 1, lime) & nummod(n 1, 36). Finally, logic inference is performed on the derived logic statements to obtain the answer.

To sum up, these statistical-based methods have two drawbacks that limit their usability. First, it requires additional annotation overhead that prevents them from handling large-scale datasets. Second, these methods are essentially based on a set of predefined templates, which are brittle and rigid. It will take great efforts to extend the templates to support other operators like multiplication and division.

2.3 Tree-Based Methods

The arithmetic expression can be naturally represented as a binary tree structure such that the operators with higher priority are placed in the lower level and the root of the tree contains the operator with the lowest priority. The idea of tree-based approaches is to transform the derivation of the arithmetic expression to constructing an equivalent tree structure step by step in a bottom-up manner. One of the advantages is that there is no need for additional annotations such as equation template, tags, or logic forms. Figure 2 shows two tree examples derived from the math word problem in Fig. 1. One is called an expression tree that is used in (Roy and Roth 2015, 2017; Wang et al. 2018b), and the other is called an equation tree (Koncel-Kedziorski et al. 2015). These two types of trees are essentially equivalent and result in the same solution, except that equation tree contains a node for the unknown variable x.

Fig. 2
figure 2

Examples of expression tree and equation tree for Fig. 1

Full size image

The overall algorithmic framework common to the tree-based approaches consists of two processing stages. In the first stage, the quantities are extracted from the text and form the bottom level of the tree. The candidate trees that are syntactically valid, but with different structures and internal nodes, are enumerated. In the second stage, a scoring function is defined to pick the best matching candidate tree, which will be used to derive the final solution. A common strategy among these algorithms is to build a local classifier to determine the likelihood of an operator being selected as the internal node. The input of the classifier consists of the contextual embeddings for its two child nodes and the output is a label in the operator set {+, −, ∗, ÷}. Such local likelihood is taken into account in the global scoring function to determine the likelihood of the entire tree.

Roy and Roth (2015) proposed the first algorithmic approach that leverages the concept of an expression tree to solve arithmetic word problems. Its first strategy to reduce the search space is training a binary classifier to determine whether an extracted quantity is relevant or not. Only the relevant ones are used for tree construction and placed in the bottom level. The irrelevant quantities are discarded. The tree construction procedure is mapped to a collection of simple prediction problems, each determining the lowest common ancestor operation between a pair of quantities mentioned in the problem. The global scoring function for an enumerated tree takes into account two terms. The first one is the likelihood of quantity being irrelevant, i.e., the quantity is not used in creating the expression tree. The other term is the likelihood of selecting an operator in one of the internal tree nodes. The service is also published as a web tool (Roy and Roth 2016), and it can respond promptly to a math word problem.

ALGES (Koncel-Kedziorski et al. 2015) differs from (Roy and Roth 2015) in two major ways. First, it adopts a more brute-force manner to exploit all the possible equation trees. More specifically, ALGES does not discard irrelevant quantities but enumerates all the syntactically valid trees. Second, its scoring function is different. There is no need to measure quantity relevance because ALGES does not build such a quantity classifier. The goal of (Roy et al. 2016) is also to build an equation tree by parsing the problem text. It makes two assumptions that can simplify the tree construction, but sacrifice its applicability. First, the final output equation form is restricted to have at most two variables. Second, each quantity mentioned in the sentence can be used at most once in the final equation. The tree construction procedure consists of a pipeline of predictors that identify irrelevant quantities, recognize grounded variables, and generate the final equation tree. With customized feature selection and SVM (support vector machine)-based classifier, the relevant quantities and variables are extracted and used as the leaf nodes of the equation tree. Finally, the tree is built in a bottom-up manner.

UnitDep (Roy and Roth 2017) can be viewed as an extension of work by the same authors (Roy and Roth 2015). An important concept, named Unit Dependency Graph (UDG), is proposed to enhance the scoring function. The vertices in UDG consist of the extracted quantities. If the quantity corresponds to a rate (e.g., 8 dollars per hour), the vertex is marked as RATE. There are six types of edge relations to be considered, such as whether two quantities are associated with the same unit. Building the UDG requires additional annotation overhead as we need to train two classifiers for the nodes and edges. The node classifier determines whether a node is associated with a rate. The edge classifier predicts the type of relationship between any pair of quantity nodes. This facilitates the processing of operators “*” and “/.”

2.4 Deep Learning Models

In recent years, deep learning (DL) has witnessed great success in a wide spectrum of “smart” applications. The main advantage is that with enough training data, DL is able to learn an effective feature representation in a data-driven manner without human intervention. It is not surprising that several efforts have sought to apply DL for math word problem solving. Deep Neural Solver (DNS) (Wang et al. 2017) is the first deep learning-based algorithm that does not rely on hand-crafted features. This is a milestone contribution because all the previous methods required human intelligence to help extract features that are effective. The deep model used in DNS is a typical sequence to sequence (seq2seq) model (Sutskever et al. 2014). The readers without deep learning background can view it as a black box to magically encode the input sequence, which refers to the problem text, and generate a math expression as the output. To ensure that the output equations by the model are syntactically correct, five rules are predefined as validity constraints. For example, if the ith character in the output sequence is an operator in {+, −, ×, ÷}, then the model cannot result in c ∈{+, −, ×, ÷, ), =} for the (i + 1)th character.

Following DNS, there have emerged multiple DL-based solvers for arithmetic word problems. Seq2SeqET (Wang et al. 2018a) extended the idea of DNS by using expression tree as the output sequence. In other words, it applied seq2seq model to convert the problem text into an expression tree (as depicted in Fig. 2). Given the output of an expression tree, we can easily infer the numeric answer. T-RNN (Wang et al. 2019) can be viewed as an improvement of Seq2SeqET, in terms of quantity encoding, template representation, and tree construction. First, an effective embedding network (with Bi-LSTM and self-attention) is used to vectorize the quantities. Second, the detailed operators in the templates are encapsulated to further reduce the number of template space. For example, n 1 + n 2, n 1 − n 2, n 1 × n 2, and n 1 ÷ n 2 are mapped to the same template n 1〈op〉n 2. Third, they are the first to adopt recursive neural network (Goller and Kuchler 1996) to infer the unknown variables in the expression tree in a recursive manner.

Wang et al. made the first attempt of applying deep reinforcement learning to solve arithmetic word problems (Wang et al. 2018b). The motivation is that deep Q-network has witnessed success in solving various problems with large search space. To fit the math problem scenario, they formulate the expression tree construction as a Markov Decision Process and propose the MathDQN that is customized from the general deep reinforcement learning framework. Technically, they tailor the definitions of states, actions, and reward functions which are key components in the reinforcement learning framework. The framework learns model parameters from the reward feedback of the environment and iteratively picks the best operator for two selected quantities.

A recent breakthrough comes from the observation that tree structures (e.g., the expression trees in Fig. 2) provide a more informative data structure than sequential expression (e.g., 17 + (7 ∗ x) = 80) to leverage. Following the idea, the sequence-to-sequence generation model can be replaced by sequence-to-tree model to improve performance. GTS (Xie and Sun 2019) is a representative sequence-to-tree model and is still considered as a competitive method in solving MWPs. Its decoder recursively generates an expression tree in a top-down manner. During the decoding process, it takes into account the encodings of parent node and sibling nodes as more informative context. There have also emerged several incremental works on top of seq2seq or seq2tree models, either by replacing the encoder with graph-based embedding or using a graph as a more general structure than trees to represent math expressions. For example, Graph2Tree (Zhang et al. 2020) replaces the sequential model with graph-based embedding to better capture the relationships and order information among the quantities. Seq2DAG (Cao et al. 2021) works by extracting the equation as a Direct Acyclic Graph (DAG) structure upon problem description.

In Table 1, we summarize the performance of these models in benchmark datasets. There are three datasets commonly used, including Math23K, Math23K*, and MAWPS.

  1. 1.

    Math23K (Wang et al. 2017). The dataset contains Chinese math word problems for elementary school students and is created by web crawling from multiple online education websites. Initially, 60, 000 problems with only one unknown variable are collected. The equation templates are extracted in a rule-based manner. To ensure high precision, a large number of problems that do not fit the rules are discarded. Finally, 23, 162 math problems remained. Since the test set in Math23K is predefined, some researchers use its modified version called Math23K*. This dataset applies fivefold cross-validation and is considered to be more challenging than Math23K.

  2. 2.

    MAWPS (Koncel-Kedziorski et al. 2016) is another testbed in English language for arithmetic word problems with one unknown variable in the question. Its objective is to compile a dataset of varying complexity from different websites. Operationally, it combines the published word problem datasets used in the previous literature. There are 2373 questions in the harvested dataset.

Table 1 Performance of deep learning models on benchmark datasets
Full size table

From the results, we can see that accuracy continues to improve as a more complex encoder or decoder is applied. Seq2DAG achieves state-of-the-art performance in Math23K*. It is worth noting that there is a recent trend to leverage the power of pretrained language models, such as BERT (Devlin et al. 2019) or its variants (Clark et al. 2020; Lewis et al. 2020), to further boost the accuracy. For instance, MWP-BERT (Liang et al. 2021) incorporates BERT and TM-generation model (Lee et al. 2021) adopts ELECTRA (Clark et al. 2020) as the pretraining model. These models are pretrained using a very large number of documents with billions of words in total. The training of BERT and ELECTRA consumes enormous hardware resources and computation time and the trained model contains hundreds of millions of parameters (110M for BERT-Base and 340M for BERT-Large). When they are applied to solve MWPs, we can observe significant performance improvement.

2.5 Geometry Problem Solving

Geometry problem solving is more challenging because they require considering visual diagram and textual expressions simultaneously. As illustrated in Fig. 3, a typical geometry word problem contains text descriptions or attribute values of geometric objects. The visual diagram may contain essential information that is absent from the text. For instance, points O, B, and C are located on the same line segment, and there is a circle passing points A, B, C, and D. To well solve geometry word problems, three main challenges need to be tackled: (1) diagram parsing requires the detection of visual mentions, geometric characteristics, the spatial information, and the co-reference with text, (2) deriving visual semantics that refer to the textual information related to the visual analogue involves assigning semantic and syntactic interpretation to the text, and (3) the inherent ambiguities lie in the task of mapping visual mentions in the diagram to the concepts in real world.

Fig. 3
figure 3

An example of geometric problem

Full size image

G-ALINGER (Seo et al. 2014) is an algorithmic work that addresses the geometry diagram understanding and text understanding simultaneously. To detect primitives from a geometric diagram, the Hough transform (Shapiro and Stockman 2001) is first applied to initialize lines and circles segments. An objective function, which incorporates pixel coverage, visual coherence, and textual–visual alignment, is applied. The function is sub-modular, and a greedy algorithm is designed to pick the primitive with the maximum gain in each iteration. The algorithm stops when no positive gain can be obtained according to the objective function. GEOS (Seo et al. 2015) can be considered as the first work to tackle a complete geometric word problem as shown in Fig. 3. Its method consists of two main steps: (1) parsing text and diagram, respectively, by generating a piece of logical expression to represent the key information of the text and diagram as well as the confidence scores, and (2) addressing the optimization problem by aligning the satisfiability of the derived logical expression in a numerical method that requires manually defining the indicator function for each predicate. It is noticeable that G-ALINGER is applied in GEOS (Seo et al. 2014) for primitive detection. Despite the superiority of automated solving process, the performance of the system would be undermined if the answer choices are unavailable in a geometry problem and the deductive reasoning based on geometric axioms is not used in this method. Inter-GPS (Lu et al. 2021) adopts a similar strategy to parse the problem text and diagram into formal language automatically via rule-based text parsing and neural object detecting, respectively. It incorporates theorem knowledge as conditional rules and performs symbolic reasoning in a stepwise manner. A subsequent improver of GEOS is presented in Sachan et al. (2017). It harvests axiomatic knowledge from 20 publicly available math textbooks and builds a more powerful reasoning engine that leverages the structured axiomatic knowledge for logical inference.

GeoShader (Alvin et al. 2017) is the first tool to automatically handle geometry problems with shaded area, presenting an interesting reasoning technique based on an analysis hypergraph. The nodes in the graph represent intermediate facts extracted from the diagram and the directed edges indicate the relationship of deductibility between two facts. The calculation of the shaded area is represented as the target node in the graph and the problem is formulated as finding a path in the hypergraph that can reach the target node.

3 Conclusions

In summary, despite the great success achieved by applying DL models to solve MWPs, the current status in this research domain still has room for improvement. We now consider a number of possible future directions that may be of interest to the AI in education community.

First, aligning visual understanding with text mention is an emerging direction that is particularly important for solving geometry word problems. However, this challenging problem has only been evaluated in self-collected and small-scale datasets, similar to those early efforts on evaluating the accuracy of solving algebra word problem. There is a chance that these proposed aligning methods fail to work well in a large and diversified dataset. Hence, it calls for a new round of evaluation for generality and robustness with a better benchmark dataset yet to be developed for geometry problems.

Second, interpretability plays a key role in measuring the usability of MWP solvers in the application of online tutoring but may pose new challenges for the deep learning-based solvers. For instance, AlphaGo (Silver et al. 2016) and AlphaZero (Silver et al. 2017) have achieved astonishing superiority over human players, but their near-optimal actions could be difficult for human to interpret. Similarly, for MWP solvers, domain knowledge and reasoning capability are useful and they are easy to interpret and understandable for human beings. It may be interesting to combine the merits of DL models, domain knowledge, and reasoning capability to develop more powerful MWP solvers.

Last but not the least, solving math word problems in English plays a dominating role in the literature. We only observed a very rare number of math solvers proposed to cope with other languages. This research topic may grow into a direction with significant impact. To our knowledge, many companies in China have harvested an enormous number of word problems in K12 education. As reported in 2015,Footnote 2 Zuoyebang, a spin off from Baidu, has collected 950 million questions and solutions in its database. When coupled with deep learning models, this is an area ripe for investigatory imagination and exciting achievements can be expected.