Morphodynamic Modelling in Marine Environments: Model Formulation and Solution Techniques

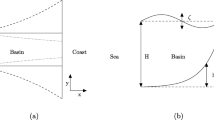
Abstract

The bathymetry and geometry of coastal seas, barrier coasts and estuaries strongly influence tides and currents, and the associated transport of sediments. In turn, these transports result in a constantly evolving bathymetry and geometry, thus resulting in a feedback loop between bathymetry and geometry, water motion and sediment transport. To capture this evolution, morphodynamic models are employed. In this chapter, first the conservation laws are derived, resulting in a system of strongly coupled partial differential equations that model the morphodynamic evolution. Subsequently, two different solution strategies, indicated as the initial value and the bifurcation approach, are discussed. In the former approach, the emphasis is on the temporal evolution of bathymetric patterns, whereas the latter approach focuses on the direct identification of asymptotic states of the system under consideration. To exemplify these two approaches, the morphodynamic evolution and asymptotic states of a short, rectangular tidal inlet are considered, showing that these two model approaches result in different and complementary insights.

Appendix

In this appendix, specific parameterisations will be chosen and the depth–averaged morphodynamic system of equations, given in Eqs. (10.16)–(10.20), will be scaled using characteristic dimensions of short tidal inlet systems. Using the non–dimensional equations, an asymptotic expansion of the physical variables is proposed and the leading order system of equations is derived.

As a first step, the bottom shear stresses $(\tau _x,\tau _y)^T$, the erosion function E and the deposition function D have to expressed in terms of relevant physical variables. Concerning the bed shear stresses, observations for turbulent flow conditions and dimension analysis suggest a quadratic dependency on the depth–averaged velocity. However, the gross features of the water motion are well captured by linearizing this quadratic dependency, resulting in a linearized friction law (Lorentz 1922; Zimmerman 1982, 1992), which is the approach taken here:

$$\begin{aligned} (\tau _x,\tau _y)^T = \rho r_\star \hat{\textbf{u}}. \end{aligned}$$

(10.38)

In this expression, $r_\star$ is a friction parameter with units $\text {m} \text {s}^{-1}$. The parameter $r_\star$ is chosen such that the net dissipation of energy (averaged over the tidal cycle and embayment) due to the linearized shear stress (10.38) equals that of the bed shear stress based on the quadratic friction law. This implies that the parameter $r_\star$ is proportional to the tidal current amplitude U and the bottom roughness.

The parameterisation of the friction terms $\hat{\textbf{F}}^b$ in the depth–averaged momentum Eqs. (10.17) and (10.18), which read

$$\begin{aligned} \hat{\textbf{F}}^b = \frac{(\tau _x,\tau _y)^T}{\rho (H-h+\zeta )}, \end{aligned}$$

becomes unbounded if the water depth tends to zero, as observed near tidal flats. As our model is designed to give only a global description of the tidal flow in an embayment, the friction terms are regularized by increasing the water depth in the denominator of the friction term by a constant $h_0$ (see Ter Brake and Schuttelaars 2010 for a detailed discussion, and the influence of this parameter on the morphodynamic equilibria).

The erosion function E and deposition function D are due to the pick–up and deposition of the sediment near the bottom. Motivated by field observations (Dyer and Soulsby 1988) and theoretical considerations, the sediment pick–up term E is taken proportional to some power of the absolute value of the difference between the actual bed shear stress and the critical shear stress for erosion. Taking this power to be equal to one (which provides a fair approximation and is computationally beneficial) and assuming the critical shear stress for erosion to be much smaller than the typical bed shear stress in a tidal inlet system, the sediment pick–up term is parameterised as:

$$\begin{aligned} E = \hat{\alpha } \left( \hat{u}^{2} + \hat{v}^2 \right) , \end{aligned}$$

where $\hat{\alpha }$ is a constant which depends on the sediment characteristics. For fine sand (grain size $2 \cdot 10^{-4} \, \text {m}$) a typical value is $\hat{\alpha } \sim 10^{-2} \text {kg} \, \text {m}^{-2} \, \text {s}^{-1}$.

The deposition function D is obtained by assuming an approximate balance between settling and vertical diffusion in the three dimensional concentration equation (10.1). Assuming the verical eddy diffusivity to be constant in space and time and that the sediment Peclet number $w_s H/K_v \gg 1$, the resulting bottom concentration can be expressed in terms of the depth–integrated concentration, resulting in $D = \gamma C$, with $\gamma = K_v/w_s^2$.

Using these parameterisations, the morphodynamic system of equations is made non–dimensional by introducing characteristic scales for all physical variables. Focussing on basin–wide phenomena, the tidally averaged basin length L is used as a typical horizontal length scale, and the inverse of the angular frequency $\sigma$ of the semidiurnal tide as a typical time scale. As a typical water depth the tidally and width-averaged water depth at the open boundary $\overline{H}$ is used, and for the $M_2$ amplitude of the free surface elevation the width–averaged water level amplitude at the open boundary $\overline{A_{M_2}}$ is employed. The velocity scale follows from the continuity equation (10.16) by requiring a balance between the temporal change in the free surface elevation and the convergence of the water transport, resulting in $U = \sigma \overline{A_{M_2}}L/\overline{H}$. The depth-integrated suspended sediment concentration is obtained by assuming an approximate balance between erosion E and deposition D. Substituting the resulting non–dimensional variables (indicated by an asterisk),

$$\begin{aligned}&(x,y)=L(x^*,y^*); \quad t={\sigma }^{-1}t^*; \quad \zeta =\overline{A_{M_2}}\zeta ^*; \quad (z,h) = \overline{H}(z^*,h^*); \nonumber \\&(u,v)=U(\hat{u}^*,\hat{v}^*); \quad C=\frac{\hat{\alpha } {U}^2}{\gamma } C^*, \quad \end{aligned}$$

(10.39)

into the morphodynamic equations results in the following non–dimensional system of equations:

$$\begin{aligned} \frac{\partial \zeta ^*}{\partial t^*} + \nabla ^* \cdot \left[ (1 - h^* + \varepsilon \zeta ^*) \boldsymbol{\hat{u}}^*\right]&= 0, \end{aligned}$$

(10.40)

$$\begin{aligned} \frac{\partial \hat{u}^*}{\partial t^*} + \varepsilon \boldsymbol{\hat{u}}^* \cdot \nabla ^* \hat{u}^* + f^* \hat{v}^* + \left( \frac{1}{\varLambda ^*}\right) ^2 \frac{\partial \zeta ^*}{\partial x^*}&= -\frac{r^* u^*}{(1-h^*+ \varepsilon \zeta ^*)}, \end{aligned}$$

(10.41)

$$\begin{aligned} \frac{\partial \hat{v}^*}{\partial t^*} + \varepsilon \boldsymbol{\hat{u}}^* \cdot \nabla ^* \hat{v}*^ - f^* \hat{u}^* + \left( \frac{1}{\varLambda ^*} \right) ^2 \frac{\partial \zeta ^*}{\partial y^*}&= -\frac{r^* \hat{v}^*}{(1-h^*+\varepsilon \zeta ^*)}, \end{aligned}$$

(10.42)

$$\begin{aligned} a^* \left\{ \frac{\partial C^*}{\partial t^*} + \varepsilon \nabla ^*\cdot \left( \boldsymbol{\hat{u}}^* C^* \right) - K_h^* \nabla ^{*2} C^* \right\}&= \left[ \left( \hat{u}^*\right) ^2 + \left( \hat{v}^*\right) ^2\right] - C^*, \end{aligned}$$

(10.43)

$$\begin{aligned} \frac{\partial h^*}{\partial t^*} - \lambda ^* \delta _b^*\nabla ^{*2} h^*&= \delta _s^* \left\{ C^* - \left[ \left( \hat{u}^*\right) ^2 + \left( \hat{v}^*\right) ^2\right] \right\} . \end{aligned}$$

(10.44)

For simplicity, the diffusive transport resulting from topographic variations is neglected in the concentration equation. Furthermore, the bedload transport has been significantly simplified (compare with Eq. (10.9)): only the contribution related to the topography is retained. Furthermore, this contribution is assumed to be isotropic in space (with the second–rank tensor $\boldsymbol{\lambda }$ reduced to a scalar coefficient $\lambda$).

The non–dimensional numbers in Eqs. (10.40)–(10.43) are $\varepsilon = \overline{A_{M_2}}/\overline{H} \equiv U/\sigma L$, which is the ratio of the mean $M_2$ tidal amplitude at the seaward boundary and the mean water depth at this boundary, $f^* =f/\sigma$ the non–dimensional Coriolis parameter, $1/\varLambda ^* = \sigma ^2 L^2/g H$ the square of the product of the frictionless tidal wavenumber and the typical lengthscale L, $r^*= r_*/\sigma H$ the non–dimensional friction parameter, $K_h^* = K_h/\sigma L^2$ the non–dimensional horizontal eddy viscosity coefficient, and $a^*=\sigma /\gamma$ the ratio of the deposition time scale and the tidal time scale $1/\sigma$.

In the bed evolution equation (10.44), apart from the non–dimensional parameter $\lambda ^* = H \lambda /L$, two other non–dimensional parameters appear. The first one is denoted by $\delta _s^* = \hat{\alpha } U^2/\rho _s(1-p) \sigma H$ which is the ratio of the tidal time scale and the typical time scale $T_{\text {s}}$ at which the bed changes due to spatial gradients in suspended sediment transport. The second non–dimensional parameter reads $\delta _b^* = \hat{s}/\sigma H L$, with $\hat{s} = (1-p) \rho _{\text {s}} \hat{q}_{\text {b}} \sqrt{g'd_{\text {s}}^3} (\theta - \theta _c)^{b_{\text {bl}}}$. This parameter $\delta _b^*$ is the ratio of the tidal time scale and the time scale $T_{\text {b}}$ of the bed evolution due to spatial gradients in bedload transport. In the systems under study the time scale $T_{\text {b}}$ is much larger than $T_{\text {s}}$, hence the bedload transport is much smaller than the suspended load transport. However, bedload effects cannot be neglected because they are necessary to suppress the growth of small–scale bedforms (Schuttelaars and De Swart 1999; Ter Brake and Schuttelaars 2011).

The fact that both morphodynamic time scales $T_{\text {s}}$ and $T_{\text {b}}$ are much larger than the hydrodynamic time scale $\sigma ^{-1}$ implies that the bed level h can be regarded as slowly varying compared to the other physical variables. Consequently the method of time–averaging can be used: the sediment and the bedrock layer thickness may be considered stationary on the comparatively short tidal time scale and its evolution is only determined by spatial gradients in the sediment transports averaged over a tidal cycle. The mathematical foundations of this approach are discussed in Sanders and Verhulst (1985) and Krol (1991).

This results in the following non–dimensional bottom evolution equation:

$$\begin{aligned} h^*_{\tau ^*} = \bigl < C^* - \left[ \left( \hat{u}^*\right) ^2 + \left( \hat{v}^*\right) ^2 \right] \bigl > + \lambda ^* \langle \nabla ^{*2} h^* \rangle , \end{aligned}$$

(10.45)

with $\langle \cdot \rangle$ denoting averaging over the tidal time scale, $\tau ^* = \delta _{s}^* t^*$ denotes the slow time coordinate, and $\lambda ^* = \kappa ^* \delta _b/\delta _s$. Using Eq. (10.43), this expression can be rewritten as

$$\begin{aligned} h^*_{\tau ^*} = - \nabla ^* \cdot \left( \boldsymbol{q}^*_{\text {diff}} + \boldsymbol{q}^*_{\text {adv}} + \boldsymbol{q}^*_{\text {bl}} \right) , \end{aligned}$$

(10.46)

with the sediment transport contributions defined as

$$\begin{aligned} \boldsymbol{q}^*_{\text {diff}}&= -a^* K_h^* \langle \nabla ^* C^* \rangle , \nonumber \\ \boldsymbol{q}^*_{\text {adv}}&= a^* \varepsilon \langle \boldsymbol{\hat{u}}^* C^* \rangle , \\ \boldsymbol{q}^*_{\text {bed}}&= -\lambda ^* \langle \nabla ^* h^* \rangle . \nonumber \end{aligned}$$

(10.47)

Considering the rectangular basin geometry, described in Sect. 10.5, the non–dimensional boundary conditions at the sidewalls are given by

$$\begin{aligned} (1-h^* +\varepsilon \zeta ^* ) \hat{v}^* = 0, \qquad K_h^* \frac{\partial C^*}{\partial y^*} = 0, \qquad \lambda ^* \frac{\partial h^*}{\partial y^*} = 0 \qquad \text {at }y^*=0, y^*=\frac{B}{L}, \end{aligned}$$

where the first condition requires the normal transport of water through the wall to vanish, and the second and third conditions require that both the suspended sediment transport and the bedload transport through the sidewalls vanish.

To obtain boundary conditions at the landward boundaries, define the location where the water depth vanishes as $X^*(t)$. At this moving boundary, the velocity is given by $\hat{u}^* = dX^*/dt^*$ and the tidally averaged (diffusive) sediment transport is assumed to vanish. The tidally averaged non–dimensional embayment length is 1, with deviations from this averaged length of $O(\varepsilon )$. Introducing this expansion in the condition of vanishing water depth at $x^*=X^*$, $1-h(X^*)+ \varepsilon \zeta (X^*,t^*) = 1$, using a Taylor expansion, it follows that in leading order $h^* = 1$ at $x^* = 1$. After substitution of this condition in the continuity equation, the boundary condition at the end of the embayment can be reformulated as a boundary condition at $x^* = 1$ and is given by $u^*_{x^*}$ is finite at $x^*=1$ (Van Leeuwen and De Swart 2001; Ter Brake and Schuttelaars 2011). Apart from this condition, the following boundary conditions are imposed:

$$\begin{aligned} K_h^* \frac{\partial C^*}{\partial x^*} + \lambda ^* \frac{\partial h^*}{\partial x^*} = 0, \qquad h^*=1 \qquad \text {at }x^* = 1. \end{aligned}$$

At the seaward boundary the water motion is forced by a single tidal constituent, the bed level is kept fixed, meaning that erosion is assumed to balance deposition:

$$\begin{aligned} \zeta ^* = \left( {A_{M_2}}/{\overline{A_{M_2}}}\right) \cos (t^*), \qquad \bigl < C^* - \left[ \left( \hat{u}^*\right) ^2 + \left( \hat{v}^*\right) ^2 \right] \bigl > = 0, \qquad \bar{h}^* = 0 \qquad \text {at }x^* = 0. \end{aligned}$$

The latter expression requires that the bed elevation $\bar{h}^*$, which is $h^*$ averaged over the seaward boundary, is equal to zero. For a more detailed discussion of these boundary conditions, see Schuttelaars and De Swart (1999), Ter Brake and Schuttelaars (2011), Boelens et al. (2021).

Equations (10.40)–(10.43) and (10.46) can be solved using an asymptotic expansion in the small parameter $\varepsilon$, reflecting comparatively small deviations from the O(1) values of primary parameters, see Schuttelaars and De Swart (2000), Ter Brake and Schuttelaars (2011). Assuming that all parameters are O(1), the focus will be on the O(1) equations, neglecting terms of $O(\varepsilon )$ and smaller. Furthermore, for the system under consideration $1/\varLambda ^* \gg 1$ which allows for a further simplification of the momentum equations (10.41) and (10.42):

$$\begin{aligned} \frac{\partial \zeta ^*}{\partial x^*} = \frac{\partial \zeta ^*}{\partial y^*} = 0, \end{aligned}$$

which states that the variations in the free surface elevations are spatially uniform. Information on the zeroth–order velocity field is obtained from the $O((\varLambda ^*)^2)$ momentum balance: elimination of the pressure terms results in a vorticity equation, which reads (neglecting earth rotation effects):

$$\begin{aligned} \frac{\partial ^2 \hat{v}^*}{\partial x^* \, \partial t^*} - \frac{\partial ^2 \hat{u}^*}{\partial y^* \, \partial t^*} = -\frac{\partial }{\partial x^*} \left( \frac{r^* \hat{v}^*}{1-h^*+h_0^*} \right) + \frac{\partial }{\partial y^*} \left( \frac{r^* \hat{u}^*}{1-h^*+h_0^*} \right) . \end{aligned}$$

(10.48)

Converting the system of non–dimensional equations and the associated boundary conditions back to dimensional ones resulting in the equations of Sect. 10.5.3.