Streaming Process Mining

Abstract

Streaming process mining refers to the set of techniques and tools which have the goal of processing a stream of data (as opposed to a finite event log). The goal of these techniques, similarly to their corresponding counterparts described in the previous chapters, is to extract relevant information concerning the running processes. This chapter presents an overview of the problems related to the processing of streams, as well as a categorization of the existing solutions. Details about control-flow discovery and conformance checking techniques are also presented together with a brief overview of the state of the art.

1 Introduction

Process mining techniques are typically classified according to the task they are meant to accomplish (e.g., control-flow discovery, conformance checking). This classification, though very meaningful, might come short when it is necessary to decide which algorithm, technique, or tool to apply to solve a problem in a given domain, where nonfunctional requirements impose specific constraints (e.g., when the results should be provided or when the events are recorded).

Most algorithms, so far, have been focusing on a static event log file, i.e., a finite set of observations referring to data collected during a certain time frame in the past (cf. Definition 1 [1]). In many settings, however, it is necessary to process and analyze the events as they happen, thus reducing (or, potentially, removing) the delay between the time when the event has happened in the real world and when useful information is distilled out of it. In addition, the amount of events being produced is becoming so vast and complex [22] that storing them for further processing is becoming less and less appealing. To cope with these issues, event-based systems [4] and event processing systems [19] can become extremely valuable tools: instead of storing all the events for later processing, these events are immediately processed and corresponding reactions can be taken immediately. In addition, event-based systems are also responsive systems: this means they are capable of reacting autonomously when deemed necessary (i.e., only when new events are observed).

Coping with the above-mentioned requirements in the context of data analysis led to the development of techniques to analyze streams of data [3, 21]. A data stream is, essentially, an unbounded sequence of observations (e.g., events), whose data points are created as soon as the event happens (i.e., in real-time). Many techniques have been developed, over the years, to tackle different problems, including frequency counting, classification, clustering, approximation, time series analysis and change diagnosis (also known as novelty detection or concept drift detection) [20, 46]. Process mining techniques applied to the analysis of data streams fall into the name of streaming process mining [8] and both control-flow discovery as well as conformance checking techniques will be discussed later in the chapter.

The rest of this chapter is structured as follows: this section presents typical use cases for streaming process mining and the background terminology used throughout the chapter. Section 2 presents a possible taxonomy of the different approaches for streaming process mining, which can be used also to drive the construction and the definition of new ones. Section 3 introduces the problem of streaming process discovery, by presenting a general overview of the state of the art and the details of one algorithm. Section 4 sketches the basic principles of streaming conformance checking. As for the previous case, also this section starts with a state-of-the-art summary and then dives into the details of one algorithm. Section 5 mentions other research endeavors of streaming process mining and then concludes the chapter.

1.1 Use Cases

This subsection aims at giving an intuition of potential use cases for streaming process mining. In general, every setting that requires drawing conclusions before the completion of a running process instance is a good candidate for the application of streaming process mining. In other words, streaming process mining is useful whenever it is important to understand running processes rather than improving future ones or “forensically” investigate those from the past.

Process discovery on event streams is useful in domains that require a clear and timely understanding of the behavior and usage of a system. For example, let’s consider a web application to self-report the annual tax statement for the citizens of a country. Such a system, typically, requires a lot of data to be inserted over many forms and, usually, the majority of its users have to interact with help pages, FAQs, and support information. In this case, it might be useful to understand and reconstruct the flow of a user (i.e., one process instance) to understand if they are getting lost in a specific section, or in specific cycles and, if necessary, provide tailored help and guidance support. Since the ultimate goal is to improve the running process instances (i.e., helping the users currently online), it is important that the analyses process the events immediately and that corresponding reactions are implemented straight away.

Conformance checking on event streams is useful whenever it is important to immediately detect deviations from reference behavior to enact proper countermeasures. For example, let’s consider operational healthcare processes [31], in most of these cases (in particular in the case of non-elective care processes, such as urgent or emergency ones) it is critically important to have a sharp understanding of each individual patient (i.e., one process instance), their treatment evolution, as well as how the clinic is functioning. For example, when treating a patient having acute myeloid leukemia it is vital to know that the treatment is running according to the protocol and, if deviations were to occur, it is necessary to initiate compensation strategies immediately.

Another relevant example of streaming conformance checking could derive from the investigation of the system calls of the kernel of an operating system when used by some services or applications. These calls should be combined in some specific ways (e.g., a file should be open(), then either write() or read() or both appear, and eventually the file should be close()) which represent the reference behavior. If an application is observed strongly violating such behavior it might be an indication of strange activities going on, for example trying to bypass some limitations or privileges. Exactly the same line of reasoning could be applied when consuming RESTful services.

Additional use cases and real scenarios are depicted in the research note [5], where real-time computing¹, to which streaming process mining belongs, is identified as one of the impactful information technology enablers in the BPM field.

1.2 Background and Terminology

This section provides the basic background on streams as well as the terminology needed in the rest of the chapter.

A stream is a sequence of observable units which evolves over time by including new observations, thus becoming unbounded². An event stream is a stream where each observable unit contains information related to the execution of an event and the corresponding process instance. In the context of this chapter, we assume that each event is inserted into the stream when the event itself happens in the real world. The universe of observable units $\mathcal {O}$ can refer to the activities executed in a case, thus having $\mathcal {O} \subseteq \mathcal {U}_\textit{act} \times \mathcal {U}_\textit{case}$ (cf. Definition 1 [1]), as discussed in Sect. 3) or to other properties (in Sect. 4 the observable units refer to relations B between pairs of activities, i.e., $\mathcal {O} \subseteq (B \times \mathcal {U}_\textit{act} \times \mathcal {U}_\textit{act}) \times \mathcal {U}_\textit{case}$).

Definition 1 (Event stream)

Given a universe of observable units $\mathcal {O}$, an event stream is an infinite sequence of observable units: $S : \mathbb {N}_{\ge 0} \rightarrow \mathcal {O}$.

We define an operator $observe$ that, given a stream S, it returns the latest observation available on the stream (i.e., $observe (S) \in \mathcal {O}$ is the latest observable unit put on S).

Due to the nature of streams, algorithms designed for their analyses are required to fulfill several constraints [6, 7], independently from the actual goal of the analyses. These constraints are:

• it is necessary to process one event at a time and inspect it at most once;

• only a limited amount of time and memory is available for processing an event (ideally, constant time and space computational complexity for each event);

• results of the analyses should be given at any time;

• the algorithm has to adapt to changes over time.

As detailed in [21, Table 2.1], it is possible to elaborate on the differences between systems consuming data streams and systems consuming static data (from now on, we will call these “offline”): in the streaming setting, the data elements arrive incrementally (i.e., one at the time) and this imposes the analysis to be incremental as well. These events are transient, meaning that they are available for a short amount of time (during which they need to be processed). In addition, elements can be analyzed at most once (i.e., no unbounded backtracking), which means that the information should be aggregated and summarized. Finally, to cope with concept drifts, old observations should be replaced by new ones: while in offline systems, all data in the log is equally important, when analyzing event stream the “importance” of events decreases over time.

In the literature, algorithms and techniques handling data streams are classified into different categories, including “online”, “incremental”, and “real-time”. While real-time systems are required to perform the computation within a given deadline – and, based on the consequences of not meeting the deadline, they are divided into hard/soft/firm –, incremental systems just focus on processing the input one element at the time with the solution being updated consequently (no emphasis/limit on the time). An online system is similar to an incremental one, except for the fact that the extent of input is not known in advance [37]. Please note that, in principle, both real-time and online techniques can be used to handle data streams, thus we prefer the more general term streaming techniques. In the context of this chapter, the streaming techniques are in between the family of “online” and “soft real-time”: though we want to process each event fast, the notion of deadline is not always available, and, when it is, missing it is not going to cause a system failure but just degradation of the usefulness of the information.

Fig. 1.

Process mining implications of some streaming requirements.

When instantiating the streaming requirements in the process mining context, some of the constraints bring important conceptual implications, which are going to change the typical way process mining is studied. For example, considering that each event is added to the stream when it happens in the real world means that the traces we look at will be incomplete most of the time. Consider the graphical representation reported in Fig. 1a, where the red area represents the portion of time during which the streaming process mining is active. Only in the first case (i.e., instance i), events referring to a complete trace are seen. In all other situations, just incomplete observations are available, either because events happened before we started observing the stream (i.e., instance l, suffix trace) because the events have still to happen (i.e., instance k, prefix trace), or because of both (i.e., instance j, subsequence trace). Figure 1b is a graphical representation of what it means to give results at any time in the case of conformance: after each event, the system needs to be able to communicate the conformity value as new events come in. Also, the result might change over time, thus adapting the computation to the new observations.

2 Taxonomy of Approaches

Different artists are often quoted as saying: “Good artists copy, great artists steal”. Regardless of who actually said this first³, the key idea is the importance of understanding the state of the art to incorporate the key elements into newly designed techniques. Streaming process mining techniques have been around for some years now, so it becomes relevant to understand and categorize them in order to relate them to each other and derive new ones.

It is possible to divide the currently available techniques for streaming process mining into four categories. A graphical representation of such taxonomy is available in Fig. 2, where three main categories are identified, plus a fourth one, which represents possible mixes of the others. In the remainder of this section, each category will be briefly presented.

Fig. 2.

Taxonomy of the different approaches to solve the different stream process mining problems. For each technique, corresponding general steps are sketched [10].

Window Models. The simplest approach to cope with infinite streams consists of storing only a set of the most recent events and, periodically, analyzing them. These approaches store a “window” of information that can be converted into a static log. Then, standard (i.e., offline) analyses can be applied to the log generated from such a window. Different types of windowing models can be used and classified based on how the events are removed [34]. These models can be characterized along several dimensions, including the unit of measurement (i.e., whether events are kept according to some logical or physical units such as the time of the events or the number of events); the edge shift (so whether any of two bounds of a window is fixed to a specific time instant or if these change over time); and the progression step (i.e., how the window evolves over time, assuming that either of the bounds advances one observation at a time or several data points are incorporated at once). These profiles can create different window models, such as:

• count-based window: at every time instance, the window contains the latest N observations;

• landmark window: one of the window bounds is fixed (e.g., the starting time or the end time, far in the future) whereas the other progresses with time;

• time-based sliding window: in this case, the sliding window progresses according to two parameters: a time window duration and a time progression step;

• time-based tumbling window: similar to the time-based sliding window but where entire batches of events are observed so that two consecutive windows do not overlap.

Algorithm 1 reports a possible representation of an algorithm for process mining on a count-based window model. The algorithm uses as a memory model a FIFO queue and it starts with a never-ending loop which comprises, as the first step, the observation of a new event. After that, the memory is checked for maximum capacity and, if reached, the oldest event observed is removed. Then, the mining can take place, initially converting the memory into a process mining capable log and then running the actual mining algorithm on the given log.

Window-based models come with many advantages such as the capability of reusing any offline process mining algorithm already available for static log files. The drawback, however, comes from the inefficient handling of the memory: window-based models are not very efficient for summarizing the stream, i.e., the logs generated from a window suffer from strong biases due to the rigidity of the model.

Problem Reduction. To mitigate the issues associated with window models, one option consists of employing a problem reduction technique (cf. Fig. 2). In this case, the idea is to reduce the process mining problem at hand to a simpler yet well-studied problem in the general stream processing field in order to leverage existing solutions and derive new ones. An example of a very well studied problem is frequency counting: counting the frequencies of variables over a stream (another example of a relevant and well-studied problem is sampling). To properly reduce a process mining problem to a frequency counting one, it is important to understand what a variable is in the process mining context and if it is indeed possible to extract information by counting how often a variable occurs.

An algorithm to tackle the frequency counting problem is called Lossy Counting [30], described in Algorithm 2 and graphically depicted in Fig. 3. Conceptually, the algorithm divides the stream into “buckets”, each of them with a fixed size (line 6). The size of the bucket is derived from one of the inputs of the algorithm ($\epsilon \in [0,1]$) which indicates the maximal acceptable approximation error in the counting. Lossy Counting keeps track of the counting by means of a data structure T, where each component $(e, f, \varDelta )$ refers to the element e of the stream (the variable to count), its estimated frequency f, and the maximum number of times it could have occurred $\varDelta$ (i.e., the maximum error). Whenever a new event is observed (line 5), if the value is already in the memory T, then the counter f is incremented by one (line 8), instead, if there is no such value, a new entry is created in T with the value e corresponding to the observed variable, frequency $f = 1$, and maximum error equal to the number of the current bucket minus one (from here it is possible to understand that since the buck size depends on the maximum allowed error, the higher the error, the larger the bucket size and hence the higher the approximation error) (line 10). With a fixed periodicity (i.e., every time a new conceptual bucket starts) the algorithm cleans the memory, by removing elements not frequently observed (lines 12–16). Please note that this specific algorithm has no memory bound: the size of its data structure T depends on the stream and on the max approximation error (i.e., if the error is set to 0 and the observations never repeat, the size of T will grow indefinitely). Variants of the algorithm enforcing a fixed memory bound is available as well [18] but are not described in detail here. In the rest of this chapter, a set whose entries are structured and updated using the Lossy Counting algorithm (i.e., T in Algorithm 2) will be called Lossy Counting Set.

Fig. 3.

Graphical representation of the Lossy Counting algorithm.

Fig. 4.

Demonstration of the evolution of the internal data structure constructed by the Lossy Counting on a simple stream. Each color refers to a variable.

Figure 4 shows a demonstration of the evolution of the Lossy Counting Sets over time (at the end and at the beginning of each virtual bucket) for the given stream. In this case, for simplicity purposes, the background color of each box represents the variable that we are counting. The counting is represented as the stacking of the blocks, and below, in red, the maximum error for each variable is ported.

The most relevant benefit of reducing the problem to a known one is the ability to employ existing as well as new solutions in order to improve the efficiency of the final process mining solution. Clearly, this desirable feature is paid back in terms of the complexity of the steps (both conceptual and computational) required for the translation.

Offline Computation. Due to some of the constraints imposed by the streaming paradigm, one option consists of moving parts of the computation offline (cf. Fig. 2) so that performance requirements are met when the system goes online. This idea implies decomposing the problem into sub-problems and reflecting on whether some of them can be solved without the actual streaming data. If that is the case, these sub-problems will be solved beforehand and corresponding pre-computed solutions will be available as the events are coming in.

Such an approach comes with the advantage of caching the results of computations that would otherwise require extremely expensive computations. This approach, still, suffers from several limitations since it is not possible to apply this approach to all streaming process mining problems. Additionally, by computing everything in advance, we lose the possibility of adapting the pre-computed solutions to the actual context, which might be uniquely specific to the running process instance.

Hybrid Approaches. As a final note, we should not rule out the option of defining ensemble methods that combine different approaches together (see Fig. 2).

3 Streaming Process Discovery

After introducing the general principles and taxonomy of techniques to tackle streaming process mining, in this section, we will specifically analyze the problem of streaming process discovery.

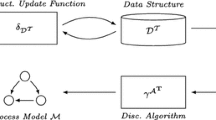
A graphical conceptualization of the problem is reported in Fig. 5: the basic idea is to have a source of events that generates an event stream. Such an event stream is consumed by a miner which keeps a representation of the underlying process model updated as the new events are coming in.

Fig. 5.

Conceptualization of the streaming process discovery. Figure from [16].

3.1 State of the Art

In this section, the main milestones of the streaming process discovery will be presented. The first available approach to tackle the streaming process discovery problem is reported in [15, 16]. This technique employs a “problem reduction” approach (cf. Fig. 2) rephrasing the Heuristics Miner [38] as a frequency counting problem. The details of this approach will be presented in Sect. 3.2. In [23], authors present StrProM which, similarly to the previous case, tracks the direct following relationship by keeping a prefix tree updated with Lossy Counting with Budget [18].

More recently, an architecture called S-BAR, which keeps an updated abstract representation of the stream (e.g., direct follow relationships), is used as starting point to infer an actual process model, as described in [44]. Different algorithms (including $\alpha$. [39], Heuristics Miner [38] and Inductive Miner [26]) have been incorporated to be used with this approach. Also in this case authors reduced their problem to frequency counting, thus using Lossy Counting, Space Saving [32], and Frequent [24].

Declarative processes (cf. Chapter 4) have also been investigated as the target of the discovery. In [12, 14, 27], authors used the notion of “replayers” – one for each Declare [35] template to mine – to discover which one are fulfilled. Also in this case, Lossy Counting strategies have been employed to achieve the goal. A newer version of the approach [33], is also capable of discovering data conditions associated with the different constraints.

3.2 Heuristics Miner with Lossy Counting (HM-LC)

This section describes in more detail one algorithm for streaming process discovery: Heuristics Miner with Lossy Counting (HM-LC) [16].

The Heuristics Miner algorithm [38] is a discovery algorithm which, given the frequency of the direct following relations observed (reported as $|a>b|$ and indicating the number of times b is observed directly after a), calculates the dependency measure, a measure of the strength of the causal relation between two activities a and b:

$$\begin{aligned} a \Rightarrow b = \frac{|a> b| - |b> a|}{|a> b| + |b > a| + 1} \in [-1,1]. \end{aligned}$$

(1)

The closer the value of such metric is to 1, the stronger the causal dependency from a to b. Based on a given threshold (parameter asked as input), the algorithm considers only those dependencies with values exceeding the threshold, deeming the remaining as noise. By considering all dependencies which are strong enough, it is possible to build a dependency graph, considering one node per activity and one edge for each dependency. In such a graph, however, when splits or joins are observed (i.e., activities with more than one outgoing or incoming connection) it is not possible to distinguish the type of the splits. In the case of a dependency from a to b and also from a to c, Heuristics Miner disambiguates between an AND and an XOR split by calculating the following metric (also based on the frequency of direct following relations):

$$\begin{aligned} a \Rightarrow (b \wedge c) = \frac{|b> c| + |c> b|}{|a> b| + |a > c| + 1} \in [0,1]. \end{aligned}$$

(2)

When the value of this measure is high (i.e. close to 1), it is likely that b and c can be executed in parallel, otherwise, these will be mutually exclusive. As for the previous case, a threshold (parameter asked as input) is used to make the distinction.

It is important to note that the two fundamental measures employed by the Heuristics Miner rely on the frequency of the directly-follows measure (e.g. $|a > b|$), and so the basic idea of Heuristics Miner with Lossy Counting is to consider such values as “variables” to be observed in a stream, thus reducing the problem to frequency counting.

As previously mentioned, Lossy Counting is an algorithm for frequency counting. In particular, the estimated frequencies can be characterized both in terms of lower and upper bounds as follows: given the estimated frequency f (i.e., the frequency calculated by the algorithm), the true frequency F (i.e., the actual frequency of the observed variable), the maximum approximation error $\epsilon$ and the number of events observed N, these inequalities hold

$$ f \le F \le f+\epsilon N. $$

To calculate the frequencies, Lossy Counting uses a set data structure where each element refers to the variable being counted, its current (and approximated) frequency, and the maximum approximation error in the counting of that variable.

For the sake of simplicity, in Heuristics Miner with Lossy Counting, the observable units of the event stream comprises just the activity name and the case id (cf. Definition 1). In other words, each event observed from the stream comprises two attributes: the activity name and the case id (cf. Definition 1 [1], Sect. 3.2 [1]), so an event e is a tuple with $e = (c,a)$, where $\#_{ case }(e) = c$ and $\#_{ act }(e) = a$.

Fig. 6.

Conceptualization of the need to isolate different traces based on a single stream. Boxes represent events: their background colors represent the case id, and the letters inside are the activity names. First line reports the stream, following lines are the single cases. Figure from [16].

The pseudocode of HM-LC is reported in Algorithm 3. The fundamental idea of the approach is to count the frequency of the direct following relations observed. In order to achieve this goal, however, it is necessary to identify the direct following pairs in the first place. As depicted in Fig. 6, to identify direct following relations it is first necessary to disentangle the different traces that are intertwined in an event stream. To this end, the HM-LC instantiates two Lossy Counting Sets: $\mathcal {D}_C$, and $\mathcal {D}_R$. The first keeps track of the latest activity observed in each process instance whereas the second counts the actual frequency of the directly follow relations. These data structures are initialized at the first line of the algorithm, which is followed by the initialization of the counter of observed events (line 2) and the calculation of the size of the buckets (line 3). After the initial setup of the data structure, a never-ending loop starts by observing events from the stream (line 5, cf. Definition 1), where each event is the pair $(c_N, a_N)$, indicating that the case id observed as event N is $c_N$ (resp., the activity is $a_N$). The id of the current bucket is calculated right afterwards (line 6). The whole algorithm is then divided into three conceptual steps: in the first the data structures are updated; in the second periodic cleanup takes place; in the third the data structures are used to construct and update the actual model.

Step 1: Updating the Data Structure. The Lossy Counting Set $\mathcal {D}_C$ has been defined in order not only to keep a count of the frequency of each case id observed in the events but also to keep track of the latest activity observed in the given trace. To achieve this goal, the entries of the data structure are tuples themselves, comprising the case id as well as the name of the latest activity observed in the case. Therefore, the first operation within the step consists of checking for the presence of an entry in $\mathcal {D}_C$ matching the case id of the observed event (but not the activity name), as reported in line 7. If this is the case, the data structure $\mathcal {D}_C$ is updated, not only by updating the frequency but also by updating the latest activity observed in the given case (lines 8 and 9). In addition, having already an entry in $\mathcal {D}_C$ means that a previous event within the same trace has already been seen and, therefore, it is possible to construct a direct following relation (cf. line 10 of Algorithm 3). This relation is then treated as a normal variable to be counted and the corresponding Lossy Counting Set is updated accordingly (lines 11–16). In case $\mathcal {D}_C$ did not contain an entry referring to case id $c_N$, it means that the observed event is the first event of its process instance (up to the approximation error) and hence just a new entry in $\mathcal {D}_C$ is inserted and no direct following relation is involved (line 18).

Step 2: Periodic Cleanup. With a periodicity imposed by the maximum approximation error ($\epsilon$), i.e., at the end of each bucket (line 20), the two Lossy Counting Sets are updated by removing entries that are not frequent or recent enough (lines 21–26). Please note that the algorithm expects that observing an event belonging to a process instance that has been removed from $\mathcal {D}_C$ corresponds to losing one direct following relation from the counting in $\mathcal {D}_R$. From this point of view, the error on the counting of the relations is not only affected by $\mathcal {D}_R$ but, indirectly, also by the removal of instances from $\mathcal {D}_C$ which causes a relation not to be seen at all (and therefore, it cannot be counted).

Step 3: Consumption of the Data Structures. The very final step of the algorithm (line 29) consists of triggering a periodic update of the model. The update procedure (not specified in the algorithm) extracts all the activities involved in a direct following relations from $\mathcal {D}_R$ and uses the dependency measure (cf. Eq. 1) to build a dependency graph, by keeping the relations with dependency measure above a threshold. To disambiguate AND/XOR splits Eq. 2 is used. Both these measures need to be adapted in order to retrieve the frequency of the relations from $\mathcal {D}_R$.

The procedure just mentioned recomputes the whole model from scratch. However, observing a new event will cause only local changes to a model. Hence a complete computation of the whole model is not necessary. In particular, it is possible to rearrange Eqs. 1 and 2 in order to signal when a dependency has changed. Specifically, given a dependency threshold $\tau _ dep$, we know that a dependency should be present if these inequalities hold:

$$\begin{aligned} |a> b| \ge \frac{|b> a|(1 + \tau _\textit{dep}) + \tau _\textit{dep}}{1 - \tau _\textit{dep}} \quad \text {or} \quad |b> a| \le \frac{|a > b|(1 - \tau _\textit{dep}) - \tau _\textit{dep}}{1 + \tau _\textit{dep}} \end{aligned}$$

In a similar fashion, we can rewrite Eq. 2 so that, given an AND threshold parameter $\tau _\textit{and}$, a split (i.e., from activity a to both activities b and c) has type AND if all these inequalities hold:

$$\begin{aligned} |b> c| \le&\tau _\textit{and}\left( |a> b| + |a> c| + 1\right) - |c> b| \\ |c> b| \le&\tau _\textit{and}(|a> b| + |a> c| + 1) - |b> c| \\ |a> b| \le&\frac{|b> c| + |c> b|}{\tau _\textit{and}} - |a> c| - 1 \\ |a> c| \le&\frac{|b> c| + |c> b|}{\tau _\textit{and}} - |a > b| - 1 \end{aligned}$$

If this is not the case, the type of the split will be XOR. Therefore, by monitoring how the frequencies of some of the relations in $\mathcal {D}_R$ (which should be used as an approximation of the direct following frequencies) are evolving, it is possible to pinpoint the changes appearing in a model, with no need for rebuilding it from scratch all the times.

In this section, we did not exhaustively cover the reduction of the Heuristics Miner to Lossy Counting (for example, we did not consider the absolute number of observations for an activity or parameters such as the relative-to-best) but we focused on the core aspects of the reduction. The goal of the section was to present the core ideas behind a streaming process discovery algorithm while, at the same time, showing an example of an algorithm based on the problem reduction approach (cf. Fig. 2).

4 Streaming Conformance Checking

Computing the conformity of running instances starting from events observed in a stream is the main goal of streaming conformance checking.

Fig. 7.

Reference process model used to calculate the conformance of traces in Table 1, from [17].

Table 1. Example traces with corresponding offline conformance.

Consider, for example, the process model reported in Fig. 7 as a reference process, and let’s investigate the offline conformance (calculated according to the alignment technique reported in [2]) for the traces reported in Table 1. Trace $t_1$ is indeed conforming with respect to the model as it represents a possible complete execution of the process. This information is already properly captured by the offline analysis. Trace $t_2$, on the other hand, is compliant with the process but just up to activity B, as reported by the conformance value 0.8: offline systems assume that the executions are complete, and therefore observing an incomplete trace represents a problem. However, as previously discussed and as shown in Fig. 1a, in online settings it could happen that parts of the executions are missing due to the fact that the execution has not yet arrived at this part of the computation. This could be the case with trace $t_2$ (i.e., $t_2$ is the prefix of a compliant trace). Trace $t_3$ suffers from the opposite problem: the execution is conforming to the model, but just from activity B onward. While offline conformance, in this case, is calculated to the value of 0.68, as for the previous case, we cannot rule out the option that the trace is actually compliant but, since the trace started before the streaming conformance checker was online, it was incapable of analyzing the beginning of it (i.e., $t_3$ is the suffix of a compliant trace). Trace $t_4$, finally, seems compliant just between activities B and D. Though offline conformance, in this case, is 0.62, as for the previous two cases, in a streaming setting, we cannot exclude that the issue actually derives from the combination of the trace starting before the streaming conformance was online and the trace not being complete (i.e.,$t_4$ is a subsequence of a compliant trace).

Hopefully, discussing the previous examples helped to point out the limit of calculating the extent of the conformance using only one numerical value in a streaming setting. Indeed, when the assumption that executions are complete is dropped, the behavior shown in the traces of Table 1 could become 100% compliant since the actual issue does not lie in the conformity but in the amount of observed behavior.

4.1 State of the Art

Computing the conformity of a stream with respect to a reference model has received a fairly large amount of attention, in particular in the case of declarative processes. Under the name “operational support”, research has been focusing [28, 29] on understanding if and which constraints are violated and satisfied as new events are coming in. In particular, each constraint is associated with one of four possible truth values: permanently or temporarily violated or fulfilled which are computed by representing the behavior as an automaton with all executions replayed on top of it.

Streaming conformance checking on imperative models has also received attention, though more recently. Optimal alignments can be computed for the prefix (i.e., prefix-alignments) of the trace seen up to a given point in time [41], resulting in a very reliable approach which, however, meets only to some extent the streaming scenario (cf. Sect. 1.2). A more recent approach [36] is capable of improving the performance of calculating a prefix-alignment, by rephrasing the problem as the shortest path one and by incrementally expanding the search space and reusing previously computed intermediate results.

A different line of research focused on calculating streaming conformance for all scenarios (cf., Fig. 1a). In this case, techniques employed “offline computation” approaches [11, 17, 25] to construct data structures capable of simplifying the computation when the system goes online. These approaches not only compute the conformity of a running instance but also try to quantify the amount of behavior observed or still to come.

In addition to these, one of the first approaches [45] focused on a RESTful service capable of performing the token replay on a BPMN model (via a token pull mechanism). No explicit guarantees, however, are reported concerning the memory usage, the computational complexity, or the reliability of the results, suggesting that the effort was mostly on the interface type (i.e., online as in RESTful).

4.2 Conformance Checking with Behavioral Patterns

This section presents in more detail one algorithm for streaming conformance checking using behavioral patterns [17]. The algorithm belongs to the category of offline computation (cf. Fig. 2), where the heaviest computation is moved before the system goes online, thus meeting the performance requirement of streaming settings.

The fundamental idea of the approach is that using just one metric to express conformity could lead to misleading results, i.e. cases that already started and/or that are not yet finished get falsely penalized. To solve these issues, the approach proposes to break the conformity into three values:

• 1. Conformance: indicating the amount of actually correct behavior seen;

• 2. Completeness: providing an estimate of the extent to which the trace has been observed since the beginning; and

• 3. Confidence: indicating how much of the trace has been seen, and therefore to what extent the conformance is likely to remain stable.

A graphical representation of these concepts is reported in Fig. 8. In addition, the approach does not assume any specific modeling language for the reference process. Instead, the approach takes the reference process as a constraining of the relative orders of its activities. Such constraints are defined in terms of behavioral patterns, such as weak ordering, parallelism, causality, and conflict. Such behavioral patterns (with the corresponding activities involved) represent also what the conformance checking algorithm observes. In the context of this chapter, we will consider the directly follow relation as a pattern.

Fig. 8.

General idea of the 3 conformance measures computed based on a partially observed process instance: conformance, completeness, and confidence. Figure from [17].

Please note that the input of the algorithm is not a stream of events, but a stream of observed behavioral patterns, which could require some processing of the raw events. This, however, does not represent a problem for the behavioral pattern considered (i.e., directly follow relation), since these can be extracted using the technique described in Sect. 3.2.

As previously mentioned, the technique offloads the computation to a pre-processing stage which takes place offline, before the actual conformance is computed. During such a step, the model is converted into another representation, better suited for the online phase. Specifically, the new model contains:

• 1. The set of behavioral patterns that the original process prescribes;

• 2. For each of the behavioral patterns identified, the minimum and maximum number of distinct prescribed patterns that must occur before it, since the very beginning of the trace;

• 3. For each behavioral pattern, the minimum number of distinct patterns still to observe to reach a valid accepting state of the process (as prescribed by the reference model).

These requirements drive the definition of the formal representation called “Process Model for Online Conformance” (PMOC). A process model for online conformance $M = (B, P, F)$ is defined as a triplet containing the set of prescribed behavioural patterns B. Each pattern $b(a_1, a_2)$ is defined as a relation b (e.g., the directly follow relation) between activities $a_1,a_2 \in \mathcal {U}_ act$ (cf. Definition 1 [1]). P contains, for each behavioral pattern $b \in B$, the pair of minimum and maximum number distinct prescribed patterns (i.e., B) to be seen before b. We refer to these values as $P_{\min }(b)$ and $P_{\max }(b)$. For each pattern, $b \in B$, F(b) refers to the minimum number of distinct patterns (i.e., B) required to reach the end of the process from b.

Once such a model is available, the conformance values can be calculated according to Algorithm 4 which executes three steps for each event: updating the data structures, calculating the conformance values, and housekeeping cleanup. After two maps are initialized (lines 1, 2), the never-ending loop starts and, each observation from the stream (which refers to a behavioral patter b for case id c, cf. Definition 1) triggers and update of the two maps: if the pattern refers to a prescribed relation, then it is added to the $\textsf {obs}(c)$ set (line 6)⁴, otherwise, the value of incorrect observations for the process instance $\textsf {obs}(c)$ is incremented (line 8)⁵. In the second step, the algorithm calculates the new conformance values. The actual conformance, which resembles the concept of precision, is calculated (lines 10, 11) as the number of distinct observed prescribed patterns in c (i.e., $|\textsf {obs}(c)|$) divided by the sum of the number of prescribed observed patterns and the incorrect patterns (i.e., $|\textsf {obs}(c)| + \textsf {inc}(c)$): 1 indicates full conformance (i.e., only correct behaviour) and 0 indicates no conformance at all (i.e., only incorrect behaviour). Completeness and confidence are updated only when a prescribed behavioral pattern is observed (line 12) since they require locating the pattern itself in the process. Concerning completeness, we have perfect value if the number of distinct behavioral patterns observed so far is within the expected interval for the current pattern (lines 13, 14). If this is not the case, we might have seen fewer or more patterns than expected. If we have seen fewer patterns, the completeness is the ratio of observed patterns over the minimum expected; otherwise, it’s just 1 (i.e., we observed more patterns than needed, so the completeness is not an issue). Please bear in mind that these numbers confront the number of distinct patterns, not their type, thus potentially leading to false positives (line 16). The confidence is calculated (line 18) as 1 minus the proportion of patterns to observe (i.e., F(b)) and the overall maximum number of future patterns (i.e., $\max _{b' \in B} F(b')$): a confidence level 1 indicates strong confidence (i.e., the execution reached the end of the process), 0 means low confidence (i.e., the execution is still far from completion, therefore there is room for change). The final step performs some cleanup operations on $\textsf {obs}$ and $\textsf {inc}$ (lines 21–23). The algorithm does not specify how old entries should be identified and removed, but, as seen on the previous section, existing approaches can easily handle this problem (e.g., by using a Lossy Counting Set).

It is important to note once again that the actual algorithm relies on a data structure (the PMOC) that is tailored to the purpose and that might be computational very expensive to obtain. However, since this operation is done only once and before any streaming processing, this represents a viable solution. The details on the construction of the PMOC are not analyzed in detail here but are available in [17]. Briefly, considering the directly follow relation as the behavioral pattern, the idea is to start from a Petri net and calculate its reverse (i.e., the Petri net where all edges have opposite directions). Both these models are then unfolded according to a specific stop criterion and, once corresponding reachability graphs are computed, the PMOC can be easily derived from the reachability graph of the unfolded original Petri net and the reachability graph of the unfolded reverse net.

Considering again the traces reported in Table 1 and the reference model in Fig. 7, all traces have a streaming conformance value of 1 (when calculated using the approach just described). The completeness is 1 for $t_1$ and $t_2$, 0.6 for $t_3$, and 0.5 for $t_4$. The confidence is 1 for $t_1$ and $t_3$, 0.5 for $t_2$, and 0.75 for $t_4$. These values indeed capture the goals mentioned at the beginning of this section: do not penalize the conformance but highlight the actual issues concerning the missing beginning or end of the trace.

As for the streaming process discovery case, in this section, we did not exhaustively cover the algorithm for streaming conformance checking presented. Instead, we focused on the most important aspects of the approach, hopefully also giving an intuition of how an offline computation approach could work (cf. Fig. 2).

5 Other Applications and Outlook

It is worth mentioning that the concepts related to streaming process mining have been applied not only to the problem of discovery and conformance but, to a limited extent, to other challenges.

Examples of such applications are the discovery of cooperative structures out of event streams, as tackled in [43], where authors process an event stream and update the set of relationships of a cooperative resource network. In [40], several additional aspects of online process mining are investigated too.

Supporting the research in streaming process mining has also been a topic of research. Simulation techniques have been defined both as standalone applications [9], as ProM plugins [42], or just as communication protocols [13].

Finally, from the industrial point of view, it might be interesting to observe that while some companies are starting to consider some aspects related to the topics discussed in this chapter (e.g., Celonis’ Execution Management Platform supports the real-time data ingestion, though not the analysis), none of them offers actual solutions for streaming process mining. A report from Everest Group⁶ explicitly refers to real-time monitoring of processes as an important process intelligence capability not yet commercially available.

This chapter presented the topic of streaming process mining. While the field is relatively young, several techniques are already available both for discovery and conformance checking.

We presented a taxonomy of the existing approaches which, hopefully, can be used proactively, when new algorithms need to be constructed, to identify how a problem can be tackled. Then two approaches, one for control-flow discovery and one for conformance checking, are presented in detail which, in addition, belong to different categories of the taxonomy. Alongside these two approaches, window models can also be employed, yet their efficacy is typically extremely low compared to algorithms specifically designed for the streaming context.

It is important to mention that streaming process mining has very important challenges still to be solved. For example, dealing with a stream where the arrival time of events does not coincide with their actual execution. In this case, it would be necessary to reorder the list of events belonging to the same process instance before processing them. Another relevant issue might be the inference of the termination of process instances. Finally, so far, we always considered an insert-only stream model, where events can only be added in a monotonic fashion. Scenarios where observed events can be changed or removed (i.e., insert-delete models) are yet to be considered.