Abstract
Process mining enables organizations to uncover their actual processes, provide insights, diagnose problems, and automatically trigger corrective actions. Process mining is an emerging scientific discipline positioned at the intersection between process science and data science. The combination of process modeling and analysis with the event data present in today’s information systems provides new means to tackle compliance and performance problems. This chapter provides an overview of the field of process mining introducing the different types of process mining (e.g., process discovery and conformance checking) and the basic ingredients, i.e., process models and event data. To prepare for later chapters, event logs are introduced in detail (including pointers to standards for event data such as XES and OCEL). Moreover, a brief overview of process mining applications and software is given.
You have full access to this open access chapter, Download chapter PDF
Similar content being viewed by others
Keywords
1 Introduction
Process mining can be defined as follows: process mining aims to improve operational processes through the systematic use of event data [1, 2]. By using a combination of event data and process models, process mining techniques provide insights, identify bottlenecks and deviations, anticipate and diagnose performance and compliance problems, and support the automation or removal of repetitive work. Process mining techniques can be backward-looking (e.g., finding the root causes of a bottleneck in a production process) or forward-looking (e.g., predicting the remaining processing time of a running case or providing recommendations to lower the failure rate). Both backward-looking and forward-looking analyses can trigger actions (e.g., countermeasures to address a performance or compliance problem). The focus of process mining is on operational processes, i.e., processes requiring the repeated execution of activities to deliver products or services. These can be found in all organizations and industries, including production, logistics, finance, sales, procurement, education, consulting, healthcare, maintenance, and government. This chapter provides a 360\(^\circ \) overview of process mining, introducing basic concepts and positioning process mining with respect to other technologies.
The idea of using detailed data about operational processes is not new. For example, Frederick Winslow Taylor (1856–1915) collected data on specific tasks to improve labor productivity [35]. With the increasing availability of computers, spreadsheets and other business intelligence tools were used to monitor and analyze operational processes. However, in most cases, the focus was on a single task in the process, or behavior was reduced to aggregated Key Performance Indicators (KPIs) such as flow time, utilization, and costs. Process mining aims to analyze end-to-end processes at the level of events, i.e., detailed behavior is considered in order to explain and improve performance and compliance problems.
Process mining research started in the late 1990s [23]. In 2004 the first version of the open-source platform ProM was released with 29 plug-ins. Over time the ProM platform was extended and now includes over 1500 plug-ins. The first commercial process mining tools appeared around 15 years ago. Today, there are over 40 commercial process mining tools and process mining is used by thousands of organizations all over the globe. However, only a small fraction of its potential has been realized. Process mining is generic and can be applied in any organization.
Figure 1 shows that process mining can be seen as the intersection of data science and process science. In [2], the following definition is proposed: “Data science is an interdisciplinary field aiming to turn data into real value. Data may be structured or unstructured, big or small, static or streaming. Value may be provided in the form of predictions, automated decisions, models learned from data, or any type of data visualization delivering insights. Data science includes data extraction, data preparation, data exploration, data transformation, storage and retrieval, computing infrastructures, various types of mining and learning, presentation of explanations and predictions, and the exploitation of results taking into account ethical, social, legal, and business aspects.” In [2], process science is used as an umbrella term to refer to the broader discipline that combines knowledge from information technology and knowledge from management sciences to improve and run operational processes. In the more recent [12], the following definition is proposed: “Process science is the interdisciplinary study of continuous change. By process, we mean a coherent series of changes that unfold over time and occur at multiple levels.” In [12], we emphasize the following key characteristics of process science: (1) processes are in focus, (2) processes are investigated using scientific methods, (3) an interdisciplinary lens is used, and (4) the goal of process science is to influence and change processes to realize measurable improvements. As stated in [2] and visualized in Fig. 1; process mining can be viewed as the link between data science and process science. Process mining seeks the confrontation between event data (i.e., observed behavior) and process models (hand-made models or automatically discovered models), and aims to exploit event data in a meaningful way, for example, to provide insights, identify bottlenecks, anticipate problems, record policy violations, recommend countermeasures, and streamline processes.
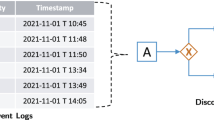
Figure 2 shows a high-level view of process mining. Event data need to be extracted from information systems used to support the processes that need to be analyzed. Customer Relationship Management (CRM), Enterprise Resource Planning (ERP), and Supply Chain Management (SCM) systems store events. Examples are SAP S/4HANA, Oracle E-Business Suite, Microsoft Dynamics 365, and Salesforce CRM. Next to these sector-agnostic software systems, there are more specialized systems such as Health Information Systems (HIS). All of these systems have in common that they are loaded with event data. However, these are scattered over many database tables and need to be converted into a format that can be used for process mining. As a consequence, data extraction is an integral part of any process mining effort, and may be time-consuming. Events are often represented by a case identifier, an activity name, a timestamp, and optional attributes such as resource, location, cost, etc. Object-centric event data allow events to point to any number of objects rather than a single case (see Sect. 3).
Once extracted, event data can be explored, selected, filtered, and cleaned (see Fig. 2). Data visualization techniques such as dotted charts and sequence diagrams can be used to understand the data. Often, the data need to be scoped to the process of interest. One can use generic query languages like SQL, SPARQL, and XQuery or a dedicated Process Query Language (PQL). Data may be incomplete, duplicated, or inconsistent. For example, month and day may be swapped during manual data entry. There is a variety of techniques and approaches to address such data quality problems [34].
The resulting dataset is often referred to as an event log, i.e., a collection of events corresponding to the selected process. Process discovery techniques are used to automatically create process models. Commercial tools typically still resort to learning the so-called Directly-Follows Graph (DFG) which typically leads to underfitting process models [3]. If two activities do not occur in a fixed order, then loops are created. This leads to Spaghetti-like diagrams suggesting repetitions that are not supported by the data. However, there are numerous approaches to learning higher-level models represented using Business Process Model and Notation (BPMN), Petri nets, or Unified Modeling Language (UML) activity diagrams. In contrast to DFGs, such models are able to express concurrency. Example techniques to discover such models are the Alpha algorithm [8], region-based approaches [11, 13, 33, 36], inductive mining techniques [28, 29], and the split miner [9]. The process model returned may aim to describe all behavior observed or just the dominant behavior. Note that the event log only contains example behavior, is likely to be incomplete, and at the same time may contain infrequent behavior.
The combination of a process model and event data can be used to conduct conformance checking and performance analysis (Fig. 2). The process model may have been discovered or made by hand. Discovered process models are descriptive and hand-crafted models are often normative. Conformance checking relates events in the event log to activities in the process model and compares both. The goal is to find commonalities and discrepancies between the modeled behavior and the observed behavior. If the process model is normative, deviations correspond to undesired behavior (e.g., fraud or inefficiencies). If the model was discovered automatically with the goal of showing the dominant behavior, then deviations correspond to exceptional behavior (i.e., outliers). Note that most processes have a Pareto distribution, e.g., 80% of the cases can be described by only 20% of the process variants. It is often easy and desirable to create a process model describing these 80%. However, the remaining 20% cannot be discarded since these cases cover the remaining 80% of the process variants and often also the majority of performance and compliance problems. Sometimes event logs are even more unbalanced, e.g., it is not uncommon to find logs where 95% of the cases can be described by less than 5% of the process variants. In the latter case, it may be that the remaining 5% of cases (covering 95% of the process variants) consume most of the resources due to rework and exception handling.
Since events have timestamps, it is easy to overlay the process model with performance diagnostics (service times, waiting times, etc.). After discovering the control-flow, the process model can be turned into a stochastic model that includes probabilities and delay distributions.
After applying conformance checking and performance analysis techniques, users can see performance and compliance problems. It is possible to perform root-cause analysis for such problems. One may find out that critical deviations are often caused by a particular machine or supplier, or that the main bottleneck is caused by poor resource planning or excessive rework for some product types. In a procurement process, price changes by a particular supplier may explain an increase in rework. If “Receive Invoice” often occurs before “Create Purchase Requisition”, then this signals a compliance problem in the same process. These are just a few examples. In principle, any process-related problem can be diagnosed as long as event data are available.
The right-hand side of Fig. 2 shows that process mining can be used to (1) transform and improve the process and (2) automatically address observed and predicted problems. The stochastic process models discovered from event data can be used to conduct “what-if” analysis using simulation or other techniques from operations research (e.g., planning). The combination of event data and process models can be used to generate Machine Learning (ML) problems. ML techniques can be used to predict outcomes without being explicitly programmed to do so. The uptake of ML in recent years can be attributed to progress in deep learning, where artificial neural networks having multiple layers progressively extract higher-level features from the raw input. ML techniques cannot be applied directly to event data. However, by replaying event data on discovered process models, it is possible to create a range of supervised learning problems. Examples include:
-
What is the remaining processing time of a particular insurance claim?
-
Are we able to handle 95% of the cases within one week?
-
Is this application going to deviate from the normative process?
-
Will this patient be moved to the intensive care unit?
-
Will we have enough free beds in the intensive care unit tomorrow?
It is important to note that the right-hand side of Fig. 2 (i.e., extraction, discovery, conformance checking, and performance analysis) cannot be supported using mainstream Artificial Intelligence (AI) and Machine Learning (ML) technologies (e.g., neural networks). One first needs to discover an explicit process model tightly connected to the event data, to pose the right questions. However, process mining can be used to create AI/ML problems. The combination can be used to trigger corrective actions or even complete workflows addressing the problem observed. This way, event data can be turned into actions that actively address performance and compliance problems.
2 Process Models
There are many notations to describe processes, ranging from Directly-Follows Graphs (DFGs) and transition systems, to BPMN and Petri nets. We will use an example to gently introduce these notations. Consider a process involving the following activities: buy ingredients (bi), create base (cb), add tomato (at), add cheese (ac), add salami (as), bake in oven (bo), eat pizza (ep), and clean kitchen (ck). We will call this fictive process the “pizza process” and use this to illustrate the key concepts and notations.
Figure 3 shows a process model using Business Process Model and Notation (BPMN) [17]. The process starts with activity buy ingredients (bi) followed by activity create base (cb). Then three activities are executed in any order: add tomato (at), add cheese (ac), and add salami (as). After all three toppings (tomato, cheese, and salami) have been added, the activities bake in oven (bo), eat pizza (ep), and clean kitchen (ck) are performed in sequence. Assuming that the three concurrent activities are performed in some order (i.e., interleaved), there are \(3!=6\) ways to execute the “pizza process”. The two diamond-shaped symbols with a + inside denote parallel gateways. The first one is a so-called AND-split starting the three concurrent branches and the second one is a so-called AND-join. The BPMN process starts with a start event (shown as a circle) and ends with an end event (shown as a thick circle).
Figure 4 models the same process in terms of a Petri net. This model also allows for \(3!=6\) ways to execute the “pizza process”. The circles correspond to places (to model states) and the squares correspond to transitions (to model activities). Places may hold tokens. A place is called marked if it contains a token. A marking is a distribution of tokens over places. In Fig. 4, the source place (i.e., the input place of transition \( bi \)) is marked, as is indicated by the token (the black dot). A transition is enabled if all input places are marked. In the initial marking shown in Fig. 4, transition \( bi \) (corresponding to activity buy ingredients) is enabled. A transition that is enabled may fire (i.e., it may occur). This means that a token is removed from each of the input places and a token is produced for each of the output places. Note that transition \( cb \) consumes one token and produces three tokens (one for each output place) and transition \( bo \) consumes three tokens (one for each input place) and produces one token. The process ends when a token is put on the sink place, i.e., the output place of \( ck \). In total there are \(2+2^3+3=13\) reachable markings. Although the behavior of the Petri net in Fig. 4 is the same as the BPMN model in Fig. 3, it is easier to refer to the states of the process model.
Figure 5 models the “pizza process” using a process tree. This representation is rarely presented to end-users, but several mining algorithms use this internally. Process trees are closer to programming constructs, process algebras, and regular expressions. The graphical representation can be converted to a compact textual format: \({{\,\mathrm{\rightarrow }\,}}( bi , cb ,{{\,\mathrm{\wedge }\,}}( ac , at , as ), bo , ep , ck )\). A sequence operator \({{\,\mathrm{\rightarrow }\,}}\) executes its children in sequential order. The root node in Fig. 5 denotes such a sequence, i.e., the six child nodes are executed in sequence. The third child node models the parallel execution of its three children. This subtree can be denoted by \({{\,\mathrm{\wedge }\,}}( ac , at , as )\). Later we will see that there are four types of operators that can be used in a process tree: \({{\,\mathrm{\rightarrow }\,}}\) (sequential composition), \({{\,\mathrm{\times }\,}}\) (exclusive choice), \({{\,\mathrm{\wedge }\,}}\) (parallel composition), and \({{\,\mathrm{\circlearrowleft }\,}}\) (redo loop). The semantics of a process tree can be expressed in terms of Petri nets, e.g., Fig. 5 and Fig. 4 represent the same process.
Most of the process mining tools directly show a Directly-Follows Graph (DFG) when loading an event log. This helps get a first impression of the behavior recorded. Figure 6 shows a DFG for our running example. There are two special nodes to model start (\(\blacktriangleright \)) and end (\(\blacksquare \)). The other nodes represent activities. The arcs in a DFG denote the “directly-follows relation”, e.g., the arc connecting \( cb \) to \( at \) shows that immediately after creating the pizza base \( cb \) one can add tomato paste \( at \). Activity \( cb \) has three outgoing arcs denoting a choice, i.e., \( cb \) is directly followed by \( at \), \( ac \), or \( as \). Activity \( at \) also has three outgoing arcs denoting that one can add another topping (\( ac \) or \( as \)) or bake the pizza (\( bo \)). Note that the behavior of the DFG in Fig. 6 is different from the three models shown before (i.e., the BPMN model, the Petri net, and the process tree). The DFG allows for infinitely many ways to execute the “pizza process” (instead of \(3!=6\)). For example, it is possible to create a pizza where each of the toppings was added 10 times. The problem is that whenever two activities can occur in any order (e.g., \( at \) and \( ac \)), there is immediately a loop in the DFG (even when both happen only once).
To explain other process constructs such as choice, skipping, and looping we extend the “pizza process”. First of all, we allow for adding multiple servings of cheese, i.e., activity \( ac \) can be executed multiple times after creating the pizza base and before putting the pizza in the oven. Second, instead of adding salami as a topping one can add mushrooms, i.e., there is a choice between \( as \) (add salami) and \( am \) (add mushrooms). Third, the eating of the pizza may be skipped (i.e., activity \( ep \) is optional).
Figure 7 shows the BPMN model with these three extensions. In total six exclusive gateways were added: three XOR-splits and three XOR-joins (see the diamond-shaped symbols with a \(\mathbf {\times }\) inside). After adding cheese, one can loop back. There is a choice between adding salami and adding mushrooms. Also the eating of the pizza can be skipped.
Figure 8 shows a Petri net modeling the extended process. A new transition \( am \) (add mushrooms) has been added. Transitions \( as \) and \( am \) share an input place. If the input place is marked, then both transitions are enabled, but only one of them can occur. If \( as \) consumes the token from the shared input place, then \( am \) gets disabled. If \( am \) consumes the token from the shared input place, then \( as \) gets disabled. This way, we model the choice between two toppings: salami and mushrooms. Figure 8 also has two new so-called silent transitions denoted by the two black rectangles. Sometimes such silent transitions are denoted as a normal transition with a \(\tau \) label. Silent transitions do not correspond to activities and are used for routing only, e.g., skipping activities. In Fig. 8, there is one silent transition to repeatedly execute \( ac \) (to model adding multiple servings of cheese) and one silent transition to skip \( ep \).
The process tree in Fig. 9 has the same behavior as the BPMN model and Petri net just shown. The process tree uses all four operators: \({{\,\mathrm{\rightarrow }\,}}\) (sequential composition), \({{\,\mathrm{\times }\,}}\) (exclusive choice), \({{\,\mathrm{\wedge }\,}}\) (parallel composition), and \({{\,\mathrm{\circlearrowleft }\,}}\) (redo loop). A silent activity is denoted by \(\tau \) and cannot be observed. The process tree in Fig. 9 can also be visualized in textual form: \({{\,\mathrm{\rightarrow }\,}}( bi , cb , {{\,\mathrm{\wedge }\,}}({{\,\mathrm{\circlearrowleft }\,}}( ac ,\tau ), at ,{{\,\mathrm{\times }\,}}( as , am )), bo ,{{\,\mathrm{\times }\,}}( ep ,\tau ), ck )\).
To understand the notation, we first look at a few smaller examples. Process tree \({{\,\mathrm{\times }\,}}(a,b)\) models a choice between activities a and b. Process tree \({{\,\mathrm{\times }\,}}(a,\tau )\) can be used to model an activity a that can be skipped. Process tree \({{\,\mathrm{\circlearrowleft }\,}}(a,\tau )\) can be used to model the process that executes a at least once. The “redo” part is silent, so the process can loop back without executing any activity. Process tree \({{\,\mathrm{\circlearrowleft }\,}}(\tau ,a)\) models a process that executes a any number of times. The “do” part is now silent and activity a is in the “redo” part. This way it is also possible to not execute a at all.
Now let us take a look at the three modifications of our extended “pizza process”: \({{\,\mathrm{\circlearrowleft }\,}}( ac ,\tau )\) models that multiple servings of cheese can be added, \({{\,\mathrm{\times }\,}}( as , am )\) models the choice between salami and mushrooms, and \({{\,\mathrm{\times }\,}}( ep ,\tau )\) models the ability to skip eating the pizza.
The DFG shown in Fig. 10 incorporates the three extensions. Again, the behavior is different from Figs. 7, 8, and 9. Unlike the other models, the DFG allows for adding multiple servings of salami, mushrooms, and tomato paste. It is impossible to model concurrency properly, because loops are added the moment the order is not fixed. Therefore, DFGs are suitable for a quick first view of the process, but for more advanced process analytics, higher-level notations such as BPMN, Petri nets, and process trees are needed.
Note that, in this section, we focused on control-flow. However, process models can be extended with frequencies, probabilities, decision rules, roles, costs, and time delays (e.g., mean waiting times). After discovering the control-flow and replaying the event data on the model, it is easy to extend process models with data, resource, cost, and time perspectives.
3 Event Data
Using process mining, we would like to analyze and improve processes using event data. Table 1 shows a fragment of an event log in tabular form. One can think of this as a table in a relational database, a CSV (Comma Separated Value) file, or Excel spreadsheet. Each row in the table corresponds to an event. An event can have many different attributes. In this simple example, each event has five attributes: case, activity, timestamp, resource, and customer. Most process mining tools and approaches require at least three attributes: case (refers to a process instance), activity (refers to the operation, action, or task), and timestamp (when did the event happen). These three attributes are enough to discover and check the control-flow perspective. A case may refer to an order, a patient, an application, a student, a loan, a car, a suitcase, a speeding ticket, etc. In Table 1, each case refers to a pizza being produced and consumed. In Sect. 2 we showed process models describing this process. However, now we start from the observed behavior recorded in the event log. We can witness the same activities as before: buy ingredients (\( bi \)), create base (\( cb \)), add cheese (\( ac \)), add tomato (\( at \)), add salami (\( as \)), add mushrooms (\( am \)), bake in oven (\( bo \)), eat pizza (\( ep \)), and clean kitchen (\( ck \)). Table 1 uses a simple time format (e.g., 18:10) to simplify the presentation (i.e., we skipped the date). Systems often use the ISO 8601 standard (or similar) to exchange date- and time-related data, e.g., 2021-09-21T18:10:00+00:00. In the remainder, we formalize event data and provide useful notions to reason about both observed and modeled behavior. We start with some basic mathematical notations.
3.1 Notations
\(\mathcal {B}(A)\) is the set of all multisets over some set A. For some multiset \(b\in \mathcal {B}(A)\), b(a) denotes the number of times element \(a\in A\) appears in b. Some examples: \(b_1 = [~]\), \(b_2 = [x,x,y]\), \(b_3 = [x,y,z]\), \(b_4 = [x,x,y,x,y,z]\), and \(b_5 = [x^3,y^2,z]\) are multisets over \(A=\{x,y,z\}\). \(b_1\) is the empty multiset, \(b_2\) and \(b_3\) both consist of three elements, and \(b_4 = b_5\), i.e., the ordering of elements is irrelevant and a more compact notation may be used for repeating elements. The standard set operators can be extended to multisets, e.g., \(x\in b_2\), \(b_2 \uplus b_3 = b_4\), \(b_5 \setminus b_2 = b_3\), \(|b_5|=6\), etc. \(\{a \in b\}\) denotes the set with all elements a for which \(b(a) \ge 1\). \(b(X) = \sum _{a \in X}\ b(x)\) is the number of elements in b belonging to set X, e.g., \(b_5(\{x,y\}) = 3+2=5\). \(b \le b'\) if \(b(a) \le b'(a)\) for all \(a \in A\). Hence, \(b_3 \le b_4\) and \(b_2 \not \le b_3\) (because \(b_2\) has two x’s). \(b < b'\) if \(b \le b'\) and \(b \ne b'\). Hence, \(b_3 < b_4\) and \(b_4 \not < b_5\) (because \(b_4 = b_5\)).
\(\sigma = \langle a_1,a_2, \ldots , a_n\rangle \in X^*\) denotes a sequence over X of length \(\left| {\sigma }\right| = n\). \(\sigma _i = a_i\) for \(1 \le i \le \left| {\sigma }\right| \). \(\langle ~\rangle \) is the empty sequence. \(\sigma _1 \cdot \sigma _2\) is the concatenation of two sequences, e.g., \(\langle x,x,y\rangle \cdot \langle x,y,z\rangle = \langle x,x,y,x,y,z\rangle \). The notation \([a \in \sigma ]\) can be used to convert a sequence into a multiset. \([a \in \langle x,x,y,x,y,z\rangle ] = [x^3,y^2,z]\).
\(f \in X \rightarrow Y\) is a total function, i.e., \(f(x) \in Y\) for any \(x \in X\). \(f \in X \not \rightarrow Y\) is a partial function with domain \( dom (f) \subseteq X\). If \(x \not \in dom (f)\), then we write \(f(x) = \bot \), i.e., the function is not defined for x.
3.2 Standard Event Log
An event log is a collection of events. An event e can have any number of attributes, and often we require the following three attributes to be present: case \(\#_{ case }(e)\), activity \(\#_{ act }(e)\), and timestamp \(\#_{ time }(e)\). Table 1 shows example events. If e is the first visible event, then \(\#_{ case }(e)= \text{ pizza-56 }\), \(\#_{ act }(e) = bi \) (buy ingredients), and \(\#_{ time }(e) =\) 18:10. For simplicity, we write 18:10, but the full timestamp includes a date and possibly also seconds and milliseconds.
To formalize event logs, we introduce some basic notations.
Definition 1 (Universes)
\(\mathcal{U}_{ ev }\) is the universe of events, \(\mathcal{U}_{ act }\) is the universe of activities, \(\mathcal{U}_{ case }\) is the universe of cases, \(\mathcal{U}_{ time }\) is the universe of timestamps, \(\mathcal{U}_{ att }= \{ act , case , time , \ldots \}\) is the universe of attributes, \(\mathcal{U}_{ val }\) is the universe of values, and \(\mathcal{U}_{ map }= \mathcal{U}_{ att }\not \rightarrow \mathcal{U}_{ val }\) is the universe of attribute-value mappings. We assume that \(\mathcal{U}_{ act }\cup \mathcal{U}_{ case }\cup \mathcal{U}_{ time }\subseteq \mathcal{U}_{ val }\), \(\bot \not \in \mathcal{U}_{ val }\), and for any \(f \in \mathcal{U}_{ map }\): \(f( act ) \in \mathcal{U}_{ act }\cup \{\bot \}\), \(f( case ) \in \mathcal{U}_{ case }\cup \{\bot \}\), and \(f( time ) \in \mathcal{U}_{ time }\cup \{\bot \}\).
Note that standard attributes of an event (activity, case, timestamp, etc.) are treated as any other attribute. \(f \in \mathcal{U}_{ map }\) is a function mapping any subset of attributes onto values. For example, f could be such that \( dom (f)=\{ case , act , time , resource , customer , cost , size \}\), \(f(case)= \text{ pizza-56 }\), \(f(act)= bi \), \(f(time)=\) 2021-09-21T18:10:00+00:00, \(f(resource) = \text{ Stefano }\), \(f(customer) = \text{ Valentina }\), \(f(size)= 33\text{ cm }\), and  . Note that the last two attributes are not shown in Table 1. and that 2021-09-21T18:10:00+00:00 is abbreviated to 18:10.
. Note that the last two attributes are not shown in Table 1. and that 2021-09-21T18:10:00+00:00 is abbreviated to 18:10.
To be general, we assume that events are partially ordered. Recall that a strict partial order is irreflexive (\(e\not \prec e\)), transitive (\(e_1\prec e_2\) and \(e_2\prec e_3\) implies \(e_1\prec e_3\)), and asymmetric (if \(e_1\prec e_2\), then \(e_2\not \prec e_1\)).
Definition 2 (Event Log)
An event log is a tuple \(L=(E,\#,\prec )\) consisting of a set of events \(E \subseteq \mathcal{U}_{ ev }\), a mapping \(\# \in E \rightarrow \mathcal{U}_{ map }\), and a strict partial ordering \(\prec \, \subseteq E \times E\) on events.
For any \(e \in E\) and \( att \in dom (\#(e))\): \(\#_{ att }(e) = \#(e)({att})\) is the value of attribute \( att \) for event e. For example, \(\#_{ act }(e)\), \(\#_{ case }(e)\), and \(\#_{ time }(e)\) are the activity, case, and timestamp of an event e.
The ordering of events respects time, i.e., if \(e_1,e_2 \in E\), \(\#_{ time }(e_1) \ne \bot \), \(\#_{ time }(e_2) \ne \bot \), and \(\#_{ time }(e_1) < \#_{ time }(e_2)\), then \(e_2 \not \prec e_1\).
To be general, events can have any number of attributes and no attribute is mandatory. However, when using simplified event logs, we only consider events having a case and activity (with an order derived using timestamps).
Assume \(L=(E,\#,\prec )\) is the event log in Table 1. The whole event log has 6400 events, i.e., the table has many more rows. Let \(E = \{ e_1,e_2, \ldots , e_{6400} \}\) be the whole set of events and assume the first event shown in Table 1 is \(e_{433}\). \(\#(e_{433})\) is a mapping with \( dom (\#(e_{433})) = \{ case , act , time , resource , customer \}\) (the columns shown in the table). \(\#_{ case }(e_{433}) = \text{ pizza-56 }\), \(\#_{ act }(e_{433}) = bi \) (buy ingredients), \(\#_{ time }(e_{433}) = \text{18:10 }\), \(\#_{ resource }(e_{433}) = \text{ Stefano }\), and \(\#_{ customer }(e_{433}) = \text{ Valentina }\). Assuming that the event identifiers follow the order shown in Table 1, the last event visible in the table is \(e_{456}\), and \(\#_{ case }(e_{456}) = \text{ pizza-58 }\), \(\#_{ act }(e_{456}) = ck \) (clean kitchen), \(\#_{ time }(e_{456}) = \text{20:51 }\), \(\#_{ resource }(e_{456}) = \text{ Mario }\), and \(\#_{ customer }(e_{456}) = \text{ Laura }\). Assuming a total order as shown in the Table, \(e_{433} \prec e_{434}\), \(e_{434} \prec e_{435}\), \(e_{455} \prec e_{456}\), \(e_{433} \prec e_{456}\), etc.
As stated in Definition 2, \(\prec \) is a strict partial order and it is not allowed that timestamps (when present) and the partial order disagree. Using Table 1 and the event identifiers \(e_{433}\) and \(e_{456}\). It cannot be that \(e_{456} \prec e_{433}\), because \(\#_{ time }(e_{456}) > \#_{ time }(e_{433})\). For two arbitrary events \(e_1\) and \(e_2\) it cannot be that both \(\#_{ time }(e_1) < \#_{ time }(e_2)\) and \(e_2 \prec e_1\). However, it can be that \(\#_{ time }(e_1) < \#_{ time }(e_2)\) and \(e_1 \not \prec e_2\) (the time perspective is more fine grained) or that \(\#_{ time }(e_1) = \#_{ time }(e_2)\) and \(e_1 \prec e_2\) (the partial order is more fine grained). Optionally, the partial order can be derived from the timestamps (when present): \(\prec \, = \{(e_1,e_2) \in E \times E \mid \#_{ time }(e_1) < \#_{ time }(e_2)\}\). In this case, the event log is fully defined by \(L=(E,\#)\) (no explicit ordering relation is needed).
It should be noted that in the often used BPI Challenge 2011 log provided by a Dutch academic hospital [16], 85% of the events have the same timestamp as the previous one. This is because, for many events, only dates are available. Many publicly available event logs have similar issues, for example, in the so-called Sepsis log [30], 30% of the events have the same timestamp as the previous one. In this event log, activities for the same case are sometimes batched, leading to events with the same timestamp. These examples illustrate that one should inspect timestamps and not take the order in the event log for granted. It may be beneficial to use partially ordered event data in case of data quality problems or when there is explicit causal information.
3.3 Simplified Event Log
For process mining techniques focusing on control-flow, it often suffices to focus only on the activity attribute and the ordering within a case. This leads to a much simpler event log notion.
Definition 3 (Simplified Event Log)
A simplified event log \(L \in \mathcal {B}({\mathcal{U}_{ act }}^*)\) is a multiset of traces. A trace \(\sigma = \langle a_1,a_2, \ldots a_n \rangle \in {\mathcal{U}_{ act }}^*\) is a sequence of activities. \(L(\sigma )\) is the number of times trace \(\sigma \) appears in event log L.
Consider case \(\text{ pizza-56 }\) in Table 1. There are eight events having this case attribute. By ordering these events based on their timestamps we get the trace  . We can do the same for the other two cases shown in Table 1:
. We can do the same for the other two cases shown in Table 1:  and
and  . We are using the same shorthands as before, i.e., buy ingredients (\( bi \)), create base (\( cb \)), add cheese (\( ac \)), add tomato (\( at \)), add salami (\( as \)), add mushrooms (\( am \)), bake in oven (\( bo \)), eat pizza (\( ep \)), and clean kitchen (\( ck \)).
. We are using the same shorthands as before, i.e., buy ingredients (\( bi \)), create base (\( cb \)), add cheese (\( ac \)), add tomato (\( at \)), add salami (\( as \)), add mushrooms (\( am \)), bake in oven (\( bo \)), eat pizza (\( ep \)), and clean kitchen (\( ck \)).
The same trace may appear multiple times in a log. For example, \(L = [\langle a,b,c,e \rangle ^{10},\langle a,c,b,e \rangle ^5,\langle a,d,e \rangle ]\) is a simple event log with \(10+5+1=16\) cases and \(40+20+3=63\) events.
An event log with events having any number of attributes (Definition 2) can be transformed into a simplified event log by ignoring the additional attributes and sequentializing the events belonging to the same case. Events without a case or activity attribute are ignored in the transformation process.
Definition 4 (Conversion)
An event log \(L=(E,\#,\prec )\) defines a simplified event log \(\tilde{L} \in \mathcal {B}({\mathcal{U}_{ act }}^*)\) that is constructed as follows:
-
\(E' = \{ e \in E \mid \#_{ case }(e)\ne \bot \wedge \#_{ act }(e)\ne \bot \}\) are all events having an activity and a case attribute.
-
\(C = \{ \#_{ case }(e) \mid e \in E'\}\) and \(A = \{ \#_{ act }(e) \mid e \in E'\}\) are the cases and activities in L.
-
For any case \(c\in C\):
-
\(E_c = \{ e \in E'\mid \#_{ case }(e)=c\}\) are the events in c,
-
\(\sigma _c = \langle e_1, e_2, \dots , e_n \rangle \) is a (deterministically chosen) sequentialization of the events in c, i.e., \(\sigma _c\) is such that \(\{ e_1, e_2, \dots ,e_n \} = E_c\), \(\left| {E_c}\right| = \left| {\sigma _c}\right| \), and for any \(1 \le i < j \le n\): \(e_j \not \prec e_i\).
-
\(\tilde{\sigma }_c = \langle \#_{ act }(e_1), \#_{ act }(e_2), \dots , \#_{ act }(e_n) \rangle \in A^*\) is the trace corresponding to c (i.e., the events in \(\sigma _c\) are replaced by the corresponding activities).
-
-
\(\tilde{L} = [ \tilde{\sigma }_c \mid c \in C] \in \mathcal {B}(A^*)\) is the simplified event log derived from L.
Let \(L=(E,\#,\prec )\) be the event log corresponding to the events visible in Table 1 (assuming the order in the table). Then: \(\tilde{L} = [ \langle bi , cb , ac , at , as , bo , ep , ck \rangle ,\langle bi , cb , at , ac , as , bo , ep , ck \rangle ,\langle bi , cb , as , at , ac , bo , ep , ck \rangle ]\). Table 1 only shows a fragment of the whole event log. For the whole event log \(L=(E,\#,\prec )\), we have \(\tilde{L} = [ \langle bi , cb , ac , at , as , bo , ep , ck \rangle ^{400},\) \(\langle bi , cb , at , ac , as , bo , ep , ck \rangle ^{200},\) \(\langle bi , cb , as , at , ac , bo , ep , ck \rangle ^{100},\) \(\langle bi , cb , ac , as , at , bo , ep , ck \rangle ^{50},\) \(\langle bi , cb , at , as , ac , bo , ep , ck \rangle ^{25},\) \(\langle bi , cb , as , ac , at , bo , ep , ck \rangle ^{25} ]\). This event log has 800 cases and 6400 events. Using process discovery techniques we can automatically discover the models in Figs. 3, 4, 5 and 6 from such an event log. If the event log also has cases where cheese is added multiple times (e.g., \(\langle bi , cb , ac , at , ac , ac , as , bo , ep , ck \rangle \)), mushrooms are added instead of salami (e.g., \(\langle bi , cb , ac , at , am , bo , ep , ck \rangle \)), and the eating activity is skipped (e.g., \(\langle bi , cb , ac , at , as , bo , ck \rangle \)), then we can automatically discover the models in Figs. 7, 8, 9 and 10 using suitable process mining techniques.
3.4 Object-Centric Event Logs
Table 1 corresponds to a conventional “flat” event log where each event (i.e., row) refers to a case, activity, and timestamp. It is very natural to assume that an event has indeed a timestamp and refers to an activity. However, the assumption that it refers to precisely one case may cause problems [4]. Object-Centric Event Logs (OCEL) aim to overcome this limitation [22]. In OCEL, an event may refer to any number of objects (of different types) rather than a single case. Object-centric process mining techniques may produce Petri nets with different types of objects [7] or artifact-centric process models [18, 19].
To understand the problem, we use Table 2, which shows OCEL data in tabular form. Compared to Table 1, we do not assume a single case notion. Instead, an event may refer to any number of objects. In this toy example, we assume four types of objects: pizza, resource, customer, and location. Assume that e is the first event listed in Table 2. \(\#_{ act }(e) = bi \) (buy ingredients), \(\#_{ time }(e) =\) 18:10, \(\#_{ pizza }(e) = \{\text{ pizza-56 },\text{ pizza-57 },\text{ pizza-58 }\}\), \(\#_{ resource }(e) = \{\text{ Stefano }\}\), \(\#_{ customer }(e) = \{\text{ Valentina },\text{ Giulia },\text{ Laura }\}\), and \(\#_{ location }(e) = \{\text{ supermarket }\}\). Note that in Table 1 there were three \( bi \) (buy ingredients) events, one for each pizza. Hence, Table 2 is closer to reality if the ingredients were indeed bought in the same visit to the supermarket. In a classical event log with a single case identifier, we need to artificially replicate events (one \( bi \) event per pizza). This may lead to misleading statistics, i.e., there was just one trip to the supermarket and not three. The three pizzas were created on demand, so the \( bi \) event also refers to the three customers. Table 2 also shows that creating the pizza base is team work, i.e., all \( cb \) events are done by both Mario and Stefano. If we assume that e is the last event visible in Table 2, then \(\#_{ act }(e) = ck \) (clean kitchen), \(\#_{ time }(e) = 20.51\), \(\#_{ pizza }(e) = \emptyset \), \(\#_{ resource }(e) = \{\text{ Mario }\}\), \(\#_{ customer }(e) = \emptyset \), and \(\#_{ location }(e) = \{\text{ kitchen-2 }\}\). This expresses that, according to this event log, cleaning the second kitchen is unrelated to the pizza prepared in it.
Definition 2 can be easily extended to allow for Object-Centric Event Logs (OCEL). We just need to assume that event attributes include object types and that attribute-value mappings may yield sets of values (e.g., objects) rather than individual values. Without fully formalizing this, we simply assume that \(\mathcal{U}_{ objtyp } \subseteq \mathcal{U}_{ att }\) is the universe of object types, \(\mathcal{U}_{ objs }\) is the universe of objects, and \(\mathcal {P}(\mathcal{U}_{ objs }) \subseteq \mathcal{U}_{ val }\) (i.e., values can be sets of objects). Moreover, for any \(f \in \mathcal{U}_{ map }\) and \( ot \in \mathcal{U}_{ objtyp } \cap dom (f)\): \(f( ot ) \subseteq \mathcal{U}_{ objs }\). Hence, attribute value mappings can be used to also map object types onto sets of objects.
To apply classical process mining techniques, we need to convert the object-centric event data to traditional event data. For example, we need to convert Table 2 into Table 1 if we pick object type pizza as a case notion. This is called “flattening the event log” and always requires picking an object type as a case notion. This can be formalized in a rather straightforward manner.
Definition 5 (OCEL Conversion)
Let \(L=(E,\#,\prec )\) be an event log having an object type \( ot \in \mathcal{U}_{ objtyp }\) such that for any \(e\in E\): \(\#_{ ot }(e) \subseteq \mathcal{U}_{ objs }\) is the set of objects of type \( ot \) involved in event e. Based on this assumption, we can create a “flattened event log” \(\tilde{L}_{ ot } \in \mathcal {B}({\mathcal{U}_{ act }}^*)\) that is constructed as follows:
-
\(E' = \{ e \in E \mid \#_{ ot }(e)\ne \emptyset \wedge \#_{ act }(e)\ne \bot \}\) are all events having an activity and referring to at least one object of type \( ot \).
-
\(O = \bigcup _{e \in E'} \#_{ ot }(e)\) and \(A = \{ \#_{ act }(e) \mid e \in E'\}\) are the objects of type \( ot \) and activities in L.
-
For any object \(o\in O\):
-
\(E_o = \{ e \in E'\mid o \in \#_{ ot }(e)\}\) are the events involving object o,
-
\(\sigma _o = \langle e_1, e_2, \dots , e_n \rangle \) is a (deterministically chosen) sequentialization of the events involving o, i.e., \(\sigma _o\) is such that \(\{ e_1, e_2, \dots ,e_n \} = E_o\), \(\left| {E_o}\right| = \left| {\sigma _o}\right| \), and for any \(1 \le i < j \le n\): \(e_j \not \prec e_i\).
-
\(\tilde{\sigma }_o = \langle \#_{ act }(e_1), \#_{ act }(e_2), \dots , \#_{ act }(e_n) \rangle \in A^*\) is the trace corresponding to o (i.e., the events in \(\sigma _o\) are replaced by the corresponding activities).
-
-
\(\tilde{L} = [ \tilde{\sigma }_o \mid o \in O] \in \mathcal {B}(A^*)\) is the simplified event log derived from L.
Definition 5 shows that any OCEL can be transformed into a simplified event log. The simplified event log is a multiset of traces where each trace refers to the “lifecycle” of an object. Consider for example  showing the lifecycle of pizza-56 in Table 2.
showing the lifecycle of pizza-56 in Table 2.  is the trace corresponding to resource Stefano.
is the trace corresponding to resource Stefano.  is the trace corresponding to customer Valentina. This trace is now the same as
is the trace corresponding to customer Valentina. This trace is now the same as  , but this would not be the case if Valentina eats multiple pizzas (e.g., in subsequent visits to the restaurant).
, but this would not be the case if Valentina eats multiple pizzas (e.g., in subsequent visits to the restaurant).  is the trace corresponding to the location “supermarket” (assuming there was just one visit to the supermarket).
is the trace corresponding to the location “supermarket” (assuming there was just one visit to the supermarket).  is the trace corresponding to the location “restaurant” (again considering only the events visible in Table 2). These traces are rather short because we only consider the events shown in Table 2.
is the trace corresponding to the location “restaurant” (again considering only the events visible in Table 2). These traces are rather short because we only consider the events shown in Table 2.
By converting an OCEL to a conventional event log, we can apply all existing process mining techniques. For each object type, we can create a process model showing the “flow of objects” of that type. However, flattening the event log using \( ot \) as a case notion potentially leads to the following problems.
-
Deficiency: Events in the original event log that have no corresponding events in the flattened event log disappear from the data set (i.e., \(\#_{ ot }(e) = \emptyset \)). For example, when selecting object type pizza as a case notion, the clean kitchen events disappear from the event log.
-
Convergence: Events referring to multiple objects of the selected type are replicated, possibly leading to unintentional duplication (i.e., \(\left| {\#_{ ot }(e))}\right| \ge 2\)). For example, when selecting object type pizza as a case notion, the first event in Table 2 will be mapped onto three events in the flattened event log. When selecting object type resource as a case notion, all create pizza base events are duplicated in the flattened event log. The replication of events can lead to misleading diagnostics.
-
Divergence: Events referring to different objects of a type not selected as the case notion may still be considered causally related because a more coarse-grained object is shared. For example, when selecting object type location as a case notion, events corresponding to different pizzas are interleaved and one can no longer see the causal dependencies.
The first two problems are easy to understand: events disappear completely (deficiency) or are replicated leading to potentially misleading management information (convergence). The problem of divergence is more subtle. To understand this better, consider  describing the “lifecycle” of the first kitchen. In this trace one can see \( cb \) followed by \( cb \) (two subsequent create pizza base events) and \( ac \) followed by \( ac \) (two subsequent add cheese events). However, these events refer to different pizzas and are not causally related. The discovered process model is likely to show loops involving \( cb \) and \( ac \), although these events occur precisely once per pizza.
describing the “lifecycle” of the first kitchen. In this trace one can see \( cb \) followed by \( cb \) (two subsequent create pizza base events) and \( ac \) followed by \( ac \) (two subsequent add cheese events). However, these events refer to different pizzas and are not causally related. The discovered process model is likely to show loops involving \( cb \) and \( ac \), although these events occur precisely once per pizza.
In summary, one can create different views on the process by flattening the event data for selected object types, but one should be careful to interpret these correctly (e.g., be aware of data duplication and the blurring of causalities).
The running “pizza process” example is not very realistic, and is only used to introduce the basic concepts in a clear manner. Earlier, we mentioned CRM systems like Salesforce and ERP systems like SAP S/4HANA, Oracle E-Business Suite, and Microsoft Dynamics 365. These systems are loaded with event data scattered over many database tables. ERP and CRM systems are widely used, broad in scope, and sector-agnostic. Also, more sector-specific systems used in banking, insurance, and healthcare have event data distributed over numerous tables. These tables refer to different types of objects that are often in a one-to-many or many-to-many relation. This immediately leads to the challenges described before.
Let us consider two of the processes almost any organization has: Purchase-to-Pay (P2P) and Order-to-Cash (O2C). The P2P process is concerned with the buy-side of an organization. The O2C process is concerned with the sell-side of a company. In the P2P process the organization is dealing with purchasing documents, items, suppliers, purchase requisitions, contracts, receipts, etc. Note that there may be many purchase orders per supplier and an order may consist of multiple items. Hence, events may refer to different objects and also multiple objects of the same time. In the O2C process, we can witness similar phenomena. A customer may place three orders on the same day and each order may have several items. Items from different orders may end up in the same delivery. Moreover, items in the same order may end up in different deliveries.
P2P and O2C processes are considered simple and there is a lot of experience with extracting such data from systems such as SAP. Still, these processes are more complicated than what many people think. It is not uncommon to find thousands of process variants. This offers great opportunities for process mining, because unexpected variants provide hints on how to improve the process. However, one should not underestimate the efforts needed for data extraction. Therefore, we discussed OCEL as it sits in-between the real database tables in systems such as SAP, Oracle, and Salesforce, and the flattened event logs assumed by most systems.
3.5 XES Standard
The initial version of the XES (eXtensible Event Stream) format was defined by the IEEE Task Force on Process Mining in September 2010. After several iterations, XES became the official IEEE standard for storing event data in 2016 [24]. XES is supported by most of the open-source process mining tools and many of the leading commercial tools. The goal is to facilitate the seamless exchange of event data between different systems. Of course, it is also possible to do this using relational databases or simple file formats. However, XES adds semantics to the data exchanged. Therefore, we focus on the concepts and refer to [24] for the syntax.
Meta model of XES [24]. A log contains traces and each trace contains events [2, 24]. Log, traces, and events have attributes. Extensions may define new attributes and a log should declare the extensions used in it. Global attributes are attributes that are declared to be mandatory. Such attributes reside at the trace or event level. Attributes may be nested. Event classifiers are defined for the log and assign a “label” (e.g., activity name) to each event. There may be multiple classifiers.
Figure 11 shows the XES meta model expressed in terms of a UML class diagram. A XES document (e.g., an XML file) contains one log consisting of any number of traces. Each trace describes a sequential list of events corresponding to a particular case. The log, its traces, and its events may have any number of attributes. Attributes may be nested. There are five core types: String, Date, Int, Float, and Boolean. XES does not prescribe a fixed set of mandatory attributes for each element (log, trace, and event), e.g., an event can have any number of attributes. However, to provide semantics for such attributes, the log refers to so-called XES extensions. An extension gives semantics to particular attributes. For example, the Time extension defines a timestamp attribute of type xs:dateTime. This corresponds to the \(\#_{ time }(e)\) attribute used before. The Organizational extension defines a resource attribute of type xs:string, i.e., the \(\#_{ resource }(e)\) attribute. Users can define their own extensions. For example, it is possible to develop domain-specific or even organization-specific extensions.
XES also supports three concepts that are of general interest and important for process mining: classifiers, lifecycle information, and activity instances. These concepts are interrelated as is discussed next.
Classifiers are used to attach labels to events. There is always at least one classifier and by default; this is the activity name. When turning an event log L into a simplified event log \(\tilde{L} \in \mathcal {B}({\mathcal{U}_{ act }}^*)\) in Definition 4, we are using this default classifier: each event e is mapped onto \(\#_{ act }(e)\). However, it is also possible to project events onto resources, locations, departments, etc., or combinations of attributes. An event classifier assigns to each event an identity, which makes it comparable to other events (via their assigned identity). Event classifiers are defined for the whole log, and there may be an arbitrary number of classifiers.
Thus far, we implicitly assumed that events are atomic. Therefore, an event has a timestamp. To handle activities that take time, XES provides the possibility to represent lifecycle information and to connect events through activity instances. An activity instance is a collection of related events that together represent the execution of an activity for a case. For example, an activity instance may be composed of a start event and a complete event. This way, we can derive information about the duration of an activity instance. The XES lifecycle model distinguishes between the following types of events: schedule, assign, withdraw, reassign, start, suspend, resume, abort, complete, autoskip, and manualskip. Using this XES extension, an event e has an attribute \(\#_{ type }(e)\). For example, assume that \(e_1\) and \(e_2\) are two events that belong to the same activity instance and \(\#_{ type }(e_1)=\text{ start }\) and \(\#_{ type }(e_2)=\text{ complete }\). \(\#_{ time }(e_2)-\#_{ time }(e_1)\) is the duration of the activity. Similarly, we can measure waiting times, etc. Note that classifiers can also use lifecycle information, e.g., an event e is identified by the pair \((\#_{ act }(e),\#_{ type }(e))\). This implies that when we discover process models, there may be activities \((a,\text{ start})\) and \((a,\text{ complete})\).
Many XES logs contain lifecycle information, but few contain explicit activity instances. This implies that heuristics are needed to link events. For example, \((a,\text{ start})\) is coupled to the first \((a,\text{ complete})\) following it. However, in the trace \(\langle \ldots ,(a,\text{ start}),\ldots ,\) \((a,\text{ start}),\ldots ,\) \((a,\text{ complete}),\ldots ,\) \((a,\text{ complete}),\ldots \rangle \), there are two possible ways to match starts and ends. Fortunately, it is often possible to extract activity instances from the original data source.
4 Different Types of Process Mining
After introducing multiple ways to represent process models (BPMN, Petri nets, process trees, and DFGs) and different types of events logs (e.g., XES and OCEL), we now briefly introduce some of the standard process mining tasks (see Fig. 12). As a starting point, we assume that high-quality event data are available. In practice, it is often time-consuming to extract event data from existing systems. As mentioned before, events may be scattered over multiple database tables or even multiple information systems using different identifiers. When starting with process mining, data extraction and data cleaning may take 80% of the time. Of course, the exact percentage depends on the type of process and information system. Also if the data pipeline is set up properly, this is a one-time effort that can be reused continuously.
4.1 Process Discovery
Event logs contain example behavior. The challenge is to discover a process model based on such example behavior. The model should not be “overfitting” (i.e., simply enumerating the observed example traces) and not “underfitting” (i.e., allow for behavior unrelated to what was observed). This is a difficult task and numerous algorithms have been proposed in literature, including the Alpha algorithm [8], region-based approaches [11, 13, 33, 36], inductive mining techniques [28, 29], and the split miner [9]. A baseline approach is the creation of a DFG, where the observed activities are added as nodes and two nodes a and b are connected through a directed arc if activity a is directly followed by activity b at least once. Obviously, such an approach is too simplistic and leads to underfitting process models. If activity a is directly followed by activity b in one case and activity b is directly followed by activity a in another case, then a loop is introduced. The techniques mentioned above address this problem and are able to uncover concurrency. However, there are many other challenges. The event log may contain infrequent behavior, i.e., traces or patterns which are less frequent compared to the mainstream behavior. Should this infrequent behavior be included or not? Hence, most approaches are parameterized to discard rare behavior. On the one hand, we often want to leave out infrequent behavior to simplify models. On the other hand, one cannot assume to have seen all behavior. Concurrency leads to an exponential number of states and a factorial number of possible traces. An unbounded loop leads to infinitely many possible traces. Process discovery is further complicated by the fact that event logs do not contain negative examples (i.e., traces that cannot happen) and are often incomplete (i.e., only a small fraction of all possible behavior is observed).
It is important to focus on a particular process or problem, having a particular goal in mind. One needs to select and filter the data based on a well-defined goal. Randomly using sliders to simplify process models may be useful for a first exploration, but will rarely lead to the desired insights.
To introduce process discovery, we focus on the control-flow, i.e., the ordering of activities. However, process models may include other perspectives, including time, data, resources, costs, etc. For example, a choice may be based on the attributes of the case or preceding event, and we may attach resource allocation rules to activities (e.g., role information and authorizations). Process discovery may add such perspectives, but we typically try to get clarity on the control-flow first. If no reasonable control-flow can be established, one should not try to add additional perspectives. Several process discovery techniques are explained in detail in [5, 10].
4.2 Conformance Checking
Conformance checking requires both an event log and a process model as input. The goal is to indicate where log and model disagree. To illustrate this consider Figs. 7, 8, and 9. These three models describe exactly the same behavior of the extended “pizza process” that can be compactly described as \({{\,\mathrm{\rightarrow }\,}}( bi , cb , {{\,\mathrm{\wedge }\,}}({{\,\mathrm{\circlearrowleft }\,}}( ac ,\tau ), at ,{{\,\mathrm{\times }\,}}( as , am )), bo ,{{\,\mathrm{\times }\,}}( ep ,\tau ), ck )\). Let \(M = \{ \langle bi , cb , ac , at , as , bo , ep , ck , \rangle , \ldots \langle bi , cb , am , at , ac , ac , ac , bo , ep , ck , \rangle , \ldots \langle bi , cb , at , ac , am , bo , ck \rangle \}\) be the infinite set of all traces allowed by the BPMN model, Petri net, and process tree depicted in the three figures. Let \(L \in \mathcal {B}({\mathcal{U}_{ act }}^*)\) be an event log containing 800 traces. Assume \(\sigma _1 = \langle bi , cb , ac , at , as , bo , ep , ck \rangle \in L\), \(\sigma _2 = \langle bi , cb , ac , ac , at , am , ep , ck \rangle \in L\), and \(\sigma _3 = \langle bi , cb , at , ac , at , as , bo , ck \rangle \in L\). Hence, \(L = [\sigma _1,\sigma _2,\sigma _3, \ldots ]\) and \(\left| {L}\right| =800\). \(\sigma _1 \in M\), i.e., this is a perfectly fitting trace. \(\sigma _2 \not \in M\) because activity \( bo \) (bake in oven) is missing, i.e., someone was eating an uncooked pizza. \(\sigma _3 \not \in M\) because activity \( at \) (add tomato) occurs twice. The goal of conformance checking is to detect such deviations.
\(L_{ fit } = [\sigma \in L \mid \sigma \in M]\) is the multiset of fitting traces and \(L_{ dev } = [\sigma \in L \mid \sigma \not \in M]\) is the multiset of deviating traces. Hence, fitness at the trace level can be defined as \(\left| {L_{ fit }}\right| / \left| {L}\right| \). The fraction is 1 if all traces are fitting and 0 if none of the traces is fitting.
There are many measures for fitness. For example, the above fraction does not take into account to what degree a trace is fitting or not. Trace \(\sigma _4 = \langle bo , bo , bo , at , at , at , at , at \rangle \in L\) is obviously more deviating than \(\sigma _2\) and \(\sigma _3\). Moreover, it is not enough to produce a number. In practice, good diagnostics are much more important than a single quality measure.
There are many techniques for conformance checking. The two most frequently used approaches are token-based replay [32] and alignments [6, 14]. For token-based replay, the process model is represented as a Petri net and traces in the event log are replayed on the model. If the trace indicates that an activity needs to take place, the corresponding transition is executed. If this is not possible because an input place is empty, a so-called missing token is added. Tokens that are never consumed are called remaining tokens. The numbers of missing and remaining tokens relative to the numbers of consumed and produced tokens indicate the severity of the conformance problem. Token-based replay can be extended to Petri nets with silent and duplicate activities using heuristics. For example, if there are two activities with the same label, pick the one that is enabled. If both are enabled, pick one of them. Similarly, silent transitions (i.e., transitions not corresponding to recorded activities) are executed when they enable a transition corresponding to the next activity in the event log. This requires an exploration of the states reachable from the current state and may lead to inconclusive results.
Compared to computing alignments, token-based replay is fairly efficient, but does not always produce valid paths through the process model. Alignments are often seen as the gold standard for conformance checking because they provide paths through the process model that are as close to the observed behavior as possible. We would like to map observed behavior onto modeled behavior to provide better diagnostics and to relate also non-fitting cases to the model. Alignments were introduced to overcome the limitations of token-based replay. The diagnostics are more detailed and more precise, because each observed trace is mapped onto a model behavior that is as close to what was observed as possible. The alignment shows common behavior, but also skipped and inserted events signaling deviations. Such skipped and inserted events are easier to interpret than missing and remaining tokens. However, for large event logs and processes, alignment computations may be intractable. Moreover, there may be many optimal alignments, making the diagnostics non-deterministic.
Several conformance checking techniques are explained in detail in [15]. When comparing observed and modeled behavior, we typically consider four main quality dimensions [1, 2, 6]:
-
Recall (also called replay fitness): the discovered model should allow for the behavior seen in the event log. This can be quantified by the minimal number of edit operations needed to make all traces in the event log fitting into the model (or simply the fraction of perfectly fitting traces).
-
Precision: the discovered model should not allow for behavior completely unrelated to what was seen in the event log. This can be quantified by the number of possible continuations in the model never observed in the event log.
-
Generalization: the discovered model should generalize the example behavior seen in the event log. It is easy to create a process model that only allows for the behavior observed and nothing more. However, such a model is likely to overfit. To avoid overfitting, the model should generalize. This can only be tested on “fresh unseen” event data. To evaluate a process discovery algorithm, standard cross-validation can be used to detect overfitting problems. This is less clear when evaluating a process model rather than a discovery algorithm [6].
-
Simplicity: the discovered model should be as simple as possible. This fourth quality criterion is related to Occam’s Razor, which states that “one should not increase, beyond what is necessary, the number of entities required to explain anything”.
4.3 Performance Analysis
The goal of process mining is to improve processes by uncovering problems. These may be the conformance problems just described, but (of course) also include performance problems such as untimely completion of a case, limited production, missed deadlines, tardiness, excessive rework, and recurring quality problems. Using token-based replay [32] and alignments [6, 14] it is possible to relate event data to a process model. As a result, it is fairly straightforward to annotate the process model with frequency and time information. Frequencies of undesired activities and loops can be used to identify quality and efficiency problems. Since events have timestamps, it is possible to measure times in-between activities, including statistics such as mean, median, standard deviation, minimum, and maximum. This allows for analyzing performance indicators, e.g., waiting times, response times, and service times.
A Service Level Agreement (SLA) is an agreement between a service provider and a client. Process mining can be used to analyze SLAs, e.g., when is a particular SLA not met. Some well-known SLAs are churn/abandonment rate (number of cases lost), average speed to answer (response time seen by customer), percentage of cases handled within a predefined timeframe, first-call resolution (cases successfully handled without rerouting), percentage of duplicated cases (e.g., multiple procurement documents corresponding to the same order), mean time between failures, mean time to recovery, etc.
4.4 Comparative Process Mining
Comparative process mining uses as input multiple event logs, e.g., \(L_1,L_2, \ldots , L_n \in \mathcal {B}({\mathcal{U}_{ act }}^*)\). These event logs may refer to different locations, periods, or categories of cases. For example, we may have the event logs \(L_{ Aachen }\) and \(L_{ Munich }\) referring to the same processes performed at two locations. We may have the event logs \(L_{ Jan },L_{ Feb },L_{ Mar }, \ldots ,L_{ Dec }\) referring to different periods or \(L_{ Gold }\) and \(L_{ Silver }\) referring to gold and silver customers.
Having multiple event logs allows for comparison and highly relevant questions. What are the striking differences and commonalities? What factors lead to these differences? Root cause analysis can be used to explain the observed differences. For example, in \(L_{ Feb }\) waiting times may be much longer than in \(L_{ Jan }\) due to limited resource availability. Comparative process mining may focus on frequently occurring problems, sometimes referred to as execution gaps. Such execution gaps include lost customers, additional work due to price changes, the merging of duplicate orders, and rework due to quality problems.
Comparative process mining is also a great tool for inter- or intra-organizational benchmarking. For example, an insurance company may have different regional offices. Using comparative process mining, these offices can learn from each other and increase the overall performance.
4.5 Predictive Process Mining
Process discovery, conformance checking, performance analysis, and comparative process mining are backward-looking. Although the value of such techniques is obvious, the actual goal is to continuously improve processes and respond to changes. Operational processes are subject to many changes, e.g., a sudden increase in the number of orders or disruptions in the supply chain. Moreover, many compliance and performance problems can be foreseen and addressed proactively. Fortunately, process models discovered and enriched using process mining can be used in a forward-looking manner.
Process mining can be used to create a range of ML questions that can be answered using standard software libraries. For example, when detecting a recurring bottleneck or deviation, it is possible to extract features from the event log and create a predictive model. This leads to a so-called situation-feature table with several descriptive features (e.g., people involved, path taken, and time of day) and one target feature (e.g., waiting time or decision). Then standard ML techniques ranging from regression and decision trees to neural networks can be applied to explain the target feature in terms of descriptive features. This leads to better diagnostics and explanations. Moreover, the models can be used in a predictive manner.
Predictive process mining questions also create specific ML challenges. Most ML techniques assume a fixed number of features as input (i.e., a fixed-length feature vector) and assume inputs to be independent. Artificial recurrent neural network architectures such as Long Short-Term Memory (LSTM) can be used to handle traces of variable length. Contextual features can be added to include information about the utilization of resources. However, this requires fine-tuning and domain knowledge.
A discovered process model can be viewed as a description of the as-is situation. Using simulation and model adaptation, it is possible to explore possible to-be situations. Simulation enables forward-looking forms of process mining. Comparative process mining can be used to compare the different alternatives.
4.6 Action-Oriented Process Mining
Process mining can be used to show (1) what has happened, (2) what is happening now, and (3) what will happen next in the process. Hence, it covers the full spectrum from backward-looking to forward-looking types of analysis. Backward-looking forms of process mining can lead to process redesigns and organizational changes. Forward-looking forms of process mining and diagnostics of the current state of a process can trigger improvement actions. Action-oriented process mining aims to turn diagnostics into actions. Assisted by low-code automation platforms, process mining software can trigger workflows. Some examples:
-
The moment the average waiting time exceeds 2 h, additional resources are added and no new orders are accepted.
-
If a supplier changes prices repeatedly for a longer period, then the supplier is blacklisted.
-
If a check is repeatedly skipped by an employee, the manager is notified.
Next to triggering improvement actions, process mining can also detect repetitive work that may be automated using Robotic Process Automation (RPA). RPA can be used to automate repetitive tasks done by humans without changing the underlying systems. Typical examples include copying information from one system into another system. Process mining can be used to discover such repetitive tasks. The term task mining is often used to refer to the discovery of processes based on user-interface interactions (filling out a form, pushing a button, copying text, etc.). Task mining can be used to uncover repetitive processes that can be automated. There is also a connection to online scheduling and other Operations Research (OR) techniques. For example, based on historical information, it is possible to create a robust schedule with events taking place in the future. Differences between scheduled events and the actual events may trigger improvement actions.
5 Applications and Software
Process mining started as an exercise in the late 1990s trying to automatically create a Petri net from example traces [2]. According to Gartner there are now over 40 process mining vendors [26]. Some of them are listed in Table 3. Note that the list is very dynamic with new vendors emerging and large IT companies acquiring smaller process mining vendors. For an up-to-date overview, see the website www.processmining.org which lists all process mining tools.
All of the tools in Table 3 support the discovery of Directly-Follows Graphs (DFGs) with frequencies and times. Most of them (but not all) support some form of conformance checking and BPMN visualization. Some of the tools target process or data analysts rather than people managing or executing processes. These tools are typically lightweight and can be deployed quickly. Enterprise-level process mining tools are more difficult to deploy, but aim to be used by many stakeholders within an organization. For example, within Siemens, over 6000 employees are using the Celonis software to improve a range of processes. Enterprise-level process mining tools have automated connections to existing information systems (e.g., SAP, Salesforce, Oracle, ServiceNow, and Workday) to allow for the continuous ingestion of data. These tools also allow for customized dashboards to lower the threshold to use process mining. In 2020, Gartner estimated the process mining software market revenue to be $550 million, which was over 70% market size growth from the previous year [26]. The process mining market is forecast to keep growing 50% per year (Compound Annual Growth Rate) in the coming years. Note that this does not include consultancy based on process mining. The Big Four (i.e., Deloitte, Ernst & Young, KPMG, and PwC) all have process mining competence centers providing process mining services all over the globe.
The technology is generic and can be used in any domain. For example, process mining is used in
-
finance and insurance (Rabobank, Wells Fargo, Hypovereinsbank, Caixa General, ADAC, APG, Suncorp, VTB, etc.),
-
logistics and transport (Uber, Deutsche Bahn, Lufthansa, Airbus, Schukat, Vanderlande, etc.),
-
production (ABB, Siemens, BMW, Fiat, Bosch, AkzoNobel, Bayer, Neste, etc.),
-
healthcare, biomedicine, and pharmacy (Uniklinik RWTH Aachen, Charite University Hospital, GE Healthcare, Philips, Medtronic, Pfizer, Bayer, AstraZeneca, etc.),
-
telecom (Deutsche Telekom, Vodafone, A1 Telekom Austria, Telekom Italia, etc.),
-
food and retail (Edeka, MediaMarkt, Globus, Zalando, AB InBev, etc.),
-
energy (Uniper, Chevron, Shell, BP, E.ON, etc.), and
-
IT services (Dell, Xerox, IBM, Nokia, ServiceNow, etc.).
In [31], several use cases are described in detail. In [26, 27], typical applications are described, and in [21] the results of a global process mining survey are presented. These show that the adoption is increasing, e.g., according to the global survey, 83% of companies already using process mining on a global scale plan to expand their initiatives [21]. Process mining helps organizations to improve processes, provide transparency, reduce costs, ensure compliance, avoid risks, eliminate waste, and redesign problematic processes [21]. To get a glimpse of the possible applications, the reader can take a look at the use cases collected by the IEEE Task Force on Process Mining [25] and HSPI Management Consulting [20]. Note that these cover just a fraction of the actual applications of process mining. It has become fairly standard to apply process mining to standard processes such as Purchase-to-Pay (P2P) and Order-to-Cash (O2C).
6 Summary and Outlook
This chapter aimed to provide a 360\(^\circ \) overview of the field of process mining. We showed that process mining connects data science and process science leading to data-driven process-centric techniques and approaches. Event data and process models were introduced. Events can be grouped in event logs, but also stored in databases. In the standard setting an event has a few mandatory attributes such as case, activity, and timestamp. This can be further reduced to representing an event log by a multiset of traces where each trace is a sequence of activities. This format is often used for control-flow discovery. However, in real-life settings it is not so easy to find a single case notion. Often events may refer to multiple objects of different types. There may also be data quality problems and data may be scattered over multiple source systems. Moreover, additional attributes such as costs, time, and resources need to be incorporated in models. We introduced Directly-Follows Graphs (DFG), Petri nets, BPMN models, and process trees as basic control-flow representations. These will be used in the remainder.
We informally described six common types of process mining: (1) process discovery, (2) conformance checking, (3) performance analysis, (4) comparative process mining, (5) predictive process mining, and (6) action-oriented process mining. These characterize the scope of process mining and challenges. The chapter also provided pointers to the over 40 process mining tools and case studies.
Although process mining is already used by many of the larger organizations, it is a relatively new technology and only a fraction of its potential is realized today. Three important trends can be witnessed that together lead to a wider adoption.
-
Supporting data extraction and analysis through process-specific and domain-specific adapters and applications (“process mining apps”). This reduces the effort to get started with process mining and leverages past experiences in other organizations.
-
Initially, process mining software aimed at experts involved in process improvement projects. However, process mining should be done continuously and at a large scale. It is a generic technology that should be accessible for many users every day. By scaling (both in terms of processes and users) and continuous use, the return on investment is the highest.
-
Increasingly, process mining and automation are combined. Process mining diagnostics trigger corrective actions through low-code automation platforms. This is the only way to ensure that improvements are realized. Without some form of automation, workers may slip back into the old ineffective ways of working that were exposed using process mining.
Process mining can also play a role in realizing sustainability goals and help to address environmental, social and economic challenges. Process mining can help to quantify and steer sustainability efforts, e.g., by removing waste and quantifying emissions. Process mining can easily handle multiple dimensions, such as time, cash flow, resource usage, and CO\({}_2\) emissions, during analysis. Sustainability is just one of many topics where process mining can play a role. Moreover, these applications also pose interesting research questions leading to new concepts and techniques.
References
van der Aalst, W.M.P.: Process Mining: Discovery, Conformance and Enhancement of Business Processes. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-19345-3
van der Aalst, W.M.P.: Process Mining: Data Science in Action. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49851-4
van der Aalst, W.M.P.: A practitioner’s guide to process mining: limitations of the directly-follows graph. Procedia Comput. Sci. 164, 321–328 (2019)
Aalst, W.M.P.: Object-centric process mining: dealing with divergence and convergence in event data. In: Ölveczky, P.C., Salaün, G. (eds.) SEFM 2019. LNCS, vol. 11724, pp. 3–25. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-30446-1_1
van der Aalst, W.M.P.: Foundations of process discovery. In: van der Aalst, W.M.P., Carmona, J. (eds.) Process Mining Handbook. LNBIP, vol. 448, pp. xx–yy. Springer, Cham (2022)
van der Aalst, W.M.P., Adriansyah, A., van Dongen, B.: Replaying history on process models for conformance checking and performance analysis. WIREs Data Min. Knowl. Discovery 2(2), 182–192 (2012)
van der Aalst, W.M.P., Berti, A.: Discovering object-centric Petri nets. Fund. Inform. 175(1–4), 1–40 (2020)
van der Aalst, W.M.P., Weijters, A.J.M.M., Maruster, L.: Workflow mining: discovering process models from event logs. IEEE Trans. Knowl. Data Eng. 16(9), 1128–1142 (2004)
Augusto, A., Conforti, R., Marlon, M., La Rosa, M., Polyvyanyy, A.: Split miner: automated discovery of accurate and simple business process models from event logs. Knowl. Inf. Syst. 59(2), 251–284 (2019)
Augusto, A., Carmona, J., Verbeek, E.: Advanced process discovery techniques. In: van der Aalst, W.M.P., Carmona, J. (eds.) Process Mining Handbook. LNBIP, vol. 448, pp. xx–yy. Springer, Cham (2022)
Bergenthum, R., Desel, J., Lorenz, R., Mauser, S.: Process mining based on regions of languages. In: Alonso, G., Dadam, P., Rosemann, M. (eds.) BPM 2007. LNCS, vol. 4714, pp. 375–383. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-75183-0_27
vom Brocke, J., et al.: Process Science: The Interdisciplinary Study of Continuous Change. SSRN (2021). http://ssrn.com/abstract=3916817
Carmona, J., Cortadella, J., Kishinevsky, M.: A region-based algorithm for discovering petri nets from event logs. In: Dumas, M., Reichert, M., Shan, M.-C. (eds.) BPM 2008. LNCS, vol. 5240, pp. 358–373. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-85758-7_26
Carmona, J., van Dongen, B., Solti, A., Weidlich, M.: Conformance Checking: Relating Processes and Models. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-99414-7
Carmona, J., van Dongen, B., Weidlich, M.: Conformance checking: foundations, milestones and challenges. In: van der Aalst, W.M.P., Carmona, J. (eds.) Process Mining Handbook. LNBIP, vol. 448, pp. xx–yy. Springer, Cham (2022)
van Dongen, B.F.: Real-Life Event Logs: Hospital Log (4TU.ResearchData) (2011). https://doi.org/10.4121/uuid:d9769f3d-0ab0-4fb8-803b-0d1120ffcf54
Dumas, M., La Rosa, M., Mendling, J., Reijers, H.: Fundamentals of Business Process Management. Springer, Heidelberg (2018). https://doi.org/10.1007/978-3-662-56509-4
van Eck, M.L., Sidorova, N., van der Aalst, W.M.P.: Guided interaction exploration and performance analysis in artifact-centric process models. Bus. Inf. Syst. Eng. 61(6), 649–663 (2018). https://doi.org/10.1007/s12599-018-0546-0
Fahland, D.: Describing behavior of processes with many-to-many interactions. In: Donatelli, S., Haar, S. (eds.) PETRI NETS 2019. LNCS, vol. 11522, pp. 3–24. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-21571-2_1
Cotroneo, G., Carbone, R., Boggini, S., Cerini, M.: Process Mining: A Database of Applications (2021). HSPI Management Consulting 2021. http://www.hspi.it/
Galic, G., Wolf, M.: Global Process Mining Survey 2021: Delivering Value with Process Analytics - Adoption and Success Factors of Process Mining. Deloitte (2021). https://www2.deloitte.com/de/de/pages/finance/articles/global-process-mining-survey-2021.html
Ghahfarokhi, A.F., Park, G., Berti, A., van der Aalst, W.M.P.: OCEL Standard (2021). http://www.ocel-standard.org/
van der Aalst, W., et al.: Process mining manifesto. In: Daniel, F., Barkaoui, K., Dustdar, S. (eds.) BPM 2011. LNBIP, vol. 99, pp. 169–194. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-28108-2_19
IEEE Task Force on Process Mining. XES Standard Definition (2016). http://www.xes-standard.org/
IEEE Task Force on Process Mining. Case Studies (2022). http://www.tf-pm.org/
Kerremans, M., Srivastava, T., Choudhary, F.: Gartner Market Guide for Process Mining, Research Note G00737056 (2021). www.gartner.com
Koplowitz, R., Mines, C., Vizgaitis, A., Reese, A.: Process Mining: Your Compass For Digital Transformation: The Customer Journey Is The Destination (2019). www.forrester.com
Leemans, S.J.J., Fahland, D., van der Aalst, W.M.P.: Discovering block-structured process models from event logs containing infrequent behaviour. In: Lohmann, N., Song, M., Wohed, P. (eds.) BPM 2013. LNBIP, vol. 171, pp. 66–78. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-06257-0_6
Leemans, S.J.J., Fahland, D., van der Aalst, W.M.P.: Scalable process discovery with guarantees. In: Gaaloul, K., Schmidt, R., Nurcan, S., Guerreiro, S., Ma, Q. (eds.) CAISE 2015. LNBIP, vol. 214, pp. 85–101. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-19237-6_6
Mannhardt, F.: Road Traffic Fine Management Process (4TU.ResearchData) (2016). https://doi.org/10.4121/uuid:915d2bfb-7e84-49ad-a286-dc35f063a460
Reinkemeyer, L.: Process Mining in Action: Principles, Use Cases and Outlook. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-40172-6
Rozinat, A., van der Aalst, W.M.P.: Conformance checking of processes based on monitoring real behavior. Inf. Syst. 33(1), 64–95 (2008)
Solé, M., Carmona, J.: Process mining from a basis of state regions. In: Lilius, J., Penczek, W. (eds.) PETRI NETS 2010. LNCS, vol. 6128, pp. 226–245. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-13675-7_14
Suriadi, S., Andrews, R., ter Hofstede, A.H.M., Wynn, M.T.: Event log imperfection patterns for process mining: towards a systematic approach to cleaning event logs. Inf. Syst. 64, 132–150 (2017)
Taylor, F.W.: The Principles of Scientific Management. Harper and Brothers Publishers, New York (1919)
van Zelst, S.J., van Dongen, B.F., van der Aalst, W.M.P., Verbeek, H.M.W.: Discovering workflow nets using integer linear programming. Computing 100(5), 529–556 (2018)
Acknowledgment
Funded by the Alexander von Humboldt (AvH) Stiftung and the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany’s Excellence Strategy – EXC 2023 Internet of Production – 390621612.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2022 The Author(s)
About this chapter
Cite this chapter
van der Aalst, W.M.P. (2022). Process Mining: A 360 Degree Overview. In: van der Aalst, W.M.P., Carmona, J. (eds) Process Mining Handbook. Lecture Notes in Business Information Processing, vol 448. Springer, Cham. https://doi.org/10.1007/978-3-031-08848-3_1
Download citation
DOI: https://doi.org/10.1007/978-3-031-08848-3_1
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-08847-6
Online ISBN: 978-3-031-08848-3
eBook Packages: Computer ScienceComputer Science (R0)