The Role of Construct Specification Equations and Entropy in the Measurement of Memory

Abstract

Memory ability, together with many other constructs related to disability and quality of life, is of growing interest in the social sciences, psychology and in health care examinations. This chapter will focus on two elements aiming at understanding, predicting, measuring and quality-assuring constructs with examples from memory measurements: (i) explicit methods for testing theories of the measurement mechanism and establishment of metrological standards and (ii) substantive theories explaining the constructs themselves. Building on entropy as a principal explanatory variable, analogous to its use in thermodynamics and information theory, we demonstrate how more fit-for-purpose and valid memory measurements can be enabled. Firstly, memory task difficulty, extracted from a Rasch psychometric analysis of memory measurements of experimental data such as from the European NeuroMET project, can be explained with a construct specification equation (CSE). Based on that understanding, the CSE can facilitate the establishment of objective and scalable units through the generation of novel certified reference “materials” for metrological traceability and comparability. These formulations of CSEs can also guide how best to compose new memory metrics, through a judicious choice of items from various legacy tests guided by entropy-based equivalence, which opens up opportunities for formulating new, less onerous but more sensitive and representative tests. Finally, we propose and demonstrate how to formulate CSEs for person ability, correlated statistically and clinically with sets of biomarkers, that can be a means of providing diagnostic information to enhance clinical decisions and targeted interventions.

10.1 Introduction

Typical responses to tests of memory, and similar constructs, inform decisions of conformity but, as raw scores, the responses are challenging to handle since they lie on ordinal scales, and often lack construct theories and established metrological standards. In response to a call for consensus methods and procedures to enable measurable quantities for constructs such as memory in clinical tests and examinations [9] we focus in this chapter on:

• (i) explicit methods for testing theories of the measurement mechanism and for the establishment of metrological standards for the measured constructs deduced from response data from for example memory tests and examinations; and

• (ii) substantive theories explaining the constructs themselves.

Differences between these – the quantity as measured compared with the quantity itself, respectively – reflect imperfections in the measurement system used, expressed as measurement errors and measurement uncertainties.

The methods and theories presented in this chapter build on pioneering work by Stenner and his colleagues (e.g., [67,68,69,70,68]). Like those authors, we adopt Rasch measurement theory (RMT) [56] as a key technique of handling raw scores in preparation for formulation of construct specification equations. But, in the interests of advancing quality assurance of the relevant constructs, we examine here the concept of causality further as well as adopt a more explicit measurement system approach. To draw on the full benefits of analogies with engineering measurement system analysis (MSA) [3], we make a clearer distinction between the responder – regarded as a “measurement instrument” – and the test item construct associated with the measurement object than originally proposed by Rasch [56, 57].

After a brief section on the definitions of terms, the chapter starts with a short description of the measurement system approach. Thereafter, the main part of the chapter presents the rational for CSEs as substantive construct theories, including contrasting our approach with related work, and the role of entropy in a metrological framework both for each construct – such as person ability and task difficulty – of interest in itself as well as constructs explicitly connected with the measurement mechanism, i.e., quantities as measured. The chapter closes with an account where those explicit methods are applied, together with substantive theories in the context of memory measurements, to overcome some of the shortcomings of current neuropsychological assessments and to ensure that quantities are traceable as far as possible to metrological standards and are metrologically legitimated. Illustrations are provided with two tests of short-term memory: a non-verbal tap recalling test (Corsi Block Test (CBT), [13]) and a verbal digit recalling test (Digit Span Test (DST), [74]). The chapter is then closed by addressing some limitations and providing a summary and outlook for the future where we highlight the possibility of formulating CSEs based on entropy for memory task difficulty to design new, less onerous but more sensitive and representative tests largely by “cherry-picking the best” items from existing batteries of cognitive tests, such as exemplified with CBT and DST.

10.2 Definitions

There are many different terms used in the literature such as observed outcomes, rating scores, counts etc. when referring to test responses. To avoid any conflation and/or misunderstanding we will use the term raw scores throughout this chapter to denote test responses which are classifications (assignments P_success to categories, e.g., pass or fail or 1–5 ratings); that is, the observed outcome before measurement restitution. Raw scores are thus distinct from the measurement outcome which is the measurement result after both observation and restitution [53].

The term “examination” is used here in the sense common in medical care and is considered a synonym for “inspection” as defined for example in ISO/IEC 17000:2004 §4.3, as including a determination of conformity (of the entity being inspected) with specified requirements. In a typical medical examination, a clinician in making a judgment will often weigh together several factors, including for instance the results of memory tests but also anamnesis, biomarkers etc. The term “testing” is the determination of one or more characteristics of an object (entity) of conformity assessment, according to the same standard (§4.2). “Examination” and “testing” are thus not synonyms for “measurement” [16] since a “measurement” (on any scale) does not necessarily involve a questioning or an assessment of conformity.

10.3 Methods for Testing Theories of What Is Being Measured

The present section has two aims. The first aim is to posit explicit methods for testing theories of the measurement mechanism in for example memory tests and examinations and for the establishment of measurement standards (etalons) in a metrological framework in such tests by adopting measurement system analysis (MSA) (ASTM 2012). MSA is the classic approach in engineering to describe indirect measurements, in the sense that an operator usually needs some kind of instrument to get a measure of the attribute of the object of interest. In both psychometric and psychophysical measurement systems, a human being – an “agent” – can be regarded as acting as a measurement instrument [49, 50]. In this sense, the MSA approach accords well with the (dichotomous) RMT:

$$ \theta -\delta =\mathit{\log}\left(\frac{P_{success}}{1-{P}_{success}}\right) $$

(10.1)

and statements about specific objectivity by Rasch ([58], p. 5) himself:

The parameters δ_j signify manifestations of a certain property of a set of "objects" which are investigated by means of a set of "agents" characterized by the parameters θ_i. Thus in principle the δ_j stand for properties of the objects per se, irrespective of which θ_i might be used for locating them. Therefore they really ought to be appraised without any reference to the θ_i actually employed for this purpose – just like reading a temperature of an object should give essentially the same result whichever adequate thermometer were used.

The MSA approach focusses on quantities as measured which in general differ from the same quantities in themselves – e.g., for the object of interest – owing to imperfections in the measurement mechanism which leads to measurement errors and uncertainties. Further description of MSA, including the process of restitution of the measurand (i.e., the measurement outcome) from the response (i.e., raw scores), can be found in the accompanying chapter in this book by Pendrill and Melin [53] which focusses on person-centred care but draws explicitly on the benefits of analogies between RMT and approaches which are more widely applicable and established in the engineering measurement community.

The second aim of this section is to posit theories which substantively explain constructs, which will take up the remaining and major part of this section.

We start our discussion by examining the concept of causality, being careful as far as possible to present separate descriptions of the measurement mechanism and of the constructs. Thereafter, presentations will be given of how Construct Specification Equations (CSEs) support substantive construct theories and enable metrological links to Certified Reference Materials (CRMs). This section concludes with a detailed description of the formulation of CSE.

10.3.1 Different Levels of Causality in the Measurement Mechanism and in Constructs

In their seminal paper, Stenner et al. [67] introduce what they term a “causal Rasch model”, which in their words: “may be seen as formalizing how a measurement mechanism and an attribute measure cooperate to produce (cause) the observed outcome.” Here we examine this causality further in terms of three distinct relations:

The first relation holds that raw scores, for instance from memory tests, can be transformed mathematically onto interval scales. In the words of Linacre and Wright [36]:

The mathematical unit of Rasch measurement, the log-odds unit or “logit”, is defined prior to the experiment. One logit is the distance along the line of the variable that increases the odds of observing the event specified in the measurement model by a factor of 2.718…, the value of “e”, the base of “natural” or Napierian logarithms used for the calculation of “log-” odds. All logits are the same length with respect to this change in the odds of observing the indicative event.

Salzberger [60] wrote later:

The Rasch model tests whether an a priori absolutely scaled raw score represents an a posteriori … non-linear raw score, which can be transformed into a linear interval-scaled measure of the latent variable.

In our opinion, this first transformation is not an expression of causality, but rather a purely mathematical relation (in line with [36]) between raw scores and test attributes. That mathematical relation provides the formula when restituting quantitative estimates of the measurand from the ordinality of the raw score responses [52].

A second relation, between raw scores and differences between test attribute variables – such as task difficulty δ_j and person ability θ_i – which RMT enables to be estimated separately and conjointly (Eq. 10.1), is a kind of causal relation but a special kind, which describes the measurement mechanism. In line with MSA, causality in this second relation has to do with how measurement information propagates from the measurement object (e.g., a memory task), through the instrument (the person tackling the task), to the system observer, who in a memory test can be a clinician [49]. However, because of the ordinality in the response to the tests considered here – such as memory tests – we refrain from calling the raw scores the dependent variables in a cause-and effect relation since the observed outcomes are in themselves strictly not quantities (i.e., measurable properties).

A third relation – which we consider as expressing a stricter kind of causality than the first two relations above – is between an RMT-derived attribute as dependent variable and one or more explanatory (independent) variables, X (Eq. 10.2 below). Examples of this are constructs such as memory task difficulty δ_j and person memory ability θ_i explained in terms, respectively, of test item characteristics and person characteristics and biomarkers. Such relations – termed Construct Specification Equations (CSE) by Stenner and Smith [64] – are not in the first hand to do with the measurement mechanism but are used to describe the attributes associated with the object or entity in themselves. The next section describes this in more detail.

To sum up, with a CSE as a kind of substantive construct theory addressed in the third kind of strictly causal relation above, the object or entity in itself does not need to be associated with a measurement mechanism. However, as examples of special cases of CSEs, we can also formulate theories of the attributes associated with measurement, that is, of the attributes associated with various elements of a measurement system. In addition to Rasch’s [56] emphasis on the importance of providing separate estimates of the attribute of the object being measured (e.g., memory task difficulty) and the instrument being used to make the measurements (e.g., person memory ability corresponding to an attribute of the instrument used for measurement), one should be careful to distinguish construct theories which address the object itself from those describing an element of the measurement system being used in the process. Previous measurement models – such as developed since the 1980s by Stenner et al. – chose to call a test item for an “instrument” and a human responder as an “object”. Rasch’s original [56] description emphasized that the choice of “object” and “instrument” was agnostic since both attributes appear symmetrically (apart from a change of sign) in the Rasch formula. This flexibility is also present in our own MSA-based approach [49, 50] but to get the full benefit of analogies with engineering MSA it is preferable to describe the human responder as the instrument rather than the item, as cited in the previous section.

Two additional comments: Firstly, notwithstanding that CSEs represent a stricter causality than RMT, construct and measurement theories are handled here as far as possible with equal priority: we do not share the view of others, paraphrasing Michell ([47], pp. 75–77), that the instrumental task of quantification, i.e., construction of measurement devices and instruments, is secondary to the scientific task of discovering quantitative structure. We give equal attention here to variations in item scores and in person scores, which is not new. As early as the 1920s, Thurstone stated: “there is at present a wide but artificial break between the group of men who work in psychophysics with the traditional stimuli and those who attempt to measure educational and social values with little interest in psychophysical theory. … It is our hope again to unify the efforts to measure social values with the advancement in psychophysical theory” [70].

10.3.2 Construct Specification Equations (CSEs) as Substantive Construct Theories

In the words of Stenner et al. [67]: “Rasch analysis, absent construct theory and an associated specification equation, is a black box in which understanding may be more illusory than not.” Therefore, when formulating an overall attribute construct to be determined in a quality assured manner, various quality characteristics of the entity of interest need to be identified, described, measurable, predictable and prioritized. In the present context of memory measurement, a construct theory must attempt to explain both memory task difficulty and person memory ability in terms, respectively, of a variety of explanatory variables, such as trial length, entropy and biomarkers.

10.3.2.1 Construct Specification Equations (CSEs) and Validity

Richard Feynman wrote on his last classroom blackboard: “What I cannot create, I do not understand”. Substantive construct theories – with which constructs can be “created” – have been described in the literature as keys to demonstrating the crucial notion of validity which refers to the conformity of observations with the intended goal of measurement. For this conformity to be achieved, the construct must exist, and variations in it must cause reproducible variations in the observations taken as evidence supporting measurement [1, 6]. In contrast to those works, again here we stress the importance of distinguishing between the construct itself and the construct as measured [52].

For testing the existence and variation of a construct, CSEs are considered to be at the highest level of construct validation available for social, psychological and health measurements, and correspond to Feynman’s ambition to create and understand. The CSEs provide a more specific and rigorously mathematical and causal conceptualization of item attributes (e.g., task difficulties) and person characteristics (e.g., person abilities) than any other construct theory. The relationships between measured quantities in the memory tests illustrated later in this chapter, e.g., from easy to difficult tasks or from low to high abilities of persons, can be explained in terms of the “something” – i.e., the explanatory variables – that causes each variation.

Early work on CSE stem from Fischer’s [18] and Prien’s [54] studies of mathematics abilities, Latimer’s [34] application of Fischer’s linear logistic test model (LLTM) to reading ability, and Wright and Stone’s [77] and Stenner and Smith’s work in the 1970s and 1980s on the Knox Cube Test (KCT) and the Peabody Picture Vocabulary Test [64, 65]. The CSE concept has been advanced considerably in education science in the context of reading comprehension [66], whilst it has largely remained an undiscovered country in health care and other areas. Commercial measures linking reading ability with text complexity in assessments and instruction are the domain of the most well-known example of CSE [66] which uses a 2-variable equation to explain text difficulty: the log mean frequency, based on the sum of frequencies of all words in the same word family in use in written or oral communications, and the log of the text’s mean sentence length as a proxy for syntactic complexity [63]. In the next section, Theories explaining what is being measured, you find more discussion of construct theories, particularly those based on the concept of entropy.

Extending our introduction to causality, CSE relations have precedence in terms of causality over the two other relations (link functions in GLM and the measurement mechanism in IRT) when one seeks to express how the constructs of interest are to be understood, predicted, measured and quality assured, that is, “created” in Feynman’s words. Only when one has the strict causality that a CSE describes [52], can it be said that one has a relation in a form similar to the relations between (so-called derived) quantities in Physics. An example of the latter derives the quantity “force” from two quantities, namely “mass” and “acceleration”, where the quantity relation (also a CSE) in this case follows Newton’s physical law of motion as an expression of causality. But such universal relations are rare: most CSEs, while objective and causal to a certain extent, will usually not enjoy the universality of relations such as Newton’s laws (where the latter apply to all bodies throughout the universe and on all scales, from the microscopic to cosmological), but are instead expressions of limited local validity, analogous to engineering sensor relations and the weaker objectivity characteristic of the social sciences [52]. Together with this, as emphasized in the introduction, again, it is important to distinguish between quantities as such and quantities as measured. Statistics can be applied to either of these, respectively, describe errors/anomalies in quantities (e.g., local inconsistences in object attributes) as well as measurement errors and uncertainties arising from imperfect measurement systems. That is, not all of statistics is measurement-related. For a discussion on descriptive purposes of statistical modelling and the prescriptive purposes of measurement modelling see the accompanying chapter by Fisher.

In a critique, Kyngdon [33] claimed that: ‘the Rasch model is not conjoint measurement because the Rasch model ’simply map[s] a set of real numbers (probabilities) into another set of real numbers (differences between logarithmic unit parameters).’ While we agree – as stated above – that the Rasch model can be regarded as a purely mathematical relation, RMT is nevertheless also a uniquely metrological approach where attributes for item/object and agent/instrument are linked conjointly. At the same time, we do not consider relations in Physics – such as the associative relation between density, volume and mass, or the fundamental law of Nature: Force = Mass x Acceleration – to be “conjoint measurement”, as claimed by Kyngdon [33] and Luce and Tukey [37]. Such relations – such as Newton’s 2^nd law or the formula for a strain gauge – admittedly might form the basis of a sensor in some cases but do not in our opinion uniquely define conjoint measurement per se. Such relations are in the first case amongst quantities in themselves, irrespective of whether they have been measured or not.

Indeed, when formulating CSEs, the choices of explanatory variables, X, (Eq. 10.2 below) are not restricted to observed quantities. Rather, various combinations of variables should be explored as guided by our understanding of the construct and by multivariate analyses. Two examples given in this chapter are, respectively: (i) formulation of explanatory variables based on the concept of entropy as a measure of information [40] and (ii) identification of principal components of variation, based on a principal component analysis (PCA), which are various combinations of attributes and which better explain the construct than these directly observed quantities themselves.

In the literature, the CSE approach in psychometrics has mostly been used and advocated in item response tests in relation to explaining items’ levels of difficulty. However, only when synthetic constructs created from theory enable the consistent and reliable prediction of both memory item (difficulty) and person memory (ability) location calibrations, can we claim to fully understand what our memory test measures. Thus, the role of CSE should not be considered only as a matter for task difficulty, as in the pioneering work [18, 34, 54, 64, 65, 77]. The CSE approach indeed adds further to metrology – as promised in the Introduction – and can be applied in principle to all elements of the measurement system (i.e., the object, the instrument, the operator, the environment and the method). The examples provided in our third section, Memory measurements below, will exemplify CSEs for memory task difficulty and person memory ability in experimental case studies.

10.3.2.2 Construct Specification Equations and Construct Modelling

In the light of construct theories, the work by Wilson [75] on Construct Modelling is also worth relating to the methods for CSEs in this chapter. Wilson outlined ‘four building blocks’ for measurements and test development: (a) construct map, (b) items design, (c) outcome space, and (d) measurement model. Wilson presents the construct related to the person attribute, e.g., person memory ability, but not the other RMT-derived attribute, viz. memory item difficulty. However, as the measurement outcome for person ability is usually the attribute one wants to use e.g., for health examinations or performance tests, it is natural to start by defining the attribute related to the person and thereafter designing items to be met for persons going up or down the scale of the person attribute. In turn, one should have an ordinal theory with ordering of groups of items and person attributes, respectively [41].

Wilson, while close, did not reach the level of CSE construct validation in his ‘four building blocks’ but did develop this concept together with de Boeck elsewhere [14]. While a CSE mathematically explains the relationship between items, a confirmatory theory tests the ordinal theory by means of empirically estimated item locations [41], which is what Wilson [75] stresses is facilitated via a Wright map’s correspondence to the construct map. With a well-developed construct modelling approach, we will gain a better understanding of our measurements, and will also inform the further development of CSE. To advance construct theories and to elaborate CSE, we need a deeper and quantitative understanding associated to each memory task than what is qualitatively considered to be an easy or difficult task. As will be demonstrated in the following sections, task difficulty varies with the degree of order in a task, with less or more entropy, and similarly for different degrees of person ability.

10.3.3 Construct Specification Equations and Metrology

For the quality assurance of any object (a product, service etc.), it is necessary that any measurements of that object are also quality assured [53]. If we are seeking objects with comparable properties, then it is recommended to ensure that the measurements of their properties are also comparable in themselves. Measurement comparability is ensured in metrology, i.e., quality-assured measurement, by traceability to metrological references through calibration.

As said above, CSEs represent the highest level of construct theory. From the metrological point of view, CSEs for task difficulty (an attribute of the object of interest) can be considered to constitute metrological references [52] analogous to ‘recipes for certified reference materials (CRMs)’ which provide traceability in fields such as chemistry and materials science. Serving as measurement objects with known values of their characteristic quantities, chemical CRM enable instrument calibration to provide reliable and traceable measurements and are essential as a form of measurement standard in both verification and validation in chemical metrology.

Analogously, in memory measurements, recipes for metrological references (i.e., Rasch estimates for memory task difficulty, δ_j) established through measurand restitution could be formulated in terms of causality as a CSE for memory task difficulty, providing objective and scalable metrological units for traceability. In the same way that chemical CRMs often allow for matrix effects where the surroundings of a chemical component can affect its concentration, the proposed psychometric CRMs could include account of the effects of context. To be qualified as a “certified” reference material (or procedure, RMP), CSEs in any application (such as person-centred healthcare) would need to be subject to requirements analogous to those stipulated for CRM and RMP in analytical chemistry and materials science [25, 27].

In some cases, a calibrated measurement instrument can act as a metrological reference as an alternative to a calibrated measurement object. In the context of memory measurement, this would involve formulation of a CSE for the measurement instrument, in terms of Rasch estimates for person memory ability, θ_j. Elsewhere, we have argued for starting with CSE for task difficulty as CRM is done for practical reasons, analogous to the procedure in quantitative metrology where a metrological standard (etalon) is associated in the first case with an attribute of an object – such as the mass of a weight – rather than the instrument used to measure it, since the latter is arguably less suitable as a metrological reference owing to its complexity and lack of robustness compared with a simple object weight [42].

We are so far refraining from talking about certified reference materials for person ability until we have a valid CSE for task difficulty. Specifically, a CSE for person memory ability can be used for well-designed measurement systems and in turn improve the reliability of task difficult estimates, and a basis for discussions with clinicians about the understanding of the person’s memory ability.

10.3.4 Formulation of Construct Specification Equations

The formulation of CSE for an attribute of interest (Y, such as task difficulty or person ability, as a dependent variable) is often defined as a linear combination of a set, k, of explanatory (independent) variables, X:

$$ \hat{\textbf{Y}}={\sum}_k{\beta}_k\cdot {x}_k $$

(10.2)

For memory measurements, Rasch estimates, δ_j or θ_j, for each item, j, or person, i, (Eq. 10.1) can be the attributes of interest to be verified and validated by CSEs. The ‘something’ that causes variation in the attribute of interest are variables that can be used to explain why some memory items are easier than others or why some persons have better memory abilities than others, i.e., the explanatory variables, X_k.

The explicit identification of the dependent variable follows from cause-and-effect considerations and differs from an implicit function which includes all variables of interest on the same side of the equation. An example of the latter is the Disease State Index for the evaluation of Alzheimer’s disease of Mattila et al. [38].

In addition to defining the attribute of interest and identifying its explanatory variables, state-of-the-art multivariate methods for CSEs include subsequently three steps of a principal component regression (PCR) [52]: (the programs and algorithms used in this PCR work are detailed in an appendix at the end of this chapter.)

• (i) Principal component analysis (PCA) amongst the set of explanatory variables, X_k: The initial set, X, of explanatory variables in Eq. 10.2 may exhibit correlation, making it unsuitable for direct regression. Principal component analysis (PCA), where a matrix P of the principal components of variation is formulated, can be used to transform X into an orthonormal set X’:

  $$ {\textbf{X}}^{\prime }=\textbf{T}=\textbf{X}\cdot \textbf{P} $$

The principal components of variation are the eigenvectors, p, of the covariance of X, with eigenvalues λ:

$$ Cov\left(\textbf{X}\right)\cdot {\textbf{p}}_n={\lambda}_n\cdot {\textbf{p}}_n $$

• (ii) Linear regression of the Rasch estimates, δ_j or θ_j, against X’ in terms of the principal components, P: As a second step, the Rasch construct Y [Eq. 10.1], e.g., task difficulty, δ, or person ability, θ, with ɛ variation) is expressed

  $$ \textbf{Y}=\textbf{T}\cdot \textbf{C}+{\upvarepsilon}_y $$

by performing a least-squares regression against the principal components:

$$ \hat{\textbf{C}}={\left({\textbf{T}}^{\textbf{T}}\cdot \textbf{T}\right)}^{-\textbf{1}}\cdot {\textbf{T}}^{\textbf{T}}\cdot \textbf{Y} $$

(10.3)

• (iii) Conversion back from principal components (PC) to the explanatory variables, X_k, in order to express the CSE for the item attribute or person characteristic is the final transforming back into the measurement space:

  $$ \hat{{\textbf{Y}}_{\textbf{0}}}={\textbf{X}}_{\textbf{0}}\cdot \textbf{P}\cdot \hat{\textbf{C}} $$

to yield a linear combination of the explanatory variables, X, as shown in Eq. 10.2, where the coefficients in the linear predictor (construct specification equation):

$$ \beta =\textbf{P}\cdot \hat{\textbf{C}}. $$

Thus, the formulation of CSEs includes two essential multivariate steps, equally applicable and important to explaining memory task difficulty or person memory ability: First, the explanatory variables may not be the experimentally observed quantities, but some combination of these in cases where there is significant correlation between them. At step (i) in the PCR above, the procedures of multivariate analysis – such as PCA – can be used to identify the main components of variation (found by “rotating” in the explanatory-variable space from the experimental dimensions to the PC dimensions). Secondly, the CSE β-coefficients can then be determined with advantage by linear regression to the PCs (step (ii), as opposed to the experimentally observed quantities) which, together with principal component analysis, form PCR.

The resulting CSE from this PCR analysis provides an important source of information: how much each explanatory variable contributes to explain and predict the variation in the attribute of interest. For instance, in the memory tests exemplified later in this chapter, it will be shown how much variables such as Entropy, Reversals and Average distance contribute to explaining memory task difficulty. By regressing measured values, Y, of the attribute of interest against corresponding predicted values, zR, yielded by the CSE, the R² index indicates the amount of variance in task difficulty or person ability accounted for by the construct theory. As explained above, the CSE, when combined with RMT, sets forth a measurement theory of raw score variation as well as simultaneously providing the vehicle for confirmation or falsification of the construct theory. Although on an ordinal scale, raw scores as outcomes are still preferred to logits by some users. The Rasch formula (Eq. 10.1) provides a simple means of converting between them.

As will be presented in next section and further illustrated in the third section, our understanding of a construct may suggest combining several quantities to form one major explanatory variable. Entropy, as a measure of order in either task or person and related to the amount of “useful” information, is one actual example explored here. An easier task or a more able person both have more order and less entropy. Once such causality has been recognized, it will be possible not only to formulate CSEs for these constructs but also to argue for the equivalence of items in different tests, with a view to eventually combining these when formulating a new and improved test, with better coverage and less items, as well as linking tests performed in different cultures.

In addition to the above-mentioned PCA when formulating CSEs, it is common to examine the unidimensionality of item attributes also using a PCA, particularly in view of the basic assumption of unidimensionality in RMT. A second kind of PCA is used to examine item residuals of the logistic regression in RMT [35]. Despite the differences between these two kinds of PCA, the results from the two can be expected to yield results which are connected. If there is more than one explanatory variable revealed in the first step of formulating a CSE with PCR, it is also likely to be accompanied by indications of a second dimension in item residual PCA (where the first PC is the primary Rasch attribute). Therefore, one could surmise that, for instance, memory item difficulty might depend on more than one factor – in addition to the degree of order (captured by the entropy term), perhaps a second “dimension” connected with another cause (such as the number of reversals in a sequence), which might scale differently. This is further illustrated below.

All in all, CSE formulation has advantages (familiar from simpler calculations such as forming a mean value and increasing reliability by adding more items or test persons) of reducing measurement uncertainties by including increased numbers of degrees of freedom through combining several explanatory variables as opposed to analyzing each variable singly. The multivariate coefficients determined experimentally (below) have smaller uncertainties than the corresponding relation for each explanatory variable taken univariately.

10.3.4.1 Measurement Uncertainties of Construct Specification Equations

There are always parameters associated with both the object (task) and person attribute values, which characterize the dispersion of the values as indications of doubt in the measured values, i.e., measurement uncertainties. In addition to the measurement uncertainties for each attribute of interest (i.e., u(δ) for each memory task’s difficulty and u(θ) for each person’s memory ability), there two further expressions of measurement uncertainties will be given in this chapter: for each β-coefficient of the CSE (Eq. 10.2) and for the predicted values zR.

10.3.4.2 Measurement Uncertainty for β-Coefficients in CSE

It is of interest to express corresponding means and standard uncertainties in the regression β-coefficients of the CSE relating the attribute value, Y, (in the examples here: memory task difficulty or person memory ability) to a set of explanatory variables, X, as well as statistics for significance testing of various differences amongst attribute values.

The measurement uncertainties in the attribute values (i.e., u(δ) for each memory task’s difficulty and u(θ) for each person’s memory ability [53] will propagate through the principal component regression described in section 1.4. An initial set of uncertainties in the estimates, $\hat{\textbf{C}}={\left({\textbf{T}}^{\textbf{T}}\cdot \textbf{T}\right)}^{-\textbf{1}}\cdot {\textbf{T}}^{\textbf{T}}\cdot \textbf{Y}$ (where X^′ = T = X ∙ P and P is the matrix of principal components) of the coefficients from the present least-squared analyses, e.g., for the CBT exemplified below, is

$$ \hat{\textbf{C}}=\left[\begin{array}{cc}1,95& 0,74\\ {}-0,75& 1.23\\ {}-0,1& 0.3\end{array}\right] $$

where the second column indicates the (expanded, k = 2) uncertainties, $\textbf{U}\left(\hat{\textbf{C}}\right)=\boldsymbol{k}\cdot \boldsymbol{u}\left(\hat{\textbf{C}}\right)$, in each coefficient (first column) for the three principal components of variation for memory task difficulty, δ, and three explanatory variables, Entropy, Reversals and Average distance, respectively.

To account for the possible effects of heteroscedasticity in the uncertainties, u(δ) or u(θ), in the attribute values which are different for the different tasks or persons [11, 30], one approach is to use a standard, weighted least-squares fit in which Eq. 3 is replaced by:

$$ \hat{\textbf{C}}={\left({\textbf{T}}^{\textbf{T}}\cdot \textbf{W}\cdot \textbf{T}\right)}^{-\textbf{1}}\cdot {\textbf{T}}^{\textbf{T}}\cdot \textbf{W}\cdot \textbf{Y} $$

where the weighting matrix ${W}_{i,j}=\frac{1}{u_i^2};i=j;0,\textrm{otherwise}$. In the cases studies presented later in this chapter, heteroscedasticity in the different memory tasks and person abilities uncertainties is mostly small, so possible bias and scatter from this is expected not to be a dominant effect.

10.3.4.3 Measurement Uncertainty in the zR Yielded from the CSE

The above-mentioned uncertainties, $\textbf{u}\left(\hat{\textbf{C}}\right)$, in the least-squared coefficient estimates will propagate to produce uncertainties in the CSE (i.e., the linear predictor, Eq. 10.2), where the CSE coefficient expression $\upbeta =\textbf{P}\cdot \hat{\textbf{C}}$ used when transforming back from PCs P to the original explanatory variables X.

Corresponding uncertainties in the zR yielded from the CSE will be given by the combined (standard, k = 1) uncertainties from each β-coefficient in Eq. 10.2:

$$ u\left(\hat{\textbf{Y}}\right)=\sqrt{\sum \limits_ku{\left({\beta}_k\right)}^2\cdot {\left({x}_k\right)}^2} $$

10.3.5 Construct Specification Equation: Ad-hoc or Pre-defined?

In an ideal world, ordinal theories should be adopted in an early phase of measurement construction. However, as stated by Fisher and Wilson [20]: ’if data are available but were generated via a process omitting construct definition and item design, application of a measurement model could still be a useful initial step in beginning to define a construct’. In the case of memory measurements such as the classic Knox Cube Test (KCT) [32] where block tapping sequences are to be recalled (similar to the CBT exemplified in this chapter), Knox initially specified different lengths of block tapping sequences to match the anticipated achievements of the mental age of each child, i.e., he assumed that longer sequences were more difficult and persons able to manage longer sequences had a higher degree of mental capacity. However, this is neither the case of all memory tests nor a complete means of developing a CSE, but it can serve as a basis for further developing ad-hoc explanatory variables to be used in a CSE. For instance, Knox considered the children’s age to be a key in terms of their performance which can guide identification of further person factors related to how mental and memory capacity develop. Similarly, any known pathology may explain memory decline and should be included in a substantive CSE theory.

An example of how a pre-defined understanding of how explanatory variables for memory item difficulty can be used is conditional likelihood estimation of component parameters specified with a linear logistic test model (LLTM) of the relationship between item difficulty and component weights (i.e., explanatory variables). For a memory measurement, in LLTM, memory item difficulties are a linear function of the number and difficulty of the cognitive operations. For instance, Green and Smith [21] formulate LLTM models of KCT memory task difficulties as: ${\delta}_j^{\ast }=-\left({\sum}_k{\beta}_{j,k}\cdot {x}_k+{\upvarepsilon}_{\delta}\right)$, where x_k denotes the difficulty of cognitive operation (e.g., tapping sequence) k, and β_{j, k} is the number of times each cognitive operation occurs in item j. A fit of the data to the model can be examined by comparing Rasch model estimates of item difficulties, δ_j, with those estimated by calculating difficulties from the component difficulty estimates, ${\delta}_j^{\ast }$, using a maximum likelihood statistic. The factor ɛ_δ is regarded as a centering constant, i.e., ${\upvarepsilon}_{\delta }+\frac{1}{L}\cdot \left({\sum}_j{\sum}_k{\beta}_{j,k}\cdot {x}_k\right)=0$. Green and Smith [21] report little difference for the KCT in the estimated component difficulties from their LLTM and the regression results of Stenner and Smith [64], where in both models X₁ is the number of taps; X₂ the distance; and X₃ the number of reversals.

Another example of how pre-defined qualitative explanatory variables can be used for supporting construct validity, although beyond memory measurements, is Adroher and Tennant’s [1] recent work in activities of daily living. Seven properties of the items in Evaluation of Daily Activity Questionnaire (EDAQ) were identified and rated in ordinal scales by 39 Occupational Therapists worldwide. Aggregated metric estimates – the weights used to predict item difficulties in LLTM – were derived from the ratings using seven cumulative link mixed models. Parallel to this, classic Rasch estimations of task difficulty, δ_j for each item, j, were assessed and compared with the predictions from the LLTM. In turn, a combination of a theoretical and empirical model enhances the understanding of what is being measured and what causes reproducible variations.

10.4 Theories Explaining Attributes of Interest

In this second section we focus on information theory and entropy as an explanatory variable, X, in CSEs. As explained above, when formulating CSEs (Eq. 10.2), experimentally observed quantities characteristic of the items or person may be combined to form new quantities which capture our understanding of the constructs – such as task difficulty and person ability in memory tests. If our understanding is correct, these combinations will turn out to explain variations better than just using the observed quantities, as can be verified experimentally. Here we consider in particular the concept of entropy in describing the causality linking factors determining the effects on each construct.

We start this section by providing a generic conceptualization of entropy and its link to measurement uncertainties and the propagation of information in a measurement system. This is then followed by illustrations of how entropy theoretically and causally relates to constructs such as memory task difficulty, where a more ordered task (less entropy) is expected to be easier, and person memory ability, where a more “ordered” person (less entropy) is expected to be more able. Experimental tests of these theories are then subsequently exemplified for memory examinations.

10.4.1 Entropy in General Terms

Entropy is simply and generally described as a measure of order related to the amount of ”useful” information or “useful” energy [10]: higher entropy implies less order giving an increased risk of more uncertainties due to loss of information or energy, and vice versa, lower entropy implies higher order and less uncertainties.

Entropy was conceived, though not named or expressed mathematically, in thermodynamics by Lazare Carnot [10] who was concerned that ‘In any machine the accelerations and shocks of the moving parts represent losses of moment of activity […] In other words, in any natural process there exists an inherent tendency towards the dissipation of “useful” energy’ ([10], p. 255, §279). All mechanical processes in a closed system involve some irreversible energy loss. Therefore, entropy (i.e., the loss of useful energy) will always increase over time according to what is known now as the second law of thermodynamics, as formulated later by Kelvin [31] and Clausius [12].

Since World War II, entropy has also been a central concept in the field of information theory [62]. For instance, the performance of a communication system depends on how well information (analogously to Carnot’s energy) is “usefully” transmitted – lost or distorted – which can be described in terms of informational entropy. In this context, like energy loss in thermodynamics, entropy in communication systems tends to increase over time and useful information is lost. A measurement system is a kind of communication system where each element bears a certain amount of information.

Apart from the rattling machines of the early Industrial Revolution or complex communication systems, we consider how well any task of a certain difficulty is performed by a person with a certain ability in terms of entropy. Entropy enables not only descriptions but also explanations and predictions of performance. As illustrated further below, how well a memory test is performed is considered by taking the measurement mechanism as information and communication described in terms of entropy. “Useful” measurement information – paraphrasing Carnot [10] – can be lost (and sometimes gained) at each of the three main stages – object, instrument and operator – identified in a measurement system as a communication system. Thus, entropy can increase overall through distortion and loss of information anywhere in the measurement system.

Rasch’s models for measurement set the stage for our focus here on entropy and information. A broader perspective on entropy in the formulation of concepts is given by Fisher [19].

10.4.2 Entropy, Measurement Uncertainties and Validity

As described above, higher entropy is associated with more loss of “useful” energy or information. In turn, this implies less information and greater uncertainties. Even though measurement uncertainty is more closely related to reliability, as often coupled together with validity, more loss of information and greater measurement uncertainties also give rise to questions about the validity of the measurement. Ultimately the aim of any measurement theory is to compensate as far as possible for the effects of imperfections in the measurement process, in order to obtain the most faithful measure of the quantities of interest. As such, substantive theories explaining the constructs being measured are key to claiming their validity. As said in the Introduction, measurement theories and construct theories are equally important but should also be considered separate issues.

Entropy can be deployed quite generally when extending the probabilistic theory for treating measurement error and uncertainty. In fact, entropy has the advantage of being applicable to all kind of scales, including nominal and ordinal scales, and not only to probability theory but also other inferences in terms of plausibility and belief. Error and uncertainty estimates in qualitative measurements can be expressed in terms of the distortion, fuzziness and lack of clarity of a wide range of characteristics using basic measures of information content, while undistorted, unambiguous and clear patterns and figures are characterized by low values of entropy. Hence, entropy is a useful concept for quality-assurance throughout the measurement process, from stimulation to restitution. Information content can range from basic examples, such as the number of elementary symbols, to increasingly sophisticated information, through syntax, semantic and pragmatic aspects of meaningful information in many contexts.

10.4.3 Entropy, Measurement System and Rasch Measurement Theory

The passage of information through the measurement system can be described in terms of the well-known conditional entropy expression for the corresponding communication system [52]:

$$ H\left(Y|Z\right)=H\left(Z,Y\right)-H(Z) $$

the entropy in the response (Y) when observing the quantity (Z) as the joint entropy reduced by the entropy associated with the measurement object (A) prior to measurement.

The link between a probabilistic description [59] and a corresponding entropy-based approach is based on the informational ‘Shannon’ entropy, H, of any ‘message’ of probability P being proportional to log(P) [62]. This formulation captures the fact that the less expected a message is (i.e., smaller P), the greater the amount of information conveyed (‘surprisal’). Taking the logarithm also facilitates addition and subtraction of different amounts of information.

The “Shannon” entropy terms can thus be expressed in terms of the probability distributions associated with each variable in the measurement process, where these probabilities are multiplied in the expression P(z, y, z_R) = P(z) ∙ P(y| z) ∙ P(z_R| z, y) using the notation used by Rossi in his probabilistic model of the measurement process [59]); and R denotes restitution.

The above expression states how the amount of information changes during transmission in a measurement system. At the start of the measurement process, there is an initial ‘deficit’ in entropy (i.e., ‘surplus’ information) coming from prior knowledge, H(Z; A), of the measurand (attribute, Z, of entity A), again using a notation analogous to that used by Rossi in a probabilistic model of the measurement process [59]. Losses and distortions H(Y, Z) from imperfections in the measurement process increase the entropy, leading finally to a posterior distribution (Q) with entropy H(Y| Z) as the result of the measurement process.

This implies further, in the measurand restitution of memory measurements (i.e., with the Rasch probabilistic formula, Eq. 10.1), that the odds ratio of succeeding with a task, is simply equal to sums and differences of entropy and this connection can be done with the expression:

$$ \mathit{\log}(P)=\mathit{\log}\left(\lambda \right)=\mathit{\log}(k)-\mathit{\log}(h) $$

where the average probability P is taken equal to the Poisson distribution factor λ, and h and k enter the equation for the conditional entropy expression above. As recalled by Pendrill and Melin [53], an early form of the psychometric Rasch model (RMT) posits that the odds ratio of successfully performing a task is equal to the ratio of an ability, h, to a difficulty, k [57].

$$ \frac{P_{success}}{1-{P}_{success}}=\frac{h}{k} $$

which can be written as Eq. 10.1 where the test person ability, θ =  log (h), and task difficulty, δ =  log (k), can be evaluated by logistic regression to the score data in terms of the probabilities q (P_success). Rasch [60] was keen to point out that his “discovery was a somewhat intuitive achievement …, with no relation to any actual item analysis problem” or any analogy to the laws of Physics.

The assumptions behind RMT need of course to be tested, such as the separability of two independent variables contributing to an overall effect or response, which have been questioned over the years, e.g., by Luce and Tukey [37] in their work on simultaneous conjoint measurement. This is done in our case using a battery of tests, based on analyses of variance and regression fit residuals, as exemplified below.

Apart from task difficulty and instrument ability, there is an additional factor – called in IRT the discrimination of the person responding – as can be captured in some IRT models with a second and/or third parameter, viz the finite resolution, ρ, of the instrument (i.e., the person taking the test). This discrimination term [24] can be modelled as a change in task difficulty (or corresponding expression for person ability): Δδ =  − (ρ − 1) ∙ δ, in turn giving an additional entropy term $H\left(Z,Y\right)\sim \Delta \delta =\ln \left(\sqrt{3}\cdot 2\cdot u\right)$ which relates discrimination to measurement uncertainty, u, (here for the case of a uniform distribution) in the response (Y) when observing the quantity (Z). As also discussed in Pendrill and Melin [53], the steepness of the characteristic ogive curve of the item response (in the binary case where one classification – zero, say – goes over to one) is determined by the uncertainty of the person making the classification for a given task. That steepness in turn determines the width – that is, the measurement uncertainty – in each experimental estimate of construct attributes such as task difficulty and person ability, where each estimate is not sharp but broadened to a width u(δ) and u(θ), respectively. (As in traditional metrology, provided measurement uncertainties and heteroscedasticity are small, this will not in general hinder the establishment of metrological references with RMT.)

With links to “useful information” and to causality in mind, a task will be easier if there is some degree of order and a poorly performing person can be explained in terms a lack of coordination explained in terms of increases in entropy. Conversely, a task will be more challenging when there is less order and a well performing person can be explained in terms of good coordination. This is further discussed in the next sections for memory task difficulty and person memory ability, respectively.

10.4.4 Entropy to Explain Memory Tasks

The forward sequences of Corsi Block Test (CBT) [13], and Digit Span Test (DST) [74] will be used as examples. In CBT the person is asked to reproduce the same sequences with different tasks with increasing length and the DST requires a similar recall task, but instead of a tapping sequence the participants are asked to recall digit sequences. As stressed above, the ‘something’ that causes variation in memory task difficulty needs to explain why some memory items are easier to perform than others.

To include entropy in CSE formulation in memory measurements, the first step is to attempt to explain memory tasks in terms of entropy. The different memory tasks to be recalled – for both non-verbal taps and verbal digits – can be characterized in general in terms of a message in which a number, N_j, (j = 1,…,J) of symbols of J different types (taps or digits) can be distributed in a number, G, of categories (or cells) $G={\sum}_{j=1}^J{N}_j$. The probability of encountering the jth symbol is ${p}_j=\frac{N_j}{G}$, which can be summed to unity. According to Léon Brillouin [7], the total number, P, of messages that can be obtained by distributing the symbols at random over the G cells (with never more than one symbol per cell) is $P=\frac{G!}{\prod \limits_{j=1}^J{N}_j!}$. In turn, the information theoretical entropy, which is a measure of the amount of information in these messages, is then:

$$ I=M\cdot lnP=M\cdot \left[\ln \left(G!\right)-{\sum}_{j=1}^J\ln \left({N}_j!\right)\right]\cong M\cdot \left[G\cdot \ln (G)-{\sum}_{j=1}^J{N}_j\cdot \ln \left({N}_j\right)\right] $$

(10.4)

where M is an arbitrary constant. Stirling’s approximation in the final terms of the righthand side of Eq. 10.4 applies when G and N are large, but with modern computer power the approximation is no longer necessary when evaluating the factorial terms. Consequently, this basic expression will be applicable when explaining task difficulty in CBT and DST.

The expression proposed by Brillouin [7] enables entropy to be evaluated for sequences which not only have increasing length (i.e., taps or digits), G, but also some repeats, N, of the same block tapped or digit. In particular, the second entropy term in Eq. 10.4 above shows the expected increase in entropy – and thus the decreased task difficulty – from N repeats.

Other effects which can make a task easier (or more aesthetically pleasing) include some aspect of simplicity, symmetry and the like where the observer recognizes a familiar pattern (similar to seeing the same figure in a digit span test) instead of just a random cloud of dots. In those cases, the extra term in the Brillouin [7] expression shows how the entropy is reduced (making the task easier) by the recognition of a number of symmetric groupings. The difficulty of remembering different block sequences (such as the Corsi block test) was described, for instance by Schnore and Partington [61], in terms of a sum of a set of basic patterns (or chunks) with different information content expressed in terms of entropy and the symmetry of each pattern.

In other work reported separately, we have demonstrated how entropy can explain reductions in task difficulty due to serial position effects (e.g., in word list tests such as R-AVLT) such as primacy and recency [43]. In that work, we propose that a CSE for task difficulty in word learning list tests such RAVLT (length L = 15) can be based theoretically on a sum of entropy terms for primary, recency, mid-list recall and word frequency (f) as given, respectively, by:

$$ {\delta}_j={\delta}_{j, primacy}+{\delta}_{j, midrange}+{\delta}_{j, recency}+{\delta}_{j, freq} $$

(10.5)

where

$$ {\delta}_{j, primacy}=-M\cdot \ln \left({G}_j!\right);G= ite\textrm{m}\ order $$

$$ {\delta}_{j, midrange}=+2\cdot \left[M\cdot \ln \left(\frac{L}{2}!\right)\right] $$

$$ {\delta}_{j, recency}=-M\cdot \ln \left({G}_j!\right);G=L-1- ite\textrm{m}\ order $$

$$ {\delta}_{j, freq}=-M\cdot \ln {f}_j $$

and the normalization factor $M=\frac{1}{\mathit{\ln}(L)}$ [7]. In the case of an odd list length, L, the expression $\mathit{\ln}\left(\frac{L}{2}!\right)$ is evaluated by rounding $\frac{L}{2}$ to the nearest integer.

Using the same basic model as in Eq. 10.4, we have recently been able to explain SPE in the immediate recall (IR) of the 15-word learning memory test RAVLT [43].

10.4.5 Entropy to Explain Person Abilities

Having explained task difficulty, we now turn to person ability. The first stage in defining, and testing, explanatory variables for any ability is to formulate an understanding of what causes a low respectively high ability, e.g., is there any known pathology behind? Is it an ability characterized by certain training or learning processes? In the case of measuring person memory ability in Alzheimer’s Diseases (AD) spectrum there are some AD-related biomarkers of interest related to amyloid pathology, tau pathology and neurodegeneration [29] as well as brain volumes and other structural parameters related to memory function associated with regions such as the hippocampus.

In general, explanations of persons’ abilities are characterized by complexity. This is especially true for cognitively related activities, such as memory abilities as there is an information processing system with 10–100 billion neurons and ~10¹⁴ synapses in the brain [73]. This system exhibits the highest degree of complexity among all organs in the human body. Connectivity, in particular, is a key to explaining cognitive ability and parallels can be drawn to other high demanding systems in thermodynamic or information theory, and therefore, Functional Magnetic Resonance Imaging (fMRI) are gaining more attention in order to explain brain complexity including several entropy-based measures [46, 72].

It should also be noted that a person’s memory ability to pay attention to the task to be performed and his or her executive functions may also partly be used to explain the person’s ability for tasks requiring recall of a variety of ordered information. There are also potentially other factors within the other elements of the measurement system (i.e., the object, the environment and the method) that can affect the person’s memory ability such as how the test is administered (i.e., the method) or if there are surrounding noises and disturbances which might cause stress (i.e., the environment). Such factors should however be separate from the explanatory variables for the person’s memory ability in the same way as they are separate from explaining task difficulty, as can be modelled in MSA.

10.5 Examples and Illustrations in Memory Measurements

In this penultimate section, we combine the explicit methods for testing the theories explaining memory item difficulty and person memory ability. We start with a brief review of memory measurements, followed by CSEs based on entropy. It will be demonstrated on the basis of measures of memory task difficulty for two short-term memory recalling tests: CBT and DST, and a CSE for measures of person memory ability will be exemplified based on known biomarkers related to Alzheimer’s Disease (AD) spectrum. At the end we summarize the limitations and strengths in the present examples and implications.

10.5.1 Memory Measurements

Since the Ancient Greeks, attempts have been made to understand how the human brain works, such as cognition and mental processes. Today, in the field of ‘the measured mind’, there are many different person attributes of interest ranging from capacities and abilities to attitudes and personality factors [5]. Our interests are not only in the measured mind but in mind attributes in themselves, irrespective of whether they have been measured. Those interests go well beyond examinations in clinical setting and quantification of health status, such as the field of educational sciences and development psychology.

10.5.1.1 The Broad Picture of Cognition and Mental Processes

Pioneers such as Binet Simon and David Wechsler appeared in the early 20th-century when the first intelligence tests aiming to measure one’s underlying mental ability were formulated, including the Binet Simon Intelligence Scale and Wechsler Bellevue Intelligence Scale [4]. Those tests, as well as similar later intelligence tests, were built on tasks for several aspects of cognition such as recalling, comparing and defining numbers, words and pictures.

Already in the pioneering work, the idea of construct maps (cf. [75]) was present based on the child’s age and corresponding longer tests for older children. Likewise, the Knox Cube Test (KCT, similar to the CBT introduced above), introduced at Ellis Island over 100 years ago for the testing of mental limitations in immigrants, had different sequence lengths to be recalled and defined what should be accomplished at different ages. These were structured tests with an objective scoring; either the person could or could not perform the requested task. However, test results were, and still mostly are, based on counts of raw scores, i.e., not measurement outcomes that separate, as in RMT, the raw data into quantitative measures of task difficulty and person ability. In turn, there are often quite large variations in the meaning of score differences and a less than comprehensive understanding of what is being measured.

The idea of constructing tests including several aspects of cognition corresponds to what later became known as a higher ordered construct and Andrich’s [2] metaphor of a rope made up of strands. This way of scaling tests together requires that the tests included work in a uniform way from less to more to build one construct to be measured on the same scale. In fact, the CSE approach – which reflects how well each construct is understood – can provide an indication of the equivalence of items in different tests, and thus guidance about which equivalent constructs can be reasonably combined to form, hopefully, better and more reliable tests [44]. On the other hand, in the clinical examination, it is common that tests for different cognitive abilities and biological aspects are used parallel, and in turn require that the clinician combine the information to decide diagnosis, drugs and treatment. Similar, this multi-source of information can obviously provide deeper understanding of how cognitive processes occur and relate to each other, while not necessarily explaining a particular construct in itself and what causes its variation.

Moreover, historically, psychological effects in measurement were initially introduced into measurement science [69] in the field of psychophysics during the nineteenth Century, in attempts to relate abstract human sensations to quantifiable physical external stimuli (such as touch pressure, sound pitch). In contrast, psychometrics developed thereafter to include other mental attributes (such as attitude, knowledge, empathy) which are not simply responses to physical stimuli. Tesio [69], in comparing and contrasting the two disciplines, claimed that “psychophysics is deterministic: a cause-effect relationship is assumed between stimulus and response…(whereas) the psychometric approach is probabilistic, in that it implies inferences.”

Compare Tesio’s claim with our description of causality and the responses to entropy. A key enabling insight, in our view, is to connect the treatment of decision risks associated with measurement uncertainty to generalized linear modelling, indeed not only in psychometrics but also across the disciplines. Handling certain more qualitative measurements in the social sciences, psychology and health care examinations in this way unite information theory (the perceptive identification and choice paradigms of psychophysics [28], with a particular focus on the RMT psychometric approach. The idea in psychophysics of modelling responses through the five human senses has been extended to a metrological model of RMT in psychometrics where the human acts as a measurement instrument [49]. But note that, although RMT is also a logarithmic expression (Eq. 10.1), the general linearized model expression in psychometrics is more general than the Weber–Fechner Law of psychophysics, which has a different logarithmic dependence derived in the particular case where a change in the psychometric function is proportional to the fractional change in the stimulus level.

10.5.1.2 Neurodegenerative Diseases and Memory Measures

There are contemporary initiatives calling for biological definitions of neurodegenerative diseases such as Alzheimer’s Disease (AD). However, prevailing AD spectrum core criterion are based not only on biomarkers but also on examinations of example cognitive function and ability to function in everyday life [39]. In the clinic, the patient is examined through a combination of history-taking from the patient and a knowledgeable informant together with neuropsychological testing.

Since measures of memory (and other cognitive aspects) currently lack established international standards, it is of course challenging to correctly make fully diagnoses as well as monitor pharmaceutical intervention effects and actual disease progression. In fact, efforts on drugs or therapies delaying or stopping disease progression, in particular in early phases, have mostly been unsuccessful. Such failures, as stressed by Raket ([55], p. 2) may be due to wrong therapeutic targets or non-efficacious therapies, but it is conceivable that a proportion of trial failure could be attributed to other factors such as study design, endpoints and non-optimal patient populations selection. To pick up on Raket’s first point, about wrong therapeutic targets or non-efficacious therapies: we would emphasize that, without proper measures, it will be challenging to identify the right target needed to be treated. This is especially true in early phases of disease where symptoms (such as memory decline) and signs (such as Amyloid and Tau pathology) are small as well as can be a pre-stage of many different diseases and may not lead to AD spectrum.

To also pick up on Raket’s comment on endpoints. There are numbers of widespread neuropsychological tests for different cognitive aspects such as learning and episodic memory; speed and attention; visuospatial functions; language; and executive functions. However, the most commonly used legacy neuropsychological tests (e.g., Mini Mental State Examination [23]) and Alzheimer’s Disease Assessment Scale-Cognitive Behavior section [22]) can neither claim accuracy to distinguish between patients (especially in early stage disease due to person-to-item targeting is commonly skewed and there are large measurement uncertainties associated with persons with early memory decline) nor are metrologically legitimated (i.e. lacking metrological references to ensure comparable measurement results) [22, 23, 42]. Despite well-known issues with those tests, the tests are frequently used incorrectly, for instance in studies of biomarker correlations [51].

Of the cognitive aspects related to AD, memory decline is one of the early symptoms. Current AD therapies focus mainly on early-stage disease, which necessitates fit-for-purpose measures to capture early memory decline. Thus, measures of memory decline (or improvement) on individual level needs comparisons at least to specific time points, e.g., annual clinical examinations or longitudinal studies. However, an impaired memory ability can also be established by comparisons e.g., with references values for the same age group or in cross-sectional studies. Both of these comparisons require that the shortcomings of current neuropsychological tests are solved to ensure that the memory quantities are traceable as far as possible to metrological standards and are metrologically legitimated. Thus, this section will illustrate possible solutions in the context of memory measurements based on the explicit methods introduced in the first section and the substantive theories introduced in the second section.

10.5.2 Subjects and Data Analyses

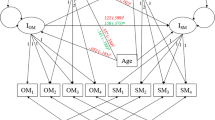
The subjects and data used stem from the project NeuroMET [17] comprising a cohort of 88 subjects with dementia due to suspected AD (n = 26), mild cognitive impairment (MCI) (n = 23) and healthy controls (HC) (n = 39). The mean age was 72 years (range 55–84 years) and 47% were women and 53% men. Of the 88 subjects, 77 had a complete set of memory assessments and biomarkers used for developing CSEs for person memory ability.

During the neuropsychological testing, a correct recall was scored 1 and an incorrect recall was scored 0 for both CBT and DST. This is, however, raw data that needed to be transformed into separate and linear measures for memory task difficulty (δ-parameter) and person memory ability (θ-parameter). To enable this, the Rasch Dichotomous Model was applied to the raw data in the software WINSTEPS^®, and consequently used for the formulation of CSEs as described for the two attributes of interest, Y, i.e., memory task difficulty and person memory ability.

Motivation of explanatory variables, X, for memory task difficulty and person ability is provided, respectively, elsewhere in this Chapter. Explanatory variables for memory task difficulty have been derived based on the variation in the recalling sequences provided; Entropy is based on Eq. 10.4, Reversal corresponds to the number of times one changes from clockwise to counter-clockwise and the other way around in CBT or counting forward to backward and the other way around in DST, Average distance is the average centimeters between blocks in CBT and the average distance between digits in DST [44]. Explanatory variables for person memory ability are well-known AD-related biomarkers, i.e., physical and chemical quantities, for each person in the cohort. Cortical thickness and left hippocampus volume (normalized to each test person’s intercranial volume) were obtained by magnetic resonance imaging (MRI) with a 7T scanner and blood-based biomarkers, neurofilament light (NfL), amyloid peptides 1-42/1-40 ratio (Aβ42/40) and total tau proteins (Tau) were measured in plasma [45]. Subsequently, the formulation of CSEs for each attribute and estimations for measurement uncertainties. PTC MathCad Prime 3.1 and its specific modules for the steps in the PCR were used for the analyses and are described in Appendix.

10.5.3 Explaining Memory Task Difficulty

Early CSE work was done in the 1980s by Stenner and Smith [64] and Stenner et al [65] on the Knox Cube Test (KCT) [32]. As explanatory variables, X, these early authors were using Length, Reversals and Distance and, like the present studies, they used Rasch transformation. However, by considering the significance of entropy in measurements, the Brillouin [7] expression for entropy seems in our studies theoretically to be more appropriate. With entropy, it is expected that more ordered sequences will be easier to remember, i.e., the informational entropy (by analogy with thermodynamic entropy) is lower (i.e., more information) when the order of the test (e.g., sequence of blocks or digits) is greater. Thus, the proposal of entropy is in line with studies which showed that inconsistency in performance at longer sequences should be a function of path complexity (as defined by [8]); that memory span is greater for structured than unstructured paths [26, 61]; and that the success rates for different lengths of sequences are overlapping [48], which are properties shared by CBT and DST.

Moreover, in contrast to previous workers who considered the distance between taps as an explanation of KCT task difficulty, the average distance is used below instead. This is to not confound with another explanatory variable – namely the number of taps which enters into the distance – which is already dealt with above. Average distance can be conceptualized as a ratio of signal to noise. Thus, a two-tap sequence such as “2-3” is easier to remember than a two-tap sequence which is spread out over more blocks, such as “1-4”. In the latter case, there is more background noise which the individual must process and filter out.

Below the CBT and DST cases are first handled separately and then related to each other and as a combined measure.

10.5.3.1 Case 1: Tapping Recall

For the CBT, the memory task difficulty values, δ, ranged from −6.5 ± 3.8 to 8.5 ± 3.7 logits where the shortest tapping sequences were easier than the longer. It was, however, evident that the sequence 3-5-1-7-2 was much easier than the other sequence with the same length. The item reliability was 0.95 and fit statistics were satisfactory. In the test situation, there is a possibility for an 8-block-tapping-sequence, but this was eliminated as only one subject achieved that level. Table 10.1 shows the memory task difficulty values, δ, and corresponding explanatory variables used for developing the CSE for CBT.

Table 10.1 The Rasch estimates, δ_j, for each item, j, and its explanatory variables in CBT

The above-mentioned PCA when formulating CSEs [section 1.4] indicates firstly that particularly the pair of explanatory variable Entropy and Reversals are rather

strongly correlated, with the correlation matrix based on the covariance matrix of the explanatory variables indicating a Pearson correlation r $=\sqrt{R^2}$ = 0.91. This is to be expected, since longer series (with consequent lower entropy) will also allow for more reversals to be made in each sequence.

As shown in the following equation, the PCA-based CSE for CBT is dominated by entropy and there is a negligible contribution to the CSEs of Reversals and Average distances:

$$ {zR}_j=-7(3)+2.0(7)\times {Entropy}_j-0.8(1.2)\times {Reversals}_j-0.1(3)\times {AveDistance}_j $$

Here the term Entropy is evaluated using the Brillouin [7] expression (Eq. 10.4) as a function of solely the number of blocks tapped. (That is, other effects discussed above, such as reduced entropy associated with symmetrical patterns and serial position effects such as primacy and recency, were found in the present studies to be negligibly small.) The contributions – or in fact the lack of contributions – from other explanatory variables are also illustrated in Fig. 10.1 where it is evident how Entropy increases with observed memory task difficulty while Reversals and Average distances only provide some noise around 0. The CSE have also larger measurement uncertainties for β-coefficients (Eq. 10.2) for Reversals and Average distance compared to Entropy.

Fig. 10.1

Predicted contributions, Δδ, to task difficulty from the three explanatory variables Entropy, Reversals and Average distance for the CBT. Item sequence corresponds to Table 10.1

As mentioned in above, a second but connected PCA is commonly performed to examine the unidimensionality of item attributes by examination of the residuals of the logistic regression of the Rasch measurement model to the observed outcomes. In the present case of CBT, this second PCA indicated only a weak additional dimension (where the first PC is the primary Rasch attribute) as a 1^st contrast contributing as little as 9.9% unexplained variance. The two PCAs thus yield results here which are connected as expected: one dominant explanatory variable revealed in the first step of formulating a CSE with PCR is likely to be accompanied by indications of one single dimension in a Rasch residual PCA.

By regressing the observed memory task difficulty values, δ, against corresponding estimated zR from the CSE, the R² index indicates high accuracy of the prediction (Pearson coefficient r $=\sqrt{R^2}$= 0.98) (Fig. 10.2) and the observed memory task difficulty values, δ, were found to lie within the corridor of predicted uncertainties. i.e., zR + UzR (Fig. 10.3).

Fig. 10.2

Linear regression of the observed CBT memory task difficulty, δ, against the CSE predicted zR for the CBT. Uncertainties coverage factor k = 2. Item sequence corresponds to Table 10.1

Fig. 10.3

Dots with uncertainty intervals shows the CBT observed memory task difficulty, δ and corridors of modelled uncertainties shows zR+UzR (grey lines) for the predicted zR values, coverage factor k = 2. Item sequence corresponds to Table 10.1

The CSE for CBT illustrated here is very similar (within uncertainties) to a recently derived CSE for memory task difficulty in KCT [40, 52]:

$$ {zR}_j=-9(5)+2(1)\times {Entropy}_j+0.8(1.4)\times {Reversals}_j+0.7(2.9)\times {AveDistance}_j $$

At the same time, in earlier formulated CSEs for KCT, entropy was not considered, and distance and number of taps were confounded, making comparisons difficult.

10.5.3.2 Case 2: Digit Recall

The memory task difficulty values, δ, ranged from 8.5 ±3.7 to 6.8 ± 2.2 logits in DTS. As for the CBT, the shortest tapping sequences were easier than the longer, but, although larger measurement uncertainties, the two longest sequences differ quite a lot in their observed memory task difficulty, δ. This is explained by 9 of 21 subjects remembered the 1^st 8-digit sequence whilst only 2 of 21 remembered the 2nd 8-digit sequence. The item reliability was 0.96 and fit statistics were satisfactory, although, the two shortest sequences were classified as minimum measures due to all 86 subjects took the test passed. A summary of the memory task difficulty values, δ, and corresponding explanatory variables used for developing a CSE for DST are presented in Table 10.2.

Table 10.2 The Rasch estimates, δ_j, for each item, j, and its explanatory variables in DST

The CSE for DST is very similar to the above illustrated CSE for CBT with Entropy as the dominating term and larger measurement uncertainties for β-coefficient (Eq. 10.2) for Reversals and Average distance compared to Entropy (Fig. 10.4):

$$ {zR}_j=-10(3)+1.5(3)\times {Entropy}_j+0.2(4)\times {Reversals}_j-0.2\left(1,5\right)\times {AveDistance}_j $$

This is further illustrated in Fig. 10.5. Figure 10.5 shows the regressed observed memory task difficulty values, δ, against corresponding estimated zR from the CSE, the R² index indicates high accuracy of the prediction (Pearson coefficient r $=\sqrt{R^2}$ = 0.98) and Fig. 10.6 shows the observed memory task difficulty values, δ, lying within the corridor of predicted uncertainties. i.e., zR ± UzR.

Fig. 10.4

Predicted contributions, Δδ, to task difficulty from the three explanatory variables Entropy, Reversals and Average distance for the DST. Item sequence corresponds to Table 10.2

Fig. 10.5

Linear regression of the observed DST memory task difficulty, δ, against the CSE predicted zR for the DST. Uncertainties coverage factor k = 2. Item sequence corresponds to Table 10.2

Fig. 10.6

Dots with uncertainty intervals shows the DST observed memory task difficulty, δ and corridors of modelled uncertainties shows zR+UzR (grey lines) for the predicted zR values, coverage factor k = 2. Item sequence corresponds to Table 10.2

The DST sequences used here did not include any repeated digits, which however do occur, for example, in a 9-digit sequence in another version of DST. That data were retrieved from GBG MCI study [71], which included 268 individual tests involving 213 MCI patients (79%) and 55 HC patients (21%). The same procedure for transforming raw data into δ parameters for task difficulty was applied. In the GBG MCI study [71], three digits are repeated twice each. This has implications for the entropy contribution from the replicated digits [40, 44]. The sequence exemplified has higher order and convey less information compared to a digit sequence with similar number of digits but no duplicates. This is illustrated to the right in Fig. 10.7; the prediction of that item is easier than another other 9-digit sequence without duplicates. Likewise, as also illustrated to the left in Fig. 10.7, that item has a corresponding entropy contribution and predicted task difficulty which turn out to be comparable with those properties of the 8-digits items studied here, thus indicating a degree of equivalence between items of different tests. Consequently, this also complements the theoretical justification for considering an information theoretical approach including Entropy as an explanatory variable when explaining memory task difficulty.

Fig. 10.7

Blue triangles for observed DST [GBG MCI study] memory task difficulty, δ, and blue dots for predicted zR task difficulty for 8-digits and 9-digits sequences, respectively, and their corresponding explanatory variables

10.5.3.3 Case 3: Taps and Digits Combined

The similarities in the administration of CBT and DST as well as their CSEs, respectively, invite to combine the items into one set of memory tasks. The item reliability was 0.93 and the memory task difficulty values, δ, ranged from −6.4 ± 3.7 to 6.8 ± 3.7 logits (and person ability values, θ, to be used in next section ranged from −4.0 ± 2.1 to 3.2 ± 1.5 logits). Three items showed Maximum measures (all from CBT) and two items showed Minimum measures (both from DST).

The main advantage of combining block and digit items in an extended CSE is that, with more information, uncertainties for assessing the persons’ memory abilities reduces. This is illustrated in Fig. 10.8 where uncertainties, U(θ), for each person’s memory ability are reduced approximately with 0.5 when comparing with U(θ) derived from only CBT.

Fig. 10.8

Measurement uncertainties (U(θ), y-axis) for each person’s memory ability from CBT in blue and from the combined CBT and DST in grey. At x-axis, from left to right least able persons to most able persons. Measurement uncertainties coverage factor k = 2

Moreover, scaling CBT and DST together enables not only a hierarchical ordering of tasks, but also numerical values with which to compare the different recall sequences. As shown in Fig. 10.9, the two easiest DST memory tasks, i.e., 3-digit sequences are approximately 2 logits easier than corresponding 3-tapping sequences for CBT. Similarly, CBT memory tasks are somewhat more challenging than DST, even though the two sets of sequence tests have roughly the same number of entities i.e., lengths of sequence. However, with the same length, and without duplicates, predicted task difficulty zR for item j would be the same if entropy were the only explanatory variable, but those 3-taps/digits sequences differ in the number of reversals and the average distance (Tables 10.1 and 10.2).

Fig. 10.9

Histogram of memory task difficulty for CBT in blue and DST in grey scaled together from left to right easiest tasks to most challenging tasks. Item order corresponds to Table 10.1 for CBT and Table 10.2 for DST. Error bars indicate measurement uncertainties coverage factor k = 2

10.5.4 Explaining Person Memory Ability

The previous section deal with a description of the objects itself, i.e., explaining memory tasks difficulties. CSEs or construct theories for task difficulty are the most common way of talking about the measurement validity. However, scores typically determined by identifying person locations along a single proficiency continuum do not in themselves naturally provide diagnostic information [15]. So, to recap, only when synthetic constructs created from theory enable the consistent and reliable prediction of both memory item (difficulty) and person memory (ability) location calibrations, can we claim to understand our memory measurements. Thus, the following section will provide an example on how a CSE for person memory ability might look like.

For the purpose of this demonstration the attribute of interest, Y, were person memory abilities estimated based on the combination of CBT and DST assessments. The ‘something’ that causes variation in the attribute of interest are variables that can be used to explain why some persons have better memory abilities than others such as well-known AD-related biomarkers:

• cortical thickness (mm³)

• left hippocampus volume (mm³; normalized to each test person’s intercranial volume)

• neurofilament light (NfL) (pg/ml)

• amyloid peptides 1-42/1-40 ratio (Aβ42/40)

• total tau proteins (Tau) (pg/ml)

where the latter three were measured in plasma.

CSEs for Person Memory Ability Based on Biomarkers

The person memory ability values, θ, ranged from −4.0 ± 2.1 to 3.2 ± 1.5 logits with a person reliability of 0.70. To correspond to memory task difficulty, from easier tasks to more challenging tasks, a lower value of person memory ability indicates a less able person, while a higher value of person memory ability indicates a more able person.

The CSE yielded from the PCR where the five biomarkers were used to explain person memory ability showed a less clear contribution from a single biomarker compared to entropy as explanatory variable for memory task difficulty:

$$ {zR}_i=-2(3)+0.24(2)\times {thickness}^3+1(2)\times lHip-0.03(3)\times NfL-0.2(4.9)\times A\upbeta 42/40+0.4(4)\times Tau $$

As shown in the CSE as well as in Fig. 10.10; NfL has a negative contribution, while cortical thickness and hippocampus volume exhibits a positive contribution. This corresponds to the accepted clinical interpretation of disease progress where higher levels of NfL are seen in patients with AD compared to more able persons within the AD spectrum and brain volume is decreasing as the disease progresses. However, there were negligible contribution from Aβ42/40 and Tau to explain person memory ability and the U(β) shown for each explanatory variable in the CSE are larger than their coefficient itself for Aβ42/40 and similar for Tau, while the three others have minor uncertainties.

Fig. 10.10

Predicted contributions, Δθ, to person ability from the five explanatory variables Thickness, left Hippocampus, NfL, Aβ42/40 and Tau

The R² index indicates lower accuracy of the prediction compared to the CSEs for memory task difficulty presented above (Pearson coefficient r $=\sqrt{R^2}$ = 0.57). At the same time the regression based on multivariable express higher accuracy than any of the individual biomarkers in univariate correlations (Person coefficient r ranging from 0.04 (Tau) to 0.51 (Thickness). Even though Thickness has close to similar Pearson coefficient as the CSE, the relative uncertainty for the β-coefficient is greatly reduced within the CSE compared to the univariate correlation (Thickness β-coefficient and U(β) in CSE/multivariate is 0.24 ± 0.02 compared to univariate 0.4 ± 0.2).

Figure 10.11 illustrates a corridor of the zR+UzR around the U(θ) for each person’s memory ability, which at some parts is considerably wider than the U(θ), probably because there are additional components of variation not yet included in the CSE model.

Fig. 10.11

Dots with uncertainty intervals shows the observed person memory ability, θ, and corridors of modelled uncertainties shows zR+UzR (grey lines) for the predicted zR values, coverage factor k = 2

10.6 Limitations and Implications in Interpreting CSEs

Only a fully comprehensive multivariate and PCR study including all potentially important explanatory variables will give a true picture. A fully comprehensive CSE for either memory task difficulty or person memory ability are not yet evident in the cases illustrated- they all have their limitations. In their critical review of what they termed “decomposing item difficulties”, Green and Smith [21] mentioned a number of potential general limitations in various multivariate and regression approaches – such as “effects of sample size, collinearity, a measurement disturbance, and multidimensionality on the estimation of component difficulties” These limitations are still valid today when forming CSEs for task difficulty, and also apply equally to person ability estimation as well.

With regards to the effects of sample size, it is well-known that large well-targeted samples provide more information about each item, and consequently, as the sample size increases, the measurement uncertainties for estimates of task difficulty are reduced [76]. And similarly, the other way around, with increased test length (i.e., number of items), measurement uncertainties are reduced for estimates of person ability, as illustrated in Fig. 10.8. However, as also mentioned earlier in this Chapter, the measurement uncertainties for each memory task difficulty, u(δ), and for each person’s memory ability, u(θ), propagate through the PCR. In turn the u(δ) and u(θ), respectively, will have implications for U(β) and UzR together with uncertainties in the fit itself, which brings us to the issue of collinearity and measurement disturbance. As is evident from Figs. 10.3, 10.6 and 10.11, the “corridor” of modelled uncertainties, UzR, is (much) wider than the observed memory task difficulty, δ, and person memory ability, θ, with its measurement uncertainties, respectively. This we interpret as indicating that there are sources of dispersion when making the multivariate regression which are not accounted for in terms only of measurement uncertainty. Some such dispersion could arise from one or more additional explanatory variables of variation associated with unrecognized explanatory variables but could also be signs of collinearity and other disturbances and warrants further investigation. Examples of additional explanatory variables for person memory ability could be the brain entropy and connectivity, as well as, but not limited to biomarkers, the person’s ability to pay attention to the task to be performed and his or her executive functions.

One way to reduce the limitations stemming from collinearity is by implementing the PCA in the first step of developing the CSE. With the PCA, the main components of variation (found by “rotating” in the explanatory-variable space from the experimental dimensions to the PC dimensions) can be obtained. Nevertheless, before that, one needs to consider each explanatory variable, X in terms of our understanding. For instance, to avoid collinearity, we have chosen to only include the left hippocampus volume, and not also the right hippocampus volume, even though both show univariate Pearson coefficients of approximately 0.45 with person memory ability. Left and right hippocampus volumes showed a Pearson coefficients r $=\sqrt{R^2}$ = 0.90, and in turn, adding both did not provide any additional predictive value in the CSE.

We performed an initial study of multidimensionality above, for instance in the discussion about task difficulty for the tapping test CBT where the PCA of item residuals indicated one dimension, and corresponding one dominant explanatory variable. As mentioned by Green and Smith [21], unidimensionality is an assumption of the Rasch model and a straightforward use of regression will be of only marginal value unless the items form a cohesive set, that is, that the same underlying variable explains response to every item in that set. However, in general terms, as mentioned by Green and Smith [21], the less well-defined or well-constructed items are, e.g., by including non-fitting items or appearance of multidimensionality, the less likely it is that the appropriate model will be identified. This brings us back to the significance of proper construct modelling [75] including a substantive theory. In our case, there is however one possible limitation in terms of the subjects included and the choice of AD related biomarkers as explanatory variables X. Even though the memory abilities are ordered as expected – AD patients having lowest abilities and health controls having highest ability – it is not necessary that all persons’ memory abilities only can be explained in terms of AD related biomarkers, e.g., a person with MCI might not progress to AD as it could also be other dementia characterized by other biomarkers.

Despite those limitations, the benefits are more important, e.g., when contrasting univariate and multivariate correlation studies. A main disadvantage of univariate fits is that the observed correlation between the attribute and a chosen explanatory variable might be explained by another covariate not considered. Where multivariate correlation studies can be reliably performed, lower measurement uncertainties than univariate fits are to be expected which is of great significance in the present field of memory measurements, and beyond.

10.7 Chapter Summary, Strengths and Future Recommendations

This chapter has focused on two elements to ensure understanding, measuring and quality-assuring constructs with examples of memory measurements; explicit methods for testing theories of the measurement mechanism and establishment of metrological standards; and substantive theories explaining the constructs themselves. We have demonstrated advancement in both those elements gained by adopting a measurement system approach, including modelling Man as a Measurement Instrument, exploring the principal components in explanatory variables for Construct Specification Equations (CSE) and introducing the concept of entropy as an explanatory variable.

Especially building on entropy, as described in thermodynamics and information theory, further enables more fit-for-purpose and valid memory measurements. The significance of a CSE for memory task difficulty in memory measurements is that it can facilitate establishing objective and scalable metrological units through the generation of certified reference ‘materials’ for traceability. Moreover, formulation of CSEs based on entropy for memory task difficulty in turn opens opportunities of formulating new, less onerous but more sensitive and representative tests largely by ‘cherry-picking the best’ items from existing batteries, such as exemplified with CBT and DST. Formulation of CSEs for person ability can be a means of providing diagnostic information to enhance clinical decisions and targeted interventions, although, there are probably additional components of variation (e.g., entropy-based measures of brain connectivity) not yet included in the CSE model to further improve the understanding what causes lower or higher memory ability.

Appendix: PCR Algorithms

The various terms on both sides of each PCR equation [section 1.4] were evaluated in this work using several modules (Table 10.3) of the program PTC^® MathCad^®, which is a high-level, matrix-based language with which text and illustrations can be combined with data handling (such as input/output), calculations and graphs in an active way. This has the advantage of providing immediate and explicit feedback when designing and formulating new programming routines as well as clear documentation for communicating with third parties and for future retrievable archiving.

Table 10.3 Mathematical expressions in PCR and corresponding PTC^® MathCad^® modules