Drop-Out Decisions in a Cohort of Italian Universities

Abstract

In this chapter, we study the determinants of student drop-out decisions using data on a cohort of over 230,000 students enrolled in the Italian university system. The empirical analysis reveals that the probability of dropping out of university negatively correlates with high school grades and student age, controlling for the course of study and university fixed effects. The benchmark estimation suggests a negative correlation between high school final grade and drop-out probability. We also find that enrolling late at the university increases the likelihood of dropping out. In line with the literature, our results suggest that women have a lower propensity to drop out. Our dataset allows differentiating between students who leave their homes to enroll at university (off-site students) and on-site students. We find that off-site students drop out significantly less than those who study in their hometowns. We provide significant evidence that off-site students are a self-selected sample of the total population. Accordingly, we use an instrumental variable (IV) approach to identify the causal relationship. The IV estimation shows that studying off-site negatively affects drop-out decisions and more so for students growing up in the south of Italy who typically study off-site in the Center-North of Italy. Taking advantage of a more detailed dataset concerning students enrolled at the Università di Sassari, we show that the choice of the degree is also important to predict the magnitude of drop-out. Specifically, we resort to a bivariate probit specification to account for self-selection into the course of study, finding that the estimates of the determinants of drop-out and the predicted probabilities are heavily affected. Accounting for self-selection, we show that an unconditional comparison among degrees is misleading, as some degrees attract more heterogeneous students than others, as far as skills and motivation are concerned. For instance, regarding the effect of gender, we show that while the estimation without selection suggests that women drop out less, once we account for selection, the contribution of women to drop-out becomes either positive or negative, depending on which course of study they choose. In line with these results, policymakers should tailor drop-out reducing policy interventions to the specificities of each course of study.

We wish to thank Bianca Biagi, Claudio Deiana, Claudio Detotto, Alessandra Faggian, Masood Gheasi, and Jacques Poot for their precious suggestions. We would like to acknowledge the participants to the workshops “Anvur: III concorso pubblico idee per la ricerca” (2019, Rome) and “International and Internal Migration: Challenges and Opportunities in Europe” (2020, L’Aquila). We thank for precious research assistance Paolo Deledda (UNISS). The authors gratefully acknowledge financial support by Regione Autonoma della Sardegna (Legge n. 7), Anvur, III Concorso Pubblico Idee di Ricerca (ANVUR) and Università degli studi di Sassari (bando una tantum ricerca 2019).

1 Introduction

There is robust evidence that more educated individuals earn higher salaries and enjoy higher employment rates, see OECD (2019). Empirical studies indicate a sizable effect, with an average increase in annual earnings of around 10% per additional year of education (see Card 2001). Nevertheless, in “[..] all developed countries the percentage of students dropping out of university or graduating beyond legal terms is very large [..],” see Aina et al. (2018), page 2. In general, delayed completion of studies reduces the average and the overall skill levels of the working population. Reducing drop-out rates could therefore have a positive impact on the skill composition of the workforce. In turn, this may trigger a positive feedback effect on the economy in terms of both efficiency and inequality. First of all, a more educated workforce would facilitate technological change and technology adoption, see Acemoglu (2002). Second, it could push down the wage skill premium, thereby reducing inequality, see Katz and Murphy (1992). Along with the USA, Italy is one of the OECD countries where the drop-out phenomenon reaches dramatic levels, with more than one student in two dropping out of university before completion, see Aina et al. (2018).

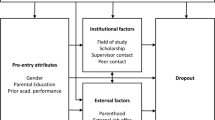
The focus of the chapter is the impact of studying off-site on drop-out behavior. We define off-site students as those who leave their homes to pursue higher education. Although Italian universities are evenly distributed across the national territory, a nonnegligible fraction of students enroll in universities located in a region or province different from residence.¹

We exploit the Anagrafe Nazionale Studenti (ANS), a dataset produced by the Ministero dell’ Università e della Ricerca (MUR), to study the determinants of the drop-out rate of undergraduates enrolled in Italian universities. The ANS collects information about all students who enrolled in the Italian university system. We rely on three years of data regarding undergraduate (i.e., bachelor) students who enrolled in the academic year 2013–2014. In particular, we study the correlation between drop-out rates and characteristics of students, courses, and universities. Regrettably, the ANS dataset does not provide specific information on the off-site status of the student. However, it provides precise information on the place of residence of the student. Linking this information with the university’s geographical location, we construct several indicators that work as proxy variables of the off-site status of the students. In our dataset, 22% of the individuals enrolled in universities located in a region different from that of their residential place. Similarly, 53.5% of the students study in a province different from their residence place. Italian inter-regional student mobility is probably eased by the homogeneous distribution of university fees across all public universities, see (Beine et al. 2020). Indeed, financial barriers to education access are quite low in Italy as poor students have access to a generous system of government grants (Checchi 2000).

Using the region of origin to define the off-site status, we estimate a reduction of the probability of dropping out associated with the off-site status of 1.62%. The results are also robust to other measures of the off-site status,² different estimation strategies, and when we cluster individuals by macro-area.

Our empirical analysis reveals that the probability of dropping out of university is negatively correlated with the high school grades and the age of the students. Our benchmark estimation suggests that one additional point in the high school final grade reduces the probability of dropping out by 4%.³ Furthermore, enrolling one year later at the university increases the probability of dropping out by 9.8%. Flunking out of high school is the main reason that explains late university enrollment in Italy.⁴ Consistently with the literature, our results also show that women have a lower probability of dropping out than men. Interestingly, our results suggest that men have a larger probability of drop-out, slightly less than 3 percent. In line with the literature, we find that individuals who attended a Liceum have a substantially lower probability of dropping out than their peers who attended vocational high school. Indeed, these estimates do not change in all variants that we consider and remain stable under our instrumental variable analysis.

Leaving home to pursue a university education may affect the educational outcomes in several ways. On the one hand, studying far from home requires additional efforts in organizing daily life, building new relationships, and so on. On the other hand, studying off-site requires more financial support, often provided by parents, that may motivate off-site students. Checchi (2000) and Contini and Zotti (2021) report that economic conditions greatly influence the likelihood of completing university studies.

It is widely known that there exist sizable differences between the North and the South of Italy, both in terms of wages and in terms of job opportunities. We interpret these findings in the light of Roy’s model of self-selection, see Borjas (1987), with Roy’s model predicting self-selection in the flow of migrants. We document that students from the South of Italy are more likely to enroll outside their home region or district than their peers from the country’s North. Moreover, southern students tend to move to a university located in the Center-North of Italy. In line with Roy’s model predictions, we show that the flow of students follows mostly the South-Center∖North direction and that very few northern students move to the South to pursue higher education. Besides, we document that off-site students’ skills are higher than the overall population in terms of high school grades. Also, students who attended a Liceum are overrepresented among off-site students. As postulated by the Roy model, evidence of self-selection is reinforced when we run separated estimates by macro-area of origin. For instance, for the northern students, we do not obtain a significant negative coefficient for the off-site proxies, and this can be partially explained by a lower strength of the selection channel for these students compared to what happens in the southern ones.

Our results are in line with Johnes and McNabb (2004), one of the few existing contributions that explicitly address the impact of the off-site status on drop-out rates. In particular, they find that the probability of dropping out is lower for students attending a university far from the one in their parental hometown. Similarly, Modena et al. (2018) report a negative correlation between drop-out rates and studying off-site.⁵

The above discussion leads us to the conclusion that addressing causality with OLS estimates is problematic for two reasons. First, our OLS significant negative coefficient for the off-site status proxies in our drop-out regression is potentially an artifact of sample selection bias. Second, off-site students go through a significant change in their daily life that, ceteris paribus, may affect their studies. We attempt to tackle this issue by resorting to an instrumental variable (IV) procedure which, taking advantage of a variable correlated with the decision of studying off-site but independent from the outcome (drop-out behavior), should allow isolating the effect of studying off-site on drop-out behavior, removing from the estimate the confounding effects mentioned above.

Technically, we instrument the off-site status proxy with the minimum distance from the closest university (our instrument), controlling for characteristics of the districts by fixed effects. Our IV estimates still uncover a negative relationship, with an impact larger in magnitude than the one suggested by the standard OLS procedure. We also implement the IV procedure by splitting our dataset according to the macro-origin of the students. Interestingly, for the subsample of southern students, the off-site status coefficient substantially increases in terms of magnitude while remaining statistically significant and negative. We suggest interpreting this result as evidence that going off-site eventually positively affects students’ motivation coming from more distressed districts. Indeed, aside from identification issues, the causal effect of studying off-site is potentially ambiguous. Studying off-site is more costly in terms of the organization of daily life and from an economic viewpoint. Extra financial support is therefore necessary, which is often provided by off-site students’ parents. The extra costs have two opposing effects. On the one hand, the fact that off-site faces a higher cost of studying compared to their peers who study in their hometown undermines the sustainability of the off-site choice, which induces higher drop-out rates. On the other hand, the extra costs might provide extra motivation to the off-site students, which would result in a lower drop-out rate. Accordingly, a negative and significant effect is compatible with the idea that the second effect dominates. Nevertheless, we are fully aware that uncovering robust causal relationships regarding the determinants of drop-out requires particular care due to the pervasiveness of self-selection and unobservables.

Self-selection bias relates to the fact that students choose where to study and which course to enroll in based on unobservable factors that can also affect drop-out. To investigate this issue, we take advantage of a more detailed dataset concerning 16 cohorts of students enrolled at the Università di Sassari. Specifically, we are interested in investigating whether the magnitude of drop-out is also affected by the choice of course of study. It is well known that students’ choice of which course to enroll in is influenced by factors such as the likelihood of finding a job after graduation or the popularity of certain studies among teenagers. This may cause a systematic mismatch between the student’s abilities and those required to complete a degree successfully. If this deviation were systematic, it would generate a higher level of drop-out in the courses affected by this phenomenon, not depending on the organization’s quality or teaching. Our results show that the estimated probability of drop-out in the five most popular departments, i.e., with an above-average enrolment rate, is always lower than that estimated without taking the selection mechanism into account. These results suggest that an unconditional comparison among degrees is misleading, as some degrees attract more heterogeneous students in terms of skills and motivation. The selection approach also shows that a univariate probit model’s estimated parameter without selection may be biased. There is abundant evidence that women drop out less than men. However, this finding may result from women being overrepresented in degrees where drop-out is below average. Once we account for selection, we find that the contribution of women to drop-out is either positive or negative, depending on the choice of the course of study.

The chapter is organized as follows. In Sect. 2, we describe our data and provide some stylized facts on drop-out rates. In Sect. 3, we outline our econometric approach. In Sect. 4, we present the OLS empirical estimates along with several robustness checks. In Sect. 5, we describe and implement the IV estimation procedure to tackle the causality issue. In a separate box, we present the synthesis of the analysis on the relationship between drop-out and choice of study course. Section 6 concludes.

2 Data and Variables

In the following, we describe our dataset and the definition of the variables employed in our empirical analysis. Then, we provide some descriptive evidence coming from our data.

2.1 Dataset

Our data from the ANS contain information about all population students enrolled in all Italian universities for the cohort of bachelor degree students enrolled in 2013–14 for the first time. We follow the students along with their academic career until the 21st of March 2018. Abstracting from PhD programs, which we do not deal with in this study, Italian universities offer three types of degrees: “Laurea triennale,” which is equivalent to a Bachelor degree, “Laurea specialistica,” which is equivalent to a 2-year Master degree, and “Laurea a ciclo unico,” which combines bachelor and master degrees.

We choose to exclude students enrolled in “Laurea specialistica” or “Laurea a ciclo unico,” because we lack information about the final grade they got in their previous careers as bachelor students. Moreover, we exclude international students, as they seem to be selected from a different population compared to national students and constitute a self-selected group so that drop-out mechanisms would probably be different from those that characterize domestic students. We also exclude students enrolled in online universities.⁶ Finally, the above choices lead to a dataset that contains information on 230, 336 students.

The next step is to provide a precise definition of university drop-out. First of all, notice that due to the peculiar characteristics of the Italian university system, differently from Johnes and McNabb (2004), we cannot differentiate between voluntarily and involuntarily drop-out. We proceed as follows. First, we classify students in four main categories: (A) students who successfully completed their degree by the 21st of March 2018, (B) students who were still enrolled by the 21st of March 2018, having not completed their degree yet, (C) students who changed course/university the year after the first year of enrollment, and (D) students who left the Italian university system.

We build a dummy variable D_i,j,c,t which takes value 1 if a student i enrolled in course c at university j drops out at time t and 0 otherwise. Concerning the measurement of the student’s off-site status, unfortunately, our dataset does not contain direct information on whether the student is actually off-site or not. Hence, to capture the off-site status, we combine information on both the place of residence of the student and university location. We use this information to construct the following three alternative discrete proxies of the off-site status:

• 1. OD (out of district): This variable takes value 1 if the student enrolls in a university located outside her home district. Notice that for a sizable percentage of students, this variable always takes value 1 given that 52 out of the 110 Italian districts do not host any university.

• 2. OR (out of region): This variable takes value 1 when the student i enrolls in a university located outside the home region. Each Italian region hosts at least one university. Therefore the value of this variable is not prearranged as it is the case for the OD variable for a sizable fraction of districts.

• 3. OFF_km: This variable takes value 1 when the student i enrolls in a university located further away than a threshold distance from the student’s home. We take advantage of the ANS information on students’ home residence for all students enrolled in any given university j. Then, after having obtained geographic coordinates for university j, we compute travel distance, between the university j and the home of student i.⁷ This measure rules out the cases of students whose house is close to the regional border who enroll outside the region without changing residence. To deal with this shortcoming, we consider two thresholds, 150 km and 200 km, that give rise to two indicators, OFF₁₅₀ and OFF₂₀₀.

In addition, to capture the off-site status of the student, we also construct two continuous variables. We consider both the travel and geodesic distances between the university j and the home student i.

2.2 Descriptive Statistics

Due to missing values in some variables, we end up with a dataset containing information on 226, 094 individuals, representing the 98% of the population of students we initially included. We find that 38.40% of the students completed their degree by the 21st of March 2018, the 17.8% of the student changed course/university, the 38.3% completed higher education, and finally the 12.9% left the university system. We define this last set of students as the droppers. Students enroll in 708 different courses, which belong to 46 different classes, clustered in the four general subject areas: (1) Health, (2) Science, (3) Social Science, and (4) Humanities. Science is the area with more students, representing 38.4% of the sample. Interestingly, slightly more than the majority of students are enrolled either in Humanities or in Social Science. Regarding gender, 54.2% of students are female, while men mainly enroll in Science and only 2.5% enroll in Health. We find that the percentage of women who leave the university, 14.8%, is lower than that of men, 11.2%. Our data show a significant difference in the percentage of drop-outs across the areas of study. While drop-outs are equal only to 5.3% in the Health∖Medical area, they reach the sizable figure of 15.1% in Humanities. To account for these patterns, we include fixed effects for the area of study in our empirical estimations. Men leave graduate studies more compared to women in any of the four areas of study. For instance, although women are underrepresented in the area of Science, the percentage of men who drop out is substantially larger than that of women. Accordingly, in our estimation, we include a dummy variable that captures the students’ gender. Another finding is that drop-out rates are much larger for students from vocational high schools; this holds for all areas. Students coming from a Liceum show a drop-out rate that is 10% lower. Conversely, students from vocational schools show a much larger drop-out rate, which reaches 21% for the Science area.

One may expect individuals with a low high school grade are overrepresented among the droppers, leading us to include a continuous variable capturing the students’ high school grades among the drop-out determinants.

Besides, we find that the drop-out rates exhibit significant variation across the home regions of the individuals. To account for this heterogeneity, fixed effects for the district and region of origin of the student are included in our econometric specification.

The percentage of students studying off-site is unevenly distributed across Italian districts. Measuring off-site students through the variable OFF₁₅₀, we find that off-site students reach the sizable figure of 33% among the students who come from the South. Instead, for those both coming from the Center and the North of Italy, the percentages are much lower and amount to 16% and 17%, respectively. Figure 1 confirms that most of the off-site students move from South Italy to study in the North. Very few individuals (only 128) move from the North to the South. We count 23,084 students from the South and enroll in universities located either in the Center or in the North of Italy. Also, we document that internal mobility of students⁸ is sizable in the Center∖North of Italy and modest in the South.⁹

Fig. 1

Migration Corridors: number of students enrolled out of region by Macro-Regions—North, Center, and South

The variables that we use for our estimation are:

• G_i, which is a dummy variable that takes value 1 if the gender of student i is male and 0 otherwise.

• HT_i is a dummy variable that takes value 1 if the high school attended by the student is a Liceum and 0 otherwise.

• HG_i is the high school grade rescaled, see Table A.1. It is a discrete variable that measures the high school grade, which takes values in the interval $\left [0\: 41\right ]$. A student enrolled in an Italian high school needs to achieve a minimum final grade of 60∕100 in order to graduate.¹⁰

• $AGE_{i}=-1\left (Yearfofbirth-1995\right )$, which is a variable aimed at capturing late enrollment at the university. Late enrollment can be the result either of grade repetition in the high school or general late enrollment. Most of the Italian students end high school at the age of nineteen. However, some may start university earlier, given the possibility to anticipate entrance at the primary school.

According to Rosenzweig et al. (2006), two main reasons explain why students move elsewhere to complete higher education.¹¹ First, individuals move elsewhere due to the lack of higher education institutions in their home region. However, this does not apply to Italy, given that universities are evenly distributed within the country’s territory. At the same time, we may expect that the percentage of off-site students is larger in better universities, as there is substantial evidence that university quality is a key pull factor of student mobility (Beine et al. 2020). Moreover, Italian universities with the best rankings are located in the Center-North of Italy. The second model explains student migration with individuals intending to move to areas where skilled labor is better paid. This model fits better the Italian experience where many individuals leave the South to join universities located in most of the Center-North area in Italy, which provides better working opportunities after graduation. We also check whether drop-out rates are different, conditioning for the area of the primary area of study, concerning the off-site status (defined here by the dummy variable OR). Except the area of Health,¹² where the percentage of droppers is only slightly lower among off-site students (5.4 for off-site and 5.1 for on-site), for the other areas, the average drop-out rate of off-site students is always considerably lower. In the area of Science, the average drop-out rate is equal to 9.6% among on-site students while equal to 12.6 among on-site students. In Social Science, the percentage of droppers is equal to 9.9 among off-site students, while among on-site students it is equal to 15.6. Finally, in Humanities, the percentage of droppers is equal to 11.5 among off-site students and is substantially larger among on-site students (16%).

Descriptive statistics seem to suggest that off-site students are a self-selected sub-population. Additional support to this hypothesis is obtained by computing the difference in means and computing the t-test. Similar results obtain if we define off-site students either using the indicator OR or using the indicator OFF₁₅₀. For instance, HG takes a mean value equal to 20.60 among students for which the variable OFF₁₅₀ takes value 1. On the contrary, among on-site students, the value is substantially lower equal to 18.08. The difference in means highlights that among off-site students, the fraction of students who attended a Liceum high school is larger than for other types of high school, and the same pattern holds when we consider the age of the students with off-site students being on average younger. We also find that the percentage of female students is slightly larger among off-site students, which holds for all the indicators that we employ. This preliminary analysis suggests interpreting with extreme caution analysis to uncover a causal link between off-site status and drop-out behavior.

3 Empirical Analysis

The existing literature provides evidence that the characteristics of universities, the field of study, and the social and economic conditions of the students’ home districts are correlated with drop-out rates.¹³ Within this literature, we aim to document the relationship between distance, namely studying off-site, and drop-out rates in the case of Italian students. In order to do so, in this section, we discuss the results of our benchmark estimations complemented with several robustness checks. Then, we address the causality issues due to self-selection and omitted variables using an instrumental variable approach.

To uncover this relation, we set up the following empirical specification:

$$\displaystyle \begin{aligned} D_{i,u,o,f,c}& =\alpha+\mathrm{A}_{u}+\mathrm{A}_{f}+ \mathrm{A}_{o}+\beta_{1}G_{i}+\beta_{2}AGE_{i}+\beta_{3}HT_{i}\notag\\ &\quad +\beta_{4}HG_{i}+\beta_{5}OffSite_{i,t}+\varepsilon_{i}, \end{aligned} $$

(1)

where ε_i is the error term, and we recall that D_i,u,o,f,c, is the dummy variable that captures the drop-out decision of student, i, coming from the place of origin, o, enrolled in university, u, the field of study, f, and course c. The variables on the RHS of Eq. 1 include gender, G_i, age, AGE_i, type of high school, HT_i, and high school grade, HG_i, which were already defined.

• A_u, which is a set of fixed effects that we include to control for differences in university characteristics.

• A_f, which is a set of fixed effects we include to control for the different fields of study.

• A_o, which is a set of fixed effects controlling for all factors specific to the home districts of students. With fixed effects, we also aim to capture differences in high school education quality among Italian districts.

• OffSite_i, which is the measure of the off-site status of students. We code this variable, the focus of our analysis, in different ways:

  • 1. OD, which takes value 1 if the student enrolls in a university located outside the home district, and zero otherwise.

  • 2. OR, which takes value 1 when the student enrolls in a university located outside the home region, and zero otherwise.

  • 3. OFF_km, which takes value 1 when the student enrolls in a university located more than km away from her home, and zero otherwise. We consider two thresholds: 150km and 200km.

  • 4. TD, the travel distance between the university and the student’s place of residence measured in hundreds of km. We also employed GD, which is the geodesic distance between the university and the student’s place of residence. One unit is equal to 100 km, results are quite similar, and we do not report the ones obtained using the latter.

A detailed table, see appendix at the end of the chapter, provides a brief description detailing definition, data source, and remarks for all the variables employed in our analysis. According to the above description, specification 1 controls for university, district of origin, and field of studies characteristics through fixed effects, as well as for other individual characteristics, for which the ANS dataset provides information including, gender, the final high school grade, the age of the individual, and the type of the high school attended.¹⁴ We note that a limitation of the ANS dataset is the lack of information on both family income and parental background.¹⁵ Also, we lack unambiguous information on the amount of tuition fees charged to each student.¹⁶

We obtain our baseline estimates of Eq. 1 through an OLS estimation procedure. Several reasons lead us to stick with the LPM (Linear Probability Model) as a baseline. Among others, Angrist and Pischke (2009) advocate the use of the LPM. Nonlinear estimation methods may provide an efficiency gain, but at the cost to commit to a precise distributional assumption of the error term and, notably, Probit and Logit average marginal effect estimates, quite often, do not differ much from LPM estimates and the interpretation of the regression coefficients is much more straightforward with the LPM.¹⁷ Also, we evaluate the robustness of our findings to selection employing the method developed in Oster (2019). Finally, to tackle the endogeneity of our variable capturing the off-site status, we complement our estimation results by means of an IV procedure.

4 Results

In what follows, we present and discuss the empirical estimates of the benchmark model described by Eq. 1. We consider all different measures of studying off-site.

Columns 1–3 of Table 1 report the estimation results when we use the dummy variables OD and OR to measure the off-site status of the students.¹⁸ The drop-out rates are negatively correlated with the high school grade, with the age of the student, with being a woman, and with a diploma from a Liceum. Interpreting our coefficient estimates as marginal effects, we find that, ceteris paribus, one additional point in the high school grade reduces the probability of dropping out by 0.4%. Being graduated in a Liceum is correlated with a reduction of drop-out by 10%. Concerning the correlation between drop-out and being an off-site student, we find a significant negative sign. When we employ OD, we find that the off-site status is associated with a 1.25% reduction of the probability of dropping out. When we proxy the off-site status with the dummy OR, the estimated correlation becomes stronger neither the sign nor the magnitude of any of the other coefficients changes across the two specifications. A comparison of columns (1)–(3) of Table 1 shows that our estimates are robust to different measurements of the off-site status.

Table 1 Determinants of drop-out rates. Benchmark (1)

As pointed out in the introduction, for many students, the home district does not host any university, so that the only option is to leave the district to pursue a university education. Specifically, this implies that for students coming from 52 out of the 110 Italian districts, the dummy, OD, always takes one as value. In that respect, OR, which is based on regions, provides a more conservative definition of the off-site status. Still, both OR and OD might not be meaningful measures of the off-site status for various reasons. For instance, using either OR or OD, we might end up classifying them as off-site students who enroll in universities that, while located in a different district or region, might be geographically very close to their home location close enough to allow for daily commuting. Therefore, we also consider alternative measures of the off-site status based on travel and geodesic distance between the student’s home and the student’s university. Specifically, in columns 4 and 5 of Table 1, the dummy variables OD and OR are replaced with the continuous variable TD, respectively, where TD is the travel distance.¹⁹ Column 4 of Table 1 suggests that a 100 km increase in the average travel distance is associated with a 0.3% reduction in the probability of drop-out. In Column (5) of Table 1, we also report the results for a regression model that include the square of distance. Including this variable, we test the hypothesis of a nonlinear relationship, and we find that the marginal effect of distance diminishes with the distance. Finally, we also report the results we obtain measuring the off-site status with the dummy variable OFF_km. We consider two specifications of this indicator: OFF₁₅₀ and OFF₂₀₀. Notice that OFF₁₅₀ and OFF₂₀₀ take value equal to 1 if the student is enrolled in a university more than 150 and 200 km distant from her home, respectively. Table 2 reports the empirical estimates obtained using these two measures of studying off-site.

Table 2 Determinants of drop-out rates. Benchmark (2)

Two results stand out from Table 2. First, the magnitude of the coefficients capturing the off-site status is strikingly close to the one delivered by the empirical estimate of OR, see Table 1. Also, we notice that the magnitude of the coefficient OFF₂₀₀ is smaller than the one of OFF₁₅₀.

To summarize, all our measures of studying off-site confirm a strong negative and significant correlation between the drop-out decision and off-site status. The estimates of the other variables of interest are in line with the findings in the literature. Women show a lower propensity to drop out. Also, there is evidence that older individuals tend to leave university more frequently and that the high school grade negatively correlates with drop-out rates, with students that earned a better high school grade eventually dropping out less.²⁰ Finally, students who attend a Liceum tend to drop less than students coming from the vocational schools.

Our findings concerning the off-site status can be questioned on several grounds. First, we evaluate whether the correlations reported in Tables 1 and 2 remain stable independently of the home macro-area of the off-site students. Accordingly, we run regressions clustering students depending on their home macro-area. We consider three macro-areas: North, Center, and South of Italy. To capture the off-site status, we use two indicators: OFF₁₅₀ and OR. Table 3 shows that the magnitude of our proxy varies substantially once we consider regressions by macro-area.

Table 3 Determinants of drop-out rates: estimates by macro-area

The use of OR or OFF yields almost identical results. Interestingly, the off-site status of the students is not significantly associated with drop-out when we run the regressions considering only students from the North of Italy. Also, it is important to notice that the magnitude of the HG coefficient is larger, in absolute value, for the sub-population of students from the South. Remarkably, the coefficient of HG is almost identical when we run regressions separately for Center and Northern students.

Several reasons may explain the lack of significance of both OR and OFF coefficients for the sample of North students. One for all, the vast majority of off-site students from the North opt to enroll in a university still located in the North and therefore at a short distance from the student’s home. Maybe distance from home is so short that it does not affect students’ life in a particular way, and therefore it does not affect their performance.

Also, the literature often estimates drop-out determinants through nonlinear models.²¹ As a robustness,²² we compute the marginal effects by estimating a Logit specification of Eq. 1. We find that the estimated marginal effects do not change significantly when we employ a Logit specification in place of our benchmark LPM. In line with previous results, we obtain negative and significant coefficients for our measures of off-site status. In the introduction, we highlighted how the possibility of self-selection and omitted variables induce particular caution in interpreting our results; thus, this analysis does not allow interpreting the partial correlation between off-site status and drop-out as evidence of a causal relationship.

To evaluate the role of selection on unobservables, we employ the procedure outlined in Oster (2019). Two reasons may explain the negative correlation between off-site status and drop-out rates: (1) selection, the best and the brightest leave their hometown to get higher education and (2) omitted variable bias, our off-site indicators are absorbing the role of omitted variables, such as family income. The method outlined in Oster (2019) assumes that the relationship between observables and the treatment is informative of the relationship between treatment and unobservables. Therefore, we assume that HG, HT, and AGE are similarly related with the treatment, the off-site status, as the observable. More clearly, in our estimation, the unobservable includes parents’ education, family income, and unobserved ability.²³ The implementation of the Oster (2019) method confirms previous results, suggesting that the off-site status affects drop-out behavior. If selection on unobservables has the same strength as the selection of observables, our estimate of the off-site status coefficient is only slightly reduced. Selection on unobservables should be at least five times stronger than selection on observables to make the relationship between the off-site status and the drop-out behavior negligible.

5 Causality: Instrumental Variable Approach

The descriptive evidence previously discussed suggests that off-site students’ sub-population is a self-selected group with systematic characteristics different from the overall population. Due to the possibility of self-selection and omitted variables, interpreting the evidence from the regression models already presented is problematic.

In other words, the evidence of a strong negative correlation between drop-out rates and off-site status does not legitimate us to conclude anything about the causality direction of that relationship due to both unobservables and self-selection.

Notably, the decision to study far from home implies sunk costs, both monetary and non, which, see Checchi (2000), affect students’ effort. Off-site students leave back home both family and friends, need to get used to the new city social norms and, last but not least, a substantial monetary investment is required (think about rent of the room/apartment, transportation cost). These costs are likely to be positively correlated with distance. As Checchi (2000) shows, students’ effort is sensitive to monetary costs in general, and those studying off-site may exert more effort in their studies because in the event of dropping out, the sunk cost is higher compared to the ones faced by on-site students. Also, Garibaldi et al. (2012) show that an increase in tuition fees reduces late graduation providing evidence that students’ effort depends on investments incurred.²⁴ Besides, among off-site students, there may be heterogeneity concerning the sunk cost. We may have type 1 students, with higher ability and motivation, who choose to study off-site to enroll in a better university, and type 2 students, from high-income households, who may choose to study off-site merely because they can afford it, although equipped with average (or below average) motivation and ability. For type 1 students, the decision to study off-site is driven by motivation. For type 2 students, it is driven by family wealth. It is evident that both motivation and wealth are negatively correlated to drop-out. As motivation and family income fell in the unobservable component in specification 1, we are not able to say whether the negative correlation between drop-out rates and offsite status is fostered by the link between higher costs and motivation or between higher costs and family wealth or by both.

The above discussion suggests the need of an appropriate estimation strategy to address the bias that self-selection along with omitted variables generates.²⁵ Following Card (1993), we exploit information on the distance from the closest university to construct an instrument for the off-site status. For each student, we determine the distance from her place of residence to the closest university. Taking advantage of this information, we identify two possible instruments:²⁶

• 1. The distance from the closest university, which we label minD

• 2. A dummy variable that we set equal to one if the closest university is distant more than 20 km from the student’s place of residence.²⁷ We label this instrument dD.

We acknowledge that there are some arguments that question the validity of our instrument, similar to the one mentioned in Card (1993) and Card (2001).²⁸ First, we collect some evidence on the validity of the exclusion restriction. Subsequently, we present and discuss our IV estimates.

5.1 Exclusion Restriction and Reduced Form

Our model is just identified, thus preventing us from performing the Sargan–Hansen to check whether the correlation among the error term and the instrument are statistically not different from zero. Despite the impossibility of performing the overid test, we can check how minD correlates with the other drop-out determinants to evaluate the exclusion restriction assumption. A good instrument should not be correlated with strong determinants of the dependent variable. Our instrument minD is almost uncorrelated with the determinants of the drop-out rate previously discussed (HT, HG, and Age). Also, we check for the reduced-form estimates. We compute such regressions for both our instruments, minD and dD. Our reduced-form estimates are both negative and slightly statistically significant.

5.2 IV: Results

Table 4 reports our empirical estimates, where we instrumented the measures of off-site status.

Table 4 IV estimates (1)—drop-out decision: instrumented indicators: OR, TD and OFF_km

Table 4 reports our empirical estimates, where we instrumented the measures of off-site status. First-stage estimates confirm that our instruments are strong.²⁹ Column (1) instruments the dummy variable OR with the instrument dD. Notice that the sign of the OR coefficient is still negative and significant and increases in magnitude compared to the OLS estimation with no instrumental variables.

Significantly, the standard errors increase, a typical consequence of the IV procedure. Column (2) reports similar findings. Here, we instrument OR with the actual minimum distance, minD. Column (3) and column (4) report results when we employ the variable TD as a proxy of the off-site status. Notice that the magnitude and the sign of all the other control variables stay almost unchanged as we vary either the instrument or the variable measuring the off-site status. In conclusion, we notice that the coefficients on distance lose statistical significance for all cases, which may be due to the lower precision implied by IV estimation. To check whether it is sensible to run the IV procedure, we report the Wu–Hausman test. The null hypothesis is that both estimators, OLS and IV, are consistent. We do not obtain strong evidence for the non-consistency of the OLS estimates. However, even if we fail to reject the null hypothesis, the test does not allow us to claim that the OLS estimates are consistent. Hence, such values of the WU–Hausman test do not invalidate our IV estimates. Indeed, this situation is typical when the standard error of the IV estimator is large as it is for Table 4 estimates. In Columns (5) and (6), we use as a proxy of the off-site status the variable OFF₁₅₀, while columns (7) and (8) employ OFF₂₀₀. Notice that the results reported in Table 4 slightly change depending on the indicator used.

The exclusion restriction of our IV might be questioned on several grounds. Our estimations control for several drop-out determinants, the high school grade, the type of the high school attended, age, and gender. However, we already acknowledge that we lack information on some determinants such as family income. Furthermore, it may be that households that give more weight to education have a larger propensity to live closer to a university.

We resort to the method proposed by Conley et al. (2012) to account for possible deviations from the exclusion restriction. This method allows considering the parameter capturing the exclusion restriction (the IV’s coefficient in the structural equation) as a random parameter drawn from a given distribution. Also, the method allows considering asymmetric deviations from the exclusion restriction. We employ the method labeled Union of Confidence Intervals taking advantage of the STATA routine developed in Clarke and Matta (2018). We conducted this robustness with the instrument dD employing as an indicator of the off-site status the dummy variable OFF₁₅₀. As long as the interval is sufficiently tiny, our estimates remain statistically significant, and the coefficient’s magnitude is only slightly affected.³⁰ Once we consider wider intervals for the parameter capturing the exclusion restriction, our estimates lose statistical significance. Furthermore, this procedure allows for assessing the instrument’s validity when the degree of the over-identification is not positive.

Our previous findings suggest that the impact of the off-site status on drop-out rates is much stronger among students coming from the South. In Table 5, we report IV estimation clustering individuals along the home macro-areas. We employ the variable OFF₁₅₀ as a proxy of the off-site status, which we instrument using minD. Column (1) considers only students from the South. It reports a highly significant and negative estimate for the off-site measure, OFF₁₅₀. This suggests that, once we account for the selection effect, for a southern student, going off-site has a considerable impact on the decision of not leaving the university. Interestingly, this does not happen to be the case for students originating from the Center and the North of Italy, for whom we do not find any significant impact of the off-site status on the decision to drop out. Our results are in line with the model and empirical findings of Checchi (2000). Students moving from the South to the North face larger sunk cost. Large sunk cost appears to have eventually a positive effect in the decision to not drop out. Similar evidence is not obtained once we consider separately students originating either from the Center or from the North. Most of them attend universities located in the same area, and therefore they face lower sunk cost and, as our estimate suggest, the positive effect on the drop-out decision eventually does not materialize.

Table 5 IV estimates, by macro-area (3)

So far, our interpretation of our IV estimates builds on the basic homogeneous treatment effect framework. However, in the more general case of heterogeneous treatment effects, the IV estimates only capture the LATE, local average treatment effect, the impact of studying off-site on the sub-population of compliers. In our case, compliers are individuals who enrolled in an off-site university because there was no university close to their place of residence. Notice that our IV estimates are substantially larger than the OLS ones. However, one may argue that after taking into account endogeneity issues, we should uncover, at least, an estimate with a lower magnitude. In our benchmark estimations, the off-site status was absorbing the impact of variables negatively correlated with our outcome variable (i.e., parents’ income, individuals’ ability). The same counterintuitive effect materializes in Card (1993); the impact of education on wages gets larger once endogeneity issues are tackled. However, it is legitimate to expect a larger effect of the off-site status on the outcome with a heterogeneous treatment effect. Compliers should come, on average, from families with a lower average income than the rest of off-site students. Ceteris paribus, families with low income, incur a relative higher education cost, leading off-site students to think twice before dropping university and putting more effort into their studies. Notably, this interpretation accounts for the substantial difference obtained once we separate estimations clustering individuals by macro-area of origin.

BOX: Course Heterogeneity, Selection Bias, and Drop-Out

As widely discussed, dropping out of university has a course- and student-specific causes. The former include those typical for each degree, which may require a relatively different level of effort. Student-specific causes include, for example, the student’s own abilities, the financial viability of those who finance the studies, and the impact on the effort that studying off-site may generate. Moreover, drop-out can be largely influenced by the mismatch between the student’s abilities and his/her most suitable degree. For these mismatches to have a significant effect, they have to be systematic. A possible explanation for why students may systematically make such misjudgments about the adequacy of their abilities with the skills and knowledge required by a degree is, for instance, that some degrees offer more job opportunities and that students may follow a herding behavior. If such students target more frequently some type of degree than others, then the mismatch between skills and motivation affects the target degrees more than the others. Among the target degree, the drop-out rate may result exceptionally higher due to the negative self-selection effect.

We use the sample selection approach to account for the correlation between unobserved heterogeneity in the enrolment decision (selection) and unexplained factors driving drop-out (outcome). We rely on 16 cohorts of students from the Università di Sassari enrolled in degrees supplied by ten departments to investigate this aspect. The cohorts allow monitoring students enrolled in the same year to determine who drops out from the Università di Sassari. Considering one university, a student leaving the degree between the first and the second year is a drop-out, although we cannot exclude that droppers enroll to other universities. Since we do not have any direct measure of popularity of departments, we label as popular the departments with relatively more students, as they attract an above-average number of students. The observations in each cohort are merged into a single pool of 57,974 observations. We choose the ten departments as the observation unit, and we use this criterion to cluster the data.

Across the 16 cohorts, five departments (Architecture, Agricultural Science, Biomedical Science, Chemistry, Pharmacy, and Veterinary Medicine) have an enrolment rate below the university average (10%). Architecture and Veterinary Medicine are one standard deviation below the average enrolment rate, while Agricultural Science, Biomedical Science, Chemistry, and Pharmacy are close to the university mean. The other five departments (Economics, History, Humanities, Law, and Medical Science) have an enrolment rate above average. Law and History are one standard deviation above the mean.

We hypothesize that drop-out is affected by the mismatch between student ability and motivation and those required in each degree. Popular degrees, with an above-average number of students, may attract relatively more individuals with low motivation. As motivation is unobservable, this determines a negative self-selection effect because in these degrees, less motivated students are overrepresented.

We estimate the probability of drop-out, i.e., to leave a degree course between the first and the second year of enrolment, by estimating Eq. 2, where the variable drop_i is a dummy variable that takes value 1 for droppers.

$$\displaystyle \begin{aligned} drop_i & =\beta_1 (final\; high\; school\; grade)_i+ \beta_2 (ECTS\; credits)_i\notag\\ &\quad +\beta_3 (exempted\; from\; tuition)_i \notag\\ &\quad +\beta_{4} (years\; from\; college\; graduation\; to\; university\; enrollment)_i\notag\\ &\quad +\beta_{5} (tuition\; fees)_i\notag\\ &\quad +\beta_{6}(lyceum)_i +\beta_{7}(technical\; vocational\; high\; school)_i\notag\\ & \quad +\beta_{8}(training\; high\; school)_i+\beta_{9}(woman)_i\notag\\ &\quad + \beta_{10-35}(cohorts\; fixed\; effects)_i+\epsilon_i\end{aligned} $$

(2)

After estimating Eq. 2 we compute the marginal predicted probability of drop-out for the whole university sample and separately for each of the ten departments. In each cohort, we average the individual marginal probability to obtain a mean by cohorts and departments. We compare these probabilities with the average marginal predicted probabilities of drop-out obtained estimating the following bivariate probit with selection defined by Eqs. 3 and 4. Equation 3 is the selection equation (choice of the department), while Eq. 4 is the drop-out equation.

$$\displaystyle \begin{aligned} &department^{k}_{i} \notag\\ &\quad = \alpha_1 (final\; high\; school\; grade)_i + \alpha_2 (beneficiary\; of\; scholarship)_i\notag\\ &\qquad + \alpha_3 (enrolled\; first\; time)_i\notag\\ &\qquad + \alpha_4 (years\; from\; college\; graduation\; to\; university\; enrollment)_i\notag\\ &\qquad + \alpha_5 (year\; of\; birth)_i+ \alpha_6 (woman)_i + \alpha_7 (lyceum)_i\notag\\ &\qquad + \alpha_8 (technical\; vocational\; high\; school)_i\kern-1pt+\kern-1pt\alpha_9 (training\; high\; school)_i\notag\\ &\qquad + \alpha_{10}( number\; of\; enrollments)_i + \alpha_{11}(tuition\; fees)_i+\epsilon_{1, i},\end{aligned} $$

(3)

$$\displaystyle \begin{aligned} drop^{k}_j& =\gamma_1 (final\; high\; school\; grade)_j+ \gamma_2 (ECTS\; credits)_j\notag\\ &\quad +\gamma_3 (exempted\; from\; tuition)_j \notag\\ &\quad +\gamma_{4} (years\; from\; college\; graduation\; to\; university\; enrollment)_j\notag\\ &\quad +\gamma_{5} (tuition\; fees)_j\notag\\ &\quad +\beta_{6}(lyceum)_j +\beta_{7}(technical\; vocational\; high\; school)_j\notag\\ &\quad +\gamma_{8}(training\; high\; school)_j+ \gamma_{9-34}(cohorts\; fixed\; effects)_j+\epsilon_i. \end{aligned} $$

(4)

The model is estimated employing maximum likelihood.³¹ The outcome Eq. 4 is estimated for all the k = 1, …, 10 departments. The estimation results for each of the ten departments (not reported) show that, once we account for selection, the average marginal predicted probability of drop-out in the five departments with above-average enrolment rate is systematically below the one computed employing the standard probit. For the least popular departments, Architecture, and Veterinary Medicine, results are as expected, i.e., that predicted probability considering selection is way above the one resulting from the standard probit. Biomedical Science, Chemistry and Pharmacy, and Agricultural Science (see Fig. 2 in the Appendix), which have an enrolment rate close to the university average, follow a pattern similar to the popular departments.

Fig. 2

Predicted probabilities of drop-out by departments

Remarkably, predicted probabilities with and without selection tend to be similar for Medical Science. Note that this is the only department during the sample period in which students have to pass a national-based test to enroll. It seems that the selection process prevents students with below-average motivation and skills from enrolling in this department.

The selection of the degree may also affect the magnitude, significance, and sign of estimated parameters. In some cases, it helps to uncover effects that are confounded because one variable may positively affect the department’s selection and negatively the drop-out, or vice versa. This is particularly interesting for the case of gender. In our estimation, the parameter of the dummy woman (α₉ in Eq. 2) is negative and significant for the whole sample and for all departments but Architecture (positive but not significant). We cannot say that this result depends on the fact women choose more likely departments with lower drop-out rates or that women are better students, thereby reducing drop-out when they are numerous. Descriptive statistics do not suggest a clear-cut. Indeed, women are relatively underrepresented in the department where drop-out rate is higher (Economics and Law), but they are also overrepresented in departments where drop-out rate is still high (History and Humanities). We cannot say whether is drop-out that causes the gender mix in a department or the opposite. However, we can compute the marginal contribution of a gender on the selection and that of the selection on drop-out.

Selection estimation is used to compute the marginal contribution on drop-out of an additional woman who decides to enroll in a department. To this purpose, we compute the marginal effect for the dummy woman on the conditional probability of drop-out. The change in conditional probability due to women is the change of the ratio between the joint probability and the marginal probability due to a discrete change of the dummy woman included in the selection equation:

$$\displaystyle \begin{aligned} \frac{\partial Prob(drop_k=1| k=1)}{\partial woman}=\frac{\partial [Prob(drop_k=1,k=1)/Prob(k=1)]}{\partial woman} \end{aligned} $$

(5)

for all k = 1, …, 10 departments.

Note that we include the dummy woman in the selection equation only. A positive sign of the dummy woman means positive selection and positive effect on the marginal probability of choosing department k, the denominator of conditional probability. If we obtain a positive marginal effect on the conditional probability of drop-out, the joint probability is positive, i.e., women contribute positively to the joint event drop-out and department k selected. We interpret this as a positive contribution of women to the probability of drop-out in that department. A negative marginal effect on the conditional probability suggests the opposite.

In case of negative selection, results are reversed. A positive marginal effect on the conditional probability of drop-out means that the joint probability is negative. On the contrary, a negative marginal effect on the conditional probability means women contribute positively to the joint event.

We classify the above results as follows. For the cases of positive selection:

• i. $\frac {\partial Prob(drop_k=1| k=1)}{\partial woman}>0$, more women, more drop-out

• ii. $\frac {\partial Prob(drop_k=1| k=1)}{\partial woman}<0$, more women, less drop-out

for the cases of negative selection

• iii. $\frac {\partial Prob(drop_k=1| k=1)}{\partial woman}>0$, less women, less drop-out

• iv. $\frac {\partial Prob(drop_k=1| k=1)}{\partial woman}<0$, less women, more drop-out

selection:

Our dataset has 6 departments with positive selection (Humanities, History, Veterinary Medicine, Medical Science, Biomedical Science, Chemistry, and Pharmacy). In Veterinary Medicine, the marginal probability and the conditional of drop-out for women are not significant. Medical science is an example of case i. Although the dummy woman is not significant in the single probit, we uncover a positive contribution of women on drop-out. The other five departments fall in case ii., excluding Chemistry and Pharmacy, for which the dummy woman is not significant in the selection equation.

The remaining four departments (Economics, Agricultural Science, Law, and Architecture) exhibit a negative selection. The first three fall in case iii., while Architecture is an example of case iv., although in the single probit, the dummy woman is not significant.

We conclude that women contribute to increasing the drop-out rate in Medical Science and Architecture, although both marginal effects are very small. On the contrary, women reduce drop-out rates in Humanities, History, Economics, Agricultural Science, Biomedical Science, and Law. There is no evidence of any contribution to drop-out of women in Veterinary science, Chemistry, and Pharmacy.

6 Conclusions

In this chapter, we investigated the determinants of the drop-out decision in the population of students enrolled at the public university system in Italy. We document that off-site students, who left home to pursue university, are a self-selected population for various characteristics that are candidate determinants of the drop-out decision. Then, we show a robust and strong negative correlation between the likelihood of dropping out of university and the off-site status of students. To go beyond correlation and assess the causal link between the off-site status and the decision to drop out, we employ an instrumental variable approach. The estimates provide strong evidence that off-site status reduces the likelihood of dropping out among southern students, who typically study in universities in the Center-North of Italy. The negative effect is still present considering the whole population of students, although lower in magnitude and barely significant. Our findings have relevant policy implications.

First, due to the documented sizable self-selection, our estimates suggest that it is not fair to rank university quality through a naive comparison of drop-out rates. We produce abundant evidence that a significant fraction of the best southern students moves to complete higher education at institutions located in the Center-North of Italy. On the contrary, the flow of students from the Center-North to the south is negligible. Our empirical results suggest that self-selection among off-site status explains part of the sizable difference in drop-out rates between northern and southern institutions. Second, our result suggests that universities aiming to improve the quality of their students’ pool shall set policies to attract off-site students.

We address whether there is any causal relationship between off-site status and drop-out behavior. We conduct our analysis taking advantage of the instrumental variable approach. We employ as an instrument of our off-site indicators variables capturing the proximity from the closest university. Our results show that, especially for off-site students originating from the south, there is substantial evidence that going off-site reduces the likelihood of dropping out of university. In line with Checchi (2000) we argue that studying off-site by requiring substantial investments (not only monetary ones), eventually positively impact the students’ effort.

However, we are aware of some shortcomings of our IV approach. Although our sample is large, our IV estimates provide strong evidence for an effect of the off-site status on drop-out rates only for the subset of southern students. To conclude, we acknowledge the limitation of our IV exercise, calling for further research to determine better both the magnitude and significance of the relationship between off-site and drop-out status.

Our analysis that exploits detailed data from the Università di Sassari highlights that, without taking into account selection, it is not sensible to naively compare drop-out rates among different departments. In addition, we shed light on the marginal contribution of women on drop-out rates, showing that the estimated parameter for women in a univariate probit model is not informing on this issue.

Appendix

The table below provides a detailed description of each variable employed in the main analysis:

Table A.1 Data sources and definitions