Abstract
In recent years, artificial intelligence and specifically artificial neural networks (NNs) have shown great success in solving complex, nonlinear problems in earth sciences. Despite their success, the strategies upon which NNs make decisions are hard to decipher, which prevents scientists from interpreting and building trust in the NN predictions; a highly desired and necessary condition for the further use and exploitation of NNs’ potential. Thus, a variety of methods have been recently introduced with the aim of attributing the NN predictions to specific features in the input space and explaining their strategy. The so-called eXplainable Artificial Intelligence (XAI) is already seeing great application in a plethora of fields, offering promising results and insights about the decision strategies of NNs. Here, we provide an overview of the most recent work from our group, applying XAI to meteorology and climate science. Specifically, we present results from satellite applications that include weather phenomena identification and image to image translation, applications to climate prediction at subseasonal to decadal timescales, and detection of forced climatic changes and anthropogenic footprint. We also summarize a recently introduced synthetic benchmark dataset that can be used to improve our understanding of different XAI methods and introduce objectivity into the assessment of their fidelity. With this overview, we aim to illustrate how gaining accurate insights about the NN decision strategy can help climate scientists and meteorologists improve practices in fine-tuning model architectures, calibrating trust in climate and weather prediction and attribution, and learning new science.
You have full access to this open access chapter, Download chapter PDF
Similar content being viewed by others
Keywords
- eXplainable Artificial Intelligence (XAI)
- Neural Networks (NNs)
- Geoscience
- Climate science
- Meteorology
- Trust
- Black box models
1 Introduction
In the last decade, artificial neural networks (NNs) [38] have been increasingly used for solving a plethora of problems in the earth sciences [5, 7, 21, 27, 36, 41, 60, 62, 68, 72], including marine science [41], solid earth science [7], and climate science and meteorology [5, 21, 62]. The popularity of NNs stems partially from their high performance in capturing/predicting nonlinear system behavior [38], the increasing availability of observational and simulated data [1, 20, 56, 61], and the increase in computational power that allows for processing large amounts of data simultaneously. Despite their high predictive skill, NNs are not interpretable (usually referred to as “black box” models), which means that the strategy they use to make predictions is not inherently known (as, in contrast, is the case for e.g., linear models). This may introduce doubt with regard to the reliability of NN predictions and it does not allow scientists to apply NNs to problems where model interpretability is necessary.
To address the interpretability issue, many different methods have recently been developed [3, 4, 32, 53, 69, 70, 73, 75, 77, 84] in the emerging field of eXplainable Artificial Intelligence (XAI) [9, 12, 78]. These methods aim at a post hoc attribution of the NN prediction to specific features in the input domain (usually referred to as attribution/relevance heatmaps), thus identifying relationships between the input and the output that may be interpreted physically by the scientists. XAI methods have already offered promising results and fruitful insights into how NNs predict in many applications and in various fields, making “black box” models more transparent [50]. In the geosciences, physical understanding about how a model predicts is highly desired, so, XAI methods are expected to be a real game-changer for the further application of NNs in this field [79].
In this chapter, we provide an overview of the most recent studies from our group that implement XAI in the fields of climate science and meteorology. We focus here on outlining our work, the details of which we are more knowledgeable of, but we highlight that relevant work has been also established by other groups (see e.g., [18, 34, 52, 74]). The first part of this overview presents results from direct application of XAI to solve various prediction problems that are of particular interest to the community. We start with XAI applications in remote sensing, specifically for image-to-image translation of satellite imagery to inform weather forecasting. Second, we focus on applications of climate prediction at a range of timescales from subseasonal to decadal, and last, we show how XAI can be used to detect forced climatic changes and anthropogenic footprint in observations and simulations. The second part of this overview explores ways that can help scientists gain insights about systematic strengths and weaknesses of different XAI methods and generally improve their assessment. So far in the literature, there has been no objective framework to assess how accurately an XAI method explains the strategy of a NN, since the ground truth of what the explanation should look like is typically unknown. Here, we discuss a recently introduced synthetic benchmark dataset that can introduce objectivity in assessing XAI methods’ fidelity for weather/climate applications, which will lead to better understanding and implementation.
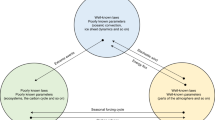
The overall aim of this chapter is to illustrate how XAI methods can be used to help scientists fine tune NN models that perform poorly, build trust in models that are successful and investigate new physical insights and connections between the input and the output (see Fig. 1).
-
i) XAI to guide the design of the NN architecture. One of the main challenges when using a NN is how to decide on the proper NN architecture for the problem at hand. We argue that XAI methods can be an effective tool for analysts to get insight into a flawed NN strategy and be able to revise it in order to improve prediction performance.
-
ii) XAI to help calibrate trust in the NN predictions. Even in cases when a NN (i.e., or any black model in general) exhibits a high predictive performance, it is not guaranteed that the underlying strategy that is used for prediction is correct. This has famously been depicted in the example of “clever Hans”, a horse that was correctly solving mathematical sums and problems based on the reaction of the audience [35]. By using XAI methods, scientists can verify when a prediction is successful for the right reasons (i.e., they can test against “clever Hans” prediction models [35]), thus helping build model trust.
-
iii) XAI to help learn new science. XAI methods allow scientists to gain physical insights about the connections between the input variables and the predicted output, and generally about the problem at hand. In cases where the highlighted connections are not fully anticipated/understood by already established science, further research and investigation may be warranted, which can accelerate learning new science. We highlight though that XAI methods will most often motivate new analysis to learn and establish new science, but cannot prove the existence of a physical phenomenon, link or mechanism, since correlation does not imply causation.
The content of the chapter is mainly based on previously published work from our group [6, 16, 25, 29, 43, 47, 80], and is re-organized here to be easily followed by the non-expert reader. In Sect. 2, we present results from various XAI applications in climate science and meteorology. In Sect. 3, we outline a new framework to generate attribution benchmark datasets to objectively evaluate XAI methods’ fidelity, and in Sect. 4, we state our conclusions.
2 XAI Applications
2.1 XAI in Remote Sensing and Weather Forecasting
As a first application of XAI, we focus on the field of remote sensing and short-term weather forecasting. When it comes to forecasting high impact weather hazards, imagery from geostationary satellites has been excessively used as a tool for situation awareness by human forecasters, since it supports the need for high spatial resolution and temporally rapid refreshing [40]. However, information from geostationary satellite imagery has less frequently been used in data assimilation or integrated into weather-forecasting numerical models, despite the advantages that these data could offer in improving numerical forecasts.
In recent work [25], scientists have used XAI to estimate precipitation over the contiguous United States from satellite imagery. These precipitating scenes that are typically produced by radars and come in the form of radar reflectivity can then be integrated into numerical models to spin up convection. Thus, the motivation of this research was to exploit the NNs’ high potential in capturing spatial information together with the large quantity, high quality and low latency of satellite imagery, in order to inform numerical modeling and forecasting. This could be greatly advantageous for mitigation of weather hazards.
For their analysis, Hilburn et al. (2021) [25] developed a convolutional NN with a U-Net architecture (dubbed GREMLIN in the original paper). The inputs to the network were four-channel satellite images, each one containing brightness temperature and lightning information, over various regions around the US. As output, the network was trained to predict a single-channel image (i.e., an image-to-image translation application) that represents precipitation over the same region as the input, in the form of radar reflectivity and measured in dBZ. The network was trained against radar observations, and its overall prediction performance across testing samples was quite successful. Specifically, predictions from the GREMLIN model exhibited an overall coefficient of determination on the order of \(R^{2}=0.74\) against the radar observations and a root mean squared difference on the order of 5.53 dBZ.
Apart from statistically evaluating the performance of GREMLIN predictions in reproducing reflectivity fields, it was also very important to assess the strategy upon which the model predicted. For this purpose, Hilburn et al. made use of a well-known XAI method, the Layer-wise Relevance Propagation (LRP [4]). Given an input sample and an output pixel, LRP reveals which features in the input contributed the most in deriving the value of the output. This is accomplished by sequentially propagating backwards the relevance from the output pixel to the neurons of the previous layers and eventually to the input features. So far, numerous different rules have been proposed in the literature as to how this propagation of relevance can be performed, and in this XAI application the alpha-beta rule was used [4], with alpha = 1 and beta = 0. The alpha-beta rule distinguishes between strictly positive and strictly negative pre-activations, which helps avoid the possibility of infinitely growing relevancies in the propagation phase, and it provides more stable results.
In Fig. 2, we show LRP results for GREMLIN for a specific sample, and a specific output pixel (namely, the central location of the shown sample), chosen for its close proximity to strong lightning activity. The first row of the figure shows the input channels and the corresponding desired output (i.e., the radar observation). The second row shows the LRP maps, highlighting which features in the input channels the neural network paid attention to in order to estimate the value of the chosen central output pixel for this sample.
The LRP results for the channel with lightning information show that the network focused only on regions where lightning was present in that channel. The LRP results for the other channels show that even in those channels the NN’s attention was drawn to focus on regions where lightning was present. Hilburn et al. then performed a new experiment by modifying the input sample to have all lightning removed, that is, all the lightning values were set to zero. In this case, LRP highlighted that the network’s focus shifted entirely in the first three input channels, as expected. More specifically, the focus shifted to two types of locations, namely, (i) cloud boundaries, or (ii) areas where the input channels had high brightness (cold temperatures), as can be seen by comparing the three leftmost panels of the first, and third row. In fact, near the center of the third-row panels, it can be seen that the LRP patterns represent the union of the cloud boundaries and the locations of strongest brightness in the first row. LRP vanishes further away from the center location, as it is expected considering the nature of the effective receptive field that corresponds to the output pixel.
LRP results for the GREMLIN model. (top) The four input channels and the corresponding observed radar image (ground truth). (middle) LRP results for the original four input channels and the chosen output pixel, and the prediction from GREMLIN. (bottom) The equivalent of the middle row, but after all lighting values were set to zero. Note that all images are zoomed into a region centered at the pixel of interest. Adapted from Hilburn et al., 2021 [25].
The LRP results as presented above provide very valuable insight about how the network derives its estimates. Specifically, the results indicate the following strategy used by GREMLIN: whenever lightning is present near the output pixel, the NN primarily focuses on the values of input pixels where lightning is present, not only in the channel that contains the lightning information, but in all four input channels. It seems that the network has learned that locations containing lightning are good indicators of high reflectivity, even in the other input channels. When no lightning is present, the NN focuses primarily on cloud boundaries (locations where the gradient is strong) or locations of very cold cloud tops. The network seems to have learned that these locations have the highest predictive power for estimating reflectivity.
In this application of XAI in remote sensing, the obtained insights from LRP have given scientists the confidence that the network derived predictions based on a physically reasonable strategy and thus helped build more trust about its predictions. Moreover, if scientists wish to improve the model further by testing different model architectures, knowing how much physically consistent the different decision strategies of the models are offers a criterion to distinguish between models, which goes beyond prediction performance.
2.2 XAI in Climate Prediction
Similar to weather forecasting, climate prediction at subseasonal, seasonal and decadal timescales is among the most important challenges in climate science, with great societal risks and implications for the economy, water security, and ecosystem management for many regions around the world [8]. Typically, climate prediction draws upon sea surface temperature (SST) information (especially on seasonal timescales and beyond), which are considered as the principal forcing variable of the atmospheric circulation that ultimately drives regional climate [19, 23, 30, 44, 57]. SST information is used for prediction either through deterministic models (i.e., SST-forced climate model simulations) or statistical models which aim to exploit physically- and historically- established teleconnections of regional climate with large-scale modes of climate variability (e.g., the El Niño-Southern Oscillation, ENSO; [11, 17, 44, 45, 48, 49, 54, 59, 67]). Limits to predictive skill of dynamical models arise from incomplete knowledge of initial conditions, uncertainties and biases in model physics, and limits on computational resources that place constraints on the grid resolution used in operational systems. Similarly, empirical statistical models exhibit limited predictive skill, arising primarily from the complex and non-stationary nature of the relationship between large scale modes and regional climate.
To address the latter, in more recent years, data-driven machine learning methods that leverage information from the entire globe (i.e., beyond predefined climate indices) have been suggested in the literature and they have shown improvements in predictive skill [13, 76]. A number of studies have specifically shown the potential of neural networks in predicting climate across a range of scales, capitalizing on their ability to capture nonlinear dependencies (see e.g., [21]), while more recent studies have used XAI methodsFootnote 1 to explain these networks and their strategies to increase trust and learn new science [47, 79, 80].
In the first study outlined herein, Mayer and Barnes (2021) [47] used XAI in an innovative way to show that NNs can identify when favorable conditions that lead to enhanced predictive skill of regional climate are present in the atmosphere (the so called “forecasts of opportunity”) or not. More specifically, the authors based their analysis on the known climate teleconnections between the Madden-Julian Oscillation in the tropics (MJO; an eastward moving disturbance of convection in the tropical atmosphere) and the North Atlantic atmospheric pressure [10, 24]. When the MJO is active, it leads to a consistent and coherent modulation of the midlatitude climate on subseasonal timescales, and thus, corresponds to enhanced predictive potential for the midlatitudes. The question that Mayer and Barnes put forward was whether or not NNs can capture this inherent property of the climate system of exhibiting periods of enhanced predictability (i.e. forecasts of opportunity).
The authors used daily data of outgoing longwave radiation (OLR; a measure of convective activity) over the tropics of the globe and trained a fully connected NN to predict the sign of the 500 hPa geopotential height anomalies (a measure of atmospheric pressure) over the North Atlantic, 22 days later. Their results showed that when the network was assigning higher confidence to a prediction (i.e., the likelihood of either the positive or the negative geopotential height class was much higher than the opposite class), it was much more likely for that prediction to end up being correct. On the contrary, when the network was assigning low confidence to a prediction (i.e., the likelihoods of the positive or negative geopotential height classes were very similar), the predictive performance of the network was much poorer, almost identical to a random guess. This meant that the NN was able to correctly capture the presence of forecasts of opportunity in the climate system.
Maps of LRP composites corresponding to the 10% most confident and correct predictions of positive and negative geopotential height anomalies. Contours indicate the corresponding composite fields of the outgoing longwave radiation with solid lines representing positive values and dashed lines negative values. Adapted from Mayer and Barnes et al., 2021 [47].
Mayer and Barnes continued in exploring which features over the tropics made the network highly confident during forecasts of opportunity, by using the LRP method. Figure 3 shows the LRP heatmaps for positive and negative, correctly predicted, anomalies of geopotential height over the North Atlantic. Note that only the top 10% of the most confident correct predictions were used for the LRP analysis (these predictions ought to represent cases of forecast of opportunity). As it is shown, LRP identified several sources of predictability over the southern Indian Ocean, the Maritime Continent and the western Pacific Ocean for positive predictions, and over the Maritime Continent, the western and central Pacific and over the western side of Hawaii for negative predictions. Judging by the OLR contours, the highlighted patterns correspond to dipoles of convection over the Indian Ocean and into the Maritime Continent in the first case and over the Maritime Continent and into the western Pacific in the second case. These patterns are consistent with the MJO structure and correspond to specific phases of the phenomenon, which in turn have been shown to be connected with the climate of the North Atlantic [10, 24]. Thus, the implementation of LRP in this problem confirms that the network correctly captured the MJO-modulated forecasts of opportunity on subseasonal scales, and it further builds trust for the network’s predictive performance.
In a second climate prediction application, this time on decadal scales, Toms et al. (2021) [80] used simulated data from fully-coupled climate models and explored sources of decadal predictability in the climate system. Specifically, Toms et al. used global SST information as the predictor, with the aim of predicting continental surface temperature around the globe; for each grid point over land, a separate dense network was used. In this way, by combining the large number of samples provided by the climate models (unrealistically large sample size compared to what is available in the observational record) and the ability of NNs to capture nonlinear dynamics, the authors were able to assess the predictability of the climate system in a nonlinear setting. Note that assessing predictability using observational records has been typically based on linear models of limited complexity to avoid overfitting, given the short sample sizes that are usually available [13, 76]. Since the climate system is far from linear, the investigation by Toms et al. may be argued to provide a better estimate of predictability than previous work. The results showed that there are several regions where surface temperature is practically unpredictable, whereas there are also regions of high predictability, namely, “hotspots” of predictability, i.e., regions where the predictive skill is inherently high. The presence of hotspots of predictability is conceptually the same with the presence of forecasts of opportunity on subseasonal scales that was discussed in the previous application.
Composite of LRP maps for the sea surface temperature (SST) field for accurate predictions of positive surface temperature anomalies at four locations across North America. The continental locations associated with the composites are denoted by the red dots in each panel. The LRP map for each sample is normalized between a value of 0 and 1 before compositing to ensure each prediction carries the same weight in the composite. The number of samples used in each composite is shown within each sub-figure. Adapted from Toms et al., 2021 [80].
Toms et al. explored the sources of predictability of surface temperature over North America by using the LRP method. Figure 4 shows the composite LRP maps that correspond to correctly predicted positive temperature anomalies over four different regions in the North America. One can observe that different SST patterns are highlighted as sources of predictability for each of the four regions. Perhaps surprisingly, temperature anomalies over Central America are shown to be most associated with SST anomalies off the east coast of Japan (Fig. 4a), likely related to the Kuroshio Extension [58]. SST anomalies over the North-Central Pacific Ocean are associated with continental temperature anomalies along the west coast (Fig. 4b), while those within the tropical Pacific Ocean contribute to predictability across central North America (Fig. 4c). Lastly, the North Atlantic SSTs contribute predictability to all four regions, although their impacts are more prominent across the northeastern side of the continent (Fig. 4d). The highlighted patterns of predictability as assessed by LRP resemble known modes of SST variability, such as the El Niño-Southern Oscillation (e.g.,[55, 81]), the Pacific Decadal Oscillation [46, 54], and the Atlantic Multidecadal Oscillation [17]. These modes are known to affect hydroclimate over North America [11, 17, 48, 49, 54], thus, this application constitutes one more case where XAI methods can help scientists build model trust. More importantly, in this setting, physical insights can be extracted about sources of temperature predictability over the entire globe, by sequentially applying LRP to each of the trained networks. As Toms et al. highlight, such an analysis could motivate further mechanistic investigation to physically establish new climate teleconnections. Thus, this application also illustrates how XAI methods can help advance climate science.
2.3 XAI to Extract Forced Climate Change Signals and Anthropogenic Footprint
As a final application of XAI to meteorology and climate science, we consider studies that try to identify human-caused climatic changes (i.e. climate change signals) and anthropogenic footprint in observations or simulations. Detecting climate change signals has been recognized in the climate community as a signal-to-noise problem, where the warming “signal” arising from the slow (long timescales), human-caused changes in the atmospheric concentrations of greenhouse gases is superimposed on the background “noise” of natural climate variability [66]. By solely using observations, one cannot identify which climatic changes are happening due to anthropogenic forcing, since there is no way to strictly infer the possible contribution of natural variability to these observed changes. Hence, the state-of-the-art approach to quantify or to account for natural variability within the climate community is the utilization of large ensembles of climate model simulations (e.g., [14, 28]). Specifically, researchers simulate multiple trajectories of the climate system, which start from slightly different initial states but share a common forcing (natural forcing or not). Under this setting, natural variability is represented by the range of the simulated future climates given a specific forcing, and the signal of the forced changes in the climate can be estimated by averaging across all simulations [51].
Utilizing these state-of-the-art climate change simulations, Barnes et al. (2020) [6] used XAI in an innovative way to detect forced climatic changes in temperature and precipitation. Specifically, the authors trained a fully connected NN to predict the year that corresponded to a given (as an input) map of annual-mean temperature (or precipitation) that had been simulated by a climate model. For the NN to be able to predict the year of each map correctly, it needs to learn to look and distinguish specific features of forced climatic change amidst the background natural variability and model differences. In other words, only robust (present in all models) and pronounced (not overwhelmed by natural variability) climate change signals arising from anthropogenic forcing would make the NN to distinguish between a year in the early decades versus late decades of the simulation. Climate change signals that are weak compared to the background natural variability or exhibit high uncertainty across different climate models will not be helpful to the NN.
In the way Barnes et al. have formed the prediction task, the prediction itself is of limited or no utility (i.e., there is no utility in predicting the year that a model-produced temperature map corresponds to; it is already known). Rather, the goal of the analysis is to explore which features help the NN distinguish each year and gain physical insight about robust signals of human-caused climate change. This means that the goal of the analysis lies on the explanation of the network and not the prediction. Barnes et al. trained the NN over the entire simulation period 1920–2099, using 80% of the climate model simulations and then tested on the remaining 20%. Climate simulations were carried out by 29 different models, since the authors were interested in extracting climate change signals that are robust across multiple climate models. Results showed that the NN was able to predict quite successfully the correct years that different temperature and precipitation maps corresponded to. Yet, the performance was lower for years before the 1960s and much higher for years well into the 21st century. This is due to the fact that the climate change signal becomes more pronounced with time, which makes it easier to distinguish amidst the background noise and the model uncertainty.
Next, Barnes et al. used LRP to gain insight into the forced climatic changes in the simulations that had helped the NN to correctly predict each year. Figure 5 shows the LRP results for the years 1975, 2035 and 2095. It can be seen that different areas are highlighted during different years, which indicates that the relative importance of different climate change signals varies through time. For example, LRP highlights the North Atlantic temperature to be a strong indicator of climate change during the late 20th and early 21st century, but not during the late 21st century. On the contrary, the Southern Ocean gains importance only throughout the 21st century. Similarly, the temperature over eastern China is highlighted only in the late 20th century, which likely reflects the aerosol forcing which acts to decrease temperature. Thus, the NN learned that strong cooling over China relatively to the overall warming of the world is an indicator for the corresponding temperature map to belong to the late 20th century.
LRP heatmaps for temperature input maps composited for a range of years when the prediction was deemed accurate. The years are shown above each panel along with the number of maps used in the composites. Darker shading denotes regions that are more relevant for the NN’s accurate prediction. Adapted from Barnes et al., 2020 [6].
The above results (see original study by Barnes et al. for more information) highlight the importance and utility of explaining the NN decisions in this prediction task and the physical insights that XAI methods can offer. As we mentioned, in this analysis the explanation of the network was the goal, while the predictions themselves were not important. Generally, this application demonstrates that XAI methods constitute a powerful approach for extracting climate patterns of forced change amidst any background noise, and advancing climate change understanding.
A second application where XAI was used to extract the anthropogenic footprint was published by Keys et al. (2021) [29]. In that study, the authors aimed at constructing a NN to predict the global human footprint index (HFI) solely from satellite imagery. The HFI is a dimensionless metric that captures the extent to which humans have influenced the terrestrial surface of the Earth over a specific region (see e.g., [82, 83]). Typically, the HFI is obtained by harmonizing eight different sub-indices, each one representing different aspects of human influence, like built infrastructure, population density, land use, land cover etc. So far, the process for establishing the HFI involves significant data analysis and modelling that does not allow for fast updates and continuous monitoring of the index, which means that large-scale, human-caused changes to the land surface may occur well before we are able to track them. Thus, estimating the HFI solely from satellite imagery that supports spatial resolution and temporally rapid refreshing can help improve monitoring of the human pressure on the Earth surface.
Keys et al. trained a convolutional NN to use single images of the land surface (Landsat; [22]) over a region to predict the corresponding Williams HFI [83]. The authors trained different networks corresponding to different areas around the world in the year 2000, and then used these trained networks to evaluate Landsat images from the year 2019. Results showed that the NNs were able to reproduce the HFI with high fidelity. Moreover, by comparing the estimated HFI in 2000 with the one in 2019, the authors were able to gain insight into the changes in the human pressure to the earth surface during the last 20 years. Patterns of change were consistent with a steady expansion of the human pressure into areas of previously low HFI or increase of density of pressure in regions with previously high HFI values.
Consequently, Keys et al. applied the LRP method for cases where the HFI increased significantly between the years 2000 and 2019. In this way, the authors aimed to gain confidence that the NN was focusing on the correct features in the satellite images to predict increases of the human footprint. As an example, in Fig. 6, we present the LRP results for a region over Texas, where wind farms were installed between the years 2000 and 2019; compare the satellite images in the left and middle panels of the figure. As shown in the LRP results, the NN correctly paid attention to the installed wind farm features in order to predict an increase of the HFI in the year 2019. By examining many other cases of increase in HFI, the authors reported that in most instances, the NN was found to place the highest attention to features that were clearly due to human activity, which provided them with confidence that the network performed with high accuracy for the right reasons.
Satellite imagery from the Global Forest Change dataset over Texas, USA, in (left) 2000 and (middle) 2019. (right) the most relevant features to the NN for its year-2019 prediction of the HFI, as estimated using LRP. Adapted from Keys et al., 2021 [29].
3 Development of Attribution Benchmarks for Geosciences
As was illustrated in the previous sections, XAI methods have already shown their potential and been used in various climate and weather applications to provide valuable insights about NN decision strategies. However, many of these methods have been shown in the computer science literature to not honor desirable properties (e.g., “completeness” or “implementation invariance”; see [77]), and in general, to face nontrivial limitations for specific problem setups [2, 15, 31, 63]. Moreover, given that many different methods have been proposed in the field of XAI (see e.g., [3, 4, 32, 53, 69, 70, 73, 75, 77, 84] among others) with each one explaining the network in a different way, it is key to better understand differences between methods, both their relative strengths and weaknesses, so that researchers are aware which methods are more suitable to use depending on the model architecture and the objective of the explanation. Thus, thorough investigation and objective assessment of XAI methods is of vital importance.
So far, the assessment of different XAI methods has been mainly based on applying these methods to benchmark problems, where the scientist is expected to know what the attribution heatmaps should look like, hence, being able to judge the performance of the XAI method in question. Examples of benchmark problems in climate science include the classification of El Niño or La Niña years or seasonal prediction of regional hydroclimate [21, 79]. In computer science, commonly used benchmark datasets for image classification problems are, among others, the MNIST or ImageNet datasets [39, 64]. Although the use of such benchmark datasets help the scientist gain some general insight about the XAI method’s efficiency, this is always based on the scientist’s subjective visual inspection of the result and their prior knowledge and understanding of the problem at hand, which has high risk of cherry-picking specific samples/methods and reinforcing individual biases [37]. In classification tasks, for example, just because it might make sense to a human that an XAI method highlights the ears or the nose of a cat for an image successfully classified as “cat”, this does not necessarily mean that this is the strategy the model in question is actually using, since there is no objective truth about the relative importance of these two or other features to the prediction. The actual importance of different features to the network’s prediction is always case- or dataset-dependent, and the human perception of an explanation alone is not a solid criterion for assessing its trustworthiness.
With the aim of a more falsifiable XAI research [37], Mamalakis et al. (2021) [43] put forward the concept of attribution benchmark datasets. These are synthetic datasets (consisting of synthetic inputs and outputs) that have been designed and generated in a way so that the importance of each input feature to the prediction is objectively derivable and known a priori. This a priori known attribution can be used as ground truth for evaluating different XAI methods and identifying systematic strengths and weaknesses. The authors referred to such synthetic datasets as attribution benchmark datasets, to distinguish from benchmarks where no ground truth of the attribution/explanation is available. The framework was proposed for regression problems (but can be extended into classification problems too), where the input is a 2D field (i.e., a single-channel image); commonly found in geoscientific applications (e.g., [13, 21, 76, 79]). Below we briefly summarize the proposed framework and the attribution benchmark dataset that Mamalakis et al. used, and we present comparisons between different XAI methods that provide insights about their performance.
3.1 Synthetic Framework
Mamalakis et al. considered a climate prediction setting (i.e., prediction of regional climate from global 2D fields of SST; see e.g., [13, 76]), and generated N realizations of an input random vector X \(\in {\Re ^d}\) from a multivariate Normal Distribution (see step 1 in Fig. 7); these are N synthetic inputs representing vectorized 2D SST fields. Next, the authors used a nonlinear function \(F: \Re ^d\rightarrow \Re \), which represented the physical system, to map each realization \({\boldsymbol{x}}_{\boldsymbol{n}}\) into a scalar \(y_n\), and generated the output random variable Y (see step 2 in Fig. 7); these synthetic outputs represented the series of the predictand climatic variable. Subsequently, the authors trained a fully-connected NN to approximate function F and compare the model attributions estimated by different XAI methods with the ground truth of the attribution. The general idea of this framework is summarized in Fig. 7, and although the dataset was inspired from a climate prediction setting, the concept of attribution benchmarks is generic and applicable to a large number of problem settings in the geosciences and beyond.
Regarding the form of function F that is used to generate the variable Y from X, Mamalakis et al. claimed that it can be of an arbitrary choice, as long as it has such a form so that the importance/contribution of each of the input variables to the response Y is objectively derivable. The simplest form for F so that the above property is honored is when F is an additively separable function, i.e. there exist local functions \(C_i\), with \(i=1,2,...,d\), so that:
where, \(X_i\) is the random variable at grid point i, and the local functions \(C_i\) are nonlinear; if the local functions \(C_i\) are linear, Eq. 1 falls back to a trivial linear problem, which is not particularly interesting to benchmark a NN or an XAI method against. Mamalakis et al., defined the local functions to be piece-wise linear functions, with number of break points \(K=5\). The break points and the slopes between the break points were chosen randomly for each grid point (see the original paper for more information). Importantly, with F being an additively separable function as in Eq. 1, the relevance/contribution of each of the variables \(X_i\) to the response \(y_n\) for any sample n, is by definition equal to the value of the corresponding local function, i.e., \(R_{i,n}^{true}=C_i(x_{i,n})\); that is when considering a zero baseline. This satisfies the basic desired property for F that any response can be objectively attributed to the input.
Schematic overview of the framework to generate synthetic attribution benchmarks. In step 1, N independent realizations of a random vector X \(\in {\Re ^d}\) are generated from a multivariate Normal Distribution. In step 2, a response Y \(\in {\Re ^d}\) to the synthetic input X is generated using a known nonlinear function F. In step 3, a fully-connected NN is trained using the synthetic data X and Y to approximate the function F. The NN learns a function \(\hat{F}\). Lastly, in step 4, the attribution heatmaps estimated from different XAI methods are compared to the ground truth (that represents the function F), which has been objectively derived for any sample \(n=1,2,. . .,N\). Similar to Mamalakis et al., 2021 [43].
Mamalakis et al. generated \(N=10^6\) samples of input and output and trained a fully connected NN to learn the function F (see step 3 in Fig. 7), using the first 900,000 samples for training and the last 100,000 samples for testing. Apart from assessing the prediction performance, the testing samples were also used to assess the performance of different post hoc, local XAI methods. The sample size was on purpose chosen to be large compared to typical samples in climate prediction applications. In this way, the authors aimed to ensure that they could achieve an almost perfect training and establish a fair assessment of XAI methods; they wanted to ensure that any discrepancy between the ground truth of the attribution and the results of XAI methods came from systematic pitfalls in the XAI method and to a lesser degree from poor training of the NN. Indeed, the authors achieved a very high prediction performance, with the coefficient of determination of the NN prediction in the testing data being slightly higher than \(R^2= 99\%\), which suggests that the NN could capture 99% of the variance in Y.
3.2 Assessment of XAI Methods
For their assessment, Mamalakis et al. considered different post hoc, local XAI methods that have been commonly used in the literature. Specifically, the methods that were assessed included Gradient [71], Smooth Gradient [73], Input*Gradient [70], Intergradient Gradients [77], Deep Taylor [53] and LRP [4]. In Fig. 8, we present the ground truth and the estimated relevance heatmaps from the XAI methods (each heatmap is standardized by the corresponding maximum absolute relevance within the map). This sample corresponds to a response \(y_n= 0.0283\), while the NN predicted 0.0301. Based on the ground truth, features that contributed positively to the response \(y_n\) occur mainly over the northern, eastern tropical and southern Pacific Ocean, the northern Atlantic Ocean, and the Indian Ocean. Features with negative contribution occur over the tropical Atlantic Ocean and the southern Indian Ocean.
The results from the method Gradient are not consistent at all with the ground truth. In the eastern tropical and southern Pacific Ocean, the method returns negative values instead of positive, and over the tropical Atlantic, positive values (instead of negative) are highlighted. The pattern (Spearman’s) correlation is very small on the order of 0.13, consistent with the above observations. As theoretically expected, this result indicates that the sensitivity of the output to the input is not the same as the attribution of the output to the input [3]. The method Smooth Gradient performs poorly and similarly to the method Gradient, with a correlation coefficient on the order of 0.16.
Performance of different XAI methods. The XAI performance is assessed by comparing the estimated heatmaps to the ground truth. All heatmaps are standardized with the corresponding maximum (absolute) value. Red (blue) color corresponds to positive (negative) contribution to the response/prediction, with darker shading representing higher (absolute) values. The Spearman’s rank correlation coefficient between each heatmap and the ground truth is also provided. Only for the methods Deep Taylor and \(\text {LRP}_{\alpha =1,\beta =0}\), the correlation with the absolute ground truth is given. Similar to Mamalakis et al., 2021 [43]. (Color figure online)
Methods Input*Gradient and Integrated Gradients perform very similarly, both capturing the ground truth very closely. Indeed, both methods capture the positive patterns over eastern Pacific, northern Atlantic and the Indian Oceans, and to an extend the negative patterns over the tropical Atlantic and southern Indian Oceans. The Spearman’s correlation with the ground truth for both methods is on the order of 0.75, indicating the very high agreement.
Regarding the LRP method, first, results confirm the arguments in [53, 65], that the Deep Taylor leads to similar results with the \(\text {LRP}_{\alpha =1,\beta =0}\), when a NN with ReLU activations is used. Second, both methods return only positive contributions. This was explained by Mamalakis et al. and is due to the fact that the propagation rule of \(\text {LRP}_{\alpha =1,\beta =0}\) is performed based on the product of the relevance in the higher layer with a strictly positive number. Hence, the sign of the NN prediction is propagated back to all neurons and to all features of the input. Because the NN prediction is positive in Fig. 8, then it is expected that \(\text {LRP}_{\alpha =1,\beta =0}\) (and Deep Taylor) returns only positive contributions (see also remarks by [33]). What is not so intuitive is the fact that the \(\text {LRP}_{\alpha =1,\beta =0}\) seems to highlight all important features, independent of the sign of their contribution (compare with ground truth). Given that, by construction, \(\text {LRP}_{\alpha =1,\beta =0}\) considers only positive preactivations [23], one might assume that it will only highlight the features that positively contribute to the prediction. However, the results in Fig. 8 show that the method highlights the tropical Atlantic Ocean with a positive contribution. This is problematic, since the ground truth clearly indicates that this region is contributing negatively to the response \(y_n\) in this example. The issue of \(\text {LRP}_{\alpha =1,\beta =0}\) about highlighting all features independent of whether they are contributing positively or negatively to the prediction has been very recently discussed in other applications of XAI as well [33].
Lastly, when using the \(\text {LRP}_{z}\) rule, the attribution heatmap very closely captures the ground truth, and it exhibits a very high Spearman’s correlation on the order of 0.76. The results are very similar to those of the methods Input*Gradient and Integrated Gradients, making these three methods the best performing ones for this example. This is consistent with the discussion in [2], which showed the equivalence of the methods Input*Gradient and \(\text {LRP}_{z}\) in cases of NNs with ReLU activation functions, as in this work.
Summary of the performance of different XAI methods. Histograms of the Spearman’s correlation coefficients between different XAI heatmaps and the ground truth for 100,000 testing samples. Similar to Mamalakis et al., 2021 [43].
To verify that the above insights are valid for the entire testing dataset and not only for the specific example in Fig. 8, we also generated the histograms of the Spearman’s correlation coefficients between the XAI methods and the ground truth for all 100,000 testing samples (similarly to Mamalakis et al.). As shown in Fig. 9, methods Gradient and Smooth Gradient perform very poorly (both exhibit almost zero average correlation with the ground truth), while methods Input*Gradient and Integrated Gradients perform equally well, exhibiting an average correlation with the ground truth around 0.7. The \(\text {LRP}_{z}\) rule is seen to be the best performing among the LRP rules, with very similar performance to the Input*Gradient and Integrated Gradients methods (as theoretically expected for this model setting; see [2]). The corresponding average correlation coefficient is also on the order of 0.7. Regarding the \(\text {LRP}_{\alpha =1,\beta =0}\) rule, we present two curves. The first curve (black curve in Fig. 9) corresponds to correlation with the ground truth after we have set all the negative contributions in the ground truth to zero. The second curve (blue curve) corresponds to correlation with the absolute value of the ground truth. For both curves we multiply the correlation value with -1 when the NN prediction was negative, to account for the fact that the prediction’s sign is propagated back to the attributions. Results show that when correlating with the absolute ground truth (blue curve), the correlations are systematically higher than when correlating with the nonnegative ground truth (black curve). This verifies that the issue of \(\text {LRP}_{\alpha =1,\beta =0}\) highlighting both positive and negative attributions occurs for all testing samples.
In general, these results demonstrate the benefits of attribution benchmarks for the identification of possible systematic pitfalls of XAI. The above assessment suggests that methods Gradient and Smooth Gradient may be suitable for estimating the sensitivity of the output to the input, but this is not necessarily equivalent to the attribution. When using the \(\text {LRP}_{\alpha =1,\beta =0}\) rule, one should be cautious, keeping always in mind that, i) it might propagate the sign of the prediction back to all the relevancies of the input layer and ii) it is likely to mix positive and negative contributions. For the setup used here (i.e. to address the specific prediction task using a shallow, fully connected network), the methods Input*Gradient, Integrated Gradients, and the \(\text {LRP}_{z}\) rule all very closely captured the true function F and are the best performing XAI methods considered. However, this result does not mean that the latter methods are systematically better performing for all types of applications. For example, in a different prediction setting (i.e. for a different function F) and when using a deep convolutional neural network, the above methods have been found to provide relatively incomprehensible explanations due to gradient shattering [42]. Thus, no optimal method exists in general and each method’s suitability depends on the type of the application and the adopted model architecture, which highlights the need to objectively assess XAI methods for a range of applications and develop best-practice guidelines.
4 Conclusions
The potential of NNs to successfully tackle complex problems in earth sciences has become quite evident in recent years. An important requirement for further application and exploitation of NNs in geoscience is their interpretability, and newly developed XAI methods show very promising results for this task. In this chapter we provided an overview of the most recent work from our group, applying XAI to meteorology and climate science. This overview clearly illustrates that XAI methods can provide valuable insights on the NN strategies, and that they are used in these fields under many different settings and prediction tasks, being beneficial for different scientific goals. For many applications that have been published in the literature, the ultimate goal is a highly-performing prediction model, and XAI methods are used by the scientists to calibrate their trust to the model, by ensuring that the decision strategy of the network is physically consistent (see e.g., [18, 21, 25, 29, 35, 47, 80]). In this way scientists can ensure that a high prediction performance is due to the right reasons, and that the network has learnt the true dynamics of the problem. Moreover, in many prediction applications, the explanation is used to help guide the design of the network that will be used to tackle the prediction problem (see e.g., [16]). As we showed, there are also applications where the prediction is not the goal of the analysis, but rather, the scientists are interested solely in the explanation. In this category of studies, XAI methods are used to gain physical insights about the dynamics of the problem or the sources of predictability. The highlighted relationships between the input and the output may warrant further investigation and advance our understanding, hence, establishing new science (see e.g., [6, 74, 79, 80]).
Independent of the goal of the analysis, an important aspect in XAI research is to better understand and assess the many different XAI methods that exist, in order to more successfully implement them. This need for objectivity in the XAI assessment arises from the fact that XAI methods are typically assessed without the use of any ground truth to test against and the conclusions can often be subjective. Thus, here we also summarized a newly introduced framework to generate synthetic attribution benchmarks to objectively test XAI methods [43]. In the proposed framework, the ground truth of the attribution of the output to the input is derivable for any sample and known a priori. This allows the scientist to objectively assess if the explanation is accurate or not. The framework is based on the use of additively separable functions, where the response Y \(\in {\Re }\) to the input X \(\in {\Re ^d}\) is the sum of local responses. The local responses may have any functional form, and independent of how complex that might be, the true attribution is always derivable. We believe that a common use and engagement of such attribution benchmarks by the geoscientific community can lead to a more cautious and accurate application of XAI methods to physical problems, towards increasing model trust and facilitating scientific discovery.
Notes
- 1.
We note here that a newly introduced line of research in XAI that is potentially relevant for climate prediction applications is in the concept of causability. Although XAI is typically used to address transparency of AI, causability refers to the quality of an explanation and to the extend to which an explanation may allow the scientist to reach a specified level of causal understanding about the underlying dynamics of the climate system [26].
References
Agapiou, A.: Remote sensing heritage in a petabyte-scale: satellite data and heritage earth engine applications. Int. J. Digit. Earth 10(1), 85–102 (2017)
Ancona, M., Ceolini, E., Öztireli, C., Gross, M.: Towards better understanding of gradient-based attribution methods for deep neural networks. arXiv preprint arXiv:1711.06104 (2017)
Ancona, M., Ceolini, E., Öztireli, C., Gross, M.: Gradient-based attribution methods. In: Samek, W., Montavon, G., Vedaldi, A., Hansen, L.K., Müller, K.-R. (eds.) Explainable AI: Interpreting, Explaining and Visualizing Deep Learning. LNCS (LNAI), vol. 11700, pp. 169–191. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-28954-6_9
Bach, S., Binder, A., Montavon, G., Klauschen, F., Müller, K.R., Samek, W.: On pixel-wise explanations for non-linear classifier decisions by layer-wise relevance propagation. PLoS ONE 10(7), e0130140 (2015)
Barnes, E.A., Hurrell, J.W., Ebert-Uphoff, I., Anderson, C., Anderson, D.: Viewing forced climate patterns through an AI lens. Geophys. Res. Lett. 46(22), 13389–13398 (2019)
Barnes, E.A., Toms, B., Hurrell, J.W., Ebert-Uphoff, I., Anderson, C., Anderson, D.: Indicator patterns of forced change learned by an artificial neural network. J. Adv. Model. Earth Syst. 12(9), e2020MS002195 (2020)
Bergen, K.J., Johnson, P.A., Maarten, V., Beroza, G.C.: Machine learning for data-driven discovery in solid earth geoscience. Science 363(6433), eaau0323 (2019)
Ocean Studies Board, The National Academies of Sciences, Engineering, and Medicine et al.: Next Generation Earth System Prediction: Strategies for Subseasonal to Seasonal Forecasts. National Academies Press (2016)
Buhrmester, V., Münch, D., Arens, M.: Analysis of explainers of black box deep neural networks for computer vision: a survey. arXiv preprint arXiv:1911.12116 (2019)
Cassou, C.: Intraseasonal interaction between the Madden-Julian oscillation and the North Atlantic oscillation. Nature 455(7212), 523–527 (2008)
Dai, A.: The influence of the inter-decadal pacific oscillation on us precipitation during 1923–2010. Clim. Dyn. 41(3–4), 633–646 (2013)
Das, A., Rad, P.: Opportunities and challenges in explainable artificial intelligence (XAI): a survey. arXiv preprint arXiv:2006.11371 (2020)
DelSole, T., Banerjee, A.: Statistical seasonal prediction based on regularized regression. J. Clim. 30(4), 1345–1361 (2017)
Deser, C., et al.: Insights from earth system model initial-condition large ensembles and future prospects. Nat. Clim. Chang. 10(4), 277–286 (2020)
Dombrowski, A.K., Anders, C.J., Müller, K.R., Kessel, P.: Towards robust explanations for deep neural networks. Pattern Recogn. 121, 108194 (2021)
Ebert-Uphoff, I., Hilburn, K.: Evaluation, tuning, and interpretation of neural networks for working with images in meteorological applications. Bull. Am. Meteor. Soc. 101(12), E2149–E2170 (2020)
Enfield, D.B., Mestas-Nuñez, A.M., Trimble, P.J.: The Atlantic multidecadal oscillation and its relation to rainfall and river flows in the continental us. Geophys. Res. Lett. 28(10), 2077–2080 (2001)
Gagne, D.J., II., Haupt, S.E., Nychka, D.W., Thompson, G.: Interpretable deep learning for spatial analysis of severe hailstorms. Mon. Weather Rev. 147(8), 2827–2845 (2019)
Goddard, L., Mason, S.J., Zebiak, S.E., Ropelewski, C.F., Basher, R., Cane, M.A.: Current approaches to seasonal to interannual climate predictions. Int. J. Climatol. J. R. Meteorol. Soc. 21(9), 1111–1152 (2001)
Guo, H.: Big earth data: a new frontier in earth and information sciences. Big Earth Data 1(1–2), 4–20 (2017)
Ham, Y.G., Kim, J.H., Luo, J.J.: Deep learning for multi-year ENSO forecasts. Nature 573(7775), 568–572 (2019)
Hansen, M.C., et al.: High-resolution global maps of 21st-century forest cover change. Science 342(6160), 850–853 (2013)
Hao, Z., Singh, V.P., Xia, Y.: Seasonal drought prediction: advances, challenges, and future prospects. Rev. Geophys. 56(1), 108–141 (2018)
Henderson, S.A., Maloney, E.D., Barnes, E.A.: The influence of the Madden-Julian oscillation on northern hemisphere winter blocking. J. Clim. 29(12), 4597–4616 (2016)
Hilburn, K.A., Ebert-Uphoff, I., Miller, S.D.: Development and interpretation of a neural-network-based synthetic radar reflectivity estimator using GOES-R satellite observations. J. Appl. Meteorol. Climatol. 60(1), 3–21 (2021)
Holzinger, A., Malle, B., Saranti, A., Pfeifer, B.: Towards multi-modal causability with graph neural networks enabling information fusion for explainable AI. Inf. Fusion 71, 28–37 (2021). https://doi.org/10.1016/j.inffus.2021.01.008
Karpatne, A., Ebert-Uphoff, I., Ravela, S., Babaie, H.A., Kumar, V.: Machine learning for the geosciences: challenges and opportunities. IEEE Trans. Knowl. Data Eng. 31(8), 1544–1554 (2018)
Kay, J.E., et al.: The community earth system model (CESM) large ensemble project: a community resource for studying climate change in the presence of internal climate variability. Bull. Am. Meteor. Soc. 96(8), 1333–1349 (2015)
Keys, P.W., Barnes, E.A., Carter, N.H.: A machine-learning approach to human footprint index estimation with applications to sustainable development. Environ. Res. Lett. 16(4), 044061 (2021)
Khan, M.Z.K., Sharma, A., Mehrotra, R.: Global seasonal precipitation forecasts using improved sea surface temperature predictions. J. Geophys. Res. Atmos. 122(9), 4773–4785 (2017)
Kindermans, P.-J., et al.: The (un)reliability of saliency methods. In: Samek, W., Montavon, G., Vedaldi, A., Hansen, L.K., Müller, K.-R. (eds.) Explainable AI: Interpreting, Explaining and Visualizing Deep Learning. LNCS (LNAI), vol. 11700, pp. 267–280. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-28954-6_14
Kindermans, P.J., et al.: Learning how to explain neural networks: PatternNet and PatternAttribution. arXiv preprint arXiv:1705.05598 (2017)
Kohlbrenner, M., Bauer, A., Nakajima, S., Binder, A., Samek, W., Lapuschkin, S.: Towards best practice in explaining neural network decisions with LRP. In: 2020 International Joint Conference on Neural Networks (IJCNN), pp. 1–7. IEEE (2020)
Lagerquist, R., McGovern, A., Homeyer, C.R., Gagne, D.J., II., Smith, T.: Deep learning on three-dimensional multiscale data for next-hour tornado prediction. Mon. Weather Rev. 148(7), 2837–2861 (2020)
Lapuschkin, S., Wäldchen, S., Binder, A., Montavon, G., Samek, W., Müller, K.R.: Unmasking clever HANs predictors and assessing what machines really learn. Nat. Commun. 10(1), 1–8 (2019)
Lary, D.J., Alavi, A.H., Gandomi, A.H., Walker, A.L.: Machine learning in geosciences and remote sensing. Geosci. Front. 7(1), 3–10 (2016)
Leavitt, M.L., Morcos, A.: Towards falsifiable interpretability research. arXiv preprint arXiv:2010.12016 (2020)
LeCun, Y., Bengio, Y., Hinton, G.: Deep learning. Nature 521(7553), 436–444 (2015)
LeCun, Y., Bottou, L., Bengio, Y., Haffner, P.: Gradient-based learning applied to document recognition. Proc. IEEE 86(11), 2278–2324 (1998)
Line, W.E., Schmit, T.J., Lindsey, D.T., Goodman, S.J.: Use of geostationary super rapid scan satellite imagery by the storm prediction center. Weather Forecast. 31(2), 483–494 (2016)
Malde, K., Handegard, N.O., Eikvil, L., Salberg, A.B.: Machine intelligence and the data-driven future of marine science. ICES J. Mar. Sci. 77(4), 1274–1285 (2020)
Mamalakis, A., Barnes, E.A., Ebert-Uphoff, I.: Investigating the fidelity of explainable artificial intelligence methods for applications of convolutional neural networks in geoscience. arXiv preprint arXiv:2202.03407 (2022)
Mamalakis, A., Ebert-Uphoff, I., Barnes, E.A.: Neural network attribution methods for problems in geoscience: a novel synthetic benchmark dataset. arXiv preprint arXiv:2103.10005 (2021)
Mamalakis, A., Yu, J.Y., Randerson, J.T., AghaKouchak, A., Foufoula-Georgiou, E.: A new interhemispheric teleconnection increases predictability of winter precipitation in southwestern us. Nat. Commun. 9(1), 1–10 (2018)
Mamalakis, A., Yu, J.Y., Randerson, J.T., AghaKouchak, A., Foufoula-Georgiou, E.: Reply to: a critical examination of a newly proposed interhemispheric teleconnection to southwestern us winter precipitation. Nat. Commun. 10(1), 1–5 (2019)
Mantua, N.J., Hare, S.R.: The pacific decadal oscillation. J. Oceanogr. 58(1), 35–44 (2002)
Mayer, K.J., Barnes, E.A.: Subseasonal forecasts of opportunity identified by an explainable neural network. Geophys. Res. Lett. 48(10), e2020GL092092 (2021)
McCABE, G.J., Dettinger, M.D.: Decadal variations in the strength of ENSO teleconnections with precipitation in the western united states. Int. J. Climatol. J. R. Meteorol. Soc. 19(13), 1399–1410 (1999)
McCabe, G.J., Palecki, M.A., Betancourt, J.L.: Pacific and Atlantic ocean influences on multidecadal drought frequency in the united states. Proc. Natl. Acad. Sci. 101(12), 4136–4141 (2004)
McGovern, A., et al.: Making the black box more transparent: understanding the physical implications of machine learning. Bull. Am. Meteor. Soc. 100(11), 2175–2199 (2019)
McKinnon, K.A., Poppick, A., Dunn-Sigouin, E., Deser, C.: An “observational large ensemble’’ to compare observed and modeled temperature trend uncertainty due to internal variability. J. Clim. 30(19), 7585–7598 (2017)
Molina, M.J., Gagne, D.J., Prein, A.F.: A benchmark to test generalization capabilities of deep learning methods to classify severe convective storms in a changing climate. Earth and Space Science Open Archive ESSOAr (2021)
Montavon, G., Lapuschkin, S., Binder, A., Samek, W., Müller, K.R.: Explaining nonlinear classification decisions with deep Taylor decomposition. Pattern Recogn. 65, 211–222 (2017)
Newman, M., et al.: The pacific decadal oscillation, revisited. J. Clim. 29(12), 4399–4427 (2016)
Newman, M., Compo, G.P., Alexander, M.A.: Enso-forced variability of the pacific decadal oscillation. J. Clim. 16(23), 3853–3857 (2003)
Overpeck, J.T., Meehl, G.A., Bony, S., Easterling, D.R.: Climate data challenges in the 21st century. Science 331(6018), 700–702 (2011)
Palmer, T.N., Anderson, D.L.T.: The prospects for seasonal forecasting-a review paper. Q. J. R. Meteorol. Soc. 120(518), 755–793 (1994)
Qiu, B., Chen, S.: Variability of the Kuroshio extension jet, recirculation gyre, and mesoscale eddies on decadal time scales. J. Phys. Oceanogr. 35(11), 2090–2103 (2005)
Redmond, K.T., Koch, R.W.: Surface climate and streamflow variability in the western united states and their relationship to large-scale circulation indices. Water Resour. Res. 27(9), 2381–2399 (1991)
Reichstein, M., Camps-Valls, G., Stevens, B., Jung, M., Denzler, J., Carvalhais, N., et al.: Deep learning and process understanding for data-driven earth system science. Nature 566(7743), 195–204 (2019)
Reinsel, D., Gantz, J., Rydning, J.: The digitization of the world from edge to core. Framingham: International Data Corporation, p. 16 (2018)
Rolnick, D., et al.: Tackling climate change with machine learning. arXiv preprint arXiv:1906.05433 (2019)
Rudin, C.: Stop explaining black box machine learning models for high stakes decisions and use interpretable models instead. Nat. Mach. Intell. 1(5), 206–215 (2019)
Russakovsky, O., et al.: ImageNet large scale visual recognition challenge. Int. J. Comput. Vis. 115(3), 211–252 (2015)
Samek, W., Montavon, G., Binder, A., Lapuschkin, S., Müller, K.R.: Interpreting the predictions of complex ml models by layer-wise relevance propagation. arXiv preprint arXiv:1611.08191 (2016)
Santer, B.D., et al.: Separating signal and noise in atmospheric temperature changes: the importance of timescale. J. Geophys. Res. Atmos. 116(D22), D22105 (2011)
Schonher, T., Nicholson, S.: The relationship between California rainfall and ENSO events. J. Clim. 2(11), 1258–1269 (1989)
Shen, C.: A transdisciplinary review of deep learning research and its relevance for water resources scientists. Water Resour. Res. 54(11), 8558–8593 (2018)
Shrikumar, A., Greenside, P., Kundaje, A.: Learning important features through propagating activation differences. In: International Conference on Machine Learning, pp. 3145–3153. PMLR (2017)
Shrikumar, A., Greenside, P., Shcherbina, A., Kundaje, A.: Not just a black box: learning important features through propagating activation differences. arXiv preprint arXiv:1605.01713 (2016)
Simonyan, K., Vedaldi, A., Zisserman, A.: Deep inside convolutional networks: visualising image classification models and saliency maps. arXiv preprint arXiv:1312.6034 (2013)
Sit, M., Demiray, B.Z., Xiang, Z., Ewing, G.J., Sermet, Y., Demir, I.: A comprehensive review of deep learning applications in hydrology and water resources. Water Sci. Technol. 82(12), 2635–2670 (2020)
Smilkov, D., Thorat, N., Kim, B., Viégas, F., Wattenberg, M.: SmoothGrad: removing noise by adding noise. arXiv preprint arXiv:1706.03825 (2017)
Sonnewald, M., Lguensat, R.: Revealing the impact of global heating on north atlantic circulation using transparent machine learning. Earth and Space Science Open Archive ESSOAr (2021)
Springenberg, J.T., Dosovitskiy, A., Brox, T., Riedmiller, M.: Striving for simplicity: the all convolutional net. arXiv preprint arXiv:1412.6806 (2014)
Stevens, A., et al.: Graph-guided regularized regression of pacific ocean climate variables to increase predictive skill of southwestern us winter precipitation. J. Clim. 34(2), 737–754 (2021)
Sundararajan, M., Taly, A., Yan, Q.: Axiomatic attribution for deep networks. In: International Conference on Machine Learning, pp. 3319–3328. PMLR (2017)
Tjoa, E., Guan, C.: A survey on explainable artificial intelligence (XAI): toward medical XAI. IEEE Trans. Neural Netw. Learn. Syst. 32, 4793–4813 (2020)
Toms, B.A., Barnes, E.A., Ebert-Uphoff, I.: Physically interpretable neural networks for the geosciences: applications to earth system variability. J. Adv. Model. Earth Syst. 12(9), e2019MS002002 (2020)
Toms, B.A., Barnes, E.A., Hurrell, J.W.: Assessing decadal predictability in an earth-system model using explainable neural networks. Geophys. Res. Lett. 48, e2021GL093842 (2021)
Trenberth, K.E.: The definition of El Nino. Bull. Am. Meteor. Soc. 78(12), 2771–2778 (1997)
Venter, O., et al.: Sixteen years of change in the global terrestrial human footprint and implications for biodiversity conservation. Nat. Commun. 7(1), 1–11 (2016)
Williams, B.A., et al.: Change in terrestrial human footprint drives continued loss of intact ecosystems. One Earth 3(3), 371–382 (2020)
Zeiler, M.D., Fergus, R.: Visualizing and understanding convolutional networks. In: Fleet, D., Pajdla, T., Schiele, B., Tuytelaars, T. (eds.) ECCV 2014. LNCS, vol. 8689, pp. 818–833. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-10590-1_53
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2022 The Author(s)
About this chapter
Cite this chapter
Mamalakis, A., Ebert-Uphoff, I., Barnes, E. (2022). Explainable Artificial Intelligence in Meteorology and Climate Science: Model Fine-Tuning, Calibrating Trust and Learning New Science. In: Holzinger, A., Goebel, R., Fong, R., Moon, T., Müller, KR., Samek, W. (eds) xxAI - Beyond Explainable AI. xxAI 2020. Lecture Notes in Computer Science(), vol 13200. Springer, Cham. https://doi.org/10.1007/978-3-031-04083-2_16
Download citation
DOI: https://doi.org/10.1007/978-3-031-04083-2_16
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-04082-5
Online ISBN: 978-3-031-04083-2
eBook Packages: Computer ScienceComputer Science (R0)