This chapter implements a design feature in which investors in the modern tontine are assured they will be made whole if they happen to die prior to receiving their original investment back in periodic payments. This is the symmetric equivalent of a cash-refund income annuity, which incidentally is the most popular rider in the US market. Now obviously, being that we are operating in a universe of modern tontines it’s impossible to guarantee or to promise anything. Nevertheless, this chapter begins by presenting what I am officially labelling v2.0 of the tontine R-script. In contrast to v1.0, this simulation algorithm adds an expected cash refund payment to those investors who aren’t fortunate enough to be blessed with longevity. In other words, both people who die (early) and people who live (late) will get something from the modern tontine. This feature must come at the expense of reduced tontine dividend payouts. How much this actually costs investors in basis points and whether or not the fund is able to deliver on this expected money back feature are questions that will be addressed under a variety of numerical scenarios. Finally, the chapter concludes with another feature, one in which investors are allowed to change their mind and lapse or surrender the tontine. This is v3.0 and the final version for this book.

5.1 Set Your Seed

I have noted that your simulation results will differ from what you see in the chapter due to the nature of randomness. The time has come to dispense with that rather inconvenient discrepancy with a simple fix: set.seed(). Do that before you generate random numbers with the same seed as mine and your results will be identical. Let’s give it a try. Start with 1000 investors who are x = 65 years old and simulate deaths before the age of y = 80. Recall that in a Gompertz model in which (x = 65, m = 90, b = 10), the 15-year survival probability is: TPXG(65,15,90,10) is 75.14%, and probability of dying during those 15 years is: 24.86%. We anticipate losing one quarter within the first 15 years, but the realized number will be random. It can be generated with the following script:

set.seed(1693) rbinom(5,1000,0.2486) > 254 242 264 242 279

The rbinom() command is quite familiar by now, but the new set.seed(1693) command assures the user they will generate and see the same 5 random numbers noted above. Give it a try and see how it works. Run the above command rbinom(5,1000,0.2486) without setting the seed first and your five numbers will obviously differ from mine. But by forcing the R-script to initialize the random numbers at a starting seed value of 1693—which is completely arbitrary, by the way—your simulation results will match mine. The results and set of five random numbers represent possible realizations of total deaths over the first 15 years of the tontine pool. As a refresher, in one scenario 254 people die and in another 242 die, etc. The important thing is that you have now learned how to generate simulation results that precisely match the ones in the text. If you want to see different results—-or you don’t like mine—then pick any other initial number for the seed; other than 1693 of course. If you are curious about what exactly the set.seed() does and how it relates to linear congruential generators, then please google exactly that phrase. And, if you are wondering why I personally picked those four numbers for my seed, when in fact you can select any number of digits, the answer is rather trite: It’s the year in which England launched its first government-sponsored tontine, a.k.a. King William’s Tontine.

5.2 Can You Get Your Money Back?

Although it’s possible for traditional insurance companies to sell conventional life annuities with a guaranteed refund-at-death feature, an investment company attempting to do so with a modern tontine is likely to run into some problems. There are three subtle reasons for this. First, conventional life annuity offerings are predicated on the law of large numbers, which assumes a very (very) large pool of annuitants. This (theoretically) guarantees that realized mortality will converge to the assumed mortality and that what happens is exactly as expected. In other words, by virtue of the large size of the annuitant pool an insurance company can predict with much greater certainty when they will have to pay death benefits, as well as the magnitude of those payments. In contrast, an investment fund company sponsoring a modern tontine with a mere few thousand investors can’t afford to rely on the LLN. Recall that our simulations assumed a small finite group, a far cry from infinity, especially later when survivors decline. Second, insurance companies issue life annuities to different ages and issue life insurance policies across the entire lifecycle. Indeed, the nature of their business centres around continuously increasing the size of the pool. In our basic v1.0 design, the pool is closed and doesn’t admit newcomers after the initial period.

The third and final reason conventional insurance companies can offer and guarantee life annuities with a refund-at-death with confidence is that they invest the underlying assets in ultra-safe bonds and fixed-income products, which yield positive interest rates under most normal economic circumstances. Yes, interest rates might be at historical lows (today) and bonds themselves can lose value (tomorrow) if-and-when rates increase, but the investment portfolio of life insurers (or at least their general account) is extremely safe and highly regulated. What this effectively means is that insurance companies are unlikely to find themselves in a situation or simulated scenario in which they don’t have enough money to pay promised death benefits. Contrast those safe and staid companies with an upstart investment or fund company that allocates the assets underlying the modern tontine to fluctuating stocks and bonds. Even if the standard deviation of returns σ is quite low, there is still a non-zero probability returns will be negative during the first few years (a.k.a. sequence of returns) and a large number of investors die early, leading to the rapid decline and perhaps even bankruptcy of the modern tontine.

At the risk of yelling—and although the next few pages are entirely focused on allowing for a refund-at-death feature—I should warn readers and users that unlike the basic (v1.0) modern tontine with a self-correcting payout thermostat, death benefits introduce a completely new risk into the picture: mission failure, financial ruin and bankruptcy. So, while a few hundred or even thousand simulations might not uncover or locate those rare scenarios, it’s a theoretical possibility that is ever present. Moreover, at the end of this chapter when I introduce additional features that allow for ongoing liquidity this concern will be even more acute. My yelling will get louder. This is exactly why sponsors of modern tontines should be (and are) careful to attach the appellation expected to the phrase refund-at-death, or anything else for that matter. I will call it a death covenant and thus avoid the charged term guarantee.

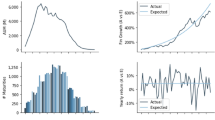
To set the stage for why the R-script must be modified in a non-trivial manner, Fig. 5.1 graphically displays what would happen if a tontine sponsor decided to manage a fund in which the dividend is (imprudently) set at the original κ 1 value of 7.67%, per the results in the prior chapter but also provides a death benefit to beneficiaries. If at the time of (early) death the annuitant had not received a sum total of f 0 = $100, 000 back in dividends, the beneficiaries would receive the unpaid capital. That is akin to a cash-refund immediate annuity, when sold and issued by an insurance company. Go back to the end of Chap. 2 for a refresher.

Fig. 5.1
figure 1

When promises are greater than reserves (98% C.I.)

Full size image

If you look at the figure from a distance, it echoes the footprint of a normal (stochastic) tontine dividend whose cone of uncertainty increases over time. But upon careful inspection and regression, you will notice that the average tontine dividend drifts downward over time, and in a statistically significant manner. The original 7.67% tontine dividend is not sustainable over time because the fund assets are leaking death benefits, and rather large amount in the early life of the fund when TCPAY is rather small. Yes, eventually this fund stabilizes when everyone has received more than their original f 0 = $100, 000 back in dividends, but the new plateau is at a much lower (average) level than $7, 671. What does all of this mean? Well, if the tontine sponsor wants a stable tontine dividend stream (a.k.a. regression coefficient of zero), they must reduce the original payout. The usual κ 1 is too generous.

5.3 Modern Tontine v2.0

In this section I present the basic R-script for a modern tontine that anticipates and reserves for a refund-at-death. To be clear and perhaps at the risk of over-explaining, this entails promising investors some tontine dividend, plus if they happen to die before receiving their entire (for example) $100,000 investment back, their beneficiary will receive a one-time death benefit of $100,000 minus (what I previously labelled) TCPAY(), if positive. The relevant question then becomes how much does this design feature cost? More importantly, how much can the fund sponsors afford to pay out in stable tontine dividends each year, and yet still have enough reserves to pay those anticipated death benefits? The following script does all that (and more). I will break down the script into three distinct segments that should be fused and run together, but will explain the main features of each individually. Many of the commands, loops and algorithms will look familiar and echo v1.0.

# Modern Tontine (MoTo) Fund Version 2.0 # Cash Refund at Death with Proper Reserve set.seed(1693) # Calculate Gompertz survival probability. TPXG<-function(x,t,m,b){exp(exp((x-m)/b)*(1-exp(t/b)))} # Calculate probability of death between times t1 and t2. TQXG<-function(x,t1,t2,m,b){TPXG(x,t1,m,b)-TPXG(x,t2,m,b)} # Value temporary life annuity from age x to age y. TLIA<-function(x,y,r,m,b){   APV<-function(t){exp(-r*t)*TPXG(x,t,m,b)}   sum(APV(1:(y-x)))} # Value temporary life annuity with $1 reducing death benefit. TLIA_RDB<-function(x,y,r,m,b,RDB){   periods<-(y-x)   value<-0   for(i in 1:periods){     PV<-exp(-r*i)     # The next two lines should be combined.     value<-value+TPXG(x,i,m,b)*PV+max(RDB-(i-1),0)     *TQXG(x,(i-1),i,m,b)*PV}   value} # Function searches for RDB value that equals TLIA_RDB. RTLIA<-function(x,y,r,m,b){   RTLIA1<-function(a){abs(TLIA_RDB(x,y,r,m,b,a)-a)}   optimize(RTLIA1,interval =c(0,1/(r+0.0001)))$minimum}

After the set.seed() command that ensures readers and users can replicate my numbers, the R-script refreshes TPXG() and introduces the TQXG command, which is the probability of dying in between two given times t1<t2, assuming the annuitant is alive at age x. After those relatively basic Gompertz-based functions, the R-script moves-on to define the previously used temporary life annuity factor TLIA, and then the temporary life annuity with a reducing death benefit, denoted by TLIA_RDB. As explained in the technical background of Chap. 2, such an annuity offers annual payments of $1 plus an additional death benefit of RDB, but reduced by $1 for every year the person has lived. So, if they die after 5 years, the death benefit is RDB minus 5, etc.

Remember that if-and-when the entire RDB has been returned to the investor (while they are alive), the death benefit obligation disappears ceases to exist. For example, if the RDB was set to $10 and the individual happens to die after year 10, their death benefit will be zero in that scenario. Note that in this function the RDB is a completely free parameter, entirely arbitrary and up to the user. It could be $100, which will take 100 years to reduce to zero, or a mere $5, which will terminate after 5 years. Of course, the higher the RDB specified by the user, the higher the numerical value of TLIA_RDB. It costs more.

The final RTLIA function in the above-segment uses the built-in R function optimize to locate the numerical value of the TLIA_RDB function that is equal to RDB itself. This is a fixed point argument of iterative technique required to obtain the present value of the annuity. For example RTLIA(65,100,0.04,90,10)=14.335, which means that TLIA_RDB with a reducing death benefit of $14.335, is exactly equal to $14.335. Play around with this function before you move-on to the next segment, so you get a sense of how TLIA differs from RTLIA, and why the latter is higher (and more expensive) than the former.

The next (second) segment within the v2.0 code is almost identical to its sibling in v1.0. It starts out by initializing the parameters used in the simulation, and no new parameters are added or used at this stage. The only change from the initial version of the algorithm—and really this is the only difference—is that I have added a new matrix AGDEB that is intended to keep track of the total amount that is paid to the people who die in each one of the N simulation paths, during each of the TH years. The simulation of life and death, as well as the investment returns is identical to v1.0. One can easily randomize the modal value of the Gompertz parameter m, or the dispersion parameter b, using the ideas discussed in Chap. 3.

set.seed(1693) # All base parameters are set here. x<-65; m<-90; b<-10; GL0<-1000; TH<-30; N<-10000 EXR<-0.04; SDR<-0.03; r<-0.04; f0<-100 # Placeholder for our data. kappa<-c() GLIVE<-matrix(nrow=N,ncol=TH) GDEAD<-matrix(nrow=N,ncol=TH) TCPAY<-matrix(nrow=N,ncol=TH) AGDEB<-matrix(nrow=N,ncol=TH) PORET<-matrix(nrow=N,ncol=TH) DETFV<-matrix(nrow=N,ncol=TH) TONDV<-matrix(nrow=N,ncol=TH) # Compute Deaths and Survivors Here (V2.0, no change). for (i in 1:N){   GDEAD[i,1]<-rbinom(1,GL0,1-TPXG(x,1,m,b))   GLIVE[i,1]<-GL0-GDEAD[i,1]   for (j in 2:TH){     GDEAD[i,j]<-rbinom(1,GLIVE[i,j-1],1-TPXG(x+j-1,1,m,b))     GLIVE[i,j]<-GLIVE[i,j-1]-GDEAD[i,j]   }} # Compute Investment Returns Here (V2.0, no change) for (i in 1:N){   PORET[i,]<-exp(rnorm(TH,EXR,SDR))-1}

The third and final segment is the primary source of the difference between the “no death benefit” v1.0 and the “reimbursement covenant” v2.0. More specifically, the new matrix AGDEB, which was defined in the second segment and which keeps track of the new death benefits, now gets populated. This then affects the evolution of the fund itself DETFV as well as the tontine dividends TONDV. I’ll delve into specific aspects of the code a little bit later. For now, the R-script must start by adjusting the payout rate vector κ, a process that isn’t as simple or easy as the prior temporary life annuity factor.

# Revised Initial Payout Rate to Provide Death Benefit kappa[1]<-1/RTLIA(x,x+TH,r,m,b) # The next two lines should be combined. for (j in 2:TH){kappa[j]<-1/   TLIA_RDB(x+j-1,x+TH,r,m,b,max(1/kappa[1]-j+1,0))} # Compute fund values and dividends. for (i in 1:N){   # First we address the first period.   # Define first dividend (per individual).   TONDV[i,1]<-kappa[1]*f0   # Define cumulative dividends paid (per individual).   TCPAY[i,1]<-TONDV[i,1]   # Define aggregate death benefits paid (for fund).   AGDEB[i,1]<-f0*GDEAD[i,1]   # Define total paid out by fund this period.   outflow<-TONDV[i,1]*GLIVE[i,1]+AGDEB[i,1]   # Define fund value.   DETFV[i,1]<-f0*GL0*(1+PORET[i,1])-outflow   # Loop through remaining periods.   for (j in 2:TH){     if (GLIVE[i,j]>0){       # Define dividend per individual in year j.       TONDV[i,j]<-kappa[j]*DETFV[i,j-1]/GLIVE[i,j-1]}     else {TONDV[i,j]<-0}     # Define cumulative dividends paid to date (per person).     TCPAY[i,j]<-TCPAY[i,j-1]+TONDV[i,j]     # Define aggregate death benefits paid (for fund).     AGDEB[i,j]<-max(f0-TCPAY[i,j-1],0)*GDEAD[i,j]     # Define total paid out by fund this period.     outflow<-TONDV[i,j]*GLIVE[i,j]+AGDEB[i,j]     # Define current fund value.     DETFV[i,j]<-DETFV[i,j-1]*(1+PORET[i,j])-outflow}}

For now, I suggest readers run the above-noted code as-is and ensure that it compiles correctly on their platform or system. To verify that your code is indeed working properly, please confirm the following three numbers. First, the mean(TONDV) should be exactly 7.123656, which is 12 cents over 7 dollars in tontine dividends per $100 investment. Second, the mean value of the underlying fund value in year 30 should be mean(DETFV[,30])=0.6662558 thousand dollars. Third and finally the slope coefficient of the above regression should be -0.0019254 and statistically indistinguishable from zero. Remember that that lack of trend (or slope) is good news and a sign of tontine stability, which is something I explained previously in Chap. 4.

Although all these numbers were generated by simulation, the set.seed (1693) ensures that your results are identical to mine. Once you confirm v2.0 is indeed working correctly, I would urge users to plot the tontine dividends and plot the fund values with the usual scripts, to visually confirm everything is in good order.

In fact, perhaps change the (x, m, b) parameters up or down, to confirm the tontine payouts move in the proper direction. Change (r = ν, σ) and confirm that your results are reasonable, and perhaps even change the set.seed() a few times, to see how the simulation results change with different initial seed values.

Congratulations! You have learned to ride a simple bike without falling off, even though you aren’t a mechanical engineer. Now it’s time to dig deeper into the theory and understand exactly what this algorithm (or mechanism) is doing, and specifically how to use and interpret the new AGDEB numbers.

5.4 The Intuition of Refunds

Start by examining Fig. 5.2, which is a picture that simply doesn’t exist in v1.0 of the tontine design. It displays the range of payouts that the tontine sponsor must make to all the investors who die in the first few years, and whose beneficiaries demand a return of the unearned investment under the reimbursement covenant. Notice the interesting parabolic shape of this figure. Initially, around age x = 65, few investors are “expected” to die, so the payout is relatively small. Then, as age increases and mortality rates accelerate the number of investors dying continue to increase—think of the PDF of the remaining lifetime random variable—but the deceased have died sufficiently late enough so they have recovered a large part of their original investment. Finally, somewhere around year 15 or so, although deaths continue to accelerate (per the Gompertz law) most of the deceased have already received their original investment back in tontine dividends and the beneficiaries have no claim on the tontine fund. The obligation is very quickly and rapidly defused somewhere between the 17th and 18th year. After that date, the sponsors can concern themselves exclusively with the living, since the deaths will generate no obligations. The next and final question with this revised mandate is but are the dividends stable?

Fig. 5.2
figure 2

Total death benefits paid to investors (98% C.I.)

Full size image

5.5 The Tontine Dashboard

In this section I would like to introduce and present a standardized way of reporting simulation results and in particular displaying the distribution of tontine dividends, fund values and other related financial information. I call this the dashboard. Here is how to interpret the results in Table 5.1.

Table 5.1 Tontine dashboard: dividend distribution; replicate with set.seed(1693)
Full size table

We start with GL0=1000 investors, each of whom contribute $100, 000 to the tontine pool, for a total initial fund of $100 Million, which is invested in a portfolio of assets that are expected to grow at a (continuously compounded) rate of: ν = 4% per year, with a standard deviation of: σ = 3%. The valuation (a.k.a. crediting) interest rate denoted by r is also set to be 4%, which doesn’t necessarily have to be the case. Finally, the demographic or biometric parameters are Gompertz, with (x = 65, m = 90, b = 10), and a time horizon of TH=30 years, with a fund liquidation age of y = 95, for those who survive. Now, being that we are simulating a v2.0 modern tontine with a refundable investment death benefit, the initial tontine dividend must be set using the RTLIA function, and not the TLIA function from Chap. 3.

1/RTLIA(65,95,0.04,90,10) > 0.07073756 1/TLIA(65,95,0.04,90,10) > 0.07670865

This means that the first year’s tontine dividend—paid at the very end of year one, when investors are all about to turn 66—is 7.073756% of $100,000, or $7, 074 per survivor. That is the first data column in Table 5.1 and doesn’t vary by scenario. That dividend is set in stone at time T = 0 and will have to be paid out to all survivors regardless of the performance of markets as reflected by PORET or the actual number of survivors as reflected by GLIVE.

It’s important to remember this small modicum of risk that affects the way I have constructed the modern tontine. Namely, the payout rates are stated and declared at the start of the year (or period), but only paid to survivors at the end. This is like an interest rate on a bank deposit, or a dividend that is declared today but payable to the holders of record at some future time. Note that investors who die in that first year, before reaching the end of their 65th year of life, will be entitled to receive their entire f 0 = $100, 000 investment as part of the death benefit reimbursement covenant. All of this discrepancy in timing adds some additional commitments and risks to the sponsor of the modern tontine. Moreover, they certainly can’t allocate the $100 Million fund to bitcoin or something equally volatile, unless the payments themselves are made in those units. The reimbursement covenant is the precise reason the payout to survivors is pegged at the RTLIA value of approximately 707 basis points, versus the TLIA value of 767 basis points. The survivors sacrifice 60 basis points of dividends (every year, for 30 years) to ensure enough funds are set aside for those who die.

Moving on to the other columns, which by now should be familiar and well understood, the table displays the range of values—from the 1st percentile to the 99th percentile—in years 5, 10, 20 and 30. To be precise, they are values at the end of those years but are set and known at the beginning of the year. Think of an ordinary annuity versus an annuity due in the basic time value of money. The median tontine dividend is stable—remember the regression coefficient is statistically indistinguishable from zero—and fluctuates between $7000 and $7100 per year. But, what’s clear from the columns is that as time marches on the pool shrinks and the number of survivors diminish, the range (and standard deviation) grows.

5.6 Lapses, Surrenders and Other Regrets

In this final section of the chapter I would like to address a more complex question. Namely, whether or not it’s possible to design a modern tontine in which individual investors are allowed to voluntarily liquidate, sell or surrender (also known as lapse) and receive the market value in cash instead of units. Let’s think about this process carefully before we rush to the R-scripts and the simulation laboratory. At first glance—especially obvious to anyone within the actuarial and insurance world—providing this sort of liquidity to investors would lead to a problem economists call anti-selection. Namely, if the investor happened to (sadly, unfortunately) get diagnosed with a life threatening disease, meaning they won’t be around for much longer and won’t benefit from the longevity insurance, they would immediately liquidate and ask for their money back. So what, you ask? Well, the problem with that behaviour is that it would leave only the healthy people in the modern tontine pool, which would then erode if not eliminate the mortality credits for everyone else. Of course, selling you shares and liquidating your investments might not be the first (or even second or third) thing on your mind should you happen to receive such horrible news, but it would definitely be something on the To Do list, as the end came near. Namely, sell, liquidate, lapse and get some money from this before it dies with you.

In fact, my first reaction when I was asked about adding a liquidity provision to a modern tontine was a straight out no. It would spring a leak in the pool and wouldn’t allow me to assume (nice, smooth) Gompertz mortality and longevity terminations.

But on further and deeper inspection it really depends on how high (or low) the initial payout rate was set, and what was assumed at the time of pricing. After all, if the payout rate κ is set low-enough (think zero) you could allow any behaviour. Moreover, it should be possible to offer some amount of liquidity (although certainly not 100%), when the modern tontine includes a covenant that rebates unreturned capital (UC) at death, which was associated with a lower κ value. Here’s the logic. If investors are allowed to leave the fund early and voluntarily but are penalized for this premature departure by forfeiting some of their equity in the fund to the benefit of others, perhaps such behaviour might actually benefit everyone else. After all, had this person who was just diagnosed with cancer died with unreturned capital, they would have received 100% of the UC. Hence, if the modern tontine sponsor allows them to leave early out of compassion, and they forfeit some of the UC, then the rest of the investors in the fund might not lose from this leniency and could actually benefit. Remember that the initial κ payout is lower when the fund includes a death benefit covenant.

Another point to keep in mind is that the more of the UC investors forfeit if they choose to lapse, the less likely it is that investors would actually choose to lapse and take this lower payout. So the lapsation rate and the lapsation penalty are not independent in the real world; however, for simplicity here we will treat them as two independent parameters.

In sum, despite concerns over anti-selection, it’s possible to offer liquidity provided that nothing is guaranteed and that this feature—like the death benefit—is positioned as a covenant, one that can be bypassed or even ignored in extreme (negative) market conditions.

With this out of the way, we can get back to the simulation laboratory and modify the script so that it accounts for this feature. Namely, we will now simulate tontine payouts when a random number of investors decide to liquidate their investment every year—while there is still some UC left—and then pay a penalty. Now, one could model the rate at which investors lapse or surrender the modern tontine in many different ways, but in what follows I will assume that lapsing is just another form of dying. Namely, there is a force of lapsation similar to a force of mortality and it removes people from the GLIVE matrix, just like dying does.

I won’t assume Gompertz lapsation—which has no empirical basis and is unnecessarily complex—and instead will assume a constant force of lapsation, which means that lapse time is exponentially distributed. Yes, this assumption is completely ad hoc, but I think of this as (for example) decrementing or losing 2% of people every single year for the first few years, but to a third state that is neither live nor dead. Those who move into that third state are entitled to receive 80% or 70% or perhaps as low as 50% of their unreturned capital. Had they (patiently) waited to die their heirs and estate would have received 100% of the UC, but perhaps they need the money now, or they don’t want to wait, etc. Remember though, once the UC has been reduced to zero and all the original money has been returned as tontine dividends, those who lapse or die receive nothing back.

In the next few pages I will describe how to simulate the tontine dividends when random (non-strategic) lapsation is allowed, which will require two more new parameters, or perhaps even vectors that are time dependent. The first is the (deterministic, known, fixed) annual lapse rate, which I’ll label η j (Greek eta), think of 2% a year for the first 15 years for example. And the second is the penalty or surrender charge that is paid upon live exit—money that is shared between the remaining investors over time—when the shares are lapsed. I’ll use the symbol and variable dsc to remind us this is a type of deferred surrender charge. I repeat that the η j parameter represents a deterministic force of lapsation that is uncorrelated with either investment returns PORET or the number of deaths GDEAD or anything else that is moving in the model. It’s superimposed exogenously without assuming any dynamic behaviour or optimizing behaviour. This is the first (baby) step. That said, to keep everyone safe, I will not change or increase the initial payout κ to account for this lapsation in advance. In other words, using an actuarial term, the tontine will not be lapse supported. If-and-when these investors lapse, the extra money will be added to the tontine fund as if it were another type of investment return and then shared over time.

With all of that preamble and introduction out of the way, here are the changes that must be made to v2.0 so that users can simulate tontine dividends, fund values and survivors when we add a (deterministic) lapsation rate. For the sake of preserving space, I will display the changes that have to be made to the R-script, as opposed to printing yet-again the entire script, which I will present at the very end of this chapter. Here is the first addition to the script, to create version v3.0.

# Parameters that Govern Lapsation and Redemption eta<-c(rep(0.02,15),rep(0,TH-15)); dsc<-0.25 LAPSE<-matrix(nrow=N, ncol=TH) AGLAP<-matrix(nrow=N,ncol=TH)

Note that these few lines initialize the lapsation rate vector η at 2% per year for the first 15 years, and then zero lapsation after year 15. Why? Because for the most part there is nothing left to lapse (or die) for, since the UC value is zero and the entire original principal has been returned. Remember that if you are paying out (on average) κ 1 = 7.07%, then after 1∕κ 1 = 14.14 years the original principal has been paid out (again, on average). By year 15, those who lapse or die would get nothing, even in the absence of a dsc. The above segment also includes the initialization of the two new matrices that will keep track of the number of people who lapse, as well as the amount of money they will extract from the fund.

The next step is to actually generate and fill-in the LAPSE matrix, which requires the following bit of R-script. Technically this requires just two extra lines of code, and modifications to two other ones, but I have reproduced the entire section here so that readers can see the parallels and symmetry between GDEAD and LAPSE.

set.seed(1693) for (i in 1:N){   LAPSE[i,1]<-rbinom(1,GL0,eta[1])   GDEAD[i,1]<-rbinom(1,GL0-LAPSE[i,1],1-TPXG(x,1,m,b))   GLIVE[i,1]<-GL0-GDEAD[i,1]-LAPSE[i,1]   for (j in 2:TH){     LAPSE[i,j]<-rbinom(1,GLIVE[i,j-1],eta[j])     # The following two lines should be combined.     GDEAD[i,j]<-rbinom(1,GLIVE[i,j-1]-LAPSE[i,j]                        ,1-TPXG(x+j-1,1,m,b))     GLIVE[i,j]<-GLIVE[i,j-1]-GDEAD[i,j]-LAPSE[i,j]   } }

Note that the first thing that happens each year is people decide whether or not to lapse. If people choose to lapse they are out of the model and can no longer be added to the GDEAD count, even if they die that year. Here is the logical flow. We simulate people who lapse during the year by using the familiar rbinom random number generator based on the number of investors alive at the beginning of the year, and our lapsation parameter η. Then we use the same process, but with the Gompertz probability, for the number of people who die, out of the people who did not lapse. In this particular run we assume the annual lapsation rate η (eta) is 2% per year for the first 15 years, and then zero afterwards. To delve deeper into the code, once the η vector is zero the LAPSE matrix will consist of a bunch of zeros (which might be a bit wasteful in terms of storage space). All those zeros are generated from a binomial distribution that is degenerate (which is also a bit wasteful). The point here is to visualize and intuit the three states: Alive, Dead and Lapsed. Finally, we are ready to compute tontine payouts and fund values. That actually requires a wholesale rewriting of the final section in the code.

# Compute fund values and dividends. for (i in 1:N){   # First we address the first period.   # First dividend (per individual).   TONDV[i,1]<-kappa[1]*f0   # Cumulative dividends paid (per individual).   TCPAY[i,1]<-TONDV[i,1]   # Aggregate death benefits paid (for fund).   AGDEB[i,1]<-f0*GDEAD[i,1]   # Aggregate lapsation payout (for fund).   AGLAP[i,1]<-f0*LAPSE[i,1]*(1-dsc)   # Total paid out by fund this period.   outflow<-TONDV[i,1]*GLIVE[i,1]+AGDEB[i,1]+AGLAP[i,1]   # Fund value.   DETFV[i,1]<-f0*GL0*(1+PORET[i,1])-outflow   # Loop through remaining periods.   for (j in 2:TH){     if (GLIVE[i,j]>0){       # Dividend in year j (per individual).       TONDV[i,j]<-kappa[j]*DETFV[i,j-1]/GLIVE[i,j-1]}     else {TONDV[i,j]<-0}     # Cumulative dividends paid to date (per individual).     TCPAY[i,j]<-TCPAY[i,j-1]+TONDV[i,j]     # Aggregate death benefits paid (for fund).     AGDEB[i,j]<-max(f0-TCPAY[i,j-1],0)*GDEAD[i,j]     # Aggregate lapsation payout (for fund).     AGLAP[i,j]<-max(f0-TCPAY[i,j-1],0)*LAPSE[i,j]*(1-dsc)     # Total paid out by fund this period.     outflow<-TONDV[i,j]*GLIVE[i,j]+AGDEB[i,j]+AGLAP[i,j]     # Current fund value.     DETFV[i,j]<-DETFV[i,j-1]*(1+PORET[i,j])-outflow   } }

The above segment replaces the relevant section in v2.0. Note that the PORET matrix doesn’t change, since lapsation doesn’t really affect investment returns, although it does behave like a subsidy at time. In fact, the tontine dividend in the first year doesn’t change from the basic simulation. The new matrix AGLAP computes the total amount that is paid out to all the lapsers. Notice how I have (once again) broken the computation down into two parts: The first year (loop) and then the remaining (TH-1) years. In either loop, the amount of money the lapsers are entitled to is their unreturned capital (UC), which is the original investment f0 minus the TCPAY matrix, multiplied by one minus the surrender charge dsc. Note that I have also added the variable outflow just to keep things clear and neat. Other than this extra little leakage from decumulation tontine fund, nothing much has changed. We are ready for some numerical results and figures.

Running v3.0 in which the Gompertz and return parameters are the usual suspects, but the new η = 2% for 15 years and the surrender charge is 25%, and seed of 1693 leads to a median tontine dividend (for survivors) of $7, 964 per year. Make sure you replicate this (with my seed). The total standard deviation across the N = 1000 scenarios is 18.5%. The slope of the canonical diagnostic regression is positive $71 per year, and the intercept is 7.122 units and obviously quite significant statistically. What does this all mean? Well, survivors can expect higher, larger and better tontine dividends over time. Recall from earlier in the chapter that when the lapse rate was set to zero (v2.0) the median tontine dividend was $7, 074, which was almost $900 per year lower. Why better now? Thank the lapsers who leave behind 25% of their UC.

Now, what happens if we reduce the dsc value from a 25% penalty to no penalty at all, but still assume that 2% of live investors lapse and surrender their investment every year? You can die or you can lapse. In both cases you get the UC. Well, if you run the R-script, the median tontine dividend is now $7584, which is lower than the earlier-noted $7964, applicable when the dsc is set to 25%. Intuition? Less money is forfeited to the fund so the average tontine dividend over time is lower. But even so, the $7584 is still higher than the baseline (non-lapsing) $7074 tontine dividend. Why? Because the lapsers are forfeiting the interest and investment gains they would have earned on the unreturned capital. Think about this carefully and perhaps even play around with different values of dsc so you can intuit how it impacts tontine dividends. Figure 5.3 displays the (90% CI) output from four different values of the surrender charge. In the upper left-hand corner you can see the case when the dsc=0 and 100% of the UC is paid out upon lapse, and the lower right-hand corner represents the case when those who lapse get a mere 1% (i.e. almost nothing) back. Naturally, everyone else gains (more) from that. Finally, play around with different lapse rate assumptions and see what happens. Things get a bit wild towards the end, and you will see why I chose to display the 90% and not 99% confidence intervals.

Fig. 5.3
figure 3

Tontine dividends with liquidity (90% C.I.)

Full size image

Note that in this script we did not change κ to account for lapsation. Therefore the dividends in this model are not expected to be constant (as you can see in Fig. 5.3), like we would like to see in a proper tontine model. We did not create a new type of tontine that allows for lapsation, and we merely demonstrated what dividends would look like if we allowed lapsation but kept the original v2.0 tontine dividend structure. To actually create a tontine that accommodates lapastion and keeps expected dividends constant, we may require numerical (non-analytic) methods.

5.7 The Final Act: Version 3.0

Finally, although some of this might seem repetitive, for the sake of completeness I now reproduce the entire and most recent version of the R-script in one central location. This version 3.0 represents the final structural evolution of the modern tontine simulation.

# Modern Tontine Fund (MoTo) Version 3.0 # Cash Refund at Death with Reserves and Lapses. set.seed(1693) # All base parameters are set here. x<-65; m<-90; b<-10; GL0<-1000; TH<-30; N<-10000 EXR<-0.04; SDR<-0.03; r<-0.04; f0<-100 # Parameters that Govern lapsation and redemption. # Replace 0.00 with appropriate rate during 15 years. eta<-c(rep(0.00,15),rep(0,TH-15)); dsc<-0.0 # Calculates Gompertz survival probability. TPXG<-function(x,t,m,b){exp(exp((x-m)/b)*(1-exp(t/b)))} # Calculate probability of death between times t1 and t2. TQXG<-function(x,t1,t2,m,b){TPXG(x,t1,m,b)-TPXG(x,t2,m,b)} # Values temporary life annuity from age x to age y. TLIA<-function(x,y,r,m,b){   APV<-function(t){exp(-r*t)*TPXG(x,t,m,b)}   sum(APV(1:(y-x)))} # Values temporary life annuity with $1 reducing death benefit. TLIA_RDB<-function(x,y,r,m,b,RDB){   periods<-(y-x)   value<-0   for(i in 1:periods){     PV<-exp(-r*i)     # The next two lines should be combined.     value<-value+TPXG(x,i,m,b)*PV+max(RDB-(i-1),0)     *TQXG(x,(i-1),i,m,b)*PV}   value} # Function searches for RDB value that equals TLIA_RDB. # This is the fixed point of the TLIA_RDB function. # RTLIA Provides Declining Death Benefit, Replacing Basic TLIA. RTLIA<-function(x,y,r,m,b){   RTLIA1<-function(a){abs(TLIA_RDB(x,y,r,m,b,a)-a)}   optimize(RTLIA1,interval =c(0,1/(r+0.0001)))$minimum} # Placeholder for our data. kappa<-c() GLIVE<-matrix(nrow=N,ncol=TH) GDEAD<-matrix(nrow=N,ncol=TH) LAPSE<-matrix(nrow=N, ncol=TH) TCPAY<-matrix(nrow=N,ncol=TH) AGDEB<-matrix(nrow=N,ncol=TH) AGLAP<-matrix(nrow=N,ncol=TH) PORET<-matrix(nrow=N,ncol=TH) DETFV<-matrix(nrow=N,ncol=TH) TONDV<-matrix(nrow=N,ncol=TH) # Compute lapses, deaths and survivors. for (i in 1:N){   LAPSE[i,1]<-rbinom(1,GL0,eta[1])   GDEAD[i,1]<-rbinom(1,GL0-LAPSE[i,1],1-TPXG(x,1,m,b))   GLIVE[i,1]<-GL0-GDEAD[i,1]-LAPSE[i,1]   for (j in 2:TH){     LAPSE[i,j]<-rbinom(1,GLIVE[i,j-1],eta[j])     # The next two lines should be combined.     GDEAD[i,j]<-rbinom(1,GLIVE[i,j-1]                        -LAPSE[i,j],1-TPXG(x+j-1,1,m,b))     GLIVE[i,j]<-GLIVE[i,j-1]-GDEAD[i,j]-LAPSE[i,j]}} # Continuously Compounded Return is Normally Distributed. # The Effective Annual Return is placed into PORET. for (i in 1:N){   PORET[i,]<-exp(rnorm(TH,EXR,SDR))-1} # The initial payout rate for Modern Tontine fund. # RTLIA (instead of TLIA) includes the declining death benefit. kappa[1]<-1/RTLIA(x,x+TH,r,m,b) # The next two lines should be combined. for (j in 2:TH){kappa[j]<-   1/TLIA_RDB(x+j-1,x+TH,r,m,b,max(1/kappa[1]-j+1,0))} # Compute fund values and dividends. for (i in 1:N){   # First we address the first period.   # Define first dividend (per individual).   TONDV[i,1]<-kappa[1]*f0   # Define cumulative dividends paid (per individual).   TCPAY[i,1]<-TONDV[i,1]   # Define aggregate death benefits paid (for fund).   AGDEB[i,1]<-f0*GDEAD[i,1]   # Define aggregate lapsation payout (for fund).   AGLAP[i,1]<-f0*LAPSE[i,1]*(1-dsc)   # Define total paid out by fund this period.   outflow<-TONDV[i,1]*GLIVE[i,1]+AGDEB[i,1]+AGLAP[i,1]   # Define fund value.   DETFV[i,1]<-f0*GL0*(1+PORET[i,1])-outflow   # Loop through remaining periods.   for (j in 2:TH){     # Define dividend per person in year j.     TONDV[i,j]<-kappa[j]*DETFV[i,j-1]/GLIVE[i,j-1]     # Define cumulative dividends paid to date per individual.     TCPAY[i,j]<-TCPAY[i,j-1]+TONDV[i,j]     # Define aggregate death benefits paid (for fund).     AGDEB[i,j]<-max(f0-TCPAY[i,j-1],0)*GDEAD[i,j]     # Define aggregate lapsation payout (for fund).     AGLAP[i,j]<-max(f0-TCPAY[i,j-1],0)*LAPSE[i,j]*(1-dsc)     # Define total paid out by fund this period.     outflow<-TONDV[i,j]*GLIVE[i,j]+AGDEB[i,j]+AGLAP[i,j]     # Define current fund value.     DETFV[i,j]<-DETFV[i,j-1]*(1+PORET[i,j])-outflow}} # Regression model on median dividend as a function of time. mtd<-c(); t<-1:TH for (j in 1:TH){mtd[j]<-median(TONDV[,j])} fit<-lm(mtd~t) # Intercept summary value, slope should be statistically zero. summary(fit)

As with prior R-scripts that included commands that are too long, please remember to append them when you compile these scripts. They should be clear from the context.

5.8 Conclusion

With this chapter, you should now be able to create and offer a modern tontine that consumers might actually be interested in purchasing. So, while the initial yield and payout might not be as high, as lucrative or with full mortality credits, it should offer a proper balance between the best cold hard mathematical economics and behavioural psychology. Finally, the last section of this chapter provides users with the definitive updated R-script v3.0 for simulating the modern tontine.

5.9 Test Yourself

  1. 1.

    Please generate a tontine dividend dashboard in which the initial seed is changed from (the year) 1693 to 3961. Discuss how (all) the results change, and why.

  2. 2.

    Please create, report and display a tontine dashboard (similar to Table 5.1), but for the aggregate amount of death benefits paid to those who die in the years T = 1, 5, 10, 15, 20. That is the AGDEB[i,j] matrix. Explain qualitatively what happens in the (later year’s) columns and discuss the statistical distribution of those death benefit payouts. Do they seem normally distributed around the mean value? Discuss.

  3. 3.

    Assume that a (nefarious or misguided) tontine sponsor claims they will offer a death reimbursement covenant, but instead decides to pay the beneficiaries of the deceased a tontine dividend until the entire f 0 := $100, 000 is returned to the heirs. The death benefit is stretched out over time, instead of being paid out at once. They say: Don’t worry, we will make your family whole again, but slowly… Please modify the core simulation v2.0 to account for this feature, discuss whether it makes any difference at all on the tontine dividend payouts and carefully explain your results.

  4. 4.

    Please generate simulation results and create a table similar to the canonical dashboard, in which the reimbursement covenant is weakened in the following manner. If at the end of the year the aggregate value of the decumulation tontine fund is less than the original investment minus dividends received, those who died during that year receive the lower of the two values. So, for example, consider the following scenario. Tontine dividends of exactly $7000 are received for 3 years, and in the 4th year the investor dies. Under the normal covenant, the beneficiaries of the deceased should receive a death benefit of $100, 000 minus the $21, 000 already received, which is: $79, 000 at the end of year 4. But imagine that the total fund value happens to only be worth $60 million, perhaps due to a (very) bad year in the markets, and there are 800 survivors at the end of year #4. This implies that the notional value of the fund at the end of the 4th year is $75, 000 per live survivor. One can think of this as the reserve per person. But, this is also $4000 less than the death benefit promised under a strong covenant. Well then, under the weak one proposed here, it would be reduced to $75, 000. Obviously this situation is somewhat artificial, but nevertheless please generate dashboard results under this particular design and report the distribution of the number of people—from an original pool of 1000 investors—who die and do not get their entire money back. Discuss the qualitative impact of fund values and tontine dividends, when initially RTLIA is used to set payouts but then weakened when someone actually dies.

  5. 5.

    Modify the v3 script to allow new members to join the tontine in the first 15 years. You can do this by adding LAPSE to our GLIVE values (instead of subtracting LAPSE). When a new person joins during the first 15 years, they pay a lower f0 into the fund, their initial investment is reduced by 30% of TCPAY (30% of the dividends they missed out on by joining late). After 15 years, we no longer allow people to join. Also note that we do not allow people to lapse in this specific fund. Find the median tontine dividend for this fund.