Keywords

1 Protect and Safeguard the word’s Cultural Masonry Heritage

1.1 Introduction

Among the 17 Sustainable Development Goals (SDGs) this dissertation concerns the 11th goal: ‘Make cities inclusive, safe, resilient and sustainable’. The focus is on the target 11.4 ‘Strengthen efforts to protect and safeguard the world’s cultural and natural heritage’. Here the method of limit analysis is used for the study of historical masonry structures concerning cultural heritage such as domes and vaults. In order to do that, the first aim of the work is to develop simple discrete algorithms based on the two theorems of limit analysis (static and kinematic theorem). The models introduced are here shown and used for the structural study of barrel vaults, rotational domes, and polygonal domes. These algorithms use optimization of a load multiplier, to calculate the collapse multiplier and the collapse mechanism, but also the multiplier leading to crack initiation. The study of the actual state of the structure with the static method, that allows to find an equilibrated solution based on membrane behaviour, is one of the aims of the work. This is possible by considering the tensile strength at the block interfaces. To consider the three different states of the structure (un-cracked, cracked and collapse) allows a better understanding of the safety state of the structure. It must be underlined that the collapse of cultural heritage structures is strictly related to the cracked state. The focus on the geometry and its proportion reported in the work aims at understanding the role they play in the structural behaviour. Thanks to the simplicity of these models, it was possible to compare different geometries, load conditions and strength criteria, without any relevant computational effort. Two interesting typology of dome was investigated: hemispherical and polygonal domes. This allows to analyse the different behaviour of single and double curvature shells. This work is part of a research project that aims at developing an interdisciplinary methodology for structural analysis of historical masonry elements, to understand the causes of existing damage, verify the structural safety and study possible structural strengthening. This is pursued by using an integrated method of limit analysis with the survey and measurement of geometry, considering deformations, crack patterns and other damage. The multidisciplinary method includes the study of historical construction phases, the analysis of the actual configuration, with the survey of the building and the annotation of the damage, and the structural analysis, with the suggested method of limit analysis.

1.2 The Geometry Considered

In the ensemble of cultural masonry heritage, different shell shapes give different structural response. Since there is a close correlation between the geometry of a surface and its main failure mechanisms, the focus on geometry is a topic of interest. A vault can be obtained by translation of the arch, as in barrel vaults (Fig. 1.) or by revolution around a vertical axis, as in the hemispherical dome (Fig. 2). The different typologies of vaults can be subdivided into “simple vaults” and “composite vaults”. The “simple vaults” are those where the surface does not have solutions of continuity because there is no point in which the curvature changes as: (i) Barrel vault, (ii) Hemispherical dome, (iii) Sail vault (deriving from the dome). The “composed vaults” are those realized through the intersection of two or more parts of a simple vault, so that the surface has several zones in which the curvature changes. In order to describe a composite vault, it is necessary to observe the elements obtained by sectioning a barrel vault along the two diagonals. There will be two “spindles” and two “nails”. If four nails are combined a cross vault is obtained, while with four spindles a cloister vault is obtained. The typical typologies are: (i) Cross vaults/groin vault, (ii) Cloister vaults, (iii) Ribbed vaults (cross vault with ribs) (iv) Polygonal vaults, (v) Stellar vaults, (vi) Fan vaults. In this work the focus is on: (i) barrel vault, (ii) dome, (iii) polygonal dome.

Fig. 1
figure 1

Barrel vault with the geometry of the construction

Full size image
Fig. 2
figure 2

Hemispherical dome with the geometry of the construction

Full size image

1.3 Barrel Vault

The barrel vault (Fig. 3), is the simplest typology of vault and is the base for many vaults of more complicated shape. It is composed of the translation of an arch in its perpendicular direction. It is mostly used as coverage of monumental buildings of a civil and religious nature.

Fig. 3
figure 3

Barrel vault, with square base and rounded arch

Full size image

The barrel vault has a semi-cylindrical intrados surface, but the vertical section can be ogival section if it is based on a translation of a pointed arch, but also parabolic or any other curved shape. In plan it is possible to have different quadrilateral shapes, and two opposite parallel walls are the typical vertical supports. A barrel vault subjected to self-weight only has “arch behaviour”, but with different load positions or in presence of soil settlements, it could have a different behaviour, such as torsion. If the limit stress is reached, cracks will appear in the direction of the tension, on the intrados or on the extrados, as in the hinged mechanism for the arch.

1.4 Hemispherical Dome

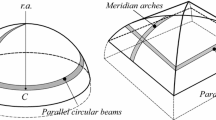
The geometry of a dome is a revolution membrane generated by an arch that rotates around its central axis. It is a convex rounded vault with a horizontal section that may be circular elliptical or polygonal. In vertical section the dome may be hemispherical (Fig. 4), circular, parabolic, or partly elliptical. If the horizontal section is a circle and the vertical section is a round arch, the dome assumes the form of a portion of a sphere and is called hemispherical dome. A dome may be smooth or coffered as in the famous case of the Pantheon in Rome, where the dome is supported upon walls of circular plan. One of the main characteristics of a dome with respect to vaults is that of minor thickness to the other dimensions of the structure. In membrane static solution only internal forces, such as the meridian and parallel, lying on the tangent plane are considered. In this behaviour the compression along the meridians grows from the crown to the base. The parallels are compressed in the key and in tension at near to the springer, in a hemispherical dome the change is at 51°50′° if a dome subjected to self-weight is considered. For axial symmetrical load a hemispherical dome, along the same parallel, has constant stresses.

Fig. 4
figure 4

Hemispherical dome

Full size image

The problem of the stability of a dome is an ancient topic, due to the tensional state that determines lack of stability over time; when the tensile strength is overcome, cracks will appear at the base of the dome along the meridians. In such cases there is no more membrane behaviour, but if a series of half arches is considered, by dividing the dome into slices cut along the meridian plane, and if it is possible to draw a thrust line inside every arch, the dome can be considered safe [14]. The simplification of the behaviour of a cracked dome by dividing it into a series of arches was firstly developed by Poleni for his study on the Vatican Dome [20], who made one of the first examples of a drawing of crack pattern on a dome was applied to the dome of San Pietro in Rome. Here an algorithm is formulated that allows to analyse domes in their actual state and in their collapse state, considering different configurations. These different configurations concern geometrical parameters such as span, thickness, number of slices, different load conditions, also considering the effect of strengthening.

1.5 Polygonal Dome

The polygonal domes (Fig. 5) are a very particular type of dome, divided into slices. Unlike simple domes, which have a double-curved structure, resembling the shape of a spherical surface, the slices of polygonal domes are single-curved and derive from the section of a cylindrical surface. They are called polygonal domes because if sectioned with a horizontal plane parallel to the floor, the resulting section has the shape of a regular polygon. This structure geometry is similar to a pavilion vault, but with more than four edges. As it was demonstrated in this work, these domes have the characteristic of concentrating the loads in the corners of the polygon, developing concentrated and pushing forces on pointed vertical supports, such as pillars. A support on the structural behaviour is given by the diagonal ribs, often present in the polygonal domes. These typologies of dome are little analysed, Flügge [10] proposed an infinitesimal equilibrium solution for a dome subjected to self-weight only. Here a discrete algorithm is formulated that allows to analyse polygonal domes in their actual state considering different configurations. These different configurations concern geometrical parameters such as span, thickness, number of slices, different load conditions (Fig. 6).

Fig. 5
figure 5

Polygonal dome

Full size image
Fig. 6
figure 6

Rotations and displacements considered in three-dimensional space

Full size image

2 The Limit Analysis Algorithms for Shell Structures

2.1 The Kinematic Algorithm Applied to Barrel Vaults

With respect to the kinematic theorem of limit analysis applied to shell structures, the aim of this chapter is to study the behaviour of masonry shell structures in their collapse mechanism. The kinematic method of limit analysis is applied to a three-dimensional shell problem with a formulation inspired by ‘discontinuity layout optimization’ (DLO), that was formulated for plane plasticity problems [22]. The method was successfully used for geotechnical [22], plate and slab problems of arbitrary geometry [11], and on three dimensional problems [13]. Here the innovation is to use it to analyse shell structures, also considering the effect of structural strengthening. An application of the kinematic theorem of limit analysis to barrel vault problems is here addressed. The main results are related to: (i) identification of the collapse mechanism; (ii) identification of the ultimate load carrying capacity: analysis of the amount of live load that can be applied before structural collapse; (iii) analysing strengthened barrel vaults.

Different yield domains and different behaviour of the material are considered. A case with infinite compression strength, no tensile strength and no sliding as stated by Heyman [15]. Then tensile strength different from zero and even the non-symmetric behaviour of a reinforced vaults is contemplated, considering different values of tensile strength according to the different types of reinforcement used. The contribution of the friction angle, mostly in the case of a torsion mechanism is also considered. The plastic dissipation, investigated for reinforced vaults, is governed by three dimensional hinges coupled with normal displacements at the interfaces. Strength criteria formulated in terms of force are opportunely converted into a displacement flow rule to fulfil the formulation that characterizes the DLO method.

This kinematic algorithm, which involves the achievement of collapse, was validated thanks to experimental tests concerning masonry vaults collapse reported in articles that were found in the literature. Some experimental tests on collapse of masonry barrel vaults are considered the benchmark, in particular the barrel rectangular vault tested by Vermeltfoort [27] was considered, that was also used as benchmark for the numerical simulations of [19]. From these experimental tests even barrel vaults with skew arches were investigated, to validate the behaviour of collapse due to torsion. In addition, the experimental tests performed by Girardello [12] allow to validate the work on reinforced vaults, considering two different materials for strengthening.

2.2 The Static Algorithm Applied to Rotational Domes

A discrete model is formulated, based on the static theorem of limit analysis to analyse domes. The structure is divided into rigid blocks, with forces acting on the interfaces. The equilibrium is imposed at each block and a resistance criterion is imposed at each interface. Two different behaviours are considered, membrane behaviour to analyse the actual state and flexural behaviour to analyse the collapse state. The internal forces of redundant structure with crack initiation load multiplier and the collapse load multiplier with corresponding mechanism are obtained after a simplex algorithm imposed. It is possible to analyse the structural behaviour considering different variables, such as geometry, loads variations and the presence of a reinforcement. Two different typologies of shell are analysed: the rotational dome and the polygonal dome. The former has a double curvature and a circular base, while the latter has a single curvature, in zenith direction.

In the literature, regarding the hemispherical domes, the solutions of differential equilibrium equations based on membrane theory have been acquired for self-weight and a few other loading conditions [10]. Membrane theory considers the stresses acting on an infinitesimal element, considering meridian and hoop stresses, and shear forces tangent to the mid surface. In this work it is proven that it is possible to analyse these structures using a discrete model, applying the static limit analysis theorem. The focus here is on the interaction between the geometry of the dome and its structural behaviour. Double curvature domes, rotational domes with round arch and pointed arch shape, are analysed with the static model in their membrane behaviour (Fig. 7), focusing on the response related to the different geometries. Furthermore, with the same discrete algorithm configuration, and using a flexural approach (Fig. 8), rotational domes are analysed up to collapse, finding the corresponding load multiplier and the collapse mechanism.

Fig. 7
figure 7

Scheme of a rotational dome block in membrane behaviour

Full size image
Fig. 8
figure 8

Forces acting on a block of the double curvature dome, flexural behavior

Full size image

2.3 The Static Algorithm Applied to Polygonal Domes

The analysis of polygonal domes is investigated, in their membrane behaviour, developing the static algorithm for polygonal domes that have straight line in the hoop force direction for their single curvature shell. Since the geometry of the surface between double curvature and single curvature domes differs, consequently, the response of the structure to load is also different. With the aim of describing the membrane behaviour of polygonal domes some geometric characteristics have been modified in the static model. The focus here is on the interaction between the geometry of the dome and the structural behaviour (Fig. 9).

Fig. 9
figure 9

Reference systems for the dome section and the forces acting on a block of polygonal dome

Full size image

In the literature, Flügge [10] directly analyses the polygonal domes subjected to self-weight, solving the differential equations of the membrane state for the specific case. D'Ayala [9, 23] and Como [8] consider pavilion vaults, that have a similar structure with single curvature surface, starting from their geometric configuration as portions of cylinders that concentrate most of the part of the loads along the diagonal ribs. In the work of D’Ayala and Tomasoni [9], a theory was formulated, based on lower bound approach of limit analysis, for the structural analysis of pavilion vaults. The formulation includes an optimized solution that allows to find the optimal thrust surface of a vault by minimizing the distance between thrust surface and middle surface. A strength criterion with finite friction is considered among block interfaces considering 3D effects that develop in vaults of complex geometry such as pavilion vaults, in the angular parts where different surfaces are connected. In this dissertation, the membrane behaviour of a single curvature dome is analysed, in a structure divided into blocks, considering the thrust surface coincident with the middle surface, analysing the maximum load that could be reached before the structure begins to crack. At this point the discrete static algorithm is applicable to polygonal domes: (i) to evaluate the action of a dome on underlying structures for single curvature dome; (ii) to solve the problem of the equilibrium of the diagonal rib; (iii) to compare maximum forces with crack positions both for double curvature dome and for single curvature dome. In the existing case of Chiaravalle abbey in Milan described in [6] the work allowed to: (i) consider load different from the self-weight adding the load of a lantern tower; (ii) to analyse and compare the behaviour of a polygonal dome in membrane behaviour and in a cracked state, by the integration of the structural analysis and the crack pattern.

2.4 Application to Real Case Studies

Some analytical cases are considered in order to analyse the effect of the geometry on the structural response. Amongst the topics dealt with are: (i) different spans; (ii) dome based on a round arch or on a pointed arch; (iii) the difference derived from tapering i.e. a reduction of the section thickness of the dome; (iv) the effects of different load conditions, such as the presence of a lantern; (v) the effect of proper structural strengthening with circular tie rods. Some existing cases of rotational domes with a lantern are analysed: the churches of (i) Sant' Agnese in Agone in Rome [3, 17] (Fig. 10); (ii) San Nicolò l'Arena in Catania [17, 18] (Fig. 11); (iii) San Giorgio in Ragusa [16] (Fig. 12).

Fig. 10
figure 10

Sant’Agnese in Agone

Full size image
Fig. 11
figure 11

San Nicolò L'Arena

Full size image
Fig. 12
figure 12

San Giorgio

Full size image

Then the polygonal dome of Chiaravalle abbey in Milan is analysed. In this case the weight of a lantern tower called Ciribiciaccola is analysed with surveys, drawings and 3D model, showing the importance of the integrated approach to understand the geometrical configuration. After the analysis of the crack pattern, it is possible to analyse the behaviour of this dome. The analysis of geometry and materials is used as input to be included in the discrete algorithm and the application to Chiaravalle abbey also shows the information deriving from the crack pattern for the structural analysis. The analysis of the dome shells both cracked and un-cracked are analysed and compared in their different structural response. Finally, the equilibrium of the rib with radial wall is calculated to evaluate their contribution to the structural behaviour.

3 Conclusions

Two methods are used to analyse shell masonry elements for calculating the safety of the structure to ensure conservation, protect and safeguard of cultural heritage, to ensure the target 11.4 of the 11th goal of the 17 Sustainable Development Goals (SDGs).

The kinematic theorem of limit analysis is applied to a discrete model with simplex method of optimization that allows to calculate the collapse load and the mechanism for shell structures such as barrel vaults. It also allows to evaluate behaviour of a vault after an intervention of structural strengthening like reinforced with FRPM material. One advantage of the kinematic code is that only a few parameters are needed to obtain a response. Material properties considered as input parameter: (i) cohesion; (ii) friction angle; (iii) tensile strength. The innovation of this work with respect to the previous formulations of DLO are: (i) three-dimensional shell structure is studied; (ii) the effect of structural strengthening is considered. Different barrel vault shapes are considered: (i) round barrel vaults; (ii) ogive barrel vaults; (iii) lowered barrel vaults; (iv) skew barrel vaults. Dead and live loads in different positions are considered. Among the loads analysed: (i) uniformly distributed load; (ii) linear load; (iii) punctual force; (iv) inclined linear load. Regarding the boundary condition with four external boundaries, the available behaviour considered are: (i) rigid; (ii) symmetry plane; (iii) free.

In order to validate the formulation, the model is applied to experimental tests of vaults up to collapse. Close agreement with experimental examples Vermeltfoort [27] and homogenized limit analysis numerical solutions Milani [19] was obtained. Even in the case of reinforced vaults, a close agreement with Girardello [12] and Valluzzi [25, 26] was reached. Foreseen developments of the model are the design of optimal strengthening intervention for vaul ts, and the consideration of vertical movements at the supports of the vaults.

The static discrete algorithms for the membrane behaviour evaluate static regimes for masonry domes, of different typologies, considering the presence of a minimum tensile and shear strength before the structure begins to crack. Through the optimized solution, the static algorithms return the value of the forces acting on the structure, and the value of the multiplier for which the load for first cracking is reached. New possibilities arise to safeguard the artistic heritage. The first cracks do not lead to collapse, which to occur requires a load such as to trigger a mechanism, with an adequate number of cracks related to membrane forces and hinges related to the flexural regime.

The collapse, with load multiplier and collapse mechanism, is also considered with a model including flexural behaviour response. The analyses allow to consider the behaviour of a dome under different conditions, with and without cracks.

The fact that the algorithms consider the strength of the material allows us to comprehend the contribution of restoration interventions involving reinforcement on the dome. A typical example of reinforcement is represented by the traditional iron tie rods and by the more modern strips of composite material in which fibres with very high tensile strength are added to a mortar matrix that strengthen the structure. Moreover, the design of proper circumferential strengthening can be studied, to avoid cracking during intervention woks.

The model shows that with the same algorithm structure and some punctual modification different geometries can be analysed and compared. Considering single or double curvature domes, this feature modifies the response of the structure to loads and the positions of weight transfer. The role of geometry analysed shows the different response given by a double-curved dome, which distributes the load over the entire support surface, and a single-curved dome, which with to the development of shear forces concentrates the weight on the diagonal ribs.

The discrete algorithm allows: (i) to calculate the multiplier value, beyond which the structure cracks; (ii) to calculate collapse multiplier and mechanism in flexural regime; (ii) to consider different load conditions; (iv) to consider the performance of the structure in the presence of structural reinforcement; (v) to obtain, with limited input data, the forces acting on the boundaries of hyper-static structures, which often require very long and complex analyses; (vi) the discrete formulation allows to change the geometry of the structure quickly by the modification of only a few parameters, this allows to compare different geometries and configurations, thus considering the role of proportions in the design of ancient structures; (vii) the simple solution obtained can be used as benchmark for more complex analysis like Finite Element Model [2].

Amongst further future developments it will be possible to focus on non-axial symmetric conditions, such as effect of soil settlements or variable lateral loads, due to wind effect or seismic events.