Light-Shining-Through-Walls Experiments

Abstract

The light-shining-through-walls (LSW) method of searching for ultralight bosonic dark matter (UBDM) uses lasers and strong dipole magnets to probe the coupling between photons and UBDM in the presence of a magnetic field. Since these experiments take place entirely in the laboratory, they offer a unique opportunity to perform a model independent measurement of this interaction. This involves shining a high-power laser through a magnetic field toward a wall which blocks the light. The interaction between the laser and the magnetic field generates a beam of UBDM that passes through the wall. Beyond the wall is another region of strong magnetic field that reconverts the UBDM back to photons that can then be measured by a single photon detection system. The sensitivity of these kinds of experiments can be improved further by implementing optical cavities before and after the wall to amplify the power of the light propagating through the magnetic fields. This chapter gives an introduction to LSW experiments and discusses a number of interesting challenges associated with the technique.

9.1 Introduction

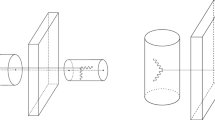
Light-shining-through-walls (LSW) experiments offer the unique ability to measure the coupling between photons and the UBDM field over a wide range of masses in a purely laboratory setting. As Fig. 9.1 shows, these experiments work by shining a high-power source of light through a static magnetic field toward an opaque wall. While the wall blocks the light, the interaction between the photons and the magnetic field will generate a UBDM field which travels through it. Past the wall is another region of static magnetic field where the UBDM field converts back to photons which can then be measured with a detector. One of the strengths of LSW experiments is that since they do not rely on model-dependent astrophysical sources to produce UBDM fields, their systematic uncertainty is related only to the experimental apparatus itself.

Fig. 9.1

A simple layout for an LSW experiment. The laser field is the red solid line, while the blue line is the UBDM field. A wall then blocks the light from the laser, while the UBDM field passes directly through it. The regenerated field is then shown as a red dotted line. The detector measures the regenerated field and does not interact with the UBDM field

In this chapter, we will refer to the region of magnetic field before the wall as the “production area” and the magnetic field after the wall as the “regeneration area.” The electromagnetic field reconverted from the UBDM field in the regeneration area will be called the “regenerated field” or “regenerated photon signal.”

We will also use the Any Light Particle Search II (ALPS II) [4, 5] as a reference point for the design of these experiments. From Fig. 9.2, we can see that ALPS II will be able to probe the coupling constant g between photons and the UBDM field down to g < 2 × 10⁻¹¹ GeV⁻¹ for masses below 0.1 meV. This will allow ALPS II to explore a very important region of the parameter space where there are several hints of the existence of UBDM fields from astronomical observations mentioned earlier in Chap. 3. These include measurements of highly energetic photons from distant sources that indicate the universe is more transparent at these energies than predictions of the standard model would suggest [2]. This is shown in Fig. 9.2 as the circular region in the lower left corner. In addition to this, UBDM fields could also explain why stellar cooling rates uniformly exceed the expectations of their models [3]. This is shown as the band from 10⁻¹¹ < g < 10⁻¹⁰. While other experiments may have investigated parts of these regions before, ALPS II will be the first to measure this range of g without relying on any astrophysical models of the production–regeneration process of the UBDM fields or the interstellar magnetic fields.

Fig. 9.2

Limits on g set from ALPS I [1] in orange and the projected sensitivity of ALPS II in blue. The hints from the transparency of the universe for TeV photons are shown in red [2], while the range of g that could cause stars to cool faster than their models predict is shown in pink [3]. ALPS II will be the first experiment to search for the UBDM coupling to photons over the mass range that could cause these phenomena in a purely laboratory setting

9.1.1 UBDM Interaction with Photons in a Magnetic Field

As we saw in Chap. 2, the term in the Lagrangian that defines the interaction between the photons and the UBDM field is

$$\displaystyle \begin{aligned} \mathcal{L}_{{}_{\mathrm{UBDM}}} = - \frac{1}{4} g \varphi F_{\mu\nu} \tilde F^{\mu\nu}~. {} \end{aligned} $$

(9.1)

In this equation, g is the coupling constant mentioned in the previous section. For LSW experiments, we can define the amplitude of the pseudoscalar UDBM fields φ_p generated in the production area as an integral of the dot product between an oscillating electric field E, supplied by the laser, and a static magnetic field B over an interaction length x,

$$\displaystyle \begin{aligned} \varphi_p(x,t) = e^{-i{\left(\omega t - k_\varphi x\right)}}\frac{i g}{2 k_\varphi}\int dx' \boldsymbol{E}{\left(x'\right)}\cdot \boldsymbol{B}{\left(x'\right)} e^{-ik_\varphi x'}~, {} \end{aligned} $$

(9.2)

where ω is the angular frequency of the electric field, while k_φ is the wavenumber of the UBDM field described by the following equation:

$$\displaystyle \begin{aligned} k_{\varphi}=\sqrt{\omega^2-m_\varphi^2}~. {} \end{aligned} $$

(9.3)

The maximum amplitude in Eq. (9.2) will occur when E ∥B, while no field is produced if E ⊥B. Likewise, opposite is true of scalar fields and the amplitude will be largest when E ⊥B and zero when E ∥B. Therefore, LSW experiments can search for pseudoscalar fields by aligning the polarization of the laser to the magnetic field, while tuning the polarization of the laser orthogonal to the magnetic field when searching for scalar fields.

If we assume that B is static in time and uniform over a length L, the amplitude of the UBDM field can be simplified using plane wave approximations for E and B:

$$\displaystyle \begin{aligned} \varphi(x,t) = \frac{i g}{2 k_\varphi} B E_0 e^{-i{\left(\omega t - k_\varphi x\right)}} \int dx' e^{iqx'}~. {} \end{aligned} $$

(9.4)

In this equation, q is a parameter that helps quantify the phase matching between the UBDM field generated at different points along the static magnetic field and is described by

$$\displaystyle \begin{aligned} q = n\omega - \sqrt{\omega^2 - m_\varphi^2} \approx \omega {\left(n-1\right)} + \frac{m^2_\varphi}{2\omega}~. {} \end{aligned} $$

(9.5)

From Eq. (9.4), it is apparent that when the mass is large enough or the interaction length is long enough that qL > 1, the experiment will lose some sensitivity as the UBDM field generated in the production area does not sum coherently. In the case where qL is some integer multiple of 2π greater than zero, the destructive interference prevents any field from being generated at all.

By evaluating the integral in Eq. (9.4), we can find the probability $\mathcal {P}_{\gamma \rightarrow \varphi }$ that a photon in the production area will convert to a UBDM field:

$$\displaystyle \begin{aligned} \mathcal{P}_{\gamma\rightarrow\varphi} = \frac{1}{4}\frac{\omega}{k_\varphi}{\left(gBL\right)}^2 |F{\left(qL\right)}|{}^2~. {} \end{aligned} $$

(9.6)

In the equation above, $F{\left (qL\right )}$ represents the form factor for the magnetic field and can be simplified to

$$\displaystyle \begin{aligned} \left|F_{\mathrm{single}}{\left(qL\right)}\right| = \left|\frac{2}{qL}\sin{\left(\frac{qL}{2}\right)}\right|~. {} \end{aligned} $$

(9.7)

Here, we can again see the effect of destructive interference in the generation of the UBDM field as the form factor goes to zero when qL = 2πN for positive integer values of N. This effect, along the 1∕qL factor outside the sine function, limits the sensitivity of LSW experiments at higher masses. This is apparent in the sensitivity curves for ALPS I and ALPS II shown in Fig. 9.2. There we can also see how a more detailed model of the magnetic field, which considers the gaps between the magnets, can produce patterns in the sensitivity at higher masses [6].

As it happens, the probability $\mathcal {P}_{\varphi \rightarrow \gamma }$ of the reverse process occurring and the UBDM field reconverting back to a photon in the regeneration area is the same as $\mathcal {P}_{\gamma \rightarrow \varphi }$. Therefore, a simple LSW experiment with the same magnetic field before and after the wall using a laser that travels only a single pass through the generation area will produce the following number of photons N_γ, in the regenerated field over a measurement time τ, for masses in which qL ≪ 1:

$$\displaystyle \begin{aligned} N_\gamma = \frac{1}{16}{\left(gBL\right)}^4 \tau P_i~. {} \end{aligned} $$

(9.8)

We should make note of the fact here that these regenerated photons will have an identical energy to those that were used to generate the UBDM field. The magnetic field and length are obviously critical to the sensitivity of the experiment as the regenerated power is proportional to ${\left (BL\right )}^4$. The input power P_i, shown in units of photons per second, matters as well, but in this case the number of regenerated photons “only” scales linearly with it.

Plugging in the ALPS II parameters of 560 T⋅m of magnetic field length and an input power of 50 W gives an interesting result. For couplings down to g < 2 × 10⁻¹¹ GeV⁻¹, this would only produce 1 regenerated photon over the course of 700 000 years. This is no mistake, remember that the N_γ above is only the number of regenerated photons for our simple example of an LSW experiment. This helps illustrate the importance of the additional techniques that LSW experiments like ALPS II can use to boost the power of the regenerated signal. These systems and how they impact the sensitivity are discussed in the later sections.

9.1.2 Magnets

As we just discussed, LSW experiments rely on strong magnetic fields to promote an interaction between photons and the UBDM field. The magnets used for LSW experiments can be evaluated based on three critical parameters: (1) the strength and orientation of their static magnetic dipole field, (2) their length, and (3) the size of the bore. While it should be obvious why the length and magnetic field strength are important, a sufficient bore diameter is also crucial for LSW experiments so that light is not lost due to clipping as the lasers propagate through the beam tube. We will discuss later how this is essential when cavities are used to amplify the power of the input laser field and the reconverted field.

Fortunately, superconducting dipole magnets that were originally developed for particle accelerators are well suited for LSW experiments as they can produce strong dipole fields over very long distance with bore diameters sufficient to accommodate the accelerator beams. These magnets are constructed by coiling a superconducting thread to form many layers of wire, increasing the total current to induce very strong magnetic fields. They can also be connected in strings to produce magnetic fields with km lengths.

Reaching and maintaining superconductivity of course requires a cryogenic system that constantly supplies liquid He to cool the thread. Nevertheless, since they are a core element in modern accelerators, there are facilities all around the world that possess the cryogenic infrastructure necessary for operating them. Furthermore, after many years of development, the technology is very mature and magnets that can produce static dipole fields as high as 9 T with a uniform polarization over long distances and sufficient free apertures for LSW experiments are even currently in use at the LHC [7].

9.1.3 Light-Tightness

For LSW experiments to reach their optimal sensitivity, background signals must be suppressed below the sensitivity of the detection system. You may remember from earlier that the regenerated photons will have the same energy of those used to generate the UBDM field. Therefore, one source of background that all LSW experiments must cope with is light leaking through the wall from the production area to the regeneration area, as this would create a signal at the detector that is indistinguishable from one induced by an interaction with the UBDM field.

While sufficiently suppressing this light may seem like a trivial task, it is complicated by two points. First, current detection systems are capable of sensitivities on the order of a single photon per week. Second, as we will see later, the optical systems for LSW experiments are very sophisticated and need to transfer light between the production and regeneration areas of the experiment while a measurement is taking place. This interface is a particularly vulnerable point in terms of light-tightness. On top of that, there also needs to be systems that can verify the sensitivity of the experiment by checking parameters such as the alignment of the laser that generates the UBDM field. This involves having a shutter in the wall that can be opened to allow light to propagate directly from the production area to the regeneration area. This is another vulnerable point as stray light can find some scattering path through the shutter. The chance of a laser field actually transmitting through the bulk material of the shutter, on the other hand, is not a major concern. Even a few µm of material is enough to prevent any light from reaching the regeneration area, and in reality, the shutter will be substantially thicker than this.

9.2 Boosting Sensitivity with a Production Cavity

One way to increase the power in the reconverted signal is to amplify the power of the circulating light in the production area. Optical cavities or resonators can be very useful in this regard as state-of-the-art mirror coatings will allow cavities on the order of 100 m to amplify their circulating power by four orders of magnitude or more. As we saw in the previous section, the power in the regenerated photon signal scales linearly with the power circulating through the static magnetic field in the production area. Therefore, installing a production cavity (PC) there will amplify the power of the regenerated photon signal by the power build-up factor of the cavity $\beta _{{ }_{\mathrm {P}}}$, if full power build-up can be achieved. Because of this caveat, in practice, it is more precise to quantify this in terms of circulating power in the PC P_c. With this, we can calculate the number of photons in the regenerated signal over a measurement time of τ from the following:

$$\displaystyle \begin{aligned} N_\gamma = \frac{1}{16}{\left(g_{a\gamma\gamma}BL\right)}^4 P_{\mathrm{c}}\tau~. {} \end{aligned} $$

(9.9)

Therefore, a PC with power build-up of 10,000 will boost the sensitivity of the experiment with respect to g by a factor of ten.

9.2.1 Linear Cavity

While a variety of resonator designs exist, two mirror linear optical cavities are the most relevant for LSW experiments. As Fig. 9.3 shows, these types of cavities use two partially transmissive mirrors separated by a distance L and aligned with their surfaces normal to each other. The laser field enters the cavity through the input mirror M₁ and exits through the output mirror M₂. Let us suppose that these mirrors have a reflectivity of R₁ and R₂, transmissivity of T₁ and T₂. For lossless mirrors, these quantities are related by the following expression:

$$\displaystyle \begin{aligned} 1 = R+T. {} \end{aligned} $$

(9.10)

While these can also be expressed as field coefficients, in this chapter we will work in the convention that these are in terms of power.

Fig. 9.3

Diagram of a two-mirror linear optical cavity with an input mirror M₁ and an output mirror M₂. The input power is given by P_i, while the circulating power is P_c, the transmitted power is P_t, and the length of the cavity is L

In the 1D example, a laser field that is incident on the input mirror will be resonant if the length of the cavity is some integer multiple of the wavelength of the laser. The frequency spacing between the resonances of the cavity is known as its free spectral range (FSR) and can be found from $f_{{ }_{\mathrm {FSR}}} = c/2L$. If the resonance condition is satisfied, the ratio of circulating power to input power can then be approximated by the following equation when T₁, T₂, ρ ≪ 1:

$$\displaystyle \begin{aligned} \beta_{{}_{\mathrm{P}}}\equiv{\left(\frac{P_{\mathrm{c}}}{P_i}\right)}_{\mathrm{max}}\approx \frac{4T_1 }{{\left(T_1+T_2+\rho\right)}^2}~. {} \end{aligned} $$

(9.11)

This is what we referred to earlier as the power build-up factor of the cavity. In this equation, ρ is the power losses that the circulating field accrues after each round trip. To reemphasize a point we made on the previous page, if the combined mirror transmissivities and losses are on the order of 100 ppm, the PC can amplify the power converted to the UBDM field by more than four orders of magnitude.

The dependence of circulating power on the laser frequency can be found from the cavity Lorentzian:

$$\displaystyle \begin{aligned} P_{\mathrm{c}} = \frac{\beta P_i}{1+{\left(\frac{2\mathcal{F}}{\pi}\sin{\left(\pi\frac{\Delta f}{f_{{}_{\mathrm{FSR}}}}\right)}\right)}^2}~. {} \end{aligned} $$

(9.12)

In this equation, the finesse of the cavity, $\mathcal {F}$, is defined as the ratio between the linewidth (full width half maximum, FWHM) of the cavity resonance f_c and the FSR:

$$\displaystyle \begin{aligned} \mathcal{F} \equiv \frac{f_{{}_{\mathrm{FSR}}}}{f_{\mathrm{c}}} \approx\frac{2\pi}{{\left(T_1 +T_2 + \rho\right)}} \mbox{ ~ ~ ~ (when ~} T,\rho\ll1 )~. {} \end{aligned} $$

(9.13)

Therefore, in order to achieve the maximum circulating power in the cavity, the input laser must be controlled such that the difference between its frequency and the cavity resonance is much less than f_c or $f_{{ }_{\mathrm {FSR}}}/\mathcal {F}$.

9.2.2 Cavity Spatial Modes

In the previous section, we only discussed the longitudinal mode of the cavity, and however it is important to also consider the spatial profile of the cavity eigenmodes. This is especially true for longer baseline LSW experiments since the modes are constrained by the magnet bore and the power build-up factor can be limited by its diameter. In addition to this, in the next section, we will discuss dual cavity LSW experiments that also use a resonator in the regeneration area. When this technique is used, it is also important to ensure that the cavities share nearly the same transversal mode.

The transversal modes of the cavity resonances are commonly expressed in a basis set of Hermite–Gauss or Laguerre–Gauss modes, and the higher order modes can therefore be described as the product of the fundamental mode and Hermite or Laguerre polynomials. For LSW experiments, it is advantageous to operate with the fundamental mode since it will provide the smallest beam sizes over the longest baseline, thus reducing the clipping losses on the magnet bore. Therefore, while there are cases where the Hermite–Gauss and Laguerre–Gauss description can be very useful, we will not explore it further.

The field, when in the fundamental mode, follows a Gaussian distribution that can be described by the following equation when using the paraxial approximation:

$$\displaystyle \begin{aligned} E{\left(r,z\right)} = E_0\frac{w_0}{w{\left(z\right)}}\exp{\left(-\frac{r^2}{w{\left(z\right)}^2}\right)}\exp{\left(i\left [kz - \psi{\left(z\right)} +\frac{kr^2}{2R{\left(z\right)}}\right ]\right)}~. {} \end{aligned} $$

(9.14)

The intensity distribution for a beam with a power of P is then given by

$$\displaystyle \begin{aligned} I{\left(r,z\right)} = \frac{2P}{\pi w{\left(z\right)}^2}\exp{\left(-2\frac{r^2}{w{\left(z\right)}^2}\right)}~. {} \end{aligned} $$

(9.15)

In these equations, $w{\left (z\right )}$ represents the 1∕e² radius of the intensity distribution as the following function of z:

$$\displaystyle \begin{aligned} w{\left(z\right)} = w_0\sqrt{1+{\left(\frac{z}{z_r}\right)}^2}~. {} \end{aligned} $$

(9.16)

Figure 9.4 shows a visual representation of the spatial mode of a Gaussian beam as it propagates through its waist position. As we can see, the radius of the distribution, shown as the thick black line, has the minimum waist w₀ at the position z = 0. In the near field (z ≪ z_r), the beam is collimated and its size remains relatively constant, while in the far field (z ≫ z_r) the waist expands linearly with z. The parameter z_r is known as the Rayleigh length and is defined as the distance from the waist position at which $w{\left (z_r\right )}=\sqrt {2}w_0$. It depends only on the minimum waist size and the laser wavelength:

$$\displaystyle \begin{aligned} z_r = \frac{\pi w_0^2}{\lambda}~. {} \end{aligned} $$

(9.17)

From this equation, we can see that the Rayleigh length is proportional to the area of the beam at the minimum waist position and inversely proportional to the wavelength. Therefore, producing a beam that is well collimated over long distances requires using a larger beam as smaller beams will only remain collimated for shorter distances. Furthermore, shorter wavelength lasers can produce the same Rayleigh length as longer wavelength lasers using smaller beam sizes. This is a critical point for LSW experiments as the diameter of the magnet bore will typically limit the length of the experiment, and once the waist size approaches some fraction of the bore diameter, clipping losses will limit the possible power build up factor of the cavities.

Fig. 9.4

Profile of a Gaussian beam with a minimum waist size of w₀, a Rayleigh length of z_r, and a divergence half-angle of θ. The waist size is shown as the thick black line, while wavefronts at different positions are shown as gray lines. As the beam propagates further into the far field, it will asymptotically approach the dotted lines that illustrate the divergence angle

This can also be seen by looking at the divergence half angle θ, of the beam in the far field. In this regime, the dependence of the waist size on z can be approximated by the linear relation $w{\left (z\right )} \approx w_0 z /z_r$, and by plugging in for z_r we can define θ as

$$\displaystyle \begin{aligned} \theta = \frac{\lambda}{\pi w_0}. {} \end{aligned} $$

(9.18)

There are also several terms in the complex exponential of Eq. (9.14). The first term, kz, is just the product of the wavenumber and the longitudinal position. The second term, $\psi {\left (z\right )}$, is known as the Gouy phase and represents the natural phase shift that the field will experience passing through the waist. The fields will also have spherical wavefronts, shown as light gray lines in Fig. 9.4, and the final term in the exponential, $kr^2/2R{\left (z\right )}$, introduces the curvature $R{\left (z\right )}$ of the wavefronts. The dependence of the wavefront curvature on the longitudinal position is given by

$$\displaystyle \begin{aligned} R{\left(z\right)} = z\left[1+{\left(\frac{z_r}{z}\right)}^2\right]~. {} \end{aligned} $$

(9.19)

Here, it is apparent that at the minimum waist position the wavefronts are flat ($R{\left (0\right )}=\infty$), while at the Rayleigh length $R{\left (z_r\right )}=2z_r$ and in the far field $R{\left (z\right )}\approx z$. This is important as the radius of curvature of the mirrors sets the wavefront curvature at their position, and this will determine the shape of the transversal mode throughout the cavity.

In order for the cavity to achieve full power build-up, the input beam must be in the same spatial mode as the eigenmode of the cavity. The coupling efficiency between the laser and the cavity can be found by calculating the spatial overlap η, between the input laser field, shown in this equation as E, and the cavity eigenmode, expressed here as E′:

$$\displaystyle \begin{aligned} \eta = \frac{\left|\int E^*E' dA \right|{}^2}{\int\left|E\right|{}^2dA \int\left|E' \right|{}^2dA}~. {} \end{aligned} $$

(9.20)

In this equation, we evaluate the overlap integral between the two normalized fields over an area A and then take its absolute square. Any spatial dependence in the differential phase between the wavefronts of the two fields or mismatch in the spatial distribution of their amplitudes will lead to a loss in the coupling of the field to the cavity. We should note the fact that the spatial overlap is independent of the longitudinal position of the plane it is evaluated over.

9.2.3 Stabilization of Optical Cavities

So far we have only considered static cavities using an input laser with a fixed frequency. In reality, though, both the laser frequency and cavity length will have some noise and a control system is needed to maintain the frequency of the laser with respect to the length of the cavity or vice versa. Much of the pioneering work in this field was done by the gravitational wave community as these types of control systems are critical to sensing the tiny phase fluctuations that gravitational waves introduce into detectors such as Advanced LIGO [8] and LSW experiments benefit considerably from this.

One of the most well-known and widely used techniques is the Pound–Drever–Hall (PDH) laser frequency stabilization [9, 10]. PDH takes advantage of the fact that close to resonance, the phase of the field reflected by the cavity will be linearly proportional to the frequency difference between the input laser and the cavity. Using phase modulation sidebands, the reflected phase can be measured to generate an electronic signal that can then be fed back to the laser frequency or the cavity length to maintain the resonance condition.

A similar technique known as differential wavefront sensing is capable of sensing the alignment of the laser with respect to the spatial eigenmode [11,12,13]. Here, a quadrant photodetector (QPD) measures the four quadrants of reflected power distribution. Again with phase modulation sidebands, misalignments between the wavefronts of the incident laser field and the circulating field that is leaking out of the input mirror of the cavity can be measured. By feeding this signal back to alignment actuators, the spatial overlap between the laser and the cavity eigenmode can be maintained.

9.2.4 Achieving High Finesse

Of course, achieving a high finesse or power build-up comes with its own set of challenges. As Problem 9.2 illustrates, the highest possible power build can be achieved when the losses (ρ) and the output mirror transmissivity (T₂) are as low as possible, while the input mirror transmissivity (T₁) obeys the condition T₁ = T₂ + ρ.

While we have some control on the transmissivities of the mirrors, there is a limit to how much we can suppress the losses. Three of the most common causes of the intracavity losses that LSW experiments must consider are scattering and absorption from the cavity mirrors and clipping on the free aperture of the magnet bore.

The scattering losses for mirrors used in high-finesse long-baseline cavities are typically driven by the surface roughness of the substrates themselves. In this case, the total integrated scatter (TIS) at normal incidence for smooth surfaces can be approximated by

$$\displaystyle \begin{aligned} \mathrm{TIS} = {\left(\frac{4\pi \sigma}{\lambda}\right)}^2~. {} \end{aligned} $$

(9.21)

In this equation, σ is the integrated RMS deviation from a perfect spheroid of the reflective surface of the mirror evaluated over the area of the beam. Therefore, larger beams will be exposed to features at lower spatial frequencies than smaller beams. Since the amplitude of these features tends to increase as the spatial frequency decreases, larger beams will typically experience higher scattering losses than smaller beams. For longer baseline cavities, this can limit in the maximum possible power build-up factor.

For LSW experiments, the clipping losses from the magnet aperture must also be considered. For this purpose, the magnet strings can be thought of as series of connected pipes. If we form a cavity by placing mirrors at the ends of the string, the clipping losses will be the percentage of light lost from scattering off of the walls of the pipes. When straight magnets are used, this can be approximated by integrating the power of the Gaussian beam at the position of its widest radius inside the magnets over the free aperture of the string. For long-baseline high-finesse cavities, this can create a problem as longer cavities will have larger eigenmodes. Unless magnets with extremely large bore diameters are used, clipping losses on the magnet bore will actually limit the maximum length of the string. To help compensate for this, the production cavity can be designed such that the Rayleigh length of the eigenmode is roughly equal to half the length of magnet string that contains it. If a cavity is also used in the regeneration area, then we must consider the clipping losses there as well. In this case, the Rayleigh length of both cavities should be half the combined length of the two strings. This will allow for the smallest possible beams at the exits of the string.

9.2.5 High-Power Operation

As we have already discussed, the higher the power the PC can support, the more sensitive the experiment will be. This can be complicated, though, by a number of effects that degrade the performance of the cavity as higher powers are used due to absorption in the optical coatings.

One of the issues with absorption in the optical coatings is that areas with a higher incident intensity will reach a higher steady-state temperature than the areas of the mirror with a lower incident intensity [14]. This will cause larger thermal expansion in the central region of the mirror creating a change in its effective radius of curvature that makes it more convex. With this, the Rayleigh length of the cavity eigenmode will increase resulting in a larger beam size of the circulating field. If the beam size increases enough, this can lead to power losses due clipping on the free aperture of the magnets or a reduction in the spatial mode matching.

High-power operation can also lead to an increase in the cavity losses if there are point absorbers on the surface of the optical coating or embedded in it [15]. These points will also reach higher steady state-temperatures than the rest of the mirror and can introduce low-frequency spatial features through thermal expansion. If the spatial features are smaller than the beam size, this can lead to additional scattering losses.

9.3 Dual Cavity LSW Experiments

The sensitivity of LSW experiments can be increased further by using a regeneration cavity (RC) after the wall to amplify the regenerated field by a resonant enhancement factor. While this factor is nearly identical to the expression we used earlier for the power build-up, the concepts are somewhat distinct as the regenerated signal is injected without its power being attenuated by one of the mirrors. There it is amplified and then attenuated only as it leaves the cavity. In this way, the resonant enhancement factor is an expression of the amplification, in power, of the regenerated field that is actually incident on the detector. The power build-up in the PC, on the other hand, is the amplification of the power of the input laser while that field is still circulating in the PC.

With this, the resonant enhancement factor, β_R, can be expressed as the following approximation:

$$\displaystyle \begin{aligned} \beta_{\mathrm{R}}\approx \frac{4T_{\mathrm{out}} }{{\left(T_1+T_2+\rho\right)}^2}~. {} \end{aligned} $$

(9.22)

In this equation, T_out refers to the transmissivity of the mirror at the detector port of the RC and could be either T₁ or T₂. As we discussed in the previous section, if we say mirror “1” is the mirror at the detector, the highest possible power build-up will be achieved when T₁ = T₂ + ρ and T₂ is chosen to be as low as possible.

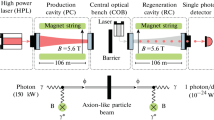
Figure 9.5 shows a simplified optical setup where the flat mirrors of the PC and RC are coupled to a central optical bench (COB) in the middle of the experiment. In this setup, the radius of curvature of the curved mirrors at the end stations can be chosen to be roughly the length of the entire such that the Rayleigh length of the cavity eigenmodes is half the length of the entire magnet string, to minimize clipping losses on the magnet bore. It is important that the Rayleigh length is not the exact length of the cavities as this could lead to higher order mode degeneracies that will interfere with their performance. The wall is then located in between the mirrors on the COB. We should note that the distance between these mirrors is much smaller than the length of the cavities.

Fig. 9.5

Standard layout for a dual cavity LSW experiment with a COB at the center that houses the flat mirrors and wall, with curved mirrors located at the end stations

When the dual cavity configuration is used, the number of regenerated photons at the detector will be

$$\displaystyle \begin{aligned} N_\gamma = \frac{1}{16}{\left(g_{a\gamma\gamma}BL\right)}^4 \eta \beta_{\mathrm{R}} P_{\mathrm{c}}\tau, {} \end{aligned} $$

(9.23)

where η is the spatial overlap between the two cavity eigenmodes and P_c is the total circulating power in the PC. With a spatial overlap on the order of one, 150 kW circulating in the PC, an RC resonant enhancement factor of 20,000, and BL of 560 T⋅m, a two-week measurement will produce roughly 50 photons at the detector for a g_aγγ of 2 × 10⁻¹¹GeV⁻¹. From this, we see that the product of the PC power build-up and RC resonant enhancement factor can help LSW experiments gain more than 8 orders of magnitude in the signal strength in the regenerated field. This can increase their sensitivity in terms of g_aγγ by a factor of 100.

The regenerated field can be treated like a weak input field and thus will need to be resonant with the length of the RC and in its spatial eigenmode. Since the PC transmitted field should be an accurate representation of the regenerated field, it can be used to verify the resonance condition and spatial overlap.

9.3.1 Dual Resonance

Remember that the regenerated field will be in the same spatial mode and have the same frequency as the field circulating in the RC. Therefore, for the regenerated field to be resonant with the RC, the field circulating in the PC must also be resonant with the RC. For this to occur, the frequency of the PC circulating field $f_{{ }_{\mathrm {PC}}}$ must meet the condition

$$\displaystyle \begin{aligned} f_{{}_{\mathrm{PC}}} = N\frac{c}{2L_{{}_{\mathrm{RC}}}}~, {} \end{aligned} $$

(9.24)

where the right side of the equation gives the corresponding resonance of the RC. Here, N is some whole integer number and ${c}/{2L_{{ }_{\mathrm {RC}}}}$ is the FSR of the RC. Any static offset from the resonance condition will lead to a loss in the resonant enhancement factor that follows the cavity Lorentzian expressed earlier in Eq. (9.12). As the input laser to the PC is frequency stabilized to its length, this tuning can actually be done by adjusting the length of either of the cavities.

Once the cavities are set to the correct length, the resonance condition must then be maintained in the presence of environmental noise. To do this, the frequency changes of the PC circulating field must somehow track the length changes of the RC or vice versa. This requires a sensing system capable of comparing these two parameters. This can be done by stabilizing the frequency of a reference laser (RL) to the length of the RC using PDH and interfering it with the light transmitted from the PC. With this system, a direct measurement can be made of the frequency difference between the PC circulating field and the RC resonance. This is important as this information can then be fed back to stabilize the length of one of the cavities with respect to the other.

This transfer of the frequency information between the RC resonance and the PC circulating field must be done while still preventing the light circulating in the PC from entering the RC. This would create background signals that are indistinguishable from the regenerated signal. Therefore, it is clear that we cannot use the same frequency for RL as the light circulating in the PC. The limits on the available frequency that we can choose for RL are actually dependent on the energy resolution of our detection method. This system must be able to tell the difference between the light we are using to sense the length of the RC and the actual regenerated signal we are trying to measure.

As we will see in the next section, the COB is one of the critical design features of dual cavity LSW experiments and its passive stability can be used to maintain the alignment between the flat mirrors. Therefore, it makes sense to actuate on the length of the cavity via one of the curved mirrors at the end stations instead.

Stabilizing the length of one of the cavities requires an actuator capable of moving the mirror fast enough and with enough dynamic range to overcome the differential length noise between the cavities over the course of a measurement. One way to do this is to mount the mirror to a piezo-electric actuator which can expand or contract based on an input voltage. The information from the measurement of the frequency difference between the PC field and the RC can be used to stabilize the length of one of the cavities by feeding back to the piezo actuator.

Without additional seismic isolation, these systems will require control bandwidths in the kHz range. This can be difficult as the mass of the mirror, internal resonances of the piezo, and the rigidity of the mount can limit the speed with which actuation is possible. As we saw from the previous section, the longer the length of the cavities is, the larger their mirrors must be to avoid clipping losses. As the mirror gets larger, it quickly becomes difficult to actuate with the necessary speed as their mass typically increases nonlinearly with the active area. Therefore, if the cavities in future LSW experiments are much longer than 100 m, they may also require more sophisticated systems that use passive isolation to suppress the seismic noise in addition to actively controlling the lengths of the cavities.

9.3.2 Spatial Overlap

Just as it is important to maintain the resonance condition of the regenerated field with respect to the RC length, this field must also be spatially coherent with the eigenmode of the RC. Any lateral displacement or angular misalignment between the modes will lead to a reduction in the coupling efficiency of the regenerated field to the RC. Just as we discussed in the previous section, the spatial mode of the regenerated field will be a replica of the PC circulating field. Therefore. the spatial overlap η [Eq. (9.20)] between the PC and RC eigenmodes can be used to estimate the coupling of the regenerated field to the RC.

For small mode-matching errors, η can be approximated by Eq. (9.25), where Δx is a transversal offset in the minimum waist position between the input field and the cavity eigenmode, Δθ is an angular offset between their optical axes, Δw is a difference in the minimum waist size, and Δz is a difference in the position of the waist along the optical axis:

$$\displaystyle \begin{aligned} \eta = 1 - {\left(\frac{\Delta x}{w_0}\right)}^2 - {\left(\frac{\Delta \theta}{\theta}\right)}^2 - {\left(\frac{\Delta w_0}{w_0}\right)}^2 - {\left(\frac{\Delta z}{2z_r}\right)}^2~. {} \end{aligned} $$

(9.25)

Due to the length of the cavities being much larger than the separation between their waist positions, Δz∕2z_r is much less than one and should not cause a significant reduction in coupling efficiency. Likewise, Δw₀∕w₀ is also insignificant as the waist size in cavities with this geometry is determined only by their length and the radius of curvature of the end mirrors, and these values should be nearly identical for the PC and RC.

The angular misalignment and transversal displacement of the eigenmodes, on the other hand, can cause a significant loss in the spatial overlap and Fig. 9.6 shows examples of how each of these effects can occur in dual cavity setups. The angular misalignment of the cavity eigenmodes will be determined by the alignment error between the flat cavity mirrors since the optical axes of the cavities must be perpendicular to them. To ensure that there is less than 1% loss in the spatial coupling from this effect, their alignment must be within one-tenth of the cavity divergence half-angle. To put this in context, for ALPS II, this is 57 µrad and the requirement on the misalignment between the central mirrors is < 5 µrad. In ALPS II, this is achieved by rigidly mounting the mirrors to a COB. The COB is effectively just a large metallic plate which has demonstrated the necessary alignment stability in tests of prototypes.

Fig. 9.6

Examples of an angular misalignment (top) and lateral shift (bottom) between the cavity spatial eigenmodes. The angle of the optical axes is determined by the alignment of flat mirrors, while their transversal positions are controlled by the alignment and position of the curved mirrors relative to the flat mirrors

The transversal waist position of each of the cavity eigenmodes will be determined by the position and alignment of the curved mirror. Since the optical axis will be normal to both mirrors, a transversal displacement of the curved cavity mirror will lead to an equal shift in the position of its optical axis. Changes in the alignment of the curved mirrors will produce a shift in the optical axis equal to the product of the angular displacement of the curved mirror and the radius of curvature of the mirror:

$$\displaystyle \begin{aligned} \Delta x = R \Delta \theta{{}_{\mbox{ curved}}}~. {} \end{aligned} $$

(9.26)

The lower diagram in Fig. 9.6 shows an example of this effect. To put some numbers on this, in ALPS II, w₀ = 6 mm and the requirements on the transversal shift between the cavities eigenmodes are < 1 mm or a < 3% power loss. With a radius of curvature of 214 m for the curved mirrors, this means that their alignment must be controlled with better than 5 µrad precision.

The relative transversal shift between the cavity eigenmodes can be sensed by measuring cavity fields transmitted from flat mirrors with QPDs on the COB. The changes in the transversal position of the cavity eigenmodes relative to the COB will then lead to changes in the differential power level measured between the quadrants. By feeding back to alignment actuators on the curved cavity end mirrors, a control loop can be used to stabilize the positions of the eigenmodes.

Like cavity length stabilization, alignment stabilization can also be tricky. A difference here is that the requirements on the alignment stability of the cavities are usually much more forgiving relative to the environmental noise than the length stability requirements. Because of this, the cavity alignment control can be much slower (control bandwidths on the order of 1 Hz) than the length control (control bandwidths on the order of 1 kHz) while still sufficiently suppressing the noise. If the alignment noise is low enough, it can even be the case that no active alignment stabilization is necessary for the cavities.

9.3.3 Verification of the Resonance Condition and Spatial Overlap

When using a dual cavity setup to amplify the regenerated photon signal, it becomes all the more important to verify that the optical system is aligned and properly tuned. In particular, the resonance condition and spatial overlap must be checked. As we mentioned earlier, one of the design features of LSW experiments is a shutter in the wall that will allow light to freely propagate from the production area to the regeneration area when it is opened.

In dual cavity LSW experiments, the shutter must be located in between the flat cavity mirrors on the COB. When the control systems are sufficiently suppressing the environmental noise and the shutter is open, the PC transmitted field should couple directly to the RC. With prior knowledge of the reflectivities of the RC mirrors, the total coupling efficiency of the regenerated field to the RC can be estimated by measuring the ratio of the PC power incident on the RC to the power that transmits through it.

9.4 Detection Techniques

As we mentioned in the introduction, LSW experiments require detection systems capable of measuring single photons over time scales of weeks in order to reach their target sensitivity. This section will discuss two different detection schemes which are capable of this, both of which will be implemented in ALPS II. These are heterodyne interferometry and transition edge sensors. We should emphasize that each of these systems places distinct constraints on the optical setup, and therefore they cannot be operated in parallel.

9.4.1 Heterodyne Interferometry

Heterodyne interferometry works by optically mixing a laser, which we will refer to as the local oscillator (LO), with the regenerated field to create an interference beat note in the power which we can then measure. By using the coherence between the two fields, we can distinguish between this low power signal and noise. Figure 9.7 shows how a detection system using heterodyne interferometry could be implemented in a dual cavity LSW experiment. In this diagram, the high-power laser (red) is coupled to the PC and has an angular frequency of ω_s, while the local oscillator (blue), with an angular frequency of $\omega _{{ }_{\mathrm {LO}}}$, is injected to the RC through a Faraday isolator (FI). As the regenerated field, shown as the dotted red line, circulates in the RC, it naturally mixes with the LO field. This produces an interference beat note at the difference frequency Δω, between the two fields. This beat note on the LO power can then be measured at the science photodetector PD_S.

Fig. 9.7

Simplified design of a heterodyne detection system for a dual cavity LSW experiment

As we discussed in the previous section, for optimal resonant enhancement of the regenerated signal, the cavity lengths must be tuned such that the frequency difference between the two fields is held at some integer number of FSRs of the RC. Furthermore, since heterodyne detection systems rely on the absolute phase coherence of the local oscillator to the regenerated signal, any drift in the relative phase between these signals will lead to a reduction in sensitivity. We should note that this goes beyond even the requirements of dual resonance.

This necessitates some additional system that can sense the phase relationship between the local oscillator and the PC transmitted field. As we can see in Fig. 9.7, the simplest way to do this would be to interfere the fields transmitted by the cavities at a beam splitter on the COB. The phase of the interference beat note can then be monitored by a photodetector PD_M. This system must also be capable of sensing the optical path-length changes between the flat cavity mirrors on the COB [16], although the components that perform this function are not shown in the figure. The technical challenges become even more significant when considering that all of this must be accomplished without compromising the light-tightness of the experiment.

We can see how difficult it is to measure the power of the regenerated field by looking at the expression for the expected power at PD_S:

$$\displaystyle \begin{aligned} \begin{array}{cc} P{\left(t\right)} = P_{{}_{\mathrm{LO}}} +P_{{}_{\mathrm{S}}} + 2\sqrt{P_{{}_{\mathrm{LO}}}P_{{}_{\mathrm{S}}}}\cos {\left(\Delta\omega t-\phi\right)} +\chi_{{}_{\mathrm{SN}}} & {\left(\Delta \omega = \omega_{{}_{\mathrm{LO}}} - \omega_{{}_{\mathrm{S}}}\right)}. \end{array} {} \end{aligned} $$

(9.27)

The static terms $P_{{ }_{\mathrm {LO}}}$ and $P_{{ }_{\mathrm {S}}}$ represent the DC power of the local oscillator laser and the weak signal field. In LSW experiments, these powers differ by over 20 orders of magnitude effectively making a measurement of the $P_{{ }_{\mathrm {S}}}$ term impossible. The third term shows the interference beat note between the local oscillator and the regenerated field. The beat note has an amplitude of $2\sqrt {P_{{ }_{\mathrm {LO}}}P_{{ }_{\mathrm {S}}}}$, which corresponds to sub-pW amplitudes for a regenerated signal of one photon per day when a 10 mW local oscillator is used. This means we need to measure an oscillation in the power with an amplitude that is over 10 orders of magnitude lower than its mean value.

Furthermore, the beat note will also be embedded within what is known as shot noise due to photon counting statistics. This will make it impossible to identify the interference beat note simply from a time series of the power. Instead, we can calculate the power spectral density (PSD) to find the signal. The PSD is a measure of the density of power in each of the frequency components that make up the signal. As we will see, heterodyne interferometry takes advantage of the fact that the PSD of coherent signals will increase with the measurement time, while the PSD of incoherent signals will remain the same over time.

The PSD of shot noise measured by the photodetector will be equal to

$$\displaystyle \begin{aligned} \mathrm{PSD}_{{}_{\mathrm{SN}}} = P_{{}_{\mathrm{LO}}} h\nu~, {} \end{aligned} $$

(9.28)

where hν is the energy per photon of the laser. The single-sided PSD of the interference beat note at the difference frequency in the absence of noise is given by the following equation for a measurement time τ:

$$\displaystyle \begin{aligned} \mathrm{PSD}_{{}_{\mathrm{IB}}} {\left(\Delta\omega\right)} = P_{{}_{\mathrm{S}}} P_{{}_{\mathrm{LO}}}\tau~. {} \end{aligned} $$

(9.29)

The signal-to-noise ratio (SNR) can then be found by calculating the ratio of these PSDs [17],

$$\displaystyle \begin{aligned} \mathrm{SNR} = \frac{S_{{}_{\mathrm{IB}}}{\left(\Delta\omega\right)} }{S_{{}_{\mathrm{SN}}}{\left(\Delta\omega\right)} }= \frac{P_{{}_{\mathrm{S}}}}{h\nu} \tau = \langle N_{{}_{\mathrm{S}}}\rangle. {} \end{aligned} $$

(9.30)

As expected, the signal-to-noise ratio is proportional to the measurement time, but what is also apparent is that the signal-to-noise ratio is equal to the expected number of regenerated photons. This is, of course, contingent on several factors such as the shot noise being at a level well above the technical noise of the photodetector. Also, the beat note between the regenerated signal and LO remaining coherent with the oscillator used to perform the PSD. Additionally, for this condition to be valid stray light and other sources of background signals must be sufficiently suppressed.

The power in the regenerated field can then be calculated by dividing the PSD at Δω by the measurement time and LO power:

$$\displaystyle \begin{aligned} P_{{}_{\mathrm{S}}} = \frac{\mathrm{PSD}_{{}_{\mathrm{IB}}} {\left(\Delta\omega\right)} }{P_{{}_{\mathrm{LO}}}\tau}~. {} \end{aligned} $$

(9.31)

In principle, heterodyne interferometry should not be limited by any fundamental backgrounds. Nevertheless, the system must be well designed such that the various electronic signals used to maintain the coherence of the fields only experience a limited coupling to the detection electronics. Otherwise, this will create background signals that cannot be distinguished from the regenerated field.

9.4.2 Transition Edge Sensors

An entirely different technology that can also be used to measure the regenerated field is transition edge sensors (TES) [18]. These devices are capable of measuring the heat induced by the incidence of single photons on an absorptive chip. They are well equipped to face the challenges posed by LSW experiments due to their low noise and high efficiency.

The diagram to the left of Fig. 9.8 shows a simplified version of the TES electrical circuit. TESs work by holding a small chip, typically made of tungsten, at the temperature threshold to superconductivity. When a photon is absorbed by the chip, it will cause a sudden spike in its temperature that provokes a change in its resistance and thus the current passing through the sensor. An inductive coil (L) in series allows the pulse in the current to be measured using a SQUID.

Fig. 9.8

On the left is a simplified diagram of the TES circuit. Here, the chip has a resistance R₀ when held at a temperature T with a current I passing through it. The current passing through the inductive coil L is measured with a SQUID. The center plot shows an R versus T curve of the chip at the superconducting transition, with the set point $T_{{ }_{\mathrm {C}}}$. The plot on the right shows an ideal pulse and how the rise time τ_rise and fall time τ_fall effect the pulse shape

A bias current can be introduced which, when traveling over a shunt resistor R_L, can be treated as a constant voltage source (V_bias) . This configuration is critical to the stability of the system as when R_L ≪ R₀ the electrothermal feedback is negative and the sensor operates at a steady state between heat introduced by the flow of current through it and the heat dissipated by a thermal link to a cold bath held at a lower temperature T_bath.

Since the bias current puts an additional heat load on the chip, it can also be used to tune and maintain the working point of the system. The R versus T curve in the middle of Fig. 9.8 shows how the chip transitions from a normal state to the superconducting state as its temperature drops. The set point is chosen at some temperature $T_{{ }_{\mathrm {C}}}$ along this curve, below the point where the derivative ∂R∕∂T is at a maximum, to optimize the dynamic range of the system.

As the right-hand plot in Fig. 9.8 shows, pulses in current will have several defining features that help identify whether or not they were indeed the result of an incident photon, and if so how much energy was transferred to the chip. One of these is the rise time τ_rise, a measure of the time constant of the initial leveling off of the change in current after the photon is absorbed. The rise time is dependent on the inductance of the coil and the total dynamic resistance of the circuit. Then, there is the fall time τ_fall or the time constant of the decay of the current back to its steady-state value. The fall time will also be determined by the same parameters which set the rise time along with several others. These additional parameters are the derivative of the resistance with respect to the bias current ∂R∕∂I and temperature of the chip ∂R∕∂T, along with the temperature of the chip itself $T_{{ }_{\mathrm {C}}}$, all at the working point, as well as the thermal conductivity of the link to the cold bath. Finally, there is the height of the pulse, which will depend on the energy introduced by the incident photon.

The following expression can be used as a simple model for a pulse with A as a scaling constant:

$$\displaystyle \begin{aligned} \delta I{\left(t\right)} = A {\left(e^{-t/\tau_{{}_{\mathrm{rise}}}} - e^{-t/\tau_{{}_{\mathrm{fall}}}}\right)}~. {} \end{aligned} $$

(9.32)

All incident photons will produce pulses with the same rise time and fall time, with the energy of the photon determining the pulse height. Simply integrating the pulse will give energy induced by the photon. However, for robustness a pulse fitting algorithm is typically applied to the measured data, which not only provides data on the photon energy, but can also help distinguish whether or not the source of the pulse was actually an incident photon, rather than the intrinsic noise of the system.

The energy resolution of the TES can be determined by measuring many photons from a single frequency source and constructing a histogram of energies with the template fitting routine. A perfect energy resolution would result in the same measured energy for all of the incident photons. The noise of the system will, however, lead to spreading of the histogram with the energy resolution of the TES being the width of the distribution. This is a critical parameter for LSW experiments as the better the energy resolution is, the better the TES can distinguish background events from signal photons. Energy resolutions down to 5% have been demonstrated [19].

One of the limiting sources of background events when using TESs for LSW experiments is black-body radiation. The primary concern is not actually events at the signal energy, since the lasers typically operate at energies outside the black-body spectrum at room temperature. Instead, the main issues arise from events called “pile-ups”, in which two pulses occur so close close together in time that is is impossible to distinguish them from a single event. If the energies of the two black-body photons sum to an energy close to that of the regenerated field, they can be mistaken as a signal.

One way to mitigate this problem is to filter out the black-body photons before they are incident on the chip. This is complicated by the fact that the filter must be operated in a cryogenic environment, and any optics after the filter that couple the light to the TES must also be cold. Otherwise, the filter itself along with the warm optics would generate their own black-body spectrum creating a background. This is further complicated by the fact that the regenerated field is normally coupled to the TES via an optical fiber.

We should note here that the black-body spectrum does not need to be completely eliminated, only reduced to the point where the background rate no longer effects the sensitivity of the experiment. If the black-body pile-up can be sufficiently suppressed, it is possible for TESs to achieve background rates below to 1 × 10⁻⁵s⁻¹ before other backgrounds, such as the radioactivity of the materials in the vicinity of the chip, become limiting.

9.5 Conclusion

As we have discussed, LSW experiments are capable of measuring the coupling between a UBDM field and electromagnetic fields without relying on model-dependent astrophysical sources. Instead, the UBDM fields are generated in the laboratory with a laser and a string of magnets. Using such a well understood mechanism of production for the UBDM field is a major advantage of LSW experiments over other types of searches.

In order to increase further their sensitivity, these experiments can use optical cavities on both sides of the wall to increase the power of the regenerated field at the detector. This, however, requires a sophisticated optical system to stabilize the length and alignment of the cavities. Furthermore, the system must have the ability to verify that it is properly tuned, all while suppressing background signals below the sensitivity of the detectors. With detection systems capable of sensitivities on the order of one photon per day, modern LSW experiments such as ALPS II will be able to probe the electromagnetic–UBDM field interaction down to couplings ∼ 2 × 10⁻¹¹ GeV⁻¹.