Solar Production of Ultralight Bosons

Abstract

This chapter will spotlight axions produced in the core of the Sun. A first focus will be put on the production mechanism for axions in the solar interior through coupling of axions to photons via the Primakoff effect as well as their interactions with electrons. In addition to the axion production, the axion-to-photon conversion probability is a crucial quantity for solar axion searches (also referred to as helioscopes) and determines the expected number of photons from solar axion conversion that are detectable in a ground-based search. After these basic considerations, the helioscope concept will be detailed, and past, current, and future experimental realizations of axion helioscopes will be discussed. This includes the analysis used to aim at axion detection and upper limit calculations in case no signal above background is detected in experimental data. For completeness, alternative approaches other than traditional helioscopes to search for solar axions are discussed.

5.1 Production of Axions in the Sun

5.1.1 Solar Models and the Origin of Solar Axions

Axions can be produced in the core of stars via the Primakoff effect [1], which converts axions to photons and vice versa in strong electromagnetic fields as shown in the Feynman graphs of Fig. 5.1. In the extremely hot and dense core of the Sun—the closest celestial axion source to Earth—the two-photon coupling of pseudoscalars allows for the conversion of blackbody (BB) photons into axions. The BB photons in this case have energies in the keV range. The virtual photon is hereby provided by the strong electromagnetic field, originating from the charged particles in the plasma. In nonrelativistic conditions, the Primakoff effect is relevant, since in this case, electrons and nuclei can be considered heavy in comparison to the energies of the surrounding photons. Therefore, the differential cross section here (not taking into account recoil effects) is given by [2]

$$\displaystyle \begin{aligned} \frac{d\sigma_{\gamma\rightarrow a}}{d\Omega}=\frac{g_{a\gamma\gamma}^{2}Z^{2}\alpha}{8\pi}\frac{|\boldsymbol{p}_{\gamma}\times\boldsymbol{p}_{a}|{}^{2}}{\boldsymbol{q}^{~4}}, \end{aligned} $$

(5.1)

Fig. 5.1

Left: Feynman diagram of the Primakoff effect in the solar interior. Photons can be converted into axions in the electric field of the charged particles in the plasma. Right: in a laboratory magnetic field, the axion couples to a virtual photon from the transverse component of the magnetic field via the inverse Primakoff effect

where the axion and photon energies are considered equal and the momentum transfer is given by q = p_γ −p_a with p_γ and p_a being the momentum of the photon and the axion, respectively. The axion-to-photon coupling constant is represented by g_aγγ, Z is the atomic number, and α denotes the fine-structure constant. The cutoff of the long-range Coulomb potential in vacuum for massive axions is given by the minimum required momentum transfer

$$\displaystyle \begin{aligned} q_{\mathrm{min}}=\frac{m_{a}^{2}}{2E_{a}}, \end{aligned} $$

(5.2)

for the axion mass being small compared to its energy (m_a ≪ E_a), yielding a total cross section of

$$\displaystyle \begin{aligned} \sigma_{\gamma\rightarrow a}=Z^{2}g_{a\gamma\gamma}^{2}\left[\frac{1}{2}\mathrm{ln}\left(\frac{2E_{a}}{m_{a}}\right)-\frac{1}{4}\right]. \end{aligned} $$

(5.3)

The cutoff of the long-range Coulomb potential in a plasma is the consequence of screening effects resulting in an additional factor in the differential cross section such that

$$\displaystyle \begin{aligned} \frac{d\sigma_{\gamma\rightarrow a}}{d\Omega}=\frac{g_{a\gamma\gamma}^{2}Z^{2}\alpha}{8\pi}\frac{|\boldsymbol{p}_{\gamma}\times\boldsymbol{p}_{a}|{}^{2}}{\boldsymbol{q}^{~4}}\frac{\boldsymbol{q}^{~2}}{\kappa^{2}+\boldsymbol{q}^{~2}}. \end{aligned} $$

(5.4)

The Debye–Hückel scale κ represents screening effects via [3]

$$\displaystyle \begin{aligned} \kappa^{2}=\frac{4\pi\alpha}{T_{\odot}}\sum_{j}Z_{j}^{2}n_{j}, \end{aligned} $$

(5.5)

with T_⊙ describing the temperature in the solar core plasma and n_j is the number density of charged particles carrying the charge Z_je. Near the center of the Sun, the Debye–Hückel scale κ ≈ 9 keV. The total scattering cross section taking into account this modification was calculated by Raffelt [3, 4]. Under the assumption of a nonrelativistic medium and negligible recoil effects, an expression for the transition rate Γ_γ→a can be obtained by summing over all target species of the medium

$$\displaystyle \begin{aligned} \Gamma_{\gamma\rightarrow a}=\frac{T_{\odot}\kappa^{2}g_{a\gamma\gamma}^{2}}{32\pi^{2}}\frac{|\boldsymbol{p}_{\gamma}|}{E_{\gamma}}\int{d\Omega\frac{|\boldsymbol{p}_{\gamma}\times\boldsymbol{p}_{a}|{}^{2}}{\boldsymbol{q}^{~2}\left(\boldsymbol{q}^{~2}+\kappa^{2}\right)}}. \end{aligned} $$

(5.6)

Angular integration then yields [4]

$$\displaystyle \begin{aligned} \begin{array}{rcl} \Gamma_{\gamma\rightarrow a} & = &\displaystyle \frac{T_{\odot}\kappa^{2}g_{a\gamma\gamma}^{2}}{32\pi}\frac{p_{\gamma}}{E_{\gamma}}\left\{\frac{\left[\left(p_{\gamma}+p_{a}\right)^{2}+\kappa^{2}\right]\left[\left(p_{\gamma}-p_{a}\right)^{2}+\kappa^{2}\right]}{4p_{\gamma}p_{a}\kappa^{2}}\right. \\ & &\displaystyle \times\ln\left[\frac{\left(p_{\gamma}+p_{a}\right)^{2}+\kappa^{2}}{\left(p_{\gamma}-p_{a}\right)^{2}+\kappa^{2}}\right] \left.{}-\frac{\left(p_{\gamma}^{2}-p_{a}^{2}\right)^{2}}{4p_{\gamma}p_{a}\kappa^{2}}\ln\left[\frac{\left(p_{\gamma}+p_{a}\right)^{2}}{\left(p_{\gamma}-p_{a}\right)^{2}}\right]-1\right\}, {}\quad \end{array} \end{aligned} $$

(5.7)

where p_γ = |p_γ| and p_a = |p_a| are the absolute values of the photon and axion momenta, respectively. For the Sun, the effective mass of the photon in the medium, i.e., the plasma frequency ω_p, is small. Typically, it is around 0.3 keV, while the solar core temperature is T_⊙ = 15.6 × 10⁶ K = 1.3 keV, leading to typical photon energies of about 3T_⊙≈ 4 keV. We therefore neglect the plasma frequency in the following, and photons will be treated as massless. Recoil effects can be ignored, such that E_γ = E_a in the photon-to-axion conversion and p_γ = E_γ = E_a and $p_{a}=\sqrt {E_{a}^{2}-m_{a}^{2}}$ can be assumed, simplifying Eq. (5.7) to

$$\displaystyle \begin{aligned} \begin{array}{rcl} \Gamma_{\gamma\rightarrow a} & = &\displaystyle \frac{T_{\odot}\kappa^{2}g_{a\gamma\gamma}^{2}}{32\pi}\left\{\frac{\left(m_{a}^{2}-\kappa^{2}\right)^{2}+4E_{a}^{2}\kappa^{2}}{4E_{a}p_{a}\kappa^{2}}\ln\left[\frac{\left(E_{a}+p_{a}\right)^{2}+\kappa^{2}}{\left(E_{a}-p_{a}\right)^{2}+\kappa^{2}}\right]\right. \\ & &\displaystyle \left. {} -\frac{m_{a}^{4}}{4E_{a}p_{a}\kappa^{2}}\ln\left[\frac{\left(E_{a}+p_{a}\right)^{2}}{\left(E_{a}-p_{a}\right)^{2}}\right]-1\right\}. {} \end{array} \end{aligned} $$

(5.8)

For axion masses small compared to the axion energy, i.e., p_a ≈ E_a, the next to last term tends to zero and the above equation reduces further to

$$\displaystyle \begin{aligned} \Gamma_{\gamma\rightarrow a}=\frac{T_{\odot}\kappa^{2}g_{a\gamma\gamma}^{2}}{32\pi}\left[\left(1+\frac{\kappa^{2}}{4E^{2}}\right)\mathrm{ln}\left(1+\frac{4E^{2}}{\kappa^{2}}\right)-1\right]. {} \end{aligned} $$

(5.9)

The differential axion flux expected at Earth is then simply the convolution of the transition rate with the distribution of blackbody photons of the Sun followed by an integration using a standard solar model

$$\displaystyle \begin{aligned} \frac{d\Phi_{a}\left(E_{a}\right)}{dE_{a}}=\frac{1}{4\pi d_{\odot}^{2}}\int_{0}^{R_{\odot}}{d^{3}\boldsymbol{r}~\frac{1}{\pi^{2}}\frac{E_{a}^{2}}{\mathrm{e}^{E_{a}/T}-1}\Gamma_{\gamma\rightarrow a}}, \end{aligned} $$

(5.10)

where an average distance to the Sun of d_⊙≈ 1.50 × 10¹³ cm can be assumed. Van Bibber et al. [5] were the first to derive an approximate formula by including the standard solar model developed by Bahcall et al. [6] in 1982. Raffelt and Serpico revised the early results using an updated solar model [7] by fitting the following function to the solar data:

$$\displaystyle \begin{aligned} \frac{d\Phi_{a}(E_{a})}{dE_{a}}=A\left(\frac{E_{a}}{E_{0}}\right)^{\beta}\mathrm{e}^{-\left(\beta+1\right)E_{a}/E_{0}}, \end{aligned} $$

(5.11)

where A is a normalization factor, E₀ corresponds to the average axion energy 〈E_a〉, and β is related to higher moments of energy. The best fit is obtained as

$$\displaystyle \begin{aligned} \frac{d\Phi_{a}(E_{a})}{dE_{a}}=6.020\times10^{10}\left(g_{10}\right)^{2}\frac{\left(E_{a}/\mathrm{keV}\right)^{2.481}}{\mathrm{e}^{\left(\left(E_{a}/\mathrm{keV}\right)/1.205\right)}}\left[\mathrm{cm}^{-2}\mathrm{s}^{-1}\mathrm{keV}^{-1}\right], \end{aligned} $$

(5.12)

with an accuracy at the 1% level for energies in the 1–11 keV range and g₁₀ defined as

$$\displaystyle \begin{aligned} g_{10}=\frac{g_{a\gamma\gamma}}{10^{-10}~\mathrm{GeV}^{-1}}. \end{aligned} $$

(5.13)

The average axion energy is $\left \langle E_{a}\right \rangle =4.2~\mathrm {keV}$, and the maximum of the axion energy distribution is expected to be around 3 keV. Note that this is the case for KSVZ axions (hadronic axions, proposed by Kim [8], Shifman et al. [9]), for which the Primakoff production mechanism dominates. For the Dine–Fischler–Srednicki–Zhitnitsky (DFSZ) model axions [10, 11], with axion-electron interaction present at tree level, for which “ABC processes” (axio-recombination, bremsstrahlung, and Compton scattering) dominate, the peak is shifted toward lower energies.¹ The total axion flux for hadronic models is then proportional to $g_{10}^{2}$ as

$$\displaystyle \begin{aligned} \Phi_{a} = 3.75\times10^{11}\left(g_{10}\right)^{2}~\mathrm{cm}^{-2}~\mathrm{s}^{-1}. \end{aligned} $$

(5.14)

The axion luminosity for the standard solar model is

$$\displaystyle \begin{aligned} L_{a} = 1.85\times10^{-3}\left(g_{10}\right)^{2}L_{\odot}, \end{aligned} $$

(5.15)

where L_⊙ refers to the solar photon luminosity. No major updates to the solar models have been made since then, so these predictions still hold. Figure 5.2 shows the differential solar axion flux for hadronic and non-hadronic axion models.

Fig. 5.2

Solar axion flux on Earth. The coupling of axions to photons here is assumed to be g_aγγ = 10⁻¹² GeV⁻¹, the interaction strength with electrons g_aee = 10⁻¹³. For a typical KSVZ (hadronic model, see Chap. 2 for details on axion models), the Primakoff effect is the dominant component and the differential axion flux is represented by the blue line, while for the DFSZ model, in which axions and electrons interact at tree level, the various components of the ABC flux take over (red lines): FF = free-free (bremsstrahlung), FB = free-bound (axio-recombination), and BB = bound-bound (axio-deexcitation). The black line is the total ABC flux. Please note that to show ABC and Primakoff spectra in the same plot, the latter has been multiplied by a factor of 50. Figure from Ref. [12]

When using an imaging device—such as an X-ray telescope—to detect photons from axion-to-photon conversion, as common in solar axion search experiments (referred to as helioscopes), a helpful approach is to consider the differential axion flux as an apparent surface luminosity $\varphi _{a}\left (E_{a},r\right )$ of the solar disk. This implies that the flux (for g₁₀ = 1) is calculated per unit surface area of the apparent 2-dimensional solar disk. It is a function of the axion energy E_a and a dimensionless radial coordinate r (0 ≤ r ≤ 1), representing the radius normalized to the solar radius R_⊙. The apparent surface luminosity $\varphi _{a}\left (E_{a},r\right )$ can be formulated as [13]

$$\displaystyle \begin{aligned} \varphi_{a}\left(E_{a},r\right)=\frac{R_{\odot}^{3}}{2\pi^{3}d_{\odot}^{2}}\int_{r}^{1}ds\frac{s}{\sqrt{s^{2}-r^{2}}}E_{a}~k~f_{B}\Gamma_{a\rightarrow\gamma} \end{aligned} $$

(5.16)

and is given in units of cm⁻² s⁻¹ keV⁻¹ per unit surface area; d_⊙ is the average distance of Earth from the Sun as in Eq. (5.10), s represents the radial position in the Sun, determining physical quantities, such as temperature and density, and k is the wavenumber. $f_{B}=\left (\mathrm {e}^{E_{a}/T_{\odot }}-1\right )^{-1}$ denotes the Bose-Einstein distribution. In Fig. 5.3, the axion surface luminosity as seen on Earth is shown as a function of axion energy E_a and radial coordinate r. Only Primakoff conversion has been taken into account here (hadronic models), but a similar plot can also be derived for non-hadronic models, in which axions also significantly interact with electrons. The color scale is given in units of axions/(cm² ⋅s⋅keV) per unit surface area on the solar disk. This shows that most axions originate from the inner 20% of the solar radius. Furthermore, the axion flux is expected to be largest at energies around 3 keV for hadronic axions. Figure 5.4 illustrates the energy dependence of the axion surface luminosity for several radial coordinates obtained by integration up to the corresponding values of r. The total axion flux at Earth can be obtained from the apparent surface luminosity $\varphi _{a}\left (E_{a},r\right )$ using

$$\displaystyle \begin{aligned} \Phi_{a}=2\pi\int_{0}^{1}dr~r\int_{\omega_{p}}^{\infty}dE~\varphi_{a}\left(E_{a},r\right), \end{aligned} $$

(5.17)

where ω_p is again the plasma frequency.

Fig. 5.3

Contour plot of the axion surface luminosity of the Sun resulting from the Primakoff effect as a function of energy and dimensionless radial coordinate r. The units, in which the flux is given, are axions/(cm² ⋅s⋅keV) per unit surface area on the solar disk. Here, g₁₀ = 1 has been assumed

Fig. 5.4

Solar axion surface luminosity depending on energy for various values of the radial coordinate r. It has been derived by integrating up to different values of r. Here, the same units as in Fig. 5.3 have been used. Credit: J. Ruz

5.1.2 Non-Primakoff Solar Axions

In non-hadronic models, like the DFSZ models (see Chap. 2), axions couple with electrons at tree level. This coupling allows for additional mechanisms of axion production in the Sun, namely: atomic axio-recombination and axion-deexcitation, axio-bremsstrahlung in electron-ion or electron-electron collisions, and Compton scattering with emission of an axion. Figure 5.5 shows the Feynman diagrams of all these processes. Collectively, solar axions from the flux generated by all these channels are referred to as ABC (or BCA) solar axions, from the initials of the aforementioned processes. The most up-to-date computations of these production channels can be found in [12].

Fig. 5.5

Different processes responsible for axion production in the Sun, including both the Primakoff process and the ABC processes. Figure from Ref. [12]

The spectral distribution of ABC solar axions, as well as of each of the individual components, is shown in Fig. 5.2. Although the relative strength of ABC and Primakoff fluxes depends on the particular values of the g_aee and g_aγγ couplings, and therefore on the details of the axion model being considered, for non-hadronic models the ABC flux is expected to dominate. For example, for the representative values taken to produce Fig. 5.2, the Primakoff spectrum has been multiplied by 50 to make it comparable with the ABC spectrum.

Although all processes contribute substantially, free-free (bremsstrahlung) processes constitute the most important component and are responsible for the fact that ABC axions are of somewhat lower energies than Primakoff axions, with a spectral maximum around ∼1 keV. This is because the axio-bremsstrahlung cross section increases for lower energies and, in the hot solar core, electrons are more abundant than photons, and their energies are high with respect to atomic orbitals. In addition, the axio-deexcitation process is responsible for the presence of several narrow peaks, each one associated with different atomic transitions of the species present in the solar core. These two features would be of crucial importance in the case of a positive detection to confirm an axion discovery, as will be discussed in Sect. 5.4.2.3.

Despite the above, due to the fact that g_aee is more strongly bounded from astrophysical considerations than g_aγγ (see Chap. 3), the sensitivity of experiments to ABC axions has so far not been sufficiently high to reach and study unconstrained values of g_aee. This may change with the next generation of solar axion helioscopes, like the International AXion Observatory (IAXO), that will enjoy sensitivity to values down to g_aee ∼ 10⁻¹³ (Sect. 5.4).

For the sake of completeness, we should mention that the existence of axion-nucleon couplings g_aNN also allows for additional mechanisms of axion production in the Sun. These emissions are monoenergetic and are associated with particular nuclear reactions in the solar core. Some examples of the emissions that have been searched for experimentally are 14.4 keV axions emitted in the M1 transition of⁵⁷Fe nuclei and MeV axions from ⁷Li and D(p, γ)³He nuclear transitions or ¹⁶⁹Tm (see Ref. [14] for details and references).

Note that while the above considerations are mainly focusing on axions, axionlike particles (ALPs, [15,16,17], see also Chap. 2) share—to a large extent—the same theory and phenomenology as axions. Interestingly, most of the experiments searching for the effects of axion couplings to standard model particles (photons, electrons, nucleons) are therefore also sensitive to these more generic axionlike particles. Generally speaking, ALPs are pseudo-Nambu-Goldstone bosons with small masses and rather weak interaction strength originating from the spontaneous breaking of a symmetry at very high energy scales (Chap. 2, Sect. 2.3). They generally mix with photons similarly to axions but do not exhibit the axion-typical relation between axion mass m_a and coupling constant g_aγγ, i.e., they are not a part of the Peccei-Quinn (PQ) mechanism [18, 19] for quantum chromodynamics (QCD) axions and do not acquire their masses from effects in QCD but rather through corresponding dynamics that explicitly break a global symmetry. These more generic particles (every axion is an ALP, but not every ALP is an axion) are invoked in various scenarios, theoretically well motivated at the low-energy frontier of particle physics (see Ref. [14] and also Chap. 2, Sect. 2.5). They are sometimes also referred to as non-QCD or non-PQ axions, which is why the term axions is often used to refer to both QCD axions and ALPs.

5.1.3 Constraints on the Solar Axion Flux

The solar axion flux expectation can be constrained by using known solar properties. First, an additional energy loss channel via axion emission would increase the consumption of nuclear fuel, and since the Sun has lived through about half of its helium burning phase, its solar axion luminosity should not exceed the solar photon luminosity. This consideration can, for example, rule out apparent “signals” of the PVLAS-type [20], since these would require an axion luminosity of L_a > 10⁶ × L_⊙, such that the solar lifetime would be about 1000 years [21]. Indeed, for g₁₀ ≳ 20, it becomes basically impossible to construct a self-consistent solar model due to excessive axion losses [22].

Precision helioseismology and the measured solar neutrino flux are another avenue to constrain the axion-photon coupling strength. In an updated statistical analysis [23], these two observations were combined to provide a stringent upper limit on the coupling constant of g₁₀ < 4.1 at the 4σ confidence level. Helioscope upper limits on g_aγγ are consistent with these solar constraints, in that the solar axion flux, which corresponds to the published limits, is too small to significantly affect the abovementioned observations. A similar argument holds to constrain the coupling of axions to electrons g_aee [24]. Axion losses can thus be seen as minor perturbations of solar models.

5.1.4 Do Axions Escape from the Sun?

In order to be detected in an experiment, solar axions first need to escape the Sun. Their mean free path (MFP) ℓ_a must therefore be larger than the solar radius. In natural units, the photon-axion conversion rate given in Eq. (5.9) and the inverse MFP of a photon of energy E_γ considering the Primakoff effect are identical. Thus, the MFP can be obtained from Eq. (5.9) in the static limit (no recoil, screening included). With a temperature T ≈ 1.3 keV and κ ≈ 9 keV at the solar center, ℓ_a for 4 keV axions is

$$\displaystyle \begin{aligned} \ell_{a}\approx 6\times 10^{24}g_{10}^{-2}\mbox{cm }\approx 8\times 10^{13}g_{10}^{-2}R_{\odot}\mbox. \end{aligned} $$

(5.18)

Thus, the coupling constant g_aγγ would have to be larger than the best solar axion limits as observed by the CERN Axion Solar Telescope (CAST, [13, 25,26,27,28,29,30,31]) by a factor of 10⁷ in order to have reabsorption of axions in the Sun.

In the extreme case of such a strong coupling, axions would influence the solar structure. They would be responsible for the bulk of the energy transport within the Sun, which is otherwise carried by the photons. In order to be trapped in the Sun, axions would have to interact strongly enough to have an MFP smaller than that of photons, which is ≈ 1 mm in the solar interior. Thus, the solar structure will only remain unaffected if the MFP ℓ_a of axions is not much larger than a millimeter. Otherwise, the energy transfer rate in the Sun would be extremely accelerated and the solar structure would be dramatically altered. This condition is so stringent that reabsorption is not a possibility worth considering for axions or axionlike particles [21].

5.2 Axion-to-Photon Conversion Probability for Solar Axions

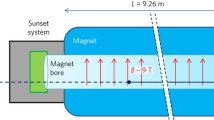
To detect solar axions in a laboratory experiment, helioscopes employ magnetic fields to convert axions into X-ray photons via the inverse Primakoff effect (see the right part of Fig. 5.1). The virtual photon in this interaction is provided by the transverse component of the magnetic field. The conversion process works in a manner analogous to neutrino oscillations [2].

Although the photon has spin-one and axions are spin-zero particles, mixing is possible in an external magnetic or electric field that enables matching of the missing quantum numbers. The conversion from a free photon into a spin-zero axion requires a change in the azimuthal quantum number of angular momentum (J_z) which for photons equals J_z = ±1 and J_z = 0 for axions. Therefore, a longitudinal field, i.e., a field with azimuthal symmetry, does not allow for these transitions given the fact that it cannot change J_z. A transverse field, however, does allow for mixing between photons and axions.

The determining wave equation for particles propagating perpendicular to a transverse magnetic field B has been derived by Raffelt and Stodolsky [32] as

$$\displaystyle \begin{aligned} \left[\left(\begin{array}{cc} \displaystyle \omega-\frac{m_{\gamma}^{2}}{2\omega} -i\frac{\Gamma}{2} & g_{a\gamma\gamma}\frac{B}{2} \\[0.3cm] \displaystyle g_{a\gamma\gamma}\frac{B}{2} & \omega-\frac{m_{a}^{2}}{2\omega} \end{array} \right)- i\partial_{z}\right] \left(\begin{array}{c} \displaystyle A_{\parallel}\\[0.3cm] \displaystyle a \end{array} \right)=0. \end{aligned} $$

(5.19)

A_∥ is the amplitude of the photon field component parallel to the magnetic field B, a is the amplitude of the axion field, ω represents the frequency, m_γ is the effective photon mass in the gas, and m_a is the axion mass. Damping is included via the inverse absorption length Γ of photons. Up to a global phase, a first-order solution can be found by using a perturbative approach as

$$\displaystyle \begin{aligned} \begin{array}{rcl} \langle A_{\parallel}(z)|a(0)\rangle & = &\displaystyle \frac{1}{2}g_{a\gamma\gamma}\exp{\left(-\int_{0}^{z}dz'~\frac{\Gamma}{2}\right)}\\ & &\displaystyle \times\int_{0}^{z}dz'B~\exp\left(i\int_{0}^{z'}dz''\left[\frac{m_{\gamma}^{2}-m_{a}^{2}}{2\omega}-i\frac{\Gamma}{2}\right]\right). \end{array} \end{aligned} $$

(5.20)

The conversion probability P_a→γ of axions into photons at a length z = L of the magnetic field can be obtained in Lorentz–Heaviside units (see Problem 5.1) as

$$\displaystyle \begin{aligned} P_{a\rightarrow\gamma}=|\langle A_{\parallel}(z)|a(0)\rangle|{}^{2}=\left(\frac{Bg_{a\gamma\gamma}}{2}\right)^{2}\frac{1}{q^{2}+\Gamma^{2}/4}\left[1+\mathrm{e}^{-\Gamma L}-2\mathrm{e}^{-\Gamma L/2}\cos\left(qL\right)\right], {} \end{aligned} $$

(5.21)

where q is the absolute momentum transfer between the real photon in the medium and the axion (see Problem 5.2) given by

$$\displaystyle \begin{aligned} q=\left|\frac{m_{\gamma}^{2}-m_{a}^{2}}{2E_{a}}\right|~, {} \end{aligned} $$

(5.22)

where E_a is the energy of the axion.

There are two cases to consider for the probability of conversion in experimental solar axion searches: (1) an evacuated conversion region and (2) a conversion volume filled with a low-Z buffer gas. Both scenarios will be discussed in the following.

5.2.1 Coherence Condition and Conversion Probability in Vacuum

Using Eq. (5.21) in the limit of m_γ → 0, the probability of axion-to-photon conversion in a magnetic field in vacuum can be derived. Assuming negligible absorption (Γ ≈ 0) results in

$$\displaystyle \begin{aligned} P_{a\rightarrow\gamma}=\left(\frac{BLg_{a\gamma\gamma}}{2}\right)^{2}\left(\frac{\sin\left(\frac{qL}{2}\right)}{\left(\frac{qL}{2}\right)}\right)^{2}, {} \end{aligned} $$

(5.23)

again with magnetic field strength B and length L. The momentum transfer q as given in Eq. (5.22) simplifies to

$$\displaystyle \begin{aligned} q=\frac{m_{a}^{2}}{2E_{a}}. \end{aligned} $$

(5.24)

This enables a coherence condition for which photon and axion waves are in phase and nonzero conversion probability can be obtained. This coherence condition can be expressed as

$$\displaystyle \begin{aligned} \frac{qL}{2}\ll\pi, \end{aligned} $$

(5.25)

which is shown in Fig. 5.6 where the $(\sin {(x)}/x)^{2}$ term of Eq. (5.23) with x = qL∕2 is plotted as a function of x and it nicely illustrates that the largest contributions are found for values $x\lesssim \pi$. In terms of axion mass, the condition can be written as

$$\displaystyle \begin{aligned} m_{a}\ll \sqrt{\frac{4\pi E_{a}}{L}}, {} \end{aligned} $$

(5.26)

such that the coherence condition is fulfilled for axion masses smaller than 0.02 eV for a realistic example of a 10 m long magnet and a typical solar axion energy of E_a ≈ 4.2 keV. In the limit of x → 0, the $\sin ^{2}{(x)}/x^{2}$ term tends to 1 and Eq. (5.23) reduces to

$$\displaystyle \begin{aligned} P_{a\rightarrow\gamma}=\left(\frac{BLg_{a\gamma\gamma}}{2}\right)^{2}, \end{aligned} $$

(5.27)

i.e., the conversion probability in vacuum.

Fig. 5.6

Dependence of the coherence term on different values of its argument qL∕2. The major contributions to the probability function result from values of qL∕2 which are smaller than π

5.2.2 Coherence Condition and Conversion Probability in a Buffer Gas

Accessing higher axion masses than possible in a conversion volume under vacuum in a given experiment can be achieved by filling the magnetic field region with a buffer gas. In order to minimize the absorption of X-ray photons in the buffer gas, elements with low atomic number Z are strongly preferred. Additional constraints due to operation of the magnet as a superconductor often require low operating temperatures of a few Kelvin and therefore usually only helium and hydrogen are good options since others are not gaseous given the required operating pressure. In the case of buffer gas use, Eqs. (5.21) and (5.22) no longer simplify as in the vacuum case.

5.2.2.1 Effective Mass of the Photon

While photons in vacuum can be considered massless and travel at the speed of light c, they acquire an effective mass when passing through a transparent medium at a speed v < c. In the classical wave picture, the slowdown can be explained as a delay of the photon wave due to interference of the incident light with photons coming from matter polarized by the original photons. Considering the situation from the particle view, it can be understood as a mixing effect between initial photon and quantum excitations of the traversed matter, resulting in a particle with effective mass. The photon energy is given by $E_{\gamma }^{2}=m_{\gamma }^{2}=\hbar ^{2} \omega _{p}^{2}$, where ω_p is the plasma frequency, and the effective photon mass in helium can be derived (see Problem 5.3) as

$$\displaystyle \begin{aligned} m_{\gamma}=\sqrt{0.020 \frac{p/\mathrm{mbar}}{T/\mathrm{K}}}\mathrm{eV}. \end{aligned} $$

(5.28)

5.2.2.2 Momentum Transfer

With the effective photon mass, the momentum transfer between an axion and a (real) photon can be calculated. q will be minimal for axion masses close to the corresponding effective photon mass of the considered buffer gas pressure. Since the momentum transfer has to be small in order to fulfill the coherence condition of Eq. (5.25), only a narrow range of axion masses can be studied at a specific gas pressure.

5.2.2.3 The Absorption of Photons in a Buffer Gas

The absorption of the photons originating from axions via the Primakoff effect in a buffer gas is another important factor influencing the conversion probability. In general, the absorption Γ of these photons is defined as the inverse of the absorption length ℓ:

$$\displaystyle \begin{aligned} \Gamma(E_{a})=\frac{1}{\ell(E_{a})}=\rho\mu(E_{a}), \end{aligned} $$

(5.29)

where ρ is the density of the gas and μ(E_a) represents the energy-dependent mass absorption coefficient, which is given by

$$\displaystyle \begin{aligned} \mu(E_{a})=\frac{N_{A}}{A}\sigma_{A}(E_{a}), \end{aligned} $$

(5.30)

with Avogadro’s constant N_A and mass number A. The scattering cross section σ_A takes into account photoelectric, coherent, and incoherent contributions. In practice, the magnetic field region of an axion helioscope will be filled with a low-Z buffer gas at a certain pressure p_gas and temperature T_gas. It is therefore useful to consider that at standard temperature and pressure (STP), the ideal gas equation yields

$$\displaystyle \begin{aligned} \ell_{\mathrm{STP}}=\ell \times {\left(\frac{T_{\mathrm{STP}}}{T_{\mathrm{He}}}\right)} \times {\left(\frac{p_{\mathrm{He}}}{p_{\mathrm{STP}}}\right)}~, \end{aligned} $$

(5.31)

for helium gas, and thus Eq. (5.29) is

$$\displaystyle \begin{aligned} \Gamma(E_{a})=\mu(E_{a})\rho_{\mathrm{STP}}\frac{T_{\mathrm{STP}}p_{\mathrm{He}}}{p_{\mathrm{STP}}T_{\mathrm{He}}}. \end{aligned} $$

(5.32)

The density under standard conditions ρ_STP for ⁴He is 0.1786 g/L.

5.2.2.4 Mass Range of Coherence

Restoring coherence by means of a buffer gas in the magnetic field region makes small axion mass ranges around the effective photon mass accessible as can be seen from Eq. (5.22) and the coherence condition of Eq. (5.25), i.e.,

$$\displaystyle \begin{aligned} \sqrt{m_{\gamma}^{2}-\frac{4\pi E_{a}}{L}}<m_{a}<\sqrt{m_{\gamma}^{2}+\frac{4\pi E_{a}}{L}}. {} \end{aligned} $$

(5.33)

Since the effective photon mass depends on the pressure and the axion mass range that can be explored varies with axion energy and length of the magnetic field region in a given experiment, the accessible axion mass range changes. For example, axion masses around a photon mass of 0.43 eV can be scanned with ⁴He at 1.8 K, since the maximum operating pressure before the ⁴He gas liquefies at these temperatures is 16.4 mbar. If an axion helioscope is operated at room temperature (293 K) instead, a similar photon mass is obtained for an operating gas pressure of 2.7 bar. Depending on the buffer gas, the magnet length, and the operating temperature, different solar axion experiments will be able to access slightly different mass ranges around the calculated photon mass.

5.3 Expected Number of Photons from Solar Axion Conversion

The expected number of photons N_γ from axion-to-photon conversion in a magnetic field can be obtained as a function of axion mass and the coupling constant (for a given pressure of the buffer gas) as

$$\displaystyle \begin{aligned} N_{\gamma}=\int_{E}\frac{d\Phi(E_{a},g_{a\gamma\gamma}^{2})}{dE_{a}}P_{a\rightarrow\gamma}(E_{a},m_{a}, g_{a\gamma\gamma}^{2})~\epsilon(E_{a})~\Delta t~A~dE_{a}, \end{aligned} $$

(5.34)

with detection area A and detection efficiency 𝜖(E_a). The exposure time, i.e., the time an axion helioscope is able to point at the solar core while tracking the Sun, is Δt. Since the expected solar axion flux and the conversion probability each depend quadratically on g_aγγ, the number of expected photons relates to the axion-photon coupling constant as

$$\displaystyle \begin{aligned} N_{\gamma}\propto g_{a\gamma\gamma}^{4}~. \end{aligned} $$

(5.35)

The number of expected photons from conversion of axions in vacuum and at a particular pressure p of a buffer gas (⁴He is used as an example) at 1.8 K in the magnetic field region is shown in Fig. 5.7 for the experimental conditions of a typical axion helioscope (i.e., CAST). An exposure time of 90 min and 100% efficiency of the detector (𝜖 = 1) have been assumed for this plot along with a magnetic field of 9 T throughout a 10 m long region. The sensitive area included is 14.52 cm², corresponding to the size of the magnet bore for the current leading axion helioscope (CAST).

Fig. 5.7

Expected number of photons from axion-to-photon conversion in a magnetic field for a typical axion helioscope as described in the text (namely, CAST). The pressure of the buffer gas (here, ⁴He) is given at 1.8 K and therefore 5.49 mbar corresponds to a density of 0.147 kg/m³

5.4 Axion Helioscope Experiments

As discussed in Sect. 5.2, axion helioscopes employ strong transverse magnetic fields B over a length L to convert solar axions into photons. Due to the fact that axions have a mass, axion and photon waves will be out of phase after a certain distance which determines the coherence condition (Eq. 5.25). For typical solar axion energies and a magnet length of ≈ 10 m, coherence is conserved for axion masses up to about 10⁻² eV, while for higher masses coherence in vacuum is lost and the experimental sensitivity decreases. It can be restored by the use of a buffer gas in the magnetic field region for higher axion masses due to the photon acquiring an effective mass in a medium. Thus, the coherence condition will be fulfilled for axion masses close to the effective photon mass. By changing the pressure of the gas inside the magnetic field region systematically, the photon mass can be increased in a controlled manner and higher masses can be scanned via pressure-step scanning.

5.4.1 Concept of Axion Helioscopes

A typical axion helioscope requires at least two key components: a powerful magnet and one or more high-sensitivity, ultralow background X-ray detectors. In latest implementations of the concept, as shown in Fig. 5.8, an X-ray focusing device is added at the end of the magnet to concentrate the signal photons and increase the signal-to-noise ratio. Such an X-ray telescope also enables the use of large cross-sectional magnets (to boost conversion probability) and simultaneously small-area detectors (to enable ultralow background levels), which in combination boost helioscope experiments to the next level. By aligning the magnet with the core of the Sun and tracking its movement, an excess of X-rays at the end of the magnet is expected as compared to background measurements when the magnet is not pointing at the Sun. The helioscope detection concept was first proposed in the 1980s [5, 33] and initially experimentally implemented by Lazarus et al. with a few hours of data acquired [34]. Later, the second-generation helioscope SUMICO [35] was built at the University of Tokyo, providing the first self-consistent limit to solar axions compatible with solar physics. During the last two decades, the helioscope principle has been advanced by the CERN Axion Solar Telescope (CAST [13, 25,26,27,28,29,30,31]) pushing the sensitivity to solar axions significantly due to innovative concepts employed by the experiment: a superior magnet, X-ray optics, and enhanced detectors. The next generation of axion helioscopes, the International AXion Observatory (IAXO, [36,37,38,39]) and its intermediate-scale phase BabyIAXO, will build on these improvements and further enhance solar axion searches by pushing sensitivities far beyond the ones reached by CAST.

Fig. 5.8

A conceptual setup of an axion helioscope using X-ray focusing to enhance the experimental sensitivity. Axions from the Sun are converted in a strong transverse magnetic field and the emerging photons are then focused by an X-ray telescope into a small focal spot. A low background detector is located in the focal plane of the optics to capture an image of the photons produced by conversion from axions. Figure adapted from Ref. [36]

Generally speaking, so far each generation of axion helioscopes improved the sensitivity to g₁₀ by a factor of ≈ 7, mostly by successfully recycling existing magnets and other equipment. Improving over the current state of the art provided by CAST requires purpose-designed components for the key helioscope pieces (magnet, detectors) as well as focusing devices without which the use of the full potential of these new components would be impossible. To maximize the figure of merit (FOM) f of a helioscope

$$\displaystyle \begin{aligned} f=f_{M}\times f_{O}\times f_{D}\times f_{T}, \end{aligned} $$

(5.36)

a global optimization of the FOM for magnet f_M, optics f_O, detectors f_D, and exposure f_T is needed. These are defined as

$$\displaystyle \begin{aligned} \begin{array}{rcl} f_{M}& =&\displaystyle B^{2}L^{2}A,{} \end{array} \end{aligned} $$

(5.37)

$$\displaystyle \begin{aligned} \begin{array}{rcl} f_{O}& =&\displaystyle \frac{\epsilon_{o}}{\sqrt{a}},{} \end{array} \end{aligned} $$

(5.38)

$$\displaystyle \begin{aligned} \begin{array}{rcl} f_{D}& =&\displaystyle \frac{\epsilon_{d}}{\sqrt{b}},{} \end{array} \end{aligned} $$

(5.39)

$$\displaystyle \begin{aligned} \begin{array}{rcl} f_{T}& =&\displaystyle \sqrt{\epsilon_{t}t},{} \end{array} \end{aligned} $$

(5.40)

where B, L, and A are the magnet parameters (field strength, field length, and cross-sectional area), and 𝜖_o, 𝜖_d, and 𝜖_t efficiencies of optics, detectors, and data acquisition, respectively. Furthermore, a is the total focal spot area of the telescopes and b the detector background normalized to unit area and time, while t is the total exposure time for observations of the solar disk center. It is worth noting that in order to maximize f, all components need to be optimized simultaneously in a multi-parameter process considering the expected axion spectrum. The helioscope figure of merit is directly proportional to the signal-to-noise (S∕N) enhancement, and therefore a measure for the sensitivity to the coupling that can be used to easily compare experiments.

Tutorial: Figure of Merit for Helioscopes

According to Eqs. (5.37)–(5.40), the figure of merit for a helioscope can most easily be boosted by improving the magnet if optics and detectors can be built to fully enable the use of these improvements. As Eq. (5.37) clearly shows, increasing the magnetic field strength B and the length L of the magnet would be the most efficient ways. Why do next-generation helioscopes opt to increase the cross-sectional area A instead?

Since the magnet parameters (B, L, and A) are all interconnected, they need to be optimized together. While magnets with larger fields (> 10 Tesla) have been previously built, they are usually much shorter than the current state of the art (CAST, with magnet length ≈ 10 m) or cannot be tilted sufficiently to track the Sun without impairing the cooling needed for superconductive operation. Increasing the length while keeping a (relatively) lower magnetic field B would be technologically feasible. However, the length L feeds into the coherence condition (see Eq. 5.25), i.e., for efficient conversion the product of momentum transfer q and length L must be small. For large L, the accessible axion masses become small as can be seen from Eqs. (5.26) and (5.33). Therefore, the best approach is to increase the cross-sectional area A of the magnet. Note that this in turn, however, requires the use of large focusing optics covering the complete magnet bore in order to focus the putative signal onto a small spot such that small-area detectors can be used. This is necessary since axion searches are by definition rare-event searches and the detector background needs to be as low as possible (zero background is the goal), which is generally only achievable with small-area detectors. Increasing the exposure time increases the sensitivity, but the upper limit on g_aγγ (in the absence of an axion signal) goes with the 8th root of time following Eqs. (5.34) and (5.35), i.e., in order to improve the limit by a factor of 2, one would need to measure a factor of 2⁸ times longer. Considering that scanning axion masses with a buffer gas in the magnetic field region needs many pressure steps and each step is usually measured for one solar tracking, one would have to spend 256 days instead of 1 to achieve a factor 2 improvement in the upper limit on the coupling.

End of Tutorial

5.4.2 Current and Future Axion Helioscopes

5.4.2.1 The CERN Axion Solar Telescope (CAST)

To date, the CAST experiment has been the most powerful axion helioscope ever built. The magnet drives the sensitivity of any helioscope due to the B²L² dependence of the conversion probability as seen from Eq. (5.37): a 9 Tesla, 9.3 m superconducting magnet is the primary element at the heart of the CAST experiment. With its two magnet bores of 14.5 cm² each, it was originally built as one of the early prototypes for the Large Hadron Collider (LHC) at CERN, which had straight bores as opposed to the bent ones fabricated later on and eventually used in the LHC, and then it was repurposed for axion searches with CAST. The magnet itself boosts the conversion probability by 2 orders of magnitude [26] compared to the predecessor helioscope [35]. CAST is equipped with an elevation and azimuthal drive, such that the experiment is able to follow the Sun twice a day during sunrise and sunset for 90 min each. When not tracking the Sun, CAST acquires background data in a magnet parking position. Right from the start, this helioscope employed an X-ray telescope in combination with a Charge Coupled Device (CCD) as a focal plane detector [40] on one of its four magnet bore exits. A second optic was installed later on [41]. CCDs are highly sensitive, pixelated photon detectors based on semiconductor technology (less sensitive versions can be found in many digital cameras and imaging devices). The CCD of CAST is a spare flight detector from the European Space Agency’s XMM Newton mission and has greatly enhanced the sensitivity of the helioscope. A variety of other detectors have been used over the course of the experiment, including several generations of novel MICROMEsh GAseous Structure (MICROMEGAS, MM, [42]) and microbulk MM detectors (i.e., a more advanced version of MM detectors), a time projection chamber (TPC, [43]) and other more specialized equipment (see [31] and the references therein for further details). Both TPCs and MMs are gaseous, low background particle detectors combining elements of Multiwire Proportional Chambers (MWPC) and conventional drift chambers. While TPC and MM share the same detection principles of amplifying charges that are created by ionization in the gas volume of the detectors, the MM detectors represent a more recent evolution that includes a metallic micro-mesh positioned in close proximity to the readout electrode dividing the gas region into two. This is a key feature that enables high gain as well as the ability to detect fast signals and also allows for ultralow background performance benefiting from the use of low-radioactivity materials used to build the detectors. Figure 5.9 shows the CAST experiment including all its main components: magnet, optics, and detectors.

Fig. 5.9

Experimental setup of the CERN Axion Solar Telescope (CAST). The magnet (blue) is installed on a movable platform (green), and detectors are mounted on either end of the magnet. On the right side, the original telescope used at CAST is visible (silver). Also shown is the cryo cooling tower of the experiment with the helium supply lines. Credit: CERN/CAST

The experiment was divided into two main phases: (1) CAST Phase I (vacuum) and (2) Phase II (gas phase with ⁴He and ³He in the magnet bores). After completion of both phases, the experiment revisited some vacuum measurements to make use of improved detection techniques and dedicated some time to chameleon² searches [47,48,49], which are candidates for dark energy, and the use of microwave cavities within the CAST magnet. During its initial observational program (Phase I), CAST operated with evacuated magnet bores studying axion masses m_a < 0.02 eV yielding an upper limit result of g_aγγ < 8.8 × 10⁻¹¹ GeV⁻¹ at the 95% confidence level [13, 26]. During CAST Phase II operations, the magnet bores were filled with ⁴He and ³He to extend the search range up to axion masses of m_a = 1.17 eV with average limits of g_aγγ ≲ 2.3–3.3 × 10⁻¹⁰ GeV⁻¹ at 95% C.L. for masses larger than 0.02 eV [27, 28]. For Phase II, the exact values depend on the individual pressure setting of the buffer gases. In recent years, improvements of the previous vacuum data results have been enabled with upgraded MM detector systems coupled to a novel X-ray telescope, the IAXO pathfinder system [41]. This approach using improved instrumentation resulted in a new benchmark limit for m_a < 0.02 eV of g_aγγ < 0.66 × 10⁻¹⁰ GeV⁻¹ (95% C.L.) [31]. One of the main goals of the CAST experiment has been to supersede the most stringent limits from astrophysical observations of horizontal branch stars (see Chap. 3) at the level of $g_{a\gamma \gamma }\lesssim 0.8\times 10^{-10}$ GeV⁻¹ [50]. CAST has studied both QCD and non-QCD axions, but most notably excluded KSVZ axions (see Chap. 3) around the 1 eV axion mass as shown in Fig. 5.10. Furthermore, the experiment has delivered results on more exotic physics cases of solar axions from M1 transition of Fe-57 nuclei [51], high-energy (MeV) axions from ⁷Li and D(p, γ)³He nuclear decays [52], axion–electron coupling constants for solar axions [53], and other ALP searches, such as for chameleons [47,48,49].

Fig. 5.10

CAST exclusion plot showing the recent benchmark result [31] of the experiment obtained with the IAXO pathfinder system [41]. The exclusion limits for g_aγγ at 95% C.L. are shown for previous data (black) and the latest results (red). QCD axions are expected to live in the yellow model band and the green line indicates the standard KSVZ axion model with E∕N = 0. This ratio is the quotient of electromagnetic anomaly E and color anomaly N of the axion current [54, 55] and can acquire various values depending on the different axion models (see Chap. 2). Figure taken from Ref. [31], in which the interested reader will also be able to find additional details and references

Tutorial: Understanding Helioscope Exclusion Plots

Figure 5.10 is a typical example of a helioscope exclusion plot, showing the upper limit obtained by a solar axion search in the case where no signal was detected above background. Why does the red line (measurements in vacuum) sharply rise at m_a ≈ 10⁻² eV and why does the black upper limit (combined previous vacuum and buffer gas phase results) display a “wiggly” structure for the higher axion masses?

The sharp rise of both curves at around 10⁻² eV is the result of a loss of coherence when operating with vacuum in the magnetic field region. Note that the value of m_a for which coherence is lost depends on the length L of the magnetic field, as seen from Eq. (5.25), and therefore depends on the specific helioscope. The black line is a combination of vacuum and buffer gas measurements, i.e., here coherence is restored—as can be seen from Eq. (5.33)—by scanning through small pressure steps with a buffer gas (⁴He and ³He, in the case of CAST). Each “wiggle” in the upper limit corresponds roughly to one specific pressure setting, i.e., a specific narrow axion mass range. The exact values depend on the number of actually observed (background) counts during the tracking, the exact time spent at the respective pressure setting, detectors active during tracking, and so on. Note also that the factor of roughly 2–3 between the vacuum and buffer gas measurements is due to the different exposure times (as well as improved detection systems): the vacuum phase includes about 2 years of tracking data, while 2 +  pressure steps were measured per day during the gas phase.

End of Tutorial

5.4.2.2 The International Axion Observatory (IAXO)

The most straightforward way to improve over current helioscope designs (see the tutorial on helioscope figures of merit earlier in this chapter) is to boost the cross-sectional area of the magnet, equip all magnet bores with X-ray focusing devices, and utilize ultralow background detectors—these improvements are the basis for the next-generation axion helioscope IAXO [37]. The expected gain of IAXO over CAST is a factor of 10⁴–10⁵ in signal-to-noise ratio, which corresponds to an improvement in sensitivity to the coupling constant g_aγγ by ≈ 30 ×. These advances promise sensitivities to discover axionlike particles with a coupling to photons as small as g_aγγ ≈ 10⁻¹² GeV⁻¹ or to electrons down to g_aee ≈ 10⁻¹³. IAXO also has the potential to find QCD axions in the 1 meV–1 eV mass range where these particles are able to solve the strong CP problem. Figure 5.11 shows the envisioned layout of the IAXO experiment.

Fig. 5.11

Schematic view of the IAXO experiment. The 25 m long magnet with its 8 bores is shown along with eight X-ray optics and detectors, the flexible service lines, cryogenics, power service units, and the horizontal and vertical drive system. A lifesize person has been added for comparison. Figure taken from Ref. [39]

Currently being designed, IAXO represents the next generation of axion helioscopes and builds on technologies with a proven track record in CAST as well as other particle physics experiments [56, 57] and astronomy missions [58, 59]. The key piece of IAXO is a 25 m long magnet with a 2.5 T (5.1 T) average (peak) field. For the first time, a helioscope will use a toroidal multibore configuration [60] with 8 coils of 70 cm diameter each and a total diameter of 5.1 m resulting in an intense field over a large conversion volume. The magnet figure of merit f_M alone provides a 300 × improvement over CAST.

Each of IAXO’s 8 bores will be covered by a 70 cm diameter telescope adopted from space science and optimized for axion searches. Telescopes for X-rays are based on the principle of total external reflection of light at grazing incidence. Therefore, the angle of incoming photons in the keV range needs to be below a critical angle (≈ 1 deg) in order for the X-rays to be reflected rather than absorbed. Reflectivity can be further enhanced by making use of Bragg’s law, resulting in constructive interference via coating the mirror substrates with a “multilayer.” Multilayers consist of periodic or non-periodic structures of alternating thin film layers of two or more materials (absorbers and spacers) deposited on an optical substrate. The focusing devices for IAXO will be built based on segmented glass technology originally developed for NASA’s Nuclear Spectroscopic Telescope Array (NuSTAR, [58]) mission and replicated optics similar to those flown on the JAXA/NASA satellites Hitomi (ASTRO-H, see [59]) and XRISM [61]. While segmented glass optics are assembled out of thousands of individual mirror pieces, replicated optics are built up from multiple full revolution shells. For IAXO, the number and position of the substrates as well as the exact prescription for the coating are being carefully designed to optimize the throughput of the optics and match both the axion spectrum and the detector responses [62], making use of the IAXO pathfinder results [41].

The focal plane detectors will be ultralow background, pixelated devices to image the focused signal. In order to achieve the low background levels required for an efficient axion search (≲ 10⁻⁷–10⁻⁸ counts/keV⁻¹cm⁻²s⁻¹), these detectors are fabricated from radiopure materials and require sophisticated shields. The baseline technology for IAXO will use small gaseous detectors with pixelized readout planes (Microbulk MICROMEGAS [42, 63]) as previously developed and tested at CAST. In addition, other detector technologies are being studied [39] to reach higher sensitivities, lower energy thresholds, and better energy resolution for applications such as detection of solar axions from ABC processes via their g_aee coupling (see Sect. 5.1.2). Just like CAST before, IAXO will have a gas phase extending the helioscope’s sensitivity to QCD axions at the higher axion masses.

As an intermediate step toward IAXO, BabyIAXO [64] is being designed and is just moving into the beginnings of its construction phase. BabyIAXO will be a scaled-down version of IAXO to test all IAXO components while simultaneously delivering first significant science results to supersede CAST’s latest benchmark results. BabyIAXO will feature a 10 m long magnet with 2 bores of 60–70 cm diameter and two optic detector systems similar in design and layout to the ones of the full-scale IAXO experiment. Most likely, the experiment will be equipped with custom-designed optics close to the final IAXO telescope specifications and a telescope that is a flight spare from ESA’s XMM Newton mission [65]. The baseline detectors for BabyIAXO are envisioned to be building on MICROMEGAS microbulk technology.

5.4.2.3 Physics Prospects of IAXO

The physics prospects for IAXO and BabyIAXO in comparison to current best limits from CAST and astrophysical hints (see Chap. 3) are shown in Fig. 5.12: at the high-mass end of the axion mass range large parts of QCD axion model space (KSVZ [8, 9] and DFSZ [10, 11]) can be tested, including viable dark matter models. Furthermore, the ALP miracle [66] parameter space in which ALPs simultaneously solve dark matter and inflation can be studied. Also, at the high-mass end, IAXO will test non-hadronic models (axion–electron coupling) that would be able to explain the stellar cooling anomaly [67]. At the lower end of the axion masses, ALP parameter space invoked by observed hints of the anomalous transparency of the Universe to ultrahigh-energy (UHE) photons will be accessible to IAXO (partially with BabyIAXO), and in the intermediate axion mass range, there is a large region of parameter space that BabyIAXO and IAXO can probe for the very first time and in which viable ALP cold dark matter could exist.

Fig. 5.12

Sensitivity prospects for BabyIAXO and IAXO in the context of other experimental and observational bounds. The interested reader is referred to Ref. [14] for a detailed recent review of axion researches, their results, and future prospects. Figure taken from Ref. [36]

In the case of a discovery, the study of the spectral features of the signal would provide additional insight into the nature of the new axionlike particle. With sufficient energy resolution and statistics, the measured spectrum could be decomposed as a sum of an ABC contribution and a Primakoff component. For adequate parameter ranges, it has been shown that independent determination of g_aγγ and g_aee should then be possible [68]. In particular, the narrow lines of Fig. 5.2 could first be used to unambiguously identify an ABC component and, eventually, they could be studied as a probe for solar metallicity [69]. Moreover, for values of m_a at the onset of loss of coherence, the measured spectrum gets distorted (depleted) at low energies. Again, with sufficient energy resolution and statistics, this effect can be used to determine the mass of the axion for a certain region of parameters [70].

Although this chapter is devoted to axions from the Sun, it is worth mentioning that there is another astrophysical source whose axions could potentially be detected with the help of helioscopes: namely, a nearby supernova (SN) explosion. In the first 10 s after the bounce of a core-collapse SN, axions are copiously produced via nucleon–nucleon axion-bremsstrahlung [71]. The energy of these axions can be several tens of MeVs, and they could in principle convert back into photons in a helioscope and be detected there, provided the experiment is equipped with appropriate high-energy detectors. According to [72], if the SN explosion occurs within a few hundred parsecs from Earth, the axions arrive in sufficiently high numbers, and one can expect a detectable, even though potentially small, signal in future helioscopes like BabyIAXO or IAXO. Apart from being equipped with gamma-ray detectors, the helioscope should point to the SN in advance of the actual explosion, something that could be accomplished with the help of a pre-SN neutrino alert.

In summary, IAXO and BabyIAXO are the next generation of axion helioscopes and will dramatically increase the sensitivity to solar axions compared to CAST, the currently most powerful axion helioscope. Furthermore, these novel, large-scale experiments also have the potential to serve as a multi-purpose facility for generic axion and ALP research in the coming decade, e.g., by incorporating microwave cavities and functioning as a haloscope (amongst other options). Together helioscopes, haloscopes, and laboratory searches provide complementary approaches to finally close in on QCD axions, axionlike particles, and other dark matter candidates to either discover these elusive particles or strongly constrain and potentially rule out their existence. For an instructive and detailed recent review of experimental axion and ALP searches, see Ref. [14].

5.5 Alternative Experiments to Search for Solar Axions

5.5.1 Stationary Helioscopes

While conventional axion helioscopes are constructed to point at and follow the Sun, other approaches have also been considered. One such novel modulation helioscope technique uses a stationary setup in which a gaseous time projection chamber (TPC) is installed in a strong magnetic field, such as the Axion Modulation hELIoscope Experiment (AMELIE, see [73]). Since solar axions are most efficiently converted when their incidence direction is perpendicular to the magnetic field, a modulation signal varying during the day due to Earth’s rotation is expected. Given that the signal would furthermore vary over the course of the year, axions would leave a distinct temporal signature in addition to their usual spectral one. This novel helioscope technology is not competitive with the standard helioscope technique for low axion masses ($m_{a}\lesssim 0.1$ eV) due to the fact that coherence of conversion is lost because of the short range of the X-rays from axion conversion in the high-pressure or high-Z gas used for large photon absorption. For higher axion masses, however, the approach might prove useful since the scanning of axion masses with a buffer gas in a conventional axion helioscope to study model-compatible axions at the higher end of the mass range remains challenging.

5.5.2 Crystalline Detectors Using Primakoff–Bragg Conversion

Instead of an external magnetic field, axion–photon conversion can also take place in the electromagnetic field at the atomic level inside materials. Therefore, crystalline detectors can be used to coherently convert solar axions into photons, which is the case when the angle of incidence of the axion fulfills the Bragg condition with the plane of the crystal [74, 75]. Pioneering results investigating these Bragg patterns were achieved with the SOLAX, COSME, and DAMA experiments. SOLAX used a Germanium spectrometer to study axion masses $m_{a}\lesssim 1$ keV and derived an upper limit on the coupling constant of g_aγγ(95% CL) < 2.7 × 10⁻⁹ GeV⁻¹ for this range [76]. COSME provided a similar result with its Ge detector yielding g_aγγ(95% CL) < 2.78 × 10⁻⁹ GeV⁻¹, independent of the axion mass [77]. The best result so far was achieved by DAMA with a NaI(Tl) crystal [78]: g_aγγ(90% CL) < 1.7 × 10⁻⁹ GeV⁻¹, again independent of the axion mass. It is worth noting that these bounds are not as strong as those derived from solar physics. Even though future experiments like CUORE [79] are expected to provide improved sensitivity to g_aγγ, they will not be able to compete with axion helioscopes for axion masses below 1 eV. While for higher masses they become more competitive, these heavy axions are disfavored by cosmology and astrophysics [80] (see also Chap. 3).

5.5.3 Non-Primakoff Effect Conversions

While the axion–photon coupling constant is the preferred parameter to study for most axion searches, since it is generic to all axion models, axions could also interact with matter via their coupling to electrons and nucleons. WIMP searches using liquid xenon detectors [81,82,83] have looked for potential signals due to the axio-electric effect [84] in their ionization detectors [85, 86]. The axio-electric effect is similar to the photo-electric effect, but, instead of a photon, an axion hits the electron and ionizes the target atom (e.g., xenon). The advantage here is that the final signals depend directly on g_aee rather than on a product of the axion–electron and the axion–photon coupling. LUX sets the most competitive limit at a 90% C.L. as g_aee < 3.5 × 10⁻¹², which is, however, not yet able to compete with limits from astrophysics [67]. Recently, the XENON collaboration reported a 3.5σ excess compatible with a potential axion signal [87] but cautioned that tritium background could explain the observed feature and cannot be excluded as the real cause for the excess at present time. Measurements with the next-generation XENONnT experiment will enable further studies of the observed feature. (Editor’s note: indeed, after this chapter was written, the XENONnT experiment ruled out axions as the cause of this excess, see arXiv:2207.11330.)

To probe axion–nucleon couplings, monochromatic solar axions emitted in M1 nuclear transitions can be searched for with detectors containing the same nuclide (see [14] and the references therein for a more detailed discussion). These experiments are however not able to compete with astrophysical limits.

However, for the time being, helioscopes remain the most promising approach to find solar axions and ALPs.