Abstract
Most dark matter searches to date employ a single sensor for detection. In this chapter, we explore the power of distributed networks in dark matter searches. Compared to a single sensor, networks offer several advantages, such as the ability to probe spatiotemporal signatures of the putative signal and, as a result, an improved rejection of false positives, better sensitivity, and improved confidence in the dark matter origin of the sought-after signal. We illustrate our general discussion with two examples: (1) the Global Network of Optical Magnetometers for Exotic physics searches (GNOME) and (2) the constellation of atomic clocks on board satellites of the Global Positioning System (GPS).
You have full access to this open access chapter, Download chapter PDF
Similar content being viewed by others
10.1 Introduction
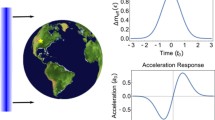
The goal of this chapter is to give an introduction to direct searches for ultralight dark matter (UBDM) using networks of precision sensors. This chapter reviews a meta-technique as it combines individual direct searches described in preceding chapters. A single apparatus couples to a dark matter (DM) field at its specific location, while a geographically distributed network can probe DM constituents at multiple locations. Thus a network approach enables testing additional signatures based on spatiotemporal correlation properties of putative DM signals. This leads to both an enhanced sensitivity and to a greater confidence in the DM origin of the sought-after signal (Fig. 10.1).
To reiterate the preceding chapters, our galaxy, the Milky Way, is embedded in a DM halo and rotates through the halo. The Sun moves through the DM halo towards the Cygnus constellation at galactic velocities vg ≈ 230 km∕s. Further, in the DM halo reference frame, the velocity distribution of DM objects is nearly Maxwellian with the dispersion of vvir ∼ 270 km∕s (virial velocity) and a cut-off at the galactic escape velocity vesc ≈ 650 km∕s. The DM energy density ρdm in the vicinity of the Solar system is estimated at the level of 0.3 GeV∕cm3, corresponding to about one hydrogen atom per three cubic cm.
All the evidence for dark matter (galactic rotation curves, gravitational lensing, peaks in the cosmic microwave background spectra, etc.—see discussion in Chap. 1) comes from galactic scale observations. The challenge in planning a laboratory experiment lies in extrapolating down from the 10-kpc characteristic galactic length scales to laboratory scales. These are truly vast extrapolation scales and a large number of theoretical models can fit the observations (as discussed in Chap. 3). For the goals of this chapter, we broadly classify DM candidates as either being “wavy” or “clumpy.” As with the ocean, one may distinguish between either a relatively calm surface with characteristic ripples or solitary perturbations such as tsunami that preserve their shape while traveling across many miles. The former is an example of the wavy DM (nearly uniform field composed of many interfering waves) and the latter of the clumpy DM candidates.
The “wavy” DM is typically composed of non-self-interacting ultralight DM candidates. Due to the large mode occupation numbers (see Chaps. 1–3), such fields behave as classical entities coherent on a scale of individual detectors. At a single node, these fields would drive a signal oscillating at the DM field Compton frequency. An important point is that such candidates are waves, and while they do induce an oscillating-in-time signal at a given spatial location, DM signals at different locations have a fixed phase relation, i.e., the signals at distinct nodes are correlated. Thereby, a discovery reach can be improved by sampling the DM wave at multiple locations. In the wavy DM models, the DM field is composed of numerous waves traveling at different velocities and in different directions. Interference of DM waves results in a stochastic field, characterized by the coherence length and coherence time (see Chaps. 1–3). Namely, the coherence properties of the DM field determine space-time correlations of the DM signal measured at different nodes. We will discuss the relevant correlation properties of wavy DM fields and network performance in Sect. 10.4.2.
“Clumpy” DM is another distinct theoretical possibility. Here, DM is not distributed uniformly but rather occurs in the form of clumps: massive, large-scale, composite DM objects. Formation of clumps generically requires some form of interaction (self-interaction) between the elementary DM constituents, but even the ever-present gravitational interaction leads to instabilities and clumping (see discussion in Chap. 3). Examples of “clumpy” objects include “dark stars” [1], Q-balls [2, 3], solitons, and clumps formed by dissipative interactions in the DM sector. Alternatively, a significant fraction of the DM mass-energy could be stored in “topological defects” manifesting as monopoles, strings, or domain walls [4]. Self-interacting fields can include bosonic and fermionic DM candidates. The characteristic spatial extent of topological defects is determined by the Compton wavelength of the underlying DM field. For an Earth-sized object, this translates into a characteristic mass of DM field quanta of ∼10−14 eV, which places such DM fields in the category of ultralight candidates.
If DM takes such a “clumpy” form, sensors would not register a continuous oscillating signal associated with the “wavy” DM but rather would observe transient events associated with a DM clump sweeping through the detector [5,6,7]. Network-based searches seek patterns of synchronous propagation of DM-induced perturbations (“glitches”) in sensor data streams; the perturbation is expected to sweep through the network at galactic velocities. The value of the network in searches for DM clumps lies in a much suppressed rate of false positives, as inevitable intrinsic noise (especially flicker noise) of a single-node sensor can mimic an encounter with a DM clump. Moreover, even if the DM-induced glitches are large, an unsuspecting experimentalist is likely to discard the event and attribute it to something perhaps unexplained but mundane (see blog post [8]). An appearance of the same glitch at all the nodes substantially raises confidence level in the detection of the sought-after signal. This strategy is analogous to that of gravitational wave observatories [9], where the same waveform is registered by multiple geographically separated detectors with the prescribed time delays. We will discuss network-based searches for clumpy DM in Sect. 10.4.3.
There are several networks of precision quantum sensors in existence. The authors are involved in the DM searches with atomic clocks and atomic magnetometers and, for concreteness, we focus on networks comprised of these two sensor types. We illustrate our general discussion with two examples: (1) the Global Network of Optical Magnetometers for Exotic physics searches (GNOME) and (2) the constellation of atomic clocks onboard satellites of the Global Positioning System (GPS). Section 10.2 introduces couplings (portals) of ultralight DM fields to the clocks and magnetometers. Essentially, we are interested in interactions that either vary fundamental constants or lead to fictitious magnetic fields coupled to atomic or nuclear spins. Section 10.3 introduces basics of atomic clocks and magnetometers. Section 10.4.1 reviews existing networks of quantum sensors. Network detection of wavy dark matter is discussed in Sect. 10.4.2 and of clumpy dark matter in Sect. 10.4.3. Some of the recent results are presented in Sect. 10.5 and conclusions are drawn in Sect. 10.6. Since the intended audience includes broader physics community, we restore ħ and c in the formulae in favor of using natural or atomic units.
10.2 Portals Into Dark Sector
Quantitative studies of interaction between the DM and Standard Model (SM) particles/fields require specification of how the two sectors interact. We follow a phenomenological approach of the so-called portals, when the gauge invariant operators of the SM fields are coupled to the operators that contain fields from the dark sector (see, e.g., Ref. [10] and Sect. 2.4.1 of Chap. 2). While a large number of Lorentz-invariant portals can be constructed, here we focus on those that can affect atomic clocks and magnetometers. In this section, we spell out these portals and discuss existing, DM-model independent, constraints on the portals. Proposals for direct DM searches should be more sensitive to new interactions than these established constraints.
In the following, we focus on either scalar or pseudoscalar DM fields ϕ. We consider interaction Lagrangians that are linear, \(\mathcal {L}^{(1)}\), and quadratic, \(\mathcal {L}^{(2)}\), in ϕ. While linear interactions invariably arise in perturbative treatments, quadratic interactions naturally appear for scalars possessing either \(\mathbb {Z}_2\)Footnote 1 or \(\mathbb {U}(1)\) intrinsic symmetries.
For atomic clocks,
The structure of these portals is such that various parts of the SM Lagrangian are multiplied by DM fields, with Γ’s being the associated coupling constants (to be determined or constrained). In the above interactions, f runs over all the SM fermions (fields ψf and masses mf), and Fμν is the electromagnetic Faraday tensor. Here we used the Lorentz-Heaviside system of electromagnetic units that is common in particle physics. In these expressions, the combination \(\sqrt {\hbar c}\,\phi \) is measured in units of energy, [E], i.e., \(\Gamma _X^{(1)}\) are measured in [E]−1 and \(\Gamma _X^{(2)}\) in [E]−2 . The \(\mathcal {L}_{\mathrm {clk}}\) portals effectively alter fundamental constants [7], such as the electron mass me and the fine-structure constant α = q2∕ħc.

It is conventional to recast the linear coupling strengths \(\Gamma ^{(1)}_X\) in terms of dimensionless “moduli” [11] (see Sect. 2.5.3)
with \(E_{\mathrm {Pl}}=\sqrt {\hbar c^5/G_N}\) being the Planck energy and GN being the Newtonian constant of gravitation. We focus on the electron mass modulus \(d_{m_e}\) and the electromagnetic gauge modulus de, where X = α in this case. The most stringent limits on these moduli come from the tests of Einstein’s equivalence principle violation (see Fig. 1 of Ref. [11]). For the parameter space relevant to atomic clocks, the excluded regions are de ≳ 10−3 and \(d_{m_e} \gtrsim 10^{-2}\).
For quadratic couplings, for consistency with prior literature, we work with energy scales
The most stringent (DM-model independent) constraints on the energy scales, \( \Lambda _{m_e,\alpha } \gtrsim 3 \, \mathrm {TeV}\) and \(\Lambda _{m_p} \gtrsim 10 \, \mathrm {TeV} \), come from the bounds on the thermal emission rate from the cores of supernovae [12]. The authors of Ref. [12] estimated emissivity of ϕ quanta due to the pair annihilation of photons and other processes such as the bremsstrahlung-like emission. They also considered tests of the gravitational force which resulted in similar constraints; compared to the linear Lagrangians \(\mathcal {L}_{\mathrm {clk}}^{(1)}\) these are milder, because the quadratic Lagrangians lead to the interaction potentials that scale as an inverse cube of the distance between the test bodies as only the exchange of pairs of ϕ’s are allowed (for linear Lagrangians, the ϕ-mediated interaction potentials scale as the inverse distance). There are additional limits on quadratic couplings arising from Big Bang nucleosynthesis, black-hole superradiance and other mechanisms which are beyond the scope of this chapter (see Ref. [13] for details).
For magnetometers, we consider the following interaction Lagrangians [5]
In these expressions, \(J^\mu = \bar {\psi } \gamma ^\mu \gamma _5 \psi \) is the axial-vector current for SM fermions and fl and fq are the characteristic energy scales (decay constants) associated with the linear and quadratic spin portals. These Lagrangians give rise to the effective spin-dependent interactions
where S is the atomic or nuclear spin.

Similar to the clocks, the most stringent limits on axion spin couplings fl and fq come from astrophysical observations, in particular, supernova 1987A (see discussion in Chap. 3). The basic framework for setting up the constraints comes from analysis of axion production through N + N → N + N + a, where N is the nucleon and a is the axion. If such a reaction occurs, it would lead to core emission of axions and increased supernova cooling rate. In turn, this would result in shortening of neutrino pulses from the supernova explosion, which was not observed with detectors such as Kamiokande, IMB, and Baksan [14]. However, the axion production would occur under conditions difficult to fully describe, thus a rather conservative limit on the decay constant fl at 2 × 108 GeV is derived from the observations [15]. Alternatively, the constraint can be formulated based on the kaon decay K → πa, which gives comparable value of 108 GeV [16]. For the quadratic coupling fq the limit is much weaker yielding 104 GeV [5, 12]. It is important to note, however, that there do exist theoretical scenarios where these astrophysical bounds can be circumvented [17], and therefore laboratory-based detection experiments as described here play a crucial role.
10.3 How Do Atomic Clocks and Magnetometers Work?
Although atomic clocks and atomic magnetometers measure different physical quantities, at the most fundamental level, both devices effectively measure the energy/frequency splitting between atomic states. For clocks, the atomic levels are chosen in such a way that the transition frequency, ideally, remains independent of external fields and environmental dynamics. Thereby, measurements of the transition frequency provide a reference that can be used for telling time. In contrast, the measured energy-level splitting in atomic magnetometers depends on the spin state and hence the applied magnetic field. In such a way, measurement of the splitting provides information about the strength (and often direction) of the magnetic field. Additionally, a common feature of atomic clocks and magnetometers is that they both employ photons for preparation and monitoring, and sometimes also manipulation, of the atoms used for the measurement.
10.3.1 Atomic Clocks
Measuring time requires observation of a stable periodic process. The elapsed time is simply a product of the number of counted periods and the fixed duration of each period. A grandfather clock is a mechanical realization of this formula: each swing of the pendulum is counted by the escapement mechanism, which advances the clock’s hands. In atomic clocks, an atomic transition serves as a frequency reference for an external source of electromagnetic radiation, referred to as the local oscillator (LO). The frequency source is tunable and once its frequency is in resonance with the atomic transition, the period of oscillation is fixed and one counts the number of oscillations at the source. The simple formula “time = number of oscillations × known oscillation period” applies once again.
One may generally distinguish between two types of atomic clocks: microwave and optical clocks. This dichotomy is based on the frequency band of the reference atomic transition. In the microwave clocks, two hyperfine levels, associated with a state of a given electronic angular momentum, are used. In the case of alkali-metal atoms, which are often used in atomic-physics experiments, the splitting of two ground-state hyperfine levels ranges between hundreds of MHz (in lithium) to nearly 10 GHz (in cesium). In fact, the ground-state hyperfine level splitting in 133Cs defines the SI unit of time, the second. Alternatively, in optical clocks, it is the energy splitting between two different electronic states that serves as the frequency reference. As these are typically separated by hundreds of THz, compared to GHz in microwave clocks, optical clocks have better fractional frequency accuracies than their microwave counterparts.
We focus on microwave clocks, as these are used in GPS. The atoms (quantum oscillators) are interrogated with light and microwave radiation. The microwave field is driven from the LO referenced to a microwave cavity. The cavity frequency is tunable and a feedback (servo) loop drives the LO frequency to be in resonance with the reference atomic transition. Technically, atomic clocks measure the quantum phase Φ of an atomic oscillator with respect to that of the LO. The accumulated phase and thereby the quantum probability of a resonant transition is determined by a time integral of the difference in frequencies between the clock atom and the LO. Both the atomic oscillator and the LO can be affected by the DM fields. The DM-induced accumulated-phase difference over measurement time t0 = tj − tj−1 is
This DM-induced phase is interpreted by the servo-loop logic as if the cavity frequency νLO has drifted away from its nominal value νclock. Technically, the servo-loop would introduce a correction \(\Phi _j^{\mathrm {DM}}/(2\pi t_0)\) to the LO frequency νLO. In other words, DM affects the time as measured by the clocks.
One can simplify the DM-induced phase in two practically relevant cases. If we assume that the characteristic duration τ of DM field action on the clock is much longer than t0 (slow regime), \( \Phi _j^{\mathrm {DM}} \approx 2\pi [\nu _{\mathrm {atom}}^{\mathrm {DM}}(t_j) - \nu _{\mathrm {LO}}^{\mathrm {DM}} (t_j)] t_0 \,. \) In the opposite limit of a short transient of duration τ ≪ t0 occurring at time t′∈ (tj−1,tj), \( \Phi _j^{\mathrm {DM}} \approx 2\pi [\nu _{\mathrm {atom}}^{\mathrm {DM}}(t_j) - \nu _{\mathrm {LO}}^{\mathrm {DM}} (t_j)] \tau \,. \) Then DM leads to fractional frequency excursions
where the second factor accounts for both the slow and fast regimes.
As discussed in Sect. 10.2, we are interested in portals that lead to variation of fundamental constants, such as the fine-structure constant α or electron mass me. Atomic frequencies are primarily affected by the induced variation of the Rydberg constant, R∞ = mec2α2. Optical clocks can exhibit additional α dependence due to relativistic effects for atomic electrons. Microwave clocks operate on hyperfine transitions and are additionally affected by the variation in the quark masses, mq and the strong coupling constant. The reference cavity is also a subject to the DM influence. For example, the variation in the Bohr radius a0 = α−1ħ∕(mec) affects cavity length L ∝ a0 and thus the cavity resonance frequencies. Conventionally, one introduces coefficients \(\kappa _X=\partial \ln \nu /\partial \ln X\) quantifying sensitivity of a resonance frequency ν to the variation in the fundamental constant X. Then
It is worth noting that there are exceptional cases of enhanced sensitivity to variation of fundamental constants, for example, in the actively pursued 229Th nuclear clock (κα ≈ 104) [18], and clocks based on highly charged ions (\(\kappa _\alpha \lesssim 10^2\)) [19].
Since DM portals pull on the fundamental constants [Eqs. (10.3) and (10.4)] and thus on the LO and atomic frequencies, the putative DM signal [Eq. (10.12)] can then be expressed as
where n = 1 or 2 for the linear and quadratic portals, respectively. Here we also introduced the effective coupling constants
where \(K_X= \kappa _X^{\mathrm {atom}} -\kappa _X^{\mathrm {LO}}\) is the differential sensitivity coefficient and the summation runs over all relevant fundamental constants.
As with any device, there are two issues that must be addressed in experiments with atomic clocks: systematic errors (accuracy) and statistical uncertainties (stability). Systematic errors quantify how well the quantum oscillator is protected from external perturbations. Although the community of physicists working on atomic clock development devotes significant efforts to characterizing clock accuracies, these are not relevant to the goal of detecting DM signals (unless conventional physics perturbations mimic the sought-after DM signatures). Sensitivity to DM portals is determined by the clock stability which quantifies statistical uncertainties. As with most statistical errors, these are reduced by increasing measurement time τmeas. The clock stabilities are characterized using the Allan variance σy(τmeas), quantifying the statistical error in fractional clock frequency as a function of the measurement time. Typically, the Allan variance scales as \(1/\sqrt {\tau _{\mathrm {meas}}}\). One can interpret σy(τmeas) as the error in the determination of the mean fractional clock frequency. In other words, namely σy(τmeas) determines the non-DM noise component of the fractional clock excursions (first factor) entering the DM signal (Eq. (10.12)). At τmeas = 1 s, modern atomic clocks have Allan deviations of ∼10−12 for GPS clocks and 10−16 for optical clocks.
10.3.2 Atomic Magnetometers
Magnetic field measurement requires monitoring of a physical quantity that depends on the magnetic field. In the case of (optical) atomic magnetometers, this quantity may be the intensity or polarization of light propagating through a medium subjected to an external magnetic field. If the medium is spin polarized, e.g., by interaction with polarized light (optical pumping), the magnetic field changes the initial spin polarization, which affects the characteristics of the transmitted light.
At the microscopic level, interaction of the field with atomic magnetic moments leads to the precession of the moments at the Larmor frequency νL = γB∕(2π), where γ is the gyromagnetic ratio for the atom. Periodic evolution of the system (i.e., precession of spins around the magnetic field direction) enables synchronous pumping of the atoms (e.g., by modulating light frequency at the Larmor frequency or its harmonic), leading to a resonant response of the atoms and hence stronger optical signals. Tracking the position of the resonance, by modifying the frequency of the LO driving the modulation, enables accurate magnetic field measurements. Alternatively, atomic magnetometers may be subjected to continuous perturbation, e.g., continuous-wave (CW) light, when competition between such processes as optical pumping, Larmor precession, and spin-polarization relaxation results in appearance of quasi-static optical signals. While this scheme allows measurements of relative field changes (unless the signal is calibrated, in which case absolute measurements can be made) and typically leads to smaller dynamic range (up to about 100 nT), the magnetometers typically have better sensitivities (1 fT/\(\sqrt {\mathrm {Hz}}\) or below), than their dynamically driven counterparts.
As shown in Eqs. (10.9) and (10.10) the axion-field gradient acts as a pseudo-magnetic field. Generally, this pseudo-magnetic field differs for electrons and nucleons. By rewriting the Hamiltonians using the total angular momentum F of an atom (F is a sum of electronic spin, electronic angular momentum, and nuclear spin), one obtains
where \(f_{l}^{\mathrm {eff}}\) and \(f_{q}^{\mathrm {eff}}\) are linear and quadratic effective decay constants. The relation of the effective decay constants \(f_{l,q}^{\mathrm {eff}}\) to the electron fe, proton fp, and neutron fn decay constants can be calculated as described, for example, in Ref. [20]. In the case of 3He and 39K, two atoms often used in atomic magnetometers, the linear coupling constants take the form
where we assumed that the angular momentum F is mostly due to an unpaired neutron in 3He and the d3∕2 valence proton in 39K.
Since the exotic spin couplings are orders of magnitude weaker than the conventional Zeeman interaction, suppression of Zeeman coupling to any uncontrollable (e.g., environmental) magnetic fields becomes of prime importance. Therefore, most experiments searching for exotic spin couplings are housed inside magnetic shields. The shields, commonly made of high permeability material (e.g., mu-metal or ferrites), passively attenuate stray magnetic fields by a factor on the order of 106. As shown in Ref. [21], for many experimental geometries and conditions, magnetic shields do not substantially reduce the sensitivity to exotic spin couplings. To further reduce the sensitivity to the magnetic fields, the magnetometers can be operated in the so-called comagnetometer arrangement, where two distinct atoms or nuclei are used for field sensing (see Chap. 8 for more information). Often, a noble gas and alkali atoms are used, as they sense the field through the coupling to the nuclear spin in the first case and predominantly through the coupling to the electronic spin in the second case. Comparison of the responses of the species to the magnetic field removes sensitivity to the field, leaving system sensitive to other, particularly exotic, couplings. Moreover, due to principally different coupling of exotic physics to different atomic species, comagnetometry also allows disentangling individual couplings to electrons, protons, and neutrons.
At the most fundamental level, the sensitivity of atomic magnetometers is determined by the quantum nature of atoms and light, i.e., by the spin-projection and photon shot noise. In an optimized system, the magnetometric sensitivity is determined as described in, e.g., Auzinsh et al. [22], Ledbetter et al. [23]
where g is the Landé factor, Nat is the number of atoms involved in field sensing, T2 is the transverse spin relaxation time, and τmeas is the duration of the measurement. This gives the fundamental sensitivity limit between 0.01 and 1 fT/\(\sqrt {\mathrm {Hz}}\) for a typical magnetometer.

10.4 DM Searches with Network of Sensors
10.4.1 Overview of Existing Networks
Networks are ubiquitous in our life, with one of the most well-known examples being the internet. In telecommunication settings, the utility of the network is proportional to the square of the number of nodes (Metcalfe’s law). This scaling law reflects the total number of unique connections Ns(Ns − 1)∕2 for the number of nodes Ns. If one considers that the price of the network increases as Ns, there is a certain critical number of nodes above which the network becomes economically viable. Similar considerations (with significant caveats) apply to networks of quantum sensors. One can argue that the sensitivity of a classical network to the exotic physics should improve generically as \(\sqrt {{N_{\mathrm {s}}}}\) since the same putative signal is measured independently by Ns sensors. However, such an argument neglects the vetoing power of the interconnected network that results in a reduced rate of false positives. In addition, the cost of deploying Ns sensors in research environment is vastly different from commercial settings. The reason is that the cost of developing a single table-top sensor in a university lab vastly exceeds the cost of the hardware. Thus the cost of the second identical sensor is mostly the cost of the hardware (economy of scale). Another possibility is an integration of already developed sensors, then the additional cost is the cost of synchronizing data acquisition or links.
Perhaps the most widely celebrated network in the physics community is LIGO (the Laser Interferometer Gravitational Wave Observatory)—a gravitational wave observatory initially consisted of two sites in the US. While this network is adding more locations, the original black-hole merger gravitational wave detection from 2015 used only two spatially separated interferometers in the waveform template matching [9]. The appearance of the same waveform in both interferometers, with the proper time delay between the two, greatly supported the credibility of the discovery claim.
There are several criteria [25] for a network to detect the signal pattern due to a macroscopic DM object sweeping through a network of Ns sensors:
-
(i)
The network should be sufficiently dense so that the string and monopole-type DM objects can overlap with at least several geographically distinct nodes.
-
(ii)
The network volume should be sufficiently large in order to increase the rate of encounters with string and monopole-type DM objects.
-
(iii)
Per the standard halo model the DM objects sweep through the network at galactic velocities (vg ∼ 300 km∕s). Thus the sampling rate should be sufficiently high to enable tracking the propagation of the DM object through the network (see Fig. 10.2). The tracking enables reconstruction of the geometry and dynamics of the encounter.
Fig. 10.2 Simulated response of an Earth-scale network of atomic clocks to a spherically symmetric Gaussian-profiled dark matter clump (a monopole or a Q-ball). The traces in the bottom panel show time-evolution of the phase of quantum oscillators for three distinct locations. From Ref. [7]
-
(iv)
Although not necessary, it is desirable that the encounters of DM objects with the network are sufficiently rare, so that only a single DM object interacts with the network at any given time.
A particular example of a global network fulfilling these criteria is the GPS. The network is nominally comprised of Ns = 32 satellites in a medium-Earth orbit (altitude ∼ 20, 000 km). Microwave Rb or Cs atomic clocks onboard the satellites drive microwave signals, which are broadcast to Earth. A network of specialized Earth-based GPS receivers measures the carrier phase of these microwave signals, which is then used to deduce the satellite clock data. The network can be extended to incorporate clocks from high-quality Earth-based receiver stations and other navigation systems, such as the European Galileo, Russian GLONASS, and Chinese BeiDou, and networks of laboratory clocks [26]. An additional and important advantage of the GPS network is the public availability of nearly two decades of archival data enabling relatively inexpensive data mining. Such searches for dark matter-induced transient variation of fundamental constants are the focus of the GPS.DM collaboration [7, 27].
GNOME is a network of shielded optical atomic magnetometers specifically targeting transient events associated with exotic physics [28]. To the best of our knowledge, this is the first network ever constructed specifically to search for physics beyond the SM. Presently, GNOME consists of Ns = 12 atomic magnetometers located at stations throughout the world (six sensors in North America, five in Europe, three in Asia, and one in Australia), with a number of new stations under construction in Israel, India, and Germany [29]. Each magnetometer is located within a multilayer magnetic shield to reduce the influence of magnetic noise. The overall network sensitivity is close to 100 fT depending on the number of stations active [30]. It is noteworthy that besides the traditional analysis technique that takes advantage of the spatiotemporal pattern of the network signal to veto false positives, GNOME offers further ability to limit the rate of false positives. Due to the pseudoscalar character of the coupling in atomic magnetometers (Sect. 10.3.2) and different directions of spin polarization in specific GNOME stations, the amplitude and sign of the putative signals also carry information about the coupling. This information can be used to further improve rejection of false positives. Additionally, several stations are implementing sensors employing a dense polarized noble gas in a comagnetometer configuration [31]. This arrangement has a reduced sensitivity to magnetic couplings and hence enhanced sensitivity to exotic spin couplings. This new network of noble-gas-based comagnetometers will form an Advanced GNOME with an anticipated sensitivity to spin couplings a hundred times better than the existing GNOME. As of the summer of 2020, there is about a year of GNOME data collected which can be analyzed to search for exotic physics signals, and results of the first search for dark matter using the GNOME data set has recently been completed as described in Ref. [32].
Let us finally reiterate a vision for a global dark matter observatory [24] (see Fig. 10.3), that is a natural extension of the GNOME architecture. Up to date, individual direct DM searches employ a broad range of sensors: atomic clocks, magnetometers, accelerometers, interferometers, cavities, resonators, permanent electric-dipole and parity-violation measurements, and extend to gravitational wave detectors (see Ref. [33] for a review). These distinct tools are typically located at geographically separated laboratories across several continents (see Fig. 10.3) or in space. These tools already form nodes of the network and only the links are missing. In the most basic version, even the physical links are not necessary as the synchronization can be implemented with a GPS-assisted time-stamping of data acquisition [6, 34]. Some of the enumerated instruments are sensitive to the same portals (e.g., atomic clocks, cavities, atom interferometers, and gravimeters are all sensitive to the DM-induced variation of fundamental constants), which would lead to an important complementarity of the searches at individual nodes.
A map of existing low-energy precision measurement laboratories (red dots) around the globe. Such a network can serve as a global dark matter observatory. Adopted from Ref. [24]

10.4.2 Network-Based Searches for “Wavy” Dark Matter
In the wavy models, DM is composed of ultralight spin-0 bosonic fields, oscillating at their Compton frequency ωϕ = mϕc2∕ħ, where mϕ is the boson mass, see Chaps. 1 and 2. Multiple proposals covered in this book focus on searching for an oscillating signal at the Compton frequency. Unfortunately, in a laboratory environment, an observation of an oscillating signal could be ascribed to some mundane ambient noise and it is desirable to establish additional DM signatures. Due to the DM virial velocity distribution, these DM fields are stochastic in nature (again, see Chap. 1) and we refer to them as virialized ultralight fields (VULFs). Their coherence times and coherence lengths are related to DM properties. An additional signature [24] relies on a VULF spatiotemporal correlations that can be probed with a network. Formally, the two-point field correlation function is defined as
where averaging is over stochastic realizations of the DM field.
DM field correlations imprint correlations on the putative DM signal. Indeed, in the assumption of the linear portals, see Sect. 10.2, the measured quantity has a DM-induced admixture \(s_{X}\left ( t,\mathbf {r}\right )\) that is proportional to the field value \(\phi \left ( t,\mathbf {r}\right )\) at the device location. Then the correlation between DM signals at the two locations is related through the DM field correlation function
The correlation function for spatiotemporal variations of fundamental constants is also expressed in terms of DM field correlation function, e.g.,
where we used the DM-induced variation (10.4) of the fine-structure constant.
The correlation function derived in Ref. [24] reads
Here \(\omega _{\phi }^{\prime }\) is the Doppler-shifted value of the Compton frequency \(\omega _{\phi }^{\prime }=\omega _{\phi }+m_{\phi }v_{g}^{2}/(2\hbar )\) and kg = mϕvg∕ħ is the “galactic” wave vector associated with the apparatus motion through the DM halo (towards the Cygnus constellation). The effective field amplitude Φ0 is related to the DM energy density as \(\Phi _{0}=\frac {\hbar }{m_{\phi }c}\sqrt {2\rho _{\mathrm {dm}}}\), which comes from directly evaluating the time-like (00) component of the stress-energy tensor for the bosonic field. Further, the amplitude and phase are defined as
where the coherence time \(\tau _{c}\equiv \left ( \xi ^{2}~\omega _{\phi }\right )^{-1}\approx 10^{6}/\omega _{\phi }\) and coherence length \(\lambda _{c}\equiv \hbar /\left (m_{\phi }\xi c\right ) \) are expressed in terms of the virial velocity ξc ≈ 10−3c. The correlation function encodes the priors on VULFs and the DM halo, such as the DM energy density in the vicinity of the Solar system, motion through the DM halo at vg and the virial velocity ξc. Thereby, the correlation function provides an improved statistical confidence in the event of an observation of a DM signal.
The N-point correlation function required for the multi-node network can be fully expressed in terms of the derived two-point correlation function since the DM field is Gaussian in nature. The statistical significance of the correlation function for a network was explored in Ref. [24]. If all Ns nodes are separated by distances larger than the coherence length λc, compared to a single apparatus, the network sensitivity improves as \(N_{\mathrm {s}}^{1/4}\). In the opposite limit of the node separations being much smaller than λc (fully coherent network), the statistical sensitivity is improved by the factor \(\sqrt {N_{\mathrm {s}}}\). Network searches for wavy DM are in their infancy, but are expected to gain in significance once the oscillating DM signal is discovered. The network will be necessary to confirm the DM origin of the signal.
10.4.3 Network-Based Searches for “Clumpy” Dark Matter
In the “clumpy” dark matter models, DM is postulated to be composed of macroscopic objects, such as topological defects (TDs). Monopoles (0D), strings (1D), and domain walls (2D) are all examples of TDs of various dimensionalities. Other examples of macroscopic DM candidates include “dark stars” [1], Q-balls [2, 3], solitons, and clumps formed due to dissipative interactions in the DM sector. A special case of clumpy DM are DM “blobs” [35], particle-like DM objects sourcing long-range Yukawa-type interactions with the SM sector.
As an illustration, we focus on topological defects. Inside the defect, the amplitude of the DM field \(\mathcal {A}\) and the energy density of the defect is related by \(\rho _{\mathrm {inside}}= \mathcal {A}^2/(\hbar c \, d^2)\), where d is the width of the defect (we use the convention where the field has units of energy). The DM object width d is treated as a free observational parameter. For topological defects, this width may be linked to the mass of the DM field particles mϕ through the healing length which is on the order of the Compton wavelength, d ∼ħ∕(mϕc). Further, the local DM energy density ρdm may be expressed in terms of d and \(\mathcal {A}\) by assuming that these objects saturate the local DM energy density,
where τ ∼ d∕vg is the characteristic duration of crossing through a point-like instrument and \(\mathcal {T}_e\) is the average time between encounters of the sensor with DM clumps. These relations hold for all types of defects.
So far both the GPS.DM and GNOME searches focused on domain walls (Fig. 10.4). Their signature is especially simple as the wall would cross all the sensors with the same amplitude of the DM signal. Domain wall-like signatures can appear naturally in the context of bubbles, i.e., domain walls closed on themselves [27]. Locally, one can neglect the bubble curvature as long as the bubble radius is much larger than the spatial extent of the sensor network. Since bubbles are spherically symmetric, gravitationally interacting ensembles of these DM objects are a subject to the equation of state for pressureless cosmological fluid as required by the ΛCDM paradigm, see Chap. 3.
An example of a DM signature for a “thin” domain wall (d∕vg < t0) sweeping through the GPS constellation is shown in Fig. 10.5. GPS clock data are reported with respect to some other fixed (reference) clock. Thus the signal pattern would involve DM-induced perturbations to both satellite clocks and the reference clock. For identical types of reference and satellite clocks, the domain wall creates a perturbation of the reference clock that leads to a “timing glitch” of equal magnitude but opposite sign as compared to those appearing when the domain wall passes through satellite clocks.Footnote 2 Consider the pattern of “glitches” in GPS clocks shown in Fig. 10.5. The domain wall first sweeps through satellites 1 and 2 in epoch 4, causing a temporary positive frequency excursion, then encounters clocks 3 and 4 in the next epoch, and so on. When the domain wall passes through the reference clock in epoch 8, most of the clocks show a temporary negative frequency excursion, since the reference clock itself experiences a positive frequency excursion (the exceptions being satellites 15 and 16 which are spatially close to the reference clock). In the case of GNOME, however, there is no reference magnetometer, i.e., all the magnetometers are independent. Thus for identical magnetometers the sought-after pattern would involve only the “diagonal” (red tiles) in Fig. 10.5.
One of the expected frequency signatures for a thin domain wall sweeping through the GPS constellation. Red (blue) tiles indicate positive (negative) DM-induced frequency excursions, while white tiles mark the absence of the signal. In this example, the satellites are listed in the order they were swept (though in general the order depends on the incident direction of the DM object and is not known a priori). The slope of the red line encodes the incident velocity of the wall. The reference clock was swept within the 30 s leading to epoch 8. Satellites 15 and 16 do not record any frequency excursions, since they are spatially close to (degenerate with) the reference clock and are swept within the same sampling period. Adopted from Ref. [27]
10.5 Putting It All Together
In this section, we illustrate the implementation of the described ideas with a search for clumpy DM [27] using archival GPS data. The archival GPS data is publicly available and the dataset includes atomic clock data and satellite positions sampled every t0 = 30 s.
Returning to the discussion of Sect. 10.3.1, we focus on “thin” domain walls and quadratic couplings. Then, with Eq. (10.22) for the DM field amplitude, the DM signal (10.13) becomes
This is the amplitude of the signal during the time interval when the wall overlaps with a sensor, otherwise there is no signal, \(s^{\mathrm {DM}}_0=0\).
The key qualifier for Eq. (10.23) is that one must be able to distinguish between the clock noise and DM-induced frequency excursions. Discriminating between the two sources relies on measuring time delays between DM events at network nodes, see Fig. 10.5. The velocity of the sweep is encoded in the time delay between two DM-induced frequency excursion and it must lie within the boundaries predicted by the standard halo model (the distributed response of the network encodes the spatial structure and kinematics of the DM object and its coupling to the sensors).
To search for domain wall signals, the GPS.DM collaboration analyzed the GPS data streams in two stages [27]. At the first stage, they scanned all the data from October 2016 to May 2000 searching for the most general patterns associated with a domain wall crossing, without taking into account the order in which the satellites were swept. They required at least 60% of the clocks to experience a frequency excursion at the same epoch, which would correspond to when the wall crossed the reference clock (vertical blue line in Fig. 10.5). This 60% requirement is a conservative choice based on the GPS constellation geometry and ensures sensitivity to walls with relative speeds of up to 700 km∕s. Then, the GPS.DM collaboration checked if these clocks also exhibit a frequency excursion of similar magnitude (accounting for clock noise) and opposite sign anywhere else within a given time window (red tiles in Fig. 10.5). Any epoch for which these criteria were met was counted as a “potential event.” Above a certain threshold for the DM signal (10.23), no potential events were seen.
The second stage of the search involved analyzing the potential events in more detail, so that their status could be elevated to “candidate events” if warranted by the evidence. GPS.DM examined a few hundred potential events that had frequency excursions magnitudes just below the threshold values, by matching the data streams against the expected patterns, where the velocity vector and wall orientation were treated as free parameters. At this second stage, GPS.DM accounted for the ordering and time at which each satellite clock was affected. This was done by matching data against a bank of signal templates that was itself generated using DM halo properties. As a result of this pattern matching, none of these events was consistent with domain wall signals.
Since GPS.DM did not find evidence for encounters with domain walls, there are two possibilities: either DM of this nature does not exist, or the DM signals are below the sensitivity. The derived limits on quadratic coupling energy scale Λα are presented in Fig. 10.6 (salmon shaded region). Here we assumed for simplicity that the DM-induced variation in the fine-structure constant α dominates. These limits represent a significant improvement over the astrophysical bounds, discussed in Sect. 10.2.
Projected discovery reach for thin wall dark matter objects along with existing constraints. The red dashed lines represent the least stringent and most stringent discovery reaches for the 2010 GPS atomic clock network. The shaded cyan region are the constraints coming from astrophysics [12], while the salmon shaded regions are the constraints placed by the GPS.DM collaboration [27]. The green shaded region contains the constraints placed by optical clock experiments [36], while the yellow region—by a global terrestrial network of laboratory clocks [37]. Adopted from Ref. [25]
The ultimate discovery reach of the clock network is given by [25]
Again we assumed that a specific coupling constant ΓX dominates so that Γeff → KX ΓX. Here \(\mathcal {C} \sim O(1)\) is a constant that depends on the confidence level and details of the network implementation, \(N_{\mathrm {E}} = {\mathcal {T}}/{\mathcal {T}}_e\) is the total number of expected encounters with DM objects during total observation time \({\mathcal {T}}\) (as of 2020 ∼ 20 years for GPS archival data). This constraint translates into projected exclusion limits on the effective energy scale \(\Lambda _{X}=1/\sqrt {|\Gamma _{X}|}\), shown in Fig. 10.6. Notice that the derived constraints from the first GPS.DM search [27] are several orders of magnitude weaker than the projected limits. Reaching the full discovery potential requires implementing more advanced statistical approaches, such as Bayesian statistics [38] or matched filter techniques [25]; these are a subject of current efforts by the GPS.DM collaboration.
10.6 Summary
Distributed sensor networks, either at a local or a global scale, are one of the powerful strategies used in scientific research. Extension of these ideas to networks of precision quantum sensors opens novel opportunities, in particular searches for a variety of dark matter candidates. While these developments are in their early stages, we believe that additional spatiotemporal signatures offered by the networks are key to improving confidence in the DM origin of a putative signal (if discovered). Networks also enable a powerful rejection of false positives.
Searching for dark matter using sensor networks is a rapidly developing research area: soon after the initial proposals [5, 7] based on atomic magnetometers and atomic clocks, several new schemes involving terrestrial networks of optical clocks, atom interferometers, and optical cavities [37, 39] have been proposed. We also mention recently proposed space missions [40, 41] that involve rudimentary networks of atomic clocks and interferometers; while these missions focus on detection of gravitational waves, DM searches are one of their secondary goals.
Finally, once a network is built, it may find other applications. For example, quantum sensor networks can be used in searches for exotic low-mass fields (ELFs) emitted in cataclysmic astrophysical events such as black-hole or neutron-star mergers [42]. This idea opens up an intriguing “exotic physics” modality in multi-messenger astronomy, where the measured exotic physics signals are correlated with gravitational wave triggers and the progenitor position in the sky.
Notes
- 1.
Qualitatively, \(\mathbb {Z}_2\) symmetry means that for a real-valued field ϕ, the Lagrangian remains invariant under sign swap operation, ϕ →−ϕ. Thus, ϕ and − ϕ obey the same equation of motion.
- 2.
This is simply a consequence of the fact that the timing glitches are determined by comparison between the reference and satellite clocks. If, for example, the glitch causes a clock to temporarily run fast, when the domain wall passes through the reference clock, satellite clocks appear to run slow with respect to the reference clock, whereas when the domain wall passes through a satellite clock, the satellite clock appears to run fast compared to the reference clock.
References
E.W. Kolb, I.I. Tkachev, Phys. Rev. Lett. 71, 3051 (1993)
S. Coleman, Nucl. Phys. B 262, 263 (1985)
A. Kusenko, P.J. Steinhardt, Phys. Rev. Lett. 87, 141301 (2001)
A. Vilenkin, Phys. Rep. 121, 263 (1985)
M. Pospelov, S. Pustelny, M.P. Ledbetter, D.F. Jackson Kimball, W. Gawlik, D. Budker, Phys. Rev. Lett. 110, 021803 (2013)
D. Budker, A. Derevianko, Phys. Today 68 (2015)
A. Derevianko, M. Pospelov, Nat. Phys. 10, 933 (2014)
A. Derevianko, When would an unanticipated “new physics” event be apparent to an unsuspecting experimentalist? http://wp.me/p2Z9xm-8Z
B.P. Abbott, et al., Phys. Rev. Lett. 116, 061102 (2016)
R. Essig, J. Jaros, W. Wester, arXiv:1311.0029 (2013)
A. Arvanitaki, S. Dimopoulos, K. Van Tilburg, Phys. Rev. Lett. 116, 031102 (2016)
K.A. Olive, M. Pospelov, Phys. Rev. D 77, 043524 (2008)
S. Sibiryakov, P. Sørensen, T.T. Yu, J. High Energ. Phys. 2020, 75 (2020)
G.G. Raffelt, Annu. Rev. Nucl. Part. Sci. 49, 163 (1999)
J.H. Chang, R. Essig, S.D. McDermott, J. High Energ. Phys. 2018, 51 (2018)
G. Marques-Tavares, M. Teo, J. High Energy Phys. 2018, 180 (2018)
W. DeRocco, P.W. Graham, S. Rajendran, Phys. Rev. D 102, 075015 (2020)
V.V. Flambaum, Phys. Rev. Lett. 97, 092502 (2006)
M.G. Kozlov, M.S. Safronova, J.R.C. López-Urrutia, P.O. Schmidt, Rev. Mod. Phys. 90, 045005 (2018)
D.F. Jackson Kimball, New J. Phys. 17, 073008 (2015)
D.F. Jackson Kimball, J. Dudley, Y. Li, S. Thulasi, S. Pustelny, D. Budker, M. Zolotorev, Phys. Rev. D 94, 082005 (2016)
M. Auzinsh, D. Budker, D.F. Kimball, S.M. Rochester, J.E. Stalnaker, A.O. Sushkov, V.V. Yashchuk, Phys. Rev. Lett. 93, 173002 (2004)
M.P. Ledbetter, I.M. Savukov, V.M. Acosta, D. Budker, M.V. Romalis, Phys. Rev. A 77, 033408 (2008)
A. Derevianko, Phys. Rev. A 97, 042506 (2018)
G. Panelli, B.M. Roberts, A. Derevianko, EPJ Quantum Technol. 7, 5 (2020)
F. Riehle, Nat. Photon. 11, 25 (2017)
B.M. Roberts, G. Blewitt, C. Dailey, M. Murphy, M. Pospelov, A. Rollings, J. Sherman, W. Williams, A. Derevianko, Nat. Comm. 8, 1195 (2017)
S. Afach, D. Budker, G. DeCamp, V. Dumont, Z.D. Grujić, H. Guo, T.W. Jackson Kimball, D. F. Kornack, V. Lebedev, W. Li, H. Masia-Roig, S. Nix, M. Padniuk, C.A. Palm, C. Pankow, C. Penaflor, X. Peng, S. Pustelny, T. Scholtes, J.A. Smiga, J.E. Stalnaker, A. Weis, A. Wickenbrock, D. Wurm, Phys. Dark Univ. 22, 162 (2018)
GNOME website. https://budker.uni-mainz.de/gnome/
H. Masia-Roig, J.A. Smiga, D. Budker, V. Dumont, Z. Grujic, D. Kim, D.F. Jackson Kimball, V. Lebedev, M. Monroy, S. Pustelny, T. Scholtes, P.C. Segura, Y.K. Semertzidis, Y.C. Shin, J.E. Stalnaker, I. Sulai, A. Weis, A. Wickenbrock, Phys. Dark Univ. 28, 100494 (2020)
T.W. Kornack, M.V. Romalis, Phys. Rev. Lett. 89, 253002 (2002)
S. Afach, B.C. Buchler, D. Budker, C. Dailey, A. Derevianko, V. Dumont, N.L. Figueroa, I. Gerhardt, Z.D. Grujić, H. Guo, et al. Nat. Phys. 17, 1396 (2021)
M.S. Safronova, D. Budker, D. DeMille, D.F. Jackson Kimball, A. Derevianko, C.W. Clark, Rev. Mod. Phys. 90, 025008 (2018)
P. Wlodarczyk, S. Pustelny, D. Budker, M. Lipinski, Nucl. Instrum. Methods 150, 763 (2014)
D.M. Grabowska, T. Melia, S. Rajendran, Phys. Rev. D 98, 115020 (2018)
P. Wcisło, P. Morzyński, M. Bober, A. Cygan, D. Lisak, R. Ciuryło, M. Zawada, Nat. Astron. 1, 0009 (2016)
P. Wcislo, P. Ablewski, K. Beloy, S. Bilicki, M. Bober, R. Brown, R. Fasano, R. Ciurylo, H. Hachisu, T. Ido, J. Lodewyck, A. Ludlow, W. McGrew, P. Morzyński, D. Nicolodi, M. Schioppo, M. Sekido, R. Le Targat, P. Wolf, X. Zhang, B. Zjawin, M. Zawada, Sci. Adv. 4, eaau486 (2018)
B.M. Roberts, G. Blewitt, C. Dailey, A. Derevianko, Phys. Rev. D 97, 083009 (2018)
L. Badurina, et al., J Cosmol. Astropart. P. 2020, 011 (2020)
G.M. Tino, et al., Eur. Phys. J. D 73, 228 (2019)
Y.A. El-Neaj, et al., EPJ Quantum Technol. 7, 6 (2020)
C. Dailey, C. Bradley, D.F. Jackson Kimball, I.A. Sulai, S. Pustelny, A. Wickenbrock, A. Derevianko, Nat. Astron. 5, 150 (2021)
Acknowledgements
We would like to thank members of GPS.DM and GNOME collaborations for numerous discussions. This work of A.D. was supported in part by the U.S. National Science Foundation under Grant Nos. PHY-1806672 and PHY-1912465 and the work of S.P. was supported in part by the National Science Centre, Poland.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2023 The Author(s)
About this chapter
Cite this chapter
Derevianko, A., Pustelny, S. (2023). Global Quantum Sensor Networks as Probes of the Dark Sector. In: Jackson Kimball, D.F., van Bibber, K. (eds) The Search for Ultralight Bosonic Dark Matter. Springer, Cham. https://doi.org/10.1007/978-3-030-95852-7_10
Download citation
DOI: https://doi.org/10.1007/978-3-030-95852-7_10
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-95851-0
Online ISBN: 978-3-030-95852-7
eBook Packages: Physics and AstronomyPhysics and Astronomy (R0)