Spatial and Temporal Variations in Plant Source Water: O and H Isotope Ratios from Precipitation to Xylem Water

Abstract

The water present within trees when sugars and cellulose are formed is the source of hydrogen and oxygen atoms that are incorporated into tree-ring cellulose (see Chaps. 10 and 11). However, the isotope composition of relevant water pools is often unknown when trying to interpret δ¹⁸O and δ²H isotopic records in tree rings. This chapter focuses on the factors that can influence the O and H isotope ratios of source waters for trees. Trees generally use water that originated as precipitation, but this does not mean that the isotope ratios of water used by trees—predominantly taken up by roots from soils—and incorporated in cellulose exactly matches precipitation isotope ratios. Precipitation isotope ratios vary in space and time, and only a fraction of all precipitation infiltrates soils, reaches roots, and is ultimately taken up by trees. Considering species, soils, and climates may allow for predicting which fraction of water resides in the root-zone during the growing seasons, and how its isotope ratios deviate from that of average precipitation. Here we provide an overview of the terrestrial water cycle and the associated transport and fractionation processes that influence the stable isotope ratios of water used by trees. We highlight obstacles and opportunities to be considered, towards more accurately interpreting the records of O and H isotope ratios in tree cellulose.

1 Introduction

Understanding the isotopic composition of the water that supplies trees (δ_Source) and is incorporated into sugars and cellulose is central to interpreting tree-ring δ¹⁸O and δ²H. When using stable isotope ratios in tree rings, δ_Source is often subtracted from the isotopic values in cellulose (δ_cellulose) to isolate the fractionation effects that reflect physiological and climatic controls over leaf gas exchange (Chap. 10, 11, 16); however, especially when using δ_cellulose as a proxy for past conditions, measurements of δ_Source are rarely available. Thus, predictions and assumptions are often necessary for interpreting tree-ring δ¹⁸O and δ²H. Analytical approaches have relied on predicting δ_Source by averaging across some compilation of isotopic values of local precipitation (e.g., Anderson et al. 1998), sometimes implicitly assuming static values (e.g., Helliker and Richter 2008). However, δ_Source varies throughout years, among years, among trees, and among sites, yielding measurement and prediction challenges.

The value of δ_Source that is recorded in an annual tree ring (after accounting for fractionation) should equal the mean isotopic ratio of xylem water (δ_xylem), weighted by the photosynthetic rate and integrated over the time when that tree grows radially. However, not only are δ_xylem measurements generally unavailable for long tree-ring records, using them would involve uncertainties (e.g., regarding the timing of sugars forming cellulose; see Chap. 13). Instead, δ_Source is commonly assumed to be constant and equal to the isotopic value of long-term-mean precipitation, but such assumptions have known limitations (e.g., as discussed in Chap. 16 and Roden and Siegwolf 2012). To better account for variations in δ_Source and more precisely interpret tree-ring cellulose isotope ratios, several factors should be considered if δ_Source estimates are needed (see Fig. 18.1).

Fig. 18.1

To estimate the isotopic composition of δ source waters to trees, we need to not only consider the average isotopic composition of precipitation at a site. We must also consider which water reaches the soil layers from which roots take up water during the time when plants are transpiring, and how the isotope ratio of that water was influenced by mixing and fractionation processes before reaching roots. While these steps can rarely be quantitatively addressed, asking these questions can help in evaluating which factors should be considered to improve the accuracy of δ_Source estimates when interpreting tree-ring isotope ratios

The objective of this chapter is to provide an overview of how precipitation, soil, and tree water-uptake processes manifest in variations in δ_Source, and how our understanding of those processes informs the interpretation of tree-ring isotope ratios. The numerous biochemical synthesis and translocation processes that further alter δ_cellulose in trees, convolving the relationship between δ_Source and δ_cellulose are discussed in Chaps. 10, 11, and 13, and not covered here. Understanding the processes that control δ_Source found in the xylem can lead to practical assumptions and new ways of using tree-ring δ¹⁸O and δ²H, despite the uncertainties in δ_Source.

2 Precipitation Inputs and Their Spatially and Temporally Varying Isotope Ratios

Isotope ratios of precipitation (δ_Precip) have been measured and monitored since the 1950s (Dansgaard 1953, 1954), producing a rich body of data and theory describing controls on meteoric-water isotope-ratio variation in space and time. Even these earliest studies recognized that isotope ratios of rainfall were related to meteorology, and that different storm systems and different climatic regimes produced rain and snow with contrasting isotope ratios (Dansgaard 1954; Craig 1961). By the mid-1960s, many of the underlying principles had been established, including equilibrium and kinetic fractionation effects that lead to isotopic differences between liquid (isotopically heavier) and vapor-phase (isotopically lighter) water (Fig. 18.2; Dansgaard 1964; Craig and Gordon 1965). These fractionation factors also lead to the progressive depletion of heavy isotopes from the atmosphere as air masses cool and lose water as liquid- or solid-phase condensate (following a so-called Rayleigh distillation process; Kendall and Caldwell 1998). Together these processes explain most of the isotopic variation in meteoric waters, though progress building on this early work has improved understanding of how dynamics and transport within the atmospheric water cycle are expressed in δ_Precip across different systems and timescales. The fundamental theory of isotope fractionation in the water cycle was reviewed by Gat (1996), and Bowen et al. (2019) provide an update focusing on the integrated expression of these processes in large-scale climatic and hydrological systems.

Fig. 18.2

Water isotope variations in dual-isotope space and the effects of climate variations on environmental water isotope ratios. Incoming precipitation generally falls along a meteoric water line (MWL) which can be described by either the global meteoric water line (GMWL, δ²H⁼8δ¹⁸O + 10), or a local meteoric water lines (LMWL) if available for a specific site. The range of precipitation isotope ratio in a given location is strongly related to its temperature, elevation, continentality. The slope of 8, reflecting the relative equilibrium fractionation factors between δ²H and δ¹⁸O, defines the GMWL but it is also common that LMWLs have similar slopes. Variation in precipitation isotope ratios along those MWLs is strongly affected by season. Phase changes result in fractionation, with lighter isotopologues favoring the vapor phase. Thus, fractionation from evaporation causes the remaining liquid water to become isotopically enriched in the heavy isotopes because the departing vapor contains more light isotopes. Fractionation caused by evaporation also results in water isotopes deviating from the MWL, following an evaporation line with a lower slope than that of the MWL. This evaporation line slope relates to the relative humidity, where evaporation lines associated with higher humidity are more similar to the equilibrium fractionation line; at very low humidity, the slope is controlled by the relative diffusivity ratios of ¹H²H¹⁶O to ¹H₂¹⁶O versus ¹H₂¹⁸O to ¹H₂¹⁶O. Deviations from the MWL can be measured as d-excess—the deviation in δ²H units from the line passing through the origin (defined by the standard V-SMOW) along the equilibrium fractionation slope (equal to 8); thus, d-excess = δ²H -8δ¹⁸O and the GMWL has a d-excess of 10. To account for LMWLs not always matching the GMWL, lc-excess—the deviation in δ²H units from the LMWL, where LMWL lc-excess = 0—better quantifies the effects of evaporative fractionation on pools supplied by local precipitation

An assumption in many tree-ring studies has been that water used by trees reflects the isotopic composition of annually- or seasonally-averaged local precipitation (e.g., Anderson et al. 2002; Danis et al. 2006; Evans 2007; Zeng et al. 2016; Lin et al. 2019), which are well-known for the modern climate across much of the Earth through a combination of monitoring and statistical modeling (Aggarwal et al. 2010; Bowen 2010). This assumption implies that the processes delivering water to trees naturally integrate across precipitation inputs at a given site. However, systematic variation in δ_Precip exists at many spatial and temporal scales relevant to ecohydrology, and the processes routing meteoric water to plants are selective so the validity of this assumption is often compromised. Here we introduce relevant sources of δ_Precip variability, working from large to small spatiotemporal scales, and we discuss the question of routing and selectivity of water uptake in subsequent sections.

Long-term, annual-average δ_Precip exhibits substantial (i.e. >1 ‰ δ¹⁸O) variation at spatial scales of tens to thousands of kilometers (Fig. 18.3a). In non-mountainous regions, local isotopic variation (at scales less than 100 km) is more limited (e.g., Price et al. 2008; Liu et al. 2010). In contrast, areas of high topographic relief form precipitation due to orographic lifting and produce strong and systematic decreases in δ_Precip with increasing elevation (Dansgaard 1964; Poage and Chamberlain 2001). The average decrease in δ¹⁸O with elevation is approximately –0.28 ‰ per 100 m (Poage and Chamberlain 2001) and approximately –2.2 ‰ δ²H per 100 m. Consequently, downslope routing of groundwater, streamwater, or other surface waters that generated in higher elevations can result in water available to trees that is isotopically lighter than local precipitation; in such systems the resulting isotopic contrast among locally-available water sources has been used to identify sources of plant water uptake (Dawson and Ehleringer 1991; Chimner and Cooper 2004).

Fig. 18.3

Maps of global variations in a typical average precipitation δ¹⁸O and b seasonal amplitude (i.e., absolute differences between mean values and either typical mid-summer or typical mid-winter values) of precipitation δ¹⁸O (adapted from Allen et al. 2019a). Circles reflect the locations of precipitation isotope monitoring sites, and their fitted average values and seasonal anomalies from those average values. In extra-tropical regions, the highest values occur in summer; elsewhere, the timing of seasonal cycles varies with the migration of the Inter Tropical Convergence Zone

Old groundwater (which could be a tree-water source in areas where that groundwater exfiltrates) can be isotopically distinct from modern precipitation. Evidence from paleo-waters, climate proxy records, and models also clearly suggest large shifts in average δ_Precip as Earth’s climate system has changed. For example, estimated δ_Precip across the northeastern USA during the last glacial period (~20,000 years ago) were likely lighter in ¹⁸O by 8 ‰ or more relative to modern precipitation (Jouzel et al. 1994). Paleo-waters are relatively common in the subsurface (Jasechko et al. 2017), and although these old waters mostly exist at depths that prohibit their use by plants, they represent an isotopically distinctive source of water that may, in rare cases, be accessed.

Potentially more common are ecosystems in which plants sample unevenly from the seasonal precipitation cycle, and thus the seasonality of δ_Precip is an important determinant of source water composition (Fig. 18.3b). Isotopic seasonality is a common feature in the atmospheric water cycle, and is typical of most regions that exhibit climatic seasonality (Bowen 2008). In the extratropics, the lowest isotope ratios are nearly ubiquitously associated with the cold season, whereas isotopic seasonality at lower latitudes is largely associated with seasonal migration of the intertropical convergence zone and associated wet/dry climate cycles (Feng et al. 2009). The largest range of seasonal variation is found in the mid- to high-latitude continental interiors of the Northern Hemisphere, where inter-seasonal δ¹⁸O ranges can exceed 20 ‰ (Bowen 2008). Allen et al. (2019a, b) illustrated how seasonality of δ_Precip influences δ_xylem, and that co-occurring species do not necessarily use the same precipitation (more below), so seasonal bias needs to be considered in δ_Source estimation.

Understanding inter-annual variations in δ_Precip is especially important for tree-ring isotope studies. Inter-annual variability in annual-mean δ_Precip can result from not only annual or seasonal δ_Precip deviating from its normal pattern, but also from anomalous amounts of summer (higher δ_Precip) or winter (lower δ_Precip) precipitation in given years. Inter-annual variations in annual mean δ_Precip often exceed 1.0 ‰ δ¹⁸O (Fig. 18.4). Among precipitation monitoring stations with at least five full years of data, standard deviations describing inter-annual variability in amount-weighted annual mean precipitation δ¹⁸O ranged from 0.2 to 1.6 ‰ (with a mean of 0.7 ‰ across 27 sites; Fig. 18.4). In general, inter-annual variability is highest—with maximum ranges among annual means exceeding 4 ‰ δ¹⁸O—in regions with larger seasonal δ¹⁸O amplitudes (r = 0.62), which also tended to have the lowest average δ_Precip values.

Fig. 18.4

Amount weighted annual precipitation δ¹⁸O means for individual years at GNIP sites. Dots represents individual years and the bars represent ± 2 standard deviations, describing inter-annual variations. These data are from GNIP sites (IAEA/WMO 2020) that have at least five full years of both monthly δ¹⁸O and monthly precipitation amounts; note that there is a several-fold larger set of sites if these criteria are loosened, allowing for gaps in records. Nonetheless, these sites (city and country code indicated on the horizontal axis) span a range of climates and latitudes (e.g., ranging from tropical sites in Uganda and Sri Lanka to northern latitudes in Canada). The monitoring sites are ranked by mean δ¹⁸O, demonstrating that the lower values are also associated with higher inter-annual variability in δ¹⁸O

The literature also includes a growing number of examples of δ_Precip variation among events or over the course of individual storm events (e.g., Munksgaard et al. 2012; Coplen et al. 2015; Fischer et al. 2017). This evidence extends back to the work of Dansgaard (1953), who measured sub-daily changes in rainfall isotope ratios in Denmark associated with the passage of weather systems. In particular, this work showed a substantial increase in ¹⁸O/¹⁶O as condensation altitude lowered throughout a warm frontal storm, and this general pattern has been subsequently documented and modeled for several other well-organized synoptic-scale events (Gedzelman and Lawrence 1990; Coplen et al. 2008; Pfahl et al. 2012; Aemisegger et al. 2015). While inter-event variations may be mostly damped out in soils and thus not detectable in tree rings, such patterns can be strongly accentuated in large-scale systems such as tropical and extratropical cyclones; in those storms, δ_Precip changes of 8–10 ‰ (δ¹⁸O; 60 to 80 ‰ for δ²H) have been observed over timescales of hours and/or spatial scales of ~100 km (Gedzelman et al. 2003; Coplen et al. 2008; Good et al. 2014a, b). These storms can produce heavy rains with unusually low isotope ratios, in particular (Lawrence and Gedzelman 1996), and evidence suggests that these isotopic anomalies can be passed along to trees and tree rings if the events are especially large or anomalous events (Weiguo et al. 2004; Miller et al. 2006; Berkelhammer and Stott 2008). The evolution of precipitating storms can be complex and spatially heterogeneous, particularly for less organized and/or convective systems. Routine prediction of isotopic variations throughout individual events has not been demonstrated, and many examples of seemingly chaotic fluctuations (Kennedy et al. 2012) suggest that within-storm variation is the norm. However, predicting these patterns remains a research frontier, and thus we do not really know their potential to bias soil water isotope ratios, relative to average δ_Precip, if different-sized events infiltrate the soil differently. With that stated, small-scale variations are often less relevant to tree rings because they integrate water signals across longer timescales.

In forests, canopy interception and interception loss can alter the isotopic composition of precipitation reaching soils. During events, slight evaporation occurs from waters stored in canopies that may evaporatively enrich the water that is eventually transmitted downward (i.e., throughfall). Perhaps more importantly (Gat and Tzur 1968), interception also involves the selective transmission of throughfall during events and the omission of the water stored at the end of events that evaporates completely. Given that δ_Precip can trend upward or downward throughout events, this selective transmission can result in erratic differences between event-mean throughfall and open-precipitation δ_Precip. A synthesis of interception studies (Allen et al. 2017) shows that, on average, the net-precipitation below forest canopies was mostly between 0.2 ‰ lighter to 0.6 ‰ heavier in δ¹⁸O than open precipitation (the mean long-term enrichment was 0.19 ‰ δ¹⁸O); while individual-event differences can be much larger than these mean values, those short-term variations are erratic. Accordingly, because individual events are small compared to the storage in soils, event-level effects due to interception are likely inconsequential to variations in δ_Source and the coarse-resolution signals inferred from tree rings. Nonetheless, enrichment is observed on average over long time scales and thus would represent a small systematic bias if ignored.

Resources to aid in predicting δ_Precip inputs to a location are widely available, although subsequent infiltration and uptake processes need to be considered to predict δ_Source. Databases of δ_Precip and volumes are available for thousands of locations with monthly or better resolution through the IAEA’s Global Network of Isotopes in Precipitation (GNIP; Aggarwal et al. 2011), and the Water Isotope Database (waterisotopes.org; Putman and Bowen 2019). Additionally, the National Ecological Observatory Network (NEON) provides a rapidly growing public dataset containing time-series of biweekly δ_Precip for sites spanning the United States; however, none are yet long time series, which are especially useful (see Sect. 18.5 and Fig. 18.4). Country-specific precipitation-isotope monitoring networks also exist for Switzerland, Austria, Germany, and elsewhere. Global interpolated data products are also available; for example, see those generated from the Water Isotope Database, which can be queried online (see IsoMap http://isomap.org and the Online Isotopes in Precipitation Calculator, http://wateriso.utah.edu/waterisotopes/) or downloaded as maps (Bowen et al. 2014). Another option is to develop predictive isoscape maps for the specific study domain (Bowen 2010). In addition to the raw isotope values provided by GNIP and elsewhere, Allen et al. (2019a) provides fitted sine coefficients that describe δ_Precip seasonality at > 600 sites globally, along with various site-characteristic covariates. Another promising source of δ_Precip estimates, especially for interpreting isotope paleo-proxy records, is isotope-enabled circulation models that output global spatiotemporal variations in δ_Precip over past centuries as estimated from sea surface temperatures (Dee et al. 2015; Konecky et al. 2019). Any of these data products can be useful for constraining δ_Source estimates in areas where δ_Precip data are not available.

3 From precipitation to Soils and Other Subsurface Storages

Nearly all water used by plants originates from precipitation, whether it be from fog, rain or snow. This precipitation is available to plants from different pools within ecosystems. Two predominant pools are water held under tension in soils (the vadose zone), and water held under pressure in groundwater (the saturated zone). Each can be complex water storages that vary spatially and temporally in isotopic values. Water enters these pools by infiltrating locally or flowing in from upslope areas. In most cases, the local infiltration of rainfall and snowmelt provides water to plants. In other cases, shallow groundwater can directly supply trees. These isotopically diverse subsurface waters largely determine the δ²H and δ¹⁸O in tree rings; therefore, considering how water resides, mixes, percolates, and evaporates in the subsurface is critical to relating precipitation patterns to plant-tissue isotope ratios.

Two aspects mainly affect the isotope ratios of the water in the vadose zone: (1) the transport, mixing and storage of precipitation with varying isotopic composition within the vadose zone; and (2) the changes of water isotope ratios caused by fractionation during evaporation from soil. Here, we introduce the processes that result in variability in subsurface pore-water isotope ratios. Understanding such processes (e.g., soil–water turnover times or typical depths of evaporative fractionation) can aid in understanding which precipitation may be stored in a soil during the growing season and to what degree soil waters might be evaporatively enriched in heavy isotopes.

3.1 Water Transport and Mixing

Given that precipitation and δ_Precip are highly variable, understanding how precipitation travels through the subsurface is key to knowing which precipitation (and associated isotope ratios) will be accessible to plants. Water transport in the unsaturated zone occurs by various mechanisms, with characteristics that can be abstractly characterized as well-mixed flow, uniform translatory (piston) flow (Hewlett and Hibbert 1967) or non-uniform preferential flow (Beven and Germann 1982); in reality, aspects of all of these flow behaviors are relevant.

Subsurface waters are rarely well mixed (Penna and Meerveld 2019), even though well-mixed assumptions are often implicit to common representations of soil and groundwater systems (e.g., Lawrence, et al. 2011). In hypothetical well-mixed systems, a single isotope ratio could be assumed for an entire storage pool, representing the mixture of new inputs and prior storages; in that scenario, the fraction of water extracted by plants, as well as that draining downward from soils, are both unbiased representations of the stored precipitation. This means that more recent precipitation will dominate the storage, and the ‘age’ of the water in storage will match the turnover time (storage/flux). This transport scenario will yield spatially uniform soil–water isotope ratios that vary in time, mimicking a damped and lagged seasonal precipitation isotope cycle. Such assumptions may not apply for soil or shallow groundwater (Penna and Meerveld 2019), but may better apply for large groundwater aquifers that store a mixture of many years or decades of past precipitation; in those conditions, values are relatively spatially and temporally uniform (Vogel and Van Urk 1975), supporting accurate estimates of δ_Source waters if it is known that trees are using groundwater.

An older conceptual model of soil–water infiltration is that of uniform translatory flow (also known as plug flow or piston flow), where newly infiltrating precipitation pushes down the previous precipitation stored in soil pores; however, this model has decreased in popularity since the majority of soil isotopic data does not fit this model (Fig. 18.5). This uniform-flow mechanism leads to depth-stratified soil waters, with the shallowest soils containing the most recent inputs (e.g., Fig. 18.5a) and increasingly older precipitation with depth. If newly infiltrated water entirely replaces previously stored water (“piston flow”), (a) no water in the profile will be older than the turnover time and (b) the temporal variations in δ_Precip would be preserved by depth in soil water isotope profiles (Fig. 18.5a), and (c) tree water isotope ratios would look similar to that of long-term mean precipitation if soils are deep enough to hold years of precipitation and roots take up soil water uniformly across the rooting profile (Sect. 18.4). Alternatively, if trees predominantly use shallow soil water, δ_Source would approximate rainfall that fell recently (i.e., usually during the growing season). The rate that this oscillating signal propagates downward (e.g., Fig. 18.5a) depends on how much precipitation falls and how much the soils store. In reality, because flow is never entirely uniform, variation in soil water isotope ratios typically decrease substantially with depth due to mixing (dispersion) during percolation (e.g., Thomas et al. 2013; Barbecot et al. 2018; also see Fig. 18.5).

Fig. 18.5

Example profiles of soil–water δ¹⁸O (left) and lc-excess (right) for (a and b) a vineyard near Freiburg, Germany, (c and d) a humid, cold, continental pine forest in southeastern Canada, and (e and f) a Mediterranean pine forest in the Pyrenees, Spain. For c–f, the error bars represent ±2 SD and the data show beginning, the middle and end of the growing season. All vertical colored and black lines represent weighted seasonal or annual averages of the δ¹⁸O for the sites. For e and f, both the so-called “mobile” (circles) and “bulk” (squares) water values are shown. For further details, see (Sprenger et al. 2016a, 2018b, 2019)

With non-uniform preferential flow, infiltrating precipitation follows the route of least resistance; new inputs differentially bypass storages to yield an isotopically heterogeneous subsurface (Brooks et al. 2010; Sprenger et al. 2018a, 2019). The more that infiltrating water bypasses storages, the more likely it is that soil matrix water will reflect older precipitation that resides across seasons and disproportionately supplies plants (often referred to ecohydrologic separation; Brooks et al. 2010). How much water flows in preferential flow paths versus trickling through the matrix can depend on soil texture, structure, wetness (Weiler and Naef 2003), biological activity (Schaik et al. 2014), and input amount or intensity (Nimmo 2011). With preferential flow, the refilling of soil water stores may occur periodically, resulting in, for example, the under-representation of precipitation that fell at higher intensities (Jasechko and Taylor 2015; Allen et al. 2019b) or when soils are wet (Brooks et al. 2010; Sprenger et al. 2019). These preferential flows have been observed through showing that (a) waters quickly passing through soils are more similar to recent precipitation than is the entirety of water in soils (including finer pores), and (b) the waters stored in the soil matrix are older than they would be if well-mixed or uniform-flow conditions dominated (Fig. 18.5c; see Berghuijs and Allen 2019). Conventional wisdom in hydrology is increasingly gravitating towards assuming that soil–water transport is highly preferential, especially in forest soils (Flury et al. 1994; Nimmo 2011), and thus δ_Source can be potentially biased towards reflecting precipitation from specific times or events when recharge occurs.

To estimate δ_Source, researchers should not only consider these soil–water transport concepts but also the general empirical patterns seen in soil–water isotope studies. Real-world soil water transport does not solely reflect any one of these processes, even if we should expect evidence of preferential flows in shallower soils and mixing in deeper soils. These dynamic subsurface flow processes affect the pattern of subsurface isotope ratios in ways that are difficult to predict; this is an active area of research in ecohydrology, with recent progress in generalizing patterns across climates (Sprenger et al. 2016b; Allen et al. 2019b) and across inter-annual climatic variations (Berkelhammer et al. 2020). In general, the isotope ratios of soil water change over the growing season from lower isotope ratios in spring to higher in summer and fall (Fig. 18.5b, c). That is to say, early growing season soil waters are typically lighter than average δ_Precip, because they reflect storage of cold-season precipitation, and (at least in shallow soils) later growing season soil waters are typically heavier than average δ_Precip (Figs. 18.5). Late growing-season shallow soil water is not only isotopically heavier because of the heavier isotopic composition of summer rainfall (e.g., compare the red and blue vertical lines in Fig. 18.5), it also results from progressive evaporative fractionation (described in the next section). Deeper soils tend to reflect a more wintry signature, even in regions with summer precipitation (Ehleringer et al. 1991; Williams and Ehleringer 2000; Martin et al. 2018; Allen et al. 2019b). Woody plant xylem frequently expresses this lighter isotope ratio associated with deeper or older precipitation.

3.2 Evaporation Fractionation of Soil Water

Just as in leaves (Chaps. 10 and 11), evaporation from soils results in the enrichment of heavy isotopes in the residual soil water because light isotopes are preferentially evaporated (Gat and Gonfiantini 1981); however, unlike in leaves, a constant resupply of water rarely exists to move up and replace the evaporated fraction. Evaporation results in heavy isotopes accumulating in the residual soil water until new precipitation mixes with or displaces the enriched pool. Thus, soil water will often be more enriched in heavy isotopes relative to the original precipitation water (Fig. 18.2). These effects are very prominent in shallow soil–water samples (Fig. 18.6), although, the most evaporatively enriched soil–water pools are generally of small volume and not necessarily a major contributor to plants (discussed further in Sect. 18.4). Nonetheless, studies inferring uptake depths or precipitation sources should consider potential alterations in δ_Source attributable to evaporation (Tang and Feng 2001).

Fig. 18.6

Soil–water isotope values compared to the estimated seasonal precipitation inputs at those sites. All soil–water values are from the growing season, when possible separated as early (April-June) versus late (July–September) growing season values. Summer and winter precipitation are defined relative to the solar cycle (thus, for the tropical sites, winter is not necessarily colder). “Shallow” includes depths from 5–30 cm; “Deep” includes depths from 30–100 cm (and to 300 cm for the Nebraska and Luxembourg sites). The studies are as follows: Arid shrubland in China (Zhou et al. 2011), Arid woodlands in Arizona (Snyder and Williams 2000), mesic woodland in Nebraska (Eggemeyer et al. 2009), Floodplain forest in Switzerland (Bertrand et al. 2014), Mediterranean oaks in Portugal (Kurz-Besson et al. 2006), sites in Luxembourg (Sprenger et al. 2016c), Subtropical forest in southern China (Rong et al. 2011), humid montane forest in North Carolina (Berry et al. 2014), a Humid conifer forest (Brooks et al. 2010), and a montane tropical rainforest (Goldsmith et al. 2012). Precipitation data are calculated using the online isotope in precipitation calculator: http://wateriso.utah.edu/waterisotopes/. Note that precipitation estimates can be imprecise; for example, in the Goldsmith et al. study, positive δ¹⁸O values for summer rainfall are common. Also, note that the most evaporative enriched soil waters are unlikely to be a substantial source to plants because there is usually minimal water content in these locations

Kinetic fractionation of stable isotopes of water leads to sources deviating from the meteoric water line (Fig. 18.2) because of differences in the relative diffusivities between ²H¹HO and ¹H₂O compared to ¹H₂¹⁸O and ¹H₂¹⁶O (Horita et al. 2008). Until recently, deviations from meteoric water lines were mostly quantified using d-excess (δ²H – 8^×δ¹⁸O), where 8 is the ratio of equilibrium fractionation factors of O and H, defining the slope of the global meteoric water line (Dansgaard 1964); however, local meteoric water lines (LMWLs) often deviate from a slope of 8 (Putman et al. 2019). Thus, variation in d-excess does not imply evaporation because precipitation inputs along a LMWL with slopes different from eight will also vary in d-excess, regardless of any subsequent evaporation. Accordingly, the line-conditioned excess (lc-excess), defined relative to LMWLs (lc-excess = δ²H – slope_LMWL × δ¹⁸O – intercept_LMWL) is more appropriate for inferring terrestrial evaporation (Landwehr and Coplen 2006). Shallow soil lc-excess values can be well below zero, even in humid climates (Sprenger et al. 2016). Low lc-excess values are especially common following extended warm periods without rain (Sprenger et al. 2018b), e.g., in summer and early autumn (Fig. 18.5d). Although few tree ring isotopic studies have used both δ²H and δ¹⁸O from plant tissue in conjunction (but see Voelker et al. 2014), this area of research is advancing because this dual-isotope approach can provide new insights into past evaporative conditions (see Chaps. 10 and 11). Alternatively, evaporation effects in dual isotope space can also be ‘compensated’ by assuming theoretical evaporation lines (which can be notably different than empirical ‘evaporation’ lines) and relating soil and plant waters to their precipitation sources (Benettin et al. 2018; Bowen et al. 2018), for insights into how soil–water is recharged by precipitation.

3.3 Predicting Soil Water Isotope Ratios from δ_Precip

Methods for predicting the complex interplay between newly infiltrating precipitation and previously stored water (that is often evaporatively fractionated) could support more accurate uses of tree-ring isotope ratios. Hydrologists use both mechanistic simulation models and statistical, “lumped” models to represent soil water processes. Parameterizing those models is data intensive, requiring measurements of soil water or outflow isotope ratios (e.g., Braud et al. 2005; Haverd and Cuntz 2010; Stumpp et al. 2012; Mueller et al. 2014; Sprenger et al. 2015) to capture the dominant mixing processes (Sect. 3.1), towards generating simulated rooting-zone water isotope time series. While such models can be effective, requiring data-driven parametrizations undermines their usefulness with long tree-ring isotopic records. Given that soil water is an ensemble of fractions of previous precipitation events, soil–water can be estimated as a distribution of those past events (Groh et al. 2018; Benettin et al. 2019); thus transfer functions capturing a statistical relationship between inputs and outputs may be more practical than mechanistic models and outperform estimates implying that soils contain an even mixture of annual precipitation. Otherwise, syntheses of growing season soil–water isotopes measurements show some generalities that aid in constraining expectations.

Soil water δ¹⁸O generally deviates from local δ_Precip across a wide range of sites (as shown here; Fig. 18.6). Shallow soil–water is isotopically heavier than the typical seasonal precipitation inputs, especially in arid regions, demonstrating strong evaporative enrichment. This pattern diminishes from arid to humid (left to right), with exceptions occurring in sites with extended dry seasons (e.g., during the dry summer in Portugal and following the dry winter in Mexico; Fig. 18.6). In regions where the growing season involves more continuous evaporation, soil water δ¹⁸O in the late growing season is usually higher than early growing season δ¹⁸O (Fig. 18.6); thus, changes in soil water δ¹⁸O throughout a season can be confounded with changes in depth of uptake. Importantly, these highly enriched shallow soil waters should be scarce and under high tension after undergoing significant evaporation, and thus they are not likely to be the primary water source to trees; furthermore, most tree radial growth occurs near the beginning of the growing season (Zweifel et al. 2006; Swidrak et al. 2013), often prior to the development of strong evaporation signatures in soil water isotope ratios. Hence, tree source waters recorded in tree ring δ_cellulose are unlikely to have δ_Source values that are as high as late-season shallow soil water values (Fig. 18.6).

In wetter regions, evaporation effects are less prominent and thus isotope ratios in soils tend to be bounded by seasonal δ_Precip; however, conditions need to be considered on a case-by-case basis. For example, the Swiss floodplain forest (Fig. 18.6) is likely influenced by a riparian aquifer, explaining its lack of evaporative signal; in general, groundwater tends to be dominated by winter precipitation (Jasechko 2019), and in this case, groundwater is likely sourced from higher elevation precipitation (Bertrand et al. 2014). Another prominent feature across these sites is that deeper soil waters are typically isotopically lighter, because they generally experience less evaporation and water with this evaporated signal only partially trickles downward (i.e., preferential flow), and less variable because of mixing with stored preferential flow; furthermore, the conventional wisdom is that winter precipitation tends to percolate deeper because surface soils are drying less during summer. The deeper soil waters are mostly enveloped by the typical summer and winter δ_Precip; notable exceptions are the driest site, where deeper soil waters may still show strong evaporative enrichment, and the tropical rainforest in Mexico, where the original study (Goldsmith et al. 2012) reports higher precipitation δ¹⁸O than those predicted by the Online Isotopes in Precipitation Calculator (waterisotopes.org). While using these precipitation predictions provides consistency across studies, δ_Precip predictions can be uncertain across topographically complex regions, especially when predicting δ_Precip in individual years (Sect. 18.2).

These patterns shown (Fig. 18.5) are explainable, albeit not necessarily a-priori predictable. Nonetheless, our first-order theoretical expectation should be that with larger fluxes (i.e., precipitation inputs) or shallower rooting zones (smaller storages), soil–water turnover times are higher and thus they should more reflect in-phase precipitation isotope values (i.e., growing season). This general pattern is shown in xylem water collected in a snapshot sample across >100 sites in Switzerland, defining steep climate and elevation gradients (Fig. 18.7a). While estimated δ_Precip decreases near monotonically with elevation, xylem water δ¹⁸O does not; these measurements highlight the influence of climate gradients on δ_Source. Deviations of xylem water (and thus soil–water available to those plants) from mean annual δ_Precip increase with elevation and precipitation amount (Fig. 18.7b), which mostly co-vary in Switzerland; thus, the drier region trees used out-of-season precipitation whereas the wet-region trees use growing-season precipitation, demonstrating the higher turnover in wetter regions. This one example demonstrates how considering the relationship between more precipitation and higher turnover times can guide evaluations of δ_Source variations across sites.

Fig. 18.7

a Annual precipitation and xylem water δ¹⁸O versus elevation and b xylem water δ¹⁸O differences from precipitation δ¹⁸O versus mean-annual precipitation amount in Switzerland; elevation and annual precipitation are largely collinear here. Panel a shows decreasing δ¹⁸O of precipitation with increasing elevation, which is true for most locations on Earth. However, xylem-water (mid-summer values) δ¹⁸O did not decrease with elevation. This probably relates to the greater precipitation amounts in higher elevations driving shorter soil–water turnover times, such that the water stored in soils is more in-phase with current precipitation (i.e., wetter climate soils store more summer precipitation in summer). Panel b shows the relationship between xylem-water δ¹⁸O at the same sites, but as deviations from annual precipitation δ¹⁸O which range from −3 to 5 ‰ δ¹⁸O; in wetter areas, this δ¹⁸O deviation increases (r = 0.59 and Spearman’s ρ = 0.47, p < 0.001), consistent with the greater soil–water turnover. Considering these relationships allows for avoiding the systematic biases that can result from assuming that xylem water equals annual precipitation across climatologically distinct sites

4 Roots and Uptake Patterns

Patterns in root water uptake add another layer of uncertainty to assumptions about how δ_xylem relates to annual δ_Precip. Earlier, we discussed how soils do not behave like sponges that store and perfectly reflect the isotopic composition of annual rainfall. Similarly, the water that roots take up does not perfectly reflect the isotopic composition of the average soil water. In this section, we highlight how roots take up water, and how those processes influence δ_Source.

Water flows from soils into plants along a passive water potential gradient known as the soil–plant atmosphere continuum (SPAC). Water enters trees primarily through their non-suberized fine roots along an apoplastic route, and minimally through a symplastic route where water is actively transported across cell membranes. Water traveling along the SPAC apoplastically does not isotopically fractionate (Dawson and Ehleringer 1991, 1993), albeit analytical errors can occur and soil and plant water are not always identical in a given instance in time (Vargas et al. 2017; Penna et al. 2018; Barbeta et al. 2020). However, plants that do use symplastic transport for water uptake, such as salt tolerant plants that exclude salts from uptake pathways, have shown isotopic fractionation of ²H during water uptake (Lin and Sternberg 1993; Ellsworth and Williams 2007). Many salt-excluding species have a highly developed Casparian strip which impedes apoplastic water movement into the endodermis, forcing water through symplastic routes crossing cell membranes. The symplastic route of water movement allows for exclusion of unwanted molecules such as salts, but costs energy for active transport. The energy required for disassociating hydrogen bonding of individual water molecules is greatest for water molecules containing ²H, compared to other isotopologues of water (Clark and Fritz 1997). As a result, water within stems of salt tolerant species has lower δ²H values relative to the source water, without having measurable differences in δ¹⁸O (Lin and Sternberg 1993; Ellsworth and Williams 2007).

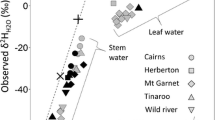
For the majority of tree species with apoplastic water uptake, water within the xylem approximates a spatially integrated mixture of soil water from a plant’s population of fine unsuberized roots, proportional to their uptake rates. Therefore, the origin of water within the xylem will depend on a plant’s root distribution and water uptake rates. Roots decline in density asymptotically with soil depth, with the majority of plant roots occurring within the upper 30 cm of the soil profile (Gale and Grigal 1987; Jackson et al. 1996; Warren et al. 2005). For tree species, the percentage of roots in the upper 30 cm varies from a high of 83% in boreal forests, to a low of 52% in temperate coniferous forests (Jackson et al. 1996). However, variation between sites was highly dependent on soil texture, water availability, and depth to water table, permafrost, or rock. In general, roots are deeper in seasonally dry regions and shallower in regions where soils remain wet (Fan et al. 2017). Thus, in humid regions, not only do soils hold waters sourced from recent, growing-season precipitation (Sect. 18.3), trees are more shallowly rooted and likely use shallower water which should generally be composed of more recent precipitation (Figs. 18.7 and 18.8). In contrast, drier regions likely contain a long-duration mixture of past precipitation and trees are more deeply rooted and thus likely use deeper waters that have dampened and lagged expressions of δ_Precip. Xylem water from deeply rooted trees should rarely express the highly evaporated waters observed in shallow soils in the same sites (Figs. 18.7 and 18.8). Some roots can extend down far below the soil bedrock interface allowing them to access deep water reserves (Canadell et al. 1996). Thus while the majority of roots are located in the top of the soil profile, rooting depths can extend below 50 m allowing trees access to many isotopically different water pools.

Fig. 18.8

Mean growing season xylem-water isotope values as a deviation from annual precipitation δ¹⁸O, plotted against site mean annual precipitation amount; these are data from the same sites as those in Fig. 18.6, minus the Luxembourg sites because they lacked xylem water measurements. Note that xylem water does not reflect evaporative enrichment above δ_Precip as strongly as does soil water (Fig. 18.6) because trees often use deeper waters, although the high variability in the driest site likely results from evaporation effects. Xylem water in wetter sites is generally more enriched compared mean precipitation (r = 0.67, p < 0.05), in contrast with the expected effects of evaporative enrichment being greater in drier sites; this presumably reflects the presence of shallower roots and more in-growing-season precipitation in soils of wetter regions

In some cases, a subset of roots can account for the majority of water uptake, which can explain dissimilarities between physical root distributions and isotope-inferred uptake depths. If all roots were equally taking up water, then the proportion of water acquired from different depths would match the distribution of fine roots; however, root water uptake rates vary with depth depending on root hydraulic properties, soil moisture content and soil water potential. When soils are at field capacity and both soil water content and plant water potential are high, small gradients in water potential are associated with relatively large fluxes of water. The majority of root water uptake during these periods is from the upper soil layer where rooting density is high. As soils dry, equivalent drops in soil water potential yield smaller and smaller volumes of water since soil moisture release curves relating water potential to water content are non-linear (Selker et al. 1999). Root water uptake shifts to deeper layers as the soil moisture content in the upper soils decreases (Warren et al. 2005; Brooks et al. 2006). The ability of roots to extract water also varies by species and with depth in the soil. Meinzer et al. (2007) found that relative uptake per root area increased with rooting depth for both Douglas-fir and western hemlock. Plants with roots extending far beyond the soil can access rock water and deep water aquifers which can sometimes make up a substantial portion of xylem water even though only a small proportion of roots extend to those depths (Schwinning 2010; Oshun et al. 2016), regardless of shallow root abundances. Phreatophytes–plants using groundwater–often have deep taproots reaching water tables which can account for a large portion of their water uptake, even though the taproot is a small portion of their rooting system (Burgess et al. 2000; Hultine et al. 2003a, b). Thus, roots at deeper depths are not only likely to be rooted in soils or substrates that maintain moisture for longer, these deep roots can transport more water, compensating for the relatively fewer roots at deeper depths in soil profiles. Ultimately, the isotopic composition of xylem water of an individual tree will reflect the integrated isotopic composition of soil water accessed by that tree’s roots, weighted by those root’s water uptake rates.

Isotopic approaches has been used extensively to understand the dynamics of root water uptake, and niche partitioning of soil water resources by plants within a community (e.g., Ehleringer et al. 1991; Meinzer et al. 2007; Goldsmith et al. 2012; Guo et al. 2018). Inferring uptake depth using isotopes requires known isotopic variation within the soil either spatially, temporally or both (see Sect. 18.3). Generally, spatial variation in soil water isotopic composition is measured along a depth profile, but spatial variation within a soil layer is also likely (e.g., Goldsmith et al. 2019), and the isotopic composition of water being extracted by roots may not match the bulk isotopic composition of soil water within a layer. Where exactly root tips are located within a layer (e.g., within or around soil pedons) will influence water potential and content they experience, and which water pool they can take up. Spatial variation in all of these factors is complicated even when soils are relatively uniform (McCully 1999; Carminati et al. 2010). While water flows passively along a water potential gradient, roots are alive and the rhizosphere around roots are filled with living organisms that can excrete compounds that can change water potentials (McCully 1999). Additionally, mycorrhiza have been shown to transport water that is taken up by plants (Warren et al. 2008). Understanding these living interactions and how they influence water traveling along the SPAC has implications for the isotopic composition of xylem water; this is an active area of research.

Another complicating factor in determining the source of water uptake within the soil is hydraulic redistribution. Hydraulic redistribution is the passive movement of soil water from one region of the soil to another via roots along a water potential gradient (Caldwell and Richards 1989; Caldwell et al. 1998; Neumann and Cardon 2012). When plants are transpiring, the water potential gradient within the plant drives water flow to the leaves and the atmosphere. However, if transpiration stops, e.g., during the night, then water can flow along potential gradients within the soil. Generally, water will flow from moist soils at depth to the dryer surface soils, and this process was originally described as hydraulic lift. However, water can flow downward via roots after rains (Ryel 2004), as well as laterally (Brooks et al. 2002, 2006), prompting the more generalized term of hydraulic redistribution. Hydraulic redistribution would act to mute isotopic variation within the soil profile, but the volumes of water that are released to the soil are small compared to the volume of water within the soil (Neumann and Cardon 2012). For example, at 5% soil water content, 10 cm of soil would hold 5 mm of water, but rates of hydraulic redistribution are around 0.02 mm within 10 cm of soil per night, several orders of magnitude smaller than the water content (Warren et al. 2007). In addition, the water excreted from the root during the night is the first water to be taken up as transpiration begins again, so isotopic differences between redistributed water and the soil water would not accumulate over time. Thus, the resulting isotopic shifts in soil water are unlikely to be detectable unless a strong isotopic label is used (Brooks et al. 2002, 2006), implying that they are unlikely to strongly influence tree-ring isotope applications.

Roots extract and integrate water from different pores and depths, and thus δ_Source variations are dampened compared to those of individual soil samples. Nonetheless, temporal variation in soils and xylem water sources can manifest in δ_Source varying spatially and temporally, introducing challenges to tree-ring δ²H and δ¹⁸O interpretations. Furthermore, xylem water concurrently sampled from individual trees or branches in the same site can vary by 1–2 ‰ δ¹⁸O (Goldsmith et al. 2019). Thus, uncertainties and variations in source waters (and thus δ_Source) should always be assumed. Nonetheless, plant-rooting characteristics are a tertiary control over δ_Source, because roots can only extract water from that which is input to the system as precipitation and held in the subsurface rooting zone (i.e., the primary and secondary controls). Therefore, discussion of how rooting depth relates to δ_Source depends on some understanding of δ_Precip, its variations, and how it resides in soils.

Foliar uptake is an alternative uptake pathway that bypasses root and soil processes. The uptake of water on leaf surfaces, typically occurring under foggy, humid conditions (Simonin et al. 2009; Gerlein-Safdi et al. 2018) when plants have lower water potentials (Goldsmith et al. 2013), represents a potentially different isotopic signature. These are generally small supplements of water (Gotsch et al. 2014), and identifying their magnitude is difficult because the isotopic effects of foliar uptake are also not always distinguishable from the back diffusion into stomata that occurs with transpiration (Goldsmith et al. 2017; Lehmann et al. 2017; also see Chaps. 10 and 11). Foliar uptake effects on tree-ring isotope ratios are not well described, but if boundary layer vapor isotope ratios are roughly in equilibrium with precipitation (see Fiorella et al. 2019), foliar uptake may not have a substantial effect on δ_Source; this is because the fluxes are small and the effects match those of the back diffusion already accounted for in leaf-atmosphere fractionation representations (Chap. 10).

5 Applications and Practical Considerations

5.1 Assuming δ_Source Values to Study Leaf-Climate Interactions

Knowing the value of δ_Source is critical for many applications using tree-ring δ¹⁸O (and δ²H) because much of the theory is based on isotopic shifts relative to δ_Source and is calculated as Δ_cellulose ≈ δ_cellulose − δ_Source (Barbour 2007). Often Δ_cellulose is used to infer leaf-atmosphere interactions, because transpiration and vapor exchange with the atmosphere alter the isotopic ratio of leaf water in systematic ways (Chaps. 10 and 11). As a result, Δ_cellulose is used as a proxy for climate and leaf physiology, after accounting for the many mixing and fractionation processes that occur during the incorporation of leaf water into cellulose (see Chaps. 10, 13, and 16). Thus, accurate knowledge or predictions of δ_Source through time are key to accurate Δ_cellulose estimates and interpretations.

A common assumption for estimating δ_Source to calculate Δ_cellulose of an annual increment is that δ_Source is equal to long-term mean δ_Precip at a given location. Indeed, trees integrate soil water both temporally and spatially so that the annual value of δ_Source is often bounded by the annual range of δ_Precip inputs to a site (unless the trees use shallow soil waters that are especially fractionated by evaporation). Soils could possibly be an unbiased mixture of a year’s precipitation, but in most scenarios (especially in more humid regions), the rooting-zone in soils can only hold a small fraction of a year’s precipitation: e.g., consider that most roots are within the upper 30 cm of soil (Gale and Grigal 1987), which could hold a maximum of 90 mm of precipitation if the field capacity is 30%. In contrasting settings with deep roots, water may only occasionally percolate to the deeper depths that disproportionately supply trees. Thus, where evaporation ratios or seasonal variation in δ_Precip is large, δ_Source could deviate (systematically) from long-term mean δ_Precip by several ‰ δ¹⁸O or tens of ‰ δ²H.

Assuming δ_Source is always equal to long-term mean δ_Precip, and thereby also assuming that δ_Precip is constant over time (Fig. 18.4) can confound interpretations of inter-annual variations in Δ_cellulose. To mitigate temporal uncertainties, where possible, one can:

• Select sites where soil or xylem water isotope ratios have been measured over years of contrasting meteorological conditions to test how dry or wet years affect the soil–water or xylem-water isotope ratios, e.g., to rule out their influence on signals that are assumed to be due to Δ_cellulose. For measuring soil water, bulk samples (e.g., taken with an auger) should be used because suction lysimeters sample water that is more likely to drain quickly and not contribute to transpiration. For xylem water, twigs or cores should be collected. Both soils and xylem material should be sampled a few times throughout the growing season and extracted water by cryogenic vacuum distillation (see the discussion on sampling in Penna et al. 2018).

• Select sites where inter-annual variations in δ_Source are small, e.g., because δ_Precip variations are small, or trees use streamwater or groundwater with a less dynamic stable isotope signature (e.g. Ulrich et al. 2019). Interestingly, these site conditions for stable δ_Source contrast with the droughty edaphic sites where tree-ring widths are more responsive to temperature, precipitation, or humidity, and thus droughty sites are often preferred for dendroclimatological applications.

• Select sites where long records of δ_Precip exist, or where magnitudes of inter-annual variations in mean δ_Precip can be constrained using publicly available δ_Precip datasets, which should provide a basis for estimations of uncertainties in assuming constant δ_Source.

• If there are no means of estimating δ_Precip and δ_Source variability, then uncertainties in δ_Source should be assumed and interpreted accordingly. While values of assumed uncertainty cannot be universally prescribed, Figs. 18.4 and 18.8 show potential ranges of inter-annual δ_Precip variability and δ_Source- δ_Precip differences that can occur.

Assuming δ_Source is always equal to long-term mean δ_Precip can confound interpretations of spatial variations in Δ_cellulose across climate gradients. For example, deviations of δ_Source from mean annual δ_Precip can depend on climate (Fig. 18.7). To mitigate spatial uncertainties associated with δ_Source, where possible, one can:

• Select sites where trees have predictable sources with relatively stable isotope ratios (e.g., obligate phreatophytes), and measure their xylem water isotopic values.

• Select sites where precipitation, xylem and/or soil water isotopic data are available or can be measured to estimate how δ_Source relates to δ_Precip.

• Select sites with similar climates, soils, and species to where past studies have estimated the relationship of δ_Source to mean δ_Precip.

• Search online isotopic databases for δ_Precip data and streamwater isotope time series (i.e. IAEA Global Network of Isotopes in Rivers, GNIR, Water Isotope Database wiDB, waterisotopes.org, etc.). These data can be used to estimate the mean isotope ratio of evapotranspired waters (see Eq. 21 in Kirchner and Allen, 2020).

• If there is no way to estimate or constrain how δ_Source differs from mean annual δ_Precip, then δ_Source can be assumed to have uncertainties of magnitudes reflecting the seasonal amplitude in δ_Precip (Fig. 18.3).

Assuming δ_Source is always equal to long-term mean δ_Precip can confound interpretations of species or individual-tree differences in Δ_cellulose, even at the same site. Many species and individuals use different water pools in the subsurface (e.g., due to differences in rooting depths). To mitigate inter species uncertainties, where possible, one can:

• Select sites where all species use groundwater or soil waters δ¹⁸O is relatively homogenous (which should involve measuring xylem water δ¹⁸O to document the similarity between species).

• Measure xylem water δ¹⁸O over a growing season to benchmark expected differences between δ_Source and δ_Precip for each species. This assumes that measurements of δ_Precip are available or are also measured.

• Select sites where rooting depth information is available for the species of interest. Insights into the relative rooting depths can be used to understand how δ_Source may differ in time for different trees at the same site (e.g., a tree that uses shallow water exclusively may experience more inter-annual variation in δ_Source than does one that uses deeper soil water with less variation in δ¹⁸O).

• Assume that trees within a single site vary substantially, and the variation is not always attributable to species. The mean within-plot range was 1.8 ‰ for the xylem-water samples in Fig. 18.7. Without some information on δ_Source or rooting depth, it may be impossible to interpret species or individual differences in Δ_cellulose.

5.2 Inferring the Source of Water from Tree Rings Isotope Ratios

Another application of tree-ring δ¹⁸O ratios is identifying the water sources used by trees. Often questions pertain to inferring changes in sources of water to trees (e.g., by depth, or between soil water, stream water and groundwater), across species, climates, landscapes, or time (e.g., (Sargeant et al. 2020; Miller et al. 2006; Sarris et al. 2013; Saurer et al. 2016; Sargeant and Singer 2016). All of these questions require first accounting for the fractionation undergone from source-water to cellulose, a sequence known to vary with meteorological conditions, species, and canopy position (this is the subject of Chaps. 10, 11 and 13); it should also be noted that constraining the leaf-atmosphere exchange fractionation sequence described in Chaps. 10, 11, and 13 also assumes knowledge of the isotopic ratio of ambient atmospheric water vapor, which can be out of equilibrium with local water sources (Fiorella et al. 2019).

After accounting for leaf-level fractionation effects, this application assumes that residual variations in cellulose δ¹⁸O reflect variations in δ_Source. Indeed δ_source can be substantially different between pools: shallow soil waters are often isotopically heavier (than deeper soil water, river water, or groundwater), because they are influenced more by evaporative fractionation, and they are also more likely to be sourced from recent growing season precipitation that is isotopically heavier than winter precipitation in most extra-tropical regions; Fig. 18.3). Alternatively, deeper soils, groundwater, and streamwater tend to be isotopically lighter than shallow soil water because they recharge more in colder seasons or often from higher elevations (Sect. 18.3). However, interpretations of source waters from cellulose need to consider the following possible confounding factors.

First, it needs to be recognized that predicting source water isotope ratios from cellulose requires estimating leaf-water evaporative enrichment and fractionation processes that occur with sugar assimilation. These processes can be uncertain and their effect size can be similar or greater in magnitude than the effects of δ_Source variation (Song et al. 2014). As a starting point to constrain those processes, inter-annual variations in temperature and relative humidity are key data, which can be applied in models to constrain expected inter-annual variability attributable to leaf fractionation processes (Sargeant et al. 2020; Cernusak et al. 2016). These processes (described in Chap. 11–13) must be constrained prior to estimating source waters from cellulose.

Second, inter-annual variations within a water source can confound the ability to separate between the use of different water sources over time. For example, source differentiation will be confounded if (a) the range of isotope ratios in those sources vary among years (e.g., shallow soils are isotopically lighter in years with less summer precipitation because they are not diluted by summer rain’s higher δ_Precip), (b) values of δ_Precip are anomalously high or low in a given year, (c) the growing seasons and thus water uptake seasons differed among years such that the rings reflect larger proportions of uptake during either spring (light, less evaporated) or late summer (heavy, more evaporated). To mitigate uncertainties in interpreting source water signals, where possible, one can:

• Select sites where seasonal and inter-annual isotope variations are smaller, such as lower elevation or more coastal regions, but where the potential sources have large isotopic differences. If the goal is to identify inter-annual differences in use of groundwater relative to soil water, select sites where groundwater is sourced by rain from much higher elevations so that its influence can be clearly distinguished (e.g., Oerter et al. 2019).

• To account for inter-annual cellulose isotopic variations attributable to inter-annual variations in δ_Precip, select regions where inter-annual δ_Precip was measured, or estimate likely ranges of inter-annual δ_Precip to see whether they could explain tree-ring variations.

• To rule out the possibility that inter-annual isotope signatures change because the mixtures of seasonal precipitation in soils, groundwater, or streams are changing, examine inter-seasonal precipitation amount variations (and δ_Precip seasonal amplitude) to see whether their effects on weighted-mean annual δ_Precip are large enough to explain inter-annual variations in ring isotope ratios (e.g., during the calibration period when data are available). These data are more widely available than records of inter-annual variation in δ_Precip.

• To rule out the influence of variations in the radial growth season, use dendrometer records of radial growth phenology to indicate how growing season varies; this issue may not matter if intra-annual (e.g., early-wood versus late-wood) isotope variations are small anyway.

Third, confounding factors in inferring site-and-species differences in source can arise, for example, when (a) comparing across soils or landscapes where water turnover times differ due to storage capacity or climate (e.g., a soil in a very wet region might hold recent precipitation whereas one in a dry site may contain several previous years of precipitation) (b) comparing across soils where infiltration processes differ and include substantial bypass flow (e.g., allowing more recent precipitation to show up lower in soil profiles or in stream or groundwater sources), or (c) species differ in growth and water-uptake seasons such that isotopic differences might reflect trees taking up water from the same pools but at different times. To mitigate uncertainties, where possible, one can:

• Select trees that co-occupy sites (or at least occupying sites with similar climates and soils) to rule out the effects of soils differences in species comparisons.

• Use multi-seasonal xylem water measurements to show that potential sources across sites similarly respond to precipitation inputs and seasonal climate variations, to rule out the possibility that tree-ring isotope variations are due to soil and δ_Precip dynamics, rather than changes in sources used by trees.

And last, confounding factors in inferring intra-annual variations (i.e., from sub-annual slices of cellulose) in sources can arise, for example when (a) water that was enriched due to evaporation from stems over winter (Treydte et al. 2014) is incorporated in early radial growth, (b) sources change isotopically throughout the growing season, confounding estimates of the relative use of each source, (e.g., rain dilutes evaporatively enriched soils resulting in profiles that are inverse to the more typical ones seen in growing seasons; Figs. 18.5 and 18.6). To mitigate uncertainties, where possible, one can:

• Interpret the earliest early-wood isotope values cautiously to avoid misinterpreting the effects of evaporative enrichment throughout the dormant seasons or of stored carbohydrates that contain source information from previous years.

• Unless the potential end-members are consistently very distinct, use a calibrated physical model to account for the source-water dynamics and interactions; these finer scale dynamics should be considered when making finer-resolution inferences from sub-annual isotopic variations.

6 Conclusions

Geographic, vertical, and temporal variations in the isotopic composition of potential water sources to plants should be considered when interpreting tree-ring δ¹⁸O or δ²H. While tree rings provide opportunity for studying these variations, there are many potential confounding factors. When interpreting tree-ring isotope ratios, the relative influences of source water variations versus climate and physiology effects on leaf-water enrichment (Chaps. 10 and 11) should both be considered; there are only few circumstances where spatiotemporal variability in source water isotopic composition can be ignored. There are many reasons why one ring, one tree, or one site may have more enriched δ¹⁸O or δ²H than another, and these could result in confounded interpretations; Table 18.1 demonstrates this challenge by offering a list of hypothetical explanations for heavier-than-normal δ¹⁸O in a ring. Nonetheless, by recognizing the full suite of controlling processes (Sects. 18.2, 18.3, and 18.4), many potential confounding factors can be eliminated when interpreting data (Sect. 18.5). Accounting for source-water isotope variations involves first examining the average and seasonal precipitation inputs to a site (Figs. 18.3 and 18.4), then considering how fast soil–water pools may turnover and how evaporation may affect their isotope ratios (Figs. 18.5, 18.6, 18.7), and last, considering which soil-waters will be taken up by trees (Figs. 18.7 and 18.8). Fortunately, soil–water-transport and plant-uptake dynamics both tend to correspond with climate, allowing source water to be partially predictable and interpretable. Understanding these processes and moving beyond assuming that source-waters isotopic compositions are constant or equal to that of long-term mean precipitation is an important step towards improved interpretation of tree-ring isotope ratios.

Table 18.1 There are many causes for high or low δ¹⁸O in tree rings. Here are many examples of diverse, potentially contrasting ecohydrological explanations for heavier-than-average δ¹⁸O in a single ring—commonly assumed to result from greater leaf water enrichment in drier years (Chap. 10)—demonstrating how the interaction among climate, soil, and tree processes can complicate interpreting tree-ring δ¹⁸O. With knowledge of the system and conditions, many of these alternative hypothetical explanations can be dismissed