Abstract
Many philosophers agree that moral responsibility often includes an epistemic requirement. Inspired by the dictum that ‘ought implies can’, this epistemic perspective induces the requirement that an agent can only be held morally responsible if she knows how to fulfil her subjective obligation yet decided not to. The central theorems of this chapter concern the characterization of both individual and collective know-how. On the one hand, I show that an individual agent knows how to do something if and only if the agent knows that it is possible for her to knowingly do it. Collective know-how, on the other hand, requires common knowledge of an effective division of tasks among the group’s members and of the fact that each member knows how to carry out her part. Accordingly, no communication is needed once the group collectively knows how to achieve some collective goal: if each member knowingly plays her part (which she knows how to do), then the group jointly achieves their collective goal. I explore some connections to the literature on knowledge, action, and ability in philosophy, economics, and artificial intelligence, and analyse the problem of responsibility voids and gaps from the perspective of informational responsibility systems.
The “epistemic condition” corresponds to the excuse of ignorance. It captures the intuition that an agent is responsible only if he both knows the particular facts surrounding his action, and acts with the proper sort of beliefs and intentions.
Fischer and Ravizza (1998, p. 13)
Parts of this chapter draw from (Duijf et al., 2021).
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
For example, Fischer and Ravizza (1998) write: “The first condition, which may be termed the ‘epistemic condition,’ corresponds to the excuse of ignorance. It captures the intuition that an agent is responsible only if he both knows the particular facts surrounding his action, and acts with the proper sort of beliefs and intentions. …The second condition of moral responsibility corresponds to the excuse of force; it pertains not so much to cognitive matters but affective, volitional, and executive features. We shall call the second condition, the ‘freedom-relevant condition,’ or perhaps the ‘control condition.’”
- 2.
Zimmerman (2008, pp. 2, 5, and 19) distinguishes between the objective, subjective and prospective views: “The Objective View (first formulation): An agent ought to perform an act if and only if it is the best option that he (or she) has. …The Subjective View (first and only formulation): An agent ought to perform an act if and only if he believes that it is the best option that he has. …The Prospective View (second formulation): An agent ought to perform an act if and only if it is the prospectively best option that he has.”
- 3.
At the end of Sect. 4.5 I briefly discuss some implications of my theory of collective know-how for cases where agreement is unproblematic and communication is possible.
- 4.
- 5.
Xu (2015) presents an excellent survey on stit theory and its epistemic extensions.
- 6.
In artificial intelligence research such indistinguishability relations are standardly used to represent an agent’s knowledge (see Fagin et al., 2003; Meyer & van der Hoek, 1995). They straightforwardly correspond to partition structures that are commonly employed in game theory and economics to model the information states of the players (see Aumann, 1999).
- 7.
In other words, these models should not be solo, i.e. they should not be based on a single moment (see Sect. 2.4).
- 8.
- 9.
More precisely, this assumption boils down to the following: if m∕h ′∈Act i(m∕h), then m∕h ∼i m∕h ′. Also see the discussion of the own-action condition in Sect. 4.3.2.
- 10.
- 11.
Some comments on the logical system. For those unfamiliar with modal logic, it may be useful to point out that one of the basic results is that the S5 axioms (reflexivity:
 , symmetry:
, symmetry:  , and transitivity:
, and transitivity:  ) jointly correspond to an accessibility relation that is an equivalence relation. Moreover, an equivalence relation corresponds to a partitioning. I refer the reader to the standard textbook treatment of modal logic (Blackburn et al., 2001). The standard interpretation for the knowledge operator is as follows: (i) reflexivity, K
i
φ → φ, requires that knowledge is factive, (ii) transitivity, K
i
φ →K
i
K
i
φ, requires that knowledge is positively introspective, and (iii) euclidity, ¬K
i
φ →K
i¬K
i
φ, requires that knowledge is negatively introspective.
) jointly correspond to an accessibility relation that is an equivalence relation. Moreover, an equivalence relation corresponds to a partitioning. I refer the reader to the standard textbook treatment of modal logic (Blackburn et al., 2001). The standard interpretation for the knowledge operator is as follows: (i) reflexivity, K
i
φ → φ, requires that knowledge is factive, (ii) transitivity, K
i
φ →K
i
K
i
φ, requires that knowledge is positively introspective, and (iii) euclidity, ¬K
i
φ →K
i¬K
i
φ, requires that knowledge is negatively introspective.This axiomatization of common knowledge is from the work of Meyer and van der Hoek (1995). Other axiomatizations of common knowledge rely on an induction rule such as \(\varphi \to \mathsf {E}_{\mathcal {G}}(\varphi \land \psi )\mid \varphi \to \mathsf {C}_{\mathcal {G}}\psi \) (Fagin et al., 2003) or \(\varphi \to \mathsf {E}_{\mathcal {G}}\varphi \mid \mathsf {E}_{\mathcal {G}}\varphi \to \mathsf {C}_{\mathcal {G}}\varphi \) (Lismont, 1993).
- 12.
- 13.
Anscombe (1963, p. 46) answers her question as follows: “In short, the only distinct action of his that is in question is this one, A. For moving his arm up and down with his finger round the pump handle is, in these circumstances, operating the pump; and, in these circumstances, it is replenishing the house water-supply; and, in these circumstances, it is poisoning the household.”
- 14.
This way of answering the question makes me a so-called ‘coarse-grained theorist’. Goldman (1971) is a classic example of the opposite ‘fine-grained theorist’, who, among other things, maintains that the man in the example performs more than one action.
- 15.
This entails that someone who considers the semantical framework as primary will be a coarse-grained theorist, while someone who takes the syntactical framework as primary may be open to the fine-grained theory of action individuation. In traditional stit theory, a semantical fine-grained theory may be formalized by letting Act i(m∕h) be a collection of subsets of moment/history pairs rather than a subset of moment/history pairs. In fact, in stit theory Broersen (2009) pioneered this way of modelling strategic action: a strategy is equated with the set of histories compatible with it; and a certain history may be compatible with multiple strategies.
- 16.
- 17.
- 18.
On my view, this issue is connected to the literature on grounding (see the SEP entry by Bliss & Trogdon, 2016). Epstein (2015) gives a uniform framework for modelling all these senses of grounding. He convincingly shows that all these senses may be modelled as a necessary implication, although they may vary in the types of facts that ground this relation, for instance, some are grounded in frame conditions, others in model properties.
- 19.
Compare Wilson (1989), who presents a teleological account of intentionality, where ‘agent iψ’d in order to φ’ is analysed as ‘agent iψ’d because he wanted to φ and believed that By(ψ, φ)’.
- 20.
Note the important difference with both
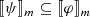 and
and  . The former drops the [i s
t
i
t]-operator and therefore misses the fact that the by-relation applies to act descriptions. The latter expresses a global by-relation rather than a local by-relation, that is, it says that whenever agent i sees to it that ψ then she sees to it that φ rather than at the current moment if agent i sees to it that ψ then she sees to it that φ.
. The former drops the [i s
t
i
t]-operator and therefore misses the fact that the by-relation applies to act descriptions. The latter expresses a global by-relation rather than a local by-relation, that is, it says that whenever agent i sees to it that ψ then she sees to it that φ rather than at the current moment if agent i sees to it that ψ then she sees to it that φ. - 21.
Note that the syntactical counterparts of
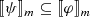 and
and  , mentioned in the previous footnote, are
, mentioned in the previous footnote, are  and
and  , respectively.
, respectively. - 22.
- 23.
I would like to thank an anonymous reviewer for bringing this issue to my attention.
- 24.
- 25.
These, and further, correspondences can be algorithmically checked using the SQEMA algorithm (Conradie et al., 2006).
Broersen (2011, Propositions 3.1 and 3.2) uses a stit logic about affecting next states, so-called Xstit, to model knowingly doing and discusses two additional properties: (i) knowledge about next states, which expresses that “agents cannot know more about next states than what is affected by the choices they have” (p. 145) and (ii) effect recollection, which expresses that “the effects of an action that is knowingly performed are known in the next state” (p. 145—it is a dynamic version of perfect recall).
- 26.
An elaborate discussion of my worries has to be postponed to another occasion.
- 27.
- 28.
It is questionable whether this property also holds under the assumption of common knowledge of rationality, which is standardly assumed in game theory. Under this assumption, it seems appropriate to say that an agent knows that her opponents are avoiding a ridiculous, yet possible, action. This would mean that she considers it impossible that her current action is compatible with such ridiculous actions of her opponents yet it is (historically) possible that her opponents perform these actions.
- 29.
This follows from the fact that
 is an S5 operator and K
i is a normal operator.
is an S5 operator and K
i is a normal operator. - 30.
See my joint work (Duijf et al., 2021) for more discussion on the uniformity of historical possibility property and, in particular, its relation to, what we called, the condition of uniformity of available action types.
- 31.
- 32.
It is certainly not my objective to give a thorough analysis of ability and all its complexities. Some think that knowing-how is merely a kind of ability, and my investigation of knowing-how proves a similar point.
- 33.
In line with the convention that her information sets can be viewed as unions of her action tokens, Fig. 4.3 does not show any dashed lines.
- 34.
In fact, the model shows that there are several distinct ways for Bob to pick a spade. After all,
 while \(m/h_{1}\vDash \lnot \Diamond (q_{\spadesuit A}\land q_{\spadesuit K})\).
while \(m/h_{1}\vDash \lnot \Diamond (q_{\spadesuit A}\land q_{\spadesuit K})\). - 35.
Unfortunately, this existential quantification cannot be captured in the current logic. This means that the concept of individual know-how is not straightforwardly characterizable in the current logic. Nevertheless, this section concludes with a central theorem that shows that individual know-how can be characterized.
- 36.
Compare Carr (1979, p. 402—notation adapted): “On the ‘bring about’ analysis of action descriptions our ability and knowing how contexts now expand as follows:
-
i is able to bring it about that φ.
-
i knows how to bring it about that φ.
It transpires on this analysis that the logical form suggested earlier, of sentences about knowing how and ability, was only the apparent form, for such sentences are really instances of one modal construction buried within another. Ability and know-how are thus seen to be concepts of third level (like e.g. the ‘know’ of self-knowledge, as it occurs in sentences like ‘i knows that he knows that φ’).” Accordingly, my notion of know-how would be a concept of fifth level.
-
- 37.
As an anonymous reviewer has pointed out, it is plausible to think that the problem of irrelevance arises for my analysis because we expect that the agent in question is also aware of the formal language or can use it to describe their actions. I believe, however, that adding awareness will not address the problem of irrelevance. To see why, let’s reconsider the example: Yuri knows how to ride his bike by riding his bike and talking to his friend. This is insufficient to conclude that Yuri explicitly knows how to ride his bike, since his talking is irrelevant to his riding. Could awareness address this problem? I think not. After all, since it is plausible that Yuri is aware of all the details mentioned in the example, he is aware that he can ride his bike by riding his bike and talking to his friend. In short: awareness of a proper refinement is insufficient for the relevance of that refinement. If this is correct, then it seems like adding awareness will not address the problem of irrelevance.
- 38.
- 39.
Lorini et al. (2014, p. 1314) write: “Each type of knowledge is defined with respect to the time of the agent’s choice: before one’s choice (ex ante knowledge), after one’s choice but before knowing the choices of others (interim knowledge), and after the choices of all agents have been made public (ex post knowledge).” Compare Horty and Pacuit (2017, pp. 31–32): “an agent’s ex ante knowledge is the information available to the agent without taking into account any actions she is currently executing, while the agent’s ex interim knowledge is information that does take into account whatever actions the agent is currently executing, along with the effects of these actions”.
- 40.
Lorini et al. (2014, Sect. 2.2.2) model agent i’s ex ante, interim, and ex post knowledge using accessibility relations \(\mathcal {E}_{i}^{\bullet \circ \circ }\), \(\mathcal {E}_{i}^{\circ \bullet \circ }\), and \(\mathcal {E}_{i}^{\circ \circ \bullet }\), respectively. The idea that these are refinements is expressed by the inclusions \(\mathcal {E}_{i}^{\bullet \circ \circ }\supseteq \mathcal {E}_{i}^{\circ \bullet \circ }\supseteq \mathcal {E}_{i}^{\circ \circ \bullet }\).
- 41.
The assumption that ex post knowledge refines ex ante knowledge is standardly referred to as ‘perfect recall’.
- 42.
Aumann (1987, p. 8) writes: “Of course, a player always knows which decision he himself takes.”
- 43.
It seems that Aumann had games of perfect information in mind, a term that became standard only after, and perhaps because of, his seminal works were published. A contemporary game theorist would reply to my worries expressed in the face-down deck of cards example by saying that the example is best modelled as a game of imperfect information. In games of imperfect information, an epistemic sense of ability is typically modelled using action types, rather than actions. We will discuss connections to action types shortly.
- 44.
Compare Horty and Pacuit (2017, p. 34—notation adapted): “if the agent has ex interim knowledge that φ no matter which of her available actions she happens to execute, this entails that she must have ex ante knowledge that φ”.
- 45.
The distributed knowledge of a group, say \(\mathcal {G}\), is typically modelled by a derived indistinguishability relation \(\sim ^{\mathsf {D}}_{\mathcal {G}}:=\bigcap _{i\in \mathcal {G}} \sim _{i}\). The evaluation rule is as follows: \(\mathcal {M},m/h\vDash \mathsf {D}_{\mathcal {G}}\varphi \) if and only if for all m ′∕h ′ satisfying \(m/h \sim ^{\mathsf {D}}_{\mathcal {G}} m^{\prime }/h^{\prime }\) it holds that \(\mathcal {M},m^{\prime }/h^{\prime }\vDash \varphi \). (Which is equivalent to requiring that for all m ′∕h ′ satisfying m∕h ∼i m ′∕h ′, for every \(i\in \mathcal {G}\), it holds that \(\mathcal {M},m^{\prime }/h^{\prime }\vDash \varphi \).)
- 46.
This is unproblematic since the game-theoretical interpretation is also not settled: “At one extreme is the ex ante stage where no decision has been made yet. The other extreme is the ex post stage where the choices of all players are openly disclosed. In between these two extremes is the ex interim stage where the players have made their decisions, but they are still uninformed about the decisions and intentions of the other players. These distinctions are not intended to be sharp. Rather, they describe various stages of information disclosure during the decision-making process” (Pacuit & Roy, 2017).
- 47.
These are sometimes called paths or computations (for example, see van der Hoek & Wooldridge, 2003).
- 48.
The analysis of epistemic abilities by Horty and Pacuit (2017) is very similar to the analysis of knowing-how by Herzig and Troquard (2006, p. 214). The latter also use operators of the form [i k s t i t]φ to express a sense of epistemic agency, where the truth conditions are spelled out using action types. Moreover, they propose to use formulas of the form ♢[i k s t i t]φ to express that agent i knows how to φ. The main difference is the following: instead of introducing action labels into stit theory (Horty & Pacuit, 2017), Herzig and Troquard (2006, p. 214) introduce an indistinguishability relation, called R UC, where “\(R_{UC_{i}}\) is the relation between indexes of identical choices lying in moments indistinguishable by agent i.”
- 49.
This equivalence also holds in the formalism of Herzig and Troquard (2006).
- 50.
- 51.
Broersen et al. (2006) show that ATL can be embedded into stit theory. The central coalitional strategic ability operator of ATL, expressed by \(\langle \langle \mathcal {G}\rangle \rangle \varphi \), corresponds to the strategic stit formula \(\Diamond [\mathcal {G}\;\mathsf {sstit}]\varphi \). (Where \([\mathcal {G}\;\mathsf {sstit}]\) is a strategic stit operator, rather than the stit operator used in this book.)
- 52.
Broersen (2011) mistakenly thinks that this formula captures the intuition of uniform strategies. This is false because an agent may know that it is possible that she ensures that she picks an ace of spades from a face-down deck of cards (K i♢[i s t i t]q ♠A holds), even though she does not know that it is possible for her to knowingly pick an ace of spades (she lacks a uniform strategy to ensure q ♠A). See the discussion surrounding Observation 4.2.
- 53.
This corresponds to the discussion of Herzig and Troquard (2006), more specifically Hypothesis 3 on page 212 and Property 2 on page 214.
- 54.
For more details and a more elaborate discussion, see (Duijf et al., 2021, Sect. 5.2).
- 55.
Horty and Pacuit (2017) argue that stit models need to be extended with action types to address certain puzzles about knowledge and action. I believe their argument is misguided due to their persistence that the indistinguishability relations are on moments. Engaging in this debate and working out the details would lead me too far astray.
- 56.
The debates usually depict two strands of anti-intellectualism: weak, which denies intellectualism, and strong, which embraces the prioricity of knowing-how over knowing-that.
- 57.
It is important to recognize that such a reduction should not be given by stipulation. It is hence important to see that my definition of knowing-how does not presuppose such a reduction (Definition 4.5). After all, the semantics of knowing-how include an existential quantification over ψ and this quantification is beyond the scope of the knowing-that operator.
- 58.
One’s take on propositional knowledge may affect one’s position in the intellectualism debate. For instance, Fantl (2008, pp. 452–453) argues that “[s]trong anti-intellectualism is most plausible if knowing that something is the case is essentially dispositional …But if knowing that something is the case is not essentially dispositional, then it seems rather implausible for knowing-that to be reduced to or a species of knowing-how”.
- 59.
Although David Carr so far agrees with my analysis, he eventually writes: “It appears to be the case that knowing how statements require as their objects, descriptions of actions construed in a much more sophisticated way [than descriptions of actions understood merely as instances of bringing about or agent-causation], as, in fact, intentional actions” (Carr, 1979, p. 409—emphasis added).
- 60.
Compare Glick (2011, p. 413—notation adapted): “Take, for instance, abilities. For any action of φ-ing, we could map i’s ability to φ onto the proposition that iφs, and instead of saying that i is able to φ, we could say that i ‘ables that he φs’. If we had this linguistic convention, we might note that ‘abling’ is a relation to a proposition, but of course, by hypothesis, we would be talking about the same thing we actually talk about with ability attributions.”
- 61.
Compare Stanley (2011, p. vii): “If it is surprising that knowledge of a fact can so immediately yield knowledge of how to swim, ride a bicycle, or play a piano, it is only so because of false assumptions about what it is to know a fact. …There are false assumptions about what it is to act on knowledge of facts, there are false assumptions about what it is to have knowledge of facts, and there are false assumptions about the nature of facts.”
- 62.
Fodor (1968, p. 634) famously writes: “Certain of the anti-intellectualist arguments fail to go through because they confuse knowing that with being able to explain how.”
- 63.
Searle (1990, p. 410) writes: “I believe one of the keys to understanding collective intentionality is to see that in general the by and by-means-of relations for achieving the collective goal have to end in individual actions.” My discussion of collective know-how, in terms of action hierarchies, relies on a similar intuition.
- 64.
Note that Chris’s and Dee’s individual situation is similar to that of Bob, which is depicted in Fig. 4.3.
- 65.
Note that in the previous example of Ann and Bob, the first property holds. The problem with that example is that it violates the second property.
- 66.
Although it is a rather artificial example, it will point to a natural concern: even though my companion’s implicit practical knowledge is opaque to me, this need not undermine our collective practical knowledge. The artificial example is meant to isolate this particular concern.
- 67.
Recall the conventions that the information sets can be viewed as unions of action tokens and that the indistinguishability relation is closed under transitivity.
- 68.
It may be helpful to point out that I will present a hierarchical task network that represents these levels in Sect. 4.6.1.
- 69.
It is important to note that this existential quantification cannot be captured in the current logic. This means that collective know-how is not straightforwardly characterizable in the current logic. In the remainder of this section it will be shown that, under the assumption that (Unif-H) holds, collective know-how is characterizable.
- 70.
- 71.
Note that Chris’s and Dee’s individual situation is similar to that of Bob, which is represented in Fig. 4.3.
- 72.
Although Chris and Dee are not able to solve their coordination game without prior communication, people are often quite effective at solving such coordination problems. Game theorists typically argue that concepts such as salience, focal points, and framing are key to understanding the coordination abilities of non-communicating agents (see Bacharach, 2006; Gauthier, 1975; Lewis, 1969; Schelling, 1960; Sugden, 1993, 1995, 2003). My notion of collective know-how is best viewed as the ability of a group of non-communicating agents that does not rely on such additional concepts.
- 73.
It is unclear how ATL-based paradigms deal with this difficulty (Ågotnes et al., 2015; Jamroga & Ågotnes, 2007; with the possible exception of Hawke, 2017). I believe that this lacuna is an artefact of the fact that these formalisms only mention two levels: the goal φ and a (maximally specific) strategy s.
- 74.
- 75.
- 76.
To be precise, (Unif-H) is used to prove (∗∗) below.
- 77.
Other subfields include conformant planning, (partially observable) Markov decision processes, and multi-agent planning.
- 78.
STRIPS, short for STanford Research Institute Problem Solver, is a problem-solving program that has been designed “to find some composition of operators that transforms a given initial world model into one that satisfies some stated goal condition” (Fikes & Nilsson, 1971). One particular formalism that has been widely used to represent hierarchical task networks is TAEMS (Decker, 1995; Horling et al., 1999).
- 79.
Compare Shoham (1993, p. 52): “Most often, when people in AI use the term ‘agent’, they refer to an entity that functions continuously and autonomously in an environment in which other processes take place and other agents exist. This is perhaps the only property that is assumed uniformly by those in AI who use the term. The sense of ‘autonomy’ is not precise, but the term is taken to mean that the agents’ activities do not require constant human guidance or intervention.”
- 80.
- 81.
Shoham (1993, p. 52) writes: “An agent is an entity whose state is viewed as consisting of mental components such as beliefs, capabilities, choices, and commitments. These components are defined in a precise fashion, and stand in rough correspondence to their common sense counterparts. In this view, therefore, agenthood is in the mind of the programmer: What makes any hardware or software component an agent is precisely the fact that one has chosen to analyse and control it in these mental terms.”
- 82.
‘BDI’ stands for ‘beliefs, desires, and intentions’.
- 83.
These should not be conflated with obligations regarding the epistemic state of the agent, which are guided by epistemic norms, such as belief consistency.
- 84.
The ‘ought implies can’ principle has often been ascribed to Immanuel Kant, although this attribution is debated. Vranas (2007) gives a defence of the principle, and writes: “I understand the claim that an agent can do something as the claim that the agent has both the ability and the opportunity to do the thing. The agent has the ability to do the thing in the sense of having the requisite skills, physical capacities, and knowledge” (p. 169).
- 85.
Horty (2019) and Ramírez Abarca and Broersen (2019a, 2019b) present a detailed account of subjective obligations for individual agents within stit theory. The main difference between these two formalisms is that the former relies on action types, whereas the latter does not. The latter also presents a complete logical system of objective and subjective obligations.
- 86.
Kolodny and MacFarlane (2010) take the example from Parfit (1988) who in turn credits Regan (1980, p. 265).
Regan (1980, p. 265) can be taken to say that if we assign equal subjective probabilities to the fact that the miners are trapped in shaft A rather than B, then act-utilitarianism requires us to block neither shaft, even though blocking neither shaft cannot possibly be the best act in the circumstances, given the actual location of the miners. Wherever the miners are located, there is an act which is preferable to blocking neither shaft. Regan (1980, p. 265—terminology adapted) concludes: “Still a reasonable approach to the [miners’] problem requires [us] to abandon all hope of producing the best consequences possible.”
- 87.
Although the obligations expressed in 1–5 take ‘we’ as a subject, these obligations depict a general individual agent rather than a collective agent.
- 88.
Kolodny and MacFarlane (2010, p. 116), in contrast, argue that “the best way to resolve the paradox is to give a semantics for deontic modals and indicative conditionals that lets us see how the argument can be invalid even with its obvious logical form”.
- 89.
Note that, given that the agent does not know the location of the miners, this means that she knowingly blocks shaft A even if it turns out that the miners are located in shaft B. It may help to indicate that the agent does not know how to block shaft A only if the miners are in shaft A.
- 90.
- 91.
Ultimately, it seems plausible that the subjective obligations depend on the morally right risk attitude: (I) if she ought to be risk-averse, then she could be obliged to knowingly block neither shaft, (II) if she ought to be risk-seeking, then she could be obliged to knowingly block one of the shafts, or (III) if she ought to be risk-neutral, then she could be obliged to knowingly do anything.
- 92.
Note that not knowingly carrying out her part is consistent with carrying out her part unknowingly.
- 93.
Causality has been a thorny issue in philosophy. For my current purposes, it is sufficient to assume that when an agent sees to it that φ, then she causes it.
- 94.
The stit model relates to what Tamminga and Duijf (2017) call a cooperation game.
- 95.
The details of our discussions differ substantially. Their framework includes subjective probabilities, relies on the NESS condition (which stands for ‘Necessary Element of a Sufficient Set’) to assess causal connections, and includes eligible options. Mine, in contrast, is non-probabilistic, relies on control (or α-effectivity) to assess causal connections, and does not include the eligibility of the available options.
- 96.
It remains to be studied whether these reasons justify the member’s divergence and thereby alleviate her individual blameworthiness.
References
Ågotnes, T., Goranko, V., Jamroga, W., & Wooldridge, M. (2015). Knowledge and ability. In H. van Ditmarsch, J. Y. Halpern, W. van der Hoek, & B. Kooi (Eds.), Handbook of epistemic logic (pp. 543–589). London: College Publications.
Ågotnes, T., & Wáng, Y. N. (2016). Resolving distributed knowledge. In R. Ramanujam (Ed.), Proceedings of the Fifteenth Conference on Theoretical Aspects of Rationality and Knowledge (pp. 37–46).
Alur, R., Henzinger, T. A., & Kupferman, O. (2002). Alternating-time temporal logic. Journal of the ACM, 49(5), 672–713.
Anscombe, G. E. M. (1963). Intention. Cambridge: Harvard University Press.
Aumann, R. J. (1987). Correlated equilibrium as an expression of Bayesian rationality. Econometrica, 55(1), 1–18.
Aumann, R. J. (1999). Interactive epistemology I: Knowledge. International Journal of Game Theory, 28(3), 263–300.
Aumann, R. J., & Dreze, J. H. (2008). Rational expectations in games. The American Economic Review, 98(1), 72–86.
Bacharach, M. (2006). Beyond Individual choice: Teams and frames in game theory, N. Gold & R. Sugden (Eds.). Princeton: Princeton University Press.
Blackburn, P., De Rijke, M., & Venema, Y. (2001). Modal logic. Cambridge: Cambridge University Press.
Bliss, R., & Trogdon, K. (2016). Metaphysical grounding. In E. N. Zalta (Ed.), The stanford encyclopedia of philosophy.
Braham, M., & M. van Hees (2012). An anatomy of moral responsibility. Mind, 121(483), 601–634.
Bratman, M. E. (2014). Shared agency: A planning theory of acting together. Oxford: Oxford University Press.
Broersen, J. (2009). A stit-logic for extensive form group strategies. In P. Boldi, G. Vizzari, G. Pasi, & R. Baeza-Yates (Eds.), Proceedings of the International Joint Conference on Web Intelligence and Intelligent Agent Technology (Vol. 3, pp. 484–487). Washington: IEEE Computer Society.
Broersen, J. (2011). Deontic epistemic stit logic distinguishing modes of mens rea. Journal of Applied Logic, 9(2), 137–152.
Broersen, J., & Herzig, A. (2015). Using STIT theory to talk about strategies. In J. van Benthem, S. Ghosh, & R. Verbrugge (Eds.), Models of strategic reasoning (pp. 137–173). Springer.
Broersen, J., Herzig, A., & Troquard, N. (2006). Embedding alternating-time temporal logic in strategic logic of agency. Journal of Logic and Computation, 16(5), 559–578.
Broersen, J., Herzig, A., & Troquard, N. (2007). A normal simulation of coalition logic and an epistemic extension. In D. Samet (Ed.), Proceedings of the Eleventh Conference on Theoretical Aspects of Rationality and Knowledge (pp. 92–101). ACM.
Brown, M. A. (1988). On the logic of ability. Journal of Philosophical Logic, 17(1), 1–26.
Carnielli, W., & Coniglio, M. E. (2020). Combining logics. In E. N. Zalta (Ed.), The Stanford Encyclopedia of Philosophy (Fall 2020 ed.). Metaphysics Research Lab, Stanford University.
Carr, D. (1979). The logic of knowing how and ability. Mind, 88(351), 394–409.
Cohen, P. R., & Levesque, H. J. (1990). Intention is choice with commitment. Artificial Intelligence, 42(2), 213–261.
Conradie, W., Goranko, V., & Vakarelov, D. (2006). Algorithmic correspondence and completeness in modal logic. I. The core algorithm SQEMA. Logical Methods in Computer Science, 2(1), 1–26.
Davidson, D. (1963). Actions, reasons, and causes. The Journal of Philosophy, 60(23), 685–700.
Davidson, D. (1980). Essays on actions and events. Oxford: Clarendon Press.
Decker, K. S. (1995). Environment centered analysis and design of coordination mechanisms. PhD Thesis, University of Massachusetts.
Duijf, H. (2015). Performing conditional strategies in strategic STIT theory. In M. Kaeshammer & P. Schulz (Eds.), Proceedings of the ESSLLI 2015 Student Session (pp. 13–24).
Duijf, H., & J. Broersen (2016). Representing strategies. In A. Lomuscio & M. Y. Vardi (Eds.), Proceedings of the Fourth International Workshop on Strategic Reasoning, Volume 218 of Electronic Proceedings in Theoretical Computer Science (pp. 15–26). Open Publishing Association.
Duijf, H., Broersen, J., Kuncová, A., & Ramírez Abarca, A. I. (2021). Doing without action types. The Review of Symbolic Logic, 14(2), 380–410.
Duijf, H., Broersen, J., & Meyer, J.-J. C. (2019). Conflicting intentions: Rectifying the consistency requirements. Philosophical Studies, 176(4), 1097–1118.
Elgesem, D. (1993). Action theory and modal logic. PhD Thesis, University of Oslo.
Epstein, B. (2015). The ant trap: Rebuilding the foundations of the social sciences. New York: Oxford University Press.
Fagin, R., Moses, Y., Vardi, M. Y., & Halpern, J. Y. (2003). Reasoning about knowledge. Cambridge: MIT Press.
Fantl, J. (2008). Knowing-how and knowing-that. Philosophy Compass, 3(3), 451–470.
Feinberg, J. (1970). Doing and deserving: Essays in the theory of responsibility. Princeton: Princeton University Press.
Fikes, R. E., & N. J. Nilsson (1971). STRIPS: A new approach to the application of theorem proving to problem solving. Artificial Intelligence, 2(3), 189–208.
Fischer, J. M., & M. Ravizza (1998). Responsibility and control: A theory of moral responsibility. Cambridge: Cambridge University Press.
Fodor, J. A. (1968). The appeal to tacit knowledge in psychological explanation. The Journal of Philosophy, 65(20), 627–640.
Gauthier, D. (1975). Coordination. Dialogue, 14(2), 195–221.
Ghallab, M., Nau, D., & Traverso, P. (2004). Automated planning: Theory and practice. Amsterdam: Elsevier.
Ginet, C. (2000). The epistemic requirements for moral responsibility. Philosophical Perspectives, 14, 267–277.
Glick, E. (2011). Two methodologies for evaluating intellectualism. Philosophy and Phenomenological Research, 83(2), 398–434.
Goldman, A. I. (1971). The individuation of action. The Journal of Philosophy, 68(21), 761–774.
Hawke, P. (2017). The logic of joint ability in two-player tacit games. The Review of Symbolic Logic, 10(3), 481–508.
Herzig, A., & F. Schwarzentruber (2008). Properties of logics of individual and group agency. In C. Areces & R. Goldblatt (Eds.), The Seventh Conference on Advances in Modal Logic (pp. 133–149). College Publications.
Herzig, A., & N. Troquard (2006). Knowing how to play: Uniform choices in logics of agency. In P. Stone & G. Weiss (Eds.), Proceedings of the Fifth International Conference on Autonomous Agents and Multiagent Systems (pp. 209–216). ACM.
van der Hoek, W., & M. Wooldridge (2003). Cooperation, knowledge, and time: Alternating-time temporal epistemic logic and its applications. Studia Logica, 75(1), 125–157.
Horling, B., Lesser, V., Vincent, R., Wagner, T., Raja, A., Zhang, S., Decker, K., & Garvey, A. (1999). The TAEMS white paper. Unpublished manuscript.
Horty, J. F. (2019). Epistemic oughts in stit semantics. Ergo, 6(20191108), 71–120.
Horty, J. F., & N. Belnap (1995). The deliberative stit: A study of action, omission, ability, and obligation. Journal of Philosophical Logic, 24(6), 583–644.
Horty, J. F., & Pacuit, E. (2017). Action types in stit semantics. The Review of Symbolic Logic, 10(4), 617–637.
Jamroga, W., & Ågotnes, T. (2007). Constructive knowledge: What agents can achieve under imperfect information. Journal of Applied Non-Classical Logics, 17(4).
Jamroga, W., & van der Hoek, W. (2004). Agents that know how to play. Fundamenta Informaticae, 63(2-3), 185–220.
Jennings, N. R. (2000). On agent-based software engineering. Artificial Intelligence, 117(2), 277–296.
Kolodny, N., & MacFarlane, J. (2010). Ifs and oughts. The Journal of Philosophy, 107(3), 115–143.
Kuncová, A., Broersen, J., Duijf, H., & Ramírez Abarca, A. I. (manuscript). Ability and knowledge: Stit theory and transition systems. Unpublished manuscript.
Lewis, D. K. (1969). Convention: A philosophical study. Cambridge: Harvard University Press.
Lismont, L. (1993). La connaissance commune en logique modale. Mathematical Logic Quarterly, 39(1), 115–130.
Lorini, E., Longin, D., & Mayor, E. (2014). A logical analysis of responsibility attribution: Emotions, individuals and collectives. Journal of Logic and Computation, 24(6), 1313–1339.
Markoff, J. (2011). Computer wins on ‘Jeopardy!’: Trivial, it’s not. The New York Times.
McNamara, P. (2019). Toward a systematization of logics for monadic and dyadic agency & ability, revisited. Filosofiska Notiser, 6(1), 157–188.
Metz, C. (2016). Google’s AI wins fifth and final game against Go genius Lee Sedol. WIRED.
Metz, C. (2017). A mystery AI just crushed the best human players at poker. WIRED.
Meyer, J.-J. C., & van der Hoek, W. (1995). Epistemic logic for AI and computer science. New York: Cambridge University Press.
Pacuit, E., & Roy, O. (2017). Epistemic foundations of game theory. In E. N. Zalta (Ed.), The stanford encyclopedia of philosophy (Summer 2017 ed.).
Parfit, D. (1988). What we together do. Unpublished manuscript.
Payette, G. (2014). Decidability of an xstit logic. Studia Logica, 102(3), 577–607.
Ramírez Abarca, A. I., & Broersen, J. (2019a). A logic of objective and subjective oughts. In F. Calimeri, N. Leone, & M. Manna (Eds.), Logics in artificial Intelligence. Lecture notes in computer science (pp. 629–641). Cham: Springer International Publishing.
Ramírez Abarca, A. I., & Broersen, J. (2019b). A logic of objective and subjective oughts (full paper with proofs). https://arxiv.org/abs/1903.10577. Unpublished manuscript.
Rao, A. S., & Georgeff, M. P. (1991). Modeling rational agents within a BDI-architecture. In J. Allen, R. Fikes, & E. Sandewall (Eds.), Proceedings of the Second International Conference on Principles of Knowledge Representation and Reasoning (Vol. 91, pp. 473–484). Morgan Kaufmann.
Regan, D. (1980). Utilitarianism and co-operation. New York: Oxford University Press.
Russell, S., & Norvig, P. (1995). Artificial intelligence: A modern approach. Englewood Cliffs: Prentice Hall.
Ryle, G. (1949). The concept of mind. London: Hutchinson.
Schelling, T. C. (1960). The strategy of conflict. Cambridge: Harvard University Press.
Schobbens, P.-Y. (2004). Alternating-time logic with imperfect recall. In W. van der Hoek, A. Lomuscio, E. de Vink, & M. Wooldridge (Eds.), Logic and communication in multi-agent systems (Vol. 85, pp. 82–93). Elsevier.
Searle, J. (1990). Collective intentions and actions. In P. R. Cohen, J. Morgan, & M. E. Pollack (Eds.), Intentions in communication (pp. 401–415). Cambridge: MIT Press.
Shoham, Y. (1993). Agent-oriented programming. Artificial Intelligence, 60(1), 51–92.
Stanley, J. (2011). Know how. Oxford: Oxford University Press.
Stanley, J., & Williamson, T. (2001). Knowing how. The Journal of Philosophy, 98(8), 411–444.
Sugden, R. (1993). Thinking as a team: Towards an explanation of nonselfish behavior. Social Philosophy and Policy, 10(1), 69–89.
Sugden, R. (1995). A theory of focal points. The Economic Journal, 105(430), 533–550.
Sugden, R. (2003). The logic of team reasoning. Philosophical Explorations, 6(3), 165–181.
Tamminga, A., & Duijf, H. (2017). Collective obligations, group plans and individual actions. Economics & Philosophy, 33(2), 187–214.
Vranas, P. B. M. (2007). I ought, therefore I can. Philosophical Studies, 136(2), 167–216.
Wang, Y. (2018). A logic of goal-directed knowing how. Synthese, 195(10), 4419–4439.
Wikipedia Contributors (2017). Automated planning and scheduling. https://en.wikipedia.org/w/index.php?title=Automated_planning_and_scheduling
Wilson, G. M. (1989). The intentionality of human action. Stanford: Stanford University Press.
Wooldridge, M. (1997). Agent-based software engineering. IEE Proceedings Software Engineering, 144(1), 26–37.
Wooldridge, M., & Jennings, N. R. (1995). Intelligent agents: Theory and practice. The Knowledge Engineering Review, 10(2), 115–152.
Xu, M. (2015). Combinations of stit with ought and know. Journal of Philosophical Logic, 44(6), 851–877.
Yu, E. (2001). Agent orientation as a modelling paradigm. Wirtschaftsinformatik, 43(2), 123–132.
Zimmerman, M. J. (1997). Moral responsibility and ignorance. Ethics, 107(3), 410–426.
Zimmerman, M. J. (2008). Living with uncertainty: The moral significance of ignorance. Cambridge: Cambridge University Press.
Author information
Authors and Affiliations
Appendices
Appendix C: Guilty Minds and Collective Know-how
C.1 Epistemic Stit Theory
Theorem 4.1 (Completeness Epistemic Stit)
The following axiom schemas, in combination with a standard axiomatization for propositional logic, and the standard rules ( such as necessitation)for the normal modal operators, provide a complete Hilbert system for the validities on epistemic stit models:
(S5 Historical Necessity) | S5 for |
(S5 Agency) | for each group \(\mathcal {G}\): S5 for \([\mathcal {G}\;\mathsf {stit}]\) |
(Agent Monotonicity) | for all groups \(\mathcal {F}\) and \(\mathcal {G}\) satisfying \(\mathcal {F}\subseteq \mathcal {G}\): \([\mathcal {F}\;\mathsf {stit}] \varphi \to [\mathcal {G}\;\mathsf {stit}] \varphi \) |
(Independence of Agency) | for all groups \(\mathcal {F}\) and \(\mathcal {G}\) satisfying \(\mathcal {F}\cap \mathcal {G}=\emptyset \): \(\Diamond [\mathcal {F}\;\mathsf {stit}] \varphi \wedge \Diamond [\mathcal {G}\;\mathsf {stit}] \psi \to \Diamond ([\mathcal {F}\;\mathsf {stit}] \varphi \wedge [\mathcal {G}\;\mathsf {stit}] \psi )\) |
(S5 Knowledge) | for each i ∈Ags: S5 for K i |
(Public Knowledge) | for each group \(\mathcal {G}\): \(\mathsf {C}_{\mathcal {G}}\varphi \to (\varphi \land \mathsf {E}_{\mathcal {G}}\mathsf {C}_{\mathcal {G}}\varphi )\) |
(Induction) | for each group \(\mathcal {G}\): \(\varphi \land \mathsf {C}_{\mathcal {G}}(\varphi \to \mathsf {E}_{\mathcal {G}}\varphi ) \to \mathsf {C}_{\mathcal {G}}\varphi \) |
Proof (Sketch)
The epistemic stit logic is a so-called fusion of epistemic logic and non-epistemic stit theory. The complete logical system for epistemic stit theory is therefore given by the simple combination of the logical systems for epistemic logic and (non-epistemic) stit logic (see Carnielli & Coniglio, 2020, Sect. 4.1).
It is well-established that the non-epistemic fragment is complete with respect to stit models, for instance, by using Sahlqvist correspondence (see the standard textbook treatment of Blackburn et al. (2001)). The completeness of the epistemic logic is standard (see, e.g. Meyer & van der Hoek, 1995). (Broersen, 2011, Theorem 2.1 proves a similar result for Xstit, the difference is that his logic concerns Xstit and excludes common knowledge.)□
C.2 Individual Practical Knowledge
Proposition 4.1
- (OAC):
-
The own-action condition , schematically expressed by K i φ →K i[i s t i t]φ, corresponds to the condition:
For all indices m∕h, \(m^{\prime }/h^{\prime }_1\) , and \(m^{\prime }/h^{\prime }_2\) , if \(m/h\sim _i m^{\prime }/h^{\prime }_1\) and \(h^{\prime }_2\in \mathit {Act}_{i}(m^{\prime }/h^{\prime }_1)\) then \(m/h\sim _i m^{\prime }/h^{\prime }_2\).
- (Unif-H):
-
The uniformity of historical possibility property , schematically expressed by ♢K i φ →K i♢φ, corresponds to the confluency condition:
For all indices m∕h 1 , m∕h 2 , and \(m^{\prime }/h^{\prime }_1\) , if \(m/h_1\sim _i m^{\prime }/h^{\prime }_1\) then there is an index \(m^{\prime }/h^{\prime }_2\) such that \(m/h_2\sim _i m^{\prime }/h^{\prime }_2\).
Proof
These correspondences can be checked using the algorithm SQEMA (Conradie et al., 2006).□
Theorem 4.2 (Impossibility Results)
Implicit individual know-how and explicit individual know-how cannot be characterized in the current logic:
-
1.
Given an agent i and a formula φ, there is noformula ψ such that for every model \(\mathcal {M}\) and every index m∕h it holds that, relative to m∕h, agent i implicitlyknows how to φ if and only if \(\mathcal {M},m/h\vDash \psi \).
-
2.
Given an agent i and a formula φ, there is noformula ψ such that for every model \(\mathcal {M}\) and every index m∕h it holds that, relative to m∕h, agent i explicitlyknows how to φ if and only if \(\mathcal {M},m/h\vDash \psi \).
Proof
Implicit individual know-how would be characterizable in \(\mathfrak {L}_{\mathit {estit}}\) if and only if, given an agent i ∈Ags and a formula φ, there is a formula ψ available such that for any model \(\mathcal {M}\) and any index m∕h it holds that \(\mathcal {M},m/h\vDash \psi \) iff i implicitly knows how to φ.
We argue by contradiction. Suppose ψ characterizes that agent i implicitly knows how to p. Let P
′⊂ P denote the set of propositional variables occurring in either ψ or p, and let q∉P
′. Consider a model \(\mathcal {M}\) and an index m∕h in which agent i has two options, that is, \(\mathit {Act}_{i}^{m}\) contains two acts. Let the epistemic indistinguishability relation ∼i be given by m
1∕h
1 ∼i
m
2∕h
2 if and only if m
2∕h
2 ∈Act
i(m
1∕h
1). Consider the valuation function V which assigns to each propositional variable the set of all indices in the model. It is now easy to see that i implicitly knows how to p, because for every formula χ we have  or
or  . The assumption implies that \(\mathcal {M},\vDash \psi \) holds. See Fig. 4.11 for the initial model in which agent i implicitly knows how to p.
. The assumption implies that \(\mathcal {M},\vDash \psi \) holds. See Fig. 4.11 for the initial model in which agent i implicitly knows how to p.
We can construct a countermodel \(\mathcal {M}^{\prime }\) from \(\mathcal {M}\) by adjusting the propositional valuation to V ′ in the following way: one choice guarantees q, the other guarantees ¬q, and both guarantee any p ′∈ P ′ (see the constructed model in Fig. 4.12). Note that V ′ only differs from V on q. It is easy to see that in \(\mathcal {M}^{\prime }\), i does not implicitly know how to p, because, in \(\mathcal {M}^{\prime }\), q is a proper refinement of p for agent i. However, because we did not alter the truth values of the propositions occurring in ψ, it is the case that ψ also holds in \(\mathcal {M}^{\prime }\). Contradiction.
In a similar way, one can prove that explicit knowledge is also not characterizable.□
Theorem 4.3 (Characterization of Individual Know-how)
Individual know-how is characterized by
That is, for every model \(\mathcal {M}\) , every index m∕h, every individual agent i, and every formula φ it holds that, relative to m∕h, agent i knows how to φ if and only if \(\mathcal {M},m/h\vDash \mathsf {K}_i\Diamond \mathsf {K}_i [i\;\mathsf {stit}]\varphi \).
Proof
(If.) Follows immediately by letting ψ := φ in Definition 4.5.
(Only if.) It is immediate for implicit know-how. For explicit know-how it follows from two facts. First,  is monotonic:
is monotonic:  , which entails
, which entails  . Replacing χ
1 with K
i[i s
t
i
t]ψ and χ
2 with K
i[i s
t
i
t]φ yields
. Replacing χ
1 with K
i[i s
t
i
t]ψ and χ
2 with K
i[i s
t
i
t]φ yields

Second, by K i-necessitation, and two applications of the K-axiom for K i it holds that:

By assumption, both the antecedent of the principal implication and the antecedent of the subordinate implication obtain. Hence, K i♢K i[i s t i t]φ holds, as desired. □
C.3 Collective Know-how
Theorem 4.4
Let \(\mathcal {M}\) be an epistemic stit model, and let m∕h be an index. Assume that \(\mathcal {M}\) satisfies (Unif-H). Suppose \(\mathcal {G}\) collectively knows how to φ, as witnessed by \((\varphi _i)_{i\in \mathcal {G}}\) . Then

and

Proof
Assume all the stated assumptions. To clarify, the crucial assumptions are (1)  and (2) \(\mathsf {C}_{\mathcal {G}}\bigwedge _{i\in \mathcal {G}} \mathsf {K}_{i}\Diamond \mathsf {K}_{i}[i\;\mathsf {stit}]\varphi _i\). It is important to note that (2) entails (2’) \(\mathsf {C}_{\mathcal {G}}\bigwedge _{i\in \mathcal {G}} \Diamond [i\;\mathsf {stit}]\varphi _i\).
and (2) \(\mathsf {C}_{\mathcal {G}}\bigwedge _{i\in \mathcal {G}} \mathsf {K}_{i}\Diamond \mathsf {K}_{i}[i\;\mathsf {stit}]\varphi _i\). It is important to note that (2) entails (2’) \(\mathsf {C}_{\mathcal {G}}\bigwedge _{i\in \mathcal {G}} \Diamond [i\;\mathsf {stit}]\varphi _i\).
First, consider the following subformula of (1), which results from ignoring the outermost modality \(\mathsf {C}_{\mathcal {G}}\): (1’)  . Let us take an arbitrary \(j\in \mathcal {G}\). The right-to-left implication of (1’) entails that at any index m∕h where (1’) obtains, we get that \(m/h\vDash \langle j\;\mathsf {stit}\rangle [\mathcal {G}\;\mathsf {stit}]\varphi \to \langle j\;\mathsf {stit}\rangle [j\;\mathsf {stit}]\varphi _j\). Note that \(\vDash \langle j\;\mathsf {stit}\rangle [j\;\mathsf {stit}]\varphi _j\to [j\;\mathsf {stit}]\varphi _j\) and, therefore, at any index m∕h where (1’) obtains, we get \(m/h\vDash \langle j\;\mathsf {stit}\rangle [\mathcal {G}\;\mathsf {stit}]\varphi \to [j\;\mathsf {stit}]\varphi _j\). Since j was arbitrary,
. Let us take an arbitrary \(j\in \mathcal {G}\). The right-to-left implication of (1’) entails that at any index m∕h where (1’) obtains, we get that \(m/h\vDash \langle j\;\mathsf {stit}\rangle [\mathcal {G}\;\mathsf {stit}]\varphi \to \langle j\;\mathsf {stit}\rangle [j\;\mathsf {stit}]\varphi _j\). Note that \(\vDash \langle j\;\mathsf {stit}\rangle [j\;\mathsf {stit}]\varphi _j\to [j\;\mathsf {stit}]\varphi _j\) and, therefore, at any index m∕h where (1’) obtains, we get \(m/h\vDash \langle j\;\mathsf {stit}\rangle [\mathcal {G}\;\mathsf {stit}]\varphi \to [j\;\mathsf {stit}]\varphi _j\). Since j was arbitrary,  is an S5 modality and \(\mathsf {C}_{\mathcal {G}}\) is a normal modality, it follows that (1) entails
is an S5 modality and \(\mathsf {C}_{\mathcal {G}}\) is a normal modality, it follows that (1) entails  .
.
For the converse, consider the subformula of (2’), which results from ignoring the outermost modality \(\mathsf {C}_{\mathcal {G}}\): (2”) \(\bigwedge _{i\in \mathcal {G}} \Diamond [i\;\mathsf {stit}]\varphi _i\). The independence of agency condition entails that at any index where (2”) holds also \(\Diamond \bigwedge _{i\in \mathcal {G}} [i\;\mathsf {stit}]\varphi _i\) obtains. Let us take an arbitrary \(j\in \mathcal {G}\). Then, at any index m∕h where (2”) obtains, we get that \(m/h\vDash [j\;\mathsf {stit}]\varphi _j\to \langle j\;\mathsf {stit}\rangle \bigwedge _{i\in \mathcal {G}} [i\;\mathsf {stit}]\varphi _i\). The left-to-right implication in (1’) entails that at any index m∕h where (1’) obtains, we get that \(m/h\vDash \langle j\;\mathsf {stit}\rangle \bigwedge _{i\in \mathcal {G}} [i\;\mathsf {stit}]\varphi _i\to \langle j\;\mathsf {stit}\rangle [\mathcal {G}\;\mathsf {stit}]\varphi \). Hence, at any index m∕h where (2”) and (1’) hold, we get \(m/h\vDash [j\;\mathsf {stit}]\varphi _j\to \langle j\;\mathsf {stit}\rangle [\mathcal {G}\;\mathsf {stit}]\varphi \). Since j was arbitrary and  and \(\mathsf {C}_{\mathcal {G}}\) are normal modalities, we have
and \(\mathsf {C}_{\mathcal {G}}\) are normal modalities, we have  , as desired.
, as desired.
Second, (∗∗) follows from (∗) and two facts. First, the fact that \(\vDash \mathsf {C}_{\mathcal {G}}\chi \to \mathsf {C}_{\mathcal {G}}\mathsf {K}_i\chi \), for each \(i\in \mathcal {G}\). Second, the fact that (Unif-H) entails that  . □
. □
Observation 4.5 (Interchangeability & Effectivity)
Let S be a game model, let \(\mathcal {G}\) be a group of agents, and let φ be a formula. The following are equivalent:
-
1.
 ;
; -
2.
\(P_{\mathcal {G}}:=\{a_{\mathcal {G}}\in A_{\mathcal {G}}\mid S,a\vDash [\mathcal {G}\;\mathsf {stit}]\varphi \}\) is interchangeable.
Proof
(1. ⇒ 2.) Assume 1. Let b, c ∈ A be such that \(b_{\mathcal {G}},c_{\mathcal {G}}\in P_{\mathcal {G}}\), and let \(i\in \mathcal {G}\). To prove 2., we take an arbitrary d ∈ A such that \(d_{\mathcal {G}}=(b_{\mathcal {G} -i},c_{i})\), and prove that \(d_{\mathcal {G}}\in P_{\mathcal {G}}\). For any \(j\in \mathcal {G}-i\) it holds that \(S,d\vDash \langle j\;\mathsf {stit}\rangle [\mathcal {G}\;\mathsf {stit}]\varphi \), because \(S,b\vDash [\mathcal {G}\;\mathsf {stit}]\varphi \) and d j = b j. Hence, \(S,d\vDash \bigwedge _{j\in \mathcal {G}-i}\langle j\;\mathsf {stit}\rangle [\mathcal {G}\;\mathsf {stit}]\varphi \). In a similar way, we can prove that \(S,d\vDash \langle i\;\mathsf {stit}\rangle [\mathcal {G}\;\mathsf {stit}]\varphi \) (note the ‘i’ here). By the right-to-left implication in 1. it follows that \(S,d\vDash [\mathcal {G}\;\mathsf {stit}]\varphi \). Hence \(d_{\mathcal {G}}\in P_{\mathcal {G}}\).
(2. ⇒ 1.) Assume 2. Take any a ∈ A. We need to show that \(S,a\vDash [\mathcal {G}\;\mathsf {stit}]\varphi \leftrightarrow \bigwedge _{i\in \mathcal {G}}\langle i\;\mathsf {stit}\rangle [\mathcal {G}\;\mathsf {stit}]\varphi \). The left-to-right implication follows immediately from the fact that [i s t i t] is reflexive, i.e. satisfies \(\vDash \chi \to \langle i\;\mathsf {stit}\rangle \chi \). To establish the right-to-left implication, assume \(S,a\vDash \bigwedge _{i\in \mathcal {G}} \langle i\;\mathsf {stit}\rangle [\mathcal {G}\;\mathsf {stit}]\varphi \). That is, for every \(i\in \mathcal {G}\) there is a \(b^{i}_{\mathcal {G}}\in P_{\mathcal {G}}\) such that \(b^{i}_{i}=a_{i}\). Using the fact that \(P_{\mathcal {G}}\) is interchangeable, one can inductively show that for any subgroup \(\mathcal {F}\subseteq \mathcal {G}\) there is a \(b^{\mathcal {F}}_{\mathcal {G}}\in P_{\mathcal {G}}\) such that \(b^{\mathcal {F}}_{\mathcal {F}}=a_{\mathcal {F}}\). Hence, \(a_{\mathcal {G}}=b^{\mathcal {G}}_{\mathcal {G}}\in P_{\mathcal {G}}\) and therefore there is an a ′∈ A such that \(a^{\prime }_{\mathcal {G}}=a_{\mathcal {G}}\) and \(S,a^{\prime }\vDash [\mathcal {G}\;\mathsf {stit}]\varphi \). Since \(\vDash [\mathcal {G}\;\mathsf {stit}]\varphi \leftrightarrow [\mathcal {G}\;\mathsf {stit}][\mathcal {G}\;\mathsf {stit}]\varphi \) and \(a^{\prime }_{\mathcal {G}}=a_{\mathcal {G}}\), it holds that \(S,a\vDash [\mathcal {G}\;\mathsf {stit}]\varphi \), as desired.□
Rights and permissions
Copyright information
© 2022 The Author(s), under exclusive license to Springer Nature Switzerland AG
About this chapter
Cite this chapter
Duijf, H. (2022). Guilty Minds and Collective Know-how. In: The Logic of Responsibility Voids. Synthese Library, vol 456. Springer, Cham. https://doi.org/10.1007/978-3-030-92655-7_4
Download citation
DOI: https://doi.org/10.1007/978-3-030-92655-7_4
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-92654-0
Online ISBN: 978-3-030-92655-7
eBook Packages: Religion and PhilosophyPhilosophy and Religion (R0)


 , symmetry:
, symmetry:  , and transitivity:
, and transitivity:  ) jointly correspond to an accessibility relation that is an equivalence relation. Moreover, an equivalence relation corresponds to a partitioning. I refer the reader to the standard textbook treatment of modal logic (Blackburn et al.,
) jointly correspond to an accessibility relation that is an equivalence relation. Moreover, an equivalence relation corresponds to a partitioning. I refer the reader to the standard textbook treatment of modal logic (Blackburn et al., 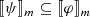 and
and  . The former drops the [i
. The former drops the [i 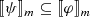 and
and  , mentioned in the previous footnote, are
, mentioned in the previous footnote, are  and
and  , respectively.
, respectively. is an S5 operator and
is an S5 operator and  while
while 


 ;
;