Abstract
In this chapter, we discuss a first application of the time derivative operator constructed in the previous chapter. More precisely, we analyse well-posedness of ordinary differential equations and will at the same time provide a Hilbert space proof of the classical Picard–Lindelöf theorem (There are different notions for this theorem. It is also called existence and uniqueness theorem for initial value problems for ordinary differential equations as well as Cauchy–Lipschitz theorem). We shall furthermore see that the abstract theory developed here also allows for more general differential equations to be considered. In particular, we will have a look at so-called delay differential equations with finite or infinite delay; neutral differential equations are considered in the exercises section.
You have full access to this open access chapter, Download chapter PDF
In this chapter, we discuss a first application of the time derivative operator constructed in the previous chapter. More precisely, we analyse well-posedness of ordinary differential equations and will at the same time provide a Hilbert space proof of the classical Picard–Lindelöf theorem.Footnote 1 We shall furthermore see that the abstract theory developed here also allows for more general differential equations to be considered. In particular, we will have a look at so-called delay differential equations with finite or infinite delay; neutral differential equations are considered in the exercises section.
We start with some information on the time derivative and its domain.
4.1 The Domain of ∂ t,ν and the Sobolev Embedding Theorem
Let H be a Hilbert space. Readers familiar with the notion of Sobolev spaces might have already realised that the domain of ∂ t,ν can be described as \(L_{2,\nu }(\mathbb {R};H)\)-functions with distributional derivative lying in \(L_{2,\nu }(\mathbb {R};H)\). We shall also use

if we want to emphasise the target Hilbert space of the \(\operatorname {dom}(\partial _{t,\nu })\)-functions. In order to stress the distributional character of the derivative introduced, we include the following result. Later on, we have the opportunity to have a more detailed look at Sobolev spaces in more general contexts.
Proposition 4.1.1
Let \(\nu \in \mathbb {R}\) and \(f,g\in L_{2,\nu }(\mathbb {R};H)\) . Then the following conditions are equivalent:
-
(i)
\(f\in \operatorname {dom}(\partial _{t,\nu })\) and ∂ t,ν f = g.
-
(ii)
For all \(\phi \in C_{\mathrm {c}}^\infty (\mathbb {R})\) we have
$$\displaystyle \begin{aligned} -\int_{\mathbb{R}}\phi'f=\int_{\mathbb{R}}\phi g, \end{aligned}$$where these integrals are Bochner integrals of the H-valued functions t↦ϕ′(t)f(t) and t↦ϕ(t)g(t), respectively.
Proof
Assume that \(f\in \operatorname {dom}(\partial _{t,\nu })\). By Proposition 3.2.4 and Corollary 3.2.6, we have that \(\mathcal {D}_H=\operatorname {lin}\left \{ \varphi \cdot x \,;\, \varphi \in C_{\mathrm {c}}^\infty (\mathbb {R}),\,x\in H \right \}\subseteq \operatorname {dom}(\partial _{t,\nu }^{*})\) (which also holds for ν = 0) and
for all x ∈ H and \(\psi \in C_{\mathrm {c}}^\infty (\mathbb {R})\). Hence, we obtain for all \(\psi \in C_{\mathrm {c}}^\infty (\mathbb {R})\)
putting  and using that multiplication by e−2ν⋅ is a bijection on \(C_{\mathrm {c}}^\infty (\mathbb {R})\), we deduce the claimed formula with g = ∂
t,ν
f.
and using that multiplication by e−2ν⋅ is a bijection on \(C_{\mathrm {c}}^\infty (\mathbb {R})\), we deduce the claimed formula with g = ∂
t,ν
f.
On the other hand, the equation involving g applied to ϕ = e−2ν⋅ ψ for \(\psi \in C_{\mathrm {c}}^\infty (\mathbb {R})\) implies that
Testing this equation with x ∈ H yields
Since \(\mathcal {D}_H\) is dense in \(\operatorname {dom}(\partial _{t,\nu })\) by Proposition 3.2.4, we infer that
for all \(h\in \operatorname {dom}(\partial _{t,\nu })\). Now, Corollary 3.2.6, yields
Thus, \(f\in \operatorname {dom}(\partial _{t,\nu }^{**})=\operatorname {dom}(\partial _{t,\nu })\) and ∂ t,ν f = g. □
The next result is a version of the Sobolev embedding theorem. It particularly confirms that functions in the domain of ∂ t,ν are continuous. This result was announced in Exercise 3.7. Here, we make use of the explicit form of the domain of ∂ t,ν as being the range space of the integral operator I ν. We define

and regard it as being endowed with the obvious norm.
Theorem 4.1.2 (Sobolev Embedding Theorem)
Let \(\nu \in \mathbb {R}\) . Then every \(f\in \operatorname {dom}(\partial _{t,\nu })\) has a continuous representative, and the mapping
is continuous.
Proof
We restrict ourselves to the case when ν > 0; the remaining cases can be proved by invoking Corollary 3.2.5. Let \(f\in \operatorname {dom}(\partial _{t,\nu })\). By definition, we find \(g\in L_{2,\nu }(\mathbb {R};H)\) such that \(f=\partial _{t,\nu }^{-1}g=I_{\nu }g.\) Then for all \(t\in \mathbb {R}\) we compute
Thus, g is integrable on \(\left (-\infty ,t\right ]\) for all \(t\in \mathbb {R}\) and dominated convergence implies that
is continuous. Moreover, for \(t\in \mathbb {R}\) we obtain
which yields the claimed continuity. □
Corollary 4.1.3
For all \(f\in \operatorname {dom}(\partial _{t,\nu })\) , we have that \(\left \Vert \mathrm {e}^{-\nu t}f(t) \right \Vert { }_{H}\to 0\) as t →±∞.
The proof is left as Exercise 4.2.
4.2 The Picard–Lindelöf Theorem
The prototype of the Picard–Lindelöf theorem will be formulated for so-called uniformly Lipschitz continuous functions. We first need a preparation.
Definition
Let X be a Banach space. Then we define

to be the set of simple functions from \(\mathbb {R}\) to X with compact support .
Lemma 4.2.1
Let X be a Banach space and \(\nu ,\eta \in \mathbb {R}\) . Then \(S_{\mathrm {c}}(\mathbb {R};X)\) is dense in \(L_{2,\nu }(\mathbb {R};X)\cap L_{2,\eta }(\mathbb {R};X)\) ; that is, for all \(f\in L_{2,\nu }(\mathbb {R};X)\cap L_{2,\eta }(\mathbb {R};X)\) there exists (f n)n in \(S_{\mathrm {c}}(\mathbb {R};X)\) such that f n → f in both \(L_{2,\nu }(\mathbb {R};X)\) and \(L_{2,\eta }(\mathbb {R};X)\) . In particular, \(S_{\mathrm {c}}(\mathbb {R};X)\) is dense in \(L_{2,\nu }(\mathbb {R};X)\).
Proof
Let \(f\in L_{2,\nu }(\mathbb {R};X)\cap L_{2,\eta }(\mathbb {R};X)\). Then for all \(n\in \mathbb {N}\) we have that  and
and  in \(L_{2,\nu }(\mathbb {R};X)\) and in \(L_{2,\eta }(\mathbb {R};X)\) as n →∞. For \(n\in \mathbb {N}\) let \((\widetilde {f}_{n,k})_{k}\) be in S(μ
2,ν;X) such that
in \(L_{2,\nu }(\mathbb {R};X)\) and in \(L_{2,\eta }(\mathbb {R};X)\) as n →∞. For \(n\in \mathbb {N}\) let \((\widetilde {f}_{n,k})_{k}\) be in S(μ
2,ν;X) such that  in \(L_{2,\nu }(\mathbb {R};X)\) as k →∞. We put
in \(L_{2,\nu }(\mathbb {R};X)\) as k →∞. We put  . Then
. Then  in \(L_{2,\nu }(\mathbb {R};X)\) and in \(L_{2,\eta }(\mathbb {R};X)\) as k →∞. □
in \(L_{2,\nu }(\mathbb {R};X)\) and in \(L_{2,\eta }(\mathbb {R};X)\) as k →∞. □
Inorder to define the notion of uniformly Lipschitz continuous functions, we first need the Lipschitz semi-norm.
Definition
Let X 0, X 1 be normed spaces, and F : X 0 → X 1 Lipschitz continuous. Then

is the Lipschitz semi-norm of F.
Definition
Let H 0, H 1 be Hilbert spaces, \(\mu \in \mathbb {R}\). Then a function \(F\colon S_{\mathrm {c}}(\mathbb {R};H_{0})\to \bigcap _{\nu \geqslant \mu }L_{2,\nu }(\mathbb {R};H_{1})\) is called uniformly Lipschitz continuous if for all \(\nu \geqslant \mu \) we have that F considered in \(L_{2,\nu }(\mathbb {R};H_{0})\times L_{2,\nu }(\mathbb {R};H_{1})\) is Lipschitz continuous, and for the unique Lipschitz continuous extensions F ν, \(\nu \geqslant \mu \), we have that
Remark 4.2.2
Another way to introduce uniformly Lipschitz continuous mappings is the following. Let H 0, H 1 be Hilbert spaces, \(\mu \in \mathbb {R}\). Let \((F^\nu )_{\nu \geqslant \mu }\) be a family of Lipschitz continuous mappings \(F^\nu \colon L_{2,\nu }(\mathbb {R};H_0)\to L_{2,\nu }(\mathbb {R};H_1)\) such that
and the mappings are consistent in the sense that for all \(\nu ,\eta \geqslant \mu \) and \(f\in L_{2,\nu }(\mathbb {R};H_0)\cap L_{2,\eta }(\mathbb {R};H_0)\) we have
Then, for \(\nu \geqslant \mu \) and \(f\in S_{\mathrm {c}}(\mathbb {R};H_0)\) we have \(F^\nu (f)\in \bigcap _{\eta \geqslant \mu }L_{2,\eta }(\mathbb {R};H_{1})\) and \(F^\nu |{ }_{S_{\mathrm {c}}(\mathbb {R};H_0)}\) is uniformly Lipschitz continuous.
Theorem 4.2.3 (Picard–Lindelöf—Hilbert Space Version)
Let H be a Hilbert space,
\(\mu \in \mathbb {R}\)
and
\(F\colon S_{\mathrm {c}}(\mathbb {R};H)\to \bigcap _{\nu \geqslant \mu }L_{2,\nu }(\mathbb {R};H)\)
uniformly Lipschitz continuous with
 . Then for all
\(\nu >\max \{L,\mu \}\)
the equation
. Then for all
\(\nu >\max \{L,\mu \}\)
the equation
admits a unique solution \(u_{\nu }\in \operatorname {dom}(\partial _{t,\nu })\) . Furthermore, for all \(\nu >\max \{L,\mu \}\) the following properties hold:
-
(a)
If F ν(u ν) is continuous in a neighbourhood of \(a\in \mathbb {R}\) , then u ν is continuously differentiable in a neighbourhood of a.
-
(b)
For all \(a\in \mathbb {R}\),
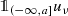 is the unique fixed point
\(v\in L_{2,\nu }(\mathbb {R};H)\)
of
is the unique fixed point
\(v\in L_{2,\nu }(\mathbb {R};H)\)
of
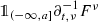 , that is, v uniquely solves
, that is, v uniquely solves
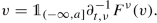
-
(c)
For all \(\eta \geqslant \nu \) we have that u ν = u η.
-
(d)
For all \(f\in L_{2,\nu }(\mathbb {R};H)\) the equation
$$\displaystyle \begin{aligned} \partial_{t,\nu}v=F^{\nu}(v)+f \end{aligned}$$admits a unique solution \(v_{\nu ,f}\in \operatorname {dom}(\partial _{t,\nu })\) , and if \(f,g\in L_{2,\nu }(\mathbb {R};H)\) satisfy f = g on \(\left (-\infty ,a\right ]\) for some \(a\in \mathbb {R},\) then v ν,f = v ν,g on \(\left (-\infty ,a\right ]\).
Proof of Theorem 4.2.3—First Part
Define \(\Phi \colon L_{2,\nu }(\mathbb {R};H)\to L_{2,\nu }(\mathbb {R};H)\) by
Since \(\left \Vert \partial _{t,\nu }^{-1} \right \Vert \leqslant \frac {1}{\nu }\) and ν > L it follows that Φ is a contraction and thus admits a unique fixed point, which by definition solves the equation in question. Moreover, we have that \(u_{\nu }=\Phi (u_{\nu })=\partial _{t,\nu }^{-1}F^{\nu }(u_{\nu })\in \operatorname {dom}(\partial _{t,\nu })\).
Differentiability of u ν as in (a) follows from Exercise 4.1 and the continuity of F ν(u ν).
For the unique existence asserted in (d), note that the unique existence of v
ν,f follows from the above considerations after realising that  defines a contraction in \(L_{2,\nu }(\mathbb {R};H)\). For the remaining statements in (d) and the statements in (b) and (c), we need some prerequisites. □
defines a contraction in \(L_{2,\nu }(\mathbb {R};H)\). For the remaining statements in (d) and the statements in (b) and (c), we need some prerequisites. □
Definition
Let H 0, H 1 be Hilbert spaces, \(\nu \in \mathbb {R}\) and \(F\colon L_{2,\nu }(\mathbb {R};H_{0})\to L_{2,\nu }(\mathbb {R};H_{1})\). Then, F is called causal if for all \(a\in \mathbb {R}\) and all \(f,g\in L_{2,\nu }(\mathbb {R};H_0)\) with f = g on \(\left (-\infty ,a\right ]\), we have that F(f) = F(g) on \(\left (-\infty ,a\right ]\).
Remark 4.2.4
Let \(\nu \in \mathbb {R}\), \(a\in \mathbb {R}\). If \(f\in L(L_{2,\nu }(\mathbb {R};H))\) with \( \operatorname {\mathrm {spt}} f\subseteq \left (-\infty ,a\right ]\) then \(f\in \bigcap _{\eta \leqslant \nu } L_{2,\eta }(\mathbb {R};H)\) and
Likewise, if \( \operatorname {\mathrm {spt}} f\subseteq \left [a,\infty \right )\), we get \(f\in \bigcap _{\rho \geqslant \nu }L_{2,\rho }(\mathbb {R};H)\) with
Lemma 4.2.5
Let H 0, H 1 be Hilbert spaces, \(\mu \in \mathbb {R}\), \(F\colon S_{\mathrm {c}}(\mathbb {R};H_{0})\to \bigcap _{\nu \geqslant \mu }L_{2,\nu }(\mathbb {R};H_{1})\) uniformly Lipschitz continuous. Then the following statements hold:
-
(a)
F ν is causal for all \(\nu \geqslant \mu \).
-
(b)
The mapping \(\partial _{t,\nu }^{-1}F^{\nu }\) is causal if \(\nu \geqslant \max \{\mu ,0\}\) and ν ≠ 0.
-
(c)
For all \(\nu \geqslant \eta \geqslant \mu \) , we have that F ν = F η on \(L_{2,\nu }(\mathbb {R};H_0)\cap L_{2,\eta }(\mathbb {R};H_0)\).
Proof
(a) We divide the proof into three steps.
-
(i)
Let \(\nu \geqslant \mu \). In order to show causality of F ν, we first note that it suffices to have F ν(f) = F ν(g) on \(\left (-\infty ,a\right ]\) for all \(f,g\in S_{\mathrm {c}}(\mathbb {R};H_0)\) with f = g on \(\left (-\infty ,a\right ]\). Indeed, let \(f,g\in L_{2,\nu }(\mathbb {R};H)\) with f = g on \(\left (-\infty ,a\right ]\) for some \(a\in \mathbb {R}\). By Lemma 4.2.1 we find (f n)n and \((\widetilde {g}_{n})_{n}\) in \(S_{\mathrm {c}}(\mathbb {R};H_{0})\) such that f n → f and \(\widetilde {g}_{n}\to g\) in \(L_{2,\nu }(\mathbb {R};H_{0})\). Next,
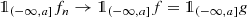 as n →∞ in \(L_{2,\nu }(\mathbb {R};H_{0})\). Thus, putting
as n →∞ in \(L_{2,\nu }(\mathbb {R};H_{0})\). Thus, putting 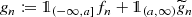 for all \(n\in \mathbb {N}\) we obtain that g
n → g in \(L_{2,\nu }(\mathbb {R};H_{0})\). Since F
ν(f
n) = F
ν(g
n) on \(\left (-\infty ,a\right ]\) for all \(n\in \mathbb {N}\) and \(F^\nu \colon L_{2,\nu }(\mathbb {R};H_0)\to L_{2,\nu }(\mathbb {R};H_1)\) is continuous, taking the limit n →∞ yields F
ν(f) = F
ν(g) on \(\left (-\infty ,a\right ]\).
for all \(n\in \mathbb {N}\) we obtain that g
n → g in \(L_{2,\nu }(\mathbb {R};H_{0})\). Since F
ν(f
n) = F
ν(g
n) on \(\left (-\infty ,a\right ]\) for all \(n\in \mathbb {N}\) and \(F^\nu \colon L_{2,\nu }(\mathbb {R};H_0)\to L_{2,\nu }(\mathbb {R};H_1)\) is continuous, taking the limit n →∞ yields F
ν(f) = F
ν(g) on \(\left (-\infty ,a\right ]\). -
(ii)
Let \(a\in \mathbb {R}\), c⩾0 and \(f\in S_{\mathrm {c}}(\mathbb {R};H_0)\) such that f = 0 on \(\left (-\infty ,a\right ]\), \(g\in \bigcap _{\nu \geqslant \mu }L_{2,\nu }(\mathbb {R};H_1)\) such that \(\left \Vert g \right \Vert { }_{L_{2,\nu }(\mathbb {R};H_1)}\leqslant c\left \Vert f \right \Vert { }_{L_{2,\nu }(\mathbb {R};H_0)}\) for all \(\nu \geqslant \mu \). Then
$$\displaystyle \begin{aligned} \begin{array}{ll} \int_{-\infty}^a \left\Vert g(t) \right\Vert {}_{H_1}^2 \mathrm{e}^{2\nu(a-t)}\,\mathrm{d} t &\leqslant \int_{\mathbb{R}} \left\Vert g(t) \right\Vert {}_{H_1}^2 \mathrm{e}^{2\nu(a-t)}\,\mathrm{d} t\\ &\leqslant c^2 \int_a^\infty \left\Vert f(t) \right\Vert {}_{H_0}^2 \mathrm{e}^{2\nu(a-t)}\,\mathrm{d} t \to 0 \end{array} \end{aligned}$$as ν →∞. Since e2ν(a−t) →∞ as ν →∞ for all t < a, the monotone convergence theorem implies g = 0 on \(\left (-\infty ,a\right ]\).
-
(iii)
Let \(f,g\in S_{\mathrm {c}}(\mathbb {R};H_0)\) such that f = g on \(\left (-\infty ,a\right ]\) for some \(a\in \mathbb {R}\). Then f − g = 0 on \(\left (-\infty ,a\right ]\). Since F is uniformly Lipschitz continuous, with
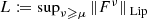 we obtain \(\left \Vert F^\nu (f)-F^\nu (g) \right \Vert { }_{L_{2,\nu }(\mathbb {R};H_1)} \leqslant L\left \Vert f-g \right \Vert { }_{L_{2,\nu }(\mathbb {R};H_0)}\) for all \(\nu \geqslant \mu \). By (ii) we conclude F
ν(f) = F
ν(g) on \(\left (-\infty ,a\right ]\) for all \(\nu \geqslant \mu \), which by (i) yields the assertion.
we obtain \(\left \Vert F^\nu (f)-F^\nu (g) \right \Vert { }_{L_{2,\nu }(\mathbb {R};H_1)} \leqslant L\left \Vert f-g \right \Vert { }_{L_{2,\nu }(\mathbb {R};H_0)}\) for all \(\nu \geqslant \mu \). By (ii) we conclude F
ν(f) = F
ν(g) on \(\left (-\infty ,a\right ]\) for all \(\nu \geqslant \mu \), which by (i) yields the assertion.The statement in (b) directly follows from (a). Note that \(\partial _{t,\nu }^{-1}F^\nu \) is uniformly Lipschitz continuous only for ν > 0.
Let us prove (c). Since F ν(f) = F(f) = F η(f) for \(f\in S_{\mathrm {c}}(\mathbb {R};H_0)\), the set \(S_{\mathrm {c}}(\mathbb {R};H_0)\) is dense in \(L_{2,\nu }(\mathbb {R};H_0)\cap L_{2,\mu }(\mathbb {R};H_0)\) by Lemma 4.2.1, and F ν and F η are Lipschitz-continuous, we obtain the assertion.
□
Proof of Theorem 4.2.3—Second Part
The remaining part in (d): Let \(f,g\in L_{2,\nu }(\mathbb {R};H)\) with f = g on \(\left (-\infty ,a\right ]\). Since \(\nu >L\geqslant 0\), we compute using Lemma 4.2.5 (b) and causality of \(\partial _{t,\nu }^{-1}\) that

The same computation also yields that

It is easy to see that  defines a contraction in \(L_{2,\nu }(\mathbb {R};H)\). Hence, the contraction mapping principle implies that
defines a contraction in \(L_{2,\nu }(\mathbb {R};H)\). Hence, the contraction mapping principle implies that  .
.
The statement in (b) follows from the fact that  defines a contraction and Lemma 4.2.5
(b).
defines a contraction and Lemma 4.2.5
(b).
For the proof of (c), we observe that for all \(n\in \mathbb {N}\), we have  . Hence, by (b) and Lemma 4.2.5
(c), it follows that
. Hence, by (b) and Lemma 4.2.5
(c), it follows that

As  satisfies the same fixed point equation, we deduce
satisfies the same fixed point equation, we deduce  for all \(n\in \mathbb {N},\) which yields the assertion. □
for all \(n\in \mathbb {N},\) which yields the assertion. □
As a first application of Theorem 4.2.3 we state and prove the classical version of the Theorem of Picard–Lindelöf.
Theorem 4.2.6 (Picard–Lindelöf—Classical Version)
Let H be a Hilbert space, \(\Omega \subseteq \mathbb {R}\times H\) be open, f : Ω → H continuous, (t 0, x 0) ∈ Ω. Assume there exists L⩾0 such that for all (t, x), (t, y) ∈ Ω we have
Then, there exists δ > 0 such that the initial value problem
admits a unique continuously differentiable solution, \(u\colon \left [t_{0},t_{0}+\delta \right ]\to H\) , which satisfies \(\left (t,u(t)\right )\in \Omega \) for all \(t\in \left [t_{0},t_{0}+\delta \right ]\).
Proof
First of all we observe that we may assume, without loss of generality, that x 0 = 0. Indeed, to solve the initial value problem
for a continuously differentiable \(v\colon \left [t_{0},t_{0}+\delta \right ]\to H\) is equivalent to solving the problem in Theorem 4.2.6 for u by setting  . Appropriately shifting the time coordinate, we may also assume that t
0 = 0.
. Appropriately shifting the time coordinate, we may also assume that t
0 = 0.
Thus, let (0, 0) ∈ Ω. Then \([0,\delta ']\times B\left [0,\varepsilon \right ]\subseteq \Omega \) for some δ′, ε > 0. Denote by P : H → H the projection onto \(B\left [0,\varepsilon \right ]\); that is, for x ∈ H, \(Px\in B\left [0,\varepsilon \right ]\) is the unique element satisfying
By Exercise 4.4, P is Lipschitz continuous with Lipschitz semi-norm bounded by 1. We then define

and will prove that F is well-defined and uniformly Lipschitz continuous. Since the mapping  is supported on \(\left [0,\delta '\right ]\), we obtain for ν⩾0 that \(F(0)\in L_{2,\nu }(\mathbb {R};H)\). Moreover, for ν⩾0 and \(g,h\in S_{\mathrm {c}}(\mathbb {R}; H)\) we estimate
is supported on \(\left [0,\delta '\right ]\), we obtain for ν⩾0 that \(F(0)\in L_{2,\nu }(\mathbb {R};H)\). Moreover, for ν⩾0 and \(g,h\in S_{\mathrm {c}}(\mathbb {R}; H)\) we estimate
which shows that F is well-defined and uniformly Lipschitz continuous.
By Theorem 4.2.3, there exists \(v\in \operatorname {dom}(\partial _{t,\nu })\) with ν > L such that
We read off from \(v=\partial _{t,\nu }^{-1}F^{\nu }(v)\) that v = 0 on \(\left (-\infty ,0\right ]\), and that v is continuous by Theorem 4.1.2. Moreover, we obtain that

from which we read off that v is continuously differentiable on \(\left (0,\delta '\right )\) since f and P are also continuous. The same equality implies for  , where
, where  , that
, that
Thus, \((t,v(t))\in \left [0,\delta '\right ]\times B\left [0,\varepsilon \right ]\subseteq \Omega \) for all \(0\leqslant t\leqslant \delta \) and so Pv(t) = v(t) for \(0\leqslant t\leqslant \delta \). Thus,  satisfies (4.1).
satisfies (4.1).
Finally, concerning uniqueness, let \(\widetilde {u}\colon \left [0,\delta \right ]\to H\) be a continuously differentiable solution of (4.1). Let \(\widetilde {v}\) be the extension of \(\widetilde {u}\) by 0 to the whole of \(\mathbb {R}\). Then we get that

Since  is the unique solution of the equation
is the unique solution of the equation  , we obtain that
, we obtain that  , which yields \(u=\widetilde {u}\). □
, which yields \(u=\widetilde {u}\). □
Remark 4.2.7
The reason for the proof of the classical Picard–Lindelöf theorem being seemingly complicated is two-fold. First of all, the Hilbert space solution theory is for L 2-functions rather than continuous (or continuously differentiable) functions. The second, maybe more important point is that the Hilbert space Picard–Lindelöf asserts a solution theory, which provides global existence in the time variable. The main body of the proof of the classical Picard–Lindelöf theorem presented here is therefore devoted to ‘localisation’ of the abstract theorem. Furthermore, note that the method of proof for obtaining uniqueness and the admittance of the initial value rests on causality. This effect will resurface when we discuss partial differential equations.
4.3 Delay Differential Equations
In this section, our study will not be as in depth as done for the local Picard–Lindelöf theorem. Of course, the solution theory would not be a very good one if it was only applicable to, arguably, the easiest case of ordinary differential equations. We shall see next that the developed theory applies to more elaborate examples.
In what follows, let H be a Hilbert space over \(\mathbb {K}\). We start out with a delay differential equation with so-called ‘discrete delay’. For this, we introduce, for \(h\in \mathbb {R}\), the time-shift operator
Lemma 4.3.1
Let \(\mu \in \mathbb {R}\) . The mapping \(\tau _{h} \colon S_{\mathrm {c}}(\mathbb {R};H) \to \bigcap _{\nu \geqslant \mu }L_{2,\nu }(\mathbb {R};H)\) is uniformly Lipschitz continuous if and only if \(h\leqslant 0\) . More precisely, for \(\nu \in \mathbb {R}\) we have
Proof
Let \(f\in S_{\mathrm {c}}(\mathbb {R};H)\). Then for \(\nu \in \mathbb {R}\) we compute
Since \(\sup _{\nu \geqslant \mu } \mathrm {e}^{2\nu h} <\infty \) if and only if \(h\leqslant 0\) we obtain the equivalence. Moreover, the above equality also yields the norm of τ h on \(L_{2,\nu }(\mathbb {R};H)\). □
We will reuse τ h for the Lipschitz continuous extensions to \(L_{2,\nu }(\mathbb {R};H)\). The well-posedness theorem for delay equations with discrete delay is contained in the next theorem. We note here that we only formulate the respective result for right-hand sides that are globally Lipschitz continuous. With a localisation technique, as has already been carried out for the classical Picard–Lindelöf theorem, it is also possible to obtain local results.
Theorem 4.3.2
Let H be a Hilbert space, \(\mu \in \mathbb {R}\), \(N\in \mathbb {N}\), \(h_{1},\ldots ,h_{N}\in \left (-\infty ,0\right ]\) , and
uniformly Lipschitz. Then there exists an \(\eta \in \mathbb {R}\) such that for all \(\nu \geqslant \eta \) the equation
admits a solution
\(u\in \operatorname {dom}(\partial _{t,\nu })\)
which is unique in
\(\bigcup _{\nu \geqslant \eta }L_{2,\nu }(\mathbb {R};H)\)
. Moreover, for all
\(a\in \mathbb {R}\)
the function
 satisfies
satisfies

Proof
The assertion follows from Theorem 4.2.3 applied to  in conjunction with Lemma 4.3.1. □
in conjunction with Lemma 4.3.1. □
Next, we formulate an initial value problem for a subclass of the latter type of equations.
Theorem 4.3.3
Let h > 0, \(f\colon \mathbb {R}_{\ge {0}}\times H\times H\to H\) continuous, and \(f(\cdot ,0,0)\in L_{2,\mu }(\mathbb {R}; H)\) for some μ > 0. Assume that there exists L⩾0 with
Let \(u_{0}\in C\left ([-h,0]; H\right )\) . Then the initial value problem
admits a unique continuous solution \(u\colon \left [-h,\infty \right )\to H\) , continuously differentiable on \(\left (0,\infty \right )\).
Proof
For t < 0 let  . We define \(F\colon S_{\mathrm {c}}(\mathbb {R}; H)\to \bigcap _{\nu \geqslant \mu }L_{2,\nu }(\mathbb {R}; H)\) by
. We define \(F\colon S_{\mathrm {c}}(\mathbb {R}; H)\to \bigcap _{\nu \geqslant \mu }L_{2,\nu }(\mathbb {R}; H)\) by

for all \(t\in \mathbb {R}\). It is easy to see that F is uniformly Lipschitz continuous. Thus, by Theorem 4.2.3, we find \(\eta \geqslant \mu \) such that for all \(\nu \geqslant \eta \) the equation
admits a solution \(v\in \bigcap _{\nu \geqslant \eta }\operatorname {dom}(\partial _{t,\nu })\) which is unique in \(\bigcup _{\nu \geqslant \eta }L_{2,\nu }(\mathbb {R}; H).\) Note that \( \operatorname {\mathrm {spt}} F^{\nu }(v)\subseteq \left [0,\infty \right )\). Hence, v = 0 on \(\left (-\infty ,0\right ].\) By Theorem 4.1.2, we obtain that v(0) = 0. We claim that  is a solution of (4.2). First of all note that u is continuous on \(\left [-h,\infty \right )\). Next, for 0 < t < h we have that t − h < 0 and thus v(t − h) = 0 and so we see that
is a solution of (4.2). First of all note that u is continuous on \(\left [-h,\infty \right )\). Next, for 0 < t < h we have that t − h < 0 and thus v(t − h) = 0 and so we see that

Similarly, for \(t\geqslant h\) we obtain
and thus, by continuity of f, u 0 and u, it follows that v is continuously differentiable on \(\left (0,\infty \right )\) and
It remains to show uniqueness. For this, let \(w\colon \left [-h,\infty \right )\to H\) be a solution of (4.2). Then
and w(t) = u
0(t) if \(t\in \left [-h,0\right ]\). Extend w by 0 on \(\left (-\infty ,-h\right )\) and set  . We infer
. We infer

for all \(t\in \mathbb {R}\). For \(a\in \mathbb {R}\) we set  and obtain, using the above formula for \(\widetilde {v}\),
and obtain, using the above formula for \(\widetilde {v}\),

By uniqueness of the solution of

it follows that  for all \(a\in \mathbb {R}\) and, thus, u = w. □
for all \(a\in \mathbb {R}\) and, thus, u = w. □
The equation to come involves the whole history of the unknown; that is, the unknown evaluated at \(\left (-\infty ,0\right ]\). For a mapping \(u\colon \mathbb {R}\to H\) and \(t\in \mathbb {R}\) we define the ‘history’ of u up to time t as \(u_t\colon \mathbb {R}_{\le {0}}\to H\),  for all \(\theta \in \mathbb {R}_{\le {0}}\). Moreover, we define the mapping
for all \(\theta \in \mathbb {R}_{\le {0}}\). Moreover, we define the mapping
which maps each \(t\in \mathbb {R}\) to the history of u up to time t.
Lemma 4.3.4
Let μ > 0. Then
is uniformly Lipschitz continuous. More precisely, for all ν > 0 we have
Proof
Let \(u\in S_{\mathrm {c}}(\mathbb {R};H)\). Then \(\Theta u(t) = u_t\in L_2(\mathbb {R}_{\le {0}};H)\) for all \(t\in \mathbb {R}\) and we compute
□
Theorem 4.3.5
Let H be a Hilbert space, \(\mu \in \mathbb {R}\) and let \(\Phi \colon S_{\mathrm {c}}\big (\mathbb {R};L_2(\mathbb {R}_{\le {0}};H)\big )\to \bigcap _{\nu \geqslant \mu }L_{2,\nu }(\mathbb {R};H)\) be uniformly Lipschitz. Then, there exists η > 0 such that for all \(\nu \geqslant \eta \) the equation
admits a solution \(u\in \bigcap _{\nu \geqslant \eta }\operatorname {dom}(\partial _{t,\nu })\) unique in \(\bigcup _{\nu \geqslant \eta }L_{2,\nu }(\mathbb {R};H).\)
Proof
This is another application of Theorem 4.2.3. □
4.4 Comments
In a way, the proof of Theorem 4.2.6 is standard PDE-theory in a nutshell; a solution theory for L p-spaces is used to deduce existence and uniqueness of solutions and a posteriori regularity theory provides more information on the properties of the solution.
Note that—of course—other proofs are available for the Picard–Lindelöf theorem. We chose, however, to present this proof here in order to provide a perspective on classical results. Furthermore, we mention that in order to obtain unique existence for the solution, it suffices to assume that f satisfies a uniform Lipschitz condition with respect to the second variable and that f is measurable. Continuity of f is needed in order to obtain C 1-solutions.
A more detailed exposition and more examples of the theory applied to delay differential equations can be found in [52] and—in a Banach space setting—[85].
There is also a way of dealing with delay differential equations by expanding the state space the problem is formulated in. In this case, it is possible to make use of the rich theory of C 0-semigroups. We refer to [10] for this.
Causality is one of the main concepts for evolutionary equations. We have provided this notion for mappings defined on L 2,ν-type spaces only. The situation becomes different if one considers merely densely defined mappings. Then it is a priori unclear, whether for a Lipschitz continuous mapping the continuous extension is also causal. For this we refer to Exercise 4.7 below and to [51, 131], and [138, Chapter 2] as well as to references mentioned there.
Exercises
Exercise 4.1
-
(a)
Let X be a Banach space, \(u\colon \left [a,b\right ]\to X\) continuous. Show that \(v\colon \left (a,b\right )\to X\) given by
$$\displaystyle \begin{aligned} v(t)=\int_{a}^{t}u(\tau)\,\mathrm{d}\tau \end{aligned}$$is continuously differentiable with v′(t) = u(t) for all t ∈ (a, b).
-
(b)
Let H be a Hilbert space, and \(\nu \in \mathbb {R}.\) Let \(u\in \operatorname {dom}(\partial _{t,\nu })\) with ∂ t,ν u continuous. Show that u is continuously differentiable and u′ = ∂ t,ν u.
Exercise 4.2
Prove Corollary 4.1.3.
Exercise 4.3
Let H be a Hilbert space. Show that

where a function \(g\colon \mathbb {R}\to H\) is said to be \(\frac {1}{2}\) -Hölder continuous if
Exercise 4.4
Let H be a Hilbert space, C ⊆ H non-empty, closed and convex. Show that the projection, P, of H onto C defines a Lipschitz continuous mapping with Lipschitz semi-norm bounded by 1, where for x ∈ H, Px ∈ C is the unique element satisfying
Exercise 4.5
Let \(h\colon \mathbb {R}\times \mathbb {R}_{\le {0}}\times \mathbb {R}^{n}\to \mathbb {R}^{n}\) be continuous satisfying
with h(⋅, ⋅, 0) = 0. Let R > 0 and \(u_{0}\in C(\mathbb {R}_{\le {0}};\mathbb {R}^{n})\) have compact support. Show that the initial value problem
admits a unique continuous solution \(u\colon \mathbb {R}\to \mathbb {R}^{n}\), which is continuously differentiable on \(\mathbb {R}_{>{0}}\).
Hint: Modify Θ from Lemma 4.3.4.
Exercise 4.6
Let H be a Hilbert space. Show that for a uniformly Lipschitz continuous \(\Phi \colon S_{\mathrm {c}}\big (\mathbb {R};L_2(\mathbb {R}_{\le {0}};H)^{2}\big )\to \bigcap _{\nu \geqslant \mu }L_{2,\nu }(\mathbb {R};H)\) the equation
admits a unique solution \(u\in \operatorname {dom}(\partial _{t,\nu })\) for ν large enough.
Exercise 4.7
Let \(D\subseteq L_2(\mathbb {R})\) be dense and suppose that \(F\colon D\subseteq L_2(\mathbb {R})\to L_2(\mathbb {R})\) admits a Lipschitz continuous extension F 0.
-
(a)
Show that F 0 is causal if and only if for all \(\phi \in S_{\mathrm {c}}(\mathbb {R};\mathbb {R})\) and all \(a\in \mathbb {R}\) there exists \(L\geqslant 0\) such that
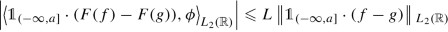
for all f, g ∈ D; that is, the mapping
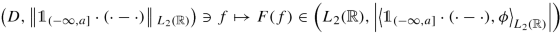
is Lipschitz continuous.
-
(b)
For \(a\in \mathbb {R}\) let
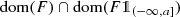 be dense in \(L_2(\mathbb {R})\) and if \(f,g\in D=\operatorname {dom}(F)\) and f = g on \(\left (-\infty ,a\right ]\) then also F(f) = F(g) on \(\left (-\infty ,a\right ]\). Show that F
0 is causal.
be dense in \(L_2(\mathbb {R})\) and if \(f,g\in D=\operatorname {dom}(F)\) and f = g on \(\left (-\infty ,a\right ]\) then also F(f) = F(g) on \(\left (-\infty ,a\right ]\). Show that F
0 is causal. -
(c)
Assume for all f, g ∈ D and \(a \in \mathbb {R}\) that f = g on \(\left (-\infty ,a\right ]\) implies that F(f) = F(g) on \(\left (-\infty ,a\right ]\). Show that this is not sufficient for F 0 to be causal. Hint: Find a dense subspace \(D=\operatorname {dom}(F)\) so that the first condition in (b) is not satisfied.
Notes
- 1.
There are different notions for this theorem. It is also called existence and uniqueness theorem for initial value problems for ordinary differential equations as well as Cauchy–Lipschitz theorem.
References
A. Bátkai, S. Piazzera, Semigroups for Delay Equations, vol. 10. Research Notes in Mathematics. (A. K. Peters, Ltd., Wellesley, MA, 2005)
B. Jacob, J.R. Partington, Graphs, closability, and causality of linear time-invariant discrete-time systems. Int. J. Control 73(11), 1051–1060 (2000)
A. Kalauch et al., A Hilbert space perspective on ordinary differential equations with memory term. J. Dyn. Differ. Equ. 26(2), 369–399 (2014)
R. Picard, S. Trostorff, M. Waurick, A functional analytic perspective to delay differential equations. Oper. Matrices 8(1), 217–236 (2014)
M. Waurick, A note on causality in Banach spaces. Indagationes Mathematicae 26(2), 404–412 (2015)
M. Waurick, On the continuous dependence on the coefficients of evolutionary equations. Habilitation. Technische Universität Dresden, 2016. http://arxiv.org/abs/1606.07731
Author information
Authors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2022 The Author(s)
About this chapter
Cite this chapter
Seifert, C., Trostorff, S., Waurick, M. (2022). Ordinary Differential Equations. In: Evolutionary Equations. Operator Theory: Advances and Applications, vol 287. Birkhäuser, Cham. https://doi.org/10.1007/978-3-030-89397-2_4
Download citation
DOI: https://doi.org/10.1007/978-3-030-89397-2_4
Published:
Publisher Name: Birkhäuser, Cham
Print ISBN: 978-3-030-89396-5
Online ISBN: 978-3-030-89397-2
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)


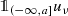 is the unique fixed point
is the unique fixed point
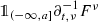 , that is, v uniquely solves
, that is, v uniquely solves
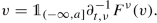
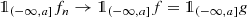 as n →∞ in
as n →∞ in 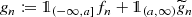 for all
for all 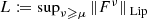 we obtain
we obtain 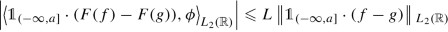
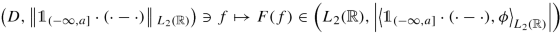
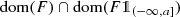 be dense in
be dense in