Abstract
It is the aim of this chapter to define a derivative operator on a suitable L 2-space, which will be used as the derivative with respect to the temporal variable in our applications. As we want to deal with Hilbert space-valued functions, we start by introducing the concept of Bochner–Lebesgue spaces, which generalises the classical scalar-valued L p-spaces to the Banach space-valued case.
You have full access to this open access chapter, Download chapter PDF
It is the aim of this chapter to define a derivative operator on a suitable L 2-space, which will be used as the derivative with respect to the temporal variable in our applications. As we want to deal with Hilbert space-valued functions, we start by introducing the concept of Bochner–Lebesgue spaces, which generalises the classical scalar-valued L p-spaces to the Banach space-valued case.
3.1 Bochner–Lebesgue Spaces
Throughout, let ( Ω, Σ, μ) be a σ-finite measure space and X a Banach space over the field \(\mathbb {K}\in \{\mathbb {R},\mathbb {C}\}\). We are aiming to define the spaces L p(μ;X) for \(1\leqslant p\leqslant \infty \). This is the space of (equivalence classes of) measurable functions attaining values in X, which are p-integrable (if p < ∞), or essentially bounded (if p = ∞) with respect to the measure μ. We begin by defining the space of simple functions on Ω with values in X and the notion of Bochner-measurability.
Definition
For a function f : Ω → X and x ∈ X we set

A function f : Ω → X is called simple if f[ Ω] is finite and for each x ∈ X ∖{0} the set A f,x belongs to Σ and has finite measure. We denote the set of simple functions by S(μ;X). A function f : Ω → X is called Bochner-measurable if there exists a sequence \((f_{n})_{n\in \mathbb {N}}\) in S(μ;X) such that
for μ-a.e. ω ∈ Ω.
Remark 3.1.1
Let us comment on the definition of Bochner-measurability.
-
(a)
For a simple function f we have

where the sum is actually finite, since
 for all x∉f[ Ω].
for all x∉f[ Ω]. -
(b)
If \(X=\mathbb {K}\), then a function is Bochner-measurable if and only if it has a μ-measurable representative. Indeed, if f is Bochner-measurable, we find a sequence (f n)n in \(S(\mu ;\mathbb {K})\) such that f n → f pointwise μ-a.e. Hence, we find a μ-nullset N ∈ Σ such that
 pointwise on all of Ω. Since g
n is μ-measurable and μ-measurable functions are stable under pointwise limits, g is μ-measurable itself. Since f = g except for a μ-nullset, f has a μ-measurable representative. If, on the other hand, f has a μ-measurable representative, let g be this representative. Approximating real and imaginary parts separately, it suffices to treat the case \(\mathbb {K}=\mathbb {R}\). Then consider for \(n\in \mathbb {N}\)
pointwise on all of Ω. Since g
n is μ-measurable and μ-measurable functions are stable under pointwise limits, g is μ-measurable itself. Since f = g except for a μ-nullset, f has a μ-measurable representative. If, on the other hand, f has a μ-measurable representative, let g be this representative. Approximating real and imaginary parts separately, it suffices to treat the case \(\mathbb {K}=\mathbb {R}\). Then consider for \(n\in \mathbb {N}\)

where
 . It is easy to see that supω ∈ Ω|s
n(ω) − g(ω)| \(\leqslant 1/n\) for all ω ∈ Ω. Hence,
. It is easy to see that supω ∈ Ω|s
n(ω) − g(ω)| \(\leqslant 1/n\) for all ω ∈ Ω. Hence, 
converges pointwise everywhere to g. In consequence, f is Bochner-measurable.
-
(c)
It is easy to check that S(μ;X) is a vector space and an \(S(\mu ;\mathbb {K})\)-module; that is, for f ∈ S(μ;X) and \(g\in S(\mu ;\mathbb {K})\) we have g ⋅ f ∈ S(μ;X).
-
(d)
If f : Ω → X is Bochner-measurable, then \(\left \Vert f(\cdot ) \right \Vert { }_{X}\colon \Omega \to \mathbb {R}\) is Bochner-measurable. Indeed, since
$$\displaystyle \begin{aligned} \left\Vert f(\cdot) \right\Vert {}_{X}=\lim_{n\to\infty}\left\Vert f_{n}(\cdot) \right\Vert {}_{X} \end{aligned}$$μ-a.e. and a sequence \((f_{n})_{n\in \mathbb {N}}\) in S(μ;X), it suffices to show that \(\left \Vert f_{n}(\cdot ) \right \Vert { }_{X}\) is simple for all \(n\in \mathbb {N}.\) The latter follows since \(A_{f_n,x}\cap A_{f_n,y}=\varnothing \) for x≠y and thus

is a real-valued simple function.
-
(e)
If one deals with arbitrary measure spaces, the definition of simple functions has to be weakened by allowing the sets A f,x to have infinite measure. However, since in the applications to follow we only work with weighted Lebesgue measures, we restrict ourselves to σ-finite measure spaces.
Definition (Bochner–Lebesgue Spaces)
For \(p\in \left [1,\infty \right ]\) we define

as well as

where ∼ denotes the usual equivalence relation of equality μ-almost everywhere. We equip L p(μ;X) with the norm

We first prove a density result.
Lemma 3.1.2
The space S(μ;X) is dense in L p(μ;X) for \(p\in \left [1,\infty \right )\).
Proof
Let f ∈ L p(μ;X). Then there exists a sequence \((f_{n})_{n\in \mathbb {N}}\) in S(μ;X) such that f n(ω) → f(ω) for all ω ∈ Ω∖ N for some nullset N ⊆ Ω. W.l.o.g. we may assume that \(\left \Vert f_n(\cdot ) \right \Vert { }_X\) and \(\left \Vert f(\cdot ) \right \Vert { }_X\) are μ-measurable on Ω ∖ N for each \(n\in \mathbb {N}\). For \(n\in \mathbb {N}\) we define the set

and set  . Then \(\widetilde {f}_{n}\in S(\mu ;X)\) and we claim that \(\widetilde {f}_{n}(\omega )\to f(\omega )\) for all ω ∈ Ω∖ N. Indeed, if f(ω) = 0 then \(\widetilde {f}_{n}(\omega )=0\) and the claim follows. If f(ω)≠0, then there is some \(n_{0}\in \mathbb {N}\) such that \(\left \Vert f_{n}(\omega ) \right \Vert { }_{X}\leqslant 2\left \Vert f(\omega ) \right \Vert { }_{X}\) for n ≥ n
0, and hence \(\omega \in \bigcap _{n\geqslant n_{0}}I_{n}.\) Consequently \(\widetilde {f}_{n}(\omega )=f_{n}(\omega )\to f(\omega ).\) By dominated convergence, it now follows that
. Then \(\widetilde {f}_{n}\in S(\mu ;X)\) and we claim that \(\widetilde {f}_{n}(\omega )\to f(\omega )\) for all ω ∈ Ω∖ N. Indeed, if f(ω) = 0 then \(\widetilde {f}_{n}(\omega )=0\) and the claim follows. If f(ω)≠0, then there is some \(n_{0}\in \mathbb {N}\) such that \(\left \Vert f_{n}(\omega ) \right \Vert { }_{X}\leqslant 2\left \Vert f(\omega ) \right \Vert { }_{X}\) for n ≥ n
0, and hence \(\omega \in \bigcap _{n\geqslant n_{0}}I_{n}.\) Consequently \(\widetilde {f}_{n}(\omega )=f_{n}(\omega )\to f(\omega ).\) By dominated convergence, it now follows that
which proves the claim. □
As a consequence of the latter lemma, we can show that Bochner-measurability is preserved by pointwise convergence almost everywhere.
Proposition 3.1.3
Let f n, f : Ω → X for \(n\in \mathbb {N}\) . Moreover, assume that f n is Bochner-measurable for each \(n\in \mathbb {N}\) and f n(ω) → f(ω) as n →∞ for μ-almost every ω ∈ Ω. Then f is Bochner-measurable.
Proof
Since f n → f almost everywhere, we have \([f\ne 0]\setminus N\subseteq \bigcup _{n\in \mathbb {N}} [f_n\ne 0]\setminus N\) for some nullset N ⊆ Ω. Moreover, since f n is Bochner-measurable, the definition of simple functions yields that \(\bigcup _{n\in \mathbb {N}} [f_n\ne 0]\subseteq \bigcup _{n\in \mathbb {N}} B_n\), where, for all \(n\in \mathbb {N}\), B n is measurable with μ(B n) < ∞. The latter implies that there exists a sequence of measurable sets \((A_n)_{n\in \mathbb {N}}\) such that A n ⊆ A n+1, μ(A n) < ∞ for all \(n\in \mathbb {N}\) and
For \(n\in \mathbb {N}\) we set  , where \(\widetilde {f}_n:\Omega \to \mathbb {R}\) is measurable and equals \(\left \Vert f_n(\cdot ) \right \Vert { }_X\)
μ-almost everywhere (cp. Remark 3.1.1
(d) and (b)). In this way we obtain a sequence of Bochner-measurable functions with g
n → f
μ-almost everywhere. Moreover, g
n ∈ L
1(μ;X) for each \(n\in \mathbb {N}\) and thus, for each \(n\in \mathbb {N}\) we find a simple function h
n with \(\left \Vert g_n-h_n \right \Vert { }_1\leqslant 2^{-n}\) by Lemma 3.1.2. Then
, where \(\widetilde {f}_n:\Omega \to \mathbb {R}\) is measurable and equals \(\left \Vert f_n(\cdot ) \right \Vert { }_X\)
μ-almost everywhere (cp. Remark 3.1.1
(d) and (b)). In this way we obtain a sequence of Bochner-measurable functions with g
n → f
μ-almost everywhere. Moreover, g
n ∈ L
1(μ;X) for each \(n\in \mathbb {N}\) and thus, for each \(n\in \mathbb {N}\) we find a simple function h
n with \(\left \Vert g_n-h_n \right \Vert { }_1\leqslant 2^{-n}\) by Lemma 3.1.2. Then
and hence, \(\sum _{n\in \mathbb {N}} \left \Vert g_n(\omega )-h_n(\omega ) \right \Vert { }_X<\infty \) for μ-almost every ω ∈ Ω, which particularily implies g n − h n → 0 μ-almost everywhere. Hence, h n → f μ-almost everywhere, which shows the Bochner-measurability of f. □
We can now prove that the spaces L p(μ;X) are actually Banach spaces.
Proposition 3.1.4
Let \(p\in \left [1,\infty \right ]\) . Then \((L_{p}(\mu ;X),\left \Vert \cdot \right \Vert { }_{p})\) is a Banach space and if X = H is a Hilbert space, then so too is L 2(μ;H) with the scalar product given by

Proof
We just show the completeness of L p(μ;X). Let \((f_{n})_{n\in \mathbb {N}}\) be a sequence in L p(μ;X) such that \(\sum _{n=1}^{\infty }\left \Vert f_{n} \right \Vert { }_{p}<\infty \). We set

Then \((g_{n})_{n\in \mathbb {N}}\) is a sequence in L p(μ) such that \(\sum _{n=1}^{\infty }\left \Vert g_{n} \right \Vert { }_{p}<\infty .\) By the completeness of L p(μ) we infer that

exists and is an element in L p(μ). In particular, g(ω) < ∞ for μ-a.e. ω ∈ Ω and thus,
for μ-a.e. ω ∈ Ω. By the completeness of X we can define

for μ-a.e. ω ∈ Ω. Note that f is Bochner-measurable by Proposition 3.1.3. We need to prove that f ∈ L p(μ;X) and that \(\sum _{n=1}^{k}f_{n}\to f\) in L p(μ;X) as k →∞. For this, it suffices to prove that
Indeed, this would imply both \(f-\sum _{n=1}^{k}f_{n}\in L_{p}(\mu ;X)\) and the desired convergence result. We prove (3.1) for p < ∞ and p = ∞ separately.
First, let p = ∞. For each \(n\in \mathbb {N}\) we have f
n ∈ L
∞(μ;X) and thus \(\left \Vert f_{n}(\omega ) \right \Vert { }_{X}\leqslant \left \Vert f_{n} \right \Vert { }_{\infty }\) for all ω ∈ Ω∖ N
n and some nullset N
n ⊆ Ω. We set  which is again a nullset. For \(k\in \mathbb {N}\) and ω ∈ Ω∖ N we then estimate
which is again a nullset. For \(k\in \mathbb {N}\) and ω ∈ Ω∖ N we then estimate
which yields (3.1).
Now, let p < ∞. For \(k\in \mathbb {N}\) we estimate
where we have used monotone convergence in the third line. This estimate yields (3.1). □
We now want to define an X-valued integral for functions in L 1(μ;X); the so-called Bochner-integral.
Proposition 3.1.5
The mapping Footnote 1
is linear and continuous, and thus has a unique continuous linear extension to L 1(μ;X), called the Bochner-integral . Moreover,
and for A ∈ Σ, f ∈ L 1(μ;X) we set

Proof
We first show linearity. Let f, g ∈ S(μ;X) and \(\lambda \in \mathbb {K}\). Then, for x ∈ X we have
and therefore μ(A λf+g,x) =∑y ∈ X μ(A f,y ∩ A g,x−λy). Thus, we compute
where we interchanged the finite sums. Now,
as well as
and therefore we conclude
In order to prove continuity, let f ∈ S(μ;X). We estimate

The remaining assertions now follow from Lemma 3.1.2 by continuous extension (see Corollary 2.1.5). □
The next proposition tells us how the Bochner-integral of a function behaves if we compose the function with a bounded or closed linear operator first. In what follows, let \(X':=L(X,\mathbb {K})\) denote the dual space of X.
Proposition 3.1.6
Let f ∈ L 1(μ;X), Y a Banach space.
-
(a)
Let B ∈ L(X, Y ). Then B ∘ f ∈ L 1(μ;Y ) and
$$\displaystyle \begin{aligned} \int_{\Omega}B\circ f\,\mathrm{d}\mu=B\int_{\Omega}f\,\mathrm{d}\mu. \end{aligned}$$ -
(b)
If X 0 ⊆ X is a closed subspace and f(ω) ∈ X 0 for μ-a.e. ω ∈ Ω, then ∫Ω f dμ ∈ X 0.
-
(c)
(Theorem of Hille) Let \(A\colon \operatorname {dom}(A)\subseteq X\to Y\) be a closed linear operator and assume that \(f(\omega )\in \operatorname {dom}(A)\) for μ-a.e. ω ∈ Ω and that A ∘ f ∈ L 1(μ;Y ). Then \(\int _{\Omega }f\,\mathrm {d}\mu \in \operatorname {dom}(A)\) and
$$\displaystyle \begin{aligned} A\int_{\Omega}f\,\mathrm{d}\mu=\int_{\Omega}A\circ f\,\mathrm{d}\mu. \end{aligned}$$
Proof
-
(a)
At first we observe that, if f ∈ S(μ;X), then

Thus, B ∘ f ∈ S(μ;Y ) since
 , the sum is finite and S(μ;Y ) is a vector space. Let now be f ∈ L
1(μ;X). Then there is \((f_{n})_{n\in \mathbb {N}}\) a sequence in S(μ;X) such that f
n → f
μ-a.e. Then B ∘ f
n ∈ S(μ;Y ) (see above) and due to the continuity of B we have that B ∘ f
n → B ∘ f
μ-a.e., hence B ∘ f is Bochner-measurable. Moreover, \(\left \Vert B\circ f(\cdot ) \right \Vert { }_{Y}\leqslant \left \Vert B \right \Vert \left \Vert f(\cdot ) \right \Vert { }_{X}\), which yields that B ∘ f ∈ L
1(μ;Y ). By continuity of both B and ∫Ω dμ, it suffices to check the interchanging property for any f ∈ S(μ;X) alone. However, this is clear, since for a simple function f
, the sum is finite and S(μ;Y ) is a vector space. Let now be f ∈ L
1(μ;X). Then there is \((f_{n})_{n\in \mathbb {N}}\) a sequence in S(μ;X) such that f
n → f
μ-a.e. Then B ∘ f
n ∈ S(μ;Y ) (see above) and due to the continuity of B we have that B ∘ f
n → B ∘ f
μ-a.e., hence B ∘ f is Bochner-measurable. Moreover, \(\left \Vert B\circ f(\cdot ) \right \Vert { }_{Y}\leqslant \left \Vert B \right \Vert \left \Vert f(\cdot ) \right \Vert { }_{X}\), which yields that B ∘ f ∈ L
1(μ;Y ). By continuity of both B and ∫Ω dμ, it suffices to check the interchanging property for any f ∈ S(μ;X) alone. However, this is clear, since for a simple function f

where the sum is actually finite and hence,

where in the third equality we have used that
 is a simple function.
is a simple function. -
(b)
Let x′∈ X′ with \(x'|{ }_{X_{0}}=0.\) It follows from (a) that
$$\displaystyle \begin{aligned} x'\left(\int_{\Omega}f\,\mathrm{d}\mu\right)=\int_{\Omega}x'\circ f\,\mathrm{d}\mu=0, \end{aligned}$$and since x′ was arbitrary, it follows that ∫Ω f dμ ∈ X 0 from the Theorem of Hahn–Banach.
-
(c)
Consider the space L 1(μ;X × Y ). By assumption, it follows that
$$\displaystyle \begin{aligned} (f,A\circ f)\in L_{1}(\mu;X\times Y). \end{aligned}$$However, \((f,A\circ f)(\omega )=(f(\omega ),\left (A\circ f\right )(\omega ))\in A\subseteq X\times Y\) for μ-a.e. ω ∈ Ω, and since A is closed we can use (b) to derive that
$$\displaystyle \begin{aligned} \int_{\Omega}(f,A\circ f)\,\mathrm{d}\mu\in A.{} \end{aligned} $$(3.2)Let π 1, π 2 be the projection from X × Y to X and Y , respectively. It then follows from part (a) that
$$\displaystyle \begin{aligned} \pi_{1}\left(\int_{\Omega}(f,A\circ f)\,\mathrm{d}\mu\right)=\int_{\Omega}\pi_{1}(f,A\circ f)\,\mathrm{d}\mu=\int_{\Omega}f\,\mathrm{d}\mu, \end{aligned}$$and analogously for π 2. Using these equalities we derive from (3.2) that \(\int _{\Omega }f\,\mathrm {d}\mu \in \operatorname {dom}(A)\) and that A∫Ω f dμ =∫Ω A ∘ f dμ.
□
As a consequence of the latter proposition, we derive the fundamental theorem of calculus for Banach space-valued functions.
Corollary 3.1.7 (Fundamental Theorem of Calculus)
Let \(a,b\in \mathbb {R},a<b\) and consider the measure space \((\left [a,b\right ],\mathcal {B}(\left [a,b\right ]),\lambda )\) , where \(\mathcal {B}(\left [a,b\right ])\) denotes the Borel-σ-algebra of \(\left [a,b\right ]\) and λ is the Lebesgue measure. Let \(f\colon \left [a,b\right ]\to X\) be continuously differentiable. Footnote 2 Then
Proof
Note first of all that continuous functions are Bochner-measurable (which can be easily seen using Theorem 3.1.10 below). Thus, the integral on the right-hand side is well-defined. Let φ ∈ X′. Then \(\varphi \circ f\colon [a,b]\to \mathbb {K}\) is continuously differentiable, and \(\left (\varphi \circ f\right )'(t)=\left (\varphi \circ f'\right )(t)\). Using Proposition 3.1.6 (a) together with the fundamental theorem of calculus for the scalar-valued case we get
Since this holds for all φ ∈ X′, the assertion follows from the Theorem of Hahn–Banach. □
Next we state a density result, which will be useful throughout the course.
Lemma 3.1.8
Let \(1\leqslant p<\infty \), \(\mathcal {D}\subseteq L_p(\mu )\) be total in L p(μ) and X a Banach space. Then the set \(\left \{ \varphi (\cdot )x \,;\, x\in X,\,\varphi \in \mathcal {D} \right \}\) is total in L p(μ;X).
Proof
By Lemma 3.1.2, we know that S(μ;X) is dense in L
p(μ;X). Thus, it suffices to approximate  for some A ∈ Σ with μ(A) < ∞ and x ∈ X. For this, however, take a sequence (ϕ
n)n in the linear hull of \(\mathcal {D}\) with
for some A ∈ Σ with μ(A) < ∞ and x ∈ X. For this, however, take a sequence (ϕ
n)n in the linear hull of \(\mathcal {D}\) with  in L
p(μ) as n →∞. Then
in L
p(μ) as n →∞. Then

Thus, the claim follows. □
The following application of Lemma 3.1.8 also deals with a dense subset of X.
Lemma 3.1.9
Let \(1\leqslant p<\infty \), \(\mathcal {D}\subseteq L_p(\mu )\) be total in L p(μ), X a Banach space, D 0 ⊆ X total in X. Then \(\left \{ \varphi (\cdot )x \,;\, x\in D_{0},\varphi \in \mathcal {D} \right \}\) is total in L p(μ;X).
Proof
The proof follows upon realising that the set \(\left \{ \varphi (\cdot )x \,;\, x\in D_{0},\,\varphi \in \mathcal {D} \right \}\) is total in the set \(\left \{ \varphi (\cdot )x \,;\, x\in X,\,\varphi \in \mathcal {D} \right \}\). From here we just apply Lemma 3.1.8. □
We conclude this section by stating and proving the celebrated Theorem of Pettis, which characterises Bochner-measurability in terms of weak measurability.
Theorem 3.1.10 (Theorem of Pettis )
Let f : Ω → X. Then f is Bochner-measurable if and only if
-
(a)
f is weakly Bochner-measurable ; that is, \(x'\circ f\colon \Omega \to \mathbb {K}\) is Bochner-measurable for each x′∈ X′, and
-
(b)
f is almost separably-valued ; that is, \(\overline {\operatorname {lin} f[\Omega \setminus N_{0}]}\) is separable for some N 0 ∈ Σ with μ(N 0) = 0.
Proof
If f is Bochner-measurable, then clearly it is weakly Bochner-measurable. Further, as f is the almost everywhere limit of simple functions, it is almost separably-valued, since each simple function attains values in a finite-dimensional subspace of X.
Assume now conversely that f satisfies (a) and (b). We define  , which is a separable Banach space by (b). Thus, there exists a sequence \((x_{n}^{\prime })_{n\in \mathbb {N}}\) in X′ such that
, which is a separable Banach space by (b). Thus, there exists a sequence \((x_{n}^{\prime })_{n\in \mathbb {N}}\) in X′ such that
Since for each \(n\in \mathbb {N}\) the function  is Bochner-measurable by (a) and Remark 3.1.1
(d), we find a μ-nullset N
n and a measurable function \(\widetilde {g}_{n}\colon \Omega \to \mathbb {R}\) such that \(g_{n}=\widetilde {g}_{n}\) on Ω ∖ N
n by Remark 3.1.1
(b). Then \(\sup _{n\in \mathbb {N}}\widetilde {g}_{n}(\cdot )\) is measurable and
is Bochner-measurable by (a) and Remark 3.1.1
(d), we find a μ-nullset N
n and a measurable function \(\widetilde {g}_{n}\colon \Omega \to \mathbb {R}\) such that \(g_{n}=\widetilde {g}_{n}\) on Ω ∖ N
n by Remark 3.1.1
(b). Then \(\sup _{n\in \mathbb {N}}\widetilde {g}_{n}(\cdot )\) is measurable and
where  , which shows that ∥f(⋅)∥ is Bochner-measurable. Let ε > 0, \((y_{n})_{n\in \mathbb {N}}\) a dense sequence in Y . Applying the previous argument to the function
, which shows that ∥f(⋅)∥ is Bochner-measurable. Let ε > 0, \((y_{n})_{n\in \mathbb {N}}\) a dense sequence in Y . Applying the previous argument to the function  for \(k\in \mathbb {N}\) we infer that ∥f
k(⋅)∥ is Bochner-measurable and hence, there is a μ-nullset \(N_{k}^{\prime }\) and a measurable funtion \(\widetilde {f_{k}}\colon \Omega \to \mathbb {R}\) such that \(\|f_{k}\|=\widetilde {f}_{k}\) on \(\Omega \setminus N_{k}^{\prime }\). Consequently, the sets
for \(k\in \mathbb {N}\) we infer that ∥f
k(⋅)∥ is Bochner-measurable and hence, there is a μ-nullset \(N_{k}^{\prime }\) and a measurable funtion \(\widetilde {f_{k}}\colon \Omega \to \mathbb {R}\) such that \(\|f_{k}\|=\widetilde {f}_{k}\) on \(\Omega \setminus N_{k}^{\prime }\). Consequently, the sets

are measurable. Moreover, by the density of \(\{y_{n}\,;\,n\in \mathbb {N}\}\) in Y , we get that \(\Omega \setminus N'\subseteq \bigcup _{k\in \mathbb {N}}E_{k}\) with  . Setting
. Setting  and \(F_{n+1}=E_{n+1}\setminus \bigcup _{k=1}^{n}F_{k}\) for \(n\in \mathbb {N}\), we obtain a sequence of pairwise disjoint measurable sets \((F_{n})_{n\in \mathbb {N}}\) with \(\Omega \setminus N'\subseteq \bigcup _{n\in \mathbb {N}}F_{n}.\) We set
and \(F_{n+1}=E_{n+1}\setminus \bigcup _{k=1}^{n}F_{k}\) for \(n\in \mathbb {N}\), we obtain a sequence of pairwise disjoint measurable sets \((F_{n})_{n\in \mathbb {N}}\) with \(\Omega \setminus N'\subseteq \bigcup _{n\in \mathbb {N}}F_{n}.\) We set

and obtain \(\|f(\omega )-g(\omega )\|\leqslant \varepsilon \) for each ω ∈ Ω∖ N′. Hence, if g is Bochner-measurable, then f is Bochner-measurable as well. Indeed, we find a sequence of such functions converging to f μ-almost everywhere and so Proposition 3.1.3 applies. For showing the Bochner-measurability of g, let \((\Omega _{k})_{k\in \mathbb {N}}\) be a sequence of pairwise disjoint measurable sets such that \(\bigcup _{k\in \mathbb {N}}\Omega _{k}=\Omega \) and μ( Ωk) < ∞ for each \(k\in \mathbb {N}.\) For \(n\in \mathbb {N}\) we set

Then \(\left (g_{n}\right )_{n\in \mathbb {N}}\) is a sequence of simple functions with g n → g pointwise as n →∞ and thus, g is Bochner-measurable. □
3.2 The Time Derivative as a Normal Operator
Now let H be a Hilbert space over \(\mathbb {K}\in \{\mathbb {R},\mathbb {C}\}\). For \(\nu \in \mathbb {R}\) and \(p\in \left [1,\infty \right )\) we define the measure

for A in the Borel-σ-algebra, \(\mathcal {B}(\mathbb {R})\), of \(\mathbb {R}\). As our underlying Hilbert space for the time derivative we set

In the same way we define

for \(p\in \left [1,\infty \right )\). If \(H=\mathbb {K}\) we abbreviate \(L_{p,\nu }(\mathbb {R}):=L_{p,\nu }(\mathbb {R};\mathbb {K})\). Thus, \(f\in L_{p,\nu }(\mathbb {R};H)\) if and only if f is Bochner measurable and
Our aim is to define the time derivative on \(L_{2,\nu }(\mathbb {R};H)\). For this, we define a suitable anti-derivative as an operator, which for ν ≠ 0 turns out to be one-to-one and bounded. Then we introduce the time derivative as the inverse of this anti-derivative. The reason for doing it that way is to easily get a formula for the adjoint for the time derivative using the boundedness of the anti-derivative.
We start our considerations with the definition of convolution operators in \(L_{2,\nu }(\mathbb {R};H)\).
Lemma 3.2.1
Let \(k\in L_{1,\nu }(\mathbb {R})\) . We define the convolution operator
by

which exists for a.e. \(t\in \mathbb {R}\) . Then, k ∗ is linear and bounded with \(\left \Vert k\ast \right \Vert \leqslant \left \Vert k \right \Vert { }_{L_{1,\nu }(\mathbb {R})}\).
Proof
Let \(f \in L_{2,\nu }(\mathbb {R};H)\). We first prove that \(s\mapsto k(s)f(t-s)\in L_{1}(\mathbb {R};H)\) for a.e. \(t\in \mathbb {R}\). The Bochner-measurability is clear since k and f are both Bochner-measurable. Moreover,
which on the one hand proves that
for a.e. \(t\in \mathbb {R}\) and on the other hand shows the norm estimate, once we have shown the Bochner-measurability of k ∗ f. For proving the latter, we apply Theorem 3.1.10. Since f is Bochner-measurable, we find a nullset N such that  is separable. Hence, for almost every \(t\in \mathbb {R}\) we have
is separable. Hence, for almost every \(t\in \mathbb {R}\) we have
by Proposition 3.1.6(b). Thus, k ∗ f is almost separably-valued. Moreover, for x′∈ H′ we have by Proposition 3.1.6(a)
almost everywhere and thus, the weak Bochner-measurability follows from the fact that the convolution of two measurable scalar-valued functions is measurable. Since the linearity of k ∗ is clear the proof is done. □
Definition
For ν≠0 we define the operator
by

Note that, by Lemma 3.2.1, I ν is bounded with \(\left \Vert I_{\nu } \right \Vert \leqslant \frac {1}{\left \vert \nu \right \vert }\).
Remark 3.2.2
For ν > 0, \(f\in L_{2,\nu }(\mathbb {R}; H)\) we have

Analogously, for ν < 0, \(f\in L_{2,\nu }(\mathbb {R}; H)\) we have
Proposition 3.2.3
Let ν≠0. Then I ν is one-to-one and \(C_{\mathrm {c}}^1(\mathbb {R};H)\) , the space of continuously differentiable, compactly supported functions on \(\mathbb {R}\) with values in H, is in the range of I ν.
Proof
We just prove the assertion for the case when ν > 0. Let \(f\in L_{2,\nu }(\mathbb {R};H)\) satisfy I ν f = 0. In particular, we obtain for all \(t\in \mathbb {R}\setminus N\) that \(0=I_{\nu }f(t)=\int _{-\infty }^{t}f(s)\,\mathrm {d} s\) for some Lebesgue nullset, \(N\subseteq \mathbb {R}\). Then for \(a,b\in \mathbb {R}\setminus N\) with a < b and x ∈ H we have that

Thus f = 0. Indeed, since \(\mathbb {R}\setminus N\) is dense in \(\mathbb {R}\),  is total in \(L_{2,\nu }(\mathbb {R})\). Hence,
is total in \(L_{2,\nu }(\mathbb {R})\). Hence,  is total in \(L_{2,\nu }(\mathbb {R};H)\) by Lemma 3.1.8. This proves the injectivity of I
ν. Moreover, if \(\varphi \in C_{\mathrm {c}}^1(\mathbb {R};H)\) then by Corollary 3.1.7 we have
is total in \(L_{2,\nu }(\mathbb {R};H)\) by Lemma 3.1.8. This proves the injectivity of I
ν. Moreover, if \(\varphi \in C_{\mathrm {c}}^1(\mathbb {R};H)\) then by Corollary 3.1.7 we have
□
Definition
For ν≠0 we define the time derivative, ∂ t,ν, on \(L_{2,\nu }(\mathbb {R};H)\) by

Note that by Lemma 3.2.1 and Proposition 3.2.3, ∂ t,ν is a closed linear operator for which \(C_{\mathrm {c}}^1(\mathbb {R};H)\subseteq \operatorname {dom}(\partial _{t,\nu })\). Since
we infer that ∂ t,ν is densely defined by Lemma 3.1.8 and Exercise 3.2. Moreover, since I ν φ′ = φ for \(\varphi \in C_{\mathrm {c}}^1(\mathbb {R};H)\) we get that
that is, ∂ t,ν extends the classical derivative of continuously differentiable functions. We shall discuss the actual domain of ∂ t,ν in the next chapter.
Proposition 3.2.4
Let ν≠0. Then
 is a core for ∂
t,ν
. Here,
\(C_{\mathrm {c}}^\infty (\mathbb {R})\)
denotes the space of smooth functions on
\(\mathbb {R}\)
with compact support.
is a core for ∂
t,ν
. Here,
\(C_{\mathrm {c}}^\infty (\mathbb {R})\)
denotes the space of smooth functions on
\(\mathbb {R}\)
with compact support.
Proof
We first prove that
is dense in \(L_{2,\nu }(\mathbb {R})\). As \(C_{\mathrm {c}}^\infty (\mathbb {R})\) is dense in \(L_{2,\nu }(\mathbb {R})\) (see Exercise 3.2), it suffices to approximate functions in \(C_{\mathrm {c}}^\infty (\mathbb {R})\). For this, let \(f\in C_{\mathrm {c}}^\infty (\mathbb {R})\). We now define

Then \(\varphi _{n}\in C_{\mathrm {c}}^\infty (\mathbb {R})\) for each \(n\in \mathbb {N}\) and
Consequently,
which shows the density of (3.3) in \(L_{2,\nu }(\mathbb {R})\). By Lemma 3.1.8 we have that
is total in \(L_{2,\nu }(\mathbb {R};H)\) and so \(\partial _{t,\nu }[\mathcal {D}_H]\) is dense in \(L_{2,\nu }(\mathbb {R};H)\). Now let \(f\in \operatorname {dom}(\partial _{t,\nu })\) and ε > 0. By what we have shown above there exists some \(\varphi \in \mathcal {D}_H\) such that
Since \(\partial _{t,\nu }^{-1}=I_{\nu }\) is bounded with \(\left \Vert \partial _{t,\nu }^{-1} \right \Vert \leqslant \frac {1}{\left \vert \nu \right \vert }\), the latter implies that
and hence, \(\mathcal {D}_H\) is indeed a core for ∂ t,ν. □
Corollary 3.2.5
For \(\nu \in \mathbb {R}\) the mapping
is unitary, and for ν, μ≠0 one has
Proof
The proof is left as Exercise 3.5. For this we recall that the equality to be proven is an equality of relations and particularly includes the equality of the (natural) domains of the operators involved. Furthermore, note that it suffices to show equality on \(C_{\mathrm {c}}^\infty (\mathbb {R};H)\) and then to use an appropriate density result. □
By Corollary 3.2.5 we can now define ∂ t,0. Let ν ≠ 0. Then

Note that in view of Corollary 3.2.5, the assertion of Proposition 3.2.4 now also holds for ν = 0.
Finally, we want to compute the adjoint of ∂ t,ν.
Corollary 3.2.6
Let \(\nu \in \mathbb {R}\) . The adjoint of ∂ t,ν is given by
In particular, ∂
t,ν
is a normal operator with
 , and ∂
t,0
is skew-selfadjoint.
, and ∂
t,0
is skew-selfadjoint.
Proof
Let ν ≠ 0 first. Integrating by parts, one obtains
for \(\varphi ,\psi \in C_{\mathrm {c}}^\infty (\mathbb {R};H)\). Since \(C_{\mathrm {c}}^\infty (\mathbb {R};H)\) is a core for ∂ t,ν by Proposition 3.2.4, the latter shows
Since we know that ∂ t,ν is onto, it suffices to prove that \(-\partial _{t,\nu }^\ast +2\nu \) is one-to-one, since this would imply equality in the latter operator inclusion. For doing so, we apply Theorem 2.2.5 to compute
Moreover, we have that − ∂ t,ν + 2ν is unitarily equivalent to − ∂ t,−ν by Corollary 3.2.5 and since ∂ t,−ν is onto, so is − ∂ t,ν + 2ν and thus \(\operatorname {ker}(-\partial _{t,\nu }^\ast +2\nu )=L_{2,\nu }(\mathbb {R};H)^\bot =\{0\}\), which yields the assertion.
The case ν = 0 follows directly from the definition of ∂ t,0. □
3.3 Comments
Standard references for Bochner integration and related results are [6, 31].
Considering the derivative operator in an exponentially weighted space goes back (at least) to Morgenstern [67], where ordinary differential equations were considered in a classical setting. In fact, we shall return to this observation in the next chapter when we devote our study to some implications of the already developed concepts on ordinary and delay differential equations.
A first occurrence of the derivative operator in exponentially weighted L 2-spaces can be found in [83], where a corresponding spectral theorem has been focussed on. We will prove in a later chapter that the spectral representation of the time derivative as a multiplication operator can be realised by a shifted variant of the Fourier transformation—the so-called Fourier–Laplace transformation.
In an applied context, the time derivative operator discussed here has been introduced in [82].
Exercises
Exercise 3.1
A sequence (φ n)n in \(C_{\mathrm {c}}^\infty (\mathbb {R}^{d})\) is called a δ-sequence if
-
(a)
φ n⩾0 for \(n\in \mathbb {N}\),
-
(b)
\( \operatorname {\mathrm {spt}}\varphi _{n}\subseteq \left [-\frac {1}{n},\frac {1}{n}\right ]^{d}\) for \(n\in \mathbb {N}\),
-
(c)
\(\int _{\mathbb {R}^{d}}\varphi _{n}=1\) for \(n\in \mathbb {N}\).
Let \(\varphi \in C_{\mathrm {c}}^\infty (\mathbb {R}^{d})\) with \( \operatorname {\mathrm {spt}}\varphi \subseteq \left [-1,1\right ]^{d}\), φ⩾0 and \(\int _{\mathbb {R}^{d}}\varphi =1\). Prove that (φ
n)n given by  for \(x\in \mathbb {R}^d\), \(n\in \mathbb {N}\) defines a δ-sequence. Moreover, give an example for such a function φ.
for \(x\in \mathbb {R}^d\), \(n\in \mathbb {N}\) defines a δ-sequence. Moreover, give an example for such a function φ.
Exercise 3.2
It is well-known that  is total in \(L_2(\mathbb {R}^{d})\).
is total in \(L_2(\mathbb {R}^{d})\).
-
(a)
Let \(\varphi \in C_{\mathrm {c}}^\infty (\mathbb {R}^{d})\), \(f\in L_2(\mathbb {R}^{d})\). Define as usual
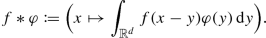
Prove that \(f\ast \varphi \in C^\infty (\mathbb {R}^d)\) with \(\partial ^{\alpha }\left (f\ast \varphi \right )=f\ast \partial ^{\alpha }\varphi \) for all \(\alpha \in \mathbb {N}_0^{d}\), where \(\partial ^{\alpha }\varphi =\partial _{1}^{\alpha _{1}}\ldots \partial _{d}^{\alpha _{d}}\varphi \). Moreover, prove that \( \operatorname {\mathrm {spt}} f\ast \varphi \subseteq \operatorname {\mathrm {spt}} f+ \operatorname {\mathrm {spt}}\varphi \).
-
(b)
Let (φ n)n be a δ-sequence and \(f\in L_2(\mathbb {R}^{d})\). Show that f ∗ φ n → f in \(L_2(\mathbb {R}^{d})\) as n →∞.
Hint: Prove that
 in \(L_2(\mathbb {R}^{d})\) for all d-dimensional bounded intervals and use that \(\left \Vert f\ast \varphi _{n} \right \Vert { }_{2}\leqslant \left \Vert f \right \Vert { }_{2}\) (see also Lemma 3.2.1).
in \(L_2(\mathbb {R}^{d})\) for all d-dimensional bounded intervals and use that \(\left \Vert f\ast \varphi _{n} \right \Vert { }_{2}\leqslant \left \Vert f \right \Vert { }_{2}\) (see also Lemma 3.2.1). -
(c)
Prove that \(C_{\mathrm {c}}^\infty (\mathbb {R}^{d})\) is dense in \(L_2(\mathbb {R}^{d})\).
Exercise 3.3
Let a < b, X 0, X 1, X 2 be Banach spaces, \(f\colon \left (a,b\right ) \to X_{0}\) and \(g\colon \left (a,b\right ) \to X_{1}\) both continuously differentiable, ℓ: X 0 × X 1 → X 2 bilinear and continuous. Prove that \(h\colon \left (a,b\right )\to X_2\) given by

is continuously differentiable with
If f, f′, g, g′ have continuous extensions to \(\left [a,b\right ],\) prove the integration by parts formula:
Exercise 3.4
For ν≠0, show that \(\left \Vert I_{\nu } \right \Vert =\frac {1}{\left \vert \nu \right \vert }\).
Exercise 3.5
Prove Corollary 3.2.5.
Exercise 3.6
Let \(\nu \in \mathbb {R}\) and H be a complex Hilbert space. Prove that \(\sigma (\partial _{t,\nu })\subseteq \left \{ \mathrm {i} t+\nu \,;\, t\in \mathbb {R} \right \}\), where ∂ t,0 is defined in Corollary 3.2.6.
Hint: For \(f\in \operatorname {dom}(\partial _{t,\nu }), z\in \mathbb {C}\) compute \(\operatorname {Re}\left \langle (z-\partial _{t,\nu })f ,f\right \rangle _{L_{2,\nu }(\mathbb {R};H)}\) by using Corollary 3.2.6. For proving the surjectivity of z − ∂ t,ν for a suitable z, use the formula
Remark: Later we will see that, actually, \(\sigma (\partial _{t,\nu })=\left \{ \mathrm {i} t+\nu \,;\, t\in \mathbb {R} \right \}\).
Exercise 3.7
Consider the differential equation

Since \(\partial _{t,\nu }^{2}-1=\left (\partial _{t,\nu }-1\right )\left (\partial _{t,\nu }+1\right )\), it follows by Exercise 3.6 that there is a unique \(u\in L_{2,\nu }(\mathbb {R})\) solving this equation if ν∉{−1, 1}. Compute these solutions.
Hint: For \(u\in \operatorname {dom}(\partial _{t,\nu })\) use the fact that u is necessarily continuous (which we shall establish in the next chapter).
Notes
- 1.
Note that the sum is indeed finite and all summands are well-defined if we set

- 2.
By this we mean that f is continuous on \(\left [a,b\right ]\), continuously differentiable on \(\left (a,b\right )\) and f′ has a continuous extension to \(\left [a,b\right ]\).
References
W. Arendt et al., Vector-Valued Laplace Transforms and Cauchy Problems. 2nd edn. (Birkhäuser, Basel, 2011)
J. Diestel, J.J. Uhl Jr., Vector Measures. With a foreword by B. J. Pettis, Mathematical Surveys, No. 15 (American Mathematical Society, Providence, RI, 1977)
D. Morgenstern, Beträge zur nichtlinearen Funktionalanalysis. PhD thesis. TU Berlin, 1952
R. Picard, A structural observation for linear material laws in classical mathematical physics. Math. Methods Appl. Sci. 32, 1768–1803 (2009)
R. Picard, Hilbert Space Approach to Some Classical Transforms (Wiley, New York, 1989)
Author information
Authors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2022 The Author(s)
About this chapter
Cite this chapter
Seifert, C., Trostorff, S., Waurick, M. (2022). The Time Derivative. In: Evolutionary Equations. Operator Theory: Advances and Applications, vol 287. Birkhäuser, Cham. https://doi.org/10.1007/978-3-030-89397-2_3
Download citation
DOI: https://doi.org/10.1007/978-3-030-89397-2_3
Published:
Publisher Name: Birkhäuser, Cham
Print ISBN: 978-3-030-89396-5
Online ISBN: 978-3-030-89397-2
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)



 for all x∉f[ Ω].
for all x∉f[ Ω]. pointwise on all of Ω. Since g
n is μ-measurable and μ-measurable functions are stable under pointwise limits, g is μ-measurable itself. Since f = g except for a μ-nullset, f has a μ-measurable representative. If, on the other hand, f has a μ-measurable representative, let g be this representative. Approximating real and imaginary parts separately, it suffices to treat the case
pointwise on all of Ω. Since g
n is μ-measurable and μ-measurable functions are stable under pointwise limits, g is μ-measurable itself. Since f = g except for a μ-nullset, f has a μ-measurable representative. If, on the other hand, f has a μ-measurable representative, let g be this representative. Approximating real and imaginary parts separately, it suffices to treat the case 
 . It is easy to see that supω ∈ Ω|s
n(ω) − g(ω)|
. It is easy to see that supω ∈ Ω|s
n(ω) − g(ω)| 


 , the sum is finite and S(μ;Y ) is a vector space. Let now be f ∈ L
1(μ;X). Then there is
, the sum is finite and S(μ;Y ) is a vector space. Let now be f ∈ L
1(μ;X). Then there is 

 is a simple function.
is a simple function.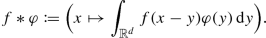
 in
in 