Abstract
This chapter is devoted to the study of evolutionary inclusions. In contrast to evolutionary equations, we will replace the skew-selfadjoint operator A by a so-called maximal monotone relation A ⊆ H × H in the Hilbert space H. The resulting problem is then no longer an equation, but just an inclusion; that is, we consider problems of the form
where \(f\in L_{2,\nu }(\mathbb {R};H)\) is given and \(u\in L_{2,\nu }(\mathbb {R};H)\) is to be determined. This generalisation allows the treatment of certain non-linear problems, since we will not require any linearity for the relation A. Moreover, the property that A is just a relation and not neccessarily an operator can be used to treat hysteresis phenomena, which for instance occur in the theory of elasticity and electro-magnetism.
You have full access to this open access chapter, Download chapter PDF
This chapter is devoted to the study of evolutionary inclusions. In contrast to evolutionary equations, we will replace the skew-selfadjoint operator A by a so-called maximal monotone relation A ⊆ H × H in the Hilbert space H. The resulting problem is then no longer an equation, but just an inclusion; that is, we consider problems of the form
where \(f\in L_{2,\nu }(\mathbb {R};H)\) is given and \(u\in L_{2,\nu }(\mathbb {R};H)\) is to be determined. This generalisation allows the treatment of certain non-linear problems, since we will not require any linearity for the relation A. Moreover, the property that A is just a relation and not neccessarily an operator can be used to treat hysteresis phenomena, which for instance occur in the theory of elasticity and electro-magnetism.
We begin to define the notion of maximal monotone relations in the first part of this chapter. In particular, we introduce the notion of the so-called Yosida approximation of A and provide a useful perturbation result for maximal monotone relations, which will be the key argument for proving the well-posedness of (17.1). For this, we prove the celebrated Theorem of Minty, which characterises the maximal monotone relations by a range condition. The second section is devoted to the main result of this chapter, namely the well-posedness of (17.1), which generalises Picard’s theorem (see Theorem 6.2.1) to a broader class of problems. In the concluding section we consider Maxwell’s equations in a polarisable medium as an application.
17.1 Maximal Monotone Relations and the Theorem of Minty
Definition
Let A ⊆ H × H. We call A monotone if
Moreover, we call A maximal monotone if A is monotone and for each monotone relation B ⊆ H × H with A ⊆ B it follows that A = B.
Remark 17.1.1
Let A ⊆ H × H be a monotone relation.
-
(a)
It is clear that A is maximal monotone if and only if for each x, y ∈ H with
$$\displaystyle \begin{aligned} \forall(u,v)\in A:\;\operatorname{Re}\left\langle u-x ,v-y\right\rangle \geqslant0 \end{aligned}$$it follows that (x, y) ∈ A.
-
(b)
From (a) it follows that A is demiclosed ; i.e., for each sequence \(((x_{n},y_{n}))_{n\in \mathbb {N}}\) in A with x n → x in H and y n → y weakly or x n → x weakly and y n → y in H for some x, y ∈ H as n →∞ it follows that (x, y) ∈ A (note that in both cases we have \(\left \langle u-x_n ,v-y_n\right \rangle \to \left \langle u-x ,v-y\right \rangle \) for each (u, v) ∈ A).
We start to present some first properties of monotone and maximal monotone relations.
Proposition 17.1.2
Let A ⊆ H × H be monotone and λ > 0. Then the following statements hold:
-
(a)
The inverse relation (1 + λA)−1 is a Lipschitz-continuous mapping, which satisfies \(\left \Vert (1+\lambda A)^{-1} \right \Vert { }_{\mathrm {Lip}}\leqslant 1.\)
-
(b)
If 1 + λA is onto, then A is maximal monotone.
Proof
For showing (a), we assume that (f, u), (g, x) ∈ (1 + λA)−1 for some f, g, u, x ∈ H. Then we find v, y ∈ H such that (u, v), (x, y) ∈ A and u + λv = f as well as x + λy = g. The monotonicity of A then yields
If now f = g, then u = x. Hence, (1 + λA)−1 is a mapping and the inequality proves its Lipschitz-continuity with \(\left \Vert (1+\lambda A)^{-1} \right \Vert { }_{\mathrm {Lip}}\leqslant 1\).
To prove (b), let B ⊆ H × H be monotone with A ⊆ B and let (x, y) ∈ B. Since 1 + λA is onto, we find (u, v) ∈ A ⊆ B such that u + λv = x + λy. Since (1 + λB)−1 is a mapping by (a), we infer that
and hence, also v = y, which proves that (x, y) ∈ A and thus, A = B. □
Example 17.1.3
Let \(B\colon \operatorname {dom}(B)\subseteq H\to H\) be a densely defined, closed linear operator. Assume \(\operatorname {Re}\left \langle u ,Bu\right \rangle \geqslant 0\) and \(\operatorname {Re} \left \langle v ,B^\ast v\right \rangle \geqslant 0\) for all \(u\in \operatorname {dom}(B)\) and \(v\in \operatorname {dom}(B^\ast )\). Then B is maximal monotone. Indeed, the monotonicity follows from the linearity of B and by Proposition 6.3.1 the operator 1 + B is continuously invertible, hence onto. Thus, the maximal monotonicity follows by Proposition 17.1.2(b). In particular, every skew-selfadjoint operator is maximal monotone. Moreover, if \(M\colon \operatorname {dom}(M)\subseteq \mathbb {C}\to L(H)\) is a material law such that there exist \(c>0,\nu _{0}\geqslant \mathrm {s}_{\mathrm {b}}\left ( M \right )\) with
then ∂ t,ν M(∂ t,ν) − c is maximal monotone for each \(\nu \geqslant \nu _{0}\).
Our first goal is to show that the implication in Proposition 17.1.2(b) is actually an equivalence. This is Minty’s theorem. For this, we start to introduce subgradients of convex, proper, lower semi-continuous mappings, which form the probably most prominent example of maximal monotone relations.
Definition
Let \(f\colon H\to \left (-\infty ,\infty \right ]\). We call f
-
(a)
convex if for all \(x,y\in H,\lambda \in \left (0,1\right )\) we have
$$\displaystyle \begin{aligned} f(\lambda x+(1-\lambda)y)\leqslant\lambda f(x)+(1-\lambda)f(y). \end{aligned}$$ -
(b)
proper if there exists x ∈ H with f(x) < ∞.
-
(c)
lower semi-continuous (l.s.c.) if for each \(c\in \mathbb {R}\) the sublevel set
$$\displaystyle \begin{aligned}{}[f\leqslant c]=\left\{ x\in H \,;\, f(x)\leqslant c \right\} \end{aligned}$$is closed.
-
(d)
coercive if for each \(c\in \mathbb {R}\) the sublevel set \([f\leqslant c]\) is bounded.
Remark 17.1.4
If \(f\colon H\to \left (-\infty ,\infty \right ]\) is convex, the sublevel sets \([f\leqslant c]\) are convex for each \(c\in \mathbb {R}\). Hence, if f is convex, l.s.c. and coercive, the sets \([f\leqslant c]\) are weakly sequentially compact (or, by the Eberlein–Šmulian theorem [50, theorem 13.1], equivalently, weakly compact) for each \(c\in \mathbb {R}.\) Indeed, if \((x_{n})_{n\in \mathbb {N}}\) is a sequence in \([f\leqslant c]\) for some \(c\in \mathbb {R}\), then it is bounded and thus, posseses a weakly convergent subsequence with weak limit x ∈ H. Since \([f\leqslant c]\) is closed and convex, Mazur’s theorem [50, Corollary 2.11] yields that it is weakly closed and thus, \(x\in [f\leqslant c]\) proving the claim.
Definition
Let \(f\colon H\to \left (-\infty ,\infty \right ]\) be convex. We define the subgradient of f by

Remark 17.1.5
Note that \(u\mapsto f(x)+\operatorname {Re}\langle y,u-x\rangle \) is an affine function touching the graph of f in x. Thus, the subgradient is the set of all pairs (x, y) ∈ H such that there exists an affine function with slope y touching the graph of f in x. It is not hard to show that if f is differentiable in x, then (x, y) ∈ ∂f if and only if y = f′(x) (see Exercise 17.1). Thus, the subgradient of f provides a generalisation of the derivative for arbitrary convex functions.
Proposition 17.1.6
Let \(f\colon H\to \left (-\infty ,\infty \right ]\) be convex and proper. Then the following statements hold:
-
(a)
If (x, y) ∈ ∂f, then f(x) < ∞. Moreover, the subgradient ∂f is monotone.
-
(b)
If f is l.s.c. and coercive, then there exists x ∈ H such that f(x) =infu ∈ H f(u).
-
(c)
Let α⩾0, x, y ∈ H and \(g\!:H\to \left (-\infty ,\infty \right ]\) with
 for u ∈ H. Then g(x) =infu ∈ H
g(u) if and only if (x, α(y − x)) ∈ ∂f.
for u ∈ H. Then g(x) =infu ∈ H
g(u) if and only if (x, α(y − x)) ∈ ∂f.
-
(d)
Let α > 0 and y ∈ H. If f is l.s.c., then \(g\!\!:H\to \left (-\infty ,\infty \right ]\) with
 for u ∈ H is convex, proper, l.s.c and coercive. In particular 1 + α∂f is onto and hence, ∂f is maximal monotone.
for u ∈ H is convex, proper, l.s.c and coercive. In particular 1 + α∂f is onto and hence, ∂f is maximal monotone.
Proof
-
(a)
If (x, y) ∈ ∂f we have \(f(u)\geqslant f(x)+\operatorname {Re}\left \langle y ,u-x\right \rangle \) for each u ∈ H. Since f is proper, we find u ∈ H such that f(u) < ∞ and hence, also f(x) < ∞. Let now (u, v), (x, y) ∈ ∂f. Then we have \(f(u)\geqslant f(x)+\operatorname {Re}\left \langle y ,u-x\right \rangle \) and \(f(x)\geqslant f(u)+\operatorname {Re}\left \langle v ,x-u\right \rangle =f(u)-\operatorname {Re}\left \langle v ,u-x\right \rangle .\) Summing up both expressions (note that f(x), f(u) < ∞ by what we have shown before), we infer
$$\displaystyle \begin{aligned} \operatorname{Re}\left\langle y-v ,u-x\right\rangle \leqslant0, \end{aligned}$$which shows the monotonicity.
-
(b)
Let \((x_{n})_{n\in \mathbb {N}}\) in H with

. Note that \(d\in \mathbb {R},\) since f is proper. Without loss of generality, we can assume that \(x_{n}\in [f\leqslant d+1]\) for each \(n\in \mathbb {N}\) and by Remark 17.1.4 we can assume that x n → x weakly as n →∞ for some x ∈ H. Let ε > 0. Since \(x_{n}\in [f\leqslant d+\varepsilon ]\) for sufficiently large \(n\in \mathbb {N},\) we derive \(x\in [f\leqslant d+\varepsilon ]\) again by Remark 17.1.4 and so, \(f(x)\leqslant d+\varepsilon \) for each ε > 0, showing the claim.
-
(c)
Assume that g(x) =infu ∈ H g(u) and let u ∈ H. Since f is proper, so is g and thus, we have g(x) < ∞, which in turn gives f(x) < ∞. Let \(\lambda \in \left (0,1\right ]\) and set
 . Then the convexity of f yields $$\displaystyle \begin{aligned} \lambda\left(f(u)-f(x)\right) & \geqslant f(w)-f(x)\\ &= g(w)-g(x)+\frac{\alpha}{2}(\left\Vert x-y \right\Vert ^{2}-\left\Vert w-y \right\Vert ^{2})\\ & \geqslant\frac{\alpha}{2}(\left\Vert x-y \right\Vert ^{2}-\left\Vert w-y \right\Vert ^{2})\\ & =\frac{\alpha}{2}\big(\left\Vert x-y \right\Vert ^{2}-\left\Vert \lambda(u-x)+x-y \right\Vert ^{2}\big)\\ & =\frac{\alpha}{2}\big(-2\lambda\operatorname{Re}\left\langle u-x ,x-y\right\rangle -\lambda^{2}\left\Vert u-x \right\Vert ^{2}\big). \end{aligned} $$
. Then the convexity of f yields $$\displaystyle \begin{aligned} \lambda\left(f(u)-f(x)\right) & \geqslant f(w)-f(x)\\ &= g(w)-g(x)+\frac{\alpha}{2}(\left\Vert x-y \right\Vert ^{2}-\left\Vert w-y \right\Vert ^{2})\\ & \geqslant\frac{\alpha}{2}(\left\Vert x-y \right\Vert ^{2}-\left\Vert w-y \right\Vert ^{2})\\ & =\frac{\alpha}{2}\big(\left\Vert x-y \right\Vert ^{2}-\left\Vert \lambda(u-x)+x-y \right\Vert ^{2}\big)\\ & =\frac{\alpha}{2}\big(-2\lambda\operatorname{Re}\left\langle u-x ,x-y\right\rangle -\lambda^{2}\left\Vert u-x \right\Vert ^{2}\big). \end{aligned} $$Dividing the latter expression by λ and taking the limit λ → 0, we infer
$$\displaystyle \begin{aligned} -\alpha\operatorname{Re}\left\langle u-x ,x-y\right\rangle \leqslant f(u)-f(x), \end{aligned}$$which proves (x, α(y − x)) ∈ ∂f.Assume now that (x, α(y − x)) ∈ ∂f. For each u ∈ H we have
$$\displaystyle \begin{aligned} \left\Vert x-y \right\Vert ^{2}-2\operatorname{Re}\left\langle y-x ,u-x\right\rangle & =\left\Vert y-x-(u-x) \right\Vert ^{2}-\left\Vert u-x \right\Vert ^{2}\leqslant\left\Vert u-y \right\Vert ^{2} \end{aligned} $$and thus,
$$\displaystyle \begin{aligned} f(u) \geqslant f(x)+\operatorname{Re}\left\langle \alpha(y-x) ,u-x\right\rangle \geqslant f(x)+\frac{\alpha}{2}\big(\left\Vert x-y \right\Vert ^{2}-\left\Vert u-y \right\Vert ^{2}\big), \end{aligned} $$which shows the claim.
-
(d)
We first show that there exists an affine function \(h\!:H\to \mathbb {R}\) with \(h\leqslant f\). For this, we consider the epigraph of f given by
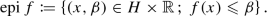
Since f is convex and l.s.c., one easily verifies that \(\operatorname {epi} f\) is convex and closed. Moreover, since f is proper, \(\operatorname {epi} f\ne \varnothing .\) Let now z ∈ H with f(z) < ∞ and η < f(z). Then \((z,\eta )\in (H\times \mathbb {R})\setminus \operatorname {epi} f\) and by the Hahn–Banach theorem we find w ∈ H and \(\gamma \in \mathbb {R}\) such that
$$\displaystyle \begin{aligned} \operatorname{Re}\left\langle w ,z\right\rangle +\gamma\eta<\operatorname{Re}\left\langle w ,x\right\rangle +\gamma\beta \end{aligned}$$for all \((x,\beta )\in \operatorname {epi} f.\) In particular
$$\displaystyle \begin{aligned} \operatorname{Re}\left\langle w ,z\right\rangle +\gamma\eta<\operatorname{Re}\left\langle w ,x\right\rangle +\gamma f(x) \end{aligned}$$for each x ∈ H and since this holds also for x = z, we infer γ > 0. Choosing
 for x ∈ H, we have found the asserted affine function.
for x ∈ H, we have found the asserted affine function.Using this, we have that
$$\displaystyle \begin{aligned} g(u)\geqslant\frac{\alpha}{2}\left\Vert u-y \right\Vert ^{2}+h(u)\quad (u\in H) \end{aligned}$$and since the right-hand side tends to ∞ as ∥u∥→∞, we derive that g is coercive. Moreover, g is convex, proper and l.s.c. (see Exercise 17.2) and thus, there exists x ∈ H with g(x) =infu ∈ H g(u) by (b). By (c), (x, α(y − x)) ∈ ∂f and thus, (x, y) ∈ 1 + α∂f. Since y ∈ H was arbitrary, 1 + α∂f is onto and so, ∂f is maximal monotone by (a) and Proposition 17.1.2(b).
□
We can now prove Minty’s theorem .
Theorem 17.1.7 (Minty)
Let A ⊆ H × H maximal monotone. Then 1 + λA is onto for all λ > 0.
Proof
Since λA is maximal monotone for each λ > 0, it suffices to prove the statement for λ = 1. Moreover, since A − (0, f) is maximal monotone for each f ∈ H, it suffices to show \(0\in \operatorname {ran}(1+A).\) For this, define \(f_{A}\colon H\times H\to \left (-\infty ,\infty \right ]\) by (note that \(A\ne \varnothing \) by maximal monotonicity)

As a supremum of affine functions, we see that f A is convex and l.s.c. Moreover, we have that
for each u, v ∈ H and since A is maximal monotone, we get by using Remark 17.1.1
and so
In particular, we get \(f_{A}(u,v)\geqslant \operatorname {Re}\left \langle u ,v\right \rangle \) for each u, v ∈ H and \(f_{A}(u,v)=\operatorname {Re}\left \langle u ,v\right \rangle \) if and only if (u, v) ∈ A. Thus, f A is proper since \(A\ne \varnothing \). By Proposition 17.1.6(d) we obtain that \(0\in \operatorname {ran}(1+\partial f_{A})\) and thus, we find (u 0, v 0) ∈ H × H with ((u 0, v 0), (−u 0, −v 0)) ∈ ∂f A. Hence, by definition of ∂f A,
for all (u, v) ∈ H × H. In particular, using that \(f_{A}(u,v)=\operatorname {Re}\left \langle u ,v\right \rangle \) for (u, v) ∈ A we get
Taking the supremum over all (u, v) ∈ A, we infer
Thus, u 0 + v 0 = 0 and instead of inequalities, we actually have equalities in the expression above. Thus, \(f_{A}(u_{0},v_{0})=\operatorname {Re}\left \langle u_{0} ,v_{0}\right \rangle \) and so, (u 0, v 0) ∈ A. From u 0 + v 0 = 0 it thus follows that \(0\in \operatorname {ran}(1+A).\) □
Next, we show how to extend maximal monotone relations on a Hilbert space H to the Bochner–Lebesgue space L 2(μ;H) for a σ-finite measure space \((\Omega ,\mathcal {A},\mu )\). The condition (0, 0) ∈ A can be dropped if μ( Ω) < ∞.
Corollary 17.1.8
Let A ⊆ H × H maximal monotone with (0, 0) ∈ A. Moreover, let \((\Omega ,\mathcal {A},\mu )\) be a σ-finite measure space and define

Then \(A_{L_2(\mu ;H)}\) is maximal monotone.
Proof
The monotonicity of \(A_{L_2(\mu ;H)}\) is clear. For showing the maximal monotonicity we prove that \(1+A_{L_2(\mu ;H)}\) is onto (see Proposition 17.1.2(b)). For this, let h ∈ L
2(μ;H) and set  for each t ∈ Ω. Note that f is well-defined by Theorem 17.1.7. Since (1 + A)−1 is continuous by Proposition 17.1.2(a) and h is Bochner-measurable, f is also Bochner-measurable. Moreover, using that (0, 0) ∈ 1 + A and \(\left \Vert (1+A)^{-1} \right \Vert { }_{\mathrm {Lip}}\leqslant 1\), we compute
for each t ∈ Ω. Note that f is well-defined by Theorem 17.1.7. Since (1 + A)−1 is continuous by Proposition 17.1.2(a) and h is Bochner-measurable, f is also Bochner-measurable. Moreover, using that (0, 0) ∈ 1 + A and \(\left \Vert (1+A)^{-1} \right \Vert { }_{\mathrm {Lip}}\leqslant 1\), we compute
and so, f ∈ L 2(μ;H). Thus, h − f ∈ L 2(μ;H), which yields \((f,h-f)\in A_{L_2(\mu ;H)}\) and so, \(h\in \operatorname {ran}(1+A_{L_2(\mu ;H)}).\) □
17.2 The Yosida Approximation and Perturbation Results
We now have all concepts at hand to introduce the Yosida approximation for a maximal monotone relation.
Definition
Let A ⊆ H × H be maximal monotone and λ > 0. We define

The family (A λ)λ>0 is called Yosida approximation of A.
Since for a maximal monotone relation A ⊆ H × H the resolvent (1 + λA)−1 is actually a Lipschitz-continuous mapping (by Proposition 17.1.2(a)), whose domain is H (by Theorem 17.1.7), the same holds for A λ. We collect some useful properties of the Yosida approximation.
Proposition 17.2.1
Let A ⊆ H × H maximal monotone and λ > 0. Then the following statements hold:
-
(a)
For all x ∈ H we have \(\left ((1+\lambda A)^{-1}(x),A_{\lambda }(x)\right )\in A\).
-
(b)
A λ is monotone and \(\left \Vert A_{\lambda } \right \Vert { }_{\mathrm {Lip}}\leqslant \frac {1}{\lambda }\).
Proof
-
(a)
For all x ∈ H we have that ((1 + λA)−1(x), x) ∈ 1 + λA, and therefore, ((1 + λA)−1(x), A λ(x)) ∈ A.
-
(b)
Let x, y ∈ H. Then we compute
$$\displaystyle \begin{aligned} &\lambda\operatorname{Re}\left\langle A_{\lambda}(x)-A_{\lambda}(y) ,x-y\right\rangle\\ &\quad =\left\Vert x-y \right\Vert ^{2}-\operatorname{Re}\left\langle (1+\lambda A)^{-1}(x)-(1+\lambda A)^{-1}(y) ,x-y\right\rangle \\ &\quad \geqslant\left\Vert x-y \right\Vert ^{2}-\left\Vert (1+\lambda A)^{-1}(x)-(1+\lambda A)^{-1}(y) \right\Vert \left\Vert x-y \right\Vert \\ &\quad \geqslant0 \end{aligned} $$by Proposition 17.1.2(a) and hence, A λ is monotone. Moreover,
$$\displaystyle \begin{aligned} &\operatorname{Re}\left\langle A_{\lambda}(x)-A_{\lambda}(y) ,x-y\right\rangle \\ &\quad =\operatorname{Re}\left\langle A_{\lambda}(x)-A_{\lambda}(y) ,(1+\lambda A)^{-1}(x)-(1+\lambda A)^{-1}(y)\right\rangle \\ & \qquad +\lambda\left\Vert A_{\lambda}(x)-A_{\lambda}(y) \right\Vert ^{2}\\ & \quad \geqslant\lambda\left\Vert A_{\lambda}(x)-A_{\lambda}(y) \right\Vert ^{2}, \end{aligned} $$where we have used (a) and the monotonicity of A. The Cauchy–Schwarz inequality now yields \(\left \Vert A_{\lambda } \right \Vert { }_{\mathrm {Lip}}\leqslant \frac {1}{\lambda }\).
□
We state a result on the strong convergence of the resolvents of a maximal monotone relation, which we already have used in previous sections for the resolvent of ∂ t,ν. For the projection P C(x) of x ∈ H onto a non-empty closed convex set C ⊆ H, recall Exercise 4.4 and that y = P C(x) if and only if y ∈ C and
Proposition 17.2.2
Let A ⊆ H × H be maximal monotone. Then
\(\overline {\mathrm {dom}\, (A)}\)
is convex and for all x ∈ H we have
\((1+\lambda A)^{-1}(x) \to P_{\overline {\mathrm {dom}\, (A)}}(x)\)
as
 , where
\(P_{\overline {\mathrm {dom}\, (A)}}\)
denotes the projection onto
\(\overline {\mathrm {dom}\, (A)}\).
, where
\(P_{\overline {\mathrm {dom}\, (A)}}\)
denotes the projection onto
\(\overline {\mathrm {dom}\, (A)}\).
Proof
We set  . Then C is closed and convex. Next, we prove that (1 + λA)−1(x) → P
C(x) as
. Then C is closed and convex. Next, we prove that (1 + λA)−1(x) → P
C(x) as  for all x ∈ H. So let x ∈ H and set
for all x ∈ H. So let x ∈ H and set  for each λ > 0. Then we have \(A_\lambda (x)=\frac {1}{\lambda }(x-x_\lambda )\) and hence, using Proposition 17.2.1(a) and the monotonicity of A, we infer \(\operatorname {Re} \left \langle x_\lambda -u ,\frac {1}{\lambda }(x-x_\lambda )-v\right \rangle \geqslant 0\) for each (u, v) ∈ A. Consequently, we obtain
for each λ > 0. Then we have \(A_\lambda (x)=\frac {1}{\lambda }(x-x_\lambda )\) and hence, using Proposition 17.2.1(a) and the monotonicity of A, we infer \(\operatorname {Re} \left \langle x_\lambda -u ,\frac {1}{\lambda }(x-x_\lambda )-v\right \rangle \geqslant 0\) for each (u, v) ∈ A. Consequently, we obtain
In particular, we see that (x λ)λ>0 is bounded as λ → 0 and so, for each nullsequence we find a subsequence (λ n)n with λ n → 0 such that \(x_{\lambda _n}\to z\) weakly for some z ∈ H. By (17.2) it follows that
It is easy to see that this inequality carries over to each u ∈ C and thus \(\operatorname {Re} \left \langle z-u ,z-x\right \rangle \leqslant 0\) for each u ∈ C which proves z = P C(x) and hence, \(x_{\lambda _n}\to P_C (x)\) weakly. Next we prove that the convergence also holds in the norm topology. From (17.2) we see that
and again, this inequality stays true for each u ∈ C. In particular, choosing u = P C(x) we infer \(\limsup _{n\to \infty } \left \Vert x_{\lambda _n} \right \Vert ^2 \leqslant \left \Vert P_C(x) \right \Vert ^2\), which together with the weak convergence, yields the convergence in norm (see Exercise 17.3). A subsequence argument (cf. Exercise 14.3) reveals x λ → P C(x) in H as λ → 0. It remains to show that \(\overline {\mathrm {dom}\, (A)}\) is convex. By what we have shown above, we have (1 + λA)−1(x) → x as λ → 0 for each x ∈ C and since (1 + λA)−1(x) ∈dom (A) for each λ > 0, we infer \(x\in \overline {\mathrm {dom}\, (A)}\). Thus, \(C\subseteq \overline {\mathrm {dom}\, (A)}\) and since the other inclusion holds trivially the proof is completed. □
We conclude this section with some perturbation results.
Lemma 17.2.3
Let A ⊆ H × H be maximal monotone and C : H → H Lipschitz-continuous and monotone. Then A + C is maximal monotone.
Proof
The monotonicity of A + C is clear. If C is constant, then the maximality of A + C is obvious. If C is non-constant we choose \(0<\lambda <\frac {1}{\left \Vert C \right \Vert { }_{\mathrm {Lip}}}\). Then for all f ∈ H the mapping
defines a strict contraction (use Proposition 17.1.2(a) and \(\operatorname {dom}((1+\lambda A)^{-1})=H\) by Theorem 17.1.7) and thus, posseses a fixed point x ∈ H, which then satisfies (x, f) ∈ 1 + λ(A + C). Thus, A + C is maximal monotone by Proposition 17.1.2(b). □
We note that the latter lemma particularily applies to C = B λ for a maximal monotone relation B ⊆ H × H and λ > 0 by Proposition 17.2.1(b).
Proposition 17.2.4
Let A, B ⊆ H × H be two maximal monotone relations, c > 0 and f ∈ H. For λ > 0 we set

Then \(f\in \operatorname {ran}(c+A+B)\) if and only if \(\sup _{\lambda >0}\left \Vert B_{\lambda }(x_{\lambda }) \right \Vert <\infty \) and in the latter case x λ → x as λ → 0 with (x, f) ∈ c + A + B, which identifies x uniquely.
Proof
Note that x λ is well-defined for λ > 0 by Lemma 17.2.3, Theorem 17.1.7 and Proposition 17.1.2.
For all λ > 0 we find y λ ∈ H such that (x λ, y λ) ∈ A and cx λ + y λ + B λ(x λ) = f.
We first assume that there exist x, y, z ∈ H such that (x, y) ∈ A, (x, z) ∈ B and cx + y + z = f. Thus, we have
which gives
where we have used the monotonicity of A in the second line and the monotonicity of B as well as Proposition 17.2.1(a) in the last line. The latter implies
and the claim follows by the Cauchy–Schwarz inequality.
Assume now that  and let μ, λ > 0. As above, we compute
and let μ, λ > 0. As above, we compute
Thus, for a nullsequence \((\lambda _{n})_{n\in \mathbb {N}}\) in \(\left (0,\infty \right )\) we infer that \((x_{\lambda _{n}})_{n\in \mathbb {N}}\) is a Cauchy sequence whose limit we denote by x. Since \((B_{\lambda _{n}}(x_{\lambda _{n}}))_{n\in \mathbb {N}}\) is bounded, we can assume, by passing to a suitable subsequence, that \(B_{\lambda _{n}}(x_{\lambda _{n}})\to z\) weakly for some z ∈ H. Then
and since \(((1+\lambda _{n}B)^{-1}(x_{\lambda _{n}}),B_{\lambda _{n}}(x_{\lambda _{n}}))\in B\) for each \(n\in \mathbb {N}\) by Proposition 17.2.1(a), the demi-closedness of B (see Remark 17.1.1) reveals (x, z) ∈ B. Moreover,

weakly and hence, by the demi-closedness of A, we infer (x, y) ∈ A, which completes the proof of the asserted equivalence. By a subsequence argument (cf. Exercise 14.3) we obtain the asserted convergence (note that x = (c + A + B)−1(f) is uniquely determined by f). □
To treat the example in Sect. 17.4 we need another perturbation result, for which we need to introduce the notion of local boundedness of a relation.
Definition
Let A ⊆ H × H and x ∈dom (A). Then A is called locally bounded at x if there exists δ > 0 such that
is bounded.
Proposition 17.2.5
Let A ⊆ H × H be maximal monotone such that \(\operatorname {int} \operatorname {conv} \mathrm {dom}\, (A)\ne \varnothing \) . Then \(\operatorname {int} \mathrm {dom}\, (A)=\operatorname {int} \operatorname {conv} \mathrm {dom}\, (A)=\operatorname {int} \overline {\mathrm {dom}\, (A)}\) and A is locally bounded at each point \(x\in \operatorname {int}\mathrm {dom}\, (A)\).
In order to prove this proposition, we need the following lemma.
Lemma 17.2.6
Let
\((D_n)_{n\in \mathbb {N}}\)
be a sequence of subsets of H with D
n ⊆ D
n+1
for each
\(n\in \mathbb {N}\)
and
 . If
\(\operatorname {int} \operatorname {conv} D\ne \varnothing \)
, then
\(\operatorname {int} \operatorname {conv} D =\bigcup _{n\in \mathbb {N}} \operatorname {int} \overline {\operatorname {conv} D_n}\).
. If
\(\operatorname {int} \operatorname {conv} D\ne \varnothing \)
, then
\(\operatorname {int} \operatorname {conv} D =\bigcup _{n\in \mathbb {N}} \operatorname {int} \overline {\operatorname {conv} D_n}\).
Proof
Set  . By Exercise 17.4 we have \(\overline {C}=\overline {\operatorname {conv} D}\). Since \((D_n)_{n\in \mathbb {N}}\) is increasing we have \(\operatorname {conv} D =\bigcup _{n\in \mathbb {N}} \operatorname {conv} D_n\) and hence, \(C\subseteq \bigcup _{n\in \mathbb {N}} \overline {\operatorname {conv} D_n}\subseteq \overline {C}\). Since C is a Baire space by Exercise 17.5, we find \(n_0\in \mathbb {N}\) such that \(\operatorname {int} \overline {\operatorname {conv} D_{n_0}} \ne \varnothing \) and hence, \( \operatorname {int} \overline {\operatorname {conv} D_{n}} \ne \varnothing \) for each \(n\geqslant n_0\). Hence, \(\overline {\operatorname {conv} D_n}=\overline {\operatorname {int} \overline {\operatorname {conv} D_n}}\) for each \(n\geqslant n_0\) by Exercise 17.4. Thus,
. By Exercise 17.4 we have \(\overline {C}=\overline {\operatorname {conv} D}\). Since \((D_n)_{n\in \mathbb {N}}\) is increasing we have \(\operatorname {conv} D =\bigcup _{n\in \mathbb {N}} \operatorname {conv} D_n\) and hence, \(C\subseteq \bigcup _{n\in \mathbb {N}} \overline {\operatorname {conv} D_n}\subseteq \overline {C}\). Since C is a Baire space by Exercise 17.5, we find \(n_0\in \mathbb {N}\) such that \(\operatorname {int} \overline {\operatorname {conv} D_{n_0}} \ne \varnothing \) and hence, \( \operatorname {int} \overline {\operatorname {conv} D_{n}} \ne \varnothing \) for each \(n\geqslant n_0\). Hence, \(\overline {\operatorname {conv} D_n}=\overline {\operatorname {int} \overline {\operatorname {conv} D_n}}\) for each \(n\geqslant n_0\) by Exercise 17.4. Thus,
Finally, since \(\bigcup _{n\in \mathbb {N}}\operatorname {int} \overline {\operatorname {conv} D_n}\) is open and convex, we infer \(C=\bigcup _{n\in \mathbb {N}}\operatorname {int} \overline {\operatorname {conv} D_n}\) by Exercise 17.4. □
Proof of Proposition 17.2.5
We first show that A is locally bounded at each point in \(\operatorname {int} \operatorname {conv} \mathrm {dom}\, (A)\). For this, we set

Then \(\mathrm {dom}\, (A)=\bigcup _{n\in \mathbb {N}} \operatorname {dom}(A_n)\) and \(\operatorname {dom}(A_n)\subseteq \operatorname {dom}(A_{n+1})\) for each \(n\in \mathbb {N}\). Since \(\operatorname {int} \operatorname {conv} \mathrm {dom}\, (A)\ne \varnothing \), Lemma 17.2.6 gives \(\operatorname {int} \operatorname {conv} \mathrm {dom}\, (A)=\bigcup _{n\in \mathbb {N}} \operatorname {int} \overline {\operatorname {conv} \operatorname {dom}(A_n)}\). Thus, it suffices to show that A is locally bounded at each \(x\in \operatorname {int} \overline {\operatorname {conv} \operatorname {dom}(A_n)}\) for each \(n\in \mathbb {N}\). So, let \(x\in \operatorname {int} \overline {\operatorname {conv} \operatorname {dom}(A_n)}\) for some \(n\in \mathbb {N}\). Then we find δ > 0 such that \(B[x,\delta ]\subseteq \overline {\operatorname {conv} \operatorname {dom}(A_n)}\). We show that \(A[B(x,\frac {\delta }{2})]\) is bounded. So, let (u, v) ∈ A with \(\left \Vert u-x \right \Vert <\frac {\delta }{2}\) and note that \(u \in \overline {\operatorname {conv} \operatorname {dom}(A_n)}\subseteq B[0,n]\). Then for each (a, b) ∈ A n we have \(\operatorname {Re} \left \langle u-a ,v-b\right \rangle \geqslant 0\) and thus
Clearly, this inequality carries over to each \(a\in \overline {\operatorname {conv} \operatorname {dom}(A_n)}\). If v≠0 we choose  , and obtain
, and obtain
which shows the boundedness of \(A[B(x,\frac {\delta }{2})]\). To complete the proof we need to show that \(\operatorname {int} \mathrm {dom}\, (A)=\operatorname {int} \operatorname {conv} \mathrm {dom}\, (A)=\operatorname {int} \overline {\mathrm {dom}\, (A)}\). First we note that \(\overline {\mathrm {dom}\, (A)}\) is convex by Proposition 17.2.2 and hence, \(\overline {\operatorname {conv} \mathrm {dom}\, (A)}=\overline {\mathrm {dom}\, (A)}\). Now Exercise 17.4(b) gives
To show the missing equality it suffices to prove that \(\operatorname {int} \operatorname {conv} \mathrm {dom}\, (A)\subseteq \mathrm {dom}\, (A)\). So, let \(x\in \operatorname {int}\operatorname {conv} \mathrm {dom}\, (A)\). Then \(x\in \overline {\mathrm {dom}\, (A)}\) and hence, we find a sequence \(((x_n,y_n))_{n\in \mathbb {N}}\) in A with x n → x. Since A is locally bounded at x, the sequence \((y_n)_{n\in \mathbb {N}}\) is bounded and hence, we can assume without loss of generality that y n → y weakly for some y ∈ H. The demi-closedness of A (see Remark 17.1.1) yields (x, y) ∈ A and thus, x ∈dom (A). □
Now we can prove the following perturbation result.
Theorem 17.2.7
Let A, B ⊆ H × H be maximal monotone, \(\big (\operatorname {int}\mathrm {dom}\, (A)\big )\cap \operatorname {dom}(B)\ne \varnothing \) . Then A + B is maximal monotone.
Proof
By shifting A and B, we can assume without loss of generality that (0, 0) ∈ A ∩ B and \(0\in (\operatorname {int} \mathrm {dom}\, (A))\cap \operatorname {dom}(B)\). We need to prove that \(\operatorname {ran}(1+A+B)=H\). So, let y ∈ H and set

Since (0, 0) ∈ A ∩ B λ and \(\left \Vert (1+A+B_\lambda )^{-1} \right \Vert { }_{\mathrm {Lip}}\leqslant 1\), we infer that \(\left \Vert x_\lambda \right \Vert \leqslant \left \Vert y \right \Vert \) for each λ > 0. For showing \(y\in \operatorname {ran}(1+A+B)\) we need to prove that \(\sup _{\lambda >0} \left \Vert B_\lambda (x_\lambda ) \right \Vert <\infty \) by Proposition 17.2.4. By definition we find y λ ∈ H such that (x λ, y λ) ∈ A and y = x λ + y λ + B λ(x λ) for each λ > 0. Since A is locally bounded at \(0\in \operatorname {int} \mathrm {dom}\, (A)\) by Proposition 17.2.5 we find R, δ > 0 with B(0, δ) ⊆dom (A) and
For λ > 0 we define  if y
λ≠0 and
if y
λ≠0 and  if y
λ = 0. Then \(\left \Vert u_\lambda \right \Vert \leqslant \frac {\delta }{2}<\delta \) and thus, u
λ ∈dom (A). Hence, there exist v
λ ∈ H with (u
λ, v
λ) ∈ A and \(\left \Vert v_\lambda \right \Vert \leqslant R\) for each λ > 0. The monotonicity of A then yields
if y
λ = 0. Then \(\left \Vert u_\lambda \right \Vert \leqslant \frac {\delta }{2}<\delta \) and thus, u
λ ∈dom (A). Hence, there exist v
λ ∈ H with (u
λ, v
λ) ∈ A and \(\left \Vert v_\lambda \right \Vert \leqslant R\) for each λ > 0. The monotonicity of A then yields
where we have used the monotonicity of B λ and B λ(0) = 0 in the fourth line. Hence, we obtain
which shows that (y λ)λ>0 is bounded and thus, also \(\sup _{\lambda >0}\left \Vert B_\lambda (x_\lambda ) \right \Vert <\infty \). □
17.3 A Solution Theory for Evolutionary Inclusions
In this section we provide a solution theory for evolutionary inclusions by generalising Picard’s theorem (see Theorem 6.2.1) to the following situation.
Throughout, we assume that A ⊆ H × H is a maximal monotone relation with (0, 0) ∈ A. Moreover, let \(M\colon \operatorname {dom}(M)\subseteq \mathbb {C}\to L(H)\) be a material law satisfying the usual positive definiteness constraint
Then for \(\nu \geqslant \max \{\nu _{0},0\}\), ν ≠ 0, we consider evolutionary inclusions of the form
where \(A_{L_{2,\nu }(\mathbb {R};H)}\) is defined as in Corollary 17.1.8. The solution theory for this kind of problems is as follows.
Theorem 17.3.1
Let
\(\nu \geqslant \max \{\nu _{0},0\}\)
, ν ≠ 0. Then the inverse relation
 is a Lipschitz-continuous mapping,
\(\operatorname {dom}(S_{\nu })=L_{2,\nu }(\mathbb {R};H)\)
and
\(\left \Vert S_{\nu } \right \Vert { }_{\mathrm {Lip}}\leqslant \frac {1}{c}\)
. Moreover, the solution mapping S
ν
is causal and independent of ν in the sense that S
ν(f) = S
μ(f) for each
\(f\in L_{2,\nu }(\mathbb {R};H)\cap L_{2,\mu }(\mathbb {R};H)\)
and
\(\mu \geqslant \nu \geqslant \max \{\nu _{0},0\}\)
, ν ≠ 0.
is a Lipschitz-continuous mapping,
\(\operatorname {dom}(S_{\nu })=L_{2,\nu }(\mathbb {R};H)\)
and
\(\left \Vert S_{\nu } \right \Vert { }_{\mathrm {Lip}}\leqslant \frac {1}{c}\)
. Moreover, the solution mapping S
ν
is causal and independent of ν in the sense that S
ν(f) = S
μ(f) for each
\(f\in L_{2,\nu }(\mathbb {R};H)\cap L_{2,\mu }(\mathbb {R};H)\)
and
\(\mu \geqslant \nu \geqslant \max \{\nu _{0},0\}\)
, ν ≠ 0.
In order to prove this theorem, we need some prerequisites. We start with an estimate, which will give us the uniqueness of the solution as well as the causality of the solution mapping S ν.
Proposition 17.3.2
Let \(\nu \geqslant \max \{\nu _{0},0\}\) , ν ≠ 0, and
Then for all \(a\in \mathbb {R}\)

Proof
By definition, we find sequences \(((u_{n},f_{n}))_{n\in \mathbb {N}}\) and \(((x_{n},g_{n}))_{n\in \mathbb {N}}\) in \(\partial _{t,\nu }M(\partial _{t,\nu })+A_{L_{2,\nu }(\mathbb {R};H)}\) such that u n → u, x n → x, f n → f and g n → g as n →∞. In particular, for each \(n\in \mathbb {N}\) we find \(v_{n},y_{n}\in L_{2,\nu }(\mathbb {R};H)\) such that \((u_{n},v_{n}),(x_{n},y_{n})\in A_{L_{2,\nu }(\mathbb {R};H)}\) and
Since (0, 0) ∈ A, we infer  and hence, we may estimate
and hence, we may estimate

where we used Corollary 17.1.8. Moreover, since z↦(zM(z))−1 is a material law, (∂
t,ν
M(∂
t,ν))−1 is causal. By Proposition 16.2.3, for \(\phi \in \operatorname {dom}(\partial _{t,\nu }M(\partial _{t,\nu }))\) we have  . Thus, we end up with
. Thus, we end up with

which yields

Letting n →∞, we derive the assertion. □
Next, we address the existence of a solution for (17.3) for suitable right-hand sides f. For this, we provide another useful characterisation for the weak differentiability of a function in \(L_{2,\nu }(\mathbb {R};H)\).
Lemma 17.3.3
Let \(\nu \in \mathbb {R}\), \(u\in L_{2,\nu }(\mathbb {R};H)\) . Then \(u\in \operatorname {dom}(\partial _{t,\nu })\) if and only if \(\sup _{0<h\leqslant h_{0}}\frac {1}{h}\left \Vert \tau _{h}u-u \right \Vert <\infty \) for some h 0 > 0. In either case
in \(L_{2,\nu }(\mathbb {R};H)\).
Proof
For h > 0 we consider the operator \(D_{h}\colon L_{2,\nu }(\mathbb {R};H)\to L_{2,\nu }(\mathbb {R};H)\) given by \(D_{h}v=\frac {1}{h}(\tau _{h}v-v)\). If \(v\in C_{\mathrm {c}}^1(\mathbb {R};H)\) we estimate

By density of \(C_{\mathrm {c}}^1(\mathbb {R};H)\) in \(H_{\nu }^{1}(\mathbb {R};H)\) we infer that

Moreover, for \(v\in C_{\mathrm {c}}^1(\mathbb {R};H)\) it is clear that D h v → v′ in \(L_{2,\nu }(\mathbb {R};H)\) as h → 0 by dominated convergence. Since \((D_{h})_{0\leqslant h\leqslant 1}\) is uniformly bounded, the convergence carries over to elements in \(H_{\nu }^{1}(\mathbb {R};H)\), which proves the first asserted implication and the convergence statement. Assume now that \(\sup _{0<h\leqslant h_{0}}\frac {1}{h}\left \Vert \tau _{h}u-u \right \Vert <\infty \) for some h 0 > 0. Choosing a suitable sequence \((h_{n})_{n\in \mathbb {N}}\) in \(\left (0,h_{0}\right ]\) with h n → 0 as n →∞, we can assume that \(\frac {1}{h_{n}}(\tau _{h_{n}}u-u)\to v\) weakly for some \(v\in L_{2,\nu }(\mathbb {R};H).\) Then we compute for each \(\phi \in C_{\mathrm {c}}^\infty (\mathbb {R};H)\)
which—as \(C_{\mathrm {c}}^\infty (\mathbb {R};H)\) is a core for \(\partial _{t,\nu }^*\) (see Proposition 3.2.4 and Corollary 3.2.6)—shows \(u\in \operatorname {dom}(\partial _{t,\nu }^{**})=\operatorname {dom}(\partial _{t,\nu }).\) □
Proposition 17.3.4
Let \(\nu \geqslant \nu _{0}\) and \(f\in \operatorname {dom}(\partial _{t,\nu }).\) Then there exists \(u\in \operatorname {dom}(\partial _{t,\nu })\) such that
Proof
We recall that  is maximal monotone by Example 17.1.3. Let λ > 0 and set
is maximal monotone by Example 17.1.3. Let λ > 0 and set

We remark that \(\big (A_{L_{2,\nu }(\mathbb {R};H)}\big )_{\lambda }=\big (A_{\lambda }\big )_{L_{2,\nu }(\mathbb {R};H)}\) (see Exercise 17.6). Hence, we have \(\tau _{h}\big (A_{L_{2,\nu }(\mathbb {R};H)}\big )_{\lambda }=\big (A_{L_{2,\nu }(\mathbb {R};H)}\big )_{\lambda }\tau _{h}\) for each h > 0. Thus, we obtain
and so, due to the monotonicity of B and \(\big (A_{L_{2,\nu }(\mathbb {R};H)}\big )_{\lambda }\) ,
Dividing both sides by h and using Lemma 17.3.3, we infer that \(u_{\lambda }\in \operatorname {dom}(\partial _{t,\nu })\) and

and hence,
Proposition 17.2.4 implies u λ → u as λ → 0 and \((u,f)\in \partial _{t,\nu }M(\partial _{t,\nu }){+}A_{L_{2,\nu }(\mathbb {R};H)}\). Moreover, since (∂ t,ν u λ)λ>0 is uniformly bounded, we can choose a suitable nullsequence \((\lambda _{n})_{n\in \mathbb {N}}\) in \(\left (0,\infty \right )\) such that \(\partial _{t,\nu }u_{\lambda _{n}}\to v\) weakly for some \(v\in L_{2,\nu }(\mathbb {R};H).\) Since ∂ t,ν is closed and hence, weakly closed (either use \(\partial _{t,\nu }^{**}=\partial _{t,\nu }\) or Mazur’s theorem [50, Corollary 2.11]) again), we infer that \(u\in \operatorname {dom}(\partial _{t,\nu }).\) □
We are now in the position to prove Theorem 17.3.1.
Proof of Theorem 17.3.1
Let \(\nu \geqslant \nu _{0}\). Since ∂
t,ν
M(∂
t,ν) − c is monotone (Example 17.1.3), the relation \(\partial _{t,\nu }M(\partial _{t,\nu })+A_{L_{2,\nu }(\mathbb {R};H)}-c\) is monotone and thus, \((\partial _{t,\nu }M(\partial _{t,\nu })+A_{L_{2,\nu }(\mathbb {R};H)})^{-1}\) defines a Lipschitz-continuous mapping with smallest Lipschitz-constant less than or equal to \(\frac {1}{c}.\) Since this mapping is densely defined by Proposition 17.3.4, it follows that \(S_{\nu }=\big (\overline {\partial _{t,\nu }M(\partial _{t,\nu })+A_{L_{2,\nu }(\mathbb {R};H)}}\big )^{-1}\) is Lipschitz-continuous with \(\left \Vert S_{\nu } \right \Vert { }_{\mathrm {Lip}}\leqslant \frac {1}{c}\) and \(\operatorname {dom}(S_{\nu })=L_{2,\nu }(\mathbb {R};H)\). Moreover, S
ν is causal, since for \(f,g\in L_{2,\nu }(\mathbb {R};H)\) with  for some \(a\in \mathbb {R}\) it follows that
for some \(a\in \mathbb {R}\) it follows that  by Proposition 17.3.2. Thus, the only thing left to be shown is the independence of the parameter ν. So, let \(f\in L_{2,\nu }(\mathbb {R};H)\cap L_{2,\mu }(\mathbb {R};H)\) for some \(\nu _{0}\leqslant \nu \leqslant \mu .\) Then we find a sequence \((\phi _{n})_{n\in \mathbb {N}}\) in \(C_{\mathrm {c}}^1(\mathbb {R};H)\) with ϕ
n → f in both \(L_{2,\nu }(\mathbb {R};H)\) and \(L_{2,\mu }(\mathbb {R};H)\). We set
by Proposition 17.3.2. Thus, the only thing left to be shown is the independence of the parameter ν. So, let \(f\in L_{2,\nu }(\mathbb {R};H)\cap L_{2,\mu }(\mathbb {R};H)\) for some \(\nu _{0}\leqslant \nu \leqslant \mu .\) Then we find a sequence \((\phi _{n})_{n\in \mathbb {N}}\) in \(C_{\mathrm {c}}^1(\mathbb {R};H)\) with ϕ
n → f in both \(L_{2,\nu }(\mathbb {R};H)\) and \(L_{2,\mu }(\mathbb {R};H)\). We set  and since 0 = S
ν(0), we derive that \(\inf \operatorname {\mathrm {spt}} u_{n}\geqslant \inf \operatorname {\mathrm {spt}}\phi _{n}>-\infty \) by Proposition 17.3.2. Thus, \(u_{n}\in L_{2,\mu }(\mathbb {R};H)\) and since \(u_{n}\in \operatorname {dom}(\partial _{t,\nu })\) by Proposition 17.3.4 and \( \operatorname {\mathrm {spt}}\partial _{t,\nu }u_{n}\subseteq \operatorname {\mathrm {spt}} u_{n}\), we infer that also \(\partial _{t,\nu }u_{n}\in L_{2,\mu }(\mathbb {R};H)\), which shows \(u_{n}\in \operatorname {dom}(\partial _{t,\mu })\) and ∂
t,μ
u
n = ∂
t,ν
u
n by Exercise 11.1. By Theorem 5.3.6 it follows that
and since 0 = S
ν(0), we derive that \(\inf \operatorname {\mathrm {spt}} u_{n}\geqslant \inf \operatorname {\mathrm {spt}}\phi _{n}>-\infty \) by Proposition 17.3.2. Thus, \(u_{n}\in L_{2,\mu }(\mathbb {R};H)\) and since \(u_{n}\in \operatorname {dom}(\partial _{t,\nu })\) by Proposition 17.3.4 and \( \operatorname {\mathrm {spt}}\partial _{t,\nu }u_{n}\subseteq \operatorname {\mathrm {spt}} u_{n}\), we infer that also \(\partial _{t,\nu }u_{n}\in L_{2,\mu }(\mathbb {R};H)\), which shows \(u_{n}\in \operatorname {dom}(\partial _{t,\mu })\) and ∂
t,μ
u
n = ∂
t,ν
u
n by Exercise 11.1. By Theorem 5.3.6 it follows that
Since we have \((u_{n},\phi _{n}-\partial _{t,\nu }M(\partial _{t,\nu })u_{n})\in A_{L_{2,\nu }(\mathbb {R};H)}\) it follows that \((u_{n},\phi _{n}-\partial _{t,\mu }M(\partial _{t,\mu })u_{n})\in A_{L_{2,\mu }(\mathbb {R};H)}\) by the definition of \(A_{L_{2,\mu }(\mathbb {R};H)}\) and thus, u n = S μ(ϕ n). Letting n →∞, we finally derive S μ(f) = S ν(f). □
17.4 Maxwell’s Equations in Polarisable Media
We recall Maxwell’s equations from Chap. 6. Let \(\Omega \subseteq \mathbb {R}^3\) open. Then the electric field E and the magnetic induction B are linked via Faraday’s law
where we assume the electric boundary condition for E. Moreover, the electric displacement D, the current j c and the magnetic field H are linked via Ampère’s law
where j 0 is a given external current. Classically, D and E as well as B and H are linked by the constitutive relations
where ε, μ ∈ L(L 2( Ω)3) model the dielectricity and magnetic permeability, respectively. In a non-polarisable medium, we would additionally assume Ohm’s law that links j c and E by j c = σE with σ ∈ L(L 2( Ω)3). In polarisable media however, this relation is replaced as follows
where E 0 > 0 is the called the threshold of ionisation of the underlying medium. The above relation is used to model the following phenomenon: Assume that the medium is not or weakly electrically conductive (i.e., σ is very small) but if the electric field is strong enough (i.e., reaching the threshold E 0), the medium polarises and allows for a current flow proportional to the electric field. Such phenomena occur for instance in certain gases between two capacitor plates, where the gas becomes a conductor if the electric field is strong enough.
Our first goal is to formulate (17.4) in terms of a binary relation. For this, we set

Lemma 17.4.1
Let u, v ∈ L 2( Ω)3 . Then (u, v) ∈ B if and only if
Proof
Assume first that (u, v) ∈ B. Then \(\left \Vert u \right \Vert \leqslant E_0\) by definition. Moreover,
and hence, if \(\left \Vert u \right \Vert <E_0\) it follows that v = 0. Moreover, if \(\left \Vert u \right \Vert =E_0\) we have equality and thus, u and v are linearly dependent; that is, we find \(\lambda _1,\lambda _2\in \mathbb {C}\) with λ
1
λ
2≠0 such that λ
1
u + λ
2
v = 0. Note that λ
2≠0 since u≠0 and hence, we get v = λu with  . We then have
. We then have
which shows \(0\leqslant \operatorname {Re} \lambda = |\lambda |\) and thus, \(\lambda \geqslant 0\). The other implication is trivial. □
The latter lemma shows that (E, j c) satisfies (17.4) if and only if (E, j c − σE) ∈ B, or equivalently (E, j c) ∈ σ + B. Thus, we may reformulate Maxwell’s equations in a polarisable medium Ω as follows
To apply our solution theory in Theorem 17.3.1, we need to ensure that

defines a maximal monotone relation on L 2( Ω)6 × L 2( Ω)6. This will be done by the perturbation result presented in Theorem 17.2.7. We start by showing the maximal monotonicity of B.
Lemma 17.4.2
We define the function \(I\colon L_2(\Omega )^3\to \left (-\infty ,\infty \right ]\) by
Then I is convex, proper and l.s.c. Moreover, B = ∂I. In particular, B is maximal monotone.
Proof
This is part of Exercise 17.7. □
Proposition 17.4.3
The relation A given by (17.5) is maximal monotone with (0, 0) ∈ A.
Proof
Since B is maximal monotone by Lemma 17.4.2, it is easy to see that \(\begin {pmatrix} B & 0 \\ 0 & 0 \end {pmatrix}\) is maximal monotone, too. Moreover, by definition we see that \(0\in \operatorname {int} \operatorname {dom} (B)\) and thus, \(0\in \operatorname {int} \operatorname {dom}\begin {pmatrix} B & 0 \\ 0 & 0 \end {pmatrix}=\operatorname {int} \operatorname {dom}(B)\times L_2(\Omega )^3\). Since clearly \(0\in \operatorname {dom} \begin {pmatrix} 0& - \operatorname {\mathrm {curl}} \\ \operatorname {\mathrm {curl}}_0 & 0 \end {pmatrix}\) and \(\begin {pmatrix} 0& - \operatorname {\mathrm {curl}} \\ \operatorname {\mathrm {curl}}_0 & 0 \end {pmatrix}\) is maximal monotone (see Example 17.1.3), the assertion follows from Theorem 17.2.7. □
Theorem 17.4.4
Let ε, μ, σ ∈ L(L 2( Ω)3) with ε, μ selfadjoint. Moreover, assume there exist ν 0, c > 0 such that
Then for each \(\nu \geqslant \nu _0\) we have that

is a Lipschitz-continuous mapping with \(\operatorname {dom}(S_\nu )=L_{2,\nu }(\mathbb {R};L_2(\Omega )^6)\) and \(\left \Vert S_\nu \right \Vert { }_{\mathrm {Lip}}\leqslant \frac {1}{c}\) . Moreover, S ν is causal and independent of ν in the sense that S ν(f) = S η(f) whenever \(\nu ,\eta \geqslant \nu _0\) and \(f\in L_{2,\nu }(\mathbb {R};L_2(\Omega )^6)\cap L_{2,\eta }(\mathbb {R};L_2(\Omega )^6)\).
Proof
This follows from Theorem 17.3.1 applied to  and A as in (17.5). □
and A as in (17.5). □
17.5 Comments
The concept of maximal monotone relations in Hilbert spaces was first introduced by Minty in 1960 for the study of networks [66] and became a well-studied subject also with generalisations to the Banach space case. For this topic we refer to the monographs [16] and [49, Chapter 3]. The concept of subgradients is older and it was found out by Rockafellar [99] that subgradients are maximal monotone. Indeed, one can show that subgradients are precisely the cyclically maximal monotone relations (see e.g. [16, Theoreme 2.5]).
The Theorem of Minty was proved in 1962, [65] and generalised to the case of reflexive Banach spaces by Rockafellar in 1970 [100]. The proof presented here follows [106] and was kindly communicated by Ralph Chill and Hendrik Vogt.
The classical way to approach differential inclusions of the form (u, f) ∈ ∂ t + A where A is maximal monotone uses the theory of nonlinear semigroups of contractions, introduced by Komura in the Hilbert space case, [56] and generalised to the Banach space case by Crandall and Pazy, [24]. The results on evolutionary inclusions presented in this chapter are based on [117, 118] and were further generalised to non-autonomous problems in [122, 126].
The model for Maxwell’s equations in polarisable media can be found in [36, Chapter VII]. We note that in this reference, condition (17.4) is replaced by
which should hold almost everywhere. To solve this problem, one cannot apply Theorem 17.2.7, since 0 is not an interior point of the domain of the corresponding relation and thus, a weaker notion of solution is needed to tackle this problem, see [36, Theorem 8.1].
Exercises
Exercise 17.1
Let \(f\colon H\to \left (-\infty ,\infty \right ]\) be convex, proper and l.s.c. Moreover, assume that f is differentiable in x ∈ H (in particular, f < ∞ in a neighbourhood of x). Show that (x, y) ∈ ∂f if and only if y = f′(x).
Exercise 17.2
Let \(f,g\colon H\to \left (-\infty ,\infty \right ]\). Prove that
-
(a)
f + g is convex if f and g are convex.
-
(b)
f + g is l.s.c. if f and g are l.s.c.
Exercise 17.3
Let H be a Hilbert space, \((x_n)_{n\in \mathbb {N}}\) in H and x ∈ H. Show, that x n → x if and only if x n → x weakly and \(\limsup _{n\to \infty } \left \Vert x_n \right \Vert \leqslant \left \Vert x \right \Vert \).
Exercise 17.4
Let X be a normed space (or, more generally, a topological vector space) and C ⊆ X convex. Prove the following statements:
-
(a)
If \(x\in \operatorname {int} C\) and \(y\in \overline {C}\), then \((1-t)x+ty\in \operatorname {int} C\) for each \(t\in \left [0,1\right )\).
-
(b)
If \(\operatorname {int} C\ne \varnothing \), then \(\overline {C}=\overline {\operatorname {int} C}\) and \(\operatorname {int} \overline {C}=\operatorname {int} C\).
-
(c)
If C is open and K ⊆ X is open with \(\overline {K}\subseteq \overline {C}\). Then K ⊆ C.
Hint: For (a) take an open set U ⊆ X with 0 ∈ U such that x + U − U ⊆ C and show (1 − t)x + ty + (1 − t)U ⊆ C.
Exercise 17.5
Let X be a topological space and U ⊆ X open. We equip U with the trace topology. Prove the following statements:
-
(a)
For A ⊆ U we have \(\overline {A}^U=\overline {A}^X\cap U\) and \(\operatorname {int}_U A=\operatorname {int}_X A\).
-
(b)
If A ⊆ U is closed in U and \(\operatorname {int}_U A=\varnothing \), then \(\operatorname {int}_X \overline {A}^X=\varnothing \).
-
(c)
If X is a Baire space, then U is a Baire space.
Recall, that a topological space X is a Baire space if for each sequence \((A_n)_{n\in \mathbb {N}}\) of closed sets with \(\operatorname {int} A_n=\varnothing \) it follows that \(\operatorname {int} \bigcup _{n\in \mathbb {N}} A_n=\varnothing \) or, equivalently, if for each sequence \((U_n)_{n\in \mathbb {N}}\) of open and dense sets it follows that \(\bigcap _{n\in \mathbb {N}} U_n\) is dense.
Exercise 17.6
Let A ⊆ H × H be maximal monotone.
-
(a)
Let μ, λ > 0. Show that (A λ)μ = A λ+μ.
-
(b)
Let (0, 0) ∈ A and \((\Omega ,\mathcal {A},\mu )\) a σ-finite measure space. Prove that \((A_\lambda )_{L_2(\mu )}=(A_{L_2(\mu )})_\lambda \) for each λ > 0.
Exercise 17.7
Let H be a Hilbert space and C ⊆ H non-empty, convex and closed. Moreover, define \(I_C\colon H\to \left (-\infty ,\infty \right ]\) by

Show that I C is convex, proper and l.s.c. and show
Moreover, prove Lemma 17.4.2.
References
H. Brézis, Opérateurs maximaux monotones et semi-groupes de contractions dans les espaces de Hilbert, vol. 5 (Elsevier, Amsterdam, 1973)
M.G. Crandall, A. Pazy, Semi-groups of nonlinear contractions and dissipative sets. J. Funct. Anal. 3, 376–418 (1969). English.
G. Duvaut, J.L. Lions, Inequalities in Mechanics and Physics. Translated from the French by C.W. John, vol. 219 (Springer, Berlin, 1976)
S. Hu, N.S. Papageorgiou, Handbook of Multivalued Analysis. Vol. I, Vol. 419. Mathematics and Its Applications. Theory (Kluwer Academic Publishers, Dordrecht, 1997)
J. Voigt, A Course on Topological Vector Spaces (Birkhäuser-Verlag, Cham, Switzerland, 2020)
Y. Komura, Nonlinear semigroups in Hilbert space. J. Math. Soc. Jpn. 19, 493–507 (1967)
G.J. Minty, Monotone (nonlinear) operators in Hilbert space. Duke Math. J. 29, 341–346 (1962)
G.J. Minty, Monotone networks. Proc. R. Soc. Lond. Ser. A 257, 194–212 (1960)
R.T. Rockafellar, On the maximal monotonicity of subdifferential mappings. Pac. J. Math. 33, 209–216 (1970)
R.T. Rockafellar, On the maximality of sums of nonlinear monotone operators. Trans. Am. Math. Soc. 149, 75–88 (1970)
S. Simons, C. Zalinescu, A new proof for Rockafellar’s characterization of maximal monotone operators. Proc. Am. Math. Soc. 132(10), 2969–2972 (2004)
S. Trostorff, An alternative approach to well-posedness of a class of differential inclusions in Hilbert spaces. Nonlinear Anal. 75(15), 5851–5865 (2012)
S. Trostorff, Autonomous evolutionary inclusions with applications to problems with nonlinear boundary conditions. Int. J. Pure Appl. Math. 85(2), 303–338 (2013)
S. Trostorff, Well-posedness for a general class of differential inclusions. J. Differ. Equ. 268, 6489–6516 (2020)
S. Trostorff, M. Wehowski, Well-posedness of non-autonomous evolutionary inclusions. Nonlinear Anal. Theory Methods Appl. Ser. A Theory Methods 101, 47–65 (2014)
Author information
Authors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2022 The Author(s)
About this chapter
Cite this chapter
Seifert, C., Trostorff, S., Waurick, M. (2022). Evolutionary Inclusions. In: Evolutionary Equations. Operator Theory: Advances and Applications, vol 287. Birkhäuser, Cham. https://doi.org/10.1007/978-3-030-89397-2_17
Download citation
DOI: https://doi.org/10.1007/978-3-030-89397-2_17
Published:
Publisher Name: Birkhäuser, Cham
Print ISBN: 978-3-030-89396-5
Online ISBN: 978-3-030-89397-2
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)


 for u ∈ H. Then g(x) =infu ∈ H
g(u) if and only if (x, α(y − x)) ∈ ∂f.
for u ∈ H. Then g(x) =infu ∈ H
g(u) if and only if (x, α(y − x)) ∈ ∂f.
 for u ∈ H is convex, proper, l.s.c and coercive. In particular 1 + α∂f is onto and hence, ∂f is maximal monotone.
for u ∈ H is convex, proper, l.s.c and coercive. In particular 1 + α∂f is onto and hence, ∂f is maximal monotone.

 . Then the convexity of f yields
. Then the convexity of f yields 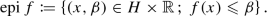
 for x ∈ H, we have found the asserted affine function.
for x ∈ H, we have found the asserted affine function.