Non-Autonomous Evolutionary Equations

Abstract

Previously, we focussed on evolutionary equations of the form

$$\displaystyle \left (\overline {\partial _{t,\nu }M(\partial _{t,\nu })+A}\right )U=F. $$

In this chapter, where we turn back to well-posedness issues, we replace the material law operator M(∂ _t,ν), which is invariant under translations in time, by an operator of the form

$$\displaystyle \mathcal {M}+\partial _{t,\nu }^{-1}\mathcal {N}, $$

where both $\mathcal {M}$ and $\mathcal {N}$ are bounded linear operators in $L_{2,\nu }(\mathbb {R};H)$. Thus, it is the aim in the following to provide criteria on $\mathcal {M}$ and $\mathcal {N}$ under which the operator

$$\displaystyle \partial _{t,\nu }\mathcal {M}+\mathcal {N}+A $$

is closable with continuous invertible closure in $L_{2,\nu }(\mathbb {R};H)$. In passing, we shall also replace the skew-selfadjointness of A by a suitable real part condition. Under additional conditions on $\mathcal {M}$ and $\mathcal {N}$, we will also see that the solution operator is causal. Finally, we will put the autonomous version of Picard’s theorem into perspective of the non-autonomous variant developed here.

Previously, we focussed on evolutionary equations of the form

$$\displaystyle \begin{aligned} \left(\overline{\partial_{t,\nu}M(\partial_{t,\nu})+A}\right)U=F. \end{aligned}$$

In this chapter, where we turn back to well-posedness issues, we replace the material law operator M(∂ _t,ν), which is invariant under translations in time, by an operator of the form

$$\displaystyle \begin{aligned} \mathcal{M}+\partial_{t,\nu}^{-1}\mathcal{N}, \end{aligned}$$

where both $\mathcal {M}$ and $\mathcal {N}$ are bounded linear operators in $L_{2,\nu }(\mathbb {R};H)$. Thus, it is the aim in the following to provide criteria on $\mathcal {M}$ and $\mathcal {N}$ under which the operator

$$\displaystyle \begin{aligned} \partial_{t,\nu}\mathcal{M}+\mathcal{N}+A \end{aligned} $$

(16.1)

is closable with continuously invertible closure in $L_{2,\nu }(\mathbb {R};H)$. In passing, we shall also replace the skew-selfadjointness of A by a suitable real part condition. Under additional conditions on $\mathcal {M}$ and $\mathcal {N}$, we will also see that the solution operator is causal. Finally, we will put the autonomous version of Picard’s theorem into perspective of the non-autonomous variant developed here.

In order to get grip on the domain of the anticipated operator sum, we need to assume a commutator condition of the coefficient operators and the time-derivative. Thus, the replacement for the assumption of the coefficient to be a “material law operator” (i.e., a bounded analytic function of the time-derivative) is to be evolutionary and to have a bounded commutator with the time-derivative (in a suitable sense). Since we proved in Theorem 8.2.1 that bounded analytic functions of the time-derivative are exactly the ones that are causal and autonomous (and evolutionary), one may view the following theorem as a direct generalisation of Picard’s theorem in the way that “autonomous” is dropped.

16.1 Examples

In principle finding examples for the non-autonomous theory is relatively simple. The prototype case focusses on time-dependent multiplication operators. In order to illustrate our findings below, we shall revisit the heat equation and Maxwell’s equations.

Non-Autonomous Heat Equation

Let $\Omega \subseteq \mathbb {R}^d$ be open and $a\colon \mathbb {R}\times \Omega \to \mathbb {R}^{d\times d}$ bounded and measurable. Assume there exists c > 0 such that

$$\displaystyle \begin{aligned} \operatorname{Re} a(t,x)\geqslant c\quad (\text{a.e. }(t,x)\in \mathbb{R}\times \Omega). \end{aligned}$$

Then the non-autonomous variant of the equations describing heat conduction are

The resulting block operator matrix

is then closable and continuously invertible in $L_{2,\nu }\big (\mathbb {R};L_2(\Omega )\times L_2(\Omega )^{d}\big )$ for all ν > 0 by Theorem 16.3.1.

Non-Autonomous Maxwell’s Equations

Let $\Omega \subseteq \mathbb {R}^3$ be open and $\varepsilon ,\mu ,\sigma \colon \mathbb {R}\times \Omega \to \mathbb {R}^{3\times 3}$ bounded and measurable. Assume that ε and μ are Lipschitz continuous w.r.t. the temporal variables uniformly in space; that is, there exists $L\geqslant 0$ such that

$$\displaystyle \begin{aligned} \|\varepsilon(s,x)-\varepsilon(t,x)\|{}_{\mathbb{R}^{3\times 3}}+ \|\mu(s,x)-\mu(t,x)\|{}_{\mathbb{R}^{3\times 3}}\leqslant L\left\vert t-s \right\vert \quad (s,t\in\mathbb{R},x\in \Omega). \end{aligned}$$

Assume ε(t, x)^⊤ = ε(t, x) and μ(t, x)^⊤ = μ(t, x) for all $t\in \mathbb {R}$, x ∈ Ω. Furthermore, assume there exist c, ν ₀ > 0 such that for all $\nu \geqslant \nu _0$ we have

$$\displaystyle \begin{aligned} \mu(t,x)\geqslant c,\text{ and } \nu\varepsilon(t,x)+\frac{1}{2}\varepsilon'(t)(x)+\operatorname{Re}\sigma(t,x)\geqslant c\quad ((t,x)\in \mathbb{R}\times\Omega). \end{aligned}$$

Then it will not be difficult to see that the operator

$$\displaystyle \begin{aligned} \partial_{t,\nu}\begin{pmatrix} \varepsilon(\mathrm{m}_t,\mathrm{m}_x) & 0 \\ 0 & \mu(\mathrm{m}_t,\mathrm{m}_x) \end{pmatrix} + \begin{pmatrix} \sigma(\mathrm{m}_t,\mathrm{m}_x) & 0 \\ 0 & 0\end{pmatrix}+\begin{pmatrix} 0 & -\operatorname{\mathrm{curl}} \\ \operatorname{\mathrm{curl}}_0 & 0 \end{pmatrix} \end{aligned}$$

is closable and continuously invertible in $L_{2,\nu }\big (\mathbb {R};L_2(\Omega )^3\times L_2(\Omega )^{3}\big )$ for all $\nu \geqslant \nu _0$ by Theorem 16.3.1; see also Exercise 16.1.

16.2 Non-Autonomous Picard’s Theorem—The ODE Case

Let H be a Hilbert space and ν > 0. In this section we will focus on the ODE-case first, which is modelled by A = 0 in (16.1).

Theorem 16.2.1

Let $\mathcal {M},\mathcal {M}',\mathcal {N}\in L(L_{2,\nu }(\mathbb {R};H))$ with $\mathcal {M}$, $\mathcal {N}$ causal and $\operatorname {Re} \mathcal {M}\geqslant 0$ . Assume

$$\displaystyle \begin{aligned} \mathcal{M} \partial_{t,\nu}\subseteq\partial_{t,\nu}\mathcal{M}- \mathcal{M}' \end{aligned}$$

and

$$\displaystyle \begin{aligned} \operatorname{Re}\left\langle \phi ,\left(\partial_{t,\nu}\mathcal{M}+\mathcal{N}\right)\phi\right\rangle \geqslant c\left\langle \phi ,\phi\right\rangle \end{aligned}$$

for some c > 0 and all $\phi \in \operatorname {dom}\left (\partial _{t,\nu }\mathcal {M}\right )$ . Then

$$\displaystyle \begin{aligned} 0\in\rho\left(\partial_{t,\nu}\mathcal{M} +\mathcal{N} \right), \end{aligned}$$

$\left \Vert (\partial _{t,\nu }\mathcal {M}+\mathcal {N})^{-1} \right \Vert \leqslant 1/c$ , and $\left (\partial _{t,\nu }\mathcal {M}+\mathcal {N}\right )^{-1}$ is causal. Moreover,

$$\displaystyle \begin{aligned} \operatorname{Re}\left\langle \phi ,\left(\partial_{t,\nu}\mathcal{M}+\mathcal{N}\right)^*\phi\right\rangle \geqslant c\left\langle \phi ,\phi\right\rangle \quad \left(\phi\in \operatorname{dom}\left(\left(\partial_{t,\nu}\mathcal{M}+\mathcal{N}\right)^*\right)\right). \end{aligned}$$

Remark 16.2.2

The only non-trivial condition in Theorem 16.2.1 is the commutator condition

$$\displaystyle \begin{aligned} \mathcal{M} \partial_{t,\nu}\subseteq\partial_{t,\nu}\mathcal{M} - \mathcal{M}'. \end{aligned}$$

This condition is satisfied for multiplication operators induced by a Lipschitz continuous function, see also Exercise 16.1.

We leave the proof of $0\in \rho \left (\partial _{t,\nu }\mathcal {M} +\mathcal {N} \right )$ and the norm estimate as Exercise 16.4. For the proof of causality, we need some preparations. The first result will also be of some value in the next chapter. It deals with a reformulation of causality for resolvents.

Proposition 16.2.3

Let $\mathcal {B}\colon \operatorname {dom}(\mathcal {B})\subseteq L_{2,\nu }(\mathbb {R};H)\to L_{2,\nu }(\mathbb {R};H)$ be linear, $0\in \rho (\mathcal {B})$ , and assume that there exists c > 0 such that for all $\phi \in \operatorname {dom}(\mathcal {B})$ we have

$$\displaystyle \begin{aligned} \operatorname{Re}\left\langle \phi ,\mathcal{B}\phi\right\rangle _{L_{2,\nu}(\mathbb{R};H)}\geqslant c\left\langle \phi ,\phi\right\rangle _{L_{2,\nu}(\mathbb{R};H)}. \end{aligned}$$

Then the following two statements are equivalent:

• (i) $\mathcal {B}^{-1}$ is causal.

• (ii) For all $\phi \in \operatorname {dom}(\mathcal {B})$ and all $a\in \mathbb {R}$ we have

  

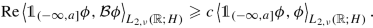
Proof

(ii)⇒(i): Let $f\in L_{2,\nu }(\mathbb {R};H)$ and $a\in \mathbb {R}$ with $\operatorname {\mathrm {spt}} f\subseteq [a,\infty )$. Then, using (ii), for we have

which yields $\operatorname {\mathrm {spt}}\phi \subseteq [a,\infty ).$ Thus, $\mathcal {B}^{-1}$ is causal.

(i)⇒(ii): Let $a\in \mathbb {R}$, $\phi \in \operatorname {dom}(\mathcal {B})$, and . Then and, using causality of $\mathcal {B}^{-1}$, we obtain

We thus compute

where in the last estimate we used that multiplication by is a contraction. □

Lemma 16.2.4

Let $\mathcal {B}\colon \operatorname {dom}(\mathcal {B})\subseteq L_{2,\nu }(\mathbb {R};H)\to L_{2,\nu }(\mathbb {R};H)$ be linear. Let $\lambda , \mu \in \rho (\mathcal {B})$ be contained in the same connected component of $\rho (\mathcal {B})$ . Assume that $(\mu -\mathcal {B})^{-1}$ is causal. Then $(\lambda -\mathcal {B})^{-1}$ is causal.

Proof

Let Z be the connected component of $\rho (\mathcal {B})$ shared by both μ and λ. Define

Then, μ ∈ M. Next, we show that M is open and closed in Z. For this, let η ₀ ∈ M. By Proposition 2.4.1, we have $B\left (\eta _0,r\right )\subseteq \rho (\mathcal {B})$ with . As $B\left (\eta _0,r\right )$ is connected, we infer $B\left (\eta _0,r\right )\subseteq Z$. Furthermore, from Proposition 2.4.1, we infer for $\eta \in B\left (\eta _0,r\right )$ that

$$\displaystyle \begin{aligned} (\eta-\mathcal{B})^{-1}= \sum_{k=0}^\infty (\eta_0-\eta)^k((\eta_0-\mathcal{B})^{-1})^{k+1}. \end{aligned}$$

Hence, since η ₀ ∈ M, we obtain for all $a\in \mathbb {R}$,

Thus, $B\left (\eta _0,r\right )\subseteq M$ and M is open in Z. Next, let (η _n)_n be a sequence in M, convergent to some η ∈ Z. For $n\in \mathbb {N}$ the equality

as well as the continuity of $(\cdot -\mathcal {B})^{-1}$ imply that η ∈ M. Hence, M is closed. We infer M = Z from the connectedness of Z and, thus, λ ∈ M. □

Lemma 16.2.5

Let $\nu \in \mathbb {R}$ and $\mathcal {M} \in L(L_{2,\nu }(\mathbb {R};H))$ be causal. If there exists c > 0 such that

$$\displaystyle \begin{aligned} \operatorname{Re}\left\langle \phi ,\mathcal{M}\phi\right\rangle _{L_{2,\nu}(\mathbb{R};H)}\geqslant c\left\langle \phi ,\phi\right\rangle _{L_{2,\nu}(\mathbb{R};H)} \quad (\phi\in L_{2,\nu}(\mathbb{R};H)), \end{aligned}$$

then $\mathcal {M}^{-1}$ is causal.

Proof

We have $0\in \rho (\mathcal {M})$ by Proposition 6.2.3(b). In particular, we obtain for all $a\in \mathbb {R}$ and $\phi \in L_{2,\nu }(\mathbb {R};H)$, using causality of $\mathcal {M}$, that

which yields causality of $\mathcal {M}^{-1}$ by Proposition 16.2.3 applied to $\mathcal {B}=\mathcal {M}$. □

Lemma 16.2.6

Let $\mathcal {M},\mathcal {N},\mathcal {M}' \in L(L_{2,\nu }(\mathbb {R};H))$ . Assume

$$\displaystyle \begin{aligned} \mathcal{M}\partial_{t,\nu}\subseteq \partial_{t,\nu}\mathcal{M}-\mathcal{M}' \end{aligned}$$

and

$$\displaystyle \begin{aligned} \operatorname{Re} \left\langle \phi ,(\partial_{t,\nu}\mathcal{M}+\mathcal{N})\phi\right\rangle \geqslant c\left\langle \phi ,\phi\right\rangle \quad (\phi\in \operatorname{dom}(\partial_{t,\nu})). \end{aligned}$$

Then

is closed.

Proof

As it was mentioned before, the proof of $0\in \rho \left (\partial _{t,\nu }(\mathcal {M}+\eta ) +\mathcal {N} \right )$ for $\eta \in \left [0,\infty \right )$ is postponed to Exercise 16.4. For all η ∈ [0, ∞) and $\phi \in \operatorname {dom}(\partial _{t,\nu })$ we have

$$\displaystyle \begin{aligned} \operatorname{Re} \left\langle \phi ,(\partial_{t,\nu}(\mathcal{M}+\eta)+\mathcal{N})\phi\right\rangle \geqslant c\left\langle \phi ,\phi\right\rangle \quad (\phi\in \operatorname{dom}(\partial_{t,\nu})). \end{aligned}$$

Note that this inequality to hold for all $\phi \in \operatorname {dom}(\partial _{t,\nu })$ is sufficient for it to hold for all $\phi \in \operatorname {dom}(\partial _{t,\nu }(\mathcal {M}+\eta ))$. Indeed, this is a consequence of $\operatorname {dom}(\partial _{t,\nu })$ being a core for $\partial _{t,\nu }(\mathcal {M}+\eta )$, which is easily seen (see also Lemma 16.3.3). Hence, by Proposition 16.2.3, η ∈ Z if and only if

Before we show closedness of Z, we shortly recall that integration by parts yields for all $a\in \mathbb {R}$

In order to show that Z is closed, let (η _n)_n be a sequence in Z, convergent to some η ∈ [0, ∞). Then we compute for all $a\in \mathbb {R}$ and $\phi \in \operatorname {dom}(\partial _{t,\nu })$ and $n\in \mathbb {N}$

Letting n →∞, we infer

for $\phi \in \operatorname {dom}(\partial _{t,\nu })$. Hence, η ∈ Z. □

Proof of Theorem 16.2.1

Keeping Exercise 16.4 in mind, we only need to show that the solution operator $(\partial _{t,\nu }\mathcal {M}+\mathcal {N})^{-1}$ is causal.

By Lemma 16.2.6, it suffices to show that for all η > 0,

$$\displaystyle \begin{aligned} (\partial_{t,\nu}(\mathcal{M}+\eta)+\mathcal{N})^{-1} \end{aligned}$$

is causal. Hence, we may assume that $0\in \rho ( \mathcal {M})$ and, using Lemma 16.2.5, that $\mathcal {M}^{-1}$ is causal. In this situation, it remains to show that

$$\displaystyle \begin{aligned} (\partial_{t,\nu}\mathcal{M}+\mathcal{N})^{-1}= \mathcal{M}^{-1}(\partial_{t,\nu}+\mathcal{N}\mathcal{M}^{-1})^{-1} \end{aligned}$$

is causal. As $\mathcal {M}^{-1}$ is causal, it furthermore suffices to show causality of

$$\displaystyle \begin{aligned} (\partial_{t,\nu}+\mathcal{K})^{-1} \end{aligned}$$

where is causal. Using $\operatorname {Re} \mathcal {M}\geqslant 0$ and the inequality assumed for $\partial _{t,\nu }\mathcal {M}+\mathcal {N}$, we conclude that $(\partial _{t,\nu }+\mu + \mathcal {K})$ is continuously invertible for all $\mu \geqslant 0$. Since $\partial _{t,\nu }^{-1}$ is causal, Lemma 16.2.4 yields that (∂ _t,ν + μ)⁻¹ is causal. From $\operatorname {Re}(\partial _{t,\nu }+\mu )\geqslant \nu +\mu$ it follows that $\left \Vert (\partial _{t,\nu }+\mu )^{-1} \right \Vert \leqslant 1/{(\nu +\mu )}$. Hence, we find μ > 0 such that $\left \Vert (\partial _{t,\nu }+\mu )^{-1}\mathcal {K} \right \Vert <1$. Thus,

$$\displaystyle \begin{aligned} \begin{array}{ll} (\partial_{t,\nu}+\mu+ \mathcal{K})^{-1} &= \big(1+ (\partial_{t,\nu}+\mu)^{-1}\mathcal{K}\big)^{-1}(\partial_{t,\nu}+\mu)^{-1}\\ &= \displaystyle\sum_{k=0}^\infty (-1)^k \big((\partial_{t,\nu}+\mu)^{-1}\mathcal{K}\big)^k(\partial_{t,\nu}+\mu)^{-1} \end{array} \end{aligned}$$

is causal as a composition of causal operators. Finally, Lemma 16.2.4 implies causality of $(\partial _{t,\nu }+ \mathcal {K})^{-1}$ as desired. □

16.3 Non-Autonomous Picard’s Theorem—The PDE Case

Let H be a Hilbert space. In Sect. 4.2, we have already discussed the notion of uniformly Lipschitz continuous mappings. Here we concentrate on linear uniformly Lipschitz continuous mappings, which we call evolutionary as a short hand:

Definition

Let $\nu _0\in \mathbb {R}$. A mapping

$$\displaystyle \begin{aligned}\mathcal{M}\colon S_{c}(\mathbb{R};H)\to\bigcap_{\nu\geqslant\nu_{0}}L_{2,\nu}(\mathbb{R};H)\end{aligned}$$

is called evolutionary (at ν ₀ ) if it is linear and uniformly Lipschitz continuous (at ν ₀); that is, for all $\nu \geqslant \nu _0$, the mapping $\mathcal {M}\colon S_{c}(\mathbb {R};H)\subseteq L_{2,\nu }(\mathbb {R};H)\to L_{2,\nu }(\mathbb {R};H)$ is linear and continuous. Moreover, its continuous extension to the whole of $L_{2,\nu }(\mathbb {R};H)$, denoted by $\mathcal {M}^\nu$, satisfies $\sup _{\nu \geqslant \nu _0}\left \Vert \mathcal {M}^\nu \right \Vert <\infty$.

The set of all evolutionary mappings is defined as

We have seen that material law operators are evolutionary (see Theorem 5.3.6 and the concluding lines of the proof). In the non-autonomous version of Picard’s theorem (Theorem 6.2.1), evolutionary mappings will replace the notion of material law operators. Hence, we allow for an explicit time-dependence in the coefficients.

Recall from Lemma 4.2.5(a), that $\mathcal {M}^\nu$ is causal and independent of ν in the sense of Lemma 4.2.5(c).

The non-autonomous version of Picard’s theorem now reads as follows.

Theorem 16.3.1

Let $\mu \in \mathbb {R}$, $\mathcal {M},\mathcal {M}',\mathcal {N}\in S_{\mathrm {ev}}(H,\mu )$, $\operatorname {Re} \mathcal {M}^\nu \geqslant 0$ for all $\nu \geqslant \mu$ and $A\colon \operatorname {dom}(A)\subseteq H\to H$ be closed and densely defined. Assume that there exists c > 0 such that the following conditions are satifsfied:

• (a) $\mathcal {M}^{\mu }\partial _{t,\mu }\subseteq \partial _{t,\mu }\mathcal {M}^{\mu }-\left (\mathcal {M}'\right )^{\mu }$,

• (b) for all $\nu \geqslant \mu$ and $\phi \in \operatorname {dom}(\partial _{t,\nu })$ we have

  $$\displaystyle \begin{aligned} \operatorname{Re}\left\langle \phi ,\left(\partial_{t,\nu}\mathcal{M}^{\nu}+\mathcal{N}^{\nu}\right)\phi\right\rangle _{L_{2,\nu}(\mathbb{R};H)}\geqslant c\left\langle \phi ,\phi\right\rangle _{L_{2,\nu}(\mathbb{R};H)}, \end{aligned}$$

• (c) for all $x\in \operatorname {dom}(A)$ and $y\in \operatorname {dom}(A^{*})$ we have

  $$\displaystyle \begin{aligned} \operatorname{Re}\left\langle x ,Ax\right\rangle _{H}\geqslant0\mathit{\text{ and }}\operatorname{Re}\left\langle y ,A^{*}y\right\rangle _{H}\geqslant0. \end{aligned}$$

Then for all $\nu \geqslant \max \{\mu ,0\}$ , ν ≠ 0, the operator

$$\displaystyle \begin{aligned} \partial_{t,\nu}\mathcal{M}^{\nu}+\mathcal{N}^{\nu}+A\colon H_{\nu}^{1}(\mathbb{R};H)\cap L_{2,\nu}\big(\mathbb{R};\operatorname{dom}(A)\big)\subseteq L_{2,\nu}(\mathbb{R};H)\to L_{2,\nu}(\mathbb{R};H) \end{aligned}$$

is closable and its closure is continuously invertible. Moreover, with $\mathcal {S}_\nu \in L(L_{2,\nu }(\mathbb {R};H))$ being the inverse of this closure, $\left \Vert \mathcal {S}_{\nu } \right \Vert { }_{L(L_{2,\nu }(\mathbb {R};H))}\leqslant 1/c$, $\mathcal {S}_{\nu }$ is eventually independent of ν and $\mathcal {S}_{\nu }$ is causal.

Remark 16.3.2

• (a) It is a consequence of Theorem 16.3.1 that the mapping

  $$\displaystyle \begin{aligned} \mathcal{S}\colon S_c(\mathbb{R};H)&\to \bigcap_{\nu\geqslant\mu} L_{2,\nu}(\mathbb{R};H) \\ f & \mapsto \left(\overline{\partial_{t,\mu}\mathcal{M}^{\mu}+\mathcal{N}^{\mu}+A}\right)^{-1}f \end{aligned} $$

  is evolutionary.

• (b) It will follow from the techniques used in the proof of Theorem 16.3.1, that a similar results holds without the assumption of evolutionarity for the operator coefficients. We refer to the formulation in Exercise 16.5 and ask the reader to provide a proof for this.

The proof of the non-autonomous version of Picard’s theorem requires some preparations. Being still a linear theory, the well-posedness result is—similar to the autonomous version of Picard’s theorem—based on Proposition 6.3.1. Furthermore, we need some results on the interaction of the time derivative and the non-autonomous coefficients. Thus, for the next lemma, we introduce the commutator

for two linear operators A and B on its natural domain

$$\displaystyle \begin{aligned} \operatorname{dom}(AB)\cap\operatorname{dom}(BA). \end{aligned}$$

Lemma 16.3.3

Let $\nu \in \mathbb {R}$, $\mathcal {M},\mathcal {M}',\mathcal {N}\in S_{\mathrm {ev}}(H,\nu ).$ For ε > 0 small enough, denote .

• (a) If $\mathcal {M}^{\nu }\partial _{t,\nu }\subseteq \partial _{t,\nu }\mathcal {M}^{\nu }-\left (\mathcal {M}'\right )^{\nu }$ , then for all ε > 0 we have

  $$\displaystyle \begin{aligned} \overline{[\partial_{t,\nu}\mathcal{M}^{\nu},S_{\varepsilon}]}=\varepsilon\partial_{t,\nu}S_{\varepsilon}(\mathcal{M}')^{\nu}S_{\varepsilon} \in L(L_{2,\nu}(\mathbb{R};H)). \end{aligned}$$

  In this case, we also have that $\overline {[\partial _{t,\nu }\mathcal {M}^{\nu },S_{\varepsilon }]}\to 0$ in the strong operator topology of $L(L_{2,\nu }(\mathbb {R};H))$.

• (b) We have that $[\mathcal {N},S_{\varepsilon }]\to 0$ as ε → 0 in the strong operator topology of $L(L_{2,\nu }(\mathbb {R};H))$.

Proof

• (a) Let ε > 0 and $\phi \in \operatorname {dom}(\partial _{t,\nu })$. Then

  $$\displaystyle \begin{aligned} \overline{[\partial_{t,\nu}\mathcal{M}^{\nu},S_{\varepsilon}]}\phi & = \partial_{t,\nu}(\mathcal{M}^\nu S_{\varepsilon} - S_{\varepsilon}\mathcal{M}^\nu)\phi \\ &= \partial_{t,\nu}S_\varepsilon((1+\varepsilon\partial_{t,\nu})\mathcal{M}^\nu - \mathcal{M}^\nu(1+\varepsilon\partial_{t,\nu}))S_{\varepsilon}\phi \\ & = \varepsilon\partial_{t,\nu}S_\varepsilon(\mathcal{M}')^\nu S_{\varepsilon}\phi, \end{aligned} $$

  which shows the first equality. Since S _ε → 1 as ε → 0 in the strong operator topology and ε∂ _t,ν S _ε = (1 − S _ε) → 0 as ε → 0 in the strong operator topology, we infer the convergence statement in (a).

• (b) This statement follows from S _ε → 1 in the strong operator topology.

  □

Lemma 16.3.4

Let $\mu \in \mathbb {R}$, $\mathcal {M},\mathcal {M}',\mathcal {N}\in S_{\mathrm {ev}}(H,\mu )$ and $A\colon \operatorname {dom}(A)\subseteq H\to H$ be closed and densely defined. Assume $\mathcal {M}^{\mu }\partial _{t,\mu }\subseteq \partial _{t,\mu }\mathcal {M}^{\mu }-\left (\mathcal {M}'\right )^{\mu }$ . Then for all $\nu \geqslant \mu$

$$\displaystyle \begin{aligned} (\partial_{t,\nu}\mathcal{M}^\nu +\mathcal{N}^\nu+A)^*& = \overline{(\partial_{t,\nu}\mathcal{M}^\nu +\mathcal{N}^\nu)^*+A^*} = \overline{(\mathcal{M}^\nu)^*\partial_{t,\nu}^* +(\mathcal{N}^\nu)^*+A^*}. \end{aligned} $$

Proof

Let $\nu \geqslant \mu$. It is not difficult to see that $\mathcal {M}^{\mu }\partial _{t,\mu }\subseteq \partial _{t,\mu }\mathcal {M}^{\mu }-\left (\mathcal {M}'\right )^{\mu }$ implies $\mathcal {M}^{\nu }\partial _{t,\nu }\subseteq \partial _{t,\nu }\mathcal {M}^{\nu }-\left (\mathcal {M}'\right )^{\nu }$, see Exercise 16.2.

Let $g\in \operatorname {dom}\big ((\partial _{t,\nu }\mathcal {M}^\nu +\mathcal {N}^\nu +A)^*\big )$. For ε > 0 small enough, we define as well as . For $u\in \operatorname {dom}(\partial _{t,\nu }\mathcal {M}^\nu +\mathcal {N}^\nu +A)$ we compute

$$\displaystyle \begin{aligned}\begin{array}{r*{20}l}{} \begin{aligned} & \left\langle (\partial_{t,\nu}\mathcal{M}^\nu +\mathcal{N}^\nu+A)u ,g_\varepsilon\right\rangle \\ & = \left\langle S_\varepsilon(\partial_{t,\nu}\mathcal{M}^\nu +\mathcal{N}^\nu+A)u ,g\right\rangle \\ & = \left\langle (\partial_{t,\nu}\mathcal{M}^\nu +\mathcal{N}^\nu+A)S_\varepsilon u ,g\right\rangle - \left\langle [\partial_{t,\nu}\mathcal{M}^\nu,S_\varepsilon]u +[\mathcal{N}^\nu,S_\varepsilon]u ,g\right\rangle . \end{aligned} \end{array}\end{aligned} $$

(16.2)

We read off that $g_\varepsilon \in \operatorname {dom}\big ((\partial _{t,\nu }\mathcal {M}^\nu +\mathcal {N}^\nu +A)^*\big )$ and

$$\displaystyle \begin{aligned} & (\partial_{t,\nu}\mathcal{M}^\nu +\mathcal{N}^\nu+A)^*g_\varepsilon\\ &\quad = S_\varepsilon^*(\partial_{t,\nu}\mathcal{M}^\nu +\mathcal{N}^\nu+A)^* g-[\partial_{t,\nu}\mathcal{M}^\nu,S_\varepsilon]^*g-[\mathcal{N}^\nu,S_\varepsilon]^*g. \end{aligned} $$

By Lemma 9.3.3, we infer that g _ε → g weakly as ε → 0. Similarly, we obtain

$$\displaystyle \begin{aligned} S_\varepsilon^*(\partial_{t,\nu}\mathcal{M}^\nu -\mathcal{N}^\nu+A)^* g+[\partial_{t,\nu}\mathcal{M}^\nu,S_\varepsilon]^*g-[\mathcal{N}^\nu,S_\varepsilon]^*g\to (\partial_{t,\nu}\mathcal{M}^\nu +\mathcal{N}^\nu+A)^* g \end{aligned}$$

weakly as ε → 0. Next, we show that $g_\varepsilon \in \operatorname {dom}(A)$ for all ε > 0. For this, we realise that $g_\varepsilon \in \operatorname {dom}(\partial _{t,\nu }^*)=\operatorname {dom}(\partial _{t,\nu })$ and, thus, revisiting (16.2), we infer

$$\displaystyle \begin{aligned} \left\langle Au ,g_\varepsilon\right\rangle & =-\left\langle (\partial_{t,\nu}\mathcal{M}^\nu +\mathcal{N}^\nu)u ,g_\varepsilon\right\rangle + \left\langle (\partial_{t,\nu}\mathcal{M}^\nu +\mathcal{N}^\nu+A)S_\varepsilon u ,g\right\rangle \\ &\quad - \left\langle [\partial_{t,\nu}\mathcal{M}^\nu,S_\varepsilon]u ,g\right\rangle -\left\langle [\mathcal{N}^\nu,S_\varepsilon]u ,g\right\rangle \\ & = -\left\langle u ,((\mathcal{M}^\nu)^*\partial_{t,\nu}^* +(\mathcal{N}^\nu)^*)g_\varepsilon\right\rangle + \left\langle u ,S_\varepsilon^*(\partial_{t,\nu}\mathcal{M}^\nu +\mathcal{N}^\nu+A)^*g\right\rangle \\ &\quad - \left\langle u ,[\partial_{t,\nu}\mathcal{M}^\nu,S_\varepsilon]^*g+[\mathcal{N}^\nu,S_\varepsilon]^*g\right\rangle . \end{aligned} $$

Since $H_\nu ^1(\mathbb {R};H)\cap L_{2,\nu }\big (\mathbb {R};\operatorname {dom}(A)\big )$ is dense in $L_{2,\nu }\big (\mathbb {R};\operatorname {dom}(A)\big )$, we read off that $g_\varepsilon \in \operatorname {dom}(A^*).$ Thus, since $g_\varepsilon \in \operatorname {dom}(\partial _{t,\nu }^*)$ anyway, we obtain by the first statements in Theorem 2.3.2 and Theorem 2.3.4 that

$$\displaystyle \begin{aligned} (\partial_{t,\nu}\mathcal{M}^\nu+\mathcal{N}^\nu+A)^*g_\varepsilon = (\mathcal{M}^\nu)^*\partial_{t,\nu}^*g_\varepsilon + (\mathcal{N}^\nu)^*g_\varepsilon + A^*g_\varepsilon, \end{aligned}$$

which together with the above convergence result shows the assertion. □

Lemma 16.3.5

Let $\mu ,\nu \in \mathbb {R}$, $\mu \geqslant \nu$ . Let $\mathcal {S}_\nu \in L(L_{2,\nu }(\mathbb {R};H))$ as well as $\mathcal {S}_\mu \in L(L_{2,\mu }(\mathbb {R};H))$ be causal and $D\subseteq L_{2,\nu }(\mathbb {R};H)\cap L_{2,\mu }(\mathbb {R};H)$ dense in $L_{2,\mu }(\mathbb {R};H)$ such that $\mathcal {S}_\nu =\mathcal {S}_\mu$ on D. Then $\mathcal {S}_\nu =\mathcal {S}_\mu$ on $L_{2,\nu }(\mathbb {R};H)\cap L_{2,\mu }(\mathbb {R};H)$.

Proof

Let $f\in L_{2,\nu }(\mathbb {R};H)\cap L_{2,\mu }(\mathbb {R};H)$. By density of D, we may find a sequence (f _n)_n in D such that f _n → f in $L_{2,\mu }(\mathbb {R};H)$. Let $a\in \mathbb {R}$. Then in $L_{2,\nu }(\mathbb {R};H)\cap L_{2,\mu }(\mathbb {R};H)$. Since both $\mathcal {S}_\mu$ and $\mathcal {S}_\nu$ are causal, we infer for $n\in \mathbb {N}$ that

Letting n →∞, we deduce that both the left-hand side as well as the right-hand side converge in $L_{2,\mathrm {loc}}(\mathbb {R};H)$. Consequently, we infer, using causality again that

This equality holds for all $a\in \mathbb {R}$, thus $\mathcal {S}^\mu f=\mathcal {S}^\nu f$ and the assertion follows. □

The following lemma is proved in the (easy) Exercise 16.7.

Lemma 16.3.6

Let H ₀ , H ₁ be Hilbert spaces. Let $B\colon \operatorname {dom}(B)\subseteq H_0 \to H_1$ be closed and densely defined. Let V  be a Hilbert space such that $V\hookrightarrow \operatorname {dom}(B)$ continuously and densely. If D ⊆ V  is a dense subspace, then D is a core for B.

Proof of Theorem 16.3.1

Define with $\operatorname {dom}(\widetilde {B})=H_\nu ^1(\mathbb {R};H)\cap L_{2,\nu }\big (\mathbb {R};\operatorname {dom}(A)\big )$. By the last equality in Lemma 16.3.4, we have $\operatorname {dom}(\widetilde {B}^*)\supseteq H_\nu ^1(\mathbb {R};H)\cap L_{2,\nu }\big (\mathbb {R};\operatorname {dom}(A^*)\big )$. Hence, $\widetilde {B}^*$ is densely defined and, therefore, by Lemma 2.2.7, $\widetilde {B}$ is closable. Next, we want to apply Proposition 6.3.1 to . For this, we let $\phi \in \operatorname {dom}(\widetilde {B})$ and compute

$$\displaystyle \begin{aligned} \operatorname{Re} \left\langle \phi ,B\phi\right\rangle & = \operatorname{Re} \left\langle \phi ,( \partial_{t,\nu}\mathcal{M}^\nu+\mathcal{N}^\nu+A)\phi\right\rangle \\ &\geqslant c\left\langle \phi ,\phi\right\rangle +\operatorname{Re} \left\langle \phi ,A\phi\right\rangle \geqslant c\left\langle \phi ,\phi\right\rangle . \end{aligned} $$

Since $\operatorname {dom}(\widetilde {B})$ is a core for B, we deduce

$$\displaystyle \begin{aligned} \operatorname{Re} \left\langle \phi ,B\phi\right\rangle \geqslant c\left\langle \phi ,\phi\right\rangle \quad (\phi\in \operatorname{dom}(B)). \end{aligned}$$

Using Lemma 16.3.4, we obtain is a core for B ^∗. Using Theorem 16.2.1, we estimate for all ψ ∈ D that

$$\displaystyle \begin{aligned} \operatorname{Re} \left\langle \psi ,B^*\psi\right\rangle & =\operatorname{Re} \left\langle \psi ,\left(\partial_{t,\nu}\mathcal{M}^{\nu}+\mathcal{N}^{\nu}\right)^*\psi+A^*\psi\right\rangle \geqslant c\left\langle \psi ,\psi\right\rangle . \end{aligned} $$

Hence,

$$\displaystyle \begin{aligned} \operatorname{Re} \left\langle \psi ,B^*\psi\right\rangle \geqslant c\left\langle \psi ,\psi\right\rangle \quad (\psi\in \operatorname{dom}(B^*)). \end{aligned}$$

Thus, Proposition 6.3.1 applies and we deduce that 0 ∈ ρ(B) and $\left \Vert B^{-1} \right \Vert \leqslant 1/c$.

Next, since $(\partial _{t,\nu }\mathcal {M}^\nu +\mathcal {N}^\nu )^{-1}$ is causal by Theorem 16.2.1, using Proposition 16.2.3 for $\phi \in H_\nu ^1(\mathbb {R};H)\cap L_{2,\nu }\big (\mathbb {R};\operatorname {dom}(A)\big )=\operatorname {dom}(\widetilde {B})$ we obtain for $a\in \mathbb {R}$ that

The inequality carries over to all $\phi \in \operatorname {dom}(B)$ using that $\operatorname {dom}(\widetilde {B})$ is, by definition, a core for B. Again appealing to Proposition 16.2.3 we obtain that B ⁻¹ is causal. Finally, in order to show that $\mathcal {S}_\nu$ is eventually independent of ν, we want to apply Lemma 16.3.5. Since we have shown that for all $\nu \geqslant \eta \geqslant \mu$, the operators $\mathcal {S}_\nu$ and $\mathcal {S}_\eta$ are continuous and causal, it remains to construct a set $U\subseteq L_{2,\nu }(\mathbb {R};H)\cap L_{2,\eta }(\mathbb {R};H)$ dense in $L_{2,\nu }(\mathbb {R};H)$ such that $\mathcal {S}_\nu =\mathcal {S}_\eta$ on U. We put

which is evidently a subset of $L_{2,\nu }(\mathbb {R};H)$. Observe that $C_{\mathrm {c}}^\infty \big (\mathbb {R};\operatorname {dom}(A)\big )\subseteq L_{2,\eta }(\mathbb {R};H)\cap L_{2,\nu }(\mathbb {R};H)$. Moreover, $\mathcal {M}^\nu =\mathcal {M}^\eta$ as well as $\mathcal {N}^\nu =\mathcal {N}^\eta$ on $L_{2,\eta }(\mathbb {R};H)\cap L_{2,\nu }(\mathbb {R};H)$. Thus, both $\mathcal {M}^\nu$ and $\mathcal {N}^\nu$ leave $L_{2,\eta }(\mathbb {R};H)\cap L_{2,\nu }(\mathbb {R};H)$ invariant, by Lemma 4.2.5. Hence, since $A\big [C_{\mathrm {c}}^\infty \big (\mathbb {R};\operatorname {dom}(A)\big )\big ]\subseteq C_{\mathrm {c}}^\infty (\mathbb {R};H)$, we infer that $U\subseteq L_{2,\eta }(\mathbb {R};H)\cap L_{2,\nu }(\mathbb {R};H)$.

Finally, by Lemma 9.4.1, $C_{\mathrm {c}}^\infty \big (\mathbb {R};\operatorname {dom}(A)\big )$ is dense in $L_{2,\nu }\big (\mathbb {R};\operatorname {dom}(A)\big )\cap H_\nu ^1(\mathbb {R};H)$. We now apply Lemma 16.3.6 to $(\mathbb {R};\operatorname {dom}(A))\cap H(\mathbb {R};H)$ and B to get that $C_{\mathrm {c}}^\infty \big (\mathbb {R};\operatorname {dom}(A)\big )$ is a core for B. Since B is surjective, this implies that $U=B\big [C_{\mathrm {c}}^\infty \big (\mathbb {R};\operatorname {dom}(A)\big )\big ]\subseteq L_{2,\nu }(\mathbb {R};H)$ is dense which yields the assertion. □

16.4 Comments

Traditionally, non-autonomous equations have been dealt with—similar to the autonomous case—by mimicking techniques and results from non-autonomous ordinary differential equations. In consequence, the fundamental solution is the central object of attention, which finds itself in the concept of so-called evolution families $(U(t,s))_{t\geqslant s}$ or propagators, see e.g. [53, 112]. Similar to the autonomous case, one is interested in the initial value problem

$$\displaystyle \begin{aligned} \begin{cases} u'(t)+A(t)u(t)=0,& t>0,\\ u(0)=u_0,&\end{cases} \end{aligned}$$

for a given parameter dependent operator family (A(t))_t of unbounded operators. The solution is then given by u(t) = U(t, 0)u ₀. In applications, for instance to parabolic equations, .

One is then interested in whether (A(t))_t gives rise to an evolution family. There, the main issue is to understand the behaviour of the possibly different domains of A(t) for any given t. Focussing on inhomogeneous problems rather than initial value problems, we again are changing the perspective in the case of evolutionary equations. The presented time-space perspective entirely dispenses with the possible domain issues and requires only mild regularity conditions of the coefficients. In particular, as it has been demonstrated for the heat equation in Sect. 16.1, we merely require boundedness and measurability for a, whereas for Maxwell’s equations we need Lipschitz continuity for the coefficients ε and μ.

The first result on the well-posedness of non-autonomous evolutionary equations has been found in [92]. In this source, the focus was on multiplication operators as coefficients and Lipschitz continuity of the operator coefficients with respect to time was assumed. The method of proof has been used to generalise this to the commutator assumption presented here, see [137, 138]. Theorem 16.3.1 also has a nonlinear analogue. This can be found in [122]. For an autonomous well-posedness result for nonlinear evolutionary inclusions we also refer to Chap. 17.

Exercises

Exercise 16.1

Let $V\colon \mathbb {R}\to \mathbb {R}$ be Lipschitz continuous.

• (a) Let $\phi \in C_{\mathrm {c}}^\infty (\mathbb {R})$. Show that $\phi V \in H^1_\nu (\mathbb {R})$ with bounded derivative. Show that there exists a bounded measurable function V ′ such that $V(t)-V(0)=\int _0^tV'(\tau ){\mathrm{d}}\tau$.

• (b) Let V  be bounded. Show that V (m) is evolutionary at 0 and that

  $$\displaystyle \begin{aligned} V(\mathrm{m})^\nu\partial_{t,\nu}\subseteq \partial_{t,\nu}V(\mathrm{m})^\nu-V'(\mathrm{m})^\nu. \end{aligned}$$

• (c) In the situation of (b), show that for $\phi \in \operatorname {dom}(\partial _{t,\nu })$, we have

  $$\displaystyle \begin{aligned} \operatorname{Re} \left\langle \phi ,\partial_{t,\nu}V(\mathrm{m})\phi\right\rangle =\nu\left\langle \phi ,V(\mathrm{m})\phi\right\rangle +\frac{1}{2}\left\langle \phi ,V'(\mathrm{m})\phi\right\rangle . \end{aligned}$$

Exercise 16.2

Let H be a Hilbert space, $\mu \in \mathbb {R}$. Let $\mathcal {M},\mathcal {M}'\in S_{\mathrm {ev}}(H,\mu )$. Assume that

$$\displaystyle \begin{aligned} \mathcal{M}^\mu\partial_{t,\mu}\subseteq \partial_{t,\mu}\mathcal{M}^\mu - (\mathcal{M}')^\mu. \end{aligned}$$

Show that then for all $\nu \geqslant \mu$ we have

$$\displaystyle \begin{aligned} \mathcal{M}^\nu\partial_{t,\nu}\subseteq \partial_{t,\nu}\mathcal{M}^\nu - (\mathcal{M}')^\nu. \end{aligned}$$

Exercise 16.3

Let H be a Hilbert space, ν, c > 0, $M\in \mathcal {M}(H,\nu ).$ Assume that

$$\displaystyle \begin{aligned} \operatorname{Re} zM(z)\geqslant c. \end{aligned}$$

Show that then

for all $\phi \in \operatorname {dom}(\partial _{t,\nu })$ and $a\in \mathbb {R}$.

Exercise 16.4

In the situation of Theorem 16.2.1, show that $0\in \rho (\partial _{t,\nu }\mathcal {M}+\mathcal {N})$ and $\left \Vert (\partial _{t,\nu }\mathcal {M}+\mathcal {N})^{-1} \right \Vert \leqslant 1/c$.

Hint: Show $\operatorname {Re}\left (\partial _{t,\nu }\mathcal {M}+\mathcal {N}\right )^{*}\geqslant c$ first.

Exercise 16.5

Prove the following ‘non-causal’ version of Theorem 16.3.1: Let H a Hilbert space, $\nu \in \mathbb {R}$. Let $\mathcal {M},\mathcal {M}',\mathcal {N}\in L(L_{2,\nu }(\mathbb {R};H))$ and $A\colon \operatorname {dom}(A)\subseteq H\to H$ be closed and densely defined. Assume that there exists c > 0 such that the following conditions are satifsfied:

• (a) $\mathcal {M}\partial _{t,\nu }\subseteq \partial _{t,\nu }\mathcal {M}-\mathcal {M}^{\prime }$,

• (b) for all $\phi \in \operatorname {dom}(\partial _{t,\nu })$ we have

  $$\displaystyle \begin{aligned} \operatorname{Re}\left\langle \phi ,\left(\partial_{t,\nu}\mathcal{M}+\mathcal{N}\right)\phi\right\rangle _{L_{2,\nu}(\mathbb{R};H)}\geqslant c\left\langle \phi ,\phi\right\rangle _{L_{2,\nu}(\mathbb{R};H)}, \end{aligned}$$

• (c) for all $x\in \operatorname {dom}(A)$ and $y\in \operatorname {dom}(A^{*})$ we have

  $$\displaystyle \begin{aligned} \operatorname{Re}\left\langle x ,Ax\right\rangle _{H}\geqslant0\text{ and }\operatorname{Re}\left\langle y ,A^{*}y\right\rangle _{H}\geqslant0. \end{aligned}$$

Then

$$\displaystyle \begin{aligned} \partial_{t,\nu}\mathcal{M}+\mathcal{N}+A\colon H_{\nu}^{1}(\mathbb{R};H)\cap L_{2,\nu}\big(\mathbb{R};\operatorname{dom}(A)\big)\subseteq L_{2,\nu}(\mathbb{R};H)\to L_{2,\nu}(\mathbb{R};H) \end{aligned}$$

is closable and its closure is continuously invertible. Denoting the respective inverse by $\mathcal {S}$, we have $\left \Vert \mathcal {S} \right \Vert { }_{L(L_{2,\nu }(\mathbb {R};H))} \leqslant 1/c$.

Exercise 16.6

Without using Theorem 16.3.1 or Exercise 16.5 show that if $M\in \mathcal {M}(H,\nu )$ and $\mathcal {N}\in \mathcal {S}_{\mathrm {ev}}(H,\nu )$ satisfy

$$\displaystyle \begin{aligned} \operatorname{Re} \left\langle \phi ,(\partial_{t,\nu}M(\partial_{t,\nu})+\mathcal{N}^\nu)\phi\right\rangle \geqslant c\left\langle \phi ,\phi\right\rangle \quad (\phi\in \operatorname{dom}(\partial_{t,\nu})) \end{aligned}$$

for some c > 0, then $0 \in \rho \big (\overline {\partial _{t,\nu }M(\partial _{t,\nu })+\mathcal {N}^\nu +A}\big )$, for all skew-selfadjoint $A\colon \operatorname {dom}(A)\subseteq H\to H$.

Hint: Compute the adjoint of $\partial _{t,\nu }M(\partial _{t,\nu })+\mathcal {N}^\nu + A$ with the help of Theorem 6.2.1 and Theorem 2.3.2.

Exercise 16.7

Prove Lemma 16.3.6.