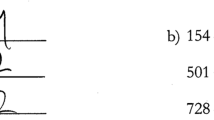Abstract
Analyzing students’ documents (e.g., their homework) can serve as a basis for diagnosing students’ learning status and thus also for adaptive teaching. When making diagnostic judgments about students’ learning status in mathematics, teachers may benefit from using theoretical models of mathematical competence because such models illustrate what tasks students should have mastered on each level of competence. Based on students’ documents and a model of mathematical competence at the primary level, we developed a simulated learning environment for (1) analyzing and (2) supporting pre-service teachers’ diagnostic processes and results. When working in the simulated environment, pre-service elementary teachers are asked to assess virtual third graders’ learning status by diagnosing their mathematical competence levels as well as their misconceptions (e.g., misconception regarding multiplication) based on the competence model. To do so, pre-service teachers analyze students’ solutions to mathematical problems that they can select from a set of problems varying in content and difficulty. First data analyses suggest that the environment can capture differences in pre-service teachers’ diagnostic processes. A better understanding of these processes can serve as a basis for further developing the learning environment.
You have full access to this open access chapter, Download chapter PDF
Similar content being viewed by others
Keywords
- Mathematical education
- Competence level model
- Misconception
- Document-based simulation
- Simulated environment
- Diagnostic competence
This chapter’s simulation at a glance
Domain | Teacher education |
Topic | Diagnosing primary students’ mathematical competence levels and misconceptions |
Learner’s task | To assume the role of a teacher and analyze students’ documents to identify primary students’ mathematical competence levels and misconceptions |
Target group | Pre-service elementary teachers |
Diagnostic mode | Document-based individual diagnosing |
Sources of information | Primary students’ solutions to mathematical tasks |
Special features | All mathematical problems and students’ solutions in the simulated environment come from pilot studies of VERA-3, a German large-scale comparison test in Grade 3, based on the primary level mathematical competence model by Reiss and Winkelmann (2009) |
3.1 Diagnosing as a Key for Adaptive Teaching
“Teachers need to be aware of what each and every student is thinking and knowing” (Hattie, 2010, p. 238). In addition to emphasizing the importance of teachers for students’ learning progress in general, Hattie identifies as one of his signposts toward excellent education that teachers must be able to diagnose their students’ current learning statuses in order to provide adequate and useful feedback (Hattie, 2010) and thus to teach adaptively. Such diagnostic competences can be defined as “individual dispositions enabling people to apply their knowledge in diagnostic activities according to professional standards to collect and interpret data in order to take decisions of high quality” (Heitzmann et al., 2019, p. 5). Diagnosing as a prerequisite for adaptive teaching has recently been studied by several research groups, including NeDiKo (e.g., Südkamp & Praetorius, 2017), DiaKom (Leuders et al., 2018) and Cosima (Chernikova et al., 2022; Heitzmann et al., 2019). Teachers’ diagnostic competences have also received increased attention on the political level. In Germany, for instance, diagnosing has been included as a standard competence for adaptive teaching in the national teacher training standards (Standing Conference of the Ministers of Education and Cultural Affairs of the Länder in the Federal Republic of Germany—Kultusministerkonferenz, 2004b).
Despite its recognized relevance, diagnosing is not yet sufficiently taught during university teacher training. Oser and Oelkers (2001) point out that there is indeed a gap between the requirements of the teaching profession, especially with respect to diagnosing, and the content taught at university and during in-service teacher training. According to Shulman (1986), teachers should have a wide range of knowledge, including content knowledge , pedagogical content knowledge and pedagogical knowledge . Förtsch et al. (2018) illustrate the applicability of these categories to the context of diagnosing. In addition to the above categories of knowledge, Shulman further defined three “forms of knowledge” that describe how to represent these categories, namely propositional knowledge , case knowledge , and strategic knowledge (Shulman, 1986, p. 10). Propositional knowledge comprises theoretical foundations, formulated as “principles, maxims, and norms” (Shulman, 1986, p. 11). In contrast, case knowledge is “knowledge of specific, well-documented, and richly described events” and comprises “examples of specific instances of practice” (Shulman, 1986, p. 11). Accordingly, case knowledge helps to apply theoretical content about diagnosing in specific situations, such as diagnosing students’ misconceptions in mathematics. Strategic knowledge is used in situations when “principles collide and no simple solution is possible” (Shulman, 1986, p. 11). However, in the everyday life of a teacher, classroom situations and in particular interactions with students may not simply be able to be abstracted to a general case, but may require adaptation to the individual circumstances. These circumstances probably also affect teachers’ diagnostic judgments about their students. In summary, possessing knowledge in all three categories as well as all three forms may be beneficial for the teaching profession in general. Thus, supporting these various knowledge facets during teacher education may have a positive impact on prospective teachers’ diagnostic processes and results. It is worth mentioning, however, that in addition to knowledge, diagnostic competences also include diagnostic activities (see Chernikova et al., 2022).
3.2 Learning from Other Disciplines About Supporting Diagnostic Processes in Simulated Learning Environments
Research on diagnosing in education has focused more strongly on the outcome of diagnosing rather than on the diagnostic process (Artelt & Rausch, 2014). Medical research on diagnosing has, however, more intensively studied diagnostic processes (see Fink et al., 2022; Radkowitsch et al., 2022). In our research, we adopt a general framework to analyze the diagnostic processes with respect to epistemic-diagnostic activities (Fischer et al., 2014), hereafter referred to as diagnostic activities. In particular, we aim to assess which diagnostic activities occur during diagnosing in educational settings, to measure their frequency and their influence on diagnostic results.
In a first practice trial (Wildgans-Lang et al., 2019), we found that we can apply the model of diagnostic activities (Fischer et al., 2014) in the educational setting under study. More specifically, we found that teachers identify problems in mathematics on the basis of questions, incorrect student solutions, or student mistakes on homework and tests. In some cases, teachers ask themselves which misconceptions can occur in a specific topic area before the lesson starts and formulate hypotheses accordingly. If teachers then create specific tasks to identify such misconceptions, this is referred to as artifact construction ; if teachers select from a set of existing tasks, this is called evidence generation . These diagnostic activities can already occur during lesson preparation. Further diagnostic activities are evidence evaluation , which involves recognizing a mistake in the student’s solution, evaluating it by applying their pedagogical content knowledge, and drawing appropriate conclusions to communicate to the student, class, parents, or colleagues (Fischer et al., 2014).
The Nediko group has developed a model in which the diagnostic activities and their sequence are discussed. The group describes that—if the diagnostic result is not obvious—the generation of hypotheses is necessary. For this, information about the student’s mathematical competences must be collected (evidence generation and evaluation) and then evaluated; that is, conclusions must be drawn, which can lead to further hypotheses (Herppich et al., 2017). The three-step diagnostic process in “error situations” (Heinrichs & Kaiser, 2018, p. 79) also refers to diagnostic activities (Heinrichs, 2015; Heinrichs & Kaiser, 2018). In summary, central to all these diagnostic processes is the generation of hypotheses, which is based on evidence generation and evaluation and from which conclusions are drawn.
3.3 Diagnosing Based on Students’ Solutions
Teachers often diagnose students’ competences or misconceptions when they identify an error in students’ work (Wildgans-Lang et al., 2019) or with the aim to evaluate their performance. Often the focus is on ranking students’ performance (Artelt & Rausch, 2014). However, a more important indicator would be to evaluate students’ competences with regard to clearly defined standards, such as the mathematical competence levels model for the primary level (Reiss & Winkelmann, 2009). This model divides the mathematical competences acquired by German primary school students in their first four school years into five levels. These range from basic technical knowledge (via routine procedures) (Level 1) to modeling complex problems and independently finding appropriate strategies (Level 5; see Reiss & Obersteiner, 2019). In addition, the competences are divided into domains, such as numbers and operations or patterns and structures, hereafter referred to as competence areas, which are in turn based on guiding principles of the national curriculum (Kultusministerkonferenz, 2004a). This theoretical classification of competences to be acquired in primary school has been reviewed in recent years via comparative studies throughout Germany (Stanat, 2012). Students’ misconceptions can also be classified into these competence areas. Misconceptions are often the reason for systematic errors (Radatz, 1980). In the first 4 years of school, students learn many basic skills in mathematics. Typical mistakes regarding such basic skills include, for example, misconceptions about place value. Such misconceptions may lead to errors when adding two numbers digit by digit. Descriptions of typical errors and misconceptions can be found in Padberg and Benz (2011). Typical errors in the modeling process encompass errors in understanding word problems, developing a solution plan, omitting steps when solving the problem, and correctly interpreting the result (Franke et al., 2010).
3.4 Supporting Diagnosing in a Simulated Environment
A simulated learning environment to support diagnosing may enhance the user’s content knowledge, pedagogical content knowledge, and pedagogical knowledge about diagnosing. Furthermore, it should give the user the opportunity to apply their knowledge about diagnosing to authentic cases. Additionally, work in the learning environment can be stopped and repeated, which seems to be helpful for reflecting on the evidence and diagnostic activities already carried out (Blomberg et al., 2013; Rich & Hannafin, 2009; Santagata, 2005). To support the transfer of the practiced diagnostic activities to real classroom situations, it might be beneficial for the learning environment to be as authentic as possible (Stammen et al., 2018).
3.5 Development of the Simulated Environment
In this section , we explain how we developed the learning environment based on the goals presented in the previous section. In order to convey case knowledge in the simulated learning environment, we developed appropriate cases. The main idea was to employ theory-driven design to generate documents depicting virtual students’ solutions to mathematical problems. Based on these documents, the users of the learning environment had to diagnose the virtual students’ mathematical competences.
The mathematical competence model on the primary level by Reiss and Winkelmann (2009) introduced above served as a foundation for developing the virtual students within the learning environment. In order to apply the model, we decided to generate virtual third graders , as students in this grade are already familiar with most of the mathematical content taught in elementary school. The virtual students were designed to have varying levels of mathematical knowledge, which in turn determined whether they would solve a given mathematical problem correctly or not. Their knowledge levels would also determine whether they made various types of mistakes when solving the problems.
All mathematical problems in the simulated environment were taken from pilot studies of VERA-3, a German large-scale comparison test for Grade 3 of elementary school. All VERA-3 problems included in the learning environment have undergone a thorough development process and are Rasch-scaled and empirically validated. The problems were developed based on the model of mathematical competence, such that each mathematical problem can be assigned to exactly one of the competence levels in the model. In other words, the competence model clearly and precisely describes which competence level is minimally necessary to solve a specific mathematical problem correctly. Furthermore, each mathematical problem is assigned to a single content area in line with curricular standards.
For simplicity’s sake, we restricted the content of the mathematical problems to two competence areas: numbers and operations and patterns and structures (see Reiss & Obersteiner, 2019; Reiss & Winkelmann, 2009). Numbers and operations comprise arithmetic problems on the primary level. Due to its central role in primary mathematics education and its fundamental importance for other competence areas (Rasch & Schütte, 2007), numbers and operations is a well-researched competence area, particularly with respect to typical student mistakes and error strategies. The competence area patterns and structures —which primarily requires recognizing connections and contexts related to the given information in mathematical problems—is also fundamentally related to other competence areas and therefore relevant to a wide range of mathematical content (Wittmann & Müller, 2007). Thus, due to their close relations to other competence areas, the competence areas numbers and operations as well as patterns and structures seem to be suitable as a starting point for developing the learning environment. Figs. 3.1 and 3.2 show mathematical problems in the two competence areas.
Sample problem for the competence area numbers and operations. The text was translated from the German original by the authors. (Further examples: https://www.iqb.hu-berlin.de/vera/aufgaben/map)
Sample problem for the competence area patterns and structures . The text was translated from the German original by the authors. (Further examples: https://www.iqb.hu-berlin.de/vera/aufgaben/map)
We carefully selected mathematical problems for the learning environment from 50,000 original student solutions by participants in VERA-3 pilot studies from 2015 to 2017. A “student solution” is a student’s response to a single mathematical problem. This means that the 50,000 student solutions include both responses by different students to the same problem and responses by the same student to different problems. The student solutions concerned problems assigned to the two competence areas discussed before. The problem selection process involved three steps:
-
In the first step, we theoretically described typical misconceptions by primary students in the two competence areas based on Padberg and Benz (2011) as well as Franke et al. (2010). We decided to focus on two facets of misconceptions: misconceptions in arithmetic (such as misconceptions concerning the place value system or the number zero) and misconceptions with regard to word problems (such as misconceptions concerning verbal answers to word problems).
-
In the second step, we studied the original student solutions from VERA-3 to identify mistakes attributable to the misconceptions defined in the first step. We grouped student solutions with mistakes stemming from the same misconception.
-
In the third step, we compared these groups of student solutions (each representing one misconception), paying particular regard to two further aspects. First, we wanted to keep the number of mathematical problems in the learning environment limited. For this reason, we preferred problems with student solutions assigned to several misconceptions. In other words, we excluded problems that did not result in mistakes regarding different competence areas and misconceptions. Second, we sought to select student solutions with similar handwriting in order to make the simulated environment as authentic as possible. As a result, we removed solutions with particularly conspicuous or unique handwriting.
After these steps, a set of 55 mathematical problems uniquely assigned to one of the five levels in the competence model were selected. For each of the 55 problems, we collected up to 15 original student solutions. In total, this resulted in 520 student solutions.
Finally, we developed virtual students with varying levels of mathematical competence. We assigned each virtual student a particular misconception determined beforehand. For simplicity’s sake, each virtual student exhibited only one misconception. Based on the groups of student solutions identified in the second step, we assigned each virtual student original VERA-3 solutions with mistakes reflecting the corresponding misconception. We also assigned each virtual student correctly solved VERA-3 solutions based on the student’s competence level.
Note that we considered the empirical solution rates from VERA for each competence level when assigning the problems and corresponding solutions to the virtual students. More precisely, we ensured that a virtual student on a particular competence level would solve at least half of the mathematical problems on this competence level correctly. Accordingly, each student solved considerably fewer problems correctly on higher competence levels, because the requirements of these problems exceed the student’s mathematical abilities. By contrast, the student solved most problems that are assigned to a lower competence level correctly.
In total, we developed 15 virtual students with different misconceptions, each of which was assigned different original VERA-3 solutions. The selected mathematical problems covered all five levels of the mathematical competence model. On the basis of their individual misconceptions and mathematical competences, the virtual students were distributed across the levels of the competence level model as follows:
-
four virtual students had Competence Level 1,
-
three virtual students had Competence Level 2,
-
four virtual students had Competence Level 3,
-
two virtual students had Competence Level 4, and
-
two virtual students had Competence Level 5.
Compared to the results of a standardization study in Germany, students on Competence Level 1 are somewhat over-represented in the simulated environment. This is due to the fact that students with the fundamental misconceptions we considered important are often at Competence Level 1.
We also assigned names to the virtual students. We selected short and common names from a list of the most popular names for newborns in Germany in 2011. This year corresponds approximately to the birth year of the virtual third graders at the time the simulated environment was developed. The virtual students’ gender was roughly equally distributed. Table 3.1 provides an overview of the 15 virtual students developed and their corresponding misconceptions.
3.6 Operating Principle of the Environment
Upon entering the simulated learning environment, users (in our case pre-service elementary teachers) first complete a knowledge test. This test assesses Shulman’s three types of knowledge (content knowledge, pedagogical knowledge, and pedagogical content knowledge; see Shulman, 1986). The test was included to be able to analyze the relations between teachers’ knowledge base and their diagnostic process and results.
After finishing the knowledge test, users are introduced to the learning setting. They are asked to imagine they are the teacher of a third-grade class and need to diagnose their students’ mathematical learning statuses. This means assigning the students to one of the five levels of the competence model, which is briefly introduced at the beginning as well. They are also asked to identify the students’ mathematical misconceptions. Users (pre-service teachers) are told that they will communicate individually with each student while all other students in the class work quietly at their desks (see also Fig. 3.3, letter A).
During the diagnostic process, pre-service teachers first choose which one of the 15 virtual students in the simulated environment they want to diagnose by analyzing his or her solutions to mathematical problems. The available problems for the selected student are sorted by difficulty according to the five competence levels (see Fig. 3.3, letter B). The pre-service teachers first select a competence level (see Fig. 3.3, letter B) and subsequently are presented with titles (see Fig. 3.4, letter D) as well as previews (see Fig. 3.4, letter E) of the available mathematical problems for the selected student on the selected competence level. For each of the 15 virtual students, between five and eight mathematical problems are available for each competence level. Evidence generation in this learning environment means that the pre-service teacher decides which problem to select and then clicks the appropriate button. The student’s solution to the mathematical problem appears right away (see Fig. 3.5). The teachers are asked to judge the correctness of the student solution (see Fig. 3.6, letter F) and to take notes (see Fig. 3.6, letter G) that may help to diagnose the student’s mathematical learning status. In this way, pre-service teachers can examine the student’s solutions to various problems and take notes until they think they have collected enough information to make a final diagnosis. The notes taken can be viewed throughout the entire process. On the one hand, the notes serve as a recall aid for teachers when they make their final diagnosis. On the other hand, we expect that these notes could provide insights into the diagnostic process. For example, it will be interesting to see whether the pre-service teachers mainly write down observations or whether they also hypothesize and draw conclusions, and how these diagnostic activities are related to the diagnostic results. A challenge will be to code the notes such that they can be assigned to different diagnostic activities (Fischer et al., 2014).
At any point, the pre-service teachers can elect to make a final diagnosis (see Fig. 3.3, letter C), which comprises several steps: First, the teachers have to choose and justify the student’s competence level and estimate the certainty of their decision on a scale from 0% to 100%. Then, the teachers have to describe the virtual student’s misconception in a free-text entry. After that, the teachers are supposed to select the student’s misconception out of a set of five misconceptions provided. Here again, the teachers are asked to rate the certainty of their decision on a scale from 0% to 100%. By asking for the certainty of the teachers’ decisions, we aim to distinguish between well-reasoned decisions and guessing. Furthermore, we want to analyze whether decisions are better justified and precise after having diagnosed several students. Finally, after making a final diagnosis for this virtual student, the teacher can continue on to diagnosing the mathematical learning status of another student.
3.7 Preliminary Findings
In a first pilot study, the simulated environment was tested with 91 participants (77 female, 14 male, M = 22.9 years old, SD = 2.96, range 20–39 years old) from two universities in Germany. They were pre-service elementary school teachers in their first to ninth semester of university teacher education studies (M = 3.6). The pre-service teachers described the simulated environment and in particular the virtual children as authentic and motivating (Wildgans-Lang et al., 2020).
First data analyses show great variation in the pre-service elementary teachers’ diagnostic processes. For instance, some participants selected a mathematical problem on Competence Level 3 to start. Depending on the student’s solution to these problems, they continued with problems with a lower or higher level of difficulty. In contrast, some pre-service teachers consistently started the diagnostic process by selecting a mathematical problem on either Competence Level 1 or 5. These participants then selected problems with an increasing or decreasing level of difficulty, respectively, until they reached a decision. Our participants’ diagnostic processes also greatly varied in the number of instances of evidence generation utilized (i.e., the number of mathematical problems used to diagnose one student). The number of problems used did not correlate with the accuracy of the diagnostic results, suggesting that viewing more evidence is not per se a good predictor of accurate diagnosing. It is also noteworthy that our participants rarely generated hypotheses, which we consider important in the diagnostic process. For a more detailed report on the results of this pilot study, see Wildgans-Lang et al. (2020).
After the pre-service teachers finished working with the learning environment, we asked them to describe in a short text how they proceeded when diagnosing their students, in particular, how they selected appropriate problems for the students and whether they found the allocation of problems to competence levels helpful. With this task, we wanted the teachers to reflect on their diagnostic process once more. In addition, we expected to identify aspects that were particularly important to teachers but that might not be recognizable from the data alone.
In general, most pre-service teachers reported that the classification of mathematical problems into competence levels was useful. One participant, for instance, reported that she began diagnosing by providing the students with problems on Level 2 in order to avoid challenging them too much at the beginning. Subsequently, this participant reported choosing problems that covered a similar mathematical topic as the previous problem, but on a higher competence level. After that, this participant selected other topics on the higher competence level. Another participant reported: “I always started with problems on Competence Level 1 and considered three student solutions. When I felt that the student solved the problems well and without mistakes, I continued with problems on the next (higher) competence level” (translated). Here again, the allocation of problems into competence levels seemed to be helpful.
However, a few participants indicated that working with the competence levels was more of a hindrance than helpful. They argued that their focus was on students’ misconceptions. Therefore, they did not select problems based on the competence level but rather on the mathematical content. Hence, sorting the problems by level of difficulty was not helpful for these participants.
This feedback suggests that the majority of prospective teachers in our study focused more strongly on diagnosing students’ competence levels rather than diagnosing their specific misconceptions. In fact, our participants diagnosed the students’ competence level correctly in 75% of cases, while they diagnosed the correct misconception in less than one-third of cases (Wildgans-Lang et al., 2020).
3.8 Conclusion, Discussion, and Outlook
Apart from the data generated while teachers make a final diagnosis concerning a student’s mathematical learning status (i.e., choosing his or her competence level and misconception), the simulated environment also records various data generated during the diagnostic process. Examples are the mathematical problems selected and their corresponding competence levels. Analyzing these data may help us understand (prospective) teachers’ approaches to diagnosing students’ mathematical learning status and compare these different approaches with the corresponding diagnostic results. Whether some approaches lead to better diagnostic results than others is an interesting question for further research. Moreover, analyzing the notes taken by teachers in the learning environment will be of particular interest for better understanding diagnostic processes. Specifically, we will categorize teachers’ notes based on the aforementioned theoretical taxonomy of diagnostic activities. This categorization is intended to make the diagnostic process more tangible. Another question for further research is whether diagnostic processes and results depend on pre-service teachers’ previous knowledge, such as that acquired during in-service teaching experiences or university courses, for example.
In summary, contributing to the first four overarching research questions mentioned in the introduction by Fischer et al. (2022) and in the concluding chapter by Opitz et al. (2022), the overarching goal for our future research will be to explore which circumstances and activities in the diagnostic process facilitate accurate diagnostic results. Identifying such factors will help us refine the simulated environment to more effectively foster pre-service teachers’ diagnostic competences. Fostering diagnostic competences includes but is not limited to effectively conveying essential categories and forms of knowledge about diagnosing (see Shulman, 1986; Förtsch et al., 2018). The learning environment we have constructed for pre-service teachers should also serve as a platform to practice diagnosing and prepare for their future careers as teachers.
As one instructional approach, we are planning on implementing scaffolds in the learning environment. The idea of scaffolds is to provide minimal and targeted support to guide the learner to engage in well-thought-out diagnostic processes leading to accurate results. Such scaffolds could be strategic tips on how to carry out diagnostic activities. Scaffolds might be also content-related, providing tips concerning the mathematical competence model or common misconceptions among elementary students.
More generally, we aim to develop a simulated environment that has been empirically found to effectively support pre-service teachers’ diagnostic competences when deployed as part of university teacher education. Such a learning environment will certainly not replace existing courses or real-life internships in schools, but may be used to complement them. Of course, how to optimally integrate such simulations into teacher education is a research question in its own right.
References
Artelt, C., & Rausch, T. (2014). Accuracy of teacher judgments. In S. Krolak-Schwerdt, S. Glock, & M. Böhmer (Eds.), Teachers’ professional development: Assessment, training, and learning (The future of education research) (Vol. 03, pp. 27–43). Sense Publishers.
Blomberg, G., Renkl, A., Gamoran Sherin, M., Borko, H., & Seidel, T. (2013). Five research-based heuristics for using video in pre-service teacher education. Journal for Educational Research Online / Journal für Bildungsforschung Online, 5(1), 90–114.
Chernikova, O., Heitzmann, N., Opitz, A., Seidel, T., & Fischer, F. (2022). A theoretical framework for fostering diagnostic competences with simulations. In F. Fischer & A. Opitz (Eds.), Learning to diagnose with simulations - examples from teacher education and medical education. Springer.
Fink, M., Siebeck, M., Fischer, F., & Fischer, M. (2022). Live and video simulations of medical history taking: Theoretical background, design, development and validation of a learning environment. In F. Fischer & A. Opitz (Eds.), Learning to diagnose with simulations - examples from teacher education and medical education. Springer.
Fischer, F., Kollar, I., Ufer, S., Sodian, B., Hussmann, H., Pekrun, R., et al. (2014). Scientific reasoning and argumentation: Advancing an interdisciplinary research agenda in education. Frontline Learning Research, 2, 28–45. https://doi.org/10.14786/flr.v2i2.96
Fischer, F., Chernikova, O., & Opitz, A. (2022). Learning to diagnose with simulations: Introduction. In F. Fischer & A. Opitz (Eds.). Learning to diagnose with simulations – examples from teacher education and medical education. Springer.
Förtsch, C., Sommerhoff, D., Fischer, F., Fischer, M., Girwidz, R., Obersteiner, A., et al. (2018). Systematizing professional knowledge of medical doctors and teachers: Development of an interdisciplinary framework in the context of diagnostic competences. Education Sciences, 8, 207. https://doi.org/10.3390/educsci8040207
Franke, M., Padberg, F., & Ruwisch, S. (2010). Didaktik des Sachrechnens in der Grundschule. Spektrum Akademischer Verlag.
Hasemann, K., & Gasteiger, H. (2014). Mathematik Primarstufe und Sekundarstufe I + II. In Anfangsunterricht Mathematik (3rd ed.). Springer Spektrum.
Hattie, J. (2010). Visible learning: A synthesis of over 800 meta-analyses relating to achievement. Routledge.
Heinrichs, H. (2015). Diagnostische Kompetenz von Mathematik-Lehramtsstudierenden: Messung und Förderung (Perspektiven der Mathematikdidaktik). Springer Spektrum.
Heinrichs, H., & Kaiser, G. (2018). Diagnostic competence for dealing with students’ errors: Fostering diagnostic competence in error situations. In T. Leuders, K. Philipp, & J. Leuders (Eds.), Diagnostic competence of mathematics teachers: Unpacking a complex construct in teacher education and teacher practice (Mathematics teacher education) (Vol. 11, pp. 79–94). Springer International Publishing.
Heitzmann, N., Seidel, T., Opitz, A., Hetmanek, A., Wecker, C., Fischer, M., Ufer, S., Schmidmaier, R., Neuhaus, B., Siebeck, M., Stürmer, K., Obersteiner, A., Reiss, K., Girwidz, R., & Fischer, F. (2019). Facilitating diagnostic competences in simulations in higher education. Frontline Learning Research, 7(4), 1–24. https://doi.org/10.14786/flr.v7i4.384
Herppich, S., Praetorius, A.-K., Hetmanek, A., Glogger-Frey, I., Ufer, S., Leutner, D., et al. (2017). Ein Arbeitsmodell für die empirische Erforschung der diagnostischen Kompetenz von Lehrkräften. In A. Südkamp & A.-K. Praetorius (Eds.), Diagnostische Kompetenz von Lehrkräften: Theoretische und methodische Weiterentwicklungen (Pädagogische Psychologie und Entwicklungspsychologie) (Vol. 94, pp. 75–94). Waxmann Verlag GmbH.
Kultusministerkonferenz. (2004a). Bildungsstandards im Fach Mathematik für den Primarbereich: Beschluss vom 15.10.2004.
Kultusministerkonferenz. (2004b). Standards für die Lehrerbildung: Bildungswissenschaften. Beschluss der KMK vom 16.12.2004. Standing conference of the ministers of education and cultural Affairs of the Länder in the Federal Republic of Germany. http://www.kmk.org/fileadmin/Dateien/veroeffentlichungen_beschluesse/2004/2004_12_16-Standards-Lehrerbildung.pdf
Leuders, T., Philipp, K., & Leuders, J. (2018). Diagnostic competence of mathematics teachers: Unpacking a complex construct in teacher education and teacher practice (Mathematics teacher education) (Vol. 11). Springer International Publishing.
Oser, F., & Oelkers, J. (Eds.). (2001). Die Wirksamkeit der Lehrerbildungssysteme: Von der Allrounderbildung zur Ausbildung professioneller Standards (Nationales Forschungsprogramm 33 - Wirksamkeit unserer Bildungssysteme). Rüegger.
Padberg, F., & Benz, C. (2011). Mathematik Primar- und Sekundarstufe I + II: Didaktik der Mathematik. In Didaktik der Arithmetik: Für Lehrerausbildung und Lehrerfortbildung (4th ed.). Spektrum Akademischer Verlag.
Radatz, H. (1980). Fehleranalysen im Mathematikunterricht. Vieweg+Teubner Verlag.
Radkowitsch, A., Sailer, M., Fischer, M., Schmidmaier, R., & Fischer, F. (2022). Diagnosing collaboratively: A theoretical model and a simulation-based learning environment. In F. Fischer & A. Opitz (Eds.), Learning to diagnose with simulations - examples from teacher education and medical education. Springer.
Rasch, R., & Schütte, S. (2007). Zahlen und Operationen. In G. Walther (Ed.), Bildungsstandards für die Grundschule: Mathematik konkret: [Aufgabenbeispiele, Unterrichtsanregungen, Fortbildungsideen]; mit CD-ROM (2nd ed., pp. 66–88). Lehrer-Bücherei.
Reiss, K., & Obersteiner, A. (2019). Competence models as a basis for defining, understanding, and diagnosing students’ mathematical competences. In A. Fritz, V. G. Haase, & P. Räsänen (Eds.), The international handbook of math learning difficulties: From the laboratory to the classroom. Springer.
Reiss, K., & Winkelmann, H. (2009). Kompetenzstufenmodelle für das Fach Mathematik im Primarbereich. In D. Granzer (Ed.), Bildungsstandards Deutsch und Mathematik: [Leistungsmessung in der Grundschule] (pp. 120–141). Beltz-Pädagogik.
Rich, P. J., & Hannafin, M. (2009). Video annotation tools: Technologies to scaffold, structure, and transform teacher reflection. Journal of Teacher Education, 60(1), 52–67.
Santagata, R. (2005). Practices and beliefs in mistake-handling activities: A video study of Italian and US mathematics lessons. Teaching and Teacher Education, 21, 491–508. https://doi.org/10.1016/j.tate.2005.03.004
Shulman, L. S. (1986). Those who understand: Knowledge growth in teaching. Educational Researcher, 15, 4–14. https://doi.org/10.3102/0013189X015002004
Stammen, A., Malone, K., & Irving, K. (2018). Effects of modeling instruction professional development on biology teachers’ scientific reasoning skills. Education Sciences, 8, 119–138. https://doi.org/10.3390/educsci8030119
Stanat, P. (Ed.). (2012). Kompetenzen von Schülerinnen und Schülern am Ende der vierten Jahrgangsstufe in den Fächern Deutsch und Mathematik: Ergebnisse des IQB-Ländervergleichs 2011. Waxmann Verlag GmbH.
Südkamp, A., & Praetorius, A.-K. (2017). Diagnostische Kompetenz von Lehrkräften: Theoretische und methodische Weiterentwicklungen. In Pädagogische Psychologie und Entwicklungspsychologie (Vol. 94). Waxmann Verlag GmbH.
Wildgans-Lang, A., Obersteiner, A., & Reiss, K. (2019). Epistemisch-diagnostische Aktivitäten im Diagnoseprozess bei Lehrkräften im Mathematikunterricht. In T. Ehmke, P. Kuhl, & M. Pietsch (Eds.), Lehrer. Bildung. Gestalten.: Beiträge zur empirischen Forschung in der Lehrerbildung (pp. 281–291). Juventa Verlag GmbH.
Wildgans-Lang, A., Scheuerer, S., Obersteiner, A., Fischer, F., & Reiss, K. (2020). Analyzing prospective mathematics teachers’ diagnostic processes in a simulated environment. ZDM, 52(2), 241–254.
Wittmann, E. C., & Müller, G. N. (2007). Muster und Strukturen als fachliches Konzept. In G. Walther (Ed.), Bildungsstandards für die Grundschule: Mathematik konkret: [Aufgabenbeispiele, Unterrichtsanregungen, Fortbildungsideen]; mit CD-ROM (2nd ed., pp. 42–65). Cornelsen Scriptor.
Acknowledgments
The research presented in this chapter was funded by a grant from the Deutsche Forschungsgemeinschaft (DFG-FOR 2385) to Kristina Reiss, Andreas Obersteiner, and Frank Fischer (RE 1247/12-1; OB 412/3-1).
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2022 The Author(s)
About this chapter
Cite this chapter
Wildgans-Lang, A., Scheuerer, S., Obersteiner, A., Fischer, F., Reiss, K. (2022). Learning to Diagnose Primary Students’ Mathematical Competence Levels and Misconceptions in Document-Based Simulations. In: Fischer, F., Opitz, A. (eds) Learning to Diagnose with Simulations . Springer, Cham. https://doi.org/10.1007/978-3-030-89147-3_3
Download citation
DOI: https://doi.org/10.1007/978-3-030-89147-3_3
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-89146-6
Online ISBN: 978-3-030-89147-3
eBook Packages: Behavioral Science and PsychologyBehavioral Science and Psychology (R0)