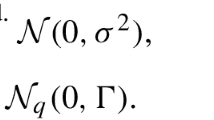Preprocessing Tools for Data Preparation

Abstract

This data preparation chapter is of paramount importance for implementing statistical machine learning methods for genomic selection. We present the basic linear mixed model that gives rise to BLUE and BLUP and explain how to decide when to use fixed or random effects that give rise to best linear unbiased estimates (BLUE or BLUEs) and best linear unbiased predictors (BLUP or BLUPs). The R codes for fitting linear mixed model for the data are given in small examples. We emphasize tools for computing BLUEs and BLUPs for many linear combinations of interest in genomic-enabled prediction and plant breeding. We present tools for cleaning, imputing, and detecting minor and major allele frequency computation, marker recodification, frequency of heterogeneous, frequency of NAs, and three methods for computing the genomic relationship matrix. In addition, scaling and data compression of inputs are important in statistical machine learning. For a more extensive description of linear mixed models, see Chap. 5.

2.1 Fixed or Random Effects

As mentioned in Chap. 1, fixed effect models in general (to design experiments, regression models, genomic prediction models, etc.) are recommended when the levels under study (collected by the scientist) are the unique levels of interest in the study, and the levels or quantities observed in the explanatory variables are treated as if they were nonrandom. For these reasons, a fixed factor is defined as a categorical or classification variable, chosen to represent specific conditions, for which the researcher has included all levels (or conditions) that are of interest for the study in the model. This means that fixed effects are unknown constant parameters associated with continuous covariates or levels of categorical factors in any fixed or mixed effects (fixed + random effects). The estimation of these fixed parameters in fixed effects models or mixed effects models is generally of intrinsic interest, since they indicate the relationships of the covariates with the response variable. Fixed effects can be associated with continuous covariates such as the weight of an animal in kilograms, maize yield in tons per hectare, qualification of a reference test or socioeconomic level, which will carry a continuous range of values, or they can be associated with factors such as gender, hybrid, or group treatment, which are categorical. This implies that fixed effects are the best option when performing an inference for the whole target population.

A random factor is a classification variable with levels that can be randomly sampled from a population with different levels of study, such as classrooms, regions, cattle herds, or clinics that are randomly sampled from a population. All possible levels of the random factor are not present in the data set, yet it is the intention of the researcher to make an inference about the entire population of levels from the selected sample of these factor levels. Random factors are included in an analysis in order for the modification in the dependent variable through the levels of the random factors to be evaluated and the results of the data analysis generalized to all levels of the population random factor. This means that random effects are represented by random variables (not observed) which, we generally assume, have a particular distribution, the normal distribution being the most common. Due to the above, random effects are suggested when we want to perform an inference for all levels of the target population.

2.2 BLUEs and BLUPs

This section presents the concepts and terminologies of BLUE and BLUP. Since these two concepts are related to a mixed model, we present the following linear mixed model as

$$ \boldsymbol{Y}=\boldsymbol{X}\boldsymbol{\beta } +\boldsymbol{Zu}+\boldsymbol{\varepsilon}, $$

(2.1)

where Y is the vector of response variables of order n × 1, X is the design matrix of fixed effects of order n × p, β is the vector of order p × 1 of beta coefficients, Z is the design matrix of random effects of order n × q, u is the vector of random effects distributed as N(0, Σ), where Σ is a variance–covariance matrix of random effects of dimension q × q, and ε is a vector of residuals distributed as N(0, R), where R is a variance–covariance matrix of residual effects of dimension n × n. The unconditional mean of Y is equal to E(Y) = Xβ, while the conditional mean of Y, given the random effects, is equal to E(Y| u) = Xβ + Zu. A solution to jointly “estimate” parameters β and u was proposed by Henderson (1950, 1963, 1973, 1975, 1984), which consists in solving the mixed model equation (MME)

$$ \left(\begin{array}{cc}{\boldsymbol{X}}^{\mathrm{T}}{\boldsymbol{R}}^{-1}\boldsymbol{X}& {\boldsymbol{X}}^{\mathrm{T}}{\boldsymbol{R}}^{-1}\boldsymbol{Z}\\ {}{\boldsymbol{Z}}^{\mathrm{T}}{\boldsymbol{R}}^{-1}\boldsymbol{X}& {\boldsymbol{Z}}^{\mathrm{T}}{\boldsymbol{R}}^{-1}\boldsymbol{Z}+{\boldsymbol{\Sigma}}^{-1}\end{array}\right)\left(\begin{array}{c}\hat{\boldsymbol{\beta}}\\ {}\hat{\boldsymbol{u}}\end{array}\right)=\left(\begin{array}{c}{\boldsymbol{X}}^{\mathrm{T}}{\boldsymbol{R}}^{-1}\boldsymbol{y}\\ {}{\boldsymbol{Z}}^{\mathrm{T}}{\boldsymbol{R}}^{-1}\boldsymbol{y}\end{array}\right) $$

(2.2)

The solution obtained for β is the BLUE and the solution obtained for u is the BLUP.

While this expression to find the estimates of $\hat{\boldsymbol{\beta}}$ and $\hat{\boldsymbol{u}}$ may look quite complex, when the number of observations is larger than the sum of the number of fixed effects and the number of random effects (p + q), it is quite efficient since only needs to calculate the inverse of the small matrices of R and Σ. Also, the matrix on the left that needs to be inverted to obtain the solution for $\hat{\boldsymbol{\beta}}$ and $\hat{\boldsymbol{u}}$ is of order (p + q) × (p + q), which in some applications is considerably less than a matrix of dimension n × n as V = ZΣZ^T + R, which is also useful to obtain the solution of these parameters by using $\hat{\boldsymbol{\beta}}={\left({\boldsymbol{X}}^{\mathrm{T}}{\boldsymbol{V}}^{-1}\boldsymbol{X}\right)}^{-1}{\boldsymbol{X}}^{\mathrm{T}}{\boldsymbol{V}}^{-1}\boldsymbol{y}$ and $\hat{\boldsymbol{u}}=\boldsymbol{\Sigma} {\boldsymbol{Z}}^{\mathrm{T}}\left(\boldsymbol{y}-\boldsymbol{X}\hat{\boldsymbol{\beta}}\right)$. Under both solutions, for $\hat{\boldsymbol{\beta}}$ and $\hat{\boldsymbol{u}}$ it is assumed that the covariance matrices are known, but in practice these are replaced by estimations and the results are known as empirical BLUE (EBLUE) and empirical BLUP (EBLUP).

The linear combinations of the parameters are called estimable functions if they can be constructed from a linear combination of unconditional means (of fixed effects only) of the observations (Littell et al. 1996). Estimable functions do not depend on random effects. Below, we provide a formal definition of an estimable function.

Definition of an estimable function

K^Tβ is estimable if there is a matrix T such that

$$ {\boldsymbol{T}}^{\mathrm{T}}\boldsymbol{E}\left(\boldsymbol{Y}\right)={\boldsymbol{T}}^{\mathrm{T}}\boldsymbol{X}\boldsymbol{\beta } ={\boldsymbol{K}}^{\mathrm{T}}\boldsymbol{\beta} \forall \boldsymbol{\beta} . $$

One way of testing candidate matrices for estimability is to use the following result:

$$ {\boldsymbol{K}}^{\mathrm{T}}\boldsymbol{\beta}\ \mathrm{is}\ \mathrm{estimable}\ \mathrm{if},\mathrm{and}\ \mathrm{only}\ \mathrm{if},{\boldsymbol{K}}^{\mathrm{T}}{\left({\boldsymbol{X}}^{\mathrm{T}}\boldsymbol{X}\right)}^{-}\left({\boldsymbol{X}}^{\mathrm{T}}\boldsymbol{X}\right)={\boldsymbol{K}}^{\mathrm{T}}, $$

where (X^TX)⁻ denotes a generalized inverse of X^TX. Quantities such as regression coefficients, treatment means, treatment differences, contrasts, and simple effects in factorial experiments are all common examples of estimable functions and their resulting estimates are examples of BLUEs (Littell et al. 2006). BLUEs correspond to broad inference because they are valid for the whole population under study, and are also called population average inference using the terminology by Zeger et al. (1998). Table 2.1 presents predictors of some regression models and some common experimental designs and also provides some functions of the predictor that are and are not estimable functions.

Table 2.1 Predictors and some estimable and non-estimable functions of each predictor of some common useful linear models

Table 2.1 indicates that estimable functions used to obtain BLUEs are only linear combinations of fixed effects, and the inference focuses on the average performance throughout the target population. Although there are many possible linear combinations of fixed effects that can be of interest to estimate with BLUEs, the most important ones are treatment means expressed as η₀ + τ_i, the difference between treatments τ_i − τ_i′ and simple effects. In general, the most common BLUEs can be obtained from any fitted generalized mixed model using the expression $\mathrm{BLUE}={g}^{-1}\Big(\boldsymbol{X}\hat{\boldsymbol{\beta}}$), where g⁻¹(·) is the inverse link used to fit the generalized mixed model and the inference is related to population-wide average (broad).

Estimability matters because many models are not full rank, such as analysis of variance (ANOVA) models, where estimating equation solutions for the effects themselves has no intrinsic meaning and solutions depend entirely on the generalized inverse used. Theory says that there is an infinite number of ways to construct a generalized inverse. While estimable functions are invariant of generalized inverse and therefore have an assignable meaning, that is, although the effect estimates per se do not have any legitimate interpretation, estimable functions do (Stroup 2012). Next, an example of how to obtain the BLUEs of genotypes (treatments) under a randomized complete block design is provided.

Example 1

Grain yield of five genotypes evaluated in a randomized complete block design. The data of this experiment are shown in Table 2.2. This example is provided to illustrate the process of estimating the BLUEs of genotypes.

Table 2.2 Grain yield (Yield) of five genotypes under a randomized complete block design

Next, we provide the R code that uses the lme4 library to fit a mixed model for the data given in Table 2.2 to estimate the BLUEs of genotypes:

Data_RCBD=read.table("Example_RCBD.csv", header =T, sep = ",") Data_RCBD library(lme4) Data_RCBD$Genotype=as.factor(Data_RCBD$Genotype) Data_RCBD$Block=as.factor(Data_RCBD$Block) Fitted=lmer(Yield~ Genotype + (1 | Block), Data_RCBD) Fitted ####Extracting design matrix of fixed effects (Intercept and Genotype) X=Fitted@pp$X X=X[!duplicated(X), ] X ####Extracting the beta coefficients Beta=Fitted@beta #fixef(Fitted) ####Obtaining the BLUEs of genotypes BLUEs_Gen=X%*%Beta BLUEs_Gen

The above code shows that Genotype was specified as a fixed effect, although Block was specified as a random effect. It is important to point out that both effects were converted to factors. The output of this fitted model is given below.

> Fitted Linear mixed model fit by REML ['lmerMod'] Formula: Yield ~ Genotype + (1 | Block) Data: Data_RCBD REML criterion at convergence: 43.1701 Random effects: Groups Name Std.Dev. Block (Intercept) 0.6922 Residual 0.6739 Number of obs: 20, groups: Block, 4 Fixed Effects: (Intercept) Genotype2 Genotype3 Genotype4 Genotype5 5.688 2.688 0.625 -1.125 0.125 > ####Extracting design matrix > X=Fitted@pp$X > X=X[!duplicated(X), ] > X (Intercept) Genotype2 Genotype3 Genotype4 Genotype5 1 1 0 0 0 0 5 1 1 0 0 0 9 1 0 1 0 0 13 1 0 0 1 0 17 1 0 0 0 1 > ####Extracting the fixed effects > Beta=Fitted@beta > ####Obtaining the BLUEs of genotypes > BLUEs_Gen=X%*%Beta > BLUEs_Gen [,1] 1 5.6875 5 8.3750 9 6.3125 13 4.5625 17 5.8125

The above code shows that the standard deviation of the random effect of blocks was equal to 0.6922, while the standard deviation of the residual was equal to 0.6739. In the part that reads “Fixed Effects” we find the beta coefficient estimates of the fixed effects with which the BLUEs of each of the genotypes can be obtained. With the Fitted@pp$X, the design matrix of fixed effects is extracted as implemented in lmer, and with X[!duplicated(X),] the rows which are duplicated due to blocks being removed. Then, with Fitted@beta, the beta coefficients for the fixed effects are extracted and, finally, with X%*%Beta, the BLUEs of each genotype are obtained. Since the estimable function (Table 2.1) for genotypes (treatments) are η₀ + τ_i, the BLUEs of each genotype are computed as 5.688 + 0 = 5.688 (BLUE of genotype 1), 5.688 + 2.688 = 8.376 (BLUE of genotype 2), 5.688 + 0.625 = 6.313 (BLUE of genotype 3), 5.688 − 1.125 = 4.563 (BLUE of genotype 4), and 5.688 + 0.125 = 5.813 (BLUE of genotype 5). Since for more complex models, obtaining the BLUEs for genotypes can be quite laborious, these can be obtained directly using the following lines of code:

library(lsmeans) Lsmeans_Gen=lsmeans(Fitted,~ Genotype) #Lsmeans_Gen BLUEs_Gen=data.frame(GID=Lsmeans_Gen$Genotype, BLUEs=Lsmeans_Gen$lsmean, SE_BLUEs=Lsmeans_Gen$SE) BLUEs_Gen

In this way we get

> BLUEs_Gen GID BLUEs SE_BLUEs 1 1 5.6875 0.4830459 2 2 8.3750 0.4830459 3 3 6.3125 0.4830459 4 4 4.5625 0.4830459 5 5 5.8125 0.4830459

Predictable functions

These are linear combinations of the fixed and random effects, K^Tβ + M^Tu, that is, they can be formed from linear combinations of the conditional means: K^Tβ + M^Tu is a predictable function if K^Tβ is estimable. The inference based on these predictable functions is referred to as narrow inference, which, unlike broad inference, has random effects such as additional terms and limits the attention to a group of the sampled random levels (Littell et al. 2006). Then, replacing the estimates obtained from the mixed model equation (2.2) in predictable functions, ${\boldsymbol{K}}^{\mathrm{T}}\hat{\boldsymbol{\beta}}$ + ${\boldsymbol{M}}^{\mathrm{T}}\hat{\boldsymbol{u}}$ results in the best linear unbiased predictors (BLUPs) of the corresponding predictable function. From a theoretical point of view, BLUP is expected to have a better genotypic predictive accuracy than BLUE, which is important for the selection of new cultivars, or even the genetic values (additive effects) for the selection of progenitors (Piepho et al. 2008). Before BLUP-based selection, selection in crop breeding was based on either simple arithmetic means or BLUEs of genotypes, which can also be calculated in a mixed model context based on fixed genotype effects (Piepho et al. 2008).

BLUP has a long tradition of selection in animal science, but its use in plant breeding is very recent. It is therefore important to provide a clear distinction between the two terms.

Table 2.3 presents the corresponding predictable functions for the same models described in Table 2.1.

Table 2.3 Some predictable functions for the same models given in Table 2.1

It is important to point out that BLUEs and BLUPs are not restricted only to linear mixed models (Eq. 2.1), because they can be obtained in an approximate manner for any fitted generalized linear mixed model using the expression $\mathrm{BLUP}={g}^{-1}\Big(\boldsymbol{X}\hat{\boldsymbol{\beta}}$+$\boldsymbol{Z}\hat{\boldsymbol{u}}$) (Stroup 2012). For example, Table 2.4 provides the BLUEs and BLUPs for some of the most popular response variables under a predictor with fixed and random effects.

Table 2.4 BLUEs for mean response and BLUPs for conditional mean response for different types of response variables

In sum, the linear combinations of fixed effects only are called estimable functions and give rise to BLUEs. The solution of mixed model equations produces estimates, or BLUEs, for linear combinations of the form K^Tβ. Linear combinations of fixed and random effects are called predictable functions. Solving the mixed model equations yields predictors, or BLUPs, which are used to obtain BLUPs of linear combinations such as K^Tβ + M^Tu. The best of both BLUEs and BLUPs means that these estimates have minimum mean square errors (see Searle et al. 2006) for the different meanings of the criteria applied to each one.

Both the BLUEs and BLUPs are not possible to be computed in real applications, since true variance–covariance values of R and Σ are required, but we only have access to estimates of these variance–covariance matrices. For this reason, only empirical BLUEs and empirical BLUPs are possible, since we use variance–covariance parameter estimates ($\hat{\boldsymbol{R}}$ and $\hat{\boldsymbol{\Sigma}}$) to solve the mixed model equations for β and u.

Below, we illustrate the calculation of the BLUPs of genotypes of the data set given in Table 2.2 for which the BLUEs of genotypes were obtained. Using the lmer() function again, but now assuming that the genotype is a random effect, instead of fixed effects we obtained the following output of the fitted model. We can see that the standard deviation of genotypes is 1.3575, the standard deviation of blocks is 0.6922, the standard deviation of residuals is 0.6739, and the intercept is equal to 6.15.

> #####BLUP of genotypes > Fitted2=lmer(Yield~ (1|Genotype) + (1 | Block), Data_RCBD) > Fitted2 Linear mixed model fit by REML ['lmerMod'] Formula: Yield ~ (1 | Genotype) + (1 | Block) Data: Data_RCBD REML criterion at convergence: 58.8152 Random effects: Groups Name Std.Dev. Genotype (Intercept) 1.3575 Block (Intercept) 0.6922 Residual 0.6739 Number of obs: 20, groups: Genotype, 5; Block, 4 Fixed Effects: (Intercept) 6.15

From the fitted model (Fitted2), we now extract the intercept with fixef(Fitted2) and the random effects of genotypes with c(ranef(Fitted2)$Genotype); then we sum up these two terms to get the BLUPs of genotypes that we called BLUP_Gen2, and finally, we calculate the correlation between the BLUPs and BLUEs (obtained above) for the same genotypes. This correlation was equal to one, which shows that we should not expect big differences between the use of BLUPs or BLUEs of genotypes, although there are large amounts of empirical evidence showing that the BLUPs should be preferred over the BLUEs and not always are the same results produced by both.

> #####Fixed effect=Intercept###### > Intercept=fixef(Fitted2) > str(Intercept) Named num 6.15 - attr(*, "names")= chr "(Intercept)" > #####Random effects of genoytpes > U_ref=c(ranef(Fitted2)$Genotype) > U_ref $'(Intercept)' [1] -0.4356567 2.0958619 0.1530686 -1.4953621 -0.3179116 > ########BLUP of Genotypes##### > BLUP_Gen2=Intercept+U_ref$'(Intercept)' > BLUP_Gen2 [1] 5.714343 8.245862 6.303069 4.654638 5.832088 > cor(c(BLUEs_Gen),BLUP_Gen2) [1] 1

2.3 Marker Depuration

First, we will define markers and their importance. Markers are beneficial in the construction of precise genetic relationships, for parental determination and for the identification and mapping of quantitative trait loci (QTL). Between 1970 and 2001, most of the genetic progress in the livestock industry was reached by using pedigree and phenotypic information. However, after the first draft of the human genome project was finished in 2001 (The International SNP Map Working Group 2001), the cost of genotyping using single nucleotide polymorphisms (SNPs) started to decrease considerably, and now its cost is at least 1000 times lower. For this reason, Stonecking (2001) points out that SNPs have become the bread and butter of DNA sequence variation and are essential in determining the genetic potential of livestock and plant breeding.

However, it is also important to point out that other types of DNA markers have been discovered, such as restriction fragment length polymorphisms (RFLP), simple sequence repeat (SSR), Diversity Arrays Technology (DArT), simple sequence length polymorphisms (SSLP), amplified fragment length polymorphisms (AFLP), etc. However, SNPs have become the main markers used to detect DNA variation for some of the following reasons: (a) SNPs are abundant and found throughout the entire genome, in intragenic and extragenic regions (Schork et al. 2000), (b) they represent the most common genetic variants, (c) the location in the DNA: they are found in introns, exons, promoters, enhancers, or intergenic regions, (d) they are easily evaluated by automated means, (e) many of them have direct repercussions on traits of interest in plant and animals, (f) they are generally biallelic, and (g) they are now cheap and easy to genotype.

It is important to remember that DNA (deoxyribonucleic acid) is organized in pairs of chromosomes, each inherited from one of the parents. The diversity found among organisms is a result of variations in DNA sequences and of environmental effects. Genetic variation is substantial and each individual of a species, with the exception of monozygotic twins, possesses a unique DNA sequence. DNA variations are mutations resulting from the substitution of single nucleotides (single nucleotide polymorphisms—SNPs), the insertion or deletion of DNA fragments of various lengths (from a single to several thousand nucleotides), or the duplication or inversion of DNA fragments (Marsjan and Oldenbroek 2007). For this reason, the genome is composed of four different nucleotides (A, C, T, and G). Next, we provide two important definitions that are keys to understanding how markers are used in genomic selection.

Genetic markers

A genetic marker is a gene or DNA sequence with a known location on a chromosome and is generally used to identify individuals, which is why it is a powerful tool to explore genetic diversity. It can be described as a variation that may arise due to a mutation or alteration in the genomic loci that can be observed. A genetic marker may be a short DNA sequence, such as a sequence surrounding a single base-pair change (single nucleotide polymorphism, SNP, see Fig. 2.1), or a long one, such as mini- and microsatellites. Molecular markers can be used in molecular biology and biotechnology to identify a particular DNA sequence in a pool of unknown DNA. For example, DNA is used to search for useful genes, and also for marker-assisted selection, paternity testing, and food traceability. In GS, genetic markers measured across the genome are used to measure genomic similarities between individuals; in theory, this can be more precise than pedigree information.

Fig. 2.1

The upper DNA molecule differs from the lower DNA molecule at a single base-pair location (a C/A polymorphism)

Markers can be used to estimate the proportion of chromosome segments shared by individuals, including the identification of genes that are identical by state (IBS). It is important to point out that probabilities generated from pedigree (A matrix) are discrete between close relatives. For example, full sibs share 0.5 of alleles (genome) that are identical by descent, that is, that are inherited from a common ancestor. A simple nucleotide polymorphism (SNP) is a widely used marker.

As an initial descriptive analysis of this type of data that could help delve into some characteristics of the structure of the genotypes data, we can compute the frequency genotypes in our data, basically the proportion of each genotype, and can help us as description of the gene variation. Rather, a more common description of the genetic variation is the allele frequency, which is the proportion of each allele present in the population, and when the individual is a diploid, its contribution of the proportion is of two alleles for each gene (Griffiths et al. 2005). In a diploid population with two alleles, A and a, if n_A, n_Aa, and n_a are the frequencies of the three genotypes (AA, Aa, aa) in a sample of n individuals, the frequency of alleles A and a are given by $\frac{2{n}_{\mathrm{A}}+{n}_{\mathrm{A}\mathrm{a}}}{2n}=\frac{n_{\mathrm{A}}}{n}+\frac{n_{\mathrm{A}\mathrm{a}}}{2n}$ and $\frac{2{n}_{\mathrm{a}}+{n}_{\mathrm{Aa}}}{2n}=\frac{n_{\mathrm{a}}}{n}+\frac{n_{\mathrm{Aa}}}{2n}$, respectively. In this case, the allele with the lower frequency is called the minor allele and the other, the major allele.

To illustrate marker recoding and depuration, consider the following example of eight plants genotyped for seven SNPs.

With the information in Table 2.5, we first proceed to find the minor (less common) and major (most common) alleles of each marker. In marker 1 (SNP1), we can see that the minor allele is G, since it only appears in G_G in one out of the eight plants; the major allele is C, since C_C appears in two out of eight plants. In SNP2, the minor allele is G since it does not appear in any of the eight plants, whereas C_C appears in three out of eight plants. Due to this, C is the major allele. In SNP3, the minor and major alleles are A (with A_A observed in 1/8) and T (with T_T observed in 2/8), respectively. Using this logic, Table 2.6 shows the minor and major alleles of each of the markers.

Table 2.5 Marker information for eight plants and seven SNPs denoted as SNP1, …, SNP7

Table 2.6 Minor allele (minorAllele) and major allele (majorAllele) for each marker

Once we have this information (minor and major alleles), it can be used to fit additive effects models, but it is first necessary to recode the marker information following the rules below:

$$ x=\left\{\begin{array}{c}0\ \mathrm{if}\ \mathrm{the}\ \mathrm{SNP}\ \mathrm{is}\ \mathrm{homozygous}\ \mathrm{for}\ \mathrm{the}\ \mathrm{major}\ \mathrm{allele}\\ {}1\ \mathrm{if}\ \mathrm{the}\ \mathrm{SNP}\ \mathrm{is}\ \mathrm{heterozygous}\\ {}2\ \mathrm{if}\ \mathrm{the}\ \mathrm{SNP}\ \mathrm{is}\ \mathrm{homozygous}\ \mathrm{for}\ \mathrm{the}\ \mathrm{other}\ \mathrm{allele}\end{array}\right. $$

The recoded information in terms of additive effects is given in Table 2.7, where the recording is now in terms of 0, 1, and 2, following the above rules. In turn, the missing genotypes are recoded as NA.

Table 2.7 Marker information recoded as 0, 1, and 2, for eight plants and seven SNPs denoted as SNP1, …, SNP7

Next, we show the minor allele frequency (MAF), the frequency of NAs and the frequency of heterozygotes genotypes (freHetero) for each marker. The frequency allele can be computed from the frequency of genotypes as described earlier and from there, the minor allele and its frequency can be deduced, but once the marker information is coded as Table 2.7, in an equivalent way, the MAF also can be calculated as the mean of each column in Table 2.7 divided by 2 without taking into account the missing values, that is, as $\mathrm{MAF}=\left({\sum}_{i=1}^{n_c}{x}_i^{\ast}\right)/\left(2{n}_c\right),$ where ${x}_i^{\ast },i=1,\dots, {n}_c$ are the coded genotyped values for non-missing individual values for a marker. For example, the MAF of marker SNP2 is equal to ${\mathrm{MAF}}_{\mathrm{SNP}2}=\frac{0+1+1+1+0+0}{2(6)}=\frac{3}{12}=0.25$. See Table 2.8 for the MAF of the remaining markers, where the frequency of NAs (freqNA) is also reported for each marker, which corresponds to the number of missing values (NAs) in each column divided by the number of individuals (8). Furthermore, the frequency of heterogeneous genotypes (freqHetero) was calculated (ratio of the summation of only the ones divided by the non-missing values).

Table 2.8 Minor allele frequency (MAF), frequency of NAs (freqNA), and frequency of heterogeneous (freqHetero) are reported for each marker

With the data formatted in this way, we are ready to compute a genomic relationship matrix or matrix of realized genetic similarities among all pairs of individuals.

It is important to point out that the recoding process for values of 0, 1, and 2 can be performed automatically using the library synbreed, but we first need to load the complete information onto R of Table 2.5. Then, for recording and imputing, we used methods available from this library; the code used for these tasks is given in Appendix 1. The output is explained below.

First, we called the library synbreed and then we loaded the marker information contained in a file called MarkersToy.csv, which is saved in an object called snp7. When all the marker information is printed, we can clearly see that it corresponds to the information given in Table 2.5, although without the first column.

> library(synbreed) > ####Loading the marker information > snp7 <- read.csv("MarkersToy.csv",header=T) > snp7=snp7[,-1] > snp7 SNP1 SNP2 SNP3 SNP4 SNP5 SNP6 SNP7 1 C_G C_C T_T G_T G_G T_C G_G 2 C_G C_G A_A G_T C_C C_C G_C 3 C_C ?_? T_A G_T G_C T_C ?_? 4 G_G ?_? T_T T_T G_C T_C G_C 5 C_C C_G T_A G_T G_C T_T C_C 6 ?_? C_G T_A G_T C_C ?_? G_G 7 C_G C_C T_A G_G G_C C_C G_C 8 C_G C_C T_A G_G G_C T_C G_G

Next, we rename the rows of the object snp7 (matrix of marker information) coded with values of ID1 to ID8. We then select the position in this matrix of values equal to ?_?, followed by these values being replaced with NA. Finally, the snp7 object is printed again and we can see that the values of ?_? were replaced by NAs.

> ####Set names for individuals > rownames(snp7) <- paste("ID",1:8,sep="") > pos.NA=which(snp7=="?_?", arr.ind=TRUE) > snp7[pos.NA]=NA > snp7 SNP1 SNP2 SNP3 SNP4 SNP5 SNP6 SNP7 ID1 C_G C_C T_T G_T G_G T_C G_G ID2 C_G C_G A_A G_T C_C C_C G_C ID3 C_C NA T_A G_T G_C T_C NA ID4 G_G NA T_T T_T G_C T_C G_C ID5 C_C C_G T_A G_T G_C T_T C_C ID6 NA C_G T_A G_T C_C NA G_G ID7 C_G C_C T_A G_G G_C C_C G_C ID8 C_G C_C T_A G_G G_C T_C G_G

Later, the object with the marker information, snp7, is transformed into an object of class gpData.

> ####Creating an object of class 'gpData' > gp <- create.gpData(geno=snp7)

Using the function codeGeno() and giving the marker object, gp, as an input, we recode the marker information to values of 0, 1, and 2. The recoded marker information is then extracted and printed, and here we can see that the recoding performed with this library is exactly equal to what we obtained manually and presented in Table 2.7.

> ####Recoding to 0, 1, and 2 values the genotypic data > gp.coded <-codeGeno(gp) > Geno_Recoded=gp.coded$geno > Geno_Recoded SNP1 SNP2 SNP3 SNP4 SNP5 SNP6 SNP7 ID1 1 0 0 1 2 1 0 ID2 1 1 2 1 0 0 1 ID3 0 NA 1 1 1 1 NA ID4 2 NA 0 2 1 1 1 ID5 0 1 1 1 1 2 2 ID6 NA 1 1 1 0 NA 0 ID7 1 0 1 0 1 0 1 ID8 1 0 1 0 1 1 0

Finally, we once again use the function codeGeno(), but we also add input=T and inpute.type=“random”, which will recode the object gp to values 0, 1, and 2, as done previously. However, it will also input the missing cells with NAs using the random method of imputation. Finally, the matrix of markers coded with values 0, 1, and 2 is presented, but with the NAs inputted with values of 0, 1, and 2 using the random method. It is important to point out that this library has other imputation options such as “family,” “beagle,” “beagleAfterFamily,” “beagleNoRand,” “beagleAfterFamilyNoRand,” and “fix,” but the technical details of each imputation method go beyond the scope of this book.

> ####Recoding to values of 0, 1, and 2 the genotypic data and inputting > Imputed_Geno<-codeGeno(gp,impute=T,impute.type="random") > Imputed_Geno$geno SNP1 SNP2 SNP3 SNP4 SNP5 SNP6 SNP7 ID1 1 0 0 1 2 1 0 ID2 1 1 2 1 0 0 1 ID3 0 0 1 1 1 1 2 ID4 2 0 0 2 1 1 1 ID5 0 1 1 1 1 2 2 ID6 2 1 1 1 0 0 0 ID7 1 0 1 0 1 0 1 ID8 1 0 1 0 1 1 0

2.4 Methods to Compute the Genomic Relationship Matrix

The three methods described here to calculate the genomic relationship matrix (GRM) are based on VanRaden’s (2008) paper “Efficient methods to compute genomic predictions” where more theoretical support for each of these methods can be found. We assume that we have a matrix of markers of order J × p, where J denotes the number of lines and p the number of markers, and that this matrix does not contain missing values and is coded as 0, 1, and 2, or −1, 0, and 1 to refer homozygotes major allele, heterozygous, and homozygous minor allele, respectively. Note that the last codification is related to the first by the relation ${\boldsymbol{X}}_2=\boldsymbol{X}+{\mathbf{1}}_J{\mathbf{1}}_p^{\mathrm{T}}$, where X₂ is a matrix of markers information coded in terms of −1, 0, and 1, while X is the coded marker information in terms of 0, 1, and 2, and 1_q is the column vector of dimension q with ones in all its entries.

• Method 1. This method calculates the GRM as

  $$ \boldsymbol{G}=\frac{1}{p}\boldsymbol{X}{\boldsymbol{X}}^{\mathrm{T}}, $$

  where X is the matrix of marker genotypes of dimensions J × p. When the marker information is coded as −1, 0, and 1 as described before, the diagonal terms of pG count the number of homozygous loci for each line, and the off-diagonal of pG is a measure of the number of alleles shared by two lines (VanRaden 2008). To illustrate how to calculate the GRM under this method, we will use the matrix of marker genotypes obtained in the previous section with Imputed_Geno$geno, which in the matrix format is equal to

  $$ \boldsymbol{X}=\left[\begin{array}{ccc}1& 0& 0\kern1em 1\kern0.5em 2\kern0.5em 1\kern0.5em 0\\ {}1& 1& \begin{array}{ccc}2& 1& \begin{array}{ccc}0& 0& 1\end{array}\end{array}\\ {}\begin{array}{c}0\\ {}2\\ {}\begin{array}{c}0\\ {}2\\ {}\begin{array}{c}1\\ {}1\end{array}\end{array}\end{array}& \begin{array}{c}0\\ {}0\\ {}\begin{array}{c}1\\ {}1\\ {}\begin{array}{c}0\\ {}0\end{array}\end{array}\end{array}& \begin{array}{c}\begin{array}{ccc}1& 1& \begin{array}{ccc}1& 1& 2\end{array}\end{array}\\ {}\begin{array}{ccc}0& 2& \begin{array}{ccc}1& 1& 1\end{array}\end{array}\\ {}\begin{array}{c}\begin{array}{ccc}1& 1& \begin{array}{ccc}1& 2& 2\end{array}\end{array}\\ {}\begin{array}{ccc}1& 1& \begin{array}{ccc}0& 0& 0\end{array}\end{array}\\ {}\begin{array}{c}\begin{array}{ccc}1& 0& \begin{array}{ccc}1& 0& 1\end{array}\end{array}\\ {}\begin{array}{ccc}1& 0& \begin{array}{ccc}1& 1& 0\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\right] $$

  Then, using the R code, we calculate the GRM under this first method as

  ##Computing the genomic relationship matrix—Method1 > G_M1=tcrossprod(X)/dim(X)[2] > G_M1 ID1 ID2 ID3 ID4 ID5 ID6 ID7 ID8 ID1 0.875 0.250 0.500 0.875 0.625 0.375 0.375 0.500 ID2 0.250 1.000 0.625 0.625 0.750 0.750 0.500 0.375 ID3 0.500 0.625 1.000 0.750 1.125 0.250 0.500 0.375 ID4 0.875 0.625 0.750 1.375 0.875 0.750 0.500 0.500 ID5 0.625 0.750 1.125 0.875 1.500 0.375 0.500 0.500 ID6 0.375 0.750 0.250 0.750 0.375 0.875 0.375 0.375 ID7 0.375 0.500 0.500 0.500 0.500 0.375 0.500 0.375 ID8 0.500 0.375 0.375 0.500 0.500 0.375 0.375 0.500

• Method 2. In this method the GRM is similar to method 1, but first each marker is centered by twice the minor allele frequency:

  $$ \boldsymbol{G}=\frac{\left(\boldsymbol{X}-{\boldsymbol{\mu}}_{\boldsymbol{E}}\right){\left(\boldsymbol{X}-{\boldsymbol{\mu}}_{\boldsymbol{E}}\right)}^{\mathrm{T}}}{2{\sum}_{j=1}^p{p}_j\left(1-{p}_j\right)}, $$

  where p_j is the minor allele frequency (MAF) of SNP j = 1, …, p and μ_E is the expected value of matrix X under the Hardy–Weinberg equilibrium (Griffiths et al. 2005) from estimates of allelic frequencies, that is, μ_E = 1_J[2p₁, …, 2p_p]. Term $2{\sum}_{j=1}^p{p}_j\left(1-{p}_j\right)$is the sum of the variance estimates of each marker and makes GRM analogous to the numerator relationship matrix (VanRaden 2008).

  Now, using the following R code, we calculate the GRM under method 2 as

  ##Computing the genomic relationship matrix—Method2 > phat=colMeans(X)/2#Minor allele frequency > phat SNP1 SNP2 SNP3 SNP4 SNP5 SNP6 SNP7 0.5000 0.1875 0.4375 0.4375 0.4375 0.3750 0.4375 > X2=scale(X,center=TRUE,scale=FALSE) > k=2*sum(phat*(1-phat)) > G_M2=tcrossprod(X2)/k > round(G_M2,3) ID1 ID2 ID3 ID4 ID5 ID6 ID7 ID8 ID1 0.930 -0.766 -0.227 0.352 -0.265 -0.227 -0.072 0.275 ID2 -0.766 0.930 -0.072 -0.419 -0.111 0.545 0.082 -0.188 ID3 -0.227 -0.072 0.776 -0.188 0.737 -0.766 0.005 -0.265 ID4 0.352 -0.419 -0.188 1.007 -0.227 0.120 -0.342 -0.304 ID5 -0.265 -0.111 0.737 -0.227 1.316 -0.805 -0.342 -0.304 ID6 -0.227 0.545 -0.766 0.120 -0.805 1.084 0.005 0.043 ID7 -0.072 0.082 0.005 -0.342 -0.342 0.005 0.467 0.198 ID8 0.275 -0.188 -0.265 -0.304 -0.304 0.043 0.198 0.545

• Method 3. Under this method, the GRM should be calculated as

  $$ \boldsymbol{G}=\frac{\boldsymbol{Z}{\boldsymbol{Z}}^{\mathrm{T}}}{p}, $$

  where Z is the matrix of scaled SNP codes and p is the number of SNPs, that is ${z}_{ij}=\left({x}_{ij}-2{p}_j\right)/\sqrt{2{p}_j\left(1-{p}_j\right).}$

  Finally, for this third method, the GRM can be calculated as

  > ##Computing the genomic relationship matrix—Method3 > X3=scale(X,center=TRUE,scale=TRUE) > G_M3=tcrossprod(X3)/ncol(X3) > round(G_M3,3) ID1 ID2 ID3 ID4 ID5 ID6 ID7 ID8 ID1 0.962 -0.880 -0.093 0.435 -0.221 -0.397 -0.028 0.223 ID2 -0.880 1.084 -0.133 -0.507 -0.014 0.667 0.012 -0.228 ID3 -0.093 -0.133 0.619 -0.112 0.490 -0.658 0.023 -0.136 ID4 0.435 -0.507 -0.112 1.058 -0.241 0.022 -0.350 -0.305 ID5 -0.221 -0.014 0.490 -0.241 1.181 -0.539 -0.391 -0.265 ID6 -0.397 0.667 -0.658 0.022 -0.539 1.053 -0.057 -0.092 ID7 -0.028 0.012 0.023 -0.350 -0.391 -0.057 0.516 0.276 ID8 0.223 -0.228 -0.136 -0.305 -0.265 -0.092 0.276 0.527

2.5 Genomic Breeding Values and Their Estimation

In plant and animal breeding, it is a common practice to rank and select individuals (plants or animals) based on their true breeding values (TBVs), also called additive genetic values. However, since we cannot see genes and breeding values, this task is not straightforward, and it is therefore estimated indirectly using observed phenotypes. The estimated values are called estimated breeding values (EBVs), which means that TBV is a latent variable that is only approximated using the observable variable (phenotype).

When the TBVs are used, the genetic change is expected to be larger than when the EBVs are used, but this difference is small when the EBVs are accurately estimated. EBVs reflect the true genetic potential or true genetic transmitting ability of individuals (plants or animals). Traditionally, they are estimated based on the performance records of their parents, sibs, progenies, and their own after correcting for various environmental factors such as management, season, age, etc. When parents are selected based on their breeding values with high reliability, a faster genetic progress is expected in the resulting population. For this reason, the process of estimating breeding values is of paramount importance in any breeding program.

There are several methods to estimate genomic estimated breeding values (GEBVs), but first we will describe the best linear unbiased predictor (BLUP) method. When using the BLUP method to estimate the GEBVs, we need to use the mixed model equations (2.2) described above to estimate BLUEs and BLUPs. Using this equation (2.2) but depending on the form taken by the matrices Z and Σ, we can end up with the GBLUP method or the SNP-BLUP method to estimate the breeding values. First, we explain the GBLUP method, where we substitute Z and Σ matrices for the incidence matrix of genotypes and genomic relationship matrix (GRM) derived from allele frequencies calculated with one of the methods of VanRaden (2008) given in Sect. 2.4. Under this GBLUP method, the GEBV can be obtained as the solution $\hat{\boldsymbol{u}}$ of the mixed model equation:

$$ \left(\begin{array}{c}\hat{\boldsymbol{\beta}}\\ {}\hat{\boldsymbol{u}}\end{array}\right)={\left(\begin{array}{cc}{\boldsymbol{X}}^{\mathrm{T}}{\boldsymbol{R}}^{-1}\boldsymbol{X}& {\boldsymbol{X}}^{\mathrm{T}}{\boldsymbol{R}}^{-1}\mathbf{1}\\ {}{\mathbf{1}}^{\mathrm{T}}{\boldsymbol{R}}^{-1}\boldsymbol{X}& {\mathbf{1}}^{\mathrm{T}}{\boldsymbol{R}}^{-1}\mathbf{1}+{\sigma}_g^{-2}\ {\boldsymbol{G}}^{-1}\end{array}\right)}^{-1}\left(\begin{array}{c}{\boldsymbol{X}}^{\mathrm{T}}{\boldsymbol{R}}^{-1}\boldsymbol{y}\\ {}{\mathbf{1}}^{\mathrm{T}}{\boldsymbol{R}}^{-1}\boldsymbol{y}\end{array}\right), $$

(2.3)

where Z was replaced by Z = 1 and Σ by ${\sigma}_g^2\boldsymbol{G}$, the genomic relationship matrix that was calculated with some of the methods described in Sect. 2.4 and the genomic variance component (${\sigma}_g^2$) should be estimated. We ended up with the system of equations given in Eq. (2.3), since the model used is Y = Xβ + u + ε, with u $\sim N\left(\mathbf{0},{\sigma}_g^2\boldsymbol{G}\right),$ where ${\sigma}_g^2$ is the genomic variance component, G is a GRM of dimension q × q calculated using any of the three methods given in Sect. 2.4, and the other terms are exactly as in Eq. (2.2). One of the greatest advantages of using the GBLUP method to obtain GEBV is that the dimensionality of the design matrices is, at most, equal to the number of lines under study. On the other hand, under the SNP-BLUP, we substitute the Z and Σ matrices in Eq. (2.2) with M (scaled marker information matrix of order n × p) and ${\sigma}_M^2\boldsymbol{I}$, respectively. Under this SNP-BLUP method, the mixed model equation is equal to

$$ \left(\begin{array}{c}\hat{\boldsymbol{\beta}}\\ {}\hat{\boldsymbol{u}}\end{array}\right)={\left(\begin{array}{cc}{\boldsymbol{X}}^{\mathrm{T}}{\boldsymbol{R}}^{-1}\boldsymbol{X}& {\boldsymbol{X}}^{\mathrm{T}}{\boldsymbol{R}}^{-1}\boldsymbol{M}\\ {}{\boldsymbol{M}}^{\mathrm{T}}{\boldsymbol{R}}^{-1}\boldsymbol{X}& {\boldsymbol{M}}^{\mathrm{T}}{\boldsymbol{R}}^{-1}\boldsymbol{M}+{\sigma}_M^{-2}{\boldsymbol{I}}^{-1}\end{array}\right)}^{-1}\left(\begin{array}{c}{\boldsymbol{X}}^{\mathrm{T}}{\boldsymbol{R}}^{-1}\boldsymbol{y}\\ {}{\boldsymbol{M}}^{\mathrm{T}}{\boldsymbol{R}}^{-1}\boldsymbol{y}\end{array}\right) $$

(2.4)

Under this mixed model equation, u is now the random effects of markers, and therefore, to obtain the GEBV, we use the estimates of marker effects ($\hat{\boldsymbol{u}}$) and GEBV = $\boldsymbol{M}\hat{\boldsymbol{u}}$, since now the model used is Y = Xβ + Mu + ε, with $\boldsymbol{u}\sim N\left(\mathbf{0},{\sigma}_M^2\boldsymbol{I}\right)$.

We then illustrate how to estimate the GEBV under both BLUP methods. For this purpose, we provide, in Table 2.9, a data set with eight lines (evaluated in two environments) for grain yield, for which, in turn, we use the seven markers imputed in Sect. 2.3.

Table 2.9 Grain yield (y) of eight lines in two environments

Below are the data of Table 2.9 that were saved in the data.for.GEBV.csv file. Library rrBLUP was used to estimate the GEBV using the mixed model equations.

> library(rrBLUP) > data=read.csv("data.for.GEBV.csv") > data X Env Lines y SNP1 SNP2 SNP3 SNP4 SNP5 SNP6 SNP7 1 1 E1 L1 5.215 1 0 0 1 2 1 0 2 2 E1 L2 4.998 1 1 2 1 0 0 1 3 3 E1 L3 5.284 0 0 1 1 1 1 2 4 4 E1 L4 5.157 2 0 0 2 1 1 1 5 5 E2 L5 6.601 0 1 1 1 1 2 2 6 6 E2 L6 5.735 2 1 1 1 0 0 0 7 7 E2 L7 5.565 1 0 1 0 1 0 1 8 8 E2 L8 5.829 1 0 1 0 1 1 0

In matrix M, only the columns corresponding to marker information are selected. This information is scaled by column using the scale command of R, and the scaled markers are saved in the MS matrix; the GRM is calculated with this information using method 3 in Sect. 2.4. Here we obtained the design matrix for environments and lines, and we also added the genomic information to the design matrix of lines by post-multiplying the design matrix of lines by the Cholesky decomposition of the GRM, which also can be used as an alternative way to obtain the breeding values. This is because the GBLUP model (2.1) can be expressed equivalently as follows:

$$ \boldsymbol{Y}=\boldsymbol{X}\boldsymbol{\beta } +{\boldsymbol{Z}}^{\ast }{\boldsymbol{u}}^{\ast }+\boldsymbol{\varepsilon}, $$

where now Z^∗ = ZL^T, G = L^TL is the Cholesky decomposition of G, and u^∗ is a random vector with distribution $N\left(\mathbf{0},{\sigma}_g^2{\boldsymbol{I}}_{\boldsymbol{q}}\right)$.

> M=data[,5:11] > MS=scale(M) #Scales matrix of markers > G=MS%*%t(MS)/ncol(MS) #Genomic relationship matrix method 3 > X_E=model.matrix(~0+Env,data=data) #Matrix design of environments > X_L1=model.matrix(~0+Lines,data=data)#Matrix design of lines > L=chol(G) #Cholesky decomposition of G > X_L=X_L1%*%t(L)#Modified matrix design of lines, Z^∗

Then, using the mixed.solve() function of the rrBLUP package, providing as input the response variable (y), the X_L1 matrix of lines and the GRM matrix, G, we solved the mixed model equation (2.3) and obtained the GEBVs, which are extracted using fm1$u.

> #######################Solution GBLUP############################ > y = data$y > fm1=mixed.solve(y=y, Z=X_L1, K=G, X=X_E, method="REML", + bounds=c(1e-09, 1e+09), SE=FALSE, return.Hinv=FALSE) > fm1$u [1] 0.08371533 -0.13384553 0.15177641 0.02540245 0.63649420 -0.22942366 -0.39877555 -0.13534366 ###################Alternative solution GBLUP###################### > fm1a=mixed.solve(y=y, Z=X_L, K=diag(dim(G)[1]), X=X_E, method="REML", bounds=c(1e-09, 1e+09), SE=FALSE, return.Hinv=FALSE) >#GEBV >X_L%*%fm1a$u

Shown below is the code to obtain the GEBV, but using the SNP-BLUP method and also using the mixed.solve() function. However, instead of giving the GRM as input, this is given by Z, which is the MS matrix, containing the matrix of the markers scaled. Now the random effects of markers are extracted with fm2$u, and to obtain the GEBV, these random effects are pre-multiplied by the scaled design matrix of markers:

> #######################Solution SNP-BLUP######################### > fm2=mixed.solve(y=y, Z=MS, X=X_E, method="REML", + bounds=c(1e-09, 1e+09), SE=FALSE, return.Hinv=FALSE) > fm2$u SNP1 SNP2 SNP3 SNP4 SNP5 SNP6 SNP7 -0.121863421 0.115618300 -0.040677892 0.083526359 0.016201822 0.184761140 -0.001827558 > beta_Mar=fm2$u > GEBV=c(MS%*%beta_Mar) > GEBV [1] 0.08373722 -0.13385647 0.15181358 0.02538892 0.63650107 -0.22940375 -0.39883111 -0.13534946

This shows that both methods (GBLUP and SNP-BLUP), give exactly the same breeding value estimates. However, although the two methods are specified in almost the same way and give similar estimates, which, based on all the SNPs (SNP-BLUP), required more computational time, this difference will be more notable for larger data sets that containing larger number of markers. Due to this, in these situations we can choose the GBLUP method.

Some advantages of using the Henderson equation to obtain the GEBV are

• (a) It fits nicely into existing BLUP software and into existing theory.

• (b) It provides measures of accuracy from the inverse of the LHS (Linear Henderson system).

• (c) It accommodates all individuals (plants or animals).

However, it has some inconveniences, such as

• (a) It can’t easily accommodate major genes (unless using weights in the construction of G).

• (b) Computation of G and inversion might be challenging.

It is important to point out that the GEBV can be obtained using other estimation methods such as Bayesian methods. Bayesian methods for GS are explained in detail in upcoming chapters, but here we will illustrate the use of the BGLR package to estimate the GBLUP Bayesian method and the SNP-BLUP Bayesian method.

We first provide the code for the GBLUP Bayesian method. The predictor ETA is a list and has two sub-list components: the first, for the effects of environments for which a FIXED model (model=“FIXED”) is used that uses a prior non-informative for each beta coefficient. The second component is an RKHS model to specify the distribution of the random effects of lines that, in general, are of the form $N\left(\mathbf{0},{\sigma}_g^2\boldsymbol{K}\right)$, and in this case, using the GRM, K = G. Then the Bayesian GBLUP model is fitted using the function BGLR(), and finally, the GEBVs are obtained with fm1$ETA$Gen$u. The response vector value is specified in the first option of the function BGLR, y=y, and with nIter=20000 and burnIn=10000, the number of iterations to run the involved MCMC method are specified, along with the number of these that will be discarded at the beginning of the MCMC, respectively.

> library(BGLR) > ####################GBLUP-BLUP Bayesian######################### > ETA=list(Env=list(X=X_E[,-1], model="FIXED"),Gen=list(K=G, model="RKHS")) > fm1=BGLR(y=y,ETA=ETA,nIter=20000,burnIn=10000,verbose=F) > fm1$ETA$Gen$u [1] 0.02581315 -0.08430838 0.12806091 0.03949064 0.32406895 -0.17367228 [7] -0.16452623 -0.09492676

The SNP-BLUP Bayesian GEBV is then fitted, but now also providing the design matrix of environments as input, and the scaled design matrix of markers in the second term. The model now used is a Bayesian Ridge regression (BRR) that gives a normal distribution with mean zero and a common variance component as a prior for each marker effect.

> ########################SNP-BLUP Bayesian######################## > ETA=list(Env=list(X=X_E[,-1], model="FIXED"), Gen=list(X=MS, model="BRR")) > fm1=BGLR(y=y,ETA=ETA,nIter=20000,burnIn=10000,verbose=F) > beta_Mar_Bayes=fm1$ETA$Gen$b > > GEBV_Bayes=c(MS%*%beta_Mar_Bayes) > GEBV_Bayes [1] 0.03187469 -0.09663427 0.12920479 0.04973765 0.34695500 -0.18172760 [7] -0.18217036 -0.09723989

Here we can observe that both methods gave GEBVs that are very similar yet slightly different due to the Monte Carlo sampling. However, these Bayesian GEBVs are different from those obtained above using Henderson’s mixed model equations, due to the fact that different machineries are used to estimate the GEBVs. Details of the Bayesian methods for GS will be provided in upcoming chapters.

Finally, it is important to point out that the advantage of the GBLUP over the SNP-BLUP is that the system of equations, when fitting the mixed model equations, is of the size of the individuals (lines or animals), which are, most of the time, fewer than the number of markers (SNPs). This advantage is also observed under the Bayesian version, because the design matrix of markers is usually larger than the dimension of the genomic relationship matrix.

2.6 Normalization Methods

This section describes four types of normalization variables (inputs and outputs). In this case, normalization refers to the process of adjusting the different inputs or outputs that were originally measured in different scales to the same scale. It is very important to carry out the normalization process before giving the inputs and outputs for most statistical machine learning algorithms because it helps improve the numerical stability in the estimation process of some algorithms; it is suggested mostly when the inputs or outputs are in different scales. However, it is important to point out that in some statistical machine learning software, the normalization process is done internally, in which case this process does not need to be carried out manually. The five normalization methods we describe next are centering, scaling, standardization, max normalization, and minimax normalization.

Centering

This normalization consists of subtracting from each variable (input or output) its mean, μ; this means that the centered values are calculated as

$$ {X}_i^{\ast }={X}_i-\mu $$

The centered variable ${X}_i^{\ast }$ has a mean of zero.

Scaling

This normalization consists of dividing each variable (input or output) by its standard deviation, σ. The scaled values are calculated as

$$ {X}_i^{\ast }=\frac{X_i}{\sigma }. $$

The scaled variable ${X}_i^{\ast }$ has unit variance.

Standardization

This process of normalization consists of calculating its mean, μ, and standard deviation, σ, for each input or output. The standardized values are then calculated as

$$ {X}_i^{\ast }=\frac{X_i-\mu }{\sigma }. $$

This process is carried out for each input or output variable, and this needs to be done with care, since we need to use the corresponding mean and standard deviation of each variable. The output of the standardized score has a mean of zero and a variance of one, which means that most standardized values range between −3.5 and 3.5.

Max normalization

This normalization consists of dividing the values of the input or output by the maximum (max) value of this variable, meaning that this score is calculated as

$$ {X}_i^{\ast }=\frac{X_i}{\max } $$

This normalization can be useful when there are no negative inputs, which guarantees that the normalized variable will be between 0 and 1.

Minimax normalization

To implement this normalization, we first need to calculate the minimum (min) and maximum (max) value for each input or output; then the minimax score is calculated using the following expression:

$$ {X}_i^{\ast }=\frac{X_i-\min }{\max -\min } $$

The resulting score of the minimax normalization is between 0 and 1. An inconvenience of this normalization method is that inputs or outputs with long-tail distributions will be dominated by inputs or outputs with uniform distributions.

It is important to point out that the normalization process is not limited to the independent variables (inputs), but can also be used for the dependent variables (outputs) when dealing with multiple outcomes in different scales. However, the normalization process of the dependent variables is not necessary for univariate prediction models or when developing a machine to predict mixed outcomes, because the original scale of the distributions can be losses, for example, to predict two types of outcomes (binary and continuous), to predict three types of outcomes (ordinal, continuous, and count), or to predict four types of outcomes (binary, ordinal, continuous, and count data). On the other hand, when developing a machine to predict four continuous outcomes in different scales (for example, grain yield in tons by hectare, plant height in centimeters, days to maturity in 0 to 120 days, and vitamin content in milligrams), in these cases, normalizing each of the response variables is suggested to avoid the training process from being dominated by the dependent variable with large variability, which implies that the trained machine would be able to predict only this response variable with the highest accuracy. However, in some statistical machine learning models, it is not necessary to normalize the dependent variables because they allow the user to put different weights on each dependent variable to be able to train the model more fairly.

2.7 General Suggestions for Removing or Adding Inputs

The following is a general guide to removing inputs:

• (a) Remove an independent variable (input) if it has zero variance, which implies that the input has a single unique value (Kuhn and Johnson 2013).

• (b) Remove an independent variable (input) if it has near-zero variance, which implies that the input has very few values.

• (c) Remove an independent variable (input) if it is highly correlated with another input variable (nearly perfect correlation), since they are measuring the same underlying information (Kuhn and Johnson 2013). Known as collinearity in statistical machine learning science, this phenomenon is important because in its presence the parameter estimates of some machine learning algorithms (for example, those based on gradient descent) are inflated (not accurately estimated).

These three issues are very common in genomic prediction, since part of the independent variables is marker information and many of them have zero or near-zero variance and other pairs have very high correlations. One of the advantages of removing input information prior to the modeling process is that this reduces the computational resources needed to implement the statistical machine learning algorithm. Also, it is possible to end up with a more parsimonious and interpretable model. Another advantage is that models with less correlated inputs are less prone to unstable parameter estimates, numerical errors, and degraded prediction performance (Kuhn and Johnson 2013).

The following are general rules for the addition of input variables:

• (a) Create dummy variables from nominal or categorical inputs.

• (b) Manually create a categorical variable from a continuous variable.

• (c) Transform the original input variable using a specific transformation.

First, we describe the process of creating dummy variables from categorical (nominal or ordinal) inputs. Transforming categorical inputs into dummy variables is required in most supervised statistical machine learning methods, since providing the original independent variable (not transformed into dummy variables) is incorrect and should be avoided by practitioners of statistical machine learning methods. However, it is important to point out that when the dependent variable is categorical, most statistical machine learning methods do not require it to be transformed into dummy variables. For example, assume that we are studying three genotypes (G1, G2, and G3) in two environments (E1 and E2) and we collected the following grain yield data.

Using the information in Table 2.10, we created the dummy variables for each categorical variable. First, we provide the dummy variables for the environments (Table 2.11).

Table 2.10 Grain yield was evaluated in two environments, and three genotypes were evaluated in each environment

Table 2.11 Resulting dummy variables for the environments

Next, we provide the dummy variables for the genotypes (Table 2.12).

Table 2.12 Resulting dummy variables for genotypes

It is important to point out that in R we can use the model.matrix() to create dummy variables from categorical independent variables. First, we create a data frame called grain.yield with the original data set:

grain.yield=data.frame(Environment=c(“E1”,“E1”, “E1”, “E2”, “E2”, “E2”), Genotype=c(“G1”,“G2”,“G3”, “G1”,“G2”,“G3”), y=c(5.3, 5.6,5.8,6.5, 6.8,6.9))

We then print the data

> grain.yield Environment Genotype y 1 E1 G1 5.3 2 E1 G2 5.6 3 E1 G3 5.8 4 E2 G1 6.5 5 E2 G2 6.8 6 E2 G3 6.9

Next, we create the dummy variables for the categorical variable environment using the model.matrix() function, as

ZE=model.matrix(~0+Environment, data=grain.yield)

The resulting matrix with the dummy variables of environments is called design matrix of environments and, in this case, it is

> ZE EnvironmentE1 EnvironmentE2 1 1 0 2 1 0 3 1 0 4 0 1 5 0 1 6 0 1

It is important to point out that, if instead of ~0+Environment, we use ~1+Environment inside the model.matrix() function, we obtain a different form of the design matrix for environments:

> ZE (Intercept) EnvironmentE2 1 1 0 2 1 0 3 1 0 4 1 1 5 1 1 6 1 1

Strictly speaking, both design matrices contain the same information due to the fact that only C − 1 dummy variables are needed to capture all the information of the categorical variable, since once we have the information of C − 1 dummy variables, we can infer the information of the missing dummy variable. However, the decision to include all dummy variables depends on the selected statistical machine learning algorithm. Under the second version of the design matrix created with the model.matrix() function, in ZE, the column (dummy variable) corresponding to the first environment was not included, but instead an intercept (a column of ones in all rows) was added. This design matrix with an intercept is very important in some statistical machine learning algorithms such as most generalized regression models, neural networks, and deep learning models. In some cases, when this intercept is not included, numerical problems occur in the estimation of the learnable parameters (beta coefficients or weights, intercepts, etc.). The reason is that for each row (observation), these variables all add up to one, and this would provide the same information as the intercept (Kuhn and Johnson 2013). However, when statistical machine learning is not sensitive to not including the intercept (as the first design matrix), using the complete set of dummy variables can help improve model interpretation.

In the same way, the design matrix (dummy variables) for genotype is created using the following R code:

ZG=model.matrix(~0+Genotype, data=grain.yield)

which provides the following dummy variables that are accommodated in the ZG matrix:

> ZG GenotypeG1 GenotypeG2 GenotypeG3 1 1 0 0 2 0 1 0 3 0 0 1 4 1 0 0 5 0 1 0 6 0 0 1

This design matrix is composed of three columns because there are three categories for the categorical variable (G1, G2, and G3). Each column represents a genotype and a dummy variable was created for each genotype using an indicator variable of 0 (not present in that row) and 1 (present in that row) for each genotype. Now, using model.matrix(~1+Genotype, data=grain.yield), we obtain the design matrix with an intercept, but without the dummy variable for genotype 1:

> ZG (Intercept) GenotypeG2 GenotypeG3 1 1 0 0 2 1 1 0 3 1 0 1 4 1 0 0 5 1 1 0 6 1 0 1

As mentioned earlier, both design matrices for genotypes are valid since they contain the same information, given that in order to capture all the information of a categorical variable, reporting only C − 1 dummy variables in the design matrix is enough. However, the choice of one or another depends mostly on the statistical machine learning model to be used. It is also important to point out that the model.matrix() function, when containing the intercept, deletes the dummy variable corresponding to the first level of the categorical variable, but from the statistical point of view, any other dummy variable can be deleted without a loss of information if, and only if, C − 1 dummy variables are maintained.

Regarding the second point (b: manually create a categorical variable from a continuous variable), we refer to the process of manually converting a continuous variable to a categorical variable. For example, let us assume that we measured plant height in centimeters and then decided to categorize this response variable into five groups (group 1 if plant height is less than 100 cm, group 2 if plant height is between 100 and 125 cm, group 3 if it is between 125 and 150 cm, group 4 if it is between 150 and 175 cm, and group 5 when plant height is greater than 175 cm). This type of categorization is sometimes required, although we suggest avoiding categorizing continuous outcomes in this way, since a significant amount of information is lost and will affect the prediction performance of the trained model. In addition, it is important to point out that the smaller the number of categories created, the greater the loss of information. Also, some researchers like Austin and Brunner (2004) reported that categorizing continuous inputs increases the rate of false positives (Kuhn and Johnson 2013). However, if researchers can justify that categorization is necessary, they should categorize the continuous input or output using a model framework to be able to do this with more precision.

Regarding the third approach to adding or creating inputs by transforming the original input variable using a specific transformation, we refer to the use of kernels, in which the input variables are transformed in such a way that the transformed input is used in the modeling process and the type of transformation depends on the objective of the study. This type of transformation with kernels will be discussed in detail in upcoming chapters. Also, many times transformations are applied to guarantee normality or any other distributional assumption on the variable of interest.

2.8 Principal Component Analysis as a Compression Method

Principal component analysis (PCA) is a method often used to compress the input data without losing as much information. The PCA works on a rectangular matrix in which the rows represent the observations (n) and the columns, the independent variables (p). The PCA creates linear combinations of the columns of matrix information, X, and generates, at most, p linear combinations, called principal components. These linear combinations, or principal components, can be obtained as follows:

$$ {\displaystyle \begin{array}{c}{\mathrm{PC}}_1={\boldsymbol{w}}_1\boldsymbol{X}={w}_{11}{X}_1+{w}_{12}{X}_2+\cdots +{w}_{1p}{X}_p\\ {}\cdots \\ {}{\mathrm{PC}}_p={\boldsymbol{w}}_p\boldsymbol{X}={w}_{p1}{X}_1+{w}_{p2}{X}_2+\cdots +{w}_{pp}{X}_p\end{array}} $$

These linear combinations are constructed in such a way that the first principal component, PC₁, captures the largest variance, the second principal component, PC₂, captures the second largest variance, and so on. For this reason, it is expected that few principal components (k < p) can explain the largest variability contained in the original rectangular matrix (X), which means that with a compressed matrix, X^∗, we contain most of the variability of the original matrix, but with a significant reduction in the number of columns. In matrix notation, the full principal components are obtained with the following expression:

$$ \mathbf{PC}=\boldsymbol{XW}, $$

where W is a p-by-p matrix of weights whose columns are the eigenvectors of Q = X^TX, that is, we first need to calculate the eigenvalue decomposition of Q, which is equal to Q = WΛW^T, where W represents the matrix of eigenvectors and Λ is a diagonal matrix of order p-by-p containing the eigenvalues. For this reason, if we use k < p principal components, the reduced (compressed) matrix is of order n × k and is calculated as

$$ {\boldsymbol{X}}^{\ast }=\boldsymbol{X}{\boldsymbol{W}}^{\ast }, $$

where W^∗ contains the same rows of W, but only the first k columns instead of the original p columns. The selection of the number of principal components to maintain is critical, and we therefore provide some classical rules for this process:

• (a) Select the required principal components to cover a certain amount of variances, such as 80% or 90%.

• (b) Order the eigenvalues from highest to lowest, then make a plot of each of the ordered eigenvalues against its position and select as the number of principal components that number from which little variance is gained by retaining additional eigenvalues. This plot is called a scree plot.

• (c) Discard those components associated with eigenvalues below a certain level, which is usually set as the average variance. In particular, when working with a correlation matrix built with the input matrix, X, the average value of the components is 1, and this rule leads to selecting eigenvalues greater than the unit.

It is important to point out that the principal components can be obtained from a covariance matrix, $\boldsymbol{Q}=\frac{1}{n-1}{\boldsymbol{X}}^{\mathrm{T}}\boldsymbol{X}$, where each column of X is centered, or from the correlation matrix, $\boldsymbol{Q}=\frac{1}{n-1}{\boldsymbol{X}}^{\mathrm{T}}\boldsymbol{X}$, where each column of the original matrix of information was standardized. The covariance matrix is used to calculate the principal components when all the independent variables were measured using the same scale, but if they were measured in different scales, we recommend calculating the principal components with the correlation matrix, which agrees with the normalization methods that are suggested when the independent variables were measured in different scales.

Assume that we measured 15 observations (lines) and five independent variables, and the collected data is given in Table 2.13.

Then we place these data (Table 2.13) in a data frame we called Data. Since the data are in different scales, each column is standardized using the function scale in R, and the first six observations of the scaled variables are given below. The complete code that provides the output given below is available in Appendix 2.

Table 2.13 Five independent variables in different scales

> Data=read.csv("Simulated_PCA.csv", header = T) > > ####We scale each column of the predictors > Rscaled=scale(Data[,-1]) > head(Rscaled) Yield PlantHeight DaysFlowering DaysMaturity WeightFreshPlant [1,] -0.2814557 -0.06307151 0.57645346 -0.8738660 -0.2214903 [2,] 0.9159136 0.97575340 0.65900049 1.4162657 0.7373101 [3,] 0.8360890 0.88300118 0.34944911 -0.1607110 1.4508360 [4,] -0.7337952 0.33576305 -0.01169416 0.2109332 0.1687191 [5,] 2.2640628 0.78097373 2.15516550 2.0490652 1.5177291 [6,] -1.2216124 -0.28567685 -0.80620937 -0.3816886 -0.4556160

We then calculate the scaled variance (correlation) $\boldsymbol{Q}=\frac{1}{n-1}{\boldsymbol{X}}^{\mathrm{T}}\boldsymbol{X}$ and from this matrix we calculate the eigenvalue decomposition using the function eigen() of R. Next, we extract the eigenvectors and eigenvalues, and using the eigenvalue information, we calculate the variance of each principal component as shown below.

> n=nrow(Rscaled) > Q_scaled=(t(Rscaled)%*%Rscaled)/(n-1) #Q_scaled=var(Rscaled) > ####Eigenvalue decomposition > SVD_Rscaled=eigen(Q_scaled) > > ####Extracting eigenvectors and eigenvalues > EVectors=SVD_Rscaled$vectors > Eigenvalues=SVD_Rscaled$values > Standar.deviations.PC=sqrt(Eigenvalues) > Standar.deviations.PC [1] 2.0090648 0.6469991 0.4964878 0.4356803 0.3297472

Afterward, we manually calculate the principal components using the expression PC = XW, where W is the matrix of eigenvectors extracted in the previous code and denoted as EVectors. The calculation used here was the scaled matrix (Rscaled) instead of the original matrix of independent variables.

> ####Principal components for all the p=5 variables > PCM=Rscaled%*%EVectors > head(PCM) [,1] [,2] [,3] [,4] [,5] [1,] -0.371645755 0.02096745 0.6294630 0.59140700 -0.58621466 [2,] 2.096405335 -0.02185667 -0.2605723 -0.54289807 0.12914892 [3,] 1.489539155 -0.30245825 0.5022823 0.73805410 0.79018009 [4,] -0.001842872 -0.78507631 -0.2113135 -0.06274286 -0.24361792 [5,] 3.931856138 1.09587334 -0.4321212 0.05736360 -0.17988334 [6,] -1.403180027 -0.72567496 -0.2400658 -0.12744453 -0.08832723

We then built the scree plot, which is one of the three tools used to select the number of principal components to maintain.

> ####Scree plot > Ordered_Eigenvalues=sort(Eigenvalues,decreasing =T ) > plot(Ordered_Eigenvalues, type = "l",ylab="Variances", xlab="Principal components")

Figure 2.2 shows that after two principal components, there are no significant gains in variance explained by adding more principal components. Due to this, we can select the first two principal components that explain 89.09% of the total variance of the complete data set.

Fig. 2.2

Scree plot for the five independent variables in different scales

Finally, the next part of the code selects only the first two principal components that will replace the whole matrix of scaled independent variables denoted here as Rscaled. Therefore, the selection process only consists of extracting the first two columns of the matrix that contain all the principal components, as shown in the following code. This reduced matrix is then replaced by the original matrix of independent variables as input in any statistical machine learning algorithm.

> ####Principal components for the first k=2 principal components > X_star=PCM[,1:2] > head(X_star) [,1] [,2] [1,] -0.371645755 0.02096745 [2,] 2.096405335 -0.02185667 [3,] 1.489539155 -0.30245825 [4,] -0.001842872 -0.78507631 [5,] 3.931856138 1.09587334 [6,] -1.403180027 -0.72567496

It is important to point out that the code given above was used to manually calculate the new variables, called principal components. However, there are also many libraries of R that can be used to carry out this process automatically. One of these functions is the prcomp(), which performs a principal component analysis when the only input provided is the original scaled (or not scaled) matrix of original inputs. Next, we show how to use this function to perform a principal component analysis. Then, with the function summary(), the standard deviation of each of the five principal components is extracted, as well as the proportion of variance that explains each principal component and the cumulative proportion of variance explained for the principal component. Here, we can see that the standard deviations obtained using this function are the same as those obtained above when the principal components were extracted manually using the eigen() function.

> ####PCA analysis using the function prcomp > PCA=prcomp(Rscaled) > summary(PCA) Importance of components: PC1 PC2 PC3 PC4 PC5 Standard deviation 2.0091 0.64700 0.4965 0.43568 0.32975 Proportion of Variance 0.8073 0.08372 0.0493 0.03796 0.02175 Cumulative Proportion 0.8073 0.89099 0.9403 0.97825 1.00000

We then show how to extract all the principal components resulting from using the prcomp() function. The principal components extracted are clearly the same, except with negative values, which is not a problem since this does not alter the solution.

> ###Extracting the principal components#### > PC_All=PCA$x > head(PCA$x) PC1 PC2 PC3 PC4 PC5 [1,] -0.371645755 -0.02096745 0.6294630 -0.59140700 -0.58621466 [2,] 2.096405335 0.02185667 -0.2605723 0.54289807 0.12914892 [3,] 1.489539155 0.30245825 0.5022823 -0.73805410 0.79018009 [4,] -0.001842872 0.78507631 -0.2113135 0.06274286 -0.24361792 [5,] 3.931856138 -1.09587334 -0.4321212 -0.05736360 -0.17988334 [6,] -1.403180027 0.72567496 -0.2400658 0.12744453 -0.08832723

Finally, we make the scree plot using the output of the prcomp() function, and the output of this figure is exactly the same as that given in Fig. 2.2.

> #####Variances of each principal component and scree plot#### > Var_PC=PCA$sdev*PCA$sdev > plot(Var_PC, type = "l",ylab="Variances", xlab="Principal components")

Appendices

Appendix 1

rm() library(synbreed) ####Loading the marker information snp7 <- read.csv("MarkersToy.csv",header=T) snp7=snp7[,-1] snp7 ####Set names for individuals rownames(snp7) <- paste("ID",1:8,sep="") pos.NA=which(snp7=="?_?", arr.ind=TRUE) snp7[pos.NA]=NA snp7 ####Creating an object of class 'gpData' gp <- create.gpData(geno=snp7) ####Recoding to 0, 1, and 2 values the genotypic data gp.coded <-codeGeno(gp) Geno_Recoded=gp.coded$geno Geno_Recoded ####Recoding to values of 0, 1, and 2 the genotypic data and inputting Imputed_Geno<-codeGeno(gp,impute=T,impute.type="random") Imputed_Geno$geno

Appendix 2

rm(list=ls()) Data=read.csv("Simulated_PCA.csv", header = T) ####We scale each column of the predictors Rscaled=scale(Data[,-1]) head(Rscaled) n=nrow(Rscaled) Q_scaled=(t(Rscaled)%*%Rscaled)/(n-1) #Q_scaled=var(Rscaled) ####Eigenvalue decomposition SVD_Rscaled=eigen(Q_scaled) ####Extracting eigenvectors and eigenvalues EVectors=SVD_Rscaled$vectors Eigenvalues=SVD_Rscaled$values Standar.deviations.PC=sqrt(Eigenvalues) Standar.deviations.PC ####Principal components for all the p=5 variables PCM=Rscaled%*%EVectors head(PCM) ####Scree plot Ordered_Eigenvalues=sort(Eigenvalues,decreasing =T ) plot(Ordered_Eigenvalues, type = "l",ylab="Variances", xlab="Principal components") ####Principal components for the first k=2 principal components X_star=PCM[,1:2] head(X_star) ####PCA analysis using the function prcomp PCA=prcomp(Rscaled) summary(PCA) ###Extracting the principal components#### PC_All=PCA$x head(PCA$x) #####Variances of each principal component and scree plot#### Var_PC=PCA$sdev*PCA$sdev plot(Var_PC, type = "l",ylab="Variances", xlab="Principal components")