Abstract
Point-free topology is the study of the category of locales and localic maps and its dual category of frames and frame homomorphisms. These notes cover the topics presented by the first author in his course on Frames and Locales at the Summer School in Algebra and Topology. We give an overview of the basic ideas and motivation for point-free topology, explaining the similarities and dissimilarities with the classical setting and stressing some of the new features.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
- 2.
That is, the opens \(U=\mathrm{int}\,\overline{U}\), “open sets without lesions”, the open sets one thinks about first.
- 3.
This proof shows indeed more: L/R is a sublocale of L, see 5.4 below.
- 4.
Nuclei in L are in a one-one correspondence with onto frame homomorphisms with domain L hence constitute an alternative representation for sublocales in L [44].
- 5.
The joins \(\mathop {\textstyle \bigsqcup }\) in S are given by \(\mathop {\textstyle \bigsqcup }s_i=\nu _S(\mathop {\textstyle \bigvee }s_i)\) (if \(t\in S\) and \(t\ge s_i\) for all i then \(t\ge \mathop {\textstyle \bigvee }s_i\) and \(t=\nu _S(t)\ge \nu _S(\mathop {\textstyle \bigvee }s_i)\)).
- 6.
The reader might have expected
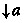 for the definition of \(\mathfrak {o}(a)\). This subset of L is not a sublocale, but the intuition is not wide from the target:
for the definition of \(\mathfrak {o}(a)\). This subset of L is not a sublocale, but the intuition is not wide from the target: 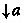 is isomorphic to \(\mathfrak o(a)\) which is the image of the localic map adjoint to the map
is isomorphic to \(\mathfrak o(a)\) which is the image of the localic map adjoint to the map  .
. - 7.
The importance of this condition is comparable with that of sobriety. Note that in a way these two conditions are dual to each other: while sobriety requires that we cannot add a point to X without changing \(\Omega (X)\), \(T_D\) says that we cannot subtract a point.
- 8.
More precisely: a map is localic iff each closed sublocale has a closed preimage whose complement is contained in the preimage of the complement of the original sublocale, and the least subocales are preserved.
- 9.
References
Aull, C.E., Thron, W.J.: Separation axioms between \(T_0\) and \(T_1\). Indag. Math. 24, 26–37 (1963)
Baboolal, D., Picado, J., Pillay, P., Pultr, A.: Hewitt’s irresolvability and induced sublocales in spatial frames. Quaest. Math. 43, 1601–1612 (2020)
Banaschewski, B.: Untersuchen uber Filterräume. Doctoral dissertation, Universität Hamburg (1953)
Banaschewski, B.: The duality of distributive continuous lattices. Can. J. Math. 32, 385–394 (1980)
Banaschewski, B.: Another look at the localic Tychonoff theorem. Comment. Math. Univ. Carolinae 29, 647–656 (1988)
Banaschewski, B.: The Real Numbers in Pointfree Topology. Textos de Matemática, vol. 12, University of Coimbra (1997)
Banaschewski, B., Hong, H.S., Pultr, A.: On the completion of nearness frames. Quaest. Math. 21, 19–37 (1998)
Banaschewski, B., Mulvey, C.J.: Stone-Čech compactification of locales I. Houston J. Math. 6, 301–312 (1980)
Banaschewski, B., Mulvey, C.J.: Stone-Čech compactification of locales II. J. Pure Appl. Algebra 33, 107–122 (1984)
Banaschewski, B., Pultr, A.: Paracompactness revisited. Appl. Categ. Struct. 1, 181–190 (1993)
Banaschewski, B., Pultr, A.: Cauchy points of uniform and nearness frames. Quaest. Math. 19, 101–127 (1996)
Banaschewski, B., Pultr, A.: A constructive view of complete regularity. Kyungpook Math. J. 43, 257–262 (2003)
Banaschewski, B., Pultr, A.: On weak lattice and frame homomorphisms. Algebra Univers. 51, 137–151 (2004)
Bénabou, J.: Treillis locaux et paratopologies. Séminaire Ehresmann, 1re année, exposé 2, Paris (1958)
Clementino, M.M.: Separação e Compacidade em Categorias. Doctoral dissertation, University of Coimbra (1992)
Ehresmann, C.: Gattungen von lokalen strukturen. Jber. Deutsch. Math. Verein 60, 59–77 (1957)
Erné, M.: Distributors and Wallman locales. Houston J. Math. 34, 69–98 (2008)
Erné, M., Picado, J., Pultr, A.: Adjoint maps between implicative semilattices and continuity of localic maps. Algebra Universalis (to appear)
Ferreira, M.J., Picado, J., Pinto, S.: Remainders in pointfree topology. Topology Appl. 245, 21–45 (2018)
Glivenko, V.: Sur quelque points de la logique de M. Brouwer. Bull. Acad. R. Belg. Cl. Sci. 15, 183–188 (1929)
Gutiérrez García, J., Mozo Carollo, I., Picado, J.: Presenting the frame of the unit circle. J. Pure Appl. Algebra 220, 976–1001 (2016)
Gutiérrez García, J., Picado, J., Pultr, A.: Notes on point-free real functions and sublocales. In: Clementino, M.M., Janelidze, G., Picado, J., Sousa, L., Tholen, W. (eds.) Categorical Methods in Algebra and Topology, vol. 46, pp. 167–200. Textos de Matemática, DMUC (2014)
Hausdorff, F.: Grundzüge der mengenlehre. Veit & Co., Leipzig (1914)
Hofmann, K.H., Lawson, J.D.: The spectral theory of distributive continuous lattices. Trans. Am. Math. Soc. 246, 285–310 (1978)
Isbell, J.R.: Atomless parts of spaces. Math. Scand. 31, 5–32 (1972)
Isbell, J.R., Kříž, I., Pultr, A., Rosický, J.: Remarks on localic groups. In: Borceux, F. (ed.) Categorical Algebra and Its Applications (Proceedings of the International Conference on Louvain-La-Neuve 1987). Lecture Notes in Mathematics, vol. 1348, pp. 154–172. Springer, Berlin (1988)
Johnstone, P.T.: Tychonoff’s theorem without the axiom of choice. Fund. Math. 113, 21–35 (1981)
Johnstone, P.T.: Stone Spaces. Cambridge Studies in Advanced Mathematics, vol. 3. Cambridge University Press, Cambridge (1982)
Johnstone, P.T.: The point of pointless topology. Bull. Am. Math. Soc. (N.S.) 8, 41–53 (1983)
Johnstone, P.T.: Wallman compactification of locales. Houston J. Math. 10, 201–206 (1984)
Johnstone, P.T.: A simple proof that localic groups are closed. Cahiers Topologie Géom. Différentielle Catég. 29, 157–161 (1988)
Johnstone, P.T.: A constructive “closed subgroup theorem’’ for localic groups and groupoids. Cahiers Topologie Géom. Différentielle Catég. 30, 3–23 (1989)
Johnstone, P.T.: Elements of the history of locale theory. In: Lowen, R., Aull, C.E. (eds.) Handbook of the History of General Topology, vol. 3, pp. 835–851. Kluwer Academic Publishers, Dordrecht (2001)
Joyal, A.: Nouveaux fondaments de l’analyse. Lectures Montréal 1973 and 1974 (unpublished)
Joyal, A., Tierney, M.: An Extension of the Galois Theory of Grothendieck, vol. 309. AMS: Memoirs of the American Mathematical Society, Providence (1984)
Klinke, O.: A presentation of the assembly of a frame by generators and relations exhibits its bitopological structure. Algebra Univers. 71, 55–64 (2014)
Kříž, I.: A constructive proof of the Tychonoff’s theorem for locales. Comment. Math. Univ. Carolinae 26, 619–630 (1985)
Macnab, D.S.: Modal operators on Heyting algebras. Algebra Univers. 12, 5–29 (1981)
Madden, J.J., Vermeer, J.: Lindelöf locales and realcompactness. In: Mathematical Proceedings of the Cambridge Philosophical Society, vol. 99, pp. 473–480 (1986)
Manes, E.G.: Algebraic Theories. Graduate Texts in Mathematics, vol. 26. Springer, Heidelberg (1976)
Niefield, S.B., Rosenthal, K.I.: Spatial sublocales and essential primes. Topology Appl. 26, 263–269 (1987)
Papert, D., Papert, S.: Sur les treillis des ouverts et paratopologies. Séminaire Ehresmann (1re année, exposé 1), Paris (1958)
Picado, J., Pultr, A.: Locales Treated Mostly in a Covariant Way. Textos de Matemática, vol. 41. University of Coimbra (2008)
Picado, J., Pultr, A.: Frames and Locales: Topology Without Points. Frontiers in Mathematics, vol. 28. Springer, Basel (2012)
Picado, J., Pultr, A.: Notes on the product of locales. Math. Slovaca 65, 247–264 (2015)
Picado, J., Pultr, A.: Axiom \(T_D\) and the Simmons sublocale theorem. Comment. Math. Univ. Carolinae 60, 541–551 (2019)
Picado, J., Pultr, A.: Separation in Point-Free Topology. Birkhäuser/Springer, Cham (2021)
Pultr, A.: Pointless uniformities I. Complete regularity. Comment. Math. Univ. Carolinae 25, 91–104 (1984)
Pultr, A., Tozzi, A.: Separation axioms and frame representation of some topological facts. Appl. Categ. Struct. 2, 107–118 (1994)
Pultr, A., Úlehla, J.: Notes on characterization of paracompact frames. Comment. Math. Univ. Carolinae 30, 377–384 (1989)
Simmons, H.: Spaces with Boolean assemblies. Colloq. Math. 43, 23–29 (1980)
Simpson, A.: Measure, randomness and sublocales. Ann. Pure Appl. Log. 163, 1642–1659 (2012)
Stone, M.H.: The theory of representations for Boolean algebras. Trans. Am. Mat. Soc. 40, 37–111 (1936)
Thron, W.J.: Lattice-equivalence of topological spaces. Duke Math. J. 29, 671–679 (1962)
Wallman, H.: Lattices and topological spaces. Ann. Math. 39, 112–126 (1938)
Acknowledgements
The authors gratefully acknowledge financial support from the Centre for Mathematics of the University of Coimbra (UIDB/00324/2020, funded by the Portuguese Government through FCT/MCTES) and from the Department of Applied Mathematics (KAM) of Charles University (Prague). The first author also acknowledges the UCL project Attractivité internationale et collaborations de recherche dans le cadre du Coimbra group 2017–2020 and an ERASMUS+ Staff Mobility Grant from the University of Coimbra that supported his visit to the Université catholique de Louvain.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2021 The Author(s), under exclusive license to Springer Nature Switzerland AG
About this chapter
Cite this chapter
Picado, J., Pultr, A. (2021). Notes on Point-Free Topology. In: Clementino, M.M., Facchini, A., Gran, M. (eds) New Perspectives in Algebra, Topology and Categories. Coimbra Mathematical Texts, vol 1. Springer, Cham. https://doi.org/10.1007/978-3-030-84319-9_6
Download citation
DOI: https://doi.org/10.1007/978-3-030-84319-9_6
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-84318-2
Online ISBN: 978-3-030-84319-9
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)


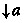 for the definition of
for the definition of 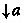 is isomorphic to
is isomorphic to  .
.