The Environmental Justice Dimension of the Mexican Emissions Trading System

Abstract

Emissions trading systems have the potential of increasing air quality given that GHG emissions are often co-produced with local pollutants such as NO_x, SO_x, and Particulate Matter (PM). Can emissions trading systems exacerbate or alleviate environmental justice concerns in emerging economies? According to the U.S. Environmental Protection Agency, Environmental Justice is achieved when no group is disproportionately affected by an environmental policy or phenomenon. The main objective of this chapter is to estimate the pollution burden faced by marginalized neighbourhoods in Mexico. This is relevant for Mexico given the beginning of the pilot program of the Mexican Emissions Trading System (ETS) and the country’s history of income inequality and poverty. Using linear regression and two-way fixed effects methods, we found that the highest emitters regulated under the ETS are located near poor populations. We estimated a 5$\%$ CO₂ emissions-reduction scenario corresponding to national targets and associated NO₂ emissions to that scenario. We find that this scenario is consistent with a decrease in the exposure of NO₂ pollution for the most marginalized neighbourhoods. This chapter also discusses other potential sources of environmental injustice that could result after the beginning of the ETS and the potential to address them.

Keywords

Introduction

In many countries, Emissions Trading Systems (ETS) as well as other market-based approaches have been considered as instruments to achieve Greenhouse Gas (GHG) emissions reductions. However, there have been concerns regarding emissions trading systems increasing existing gaps in pollution exposure across space. Much of the opposition towards emission trading systems and carbon taxes stem from environmental justice concerns. Environmental justice concerns arise if there are differences in environmental quality across income levels. More specifically, some of these environmental justice concerns are centred around vulnerable people experiencing higher levels of exposure to local pollutants. Local pollutants like particulate matter, SOx, and NOx are short-lived and their damages to nearby populations depend on where they are released, while GHG emissions cause long-lasting global damages.

Studies have analysed the distributional impacts of emissions trading systems from an empirical perspective (Fowlie et al. 2012). Whether they will be effective in reducing disparities in air pollution exposure depends on the answers to three questions. First, what is the current spatial relationship between CO₂ emissions and air pollution exposure? Second, are polluting facilities located near vulnerable populations? Third, what is the spatial relationship between regulated facilities and air pollution exposure after the policy is implemented? The objective of this chapter is to analyse the current spatial relationship between regulated emissions and air pollution exposure as well as the characteristics of the populations near regulated facilities. Understanding these questions will provide background for future work that analyses whether Mexico’s GHG emissions trading system can improve environmental justice among Mexican communities.

Mexico started the first year of the pilot of its GHG emissions trading system in January 2020. The program regulates heavily polluting industries that emit more than 100,000 metric tons of CO₂ of total annual direct emissions coming from stationary sources. This program is one of the pillars of an ambitious climate policy in Mexico and, according to authorities, already covers around 40$\%$ of national GHG emissions in the first year of its pilot phase (SEMARNAT 2019b). If the target is achieved, besides reductions in CO₂ emissions, Mexico  could expect co-benefits in air quality as is the case with other GHG emissions trading systems around the world (Hernandez-Cortes and Meng 2020; Walch 2018). However, despite Mexico having high rates of poverty and inequality, the current policy does not explicitly include a special emphasis on involving vulnerable populations as possible stakeholders in the climate policy. Other cap and trade systems in the world have had a special interest in helping vulnerable communities either through revenue recycling or investments in climate-friendly projects in these communities.¹

This chapter will discuss possible air pollution co-benefits from Mexico’s emissions trading system and analyse whether vulnerable communities could benefit from decreases in GHG emissions. Given that emissions coming from local pollutants are often co-generated with GHG emissions, by reducing GHG emissions, there could be potential gains in local pollution reductions. A large body of academic literature has documented the impacts of pollution on health, showing that pollution can be especially detrimental for vulnerable populations such as the elderly, children, and low-income groups (Deryugina et al. 2019; Arceo et al. 2016; Gutierrez 2015). Therefore, this chapter will analyse whether regulated facilities under Mexico’s ETS are located near vulnerable populations and their pollution exposure. We find that the highest CO₂ and NO₂ emitters are located close to disadvantaged communities, mainly in urban areas. These emitters are electricity generators and oil and cement producers. We find that the Mexican ETS is likely to account for nearly 90$\%$ of CO₂ emissions and 40$\%$ of NO₂ emissions coming from all stationary sources in our dataset. We simulate CO₂ emissions for the first year of the pilot program following the expectations of the Mexican government and find that disadvantaged communities might experience a large decline of NO₂ emissions compared to baseline levels. Moreover, this decrease is higher for vulnerable communities than other communities.

The rest of the chapter is structured as follows. Section 12.1 defines environmental justice and the role of emissions trading systems in exacerbating or reducing existing gaps in environmental justice. Section 12.2 describes the context of regulated facilities under Mexico’s ETS and their characteristics. Section 12.3 describes the data sources used in this chapter. Section 12.4 discusses the empirical framework as well as the results. Finally, Sect. 12.5 concludes and puts forward discussion questions for future research in the context of Mexico’s ETS.

Environmental Justice and Emissions Trading Systems

The US Environmental Protection Agency defines environmental justice as the “fair treatment and meaningful involvement of all people regardless of race, colour, national origin, or income with respect to the development, implementation, and enforcement of environmental laws, regulations, and policies”. Regarding fair treatment, this definition refers to a situation where “no group of people should bear a disproportionate share of the negative environmental consequences resulting from industrial, governmental, and commercial operations facilities” (EPA 2018). Social justice concerns about environmental policy have a longstanding history. Some of these concerns are focused on how the burden of environmental phenomena like air or water pollution falls on poor and minority communities.

Environmental justice concerns can be further divided into exposure and policy incidence. Environmental justice in exposure can be understood as vulnerable communities being systematically located near more polluting areas due to external reasons such as land prices (Banzhaf et al. 2019). Environmental justice in policy incidence can be understood as vulnerable communities being disproportionately affected by environmental policies such as relocation of facilities (Liu 2013).

Environmental justice concerns have received attention from policymakers while trying to elaborate climate policy. In the case of emissions trading systems, studies have found that poor and minority communities are located near disadvantaged communities (Cushing et al. 2018). Other studies have suggested that emissions trading systems might decrease the amount of pollution exposure that low-income and minority communities face (Grainger and Ruangmas 2018; Hernandez-Cortes and Meng 2020). In the case of the United States, current discussions about climate policy mention justice to all communities but with a special focus on low-income communities, indigenous peoples, and communities of colour.²

Existing studies suggest that low-income communities are located near heavily polluted areas (Currie et al. 2011). In the case of Mexico, Chakraborti and Margolis (2017) found that poorer communities in Mexico are located near the firms that release higher toxic pollution. The authors find that plants near vulnerable communities (measured by the Urban Marginalization Index) emit 87$\%$ more cyanide and 72$\%$ more arsenic and chromium than the average community. Other subnational studies have found a similar result: more polluting firms are located near poorer communities (Lara-Valencia et al. 2009; Grinesky and Collins 2008). These studies have found that vulnerable communities are located close to the highest polluting facilities in Mexico. This means that there might be inequality in environmental exposure to air and water quality in Mexico. Other studies that have approached environmental justice concerns in Mexico are Mahady et al. (2020) and Lome-Hurtado et al. (2019). However, there are no estimates on the incidence of environmental policy on environmental justice. To our knowledge, this is the first effort to analyse the potential environmental justice benefits of a GHG policy in the context of Mexico.

This chapter aims to provide descriptive evidence of the characteristics of the populations living near the facilities regulated by the Mexican ETS. Although the Mexican ETS is regulating greenhouse gases that have no direct impact on local air quality, there could be co-benefits associated with the reduction of CO₂ emissions. By setting a cap on the amount of CO₂ emissions, facilities might emit lower emissions coming from stationary sources such as SO₂ and NO_2. At the same time, these pollutants reduce the amount of harmful secondary pollutants such as PM_2.5, which have been found to have severe consequences to long-term health in affected populations (Deryugina et al. 2019).

Mexico ETS Context and Inequality

The Mexican ETS started its pilot phase in January 2020. This phase will last three years with a transition period in the third year to the fully operating system in 2022. The rules currently regulate facilities in the energy and industrial³ sectors that have emitted at least 100,000 metric tons of CO₂ in any year during the 2016–2019 period. Throughout the pilot phase, emissions allowances will begin to be allocated via grandfathering to the facilities, according to historical emissions, the NDC target, and sectoral targets stated in the General Law of Climate Change (SEMARNAT 2019a), with the possibility of auctioning allowances after the first pilot year. The inclusion of other greenhouse gases, sectors, and allowance allocation processes will be evaluated before the start of the operating phase. The cap was announced in late November of 2019: 271.3 and 273.1 million allowances will be available in 2020 and 2021, respectively. A backup reserve of 20$\%$ additional allowances is also in place and rules for offsets will be developed during the initial phase.

Mexico faces inequality not only across income and wealth but also gender, ethnicity, access to public services, and, more generally, opportunity (Altamirano and Flamand 2018). There is also stark geographic inequality: some regions within the country are developing fast, while others have been lagging for years (Esquivel 1999; Dávila et al. 2002). The birthplace of a person may play an important role in determining the opportunities they can access, thereby limiting or enhancing the capabilities they can develop (Altamirano and Flamand 2018, p. 28). For example, according to the Social Mobility Report in Mexico 2019 (CEEY 2019), 86$\%$ of Mexicans born in poverty⁴ in the south of Mexico remain in poverty during their adult life while the same is the case for 54$\%$ of people born in poverty in the northern region.⁵ Another dimension of inequality, which may compound and intertwine with the others, is the environmental burden. While some pollutants that affect air quality may be more severe in more prosperous urban places, due to other institutional factors, high-polluting facilities may locate in relatively less developed regions, burdening the less advantaged communities inhabiting therein.

Several studies have analysed the possible sources of environmental injustice due to local climate policy. In the case of cap and trade programs, Kaswan (2008) explains some of the environmental justice concerns due to GHG cap and trade systems. The advantage of cap and trade programs is the low cost of regulation compared to other regulations like command and control. As Kaswan (2008) explains it, facilities can align their emissions to the number of allowances either by reducing emissions to the allowance levels, reducing emissions to less than the given allowances and selling the rest, or buying allowances to compensate their excess emissions. Thus, by buying and selling allowances, the spatial distribution of emissions is expected to change. Given that GHGs are produced together with other co-pollutants such as NO_x, SO_x, particulate matter, and toxic substances, a cap on GHG might decrease pollutant emissions. These pollutants and toxins are known to have several health consequences to the populations living nearby the polluting facilities. Therefore, by imposing a cap on GHG, there could be improved health outcomes for those living near regulated facilities. This relationship depends on whether GHG and local pollutant emissions are complements or substitutes in the production activity. Holland (2012) finds evidence supporting the idea that GHG and local pollutants are complements in the production process.⁶

Whether a GHG cap and trade will decrease the production of co-pollutants depends on facilities’ technology and abatement options. Fowlie et al. (2012) explain that cap and trade programs could exacerbate pollution in historically disadvantaged communities. The authors mention that large polluting facilities can purchase allowances and produce higher pollution, which could increase pollution exposure near these areas. However, under a cap and trade program, we would expect a higher reduction of pollution coming from low-abatement cost facilities than other facilities (Fowlie et al. 2012; Burtraw et al. 2005). If these low-abatement cost facilities are located near disadvantaged communities, there could be environmental justice co-benefits from a GHG emissions trading system.

Other GHG emissions trading programs have tried to address existing environmental inequalities and future differences in emissions by implementing policies that monitor pollution from regulated facilities in vulnerable communities. For instance, California’s emissions trading program under AB 32 has an explicit target to help disadvantaged communities by funding public investments that could improve air quality among these communities using the auction proceeds from the cap and trade system. Moreover, California’s AB 32 has implemented environmental justice committees in disadvantaged communities where community leaders can propose new programs to improve air quality in their communities. Other jurisdictions, such as the EU-ETS, address fairness issues at the Member State level, reflecting income disparities between countries: Distributing 10$\%$ of allowances for growth and solidarity reasons, financially supporting the modernization of the energy sector, and offering partial free allocation to the power sector in exchange for low-carbon investments (Meadows et al. 2020). Revenues from auctioning allocations are mostly used on further reducing GHG emissions in other sectors, R&D, and supporting lower- and middle-income households in order to address social aspects (Borghesi et al. 2016).

In the case of Mexico’s ETS, environmental justice concerns have not yet been fully operationalized as a policy target. However, in supporting documents to the design of the Mexican ETS, the Ministry of Environment (SEMARNAT) has considered the potential of directing revenue collected through the auctioning of emissions allowances to decarbonization projects or to mitigate unwanted distributional effects (SEMARNAT and GIZ 2018). Additionally, the Ministry of Environment will be able to conduct auctions from the second pilot year on, to gain experience in this regard and further discuss the use of these revenues (SEMARNAT 2019b).

Data Sources

This chapter analyses whether vulnerable communities are located close to the higher polluting facilities in Mexico and simulate likely CO₂ reductions under the ETS. In order to do so, we use data on vulnerability measures as well as emissions data from all polluting facilities in Mexico.

Vulnerability data: We used two main data sources to classify the vulnerability level in communities across Mexico. For the urban areas, we used the 2010 Index of Urban Marginalization calculated by CONAPO at the urban AGEB level. AGEBs are the smallest spatial unit in Mexico used by INEGI.⁷ Similar to census tract information, AGEBs are small spatial units comprised of less than 50 street blocks. CONAPO calculates the urban marginalization index for all urban AGEBs by using AGEB-level census data on a set of poverty and income indicators.⁸ CONAPO then divides the AGEBs into five different categories regarding their marginalization index at the national level: “very low”, “low”, “medium”, “high”, and “very high”. We should expect higher income communities to be in the “low” and “very low” marginalization groups and poorer communities to be in the “high” and “very high” categories. To account for rural areas, we also included the 2010 locality index of marginalization at the rural locality level. Rural localities are smaller in extension and population than their urban counterparts; therefore, they are more comparable in extension to urban AGEBs than urban localities. Analogous to the urban marginalization index, the locality marginalization divides localities as “very low”, “low”, “medium”, “high”, and “very high” with the same indicators.

Emissions data: Emissions data at the facility level come from the Registro de Emisiones y Transferencia de Contaminantes (RETC) compiled by SEMARNAT. This registry contains all toxic emissions as well as CO₂ and NO₂ at the plant level for regulated entities by NOM-165-SEMARNAT-2013. This dataset contains year-level pollution emissions emitted by regulated stationary sources.⁹ We consider the toxic, local pollution (NO₂) and CO₂ emissions of all these facilities. We focus on NO₂ given that is the only local pollutant consistently reported in RETC throughout the years we analysed. NO₂ has harmful health effects such as lung damage and is an important precursor of PM_2.5 and ground ozone, both of which are associated with other health effects such as asthma and chronic bronchitis among others. Although RETC has a very complete record of pollution emissions, it is not the main GHG emissions registry used for Mexico’s emissions trading systems. The system used for regulating and monitoring these emissions is the Registro Nacional de Emisiones (RENE). However, this system is confidential and the data are not available. This chapter considers the emissions in RETC a good proxy of GHG and pollution emissions coming from stationary sources. RETC only considers stationary sources whereas RENE considers additional mobile sources and indirect emissions coming from electricity use. Differences between RENE and RETC are expected to arise from mobile emissions and electricity use. Therefore, since RETC only has information on point sources, the emissions in RETC are a proxy for overall CO₂ emissions and a lower bound for the emissions in RENE. RETC contains data for the 2004–2018 period. However, we restrict the data to the 2016–2018 period given that these are the relevant years for inclusion into the emissions trading program.

Linking vulnerability level to emissions data: We linked the emissions data to each area’s vulnerability level by using the coordinates of the RETC facilities to link each facility to its corresponding urban AGEB. Given the scattered distribution of rural localities, we calculated a buffer of 1 km² surrounding the locality and associated the RETC facilities within this buffer. In a few cases, there is an overlap between the rural locality buffer and the urban AGEBs. We kept two records for these facilities to account for both communities.

Analysis

GHG Emissions in Mexico and Covered Entities

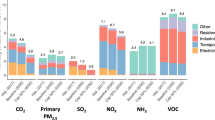
Figure 12.1 shows average emissions by industry using data from RETC. Electricity generation produces the largest CO₂ emissions, followed by cement and oil producers. In the case of NO₂, the largest emissions come from electricity generation. Figure 12.2 Panel (a) shows the location of the 2018 RETC facilities by the marginalization level of the locality/AGEB that contains it. As an example of the spatial distribution of firms, Fig. 12.2 Panel (b) shows their location in Greater Mexico City.

Fig. 12.1

Notes Authors’ estimations using publicly available data from RETC. These figures show the average CO₂ and NO₂ emissions for the 2016–2018 period classified by sector. NO₂ and CO₂ emissions are expressed in tons.

Average CO₂ and NO₂ emissions by industry

Fig. 12.2

Note Maps created by the authors using data from RETC installations and CONAPO’s urban AGEB and rural locality marginalization index. Panel (a) shows the geographic location of 2018 RETC installations in colours according to the marginalization level of the AGEB or locality that contains it. Panel (b) zooms in on the Greater Mexico City region. Transparent datapoints show facilities without matching AGEBs or localities.

Map of facilities under RETC and marginalization levels

While RETC facilities are located across the country, some areas have a higher point density, like the central region of the country—Greater Mexico City and the Bajío region—as well as some industrial areas along or near the northern border. No clear pattern of marginalization emerges although it appears that facilities with higher marginalization levels are concentrated in centre-to-south Mexico. In the case of Greater Mexico City, Panel (b) shows that there can be a juxtaposition of different marginalization levels in facilities close by, although a larger trend can be observed in which better-off AGEBs are located within the centre of Mexico City, and some other facilities are concentrated in peripheral areas with higher levels of marginalization.

Mexico’s ETS is planned to cover over 40$\%$ of total GHG emissions in the country and inclusion in the program depends on whether CO₂ emissions crossed the 100,000 tons threshold in any of the years of the 2016–2019 period. To analyse possible gains on GHG reductions due to the ETS, we considered the regulation threshold for the ETS. In Fig. 12.3, Panels a) and b) show the proportion of CO₂ and NO₂ emissions covered by the ETS as a function of the threshold above which facilities are automatically enrolled in the program. To calculate the coverage, we computed the annual average for the period 2016–2018 considering facilities above the CO₂ emissions regulation threshold. This number was then divided by the yearly average total emissions in our dataset—either CO₂ or NO₂—for the same period. Panel c) shows the number of facilities that participate in the emissions trading system, also as a function of the threshold. The coverage for CO₂ is close to 90$\%$ and above 40$\%$ of NO₂. In contrast, facilities vary more with the threshold level, showing that regulating 287 facilities (under the current threshold in our dataset) compared to 305 under a more stringent cap may have monitoring and implementation costs and not as much gains in environmental coverage.

Fig. 12.3

Note Authors’ calculations using data from RETC for the 2016–2018 period. Panels a) and b) show the percentage of CO₂ and NO₂ emissions covered by the ETS as a function of the CO₂ threshold expressed in tons, with respect to the total average emissions in our dataset during the relevant period. Panel c) shows the number of regulated facilities with the CO₂ threshold expressed in tons.

Emissions threshold, coverage, and regulated facilities

Characterization of GHG Emissions and Environmental Justice

Figure 12.4 shows average pollution emissions by marginalization level for the three largest CO₂ emitting sectors for both rural and urban areas. This figure shows that on average, electricity generators with the highest emission levels are located in urban areas with “very high” marginalization levels. However, rural areas with “high” marginalization levels also face high levels of emissions coming from electricity generation. In the case of cement production, both urban and rural communities with “high” marginalization levels have facilities that release the highest levels of CO₂ emissions.

Fig. 12.4

Note Authors’ estimations using data from RETC (CO₂ and NO₂ emissions) and the CONAPO’s urban AGEB and rural locality marginalization index. The figure shows the average CO₂ emissions during the 2016–2018 period by marginalization level for rural and urban areas. CO₂ emissions are expressed in tons.

Emissions by marginalization level for the most polluting sectors

Table 12.1 shows the descriptive statistics of facilities regulated by the ETS. As expected, regulated facilities show higher CO₂ emissions as well as other pollutants emissions. Furthermore, regulated facilities are in neighbourhoods with higher levels of marginalization than non-regulated facilities.

Table 12.1 Facilities’ descriptive statistics

In order to further explore these differences, we use a two-way fixed effect regression where we account for year and municipality fixed effects in order to control for emissions driven by year-to-year fluctuations and municipality characteristics. Equation (12.1) shows our empirical specification.

$${Y}_{it}=\mathrm{\alpha }+\sum\limits_{i=1}^{5}{\upbeta }_{i}1\{Marginalization Leve{l}_{i}\}+{X}_{i}+{\upgamma }_{t}+{\upmu }_{m}+{\upepsilon }_{it}$$

(12.1)

where ${Y}_{it}$ is CO₂ emissions at locality/AGEB $i$ in year $t$ during the period 2016–2018. $1\{MarginalizationLeve{l}_{i}\}$ are indicator variables that equal one for each marginalization level. ${\gamma }_{t}$ are year fixed effects, ${\mu }_{m}$ are municipality fixed effects, and ${X}_{i}$ is an indicator of whether the AGEB is rural or urban. ${\upepsilon }_{it}$ is the standard error clustered at the rural locality/AGEB level. Each specific ${\upbeta }_{i}$ shows the marginal difference in emissions compared to a base category, which in our case will be the “very low” marginalization level. Estimating this regression allows us to control for municipality-specific time-invariant effects during the 2016–2018 period. Examples of these variables are municipality-specific environmental programs, infrastructure, or municipality government characteristics, among others. Adding year-specific effects allows us to control for emission changes affecting all localities that are specific to one year. For example, a drop in emissions due to slower economic conditions during a specific year.

Panel (a) of Fig. 12.5 shows the coefficients estimated from Eq. (12.1) along with their confidence intervals for CO₂, NO₂, lead, and cadmium emissions. These results imply that AGEBs/rural localities with “high” marginalization levels are on average exposed to 7,600 additional tons of CO₂ from the facilities located nearby compared to communities with “very low” marginalization levels. To the extent that these CO₂ emissions are produced with co-pollutants, communities with “high” marginalization levels could be exposed to higher local pollution emissions than communities with “low” marginalization levels. This implies that an emissions trading program that targets facilities with high CO₂ emissions could potentially benefit communities with “high” marginalization levels, conditional on existing co-benefits between CO₂ emissions reductions and other local pollutants. As an illustrative comparison, we estimated Eq. (12.1) using other pollutants (NO₂) and toxic emissions (Cadmium and Lead) in subpanels (b)–(d) of Fig. 12.5. Compared to the results for CO₂, we cannot conclude that the emissions are significantly different across different income groups. However, this does not conclusively prove that there is no detectable difference in emissions by marginalization group, as we may simply lack the precision to estimate it. Future work could look at other pollution data such as air quality monitoring data near these facilities in order to further characterize this relationship. Panel (b) of Fig. 12.5 shows the corresponding coefficients for Fig. 12.5 where the “very low” marginalization level is the base category.

Fig. 12.5

Notes Authors’ estimations using data from RETC (CO₂, NO₂, Lead, and Cd emissions) and the CONAPO’s AGEB and rural locality marginalization index. Panel a): Subpanels a)–d) show a different estimation of Eq. (12.1) where the dependent variable changes for each specific pollutant. The x-axis denotes the marginalization level of the exposed communities. The y-axis denotes the difference in baseline emissions of the respective pollutant for each marginalization level with respect to the “very low” marginalization level. Panels (a)–(d) are using 21,993 observations which represent a yearly observation per plant-locality pair for the 2016–2018 period. The points are the point estimates of Eq. (12.1) with 95$\%$ confidence intervals using clustered standard errors at the locality level. Panel (b): Regression results associated with panel (a) results. Standard errors clustered at the locality level in parenthesis.

Differences in emissions by marginalization

Simulation of Mexico’s ETS and Environmental Justice

The Mexican emissions trading program has the potential to create co-benefits in air quality improvements while reducing CO₂ through cap and trade. As explained before, this will be determined by the correlation between CO₂ emissions and co-pollutants. In order to explore the potential improvements in air quality as a result of the emissions trading program, we simulate an emissions-reduction scenario, by means of decreasing CO₂ and NO₂ emissions by 5$\%$ in the first year of the program with respect to the 2016–2018 average for regulated facilities. This is consistent with the Mexican emissions reduction target for the industrial sector, as indicated in the General Law of Climate Change.¹⁰ It should be noted that other feasible scenarios include non-uniform reductions within sectors, which also would be consistent with the Mexican emissions reduction target. This is the case for the electricity sector: it typically has a lower abatement cost than other sectors such as cement production and oil refining (Friedmann et al. 2019; INECC 2018).¹¹ We could expect that installations in this sector become net sellers of emissions allowances, thereby reducing emissions and associated co-pollutants locally. Our scenario is, therefore, a lower bound for the spatial and equity consequences of emissions reductions due to the Mexican ETS.

For the 5$\%$ uniform decrease scenario, we predict the average emissions in the first year of the pilot program (2020) using the 2016–2018 data and estimating a two-way fixed effect regression given in Eq. (12.2) in order to obtain the average predicted emissions in the period after 2016–2018.

$${Y}_{it}={\mathrm{\alpha }}_{0}+{m}_{s}+{r}_{t}+{u}_{it}$$

(12.2)

where the dependent variable is either the tons of CO₂ and NO₂ emissions with sector (${m}_{s}$) and year (${r}_{t}$) fixed effects. We obtained the predicted values of CO₂ and NO₂ and simulated a 5$\%$ decrease scenario with respect to the average emissions of CO₂. Using these predicted emission reductions, we followed a similar approach to Eq. (12.1) and obtained the percent difference in emissions compared to the “very low” base category.¹²

Panel a) of Fig. 12.6 shows the findings of our simulation. Panel a) shows the results for CO₂ and panel b shows the results for NO₂. In the case of CO₂, we find that a 5$\%$ decrease in emissions results in the previous differences across marginalization levels disappearing. Whereas baseline emissions indicate that “high” marginalization areas had on average more emissions than “very low” ones, and this reduction scenario levels the situation by making differences indiscernible. In the case of NO₂, we find that there are differences in the predicted emissions across marginalization levels. Compared to the “very low” base category, communities with “medium” marginalization levels are expected to have higher NO₂ emissions with a 5$\%$ decrease in CO₂ emissions. However, in the case of NO₂, communities under the “high” marginalization level do not have higher predicted emissions compared to the “very low” marginalization communities. Therefore, we find a decrease in the exposure of NO₂ pollution for the most vulnerable areas but increases to other communities in the “medium” and “high” marginalization levels. However, for the “high” marginalization communities, the increase is not significant. Panel b) of Fig. 12.6 shows the coefficient results associated with Panel a) where “very low” is the base category.

Fig. 12.6

Notes Authors’ estimations using data from RETC (CO₂ and NO₂ emissions) and the CONAPO’s AGEB and rural locality marginalization index. Panel a): Subpanels a) and b) show the estimates for different dependent variables for the simulation where the dependent variable is the simulated emissions of each specific pollutant during the first year of the program. The x-axis denotes the marginalization level of the exposed communities. The y-axis denotes the percent difference in CO₂ and NO₂ emissions under scenario 1 for each marginalization level with respect to the “very low” marginalization level. Panel b) Regression results associated with panel a) results. Standard errors clustered at the locality level in parenthesis. Panels a) and b) are using 124 observations which represent one observation per regulated facility. The points are the point estimates of Eq. (12.1) with 95$\%$ confidence intervals using robust standard errors.

Simulation of CO₂ and NO₂ emissions under scenario 1

There are potential limitations to our methods. For instance, we do not consider the fate and transport of pollution in the environment, which could potentially change the conclusions of our NO₂ analysis. Furthermore, we assumed that technology remains constant, which means that facilities do not invest in other technologies that change the relationship in emissions releases from CO₂ and NO₂. Finally, given data limitations, we do not include information about other potential pollutants such as SO₂ or potential secondary formation of pollutants that create emissions of PM_2.5. These are two valid concerns that we plan to explore further as the pilot program ends its first compliance cycle and as new emissions data are released.

Conclusion and Discussion

Mexico has started the pilot phase of an ambitious emissions trading program with the objective of reducing domestic GHG emissions. Using data on CO₂ emissions at the plant level, we calculated that the emissions trading program will cover around 90$\%$ of CO₂ emissions from point sources and large industrial facilities in Mexico. By introducing a cap on emissions, the program will likely allow for an overall reduction in domestic CO₂ emissions. One aspect of Mexico’s climate agenda that deserves more attention is whether the cap and trade program will reduce local pollution emissions near regulated facilities. The objective of this chapter was to analyse possible complementarities of local pollutant emission reductions because of the cap and trade system and who would benefit from a decrease in pollution as a result of the program. More importantly, this chapter also examined whether low-income communities would benefit from reductions in local pollution emissions and toxins due to the GHG emissions trading system.

Consistent with other studies, we found that the electricity sector has the highest CO₂ and NO₂ emissions in Mexico. The other two highest emitting sectors are cement production and oil refining. These three sectors are likely to have the highest number of regulated facilities under the GHG cap and trade program. We also analysed the distribution of emissions across communities with different levels of marginalization. We found large disparities between urban and rural areas: high emitting facilities are generally located in urban areas with “very high” marginalization levels, as defined by the Mexican government. However, rural areas with “high” marginalization levels also face high CO₂ emissions. We estimate that communities with “high” marginalization levels are on average exposed to 7,600 more tons of CO₂ emissions than the communities with “very low” marginalization levels during the 2016–2018 period. To the extent that these emissions are produced with co-pollutants, a cap and trade program that reduces CO₂ emissions is likely to benefit these communities in terms of air pollution exposure. We also found that communities with “high” marginalization levels are also exposed to higher NO₂ emissions; however, this is not statistically significant. Finally, with a 5$\%$ reduction of CO₂ emissions consistent with the program’s target, we expect a decrease in NO₂ emissions for the most vulnerable populations. This could be likely translated to gains in co-pollutant reductions due to the ETS.

Environmental justice concerns have been part of climate policy implementation in other places of the world. These concerns have allowed the development of regulations that could potentially be implemented together with cap and trade to address disparities in air pollution exposure. For instance, California’s AB 32 establishes that at least 25$\%$ of the revenues from cap and trade need to support disadvantaged communities and 5$\%$ of the revenues need to be used for developing projects in low-income communities. Moreover, the other revenue from cap and trade is used for grants to local environmental groups to implement projects such as community-owned air quality monitoring stations. Other emissions trading systems use part of their auction proceeds to mitigate electricity ratepayer effects (RGGI) financial support to mid and low-income households (EU-ETS), or directed towards funds that finance climate actions, including awareness raising (Québec) (Borghesi et al. 2016).

These actions might not apply to Mexico in the context of its emissions trading program. Nevertheless, analysing possible co-benefits of climate policy and its environmental justice implications is likely to be an important first step in achieving emission reductions with greater equality in terms of environmental exposure. This is especially relevant in the case of Mexico, given its large inequalities in income and along other important dimensions. The Ministry of Environment might benefit from using auction revenues in an environmentally progressive way. Additionally, it might find it optimal to introduce criteria for offsetting projects to be developed in environmentally disadvantaged communities, to relax their environmental burden.

There are other potential sources of environmental injustice that were not covered by this chapter, which could be exacerbated or reduced due to the Mexican ETS. The pass-through of carbon-related costs to consumers might affect disadvantaged communities heterogeneously, creating or alleviating energy expenditure gaps (Lyubich 2020). Additional sources related to environmental inequality are related to information gaps (Hausman and Stolper 2020), direct discrimination by demographics, firm location decisions, and housing decisions influenced by income inequality, among others.

Further research is needed to address climate justice concerns from this and other environmental policies. In the context of this chapter, research is needed to explore further relationships between CO₂, NO_2, and toxic contaminants, so the feasibility of GHG and co-pollutant reductions can be assessed. Improved data availability from the RENE would better inform the ETS policy and aid in developing pathways to the maximization of its potential co-benefits. However, the environmental justice dimension detailed in this chapter is a starting point to the evaluation of the distributional aspects of the ETS and could be a fruitful agenda for Mexican climate policy.