Abstract
We are entering an age of ‘big’ computational neuroscience, in which neural network models are increasing in size and in numbers of underlying data sets. Consolidating the zoo of models into large-scale models simultaneously consistent with a wide range of data is only possible through the effort of large teams, which can be spread across multiple research institutions. To ensure that computational neuroscientists can build on each other’s work, it is important to make models publicly available as well-documented code. This chapter describes such an open-source model, which relates the connectivity structure of all vision-related cortical areas of the macaque monkey with their resting-state dynamics. We give a brief overview of how to use the executable model specification, which employs NEST as simulation engine, and show its runtime scaling. The solutions found serve as an example for organizing the workflow of future models from the raw experimental data to the visualization of the results, expose the challenges, and give guidance for the construction of an ICT infrastructure for neuroscience.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
- Computational neuroscience
- Spiking neural networks
- Primate cortex
- Simulations
- Strong scaling
- Reproducibility
- Reusability
- Complexity barrier
1 Introduction
With the availability of ever more powerful supercomputers, simulation codes that can efficiently make use of these resources (e.g., [1]), and large, systematized data sets on brain architecture, connectivity, neuron properties, genetics, transcriptomics, and receptor densities [2,3,4,5,6,7,8,9,10], the time is ripe for creating large-scale models of brain circuitry and dynamics.
We recently published a spiking model of all vision-related areas of macaque cortex, relating the network structure to the multi-scale resting-state activity [11, 12]. The model simultaneously accounts for the parallel spiking activity of populations of neurons and for the functional connectivity as measured with resting-state functional magnetic resonance imaging (fMRI). As a spiking network model with the full density of neurons and synapses in each local microcircuit, yet covering a large part of the cerebral cortex, it is unique in bringing together realistic microscopic and macroscopic activity.
Rather than as a finished product, the model is intended as a platform for further investigations and developments, for instance to study the origin of oscillations [13], to add function [14], or to go toward models of human cortex [15].
To support reuse and further developments by others we have made the entire executable workflow available, from anatomical data to analysis and visualization. Here we provide a brief summary of the model, followed by an overview over the workflow components, along with a few typical usage examples.
The model is implemented in NEST [16] and can be executed using a high-performance compute (HPC) cluster or supercomputer. We provide corresponding strong scaling results to give an indication of the necessary resources and optimal parallelization.
2 Overview of the Multi-Area Model
The multi-area model describes all 32 vision-related areas in one hemisphere of macaque cortex in the parcellation of Felleman and Van Essen [17]. Each area is represented by a layered spiking network model of a \(1\,\mathrm {mm^{2}}\) microcircuit [18], adjusted to the area- and layer-specific numbers of neurons and laminar thicknesses. Layers 2/3, 4, 5, and 6 each have an excitatory and an inhibitory population of integrate-and-fire neurons. To minimize downscaling distortions [19], the local circuits contain the full density of neurons and synapses. This brings the total size of the network to \(\sim \)4 million neurons and \(\sim \)24 billion synapses. All neurons receive an independent Poisson drive to represent the non-modeled parts of the brain.
Overview of the connectivity of the multi-area model as determined from anatomical data and predictive connectomics. A Area-level connectivity. The weighted and directed graph of the number of outgoing synapses per neuron (out-degrees) between each pair of areas is clustered using the map equation method [20]. Green, early visual areas; dark blue, ventral stream areas; purple, frontal areas; red, dorsal stream areas; light red, superior temporal polysensory areas; light blue, mixed cluster. Black arrows show within-cluster connections, gray arrows between-cluster connections. B Population-level connection probabilities (the probability of at least one synapse between a pair of neurons from the given populations). C Hierarchically resolved average laminar patterns of the numbers of incoming synapses per neuron (in-degrees). Hierarchical relationships are defined based on fractions of supragranular labeled neurons (SLN) from retrograde tracing experiments [21]: feedforward, \(SLN>0.65\); lateral, \(0.35\le SLN\le 0.65\); feedback, \(SLN<0.35\). The connections emanate from excitatory neurons and are sent to both excitatory and inhibitory neurons. For further details see [11].
The inter-area connectivity is based on axonal tracing data from the CoCoMac database on the existence and laminar patterns of connections [4], along with quantitative tracing data also indicating the numbers of source neurons in each area and their supragranular or infragranular location [22, 23]. These data are complemented with statistical predictions (‘predictive connectomics’) to fill in the missing values, based on cortical architecture (neuron densities, laminar thicknesses) and inter-area distances [24]. Figure 1 shows the resulting connectivity at the level of areas, layers, and populations. A semi-analytical mean-field method adjusts the data-based connectivity slightly in order to bring the firing rates into biologically plausible ranges [25].
By increasing the synaptic strengths of the inter-area connections, slow activity fluctuations, present in experimental recordings but not in the isolated microcircuit, are reproduced. In particular, the system needs to be poised right below an instability between a low-activity and a high-activity state in order to capture the experimental observations. The spectrum of the fluctuations and the distribution of single-neuron spike rates in primary visual cortex (V1) are close to those in lightly anesthetized macaque monkeys. At the same synaptic strengths where the parallel spiking activity of V1 neurons is most realistic, also the inter-area functional connectivity is most similar to macaque fMRI resting-state functional connectivity.
3 The Multi-Area Model Workflow
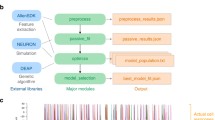
The multi-area model code is available via https://inm-6.github.io/multi-area-model/ and covers the full digitized workflow from the raw experimental data to simulation, analysis, and visualization. The model can thus be cloned to obtain a local version, or forked to build on top of it. The implementation language is Python, the open-source scripting language the field of computational neuroscience has agreed on [26]. The online documentation provides all information needed to instantiate and run the model. The tool Snakemake [27] is used to specify the interdependencies between all the scripts and execute them in the right order to reproduce the figures of the papers on the model’s anatomy [11], dynamics [12], and stabilization based on mean-field theory [25] (see Fig. 2).
Visualization of a Snakemake workflow. The interdependencies between the scripts reproducing the figures in [12], visualized as a directed acyclic graph. The label of a node corresponds to the name of the script.
Furthermore, if one of the files in the workflow is adjusted, Snakemake enables executing only that file and the ones that depend on it anew. A tutorial video (https://www.youtube.com/watch?v=YsH3BcyZBcU) gives a brief overview of the model, explains the structure of the code, and shows how to run a basic simulation.
4 Example Usage
One main property delivered by the multi-area model is the population-, layer-, and area-specific connectivity for all vision-related areas in one hemisphere of macaque cortex. We here describe how to obtain the two available versions of this connectivity: 1) based directly on the anatomical data plus predictive connectomics that fills in the missing values; 2) after slight adjustments in the connectivity in order to arrive at plausible firing rates in the model. We also refer to this procedure as ‘stabilization’ because obtaining plausible activity entails enhancing the size of the basin of attraction of the low-activity state, i.e., increasing its global stability. An example how to use the mean-field method developed in [25] for this purpose is provided in the model repository: figures/SchueckerSchmidt2017/stabilization.py. The method adjusts the number of incoming connections per neuron (in-degree). The script exports the adjusted matrix of all in-degrees as a NumPy [28] file; to have the matrix properly annotated one can instantiate the
 class with the exported matrix specified in the connection parameters as
class with the exported matrix specified in the connection parameters as
 . Afterwards, one can access the connectivity using the instantiation
. Afterwards, one can access the connectivity using the instantiation
 of the
of the
 class:
class:
 for the in-degrees or
for the in-degrees or
 for the total number of synapses between each pair of populations. To obtain the connectivity without stabilization, it is sufficient to instantiate the
for the total number of synapses between each pair of populations. To obtain the connectivity without stabilization, it is sufficient to instantiate the
 class without specifying
class without specifying
 .
.
Performing a simulation of the full multi-area model requires a significant amount of compute resources. To allow for smaller simulations, it is possible to simulate only a subset of the areas. In this case, the non-simulated areas can be replaced by Poisson processes with a specified rate. To this end, the options
 and
and
 in
in
 have to be set to
have to be set to
 and the path to a JSON file containing the rates of the non-simulated areas. Lastly, the simulated areas have to be specified as a list, for instance
and the path to a JSON file containing the rates of the non-simulated areas. Lastly, the simulated areas have to be specified as a list, for instance

before the
 class is instantiated. A simple example how to deploy a simulation is given in run_example_fullscale.py; the effect of replacing areas by Poisson processes is shown in Fig. 3.
class is instantiated. A simple example how to deploy a simulation is given in run_example_fullscale.py; the effect of replacing areas by Poisson processes is shown in Fig. 3.
Simulating subsets of the multi-area model. Bottom panels, spiking activity of excitatory (blue) and inhibitory (red) neurons in all layers of area V1 where in A and B a subset of areas is replaced by Poisson processes. Top panels, sketches visualizing which areas were simulated (white spotlights); the colors therein correspond to different clusters: lower visual (green), ventral stream (dark blue), dorsal stream (red), superior temporal polysensory (light red), mixed cluster (light blue), and frontal (purple). If all areas besides V1 are replaced by Poisson processes (A), the activity displays no temporal structure. Simulating a subset of ten areas (B) slightly increases the activity but does not give rise to a temporal structure, either. Only the simulation of the full model (C) produces a clear temporal structure in the activity. Parameters identical to [12, Fig. 5].
Strong scaling of the multi-area model. The contributions of different phases to the total simulation time and state propagation for 12 to 200 compute nodes for 1 s of biological time. Each data point consists of three random network realizations, with error bar showing the standard deviation of measurements. A The main contributions to the total time are network construction and state propagation. B The state propagation is dominated by three phases: the communication, update, and spike delivery phase. Adding more compute resources while keeping network size the same (strong scaling) decreases the latter two but increases the absolute and relative contribution of the communication phase. The combined contributions are minimized at a real-time factor of 31 (black horizontal line). Parameters identical to [12, Fig. 5].
5 Strong Scaling
The limiting factor dictating the necessary compute resources for simulating the multi-area model is the available memory. Approximately 1 TB is needed for instantiating the network alone. To ensure sufficient memory for the model, the simulation has to be distributed across multiple nodes.
We simulated the model using NEST 2.14 [29] on the JURECA supercomputer in Jülich, which provides 1872 compute nodes equipped with two Intel Xeon E5-2680 v3 Haswell CPUs per node. Each CPU has 12 cores running at 2.5 GHz. The standard compute node provides 128 GB of memory of which 96 GB are guaranteed to be available for the running application. Thus, on this machine, the multi-area model needs at least 11 nodes.
Having established the minimal hardware requirements, we are interested in the runtime of the simulation depending on the compute resources. We quantify the proximity of the time required for state propagation to biological real time by the real-time factor \(T_{\mathrm {sim}}/T_{\mathrm {bio}}\). Carrying out a strong scaling experiment, the problem size stays fixed and we increase the number of compute nodes from 12 to 200, thus reducing the load per node. In our simulations we use 6 MPI processes per node and 4 threads per MPI process, as we found this hybrid parallelization to perform better than other combinations of threading and MPI parallelism (data not shown). In particular during the construction phase, hybrid parallelization outperformed pure threading by a large margin. The threads are pinned to the cores and jemalloc is used as a memory allocator ([30], see [31] for the relevance of the allocator for NEST). In each run, we simulate 10 s of biological time.
In Fig. 4A the total runtime and its main contributions, network construction and state propagation, are shown. The contribution of state propagation is averaged to 1 s of biological time. The main share of the time is taken up by network construction. During this phase the neurons and synapses are created and connected, while during state propagation the dynamics of the model is simulated. The time spent in the former phase is fixed, as it is independent of the specified biological time, whereas the time spent propagating the state depends on the specified biological time and the state of the network. Depending on the initial conditions and the random Poisson input, the network exhibits higher or lower activity, affecting the time spent propagating the state. Hence, the ratio of both phases should not be taken at face value. In some cases, longer simulations are of interest, increasing the relevance of the time spent propagating the state. Thus, it is interesting to know how different components of the state propagation algorithm contribute to this phase.
The three main phases during state propagation are: update of neuronal states, communication between MPI processes, and delivery of spikes to the target neurons within each target MPI process. Figure 4B shows the contributions of these phases to the real-time factor. Adding more compute resources brings down the contributions of the update and delivery phases and increases the time consumption of communication. Especially the delivery of spikes is heavily dependent on the network activity. At 160 nodes, a real-time factor of 31 is achieved (mean spike rate \(14.1\,\)spikes/s). This slowdown compared to real time enables researchers to study the dynamics of the multi-area model over sufficiently long periods, for example in detailed correlation analyses, but systematic investigations of plasticity and learning would still profit from further progress.
In order to test the influence of the communication rate on the time required for state propagation, we carried out a simulation of a two-population balanced random network [32] which has been used in previous publications on neuronal network simulation technology [1, 31, 33,34,35,36]. We use the same parameters as in [1], but replace connections governed by spike-timing dependent plasticity by static connections. In addition we set the numbers of neurons and synapses to match those in the multi-area model (resulting mean spike rate \(12.9\,\)spikes/s). The communication interval is determined by the minimum delay, as the spikes can be buffered over the duration of this delay while maintaining causality [37]. The multi-area model has a minimum delay of 0.1 ms, whereas the balanced random network has a uniform delay of 1.5 ms, so that communication occurs 15 times less often. Using 160 nodes and the same configurations as before, we find a real-time factor of 17. Here, 80% of the time is spent delivering the spikes to the target neurons locally on each process, whereas only 1% of the time is spent on MPI communication. Forcing the two-population model to communicate in 0.1 ms intervals by adding a synapse of corresponding delay and zero weight indeed requires the same absolute time for MPI communication as in the multi-area model. The real-time factor increases to 34, significantly larger than for the multi-area model. The increase is entirely due to a longer spike delivery phase. How the efficiency of spike delivery is determined by the network activity remains to be answered by future investigations. Possibly relevant factors are the wide distribution of spike rates in the multi-area model compared to the narrow one in the two-population model, and the different synchronization patterns of neuronal activity in the two models. In summary, less frequent MPI communication shifts the bottleneck to another software component while almost halving the total runtime. This opens up the possibility of speeding up the simulation even more through optimized algorithms for spike delivery on each target process.
6 Conclusions
The usefulness of large-scale data-driven brain models is often questioned [38,39,40], as their high complexity limits ready insights into mechanisms underlying their dynamics, large numbers of parameters and a lack of testing of models with new data may lead to overfitting and poor generalization, and function does not emerge magically by putting the microscopic building blocks together. However, this argument can also be turned around. It seems that in recent years the complexity of the majority of models and thereby their scope of explained brain functions is not increasing anymore. One reason is that elegant publications on minimal models explaining a single phenomenon are often also end points in that they have no explanatory power beyond their immediate scope. It remains unclear how the proposed mechanisms interact with other mechanisms realized in the same brain structure, and how such models can be used as building blocks for larger models giving a more complete picture of brain function. The powerful approach of minimal models from physics needs to be integrated with the systems perspective of biology. To achieve models able to make accurate predictions for a broad range of questions, the zoo of available models of individual brain regions and hypothesized mechanisms needs to be consolidated into large-scale models tested on numerous benchmarks on multiple scales [41]. Having an accurate, if complex, model of the brain that generates reliable predictions enables in silico experiments, for instance to predict treatment outcomes for neurological conditions, potentially even for individual subjects [42]. Furthermore, combining the bottom-up, data-driven approach with a top-down, functional approach allows models to be equipped with information processing capabilities. Creating such accurate, integrative models will require overcoming the complexity barrier computational neuroscience is facing. Without progress in the software tools supporting collaborative model development and the expressive digital representation of models and the required workflows, reproducibility and reusability cannot be maintained for more complex models.
On the technical side, simulation codes like NEST have matured to generic simulation engines for a wide range of models. Recent developments in the simulation technology of NEST have considerably sped up the state propagation and reduced the memory footprint [1] of large-scale network models. The rapid state propagation causes the network construction phase to take up a large fraction of the simulation time for simulations of short to medium duration. Furthermore, the fact that hybrid parallelization currently performs better than pure threading during the construction phase indicates that the code still spends time on the Python interpreter level and does not yet optimally make use of memory locality. For these reasons, speeding up network construction should be a focus of future work.
Our strong scaling results show that communication starts to dominate at an intermediate number of nodes, so that the further speed-up in the solution of the neuron equations cannot be fully exploited. Therefore, it would be desirable to develop methods for further limiting the time required for communication, for instance by distributing the neurons across the processes according to the modular structure of the neuronal network [43], as opposed to the current round-robin distribution. The longer delays between areas compared to within areas would then allow less frequent MPI communication, by buffering the spikes for the duration of the delay [37, 43]. A major fraction of time is then spent in the spike delivery phase. Here an algorithm needs to transfer the spikes arriving at the compute node to their target neurons. It is our hope that in future a better understanding of the interplay between the intrinsically random access pattern and memory architecture will lead to more effective algorithms.
While the publication of the model code in a public repository enables downloading and executing the code, this requires setting up the simulation on the chosen HPC system, which may be nontrivial, and the HPC resources have to be available to the research group in the first place. Therefore, it would be desirable to link computing resources to the repository, enabling the code to be executed directly from it. The ICT infrastructure for neuroscience (EBRAINS) being created by the European Human Brain Project (HBP) has made first steps in this direction. A preliminary version of a digital workflow for the collaborative development of reproducible and reusable models was evaluated in [44]. Next to finding a concrete solution for the multi-area model at hand, the purpose of the present study was to extend the previous work and obtain a clearer picture of the requirements on collaborative model development and the digital representation of workflows. From the present perspective it seems effective not to reimplement the functionality of advanced code development platforms like GitHub in the HBP infrastructure but to build a bridge enabling execution of the models and storage of the results. An essential feature will be that the model repository remains portable by abstractions from any machine specific instructions and authorization information.
The microcircuit building block for this model [18] has found strong resonance in the computational neuroscience community, having already inspired multiple follow-up studies [45,46,47,48,49,50,51,52]. The multi-area model of monkey cortex developed by Schmidt et al. [11, 12] and described here has a somewhat higher threshold for reuse, due to its greater complexity and specificity. Nevertheless, it has already been ported to a single GPU using connectivity generated on the fly each time a spike is triggered, thereby trading memory storage and retrieval for computation, which is possible in this case because the synapses are static [53]. We hope that the technologies presented here push the complexity barrier of neuroscience modeling a bit further out, such that the model will find a wide uptake and serve as a scaffold for generating an ever more complete and realistic picture of cortical structure, dynamics, and function.
References
Jordan, J., et al.: Extremely scalable spiking neuronal network simulation code: from laptops to exascale computers. Front. Neuroinform. 12, 2 (2018)
van Albada, S.J., et al.: Bringing anatomical information into neuronal network models. arXiv preprint arXiv:2007.00031 (2020)
Zilles, K., et al.: Architectonics of the human cerebral cortex and transmitter receptor fingerprints: reconciling functional neuroanatomy and neurochemistry. Eur. Neuropsychopharmacol. 12(6), 587–599 (2002)
Bakker, R., Thomas, W., Diesmann, M.: CoCoMac 2.0 and the future of tract-tracing databases. Front. Neuroinform. 6, 30 (2012)
Reimann, M.W., King, J.G., Muller, E.B., Ramaswamy, S., Markram, H.: An algorithm to predict the connectome of neural microcircuits. Front. Comput. Neurosci. 9, 120 (2015)
Erö, C., Gewaltig, M.O., Keller, D., Markram, H.: A cell atlas for the mouse brain. Front. Neuroinform. 12, 84 (2018)
Tasic, B., et al.: Shared and distinct transcriptomic cell types across neocortical areas. Nature 563, 72–78 (2018)
Gouwens, N.W., et al.: Classification of electrophysiological and morphological neuron types in the mouse visual cortex. Nat. Neurosci. 22, 1182–1195 (2019)
Sugino, K., et al.: Mapping the transcriptional diversity of genetically and anatomically defined cell populations in the mouse brain. eLife 8, e38619 (2019)
Winnubst, J., et al.: Reconstruction of 1,000 projection neurons reveals new cell types and organization of long-range connectivity in the mouse brain. Cell 179(1), 268–281 (2019)
Schmidt, M., Bakker, R., Hilgetag, C.C., Diesmann, M., van Albada, S.J.: Multi-scale account of the network structure of macaque visual cortex. Brain Struct. Func. 223(3), 1409–1435 (2018)
Schmidt, M., Bakker, R., Shen, K., Bezgin, G., Diesmann, M., van Albada, S.J.: A multi-scale layer-resolved spiking network model of resting-state dynamics in macaque visual cortical areas. PLoS Comput. Biol. 14(10), e1006359 (2018)
Shimoura, R.O., Roque, A.C., Diesmann, M., van Albada, S.J.: Visual alpha generators in a spiking thalamocortical microcircuit model. In: 28th Annual Computational Neuroscience Meeting, P204 (2019)
Korcsak-Gorzo, A., van Meegen, A., Scherr, F., Subramoney, A., Maass, W., van Albada, S.J.: Learning-to-learn in data-based columnar models of visual cortex. In: Bernstein Conference 2019, W9 (2019)
Pronold, J., van Meegen, A., Bakker, R., Morales-Gregorio, A., van Albada, S.J.: Multi-area spiking network models of macaque and human cortices. In: NEST Conference 2019, p. 30 (2019)
Gewaltig, M.O., Diesmann, M.: NEST (NEural Simulation Tool). Scholarpedia 2(4), 1430 (2007)
Felleman, D.J., Van Essen, D.C.: Distributed hierarchical processing in the primate cerebral cortex. Cereb. Cortex 1, 1–47 (1991)
Potjans, T.C., Diesmann, M.: The cell-type specific cortical microcircuit: relating structure and activity in a full-scale spiking network model. Cereb. Cortex 24(3), 785–806 (2014)
van Albada, S.J., Helias, M., Diesmann, M.: Scalability of asynchronous networks is limited by one-to-one mapping between effective connectivity and correlations. PLoS Comput. Biol. 11(9), e1004490 (2015)
Rosvall, M., Axelsson, D., Bergstrom, C.T.: The map equation. Eur. Phys. J. Spec. Top. 178(1), 13–23 (2009)
Markov, N.T., et al.: Anatomy of hierarchy: feedforward and feedback pathways in macaque visual cortex. J. Compar. Neurol. 522(1), 225–259 (2014)
Markov, N.T., et al.: Weight consistency specifies regularities of macaque cortical networks. Cereb. Cortex 21(6), 1254–1272 (2011)
Markov, N.T., et al.: A weighted and directed interareal connectivity matrix for macaque cerebral cortex. Cereb. Cortex 24(1), 17–36 (2014)
Hilgetag, C.C., Beul, S.F., van Albada, S.J., Goulas, A.: An architectonic type principle integrates macroscopic cortico-cortical connections with intrinsic cortical circuits of the primate brain. Netw. Neurosci. 3(4), 905–923 (2019)
Schuecker, J., Schmidt, M., van Albada, S.J., Diesmann, M., Helias, M.: Fundamental activity constraints lead to specific interpretations of the connectome. PLoS Comput. Biol. 13(2), e1005179 (2017)
Muller, E., Bednar, J.A., Diesmann, M., Gewaltig, M.O., Hines, M., Davison, A.P.: Python in neuroscience. Front. Neuroinform. 9, 11 (2015)
Köster, J., Rahmann, S.: Snakemake–a scalable bioinformatics workflow engine. Bioinformatics 28(19), 2520–2522 (2012)
Harris, C.R., et al.: Array programming with NumPy. Nature 585(7825), 357–362 (2020)
Peyser, A., et al.: NEST 2.14.0 (2017)
Evans, J.: Scalable memory allocation using jemalloc (2011). https://www.facebook.com/notes/facebook-engineering/scalable-memory-allocation-using-jemalloc/480222803919
Ippen, T., Eppler, J.M., Plesser, H.E., Diesmann, M.: Constructing neuronal network models in massively parallel environments. Front. Neuroinform. 11, 30 (2017)
Brunel, N.: Dynamics of sparsely connected networks of excitatory and inhibitory spiking neurons. J. Comput. Neurosci. 8(3), 183–208 (2000)
Helias, M., et al.: Supercomputers ready for use as discovery machines for neuroscience. Front. Neuroinform. 6, 26 (2012)
Kunkel, S., et al.: Spiking network simulation code for petascale computers. Front. Neuroinform. 8, 78 (2014)
Kunkel, S., Schenck, W.: The nest dry-run mode: efficient dynamic analysis of neuronal network simulation code. Front. Neuroinform. 11, 40 (2017)
Kunkel, S., Potjans, T.C., Eppler, J.M., Plesser, H.E., Morrison, A., Diesmann, M.: Meeting the memory challenges of brain-scale simulation. Front. Neuroinform. 5, 35 (2012)
Morrison, A., Mehring, C., Geisel, T., Aertsen, A., Diesmann, M.: Advancing the boundaries of high connectivity network simulation with distributed computing. Neural Comput. 17(8), 1776–1801 (2005)
Eliasmith, C., Trujillo, O.: The use and abuse of large-scale brain models. Curr. Opin. Neurobiol. 25, 1–6 (2014)
Frégnac, Y.: Big data and the industrialization of neuroscience: a safe roadmap for understanding the brain? Science 358(6362), 470–477 (2017)
Bassett, D.S., Zurn, P., Gold, J.I.: On the nature and use of models in network neuroscience. Nat. Rev. Neurosci. 19(9), 566–578 (2018)
Einevoll, G.T., et al.: The scientific case for brain simulations. Neuron 102(4), 735–744 (2019)
Proix, T., Bartolomei, F., Guye, M., Jirsa, V.K.: Individual brain structure and modelling predict seizure propagation. Brain 140(3), 641–654 (2017)
Pastorelli, E., et al.: Newblock scaling of a large-scale simulation of synchronous slow-wave and asynchronous awake-like activity of a cortical model with long-range interconnections. Front. Syst. Neurosci. 13, 33 (2019)
Senk, J., et al.: A collaborative simulation-analysis workflow for computational neuroscience using HPC. In: Di Napoli, Edoardo, Hermanns, Marc-André., Iliev, Hristo, Lintermann, Andreas, Peyser, Alexander (eds.) JHPCS 2016. LNCS, vol. 10164, pp. 243–256. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-53862-4_21
Lindén, H., et al.: Modeling the spatial reach of the LFP. Neuron 72(5), 859–872 (2011)
Cain, N., Iyer, R., Koch, C., Mihalas, S.: The computational properties of a simplified cortical column model. PLoS Comput. Biol. 12(9) (2016)
Hagen, E., et al.: Hybrid scheme for modeling local field potentials from point-neuron networks. Cereb. Cortex 26(12), 4461–4496 (2016)
Schwalger, T., Deger, M., Gerstner, W.: Towards a theory of cortical columns: from spiking neurons to interacting neural populations of finite size. PLoS Comput. Biol. 13(4), e1005507 (2017)
Shimoura, R.O., et al.: [Re] the cell-type specific cortical microcircuit: relating structure and activity in a full-scale spiking network model. ReScience 4(1) (2018)
van Albada, S.J., et al.: Performance comparison of the digital neuromorphic hardware SpiNNaker and the neural network simulation software NEST for a full-scale cortical microcircuit model. Front. Neurosci. 12, 291 (2018)
Knight, J.C., Nowotny, T.: GPUs outperform current HPC and neuromorphic solutions in terms of speed and energy when simulating a highly-connected cortical model. Front. Neurosci. 12, 941 (2018)
Rhodes, O., et al.: Real-time cortical simulation on neuromorphic hardware. Phil. Trans. R. Soc. A 378, 20190160 (2019)
Knight, J.C., Nowotny, T.: Larger GPU-accelerated brain simulations with procedural connectivity. Nat. Comput. Sci. 1(2), 136–142 (2021)
Acknowledgments
Supported by the European Union’s Horizon 2020 research and innovation program under HBP SGA1 (Grant Agreement No. 720270), the European Union’s Horizon 2020 Framework Programme for Research and Innovation under Specific Grant Agreements No. 785907 and 945539 (Human Brain Project SGA2, SGA3), Priority Program 2041 (SPP 2041) “Computational Connectomics” of the German Research Foundation (DFG), and the Helmholtz Association Initiative and Networking Fund under project number SO-092 (Advanced Computing Architectures, ACA). Simulations on the JURECA supercomputer at the Jülich Supercomputing Centre were enabled by computation time grant JINB33.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2021 The Author(s)
About this paper
Cite this paper
van Albada, S.J., Pronold, J., van Meegen, A., Diesmann, M. (2021). Usage and Scaling of an Open-Source Spiking Multi-Area Model of Monkey Cortex. In: Amunts, K., Grandinetti, L., Lippert, T., Petkov, N. (eds) Brain-Inspired Computing. BrainComp 2019. Lecture Notes in Computer Science(), vol 12339. Springer, Cham. https://doi.org/10.1007/978-3-030-82427-3_4
Download citation
DOI: https://doi.org/10.1007/978-3-030-82427-3_4
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-82426-6
Online ISBN: 978-3-030-82427-3
eBook Packages: Computer ScienceComputer Science (R0)