Abstract
Partially-Observable Markov Decision Processes (POMDPs) are a well-known stochastic model for sequential decision making under limited information. We consider the EXPTIME-hard problem of synthesising policies that almost-surely reach some goal state without ever visiting a bad state. In particular, we are interested in computing the winning region, that is, the set of system configurations from which a policy exists that satisfies the reachability specification. A direct application of such a winning region is the safe exploration of POMDPs by, for instance, restricting the behavior of a reinforcement learning agent to the region. We present two algorithms: A novel SAT-based iterative approach and a decision-diagram based alternative. The empirical evaluation demonstrates the feasibility and efficacy of the approaches.
This work is partially supported by NSF grants 1545126 (VeHICaL), 1646208 and 1837132, by the DARPA contracts FA8750-18-C-0101 (AA) and FA8750-20-C-0156 (SDCPS), by Berkeley Deep Drive, and by Toyota under the iCyPhy center.
This research has been partially funded by NWO grant OCENW.KLEIN.187: “Provably Correct Policies for Uncertain Partially Observable Markov Decision Processes”.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others

1 Introduction
Partially observable Markov decision processes (POMDPs) constitute the standard model for agents acting under partial information in uncertain environments [34, 52]. A common problem is to find a policy for the agent that maximizes a reward objective [36]. This problem is undecidable, yet, well-established approximate [27], point-based [43], or Monte-Carlo-based [49] methods exist. In safety-critical domains, however, one seeks a safe policy that exhibits strict behavioral guarantees, for instance in the form of temporal logic constraints [44]. The aforementioned methods are not suitable to deliver provably safe policies. In contrast, we employ almost-sure reach-avoid specifications, where the probability to reach a set of avoid states is zero, and the probability to reach a set of goal states is one. Our Challenge 1 is to compute a policy that adheres to such specifications. Furthermore, we aim to ensure the safe exploration of a POMDP, with safe reinforcement learning [23] as direct application. Challenge 2 is then to compute a large set of safe policies for the agent to choose from at any state of the POMDP. Such sets of policies are called permissive policies [21, 31].
POMDP Almost-Sure Reachability Verification. Let us remark that in POMDPs, we cannot directly observe in which state we are, but we are in general able to track a belief, i.e., a distribution over states that describes where in the POMDP we may be. The belief allows us to formulate the following verification task:

The underlying EXPTIME-complete problem requires—in general—policies with access to memory of exponential size in the number of states [4, 18]. For safe exploration and, e.g., to support nested temporal properties, the ability to solve this problem for each belief in the POMDP is essential.
We base our approaches on the concept of a winning region, also referred to as controllable or attractor regions. Such regions are sets of winning beliefs from which a policy exists that guarantees to satisfy an almost-sure specification. The verification task relates three concrete problems which we tackle in this paper: (1) Decide whether a belief is winning, (2) compute the maximal winning region, and (3) compute a large yet not necessarily maximal winning region. We now outline our two approaches. First, we directly exploit model checking for MDPs [5] using belief abstractions. The second, much faster approach iteratively exploits satisfiability solving (SAT) [8]. Finally, we define a scheme to enable safe reinforcement learning [23] for POMDPs, referred to as shielding [2, 30].
MDP Model Checking. A prominent approach gives the semantics of a POMDP via an (infinite) belief MDP whose states are the beliefs in the POMDP [36]. For almost-sure specifications, it is sufficient to consider belief-supports rather than beliefs. In particular, two beliefs with the same support are either both in a winning region or not [47]. We abstract a belief MDP into a finite belief-support MDP, whose states are the support of beliefs. The (maximal) winning region are (all) states of the belief-support MDP from which one can almost surely reach a belief support that contains a goal state without visiting belief support states that contain an avoid state.
To find a winning region in the POMDP, we thus just have to solve almost-sure reachability in this finite MDP. The number of belief supports, however, is exponentially large in the number of POMDP states, threatening the efficient application of explicit state verification approaches. Symbolic state space representations are a natural option to mitigate this problem [7]. We construct a symbolic description of the belief support MDP and apply state-of-the-art symbolic model checking. Our experiments show that this approach (referred to as MDP Model Checking) does in general not alleviate the exponential blow-up.
Incremental SAT Solving. While the belief support model exploits the structure of the belief support MDP by using a symbolic state space representation, it does not exploit elementary properties of the structure of winning regions. To overcome the scalability challenge, we aim to exploit information from the original POMDP, rather than working purely on the belief-support MDP. In a nutshell, our approach computes the winning regions in a backward fashion by optimistically searching policies without memory on the POMDP level. Concretely, starting from the belief support states that shall be reached almost-surely, further states are added to the winning region if we quickly can find a policy that reaches these states without visiting those that are to avoid. We search for these policies by incrementaly employing an encoding based on SAT solving. This symbolic encoding avoids an expensive construction of the belief support MDP. The computed winning region directly translates to sufficient constraints on the set of safe policies, i.e., each policy satisfying these constraints satisfies, by construction, the specification. The key idea is to successively add short-cuts corresponding to already known safe policies. These changes to the structure of the POMDP are performed implicitly on the SAT encoding. The resulting scalable method is sound, but not complete by itself. However, it can be rendered complete by trading off a certain portion of the scalability; intuitively one would eventually search for policies with larger amounts of memory.
Shielding. An agent that stays within a winning region is guaranteed to adhere to the specification. In particular, we shield (or mask) any action of the agent that may lead out of the winning region [1, 39, 42]. We stress that the shape of the winning region is independent of the transition probabilities or rewards in the POMDP. This independence means that the only prior knowledge we need to assume is the topology, that is, the graph of the POMDP. A pre-computation of the winning region thus yields a shield and allows us to restrict an agent to safely explore environments, which is the essential requirement for safe reinforcement learning [22, 23] of POMDPs. The shield can be used with any RL agent [2].
Comparison with the State-of-the-Art. Similar to our approach, [15] solves almost-sure specifications using SAT. Intuitively, the aim is to find a so-called simple policy that is Markovian (aka memoryless). Such a policy may not exist, yet, the method can be applied to a POMDP that has an extended state space to account for finite memory [33, 37]. There are three shortcomings that our incremental SAT approach overcomes. First, one needs to pre-define the memory a policy has at its disposal, as well as a fixed lookahead on the exploration of the POMDP. Our encoding does not require to fix these hyperparameter a priori. Second, the approach is only feasible if small memory bounds suffice. Our approach scales to models that require policies with larger memory bounds. Third, the approach finds a single simple policy starting from a pre-defined initial state. Instead, we find a large winning region. For safe exploration, this means that we may exclude many policies and never explore important parts of the system, harming the final performance of the agent. Shielding MDPs is not new [2, 9, 10, 30]. However, those methods do neither take partial observability into account, nor can they guarantee reaching desirable states. Nam and Alur [39] cover partial observability and reachability, but do not account for stochastic uncertainty.
Experiments. To showcase the feasibility of our method, we adopted a number of typical POMDP environments. We demonstrate that our method scales better than the state of the art. We evaluate the shield by letting an agent explore the POMDP environment according to the permissive policy, thereby enforcing the satisfaction of the almost-sure specification. We visualize the resulting behavior of the agent in those environments with a set of videos.
Contributions. Our paper makes four contributions: (1) We present an incremental SAT-based approach to compute policies that satisfy almost-sure properties. The method scales to POMDPs whose belief-support states count billions; (2) The novel approach is able to find large winning regions that yield permissive policies. (3) We implement a straightforward approach that constructs the belief-support symbolically using state-of-the-art model checking. We show that its completeness comes at the cost of limited scalability. (4) We construct a shield for almost-sure specifications on POMDPs which enforces at runtime that no unsafe states are visited and that, under mild assumptions, the agent almost-surely reaches the set of desirable states.
Further Related Work. Chatterjee et al. compute winning regions for minimizing a reward objective via an explicit state representation [17], or consider almost-sure reachability using an explicit state space [16, 51]. The problem of determining any winning policy can be cast as a strong cyclic planning problem, proposed earlier with decision diagrams [7]. Indeed, our BDD-based implementation on the belief-support MDP can be seen as a reimplementation of that approach.
Quantitative variants of reach-avoid specifications have gained attention in, e.g., [11, 28, 40]. Other approaches restrict themselves to simple policies [3, 33, 45, 58]. Wang et al. [55] use an iterative Satisfiability Modulo Theories (SMT) [6] approach for quantitative finite-horizon specifications, which requires computing beliefs. Various general POMDP approaches exist, e.g., [26, 27, 29, 48, 49, 54, 56]. The underlying approaches depend on discounted reward maximization and can satisfy almost-sure specifications with high reliability. However, enforcing probabilities that are close to 0 or 1 requires a discount factor close to 1, drastically reducing the scalability of such approaches [28]. Moreover, probabilities in the underlying POMDP need to be precisely given, which is not always realistic [14].
Another line of work (for example [53]) uses an idea similar to winning regions with uncertain specifications, but in a fully observable setting. Finally, complementary to shielding, there are approaches that guide reinforcement learning (with full observability) via temporal logic constraints [24, 25].
2 Preliminaries and Formal Problem
We briefly introduce POMDPs and their semantics in terms of belief MDPs, before formalising and studying the problem variants outlined in the introduction. We present belief-support MDPs as a finite abstraction of infinite belief MDPs.
We define the support \(\textit{supp}(\mu )=\{x\in X\mid \mu (x)>0\}\) of a discrete probability distribution \(\mu \) and denote the set of all distributions with \( Distr (X)\).
Definition 1 (MDP)
A Markov decision process (MDP) is a tuple \(\mathcal {M}= \langle S, \text {Act}, \mu _\text {init}, \mathbf {P}\rangle \) with a set S of states, an initial distribution \(\mu _\text {init}\in Distr (S)\), a finite set \(\text {Act}\) of actions, and a transition function \(\mathbf {P}:S \times \text {Act}\rightarrow Distr (S)\).
Let \(\text {post}_{s}(\alpha ) = \textit{supp}(\mathbf {P}(s,\alpha ))\) denote the states that may be the successors of the state \(s \in S\) for action \(\alpha \in \text {Act}\) under the distribution \(\mathbf {P}(s,\alpha )\). If \(\text {post}_{s}(\alpha )=\{s\}\) for all actions \(\alpha \), s is called absorbing.
Definition 2 (POMDP)
A partially observable MDP (POMDP) is a tuple \(\mathcal {P}= \langle \mathcal {M}, \varOmega , \text {obs}\rangle \) with \(\mathcal {M}= \langle S, \text {Act}, \mu _\text {init}, \mathbf {P}\rangle \) the underlying MDP with finite S, \(\varOmega \) a finite set of observations, and \(\text {obs}:S \rightarrow \varOmega \) an observation function. We assume that there is a unique initial observation, i.e., that \(|\{ \text {obs}(s) \mid s \in supp (\mu _\text {init})\}| = 1\).
More general observation functions \(\text {obs}:S \rightarrow Distr (\varOmega )\) are possible via a (polynomial) reduction [17]. A path through an MDP is a sequence \(\pi \), \(\pi = (s_0,\alpha _0)(s_1,\alpha _1) \ldots s_n\) of states and actions. such that \(s_{i+1} \in \text {post}_{s_i}(\alpha _i)\) for \(\alpha _{i} \in \text {Act}\) and \(0\le i < n\). The observation function \(\text {obs}\) applied to a path yields an observation(-action) sequence \(\text {obs}(\pi )\) of observations and actions.
For modeling flexibility, we allow actions to be unavailable in a state (e.g., opening doors is only available when at a door), and it turned out to be crucial to handle this explicitly in the following algorithms. Technically, the transition function is a partial function, and the enabled actions are a set \(\text {EnAct}(s) = \{ \alpha \in \text {Act}\mid \text {post}_{s}(\alpha ) \ne \emptyset \}\). To ease the presentation, we assume that states \(s,s'\) with the same observation share a set of enabled actions \(\text {EnAct}(s)=\text {EnAct}(s')\).
Definition 3 (Policy)
A policy \(\sigma :(S\times \text {Act})^*\times S \rightarrow Distr (\text {Act})\) maps a path \(\pi \) to a distribution over actions. A policy is observation-based, if for each two paths \(\pi \), \(\pi '\) it holds that \(\text {obs}(\pi ) = \text {obs}(\pi ') \Rightarrow \sigma (\pi ) = \sigma (\pi ').\) A policy is memoryless, if for each \(\pi \), \(\pi '\) it holds that \(\mathsf {last}(\pi ) = \mathsf {last}(\pi ') \Rightarrow \sigma (\pi ) = \sigma (\pi ')\). A policy is deterministic, if for each \(\pi \), \(\sigma (\pi )\) is a Dirac distribution, i.e., if \(| supp (\sigma (\pi ))| = 1\).
Policies resolve nondeterminism and partial observability by turning a (PO)MDP into the induced infinite discrete-time Markov chain whose states are the finite paths of the (PO)MDP. Probability measures are defined on this Markov chain.
For POMDPs, a belief describes the probability of being in certain state based on an observation sequence. Formally, a belief \(\mathfrak {b}\) is a distribution \(\mathfrak {b}\in Distr (S)\) over the states. A state s with positive belief \(\mathfrak {b}(s)>0\) is in the belief support, \(s\in \textit{supp}(b)\). Let \( Pr _\mathfrak {b}^\sigma (S')\) denote the probability to reach a set \(S'\subseteq S\) of states from belief \(\mathfrak {b}\) under the policy \(\sigma \). More precisely, \( Pr _\mathfrak {b}^\sigma (S')\) denotes the probability of all paths that reach \(S'\) from \(\mathfrak {b}\) when nondeterminism is resolved by \(\sigma \).
The policy synthesis problem usually consists in finding a policy that satisfies a certain specification for a POMDP. We consider reach-avoid specifications, a subclass of indefinite horizon properties [46]. For a POMDP \(\mathcal {P}\) with states S, such a specification is \(\varphi =\langle \textit{REACH}, \textit{AVOID}\rangle \subseteq S \times S\). We assume that states in \(\textit{AVOID}\) and in \(\textit{REACH}\) are (made) absorbing and \(\textit{REACH}\cap \textit{AVOID}=\emptyset \).
Definition 4 (Winning)
A policy \(\sigma \) is winning for \(\varphi \) from belief \(\mathfrak {b}\) in (PO)MDP \(\mathcal {P}\) iff \( Pr _\mathfrak {b}^\sigma (\textit{AVOID})=0\) and \( Pr _\mathfrak {b}^\sigma (\textit{REACH})=1\), i.e., if it reaches \(\textit{AVOID}\) with probability zero and \(\textit{REACH}\) with probability one (almost-surely) when \(\mathfrak {b}\) is the initial state. Belief \(\mathfrak {b}\) is winning for \(\varphi \) in \(\mathcal {P}\) if there exists a winning policy from \(\mathfrak {b}\).
We omit \(\mathcal {P}\) and \(\varphi \) whenever it is clear from the context and simply call \(\mathfrak {b}\) winning.

The problem is EXPTIME-complete [18]. Contrary to MDPs, it is not sufficient to consider memoryless policies.
Model checking queries for POMDPs often rely on the analysis of the belief MDP. Indeed, we may analyse this generally infinite model. Let us first recap a formal definition of the belief MDP, using the presentation from [11]. In the following, let  denote the probabilityFootnote 1 to move to (a state with) observation \(z\) from state \(s\) using action \(\alpha \). Then,
denote the probabilityFootnote 1 to move to (a state with) observation \(z\) from state \(s\) using action \(\alpha \). Then,  is the probability to observe \(z\) after taking \(\alpha \) in \(\mathfrak {b}\). We define the belief obtained by taking \(\alpha \) from \(\mathfrak {b}\), conditioned on observing \(z\):
is the probability to observe \(z\) after taking \(\alpha \) in \(\mathfrak {b}\). We define the belief obtained by taking \(\alpha \) from \(\mathfrak {b}\), conditioned on observing \(z\):

Definition 5 (Belief MDP)
The belief MDP of POMDP \(\mathcal {P}= \langle \mathcal {M}, \varOmega , \text {obs}\rangle \) where \(\mathcal {M}= \langle S, \text {Act}, \mu _\text {init}, \mathbf {P}\rangle \) is the MDP  with \(\mathcal {B}= Distr (S)\), and transition function \(\mathbf {P}_\mathcal {B}\) given by
with \(\mathcal {B}= Distr (S)\), and transition function \(\mathbf {P}_\mathcal {B}\) given by

Due to (1) and the unique initial observation, we may restrict the beliefs to \(\mathcal {B}= \bigcup _{z\in \varOmega } Distr (\{ s \mid \text {obs}(s) = z\})\), that is, each belief state has a unique associated observation. We can lift specifications to belief MDPs: Avoid-beliefs are the set of beliefs \(\mathfrak {b}\) such that \( supp (\mathfrak {b}) \cap \textit{AVOID}\ne \emptyset \), and reach-beliefs are the set of beliefs \(\mathfrak {b}\) such that \( supp (\mathfrak {b}) \subseteq \textit{REACH}\).
Towards obtaining a finite abstraction, the main algorithmic idea is the following. For the qualitative reach-avoid specifications we consider, the belief probabilities are irrelevant—only the belief support is important [47].
Lemma 1
For winning belief \(\mathfrak {b}\), belief \(\mathfrak {b}'\) with \( supp (\mathfrak {b})= supp (\mathfrak {b}')\) is winning.
Consequently, we can abstract the belief MDP into a finite belief support MDP.
Definition 6 (Belief-Support MDP)
For a POMDP \(\mathcal {P}= \langle \mathcal {M}, \varOmega , \text {obs}\rangle \) with \(\mathcal {M}= \langle S, \text {Act}, \mu _\text {init}, \mathbf {P}\rangle \), the finite state space of a belief-support MDP \(\mathcal {P}_B\) is \(B= \bigl \{ b\subseteq S\mid \forall s,s'\in b:\text {obs}(s)=\text {obs}(s')\bigr \}\) where each state is the support of a belief state. Action \(\alpha \) in state \(b\) leads (with an irrelevant positive probability \(p>0\)) to a state \(b'\), if
Thus, transitions between states within \(b\) and \(b'\) are mimicked in the POMDP. Equivalently, the following clarifies the belief-support MDP as an abstraction of the belief MDP: there are transitions with action \(\alpha \) between \(b\) and \(b'\), if there exists beliefs \(\mathfrak {b},\mathfrak {b}'\) with \( supp (\mathfrak {b}) = b\) and \( supp (\mathfrak {b}') = b'\), such that \(\mathfrak {b}' \in \text {post}_{\mathfrak {b}}(\alpha )\).
We lift the specification as before:
Definition 7 (Lifted specification)
For \(\varphi = \langle \textit{AVOID}, \textit{REACH}\rangle \), we define \(\varphi _B = \langle \textit{AVOID}_B, \textit{REACH}_B \rangle \) with \(\textit{AVOID}_B = \{ b\mid b\cap \textit{AVOID}\ne \emptyset \}\), and \(\textit{REACH}_B = \{ b\mid b\subseteq \textit{REACH}\}\).
We obtain the following lemma, which follows from the fact that almost-sure reachability is a graph propertyFootnote 2.
Lemma 2
If belief \(\mathfrak {b}\) is winning in the POMDP \(\mathcal {P}\) for \(\varphi \), then the support \( supp (\mathfrak {b})\) is winning in the belief-support MDP \(\mathcal {P}_B\) for \(\varphi _B\).
Lemma 2 yields an equivalent reformulation of Problem 1 for belief supports:

3 Winning Regions
This section provides the observations on winning regions, a key concept for this paper. An important consequence of Lemma 2 and the reformulation of Problem 1 to the belief-support MDP is that the initial distribution of the POMDP is no longer relevant. Winning policies for individual beliefs may be composed to a policy that is winning for all of these beliefs, using the individual action choices.
Lemma 3
If the policies \(\sigma \) and \(\sigma '\) are winning for the belief supports \(b\) and \(b'\), respectively, then there exists a policy \(\sigma ''\) that is winning for both \(b\) and \(b'\).
While this statement may seem trivial on the MDP (or equivalently on beliefs), we notice that it does not hold for POMDP states. As a natural consequence, we are able to consider winning beliefs without referring to a specific policy.
Definition 8 (Winning region)
Let \(\sigma \) be a policy. A set \(W_{\varphi }^{\sigma } \subseteq B\) of belief supports is a winning region for \(\varphi \) and \(\sigma \), if \(\sigma \) is winning from each \(b\in W_{\varphi }^{\sigma }\). A set \(W_{\varphi } \subseteq B\) is a winning region for \(\varphi \), if every \(b\in W_{\varphi }\) is winning. The region containing all winning beliefs is the maximal winning regionFootnote 3.
Observe that the maximal winning region in MDPs exists for qualitative reachability, but not for quantitative reachability, which we do not consider here.

Using this definition of winning regions, we are able to reformulate Problem 1 by asking whether the support of some belief \(\mathfrak {b}\) is in the winning region.
Part of Problem 1 was to compute a winning policy. Below, we study the connection between the winning region and winning policies. We are interested in subsets of the maximal winning region that exhibit two properties:
Definition 9 (Deadlock-free)
A set W of belief-supports \(W\subseteq B\) is deadlock-free, if for every \(b\in W\), an action \(\alpha \in \text {EnAct}(b)\) exists such that \(\text {post}_{b}(\alpha ) \subseteq W\).
Definition 10 (Productive)
A set of belief supports \(W \subseteq B\) is productive (towards a set \(\textit{REACH}_B\)), if from every \(b\in W\), there exists a (finite) path \(\pi = b_0\alpha _1b_1\ldots b_n\) from \(b_0\) to \(b_n \in \textit{REACH}_B\) with \(b_i \in W\) and \(\text {post}_{b_i}(\alpha ) \subseteq W\) for all \(1 \le i \le n\).
Every productive region is deadlock-free, as \(\textit{REACH}\)-states are absorbing. The maximal winning region is productive towards \(\textit{REACH}_B\) (and thus deadlock-free) by definition. Intuitively, while a deadlock-free region ensures that one never has to leave the region, any productive winning region ensures that from every belief support within this region there is a policy to stay in the winning region and that can almost-surely reach a \(\textit{REACH}\)-state. In particular, to find a winning policy (Challenge 1) or for the purpose of safe exploration (Challenge 2), it is sufficient to find a productive subset of the maximal winning region. We detail on this insight in Sect. 6.

To allow a compact representation of winning regions, we exploit that for any belief support \(b' \subseteq b\) it holds that \(\text {post}_{b'}(\alpha ) \subseteq \text {post}_{b}(\alpha )\) for all actions \(\alpha \in \text {Act}\), that is, the successors of \(b'\) are contained in the successors of \(b\).
Lemma 4
For winning belief support \(b\), \(b' \subseteq b\) is winning.
4 Iterative SAT-Based Computation of Winning Regions
We devise an approach for iteratively computing an increasing sequence of productive winning regions. The approach delivers a compact symbolic encoding of winning regions: For a belief (or belief-support) state from a given winning region, we can efficiently decide whether the outcome of an action emanating from the state stays within the winning region.
Key ingredient is the computation of so-called memoryless winning policies. We start this section by briefly recapping how to compute such policies directly on the POMDP, before we build an efficient incremental approach on top of this base method. In particular, we first present a naive iterative algorithm based on the notion of shortcuts, then describe how to implicitly add shortcuts within the encoding, and then finally combine the ideas to an efficient algorithm.
4.1 One-Shot Approach to Find Small Policies from a Single Belief
We aim to solve Problem 1 and determine a winning policy. The number of policies is exponential in the actions and the (exponentially many) belief support states. Searching among doubly exponentially many possibilities is intractable in general. However, Chatterjee et al. [15] observe that often much simpler winning policies exist and provides a one-shot approach to find them. The essential idea is to search only for memoryless observation-based policies \(\sigma :\varOmega \rightarrow Distr (\text {Act})\) that are winning for the (initial) belief support \(b\).
Example 1
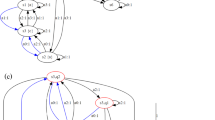
Consider the small Cheese-POMDP [35] in Fig. 1(a). States are cells, actions are moving in the cardinal directions (if possible), and observations are the directions with adjacent cells, e.g., the boldface states 6, 7, 8 share an observation. We set \(\textit{REACH}=\{10\}\) and \(\textit{AVOID}=\{9,11\}\). From belief support \(b=\{ 6,8 \}\) there is no memoryless winning policy—In states \(\{6,8\}\) we have to go north, which prevents us from going south in state 7. However, we can find a memoryless winning policy for \(\{ 1,5 \}\), see Fig. 1(b).
This problem is NP-complete, and it is thus natural to encode the problem as a satisfiability query in propositional logic. We mildly adapt the original encoding of winning policies [15]. We introduce three sets of Boolean variables: \(A_{z,\alpha }\), \(C_{s}\) and \(P_{{s,j}}\). If a policy takes action \(\alpha \in \text {Act}\) with positive probability upon observation \(z\in \varOmega \), then and only then, \(A_{z,\alpha }\) is true. If under this policy a state \(s \in S\) is reached from some initial belief support \(b_\iota \) with positive probability, then and only then, \(C_{s}\) is true. We define a maximal rank \(k\) to ensure the productivity. For each state s and rank \(0 \le j \le k\), variable \(P_{{s,j}}\) indicates rank j for s, that is, a path from s leads to \(s' \in \textit{REACH}\) within j steps.Footnote 4 A winning policy is then obtained by finding a satisfiable solution (via a SAT solver) to the conjunction \(\varPsi _{\mathcal {P}}^{\varphi }(b_\iota ,k)\) of the constraints (2a)–(5), where \({S_{?}}= S \setminus \big (\textit{AVOID}\cup \textit{REACH}\big )\).

The initial belief support is clearly reachable (2a). The conjunction in (2b) ensures that in every observation, at least one action is taken.
The conjunction (3) ensures that for any model for these formulas, the set of states \(\{s \in S \mid C_s = \mathsf {true} \}\) is reachable, does not overlap with \(\textit{AVOID}\), and is transitively closed under reachability (for the policy described by \(A_{z,\alpha }\)).
Conjunction (4) states that any state that is reached almost-surely reaches a state in \(\textit{REACH}\), i.e., that there is a path (of length at most) k to the target. Conjunctions (5) describe a ranking function that ensures the existence of this path. Only states in \(\textit{REACH}\) have rank zero, and a state with positive probability to reach a state with rank \(j{-}1\) within a step has rank at most j.
By [15, Thm. 2], it holds that the conjunction \(\varPsi _{\mathcal {P}}^{\varphi }(b_\iota ,k)\) of the constraints (2a)–(5) is satisfiable, if there is a memoryless observation-based policy such that \(\varphi \) is satisfied. If \(k=|S|\), then the reverse direction also holds. If \(k< |S|\), we may miss states with a higher rank. Large values for \(k\) are practically intractable [15], as the encoding grows significantly with \(k\). Pandey and Rintanen [41] propose extending SAT-solvers with a dedicated handling of ranking constraints.
In order to apply this to small-memory policies, one can unfold \(\log (m)\) bits of memory of such a policy into an m times larger POMDP [15, 33], and then search for a memoryless policy in this larger POMDP. Chatterjee et al. [15] include a slight variation to this unfolding, allowing smaller-than-memoryless policies by enforcing the same action over various observations.
4.2 Iterative Shortcuts
We exploit the one-shot approach to create a naive iterative algorithm that constructs a productive winning region. The iterative algorithm avoids the following restrictions of the one-shot approach. (1) In order to increase the likelihood of finding winning policies, we do not restrict ourselves to small-memory policies, and (2) we do not have to fix a maximal rank \(k\). These modifications allow us to find more winning policies, without guessing hyper-parameters. As we do not need to fix the belief-state, those parts of the winning region that are easy to find for the solver are encountered first.
The One-Shot Approach on Winning Regions. To understand the naive iterative algorithm, it is helpful to consider the previous encoding in the light of Problem 3, i.e., finding productive winning regions. Consider first the interpretation of the variables. Indeed, observe that we have found the same winning policy for all states s where \(C_s\) is true. Consequentially, any belief support \(b_z= \{ s \mid C_s~\texttt {true} \wedge \text {obs}(s) = z\}\) is winning.
Lemma 5
If \(\sigma \) is winning for \(b\) and \(b'\), then \(\sigma \) is also winning for \(b\cup b'\).
This lemma is somewhat dual to Lemma 4, but requires a fixed policy. The constraints (3) and ensure that a winning-region is deadlock-free. The constraints (4) and (5) ensure productivity of the winning region.
Adding Shortcuts Explicitly. The key idea is that we iteratively add short-cuts in the POMDP that represent known winning policies. We find a winning policy \(\sigma \) for some belief states in the first iteration, and then add a fresh action \(\alpha _\sigma \) to all (original) POMDP states: This action leads – with probability one – to a \(\textit{REACH}\) state, if the state is in the wining belief-support under policy \(\sigma \). Otherwise, the action leads to an \(\textit{AVOID}\) state.
Definition 11
For POMDP \(\mathcal {P}= \langle \mathcal {M}, \varOmega , \text {obs}\rangle \) where \(\mathcal {M}= \langle S, \text {Act}, \mu _\text {init}, \mathbf {P}\rangle \) and a policy \(\sigma \) with associated winning region \(W_\varphi ^\sigma \), and assuming w.l.o.g., \(\top \in \textit{REACH}\) and \(\bot \in \textit{AVOID}\), we define the shortcut POMDP \(\mathcal {P}\{\sigma \} = \langle \mathcal {M}', \varOmega , \text {obs}\rangle \) with \(\mathcal {M}' = \langle S, \text {Act}', \mu _\text {init}, \mathbf {P}' \rangle \), \(\text {Act}' = \text {Act}\cup \{ \alpha _\sigma \}\), \(\mathbf {P}'(s,\alpha ) = \mathbf {P}(s,\alpha )\) for all \(s \in S\) and \(\alpha \in \text {Act}\), and \(\mathbf {P}'(s,\alpha _\sigma ) = \{ \top \mapsto [\{ s \} \in W_\varphi ^\sigma ], \bot \mapsto [\{ s \} \not \in W_\varphi ^\sigma ]\}\).
Lemma 6
For a POMDP \(\mathcal {P}\) and policy \(\sigma \), the (maximal) winning regions for \(\mathcal {P}\{\sigma \}\) and \(\mathcal {P}\) coincide.
First, adding more actions will not change a winning belief-support to be not winning. Furthermore, by construction, taking the novel action will only lead to a winning belief-support whenever following \(\sigma \) from that point onwards would be a winning policy. The key benefit is that adding shortcuts may extend the set of belief-support states that win via a memoryless policy. This observation also gives rise to the following extension to the one-shot approach.
Example 2
We continue with Example 1. If we add shortcuts, we can now find a memoryless winning policy for \(b=\{ 6,8 \}\), depicted in Fig. 1(c).
Iterative Shortcuts to Extend a Winning Region. The idea is now to run the one-shot approach, extract the winning region, add the shortcuts to the POMDP, and rerun the one-shot approach. To make the one-shot approach applicable in this setting, it only needs one change: Rather than fixing an initial belief-support, we ask for an arbitrary new belief-support to be added to the states that we have previously covered. We use a data structure \(\mathsf {Win}\) such that \(\mathsf {Win}(z)\) encodes all winning belief supports with observation \(z\). Internally, the data structure stores maximal winning belief supports (w.r.t. set inclusion, see also Lemma 4) as bit-vectors. By construction, for every \(b\in \mathsf {Win}(z)\), a winning region exists, i.e., conceptually, there is a shortcut-action leading to \(\textit{REACH}\).
We extend the encoding (in partial preparation of the next subsection) and add a variable \(U_{z} \in b\) that is true if the policy is winning in a belief support that is not yet in \(\mathsf {Win}(z)\). We replace (2a) with:
For an observation \(z\) for which we have not found a winning belief support yet, finding a policy from any state s with \(\text {obs}(s)\) updates the winning region. Otherwise, it means finding a winning policy for a belief support that is not subsumed by a previous one (6).
Real-Valued Ranking. To avoid setting a maximal path length, we use unbounded (real) variables \(R_{s}\) rather than Boolean variables for the ranking [57]. This relaxation avoids the growth of the encoding and admits arbitrarily large ranks with a fixed-size encoding into difference logic. This logic is an extension to propositional logic that can be checked using an SMT solver [6].
We replace (4) and (5): A state must have a successor state with a lower rank – as before, but with real-valued ranks (7).

Algorithm. Together, the algorithm is given in Algorithm 1. We initialize the winning region based on the specification, then encode the POMDP using the (modified) one-shot encoding. As long as the SMT solver finds policies that are winning for a new belief-support, we add those belief supports to the winning region. In each iteration, \(\mathsf {Win}\) contains a winning region. Once we find no more policies that extend the winning region on the extended POMDP, we terminate.
The algorithm always terminates because the set of winning regions is finite, but in general does not solve Problem 2. Formally, the maximal winning region is a greatest fixpoint [5] and we iterate from below, i.e., the fixpoint that we find will be the smallest fixpoint (of the operation that we implement). However, iterating from above requires to reason that none of the doubly-exponentially many policies is winning for a particular belief support state; whereas our approach profits from finding simple strategies early on. Unfolding of memory as discussed earlier also makes this algorithm complete, yet, suffers from the same blow-up. A main advantage is that the algorithm often avoids the need for unfolding when searching for a winning policy or large winning regions.
Next, we address two weaknesses: First, the algorithm currently creates a new encoding in every iteration, yielding significant overhead. Second, the algorithm in many settings requires adding a bit of memory to realize behavior where in a particular observation, we first want to execute an action \(\alpha \) and then follow a shortcut from the state (with the same observation) reached from there. We adapt the encoding to explicitly allow for these (non-memoryless) policies.
4.3 Incremental Encoding of Winning Regions
In this section, instead of naively adjusting the POMDP, we realize the idea of adding shortcuts directly on the encoding. This encoding is the essential step towards an efficacious approach for solving Problem 3. We find winning states based on a previous solution, and instead of adding actions, we allow the solver to decide following individual policies from each observation. In Sect. 4.4, we embed this encoding into an improved algorithm.
Our encoding represents an observation-based policy that can decide to take a shortcut, which means that it follows a previously computed winning policy from there (implicitly using Lemma 3). In addition to \(A_{z,\alpha }\), \(C_{s}\) and \(R_{s}\) from the previous encoding, we use the following variables: The policy takes shortcuts in states s where \(D_{s}\) is true. For each observation, we must take the same shortcut, referred to by a positive integer-valued index \(I_{z}\). More precisely, \(I_{z}\) refers to a shortcut from a previously computed (fragment of a) winning region stored in \(\mathsf {Win}(z)_{I_{z}}\). The policy may decide to switch, that is, to follow a shortcut after taking an action starting in a state with observation \(z\). If \(F_{z}\) is true, the policy takes some action from \(z\)-states and from the next state, we take a shortcut. The encoding thus implicitly represents policies that are not memoryless but rather allow for a particular type of memory.
The conjunction of (6) and (8)–(13) yields the encoding \(\varPhi _{\mathcal {P}}^{\varphi }(\mathsf {Win})\):
Similar to (2b), (3), we select at least one action and AVOID-states should not be reached (8). States reached are closed under the transitive closure, however, only if we do not switch to taking a shortcut (9). Furthermore, we mark the states reached after switching (10) and need to select a shortcut for these states.
If we reach a state s after switching, then we must pick a shortcut. We can only pick an index that reflects a found winning region (11). If we pick this shortcut reflecting a winning region (fragment) for observation \(z\), then we are winning from the states in \(\mathsf {Win}(z)_i\), but not from any other state s with that observation. Thus, for \(s \not \in \mathsf {Win}(z)_i\), if we are going to follow any shortcut (that is, \(D_{s}\) holds), we should not pick this particular shortcut encoded by \(I_{z}\) (because it will lead to an \(\textit{AVOID}\)-state). In terms of the policy: Taking this previously computed policy from state s is not (known to) lead us to a \(\textit{REACH}\)-state (12). Finally, we update the ranking to account for shortcuts.
We make a slight adaption to (7): Either we have a successor state with a lower rank (as before) or we follow a shortcut—which either leads to the target or to violating the specification (13). We formalize the correctness of the encoding:
Lemma 7
If \(\eta \models \varPhi _{\mathcal {P}}^{\varphi }(\mathsf {Win})\), then for every observation \(z\), the belief support \(b_z= \{ s \mid \eta (C_{s}) = \texttt {true}, \text {obs}(s) = z\}\) is winning.
Algorithm 2 is a straightforward adaption of Algorithm 1 that avoids adding shortcuts explicitly (and uses the updated encoding). As before, the algorithm terminates and solves Problem 3. We conclude:

Theorem 1
In any iteration, Algorithm 2 computes a productive winning region.
4.4 An Incremental Algorithm
We adapt the algorithm sketched above to exploit the incrementality of modern SMT solvers. Furthermore, we aim to reduce the invocations of the solver by finding some extensions to the winning region via a graph-based algorithm.
Graph-Based Preprocessing. To reduce the number of SMT invocations, we employ polynomial-time graph-based heuristics. The first step is to use (fully observable) MDP model checking on the POMDP as follows: find all states that under each (not necessarily observation-based) policy reach an \(\textit{AVOID}\)-state with positive probability, and make them absorbing. Then, we find all states that under each policy reach a \(\textit{REACH}\)-state almost-surely. Then, we iteratively search for winning observations and use them to extend the \(\textit{REACH}\)-states. An observation \(z\) is winning, if the belief-support \(\{ s \mid \text {obs}(s) = z\}\) is winning. We start with a previously determined winning region \(W_{}\). We iteratively update \(W_{}\) by adding states \(b_z= \{ s \mid \text {obs}(s) = z\}\) for some observation \(z\), if there is an action \(\alpha \) such that from every \(s \in b_z\), it holds \(\text {post}_{s}(\alpha ) \subseteq W_{}\). The iterative updates are interleaved with MDP model checking on the POMDP as described above until we find a fixpoint.

Optimized Algorithm. We improve Algorithm 2 along four dimensions to obtain Algorithm 3. First, we employ fewer updates of the winning region: We aim to extend the policy as much as possible, i.e., we want the SMT-solver to find more states with the same observation that are winning under the same policy. Therefore, we fix the variables for action choices that yield a new winning policy, and let the SMT solver search whether we can extend the corresponding winning region by finding more states and actions that are compatible with the partial policy. Second, we observe that between (outer) iterations, large parts of the encoding stay intact, and use an incremental approach in which we first push all the constraints from the POMDP onto the stack, then all the constraints from the winning region, and finally a constraint that asks for progress. After we found a new policy, we pop the last constraint from the stack, add new constraints regarding the winning region (notice that the old constraints remain intact), and push new constraints that ask for extending the winning region to the stack. We refresh the encoding periodically to avoid unnecessary cluttering. Third, further constraints (1) make the usage of shortcuts more flexible—we allow taking shortcuts either immediately or after the next action, and (2) enable an even more incremental encoding with some minor technical reformulations. Fourth, we add the graph-preprocessing discussed above during the outer iteration.
5 Symbolic Model Checking for the Belief-Support MDP
In this section, we briefly describe how we encode a given POMDP into a belief-support MDP to employ symbolic, off-the-shelf probabilistic model checking. In particular, we employ symbolic (decision-diagram, DD) representations of the belief-support MDP as we expect this MDP to be huge. Constructing that DD representation effectively is not entirely trivial. Instead, we advocate constructing a (modular) symbolic description of the belief support MDP. Concretely, we automatically generate a model description in the MDP modeling language JANI [13],Footnote 5 and then apply off-the-shelf model checking on the JANI description.
Conceptually, we create a belief-support MDP with auxiliary states to allow for a concise encoding.Footnote 6 We use this auxiliary state \(\hat{b}\) to describe for any transition the conditioning on the observation. Concretely, a single transition \(\mathbf {P}(b,\alpha ,b')\) in the belief-support MDP is reflected by two transitions \(\mathbf {P}(b,\alpha ,\hat{b})\) and \(\mathbf {P}(\hat{b},\alpha _\bot ,b')\) in our encoding, where \(\alpha _\bot \) is a unique dummy action. We encode states using triples \(\langle \texttt {belsup},\texttt {newobs},\texttt {lact}\rangle \). \(\texttt {belsup}\) is a bit vector with entries for every state s that we use to encode the belief support. Variables \(\texttt {newobs}\) and \(\texttt {lact}\) store an observation and an action and are relevant only for the auxiliary states. Technically, we now encode the first transition from \(b\) with the nondeterministic action \(\alpha \) to \(\hat{b}\). \(\mathbf {P}(b, \alpha )\) then yields (with arbitrary positive) probability a new observation that will reflect the observation \(\text {obs}(b')\). We store \(\alpha \) and \(\text {obs}(b')\) in \(\texttt {lact}\) and \(\texttt {newobs}\), respectively. The second step is a single deterministic (dummy) action updating \(\texttt {belsup}\) while taking into account \(\texttt {newobs}\). The step also resets \(\texttt {lact}\) and \(\texttt {newobs}\).
The encoding of the transitions as follows: For the first step, we create nondeterministic choices for each action \(\alpha \) and observation \(z\). We guard these choices with \(z\) meaning that the edge is only applicable to states having observation \(z\), i.e., the guard is \(\bigvee _{\begin{array}{c} s \in S,\text {obs}(s) = z \end{array}} \texttt {belsup}(s)\). With these guarded edges, we define the destinations: With an arbitraryFootnote 7 probability p, we go to an observation \(z_1\) if there is at least one state in \(s \in \texttt {belsup}\) which has a successor state \(s' \in \text {post}_{s}(\alpha )\) with \(\text {obs}(s') = z_1\).
The following pseudocode reflects the first step in the transition encoding. The syntax is as follows: take an action if a Boolean guard is satisfied, then updates are executed with probability prob. An example for a guard is an observation \(z\).
The second step synchronously updates each state \(s'\) in the POMDP independently: The entry \(\texttt {belsup}(s')\) is set to true if \(\text {obs}(s) = \texttt {newobs}\) and if there is a state s currently true in (the old) \(\texttt {belsup}\) with \(s' \in \text {post}_{s}(\texttt {lact})\). The step thus can be captured by the following pseudocode for each \(s'\):
Finally, whenever the dummy action \(\alpha _\bot \) is executed, we also reset the variables \(\texttt {newobs}\) and \(\texttt {lact}\). The resulting encoding thus has transitions in the order of \(|S| + |\varOmega |^2\cdot |\max _{z\in \varOmega } \text {EnAct}(z)|\).
6 Almost-Sure Reachability Shields in POMDPs
In this section, we define a shield for POMDPs – towards the application of safe exploration (Challenge 2) – that blocks actions which would lead an agent out of a winning region. In particular, the shield imposes restrictions on policies to satisfy the reach-avoid specification. Technically, we adapt so-called permissive policies [21, 31] for a belief-support MDP. To force an agent to stay within a productive winning region \(W_{\varphi }\) for specification \(\varphi \), we define a \(\varphi \)-shield \(\nu :b\rightarrow 2^\text {Act}\) such that for any winning \(b\) for \(\varphi \) we have \(\nu (b) \subseteq \{ \alpha \in \text {Act}\mid \text {post}_{b}(\alpha ) \subseteq W_{\varphi } \}\), i.e., an action is part of the shield \(\nu (b)\) if it exclusively leads to belief support states within the winning region.
A shield \(\nu \) restricts the set of actions an arbitrary policy may takeFootnote 8. We call such restricted policies admissible. Specifically, let \(b_\tau \) be the belief support after observing an observation sequence \(\tau \). Then policy \(\sigma \) is \(\nu \)-admissible if \(\textit{supp}(\sigma (\tau )) \subseteq \nu (b_\tau )\) for every observation-sequence \(\tau \). Consequently, a policy is not admissible if for some observation sequence \(\tau \), the policy selects an action \(\alpha \in \text {Act}\) which is not allowed by the shield.
Some admissible policies may choose to stay in the winning region without progressing towards the \(\textit{REACH}\) states. Such a policy adheres to the avoid-part of the specification, but violates the reachability part. To enforce progress, we adapt a notion of fairness. A policy is fair if it takes every action infinitely often at any belief support state that appears infinitely often along a trace [5]. For example, a policy that randomizes (arbitrarily) over all actions is fair–we notice that most reinforcement learning policies are therefore fair.
Theorem 2
For a \(\varphi \)-shield \(\nu \) and a winning belief support \(b\), any fair \(\nu \)-admissible policy satisfies \(\varphi \) from \(b\).
We give a proof (sketch) in [32, Appendix]. The main idea is to show that the induced Markov chain of any admissible policy has only bottom SCCs that contain \(\textit{REACH}\)-states.
Remark 1
If \(\varphi \) is a safety specification (where \( Pr _\mathfrak {b}^\sigma (\textit{AVOID})=0\) suffices), we can rely on deadlock-free winning regions rather than productive winning regions and drop the fairness assumption.
7 Empirical Evaluation
We investigate the applicability of our incremental approach (Algorithm 3) to Challenge 1 and Challenge 2, and compare with our adaption and implementation of the one-shot approach [15], see Sect. 4.1. We also employ the MDP model-checking approach from Sect. 5. Experiments, videos, source code are archivedFootnote 9.
Setting. We implemented the one-shot algorithm, our incremental algorithm, and the generation of the JANI description of the belief support MDP into the model checker Storm [19] on top of the SMT solver z3 [38]. To compare with the one-shot algorithm for Problem 1, that is, for finding a policy from the
 state, we add a variant of Algorithm 3. Intuitively, any outer iteration starts with an SMT-check to see whether we find a policy covering the initial states. We realize the latter by fixing (temporarily) the \(C_{s}\)-variables. In the first iteration, this configuration and its resulting policy closely resemble the one-shot approach. For the MDP model-checking approach, we use Storm (from the C++ API) with the dd engine and default settings.
state, we add a variant of Algorithm 3. Intuitively, any outer iteration starts with an SMT-check to see whether we find a policy covering the initial states. We realize the latter by fixing (temporarily) the \(C_{s}\)-variables. In the first iteration, this configuration and its resulting policy closely resemble the one-shot approach. For the MDP model-checking approach, we use Storm (from the C++ API) with the dd engine and default settings.
For the experiments, we use a MacBook Pro MV962LL/A, a single core, no randomization, and use a 6 GB memory limit. The time-out (TO) is 15 min.
Baseline. We compare with the one-shot algorithm including the graph-based preprocessing to identify more winning observations. We use two setups: (1) We (manually, a-priori) search for
 for each instance. We search for the smallest amount of memory possible, and for the smallest maximal rank k (being a multiplicative of five) that yields a result. Guessing parameters as an “oracle” is time-consuming and unrealistic. We investigate (2) the performance of the one-shot algorithm by
for each instance. We search for the smallest amount of memory possible, and for the smallest maximal rank k (being a multiplicative of five) that yields a result. Guessing parameters as an “oracle” is time-consuming and unrealistic. We investigate (2) the performance of the one-shot algorithm by
 to two memory-states and \(k=30\). These parameters provide results for most benchmarks.
to two memory-states and \(k=30\). These parameters provide results for most benchmarks.
Benchmarks. Our benchmarks involve agents operating in \(N{\times }N\) grids, inspired by, e.g., [12, 15, 20, 50, 51]. See Fig. 2 for video stills of simulating the following benchmarks. Rocks is a variant of rock sample. The grid contains two rocks which are either valuable or dangerous to collect. To find out with certainty, the rock has to be sampled from an adjacent field. The goal is to collect a valuable rock, bring it to the drop-off zone, and not collect dangerous rocks. Refuel concerns a rover that shall travel from one corner to the other, while avoiding an obstacle on the diagonal. Every movement costs energy and the rover may recharge at recharging stations to its full battery capacity E. It receives noisy information about its position and battery level. Evade is a scenario where a robot needs to reach a destination and evade a faster agent. The robot has a limited range of vision (R), but may scan the whole grid instead of moving. A certain safe area is only accessible by the robot. Intercept is inverse to Evade in the sense that the robot aims to meet an agent before it leaves the grid via one of two available exits. On top of the view radius, the agent observes a corridor in the center of the grid. Avoid is a related scenario where a robot shall keep distance to patrolling agents that move with uncertain speed, yielding partial information about their position The robot may exploit their predefined routes. Obstacle contains static obstacles where the robot needs to reach the exit. Its initial state and movement are uncertain, and it only observes whether the current position is a trap or exit.
Results for Challenge 1. Table 1 details the numerical benchmark results. For each benchmark instance (columns), we report the name and relevant characteristics: the number of states (|S|), the number of transitions (#Tr, the edges in the graph described by the POMDP), the number of observations (\(|\varOmega |\)), and the number of belief support states (\(|b|\)). For the incremental method, we provide the run time (Time, in seconds), the number of outer iterations (#Iter.) in Algorithm 3, and the number of invocations of the SMT solver (#solve), and the approximate size of the winning region (\(|W_{}|\)). We then report these numbers when searching for a policy that wins from the initial state. For the one-shot method, we provide the time for the optimal parameters (on the next line)–TOs reflect settings in which we did not find any suitable parameters, and the time for the preset parameters (2,30), or N/A if no policy can be found with these parameters. Finally, for (belief-support) MDP model checking, we give only the run times.
The incremental algorithm finds winning policies for the
 state without guessing parameters and is often faster versus the one-shot approach with an oracle providing
state without guessing parameters and is often faster versus the one-shot approach with an oracle providing
 parameters, and significantly faster than the one-shot approach with reasonably
parameters, and significantly faster than the one-shot approach with reasonably
 ed parameters. In detail, Rocks shows that we can handle large numbers of iterations, solver invocations, and winning regions. The incremental approach scales to larger models, see e.g., Avoid. Refuel shows a large sensitivity of the one-shot method on the lookahead (going from 15 to 30 increases the runtime), while Evade shows sensitivity to memory (from 1 to 2). In contrast, the incremental approach does not rely on user-input, yet delivers comparable performance on Refuel or Avoid. It suffers slightly on Evade, where the one-shot approach has reduced overhead. We furthermore conclude that off-the-shelf MDP model checking is not a fast alternative. Its advantage is the guarantee to find the maximal winning region, however, for our benchmarks, maximal winning regions (empirically) coincide with the results from the incremental
ed parameters. In detail, Rocks shows that we can handle large numbers of iterations, solver invocations, and winning regions. The incremental approach scales to larger models, see e.g., Avoid. Refuel shows a large sensitivity of the one-shot method on the lookahead (going from 15 to 30 increases the runtime), while Evade shows sensitivity to memory (from 1 to 2). In contrast, the incremental approach does not rely on user-input, yet delivers comparable performance on Refuel or Avoid. It suffers slightly on Evade, where the one-shot approach has reduced overhead. We furthermore conclude that off-the-shelf MDP model checking is not a fast alternative. Its advantage is the guarantee to find the maximal winning region, however, for our benchmarks, maximal winning regions (empirically) coincide with the results from the incremental
 approach.
approach.
Results for Challenge 2. Winning regions obtained from running incrementally to a
 are significantly larger than when running them only until an
are significantly larger than when running them only until an
 winning policy is found (cf. the table), but requires extra computational effort.
winning policy is found (cf. the table), but requires extra computational effort.
If a shielded agent moves randomly through the grid-worlds, the larger winning regions indeed induce more permissiveness, that is, freedom to move for the agent (cf. the videos, Fig. 2). This observation can also be quantified. In Table 2, we compare the two different types of shields. For both, we give average and standard deviation over permissiveness over 250 paths. We choose to approximate permissiveness along a path as the number of cumulative actions allowed by the permissive scheduler along a path, divided by the number of cumulative actions available in the POMDP along that path. As the shield is correct by construction, each run indeed never visits avoid states and eventually reaches the target (albeit after many steps). This statement is not true for the unshielded agents.
8 Conclusion
We provided an incremental approach to find POMDP policies that satisfy almost-sure reachability specifications. The superior scalability is demonstrated on a string of benchmarks. Furthermore, this approach allows to shield agents in POMDPs and guarantees that any exploration of an environment satisfies the specification, without needlessly restricting the freedom of the agent. We plan to investigate a tight interaction with state-of-the-art reinforcement learning and quantitative verification of POMDPs. For the latter, we expect that an explicit approach to model checking the belief-support MDP can be feasible.
Notes
- 1.
We use Iverson brackets: \([x]=1\) if x holds and 0 otherwise.
- 2.
Although the probabilities are not relevant to compute almost-sure reachability, it is important to notice that almost-sure reachability is different from sure-reachability [5]: For almost-sure reachability, there can be an infinite path that never reaches the target, as long as the probability mass over all those paths is 0. Almost-sure reachability can, however, be expressed as sure-reachability in a particular game-setting [47].
- 3.
In some literature, winning region always refers to a maximal winning region.
- 4.
Notice that a state s can have multiple ‘ranks’ in this encoding. Its rank is the smallest j such that \(P_{{s,j}}\) is true.
- 5.
The description here works on a network of synchronized state machines as is also common in the PRISM language.
- 6.
The usage of message passing or indexed assignments in JANI would circumvent the need for intermediate states, but is to the best of our knowledge not supported by decision-diagram based model checkers.
- 7.
We leave this a parametric probability in model building to reduce the number of different probabilities, as this is beneficial for the size of the decision diagram that Storm constructs – it will only have leafs 0, p, 1. Technically, such MDPs are not necessarily well-defined but we can employ model checking on the graph structure.
- 8.
While memory policies based on the belief (support) are sufficient to ensure almost-sure reachability, the goal is to shield other policies that do not necessarily fall in this restricted class.
- 9.
References
Akametalu, A.K., Kaynama, S., Fisac, J.F., Zeilinger, M.N., Gillula, J.H., Tomlin, C.J.: Reachability-based safe learning with Gaussian processes. In: CDC, pp. 1424–1431. IEEE (2014)
Alshiekh, M., Bloem, R., Ehlers, R., Könighofer, B., Niekum, S., Topcu, U.: Safe reinforcement learning via shielding. In: AAAI. AAAI Press (2018)
Amato, C., Bernstein, D.S., Zilberstein, S.: Optimizing fixed-size stochastic controllers for POMDPs and decentralized POMDPs. Auton. Agents Multi Agent Syst. 21(3), 293–320 (2010). https://doi.org/10.1007/s10458-009-9103-z
Baier, C., Größer, M., Bertrand, N.: Probabilistic \(\omega \)-automata. J. ACM 59(1), 1:1–1:52 (2012)
Baier, C., Katoen, J.P.: Principles of Model Checking. MIT Press, Cambridge (2008)
Barrett, C.W., Sebastiani, R., Seshia, S.A., Tinelli, C.: Satisfiability modulo theories. In: Handbook of Satisfiability, pp. 825–885. IOS Press (2009)
Bertoli, P., Cimatti, A., Pistore, M.: Towards strong cyclic planning under partial observability. In: ICAPS, pp. 354–357. AAAI (2006)
Biere, A., Heule, M., van Maaren, H., Walsh, T. (eds.): Handbook of Satisfiability. IOS Press (2009)
Bloem, R., Jensen, P.G., Könighofer, B., Larsen, K.G., Lorber, F., Palmisano, A.: It’s time to play safe: Shield synthesis for timed systems. CoRR abs/2006.16688 (2020)
Bloem, R., Könighofer, B., Könighofer, R., Wang, C.: Shield synthesis: runtime enforcement for reactive systems. In: Baier, C., Tinelli, C. (eds.) TACAS 2015. LNCS, vol. 9035, pp. 533–548. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46681-0_51
Bork, A., Junges, S., Katoen, J.-P., Quatmann, T.: Verification of indefinite-horizon POMDPs. In: Hung, D.V., Sokolsky, O. (eds.) ATVA 2020. LNCS, vol. 12302, pp. 288–304. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-59152-6_16
Brockman, G., et al.: Open AI Gym. CoRR abs/1606.01540 (2016)
Budde, C.E., Dehnert, C., Hahn, E.M., Hartmanns, A., Junges, S., Turrini, A.: JANI: quantitative model and tool interaction. In: Legay, A., Margaria, T. (eds.) TACAS 2017. LNCS, vol. 10206, pp. 151–168. Springer, Heidelberg (2017). https://doi.org/10.1007/978-3-662-54580-5_9
Burns, B., Brock, O.: Sampling-based motion planning with sensing uncertainty. In: ICRA, pp. 3313–3318. IEEE (2007)
Chatterjee, K., Chmelik, M., Davies, J.: A symbolic SAT-based algorithm for almost-sure reachability with small strategies in POMDPs. In: AAAI, pp. 3225–3232. AAAI Press (2016)
Chatterjee, K., Chmelik, M., Gupta, R., Kanodia, A.: Qualitative analysis of POMDPs with temporal logic specifications for robotics applications. In: ICRA, pp. 325–330. IEEE (2015)
Chatterjee, K., Chmelik, M., Gupta, R., Kanodia, A.: Optimal cost almost-sure reachability in POMDPs. Artif. Intell. 234, 26–48 (2016)
Chatterjee, K., Doyen, L., Henzinger, T.A.: Qualitative analysis of partially-observable Markov decision processes. In: Hliněný, P., Kučera, A. (eds.) MFCS 2010. LNCS, vol. 6281, pp. 258–269. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-15155-2_24
Dehnert, C., Junges, S., Katoen, J.-P., Volk, M.: A Storm is coming: a modern probabilistic model checker. In: Majumdar, R., Kunčak, V. (eds.) CAV 2017. LNCS, vol. 10427, pp. 592–600. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63390-9_31
Dietterich, T.G.: The MAXQ method for hierarchical reinforcement learning. In: ICML, pp. 118–126. Morgan Kaufmann (1998)
Dräger, K., Forejt, V., Kwiatkowska, M., Parker, D., Ujma, M.: Permissive controller synthesis for probabilistic systems. In: Ábrahám, E., Havelund, K. (eds.) TACAS 2014. LNCS, vol. 8413, pp. 531–546. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-54862-8_44
Fulton, N., Platzer, A.: Safe reinforcement learning via formal methods: toward safe control through proof and learning. In: AAAI, pp. 6485–6492. AAAI Press (2018)
García, J., Fernández, F.: A comprehensive survey on safe reinforcement learning. J. Mach. Learn. Res. 16, 1437–1480 (2015)
Hahn, E.M., Perez, M., Schewe, S., Somenzi, F., Trivedi, A., Wojtczak, D.: Omega-regular objectives in model-free reinforcement learning. In: Vojnar, T., Zhang, L. (eds.) TACAS 2019. LNCS, vol. 11427, pp. 395–412. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-17462-0_27
Hasanbeig, M., Abate, A., Kroening, D.: Cautious reinforcement learning with logical constraints. In: AAMAS, pp. 483–491. IFAAMAS (2020)
Hausknecht, M.J., Stone, P.: Deep recurrent Q-learning for partially observable MDPs. In: AAAI, pp. 29–37. AAAI Press (2015)
Hauskrecht, M.: Value-function approximations for partially observable Markov decision processes. J. Artif. Intell. Res. 13, 33–94 (2000)
Horák, K., Bosanský, B., Chatterjee, K.: Goal-HSVI: heuristic search value iteration for goal POMDPs. In: IJCAI, pp. 4764–4770. ijcai.org (2018)
Jaakkola, T.S., Singh, S.P., Jordan, M.I.: Reinforcement learning algorithm for partially observable Markov decision problems. In: NIPS, pp. 345–352 (1994)
Jansen, N., Könighofer, B., Junges, S., Serban, A., Bloem, R.: Safe reinforcement learning using probabilistic shields (invited paper). In: CONCUR. LIPIcs, vol. 171, pp. 3:1–3:16. Schloss Dagstuhl - LZI (2020)
Junges, S., Jansen, N., Dehnert, C., Topcu, U., Katoen, J.-P.: Safety-constrained reinforcement learning for MDPs. In: Chechik, M., Raskin, J.-F. (eds.) TACAS 2016. LNCS, vol. 9636, pp. 130–146. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49674-9_8
Junges, S., Jansen, N., Seshia, S.A.: Enforcing almost-sure reachability in POMDPs. CoRR abs/2007.00085 (2020)
Junges, S., Jansen, N., Wimmer, R., Quatmann, T., Winterer, L., Katoen, J.P., Becker, B.: Finite-state controllers of POMDPs using parameter synthesis. In: UAI, pp. 519–529. AUAI Press (2018)
Kaelbling, L.P., Littman, M.L., Cassandra, A.R.: Planning and acting in partially observable stochastic domains. Artif. Intell. 101(1–2), 99–134 (1998)
Littman, M.L., Cassandra, A.R., Kaelbling, L.P.: Learning policies for partially observable environments: Scaling up. In: ICML, pp. 362–370. Morgan Kaufmann (1995)
Madani, O., Hanks, S., Condon, A.: On the undecidability of probabilistic planning and infinite-horizon partially observable Markov decision problems. In: AAAI, pp. 541–548. AAAI Press (1999)
Meuleau, N., Kim, K.E., Kaelbling, L.P., Cassandra, A.R.: Solving POMDPs by searching the space of finite policies. In: UAI, pp. 417–426. Morgan Kaufmann (1999)
de Moura, L., Bjørner, N.: Z3: an efficient SMT solver. In: Ramakrishnan, C.R., Rehof, J. (eds.) TACAS 2008. LNCS, vol. 4963, pp. 337–340. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-78800-3_24
Nam, W., Alur, R.: Active learning of plans for safety and reachability goals with partial observability. IEEE Trans. Syst. Man Cybern. Part B 40(2), 412–420 (2010)
Norman, G., Parker, D., Zou, X.: Verification and control of partially observable probabilistic systems. Real-Time Syst. 53(3), 354–402 (2017). https://doi.org/10.1007/s11241-017-9269-4
Pandey, B., Rintanen, J.: Planning for partial observability by SAT and graph constraints. In: ICAPS, pp. 190–198. AAAI Press (2018)
Pecka, M., Svoboda, T.: Safe exploration techniques for reinforcement learning - an overview. In: Hodicky, J. (ed.) MESAS 2014. LNCS, vol. 8906, pp. 357–375. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-13823-7_31
Pineau, J., Gordon, G., Thrun, S.: Point-based value iteration: an anytime algorithm for POMDPs. In: IJCAI, pp. 1025–1032. Morgan Kaufmann (2003)
Pnueli, A.: The temporal logic of programs. In: FOCS, pp. 46–57. IEEE CS (1977)
Poupart, P., Boutilier, C.: Bounded finite state controllers. In: NIPS, pp. 823–830. MIT Press (2003)
Puterman, M.L.: Markov Decision Processes. Wiley, Hoboken (1994)
Raskin, J., Chatterjee, K., Doyen, L., Henzinger, T.A.: Algorithms for omega-regular games with imperfect information. Log. Methods Comput. Sci. 3(3) (2007)
Shani, G., Pineau, J., Kaplow, R.: A survey of point-based POMDP solvers. Auton. Agent. Multi-Agent Syst. 27(1), 1–51 (2013). https://doi.org/10.1007/s10458-012-9200-2
Silver, D., Veness, J.: Monte-Carlo planning in large POMDPs. In: NIPS, pp. 2164–2172 (2010)
Smith, T., Simmons, R.: Heuristic search value iteration for POMDPs (2004)
Svorenová, M., et al.: Temporal logic motion planning using POMDPs with parity objectives: case study paper. In: HSCC, pp. 233–238. ACM (2015)
Thrun, S., Burgard, W., Fox, D.: Probabilistic Robotics. The MIT Press, Cambridge (2005)
Turchetta, M., Berkenkamp, F., Krause, A.: Safe exploration for interactive machine learning. In: NeurIPS, pp. 2887–2897 (2019)
Walraven, E., Spaan, M.T.J.: Accelerated vector pruning for optimal POMDP solvers. In: AAAI, pp. 3672–3678. AAAI Press (2017)
Wang, Y., Chaudhuri, S., Kavraki, L.E.: Bounded policy synthesis for POMDPs with safe-reachability objectives. In: AAMAS, pp. 238–246. IFAAMAS (2018)
Wierstra, D., Foerster, A., Peters, J., Schmidhuber, J.: Solving deep memory POMDPs with recurrent policy gradients. In: de Sá, J.M., Alexandre, L.A., Duch, W., Mandic, D. (eds.) ICANN 2007. LNCS, vol. 4668, pp. 697–706. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-74690-4_71
Wimmer, R., Jansen, N., Ábrahám, E., Katoen, J.P., Becker, B.: Minimal counterexamples for linear-time probabilistic verification. Theor. Comput. Sci. 549, 61–100 (2014)
Winterer, L., Wimmer, R., Jansen, N., Becker, B.: Strengthening deterministic policies for POMDPs. In: Lee, R., Jha, S., Mavridou, A., Giannakopoulou, D. (eds.) NFM 2020. LNCS, vol. 12229, pp. 115–132. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-55754-6_7
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2021 The Author(s)
About this paper
Cite this paper
Junges, S., Jansen, N., Seshia, S.A. (2021). Enforcing Almost-Sure Reachability in POMDPs. In: Silva, A., Leino, K.R.M. (eds) Computer Aided Verification. CAV 2021. Lecture Notes in Computer Science(), vol 12760. Springer, Cham. https://doi.org/10.1007/978-3-030-81688-9_28
Download citation
DOI: https://doi.org/10.1007/978-3-030-81688-9_28
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-81687-2
Online ISBN: 978-3-030-81688-9
eBook Packages: Computer ScienceComputer Science (R0)