figure a

1 Introduction

Systems with probabilistic uncertainty are ubiquitous, e.g., probabilistic programs, distributed systems, fault trees, and biological models. Markov chains replace nondeterminism in transition systems with probabilistic uncertainty, and probabilistic model checking [4, 7] provides model checking algorithms. A key property that probabilistic model checkers answer is: What is the (precise) probability that a target state is reached (within a finite number of steps h)? Contrary to classical qualitative model checking and approximate variants of probabilistic model checking, precise probabilistic model checking must find the total probability of all paths from the initial state to any target state.

Nevertheless, the prevalent ideas in probabilistic model checking are generalizations of qualitative model checking. Whereas qualitative model checking tracks the states that can reach a target state (or dually, that can be reached from an initial state), probabilistic model checking tracks the i-step reachability probability for each state in the chain. The \(i{+}1\)-step reachability can then be computed via multiplication with the transition matrix. The scalability concern is that this matrix grows with the state space in the Markov chain. Mature model checking tools such as Storm [36], Modest [34], and Prism [51] utilize a variety of methods to alleviate the state space explosion. Nevertheless various natural models cannot be analyzed by the available techniques.

Fig. 1.
figure 1

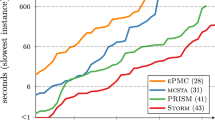
Motivating example. Figure 1(c) compares the performance of Rubicon ( ), Storm’s explicit engine ( ), Storm’s symbolic engine ( ) and Prism ( ) when invoked on a (b) with arbitrarily fixed (different) constants for \(p_i,q_i\) and horizon \(h=10\). Times are in seconds, with a time-out of 30 min.

Full size image

In parallel, within the AI community a different approach to representing a distribution has emerged, which on first glance can seem unintuitive. Rather than marginalizing out the paths and tracking reachability probabilities per state, the probabilistic AI community commonly aggregates all paths that reach the target state. At its core, inference is then a weighted sum over all these paths [16]. This hinges on the observation that this set of paths can often be stored more compactly, and that the probability of two paths that share the same prefix or suffix can be efficiently computed on this concise representation. This inference technique has been used in a variety of domains in the artificial intelligence (AI) and verification communities [9, 14, 27, 39], but is not part of any mature probabilistic model checking tools.

This paper theoretically and experimentally compares and contrasts these two approaches. In particular, we describe and motivate Rubicon, a probabilistic model checker that leverages the successful probabilistic inference techniques. We begin with an example that explains the core ideas of Rubicon followed by the paper structure and key contributions.

Motivating Example. Consider the example illustrated in Fig. 1(a). Suppose there are n factories. Each day, the workers at each factory collectively decide whether or not to strike. To simplify, we model each factory (i) with two states, striking (\(t_i\)) and not striking (\(s_i\)). Furthermore, since no two factories are identical, we take the probability to begin striking (\(p_i\)) and to stop striking (\(q_i\)) to be different for each factory. Assuming that each factory transitions synchronously and in parallel with the others, we query: “what is the probability that all the factories are simultaneously striking within h days?”

Despite its simplicity, we observe that state-of-the-art model checkers like Storm and Prism do not scale beyond 15 factories.Footnote 1 For example, Fig. 1(b) provides a Prism encoding for this simple model (we show the instance with 3 factories), where a Boolean variable \(c_i\) is used to encode the state of each factory. The “allStrike” label identifies the target state. Figure 1(c) shows the run time for an increasing number of factories. While all methods eventually time out, Rubicon scales to systems with an order of magnitude more states.

Why is This Problem Hard? To understand the issue with scalability, observe that tools such as Storm and Prism store the transition matrix, either explicitly or symbolically using algebraic decision diagrams (ADDs). Every distinct entry of this transition matrix needs to be represented; in the case of ADDs using a unique leaf node. Because each factory in our example has a different probability of going on strike, that means each subset of factories will likely have a unique probability of jointly going on strike. Hence, the transition matrix then will have a number of distinct probabilities that is exponential in the number of factories, and its representation as an ADD must blow up in size. Concretely, for 10 factories, the size of the ADD representing the transition matrix has 1.9 million nodes. Moreover, the explicit engine fails due to the dense nature of the underlying transition matrix. We discuss this method in Sect. 3.

How to Overcome This Limitation? This problematic combinatorial explosion is often unnecessary. For the sake of intuition, consider the simple case where the horizon is 1. Still, the standard transition matrix representations blow up exponentially with the number of factories n. Yet, the probability of reaching the “allStrike” state is easy to compute, even when n grows: it is \(p_1 \cdot p_2 \cdots p_n\).

Rubicon aims to compute probabilities in this compact factorized way by representing the computation as a binary decision diagram (BDD). Figure 1(d) gives an example of such a BDD, for three factories and a horizon of one. A key property of this BDD, elaborated in Sect. 3, is that it can be interpreted as a parametric Markov chain, where the weight of each edge corresponds with the probability of a particular factory striking. Then, the probability that the goal state is reached is given by the weighted sum of paths terminating in T: for this instance, there is a single such path with weight \(p_1 \cdot p_2 \cdot p_3\). These BDDs are tree-like Markov-chains, so model checking can be performed in time linear in the size of the BDD using dynamic programming. Essentially, the BDD represents the set of paths that reach a target state—an idea common in probabilistic inference.

To construct this BDD, we propose to encode our reachability query symbolically as a weighted model counting (WMC) query on a logical formula. By compiling that formula into a BDD, we obtain a diagram where computing the query probability can be done efficiently (in the size of the BDD). Concretely for Fig. 1(d), the BDD represents the formula \(c_1^{(1)} \wedge c_2^{(1)} \wedge c_3^{(1)}\), which encodes all paths through the chain that terminate in the goal state (all factories strike on day 1). For this example and this horizon, this is a single path. WMC is a well-known strategy for probabilistic inference and is currently the among the state-of-the-art approaches for discrete graphical models [16], discrete probabilistic programs [39], and probabilistic logic programs [27].

In general, the exponential growth of the number of paths might seem like it dooms this approach: for \(n=3\) factories and horizon \(h=1\), we need to only represent 8 paths, but for \(h=2\), we would need to consider 64 different paths, and so on. However, a key insight is that, for many systems – such as the factory example – the structural compression of BDDs allows a concise representation of exponentially many paths, all while being parametric over path probabilities (see Sect. 4). To see why, observe that in the above discussion, the state of each factory is independent of the other factories: independence, and its natural generalizations like conditional and contextual independence, are the driving force behind many successful probabilistic inference algorithms [47]. Succinctly, the key advantage of Rubicon is that it exploits a form of structure that has thus far been under-exploited by model checkers, which is why it scales to more parallel factories than the existing approaches on the hard task. In Sect. 6 we consider an extension to this motivating example that adds dependencies between factories. This dependency (or rather, the accompanying increase in the size of the underlying MC) significantly decreases scalability for the existing approaches but negligibly affects Rubicon.

This leads to the task: how does one go from a Prism model to a concise BDD efficiently? To do this, Rubicon leverages a novel translation from Prism models into a probabilistic programming language called Dice (outlined in Sect. 5).

Contribution and Structure. Inspired by the example, we contribute conceptual and empirical arguments for leveraging BDD-based probabilistic inference in model checking. Concretely:

  1. 1.

    We demonstrate fundamental advantages in using probabilistic inference on a natural class of models (Sect. 1 and 6).

  2. 2.

    We explain these advantages by showing the fundamental differences between existing model checking approaches and probabilistic inference (Sect. 3 and 4). To that end, Sect. 4 presents probabilistic inference based on an operational and a logical perspective and combines these perspectives.

  3. 3.

    We leverage those insights to build Rubicon, a tool that transpiles Prism to Dice, a probabilistic programming language (Sect. 5).

  4. 4.

    We demonstrate that Rubicon indeed attains an order-of-magnitude scaling improvement on several natural problems including sampling from parametric Markov chains and verifying network protocol stabilization (Sect. 6).

Ultimately we argue that Rubicon makes a valuable contribution to the portfolio of probabilistic model checking backends, and brings to bear the extensive developments on probabilistic inference to well-known model checking problems.

2 Preliminaries and Problem Statement

We state the problem formally and recap relevant concepts. See [7] for details. We sometimes use \(\bar{p}\) to denote \(1 - p\). A Markov chain (MC) is a tuple \(\mathcal {M}= \langle S, \iota , P, T \rangle \) with S a (finite) set of states, \(\iota \in S\) the initial state, \(P:S \rightarrow Distr(S)\) the transition function, and T a set of target states \(T \subseteq S\), where \(Distr(S)\) is the set of distributions over a (finite) set S. We write \(P(s,s')\) to denote \(P(s)(s')\) and call P a transition matrix. The successors of s are \(\mathsf {Succ}(s) = \{s' \mid P(s,s') > 0 \}\). To support MCs with billions of states, we may describe MCs symbolically, e.g., with Prism [51] or as a probabilistic program [42, 48]. For such a symbolic description \(\mathcal {P}\), we denote the corresponding MC with \([\![\, \mathcal {P} \, ]\!]\). States then reflect assignments to symbolic variables.

A path \(\pi = s_0 \ldots s_n\) is a sequence of states, \(\pi \in S^{+}\). We use \(\pi _\downarrow \) to denote the last state \(s_n\), and the length of \(\pi \) above is n and is denoted \(|\pi |\). Let \(\text {Paths}_h\) denote the paths of length h. The probability of a path is the product of the transition probabilities, and may be defined inductively by \(\Pr (s) = 1\), \(\Pr (\pi \cdot s) = \Pr (\pi ) \cdot P(\pi _\downarrow ,s)\). For a fixed horizon h and set of states T, let the set \([\![\, s{\rightarrow }\lozenge ^{\le h} T \, ]\!] = \{ \pi \mid \pi _0 = s \wedge |\pi | \le h \wedge \pi _\downarrow \in T \wedge \forall i < |\pi |.~\pi _i \not \in T\}\) denote paths from s of length at most h that terminate at a state contained in T. Furthermore, let \(\Pr _\mathcal {M}(s \models \lozenge ^{\le h} T) = \sum _{\pi \in [\![\, s{\rightarrow }\lozenge ^{\le h} T \, ]\!]} \Pr (\pi )\) describe the probability to reach T within h steps. We simplify notation when \(s = \iota \) and write \([\![\, \lozenge ^{\le h} T \, ]\!]\) and \(\Pr _\mathcal {M}(\lozenge ^{\le h} T)\), respectively. We omit \(\mathcal {M}\) whenever that is clear from the context.

Fig. 2.
figure 2

(a) MC toy example (b) (distinct) pMC toy example (c) ADD transition matrix

Full size image

Formal Problem: Given an MC \(\mathcal {M}\) and a horizon h, compute \(\Pr _\mathcal {M}(\lozenge ^{\le h} T)\).

Example 1

For conciseness, we introduce a toy example MC \(\mathcal {M}\) in Fig. 2(a). For horizon \(h=3\), there are three paths that reach state \(\langle 1{,}0 \rangle \): For example the path \(\langle 0,0 \rangle \langle 0,1 \rangle \langle 1,0 \rangle \) with corresponding reachability probability \(0.4 \cdot 0.5\). The reachability probability \(\Pr _\mathcal {M}(\lozenge ^{\le 3} \{ \langle 1,0 \rangle \}) = 0.42\).

It is helpful to separate the topology and the probabilities. We do this by means of a parametric MC (pMC) [22]. A pMC over a fixed set of parameters \(\mathbf {p}\) generalises MCs by allowing for a transition function that maps to \(\mathbb {Q}[\mathbf {p}]\), i.e., to polynomials over these variables [22]. A pMC and a valuation of parameters \(\mathbf {u}:\mathbf {p} \rightarrow \mathbb {R}\) describe a MC by replacing \(\mathbf {p}\) with \(\mathbf {u}\) in the transition function P to obtain \(P[\mathbf {u}]\). If \(P[\mathbf {u}](s)\) is a distribution for every s, then we call \(\mathbf {u}\) a well-defined valuation. We can then think about a pMC \(\mathcal {M}\) as a generator of a set of MCs \(\{ \mathcal {M}[\mathbf {u}] \mid \mathbf {u} \text { well-defined} \}\). Figure 2(b) shows a pMC; any valuation \(\mathbf {u}\) with \(\mathbf {u}(p), \mathbf {u}(q) \in [0,1]\) is well-defined. We consider the following associated problem:

Parameter Sampling: Given a pMC \(\mathcal {M}\), a finite set of well-defined valuations U, and a horizon h, compute \(\Pr _{\mathcal {M}[\mathbf {u}]}(\lozenge ^{\le h} T)\) for each \(\mathbf {u} \in U\).

We recap binary decision diagrams (BDDs) and their generalization into algebraic decision diagrams (ADDs, a.k.a. multi-terminal BDDs). ADDs over a set of variables X are directed acyclic graphs whose vertices V can be partitioned into terminal nodes \(V_t\) without successors and inner nodes \(V_i\) with two successors. Each terminal node is labeled with a polynomial over some parameters \(\mathbf {p}\) (or just to constants in \(\mathbb {Q}\)), \(\mathsf {val}:V_t \rightarrow \mathbb {Q}[\mathbf {p}]\), and each inner node \(V_i\) with a variable, \(\mathsf {var}:V_i \rightarrow X\). One node is the root node \(v_0\). Edges are described by the two successor functions \(E_0:V_i \rightarrow V\) and \(E_1:V_i \rightarrow V\). A BDD is an ADD with exactly two terminals labeled T and F. Formally, we denote an ADD by the tuple \(\langle V, v_0, X, \mathsf {var}, \mathsf {val}, E_0, E_1 \rangle \). ADDs describe functions \(f:\mathbb {B}^{X} \rightarrow \mathbb {Q}[\mathbf {p}]\) (described by a path in the underlying graph and the label of the corresponding terminal node). As finite sets can be encoded with bit vectors, ADDs represent functions from (tuples of) finite sets to polynomials.

Example 2

The transition matrix P of the MC in Fig. 2(a) maps states, encoded by bit vectors, \(\langle x, y \rangle , \langle x', y' \rangle \) to the probabilities to move from state \(\langle x, y \rangle \) to \(\langle x', y' \rangle \). Figure 2(c) shows the corresponding ADD.Footnote 2

3 A Model Checking Perspective

We briefly analyze the de-facto standard approach to symbolic probabilistic model checking of finite-horizon reachability probabilities. It is an adaptation of qualitative model checking, in which we track the (backward) reachable states. This set can be thought of as a mapping from states to a Boolean indicating whether a target state can be reached. We generalize the mapping to a function that maps every state s to the probability that we reach T within i steps, denoted \(\Pr _\mathcal {M}(s \models \lozenge ^{\le i} T)\). First, it is convenient to construct a transition relation in which the target states have been made absorbing, i.e., we define a matrix with \(A(s,s') = P(s,s')\) if \(s \not \in T\) and \(A(s,s') = [s = s']\)Footnote 3 otherwise. The following Bellman equations characterize that aforementioned mapping:

$$\begin{aligned} \Pr _\mathcal {M}\big (s \models \lozenge ^{\le 0} T\big )&= [s \in T],\\ \Pr _\mathcal {M}\big (s \models \lozenge ^{\le i} T\big )&= \sum _{s' \in \mathsf {Succ}(s)} \!A(s,s') \cdot \Pr _\mathcal {M}(s' \models \lozenge ^{\le i-1} T) \qquad \text { with i>0}.\end{aligned}$$

The main aspect model checkers take from these equations is that to compute the h-step reachability from state s, one only needs to combine the \(h{-}1\)-step reachability from any state \(s'\) and the transition probabilities \(P(s,s')\). We define a vector \(\mathbf {T}\) with \(\mathbf {T}(s) = [s \in T]\). The algorithm then iteratively computes and stores the i step reachability for \(i = 0\) to \(i = h\), e.g. by computing \(A^3\cdot \mathbf {T}\) using \(A \cdot (A\cdot (A \cdot \mathbf {T}))\). This reasoning is thus inherently backwards and implicitly marginalizing out paths. In particular, rather than storing the i-step paths that lead to the target, one only stores a vector \(\mathbf {x} = A^i \cdot \mathbf {T}\) that stores for every state s the sum over all i-long paths from s.

Explicit representations of matrix A and vector \(\mathbf {x}\) require memory at least in the order |S|.Footnote 4 To overcome this limitation, symbolic probabilistic model checking stores both A and \(A^i \cdot \mathbf {T}\) as an ADD by considering the matrix as a function from a tuple \(\langle s,s' \rangle \) to \(A(s,s')\), and \(\mathbf {x}\) as a function from s to \(\mathbf {x}(s)\) [2].

Fig. 3.
figure 3

Bounded reachability and symbolic model checking for the MC \(\mathcal {M}\) in Fig. 2(a).

Full size image

Example 3

Reconsider the MC in Fig. 2(a). The h-bounded reachability probability \(\Pr _\mathcal {M}(\lozenge ^{\le h} \{\langle 1,0 \rangle \})\) can be computed as reflected in Fig. 3(a). The ADD for P is shown in Fig. 2(c). The ADD for \(\mathbf {x}\) when \(h=2\) is shown in Fig. 3(b).

The performance of symbolic probabilistic model checking is directly governed by the sizes of these two ADDs. The size of an ADD is bounded from below by the number of leafs. In qualitative model checking, both ADDs are in fact BDDs, with two leafs. However, for the ADD representing A, this lower bound is given by the number of different probabilities in the transition matrix. In the running example, we have seen that a small program \(\mathcal {P}\) may have an underlying MC \([\![\, \mathcal {P} \, ]\!]\) with an exponential state space S and equally many different transition probabilities. Symbolic probabilistic model checking also scales badly on some models where A has a concise encoding but \(\mathbf {x}\) has too many different entries.Footnote 5 Therefore, model checkers may store \(\mathbf {x}\) partially explicit [49].

Fig. 4.
figure 4

The computation tree for \(\mathcal {M}\) and horizon 3 and its compression. We label states as \(s{=}\langle 0{,}0\rangle \), \(t{=}\langle 0{,}1 \rangle \), \(u{=}\langle 1{,}0\rangle ,v{=}\langle 1{,}1 \rangle \). Probabilities are omitted for conciseness.

Full size image

The insights above are not new. Symbolic probabilistic model checking has advanced [46] to create small representations of both A and \(\mathbf {x}\). In competitions, Storm often applies a bisimulation-to-explicit method that extracts an explicit representation of the bisimulation quotient [26, 36]. Finally, game-based abstraction [32, 44] can be seen as a predicate abstraction technique on the ADD level. However, these methods do not change the computation of the finite horizon reachability probabilities and thus do not overcome the inherent weaknesses of the iterative approach in combination with an ADD-based representation.

4 A Probabilistic Inference Perspective

We present four key insights into probabilistic inference. (1) Sect. 4.1 shows how probabilistic inference takes the classical definition as summing over the set of paths, and turns this definition into an algorithm. In particular, these paths may be stored in a computation tree. (2) Sect. 4.2 gives the traditional reduction from probabilistic inference to the classical weighted model counting (\(\mathsf {WMC}\)) problem [16, 57]. (3) Sect. 4.3 connects this reduction to point (1) by showing that a BDD that represents this \(\mathsf {WMC}\) is bisimilar to the computation tree assuming that the out-degree of every state in the MC is two. (4) Sect. 4.4 describes and compares the computational benefits of the BDD representation. In particular, we clarify that enforcing an out-degree of two is a key ingredient to overcoming one of the weaknesses of symbolic probabilistic model checking: the number of different probabilities in the underlying MC.

4.1 Operational Perspective

The following perspective frames (an aspect of) probabilistic inference as a model transformation. By definition, the set of all paths – each annotated with the transition probabilities – suffices to extract the reachability probability. These sets of paths may be represented in the computation tree (which is itself an MC).

Example 4

We continue from Example 1. We put all paths of length three in a computation tree in Fig. 4(a) (cf. the caption for state identifiers). The three paths that reach the target are highlighted in red. The MC is highly redundant. We may compress to the MC in Fig. 4(b).

Definition 1

For MC \(\mathcal {M}\) and horizon h, the computation tree (CT) \(\mathsf {CT}(\mathcal {M},h) = \langle \text {Paths}_h, \iota , P', T' \rangle \) is an MC with states corresponding to paths in \(\mathcal {M}\), i.e., \(\text {Paths}_h^\mathcal {M}\), initial state \(\iota \), target states \(T'= [\![\, \lozenge ^{\le h} T \, ]\!]\), and transition relation

(1)

The CT contains (up to renaming) the same paths to the target as the original MC. Notice that after h transitions, all paths are in a sink state, and thus we can drop the step bound from the property and consider either finite or indefinite horizons. The latter considers all paths that eventually reach the target. We denote the probability mass of these paths with \(\Pr _\mathcal {M}(s \models \lozenge T)\) and refer to [7] for formal details.Footnote 6 Then, we may compute bounded reachability probabilities in the original MC by analysing unbounded reachability in the CT:

\(\Pr _\mathcal {M}(\lozenge ^{\le h} T) = \Pr _{\mathsf {CT}(\mathcal {M},h)}(\lozenge ^{\le h} T') = \Pr _{\mathsf {CT}(\mathcal {M},h)}(\lozenge T').\)

The nodes in the CT have a natural topological ordering. The unbounded reachability probability is then computed (efficiently in CT’s size) using dynamic programming (i.e., topological value iteration) on the Bellman equation for \(s \not \in T\):

\(\Pr _\mathcal {M}(s \models \lozenge T) = \sum _{s' \in \mathsf {Succ}(s)} P(s,s') \cdot \Pr _\mathcal {M}(s' \models \lozenge T).\)

For pMCs, the right-hand side naturally is a factorised form of the solution function f that maps parameter values to the induced reachability probability, i.e. \(f(\mathbf {u}) = \Pr _{\mathcal {M}[\mathbf {u]}}(\lozenge ^{\le h}T)\) [22, 24, 33]. For bounded reachability (or acyclic pMCs), this function amounts to a sum over all paths with every path reflected by a term of a polynomial, i.e., the sum is a polynomial. In sum-of-terms representation, the polynomial can be exponential in the number of parameters [5].

For computational efficiency, we need a smaller representation of the CT. As we only consider reachability of T, we may simplify [43] the notion of (weak) bisimulation [6] (in the formulation of [40]) to the following definition.

Definition 2

For \(\mathcal {M}\) with states S, a relation \(\mathcal {R} \subseteq S \times S\) is a (weak) bisimulation (with respect to T) if \(s \mathcal {R} s'\) implies \(\Pr _{\mathcal {M}}(s \models \lozenge T) = \Pr _{\mathcal {M}}(s' \models \lozenge T)\). Two states \(s, s'\) are (weakly) bisimilar (with respect to T) if \(\Pr _{\mathcal {M}}(s \models \lozenge T) = \Pr _{\mathcal {M}}(s' \models \lozenge T)\)

Two MCs \(\mathcal {M}, \mathcal {M}'\) are bisimilar, denoted \(\mathcal {M}\sim \mathcal {M}'\) if the initial states are bisimilar in the disjoint union of the MCs. It holds by definition that if \(\mathcal {M}\sim \mathcal {M}'\), then \(\Pr _\mathcal {M}(\lozenge T) = \Pr _{\mathcal {M}'}(\lozenge T')\). The notion of bisimulation can be lifted to pMCs [33].

Idea 1: Given a symbolic description \(\mathcal {P}\) of a MC \([\![\, \mathcal {P} \, ]\!]\), efficiently construct a concise MC \(\mathcal {M}\) that is bisimilar to \(\mathsf {CT}([\![\, \mathcal {P} \, ]\!],h)\).

Indeed, the (compressed) CT in Fig. 4(b) and Fig. 4(a) are bisimilar. We remark that we do not necessarily compute the bisimulation quotient of \(\mathsf {CT}([\![\, \mathcal {P} \, ]\!],h)\).

4.2 Logical Perspective

The previous section defined weakly bisimilar chains and showed computational advantages, but did not present an algorithm. In this section we frame the finite horizon reachability probability as a logical query known as weighted model counting \((\mathsf {WMC})\). In the next section we will show how this logical perspective yields an algorithm for constructing bisimilar MCs.

Weighted model counting is well-known as an effective reduction for probabilistic inference [16, 57]. Let \(\varphi \) be a logical sentence over variables C. The weight function \(W_C :C \rightarrow \mathbb {R}_{\ge 0}\) assigns a weight to each logical variable. A total variable assignment \(\eta :C \rightarrow \{ 0, 1 \}\) by definition has weight \(\mathsf {weight}(\eta ) = \prod _{c \in C} W_C(c) \eta (c) + (1-W_C(c)) \cdot (1-\eta (c))\). Then the weighted model count for \(\varphi \) given W is \(\mathsf {WMC}(\varphi ,W_C) = \sum _{\eta \models \varphi } \mathsf {weight}(\eta )\). Formally, we desire to compute a reachability query using a \(\mathsf {WMC}\) query in the following sense:

Idea 2: Given an MC \(\mathcal {M}\), efficiently construct a predicate \(\varphi _{\mathcal {M}, h}^C\) and a weight-function \(W_C\) such that \(\Pr _\mathcal {M}(\lozenge ^{\le h} T) = \mathsf {WMC}(\varphi _{\mathcal {M},h}^C, W_C)\).

Consider initially the simplified case when the MC \(\mathcal {M}\) is binary: every state has at most two successors. In this case producing \((\varphi _{\mathcal {M}, h}^C, W_C)\) is straightforward:

Example 5

Consider the MC in Fig. 2(a), and note that it is binary. We introduce logical variables called state/step coins \(C= \{ c_{s,i} \mid s \in S, i < h \}\) for every state and step. Assignments to these coins denote choices of transitions at particular times: if the chain is in state s at step i, then it takes the transition to the lexicographically first successor of s if \(c_{s,i}\) is true and otherwise takes the transition to the lexicographically second successor. To construct the predicate \(\varphi _{\mathcal {M}, 3}^C\), we will need to write a logical sentence on coins whose models encode accepting paths (red paths) in the CT in Fig. 4(a).

We start in state \(s=\langle 0,0 \rangle \) (using state labels from the caption of Fig. 4). We order states as \(s = \langle 0,0 \rangle< t = \langle 0,1 \rangle< u = \langle 1, 0 \rangle < v = \langle 1,1 \rangle \). Then, \(c_{s,0}\) is true if the chain transitions into state s at time 0 and false if it transitions to state t at time 0. So, one path from s to the target node \(\langle 1,0 \rangle \) is given by the logical sentence \((c_{s,0} \wedge \lnot c_{s,1} \wedge c_{t,2})\). The full predicate \(\varphi ^C_{\mathcal {M},3}\) is therefore:

$$ \varphi ^C_{\mathcal {M},3} = (c_{s,0} \wedge \lnot c_{s,1} \wedge c_{t,2}) \vee (\lnot c_{s,0} \wedge c_{t, 1} ) \vee (\lnot c_{s,0} \wedge \lnot c_{t, 1} \wedge c_{v, 2}). $$

Each model of this sentence is a single path to the target. This predicate \(\varphi ^C_{\mathcal {M},h}\) can clearly be constructed by considering all possible paths through the chain, but later on we will show how to build it more efficiently.

Finally, we fix \(W_C\): The weight for each coin is directly given by the transition probability to the lexicographically first successor: for \(0 \le i < h\), \(W_C(c_{s,i}) = 0.6\) and \(W_C(c_{t,i}) = W_C(c_{v,i}) = 0.5\). The \(\mathsf {WMC}\) is indeed 0.42, reflecting Example 1.

When the MC is not binary, it suffices to limit the out-degree of an MC to be at most two by adding auxiliary states, hence binarizing all transitions, cf. [38].

4.3 Connecting the Operational and the Logical Perspective

Now that we have reduced bounded reachability to weighted model counting, we reach a natural question: how do we perform \(\mathsf {WMC}\)?Footnote 7 Various approaches to performing \(\mathsf {WMC}\) have been explored; a prominent approach is to compile the logical function into a binary decision diagram (BDD), which supports fast weighted model counting [21]. In this paper, we investigate the use of a BDD-driven approach for two reasons: (i) BDDs admit straightforward support for parametric models. (ii) BDDs provide a direct connection between the logical and operational perspectives. To start, observe that the graph of the BDD, together with the weights, can be interpreted as an MC:

Definition 3

Let \(\varphi ^X\) be a propositional formula over variables X and \({<}_X\) an ordering on X. Let \(\mathsf {BDD}(\varphi ^X, {<}_X) = \langle V, v_0, X, \mathsf {var}, \mathsf {val}, E_0, E_1 \rangle \) be the corresponding BDD, and let W be a weight function on X with \(0 \le W(x) \le 1\). We define the MC \(\mathsf {BDD}_\mathsf {MC}(\varphi ^X, {<}_X, W) = \langle S, \iota , P, T \rangle \) with \(S = V\), \(\iota = v_0\), \(P(s) = \{ E_0(s) \mapsto W(\mathsf {var}(s)), E_1(s) \mapsto 1-W(\mathsf {var}(s)) \}\) and \(T = \{ v \in V \mid \mathsf {val}(v) = 1 \}\).

These BDDs are intimately related to the computation trees discussed before. For a binary MC \(\mathcal {M}\), the tree \(\mathsf {CT}(\mathcal {M},h)\) is binary and can be considered as a (not necessarily reduced) BDD. More formally, let us construct \(\mathsf {BDD}_\mathsf {MC}(\varphi _{\mathcal {M},h}^C, {<}_C, \)). We fix a total order on states. Then we fix state/step coins \(C=\{ c_{s,i} \mid s \in S, i < h \}\) and the weights as in Example 5. Finally, let \({<}_C\) be an order on C such that \(i < j\) implies \(c_{s,i} {<}_Cc_{s,j}\). Then:

$$\begin{aligned} \mathsf {CT}(\mathcal {M},h) \sim \mathsf {BDD}_\mathsf {MC}(\varphi _{\mathcal {M},h}^C, {<}_C, W). \end{aligned}$$
(2)

In the spirit of Idea 1, we thus aim to construct \( \mathsf {BDD}_\mathsf {MC}(\varphi _{\mathcal {M},h}^C, {<}_C, W)\), a representation as outlined in Idea 2, efficiently. Indeed, the BDD (as MC) in Fig. 4(c) is bisimilar to the MC in Fig. 4(b).

Idea 3: Represent a bisimilar version of the computation tree using a BDD.

Fig. 5.
figure 5

Two computation trees for the motivating example in Sect. 1.

Full size image

4.4 The Algorithmic Benefits of BDD Construction

Thus far we have described how to construct a binarized MC bisimilar to the CT. Here, we argue that this construction has algorithmic benefits by filling in two details. First, the binarized representation is an important ingredient for compact BDDs. Second, we show how to choose a variable ordering that ensures that the BDDs grow linearly in the horizon. In sum,

Idea 4: \(\mathsf {WMC}\) encodings of binarized Markov Chains may increase compression of computation trees.

To see the benefits of binarized transitions, we return to the factory example in Sect. 1. Figure 5(a) gives a bisimilar computation tree for the 3-factory \(h=1\) example. However, in this tree, the states are unfactorized: each node in the tree is a joint configuration of factories. This tree has 8 transitions (one for each possible joint state transition) with 8 distinct probabilities. On the other hand, the bisimilar computation tree in Fig. 1(d) has binarized transitions: each node corresponds to a single factory’s state at a particular time-step, and each transition describes an update to only a single factory. This binarization enables the exploitation of new structure: in this case, the independence of the factories leads to smaller BDDs, that is otherwise lost when considering only joint configurations of factories.

Recall that the size of the ADD representation of the transition function is bounded from below by the number of distinct probabilities in the underlying MC: in this case, this is visualized by the number of distinct outgoing edge probabilities from all nodes in the unfactorized computation tree. Thus, a good binarization can have a drastically positive effect on performance. For the running example, rather than \(2^{n}\) different transition probabilities (with n factories), the system now has only \(4\cdot n\) distinct transition probabilities!

Causal Orderings. Next, we explore some of the engineering choices Rubicon makes to exploit the sequential structure in a MC when constructing the BDD for a \(\mathsf {WMC}\) query. First, note that the transition matrix \(P(s, s')\) implicitly encodes a distribution over state transition functions, \(S \rightarrow S\). To encode P as a BDD, we must encode each transition as a logical variable, similar to the situation in Sect. 4.2. In the case of binary transitions this is again easy. In the case of non-binary transitions, we again introduce additional logical variables [16, 27, 39, 57]. This logical function has the following form:

$$\begin{aligned} f_P :\{0, 1\}^{C} \rightarrow (S \rightarrow S). \end{aligned}$$
(3)

Whereas the computation tree follows a fixed (temporal) order of states, BDDs can represent the same function (and the same weighted model count) using an arbitrary order. Note that the BDD’s size and structure drastically depends both on the construction of the propositional formula and the order of the variables in that encoding. We can bound the size of the BDD by enforcing a variable order based on the temporal structure of the original MC. Specifically, given h coin collections \(\mathbf {C} = C \times \ldots \times C\), one can generate a function f describing the h-length paths via repeated applications of \(f_P\):

$$\begin{aligned} {\begin{matrix}&f :\{0, 1\}^{\mathbf {C}} \rightarrow \text {Paths}_h\quad f(C_1, \ldots , C_h) = \bigg ( f_P(C_h)\circ \ldots \circ f_P(C_1)\bigg )(\iota ) \end{matrix}} \end{aligned}$$
(4)

Let \(\psi \) denote an indicator for the reachability property as a function over paths, \(\psi :\text {Paths}_h\rightarrow \{0, 1\}\) with \(\psi (\pi )= [ \pi \in [\![\, \lozenge ^{\le h} T \, ]\!]]\). We call predicates formed by composition with \(f_P\), i.e., \(\varphi = \psi \circ f_P\), causal encodings and orderings on \(c_{i, t} \in \mathbf {C}\) that are lexicographically sorted in time, \(t_1< t_2 \implies c_{i, t_1} < c_{j, t_2}\), causal orderings. Importantly, causally ordered / encoded BDDs grow linearly in horizon h, [61, Corollary 1]. More precisely, let \(\varphi _{\mathcal {M},h}^{\mathbf {C}}\) be causally encoded where \(|\mathbf {C}| = h\cdot m\). The causally ordered BDD for \(\varphi _{\mathcal {M},h}^{\mathbf {C}}\) has at most \(h\cdot |S\times S_\psi | \cdot m\cdot 2^{m}\) nodes, where \(|S_\psi | = 2\) for reachability properties.Footnote 8 However, while the worst-case growth is linear in the horizon, constructing that BDD may induce a super-linear cost in the size, e.g., function composition using BDDs is super-linear!

Figure 5(b) shows the motivating factory example with 2 factories and \(h=2\). The variables are causally ordered: the factories in time step 1 occur before the factories in time step 2. For n factories, a fixed number f(n) of nodes are added to the BDD upon each iteration, guaranteeing growth on the order \(\mathcal {O}(f(n)\cdot h)\). Note the factorization that occurs: the BDD has node sharing (node \(c_2^{(2)}\) is reused) that yields additional computational benefits.

Summary and Remaining Steps. The operational view highlights that we want to compute a transformation of the original input MC \(\mathcal {M}\). The logical view presents an approach to do so efficiently: By computing a BDD that stores a predicate describing all paths that reach the target, and interpreting and evaluating the (graph of the) BDD as an MC. In the following section, we discuss the two steps that we follow to create the BDD: (i) From \(\mathcal {P}\) generate \(\mathcal {P}'\) such that \(\mathsf {CT}([\![\, \mathcal {P} \, ]\!],h) \sim [\![\, \mathcal {P}' \, ]\!]\). (ii) From \(\mathcal {P}'\) generate \(\mathcal {M}\) such that \(\mathcal {M}= [\![\, \mathcal {P}' \, ]\!]\).

5 Rubicon

We present Rubicon which follows the two steps outlined above. For exposition, we first describe a translation of monolithic Prism programs to Dice programs and then extend this translation to admit modular programs. Technical steps and extensions are deferred to [38, Appendix].

Dice Preliminaries. We give a brief description of Dice, a probabilistic programming language (PPL) introduced in [39]. A PPL is a programming language augmented with a primitive notion of random choice: for instance, in Dice, a Bernoulli random variable is introduced by the syntax flip 0.5. The syntax of Dice is similar to the programming language OCaml: local variables are introduced by the syntax , where e\(_1\) and e\(_2\) are expressions, i.e., sub-programs. Dice supports procedures, bounded integers, bounded loops, and standard control flow via if-statements.

Fig. 6.
figure 6

From Prism to Dice using Rubicon.

Full size image

One goal of a PPL is to perform probabilistic inference: compute the probability that the program returns a particular value. Inference on the tiny Dice program let x = flip 0.1 in x would yield that true is returned with probability 0.1. The Dice compiler performs probabilistic inference via weighted model counting and BDD compilation. In doing so, it accomplishes the non-trivial tasks of: (i) choosing a logical encoding for probabilistic programs (ii) establishing good variable orderings (iii) efficiently manipulating and constructing BDDs (iv) performing WMC . For details, we refer the reader to [39].

Rubicon uses Dice to effectively construct a BDD and perform WMC on a Dice program that reflects a description of some computation tree. This implementation exploits the structure that was described in Sect. 4.4: in particular, the BDD generated in Fig. 5(b) is exactly the BDD that will be generated by Dice from the output of Rubicon. The variable ordering used by Dice is given by the order in which program variables are introduced, and Rubicon’s translation was designed with this variable ordering in mind.

Transpiling Prism to Dice. We present the core translation routine implemented in Rubicon. We note that the ultimate performance of Rubicon is heavily dependent on the quality of this translation. We evaluate the performance in the next section.

The Prism specification language consists of one or more reactive modules (or partially synchronized state machines) that may interact with each other. Our example in Fig. 1(b) illustrates fully synchronized state machines. While Prism programs containing multiple modules can be flattened into a single monolithic program, this yields an exponential blow-up: If one flattens the n modules in Fig. 1(b) to a single module, the resulting program has \(2^n\) updates per command. This motivates our direct translation of PRISM programs containing multiple modules.

Monolithic Prism Programs. We explain most ideas on Prism programs that consist of a single “monolithic” module before we address the modular translation at the end of the subsection. A module has a set of bounded variables, and the valuations of these variables span the state space of the underlying MC. Its transitions are described by guarded commands of the form:

$$\begin{aligned}{{[}{} \texttt {act}]\ \ {\mathtt {guard}} \ \ \rightarrow \ \ p_1 : {\texttt {update}}_1 + \ldots \ldots + p_n : {\texttt {update}}_n}\end{aligned}$$

The action name act is only relevant in the modular case and can be ignored for now. The guard is a Boolean expression over the module’s variables. If the guard evaluates to \(\texttt {true}\) for some state (a valuation), then the module evolves into one of the n successor states by updating its variables. An update is chosen according to the probability distribution given by the expressions \(p_1, \ldots , p_n\). In every state enabling the guard, the evaluation of \(p_1,\ldots ,p_n\) must sum up to one. A set of guards overlap if they all evaluate to \(\texttt {true}\) on a given state. The semantics of overlapping guards in the monolithic setting is to first uniformly select an active guard and then apply the corresponding stochastic transition. Finally, a self-loop is implicitly added to states without an enabled guard.

Example 6

We present our translation primarily through example. In Fig. 6(a), we give a Prism program for a MC. The program contains two variables x and y, where x is either zero or one, and y between zero and two. There are thus 6 different states. We denote states as tuples with the x- and y-value. We depict the MC in Fig. 6(b). From state \(\langle 0, 0 \rangle \), (only) the first guard is enabled and thus there are two transitions, each with probability a half: one in which x becomes one and one in which y is increased by one. Finally, there is no guard enabled in state \(\langle 1, 1 \rangle \), resulting in an implicit self-loop.

Translation. All Dice programs consist of two parts: a main routine, which is run by default when the program starts, and function declarations that declare auxiliary functions. We first define the auxiliary functions. For simplicity let us temporarily assume that no guards overlap and that probabilities are constants, i.e., not state-dependent.

The main idea in the translation is to construct a Dice function step that, given the current state, outputs the next state. Because a monolithic Prism program is almost a sequential program, in its most basic version, the step function is straightforward to construct using built-in Dice language primitives: we simply build a large if-else block corresponding to each command. This block iteratively considers each command’s guard until it finds one that is satisfied. To perform the corresponding update we flip a coin – based on the probabilities corresponding to the updates – to determine which update to perform. If no command is enabled, we return the same state in accordance with the implicit self-loop. Figure 6(d) shows the program blocks for the Prism program from Fig. 6(a) with target state \([\![\, x=0,y=2 \, ]\!]\). There are two other important auxiliary functions. The init function simply returns the initial state by translating the initialization statements from Prism, and the hit function checks whether the current state is a target state that is obtained from the property.

Now we outline the main routine, given for this example in Fig. 6(c). This function first initializes the state. Then, it calls step 2 times, checking on each iteration using hit if the target state is reached. Finally, we return whether we have been in a target state. The probability to return true corresponds to the reachability probability on the underlying MC specified by the Prism program.

Fig. 7.
figure 7

Prism program with overlapping guards and its translation (conceptually).

Full size image
Fig. 8.
figure 8

Modular Prism and resulting Dice step function.

Full size image

Overlapping Guards. Prism allows multiple commands to be enabled in the same state, with semantics to uniformly at random choose one of the enabled commands to evaluate. Dice has no primitive notion of this construct.Footnote 9 We illustrate the translation in Fig. 7(a) and Fig. 7(b). It determines which guards aEn, bEn, cEn are enabled. Then, we randomly select one of the commands which are enabled, i.e., we uniformly at random select a true bit from a given tuple of bits. We store the index of that bit and use it to execute the corresponding command.

Modular Prism Programs. For modular Prism programs, the action names at the front of Prism commands are important. In each module, there is a set of action names available. An action is enabled if each module that contains this action name has (at least) one command with this action whose guard is satisfied. Commands with an empty action are assumed to have a globally unique action name, so in that case the action is enabled iff the guard is enabled. Intuitively, once an action is selected, we randomly select a command per module in all modules containing this action name. Our approach resembles that for overlapping guards described above. See Fig. 8 for an intuitive example. To automate this, the updates require more care, cf. [38] for details.

Implementation. Rubicon is implemented on top of Storm’s Python API and translates Prism to Dice fully automatically. Rubicon supports all MCs in the Prism benchmark suite and a large set of benchmarks from the Prism website and the QVBS [35], with the note that we require a single initial state and ignore reward declarations. Furthermore, we currently do not support the hide/restrict process-algebraic compositions and some integer operations.

6 Empirical Comparisons

We compare and contrast the performance of Storm against Rubicon to empirically demonstrate the following strengths and weaknesses:Footnote 10

  • Explicit Model Checking (Storm) represents the MC explicitly in a sparse matrix format. The approach suffers from the state space explosion, but has been engineered to scale to models with many states. Besides the state space, the sparseness of the transition matrix is essential for performance.

  • Symbolic Model Checking (Storm) represents the transition matrix and the reachability probability as an ADD. This method is strongest when the transition matrix and state vector have structure that enables a small ADD representation, like symmetry and sparsity.

  • Rubicon represents the set of paths through the MC as a (logical) BDD. This method excels when the state space has structure that enables a compact BDD representation, such as conditional independence, and hence scales well on examples with many (asymmetric) parallel processes or queries that admit a compact representation.

The sources, benchmarks and binaries are archived.Footnote 11

There is no clear-cut model checking technique that is superior to others (see QCOMP [12]). We demonstrate that, while Rubicon is not competitive on some commonly used benchmarks [52], it improves a modern model checking portfolio approach on a significant set of benchmarks. Below we provide several natural models on which Rubicon is superior to one or both competing methods. We also evaluated Rubicon on standard benchmarks, highlighting that Rubicon is applicable to models from the literature. We see that Rubicon is effective on Herman (elaborated below), has mixed results on BRP [38, Appendix], and is currently not competitive on some other standard benchmarks (NAND, EGL, LeaderSync). While not exhaustive, our selected benchmarks highlight specific strengths and weaknesses of Rubicon. Finally, a particular benefit of Rubicon is fast sampling of parametric chains, which we demonstrate on Herman and our factory example.

Fig. 9.
figure 9

Scaling plots comparing Rubicon ( ), Storm’s symbolic engine ( ), and Storm’s explicit engine ( ). An “(R)” in the caption denotes random parameters.

Full size image

Scaling Experiments. In this section, we describe several scaling experiments (Fig. 9), each designed to highlight a specific strength or weakness.

Weather Factories. First, Fig. 9(a) describes a generalization of the motivating example from Sect. 1. In this model, the probability that each factory is on strike is dependent on a common random event: whether or not it is raining. The rain on each day is dependent on the previous day’s weather. We plot runtime for an increasing number of factories for \(h{=}10\). Both Storm engines eventually fail due to the state explosion and the number of distinct probabilities in the MC. Rubicon is orders of magnitude faster in comparison, highlighting that it does not depend on complete independence among the factories. Figure 9(b) shows a more challenging instance where the weather includes wind which, each day, affects whether or not the sun will shine, which in turn affects strike probability.

Herman. Herman is based on a distributed protocol [37] that has been well-studied [1, 53] and which is one of the standard benchmarks in probabilistic model checking. Rather than computing the expected steps to ‘stabilization’, we consider the step-bounded probability of stabilization. Usually, all participants in the protocol flip a coin with the same bias. The model is then highly symmetric, and hence is amenable to symbolic representation with ADDs. Figures 9(c) and 9(e) show how the methods scale on Herman examples with 13 and 17 parallel processes. We observe that the explicit approach scales very efficiently in the number of iterations but has a much higher up-front model-construction cost, and hence can be slower for fewer iterations.

To study what happens when the coin biases vary over the protocol participants, we made a version of the Herman protocol where each participant’s bias is randomly chosen, which ruins the symmetry and so causes the ADD-based approaches to scale significantly worse (Figs. 9(d) and 9(f), and 9(g)); we see that symbolic ADD-based approaches completely fail on Herman 17 and Herman 19 (the curve terminating denotes a memory error). Rubicon and the explicit approach are unaffected by varying parameters.

Queues. The Queues model has K queues of capacity Q where every step, tasks arrive with a particular probability. Three queues are of type 1, the others of type 2. We ask the probability that all queues of type 1 and at least one queue of type 2 is full within k steps. Contrary to the previous models, the ADD representation of the transition matrix is small. Figure 9(h) shows the relative scaling on this model with \(K=8\) and \(Q=3\). We observe that ADDs quickly fail due to inability to concisely represent the probability vector \(\mathbf {x}\) from Sect. 3. Rubicon outperforms explicit model checking until \(h=10\).

Sampling Parametric Markov Chains. We evaluate performance for the pMC sampling problem outlined in Sect. 2. Table 1 gives for four models the time to construct the BDD and to perform WMC, as well as the time to construct an ADD in Storm and to perform model checking with this ADD. Finally, we show the time for Storm to compute the solution function of the pMC (with the explicit representation). The pMC sampling in Storm – symbolic and explicit – computes the reachability probabilities with concrete probabilities. Rubicon, in contrast, constructs a ‘parametric’ BDD once, amortizing the cost of repeated efficient evaluation. The ‘parametric BDD’ may be thought of as a solution function, as discussed in Sect. 4.1. Storm cannot compute these solution functions as efficiently. We observe in Table 1 that fast parametric sampling is realized in Rubicon: for instance, after a 40s up-front compilation of the factories example with 15 factories, we have a solution function in factorized form and it costs an order of magnitude less time to draw a sample. Hence, sampling and computation of solution functions of pMCs is a major strength of Rubicon.

Table 1. Sampling performance comparison and pMC model checking, time in seconds.
Full size table

7 Discussion, Related Work, and Conclusion

We have demonstrated that the probabilistic inference approach to probabilistic model checking can improve scalability on an important class of problems. Another benefit of the approach is for sampling pMCs. These are used to evaluate e.g., robustness of systems [1], or to synthesise POMDP controllers [41]. Many state-of-the-art approaches [17, 19, 24] require the evaluation of various instantiated MCs, and Rubicon is well-suited to this setting. More generally, support of inference techniques opens the door to a variety of algorithms for additional queries, e.g., computing conditional probabilities [3, 8].

An important limitation of probabilistic inference is that only finitely many paths can be stored. For infinite horizon properties in cyclic models, an infinite set of arbitrarily long paths would be required. However, as standard in probabilistic model checking, we may soundly approximate infinite horizons. Additionally, the inference algorithm in Dice does not support a notion of non-determinism. It thus can only be used to evaluate MCs, not Markov decision processes. However, [61] illustrates that this is not a conceptual limitation. Finally, we remark that Rubicon achieves its performance with a straightforward translation. We are optimistic that this is a first step towards supporting a larger class of models by improving the transpilation process for specific problems.

Related Work. The tight connection with inference has been recently investigated via the use of model checking for Bayesian networks, the prime model in probabilistic inference [56]. Bayesian networks can be described as probabilistic programs [10] and their operational semantics coincides with MCs [31]. Our work complements these insights by studying how symbolic model checking can be sped up by probabilistic inference.

The path-based perspective is tightly connected to factored state spaces. Factored state spaces are often represented as (bipartite) Dynamic Bayesian networks. ADD-based model checking for DBNs has been investigated in [25], with mixed results. Their investigation focuses on using ADDs for factored state space representations. We investigate using BDDs representing paths. Other approaches also investigated a path-based view: The symbolic encoding in [28] annotates propositional sub-formulae with probabilities, an idea closer to ours. The underlying process implicitly constructs an (uncompressed) CT leading to an exponential blow-up. Likewise, an explicit construction of a computation tree without factorization is considered in [62]. Compression by grouping paths has been investigated in two approximate approaches: [55] discretises probabilities and encodes into a satisfiability problem with quantifiers and bit-vectors. This idea has been extended [60] to a PAC algorithm by purely propositional encodings and (approximate) model counting [14]. Finally, factorisation exploits symmetries, which can be exploited using symmetry reduction [50]. We highlight that the latter is not applicable to the example in Fig. 1(d).

There are many techniques for exact probabilistic inference in various forms of probabilistic modeling, including probabilistic graphical models [20, 54]. The semantics of graphical models make it difficult to transpile Prism programs, since commonly used operations are lacking. Recently, probabilistic programming languages have been developed which are more amenable to transpilation [13, 23, 29, 30, 59]. We target Dice due to the technical development that it enables in Sect. 4, which enabled us to design and explain our experiments. Closest related to Dice is ProbLog [27], which is also a PPL that performs inference via WMC; ProbLog has different semantics from Dice that make the translation less straightforward. The paper [61] uses an encoding similar to Dice for inferring specifications based on observed traces. ADDs and variants have been considered for probabilistic inference [15, 18, 58], which is similar to the process commonly used for probabilistic model checking. The planning community has developed their own disjoint sets of methods [45]. Some ideas from learning have been applied in a model checking context [11].

8 Conclusion

We present Rubicon, bringing probabilistic AI to the probabilistic model checking community. Our results show that Rubicon can outperform probabilistic model checkers on some interesting examples, and that this is not a coincidence but rather the result of a significantly different perspective.