Abstract
We pursue the vision of an ideal language framework, where programming language designers only need to define the formal syntax and semantics of their languages, and all language tools are automatically generated by the framework. Due to the complexity of such a language framework, it is a big challenge to ensure its trustworthiness and to establish the correctness of the autogenerated language tools. In this paper, we propose an innovative approach based on proof generation. The key idea is to generate proof objects as correctness certificates for each individual task that the language tools conduct, on a case-by-case basis, and use a trustworthy proof checker to check the proof objects. This way, we avoid formally verifying the entire framework, which is practically impossible, and thus can make the language framework both practical and trustworthy. As a first step, we formalize program execution as mathematical proofs and generate their complete proof objects. The experimental result shows that the performance of our proof object generation and proof checking is very promising.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords

1 Introduction
Unlike natural languages that allow vagueness and ambiguity, programming languages must be precise and unambiguous. Only with rigorous definitions of programming languages, called the formal semantics, can we guarantee the reliability, safety, and security of computing systems.
Our vision is thus an ideal language framework based on the formal semantics of programming languages. Shown in Fig. 1, an ideal language framework is one where language designers only need to define the formal syntax and semantics of their language, and all language tools are automatically generated by the framework. The correctness of these language tools is established by generating complete mathematical proofs as certificates that can be automatically machine-checked by a trustworthy proof checker.
The \(\mathbb {K}\) language framework (https://kframework.org) is in pursuit of the above ideal vision. It provides a simple and intuitive front end language (i.e., a meta-language) for language designers to define the formal syntax and semantics of other programming languages. From such a formal language definition, the framework automatically generates a set of language tools, including a parser, an interpreter, a deductive verifier, a program equivalence checker, among many others [9, 24]. \(\mathbb {K}\) has obtained much success in practice, and has been used to define the complete executable formal semantics of many real-world languages, such as C [12], Java [2], JavaScript [21], Python [13], Ethereum virtual machines byte code [15], and x86-64 [10], from which their implementations and formal analysis tools are automatically generated. Some commercial products [14, 18] are powered by these autogenerated implementations and/or tools.
What is missing in \(\mathbb {K}\) (compared to the ideal vision in Fig. 1) is its ability to generate proof objects as correctness certificates. The current \(\mathbb {K}\) implementation is a complex artifact with over 500,000 lines of code written in 4 programming languages, with new code committed on a weekly basis. Its code base includes complex data structures, algorithms, optimizations, and heuristics to support the various features such as defining formal language syntax using BNF grammar, defining computation configurations as constructor terms, defining formal semantics using rewrite rules, specifying arbitrary evaluation strategies, and defining the binding behaviors of binders (Sect. 3). The large code base and rich features make it challenging to formally verify the correctness of \(\mathbb {K}\).
Our main contribution is the proposal of a practical approach to establishing the correctness of a complex language framework, such as \(\mathbb {K}\), via proof object generation. Our approach consists of the following main components:
-
1.
A small logical foundation of \(\mathbb {K}\);
-
2.
Proof parameters that are provided by \(\mathbb {K}\) as the hints for proof generation;
-
3.
A proof object generator that generates proof objects from proof parameters;
-
4.
A fast and trustworthy third-party proof checker that verifies proof objects.
The key idea that makes our approach practical is that we establish the correctness not for the entire framework, but for each individual language tasks that it conducts, on a case-by-case basis. This idea is not limited to \(\mathbb {K}\) but also applicable to the existing language frameworks and/or formal semantics approaches.
As a first step, we formalize program execution as mathematical proofs and generate their complete proof objects. The experimental result (Table 1) shows promising performance of the proof object generation and proof checking. For example, for a 100-step program execution trace, its complete proof object has 1.6 million lines of code that takes only 5.6 s to proof-check.
We organize the rest of the paper as follows. We give an overview of our approach in Sect. 2. We introduce \(\mathbb {K}\) and discuss the generation of proof parameters in Sect. 3. We discuss matching logic—the logical foundation of \(\mathbb {K}\)—in Sect. 4. We then compile \(\mathbb {K}\) to matching logic in Sect. 5, and discuss proof object generation in Sect. 6. We discuss the limitations of our current implementation and show the experiment results in Sects. 7 and 8, respectively. Finally, we discuss related work in Sect. 9 and conclude the paper in Sect. 10.
2 Our Approach Overview
We give an overview of our approach via the following four main components: (1) a logical foundation of \(\mathbb {K}\), (2) proof parameters, (3) proof object generation, and (4) a trustworthy proof checker.
Logical Foundation of \(\mathbb {K}\) . Our approach is based on matching logic [5, 22]. Matching logic is the logical foundation of \(\mathbb {K}\), in the following sense:
-
1.
The \(\mathbb {K}\) definition (i.e., the language definition in Fig. 1) of a programming language L corresponds to a matching logic theory \(\varGamma ^L\), which, roughly speaking, consists of a set of logical symbols that represents the formal syntax of L, and a set of logical axioms that specify the formal semantics.
-
2.
All language tools in Fig. 1 and all language tasks that \(\mathbb {K}\) conducts are formally specified by matching logic formulas. For example, program execution is specified (in our approach) by the following matching logic formula:
$$\begin{aligned} \varphi _ init \Rightarrow \varphi _ final \end{aligned}$$(1)where \(\varphi _ init \) is the formula that specifies the initial state of the execution, \(\varphi _ final \) specifies the final state, and “\(\Rightarrow \)” states the rewriting/reachability relation between states (see Sect. 5.1).
-
3.
There exists a matching logic proof system that defines the provability relation \(\vdash \) between theories and formulas. For example, the correctness of the above execution from \(\varphi _ init \) to \(\varphi _ final \) is witnessed by the formal proof:
$$\begin{aligned} \varGamma ^L \vdash \varphi _ init \Rightarrow \varphi _ final \end{aligned}$$(2)
Therefore, matching logic is the logical foundation of \(\mathbb {K}\). The correctness of \(\mathbb {K}\) conducting one language task is reduced to the existence of a formal proof in matching logic. Such formal proofs are encoded as proof objects, discussed below.
Proof Parameters. A proof parameter is the necessary information that \(\mathbb {K}\) should provide to help generate proof objects. For program execution, such as Eq. (2), the proof parameter includes the following information:
-
the complete execution trace \(\varphi _0,\varphi _1,\dots ,\varphi _n\), where \(\varphi _0 \equiv \varphi _ init \) and \(\varphi _n \equiv \varphi _ final \); we call \(\varphi _0,\dots ,\varphi _n\) the intermediate snapshots of the execution;
-
for each step from \(\varphi _i\) to \(\varphi _{i+1}\), the rewriting information that consists of the rewrite/semantic rule \(\varphi _ lhs \Rightarrow \varphi _ rhs \) that is applied, and the corresponding substitution \(\theta \) such that \(\varphi _ lhs \theta \equiv \varphi _i\).
In other words, a proof parameter of a program execution trace contains the complete information about how such an execution is carried out by \(\mathbb {K}\). The proof parameter, once generated by \(\mathbb {K}\), is passed to the proof object generator to generate the corresponding proof object, discussed below.
Proof Object Generation. In our approach, a proof object is an encoding of matching logic formal proofs, such as Eq. (2). Proof objects are generated by a proof object generator from the proof parameters provided by \(\mathbb {K}\). At a high level, a proof object for program execution, such as Eq. (2), consists of:
-
1.
the formalization of matching logic and its provability relation \(\vdash \);
-
2.
the formalization of the formal semantics \(\varGamma ^L\) as a logical theory, which includes axioms that specify the rewrite/semantic rules \(\varphi _ lhs \Rightarrow \varphi _ rhs \);
-
3.
the formal proofs of all one-step executions, i.e., \(\varGamma ^L \vdash \varphi _i \Rightarrow \varphi _{i+1}\) for all i;
-
4.
the formal proof of the final proof goal \(\varGamma ^L \vdash \varphi _ init \Rightarrow \varphi _ final \).
Our proof objects have a linear structure, which implies a nice separation of concerns. Indeed, Item 1 is only about matching logic and is not specific to any programming languages/language tasks, so we only need to develop and proof-check it once and for all. Item 2 is specific to the language semantics \(\varGamma ^L\) but is independent of the actual program executions, so it can be reused in the proof objects of various language executions for the same programming language L.
A Trustworthy Proof Checker. A proof checker is a small program that checks whether the formal proofs encoded in a proof object are correct. The proof checker is the main trust base of our work. In this paper, we use Metamath [20]—a third-party proof checking tool that is simple, fast, and trustworthy—to formalize matching logic and encode its formal proofs.
Summary. Our approach to establishing the correctness of \(\mathbb {K}\) is based on its logical foundation—matching logic. We formalize language semantics as logical theories, and program executions as formulas and proof goals, whose proof objects are automatically generated and proof-checked. Our proof objects have a linear structure that allows easy reuse of their components. The key characteristics of our logical-based approach are the following:
-
It is faithful to the real \(\mathbb {K}\) implementation because proof objects are generated from proof parameters, which include all execution snapshots and the actual rewriting information, provided by \(\mathbb {K}\).
-
It is practical because proof objects are generated for each program executions on a case-by-case bases, avoiding the verification of the entire \(\mathbb {K}\).
-
It is trustworthy because the autogenerated proof objects are checked using the trustworthy third-party Metamath proof checker.
3 \(\mathbb {K}\) Framework and Generation of Proof Parameters
3.1 \(\mathbb {K}\) Overview
\(\mathbb {K}\) is an effort in realizing the ideal language framework vision in Fig. 1. An easy way to understand \(\mathbb {K}\) is to look at it as a meta-language that can define other programming languages. In Fig. 2, we show an example \(\mathbb {K}\) language definition of an imperative language IMP. In the 39-line definition, we completely define the formal syntax and the (executable) formal semantics of IMP, using a front end language that is easy to understand. From this language definition, \(\mathbb {K}\) can generate all language tools for IMP, including its parser, interpreter, verifier, etc.
We use IMP as an example to illustrate the main \(\mathbb {K}\) features. There are two modules:
 defines the syntax and
defines the syntax and
 defines the semantics using rewrite rules. Syntax is defined as BNF grammars. The keyword
defines the semantics using rewrite rules. Syntax is defined as BNF grammars. The keyword
 leads production rules that can have attributes that specify the additional syntactic and/or semantic information. For example, the syntax of
leads production rules that can have attributes that specify the additional syntactic and/or semantic information. For example, the syntax of
 -statements is defined in lines 11–12 and has the attribute
-statements is defined in lines 11–12 and has the attribute
 , meaning that the evaluation order is strict in the first argument, i.e., the condition of an
, meaning that the evaluation order is strict in the first argument, i.e., the condition of an
 -statement.
-statement.
In the module
 , we define the configurations of IMP and its formal semantics. A configuration (lines 23–25) is a constructor term that has all semantic information needed to execute programs. IMP configurations are simple, consisting of the IMP code and a program state that maps variables to values. We organize configurations using (semantic) cells:
, we define the configurations of IMP and its formal semantics. A configuration (lines 23–25) is a constructor term that has all semantic information needed to execute programs. IMP configurations are simple, consisting of the IMP code and a program state that maps variables to values. We organize configurations using (semantic) cells:
 is the cell of IMP code and
is the cell of IMP code and
 is the cell of program states. In the initial configuration (lines 24–25),
is the cell of program states. In the initial configuration (lines 24–25),
 is empty and
is empty and
 contains the IMP program that we pass to \(\mathbb {K}\) for execution (represented by the special \(\mathbb {K}\) variable
contains the IMP program that we pass to \(\mathbb {K}\) for execution (represented by the special \(\mathbb {K}\) variable
 ).
).
We define formal semantics using rewrite rules. In lines 26–27, we define the semantics of variable lookup, where we match on a variable
 in the
in the
 cell and look up its value
cell and look up its value
 in the
in the
 cell, by matching on the binding
cell, by matching on the binding
 . Then, we rewrite
. Then, we rewrite
 to
to
 , denoted by
, denoted by
 in the
in the
 cell in line 26. Rewrite rules in \(\mathbb {K}\) are similar to those in the rewrite engines such as Maude [7].
cell in line 26. Rewrite rules in \(\mathbb {K}\) are similar to those in the rewrite engines such as Maude [7].
A Running Example. IMP is too complex as a running example so we introduce a simpler one:
 . Although simple,
. Although simple,
 still uses the core features of defining formal syntax as grammars and formal semantics as rewrite rules.
still uses the core features of defining formal syntax as grammars and formal semantics as rewrite rules.
 is a tiny language that defines a state machine with two counters. Its computation configuration is simply a pair \(\langle m,n \rangle \) of two integers m and n, and its semantics is defined by the following (conditional) rewrite rule:
is a tiny language that defines a state machine with two counters. Its computation configuration is simply a pair \(\langle m,n \rangle \) of two integers m and n, and its semantics is defined by the following (conditional) rewrite rule:
Therefore,
 adds n by m and reduces m by 1. Starting from the initial state \(\langle m,0 \rangle \),
adds n by m and reduces m by 1. Starting from the initial state \(\langle m,0 \rangle \),
 carries out m execution steps and terminates at the final state \(\langle 0,m(m+1)/2 \rangle \), where \(m(m+1)/2 = m + (m-1) + \dots + 1\).
carries out m execution steps and terminates at the final state \(\langle 0,m(m+1)/2 \rangle \), where \(m(m+1)/2 = m + (m-1) + \dots + 1\).
3.2 Program Execution and Proof Parameters
In the following, we show a concrete program execution trace of
 starting from the initial state \(\langle 100,0 \rangle \):
starting from the initial state \(\langle 100,0 \rangle \):
To make \(\mathbb {K}\) generate the above execution trace, we need to follow these steps:
-
1.
Prepare the initial state \(\langle 100,0 \rangle \) in a source file, say
 .
. -
2.
Compile the formal semantics
 into a matching logic theory, explained in Sect. 5.
into a matching logic theory, explained in Sect. 5. -
3.
Use the \(\mathbb {K}\) execution tool
 and pass the source file to it:
and pass the source file to it:
The option
 tells \(\mathbb {K}\) to execute for
tells \(\mathbb {K}\) to execute for
 steps and output the (intermediate) snapshot. By letting
steps and output the (intermediate) snapshot. By letting
 be 1, 2, ..., we collect all snapshots in Eq. (4).
be 1, 2, ..., we collect all snapshots in Eq. (4).
The proof parameter of Eq. (4) includes the additional rewriting information for each execution step. That is, we need to know the rewrite rule that is applied and the corresponding substitution. In
 , there is only one rewrite rule, and the substitution can be easily obtained by pattern matching, where we simply match the snapshot with the left-hand side of the rewrite rule.
, there is only one rewrite rule, and the substitution can be easily obtained by pattern matching, where we simply match the snapshot with the left-hand side of the rewrite rule.
Note that we regard \(\mathbb {K}\) as a “black box”. We are not interested in its complex internal algorithms. Instead, we hide such complexity by letting \(\mathbb {K}\) generate proof parameters that include enough information for proof object generation. This way, we create a separation of concerns between \(\mathbb {K}\) and proof object generation. \(\mathbb {K}\) can aim at optimizing the performance of the autogenerated language tools, without making proof object generation more complex.
4 Matching Logic and Its Formalization
We review the syntax and proof system of matching logic—the logical foundation of \(\mathbb {K}\). Then, we discuss its formalization, which is our main technical contribution and is a critical component of the proof objects we generate for \(\mathbb {K}\) (see Sect. 2).
4.1 Matching Logic Overview
Matching logic was proposed in [23] as a means to specify and reason about programs compactly and modularly. The key concept is its formulas, called patterns, which are used to specify program syntax and semantics in a uniform way. Matching logic is known for its simplicity and rich expressiveness. In [4,5,6, 22], the authors developed matching logic theories that capture FOL, FOL-lfp, separation logic, modal logic, temporal logics, Hoare logic, \(\lambda \)-calculus, type systems, etc. In Sect. 5, we discuss the matching logic theories that capture \(\mathbb {K}\).
The syntax of matching logic is parametric in two sets of variables \(EV\) and \(SV\). We call \(EV\) the set of element variables, denoted \(x,y,\dots \), and \(SV\) the set of set variables, denoted \(X,Y,\dots \).
Definition 1
A (matching logic) signature \(\varSigma \) is a set of (constant) symbols. The set of \(\varSigma \)-patterns, denoted \(\textsc {Pattern}(\varSigma )\), is inductively defined as follows:

where in \(\mu X \mathord {.\,}\varphi \) we require that \(\varphi \) has no negative occurrences of X.
Thus, element variables, set variables, and symbols are patterns. \(\varphi _1 \, \varphi _2\) is a pattern, called application, where the first argument is applied to the second. We have propositional connectives \(\bot \) and \(\varphi _1 \rightarrow \varphi _2\), existential quantification \(\exists x \mathord {.\,}\varphi \), and the least fixpoints \(\mu X \mathord {.\,}\varphi \), from which the following notations are defined:

We use \(\textsc {fv}(\varphi )\) to denote the free variables of \(\varphi \), and \(\varphi [\psi /x]\) and \(\varphi [\psi / X]\) to denote capture-free substitution. Their (usual) definitions are listed in Fig. 4.
Capture-free substitution are defined in the usual way and formalized later in Sect. 4.2 as a part of our proof objects.
Matching logic has a pattern matching semantics, where a pattern \(\varphi \) is interpreted as the set of elements that match it. For example, \(\varphi _1 \wedge \varphi _2\) is the pattern that is matched by those matching both \(\varphi _1\) and \(\varphi _2\). Matching logic semantics is not needed for proof object generation, so we exile it to [5, 22].
We show the matching logic proof system in Fig. 5, which defines the provability relation, written \(\varGamma \vdash \varphi \), meaning that \(\varphi \) can be proved using the proof system, with patterns in \(\varGamma \) added as additional axioms. We call \(\varGamma \) a matching logic theory. The proof system is a main component of proof objects. To understand it, we first need to define application contexts.
Definition 2
A context is a pattern C with a hole variable \(\square \). We write \(C[\varphi ] \equiv C[\varphi /\square ]\) as the result of context plugging. We call C an application context, if
-
1.
\(C \equiv \square \) is the identity context; or
-
2.
\(C \equiv \varphi \ C'\) or \(C \equiv C' \, \varphi \), where \(C'\) is an application context and \(\square \not \in \textsc {fv}(\varphi )\).
That is, the path from the root to \(\square \) in C has only applications.
The proof rules are sound and can be divided into 4 categories: FOL reasoning, frame reasoning, fixpoint reasoning, and some technical rules. The FOL reasoning rules provide (complete) FOL reasoning (see, e.g., [25]). The frame reasoning rules state that application contexts are commutative with disjunctive connectives such as \(\vee \) and \(\exists \). The fixpoint reasoning rules support the standard fixpoint reasoning as in modal \(\mu \)-calculus [17]. The technical proof rules are needed for some completeness results (see [5] for details).
4.2 Formalizing Matching Logic
We discuss the formalization of matching logic, which is our first main contribution and forms an important component in our proof objects (see Sect. 2).
Metamath [20] is a tiny language to state abstract mathematics and their proofs in a machine-checkable style. In our work, we use Metamath to formalize matching logic and to encode our proof objects. We choose Metamath for its simplicity and fast proof checking: Metamath proof checkers are often hundreds lines of code and can proof-check thousands of theorems in a second.
Our formalization follows closely Sect. 4.1. We formalize the syntax of patterns and the proof system. We also need to formalize some metalevel operations such as free variables and capture-free substitution. An innovative contribution is a generic way to handling notations (such as \(\lnot \) and \(\wedge \)) in matching logic. The resulting formalization has only 245 lines of code, which we show in [16]. This formalization of matching logic is the main trust base of our proof objects.
Metamath Overview. We use an extract of our formalization of matching logic (Fig. 6) to explain the basic concepts in Metamath. At a high level, a Metamath source file consists of a list of statements. The main ones are:
-
1.
constant statements (
 ) that declare Metamath constants;
) that declare Metamath constants; -
2.
variable statements (
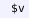 ) that declare Metamath variables, and floating statements (
) that declare Metamath variables, and floating statements (
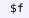 ) that declare their intended ranges;
) that declare their intended ranges; -
3.
axiomatic statements (
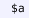 ) that declare Metamath axioms, which can be associated with some essential statements (
) that declare Metamath axioms, which can be associated with some essential statements (
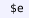 ) that declare the premises;
) that declare the premises; -
4.
provable statements (
 ) that states a Metamath theorem and its proof.
) that states a Metamath theorem and its proof.
Figure 6 defines the fragment of matching logic with only implications. We declare five constants in a row in line 1, where
 ,
,
 , and
, and
 build the syntax,
build the syntax,
 is the type of patterns, and
is the type of patterns, and
 is the provability relation. We declare three metavariables of patterns in lines 3–6, and the syntax of implication \(\varphi _1 \rightarrow \varphi _2\) as
is the provability relation. We declare three metavariables of patterns in lines 3–6, and the syntax of implication \(\varphi _1 \rightarrow \varphi _2\) as
 in line 7. Then, we define matching logic proof rules as Metamath axioms. For example, lines 18–22 define the rule
in line 7. Then, we define matching logic proof rules as Metamath axioms. For example, lines 18–22 define the rule
 .
.
In line 23, we show an example (meta-)theorem and its formal proof in Metamath. The theorem states that \(\vdash \varphi _1 \rightarrow \varphi _1\) holds, and its proof (lines 25–43) is a sequence of labels referring to the previous axiomatic/provable statements.
Metamath proofs are very easy to proof-check, which is why we use it in our work. The proof checker reads the labels in order and push them to a proof stack S, which is initially empty. When a label l is read, the checker pops its premise statements from S and pushes l itself. When all labels are consumed, the checker checks whether S has exactly one statement, which should be the original proof goal. If so, the proof is checked. Otherwise, it fails.
As an example, we look at the first 5 labels of the proof in Fig. 6, line 25:

where we show the stack status in comments. The first label
 refers to a
refers to a
 -statement without premises, so nothing is popped off, and the corresponding statement
-statement without premises, so nothing is popped off, and the corresponding statement
 is pushed to the stack. The same happens, for the second and third labels. The fourth label
is pushed to the stack. The same happens, for the second and third labels. The fourth label
 refers to a
refers to a
 -statement with two metavariables of patterns, and thus has 2 premises. Therefore, the top two statements in S are popped off, and the corresponding conclusion
-statement with two metavariables of patterns, and thus has 2 premises. Therefore, the top two statements in S are popped off, and the corresponding conclusion
 is pushed to S. The last label does the same, popping off two premises and pushing
is pushed to S. The last label does the same, popping off two premises and pushing
 to S. Thus, these five proof steps prove the wellformedness of \(\varphi _1 \rightarrow (\varphi _1 \rightarrow \varphi _1)\).
to S. Thus, these five proof steps prove the wellformedness of \(\varphi _1 \rightarrow (\varphi _1 \rightarrow \varphi _1)\).
Formalizing Matching Logic Syntax. Now, we go through the formalization of matching logic and emphasize some highlights. See [5, 6, 22] for full detail.
The syntax of patterns is formalized below, following Definition 1:

Note that we omit the declarations of metavariables (such as
 ) because their meaning can be easily inferred. The only nontrivial case above is
) because their meaning can be easily inferred. The only nontrivial case above is
 , where we require that
, where we require that
 is positive in
is positive in
 , discussed below.
, discussed below.
Metalevel Assertions. To formalize matching logic, we need the following metalevel operations and/or assertions:
-
1.
positive (and negative) occurrences of variables;
-
2.
free variables;
-
3.
capture-free substitution;
-
4.
application contexts;
-
5.
notations.
Item 1 is needed to define the syntax of \(\mu X \mathord {.\,}\varphi \), while Items 2–5 are needed to define the proof system (Fig. 5). Here, we show how to define capture-free substitution as an example. Notations are discussed in the next section.
To formalize capture-free substitution, we first define a Metamath constant

that serves as an assertion symbol:
 holds iff
holds iff
 . Then, we can define substitution following Fig. 4. The only nontrivial case is when
. Then, we can define substitution following Fig. 4. The only nontrivial case is when
 is \(\exists x \mathord {.\,}\varphi \) or \(\mu X \mathord {.\,}\varphi \), in which case \(\alpha \)-renaming is required to avoid variable capture. We show the case when
is \(\exists x \mathord {.\,}\varphi \) or \(\mu X \mathord {.\,}\varphi \), in which case \(\alpha \)-renaming is required to avoid variable capture. We show the case when
 is \(\exists x \mathord {.\,}\varphi \) below:
is \(\exists x \mathord {.\,}\varphi \) below:

There are two cases, as expected from Fig. 4.
 is when the substitution is shadowed.
is when the substitution is shadowed.
 is the general case, where we first rename
is the general case, where we first rename
 to a fresh variable
to a fresh variable
 and then continue the substitution. The
and then continue the substitution. The
 -statements state that the substitution is not shadowed and
-statements state that the substitution is not shadowed and
 is fresh.
is fresh.
Supporting Notations. Notations (e.g., \(\lnot \) and \(\wedge \)) play an important role in matching logic. Many proof rules such as
 and
and
 use notations (see Fig. 5). However, Metamath has no built-in support for notations. To define a notation, say \(\lnot \varphi \equiv \varphi \rightarrow \bot \), we need to (1) declare a constant
use notations (see Fig. 5). However, Metamath has no built-in support for notations. To define a notation, say \(\lnot \varphi \equiv \varphi \rightarrow \bot \), we need to (1) declare a constant
 and add it to the pattern syntax; (2) define the equivalence relation \(\lnot \varphi \equiv \varphi \rightarrow \bot \); and (3) add a new case for
and add it to the pattern syntax; (2) define the equivalence relation \(\lnot \varphi \equiv \varphi \rightarrow \bot \); and (3) add a new case for
 to every metalevel assertions. While (1) and (2) are reasonable, we want to avoid (3) because there are many metalevel assertions and thus it creates duplication.
to every metalevel assertions. While (1) and (2) are reasonable, we want to avoid (3) because there are many metalevel assertions and thus it creates duplication.
Therefore, we implement an innovative and generic method that allows us to define any notations in a compact way. Our method is to declare a new constant
 and use it to capture the congruence relation of sugaring/desugaring. Using
and use it to capture the congruence relation of sugaring/desugaring. Using
 , it takes only three lines to define the notation \(\lnot \varphi \equiv \varphi \rightarrow \bot \):
, it takes only three lines to define the notation \(\lnot \varphi \equiv \varphi \rightarrow \bot \):

To make the above work, we need to state that
 is a congruence relation with respect to the syntax of patterns and all the other metalevel assertions. Firstly, we state that it is reflexive, symmetric, and transitive:
is a congruence relation with respect to the syntax of patterns and all the other metalevel assertions. Firstly, we state that it is reflexive, symmetric, and transitive:

And the following is an example where we state that
 is a congruence with respect to provability:
is a congruence with respect to provability:

This way, we only need a fixed number of statements that state that
 is a congruence, making it more compact and less duplicated to define notations.
is a congruence, making it more compact and less duplicated to define notations.
Formalizing Proof System. With metalevel assertions and notations, it is now straightforward to formalize matching logic proof rules. We have seen the formalization of
 in Fig. 6. In the following, we formalize the fixpoint proof rule
in Fig. 6. In the following, we formalize the fixpoint proof rule
 , whose premises use capture-free substitution:
, whose premises use capture-free substitution:

5 Compiling \(\mathbb {K}\) into Matching Logic
To execute programs using \(\mathbb {K}\), we need to compile the \(\mathbb {K}\) language definition for language L into a matching logic theory, written \(\varGamma ^L\) (see Sect. 3.2). In this section, we discuss this compilation process and show how to formalize \(\varGamma ^L\).
5.1 Basic Matching Logic Theories
Firstly, we discuss the basic matching logic theories that are required by \(\varGamma ^L\). We discuss the theories of equality, sorts (and sorted functions), and rewriting.
Theory of Equality. By equality, we mean a (predicate) pattern \(\varphi _1 = \varphi _2\) that holds (i.e., equals to \(\top \)) iff \(\varphi _1\) equals to \(\varphi _2\), and fails (i.e., equals to \(\bot \)) otherwise. We first need to define definedness \(\lceil {\varphi }\rceil \), which is a predicate pattern that states that \(\varphi \) is defined, i.e., \(\varphi \) is matched by at least one element: \(\varphi \) is not \(\bot \).
Definition 3
Consider a symbol  , called the definedness symbol. We write \(\lceil {\varphi }\rceil \) for the application
, called the definedness symbol. We write \(\lceil {\varphi }\rceil \) for the application  . In addition, we define the following axiom:
. In addition, we define the following axiom:

 states that any element x is defined. Using the definedness symbol, we can define many important mathematical instruments, including equality, as the following notations:
states that any element x is defined. Using the definedness symbol, we can define many important mathematical instruments, including equality, as the following notations:

[22, Section 5.1] shows that the above indeed capture the intended semantics.
Theory of Sorts. Matching logic is not sorted, but \(\mathbb {K}\) is. To compile \(\mathbb {K}\) into matching logic, we need a systematic way to dealing with sorts. We follow the “sort-as-predicate” paradigm to handle sorts and sorted functions in matching logic, following [4, 6]. The main idea is to define a symbol \(\llbracket \_ \rrbracket \in \varSigma \), called the inhabitant symbol, and use the inhabitant pattern \(\llbracket s \rrbracket \) (abbreviated for the application \(\llbracket \_ \rrbracket \, s\)) to represent the inhabitant set of sort s. For example, to define a sort \( Nat \), we define a corresponding symbol \( Nat \) that represents the sort name, and use \(\llbracket Nat \rrbracket \) to represent the set of all natural numbers.
Sorted functions can be axiomatized as special matching logic symbols. For example, the successor function \( succ \) of natural numbers is a symbol with axiom:
In other words, for any x in the inhabitant set of \( Nat \), there exists a y in the inhabitant set of \( Nat \) such that \( succ \, x\) equals to y. Thus, \( succ \) is a sorted function from \( Nat \) to \( Nat \).
Theory of Rewriting. Recall that in \(\mathbb {K}\), the formal language semantics is defined using rewrite rules, which essentially define a transition system over computation configurations. In matching logic, a transition system can be captured by only one symbol \({\bullet }\in \varSigma \), called one-path next, with the intuition that for any configuration \(\gamma \), \({\bullet }\gamma \) is matched by all configurations that can go to \(\gamma \) in one step. In other words, \(\gamma \) is reached on one-path in the next configuration.
Program execution is the reflexive and transitive closure of one-path next. Formally, we define program execution (i.e., rewriting) as follows:

5.2 Kore: The Intermediate Between \(\mathbb {K}\) and Matching Logic
The \(\mathbb {K}\) compilation tool
 (explained shortly) is what compiles a \(\mathbb {K}\) language definition into a matching logic theory \(\varGamma ^L\), written in a formal language called Kore. For legacy reasons, the Kore language is not the same as the syntax of matching logic (Definition 1), but an axiomatic extension with equality, sorts, and rewriting. Thus, to formalize \(\varGamma ^L\) in proof objects, we need to (1) formalize the matching logic theories of equality, sorts, and rewriting; and (2) automatically translate Kore definitions into the corresponding matching logic theories. Figure 7 shows the 2-phase translation from \(\mathbb {K}\) to matching logic, via Kore.
(explained shortly) is what compiles a \(\mathbb {K}\) language definition into a matching logic theory \(\varGamma ^L\), written in a formal language called Kore. For legacy reasons, the Kore language is not the same as the syntax of matching logic (Definition 1), but an axiomatic extension with equality, sorts, and rewriting. Thus, to formalize \(\varGamma ^L\) in proof objects, we need to (1) formalize the matching logic theories of equality, sorts, and rewriting; and (2) automatically translate Kore definitions into the corresponding matching logic theories. Figure 7 shows the 2-phase translation from \(\mathbb {K}\) to matching logic, via Kore.
Phase 1: From \(\mathbb {K}\) to Kore. To compile a \(\mathbb {K}\) definition such as
 in Fig. 3, we pass it to the \(\mathbb {K}\) compilation tool
in Fig. 3, we pass it to the \(\mathbb {K}\) compilation tool
 as follows:
as follows:

The result is a compiled Kore definition
 . We show the autogenerated Kore axiom in Fig. 7 that corresponds to the rewrite rule in Eq. (3). As we can see, Kore is a much lower-level language than \(\mathbb {K}\), where the programming language concrete syntax and \(\mathbb {K}\) ’s front end syntax are parsed and replaced by the abstract syntax trees, represented by the constructor terms.
. We show the autogenerated Kore axiom in Fig. 7 that corresponds to the rewrite rule in Eq. (3). As we can see, Kore is a much lower-level language than \(\mathbb {K}\), where the programming language concrete syntax and \(\mathbb {K}\) ’s front end syntax are parsed and replaced by the abstract syntax trees, represented by the constructor terms.
Phase 2: From Kore to Matching Logic. We develop an automatic encoder that translates Kore syntax into matching logic patterns. Since Kore is essentially the theory of equality, sorts, and rewriting, we can define the syntactic constructs of the Kore language as notations, using the basic theories in Sect. 5.1.
6 Generating Proof Objects for Program Execution
In this section, we discuss how to generate proof objects for program execution, based on the formalization of matching logic and \(\mathbb {K}\)/Kore in Sects. 4 and 5. The key step is to generate proof objects for one-step executions, which are then put together to build the proof objects for multi-step executions using the transitivity of the rewriting relation. Thus, we focus on the process of generating proof objects for one-step executions from the proof parameters provided by \(\mathbb {K}\).
6.1 Problem Formulation
Consider the following \(\mathbb {K}\) definition that consists of K (conditional) rewrite rules:
where \(t_k\) and \(s_k\) are the left- and right-hand sides of the rewrite rule, respectively, and \(p_k\) is the rewriting condition. Consider the following execution trace:
where \(\varphi _0,\dots ,\varphi _n\) are snapshots. We let \(\mathbb {K}\) generate the following proof parameter:
where for each \(0 \le i < n\), \(k_i\) denotes the rewrite rule that is applied on \(\varphi _{i}\) (\(1 \le k_i \le K\)) and \(\theta _i\) denotes the corresponding substitution such that \(t_{k_i} \theta _i = \varphi _{i}\).
As an example, the rewrite rule of
 , restated below:
, restated below:

has the left-hand side \(t_k \equiv \langle m,n \rangle \), the right-hand side \(s_k \equiv \langle m-1,n+m \rangle \), and the condition \(p_k \equiv m \ge 0\). Note that the right-hand side pattern \(s_k\) contains the arithmetic operations “\(+\)” and “−” that can be further evaluated to a value, if concrete instances of the variables m and n are given. Generally speaking, the right-hand side of a rewrite rule may include (built-in or user-defined) functions that are not constructors and thus can be further evaluated. We call such evaluation process a simplification.
6.2 Applying Rewrite Rules and Applying Simplifications
In the following, we list all proof objects for one-step executions.

As we can see, there are two types of proof objects: one that proves the results of applying rewrite rules and one that applies simplification.
Applying Rewrite Rules. The main steps in proving \(\varGamma ^L \vdash \varphi _i \Rightarrow s_{k_i} \theta _i\) are (1) to instantiate the rewrite rule \(t_{k_i} \wedge p_{k_i} \Rightarrow s_{k_i}\) using the substitution
given in the proof parameter, and (2) to show that the (instantiated) rewriting condition \(p_{k_i} \theta _i\) holds. Here, \(x_1,\dots ,x_m\) are the variables that occur in the rewrite rule and \(c_1,\dots ,c_m\) are terms by which we instantiate the variables. For (1), we need to first prove the following lemma, called
 in [5], which states that \(\forall \)-quantification can be instantiated by functional patterns:
in [5], which states that \(\forall \)-quantification can be instantiated by functional patterns:

Intuitively, the premise \(\exists y_1 \mathord {.\,}\varphi _1 = y_1\) states that \(\varphi _1\) is a functional pattern because it equals to some element \(y_1\).
If \(\varTheta \) in Eq. (8) is the correct proof parameter, \(\theta _i\) is the correct substitution and thus \(t_{k_i}\theta _i \equiv \varphi _i\). Therefore, to prove the original proof goal for one-step execution, i.e. \(\varGamma ^L \vdash \varphi _i \Rightarrow s_{k_i}\theta _i\), we only need to prove that \(\varGamma ^L \vdash p_{k_i}\theta _i\), i.e., the rewriting condition \(p_{k_i}\) holds under \(\theta _i\). This is done by simplifying \(p_{k_i}\theta _i\) to \(\top \), discussed together with the simplification process in the following.
Applying Simplifications. \(\mathbb {K}\) carries out simplification exhaustively before trying to apply a rewrite rule, and simplifications are done by applying (oriented) equations. Generally speaking, let s be a functional pattern and \(p \rightarrow t = t'\) be a (conditional) equation, we say that s can be simplified w.r.t. \(p \rightarrow t=t'\), if there is a sub-pattern \(s_0\) of s (written \(s \equiv C[s_0]\) where C is a context) and a substitution \(\theta \) such that \(s_0 = t\theta \) and \(p\theta \) holds. The resulting simplified pattern is denoted \(C[t'\theta ]\). Therefore, a proof object of the above simplification consists of two proofs: \(\varGamma ^L \vdash s = C[t'\theta ]\) and \(\varGamma ^L \vdash p\theta \). The latter can be handled recursively, by simplifying \(p\theta \) to \(\top \), so we only need to consider the former.
The main steps of proving \(\varGamma ^L \vdash s = C[t'\theta ]\) are the following:
-
1.
to find C, \(s_0\), \(\theta \), and \(t=t'\) in \(\varGamma ^L\) such that \(s \equiv C[s_0]\) and \(s_0 = t\theta \); in other words, s can be simplified w.r.t. \(t=t'\) at the sub-pattern \(s_0\);
-
2.
to prove \(\varGamma ^L \vdash s_0 = t'\theta \) by instantiating \(t=t'\) using the substitution \(\theta \), using the same
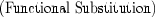 lemma as above;
lemma as above; -
3.
to prove \(\varGamma ^L \vdash C[s_0] = C[t']\) using the transitivity of equality.
Finally, we repeat the above one-step simplifications until no sub-patterns can be simplified further. The resulting proof objects are then put together by the transitivity of equality.
7 Discussion on Implementation
As discussed in Sect. 2, a complete proof object for program execution (i.e., \(\varGamma ^L \vdash \varphi _ init \Rightarrow \varphi _ final \)) consists of (1) the formalization of matching logic and its basic theories; (2) the formalization of \(\varGamma ^L\); and (3) the proofs of one-step and multi-step program executions. In our implementation, (1) is developed manually because it is fixed for all programming languages and program executions. (2) and (3) are automatically generated by the algorithms in Sect. 6.
During the (manual) development of (1), we needed to prove many basic matching logic (meta-)theorems as lemmas, such as
 in Sect. 6.2. To ease the manual work, we developed an interactive theorem prover (ITP) for matching logic, which allows us to carry out higher-level interactive proofs that are later automatically translated into the lower-level Metamath proofs. We show the highlights of our ITP for matching logic in Sect. 7.1.
in Sect. 6.2. To ease the manual work, we developed an interactive theorem prover (ITP) for matching logic, which allows us to carry out higher-level interactive proofs that are later automatically translated into the lower-level Metamath proofs. We show the highlights of our ITP for matching logic in Sect. 7.1.
In Sect. 7.2, we discuss the main limitations of our current preliminary implementation. These limitations are planned to be addressed in future work.
7.1 An Interactive Theorem Prover for Matching Logic
Metamath proofs are low-level and not human readable (see, e.g., the proof of \(\vdash \varphi \rightarrow \varphi \) in Fig. 6). Metamath has its own interactive theorem prover (ITP), but it is for general purposes and does not have specific support for matching logic. Therefore, we developed a new ITP for matching logic that has the following characteristic features:
-
Our ITP understands the syntax of matching logic patterns and has proof tactics to desugar notations in the proof goals;
-
Our ITP has an automatic proof tactic for propositional tautologies, based on the resolution method;
-
Our ITP allows dynamic proofs, meaning that new lemmas can be dynamically added during an interactive proof; this makes our ITP easier to use.
When an interactive proof is finished, our ITP will translate the higher-level proof tactics into real Metamath formal proofs, and thus ease the manual development. It is not our interest to fully introduce ITP in this paper, as more detail about the ITP is to be found in future publications.
7.2 Limitations and Threats to Validity
We discuss the trust base of the autogenerated proof objects by pointing out the main threats to validity, caused by the limitations of our preliminary implementation. It should be noted that these limitations are about the implementation, and not our approach. We shall address these limitations in future work.
Limitation 1: Need to Trust Kore. Our current implementation is based on the existing \(\mathbb {K}\) compilation tool
 that compiles \(\mathbb {K}\) into Kore definitions. Recall that Kore is a (legacy) formal language with built-in support for equality, sorts, and rewriting, and thus is different (and more complex) than the syntax of matching logic. By using Kore as the intermediate between \(\mathbb {K}\) and matching logic (Fig. 7), we need to trust Kore and the \(\mathbb {K}\) complication tool
that compiles \(\mathbb {K}\) into Kore definitions. Recall that Kore is a (legacy) formal language with built-in support for equality, sorts, and rewriting, and thus is different (and more complex) than the syntax of matching logic. By using Kore as the intermediate between \(\mathbb {K}\) and matching logic (Fig. 7), we need to trust Kore and the \(\mathbb {K}\) complication tool
 .
.
In the future, we will eliminate Kore entirely from the picture and formalize \(\mathbb {K}\) directly. To do that, we need to formalize the “front end matters” of \(\mathbb {K}\), such as concrete programming language syntax and \(\mathbb {K}\) attributes, currently handled by
 . That is, we need to formalize and generate proof objects for
. That is, we need to formalize and generate proof objects for
 .
.
Limitation 2: Need to Trust Domain Reasoning. \(\mathbb {K}\) has built-in support for domain reasoning such as integer arithmetic. Our current proof objects do not include the formal proofs of such domain reasoning, but instead regard them as assumed lemmas. In the future, we will incorporate the existing research on generating proof objects for SMT solvers [1] into our implementation, in order to generate proof objects also for domain reasoning; see also Sect. 9.
Limitation 3: Do Not Support More Complex \(\mathbb {K}\) features. Our current implementation only supports the core \(\mathbb {K}\) features of defining programming language syntax and of defining formal semantics as rewrite rules. Some more complex features are not supported; the main ones are (1) the
 attributes that specify evaluation orders; and (2) the use of built-in collection datatypes, such as lists, sets, and maps.
attributes that specify evaluation orders; and (2) the use of built-in collection datatypes, such as lists, sets, and maps.
To support (1), we should handle the so-called heating/cooling rules that are autogenerated rewrite rules that implement the specified evaluation orders. Our current implementation does not support these heating/cooling rules because they are conditional rules, and their conditions are those that state that an element is not a computation result. To prove such conditions, we need additional constructors axioms for the sorts/types that represent results of computation. To support (2), we should extend our algorithms in Sect. 6 with unification modulo these collection datatypes.
8 Evaluation
In this section, we evaluate the performance of our implementation and discuss the experiment results, summarized in Table 1. We use two sets of benchmarks. The first is our running example
 with different inputs (10, 20, 50, and 100). The second is REC [11], which is a popular performance benchmark for rewriting engines. We evaluate both the performance of proof object generation and that of proof checking. Our implementation can be found in [16] and [3].
with different inputs (10, 20, 50, and 100). The second is REC [11], which is a popular performance benchmark for rewriting engines. We evaluate both the performance of proof object generation and that of proof checking. Our implementation can be found in [16] and [3].
The main takeaways of our experiments are:
-
1.
Proof checking is efficient and takes a few seconds; in particular, the task-specific checking time is often less than one second (“task” column in Table 1).
-
2.
Proof object generation is slower and takes several minutes.
-
3.
Proof objects are huge, often of millions LOC (wrapped at 80 characters).
Proof Object Generation. We measure the proof object generation time as the time to generate complete proof objects following the algorithms in Sect. 6, from the compiled language semantics (i.e., Kore definitions) and proof parameters. As shown in Table 1, proof generation takes around 17–406 s on the benchmarks, and the average is 107 s.
Proof object generation can be divided into two parts: that of the language semantics \(\varGamma ^L\) and that of the (one-step and multi-step) program executions. Both parts are shown in Table 1 under columns “sem” and “rewrite”, respectively. For the same language, the time to generate language semantics \(\varGamma ^L\) is the same (up to experimental error). The time for executions is linear to the number of steps.
Proof Checking. Proof checking is efficient and takes a few seconds on our benchmarks. We can divide the proof checking time into two parts: that of the logical foundation and that of the actual program execution tasks. Both parts are shown in Table 1 under columns “logic” and “task”. The “logic” part includes formalization of matching logic and its basic theories, and thus is fixed for any programming language and program and has the same proof checking time (up to experimental error). The “task” part includes the language semantics and proof objects for the one-step and multi-step executions. Therefore, the time to check the “task” part is a more valuable and realistic measure, and according to our experiments, it is often less than 1 s, making it acceptable in practice.
As a pleasant surprise, the time for “task-specific”proof checking is roughly the same as the time that it takes \(\mathbb {K}\) to parse and execute the programs. In other words, there is no significant performance difference on our benchmarks between running the programs directly in \(\mathbb {K}\) and checking the proof objects.
There exists much potential to optimize the performance of proof checking and make it even faster than program execution. For example, in our approach proof checking is an embarrassingly parallel problem, because each meta-theorems can be proof-checked entirely independently. Therefore, we can significantly reduce the proof checking time by running multiple checkers in parallel.
9 Related Work
The idea of using proof generation to address the functional correctness of complicated systems has been introduced a long time ago.
Interactive theorem provers such as Coq [19] and Isabelle [26] are often used to formalize programming language semantics and to reason about program properties. These provers often provide a high-level proof script language that allows the users to develop human-readable proofs, which are then automatically translated into lower-level proof objects that can be checked by the corresponding proof checkers. For example, the proof objects of Coq are of the form \(t:t'\), where \(t'\) is a term that represents the proposition to be proved and \(t'\) represents a formal proof. The typing claim \(t:t'\) can then be proof-checked by a proof checker that implements the typing rules of the calculus of inductive constructions (CIC) [8], which is the logical foundation of Coq.
There are two main differences between provers such as Coq and our technique. Firstly, Coq is not regarded as a language framework in the sense of Fig. 1 because no language tools are autogenerated from the formal semantics. In our case, we need to be able to handle the correctness of individual tasks on a case-by-case basis to reduce the complexity. Secondly, Coq proof checking is based on CIC, which is arguably more complex than matching logic—the logical foundation of \(\mathbb {K}\) as demonstrated in this paper. Indeed, the formalization of matching logic requires only 245 LOC which we display entirely in [16].
Another application of proof generation is to ensure the correctness of SMT solvers. These are popular tools to check the satisfiability of FOL formulas, written in a formal language containing interpreted functions and predicates. SMT solvers often implement complex data structures and algorithms, putting their correctness at risk. There is recent work such as [1] studying proof generation for SMT solvers. The research has been incorporated in theorem provers such as Lean, which attempts to bridge the gap between SMT reasoning and proof assistants more directly by building a proof assistant with efficient and sophisticated built-in SMT capabilities. As discussed in Sect. 7, our current implementation does not generate proofs for domain reasoning. So, we plan to incorporate the above SMT proof generation work into our future implementation.
10 Conclusion
We propose an innovative approach based on proof generation. The key idea is to generate proof objects as proof certificates for each individual task that the language tools conduct, on a case-by-case basis. This way, we avoid formally verifying the entire framework, which is practically impossible, and thus can make the language framework both practical and trustworthy.
References
Barrett, C., De Moura, L., Fontaine, P.: Proofs in satisfiability modulo theories. In: All About Proofs, Proofs for All, vol. 55, no. 1, pp. 23–44 (2015)
Bogdănaş, D., Roşu, G.: K-Java: a complete semantics of Java. In: Proceedings of the 42nd Symposium on Principles of Programming Languages (POPL 2015), Mumbai, India, pp. 445–456. ACM (2015)
Chen, X., Lin, Z., Trinh, MT, Roşu, G.: Towards a trustworthy semantics-based language framework via proof generation (artifact image). https://zenodo.org/record/4701997#.YIAywHX0mso (2021)
Chen, X., Lucanu, D., Roşu, G.: Initial algebra semantics in matching logic. Technical Report, University of Illinois at Urbana-Champaign, July 2020. http://hdl.handle.net/2142/107781
Chen, X., Roşu, G.: Matching \(\mu \)-logic. In: Proceedings of the 34th Annual ACM/IEEE Symposium on Logic in Computer Science (LICS 2019), Vancouver, Canada, pp. 1–13. IEEE (2019)
Chen, X., Roşu, G.: A general approach to define binders using matching logic. In: Proceedings of the 25th ACM SIGPLAN International Conference on Functional Programming (ICFP 2020), New Jersey, USA, pp. 1–32. ACM (2020)
Clavel, M., et al.: Maude Manual (version 3.0). SRI International (2020)
Coq Team: Coq documents: calculus of inductive constructions. https://coq.inria.fr/refman/language/cic.html (2020)
Ştefănescu, A., Park, D., Yuwen, S., Li, Y., Roşu, G.: Semantics-based program verifiers for all languages. In: Proceedings of the 2016 ACM SIGPLAN International Conference on Object-Oriented Programming, Systems, Languages, and Applications (OOPSLA 2016), pp. 74–91. ACM (2016)
Dasgupta, S., Park, D., Kasampalis, T., Adve, V.S., Roşu, G.: A complete formal semantics of x86–64 user-level instruction set architecture. In: Proceedings of the 40th ACM SIGPLAN Conference on Programming Language Design and Implementation (PLDI 2019), Phoenix, Arizona, USA, pp. 1133–1148. ACM (2019)
Durán, F., Garavel, H.: The rewrite Engines competitions: a RECtrospective. In: Beyer, D., Huisman, M., Kordon, F., Steffen, B. (eds.) TACAS 2019. LNCS, vol. 11429, pp. 93–100. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-17502-3_6
Ellison, C., Rosu, G.: An executable formal semantics of C with applications. ACM SIGPLAN Not. 47(1), 533–544 (2012)
Guth, D.: A formal semantics of Python 3.3 (2013)
Guth, D., Hathhorn, C., Saxena, M., Roşu, G.: RV-Match: practical semantics-based program analysis. In: Chaudhuri, S., Farzan, A. (eds.) CAV 2016. LNCS, vol. 9779, pp. 447–453. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-41528-4_24
Hildenbrandt, E.: KEVM: a complete semantics of the Ethereum virtual machine. In: Proceedings of the 2018 IEEE Computer Security Foundations Symposium (CSF 2018), Oxford, UK, pp. 204–217. IEEE (2018). http://jellopaper.org
K Team: Matching logic proof checker. GitHub page (2021). https://github.com/kframework/matching-logic-proof-checker
Kozen, D.: Results on the propositional \(\mu \)-calculus. Theor. Comput. Sci. 27(3), 333–354 (1983)
Luo, Q., et al.: RV-monitor: efficient parametric runtime verification with simultaneous properties. In: Bonakdarpour, B., Smolka, S.A. (eds.) RV 2014. LNCS, vol. 8734, pp. 285–300. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-11164-3_24
Coq Team: The Coq proof assistant. LogiCal Project (2020)
Megill, N., Wheeler, D.A.: Metamath: a computer language for mathematical proofs. Lulu.com (2019)
Park, D., Ştefănescu, A., Roşu, G.: KJS: a complete formal semantics of JavaScript. In: Proceedings of the 36th Annual ACM SIGPLAN Conference on Programming Language Design and Implementation (PLDI 2015), Portland, OR, pp. 346–356. ACM (2015)
Roşu, G.: Matching logic. Log. Methods Comput. Sci. 13(4), 1–61 (2017)
Roşu, G., Schulte, W.: Matching logic–extended report. Technical Report Department of Computer Science UIUCDCS-R-2009-3026, University of Illinois at Urbana-Champaign, January 2009
Rosu, G.: K-A semantic framework for programming languages and formal analysis tools. Dependable Softw. Syst. Eng. 50, 186 (2017)
Shoenfield, J.R.: Mathematical Logic. Addison-Wesley Pub. Co, Boston (1967)
The Isabelle Development Team. Isabelle (2018). https://isabelle.in.tum.de/
Acknowledgment
The work presented in this paper was supported in part by NSF CNS 16-19275 and an IOHK grant. This material is based upon work supported by the United States Air Force and DARPA under Contract No. FA8750-18-C-0092.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2021 The Author(s)
About this paper
Cite this paper
Chen, X., Lin, Z., Trinh, MT., Roşu, G. (2021). Towards a Trustworthy Semantics-Based Language Framework via Proof Generation. In: Silva, A., Leino, K.R.M. (eds) Computer Aided Verification. CAV 2021. Lecture Notes in Computer Science(), vol 12760. Springer, Cham. https://doi.org/10.1007/978-3-030-81688-9_23
Download citation
DOI: https://doi.org/10.1007/978-3-030-81688-9_23
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-81687-2
Online ISBN: 978-3-030-81688-9
eBook Packages: Computer ScienceComputer Science (R0)








 .
. .
. into a matching logic theory, explained in Sect.
into a matching logic theory, explained in Sect.  and pass the source file to it:
and pass the source file to it: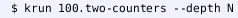



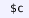 ) that declare Metamath constants;
) that declare Metamath constants;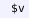 ) that declare Metamath variables, and floating statements (
) that declare Metamath variables, and floating statements (
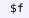 ) that declare their intended ranges;
) that declare their intended ranges;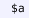 ) that declare Metamath axioms, which can be associated with some essential statements (
) that declare Metamath axioms, which can be associated with some essential statements (
 ) that declare the premises;
) that declare the premises; ) that states a Metamath theorem and its proof.
) that states a Metamath theorem and its proof.
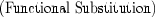 lemma as above;
lemma as above;