Abstract
Stateless model checking (SMC) is one of the standard approaches to the verification of concurrent programs. As scheduling non-determinism creates exponentially large spaces of thread interleavings, SMC attempts to partition this space into equivalence classes and explore only a few representatives from each class. The efficiency of this approach depends on two factors: (a) the coarseness of the partitioning, and (b) the time to generate representatives in each class. For this reason, the search for coarse partitionings that are efficiently explorable is an active research challenge.
In this work we present \({\text {RVF-SMC}}\), a new SMC algorithm that uses a novel reads-value-from (RVF) partitioning. Intuitively, two interleavings are deemed equivalent if they agree on the value obtained in each read event, and read events induce consistent causal orderings between them. The RVF partitioning is provably coarser than recent approaches based on Mazurkiewicz and “reads-from” partitionings. Our experimental evaluation reveals that RVF is quite often a very effective equivalence, as the underlying partitioning is exponentially coarser than other approaches. Moreover, \({\text {RVF-SMC}}\) generates representatives very efficiently, as the reduction in the partitioning is often met with significant speed-ups in the model checking task.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
The verification of concurrent programs is one of the key challenges in formal methods. Interprocess communication adds a new dimension of non-determinism in program behavior, which is resolved by a scheduler. As the programmer has no control over the scheduler, program correctness has to be guaranteed under all possible schedulers, i.e., the scheduler is adversarial to the program and can generate erroneous behavior if one can arise out of scheduling decisions. On the other hand, during program testing, the adversarial nature of the scheduler is to hide erroneous runs, making bugs extremely difficult to reproduce by testing alone (aka Heisenbugs [1]). Consequently, the verification of concurrent programs rests on rigorous model checking techniques [2] that cover all possible program behaviors that can arise out of scheduling non-determinism, leading to early tools such as VeriSoft [3, 4] and CHESS [5].
To battle with the state-space explosion problem, effective model checking for concurrency is stateless. A stateless model checker (SMC) explores the behavior of the concurrent program by manipulating traces instead of states, where each (concurrent) trace is an interleaving of event sequences of the corresponding threads [6]. To further improve performance, various techniques try to reduce the number of explored traces, such as context bounded techniques [7,8,9,10] As many interleavings induce the same program behavior, SMC partitions the interleaving space into equivalence classes and attempts to sample a few representative traces from each class. The most popular approach in this domain is partial-order reduction techniques [6, 11, 12], which deems interleavings as equivalent based on the way that conflicting memory accesses are ordered, also known as the Mazurkiewicz equivalence [13]. Dynamic partial order reduction [14] constructs this equivalence dynamically, when all memory accesses are known, and thus does not suffer from the imprecision of earlier approaches based on static information. Subsequent works managed to explore the Mazurkiewicz partitioning optimally [15, 16], while spending only polynomial time per class.
The performance of an SMC algorithm is generally a product of two factors: (a) the size of the underlying partitioning that is explored, and (b) the total time spent in exploring each class of the partitioning. Typically, the task of visiting a class requires solving a consistency-checking problem, where the algorithm checks whether a semantic abstraction, used to represent the class, has a consistent concrete interleaving that witnesses the class. For this reason, the search for effective SMC is reduced to the search of coarse partitionings for which the consistency problem is tractable, and has become a very active research direction in recent years. In [17], the Mazurkiewicz partitioning was further reduced by ignoring the order of conflicting write events that are not observed, while retaining polynomial-time consistency checking. Various other works refine the notion of dependencies between events, yielding coarser abstractions [18,19,20]. The work of [21] used a reads-from abstraction and showed that the consistency problem admits a fully polynomial solution in acyclic communication topologies. Recently, this approach was generalized to arbitrary topologies, with an algorithm that remains polynomial for a bounded number of threads [22]. Finally, recent approaches define value-centric partitionings [23], as well as partitionings based on maximal causal models [24]. These partitionings are very coarse, as they attempt to distinguish only between traces which differ in the values read by their corresponding read events. We illustrate the benefits of value-based partitionings with a motivating example.
1.1 Motivating Example
Consider a simple concurrent program shown in Fig. 1. The program has 98 different orderings of the conflicting memory accesses, and each ordering corresponds to a separate class of the Mazurkiewicz partitioning. Utilizing the reads-from abstraction reduces the number of partitioning classes to 9. However, when taking into consideration the values that the events can read and write, the number of cases to consider can be reduced even further. In this specific example, there is only a single behaviour the program may exhibit, in which both read events read the only observable value.
The above benefits have led to recent attempts in performing SMC using a value-based equivalence [23, 24]. However, as the realizability problem is NP-hard in general [25], both approaches suffer significant drawbacks. In particular, the work of [23] combines the value-centric approach with the Mazurkiewicz partitioning, which creates a refinement with exponentially many more classes than potentially necessary. The example program in Fig. 1 illustrates this, where while both read events can only observe one possible value, the work of [23] further enumerates all Mazurkiewicz orderings of all-but-one threads, resulting in 7 partitioning classes. Separately, the work of [24] relies on SMT solvers, thus spending exponential time to solve the realizability problem. Hence, each approach suffers an exponential blow-up a-priori, which motivates the following question: is there an efficient parameterized algorithm for the consistency problem? That is, we are interested in an algorithm that is exponential-time in the worst case (as the problem is NP-hard in general), but efficient when certain natural parameters of the input are small, and thus only becomes slow in extreme cases.
Another disadvantage of these works is that each of the exploration algorithms can end up to the same class of the partitioning many times, further hindering performance. To see an example, consider the program in Fig. 1 again. The work of [23] assigns values to reads one by one, and in this example, it needs to consider as separate cases both permutations of the two reads as the orders for assigning the values. This is to ensure completeness in cases where there are write events causally dependent on some read events (e.g., a write event appearing only if its thread-predecessor reads a certain value). However, no causally dependent write events are present in this program, and our work uses a principled approach to detect this and avoid the redundant exploration. While an example to demonstrate [24] revisiting partitioning classes is a bit more involved one, this property follows from the lack of information sharing between spawned subroutines, enabling the approach to be massively parallelized, which has been discussed already in prior works [21, 23, 26].
1.2 Our Contributions
In this work we tackle the two challenges illustrated in the motivating example in a principled, algorithmic way. In particular, our contributions are as follows.
-
(1)
We study the problem of verifying the sequentially consistent executions. The problem is known to be NP-hard [25] in general, already for 3 threads. We show that the problem can be solved in \(O(k^{d+1}\cdot n^{k+1})\) time for an input of n events, k threads and d variables. Thus, although the problem NP-hard in general, it can be solved in polynomial time when the number of threads and number of variables is bounded. Moreover, our bound reduces to \(O(n^{k+1})\) in the class of programs where every variable is written by only one thread (while read by many threads). Hence, in this case the bound is polynomial for a fixed number of threads and without any dependence on the number of variables.
-
(2)
We define a new equivalence between concurrent traces, called the reads-value-from (RVF) equivalence. Intuitively, two traces are RVF-equivalent if they agree on the value obtained in each read event, and read events induce consistent causal orderings between them. We show that RVF induces a coarser partitioning than the partitionings explored by recent well-studied SMC algorithms [15, 21, 23], and thus reduces the search space of the model checker.
-
(3)
We develop a novel SMC algorithm called \({\text {RVF-SMC}}\), and show that it is sound and complete for local safety properties such as assertion violations. Moreover, \({\text {RVF-SMC}}\) has complexity \(k^d\cdot n^{O(k)}\cdot \beta \), where \(\beta \) is the size of the underlying RVF partitioning. Under the hood, \({\text {RVF-SMC}}\) uses our consistency-checking algorithm of Item 1 to visit each RVF class during the exploration. Moreover, \({\text {RVF-SMC}}\) uses a novel heuristic to significantly reduce the number of revisits in any given RVF class, compared to the value-based explorations of [23, 24].
-
(4)
We implement \({\text {RVF-SMC}}\) in the stateless model checker Nidhugg [27]. Our experimental evaluation reveals that RVF is quite often a very effective equivalence, as the underlying partitioning is exponentially coarser than other approaches. Moreover, \({\text {RVF-SMC}}\) generates representatives very efficiently, as the reduction in the partitioning is often met with significant speed-ups in the model checking task.
2 Preliminaries
General Notation. Given a natural number \(i\ge 1\), we let [i] be the set \(\{ 1,2,\dots , i \}\). Given a map \(f:X\rightarrow Y\), we let \(\mathsf {dom}(f)=X\) denote the domain of f. We represent maps f as sets of tuples \(\{ (x, f(x))\}_x\). Given two maps \(f_1, f_2\) over the same domain X, we write \(f_1=f_2\) if for every \(x\in X\) we have \(f_1(x)=f_2(x)\). Given a set \(X'\subset X\), we denote by \(f|X'\) the restriction of f to \(X'\). A binary relation \(\sim \) on a set X is an equivalence iff \(\sim \) is reflexive, symmetric and transitive.
2.1 Concurrent Model
Here we describe the computational model of concurrent programs with shared memory under the Sequential Consistency (\({\text {SC}}\)) memory model. We follow a standard exposition of stateless model checking, similarly to [14, 15, 21,22,23, 28],
Concurrent Program. We consider a concurrent program \(\mathcal {H}=\{ \mathsf {thr}_i \}_{i=1}^k\) of k deterministic threads. The threads communicate over a shared memory \(\mathcal {G}\) of global variables with a finite value domain \(\mathcal {D}\). Threads execute events of the following types.
-
(1)
A write event \(w\) writes a value \(v\in \mathcal {D}\) to a global variable \(x\in \mathcal {G}\).
-
(2)
A read event \(r\) reads the value \(v\in \mathcal {D}\) of a global variable \(x\in \mathcal {G}\).
Additionally, threads can execute local events which do not access global variables and thus are not modeled explicitly.
Given an event \(e\), we denote by \(\mathsf {thr}(e)\) its thread and by \(\mathsf {var}(e)\) its global variable. We denote by \(\mathcal {E}\) the set of all events, and by \(\mathcal {R}\) (\(\mathcal {W}\)) the set of read (write) events. Given two events \(e_1, e_2\in \mathcal {E}\), we say that they conflict, denoted \(e_1 \bowtie e_2\), if they access the same global variable and at least one of them is a write event.
Concurrent Program Semantics. The semantics of \(\mathcal {H}\) are defined by means of a transition system over a state space of global states. A global state consists of (i) a memory function that maps every global variable to a value, and (ii) a local state for each thread, which contains the values of the local variables and the program counter of the thread. We consider the standard setting of Sequential Consistency (\({\text {SC}}\)), and refer to [14] for formal details. As usual, \(\mathcal {H}\) is execution-bounded, which means that the state space is finite and acyclic.
Event Sets. Given a set of events \(X\subseteq \mathcal {E}\), we write \(\mathcal {R}(X)=X\cap \mathcal {R}\) for the set of read events of X, and \(\mathcal {W}(X)=X\cap \mathcal {W}\) for the set of write events of X. Given a set of events \(X\subseteq \mathcal {E}\) and a thread \(\mathsf {thr}\), we denote by \(X_{\mathsf {thr}}\) and \(X_{\ne \mathsf {thr}}\) the events of \(\mathsf {thr}\), and the events of all other threads in X, respectively.
Sequences and Traces. Given a sequence of events \(\tau =e_1,\dots ,e_j\), we denote by \(\mathcal {E}(\tau )\) the set of events that appear in \(\tau \). We further denote \(\mathcal {R}(\tau ) = \mathcal {R}(\mathcal {E}(\tau ))\) and \(\mathcal {W}(\tau ) = \mathcal {W}(\mathcal {E}(\tau ))\).
Given a sequence \(\tau \) and two events \(e_1, e_2 \in \mathcal {E}(\tau )\), we write \(e_1 <_\tau e_2\) when \(e_1\) appears before \(e_2\) in \(\tau \), and \(e_1 \le _\tau e_2\) to denote that \(e_1 <_\tau e_2\) or \(e_1 = e_2\). Given a sequence \(\tau \) and a set of events A, we denote by \(\tau |A\) the projection of \(\tau \) on A, which is the unique subsequence of \(\tau \) that contains all events of \(A \cap \mathcal {E}(\tau )\), and only those events. Given a sequence \(\tau \) and a thread \(\mathsf {thr}\), let \(\tau _{\mathsf {thr}}\) be the subsequence of \(\tau \) with events of \(\mathsf {thr}\), i.e., \(\tau |\mathcal {E}(\tau )_{\mathsf {thr}}\). Given two sequences \(\tau _1\) and \(\tau _2\), we denote by \(\tau _1 \circ \tau _2\) the sequence that results in appending \(\tau _2\) after \(\tau _1\).
A (concrete, concurrent) trace is a sequence of events \(\sigma \) that corresponds to a concrete valid execution of \(\mathcal {H}\). We let \(\mathsf {enabled}(\sigma )\) be the set of enabled events after \(\sigma \) is executed, and call \(\sigma \) maximal if \(\mathsf {enabled}(\sigma )=\emptyset \). As \(\mathcal {H}\) is bounded, all executions of \(\mathcal {H}\) are finite and the length of the longest execution in \(\mathcal {H}\) is a parameter of the input.
Reads-From and Value Functions. Given a sequence of events \(\tau \), we define the reads-from function of \(\tau \), denoted \(\mathsf {RF}_{\tau }:\mathcal {R}(\tau )\rightarrow \mathcal {W}(\tau )\), as follows. Given a read event \(r\in \mathcal {R}(\tau )\), we have that \(\mathsf {RF}_{\tau }(r)\) is the latest write (of any thread) conflicting with \(r\) and occurring before \(r\) in \(\tau \), i.e., (i) \(\mathsf {RF}_{\tau }(r) \bowtie r\), (ii) \(\mathsf {RF}_{\tau }(r) <_\tau r\), and (iii) for each  such that
such that  and
and  , we have
, we have  . We say that \(r\) reads-from \(\mathsf {RF}_{\tau }(r)\) in \(\tau \). For simplicity, we assume that \(\mathcal {H}\) has an initial salient write event on each variable.
. We say that \(r\) reads-from \(\mathsf {RF}_{\tau }(r)\) in \(\tau \). For simplicity, we assume that \(\mathcal {H}\) has an initial salient write event on each variable.
Further, given a trace \(\sigma \), we define the value function of \(\sigma \), denoted \(\mathsf {val}_{\sigma }:\mathcal {E}(\sigma )\rightarrow \mathcal {D}\), such that \(\mathsf {val}_{\sigma }(e)\) is the value of the global variable \(\mathsf {var}(e)\) after the prefix of \(\sigma \) up to and including \(e\) has been executed. Intuitively, \(\mathsf {val}_{\sigma }(e)\) captures the value that a read (resp. write) event \(e\) shall read (resp. write) in \(\sigma \). The value function \(\mathsf {val}_{\sigma }\) is well-defined as \(\sigma \) is a valid trace and the threads of \(\mathcal {H}\) are deterministic.
2.2 Partial Orders
In this section we present relevant notation around partial orders, which are a central object in this work.
Partial Orders. Given a set of events \(X\subseteq \mathcal {E}\), a (strict) partial order P over X is an irreflexive, antisymmetric and transitive relation over X (i.e., \(<_{P}\,\subseteq X\times X\)). Given two events \(e_1,e_2\in X\), we write \(e_1\le _P e_2\) to denote that \(e_1<_Pe_2\) or \(e_1=e_2\). Two distinct events \(e_1,e_2\in X\) are unordered by P, denoted \(e_1\parallel _{P} e_2\), if neither \(e_1<_{P}e_2\) nor \(e_2<_{P} e_1\), and ordered (denoted  ) otherwise. Given a set \(Y\subseteq X\), we denote by \(P|Y\) the projection of P on the set Y, where for every pair of events \(e_1, e_2\in Y\), we have that \(e_1<_{P|Y} e_2\) iff \(e_1<_{P} e_2\). Given two partial orders P and Q over a common set X, we say that Q refines P, denoted by \(Q\sqsubseteq P\), if for every pair of events \(e_1, e_2\in X\), if \(e_1<_{P}e_2\) then \(e_1<_{Q}e_2\). A linearization of P is a total order that refines P.
) otherwise. Given a set \(Y\subseteq X\), we denote by \(P|Y\) the projection of P on the set Y, where for every pair of events \(e_1, e_2\in Y\), we have that \(e_1<_{P|Y} e_2\) iff \(e_1<_{P} e_2\). Given two partial orders P and Q over a common set X, we say that Q refines P, denoted by \(Q\sqsubseteq P\), if for every pair of events \(e_1, e_2\in X\), if \(e_1<_{P}e_2\) then \(e_1<_{Q}e_2\). A linearization of P is a total order that refines P.
Lower Sets. Given a pair (X, P), where X is a set of events and P is a partial order over X, a lower set of (X, P) is a set \(Y\subseteq X\) such that for every event \(e_1\in Y\) and event \(e_2\in X\) with \(e_2\le _{P} e_1\), we have \(e_2\in Y\).
Visible Writes. Given a partial order P over a set X, and a read event \(r\in \mathcal {R}(X)\), the set of visible writes of \(r\) is defined as
i.e., the set of write events \(w\) conflicting with \(r\) that are not “hidden” to \(r\) by P.
The Program Order \(\mathsf {PO}\). The program order \(\mathsf {PO}\) of \(\mathcal {H}\) is a partial order \(<_{\mathsf {PO}}\subseteq \mathcal {E}\times \mathcal {E}\) that defines a fixed order between some pairs of events of the same thread, reflecting the semantics of \(\mathcal {H}\).
A set of events \(X\subseteq \mathcal {E}\) is proper if (i) it is a lower set of \((\mathcal {E}, \mathsf {PO})\), and (ii) for each thread \(\mathsf {thr}\), the events \(X_{\mathsf {thr}}\) are totally ordered in \(\mathsf {PO}\) (i.e., for each distinct \(e_1,e_2 \in X_{\mathsf {thr}}\) we have  ). A sequence \(\tau \) is well-formed if (i) its set of events \(\mathcal {E}(\tau )\) is proper, and (ii) \(\tau \) respects the program order (formally, \(\tau \sqsubseteq \mathsf {PO}|\mathcal {E}(\tau )\)). Every trace \(\sigma \) of \(\mathcal {H}\) is well-formed, as it corresponds to a concrete valid execution of \(\mathcal {H}\). Each event of \(\mathcal {H}\) is then uniquely identified by its \(\mathsf {PO}\) predecessors, and by the values its \(\mathsf {PO}\) predecessor reads have read.
). A sequence \(\tau \) is well-formed if (i) its set of events \(\mathcal {E}(\tau )\) is proper, and (ii) \(\tau \) respects the program order (formally, \(\tau \sqsubseteq \mathsf {PO}|\mathcal {E}(\tau )\)). Every trace \(\sigma \) of \(\mathcal {H}\) is well-formed, as it corresponds to a concrete valid execution of \(\mathcal {H}\). Each event of \(\mathcal {H}\) is then uniquely identified by its \(\mathsf {PO}\) predecessors, and by the values its \(\mathsf {PO}\) predecessor reads have read.
A trace \(\sigma \), the displayed events \(\mathcal {E}(\sigma )\) are vertically ordered as they appear in \(\sigma \). The solid black edges represent the program order \(\mathsf {PO}\). The dashed red edges represent the reads-from function \(\mathsf {RF}_{\sigma }\). The transitive closure of all the edges then gives us the causally-happens-before partial order \(\mathsf {\mapsto }_{\sigma }\).
Causally-Happens-Before Partial Orders. A trace \(\sigma \) induces a causally-happens-before partial order \(\mathsf {\mapsto }_{\sigma } \subseteq \mathcal {E}(\sigma )\times \mathcal {E}(\sigma )\), which is the weakest partial order such that (i) it refines the program order (i.e., \(\mathsf {\mapsto }_{\sigma }\sqsubseteq \mathsf {PO}|\mathcal {E}(\sigma )\)), and (ii) for every read event \(r\in \mathcal {R}(\sigma )\), its reads-from \(\mathsf {RF}_{\sigma }(r)\) is ordered before it (i.e., \(\mathsf {RF}_{\sigma }(r)\;\, \mathsf {\mapsto }_{\sigma } \;\,r\)). Intuitively, \(\mathsf {\mapsto }_{\sigma }\) contains the causal orderings in \(\sigma \), i.e., it captures the flow of write events into read events in \(\sigma \) together with the program order. Figure 2 presents an example of a trace and its causal orderings.
3 Reads-Value-From Equivalence
In this section we present our new equivalence on traces, called the reads-value-from equivalence (\(\mathsf {RVF}\) equivalence, or \(\sim _{\mathsf {RVF}}\), for short). Then we illustrate that \(\sim _{\mathsf {RVF}}\) has some desirable properties for stateless model checking.
Reads-Value-From Equivalence. Given two traces \(\sigma _1\) and \(\sigma _2\), we say that they are reads-value-from-equivalent, written \(\sigma _1 \sim _{\mathsf {RVF}}\sigma _2\), if the following hold.
-
(1)
\(\mathcal {E}(\sigma _1) = \mathcal {E}(\sigma _2)\), i.e., they consist of the same set of events.
-
(2)
\(\mathsf {val}_{\sigma _1} = \mathsf {val}_{\sigma _2}\), i.e., each event reads resp. writes the same value in both.
-
(3)
\(\mathsf {\mapsto }_{\sigma _1} |\mathcal {R}= \mathsf {\mapsto }_{\sigma _2} |\mathcal {R}\), i.e., their causal orderings agree on the read events.
Figure 3 presents an intuitive example of \(\mathsf {RVF}\)-(in)equivalent traces.
Three traces \(\sigma _1\), \(\sigma _2\), \(\sigma _3\), events of each trace are vertically ordered as they appear in the trace. Traces \(\sigma _1\) and \(\sigma _2\) are \(\mathsf {RVF}\)-equivalent (\(\sigma _1\) \(\sim _{\mathsf {RVF}}\) \(\sigma _2\)), as they have the same events, same value function, and the two read events are causally unordered in both. Trace \(\sigma _3\) is not \(\mathsf {RVF}\)-equivalent with either of \(\sigma _1\) and \(\sigma _2\). Compared to \(\sigma _1\) resp. \(\sigma _2\), the value function of \(\sigma _3\) differs (
 reads a different value), and the causal orderings of the reads differ (
reads a different value), and the causal orderings of the reads differ (
 ).
).
Soundness. The \(\mathsf {RVF}\) equivalence induces a partitioning on the maximal traces of \(\mathcal {H}\). Any algorithm that explores each class of this partitioning provably discovers every reachable local state of every thread, and thus \(\mathsf {RVF}\) is a sound equivalence for local safety properties, such as assertion violations, in the same spirit as in other recent works [21,22,23,24]. This follows from the fact that for any two traces \(\sigma _1\) and \(\sigma _2\) with \(\mathcal {E}(\sigma _1) = \mathcal {E}(\sigma _2)\) and \(\mathsf {val}_{\sigma _1} = \mathsf {val}_{\sigma _2}\), the local states of each thread are equal after executing \(\sigma _1\) and \(\sigma _2\).
Coarseness. Here we describe the coarseness properties of the \(\mathsf {RVF}\) equivalence, as compared to other equivalences used by state-of-the-art approaches in stateless model checking. Figure 4 summarizes the comparison.
The SMC algorithms of [22] and [28] operate on a reads-from equivalence, which deems two traces \(\sigma _1\) and \(\sigma _2\) equivalent if
-
(1)
they consist of the same events (\(\mathcal {E}(\sigma _1) = \mathcal {E}(\sigma _2)\)), and
-
(2)
their reads-from functions coincide (\(\mathsf {RF}_{\sigma _1} = \mathsf {RF}_{\sigma _2}\)).
The above two conditions imply that the induced causally-happens-before partial orders are equal, i.e., \(\mathsf {\mapsto }_{\sigma _1} = \mathsf {\mapsto }_{\sigma _2}\), and thus trivially also \(\mathsf {\mapsto }_{\sigma _1} |\mathcal {R}= \mathsf {\mapsto }_{\sigma _2} |\mathcal {R}\). Further, by a simple inductive argument the value functions of the two traces are also equal, i.e., \(\mathsf {val}_{\sigma _1} = \mathsf {val}_{\sigma _2}\). Hence any two reads-from-equivalent traces are also \(\mathsf {RVF}\)-equivalent, which makes the \(\mathsf {RVF}\) equivalence always at least as coarse as the reads-from equivalence.
The work of [23] utilizes a value-centric equivalence, which deems two traces equivalent if they satisfy all the conditions of our \(\mathsf {RVF}\) equivalence, and also some further conditions (note that these conditions are necessary for correctness of the SMC algorithm in [23]). Thus the \(\mathsf {RVF}\) equivalence is trivially always at least as coarse. The value-centric equivalence preselects a single thread \(\mathsf {thr}\), and then requires two extra conditions for the traces to be equivalent, namely:
-
(1)
For each read of \(\mathsf {thr}\), either the read reads-from a write of \(\mathsf {thr}\) in both traces, or it does not read-from a write of \(\mathsf {thr}\) in either of the two traces.
-
(2)
For each conflicting pair of events not belonging to \(\mathsf {thr}\), the ordering of the pair is equal in the two traces.
Both the reads-from equivalence and the value-centric equivalence are in turn as coarse as the data-centric equivalence of [21]. Given two traces, the data-centric equivalence has the equivalence conditions of the reads-from equivalence, and additionally, it preselects a single thread \(\mathsf {thr}\) (just like the value-centric equivalence) and requires the second extra condition of the value-centric equivalence, i.e., equality of orderings for each conflicting pair of events outside of \(\mathsf {thr}\).
Finally, the data-centric equivalence is as coarse as the classical Mazurkiewicz equivalence [13], the baseline equivalence for stateless model checking [14, 15, 29]. Mazurkiewicz equivalence deems two traces equivalent if they consist of the same set of events and they agree on their ordering of conflicting events.
While \(\mathsf {RVF}\) is always at least as coarse, it can be (even exponentially) coarser, than each of the other above-mentioned equivalences. We illustrate this in Appendix B of [30]. We summarize these observations in the following proposition.
Proposition 1
\(\mathsf {RVF}\) is at least as coarse as each of the Mazurkiewicz equivalence [15], the data-centric equivalence [21], the reads-from equivalence [22], and the value-centric equivalence [23]. Moreover, \(\mathsf {RVF}\) can be exponentially coarser than each of these equivalences.
In this work we develop our SMC algorithm \({\text {RVF-SMC}}\) around the \(\mathsf {RVF}\) equivalence, with the guarantee that the algorithm explores at most one maximal trace per class of the \(\mathsf {RVF}\) partitioning, and thus can perform significantly fewer steps than algorithms based on the above equivalences. To utilize \(\mathsf {RVF}\), the algorithm in each step solves an instance of the verification of sequential consistency problem, which we tackle in the next section. Afterwards, we present \({\text {RVF-SMC}}\).
4 Verifying Sequential Consistency
In this section we present our contributions towards the problem of verifying sequential consistency (\({\text {VSC}}\)). We present an algorithm \({\text {VerifySC}}\) for \({\text {VSC}}\), and we show how it can be efficiently used in stateless model checking.
The \({\text {VSC}}\) Problem. Consider an input pair \((X, \mathsf {GoodW})\) where
-
(1)
\(X \subseteq \mathcal {E}\) is a proper set of events, and
-
(2)
\(\mathsf {GoodW}:\mathcal {R}(X) \rightarrow 2^{\mathcal {W}(X)}\) is a good-writes function such that \(w\in \mathsf {GoodW}(r)\) only if \(r \bowtie w\).
A witness of \((X, \mathsf {GoodW})\) is a linearization \(\tau \) of X (i.e., \(\mathcal {E}(\tau ) = X\)) respecting the program order (i.e., \(\tau \sqsubseteq \mathsf {PO}|X\)), such that each read \(r\in \mathcal {R}(\tau )\) reads-from one of its good-writes in \(\tau \), formally \(\mathsf {RF}_{\tau }(r) \in \mathsf {GoodW}(r)\) (we then say that \(\tau \) satisfies the good-writes function \(\mathsf {GoodW}\)). The task is to decide whether \((X, \mathsf {GoodW})\) has a witness, and to construct one in case it exists.
\({\text {VSC}}\) in Stateless Model Checking. The \({\text {VSC}}\) problem naturally ties in with our SMC approach enumerating the equivalence classes of the \(\mathsf {RVF}\) trace partitioning. In our approach, we shall generate instances \((X, \mathsf {GoodW})\) such that (i) each witness \(\sigma \) of \((X, \mathsf {GoodW})\) is a valid program trace, and (ii) all witnesses \(\sigma _1, \sigma _2\) of \((X, \mathsf {GoodW})\) are pairwise \(\mathsf {RVF}\)-equivalent (\(\sigma _1 \sim _{\mathsf {RVF}}\sigma _2\)).
Hardness of \({\text {VSC}}\). Given an input \((X, \mathsf {GoodW})\) to the \({\text {VSC}}\) problem, let \(n=|X|\), let k be the number of threads appearing in X, and let d be the number of variables accessed in X. The classic work of [25] establishes two important lower bounds on the complexity of \({\text {VSC}}\):
-
(1)
\({\text {VSC}}\) is NP-hard even when restricted only to inputs with \(k=3\).
-
(2)
\({\text {VSC}}\) is NP-hard even when restricted only to inputs with \(d=2\).
The first bound eliminates the possibility of any algorithm with time complexity \(O( n^{ f(k) })\), where f is an arbitrary computable function. Similarly, the second bound eliminates algorithms with complexity \(O( n^{ f(d) })\) for any computable f.
In this work we show that the problem is parameterizable in \(k+d\), and thus admits efficient (polynomial-time) solutions when both variables are bounded.
4.1 Algorithm for \({\text {VSC}}\)
In this section we present our algorithm \({\text {VerifySC}}\) for the problem \({\text {VSC}}\). First we define some relevant notation. In our definitions we consider a fixed input pair \((X, \mathsf {GoodW})\) to the \({\text {VSC}}\) problem, and a fixed sequence \(\tau \) with \(\mathcal {E}(\tau ) \subseteq X\).
Active Writes. A write \(w\in \mathcal {W}(\tau )\) is active in \(\tau \) if it is the last write of its variable in \(\tau \). Formally, for each \(w' \in \mathcal {W}(\tau )\) with \(\mathsf {var}(w') = \mathsf {var}(w)\) we have \(w' \le _{\tau } w\). We can then say that \(w\) is the active write of the variable \(\mathsf {var}(w)\) in \(\tau \).
Held Variables. A variable \(x \in \mathcal {G}\) is held in \(\tau \) if there exists a read \(r\in \mathcal {R}(X) \setminus \mathcal {E}(\tau )\) with \(\mathsf {var}(r) = x\) such that for each its good-write \(w\in \mathsf {GoodW}(r)\) we have \(w\in \tau \). In such a case we say that \(r\) holds x in \(\tau \). Note that several distinct reads may hold a single variable in \(\tau \).
Executable Events. An event \(e\in \mathcal {E}(X) \setminus \mathcal {E}(\tau )\) is executable in \(\tau \) if \(\mathcal {E}(\tau ) \cup \{e\}\) is a lower set of \((X,\mathsf {PO})\) and the following hold.
-
(1)
If \(e\) is a read, it has an active good-write \(w\in \mathsf {GoodW}(e)\) in \(\tau \).
-
(2)
If \(e\) is a write, its variable \(\mathsf {var}(e)\) is not held in \(\tau \).
Memory Maps. A memory map of \(\tau \) is a function from global variables to thread indices \({\text {MMap}}_{\tau }:\mathcal {G}\rightarrow [k]\) where for each variable \(x \in \mathcal {G}\), the map \({\text {MMap}}_{\tau }(x)\) captures the thread of the active write of x in \(\tau \).
Witness States. The sequence \(\tau \) is a witness prefix if the following hold.
-
(1)
\(\tau \) is a witness of \((\mathcal {E}(\tau ), \,\mathsf {GoodW}|\mathcal {R}(\tau ))\).
-
(2)
For each \(r\in X \setminus \mathcal {R}(\tau )\) that holds its variable \(\mathsf {var}(r)\) in \(\tau \), one of its good-writes \(w\in \mathsf {GoodW}(r)\) is active in \(\tau \).
Intuitively, \(\tau \) is a witness prefix if it satisfies all \({\text {VSC}}\) requirements modulo its events, and if each read not in \(\tau \) has at least one good-write still available to read-from in potential extensions of \(\tau \). For a witness prefix \(\tau \) we call its corresponding event set and memory map a witness state.
Figure 5 provides an example illustrating the above concepts, where for brevity of presentation, the variables are subscripted and the values are not displayed.
Event set X, and the good-writes function \(\mathsf {GoodW}\) denoted by the green dotted edges. The solid nodes are ordered vertically as they appear in \(\tau \). The grey dashed nodes are in \(X \setminus \mathcal {E}(\tau )\). Events
 and
and
 are executable in \(\tau \). Event
are executable in \(\tau \). Event
 is not, its good-write is not active in \(\tau \). Event
is not, its good-write is not active in \(\tau \). Event
 is also not executable, as its variable
is also not executable, as its variable
 is held by
is held by
 . The memory map of \(\tau \) is
. The memory map of \(\tau \) is
 and
and
 . \(\tau \) is a witness prefix, and \(\mathcal {E}(\tau )\) with \({\text {MMap}}_{\tau }\) together form its witness state.
. \(\tau \) is a witness prefix, and \(\mathcal {E}(\tau )\) with \({\text {MMap}}_{\tau }\) together form its witness state.

Algorithm. We are now ready to describe our algorithm \({\text {VerifySC}}\), in Algorithm 1 we present the pseudocode. We attempt to construct a witness of \((X, \mathsf {GoodW})\) by enumerating the witness states reachable by the following process. We start (Line 1) with an empty sequence \(\epsilon \) as the first witness prefix (and state). We maintain a worklist \(\mathcal {S}\) of so-far unprocessed witness prefixes, and a set \(\mathsf {Done}\) of reached witness states. Then we iteratively obtain new witness prefixes (and states) by considering an already obtained prefix (Line 3) and extending it with each possible executable event (Line 6). Crucially, when we arrive at a sequence \(\tau _{e}\), we include it only if no sequence \(\tau '\) with equal corresponding witness state has been reached yet (Line 7). We stop when we successfully create a witness (Line 4) or when we process all reachable witness states (Line 9).
Correctness and Complexity. We now highlight the correctness and complexity properties of \({\text {VerifySC}}\), while we refer to Appendix C of [30] for the proofs. The soundness follows straightforwardly by the fact that each sequence in \(\mathcal {S}\) is a witness prefix. This follows from a simple inductive argument that extending a witness prefix with an executable event yields another witness prefix. The completeness follows from the fact that given two witness prefixes \(\tau _1\) and \(\tau _2\) with equal induced witness state, these prefixes are “equi-extendable” to a witness. Indeed, if a suffix \(\tau ^*\) exists such that \(\tau _1 \circ \tau ^*\) is a witness of \((X, \mathsf {GoodW})\), then \(\tau _2 \circ \tau ^*\) is also a witness of \((X, \mathsf {GoodW})\). The time complexity of \({\text {VerifySC}}\) is bounded by \(O(n^{k + 1} \cdot k^{d + 1})\), for n events, k threads and d variables. The bound follows from the fact that there are at most \(n^{k} \cdot k^{d}\) pairwise distinct witness states. We thus have the following theorem.
Theorem 1
\({\text {VSC}}\) for n events, k threads and d variables is solvable in \(O(n^{k + 1} \cdot k^{d + 1})\) time. Moreover, if each variable is written by only one thread, \({\text {VSC}}\) is solvable in \(O(n^{k + 1} )\) time.
Implications. We now highlight some important implications of Theorem 1. Although \({\text {VSC}}\) is NP-hard [25], the theorem shows that the problem is parameterizable in \(k+d\), and thus in polynomial time when both parameters are bounded. Moreover, even when only k is bounded, the problem is fixed-parameter tractable in d, meaning that d only exponentiates a constant as opposed to n (e.g., we have a polynomial bound even when \(d=\log n\)). Finally, the algorithm is polynomial for a fixed number of threads regardless of d, when every memory location is written by only one thread (e.g., in producer-consumer settings, or in the concurrent-read-exclusive-write (CREW) concurrency model). These important facts brought forward by Theorem 1 indicate that \({\text {VSC}}\) is likely to be efficiently solvable in many practical settings, which in turn makes \(\mathsf {RVF}\) a good equivalence for SMC.
4.2 Practical Heuristics for \({\text {VerifySC}}\) in SMC
We now turn our attention to some practical heuristics that are expected to further improve the performance of \({\text {VerifySC}}\) in the context of SMC.
1. Limiting the Search Space. We employ two straightforward improvements to \({\text {VerifySC}}\) that significantly reduce the search space in practice. Consider the for-loop in Line 5 of Algorithm 1 enumerating the possible extensions of \(\tau \). This enumeration can be sidestepped by the following two greedy approaches.
-
(1)
If there is a read \(r\) executable in \(\tau \), then extend \(\tau \) with \(r\) and do not enumerate other options.
-
(2)
Let
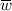 be an active write in \(\tau \) such that
be an active write in \(\tau \) such that  is not a good-write of any \(r\in \mathcal {R}(X) \setminus \mathcal {E}(\tau )\). Let \(w\in \mathcal {W}(X) \setminus \mathcal {E}(\tau )\) be a write of the same variable (
is not a good-write of any \(r\in \mathcal {R}(X) \setminus \mathcal {E}(\tau )\). Let \(w\in \mathcal {W}(X) \setminus \mathcal {E}(\tau )\) be a write of the same variable ( ), note that \(w\) is executable in \(\tau \). If \(w\) is also not a good-write of any \(r\in \mathcal {R}(X) \setminus \mathcal {E}(\tau )\), then extend \(\tau \) with \(w\) and do not enumerate other options.
), note that \(w\) is executable in \(\tau \). If \(w\) is also not a good-write of any \(r\in \mathcal {R}(X) \setminus \mathcal {E}(\tau )\), then extend \(\tau \) with \(w\) and do not enumerate other options.
The enumeration of Line 5 then proceeds only if neither of the above two techniques can be applied for \(\tau \). This extension of \({\text {VerifySC}}\) preserves completeness (not only when used during SMC, but in general), and it can be significantly faster in practice. For clarity of presentation we do not fully formalize this extended version, as its worst-case complexity remains the same.
2. Closure. We introduce closure, a low-cost filter for early detection of \({\text {VSC}}\) instances \((X, \mathsf {GoodW})\) with no witness. The notion of closure, its beneficial properties and construction algorithms are well-studied for the reads-from consistency verification problems [21, 22, 31], i.e., problems where a desired reads-from function is provided as input instead of a desired good-writes function \(\mathsf {GoodW}\). Further, the work of [23] studies closure with respect to a good-writes function, but only for partial orders of Mazurkiewicz width 2 (i.e., for partial orders with no triplet of pairwise conflicting and pairwise unordered events). Here we define closure for all good-writes instances \((X, \mathsf {GoodW})\), with the underlying partial order (in our case, the program order \(\mathsf {PO}\)) of arbitrary Mazurkiewicz width.
Given a \({\text {VSC}}\) instance \((X, \mathsf {GoodW})\), its closure P(X) is the weakest partial order that refines the program order (\(P\sqsubseteq \mathsf {PO}|X\)) and further satisfies the following conditions. Given a read \(r\in \mathcal {R}(X)\), let \(Cl(r) = \mathsf {GoodW}(r) \cap \mathsf {VisibleW}_{P}(r)\). The following must hold.
-
(1)
\(Cl(r) \ne \emptyset \).
-
(2)
If \((Cl(r), \,P|Cl(r))\) has a least element \(w\), then \(w<_{P} r\).
-
(3)
If \((Cl(r), \,P|Cl(r))\) has a greatest element \(w\), then for each
 with
with  , if
, if  then
then  .
. -
(4)
For each
 with
with  , if each \(w\in Cl(r)\) satisfies
, if each \(w\in Cl(r)\) satisfies  , then we have
, then we have  .
.
If \((X, \mathsf {GoodW})\) has no closure (i.e., there is no P with the above conditions), then \((X, \mathsf {GoodW})\) provably has no witness. If \((X, \mathsf {GoodW})\) has closure P, then each witness \(\tau \) of \({\text {VSC}}(X, \mathsf {GoodW})\) provably refines P (i.e., \(\tau \sqsubseteq P\)).
Finally, we explain how closure can be used by \({\text {VerifySC}}\). Given an input \((X, \mathsf {GoodW})\), the closure procedure is carried out before \({\text {VerifySC}}\) is called. Once the closure P of \((X, \mathsf {GoodW})\) is constructed, since each solution of \({\text {VSC}}(X, \mathsf {GoodW})\) has to refine P, we restrict \({\text {VerifySC}}\) to only consider sequences refining P. This is ensured by an extra condition in Line 5 of Algorithm 1, where we proceed with an event \(e\) only if it is minimal in P restricted to events not yet in the sequence. This preserves completeness, while further reducing the search space to consider for \({\text {VerifySC}}\).
3. VerifySC Guided by Auxiliary Trace. In our SMC approach, each time we generate a \({\text {VSC}}\) instance \((X, \mathsf {GoodW})\), we further have available an auxiliary trace \(\widetilde{\sigma }\). In \(\widetilde{\sigma }\), either all-but-one, or all, good-writes conditions of \(\mathsf {GoodW}\) are satisfied. If all good writes in \(\mathsf {GoodW}\) are satisfied, we already have \(\widetilde{\sigma }\) as a witness of \((X, \mathsf {GoodW})\) and hence we do not need to run \({\text {VerifySC}}\) at all. On the other hand, if case all-but-one are satisfied, we use \(\widetilde{\sigma }\) to guide the search of \({\text {VerifySC}}\), as described below.
We guide the search by deciding the order in which we process the sequences of the worklist \(\mathcal {S}\) in Algorithm 1. We use the auxiliary trace \(\widetilde{\sigma }\) with \(\mathcal {E}(\widetilde{\sigma }) = X\). We use \(\mathcal {S}\) as a last-in-first-out stack, that way we search for a witness in a depth-first fashion. Then, in Line 5 of Algorithm 1 we enumerate the extension events in the reverse order of how they appear in \(\widetilde{\sigma }\). We enumerate in reverse order, as each resulting extension is pushed into our worklist \(\mathcal {S}\), which is a stack (last-in-first-out). As a result, in Line 3 of the subsequent iterations of the main while loop, we pop extensions from \(\mathcal {S}\) in order induced by \(\widetilde{\sigma }\).
5 Stateless Model Checking
We are now ready to present our SMC algorithm \({\text {RVF-SMC}}\) that uses \(\mathsf {RVF}\) to model check a concurrent program. \({\text {RVF-SMC}}\) is a sound and complete algorithm for local safety properties, i.e., it is guaranteed to discover all local states that each thread visits.
\({\text {RVF-SMC}}\) is a recursive algorithm. Each recursive call of \({\text {RVF-SMC}}\) is argumented by a tuple \((X, \mathsf {GoodW}, \sigma , \mathcal {C})\) where:
-
(1)
X is a proper set of events.
-
(2)
\(\mathsf {GoodW}:\mathcal {R}(X) \rightarrow 2^{\mathcal {W}(X)}\) is a desired good-writes function.
-
(3)
\(\sigma \) is a valid trace that is a witness of \((X, \mathsf {GoodW})\).
-
(4)
\(\mathcal {C}:\mathcal {R}\rightarrow {\text {Threads}}\rightarrow \mathbb {N}\) is a partial function called causal map that tracks implicitly, for each read \(r\), the writes that have already been considered as reads-from sources of \(r\).
Further, we maintain a function \(\mathsf {ancestors}:\mathcal {R}(X) \rightarrow \{ \mathsf {true}, \mathsf {false}\}\), where for each read \(r\in \mathcal {R}(X)\), \(\mathsf {ancestors}(r)\) stores a boolean backtrack signal for \(r\). We now provide details on the notions of causal maps and backtrack signals.
Causal Maps. The causal map \(\mathcal {C}\) serves to ensure that no more than one maximal trace is explored per \(\mathsf {RVF}\) partitioning class. Given a read \(r\in \mathsf {enabled}(\sigma )\) enabled in a trace \(\sigma \), we define \(\mathsf {forbids}_{\sigma }^{\mathcal {C}}(r)\) as the set of writes in \(\sigma \) such that \(\mathcal {C}\) forbids \(r\) to read-from them. Formally, \(\mathsf {forbids}_{\sigma }^{\mathcal {C}}(r) = \emptyset \) if \(r\not \in \mathsf {dom}(\mathcal {C})\), otherwise \(\mathsf {forbids}_{\sigma }^{\mathcal {C}}(r) = \{ w\in \mathcal {W}(\sigma ) \;|\; w\text { is within first }\mathcal {C}(r)(\mathsf {thr}(w)) \text { events of }\sigma _{\mathsf {thr}} \}\). We say that a trace \(\sigma \) satisfies \(\mathcal {C}\) if for each \(r\in \mathcal {R}(\sigma )\) we have \(\mathsf {RF}_{\sigma }(r) \not \in \mathsf {forbids}_{\sigma }^{\mathcal {C}}(r)\).
Backtrack Signals. Each call of \({\text {RVF-SMC}}\) (with its \(\mathsf {GoodW}\)) operates with a trace \(\widetilde{\sigma }\) satisfying \(\mathsf {GoodW}\) that has only reads as enabled events. Consider one of those enabled reads \(r\in \mathsf {enabled}(\widetilde{\sigma })\). Each maximal trace satisfying \(\mathsf {GoodW}\) shall contain \(r\), and further, one of the following two cases is true:
-
(1)
In all maximal traces \(\sigma '\) satisfying \(\mathsf {GoodW}\), we have that \(r\) reads-from some write of \(\mathcal {W}(\widetilde{\sigma })\) in \(\sigma '\).
-
(2)
There exists a maximal trace \(\sigma '\) satisfying \(\mathsf {GoodW}\), such that \(r\) reads-from a write not in \(\mathcal {W}(\widetilde{\sigma })\) in \(\sigma '\).
Whenever we can prove that the first above case is true for \(r\), we can use this fact to prune away some recursive calls of \({\text {RVF-SMC}}\) while maintaining completeness. Specifically, we leverage the following crucial lemma, and present the proof in Appendix D of [30].
Lemma 1
Consider a call \({\text {RVF-SMC}}(X, \mathsf {GoodW}, \sigma , \mathcal {C})\) and a trace \(\widetilde{\sigma }\) extending \(\sigma \) maximally such that no event of the extension is a read. Let \(r\in \mathsf {enabled}(\widetilde{\sigma })\) such that \(r\not \in \mathsf {dom}(\mathcal {C})\). If there exists a trace \(\sigma '\) that (i) satisfies \(\mathsf {GoodW}\) and \(\mathcal {C}\), and (ii) contains \(r\) with \(\mathsf {RF}_{\sigma '}(r) \not \in \mathcal {W}(\widetilde{\sigma })\), then there exists a trace  that (i) satisfies \(\mathsf {GoodW}\) and \(\mathcal {C}\), (ii) contains \(r\) with
that (i) satisfies \(\mathsf {GoodW}\) and \(\mathcal {C}\), (ii) contains \(r\) with  , and (iii) contains a write \(w\not \in \mathcal {W}(\widetilde{\sigma })\) with \(r \bowtie w\) and \(\mathsf {thr}(r) \ne \mathsf {thr}(w)\).
, and (iii) contains a write \(w\not \in \mathcal {W}(\widetilde{\sigma })\) with \(r \bowtie w\) and \(\mathsf {thr}(r) \ne \mathsf {thr}(w)\).
We then compute a boolean backtrack signal for a given \({\text {RVF-SMC}}\) call and read \(r\in \mathsf {enabled}(\widetilde{\sigma })\) to capture satisfaction of the consequent of Lemma 1. If the computed backtrack signal is false, we can safely stop the \({\text {RVF-SMC}}\) exploration of this specific call and backtrack to its recursion parent.

Algorithm. We are now ready to describe our algorithm \({\text {RVF-SMC}}\) in detail, Algorithm 2 captures the pseudocode of \({\text {RVF-SMC}}(X, \mathsf {GoodW}, \sigma , \mathcal {C})\). First, in Line 1 we extend \(\sigma \) to \(\widetilde{\sigma }\) maximally such that no event of the extension is a read. Then in Lines 2–5 we update the backtrack signals for ancestors of our current recursion call. After this, in Lines 6–11 we construct a sequence of reads enabled in \(\widetilde{\sigma }\). Finally, we proceed with the main while-loop in Line 13. In each while-loop iteration we process an enabled read \(r\) (Line 14), and we perform no more while-loop iterations in case we receive a \(\mathsf {false}\) backtrack signal for \(r\). When processing \(r\), first we collect its viable reads-from sources in Line 17, then we group the sources by value they write in Line 18, and then in iterations of the for-loop in Line 19 we consider each value-group. In Line 20 we form the event set, and in Line 21 we form the good-write function that designates the value-group as the good-writes of \(r\). In Line 22 we use \({\text {VerifySC}}\) to generate a witness, and in case it exists, we recursively call \({\text {RVF-SMC}}\) in Line 26 with the newly obtained events, good-write constraint for \(r\), and witness.
To preserve completeness of \({\text {RVF-SMC}}\), the backtrack-signals technique can be utilized only for reads \(r\) with undefined causal map \(r\not \in \mathsf {dom}(\mathcal {C})\) (cf. Lemma 1). The order of the enabled reads imposed by Lines 6–11 ensures that subsequently, in iterations of the loop in Line 13 we first consider all the reads where we can utilize the backtrack signals. This is an insightful heuristic that often helps in practice, though it does not improve the worst-case complexity.
\({\text {RVF-SMC}}\) (Algorithm 2). Circles represent nodes of the recursion tree. Below each circle is its corresponding event set \(\mathcal {E}(\widetilde{\sigma })\) and the enabled reads (dashed grey). Writes with green background are good-writes \((\mathsf {GoodW})\) of its corresponding-variable read. Writes with red background are forbidden by \(\mathcal {C}\) for its corresponding-variable read. Dashed arrows represent recursive calls. (Color figure online)
Example. Figure 6 displays a simple concurrent program on the left, and its corresponding \({\text {RVF-SMC}}\) (Algorithm 2) run on the right. We start with \({\text {RVF-SMC}}(\emptyset , \emptyset , \epsilon , \emptyset )\) (A). By performing the extension (Line 1) we obtain the events and enabled reads as shown below (A). First we process read
 (Line 14). The read can read-from
(Line 14). The read can read-from
 and
and
 , both write the same value so they are grouped together as good-writes of
, both write the same value so they are grouped together as good-writes of
 . A witness is found and a recursive call to (B) is performed. In (B), the only enabled event is
. A witness is found and a recursive call to (B) is performed. In (B), the only enabled event is
 . It can read-from
. It can read-from
 and
and
 , both write the same value so they are grouped for
, both write the same value so they are grouped for
 . A witness is found, a recursive call to (C) is performed, and (C) concludes with a maximal trace. Crucially, in (C) the event
. A witness is found, a recursive call to (C) is performed, and (C) concludes with a maximal trace. Crucially, in (C) the event
 is discovered, and since it is a potential new reads-from source for
is discovered, and since it is a potential new reads-from source for
 , a backtrack signal is sent to (A). Hence after \({\text {RVF-SMC}}\) backtracks to (A), in (A) it needs to perform another iteration of Line 13 while-loop. In (A), first the causal map \(\mathcal {C}\) is updated to forbid
, a backtrack signal is sent to (A). Hence after \({\text {RVF-SMC}}\) backtracks to (A), in (A) it needs to perform another iteration of Line 13 while-loop. In (A), first the causal map \(\mathcal {C}\) is updated to forbid
 and
and
 for \(r_1\). Then, read
for \(r_1\). Then, read
 is processed from (A), creating (D). In (D),
is processed from (A), creating (D). In (D),
 is the only enabled event, and
is the only enabled event, and
 is its only \(\mathcal {C}\)-allowed write. This results in (E) which reports a maximal trace. The algorithm backtracks and concludes, reporting two maximal traces in total.
is its only \(\mathcal {C}\)-allowed write. This results in (E) which reports a maximal trace. The algorithm backtracks and concludes, reporting two maximal traces in total.
Theorem 2
Consider a concurrent program \(\mathcal {H}\) of k threads and d variables, with n the length of the longest trace in \(\mathcal {H}\). \({\text {RVF-SMC}}\) is a sound and complete algorithm for local safety properties in \(\mathcal {H}\). The time complexity of \({\text {RVF-SMC}}\) is \(k^{d} \cdot n^{O(k)} \cdot \beta \), where \(\beta \) is the size of the \(\mathsf {RVF}\) trace partitioning of \(\mathcal {H}\).
Novelties of the Exploration. Here we highlight some key aspects of \({\text {RVF-SMC}}\). First, we note that \({\text {RVF-SMC}}\) constructs the traces incrementally with each recursion step, as opposed to other approaches such as [15, 22] that always work with maximal traces. The reason of incremental traces is technical and has to do with the value-based treatment of the \(\mathsf {RVF}\) partitioning. We note that the other two value-based approaches [23, 24] also operate with incremental traces. However, \({\text {RVF-SMC}}\) brings certain novelties compared to these two methods. First, the exploration algorithm of [24] can visit the same class of the partitioning (and even the same trace) an exponential number of times by different recursion branches, leading to significant performance degradation. The exploration algorithm of [23] alleviates this issue using the causal map data structure, similar to our algorithm. The causal map data structure can provably limit the number of revisits to polynomial (for a fixed number of threads), and although it offers an improvement over the exponential revisits, it can still affect performance. To further improve performance in this work, our algorithm combines causal maps with a new technique, which is the backtrack signals. Causal maps and backtrack signals together are very effective in avoiding having different branches of the recursion visit the same \(\mathsf {RVF}\) class.
Beyond RVF Partitioning. While \({\text {RVF-SMC}}\) explores the \(\mathsf {RVF}\) partitioning in the worst case, in practice it often operates on a partitioning coarser than the one induced by the \(\mathsf {RVF}\) equivalence. Specifically, \({\text {RVF-SMC}}\) may treat two traces \(\sigma _1\) and \(\sigma _2\) with same events (\(\mathcal {E}(\sigma _1) = \mathcal {E}(\sigma _2)\)) and value function (\(\mathsf {val}_{\sigma _1} = \mathsf {val}_{\sigma _2}\)) as equivalent even when they differ in some causal orderings (\(\mathsf {\mapsto }_{\sigma _1} |\mathcal {R}\ne \mathsf {\mapsto }_{\sigma _2} |\mathcal {R}\)). To see an example of this, consider the program and the \({\text {RVF-SMC}}\) run in Fig. 6. The recursion node (C) spans all traces where (i)
 reads-from either
reads-from either
 or
or
 , and (ii)
, and (ii)
 reads-from either
reads-from either
 or
or
 . Consider two such traces \(\sigma _1\) and \(\sigma _2\), with
. Consider two such traces \(\sigma _1\) and \(\sigma _2\), with
 and
and
 . We have
. We have
 and
and
 , and yet \(\sigma _1\) and \(\sigma _2\) are (soundly) considered equivalent by \({\text {RVF-SMC}}\). Hence the \(\mathsf {RVF}\) partitioning is used to upper-bound the time complexity of \({\text {RVF-SMC}}\). We remark that the algorithm is always sound, i.e., it is guaranteed to discover all thread states even when it does not explore the \(\mathsf {RVF}\) partitioning in full.
, and yet \(\sigma _1\) and \(\sigma _2\) are (soundly) considered equivalent by \({\text {RVF-SMC}}\). Hence the \(\mathsf {RVF}\) partitioning is used to upper-bound the time complexity of \({\text {RVF-SMC}}\). We remark that the algorithm is always sound, i.e., it is guaranteed to discover all thread states even when it does not explore the \(\mathsf {RVF}\) partitioning in full.
6 Experiments
In this section we describe the experimental evaluation of our SMC approach \({\text {RVF-SMC}}\). We have implemented \({\text {RVF-SMC}}\) as an extension in Nidhugg [27], a state-of-the-art stateless model checker for multithreaded C/C++ programs that operates on LLVM Intermediate Representation. First we assess the advantages of utilizing the \(\mathsf {RVF}\) equivalence in SMC as compared to other trace equivalences. Then we perform ablation studies to demonstrate the impact of the backtrack signals technique (cf. Sect. 5) and the \({\text {VerifySC}}\) heuristics (cf. Sect. 4.2).
In our experiments we compare \({\text {RVF-SMC}}\) with several state-of-the-art SMC tools utilizing different trace equivalences. First we consider \({\text {VC-DPOR}}\) [23], the SMC approach operating on the value-centric equivalence. Then we consider \(\mathsf {Nidhugg/rfsc}\) [22], the SMC algorithm utilizing the reads-from equivalence. Further we consider \({\text {DC-DPOR}}\) [21] that operates on the data-centric equivalence, and finally we compare with \(\mathsf {Nidhugg/source}\) [15] utilizing the Mazurkiewicz equivalence.Footnote 1 The works of [22] and [32] in turn compare the \(\mathsf {Nidhugg/rfsc}\) algorithm with additional SMC tools, namely \(\mathsf {GenMC}\) [28] (with reads-from equivalence), \(\mathsf {RCMC}\) [29] (with Mazurkiewicz equivalence), and \(\mathsf {CDSChecker}\) [33] (with Mazurkiewicz equivalence), and thus we omit those tools from our evaluation.
There are two main objectives to our evaluation. First, from Sect. 3 we know that the \(\mathsf {RVF}\) equivalence can be up to exponentially coarser than the other equivalences, and we want to discover how often this happens in practice. Second, in cases where \(\mathsf {RVF}\) does provide reduction in the trace-partitioning size, we aim to see whether this reduction is accompanied by the reduction in the runtime of \({\text {RVF-SMC}}\) operating on \(\mathsf {RVF}\) equivalence.
Setup. We consider 119 benchmarks in total in our evaluation. Each benchmark comes with a scaling parameter, called the unroll bound. The parameter controls the bound on the number of iterations in all loops of the benchmark. For each benchmark and unroll bound, we capture the number of explored maximal traces, and the total running time, subject to a timeout of one hour. In Appendix E of [30] we provide further details on our setup.
Results. We provide a number of scatter plots summarizing the comparison of \({\text {RVF-SMC}}\) with other state-of-the-art tools. In Fig. 7, Fig. 8, Fig. 9 and Fig. 10 we provide comparison both in runtimes and explored traces, for \({\text {VC-DPOR}}\), \(\mathsf {Nidhugg/rfsc}\), \({\text {DC-DPOR}}\), and \(\mathsf {Nidhugg/source}\), respectively. In each scatter plot, both its axes are log-scaled, the opaque red line represents equality, and the two semi-transparent lines represent an order-of-magnitude difference. The points are colored green when \({\text {RVF-SMC}}\) achieves trace reduction in the underlying benchmark, and blue otherwise.
Discussion: Significant Trace Reduction. In Table 1 we provide the results for several benchmarks where \(\mathsf {RVF}\) achieves significant reduction in the trace-partitioning size. This is typically accompanied by significant runtime reduction, allowing is to scale the benchmarks to unroll bounds that other tools cannot handle. Examples of this are 27_Boop4 and scull_loop, two toy Linux kernel drivers.
In several benchmarks the number of explored traces remains the same for \({\text {RVF-SMC}}\) even when scaling up the unroll bound, see 45_monabsex1, reorder_5 and singleton in Table 1. The singleton example is further interesting, in that while \({\text {VC-DPOR}}\) and \({\text {DC-DPOR}}\) also explore few traces, they still suffer in runtime due to additional redundant exploration, as described in Sects. 1 and 5.
Discussion: Little-to-no Trace Reduction. Table 2 presents several benchmarks where the \(\mathsf {RVF}\) partitioning achieves little-to-no reduction. In these cases the well-engineered \(\mathsf {Nidhugg/rfsc}\) and \(\mathsf {Nidhugg/source}\) dominate the runtime.
RVF-SMC Ablation Studies. Here we demonstrate the effect that follows from our \({\text {RVF-SMC}}\) algorithm utilizing the approach of backtrack signals (see Sect. 5) and the heuristics of \({\text {VerifySC}}\) (see Sect. 4.2). These techniques have no effect on the number of the explored traces, thus we focus on the runtime. The left plot of Fig. 11 compares \({\text {RVF-SMC}}\) as is with a \({\text {RVF-SMC}}\) version that does not utilize the backtrack signals (achieved by simply keeping the \(\mathsf {backtrack}\) flag in Algorithm 2 always \(\mathsf {true}\)). The right plot of Fig. 11 compares \({\text {RVF-SMC}}\) as is with a \({\text {RVF-SMC}}\) version that employs \({\text {VerifySC}}\) without the closure and auxiliary-trace heuristics. We can see that the techniques almost always result in improved runtime. The improvement is mostly within an order of magnitude, and in a few cases there is several-orders-of-magnitude improvement.
Finally, in Fig. 12 we illustrate how much time during \({\text {RVF-SMC}}\) is typically spent on \({\text {VerifySC}}\) (i.e., on solving \({\text {VSC}}\) instances generated during \({\text {RVF-SMC}}\)).
Ablation studies of \({\text {RVF-SMC}}\). The left plot compares \({\text {RVF-SMC}}\) with and without backtrack signals. The right plots compares \({\text {RVF-SMC}}\) with and without the closure and auxiliary-trace heuristics of Sect. 4.2.
7 Conclusions
In this work we developed \({\text {RVF-SMC}}\), a new SMC algorithm for the verification of concurrent programs using a novel equivalence called reads-value-from (RVF). On our way to \({\text {RVF-SMC}}\), we have revisited the famous \({\text {VSC}}\) problem [25]. Despite its NP-hardness, we have shown that the problem is parameterizable in \(k+d\) (for k threads and d variables), and becomes even fixed-parameter tractable in d when k is constant. Moreover we have developed practical heuristics that solve the problem efficiently in many practical settings.
Our \({\text {RVF-SMC}}\) algorithm couples our solution for \({\text {VSC}}\) to a novel exploration of the underlying RVF partitioning, and is able to model check many concurrent programs where previous approaches time-out. Our experimental evaluation reveals that RVF is very often the most effective equivalence, as the underlying partitioning is exponentially coarser than other approaches. Moreover, \({\text {RVF-SMC}}\) generates representatives very efficiently, as the reduction in the partitioning is often met with significant speed-ups in the model checking task. Interesting future work includes further improvements over the \({\text {VSC}}\), as well as extensions of \({\text {RVF-SMC}}\) to relaxed memory models.
Notes
- 1.
The MCR algorithm [24] is beyond the experimental scope of this work, as that tool handles Java programs and uses heavyweight SMT solvers that require fine-tuning.
References
Musuvathi, M., Qadeer, S., Ball, T., Basler, G., Nainar, P.A., Neamtiu, I.: Finding and reproducing heisenbugs in concurrent programs. In: OSDI (2008)
Clarke Jr., E.M., Grumberg, O., Peled, D.A.: Model Checking. MIT Press, Cambridge (1999)
Godefroid, P.: Model checking for programming languages using VeriSoft. In: POPL (1997)
Godefroid, P.: Software model checking: the VeriSoft approach. FMSD 26(2), 77–101 (2005)
Ball, T., Musuvathi, M., Qadeer, S.: Chess: a systematic testing tool for concurrent software. Technical report (2007)
Godefroid, P.: Partial-Order Methods for the Verification of Concurrent Systems: An Approach to the State-Explosion Problem. Springer, Secaucus (1996)
Musuvathi, M., Qadeer, S.: Iterative context bounding for systematic testing of multithreaded programs. SIGPLAN Not. 42(6), 446–455 (2007)
Lal, A., Reps, T.: Reducing concurrent analysis under a context bound to sequential analysis. FMSD 35(1), 73–97 (2009)
Chini, P., Kolberg, J., Krebs, A., Meyer, R., Saivasan, P.: On the complexity of bounded context switching. In: Pruhs, K., Sohler, C. (eds.) 25th Annual European Symposium on Algorithms (ESA 2017), Leibniz International Proceedings in Informatics (LIPIcs), Dagstuhl, Germany, vol. 87, pp. 27:1–27:15. Schloss Dagstuhl-Leibniz-Zentrum fuer Informatik. (2017)
Baumann, P., Majumdar, R., Thinniyam, R.S., Zetzsche, G.: Context-bounded verification of liveness properties for multithreaded shared-memory programs. In: Proceedings of ACM Programming Language, vol. 5, no. POPL, pp. 1–31 (2021)
Clarke, E.M., Grumberg, O., Minea, M., Peled, D.: State space reduction using partial order techniques. STTT 2(3), 279–287 (1999)
Peled, D.: All from one, one for all: on model checking using representatives. In: CAV (1993)
Mazurkiewicz, A.: Trace theory. In: Brauer, W., Reisig, W., Rozenberg, G. (eds.) ACPN 1986. LNCS, vol. 255, pp. 278–324. Springer, Heidelberg (1987). https://doi.org/10.1007/3-540-17906-2_30
Flanagan, C., Godefroid, P.: Dynamic partial-order reduction for model checking software. In: POPL (2005)
Abdulla, P., Aronis, S., Jonsson, B., Sagonas, K.: Optimal dynamic partial order reduction. In: POPL (2014)
Nguyen, H.T.T., Rodríguez, C., Sousa, M., Coti, C., Petrucci, L.: Quasi-optimal partial order reduction. In: Computer Aided Verification - 30th International Conference, CAV 2018, Held as Part of the Federated Logic Conference, FloC 2018, Oxford, UK, 14–17 July, 2018, Proceedings, Part II, pp. 354–371 (2018)
Aronis, S., Jonsson, B., Lång, M., Sagonas, K.: Optimal dynamic partial order reduction with observers. In: Beyer, D., Huisman, M. (eds.) Tools and Algorithms for the Construction and Analysis of Systems, pp. 229–248. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-89963-3_14
Godefroid, P., Pirottin, D.: Refining dependencies improves partial-order verification methods (extended abstract). In: CAV (1993)
Albert, E., Arenas, P., de la Banda, M.G., Gómez-Zamalloa, M., Stuckey, P.J.: Context-sensitive dynamic partial order reduction. In: Majumdar, R., Kunčak, V. (eds.) CAV 2017. LNCS, vol. 10426, pp. 526–543. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63387-9_26
Kokologiannakis, M., Raad, A., Vafeiadis, V.: Effective lock handling in stateless model checking. In: Proceedings of ACM Programming Language, vol. 3, no. OOPSLA, pp. 1–26 (2019)
Chalupa, M., Chatterjee, K., Pavlogiannis, A., Sinha, N., Vaidya, K.: Data-centric dynamic partial order reduction. In: Proceedings of ACM Programming Language, vol. 2, no. POPL, pp. 31:1–31:30 (2017)
Abdulla, P.A., Atig, M.F., Jonsson, B., Lång, M., Ngo, T.P., Sagonas, K.: Optimal stateless model checking for reads-from equivalence under sequential consistency. In: Proceedings of ACM Programming Language, vol. 3, no. OOPSLA, pp. 1–29 (2019)
Chatterjee, K., Pavlogiannis, A., Toman, V.: Value-centric dynamic partial order reduction. In: Proceedings of ACM Programming Language, vol. 3, no. OOPSLA, pp. 1–29 (2019)
Huang, J.: Stateless model checking concurrent programs with maximal causality reduction. In: PLDI (2015)
Gibbons, P.B., Korach, E.: Testing shared memories. SIAM J. Comput. 26(4), 1208–1244 (1997)
Abdulla, P.A., Atig, M.F., Jonsson, B., Ngo, T.P.: Optimal stateless model checking under the release-acquire semantics. In: Proceedings of ACM Programming Language, vol. 2, no. OOPSLA, pp. 135:1–135:29 (2018)
Abdulla, P.A., Aronis, S., Atig, M.F., Jonsson, B., Leonardsson, C., Sagonas, K.: Stateless model checking for TSO and PSO. Acta Informatica 54(8), 789–818 (2016). https://doi.org/10.1007/s00236-016-0275-0
Kokologiannakis, M., Raad, A., Vafeiadis, V.: Model checking for weakly consistent libraries. In: Proceedings of the 40th ACM SIGPLAN Conference on Programming Language Design and Implementation, PLDI 2019, New York, NY, USA, pp. 96–110. ACM (2019)
Kokologiannakis, M., Lahav, O., Sagonas, K., Vafeiadis, V.: Effective stateless model checking for c/c++ concurrency. In: Proceedings of ACM Programming Language, 2, no. POPL, pp. 17:1–17:32 (2017)
Agarwal, P., Chatterjee, K., Pathak, S., Pavlogiannis, A., Toman, V.: Stateless model checking under a reads-value-from equivalence. CoRR/arXiv abs/2105.06424 (2021)
Pavlogiannis, A.: Fast, sound, and effectively complete dynamic race prediction. In: Proceedings ACM Programming Language, vol. 4, no. POPL, pp. 1–29 (2019)
Lång, M., Sagonas, K.: Parallel graph-based stateless model checking. In: Hung, D.V., Sokolsky, O. (eds.) ATVA 2020. LNCS, vol. 12302, pp. 377–393. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-59152-6_21
Norris, B., Demsky, B.: A practical approach for model checking C/C++11 code. ACM Trans. Program. Lang. Syst. 38(3), 10:1–10:51 (2016)
Acknowledgments
The research was partially funded by the ERC CoG 863818 (ForM-SMArt) and the Vienna Science and Technology Fund (WWTF) through project ICT15-003.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2021 The Author(s)
About this paper
Cite this paper
Agarwal, P., Chatterjee, K., Pathak, S., Pavlogiannis, A., Toman, V. (2021). Stateless Model Checking Under a Reads-Value-From Equivalence. In: Silva, A., Leino, K.R.M. (eds) Computer Aided Verification. CAV 2021. Lecture Notes in Computer Science(), vol 12759. Springer, Cham. https://doi.org/10.1007/978-3-030-81685-8_16
Download citation
DOI: https://doi.org/10.1007/978-3-030-81685-8_16
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-81684-1
Online ISBN: 978-3-030-81685-8
eBook Packages: Computer ScienceComputer Science (R0)










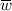 be an active write in
be an active write in  is not a good-write of any
is not a good-write of any  ), note that
), note that  with
with  , if
, if  then
then  .
. with
with  , if each
, if each  , then we have
, then we have  .
.





