Abstract
Some of the most significant high-level properties of currencies are the sums of certain account balances. Properties of such sums can ensure the integrity of currencies and transactions. For example, the sum of balances should not be changed by a transfer operation. Currencies manipulated by code present a verification challenge to mathematically prove their integrity by reasoning about computer programs that operate over them, e.g., in Solidity. The ability to reason about sums is essential: even the simplest ERC-20 token standard of the Ethereum community provides a way to access the total supply of balances.
Unfortunately, reasoning about code written against this interface is non-trivial: the number of addresses is unbounded, and establishing global invariants like the preservation of the sum of the balances by operations like transfer requires higher-order reasoning. In particular, automated reasoners do not provide ways to specify summations of arbitrary length.
In this paper, we present a generalization of first-order logic which can express the unbounded sum of balances. We prove the decidablity of one of our extensions and the undecidability of a slightly richer one. We introduce first-order encodings to automate reasoning over software transitions with summations. We demonstrate the applicability of our results by using SMT solvers and first-order provers for validating the correctness of common transitions in smart contracts.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
A basic challenge in smart contract verification is how to express the functional correctness of transactions, such as currency minting or transferring between accounts. Typically, the correctness of such a transaction can be verified by proving that the transaction leaves the sum of certain account balances unchanged.
Consider for example the task of minting an unbounded number of tokens in the simplified ERC-20 token standard of the Ethereum community [32], as illustrated in Fig. 1Footnote 1. This example deposits the minted amount (n) into the receiver’s address (a) and we need to ensure that the mint operation only changed the balance of the receiver. To do so, in addition to (i) proving that the balance of the receiver has been increased by n, we also need to verify that (ii) the account balance of every user address a\('\) different than a has not been changed during the mint operation and that (iii) the sum of all balances changed exactly by the amount that was minted. The validity of these three requirements (i)-(iii), formulated as the post-conditions of Fig. 1, imply its functional correctness.
Surprisingly, proving formulas similar to the post-conditions of Fig. 1 is challenging for state-of-the-art automated reasoners, such as SMT solvers [6, 7, 9] and first-order provers [11, 19, 34]: it requires reasoning that links local changes of the receiver (a) with a global state capturing the sum of all balances, as well as constructing that global state as an aggregate of an unbounded but finite number of
 balances. Moreover, our encoding of the problem uses discrete coins that are minted and deposited, whose number is unbounded but finite as well.
balances. Moreover, our encoding of the problem uses discrete coins that are minted and deposited, whose number is unbounded but finite as well.
In this paper we address verification challenges of software transactions with aggregate properties, such as preservation of sums by transitions that manipulate low-level, individual entities. Such properties are best expressed in higher-order logic, hindering the use of existing automated reasoners for proving them. To overcome such a reasoning limitation, we introduce Sum Logic (SL) as a generalization of first-order logic, in particular of Presburger arithmetic. Previous works [12, 21, 31] have also introduced extensions of first-order logic with aggregates by counting quantifiers or generalized quantifiers. In Sum Logic (SL) we only consider the special case of integer sums over uninterpreted functions, allowing us to formalize SL properties with and about unbounded sums, in particular sums of account balances, without higher-order operations (Sect. 3). We prove the decidability of one of our SL extensions and the undecidability of a slightly richer one (Sect. 4). Given previous results [21], our undecidability result is not surprising. In contrast, what may be unexpected is our decidability result and the fact that we can use our first-order fragment for a convenient and practical new way to verify the correctness of smart contracts.
We further introduce first-order encodings which enable automated reasoning over software transactions with summations in SL (Sect. 5). Unlike [5], where SMT-specific extensions supporting higher-order reasoning have been introduced, the logical encodings we propose allow one to use existing reasoners without any modification. We are not restricted to SMT reasoning, but can also leverage generic automated reasoners, such as first-order theorem provers, supporting first-order logic. We believe our results ease applying automated reasoning to smart contract verification even for non-experts.
We demonstrate the practical applicability of our results by using SMT solvers and first-order provers for validating the correctness of common financial transitions appearing in smart contracts (Sect. 6). We refer to these transitions as smart transitions. We encode SL into pure first-order logic by adding another sort that represents the tokens of the crypto-currency themselves (which we dub “coins”).
Although the encodings of Sect. 5 do not translate to our decidable SL fragment from Sect. 4, our experimental results show that automated reasoning engines can handle them consistently and fast. The decidability results of Sect. 5 set the boundaries for what one can expect to achieve, while our experiments from Sect. 5 demonstrate that the unknown middle-ground can still be automated.
While our work is mainly motivated by smart contract verification, our results can be used for arbitrary software transactions implementing sum/aggregate properties. Further, when compared to the smart contract verification framework of [33], we note that we are not restricted to proving the correctness of smart contracts as finite-state machines, but can deal with semantic properties expressing financial transactions in smart contracts, such as currency minting/transfers.
While ghost variable approaches [14] can reason about changes to the global state (the sum), our approach allows the verifier to specify only the local changes and automatically prove the impact on the global state.
Contributions. In summary, this paper makes the following contributions:
-
We present a generalization to Presburger arithmetic (SL, in Sect. 3) that allows expressing properties about summations. We show how we can formalize verification problems of smart contracts in SL.
-
We discuss the decidability problem of checking validity of SL formulas (Sect. 4): we prove that it is undecidable in the general case, but also that there exists a small decidable fragment.
-
We show different encodings of SL to first-order logic (Sect. 5). To this end, we consider theory-specific reasoning and variations of SL, for example by replacing non-negative integer reasoning with term algebra properties.
-
We evaluate our results with SMT solvers and first-order theorem provers, by using 31 new benchmarks encoding smart transitions and their properties (Sect. 6). Our experiments demonstrate the applicability of our results within automated reasoning, in a fully automated manner, without any user guidance.
2 Preliminaries
We consider many-sorted first-order logic (FOL) with equality, defined in the standard way. The equality symbol is denoted by \(\approx \).
We denote by \(\text {STRUCT} \left[ \varSigma \right] \) the set of all structures for the vocabulary \(\varSigma \). A structure \(\mathcal {A}\in \text {STRUCT} \left[ \varSigma \right] \) is a pair \( \left( \mathcal {D},\mathcal {I} \right) \), where for each sort \(\boldsymbol{s}\), its domain in \(\mathcal {A}\) is \(\mathcal {D}(\boldsymbol{s})\), and for each symbol S, its interpretation in \(\mathcal {A}\) is \(\mathcal {I}(S)\). Note that models of a formula \(\varphi \) over a vocabulary \(\varSigma \) are structures \(\mathcal {A}\in \text {STRUCT} \left[ \varSigma \right] \).
A first-order theory is a set of first-order formulas closed under logical consequence. We will consider, the first-order theory of the natural numbers with addition. This is Presburger arithmetic (PA) which is of course decidable [27].
We write \(\mathbb {N}\) to denote the set of natural numbers. We consider \(0 \in \mathbb {N}\) and write \(\mathbb {N}^+\) to explicitly exclude 0 from \(\mathbb {N}\). The vocabulary of PA is \( \varSigma _\text {Presburger} = \left( 0, 1, c_1, \dots , c_l, +^2 \right) \), with all constants \(0, 1, c_i\) of sort  . A structure \(\mathcal {A}= (\mathcal {D}, \mathcal {I}) \in \text {STRUCT} \left[ \varSigma _\text {Presburger} \right] \) is called a Standard Model of Arithmetic when
. A structure \(\mathcal {A}= (\mathcal {D}, \mathcal {I}) \in \text {STRUCT} \left[ \varSigma _\text {Presburger} \right] \) is called a Standard Model of Arithmetic when  and \(+^2\) is interpreted as the standard binary addition \(+\) function over the naturals. The vocabulary \(\varSigma _\text {Presburger}\) can be extended with a total order relation, yielding \(\varSigma ^*_\text {Presburger} = \left( 0, 1, +^2, \le ^2 \right) \), where \(\le ^2\) is interpreted as the binary relation \(\le \) in Standard Models of Arithmetic.
and \(+^2\) is interpreted as the standard binary addition \(+\) function over the naturals. The vocabulary \(\varSigma _\text {Presburger}\) can be extended with a total order relation, yielding \(\varSigma ^*_\text {Presburger} = \left( 0, 1, +^2, \le ^2 \right) \), where \(\le ^2\) is interpreted as the binary relation \(\le \) in Standard Models of Arithmetic.
3 Sum Logic (SL)
We now define Sum Logic (SL) as a generalization of Presburger arithmetic, extending Presburger arithmetic with unbounded sums. SL is motivated by applications of financial transactions over cryptocurrencies in smart contracts. Smart contracts are decentralized computer programs executed on a blockchain-based system, as explained in [28]. Among other tasks, they automate financial transactions such as transferring and minting money. We refer to these transactions as smart transitions. The aim of this paper and SL in particular is to express and reason about the post-conditions of smart transitions similar to Fig. 1.
SL expresses smart transition relations among sums of accounts of various kinds, e.g., at different banks, times, etc. Each such kind, j, is modeled by an uninterpreted function symbol, \(b_j\), where \(b_j(a)\) denotes the balance of a’s account of kind j, and a constant symbol \(s_j\), which denotes the sum of all outputs of \(b_j\). As such, our SL generalizes Presburger arithmetic with (i) a sort  corresponding to the (unbounded) set of account addresses; (ii) balance functions \(b_j\) mapping account addresses from
corresponding to the (unbounded) set of account addresses; (ii) balance functions \(b_j\) mapping account addresses from  to account values of sort
to account values of sort  ; and (iii) sum constants \(s_j\) of sort
; and (iii) sum constants \(s_j\) of sort  capturing the total sum of all account balances represented by \(b_j\). Formally, the vocabulary of SL is defined as follows.
capturing the total sum of all account balances represented by \(b_j\). Formally, the vocabulary of SL is defined as follows.
Definition 1
(SL Vocabulary). Let
be a sorted first-order vocabulary of SL over sorts  , where
, where
-
(Addresses) The constants \(a_1, \dots , a_l\) are of sort
 ;
; -
(Balance functions) \(b^1_1, \dots , b^1_m\) are unary function symbols from
 to
to  ;
; -
(Constants and Sums) The constants \(c_1, \dots , c_d, s_1, \dots , s_m\) and 0, 1 are of sort
 ;
; -
\(+^2\) is a binary function
 ;
; -
\(\le ^2\) is a binary relation over
 .
.
In what follows, when the cardinalities in an SL vocabulary are clear from context, we simply write \(\varSigma \) instead of \(\varSigma ^{l,m,d}_{+,\le }\). Further, by  we denote the sub-vocabulary where the crossed-out symbols are not available. Note that even when addition is not available, we still allow writing numerals larger than 1.
we denote the sub-vocabulary where the crossed-out symbols are not available. Note that even when addition is not available, we still allow writing numerals larger than 1.
We restrict ourselves to universal sentences over an SL vocabulary, with quantification only over the
 sort.
sort.
We now extend the Tarskian semantics of first-order logic to ensure that the sum constants of an SL vocabulary (\(s_1, \dots , s_m\)) are equal to the sum of outputs of their associated balance functions (\(b_j\) for each \(s_j\)) over the respective entire domains of sort  .
.
Let \(\varSigma \) be an SL vocabulary. An SL structure \(\mathcal {A}= \left( \mathcal {D},\mathcal {I} \right) \in \text {STRUCT} \left[ \varSigma \right] \) representing a model for an SL formula \(\varphi \) is called an SL model iff

We write \(\mathcal {A}\vDash _{{\textsc {SL}}{}} \varphi \) to mean that \(\mathcal {A}\) is an SL model of \(\varphi \). When it is clear from context, we simply write \(\mathcal {A}\vDash \varphi \).
Example 1
(Encoding ERC-20 in SL). As a use case of \({\textsc {SL}}{}\), we showcase the encoding of the ERC-20 token standard of the Ethereum community [32] in SL. To this end, we consider an SL vocabulary \(\varSigma ^{l,2,d}\). We respectively denote the balance functions and their associated sums as \(b, b',s, s'\) in the SL structure over \(\varSigma ^{l,2,d}\). The resulting instance of SL can then be used to encode ERC-20 operations/smart transitions as SL formulas, as shown in Table 1. Using this encoding, the post-condition of Fig. 1 is expressed as the SL formula
formalizing the correctness of the smart transition of minting n tokens in Fig. 1. In the applied verification examples in Sect. 6, rather than verifying the low-level implementation of built-in functions such as  , we assume their correctness by including suitable axioms.
, we assume their correctness by including suitable axioms.
4 Decidability of SL
We consider the decidability problem of verifying formulas in SL. We show that when there are several function symbols \(b_j\) to sum over, the satisfiability problem for SL becomes undecidableFootnote 2. We first present, however, a useful decidable fragment of SL.
4.1 A Decidable Fragment of SL
We prove decidability for a fragment of SL, which we call the \( \left( l,1,d \right) \)-FRAG fragment of SL (Theorem 4). For doing so, we reduce the fragment to Presburger arithmetic, by using regular Presburger constructs to encode SL extensions, that is the uninterpreted functions and sum constants of SL.
The first step of our reduction proof is to consider distinct models, which are models where the  constants \(a_i\) represent distinct elements in the domain
constants \(a_i\) represent distinct elements in the domain  . While this restriction is somewhat unnatural, we show that for each vocabulary and formula that has a model, there exists an equisatisfiable formula over a different vocabulary that has a distinct model (Theorem 1). The crux of our decidability proof is then proving that \( \left( l,1,d \right) \)-FRAG has small
. While this restriction is somewhat unnatural, we show that for each vocabulary and formula that has a model, there exists an equisatisfiable formula over a different vocabulary that has a distinct model (Theorem 1). The crux of our decidability proof is then proving that \( \left( l,1,d \right) \)-FRAG has small
 space: given a formula \(\varphi \), if it is satisfiable, then there exists a model where
space: given a formula \(\varphi \), if it is satisfiable, then there exists a model where  , \( \left| \varphi \right| \) is the length of \(\varphi \), and \(\kappa (.)\) is some computable function (Theorem 3)Footnote 3.
, \( \left| \varphi \right| \) is the length of \(\varphi \), and \(\kappa (.)\) is some computable function (Theorem 3)Footnote 3.
Distinct Models. An SL structure \(\mathcal {A}\) is considered distinct when the l
 constants represent l distinct elements in
constants represent l distinct elements in  . I.e.,
. I.e.,
Since each SL model induces an equivalence relation over the  constants, we consider partitions P over \( \left\{ a_1, \dots , a_l \right\} \). For each possible partition P we define a transformation of terms and formulas \(\mathcal {T}_P\) that substitutes equivalent
constants, we consider partitions P over \( \left\{ a_1, \dots , a_l \right\} \). For each possible partition P we define a transformation of terms and formulas \(\mathcal {T}_P\) that substitutes equivalent  constants with a single
constants with a single  constant. The resulting formulas are defined over a vocabulary that has \( \left| P\right| \)
constant. The resulting formulas are defined over a vocabulary that has \( \left| P\right| \)  constants. We show that given an SL formula \(\varphi \), if \(\varphi \) has a model, we can always find a partition P such that each of its classes corresponds to an equivalence class induced by that model.
constants. We show that given an SL formula \(\varphi \), if \(\varphi \) has a model, we can always find a partition P such that each of its classes corresponds to an equivalence class induced by that model.
Theorem 1
(Distinct Models). Let \(\varphi \) be an SL formula over \(\varSigma \), then \(\varphi \) has a model iff there exists a partition P of \( \left\{ a_1,\dots ,a_l \right\} \) such that \(\mathcal {T}_P(\varphi )\) has a distinct model. \(\square \)
Small
 Space. In order to construct a reduction to Presburger arithmetic, we bound the size of the
Space. In order to construct a reduction to Presburger arithmetic, we bound the size of the  sort. For a fragment of SL to be decidable, we therefore need a way to bound its models upfront. We formalize this requirement as follows.
sort. For a fragment of SL to be decidable, we therefore need a way to bound its models upfront. We formalize this requirement as follows.
Definition 2
(Small
 Space). Let FRAG be some fragment of SL over vocabulary \(\varSigma = \varSigma ^{l,m,d}_{+,\le }\). FRAG is said to have small
Space). Let FRAG be some fragment of SL over vocabulary \(\varSigma = \varSigma ^{l,m,d}_{+,\le }\). FRAG is said to have small
 space if there exists a computable function \(\kappa _\varSigma (.)\), such that for any SL formula \(\varphi \in \textsc {FRAG}\), \(\varphi \) has a distinct model iff \(\varphi \) has a distinct model \(\mathcal {A}= (\mathcal {D}, \mathcal {I})\) with small
space if there exists a computable function \(\kappa _\varSigma (.)\), such that for any SL formula \(\varphi \in \textsc {FRAG}\), \(\varphi \) has a distinct model iff \(\varphi \) has a distinct model \(\mathcal {A}= (\mathcal {D}, \mathcal {I})\) with small
 space, where
space, where  .
.
We call \(\kappa _\varSigma (.)\) the bound function of FRAG; when the vocabulary is clear from context we simply write \(\kappa (.)\).
One instance of a fragment (or rather, family of fragments) that satisfies this property is the \( \left( l,1,d \right) \)-FRAG fragment: the simple case of a single uninterpreted “balance” function (and its associated sum constant), further restricted by removing the binary function \(+\) and the binary relation \(\le \). Therefore, we derive the following theorem:
Theorem 2
(Small
 Space of \( \left( l,1,d \right) \)-FRAG).
Space of \( \left( l,1,d \right) \)-FRAG).
For any l, d, it holds \( \left( l,1,d \right) \)-FRAG, the fragment of SL formulas over the SL vocabulary

has small
 space with bound function \(\kappa (x) = l + x + 1\). \(\square \)
space with bound function \(\kappa (x) = l + x + 1\). \(\square \)
An attempt to trivially extend Theorem 2 for a fragment of SL with two balance functions falls apart in a few places, but most importantly when comparing balances to the sum of a different balance function. In Sect. 4.2 we show that these comparisons are essential for proving our undecidability result in SL.
Presburger Reduction. For showing decidability of some FRAG fragment of SL, we describe a Turing reduction to pure Presburger arithmetic. We introduce a transformation \(\tau (.)\) of formulas in SL into formulas in Presburger arithmetic. It maps universal quantifiers to disjunctions, and sums to explicit addition of all balances. In addition, we define an auxiliary formula \(\eta (\varphi )\), which ensures only valid addresses are considered, and that invalid addresses have zero balances. The formal definitions of \(\tau (.)\) and \(\eta (\varphi )\) can be found in [10].
By relying on the properties of distinctness and small
 space we get the following results.
space we get the following results.
Theorem 3
(Presburger Reduction). An SL formula \(\varphi \) has a distinct, SL model with small
 space iff \(\tau (\varphi ) \wedge \eta (\varphi )\) has a Standard Model of Arithmetic. \(\square \)
space iff \(\tau (\varphi ) \wedge \eta (\varphi )\) has a Standard Model of Arithmetic. \(\square \)
Theorem 4
(SL Decidability). Let FRAG be a fragment of SL that has small
 space, as defined in Definition 2. Then, FRAG is decidable.
space, as defined in Definition 2. Then, FRAG is decidable.
Proof
(Theorem 4). Let \(\varphi \) be a formula in FRAG. Then \(\varphi \) has an SL model iff for some partition P of \( \left\{ a_1,\dots ,a_l \right\} \), \(\mathcal {T}_P(\varphi )\) has a distinct SL model. For any P, the formula \(\mathcal {T}_P(\varphi )\) is in FRAG, therefore \(\mathcal {T}_P(\varphi )\) has a distinct SL model iff it has a distinct SL model with small
 space.
space.
From Theorem 3, we get that for any P, \(\varphi _P \triangleq \mathcal {T}_P(\varphi )\) has a distinct SL model iff \(\tau (\varphi _P) \wedge \eta (\varphi _P)\) has a Standard Model of Arithmetic. By using the PA decision procedure as an oracle, we obtain the following decision procedure for a FRAG formula \(\varphi \):
-
For each possible partition P of \( \left\{ a_1,\dots ,a_l \right\} \), let \(\varphi _P = \mathcal {T}_P(\varphi )\);
-
Using a PA decision procedure, check whether \(\tau (\varphi _P) \wedge \eta (\varphi _P)\) has a model, for each P;
-
If a model for some partition P was found, the formula \(\varphi _P\) has a distinct SL model, and therefore \(\varphi \) has SL model;
-
Otherwise, there is no distinct SL model for any partition P, and therefore there is no SL model for \(\varphi \).
Remark 1
Our decision procedure for Theorem 4 requires \(B_l\) Presburger queries, where \(B_l\) is Bell’s number for all possible partitions of a set of size l.
Using Theorem 4 and Theorem 2, we then obtain the following result.
Corollary 1
\( \left( l,1,d \right) \)-FRAG is decidable. \(\square \)
4.2 SL Undecidability
We now show that simple extensions of our decidable \( \left( l,1,d \right) \)-FRAG fragment lose its decidability (Theorem 5). For doing so, we encode the halting problem of a two-counter machine using SL with 3 balance functions, thereby proving that the resulting SL fragment is undecidable.
Consider a two-counter machine, whose transitions are encoded by the Presburger formula \(\pi (c_1, c_2, p, c'_1, c'_2, p')\) with 6 free variables: 2 for each of the three registers, one of which being the program counter (pc). We assume w.l.o.g. that all three registers are within \(\mathbb {N}^+\), allowing us to use addresses with a zero balance as a special “separator”. In addition, we assume that the program counter is 1 at the start of the execution, and that there exists a single halting statement at line H. That is, the two-counter machine halts iff the pc is equal to H.
Reduction Setting. We have 4
 elements for each time-step, 3 of them hold one register each, and one is used to separate between each group of
elements for each time-step, 3 of them hold one register each, and one is used to separate between each group of
 elements (see Table 2). We have 3 uninterpreted functions from
elements (see Table 2). We have 3 uninterpreted functions from
 to
to
 (“balances”). For readability we denote these functions as c, l, g (instead of \(b_1,b_2,b_3\)) and their respective sums as \(s_c,s_l,s_g\):
(“balances”). For readability we denote these functions as c, l, g (instead of \(b_1,b_2,b_3\)) and their respective sums as \(s_c,s_l,s_g\):
-
1.
Function \(c\,\): Cardinality function, used to force size constraints. We set its value for all addresses to be 1, and therefore the number of addresses is \(s_c\).
-
2.
Function \(l\,\): Labeling function, to order the time-steps. We choose one element to have a maximal value of \(s_c - 1\) and ensure that l is injective. This means that the values of l are distinctly \([0, s_c - 1]\).
-
3.
Function \(g\,\): General purpose function, which holds either one of the registers or 0 to mark the
 element as a separating one.
element as a separating one.
Each group representing a time-step is a 4
 element, ordered as follows:
element, ordered as follows:
-
1.
First, a separating
 element x (where g(x) is 0).
element x (where g(x) is 0). -
2.
Then, the two general-purpose counters.
-
3.
Lastly, the program counter.
In addition we have 2
 constants, \(a_0\) and \(a_1\) which represent the pc value at the start and at the end of the execution. The element \(a_1\) also holds the maximal value of l, that is, \(l(a_1) + 1\approx s_c\). Further, \(a_0\) holds the fourth-minimal value, since its the last element of the first group, and each group has four elements.
constants, \(a_0\) and \(a_1\) which represent the pc value at the start and at the end of the execution. The element \(a_1\) also holds the maximal value of l, that is, \(l(a_1) + 1\approx s_c\). Further, \(a_0\) holds the fourth-minimal value, since its the last element of the first group, and each group has four elements.
Formalization Using a Two-Counter Machine. We now formalize our reduction, proving undecidability of SL.
(i) We impose an injective labeling
(ii) We next formalize properties over the program counter pc. The
 constant that represents the program counter pc value of the last time-step is set to have the maximal labeling, that is
constant that represents the program counter pc value of the last time-step is set to have the maximal labeling, that is
Further, the
 constant that represents the pc value of the first time-step has the fourth labeling, hence
constant that represents the pc value of the first time-step has the fourth labeling, hence
Finally, the first and last values of the program counter are respectively 1 and H, that is
(iii) We express cardinality constraints ensuring that there are as many
 elements as the labeling of the last
elements as the labeling of the last
 constant (\(a_1\)) + 1. We assert
constant (\(a_1\)) + 1. We assert
(iv) We encode the transitions of the two-counter machine, as follows. For every 8
 elements, if they represent two sequential time-steps, then the formula for the transitions of the two-counter machine is valid for the registers it holds. As such, we have
elements, if they represent two sequential time-steps, then the formula for the transitions of the two-counter machine is valid for the registers it holds. As such, we have
where the conjunction \(F1 \wedge F2 \wedge F3\) expresses that \(x_1, \dots , x_8\) are two sequential time-steps, with F1, F2 and F3 defined as below. In particular, F1, F2 and F3 formalize that \(x_1, \dots , x_8\) have sequential labeling, starting with one zero-valued
 element (“separator”) and continuing with 3 non-zero elements, as follows:
element (“separator”) and continuing with 3 non-zero elements, as follows:
-
Sequential:
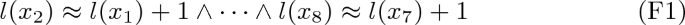
-
Time-steps:

Based on the above formalization, the formula \(\varphi = \varphi _1 \wedge \dots \wedge \varphi _6\) is satisfiable iff the two-counter machine halts within a finite amount of time-steps (and the exact amount would be given by \(\frac{s_c}{4}\)). Since the halting problem for two-counter machines is undecidable, our SL, already with 3 uninterpreted functions and their associated sums, is also undecidable.
Theorem 5
For any \(l \ge 2, m \ge 3\) and d, any fragment of SL over \(\varSigma ^{l,m,d}_{+,\le }\) is undecidable. \(\square \)
Remark 2
Note that in the above formalization the only use of associated sums comes from expressing the size of the set of
 elements. As for our uninterpreted function c(.) we have \(\forall x. c(x) \approx 1\), its sum \(s_c\) is thus the amount of addresses. Hence, we can encode the halting problem for two-counter machines in an almost identical way to the encoding presented here, using a generalization of PA with two uninterpreted functions for l(.) and g(.), and a size operation replacing c(.) and its associated sum.
elements. As for our uninterpreted function c(.) we have \(\forall x. c(x) \approx 1\), its sum \(s_c\) is thus the amount of addresses. Hence, we can encode the halting problem for two-counter machines in an almost identical way to the encoding presented here, using a generalization of PA with two uninterpreted functions for l(.) and g(.), and a size operation replacing c(.) and its associated sum.
5 SL Encodings of Smart Transitions
The definition of SL models in Sects. 3 and 4 ensured that the summation constants \(s_j\) were respectively equal to the actual summation of all balances \(b_j(.)\). In this section, we address the challenge to formalize relations between \(s_j\) and \(b_j(.)\) in a way that the resulting encodings can be expressed in the logical frameworks of automated reasoners, in particular of SMT solvers and first-order theorem provers.
In what follows, we consider a single transaction or one time-step of multiple transactions over \(s_j, b_j(.)\). We refer to such transitions as smart transitions. Smart transitions are common in smart contracts, expressing for example the minting and/or transferring of some coins, as evidenced in Fig. 1 and discussed later.
Based on Sect. 3, our smart transitions are encoded in the \(\varSigma ^{l,2,d}\) fragment of SL. Note however, that neither decidability nor undecidability of this fragment is implied by Theorem 4, nor Theorem 5. In this section, we show that our SL encoding of smart transitions is expressible in first-order logic. We first introduce a sound, implicit SL encoding, by “hiding” away sum semantics and using invariant relations over smart transitions (Sect. 5.1). This encoding does not allow us to directly assert the values of any balance or sum, but we can prove that this implicit encoding is complete, relative to a translation function (Sect. 5.2).
By further restricting our implicit SL encoding to this relative complete setting, we consider counting properties to explicitly reason with balances and directly express verification conditions with unbounded sums on \(s_j\) and \(b_j(.)\). This is shown in Sect. 5.3, and we evaluate different variants of the explicit SL encoding in Sect. 6, showcasing their practical use and relevance within automated reasoning.
To directly present our SL encodings and results in the smart contract domain, in what follows we rely on the notation of Table 1. As such, we respectively denote \(b,b'\) by old-bal, new-bal and write old-sum, new-sum for \(s,s'\). As already discussed in Fig. 1, the prefixes old- and new- refer to the entire state expressed in the encoding before and after the smart transition. We explicitly indicate this state using old-world, new-world respectively. The non-prefixed versions bal and sum are stand-ins for both the old- and new- versions—Fig. 2 illustrates our setting for the smart transition of minting one coin.
With this SL notation at hand, we are thus interested in finding first-order formulas that verify smart transition relations between old-sum and new-sum, given the relation between old-bal and new-bal. In this paper, we mainly focus on the smart transitions of minting and transferring money, yet our results could be used in the context of other financial transactions/software transitions over unbounded sums.
Example 2
In the case of minting n coins in Fig. 1, we require formulas that (a) describe the state before the transition (the old-world, thus pre-condition), (b) formalize the transition (the relation between old-bal and new-bal; (i)-(ii) in Fig. 1) and (c) imply the consequences for the new-world ((iii) in Fig. 1). These formulas verify that minting and depositing n coins into some address result in an increase of the sum by n, that is  , as expressed in the functional correctness formula (1) of Fig. 1.
, as expressed in the functional correctness formula (1) of Fig. 1.
5.1 SL Encoding Using Implicit Balances and Sums
The first encoding we present is a set of first-order formulas with equality over sorts  . No additional theories are considered. The
. No additional theories are considered. The
 sort represents money, where one coin is one unit of money. The
sort represents money, where one coin is one unit of money. The
 sort represents the account addresses as before. As a consequence, balance functions and sum constants only exist implicitly in this encoding. As such, the property
sort represents the account addresses as before. As a consequence, balance functions and sum constants only exist implicitly in this encoding. As such, the property  cannot be directly expressed in this encoding. Instead, we formalize this property by using so-called smart invariant relations between two predicates has-coin and active over coins
cannot be directly expressed in this encoding. Instead, we formalize this property by using so-called smart invariant relations between two predicates has-coin and active over coins  and
and  , as follows.
, as follows.
Definition 3
(Smart Invariants). Let  and consider
and consider  . A smart invariant of the pair
. A smart invariant of the pair  is the conjunction of the following three formulas
is the conjunction of the following three formulas
-
1.
Only active coins c can be owned by an address a:

-
2.
Every active coin c belongs to some address a:
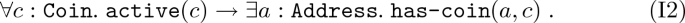
-
3.
Every coin c belongs to at most one address a:

We write  to denote the smart invariant \(\text {(I1)} \wedge \text {(I2)} \wedge \text {(I3)}\) of
to denote the smart invariant \(\text {(I1)} \wedge \text {(I2)} \wedge \text {(I3)}\) of  .
.
Intuitively, our smart invariants ensure that a coin c is active iff it is owned by precisely one address a. Our smart invariants imply the soundness of our implicit SL encoding, as follows.
Theorem 6
(Soundness of SL Encoding). Given that  and for every
and for every  it holds
it holds  , then
, then  . \(\square \)
. \(\square \)
We say that a smart transition preserves smart invariants, when

where  and
and  respectively denote the functions
respectively denote the functions  in the states before and after the smart transition. Based on the soundness of our implicit SL encoding, we formalize smart transitions preserving smart invariants as first-order formulas. We only discuss smart transitions implementing minting n coins here, but other transitions, such as transferring coins, can be handled in a similar manner. We first focus on miniting a single coin, as follows.
in the states before and after the smart transition. Based on the soundness of our implicit SL encoding, we formalize smart transitions preserving smart invariants as first-order formulas. We only discuss smart transitions implementing minting n coins here, but other transitions, such as transferring coins, can be handled in a similar manner. We first focus on miniting a single coin, as follows.
Definition 4
(Transition  ). Let there be
). Let there be  . The transition
. The transition  activates coin c and deposits it into address a.
activates coin c and deposits it into address a.
-
1.
The coin c was inactive before and is active now:
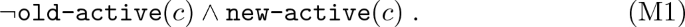
-
2.
The address a owns the new coin c:
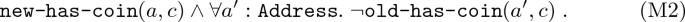
-
3.
Everything else stays the same:
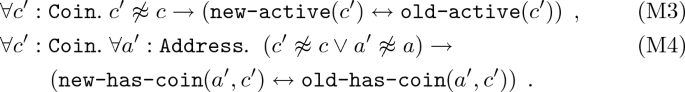
The transition  is defined as \(\text {(M1)} \wedge \text {(M2)} \wedge \text {(M3)} \wedge \text {(M4)}\).
is defined as \(\text {(M1)} \wedge \text {(M2)} \wedge \text {(M3)} \wedge \text {(M4)}\).
By minting one coin, the balance of precisely one address, that is of the receiver’s address, increases by one, whereas all other balances remain unchanged. Thus, the expected impact on the sum of account balances is also increased by one, as illustrated in Fig. 2. The following theorem proves that the definition of  is sound. That is,
is sound. That is,  affects the implicit balances and sums as expected and hence
affects the implicit balances and sums as expected and hence  preserves smart invariants.
preserves smart invariants.
Theorem 7
(Soundness of  ). Let
). Let  ,
,  such that
such that  . Consider balance functions
. Consider balance functions  ,
,  , non-negative integer constants
, non-negative integer constants  ,
,  , unary predicates
, unary predicates  ,
,  and binary predicates
and binary predicates  ,
,  such that
such that

and for every address \(a'\), we have

Then,  ,
,  . Moreover, for all other addresses \(a' \ne a\), it holds
. Moreover, for all other addresses \(a' \ne a\), it holds  . \(\square \)
. \(\square \)
Smart transitions minting an arbitrary number of n coins, as in our Fig. 1, is then realized by repeating the  transition n times. Based on the soundness of
transition n times. Based on the soundness of  , ensuring that
, ensuring that  preserves smart invariants, we conclude by induction that n repetitions of
preserves smart invariants, we conclude by induction that n repetitions of  , that is minting n coins, also preserves smart invariants. The precise definition of
, that is minting n coins, also preserves smart invariants. The precise definition of  together with the soundness result is stated in [10].
together with the soundness result is stated in [10].
5.2 Completeness Relative to a Translation Function
Smart invariants provide sufficient conditions for ensuring soundness of our SL encodings (Theorem 6). We next show that, under additional constraints, smart invariants are also necessary conditions, establishing thus (relative) completeness of our encodings.
A straightforward extension of Theorem 6 however does not hold. Namely, only under the assumptions of Theorem 6, the following formula is not valid:

As a counterexample, assume (i)  , (ii) for every
, (ii) for every  it holds that
it holds that  , that is the assumptions of Theorem 6. Further, let (iii) the smart invariants inv(has-coin, active) hold for all but the coins
, that is the assumptions of Theorem 6. Further, let (iii) the smart invariants inv(has-coin, active) hold for all but the coins  and all but the addresses
and all but the addresses  . We also assume that (iv) \(c_1\) is active but not owned by any address and (v) \(c_2\) is active and owned by the two distinct addresses \(a_1,a_2\). We thus have
. We also assume that (iv) \(c_1\) is active but not owned by any address and (v) \(c_2\) is active and owned by the two distinct addresses \(a_1,a_2\). We thus have  , yet
, yet  does not hold.
does not hold.
To ensure completeness of our encodings, we therefore introduce a translation function f that restricts the set  of
of  pairs, as follows. We exclude from \(\mathcal {F}\) those pairs
pairs, as follows. We exclude from \(\mathcal {F}\) those pairs  that violate smart invariants by both (i) not satisfying (I2), as (I2) ensures that there are not too many active coins, and by (ii) not satisfying at least one of (I1) and (I3), as (I1) and (I3) ensure that there are not too few active coins. The required translation function f (as in [10]) now assigns every pair
that violate smart invariants by both (i) not satisfying (I2), as (I2) ensures that there are not too many active coins, and by (ii) not satisfying at least one of (I1) and (I3), as (I1) and (I3) ensure that there are not too few active coins. The required translation function f (as in [10]) now assigns every pair  the set of all
the set of all  that satisfy
that satisfy  ,
,  for every address a and have not been excluded.
for every address a and have not been excluded.
Theorem 8
(Relative Completeness of SL Encoding). Let  and let
and let  be arbitrary. Then,
be arbitrary. Then,

\(\square \)
5.3 SL Encodings Using Explicit Balances and Sums
We now restrict our SL encoding from Sect. 5.1 to explicitly reason with balance functions during smart transitions. We do so by expressing our translation function f from Sect. 5.2 in first-order logic. We now use the summation constant  and the balance function
and the balance function  in our SL encoding. In particular, we use our smart invariants
in our SL encoding. In particular, we use our smart invariants  in this explicit SL encoding together with two additional axioms (Ax1, Ax2), ensuring that
in this explicit SL encoding together with two additional axioms (Ax1, Ax2), ensuring that  and
and  for all
for all  .
.
To formalize the additional properties, we introduce two counting mechanisms in our SL encoding. The first one is a bijective function  and the second one is a function
and the second one is a function  , where
, where  is bijective for every
is bijective for every  . To ensure that
. To ensure that  and
and  count coins, we impose the following two properties:
count coins, we impose the following two properties:

Figure 3 illustrates our revised SL encoding for our smart transition  . We next ensure soundness of our resulting explicit encoding for summation, as follows.
. We next ensure soundness of our resulting explicit encoding for summation, as follows.
Theorem 9
(Soundness of Explicit SL Encodings). Let there be a pair  , a pair
, a pair  , and functions
, and functions  and
and  .
.
Given that  is bijective,
is bijective,  is bijective for every
is bijective for every  , and that (Ax1), (Ax2) and
, and that (Ax1), (Ax2) and  hold, then,
hold, then,  and
and  , for every
, for every  .
.
In particular, we have  . \(\square \)
. \(\square \)
When compared to Sect. 5.1, our explicit SL encoding introduced above uses our smart invariants as axioms of our encoding, together with (Ax1) and (Ax2). In our explicit SL encoding, the post-conditions asserting functional correctness of smart transitions express thus relations among  to
to  . For example, for
. For example, for  we are interested in ensuring
we are interested in ensuring

By using two new constants \(\texttt {old-total}\), \(\texttt {new-total} \in \mathbb {N}\), we can use  as smart invariant for
as smart invariant for  . As a result, the property to be ensured is then
. As a result, the property to be ensured is then

It is easy to see that the negations of (2) and (3) are equisatisfiable. We note however that the additional constants \(\texttt {old-total}\), \(\texttt {new-total}\) used in (3) lead to unstable results within automated reasoners, as discussed in Sect. 6.
6 Experiments
From Theory to Practice. To make our explicit SL encodings handier for automated reasoners, we improved the setting illustrated in Fig. 3 by applying the following restrictions without losing any generality.
(i) The predicates has-coin and active were removed from the explicit SL encodings, by replacing them by their equivalent expressions (Ax1)-(Ax2).
(ii) The surjectivity assertions of count and idx were restricted to the relevant intervals  ,
,  respectively.
respectively.
(iii) Compared to Fig. 3, only one mutual count and one mutual idx functions were used. We however conclude that we do not lose expressivity of our resulting SL encoding, as shown in [10].
(iv) When our SL encoding contains expressions such as  , with \(a_0\), \(a_1\) being distinct addresses such that either
, with \(a_0\), \(a_1\) being distinct addresses such that either  or
or  , \(i\in \left\{ 0,1 \right\} \), then it can be assumed that the coins in those intervals are in the same order for both functions [10].
, \(i\in \left\{ 0,1 \right\} \), then it can be assumed that the coins in those intervals are in the same order for both functions [10].
Based on the above, we derive three different explicit SL encodings to be used in automated reasoning about smart transitions. We respectively denote these explicit SL encodings by int, nat and id, and describe them next.
Benchmarks. In our experiments, we consider four smart transitions  ,
,  ,
,  and
and  , respectively denoting minting and transferring one and n coins. These transitions capture the main operations of linear integer arithmetic. In particular,
, respectively denoting minting and transferring one and n coins. These transitions capture the main operations of linear integer arithmetic. In particular,  implements the smart transition of our running example from Fig. 1.
implements the smart transition of our running example from Fig. 1.
For each of the four smart transitions, we implement four SL encodings: the implicit SL encoding uf from Sect. 5.1 using only uninterpreted functions and three explicit encodings int, nat and id as variants of Sect. 5.3. We also consider three additional arithmetic benchmarks using int, which are not directly motivated by smart contracts. Together with variants of int and nat presented in the sequel, our benchmark set contains 31 examples altogether, with each example being formalized in the SMT-LIB input syntax [1]. In addition to our encodings, we also proved consistency of the axioms used in our encodings.
SL Encodings and Relaxations. Our explicit SL encoding int uses linear integer arithmetic, whereas nat and id are based on natural numbers. As naturals are not a built-in theory in SMT-LIB, we assert the axioms of Presburger arithmetic directly in the encodings of nat and id.
In our id encodings, inductive datatypes are additionally used to order coins. There exists one linked list of all coins for count and one for each  ,
,  . Additionally, there exists a “null” coin, which is the first element of every list and is not owned by any address. As shown in Fig. 4, the numbering of each coin is defined by its position in the respective list. This way surjectivity for count and idx can respectively be asserted by the formulas
. Additionally, there exists a “null” coin, which is the first element of every list and is not owned by any address. As shown in Fig. 4, the numbering of each coin is defined by its position in the respective list. This way surjectivity for count and idx can respectively be asserted by the formulas  and
and  . However, asserting surjectivity for int and nat cannot be achieved without quantifying over \(\mathbb {N}^+\). Such quantification would drastically effect the performance of automated reasoners in (fragments of) first-order logics. As a remedy, within the default encodings of int and nat, we only consider relevant instances of surjectivity.
. However, asserting surjectivity for int and nat cannot be achieved without quantifying over \(\mathbb {N}^+\). Such quantification would drastically effect the performance of automated reasoners in (fragments of) first-order logics. As a remedy, within the default encodings of int and nat, we only consider relevant instances of surjectivity.
Further, we consider variations of int and nat by asserting proper surjectivity to the relevant intervals of idx and count (denoted as surj) and/or adding the
 constants mentioned in Sect. 5.3 (denoted as with
constants mentioned in Sect. 5.3 (denoted as with
 , no
, no
 ) . These variations of int and nat are implemented for
) . These variations of int and nat are implemented for  and
and  .
.
Experimental Setting. We evaluated our benchmark set of 31 examples using SMT solvers Z3 [7] and CVC4 [6], as well as the first-order theorem prover Vampire [19]. Our experiments were run on a standard machine with an Intel Core i5-6200U CPU (2.30 GHz, 2.40 GHz) and 8 GB RAM. The time is given in seconds and we ran all experiments with a time limit of 300 s. Time out is indicated by the symbol \(\times \). The default parameters were used for each solver, unless stated otherwise in the corresponding tablesFootnote 4.
 and \(\texttt {transferFrom}_1\) using nat and int, with/without the
and \(\texttt {transferFrom}_1\) using nat and int, with/without the
 constants and with/without surjectivity.
constants and with/without surjectivity.Experimental Analysis. We first report on our experiments using different variations of int and nat. Table 3 shows that asserting complete surjectivity for int and nat is computationally hard and indeed significantly effects the performance of automated reasoners. Thus, for the following experiments only relevant instances of surjectivity, such as  were asserted in int and nat. Table 3 also illustrates the instability of using the \(\texttt {total}\) constant. Some tasks seem to be easier even though their reasoning difficulty increased strictly by adding additional constants.
were asserted in int and nat. Table 3 also illustrates the instability of using the \(\texttt {total}\) constant. Some tasks seem to be easier even though their reasoning difficulty increased strictly by adding additional constants.
Our most important experimental findings are shown in Table 4, demonstrating that our SL encodings are suitable for automated reasoners. Thanks to our explicit SL encodings, each solver can certify every smart transition in at least one encoding. Our explicit SL encodings are more relevant than the implicit encoding uf as we can express and compare any two non-negative integer sums, whereas for uf handling arbitrary values n can only be done by iterating over the  (or
(or  ) transition. This iteration requires inductive reasoning, which currently only Vampire could do [15], as indicated by the superscript \(*\). Nevertheless, the transactions
) transition. This iteration requires inductive reasoning, which currently only Vampire could do [15], as indicated by the superscript \(*\). Nevertheless, the transactions  ,
,  , which involve only one coin in uf, require no inductive reasoning as the actual sum is not considered; each of our solvers can certify these examples.
, which involve only one coin in uf, require no inductive reasoning as the actual sum is not considered; each of our solvers can certify these examples.
We note that the tasks  and
and  from Table 4 yield a huge search space when using their explicit SL encodings within automated reasoners. We split these tasks into proving intermediate lemmas and proved each of these lemmas independently, by the respective solver. In particular, we used one lemma for
from Table 4 yield a huge search space when using their explicit SL encodings within automated reasoners. We split these tasks into proving intermediate lemmas and proved each of these lemmas independently, by the respective solver. In particular, we used one lemma for  and four lemmas for
and four lemmas for  . In our experiments, we only used the recent theory reasoning framework of Vampire with split queues [13] and indicate our results in by superscript \(\dagger \).
. In our experiments, we only used the recent theory reasoning framework of Vampire with split queues [13] and indicate our results in by superscript \(\dagger \).
We further remark that our explicit SL encoding id using inductive datatypes also requires inductive reasoning about smart transitions and beyond. The need of induction explains why SMT solvers failed proving our id benchmarks, as shown in Table 4. We note that Vampire found a proof using built-in induction [15] and theory-specific reasoning [13], as indicated by superscript \(\ddagger \).
We conclude by showing the generality of our approach beyond smart transitions. It in fact enables fully automated reasoning about any two summations \(\sum _{i \in I} g(i)\), \(\sum _{i \in I} h(i)\) of non-negative integer values g(i), h(i) (\(i \in I\)) over a mutual finite set I. The examples of Table 5 affirm this claim.
7 Related Work
Smart Contract Safety. Formal verification of smart contracts is an emerging hot topic because of the value of the assets stored in smart contracts, e.g. the DeFi software [3]. Due to the nature of the blockchain, bugs in smart contracts are irreversible and thus the demand for provably bug-free smart contracts is high.
The K interactive framework has been used to verify safety of a smart contract, e.g. in [23]. Isabelle [22] was also shown to be useful in manual, interactive verification of smart contracts [17]. We, however, focus on automated approaches.
There are also efforts to perform deductive verification of smart contracts both on the source level in languages such as Solidity [4, 14, 33] and Move [35], as well as on the the Ethereum virtual machine (EVM) level [2, 29]. This paper improves the effectiveness of these approaches by developing techniques for automatically reasoning about unbounded sums. This way, we believe we support a more semantic-based verification of smart contracts.
Our approach differs from works using ghost variables [14], since we do not manually update the “ghost state”. Instead, the verifier needs only to reason about the local changes, and the aggregate state is maintained by the axioms. That means other approaches assume (a) the local changes and (b) the impact on ghost variables (sum), whereas we only assume (a) and automatically prove \(a \Rightarrow b\). This way, we reduce the user-guidance in providing and proving (b).
Our work complements approaches that verify smart contracts as finite state machines [33] and methods, like ZEUS [18], using symbolic model checking and abstract interpretation to verify generic safety properties for smart contracts.
The work in [30] provides an extensive evaluation of ERC-20 and ERC-721 tokens. ERC-721 extends ERC-20 with ownership functions, one of which being “approve”. It enables transactions on another party’s behalf. This is independent of our ability to express sums in first-order logic, as the transaction’s initiator is irrelevant to its effect.
Reasoning about Financial Applications. Recently, the Imandra prover introduced an automated reasoning framework for financial applications [24,25,26]. Similarly to our approach, these works use SMT procedures to verify and/or generate counter-examples to safety properties of low- and high-level algorithms. In particular, results of [24,25,26] include examples of verifying ranking orders in matching logics of exchanges, proving high-level properties such as transitivity and anti-symmetry of such orders. In contrast, we focus on verifying properties relating local changes in balances to changes of the global state (the sum). Moreover, our encodings enable automated reasoning both in SMT solving and first-order theorem proving.
Automated Aggregate Reasoning. The theory of first-order logic with aggregate operators has been thoroughly studied in [16, 21]. Though proven to be strictly more expressive than first-order logic, both in the case of general aggregates as well as simple counting logics, in this paper we present a practical way to encode a weakened version of aggregates (specifically sums) in first-order logic. Our encoding (as in Sect. 5) works by expressing particular sums of interest, harnessing domain knowledge to avoid the need of general aggregate operators.
Previous works [5, 20] in the field of higher-order reasoning do not directly discuss aggregates. The work of [20] extends Presburger arithmetic with Boolean algebra for finite, unbounded sets of uninterpreted elements. This includes a way to express the set cardinalities and to compare them against integer variables, but does not support uninterpreted functions, such as the balance functions we use throughout our approach.
The SMT-based framework of [5] takes a different, white-box approach, modifying the inner workings of SMT solvers to support higher-order logic. We on the other hand treat theorem provers and SMT solvers as black-boxes, constructing first-order formulas that are tailored to their capabilities. This allows us to use any off-the-shelf SMT solver.
In [8], an SMT module for the theory of FO(Agg) is presented, which can be used in all DPLL-based SAT, SMT and ASP solvers. However, FO(Agg) only provides a way to express functions that have sets or similar constructs as inputs, but not to verify their semantic behavior.
8 Conclusions
We present a methodology for reasoning about unbounded sums in the context of smart transitions, that is transitions that occur in smart contracts modeling transactions. Our sum logic SL and its usage of sum constants, instead of fully-fledged sum operators, turns out to be most appropriate for the setting of smart contracts. We show that SL has decidable fragments (Sect. 4.1), as well as undecidable ones (Sect. 4.2). Using two phases to first implicitly encode SL in first-order logic (Sect. 5.1), and then explicitly encode it (Sect. 5.3), allows us to use off-the-shelf automated reasoners in new ways, and automatically verify the semantic correctness of smart transitions.
Showing the (un)decidability of the SL fragment with two sets of uninterpreted functions and sums is an interesting step for further work, as this fragment supports encoding smart transition systems. Another interesting direction of future work is to apply our approach to different aggregates, such as minimum and maximum and to reason about under which conditions these values stay above /below certain thresholds. A slightly modified setting of our SL axioms can already handle \(\min \)/\(\max \) aggregates in a basic way, namely by using \(\ge \) and \(\le \) instead of equality and dropping the injectivity/surjectivity (respectively) axioms of the counting mechanisms.
Summing upon multidimensional arrays in various ways is yet another direction of future research. Our approach supports the summation over all values in all dimensions by adding the required number of parameters to the predicate idx and by adapting the axioms accordingly.
Notes
- 1.
The old- prefix denotes the value of a function before the mint transition, and the new- prefix denotes the value afterwards.
- 2.
Proofs of our results are given in the appendix of [10].
- 3.
The function \(\kappa (.)\) is defined per decidable fragment of SL, and not per formula.
- 4.
The precise calls and encodings are available at github.com/SoRaTu/SmartSums.
References
SMTLIB: Satisfiability Modulo Theories Library. https://smtlib.cs.uiowa.edu/papers/smt-lib-reference-v2.6-r2017-07-18.pdf
Certora Ltd: The Certora Verifier (2020). www.certora.com
Concourse Open Community: DeFi Pulse (2020). https://defipulse.com/
Alt, L.: Solidity’s SMTChecker can Automatically find Real Bugs (2019). https://medium.com/@leonardoalt/soliditys-smtchecker-can-automatically-find-real-bugs-beb566c24dea
Barbosa, H., Reynolds, A., El Ouraoui, D., Tinelli, C., Barrett, C.: Extending SMT solvers to higher-order logic. In: CADE, pp. 35–54 (2019)
Barrett, C., et al.: CVC4. In: CAV, pp. 171–177 (2011)
De Moura, L., Bjørner, N.: Z3: An efficient SMT solver. In: TACAS, pp. 337–340 (2008)
Denecker, M., De Cat, B.: DPLL (Agg): an efficient SMT module for aggregates. In: Logic and Search (2010)
Dutertre, B., De Moura, L.: The Yices SMT Solver. Tool paper at http://yices.csl.sri.com/tool-paper.pdf, pp. 1–2 (2006)
Elad, N., Rain, S., Immerman, N., Kovács, L., Sagiv, M.: Summing up smart transitions (2021). https://arxiv.org/abs/2105.07663
Emerson, A.: Modal and temporal logics. In: Handbook of Theoretical Computer Science, vol. B, pp. 995–1072 (1990)
Etessami, K.: Counting quantifiers, successor relations, and logarithmic space. In: JCSS, pp. 400–411 (1997)
Gleiss, B., Suda, M.: Layered clause selection for saturation-based theorem proving. In: IJCAR, pp. 34–52 (2020)
Hajdu, Á., Jovanovic, D.: Solc-verify: a modular verifier for solidity smart contracts. In: VSTTE, pp. 161–179 (2019)
Hajdú, M., Hozzová, P., Kovács, L., Schoisswohl, J., Voronkov, A.: Induction with generalization in superposition reasoning. In: CICM, pp. 123–137 (2020)
Hella, L., Libkin, L., Nurmonen, J., Wong, L.: Logics with aggregate operators. J. ACM. 48(8), 880–907 (2001)
Hirai, Y.: Defining the Ethereum virtual machine for interactive theorem provers. In: FC, pp. 520–535 (2017)
Kalra, S., Goel, S., Dhawan, M., Sharma, S.: ZEUS: analyzing safety of smart contracts. In: NDSS (2018)
Kovács, L., Voronkov, A.: First-order theorem proving and vampire. In: CAV, pp. 1–35 (2013)
Kuncak, V., Nguyen, H.H., Rinard, M.: An algorithm for deciding BAPA: Boolean algebra with Presburger arithmetic. In: CADE, pp. 260–277 (2005)
Libkin, L.: Logics with counting, auxiliary relations, and lower bounds for invariant queries. In: LICS, pp. 316–325 (1999)
Nipkow, T.: Interactive proof: introduction to Isabelle/HOL. In: Software Safety and Security, pp. 254–285 (2012)
Park, D., Zhang, Y., Rosu, G.: End-to-end formal verification of Ethereum 2.0 deposit smart contract. In: CAV, pp. 151–164 (2020)
Passmore, G.O., et al.: The Imandra automated reasoning system (system description). In: IJCAR, pp. 464–471 (2020)
Passmore, G.O.: Formal verification of financial algorithms with Imandra. In: FMCAD, pp. i–i (2018)
Passmore, G.O., Ignatovich, D.: Formal verification of financial algorithms. In: CADE, pp. 26–41 (2017)
Presburger, M.: Über die Vollständigkeit eines gewissen Systems der Arithmetik ganzer Zahlen, in welchem die Addition als einzige Operation hervortritt. In: Comptes Rendus du I congres de Mathématiciens des Pays Slaves, pp. 92–101 (1929)
Sadiku, M., Eze, K., Musa, S.: Smart contracts: a primer (2018)
Schneidewind, C., Grishchenko, I., Scherer, M., Maffei, M.: eThor: practical and provably sound static analysis of Ethereum smart contracts. In: CCS, pp. 621–640 (2020)
Stephens, J., Ferles, K., Mariano, B., Lahiri, S., Dillig, I.: SmartPulse: automated checking of temporal properties in smart contracts. In: IEEE S&P (2021)
Väänänen, J.A.: Generalized quantifiers. In: Bull. EATCS (1997)
Vogelsteller, F., Buterin, V.: EIP-20: ERC-20 token standard. In: EIP no. 20 (2015)
Wang, Y., et al.: Formal verification of workflow policies for smart contracts in azure blockchain. In: VSTTE, pp. 87–106 (2019)
Weidenbach, C., Dimova, D., Fietzke, A., Kumar, R., Suda, M., Wischnewski, P.: SPASS Version 3.5. In: CADE, pp. 140–145 (2009)
Zhong, J.E., et al.: The move prover. In: CAV, pp. 137–150 (2020)
Acknowledgement
We thank Petra Hozzová for fruitful discussions on our encodings and Sharon Shoham-Buchbinder for her insights and contributions to this paper. This work was partially funded by the ERC CoG ARTIST 101002685, the ERC StG SYMCAR 639270, the United States-Israel Binational Science Foundation (BSF) grant No. 2016260, Grant No. 1810/18 from the Israeli Science Foundation, Len Blavatnik and the Blavatnik Family foundation, the FWF grant LogiCS W1255-N23, the TU Wien DK SecInt and the Amazon ARA 2020 award FOREST.
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2021 The Author(s)
About this paper
Cite this paper
Elad, N., Rain, S., Immerman, N., Kovács, L., Sagiv, M. (2021). Summing up Smart Transitions. In: Silva, A., Leino, K.R.M. (eds) Computer Aided Verification. CAV 2021. Lecture Notes in Computer Science(), vol 12759. Springer, Cham. https://doi.org/10.1007/978-3-030-81685-8_15
Download citation
DOI: https://doi.org/10.1007/978-3-030-81685-8_15
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-81684-1
Online ISBN: 978-3-030-81685-8
eBook Packages: Computer ScienceComputer Science (R0)






 ;
; to
to  ;
; ;
; ;
; .
. element as a separating one.
element as a separating one. element x (where g(x) is 0).
element x (where g(x) is 0).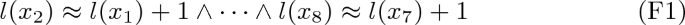


 , where
, where  .
.

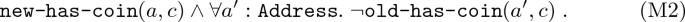
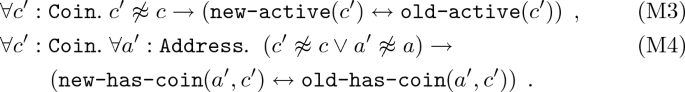

 , where
, where  .
.