Abstract
ksmt is a CDCL-style calculus for solving non-linear constraints over the real numbers involving polynomials and transcendental functions. In this paper we investigate properties of the ksmt calculus and show that it is a \(\delta \)-complete decision procedure for bounded problems. We also propose an extension with local linearisations, which allow for more efficient treatment of non-linear constraints.
This research was partially supported by an Intel research grant, the DFG grant WERA MU 1801/5-1 and the RFBR-JSPS 20-51-5000 grant.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
Solving non-linear constraints is important in many applications, including verification of cyber-physical systems, software verification, proof assistants for mathematics [1, 2, 6, 15, 21, 25]. Hence there has been a number of approaches for solving non-linear constraints, involving symbolic methods [16, 18, 23, 29] as well as numerically inspired ones, in particular for dealing with transcendental functions [13, 30], and combinations of symbolic and numeric methods [7, 11, 12].
In [7] we introduced the ksmt calculus for solving non-linear constraints over a large class of functions including polynomial, exponential and trigonometric functions. The ksmt calculusFootnote 1 combines CDCL-style reasoning [3, 22, 28] over the reals based on conflict resolution [19] with incremental linearisations of non-linear functions using methods from computable analysis [24, 31]. Our approach is based on computable analysis and exact real arithmetic which avoids limitations of double precision computations caused by rounding errors and instabilities in numerical methods. In particular, satisfiable and unsatisfiable results returned by ksmt are exact as required in many applications. This approach also supports implicit representations of functions as solutions of ODEs and PDEs [26].
It is well known that in the presence of transcendental functions the constraint satisfiability problem is undecidable [27]. However if we only require solutions up to some specified precision \(\delta \), then the problem can be solved algorithmically on bounded instances and that is the motivation behind \(\delta \)-completeness, which was introduced in [13]. In essence a \(\delta \)-complete procedure decides if a formula is unsatisfiable or a \(\delta \) weakening of the formula is satisfiable.
In this paper we investigate theoretical properties of the ksmt calculus, and its extension \(\delta \)-ksmt for the \(\delta \)-SMT setting. Our main results are as follows:
-
1.
We introduced a notion of \(\epsilon \)-full linearisations and prove that all \(\epsilon \)-full runs of ksmt are terminating on bounded instances.
-
2.
We extended the \(\texttt {ksmt} \) calculus to the \(\delta \)-satisfiability setting and proved that \(\delta \)-ksmt is a \(\delta \)-complete decision procedure for bounded instances.
-
3.
We introduced an algorithm for computing \(\epsilon \)-full local linearisations and integrated it into \(\delta \)-ksmt. Local linearisations can be used to considerably narrow the search space by taking into account local behaviour of non-linear functions avoiding computationally expensive global analysis.
In Section 3, we give an overview about the ksmt calculus and introduce the notion of \(\epsilon \)-full linearisation used throughout the rest of the paper. We also present a completeness theorem. Section 4 introduces the notion of \(\delta \)-completeness and related concepts. In Section 5 we introduce the \(\delta \)-ksmt adaptation, prove it is correct and \(\delta \)-complete, and give concrete effective linearisations based on a uniform modulus of continuity. Finally in Section 6, we introduce local linearisations and show that termination is independent of computing uniform moduli of continuity, before we conclude in Section 7.
2 Preliminaries
The following conventions are used throughout this paper. By \(\Vert \cdot \Vert \) we denote the maximum-norm \(\Vert (x_1,x_2,\ldots ,x_n)\Vert =\max \{|x_i|:1\le i\le n\}\). When it helps clarity, we write finite and infinite sequences \(\boldsymbol{x}=(x_1,\ldots ,x_n)\) and \(\boldsymbol{y}=(y_i)_i\) in bold typeface. We are going to use open balls \(B(\boldsymbol{c},\epsilon )=\{\boldsymbol{x}:\Vert \boldsymbol{x}-\boldsymbol{c}\Vert <\epsilon \}\subseteq \mathbb {R}^n\) for \(\boldsymbol{c}\in \mathbb {R}^n\) and \(\epsilon >0\) and \(\bar{A}\) to denote the closure of the set \(A\subseteq \mathbb {R}^n\) in the standard topology induced by the norm. By \(\mathbb {Q}_{>0}\) we denote the set \(\{q\in \mathbb {Q}:q>0\}\). For sets X, Y, a (possibly partial) function from X to Y is written as \(X\rightarrow Y\). We use the notion of compactness: a set A is compact iff every open cover of A has a finite subcover. In Euclidean spaces this is equivalent to A being bounded and closed [32].
Basic Notions of Computable Analysis
Let us recall the notion of computability of functions over real numbers used throughout this paper. A rational number q is an n-approximation of a real number x if \(\Vert q-x\Vert \le 2^{-n}\). Informally, a function f is computed by a function-oracle Turing machine \(M_f^?\), where \(^?\) is a placeholder for the oracle representing the argument of the function, in the following way. The real argument x is represented by an oracle function \(\varphi :\mathbb {N}\rightarrow \mathbb {Q}\), for each n returning an n-approximation \(\varphi _n\) of x. For simplicity, we refer to \(\varphi \) by the sequence \((\varphi _n)_n\). When run with argument \(p\in \mathbb {N}\), \(M_f^\varphi (p)\) computes a rational p-approximation of f(x) by querying its oracle \(\varphi \) for approximations of x. Let us note that the definition of the oracle machine does not depend on the concrete oracle, i.e., the oracle can be seen as a parameter. In case only the machine without a concrete oracle is of interest, we write \(M_f^?\). We refer to [17] for a precise definition of the model of computation by function-oracle Turing machines which is standard in computable analysis.
Definition 1
([17]). Consider \(\boldsymbol{x} \in \mathbb {R}^n\). A name for \(\boldsymbol{x}\) is a rational sequence \(\boldsymbol{\varphi }=(\boldsymbol{\varphi }_k)_k\) such that \(\forall k:\Vert \boldsymbol{\varphi }_k-\boldsymbol{x}\Vert \le 2^{-k}\). A function \(f:\mathbb {R}^n\rightarrow \mathbb {R}\) is computable iff there is a function-oracle Turing machine \(M_f^?\) such that for all \(\boldsymbol{x}\in \mathrm {dom}f\) and names \(\boldsymbol{\varphi }\) for \(\boldsymbol{x}\), \(|M_f^{\boldsymbol{\varphi }}(p)-f(\boldsymbol{x})|\le 2^{-p}\) holds for all \(p\in \mathbb {N}\).
This definition is closely related to interval arithmetic with unrestricted precision, but enhanced with the guarantee of convergence and it is equivalent to the notion of computability used in [31]. The class of computable functions contains polynomials and transcendental functions like \(\sin \), \(\cos \), \(\exp \), among others. It is well known [17, 31] that this class is closed under composition and that computable functions are continuous. By continuity, a computable function \(f:\mathbb {R}^n\rightarrow \mathbb {R}\) total on a compact \(D\subset \mathbb {R}^n\) has a computable uniform modulus of continuity \(\mu _f:\mathbb {N}\rightarrow \mathbb {N}\) on D [31, Theorem 6.2.7], that is,
A uniform modulus of continuity of f expresses how changes in the value of f depend on changes of the arguments in a uniform way.
3 The ksmt Calculus
We first describe the ksmt calculus for solving non-linear constraints [7] informally, and subsequently recall the main definitions which we use in this paper. The ksmt calculus consists of transition rules, which, for any formula in linear separated form, allow deriving lemmas consistent with the formula and, in case of termination, produce a satisfying assignment for the formula or show that it is unsatisfiable. A quantifier-free formula is in separated linear form \(\mathcal {L}\cup \mathcal {N}\) if \(\mathcal {L}\) is a set of clauses over linear constraints and \(\mathcal {N}\) is a set of non-linear atomic constraints; this notion is rigorously defined below.
In the ksmt calculus there are four transition rules applied to its states: Assignment refinement (A), Conflict resolution (R), Backjumping (B) and Linearisation (L). The final ksmt states are sat and unsat. A non-final ksmt state is a triple \((\alpha ,\mathcal {L},\mathcal {N})\) where \(\alpha \) is a (partial) assignment of variables to rationals. A ksmt derivation starts with an initial state where \(\alpha \) is empty and tries to extend this assignment to a solution of \(\mathcal {L} \cup \mathcal {N}\) by repeatedly applying the Assignment refinement rule. When such assignment extension is not possible we either obtain a linear conflict which is resolved using the conflict resolution rule, or a non-linear conflict which is resolved using the linearisation rule.
The main idea behind the linearisation rule is to approximate the non-linear constraints around the conflict using linear constraints in such a way that the conflict will be shifted into the linear part where it will be resolved using conflict resolution. Application of either of these two rules results in a state containing a clause evaluating to false under the current assignment. This is followed by either application of the backjumping rule, which undoes assignments or by termination in case the formula is unsat. In this procedure, only the assignment and linear part of the state change and the non-linear part stays fixed.
Notations. Let \(\mathcal {F}_{\mathrm {lin}}\) consist of rational constants, addition and multiplication by rational constants; \(\mathcal {F}_{\mathrm {nl}}\) denotes an arbitrary collection of non-linear computable functions including transcendental functions and polynomials over the reals. We consider the structure \((\mathbb {R},\langle \mathcal {F}_{\mathrm {lin}}\cup \mathcal {F}_{\mathrm {nl}},\mathcal {P}\rangle )\) where \(\mathcal {P}=\{{<},{\le },{>},{\ge },{=},{\ne }\}\) and a set of variables \(V=\{x_1,x_2,\ldots ,x_n,\ldots \}\). We will use, possibly with indices, x to denote variables and q, c, e for rational constants. Define terms, predicates and formulas over V in the standard way. An atomic linear constraint is a formula of the form: \(q+c_1x_1+\ldots +c_nx_n \diamond 0\) where \(q,c_1,\ldots ,c_n\in \mathbb {Q}\) and \(\diamond \in \mathcal {P}\). Negations of atomic formulas can be eliminated by rewriting the predicate symbol \(\diamond \) in the standard way, hence we assume that all literals are positive. A linear constraint is a disjunction of atomic linear constraints, also called (linear) clause. An atomic non-linear constraint is a formula of the form \(f(\boldsymbol{x})\diamond 0\), where \(\diamond \in \mathcal {P}\) and f is a composition of computable non-linear functions from \(\mathcal {F}_{\mathrm {nl}}\) over variables \(\boldsymbol{x}\). Throughout this paper for every computable real function f we use \(M_f^?\) to denote a function-oracle Turing machine computing f. We assume quantifier-free formulas in separated linear form [7, Definition 1], that is, \(\mathcal {L}\cup \mathcal {N}\) where \(\mathcal {L}\) is a set of linear constraints and \(\mathcal {N}\) is a set of non-linear atomic constraints. Arbitrary quantifier-free formulas can be transformed equi-satisfiably into separated linear form in polynomial time [7, Lemma 1]. Since in separated linear form all non-linear constraints are atomic we will call them just non-linear constraints.
Let \(\alpha :V\rightarrow \mathbb {Q}\) be a partial variable assignment. The interpretation \([\![\boldsymbol{x}]\!]^\alpha \) of a vector of variables \(\boldsymbol{x}\) under \(\alpha \) is defined in a standard way as component-wise application of \(\alpha \). Define the notation \([\![t]\!]^\alpha \) as evaluation of term t under assignment \(\alpha \), that can be partial, in which case \([\![t]\!]^\alpha \) is treated symbolically. We extend \([\![\cdot ]\!]^\alpha \) to predicates, clauses and CNF in the usual way and \(\textsf {true},\textsf {false} \) denote the constants of the Boolean domain. The evaluation \([\![t\diamond 0]\!]^\alpha \) for a predicate \(\diamond \) and a term t results in \(\textsf {true} \) or \(\textsf {false} \) only if all variables in t are assigned by \(\alpha \).
In order to formally restate the calculus, the notions of linear resolvent and linearisation are essential. A resolvent \(R_{\alpha ,\mathcal {L},z}\) on a variable z is a set of linear constraints that do not contain z, are implied by the formula \(\mathcal {L}\) and which evaluate to \(\textsf {false} \) under the current partial assignment \(\alpha \); for more details see [7, 19].
Definition 2
Let P be a non-linear constraint and let \(\alpha \) be an assignment with \([\![P]\!]^\alpha =\textsf {false} \). A linearisation of P at \(\alpha \) is a linear clause C with the properties:
-
1.
\(\forall \beta :[\![P]\!]^\beta =\textsf {true} \implies [\![C]\!]^\beta =\textsf {true} \), and
-
2.
\([\![C]\!]^\alpha =\textsf {false} \).
Wlog. we can assume that the variables of C are a subset of the variables of P. Let us note that any linear clause C represents the complement of a rational polytope R and we will use both interchangeably. Thus for a rational polytope R, \(\boldsymbol{x}\not \in R\) also stands for a linear clause. In particular, any linearisation excludes a rational polytope containing the conflicting assignment from the search space.
Transition rules. For a formula \(\mathcal {L}_0\cup \mathcal {N}\) in separated linear form, the initial ksmt state is \((\textsf {nil},\mathcal {L}_0,\mathcal {N})\). The calculus consists of the following transition rules from a state \(S=(\alpha ,\mathcal {L},\mathcal {N})\) to \(S'\):
-
(A) Assignment. \(S'=(\alpha {:}{:}z\mapsto q,\mathcal {L},\mathcal {N})\) iff \([\![\mathcal {L}]\!]^\alpha \ne \textsf {false} \) and there is a variable z unassigned in \(\alpha \) and \(q\in \mathbb {Q}\) with \([\![\mathcal {L}]\!]^{\alpha {:}{:}z\mapsto q}\ne \textsf {false} \).
-
(R) Resolution. \(S'=(\alpha ,\mathcal {L}\cup R_{\alpha ,\mathcal {L},z},\mathcal {N})\) iff \([\![\mathcal {L}]\!]^\alpha \ne \textsf {false} \) and there is a variable z unassigned in \(\alpha \) with \(\forall q\in \mathbb {Q}:[\![\mathcal {L}]\!]^{\alpha {:}{:}z\mapsto q}=\textsf {false} \) and \(R_{\alpha ,\mathcal {L},z}\) is a resolvent.
-
(B) Backjump. \(S'=(\gamma ,\mathcal {L},\mathcal {N})\) iff \([\![\mathcal {L}]\!]^\alpha =\textsf {false} \) and there is a maximal prefix \(\gamma \) of \(\alpha \) such that \([\![\mathcal {L}]\!]^\gamma \ne \textsf {false} \).
-
(L) Linearisation. \(S'=(\alpha ,\mathcal {L}\cup \{L_{\alpha , P}\},\mathcal {N})\) iff \([\![\mathcal {L}]\!]^\alpha \ne \textsf {false} \), there is P in \(\mathcal {N}\) with \([\![P]\!]^\alpha =\textsf {false} \) and there is a linearisation \(L_{\alpha ,P}\) of P at \(\alpha \).
-
\((F^ sat _{})\) Final sat. \(S'=\textsf {sat} \) if all variables are assigned in \(\alpha \), \([\![\mathcal {L}]\!]^\alpha =\textsf {true} \) and none of the rules (A), (R), (B), (L) is applicable.
-
\((F^ unsat )\) Final unsat. \(S'=\textsf {unsat} \) if \([\![\mathcal {L}]\!]^\textsf {nil} =\textsf {false} \). In other words a trivial contradiction, e.g., \(0>1\) is in \(\mathcal {L}\).
A path (or a run) is a derivation in a ksmt. A procedure is an effective (possibly non-deterministic) way to construct a path.
Termination. If no transition rule is applicable, the derivation terminates. For clarity, we added the explicit rules \((F^ sat _{})\) and \((F^ unsat )\) which lead to the final states. This calculus is sound [7, Lemma 2]: if the final transition is \((F^ sat _{})\), then \(\alpha \) is a solution to the original formula, or \((F^ unsat )\), then a trivial contradiction \(0>1\) was derived and the original formula is unsatisfiable. The calculus also makes progress by reducing the search space [7, Lemma 3].
unsat example run of ksmt using interval linearisation [7].
An example run of the ksmt calculus is presented in Figure 2. We start in a state with a non-linear part \(\mathcal {N}=\{y\le 1/x\}\), which defines the pink area and the linear part \(\mathcal {L}=\{ (x/4+1\le y), (y\le 4\cdot (x-1))\}\), shaded in green. Then we successively apply ksmt rules excluding regions around candidate solutions by linearisations, until we derive linearisations which separates the pink area from the green area thus deriving a contradiction.
Remark 1
In general a derivation may not terminate. The only cause of non-termination is the linearisation rule which adds new linear constraints and can be applied infinitely many times. To see this, observe that ksmt with only the rules (A), (R), (B) corresponds to the conflict resolution calculus which is known to be terminating [19, 20]. Thus, in infinite ksmt runs the linearisation rule (L) is applied infinitely often. This argument is used in the proof of Theorem 1 below. Let us note that during a run the ksmt calculus neither conflicts nor lemmas can be generated more than once. In fact, any generated linearisation is not implied by the linear part, prior to adding this linearisation.
3.1 Sufficient Termination Conditions
In this section we will assume that \((\alpha ,\mathcal {L},\mathcal {N})\) is a ksmt state obtained by applying ksmt inference rules to an initial state. As in [13] we only consider bounded instances. In many applications this is a natural assumption as variables usually range within some (possibly large) bounds. We can assume that these bounds are made explicit as linear constraints in the system.
Definition 3
Let F be the formula \(\mathcal {L}_0\wedge \mathcal {N}\) in separated linear form over variables \(x_1,\ldots ,x_n\) and let \(B_i\) be the set defined by the conjunction of all clauses in \(\mathcal {L}_0\) univariate in \(x_i\), for \(i=1,\ldots ,n\); in particular, if there are no univariate linear constraints over \(x_i\) then \(B_i=\mathbb {R}\). We call F a bounded instance if:
-
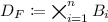 is bounded, and
is bounded, and -
for each non-linear constraint \(P:f(x_{i_1},\ldots ,x_{i_k})\diamond 0\) in \(\mathcal {N}\) with \(i_j\in \{1,\ldots ,n\}\) for \(j\in \{1,\ldots ,k\}\) it holds that \(\bar{D_P}\subseteq \mathrm {dom}f\) where
 .
.
By this definition, already the linear part of bounded instances explicitly defines a bounded set by univariate constraints. Consequently, the set of solutions of F is bounded as well.
In Theorem 1 we show that when we consider bounded instances and restrict linearisations to so-called \(\epsilon \)-full linearisations, then the procedure terminates. We use this to show that the ksmt-based decision procedure we introduce in Section 5 is \(\delta \)-complete.
Definition 4
Let \(\epsilon >0\), P be a non-linear constraint over variables \(\boldsymbol{x}\) and let \(\alpha \) be an assignment of \(\boldsymbol{x}\). A linearisation C of P at \(\alpha \) is called \(\epsilon \)-full iff for all assignments \(\beta \) of \(\boldsymbol{x}\) with \([\![\boldsymbol{x}]\!]^\beta \in B([\![\boldsymbol{x}]\!]^\alpha ,\epsilon )\), \([\![C]\!]^\beta =\textsf {false} \).
A ksmt run is called \(\epsilon \)-full for some \(\epsilon >0\), if all but finitely many linearisations in this run are \(\epsilon \)-full.
The next theorem provides a basis for termination of ksmt-based decision procedures for satisfiability.
Theorem 1
Let \(\epsilon >0\). On bounded instances, \(\epsilon \)-full ksmt runs are terminating.
Proof
Let \(F:\mathcal {L}_0 \wedge \mathcal {N}\) be a bounded instance and \(\epsilon >0\). Towards a contradiction assume there is an infinite \(\epsilon \)-full derivation \((\alpha _0,\mathcal {L}_0,\mathcal {N}),\dots , (\alpha _n,\mathcal {L}_n,\mathcal {N}), \dots \) in the ksmt calculus. Then, by definition of the transition rules, \(\mathcal {L}_k\subseteq \mathcal {L}_l\) for all k, l with \(0\le k\le l\). According to Remark 1 in any infinite derivation the linearisation rule must be applied infinitely many times. During any run of ksmt the set of non-linear constraints \(\mathcal {N}\) is fixed and therefore there is a non-linear constraint P in \(\mathcal {N}\) over variables \(\boldsymbol{x}\) to which linearisation is applied infinitely often. Let \((\alpha _{i_1},\mathcal {L}_{i_1},\mathcal {N}),\dots , (\alpha _{i_n},\mathcal {L}_{i_n},\mathcal {N}), \dots \) be a corresponding subsequence in the derivation such that \(C_{i_1}\in \mathcal {L}_{i_1+1},\ldots ,C_{i_n}\in \mathcal {L}_{i_n+1},\ldots \) are \(\epsilon \)-full linearisations of P. Consider two different linearisation steps \(k,\ell \in \{i_j:j\in \mathbb {N}\}\) in the derivation where \(k < \ell \). By the precondition of rule (L) applied in step \(\ell \) we have \([\![\mathcal {L}_\ell ]\!]^{\alpha _\ell }\ne \textsf {false} \). In particular the linearisation \(C_k\in \mathcal {L}_{k+1}\subseteq \mathcal {L}_\ell \) of P constructed in step k does not evaluate to false under \(\alpha _\ell \). Since the set of variables in \(C_k\) is a subset of those in P, \([\![C_k]\!]^{\alpha _\ell }\ne \textsf {false} \) implies \([\![C_k]\!]^{\alpha _\ell }=\textsf {true} \). By assumption, the linearisation \(C_k\) is \(\epsilon \)-full, thus from Definition 4 it follows that \([\![\boldsymbol{x}]\!]^{\alpha _\ell }\notin B([\![\boldsymbol{x}]\!]^{\alpha _k},\epsilon )\). Therefore the distance between \([\![\boldsymbol{x}]\!]^{\alpha _k}\) and \([\![\boldsymbol{x}]\!]^{\alpha _\ell }\) is at least \(\epsilon \). However, every conflict satisfies the variable bounds defining \(D_F\), so there could be only finitely many conflicts with pairwise distance at least \(\epsilon \). This contradicts the above.
Concrete algorithms to compute \(\epsilon \)-full linearisations are presented in Sections 5 and 6.
4 \(\delta \)-decidability
In the last section, we proved termination of the ksmt calculus on bounded instances when linearisations are \(\epsilon \)-full. Let us now investigate how \(\epsilon \)-full linearisations of constraints involving non-linear computable functions can be constructed. To that end, we assume that all non-linear functions are defined on the closure of the bounded space \(D_F\) defined by the bounded instance F.
So far we described an approach which gives exact results but at the same time is necessarily incomplete due to undecidability of non-linear constraints in general. On the other hand, non-linear constraints usually can be approximated using numerical methods allowing to obtain approximate solutions to the problem. This gives rise to the bounded \(\delta \)-SMT problem [13] which allows an overlap between the properties \(\delta \)-sat and unsat of formulas as illustrated by Figure 3. It is precisely this overlap that enables \(\delta \)-decidability of bounded instances.
Let us recall the notion of \(\delta \)-decidability, adapted from [13].
Definition 5
Let F be a formula in separated linear form and let \(\delta \in \mathbb {Q}_{>0}\). We inductively define the \(\delta \)-weakening \(F_\delta \) of F.
-
If F is linear, let
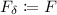 .
. -
If F is a non-linear constraint \(f(\boldsymbol{x})\diamond 0\), let

-
Otherwise, F is \(A\circ B\) with \(\circ \in \{\wedge ,\vee \}\). Let
 .
.
\(\delta \)-deciding F designates computing
In case both answers are valid, the algorithm may output any.
An assignment \(\alpha \) with \([\![F_\delta ]\!]^\alpha =\textsf {true} \) we call a \(\delta \)-satisfying assignment for F.
For non-linear constraints P this definition of the \(\delta \)-weakening \(P_\delta \) corresponds exactly to the notion of \(\delta \)-weakening \(P^{-\delta }\) used in the introduction of \(\delta \)-decidability [14, Definition 4.1].
Remark 2
The \(\delta \)-weakening of a non-linear constraint \(f(\boldsymbol{x})\ne 0\) is a tautology.
We now consider the problem of \(\delta \)-deciding quantifier-free formulas in separated linear form. The notion of \(\delta \)-decidability is slightly stronger than in [13] in the sense that we do not weaken linear constraints. Consider a formula F in separated linear form. As before, we assume variables \(\boldsymbol{x}\) to be bounded by linear constraints \(\boldsymbol{x}\in D_F\). We additionally assume that for all non-linear constraints \(P:f(\boldsymbol{x})\diamond 0\) in \(\mathcal {N}\), f is defined on \(\bar{D_P}\) and, in order to simplify the presentation, throughout the rest of paper we will assume only the predicates \(\diamond \in \{{>},{\ge }\}\) are part of formulas, since the remaining ones \({<},{\le },{=}\) can easily be expressed by the former using simple arithmetic transformations, and by Remark 2 predicates \(\ne \) are irrelevant for \(\delta \)-deciding formulas.
An algorithm is \(\delta \)-complete, if it \(\delta \)-decides bounded instances [13].
5 \(\delta \)-ksmt
Since \(\delta \)-decidability as introduced above adapts the condition when a formula is considered to be satisfied to \(\delta \)-sat, this condition has to be reflected in the calculus, which we show solves the bounded \(\delta \)-SMT problem in this section. Adding the following rule \((F^ sat _{\delta })\) together with the new final state \(\delta \)-sat to ksmt relaxes the termination conditions and turns it into the extended calculus we call \(\delta \)-ksmt.
-
\((F^ sat _{\delta })\) Final \(\delta \)-sat. If \((\alpha ,\mathcal {L},\mathcal {N})\) is a \(\delta \)-ksmt state where \(\alpha \) is a total assignment and \([\![\mathcal {L}\wedge \mathcal {N}_\delta ]\!]^\alpha =\textsf {true} \), transition to the \(\delta \)-sat state.
The applicability conditions on the rules (L) and \((F^ sat _{\delta })\) individually are not decidable [5, 27], however, when we compute them simultaneously, we can effectively apply one of these rules, as we will show in Lemma 3. In combination with \(\epsilon \)-full ness of the computed linearisations (Lemma 4), this leads to Theorem 3, showing that \(\delta \)-ksmt is a \(\delta \)-complete decision procedure.
Let us note that if we assume \(\delta =0\) then \(\delta \)-ksmt would just reduce to ksmt as \((F^ sat _{})\) and \((F^ sat _{\delta })\) become indistinguishable, but in the following we always assume \(\delta >0\).
In the following sub-section, we prove that terminating derivations of the \(\delta \)-ksmt calculus lead to correct results. Then, in Section 5.2, we present a concrete algorithm for applying rules (L) and \((F^ sat _{\delta })\) and show its linearisations to be \(\epsilon \)-full, which is sufficient to ensure termination, as shown in Theorem 1. These properties lead to a \(\delta \)-complete decision procedure. In Section 6 we develop a more practical algorithm for \(\epsilon \)-full linearisations that does not require computing a uniform modulus of continuity.
5.1 Soundness
In this section we show soundness of the \(\delta \)-ksmt calculus, that is, validity of its derivations. In particular, this implies that derivability of the final states \(\textsf {unsat} \), \(\delta \)-sat and sat directly corresponds to unsatisfiability, \(\delta \)-satisfiability and satisfiability of the original formula, respectively.
Lemma 1
For all \(\delta \)-ksmt derivations of \(S'=(\alpha ',\mathcal {L}',\mathcal {N})\) from a state \(S=(\alpha ,\mathcal {L},\mathcal {N})\) and for all total assignments \(\beta \), \([\![\mathcal {L}\wedge \mathcal {N}]\!]^\beta = [\![\mathcal {L}'\wedge \mathcal {N}]\!]^\beta \).
Proof
Let \(\beta \) be a total assignment of the variables in \(\mathcal {L}\wedge \mathcal {N}\). Since the set of variables remains unchanged by \(\delta \)-ksmt derivations, \(\beta \) is a total assignment for \(\mathcal {L}'\wedge \mathcal {N}\) as well. Let \(S'=(\alpha ',\mathcal {L}',\mathcal {N})\) be derived from \(S=(\alpha ,\mathcal {L},\mathcal {N})\) by a single application of one of \(\delta \)-ksmt rules. By the structure of \(S'\), its derivation was not caused by neither \((F^ unsat ),(F^ sat _{})\) or \((F^ sat _{\delta })\). For rules (A) and (B) there is nothing to show since \(\mathcal {L}=\mathcal {L}'\). If (R) caused \(S\mapsto S'\), the claim holds by soundness of arithmetical resolution. Otherwise (L) caused \(S\mapsto S'\) in which case the direction \(\Rightarrow \) follows from the definition of a linearisation (condition 1 in Definition 2) while the other direction trivially holds since \(\mathcal {L}\subseteq \mathcal {L}'\).
The condition on derivations of arbitrary lengths then follows by induction.
Lemma 2
Let \(\delta \in \mathbb {Q}_{>0}\). Consider a formula \(G=\mathcal {L}_0\wedge \mathcal {N}\) in separated linear form and let \(S=(\alpha ,\mathcal {L},\mathcal {N})\) be a \(\delta \)-ksmt state derivable from the initial state \(S_0=(\textsf {nil},\mathcal {L}_0,\mathcal {N})\). The following hold.
-
If rule \((F^ unsat )\) is applicable to S then G is unsatisfiable.
-
If rule \((F^ sat _{\delta })\) is applicable to S then \(\alpha \) is a \(\delta \)-satisfying assignment for G, hence G is \(\delta \)-satisfiable.
-
If rule \((F^ sat _{})\) is applicable to S then \(\alpha \) is a satisfying assignment for G, hence G is satisfiable.
Proof
Let formula G and states \(S_0,S\) be as in the premise. As S is not final in \(\delta \)-ksmt, only ksmt rules have been applied in deriving it. The statements for rules \((F^ unsat )\) and \((F^ sat _{})\) thus hold by soundness of ksmt [7, Lemma 2].
Assume \((F^ sat _{\delta })\) is applicable to S, that is, \([\![\mathcal {L}\wedge \mathcal {N}_\delta ]\!]^\alpha \) is true. Then, since \(\mathcal {L}_0\subseteq \mathcal {L}\), we conclude that \(\alpha \) satisfies \(\mathcal {L}_0\wedge \mathcal {N}_\delta \) which, according to Definition 5, equals \(G_\delta \). Therefore \(\alpha \) is a \(\delta \)-satisfying assignment for G.
Since the only way to derive one of the final states unsat, \(\delta \)-sat and sat from the initial state in \(\delta \)-ksmt is by application of the rule \((F^ unsat ),(F^ sat _{\delta })\) and \((F^ sat _{})\), respectively, as corollary of Lemmas 1 and 2 we obtain soundness.
Theorem 2 (Soundness)
Let \(\delta \in \mathbb {Q}_{>0}\). The \(\delta \)-ksmt calculus is sound.
5.2 \(\delta \)-completeness
We proceed by introducing Algorithm 1 computing linearisations and deciding which of the rules \((F^ sat _{\delta })\) and (L) to apply. These linearisations are then shown to be \(\epsilon \)-full for some \(\epsilon >0\) depending on the bounded instance. By Theorem 1, this property implies termination, showing that \(\delta \)-ksmt is a \(\delta \)-complete decision procedure.
Given a non-final \(\delta \)-ksmt state, the function nlinStep\(_\delta \) in Algorithm 1 computes a \(\delta \)-ksmt state derivable from it by application of \((F^ sat _{\delta })\) or (L). This is done by evaluating the non-linear functions and adding a linearisation \(\ell \) based on their uniform moduli of continuity as needed. To simplify the algorithm, it assumes total assignments as input. It is possible to relax this requirement, e.g., by invoking rules (A) or (R) instead of returning \(\delta \)-sat for partial assignments.

Lemma 3
Let \(\delta \in \mathbb {Q}_{>0}\) and let \(S=(\alpha ,\mathcal {L},\mathcal {N})\) be a \(\delta \)-ksmt state where \(\alpha \) is total and \([\![\mathcal {L}]\!]^\alpha =\textsf {true} \). Then nlinStep\(_\delta \)(\(\alpha ,\mathcal {L},\mathcal {N}\)) computes a state derivable by application of either (L) or \((F^ sat _{\delta })\) to S.
Proof
In the proof we will use notions from computable analysis, as defined in Section 2. Let \((\alpha ,\mathcal {L},\mathcal {N})\) be a state as in the premise and let \(P:f(\boldsymbol{x})\diamond 0\) be a non-linear constraint in \(\mathcal {N}\). Let \(M_f^?\) compute f as in Algorithm 1. The algorithm computes a rational approximation \(\tilde{y}=M_f^{([\![\boldsymbol{x}]\!]^\alpha )_i}(p)\) of \(f([\![\boldsymbol{x}]\!]^\alpha )\) where \(p\ge -\lfloor \log _2(\min \{1,\delta /4\})\rfloor \in \mathbb {N}\). \([\![\mathcal {L}]\!]^\alpha =\textsf {true} \) implies \([\![\boldsymbol{x}]\!]^\alpha \in D_P\subseteq \mathrm {dom}f\), thus the computation of \(\tilde{y}\) terminates. Since \(M_f^?\) computes f, \(\tilde{y}\) is accurate up to \(2^{-p}\le \delta /4\), that is, \(\tilde{y}\in [f([\![\boldsymbol{x}]\!]^\alpha )\pm \delta /4]\). By assumption \(\diamond \in \{{>},{\ge }\}\), thus
-
1.
\(\tilde{y}\mathrel \diamond -\delta /2\) implies \(f([\![\boldsymbol{x}]\!]^\alpha )\mathrel \diamond -\delta \), which is equivalent to \([\![P_\delta ]\!]^\alpha =\textsf {true} \), and
-
2.
\(\lnot (\tilde{y}\mathrel \diamond -\delta /2)\) implies \(\lnot (f([\![\boldsymbol{x}]\!]^\alpha )\mathrel \diamond -\delta /2+\delta /4)\), which in turn implies \([\![P]\!]^\alpha =\textsf {false} \) and the applicability of rule (L).
For Item 1 no linearisation is necessary and indeed the algorithm does not linearise P. Otherwise (Item 2), it adds the linearisation \((\boldsymbol{x}\notin B([\![\boldsymbol{x}]\!]^\alpha ,\epsilon ))\) to the linear clauses. Since \([\![\boldsymbol{x}]\!]^\alpha \in D_P\) by Eq. (2.1) we obtain that \(0\notin B(f(\boldsymbol{z}),\delta /4)\) holds, implying \(\lnot (f(\boldsymbol{z})\diamond 0)\), for all \(\boldsymbol{z}\in B([\![\boldsymbol{x}]\!]^\alpha ,\epsilon )\cap \bar{D_P}\). Hence, \((\boldsymbol{x}\notin B([\![\boldsymbol{x}]\!]^\alpha ,\epsilon ))\) is a linearisation of P at \(\alpha \).
In case nlinStep\(_\delta \)(\(\alpha ,\mathcal {L},\mathcal {N}\)) returns \(\delta \)-sat, the premise of Item 1 holds for every non-linear constraint in \(\mathcal {N}\), that is, \([\![\mathcal {N}_\delta ]\!]^\alpha =\textsf {true} \). By assumption \([\![\mathcal {L}]\!]^\alpha =\textsf {true} \), hence the application of the \((F^ sat _{\delta })\) rule deriving \(\delta \)-sat is possible in \(\delta \)-ksmt.
Lemma 4
For any bounded instance \(\mathcal {L}_0\wedge \mathcal {N}\) there is a computable \(\epsilon \in \mathbb {Q}_{>0}\) such that any \(\delta \)-ksmt run starting in \((\textsf {nil},\mathcal {L}_0,\mathcal {N})\), where applications of (L) and \((F^ sat _{\delta })\) are performed by nlinStep\(_\delta \), is \(\epsilon \)-full.
Proof
Let \(P:f(\boldsymbol{x})\diamond 0\) be a non-linear constraint in \(\mathcal {N}\). Since \(\mathcal {L}_0\wedge \mathcal {N}\) is a bounded instance, \(D_P\subseteq \mathbb {R}^n\) is also bounded. Let  where \(p\ge -\lfloor \log _2(\min \{1,\delta /4\})\rfloor \in \mathbb {N}\) as in Algorithm 1. As \(\mu _f\) is a uniform modulus of continuity, the inequalities in the following construction hold on the whole domain \(\bar{D_P}\) of f and do not depend on the concrete assignment \(\alpha \) where the linearisation is performed. Since \(\log _2\) and \(\mu _f\) are computable, so are p and \(\epsilon _P\). There are finitely many non-linear constraints P in \(\mathcal {N}\), therefore the linearisations the algorithm nlinStep\(_\delta \) computes are \(\epsilon \)-full with \(\epsilon =\min \{\epsilon _P:P~\text {in}~\mathcal {N}\}>0\).
where \(p\ge -\lfloor \log _2(\min \{1,\delta /4\})\rfloor \in \mathbb {N}\) as in Algorithm 1. As \(\mu _f\) is a uniform modulus of continuity, the inequalities in the following construction hold on the whole domain \(\bar{D_P}\) of f and do not depend on the concrete assignment \(\alpha \) where the linearisation is performed. Since \(\log _2\) and \(\mu _f\) are computable, so are p and \(\epsilon _P\). There are finitely many non-linear constraints P in \(\mathcal {N}\), therefore the linearisations the algorithm nlinStep\(_\delta \) computes are \(\epsilon \)-full with \(\epsilon =\min \{\epsilon _P:P~\text {in}~\mathcal {N}\}>0\).
We call \(\delta \)-ksmt derivations when linearisation are computed using Algorithm 1 \(\delta \)-ksmt with full-box linearisations, or \(\delta \)-ksmt-fb for short. As the runs computed by it are \(\epsilon \)-full for \(\epsilon >0\), by Theorem 1 they terminate.
Theorem 3
\(\delta \)-ksmt-fb is a \(\delta \)-complete decision procedure.
Proof
\(\delta \)-ksmt-fb is sound (Theorem 2) and terminates on bounded instances (Theorem 1 and Lemma 4).
6 Local \(\epsilon \)-full Linearisations
In practice, when the algorithm computing \(\epsilon \)-full linearisations described in the previous section is going to be implemented, the question arises of how to get a good uniform modulus of continuity \(\mu _f\) for a computable function f. Depending on how f is given, there may be several ways of computing it. Implementations of exact real arithmetic, e.g., iRRAM [24] and Ariadne [2], are usually based on the formalism of function-oracle Turing machines (see Definition 1) which allow to compute with representations of computable functions [10] including implicit representations of functions as solutions of ODEs/PDEs [9, 26]. If f is only available as a function-oracle Turing machine \(M_f^?\) computing it, a modulus \(\mu _f\) valid on a compact domain can be computed, however, in general this is not possible without exploring the behaviour of the function on the whole domain, which in many cases is computationally expensive. Moreover, since \(\mu _f\) is uniform, \(\mu _f(n)\) is constant throughout \(D_F\), independent of the actual assignment \(\alpha \) determining where f is evaluated. Yet, computable functions admit local moduli of continuity that additionally depend on the concrete point in their domain. In most cases these would provide linearisations with \(\epsilon \) larger than that determined by \(\mu _f\) leading to larger regions being excluded, ultimately resulting in fewer linearisation steps and general speed-up. Indeed, machines producing finite approximations of f(x) from finite approximations of x internally have to compute some form of local modulus to guarantee correctness. In this section, we explore this approach of obtaining linearisations covering a larger part of the function’s domain.
In order to guarantee a positive bound on the local modulus of continuity extracted directly from the run of the machine \(M_f^?\) computing f, it is necessary to employ a restriction on the names of real numbers \(M_f^?\) computes on. The set of names should in a very precise sense be “small”, i.e., it has to be compact. The very general notion of names used in Definition 1 is too broad to satisfy this criterion since the space of rational approximations is not even locally compact. Here, we present an approach using practical names of real numbers as sequences of dyadic rationals of lengths restricted by accuracy. For that purpose, we introduce another representation [31] of \(\mathbb {R}\), that is, the surjective mapping \(\xi :\mathbb {D}_\omega \rightarrow \mathbb {R}\). Here, \(\mathbb {D}_\omega \) denotes the set of infinite sequences \(\varphi \) of dyadic rationals with bounded length. If \(\varphi \) has a limit (in \(\mathbb {R}\)), we write \(\lim \varphi \).
Definition 6
-
For \(k\in \omega \) let
 and let
and let 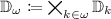 be the set of all sequences \((\varphi _k)_k\) with \(\varphi _k\in \mathbb {D}_k\) for all \(k\in \omega \). By default, \(\mathbb {D}_\omega \) is endowed with the Baire space topology, which corresponds to that induced by the metric $$ d:(\varphi ,\psi )\mapsto {\left\{ \begin{array}{ll} 0&{}\mathrm{{if}}~\varphi =\psi \\ 1/{\min \{1+n:n\in \omega ,\varphi _n\ne \psi _n\}}&{}\mathrm{{otherwise.}} \end{array}\right. } $$
be the set of all sequences \((\varphi _k)_k\) with \(\varphi _k\in \mathbb {D}_k\) for all \(k\in \omega \). By default, \(\mathbb {D}_\omega \) is endowed with the Baire space topology, which corresponds to that induced by the metric $$ d:(\varphi ,\psi )\mapsto {\left\{ \begin{array}{ll} 0&{}\mathrm{{if}}~\varphi =\psi \\ 1/{\min \{1+n:n\in \omega ,\varphi _n\ne \psi _n\}}&{}\mathrm{{otherwise.}} \end{array}\right. } $$ -
Define \(\xi :\mathbb {D}_\omega \rightarrow \mathbb {R}\) as the partial function mapping \(\varphi \in \mathbb {D}_\omega \) to \(\lim \varphi \) iff \(\forall i,j:|\varphi _i-\varphi _{i+j}|\le 2^{-(i+1)}\). Any \(\varphi \in \xi ^{-1}(x)\) is called a \(\xi \)-name of \(x\in \mathbb {R}\).
-
The representation \(\rho :(x_k)_k\mapsto x\) mapping names \((x_k)_k\) of \(x\in \mathbb {R}\) to x as per Definition 1 is called Cauchy representation.
Using a standard product construction we can easily generalise the notion of \(\xi \)-names to \(\xi ^n\)-names of \(\mathbb {R}^n\). When clear from the context, we will drop n and just write \(\xi \) to denote the corresponding generalised representation \(\mathbb {D}_\omega ^n\rightarrow \mathbb {R}^n\).
Computable equivalence between two representations not only implies that there are continuous maps between them but also that names can computably be transformed [31]. Since the Cauchy representation itself is continuous [4] we derive continuity of \(\xi \), which is used below to show compactness of preimages \(\xi ^{-1}(X)\) of compact sets \(X\subseteq \mathbb {R}\) under \(\xi \). All proofs can be found in [8].
Lemma 5
The following properties hold for \(\xi \).
-
1.
\(\xi \) is a representation of \(\mathbb {R}^n\): it is well-defined and surjective.
-
2.
Any \(\xi \)-name of \(\boldsymbol{x}\in \mathbb {R}^n\) is a Cauchy-name of \(\boldsymbol{x}\).
-
3.
\(\xi \) is computably equivalent to the Cauchy representation.
-
4.
\(\xi \) is continuous.
The converse of Item 2 does not hold. An example for a Cauchy-name of \(0\in \mathbb {R}\) is the sequence \((x_n)_n\) with \(x_n=(-2)^{-n}\) for all \(n\in \omega \), which does not satisfy \(\forall i,j:|x_i-x_{i+j}|\le 2^{-(i+1)}\). However, given a name of a real number, we can compute a corresponding \(\xi \)-name, this is one direction of the property in Item 3.
As a consequence of Item 2 a function-oracle machine \(M^?\) computing \(f:\mathbb {R}^n\rightarrow \mathbb {R}\) according to Definition 1 can be run on \(\xi \)-names of \(\boldsymbol{x}\in \mathbb {R}^n\) leading to valid Cauchy-names of \(f(\boldsymbol{x})\). Note that this proposition does not require \(M_f^?\) to compute a \(\xi \)-name of \(f(\boldsymbol{x})\). Any rational sequence rapidly converging to \(f(\boldsymbol{x})\) is a valid output. This means, that the model of computation remains unchanged with respect to the earlier parts of this paper. It is the set of names the machines are operated on, which is restricted. This is reflected in Algorithm 2 by computing dyadic rational approximations \(\tilde{\boldsymbol{x}}_k\) of \([\![\boldsymbol{x}]\!]^\alpha \) such that \(\tilde{\boldsymbol{x}}_k\in \mathbb {D}_k^n\) instead of keeping the name of \([\![\boldsymbol{x}]\!]^\alpha \) constant as has been done in Algorithm 1.

In particular, in Theorem 4 we show that linearisations for the \((L_\delta )\) rule can be computed by Algorithm 2, which – in contrast to linearise\(_\delta \) in Algorithm 1 – does not require access to a procedure computing an upper bound \(\mu _f\) on the uniform modulus of continuity of the non-linear function \(f\in \mathcal {F}_{\mathrm {nl}}\) valid on the entire bounded domain. It not just runs the machine \(M_f^?\), but also observes the queries \(M_f^\varphi \) poses to its oracle in order to obtain a local modulus of continuity of f at the point of evaluation. The function  used to define Algorithm 2 computes a dyadic approximation of \(\boldsymbol{x}\), with \(\lfloor {\cdot }\rceil :\mathbb {Q}^n\rightarrow \mathbb {Z}^n\) denoting a rounding operation, that is, it satisfies \(\forall \boldsymbol{q}:\Vert \lfloor {\boldsymbol{q}}\rceil -\boldsymbol{q}\Vert \le \frac{1}{2}\). On rationals (our use-case), \(\lfloor {\cdot }\rceil \) is computable by a classical Turing machine.
used to define Algorithm 2 computes a dyadic approximation of \(\boldsymbol{x}\), with \(\lfloor {\cdot }\rceil :\mathbb {Q}^n\rightarrow \mathbb {Z}^n\) denoting a rounding operation, that is, it satisfies \(\forall \boldsymbol{q}:\Vert \lfloor {\boldsymbol{q}}\rceil -\boldsymbol{q}\Vert \le \frac{1}{2}\). On rationals (our use-case), \(\lfloor {\cdot }\rceil \) is computable by a classical Turing machine.
Definition 7
([31, Definition 6.2.6]). Let \(f:\mathbb {R}^n\rightarrow \mathbb {R}\) and \(\boldsymbol{x}\in \mathrm {dom}f\). A function \(\gamma :\mathbb {N}\rightarrow \mathbb N\) is called a (local) modulus of continuity of f at \(\boldsymbol{x}\) if for all \(p\in \mathbb N\) and \(\boldsymbol{y}\in \mathrm {dom}f\), \(\Vert \boldsymbol{x}-\boldsymbol{y}\Vert \le 2^{-\gamma (p)}\implies \vert f(\boldsymbol{x})-f(\boldsymbol{y})\vert \le 2^{-p}\) holds.
We note that in most cases a local modulus of continuity of f at \(\boldsymbol{x}\) is smaller than the best uniform modulus of f on its domain, since it only depends on the local behaviour of f around x. One way of computing a local modulus of f at \(\boldsymbol{x}\) is using the function-oracle machine \(M_f^?\) as defined next.
Definition 8
Let \(M^?_f\) compute \(f:\mathbb R^n\rightarrow \mathbb R\) and let \(\boldsymbol{x}\in \mathrm {dom}f\) have Cauchy-name \(\varphi \). The function \(\gamma _{M_f^?,\varphi }:p\mapsto \max \{0,k: M_f^\varphi (p+2)~\text {queries index}~k~\text {of}~\varphi \}\) is called the effective local modulus of continuity induced by \(M_f^?\) at \(\varphi \).
The effective local modulus of continuity of f at a name \(\varphi \) of \(\boldsymbol{x}\in \mathrm {dom}f\) indeed is a local modulus of continuity of f at \(\boldsymbol{x}\) [17, Theorem 2.13]. Algorithm 2 computes \(\epsilon \)-full linearisations by means of the effective local modulus [8], as stated next.
Lemma 6
Let \(P:f(\boldsymbol{x})\diamond 0\) be a non-linear constraint in \(\mathcal {N}\) and \(\alpha \) be an assignment of \(\boldsymbol{x}\) to rationals in \(\mathrm {dom}f\). Whenever \(C={}\) LineariseLocal\(_\delta \)(\(f,\boldsymbol{x},\diamond ,\alpha \)) and \(C\ne \textsf {None}\), C is an \(\epsilon \)-full linearisation of P at \(\alpha \), with \(\epsilon \) corresponding to the effective local modulus of continuity induced by \(M_f^?\) at a \(\xi \)-name of \([\![\boldsymbol{x}]\!]^\alpha \).
Thus, the function lineariseLocal\(_\delta \) in Algorithm 2 is a drop-in replacement for linearise\(_\delta \) in Algorithm 1 since the condition on returning a linearisation of P versus accepting \(P_\delta \) is identical. The linearisations however differ in the radius \(\epsilon \), which now, according to Lemma 6, corresponds to the effective local modulus of continuity. The resulting procedure we call nlinStepLocal\(_\delta \). One of its advantages over nlinStep\(_\delta \) is running \(M_f^?\) on \(\xi \)-names instead of Cauchy-names, is that they form a compact set for bounded instances, unlike the latter. This allows us to bound \(\epsilon >0\) for the computed \(\epsilon \)-full local linearisations of otherwise arbitrary \(\delta \)-ksmt runs. A proof of the following Lemma showing compactness of preimages \(\xi ^{-1}(X)\) of compact sets \(X\subseteq \mathbb R\) under \(\xi \) is given in [8].
Lemma 7
Let \(X\subset \mathbb R^n\) be compact. Then the set \(\xi ^{-1}(X)\subset \mathbb D_\omega ^n\) of \(\xi \)-names of elements in X is compact as well.
The proof involves showing \(\xi ^{-1}(X)\) to be closed and uses the fact that for each component \(\varphi _k\) of names \((\varphi _k)_k\) of \(\boldsymbol{x}\in X\) there are just finitely many choices from \(\mathbb D_k\) due to the restriction of the length of the dyadics. This is not the case for the Cauchy representation used in Definition 1 and it is the key for deriving existence of a strictly positive lower bound \(\epsilon \) on the \(\epsilon \)-full ness of linearisations.
Theorem 4
Let \(\delta \in \mathbb Q_{>0}\). For any bounded instance \(\mathcal {L}_0\wedge \mathcal {N}\) there is \(\epsilon >0\) such that any \(\delta \)-ksmt run starting in \((\textsf {nil},\mathcal {L}_0,\mathcal {N})\), where applications of (L) and \((F^ sat _{\delta })\) are performed according to nlinStepLocal\(_\delta \), is \(\epsilon \)-full.
Proof
Assume \(\mathcal {L}_0\wedge \mathcal {N}\) is a bounded instance. Set  , where \(\epsilon _P\) is defined as follows. Let \(P:f(\boldsymbol{x})\diamond 0\) in \(\mathcal {N}\). Then the closure \(\bar{D_P}\) of the bounded set \(D_P\) is compact. Let E be the set of \(\xi \)-names of elements of \(\bar{D_P}\subseteq \mathrm {dom}f\) (see Definition 6) and for any \(\varphi \in E\) let \(k_\varphi \) be defined as \(\gamma _{M_f^?,\varphi }(p)\) (see Definition 8) where p is computed from \(\delta \) as in Algorithm 2 and is independent of \(\varphi \). Since the preimage of each \(k_\varphi \) is open, the function \(\varphi \mapsto k_\varphi \) is continuous. By Lemma 7 the set E is compact, thus, there is \(\psi \in E\) such that \(2^{-k_\psi }= \inf \{2^{-k_\varphi }:\varphi \in E\}\). Set
, where \(\epsilon _P\) is defined as follows. Let \(P:f(\boldsymbol{x})\diamond 0\) in \(\mathcal {N}\). Then the closure \(\bar{D_P}\) of the bounded set \(D_P\) is compact. Let E be the set of \(\xi \)-names of elements of \(\bar{D_P}\subseteq \mathrm {dom}f\) (see Definition 6) and for any \(\varphi \in E\) let \(k_\varphi \) be defined as \(\gamma _{M_f^?,\varphi }(p)\) (see Definition 8) where p is computed from \(\delta \) as in Algorithm 2 and is independent of \(\varphi \). Since the preimage of each \(k_\varphi \) is open, the function \(\varphi \mapsto k_\varphi \) is continuous. By Lemma 7 the set E is compact, thus, there is \(\psi \in E\) such that \(2^{-k_\psi }= \inf \{2^{-k_\varphi }:\varphi \in E\}\). Set  . The claim then follows by Lemma 6.
. The claim then follows by Lemma 6.
Thus we can conclude.
Corollary 1
\(\delta \)-ksmt with local linearisations is a \(\delta \)-complete decision procedure.
7 Conclusion
In this paper we extended the the ksmt calculus to the \(\delta \)-satisfiability setting and proved that the resulting \(\delta \)-ksmt calculus is a \(\delta \)-complete decision procedure for solving non-linear constraints over computable functions which include polynomials, exponentials, logarithms, trigonometric and many other functions used in applications. We presented algorithms for constructing \(\epsilon \)-full linearisations ensuring termination of \(\delta \)-ksmt. Based on methods from computable analysis we presented an algorithm for constructing local linearisations. Local linearisations exclude larger regions from the search space and can be used to avoid computationally expensive global analysis of non-linear functions.
Notes
- 1.
Implementation is available at http://informatik.uni-trier.de/~brausse/ksmt/
References
Bard, J., Becker, H., Darulova, E.: Formally verified roundoff errors using SMTbased certificates and subdivisions. In: ter Beek, M.H., McIver, A., Oliveira, J.N. (eds.) Formal Methods - The Next 30 Years - Third World Congress, FM 2019, Proceedings. LNCS, vol. 11800, pp. 38–44. Springer (2019)
Benvenuti, L., Bresolin, D., Collins, P., Ferrari, A., Geretti, L., Villa, T.: Assume–guarantee verification of nonlinear hybrid systems with Ariadne. International Journal of Robust and Nonlinear Control 24(4), 699–724 (2014)
Bonacina, M.P., Graham-Lengrand, S., Shankar, N.: Conflict-driven satisfiability for theory combination: Transition system and completeness. J. Autom. Reason. 64(3), 579–609 (2020)
Brattka, V., Hertling, P.: Topological properties of real number representations. Theor. Comput. Sci. 284(2), 241–257 (2002)
Brattka, V., Hertling, P., Weihrauch, K.: A Tutorial on Computable Analysis, pp. 425–491. Springer New York, New York, NY (2008)
Brauße, F., Khasidashvili, Z., Korovin, K.: Selecting stable safe configurations for systems modelled by neural networks with ReLU activation. In: Ivrii, A., Strichman, O. (eds.) 2020 Formal Methods in Computer Aided Design, FMCAD 2020. pp. 119–127. IEEE (2020)
Brauße, F., Korovin, K., Korovina, M.V., Müller, N.T.: A CDCL-style calculus for solving non-linear constraints. In: Herzig, A., Popescu, A. (eds.) Frontiers of Combining Systems - 12th International Symposium, FroCoS 2019, Proceedings. LNCS, vol. 11715, pp. 131–148. Springer (2019)
Brauße, F., Korovin, K., Korovina, M.V., Müller, N.T.: The ksmt calculus is a \(\delta \)-complete decision procedure for non-linear constraints. CoRR abs/2104.13269 (2021)
Brauße, F., Korovina, M.V., Müller, N.T.: Towards using exact real arithmetic for initial value problems. In: Mazzara, M., Voronkov, A. (eds.) Perspectives of System Informatics - 10th International Andrei Ershov Informatics Conference, PSI 2015, in Memory of Helmut Veith, Revised Selected Papers. LNCS, vol. 9609, pp. 61–74. Springer (2015)
Brauße, F., Steinberg, F.: A minimal representation for continuous functions. CoRR abs/1703.10044 (2017)
Cimatti, A., Griggio, A., Irfan, A., Roveri, M., Sebastiani, R.: Incremental linearization for satisfiability and verification modulo nonlinear arithmetic and transcendental functions. ACM Trans. Comput. Log. 19(3), 19:1–19:52 (2018)
Fontaine, P., Ogawa, M., Sturm, T., Vu, X.: Subtropical satisfiability. In: Dixon, C., Finger, M. (eds.) Frontiers of Combining Systems - 11th International Symposium, FroCoS 2017, Proceedings. LNCS, vol. 10483, pp. 189–206. Springer (2017)
Gao, S., Avigad, J., Clarke, E.M.: \(\delta \)-complete decision procedures for satisfiability over the reals. In: Gramlich, B., Miller, D., Sattler, U. (eds.) Automated Reasoning - 6th International Joint Conference, IJCAR 2012, Proceedings. LNCS, vol. 7364, pp. 286–300. Springer (2012)
Gao, S., Avigad, J., Clarke, E.M.: Delta-decidability over the reals. In: Proceedings of the 27th Annual IEEE Symposium on Logic in Computer Science, LICS 2012. pp. 305–314. IEEE Computer Society (2012)
Hales, T.C., Adams, M., Bauer, G., Dang, D.T., Harrison, J., Hoang, T.L., Kaliszyk, C., Magron, V., McLaughlin, S., Nguyen, T.T., Nguyen, T.Q., Nipkow, T., Obua, S., Pleso, J., Rute, J.M., Solovyev, A., Ta, A.H.T., Tran, T.N., Trieu, D.T., Urban, J., Vu, K.K., Zumkeller, R.: A formal proof of the Kepler conjecture. CoRR abs/1501.02155 (2015)
Jovanovic, D., de Moura, L.: Solving non-linear arithmetic. ACM Commun. Comput. Algebra 46(3/4), 104–105 (2012)
Ko, K.: Complexity Theory of Real Functions. Birkhäuser / Springer (1991)
Korovin, K., Kosta, M., Sturm, T.: Towards conflict-driven learning for virtual substitution. In: Gerdt, V.P., Koepf, W., Seiler, W.M., Vorozhtsov, E.V. (eds.) Computer Algebra in Scientific Computing - 16th International Workshop, CASC 2014, Proceedings. LNCS, vol. 8660, pp. 256–270. Springer (2014)
Korovin, K., Tsiskaridze, N., Voronkov, A.: Conflict resolution. In: Gent, I.P. (ed.) Principles and Practice of Constraint Programming - CP 2009, 15th International Conference, CP 2009, Proceedings. LNCS, vol. 5732, pp. 509–523. Springer (2009)
Korovin, K., Voronkov, A.: Solving systems of linear inequalities by bound propagation. In: Bjørner, N., Sofronie-Stokkermans, V. (eds.) Automated Deduction - CADE-23 - 23rd International Conference on Automated Deduction, Proceedings. LNCS, vol. 6803, pp. 369–383. Springer (2011)
Kurátko, J., Ratschan, S.: Combined global and local search for the falsification of hybrid systems. In: Legay, A., Bozga, M. (eds.) Formal Modeling and Analysis of Timed Systems - 12th International Conference, FORMATS 2014, Proceedings. LNCS, vol. 8711, pp. 146–160. Springer (2014)
de Moura, L.M., Jovanovic, D.: A model-constructing satisfiability calculus. In: Giacobazzi, R., Berdine, J., Mastroeni, I. (eds.) Verification, Model Checking, and Abstract Interpretation, 14th International Conference, VMCAI 2013, Proceedings. LNCS, vol. 7737, pp. 1–12. Springer (2013)
de Moura, L.M., Passmore, G.O.: Computation in real closed infinitesimal and transcendental extensions of the rationals. In: Bonacina, M.P. (ed.) Automated Deduction - CADE-24 - 24th International Conference on Automated Deduction, Proceedings. LNCS, vol. 7898, pp. 178–192. Springer (2013)
Müller, N.T.: The iRRAM: Exact arithmetic in C++. In: Blanck, J., Brattka, V., Hertling, P. (eds.) Computability and Complexity in Analysis, 4th International Workshop, CCA 2000, Selected Papers. LNCS, vol. 2064, pp. 222–252. Springer (2000)
Platzer, A.: Logical Foundations of Cyber-Physical Systems. Springer (2018)
Pour-El, M.B., Richards, J.I.: Computability in analysis and physics. Perspectives in Mathematical Logic, Springer (1989)
Richardson, D.: Some undecidable problems involving elementary functions of a real variable. J. Symb. Log. 33(4), 514–520 (1968)
Silva, J.P.M., Sakallah, K.A.: GRASP - a new search algorithm for satisfiability. In: Rutenbar, R.A., Otten, R.H.J.M. (eds.) Proceedings of the IEEE/ACM International Conference on Computer-Aided Design, ICCAD 1996. pp. 220–227. IEEE Computer Society / ACM (1996)
Tiwari, A., Lincoln, P.: A search-based procedure for nonlinear real arithmetic. Formal Methods Syst. Des. 48(3), 257–273 (2016)
Tung, V.X., Khanh, T.V., Ogawa, M.: raSAT: An SMT solver for polynomial constraints. In: Olivetti, N., Tiwari, A. (eds.) Automated Reasoning - 8th International Joint Conference, IJCAR 2016, Proceedings. LNCS, vol. 9706, pp. 228–237. Springer (2016)
Weihrauch, K.: Computable Analysis – An Introduction. Texts in Theoretical Computer Science. An EATCS Series, Springer (2000)
Willard, S.: General Topology. Addison-Wesly (1970)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2021 The Author(s)
About this paper
Cite this paper
Brauße, F., Korovin, K., Korovina, M.V., Müller, N.T. (2021). The ksmt Calculus Is a \(\delta \)-complete Decision Procedure for Non-linear Constraints. In: Platzer, A., Sutcliffe, G. (eds) Automated Deduction – CADE 28. CADE 2021. Lecture Notes in Computer Science(), vol 12699. Springer, Cham. https://doi.org/10.1007/978-3-030-79876-5_7
Download citation
DOI: https://doi.org/10.1007/978-3-030-79876-5_7
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-79875-8
Online ISBN: 978-3-030-79876-5
eBook Packages: Computer ScienceComputer Science (R0)







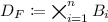 is bounded, and
is bounded, and .
.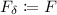 .
.
 .
.
 and let
and let 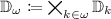 be the set of all sequences
be the set of all sequences