Abstract
 is an emerging natural proof assistant that accepts input in the controlled natural language ForTheL.
is an emerging natural proof assistant that accepts input in the controlled natural language ForTheL.
 is included in the current version of the Isabelle/PIDE which allows comfortable editing and asynchronous proof-checking of ForTheL texts. The .tex dialect of ForTheL can be typeset by
is included in the current version of the Isabelle/PIDE which allows comfortable editing and asynchronous proof-checking of ForTheL texts. The .tex dialect of ForTheL can be typeset by
 into documents that approximate the language and appearance of ordinary mathematical texts.
into documents that approximate the language and appearance of ordinary mathematical texts.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
 (for Natural Proof Checking) is an emerging natural proof assistant that accepts input in a controlled natural language, approximating ordinary mathematical language and texts. The system uses
(for Natural Proof Checking) is an emerging natural proof assistant that accepts input in a controlled natural language, approximating ordinary mathematical language and texts. The system uses
-
the dedicated input language ForTheL (Formula Theory Language),
-
natural language processing for texts with symbolic material,
-
strong automatic theorem proving (ATP) for filling in implicit or obvious proof steps.
The current version of
 also introduces a
also introduces a
 dialect of ForTheL so that high-quality mathematical typesetting is readily available.
dialect of ForTheL so that high-quality mathematical typesetting is readily available.
 allows the formalization and proof-checking of advanced mathematics in a style that is immediately readable by mathematicians. Example formalizations from various domains of undergraduate mathematics are included.
allows the formalization and proof-checking of advanced mathematics in a style that is immediately readable by mathematicians. Example formalizations from various domains of undergraduate mathematics are included.
 ships as a component in the latest release of the Isabelle prover platform [8]. When editing a ForTheL file in Isabelle/jEdit Prover IDE (PIDE), there is an auxiliary
ships as a component in the latest release of the Isabelle prover platform [8]. When editing a ForTheL file in Isabelle/jEdit Prover IDE (PIDE), there is an auxiliary
 server in the background to quickly answer requests for checking ForTheL texts, with an internal cache to avoid repeated checking of unchanged text segments. The implementation uses programming interfaces of Isabelle/PIDE that allow user-defined file formats to participate in the concurrent document model. A second auxiliary server allows the
server in the background to quickly answer requests for checking ForTheL texts, with an internal cache to avoid repeated checking of unchanged text segments. The implementation uses programming interfaces of Isabelle/PIDE that allow user-defined file formats to participate in the concurrent document model. A second auxiliary server allows the
 program to run external prover processes under the control of Isabelle, with explicit timeouts. This works reliably on the usual platforms (Linux, Windows, macOS) by re-using external provers of Isabelle/Sledgehammer [17]. From the perspective of logic, there is no connection of
program to run external prover processes under the control of Isabelle, with explicit timeouts. This works reliably on the usual platforms (Linux, Windows, macOS) by re-using external provers of Isabelle/Sledgehammer [17]. From the perspective of logic, there is no connection of
 with Isabelle/Sledgehammer or any other Isabelle/HOL tools.
with Isabelle/Sledgehammer or any other Isabelle/HOL tools.
In this paper we briefly discuss the need for natural proof assistants, provide some general information on Isabelle/Naproche, and give an overview of methods employed in the system, using an excerpt from a formalization of Euclid’s infinitude of primes as a running example. To conclude we compare
 to other projects in formal mathematics with natural language input and indicate ways to further extend
to other projects in formal mathematics with natural language input and indicate ways to further extend
 ’s naturalness and efficiency.
’s naturalness and efficiency.
2 Natural Proof Assistants
While state-of-the-art interactive theorem provers have been successfully used to prove and certify highly non-trivial research mathematics, they are still, according to Lawrence Paulson [16] “unsuitable for mathematics. Their formal proofs are unreadable.”
Natural proof assistants intend to bridge the wide gap between intuitive mathematical texts and the formal rigour of logical calculi. We propose the following criteria for natural proof assistants:
-
Input languages should be close to the mathematical vernacular, including support for common grammatical conventions and symbolic expressions. These languages should support familiar text structurings, such as the usual definition-theorem-proof style.
-
Proofs should consist of natural argumentative phrases for various proof tactics, allowing for a more declarative style.
-
The system should use familiar logics and mathematical ontologies.
-
Tedious details and obvious proof gaps should be filled in automatically.
-
An intuitive editor should allow for interactive text and theory development, where incremental proof checking can guide the formalization.
We expect that naturalness will be crucial for the adoption of formal mathematics by the wider mathematical community. This is in line with some ongoing large-scale projects in formal mathematics. For instance, the ALEXANDRIA project by Paulson [16] stipulates:
ALEXANDRIA will be based on legible structured proofs. Formal proofs should be not mere code, but a machine-checkable form of communication between mathematicians.
The Formal Abstracts project of Thomas Hales [5] intends to
-
give a statement of the main theorem of each published mathematical paper in a language that is both human and machine readable,
-
link each term in theorem statements to a precise definition of that term (again in human/machine readable form).
3 Isabelle/Naproche
The
 proof assistant stems from two long-term efforts aiming towards naturalness: the Evidence Algorithm (EA) and System for Automated Deduction (SAD) projects at the universities of Kiev and Paris [14, 15, 20, 21], and the Naproche project at Bonn [1,2,3, 10].
proof assistant stems from two long-term efforts aiming towards naturalness: the Evidence Algorithm (EA) and System for Automated Deduction (SAD) projects at the universities of Kiev and Paris [14, 15, 20, 21], and the Naproche project at Bonn [1,2,3, 10].
 extends the input language ForTheL of SAD and embeds it into
extends the input language ForTheL of SAD and embeds it into
 , allowing mathematical typesetting; the original proof-checking mechanisms of SAD have been made more efficient and varied.
, allowing mathematical typesetting; the original proof-checking mechanisms of SAD have been made more efficient and varied.
The first experimental integration of the then Naproche-SAD prover into the Isabelle Prover IDE was done in 2018 by Frerix and Wenzel [23, §1.2]. The current (refined and extended) version has now become a bundled component of Isabelle2021 [8]. After downloading and unpacking the Isabelle distribution, Isabelle/Naproche becomes immediately accessible in the Documentation panel, section Examples, entry $ISABELLE_NAPROCHE/Intro.thy. Isabelle and its add-on components work directly without manual installation, but this comes at the cost of substantial resource requirements: on Linux the total size is 1.2 GB, which includes Java 15 (330 MB), E prover 2.5 (30 MB), and
 (20 MB). The bulk of other Isabelle components are required for Isabelle/HOL theory and proof development, but
(20 MB). The bulk of other Isabelle components are required for Isabelle/HOL theory and proof development, but
 has no logical connection to that.
has no logical connection to that.
The
 prover is invoked automatically when editing ForTheL files with .ftl or .ftl.tex extensions. Further examples and an introductory tutorial are linked in the Isabelle theory file $ISABELLE_NAPROCHE/Intro.thy: as usual for Isabelle/jEdit and other IDEs, following a link works by a mouse click combined with the keyboard modifier CTRL (Linux, Windows) or CMD (macOS). The examples deal with results from undergraduate number theory, geometry, and set theory; most are available in the classic ASCII style as well as in
prover is invoked automatically when editing ForTheL files with .ftl or .ftl.tex extensions. Further examples and an introductory tutorial are linked in the Isabelle theory file $ISABELLE_NAPROCHE/Intro.thy: as usual for Isabelle/jEdit and other IDEs, following a link works by a mouse click combined with the keyboard modifier CTRL (Linux, Windows) or CMD (macOS). The examples deal with results from undergraduate number theory, geometry, and set theory; most are available in the classic ASCII style as well as in
 style and typeset in PDF.
style and typeset in PDF.
The ForTheL library FLib [13] contains a variety of formalizations for earlier versions of
 . Some substantial texts have been written as undergraduate student projects and cover, e.g., group theory up to Sylow theorems, initial chapters from Walter Rudin’s Analysis, or set theory up to Silver’s theorem in cardinal arithmetic. These texts will soon be upgraded to the new version of
. Some substantial texts have been written as undergraduate student projects and cover, e.g., group theory up to Sylow theorems, initial chapters from Walter Rudin’s Analysis, or set theory up to Silver’s theorem in cardinal arithmetic. These texts will soon be upgraded to the new version of
 and included in an interlinked formalized library of readable and proof-checked mathematical texts.
and included in an interlinked formalized library of readable and proof-checked mathematical texts.
4 Formalizing in ForTheL
4.1 Example
The following screenshot shows a proof of the infinitude of prime numbers in the Isabelle/Naproche Prover IDE taken from the bundled tutorial which itself is a proof-checked ForTheL text:

The editor buffer contains the ForTheL source, which also happens to conform to standard
 format. (The “Contradiction” lemma, now deactivated by a %, is a left-over of a typical check for hidden inconsistencies in the axiomatic setup.) The Output panel contains feedback from the
format. (The “Contradiction” lemma, now deactivated by a %, is a left-over of a typical check for hidden inconsistencies in the axiomatic setup.) The Output panel contains feedback from the
 prover about the source document: “verification successful” and some statistics; the most relevant messages are also shown in-line over the source as squiggly underline with popup on mouse-hovering. The Sidekick/latex structure overview is provided by standard plugins of the underlying text editor. This piece of mathematics is typeset by
prover about the source document: “verification successful” and some statistics; the most relevant messages are also shown in-line over the source as squiggly underline with popup on mouse-hovering. The Sidekick/latex structure overview is provided by standard plugins of the underlying text editor. This piece of mathematics is typeset by
 as follows:
as follows:

4.2 The ForTheL Language
The mathematical controlled language ForTheL has been developed over several decades in the Evidence Algorithm (EA) / System for Automated Deduction (SAD) project. It is carefully designed to approximate the weakly typed natural language of mathematics whilst being efficiently translatable to first-order logic. In ForTheL, standard mathematical types are called notions, and these are internally represented as predicates with a distinguished variable, which are treated as unary predicates with the other variables used as parameters (“types as predicates”). This leads to a flexible dependent type system where number systems can be cumulative (\(\mathbb {N} \subseteq \mathbb {R}\)), and notions can depend on parameters (subsets of \(\mathbb {N}\), divisors of n).
First-order languages of notions, constants, relations, and functions can be introduced and extended by signature and definition commands. The formalization of Euclid’s theorem, e.g., sets out like:

5 Architecture of the
 System
System
 follows standard principles of interactive theorem proving, but with a strong emphasis on the naturalness aspects explained above. The general information processing in the system is described in the following diagram. The core
follows standard principles of interactive theorem proving, but with a strong emphasis on the naturalness aspects explained above. The general information processing in the system is described in the following diagram. The core
 program is implemented in Haskell.
program is implemented in Haskell.

In the sequel we shall describe main components of
 .
.
5.1 Tokenizing and Parsing
 uses a standard tokenizing algorithm for cutting text up into a list of meaningful tokens, with precise source positions to enable PIDE messages and markup, e.g., by colours for free and bound variables. When using
uses a standard tokenizing algorithm for cutting text up into a list of meaningful tokens, with precise source positions to enable PIDE messages and markup, e.g., by colours for free and bound variables. When using
 syntax, the tokenizer also takes care of expanding certain
syntax, the tokenizer also takes care of expanding certain
 commands (see the next subsection).
commands (see the next subsection).
Parsing is carried out in Haskell’s monadic style with parser combinators. We allow ambiguous parsing, since it better fits natural language. Currently the translation into tagged first-order logic is already part of the parsing process. The following translation of our example snippet was obtained by running
 from the command line with the -T (translate) option:
from the command line with the -T (translate) option:

In order to make
 more versatile we plan on parsing into an abstract syntax tree instead, so that different logical back-ends could translate into different logics. We have already made some experiments on translating ForTheL to Lean [12].
more versatile we plan on parsing into an abstract syntax tree instead, so that different logical back-ends could translate into different logics. We have already made some experiments on translating ForTheL to Lean [12].
Moreover, with the input language growing, we shall eventually turn to some grammatical framework to speed up language development without hard-coding vocabulary or grammar rules into the
 code.
code.
5.2
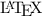 Processing
Processing
We have extended
 to support a .ftl.tex format, in addition to the original .ftl format. Files in .ftl.tex format are intended to be readable by both
to support a .ftl.tex format, in addition to the original .ftl format. Files in .ftl.tex format are intended to be readable by both
 for logical checking and by
for logical checking and by
 for typesetting.
for typesetting.
The
 tokenizer ignores the whole document, except what is inside forthel environments of the form
tokenizer ignores the whole document, except what is inside forthel environments of the form

In a forthel environment, standard
 syntax can be used for declaring text environments for theorems and definitions.
syntax can be used for declaring text environments for theorems and definitions.
In
 , users can define their own operators and phrases by defining linguistic and symbolic patterns. This mechanism has been adapted to allow
, users can define their own operators and phrases by defining linguistic and symbolic patterns. This mechanism has been adapted to allow
 constructs in patterns. In the Euclid text we use the pattern
constructs in patterns. In the Euclid text we use the pattern
 for the finite set \(\{p_1,\dots ,p_r\}\). By defining
for the finite set \(\{p_1,\dots ,p_r\}\). By defining
 as a
as a
 macro we can arrange that the ForTheL pattern will be printed in the familiar set notation:
macro we can arrange that the ForTheL pattern will be printed in the familiar set notation:

There are some primitive concepts in
 , such as the logical operators \(\vee \), \(\wedge \), \(\exists \) that are directly recognized in the
, such as the logical operators \(\vee \), \(\wedge \), \(\exists \) that are directly recognized in the
 source and expanded to corresponding internal tokens.
source and expanded to corresponding internal tokens.
The current release of
 does not differentiate between math mode and text mode in
does not differentiate between math mode and text mode in
 , since it re-uses much of the parsing machinery of the original .ftl format. Future releases shall make such a distinction to increase the robustness of the parser, improve error messages and resolve some ambiguities in the current grammar.
, since it re-uses much of the parsing machinery of the original .ftl format. Future releases shall make such a distinction to increase the robustness of the parser, improve error messages and resolve some ambiguities in the current grammar.
5.3 Logical Processing
The first-order formulas derived from ForTheL statements are put into an internal ProofText data type consisting of blocks of formulae, arranged in a tree-like fashion. The tree structure mirrors the logical structure of a text, where a statement can be seen as a node to which a subtext, e.g., its proof is attached. Since statements in a proof can have their own subproofs this leads to a recursive tree structure, on which the further checking is performed along a depth-first left-to-right traversal.
5.4 Ontological Checking by the
 Reasoner
Reasoner
An innocent mathematical statement like \(a^2+b^2=c^2\) contains a number of implicit proof tasks, even if the whole statement is not to be proved, but part of a definition or an assumption. One has to check that a, b, c are (numerical) terms to which the squaring operation can be applied, and that the resulting squares can be subjected to addition and equality. These checks are called “ontological”, and they roughly correspond to type checking in type-orientated systems. The situation here is however more complicated, as types (i.e. notions) and operations may involve first-order definitions with preconditions, which cannot be decided during the parsing process but only during proof-checking. So in the checking process each node of the aforementioned tree is first checked ontologically; if the node formula itself is marked as a conjecture, it is logically checked.
5.5 Logical Checking by the
 Reasoner
Reasoner
The various checks are organized by the
 reasoner module. In simple cases the reasoner itself can supply a proof; if not, the reasoner constructs proof tasks for the ATP. Since definitions in first-order logic are formally symmetric equivalences, they may lead to circularities in proof searches. Instead definitions are successively unfolded by replacing the definiendum by the definiens. This process may be iterated when proof attempts fail.
reasoner module. In simple cases the reasoner itself can supply a proof; if not, the reasoner constructs proof tasks for the ATP. Since definitions in first-order logic are formally symmetric equivalences, they may lead to circularities in proof searches. Instead definitions are successively unfolded by replacing the definiendum by the definiens. This process may be iterated when proof attempts fail.
The ATP is given certain timeouts to search for proofs. Ontological checking is supposed to be easier than proper mathematical proving. So the default time for each ontological check is set to 1 sec, whereas proving gets 3 sec and can be iterated for several rounds of definition unfolding.
5.6 Communication with an External ATP
Proof tasks are translated into the generic TPTP first-order format for ATPs. These can be viewed in the Output window of Isabelle/jEdit, after inserting the directive [dump on] into the ForTheL source. The final proof task in checking Euclid’s proof ends with the TPTP lines:

By default
 uses E prover [19] as external ATP, but one may switch to other provers available in the Isabelle distribution.
uses E prover [19] as external ATP, but one may switch to other provers available in the Isabelle distribution.
6 Integration into Isabelle
The initial integration of
 into the Isabelle Prover IDE happened in 2018 and is briefly reported as an example in the PIDE overview article [23] based on Isabelle2019 (June 2019). The main idea was to turn the existing Haskell command-line program into a TCP server that can answer concurrent requests for checking ForTheL texts in a purely functional manner, with proper handling of cancel messages (for interrupts caused by user editing); this required to remove a few low-level system operations, like reading physical files or exit of the process. Afterwards, the semantic operation forthel_file in Isabelle – to check ForTheL text and produce markup messages according to the PIDE protocol – was implemented as Isabelle/Isar command in Isabelle/ML as usual, but the main work is delegated to the
into the Isabelle Prover IDE happened in 2018 and is briefly reported as an example in the PIDE overview article [23] based on Isabelle2019 (June 2019). The main idea was to turn the existing Haskell command-line program into a TCP server that can answer concurrent requests for checking ForTheL texts in a purely functional manner, with proper handling of cancel messages (for interrupts caused by user editing); this required to remove a few low-level system operations, like reading physical files or exit of the process. Afterwards, the semantic operation forthel_file in Isabelle – to check ForTheL text and produce markup messages according to the PIDE protocol – was implemented as Isabelle/Isar command in Isabelle/ML as usual, but the main work is delegated to the
 server. Its implementation uses the Isabelle/Haskell library for common Isabelle/PIDE message formats, source positions, markup etc. – it is maintained within the Isabelle distribution.
server. Its implementation uses the Isabelle/Haskell library for common Isabelle/PIDE message formats, source positions, markup etc. – it is maintained within the Isabelle distribution.
The current version of Isabelle/Naproche refines this approach in various respects. In particular, Isabelle2021 now provides a standard mechanism for user-defined Isabelle/Scala services: this is both relevant for Isabelle command-line tools to build and test Isabelle/Naproche, and the Prover IDE support of ForTheL files to connect the Isabelle/jEdit front-end to the
 back-end.
back-end.
Moreover, the Java process running the Prover IDE provides an additional TCP server to launch external provers that are already distributed with Isabelle (thanks to Isabelle/Sledgehammer):
 applications mainly use the current E prover 2.5 [19], but SPASS and Vampire are available for experiments. The existing management of processes in Isabelle/Scala involves considerable efforts to robustly support interrupts and timeouts in a concurrent environment; this works on all platforms supported by Isabelle (using special tricks for Windows/Cygwin, and macOS/Rosetta on Apple Silicon).
applications mainly use the current E prover 2.5 [19], but SPASS and Vampire are available for experiments. The existing management of processes in Isabelle/Scala involves considerable efforts to robustly support interrupts and timeouts in a concurrent environment; this works on all platforms supported by Isabelle (using special tricks for Windows/Cygwin, and macOS/Rosetta on Apple Silicon).
The documentation file $ISABELLE_NAPROCHE/Intro.thy gives further hints on implementation near the end, with hyperlinks to the sources. A lot of technical Isabelle infrastructure is re-used by Isabelle/Naproche, but there is presently no connection to Isabelle/HOL, which is a much larger and better-known application of the same Isabelle framework [18].
7 Related and Future Work
Bridging the gap between mathematical practice and fully formal methods has always been a central concern in formal mathematics. The development of the Mizar system [11] was accompanied or even driven by the stepwise adaptation of its language to standard mathematical proof methods and logical foundations. In contrast, most interactive theorem provers feature formal tactic languages, with tactics scripts that can hardly be understood without stepwise tracing and reconstructing internal logical states.
The Mizar language has been a role model for other proof languages. There are, e.g., "Mizar modes" for HOL [6, 25] and Coq [4] and the widely used Isar language for Isabelle [22, 24]. These language can be read by mathematicians, with some effort, but they retain a strong bias toward computer science customs. A survey of input languages for formalization on a scale between formal and natural can be found in [9].
Only a few formal mathematics projects have aimed at processing actual mathematical language. These projects have operated in isolation and seem to be mostly inactive now. The paper [7] by Muhammad Humayoun and Christophe Raffalli, e.g., describes the MathNat project and also surveys other related attempts.
The Naproche approach can be viewed in the Mizar tradition: use a rich controlled language for mathematics, increase the proving capabilities by strong automated theorem proving, and, eventually, create an extensive library of basic mathematics and specialized theories, which simultaneously can be used as a library for human readers.
The readability and naturalness of texts which proof-check in the
 system motivate significant further extensions of the project where ad hoc methods are to be replaced by principled and established approaches:
system motivate significant further extensions of the project where ad hoc methods are to be replaced by principled and established approaches:
1. the input language ForTheL has to be extended for wide mathematical coverage; ForTheL needs an extensive formal grammar and vocabulary to be processed by strong linguistic methods; the vocabulary may also encompass standard
 symbols and semantic information;
symbols and semantic information;
2. methods of type derivation and elaboration should be provided;
3. Isabelle/Sledgehammer-like methods should lead to efficient premise selection in large texts and theories;
4. the creation of libraries of ForTheL documents requires import and export mechanisms corresponding to quoting and referencing in the mathematical literature;
5. the natural text processing of
 should be interfaced with other proof assistants to leverage their strengths and libraries. We shall in particular work on a “
should be interfaced with other proof assistants to leverage their strengths and libraries. We shall in particular work on a “
 mode” for Isabelle.
mode” for Isabelle.
References
Cramer, M.: Proof-checking mathematical texts in controlled natural language. Ph.D. thesis, University of Bonn (2013), http://hdl.handle.net/20.500.11811/5780
Cramer, M., Koepke, P., Kühlwein, D., Schröder, B.: The Naproche system (2009), https://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.211.3401
Frerix, S., Koepke, P.: Automatic proof-checking of ordinary mathematical texts. Proceedings of the Workshop Formal Mathematics for Mathematicians (2018), http://ceur-ws.org/Vol-2307/paper13.pdf
Giero, M., Wiedijk, F.: MMode, a Mizar mode for the proof assistant Coq (2003), https://www.cs.ru.nl/~freek/mmode/mmode.pdf
Hales, T.: Formal abstracts (2020), https://formalabstracts.github.io
Harrison, J.: A mizar mode for HOL. In: von Wright, J., Grundy, J., Harrison, J. (eds.) Theorem Proving in Higher Order Logics: 9th International Conference, TPHOLs’96. Lecture Notes in Computer Science, vol. 1125, pp. 203–220. Springer-Verlag, Turku, Finland (1996)
Humayoun, M., Raffalli, C.: MathNat - mathematical text in a controlled natural language. Journal on Research in Computing Science 46 (2010)
Isabelle contributors: The Isabelle 2021 release (2021), https://isabelle.in.tum.de
Kaliszyk, C., Rabe, F.: A survey of languages for formalizing mathematics. In: Benzmüller, C., Miller, B. (eds.) Intelligent Computer Mathematics. pp. 138–156. Springer International Publishing, Cham (2020). https://doi.org/10.1007/978-3-030-53518-6_9
Koepke, P.: Textbook mathematics in the Naproche-SAD system. In: Brady, E., Davenport, J., Farmer, W.M., Kaliszyk, C., Kohlhase, A., Kohlhase, M., Müller, D., Pąk, K., Coen, C.S. (eds.) Joint Proceedings of the FMM and LML Workshops (2019), http://ceur-ws.org/Vol-2634/FMM4.pdf
Mizar, http://www.mizar.org/
de Moura, L.M., Kong, S., Avigad, J., van Doorn, F., von Raumer, J.: The Lean Theorem Prover (system description). In: Felty, A.P., Middeldorp, A. (eds.) Automated Deduction – CADE-25 – 25th International Conference on Automated Deduction, Berlin, Germany, August 1-7, 2015, Proceedings. Lecture Notes in Computer Science, vol. 9195, pp. 378–388. Springer (2015). https://doi.org/10.1007/978-3-319-21401-6_26
Naproche contributors: FLib, https://github.com/naproche-community/FLib
Paskevich, A.: Méthodes de formalisation des connaissances et des raisonnements mathématiques: aspects appliqués et théoriques. Ph.D. thesis, Université Paris 12 (2007), http://tertium.org/papers/thesis-07.fr.pdf
Paskevich, A.: The syntax and semantics of the ForTheL language (2007), http://nevidal.org/download/forthel.pdf
Paulson, L.C.: ALEXANDRIA: Large-scale formal proof for the working mathematician, https://www.cl.cam.ac.uk/~lp15/Grants/Alexandria
Paulson, L.C., Blanchette, J.C.: Three years of experience with Sledgehammer, a practical link between automatic and interactive theorem provers. In: Sutcliffe, G., Schulz, S., Ternovska, E. (eds.) IWIL 2010. The 8th International Workshop on the Implementation of Logics. EPiC Series in Computing, vol. 2, pp. 1–11. EasyChair (2012). https://doi.org/10.29007/36dt
Paulson, L.C., Nipkow, T., Wenzel, M.: From LCF to Isabelle/HOL. Formal Aspects of Computing 31, 675–698 (September 2019), 1–24 (2019). https://doi.org/10.1007/s00165-019-00492-1, Springer, London
Schulz, S.: The E Theorem Prover, https://eprover.org
Verchinine, K., Lyaletski, A., Paskevich, A.: System for automated deduction (SAD): a tool for proof verification. Automated Deduction–CADE-21 pp. 398–403 (2007). https://doi.org/10.1007/978-3-540-73595-3_29
Verchinine, K., Lyaletski, A., Paskevich, A., Anisimov, A.: On correctness of mathematical texts from a logical and practical point of view. In: Autexier, S., Campbell, J., Rubio, J., Sorge, V., Suzuki, M., Wiedijk, F. (eds.) International Conference on Intelligent Computer Mathematics. pp. 583–598. Springer (2008). https://doi.org/10.1007/978-3-540-85110-3_47
Wenzel, M.: The Isar proof language in 2016 (2016), http://sketis.net/wp-content/uploads/2016/08/Isabelle_Workshop_2016_Isar.pdf
Wenzel, M.: Interaction with formal mathematical documents in Isabelle/PIDE. In: Kaliszyk, C., Brady, E., Kohlhase, A., Sacerdoti Coen, C. (eds.) Intelligent Computer Mathematics (CICM 2019). Lecture Notes in Artificial Intelligence, vol. 11617. Springer (2019). https://doi.org/10.1007/978-3-030-23250-4_1
Wenzel, M.: Isar – a generic interpretative approach to readable formal proof documents. In: Bertot, Y., Dowek, G., Théry, L., Hirschowitz, A., Paulin, C. (eds.) Theorem Proving in Higher Order Logics, pp. 167–183. Springer Berlin Heidelberg, Berlin, Heidelberg (1999)
Wiedijk, F.: Mizar light for HOL light. In: Boulton, R.J., Jackson, P.B. (eds.) TPHOLs: International Conference on Theorem Proving in Higher Order Logics. pp. 378–393. Springer (2001)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2021 The Author(s)
About this paper
Cite this paper
De Lon, A., Koepke, P., Lorenzen, A., Marti, A., Schütz, M., Wenzel, M. (2021). The Isabelle/Naproche Natural Language Proof Assistant. In: Platzer, A., Sutcliffe, G. (eds) Automated Deduction – CADE 28. CADE 2021. Lecture Notes in Computer Science(), vol 12699. Springer, Cham. https://doi.org/10.1007/978-3-030-79876-5_36
Download citation
DOI: https://doi.org/10.1007/978-3-030-79876-5_36
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-79875-8
Online ISBN: 978-3-030-79876-5
eBook Packages: Computer ScienceComputer Science (R0)




 System
System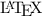 Processing
Processing Reasoner
Reasoner Reasoner
Reasoner