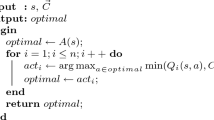A Normative Supervisor for Reinforcement Learning Agents

Abstract

We introduce a modular and transparent approach for augmenting the ability of reinforcement learning agents to comply with a given norm base. The normative supervisor module functions as both an event recorder and real-time compliance checker w.r.t. an external norm base. We have implemented this module with a theorem prover for defeasible deontic logic, in a reinforcement learning agent that we task with playing a “vegan” version of the arcade game Pac-Man.

This work was partially supported by WWTF project MA16-28 and the DC-RES run by the TU Wien’s Faculty of Informatics and the FH-Technikum Wien.

1 Introduction

Autonomous agents are an increasingly integral part of modern life. While performing activities formerly reserved for human agents, they must possess the ability to adapt to (potentially unpredictable) changes in their environment; reinforcement learning (RL) has proven a successful method for teaching agents this behaviour (see, e.g. [16, 13]). Performing human roles further requires that agents align themselves with the ethical standards their human counterparts are subject to, introducing a requirement for ethical reasoning. RL has been employed to enforce such standards as well (see, e.g., [14]); agents can be trained to act in line with further rewards/penalties assigned according to the performance of ethical/unethical behaviour through a reward function. However, this does not provide a guarantee of the desired behaviour. Moreover, such techniques are not well equipped to handle the complexities of ethical reasoning. In general, like other black-box machine learning methods, RL cannot transparently explain why a certain policy is compliant or not. Additionally, when the ethical values are embedded in the learning process, a small change in their definition would require us to retrain the policy from scratch.

To obviate the limitations of RL to represent ethical norms, the approach we follow in this paper combines RL with Deontic Logic, the branch of formal logic that is concerned with prescriptive statements; we implement a normative supervisor to inform a trained RL agent of the ethical requirements in force in a given situation. Since the pioneering works [17, 15], it has been well understood that Deontic Logic can be applied to model ethical norms; the difference between ethical and legal norms is indeed only on how they emerge, not what normative consequences are entailed by them. We implement our normative supervisor using defeasible deontic logic [8, 9]. This is a simple and computationally feasible, yet expressive, logic allowing for defeasible reasoning, and can easily accommodate changes to the norm base, should the ethical requirements become more complex (see Sect. 3.4 for a brief walk-through). Moreover, the constructive nature of this logic allows us to determine how a given conclusion has been reached.

By embedding the normative supervisor into the RL agent architecture, the agent can follow near-optimal learned policies while enforcing ethical actions in a modular and transparent way. The supervisor functions as both an event recorder and real-time compliance checker; it corrects the choice of a given action from the policy only when this violates a norm. It is furthermore used as an event logger to identify and extract new sets of (ethical) norms to promote particular goals. We demonstrate our approach on an RL agent that plays a “vegan” version of Pac-Man, with an “ethical” constraint forbidding Pac-Man from eating ghosts. Already used as a case study in [14, 10], the Pac-Man game is a closed environment for testing with clearly defined game mechanics and parameters which are easy to isolate, manipulate, and extend with variably intricate rule sets. We successfully evaluated our approach with several tests, consisting of “vegan” games and a “vegetarian” version of the game where the agent can eat only one type of ghost. The achievement of full compliance in the latter case was possible with the introduction of additional norms identified via the event recorder.

Related Work. The papers [14] and [10] on Pac-Man motivated our work. The former employs multi-objective RL with policy orchestration to impose normative constraints on vegan Pac-Man. It seamlessly combines ethically compliant behaviour and learned optimal behaviour; however, the ethical reasoning performed is still to a degree implicit, it does not provide justifications for the choices made, and it is not clear how the approach would remain reasonably transparent with more complex norm sets. [10] takes steps to integrate more complex constraints on a RL agent, but as they are embedded in the learned policy, it lacks the transparency of a logic-based implementation. [1] and [2] address the problem of transparency in the implementation of ethical behaviours in AI, but their approach has not been implemented and tested yet. Symbolic reasoning for implementing ethically compliant behaviour in autonomous agents has been used in many frameworks, such as [5], which models the behaviour from a BDI perspective. This approach does not allow for defeasible reasoning, and focuses on avoiding ethical non-compliance at the planning level. Non-monotonic logic-based approaches that extend BDI with a normative component appear in [6, 9], whose solutions remain only at the theoretical level. These papers belong to the related field of Normative Multi-Agent Systems, which is not specifically concerned with the ethical behaviour of agents [3], and whose introduced formalisms and tools (e.g. [12]) have not yet been used in combination with RL.

2 Background

Normative Reasoning. Normative reasoning differs from the reasoning captured by classical logic in that the focus is not on true or false statements, but rather the imposition of norms onto such statements.

We will deal with two types of norms: constitutive and regulative norms (see [4] for the terminology). Regulative norms describe obligations, prohibitions and permissions. Constitutive norms regulate instead the creation of institutional facts as well as the modification of the normative system itself; their content is a relation between two concepts, and they will typically take the form “in context c, concept x counts as concept y”, where x refers to a more concrete concept (e.g., walking) and y to a more abstract one (e.g., moving). We say concept x is at a lower level of abstraction than concept y in context c if there is a constitutive norm with context c asserting that x counts as y (henceforth denoted $\mathbf{C} (x, y)$).

Reinforcement Learning (RL). RL refers to a class of algorithms specialized in learning how an agent should act in its environment to maximize the expected cumulative reward. Given a function that assigns rewards/penalties to each state and successor state pair (or state-action pairs), the RL algorithm learns an optimal policy, a function from states to actions that can govern its behaviour.

In our case study we chose Q-learning [18] with function approximation as a RL algorithm. In Q-learning, the RL algorithm first learns a function Q(s, a) to predict the expected cumulative reward (Q-value) from state s taking action a. The learned policy picks the action $argmax_{a\in possible} \ Q(s, a)$ with the highest Q-value over a list of possible actions. The function Q is approximated as a linear function which is the weighted sum of features describing some elements of the environment (e.g., the distance between the agent and object X); the features which are most relevant to predicting the agent success are weighted most heavily.

Vegan Pac-Man. In the arcade game Pac-Man, an eponymous agent is situated inside a maze over a grid, where some cells contain a ‘food pellet’ which Pac-Man will eat if it moves inside the cell. Pac-Man’s goal is to maximize his score; when Pac-Man eats a food pellet he gains a reward ($+10$ points), but there is also a time penalty ($-1$ point for every time step). Pac-Man wins when he has eaten all the food pellets in the maze (resulting in $+500$ points), and he loses if he collides with one of the ghost agents wandering around the maze (resulting in $-500$ points). However, after eating a ‘power pellet’ (of which there are two), the ghosts become ‘scared’, and Pac-Man can eat them (for $+200$ points).

Inspired by [14], we consider a variation of the UC Berkeley AI Pac-Man implementation [7], where Pac-Man cannot eat ghosts (only blue ghosts in the vegetarian version). Our Pac-Man agent utilizes a Q-learning policy; for the utility function we use the game’s score, and we take the game states as states. We use the same game layout as in [14]; this is a $20\times 11$ maze populated with 97 food pellets and two ghosts (blue and orange) which follow random paths, where the maximum score available is 2170, and 1370 when eating ghosts is forbidden.

3 The Normative Supervisor

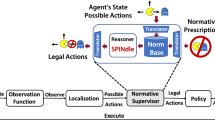
The key component of our approach is a normative supervisor whose architecture is illustrated in Fig. 1. This module consists of a normative reasoning engine (we use the SPINdle theorem prover [11]), and of other components that encode the norms and environmental data into defeasible deontic logic rules, and translate the conclusions of the reasoning engine into instructions for the agent.

Fig. 1.

Key components and placement of the Normative Supervisor.

We place the normative supervisor in the already-trained agent’s control loop between the localization and policy module. The localization module identifies the current agent’s state with respect to its environment and returns a list of possible actions to the normative supervisor. This module filters out all the actions that are not compliant with the norms. The policy will then identify, among the pool of the compliant actions, the optimal one for generating the next game state. If there are no available compliant actions the normative supervisor will select the ’lesser evil’ action. This module additionally enables the logging of events during the game for later scrutiny.

3.1 Configuring the Norm Base

We start with a simple normative prescription, consisting only of the behavioral constraint proposed in [14] that “Pac-Man must not eat ghosts”¹, represented as $vegan:\ \mathbf{F} (eat(pacman, ghost))$, where F denotes prohibition.

If this norm base is to inform our agent’s actions, it needs to reference concepts that correspond to the information directly processed by the agent, which is limited to the locations of game entities and the actions that Pac-Man can perform, which we denote as North, South, East, West, and Stop. The only way eat(pacman, ghost) can be done is if (a) the ghost is in a ‘scared’ state, and (b) Pac-Man and the ghost move into the same cell. These are expressed as scared(ghost) and inRange(pacman, ghost) respectively. Pac-Man does not know which direction the ghost will move in, but we will assume a “cautious” model of action where Pac-Man is not to perform any action that could constitute eating a ghost; that is, if Pac-Man takes an action that could reasonably lead to him violating a norm, we will consider that norm violated. Since Pac-Man’s next action determines what is in range, we will actually need five entities to express inRange(pacman, ghost), one corresponding to each action. These concepts are used to construct a constitutive norm, or a kind of strategy, regarding eating, $strategy_{North}:\ \mathbf{C} (North, eat(pacman, ghost))$, which is applicable in the context $\{scared(ghost), inNorthRange(pacman, ghost)\}$.

For inNorthRange(pacman, ghost), we have access to the positions of Pac-Man and the ghosts, so we can create another set of constitutive norms for this, which apply in the context $\{pacman(i,j)\}$, $range_{North}:\ \mathbf{C} (ghost(k,l),$ inNorthRange(pacman, ghost)), where (k, l) has a Manhattan distance of one or fewer cells from $(i,j+1)$.

Finally, we need to consider additional relationships between norms and concepts. For this norm base, we only have one regulative norm, so a mechanism for conflict resolution is not needed. However, as Pac-Man can only execute one action at a time, we have a non-concurrence relation between every action. This amounts to an inability to comply with multiple obligations over distinct actions. However, since Vegan Pac-Man does not deal with any obligations, additional rules will not be needed.

Representing the Norm Base. We need a formal language – equipped with an automated theorem prover – capable of effectively representing and reasoning with the norm base; we chose defeasible deontic (propositional) logic (DDPL for short) [8]. DDPL is defined over literals and modal literals, and the key ingredient is the rules we can construct from them. For the purposes of this paper we only consider one deontic modality (obligation $\mathbf{O}$) and define prohibition and permission as $\mathbf{F} (p) \equiv \mathbf{O} (\lnot p)$ and $\mathbf{P} (p) \equiv \lnot \mathbf{O} (\lnot p)$.

Definition 1

A rule is an expression $r:A(r)\hookrightarrow _{*} N(r)$ where r is a label uniquely identifying the rule, $A(r)=\{a_{1}, ..., a_{n}\}$ is the antecedent, N(r) is the consequent, $\hookrightarrow _{*}\in \{\rightarrow _{*}, \Rightarrow _{*}, \rightsquigarrow _{*}\}$, and the mode of each rule is designated with $*\in \{C, O\}$.

Rules labelled by C and O are constitutive and regulative rules, respectively. Strict rules ($\rightarrow _*$) are rules where the consequent strictly follows from the antecedent without exception. Defeasible rules ($\Rightarrow _*$) are rules where the consequent typically follows from the antecedent, unless there is evidence to the contrary. Defeaters ($\rightsquigarrow _*$) are rules that only prevent a conclusion from being reached by a defeasible rule; regulative defeaters are used to encode permissive rules (see [8]).

The central concept of DDPL (and our application of it) is:

Definition 2

A defeasible theory D is a tuple $\langle F, R_{O}, R_{C}, >\rangle$, where F is a set of literals (facts), $R_{O}$ and $R_{C}$ are sets of regulative and constitutive rules, and > is a superiority relation over rules.

These tools will be utilized to map Pac-Man’s to a defeasible theory; the environment translated to a set of facts and the norm base to a set of rules.

3.2 Automating Translation

We are now dealing with three kinds of syntax: our informal representation of the norm base, the input and output of the host process, and the formal language of the reasoner (DDPL and its theorem prover SPINdle [11]). If we frame the reasoner as a central reasoning facility, the agent as a front-end, and the norm base as a back-end, we can implement this dynamic as a translator with two faces, one front-facing and one back-facing, feeding information into the reasoner from the agent and the norm base respectively.

Front End Translation. The front-end translator will be continuously in use, sending new data to be translated and requiring translated proposed actions as the environment changes. This will be an algorithm that transforms input data from the agent into propositions which assert facts about the agent or the environment, and then logical conclusions into instructions the agent will understand. Each cell of the Pac-Man grid can contain characters (Pac-Man or one of the ghosts), an object (a wall or a food pellet), or nothing at all. Walls are accounted for during the localization stage of Pac-Man’s algorithm and food pellets are not an entity that appears in the norm base, so we will need to reason only about the characters. Hence we have two sets of variables in each game; $pacman_{i,j}$ and $ghost_{i,j}$ (along with scared(ghost) if the ghost is in a scared state) assert the current coordinates of Pac-Man and of each ghost, and appear in a set Facts in the defeasible theory $GameState=\langle Facts, R_{C}, R_{O}, > \rangle$.

Actions will be represented as deontic literals, in the set

$$ Actions = \{North, South, East, West, Stop\} $$

A query from Pac-Man to the reasoner will be accompanied by a representation of the current game state, along with a list of possible actions, possible, which will be translated to the corresponding literal in Actions.

Back End Translation. In this critical task it is crucial to ensure that norms dictate the same behaviour once translated into this language. Besides making sure that each component of the norm can be represented by the language, we must also analyse our translated norm base with respect to how the available metadata is accommodated by the reasoner’s rules of inference.

We represent the regulative norm of Vegan Pac-Man (vegan) as:

$$ \Rightarrow _{O} \lnot eat_{pacman,ghost} \; \in R_{O} $$

where defeasibility is given as a precautionary measure, in case we want to add (potentially conflicting) norms later.

Note that if moving North counts as eating a ghost, an obligation to go North counts as being obligated to eat a ghost, and a prohibition to eat a ghost implies a prohibition to move North. So we can rewrite $strategy_{North}$ as $\mathbf{C} (\mathbf{O} (\lnot eat(pacman, ghost)),\mathbf{O} (\lnot North) )$, or with the applicable context as:

$$scared_{ghost}, inNorthRange_{pacman, ghost},\mathbf{O} (\lnot eat_{pacman,ghost})\Rightarrow _{O} \lnot North\in R_{O}$$

Note that though this a constitutive rule, in DDPL it will be in $R_{O}$. This will work for all of the constitutive norms attached to a prohibited action, where we place the context and the prohibition in question in the antecedent, and the prohibition of the concrete action in the strategy is the consequent.

For the remaining constitutive norms, we have a rather simple conversion. These norms will be generated w.r.t. the input from the agent; for example, if the agent (Pac-Man) tells us that he is at (2, 3), the rule $range_{North}$ will be:

$$ pacman_{2,3}, ghost_{2, 4}\rightarrow _{C} inNorthRange_{pacman,ghost}\in R_{C} $$

We have found that it is more time-efficient to generate these constitutive norms anew whenever the fact set changes, instead of generating every possible constitutive norm ahead of time, and having SPINdle deal with all at once.

3.3 Classify and Assess Conclusions

Once we understand how various concepts are represented in the reasoner language, we need to parse the possible outputs of the reasoning engine into indicators as to which actions in the agent’s arsenal are compliant with the norm base.

Compliant Solutions. Ideally, we will want to locate a compliant solution – an action that constitutes a possible course of action for the agent that does not violate any norms – from the conclusions yielded by the reasoner.

Definition 3

A set of compliant solutions is: (1) non-empty, and consisting only of (2) solutions composed of possible actions, (3) solutions that do not violate any norms, and (4) solutions that are internally consistent.

The manner in which we construct such a set is heavily influenced by the output (conclusions) yielded by SPINdle. Conclusions in DDPL are established over proofs and can be classified as defeasible or definite, and positive or negative. A positive conclusion means that the referenced literal holds, while a negative indicates that this literal has been refuted. A definite conclusion is obtained by using only strict rules and facts using forward chaining of rules. A conclusion holds defeasibly (denoted by $+\partial _C$ for a factual conclusion and $+\partial _O$ for an obligation) if there is an applicable rule for it and the rules for the opposite cannot be applied or are defeated. Over the course of a proof, each rule will be classified as either applicable (i.e., the antecedent holds and the consequent follows), discarded (i.e., the rule is not applied because the antecedent doesn’t fully hold), or defeated by a defeater or a higher priority rule. For a set of rules R, R[p], $R_O$ and $R^{sd}$ are, respectively, the subsets of: the rules for p, regulative rules, and strict or defeasible rule. The definition of provability for defeasible obligations [8] (we define only defeasible conclusions, because in our formalization regulative norms were expressed as defeasible rules) is:

Definition 4

Given a defeasible theory D, if $D\vdash +\partial _{O}\ p$, then:

• 1. $\exists r\in R^{sd}_{O}[p]$ that is applicable defeasible, and

• 2. $\forall s\in R_O[\lnot p]$ either: (a) s is discarded, or (b) $s\in R^{sd}$ and $\exists t\in R_O[p]$ s.t. t is applicable, $t>s$, or (c) s is a defeater, $\exists t\in R^{sd}_{O}[p]$ s.t. t is applicable, $t>s$

A derivation in DDPL has a three phase argumentation structure, where arguments are simply applicable rules: (1) we need an argument for the conclusion we want to prove, (2) we analyse all possible counter-arguments, and (3) we rebut the counter-arguments. An argument can be rebutted when it is not applicable or when it is defeated by a stronger applicable argument. If we exclude the undercut case, in every phase the arguments attack the arguments in the previous phase. A rule attacks another rule if the conclusions of the two rules are contradictory (note that $\mathbf{P} (q)$ and $\mathbf{P} (\lnot q)$ are not a deontic contradiction). Accordingly, any regulative rule for q attacks a strict or defeasible regulative rule for $\lnot q$. However, a regulative defeater for q is not attacked by a regulative defeater for $\lnot q$ (condition 2(c) above).

We parse out a solution set by: (1) if we do not receive a full set of conclusions from SPINdle, we return an empty set; (2) we remove all conclusions that do not reference a literal in possible; (3) any action corresponding to a defeasibly proved positive literal occurs in every solution; and (4) any action corresponding to a defeasibly proved negative literal is discarded from every solution.

Claim: the above procedure yields either an empty set or a compliant solution.

Proof sketch: If our solution is not internally consistent, we can prove both $+\delta _O\ a$ and $+\delta _O \lnot a$ for some action a. In this case SPINdle will return neither, and the above procedure leads to an empty set in step (1). Only possible actions will occur in a solution as per step (2), and any solutions which fail to comply with an obligation or prohibition will be excluded through step (3) and (4) respectively.

‘Lesser of two Evils’ Solutions. If the above procedure leaves us with an empty solution set, we want to identify which non-compliant actions constitute the “best” choice (i.e. are minimally non-compliant). Our characterization of degrees of non-compliance depends on the way the reasoner constructs solutions, and what information it logs during this process. SPINdle has an inference logger that classifies every rule in the theory as discarded, applicable, or defeated. For our agent, the chosen degree is a score derived from the of norms that have been applied versus those that have been defeated (discarded norms are ignored):

$$ score:=\#complied - \#violated = \#applied - \#defeated $$

This score is computed through the theory $GameState_{a}$, which is constructed by adding a fact $\mathbf{O} (a)$ to GameState. Recall that a rule will be defeated when its defeasible theory includes a fact that conflicts with the head of this rule. So when we add $\mathbf{O} (a)$ to GameState, all norms that prescribed $\mathbf{F} (a)=\mathbf{O} (\lnot a)$ for GameState are defeated and any prescribing $\mathbf{O} (a)$ is applied. To compute the score, we use SPINdle in a rather unconventional way, ignoring conclusions yielded and checking the inference log to count which rules have been applied during reasoning ($\# applied$) and which were defeated ($\# defeated$) and set $score = \# applied - \# defeated$. This procedure is completed for every action in possible, and we select the action(s) with the highest score. If there are multiple actions with a highest score, we send multiple solutions to the agent and it will pick the best action according to its policy.

Claim: computing scores for all possible actions is completed in polynomial time.

Proof sketch: As shown in [8], conclusions in DDPL can be computed in linear time with respect to the the number of literal occurrences plus the number of the rules in the theory. The claim holds since every action in possible is a literal, and the above procedure is completed |possible| times.

3.4 Revising the Norm Base

We demonstrate the advantages of our approach – modularity, configurability, and capability as an event recorder – through revising our norm base.

Inherent to Pac-Man’s environment is the possibility of encountering a state where no compliant action is possible; in this section we explore how to address cases like this through adding or removing rules to the norm base.

Fig. 2.

Pac-Man trapped between two ghosts (a) or in a corner (b). In (c) Pac-Man consumes the power pellet and eats the ghost at the same time.

When playing “vegan” Pac-Man, we may encounter the case depicted in Fig. 2(a).

In absence of additional information Pac-Man will eat whichever ghost the policy indicates it should, and a violation report is generated. Each violation report is saved as a timestamped file accompanied with the representation of the current game state. This report can be used to retroactively examine the context in which violations occur, and we can thereby revise our norm base which is independent from the agent’s RL policy. In the case of “vegan” Pac-Man, these reports make it clear that this version of the game will be susceptible to somewhat regular violations in the form of Fig. 2(a).

If we consider instead “vegetarian” Pac-Man, we can restrict our norm base to the vegan rule only applied to the blue ghost. However, situations in which compliance is not possible can still occur; for instance the one depicted in Fig. 2(b), or the case where Pac-Man consumes a power pellet and the blue ghost at the same time, as shown in Fig. 2(c). In the latter case, the violation occurs because, prior to Pac-Man’s consumption of the power pellet, the blue ghost is not scared and Pac-Man’s strategy to comply with vegan will not be triggered. This is roughly analogous to an agent committing an unethical act because it has no way of recognizing that it is unethical.

Summarily, the violation reports show that there are four points in the maze where Pac-Man, potentially, cannot comply, given the information he has access to; in response, we add a norm danger steering Pac-Man away from these areas:

$$ \Rightarrow _{O} \lnot enter_{pacman, danger} $$

which is accompanied by constitutive norms defining the abstract action of “entering danger” (for some pre-defined location denoted as danger), such as:

$$inNorthRange_{pacman,danger}, inRange_{ghost, danger}\Rightarrow _{O}\lnot North$$

4 Evaluation and Conclusion

We have presented a modular and transparent approach that enables an autonomous agent in pursuing ethical goals, while still running an RL policy that maximizes its cumulative reward. Our approach was evaluated on six tests², in batches of 100 games. The results are displayed in the following table and discussed below; we give data on both game performance (average score and % games won) and ethical performance (ghosts eaten). Refer to Sec. 2 for a thorough description of the testing environment.

The first two baseline tests measured the performance of Pac-Man using two different (ethically agnostic) RL policies without the normative supervisor; this establishes a baseline for Pac-Man’s game performance. We refer to the first RL policy (in Test 1a) as safe because the algorithm used to train it does not differentiate between regular ghosts and scared ghosts, learning how to avoid them altogether. We refer to the other RL policy (in Test 1b) as hungry because the corresponding algorithm differentiates between regular ghosts and scared ghosts, and the agent learns how to eat the scared ghosts. The results for Test 1b (average score of 1503.5 maximum score of 2133) were comparable to the baseline version in [14] (average score of 1675.9, max score of 2144).

Tests 2a, 2b, 3, and 4 make use of the normative supervisor. In 2a and 2b, we subject Pac-Man to a “vegan” norm base, prohibiting eating all ghosts (for both the safe and hungry policies respectively). The results obtained for test 2a were comparable to those in [14]: the average number of violations was the same in both tests (0.03 ghosts), and our average score was only slightly smaller (1193.39 instead of 1268.5). Compared with the baseline, the game performance did not suffer. For test 2b we obtained instead full compliance. Test 3 and 4 both use the hungry policy. In test 3 we subject Pac-Man to a “vegetarian” norm base, where only eating blue ghosts is forbidden. Allowing Pac-Man to eat one of the ghosts allows him to further maximize his score and avoid the violations depicted in Fig. 2(a). Test 4 addresses the two edge cases of non-compliance occurring in Test 3 as depicted in Fig. 2(b) and Fig. 2(c) by adding the new rules defined in Sec. 3.4, steering Pac-Man away from entering the “dangerous” areas. Here, violations were completely eliminated.

These tests, along with the analysis of the violation reports created in non-compliant cases, yielded several insights. The module did not cause Pac-Man’s game performance to suffer, and could successfully identify non-compliant behaviour. It implemented compliant behaviour in most cases, with the exception of situations where compliance was not possible. The violation reports allowed us to identify such situations with ease.

The game used in this paper offers limited opportunities to work with meaningful (ethical) norms. We aim to explore alternative case studies with more options to define multiple (and possibly conflicting) ethical goals to test the interactions between RL and a normative supervisor based on DDPL.