Making Higher-Order Superposition Work

Abstract

Superposition is among the most successful calculi for first-order logic. Its extension to higher-order logic introduces new challenges such as infinitely branching inference rules, new possibilities such as reasoning about formulas, and the need to curb the explosion of specific higher-order rules. We describe techniques that address these issues and extensively evaluate their implementation in the Zipperposition theorem prover. Largely thanks to their use, Zipperposition won the higher-order division of the CASC-J10 competition.

1 Introduction

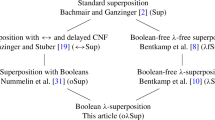
In recent decades, superposition-based first-order automatic theorem provers have emerged as useful reasoning tools. They dominate at the annual CASC [45] theorem prover competitions, having always won the first-order theorem division. They are also used as backends to proof assistants [13, 25, 35], automatic higher-order theorem provers [42], and software verifiers [17]. The superposition calculus has only recently been extended to higher-order logic, resulting in $\lambda$-superposition [6], which we developed together with Waldmann, as well as combinatory superposition [10] by Bhayat and Reger.

Both higher-order superposition calculi were designed to gracefully extend first-order reasoning. As most steps in higher-order proofs tend to be essentially first-order, extending the most successful first-order calculus to higher-order logic seemed worth trying. Our first attempt at corroborating this conjecture was in 2019: Zipperposition 1.5, based on $\lambda$-superposition, finished third in the higher-order theorem division of CASC-27 [47], 12 percentage points behind the winner, the tableau prover Satallax 3.4 [11].

Studying the competition results, we discovered that higher-order tableaux have some advantages over higher-order superposition. To bridge the gap, we developed techniques and heuristics that simulate the behavior of a tableau prover in the context of saturation. We implemented them in Zipperposition 2, which took part in CASC-J10 in 2020. This time, Zipperposition won the division, solving 84% of problems, a whole 20 percentage points ahead of the next best prover, Satallax 3.4. In this paper, we describe the main techniques that explain this reversal of fortunes. They range from preprocessing to backend integration.

Interesting patterns can be observed in various higher-order encodings of problems. We show how we can exploit these to simplify problems (Sect. 3). By working on formulas rather than clauses, tableau techniques take a more holistic view of a higher-order problem. Delaying the clausification through the use of calculus rules that act on formulas achieves the same effect in superposition. We further explore the benefits of this approach (Sect. 4).

The main drawback of $\lambda$-superposition compared with combinatory superposition is that it relies on rules that enumerate possibly infinite sets of unifiers. We describe a mechanism that interleaves performing infinitely branching inferences with the standard saturation process (Sect. 5). The prover retains the same behavior as before on first-order problems, smoothly scaling with increasing numbers of higher-order clauses. We also propose some heuristics to curb the explosion induced by highly prolific $\lambda$-superposition rules (Sect. 6).

Using first-order backends to finish the proof is common practice in higher-order reasoning. Since $\lambda$-superposition coincides with standard superposition on first-order clauses, invoking backends may seem redundant; yet Zipperposition is nowhere as efficient as E [38] or Vampire [28], so invoking a more efficient backend does make sense. We describe how to achieve a balance between allowing native higher-order reasoning and delegating reasoning to a backend (Sect. 7).

Finally, we compare Zipperposition 2 with other provers on all monomorphic higher-order TPTP benchmarks [46] to perform a more extensive evaluation than at CASC (Sect. 8). Our evaluation corroborates the competition results.

2 Background and Setting

We focus on monomorphic higher-order logic, but the techniques can easily be extended with polymorphism. Indeed, Zipperposition already supports some techniques polymorphically.

Higher-Order Logic. We define terms s, t, u, v inductively as free variables F, X, bound variables $x, y, z, \dotsc$, constants $\mathsf {f}, \mathsf {g},\mathsf {a},\mathsf {b}, \dotsc$, applications $s \, t$, and $\lambda$-abstractions $\lambda x.\> s$. The syntactic distinction between free and bound variables gives rise to loose bound variables (e.g., y in $\lambda x.\> y \, \mathsf {a}$) [32]. We let $s \, \overline{t}_n$ stand for $s \, t_1 \, \ldots \, t_n$ and $\lambda \overline{x}_n.\> s$ for $\lambda x_1. \ldots \lambda x_n. \> s$. Every $\beta$-normal term can be written as $\lambda \overline{x}_m.\> s \, \overline{t}_n$, where s is not an application; we call s the head of the term. If the type of a term t is of the form $\tau _1 \rightarrow \cdots \rightarrow \tau _n \rightarrow o$, where o is the distinguished Boolean type and $n \ge 0$, we call t a predicate. A literal l is an equation $s \approx t$ or a disequation $s \not \approx t$. A clause is a finite multiset of literals, interpreted and written disjunctively $l_1 \mathrel \vee \cdots \mathrel \vee l_n$. Logical symbols that may occur within terms are written in boldface: $\pmb {\lnot }, \pmb \wedge , \pmb \vee , \pmb \rightarrow , \pmb \leftrightarrow , \dots$. Predicate literals are encoded as (dis)equations with $\pmb \top$ based on their sign; for example, $\mathsf {even}(x)$ becomes $\mathsf {even}(x) \approx \pmb \top$, and $\lnot \,\mathsf {even}(x)$ becomes $\mathsf {even}(x) \not \approx \pmb \top$.

Higher-Order Calculi. The $\lambda$-superposition calculus is a refutationally complete inference system and redundancy criterion for Boolean-free extensional polymorphic clausal higher-order logic. The calculus relies on complete sets of unifiers (CSUs). The CSU for s and t with respect to a set of variables V, denoted by $\mathrm {CSU}_V(s,t)$, is a set of unifiers such that for any unifier $\varrho$ of s and t, there exist substitutions $\sigma \in \mathrm {CSU}_V(s,t)$ and $\theta$ such that $\varrho (X) = \sigma ( \theta (X))$ for all variables $X \in V$. The set X is used to distinguish between important and auxiliary variables. We usually omit it. A pragmatic, incomplete extension of $\lambda$-superposition with interpreted Booleans is described by Vukmirović and Nummelin [51]. This forms the basis of most of this work. Recently, a refutationally complete extension was developed by Bentkamp et al. [5]; it is not considered here.

By contrast, the combinatory superposition calculus avoids CSUs by using a form of first-order unification, but essentially it enumerates higher-order terms using rules that instantiate applied variables with partially applied combinators from the complete combinator set $\{\mathsf {S}, \mathsf {K}, \mathsf {B}, \mathsf {C}, \mathsf {I}\}$. This calculus is the basis of Vampire 4.5 [10], which finished closely behind Satallax 3.4 at CASC-J10.

A different, very successful calculus is Satallax’s SAT-guided tableaux [2]. Satallax was the leading higher-order prover of the 2010s. Its simple and elegant tableaux avoid deep superposition-style rewriting inferences. Nevertheless, our working hypothesis for the past six years has been that superposition would likely provide a stronger basis for higher-order reasoning. Other competing higher-order calculi include SMT (implemented in CVC4 [3, 4]) and extensional paramodulation (implemented in Leo-III [42]).

Zipperposition. Zipperposition [6, 12] is a higher-order theorem prover based on a pragmatic extension of $\lambda$-superposition. It was conceived as a testbed for rapidly experimenting with extensions of first-order superposition, but over time, it has assimilated many of E’s techniques and heuristics. Zipperposition 2 also implements combinatory superposition.

Several of our techniques extend the given clause procedure [30, Section 2.3], the standard saturation procedure. It partitions the proof state into a set P of passive clauses and a set A of active clauses. Initially, P contains all input clauses, and A is empty. At each iteration, a given clause C from P is moved to A (i.e., it is activated), all inferences between C and clauses in A are performed, and the conclusions are added to P. Because Zipperposition fully simplifies clauses only when they are activated, it implements a DISCOUNT-style loop [14].

Experimental Setup. To assess our techniques, we carried out experiments with Zipperposition 2. We used all 2606 monomorphic higher-order problems from the TPTP library [46], version 7.2.0, as benchmarks. Although some techniques support polymorphism, we uniformly used the monomorphic benchmarks. We fixed a base configuration of Zipperposition parameters as a baseline for all comparisons. Then, in each experiment, we varied the parameters associated with a specific technique to evaluate it. The experiments were run on StarExec [43] servers, equipped with Intel Xeon E5-2609 CPUs clocked at 2.40 GHz. Unless otherwise stated, we used a CPU time limit of 20 s, roughly the time each configuration is given in the portfolio mode used for CASC. The raw evaluation results are available online.¹

3 Preprocessing Higher-Order Problems

The TPTP library contains thousands of higher-order problems. Despite their diversity, they have a markedly different flavor from the TPTP first-order problems. Notably, they extensively use the definition role to identify universally quantified equations (or equivalences) that define symbols.

Definitions can be replaced by rewrite rules, using the orientation given in the input problem. If there are multiple definitions for the same symbol, only the first one is replaced by a rewrite rule. Then, whenever a clause is picked in the given clause procedure, it will be rewritten using the collected rules. Since the TPTP format enforces no constraints on definitions, rewriting might diverge. To ensure termination, we limit the number of applied rewrite steps. In practice, most TPTP problems are well behaved: Only one definition is given for each symbol, and the definitions are acyclic. Instead of rewriting a clause when it is activated, we can rewrite the input formulas as a preprocessing step. This ensures that the input clauses will be fully simplified when the proving process starts and no defined symbols will occur in clauses, which usually helps the heuristics.

Eagerly unfolding the definitions and $\beta$-reducing can eliminate all of a problem’s higher-order features, making it amendable to first-order methods. However, this can inflate the problem beyond recognition and compromise the refutational completeness of superposition.

To keep completeness, we can try to orient the definitions using the term order that parameterized superposition and rely on demodulation to simplify the proof state. Usually, the Knuth–Bendix order (KBO) [26] is used. It compares terms by first comparing their weights, which is the sum of all the weights assigned to the symbols it contains. Given a symbol weight assignment $\mathcal {W}$, we can update it so that it orients acyclic definitions from left to right assuming that they are of the form $\mathsf {f} \, \overline{X}_m \approx \lambda \overline{y}_n. \, t$, where the only free variables in t are $\overline{X}_m$, no free variable repeats or appears applied in t, and $\mathsf {f}$ does not occur in t. Then we traverse the symbols $\mathsf {f}$ that are defined by such equations following the dependency relation, starting with a symbol $\mathsf {f}$ that does not depend on any other defined symbol. For each $\mathsf {f}$, we set $\mathcal {W}(\mathsf {f})$ to $w + 1$, where w is the maximum weight of the right-hand sides of $\mathsf {f}$’s definitions, computed using $\mathcal {W}$. By construction, for each equation the left-hand side is heavier. Thus, the equations are orientable from left to right.

Evaluation and Discussion. The base configuration treats axioms annotated with definition as rewrite rules, and it preprocesses the formulas using the rewrite rules. We also tested the effects of disabling this preprocessing (−preprocess), disabling the special treatment of definition axioms (−RW), and disabling the special treatment of definition while using adjusted KBO[2] weights as described above (−RW$+$KBO). The results are given in Figure 1. In all of the figures in this paper, each cell gives the number of proved problems; the highest number is typeset in bold. Clearly, treating definition axioms as rewrite rules greatly improves performance. Using adjusted KBO weights is not as strong, although it proves 15 problems not proved using other configurations.

4 Reasoning about Formulas

Higher-order logic identifies terms and formulas. To prove a problem, we often need to instantiate a variable with the right predicate. Finding this predicate can be easier if the problem is not clausified. Consider the conjecture $\exists f. \, f \, \mathsf {p} \, \mathsf {q} \pmb \leftrightarrow \mathsf {p} \pmb \wedge \mathsf {q}$. Expressed in this form, the formula is easy to prove by taking $f := \lambda x \, y. \> x \pmb \wedge y$. By contrast, guessing the right instantiation for the negated, clausified form $F \, \mathsf {p} \, \mathsf {q} \not \approx \pmb \top \mathrel \vee \mathsf {p} \not \approx \pmb \top \mathrel \vee \mathsf {q} \not \approx \pmb \top , F \, \mathsf {p} \, \mathsf {q} \approx \pmb \top \mathrel \vee \mathsf {p} \approx \pmb \top$, $F \, \mathsf {p} \, \mathsf {q} \approx \pmb \top \mathrel \vee \mathsf {q} \approx \pmb \top$ is more challenging. One of the strengths of higher-order tableau provers is that they do not clausify the input problem. This might explain Satallax’s dominance in the THF division of CASC competitions until CASC-J10.

Fig. 1.

Effect of the definition rewriting methods

Fig. 2.

Effect of clausification and lightweight AVATAR

We studied techniques to incrementally clausify formulas during proof search in incomplete [51] and complete [5] extensions of $\lambda$-superposition. Both approaches include the same set of (outer) delayed clausification rules that clausify top-level logical symbols, proceeding outside in; for example, a clause $C' \mathrel \vee (\mathsf {p} \pmb \wedge \mathsf {q}) \not \approx \pmb \top$ is transformed into $C' \mathrel \vee \mathsf {p} \not \approx \pmb \top \mathrel \vee \mathsf {q} \not \approx \pmb \top$. The complete approach requires additional inference rules; it also supports inner delayed clausification. We focus on the pragmatic, incomplete approach and do not consider inner clausification due to its poor performance [5].

Delayed clausification rules can be used as inference rules (which add conclusions to the passive set) or as simplification rules (which delete premises and add conclusions to the passive set). Inferences are more flexible because they produce all intermediate clausification states, whereas simplifications produce fewer clauses. Since clausifying equivalences can destroy a lot of syntactic structure [18], we never apply simplifying clausification rules on them.

We discuss two tableau-inspired approaches for reasoning about formulas. First, we study how clause-splitting techniques interfere with delayed clausification. Second, we discuss heuristic instantiation of quantifiers during saturation.

Zipperposition supports a lightweight variant of AVATAR [49], an architecture that partitions the search space by splitting clauses into variable-disjoint subclauses. This variant of AVATAR is described by Ebner et al. [15]. Combining lightweight AVATAR and delayed clausification makes it possible to split a clause $(\varphi _1 \pmb \vee \cdots \pmb \vee \varphi _n) \approx \pmb \top$, where the $\varphi _i$’s are arbitrarily complex formulas that share no free variables with each other, into clauses $\varphi _i \approx \pmb \top$.

To finish the proof, it suffices to derive $\bot$ under each assumption $\varphi _i \approx \pmb \top$. Since the split is performed at the formula level, this technique resembles tableaux, but it exploits the strengths of superposition, such as its powerful redundancy criterion and simplification machinery, to close the branches.

Interleaving clausification and saturation allows us to simulate another tableau technique. Whenever dynamic clausification replaces the predicate variable x in a clause of the form $(\pmb \forall x.\, \varphi ) \approx \pmb \top \mathrel \vee C$ with a fresh variable X, resulting in $\varphi \{x \mapsto X\} \approx \pmb \top \mathrel \vee C$, we can create additional clauses in which x is replaced with $t \in Inst$, where $Inst$ is a set of heuristically chosen terms. This set contains $\lambda$-abstractions whose bodies are formulas and which occur in activated clauses, and primitive instantiations [51]—that is, imitations (in the sense of higher-order unification) of logical symbols that approximate the shape of a predicate that can instantiate a predicate variable.

However, as a new term t can be added to $Inst$ after a clause with a quantified variable of the same type as t has been activated, we must also keep track of the clauses $\varphi \{x \mapsto X\} \approx \pmb \top \mathrel \vee C$, so that when $Inst$ is extended, we instantiate the saved clauses. Conveniently, instantiated clauses are not recognized as subsumed, since Zipperposition uses an optimized but incomplete subsumption algorithm.

Given a disequation $\mathsf {f}\,\overline{s}_{n} \not \approx \mathsf {f}\,\overline{t}_{n}$, the abstraction of $s_i$ is $\lambda x.\, u \pmb \approx v$, where u is obtained by replacing $s_i$ with x in $\mathsf {f}\,\overline{s}_{n}$ and v is obtained by replacing $s_i$ with x in $\mathsf {f}\,\overline{t}_{n}$. For $\mathsf {f}\,\overline{s}_{n} \approx \mathsf {f}\,\overline{t}_{n}$, the analogous abstraction is $\lambda x.\, \pmb {\lnot \,}(u \pmb \approx v)$.

Adding abstractions of the conjecture literals to $Inst$ can provide useful instantiations for formulas such as induction principles for datatypes. As the conjecture is negated, the equation’s polarity is inverted in the abstraction. Consider the TPTP problem [44], whose clausified negated conjecture is $\mathsf {ap} \, \mathsf {xs} \, (\mathsf {ap} \, \mathsf {ys} \, \mathsf {zs}) \not \approx \mathsf {ap} \, (\mathsf {ap} \, \mathsf {xs} \, \mathsf {ys}) \, \mathsf {zs}$, where $\mathsf {ap}$ is the append operator defined recursively on its first argument and $\mathsf {xs}$, $\mathsf {ys}$, and $\mathsf {zs}$ are of list type. Abstracting $\mathsf {xs}$ from the disequation yields $t = \lambda x.\, \mathsf {ap} \, x \, (\mathsf {ap} \, \mathsf {ys} \, \mathsf {zs}) \pmb \approx \mathsf {ap} \, (\mathsf {ap} \, x \, \mathsf {ys}) \, \mathsf {zs}$, which is added to $Inst$. Included in the problem is the induction axiom for the list datatype: $\pmb \forall p. \, (p \, \mathsf {nil} \pmb \wedge (\pmb \forall x \, xs . \, p \, xs \pmb \rightarrow p \, (\mathsf {cons} \, x \, xs ))) \pmb \rightarrow \pmb \forall xs . \, p \, xs$, where $\mathsf {nil}$ and $\mathsf {cons}$ have the usual meanings. Instantiating p with t and using the $\mathsf {ap}$ definition, we can prove $\pmb \forall x. \, \mathsf {ap} \, x \, (\mathsf {ap} \, \mathsf {ys} \, \mathsf {zs}) \pmb \approx \mathsf {ap} \, (\mathsf {ap} \, x \, \mathsf {ys}) \, \mathsf {zs}$, from which we easily derive a contradiction.

Evaluation and Discussion. The base configuration uses immediate clausification (IC), an approach that applies a standard clausification algorithm [33] both as a preprocessing step and whenever predicate variables are instantiated. Zipperposition’s lightweight AVATAR is disabled in the base configuration. To test the merits of delayed clausification, we vary base’s parameters along two axes: We choose immediate clausification (IC), delayed clausification as inference (DCI), or delayed clausification as simplification (DCS), and we either enable ($+$LA) or disable (−LA) the lightweight AVATAR. The base configuration does not use instantiation with terms from $Inst$.

Figure 2 shows that using delayed clausification as simplification greatly increases the success rate, while using delayed clausification as inference has the opposite effect. Manually inspecting the proofs found by the DCS configuration, we noticed that a main reason for its success is that it does not simplify away equivalences. Overall, the lightweight AVATAR harms performance, but the sets of problems proved with and without it are vastly different. For example, the IC$+$LA configuration proves 60 problems not proved by IC−LA.

The Boolean instantiation technique presented above requires delayed clausification. To test its effects, we enabled it in the best configuration from Figure 2, DCS−LA. With this change, Zipperposition proves 1744 problems, 36 of which cannot be proved by any other configuration in the same figure. Boolean instantiation is the only way in which Zipperposition 2 can prove higher-order problems requiring reasoning about induction axioms (e.g., ).

5 Enumerating Infinitely Branching Inferences

As an optimization and to simplify the implementation, Leo-III [40] and Vampire 4.4 [9] (which uses a predecessor of combinatory superposition) compute only a finite subset of the possible conclusions for inferences that require enumerating a CSU. Not only is this a source of incompleteness, but choosing the cardinality of the computed subset is a difficult heuristic choice. Small sets can result in missing the unifier necessary for the proof, whereas large sets make the prover spend a long time in the unification procedure, generate useless clauses, and possibly get sidetracked into the wrong parts of the search space.

We propose a modification to the given clause procedure to seamlessly interleave unifier computation and proof state exploration. Given a complete unification procedure, which may yield infinite streams of unifiers, our modification fairly enumerates all conclusions of inferences relying on elements of a CSU. Under some reasonable assumptions, it behaves exactly like the standard given clause procedure on purely first-order problems. We also describe heuristics that help achieve a similar performance as when using incomplete, terminating unification procedures without sacrificing completeness.

Given the undecidability of the question as to whether there exists a next CSU element in a stream of unifiers, the request for the next conclusion might not terminate, effectively bringing the theorem prover to a halt. Our modified given clause procedure expects the unification procedure to return a lazily computed stream [34, Sect. 4.2], each element of which is either $\emptyset$ or a singleton set containing a unifier. To avoid getting stuck waiting for a unifier that may not exist, the unification procedure should return $\emptyset$ after it performs a number of operations without finding a unifier.

The complete unification procedure by Vukmirović et al. [52] returns such a stream. Other procedures such as Huet’s [22] and Jensen and Pietrzykowski’s [23] can easily be adapted to meet this requirement. Based on the stream of unifiers interspersed with $\emptyset$, we can construct a stream of inferences similarly interspersed with $\emptyset$ of which any finite prefixes can be computed in finite time.

To support such streams in the given clause procedure, we extend it to represent the proof state not only by the active (A) and passive (P) clause sets, but also by a priority queue Q containing the inference streams. Each stream is associated with a weight, and Q is sorted in order of increasing weight. Elsewhere [6], Bentkamp et al. described an older version of this extension. Here we present a newer version in more detail, including heuristics to postpone unpromising streams. The pseudocode of the modified procedure is as follows:

Initially, all input clauses are put into P, and A and Q are empty. Unlike in the standard given clause procedure, inference results are represented as clause streams. The first element is inserted into P, and the rest of the stream is stored in Q with some positive integer weight computed from the inference rule.

To eventually consider inference conclusions from streams in Q as given clauses, we extract elements from, or probe, streams and move any obtained clauses to P. Analogously to the traditional pick–given ratio [30, 37], we use a parameter $K_{\mathrm {fair}}$ (by default, $K_{\mathrm {fair}}= 70$) to ensure fairness: Every $K_{\mathrm {fair}}$th iteration, FairProbe probes an increasing number of oldest streams, which achieves dovetailing. In all other iterations, HeuristicProbe attempts to extract up to $K_{\mathrm {best}}$ clauses from the most promising streams (by default, $K_{\mathrm {best}}= 7$). In each attempt, the most promising stream in Q is chosen. If its first element is $\emptyset$, the rest of the stream is inserted into Q, and a new stream is chosen. This is repeated until either $K_{\mathrm {retry}}$ occurrences of $\emptyset$ have been met (by default, $K_{\mathrm {retry}}= 20$) or the stream yields a singleton set. Setting $K_{\mathrm {retry}}> 0$ increases the chance that HeuristicProbe will return $K_{\mathrm {best}}$ clauses, as desired. Finally, if P becomes empty, ForceProbe searches relentlessly for a clause in Q, as a fallback.

The function ExtractClause extracts an element from a nonempty stream not in Q and inserts the remaining stream into Q with an increased weight, calculated as follows. Let n be the number of times the stream was chosen for probing. If probing results in $\emptyset$, the stream’s weight is increased by $\max \,\{2, n-16\}$. If probing results in a clause C whose penalty is p, the stream’s weight is increased by $p \cdot \max \,\{1, n-64\}$. The penalty of a clause is a number assigned by Zipperposition based on features such as the depth of its derivation and the rules used in it. The constants 16 and 64 increase the chance that newer streams are picked, which is desirable because their first clauses are expected to be useful.

All three probing functions are invoked by GivenClause, which forms the body of the saturation loop. It differs from the standard given clause procedure in three ways: First, the proof state includes Q in addition to P and A. Second, new inferences involving the given clause are added to Q instead of being performed immediately. Third, inferences in Q are periodically performed lazily to fill P.

GivenClause eagerly stores the first element of a new inference stream in P to imitate the standard given clause procedure. If the underlying unification procedure behaves like the standard first-order unification algorithm on higher-order logic’s first-order fragment, our given clause procedure coincides with the standard one. The unification procedure by Vukmirović et al. terminates on the first-order and other fragments [32], and for problems outside these fragments, it immediately returns $\emptyset$ to avoid computing complicated unifiers eagerly.

Evaluation and Discussion. When the unification procedure of Vukmirović et al. was implemented in Zipperposition, it was observed that Zipperposition is the only competing higher-order prover that proves all Church numeral problems from the TPTP, never spending more than 5 seconds on the problem [52].

Consider the TPTP problem NUM800$^1$, which requires finding a function F such that $F \, \mathsf {c_1} \, \mathsf {c_2} \pmb \approx \mathsf {c_2} \pmb \wedge F \, \mathsf {c_2} \, \mathsf {c_3} \pmb \approx \mathsf {c_6}$, where $\mathsf {c}_n$ abbreviates the Church numeral for n, $\lambda s\, z. \> s^n(z)$. To prove it, it suffices to take F to be the multiplication operator $\lambda x \, y \, s \, z. \> x \, (y \, s) \, z$. However, this unifier is only one out of many available for each occurrence of F.

In an independent evaluation setup on the same set of 2606 problems used in this paper, Vukmirović et al. compared a complete, nonterminating variant and a pragmatic, terminating variant of the unification procedure [52, Sect. 7]. The pragmatic variant was used directly—all the inference conclusions were put immediately in P, bypassing Q. The complete variant, which relies on possibly infinite streams and is much more prolific, proved only 15 problems less than the most competitive pragmatic variant. Furthermore, it proved 19 problems not proved by the pragmatic variant. This shows that our given clause procedure, with its heuristics, allows the prover to defer exploring less promising branches of the unification and uses the full power of a complete higher-order unifier search to solve unification problems that cannot be solved by a crippled procedure.

Among the competing higher-order theorem provers, only Satallax uses infinitely branching calculus rules. It maintains a queue of “commands” that contain instructions on how to create a successor state in the tableau. One command describes infinite enumeration of all closed terms of a given function type. Each execution of this command makes progress in the enumeration. Unlike evaluation of streams representing elements of CSU, each command execution is guaranteed to make progress in enumerating the next closed functional term, so there is no need to ever return $\emptyset$.

6 Controlling Prolific Rules

To support higher-order features such as function extensionality and quantification over functions, many refutationally complete calculi employ highly prolific rules. For example, $\lambda$-superposition uses a rule FluidSup[6] that very often applies to two clauses if one of them contains a term of the form $F \, \overline{s}_n$, where $n > 0$. We describe three mechanisms to keep rules like these under control.

First, we limit applicability of the prolific rules. In practice, it often suffices to apply prolific higher-order rules only to initial or shallow clauses—clauses with a shallow derivation depth. Thus, we added an option to forbid the application of a rule if the derivation depth of any premise exceeds a limit.

Second, we penalize the streams of expensive inferences. The weight of each stream is given an initial value based on characteristics of the inference premises such as their derivation depth. For prolific rules such as FluidSup, we increment this value by a parameter $K_\mathrm {incr}$. Weights for less prolific variants of this rule, such as DupSup [6], are increased by a fraction of $K_\mathrm {incr}$ (e.g., $\lfloor K_\mathrm {incr}/3 \rfloor$).

Third, we defer the selection of prolific clauses. To select the given clause, most saturating provers evaluate clauses according to some criteria and select the clause with the lowest evaluation. For this choice to be efficient, passive clauses are organized into a priority queue ordered by their evaluations. Like E, Zipperposition maintains multiple queues, ordered by different evaluations, that are visited in a round-robin fashion. It also uses E’s two-layer evaluation functions, a variant of which has recently been implemented in Vampire [19]. The two layers are clause priority and clause weight. Clauses with higher priority are preferred, and the weight is used for tie-breaking. Intuitively, the first layer crudely separates clauses into priority classes, whereas the second one uses heuristic weights to prefer clauses within a priority class. To control the selection of prolific clauses, we introduce new clause priority functions that take into account features specific to higher-order clauses.

The first new priority function PreferHOSteps (PHOS) assigns a higher priority if rules specific to $\lambda$- or combinatory superposition were used in the clause derivation. Since most of the other clause priority functions tend to defer higher-order clauses, having a clause queue that prefers the results of higher-order inferences might be necessary to find a proof more efficiently. A simpler function, which prefers clauses containing $\lambda$-abstractions, is PreferLambda (PL).

We also introduce the priority function ByNormalizationFactor (BNF), inspired by the observation that a higher-order inference that applies a complicated substitution to a clause is usually followed by a $\beta \eta$-normalization step. If $\beta \eta$-normalization greatly reduces the size of a clause, it is likely that this substitution simplifies the clause (e.g., by removing a variable’s arguments). Thus, this function prefers clauses that were produced by $\beta \eta$-normalization, and among those it prefers the ones with larger size reductions.

Another new priority function is PreferShallowAppVars (PSAV). This prefers clauses with lower depths of the deepest occurrence of an applied variable—that is, $C[X \, \mathsf {a}]$ is preferred over $C[\mathsf {f}\,(X \, \mathsf {a})]$. This function tries to curb the explosion of both $\lambda$- and combinatory superposition: Applying a substitution to a top-level applied variable often reduces this applied variable to a term with a constant head, which likely results in a less explosive clause. Among the functions that rely on properties of applied variables we implemented PreferDeepAppVars (PDAV), which returns the priority opposite of PSAV, and ByAppVarNum (BAVN), which prefers clauses with fewer occurrences of applied variables.

Fig. 3.

Effect of the priority function on performance

Fig. 4.

Effect of the FluidSup weight increment $K_\mathrm {incr}$ on performance

Evaluation and Discussion. In the base configuration, Zipperposition visits several clause queues, one of which uses the constant priority function ConstPrio (CP). To evaluate the new priority functions, we replaced the queue ordered by CP with the queue ordered by one of the new functions, leaving the clause weight intact. The results are shown in Figure 3. It shows that the expensive priority functions PHOS and BNF, which require inspecting the proof of clauses, hardly help. Simple functions such as PL are more effective: Compared with base, PL loses one problem overall but proves 22 new problems.

FluidSup is disabled in base because it is so explosive. To test if increasing inference stream weights makes a difference on the success rate, we enabled FluidSup and used different weight increments $K_\mathrm {incr}$ for FluidSup inference queues. The results are shown in Figure 4. As expected, using a low increment with FluidSup is detrimental to performance. However, as the column for $K_\mathrm {incr}=16$ shows, nor should we use too high an increment, since that delays useful FluidSup inferences. Interestingly, even though the configuration with $K_\mathrm {incr}=1$ proves the least problems overall, it proves 7 problems not proved by base, which is more than any other configuration we tried.

7 Controlling the Use of Backends

Cooperation with efficient first-order theorem provers is an essential feature of higher-order theorem provers such as Leo-III [40, Sect. 4.4] and Satallax [11]. Those provers invoke first-order backends repeatedly during a proof attempt and spend a substantial amount of time in backend collaboration. Since $\lambda$-superposition generalizes a highly efficient first-order calculus, we expect that future efficient $\lambda$-superposition implementations will not benefit much from backends. Experimental provers such as Zipperposition can still gain a lot. We present some techniques for controlling the use of backends.

In his thesis [40, Sect. 6.1], Steen extensively evaluates the effects of using different first-order backends on the performance of Leo-III. His results suggest that adding only one backend already substantially improves the performance. To reduce the effort required for integrating multiple backends, we chose Ehoh [50] as our single backend. Ehoh is an extension of the highly optimized superposition prover E with support for higher-order features such as partial application, applied variables, and interpreted Booleans. On the one hand, Ehoh provides the efficiency of E while easing the translation from full higher-order logic: The only missing syntactic feature is $\lambda$-abstraction. On the other hand, Ehoh’s higher-order reasoning capabilities are limited. Its unification algorithm is essentially first-order and it cannot synthesize $\lambda$-abstractions.

In a departure from Leo-III and other cooperative provers, we invoke the backend at most once during a run of the prover. This is because most competitive higher-order provers use a portfolio mode in which many configurations are run for a short time, and we want to leave enough time for native higher-order reasoning. Moreover, multiple backend invocations tend to be wasteful, because currently each invocation starts with no knowledge of the previous ones.

Only a carefully chosen subset of the available clauses are translated and sent to Ehoh. Let I be the set of input clauses. Given a proof state, let $M = P \cup A$, and let $M_\mathrm {ho}$ denote the subset of M that contains only clauses that were derived using at least one $\lambda$-superposition-specific inference rule. We order the clauses in $M_\mathrm {ho}$ by increasing derivation depth, using syntactic weight to break ties. Then we choose all clauses in I and the first $K_\mathrm {size}$ clauses from $M_\mathrm {ho}$ for use with the backend reasoner. We leave out clauses in $M \setminus (I \cup M_\mathrm {ho})$ because Ehoh can rederive them. We also expect large clauses with deep derivations to be less useful.

The remaining step is the translation of $\lambda$-abstractions. We support two translation methods: $\lambda$-lifting [24] and $\mathsf {SKBCI}$ combinators [48]. For $\mathsf {SKBCI}$, we omit the combinator definition axioms, because they are very explosive [10]. A third mode simply omits clauses containing $\lambda$-abstractions.

Evaluation and Discussion. In Zipperposition, we can adjust the CPU time allotted to Ehoh, Ehoh’s own proof search parameters, the point when Ehoh is invoked, the number $K_\mathrm {size}$ of selected clauses from $M_\mathrm {ho}$, and the $\lambda$ translation method. We fix the time limit to 5 s, use Ehoh in auto mode, and focus on the last three parameters. In base, collaboration with Ehoh is disabled.

Fig. 5.

Effect of the backend invocation point $K_\mathrm {time}$

Fig. 6.

Effect of the method used to translate $\lambda$-abstractions

Fig. 7.

Effect of the number of selected clauses $K_\mathrm {size}$

Ehoh is invoked after $K_\mathrm {time}\cdot t$ CPU seconds, where $0 \le K_\mathrm {time}< 1$ and t is the total CPU time allotted to Zipperposition. Figure 5 shows the effect of varying $K_\mathrm {time}$ when $K_\mathrm {size}= 32$ and $\lambda$-lifting is used. The evaluation confirms that using a highly optimized backend such as Ehoh greatly improves the performance of a less optimized prover such as Zipperposition. The figure indicates that it is preferable to invoke the backend early. We have indeed observed that if the backend is invoked late, small clauses with deep derivations tend to be present by then. These clauses might have been used to delete important shallow clauses already. But due to their derivation depth, they will not be translated. In such situations, it is better to invoke the backend before the important clauses are deleted.

Figure 6 quantifies the effects of the three $\lambda$-abstraction translation methods. We fixed $K_\mathrm {time}= 0.25$ and $K_\mathrm {size}=32$. The clear winner is $\lambda$-lifting. Omitting clauses with $\lambda$-abstractions performs comparably to SKBCI combinators.

Figure 7 shows the effect of $K_\mathrm {size}$ on performance, with $K_\mathrm {time}= 0.25$ and $\lambda$-lifting. We find that including a small number of higher-order clauses with the lowest weight performs better than including a large number of such clauses.

8 Comparison with Other Provers

Different choices of parameters lead to noticeably different sets of proved problems. In an attempt to use Zipperposition 2 to its full potential, we have created a portfolio mode that runs up to 50 configurations in parallel during the allotted time. To provide some context, we compare Zipperposition 2 with the latest versions of all higher-order provers that competed at CASC-J10: CVC4 1.8 [4], Leo-III 1.5 [42], Satallax 3.5 [11], and Vampire 4.5 [10]. Note that Vampire’s higher-order schedule is optimized for running on a single core.

We use the same 2606 monomorphic higher-order TPTP 7.2.0 problems as elsewhere in this paper, but we try to replicate the CASC setup more faithfully. CASC-J10 was run on 8-core CPUs with a 120 s wall-clock limit and a 960 s CPU limit. Since we run the experiments on 4-core CPUs, we set the wall-clock limit to 240 s and keep the same CPU limit. Leo-III, Satallax, and Zipperposition are cooperative provers. We also run them in uncooperative mode, without their backends, to measure their intrinsic strength. Figure 8 summarizes the results.

Fig. 8.

Comparison of competing higher-order theorem provers

Among the cooperative provers, Zipperposition is the one that depends the least on its backend, and its uncooperative mode is only one problem behind Satallax’s cooperative mode. This confirms our hypothesis that $\lambda$-superposition is a suitable basis for automatic higher-order reasoning. This also suggests that the implementation of this calculus in a modern first-order superposition prover such as E or Vampire would achieve markedly better results. Moreover, we believe that there are still techniques inspired by tableaux, SAT solving, and SMT solving that could be adapted and integrated in saturation provers.

9 Discussion and Conclusion

Back in 1994, Kohlhase [27, Sect. 1.3] was optimistic about the future of higher-order automated reasoning:

The obstacles to proof search intrinsic to higher-order logic may well be compensated by the greater expressive power of higher-order logic and by the existence of shorter proofs. Thus higher-order automated theorem proving will be practically as feasible as first-order theorem proving is now as soon as the technological backlog is made up.

For higher-order superposition, the backlog consisted of designing calculus extensions, heuristics, and algorithms that mitigate its weaknesses. In this paper, we presented such enhancements, justified their design, and evaluated them. We explained how each weak point in the higher-order proving pipeline could be improved, from preprocessing to reasoning about formulas, to delaying unpromising or explosive inferences, to invoking a backend. Our evaluation indicates that higher-order superposition is now the state of the art in higher-order reasoning.

Higher-order extensions of first-order superposition have been considered by Bentkamp et al. [6, 7] and Bhayat and Reger [9, 10]. They introduced proof calculi, proved them refutationally complete, and suggested optional rules, but they hardly discussed the practical aspects of higher-order superposition. Extensions of SMT are discussed by Barbosa et al. [3]. Bachmair and Ganzinger [1], Manna and Waldinger [29], and Murray [31] have studied nonclausal resolution calculi.

In contrast, there is a vast literature on practical aspects of first-order reasoning using superposition and related calculi. The literature evaluates various procedures and techniques [21, 36], literal and term order selection functions [20], and clause evaluation functions [19, 39], among others. Our work joins the select club of papers devoted to practical aspects of higher-order reasoning [8, 16, 41, 53].

As a next step, we plan to implement the described techniques in Ehoh [50], the $\lambda$-free higher-order extension of E. We expect the resulting prover to be substantially more efficient than Zipperposition. Moreover, we want to investigate the proofs found by provers such as CVC4 and Satallax but missed by Zipperposition. Finding the reason behind why Zipperposition fails to prove specific problems will likely result in useful new techniques.