Abstract
We recently designed two calculi as stepping stones towards superposition for full higher-order logic: Boolean-free \(\lambda \)-superposition and superposition for first-order logic with interpreted Booleans. Stepping on these stones, we finally reach a sound and refutationally complete calculus for higher-order logic with polymorphism, extensionality, Hilbert choice, and Henkin semantics. In addition to the complexity of combining the calculus’s two predecessors, new challenges arise from the interplay between \(\lambda \)-terms and Booleans. Our implementation in Zipperposition outperforms all other higher-order theorem provers and is on a par with an earlier, pragmatic prototype of Booleans in Zipperposition.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
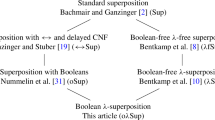
Superposition is a leading calculus for first-order logic with equality. We have been wondering for some years whether it would be possible to gracefully generalize it to extensional higher-order logic and use it as the basis of a strong higher-order automatic theorem prover. Towards this goal, we have, together with colleagues, designed superposition-like calculi for three intermediate logics between first-order and higher-order logic. Now we are finally ready to assemble a superposition calculus for full higher-order logic. The filiation of our new calculus from Bachmair and Ganzinger’s standard first-order superposition is as follows:

Our goal was to devise an efficient calculus for higher-order logic. To achieve it, we pursued two objectives. First, the calculus should be refutationally complete. Second, the calculus should coincide as much as possible with its predecessors
 and
and
 on the respective fragments of higher-order logic (which in turn essentially coincide with Sup on first-order logic). Achieving these objectives is the main contribution of this paper. We made an effort to keep the calculus simple, but often the refutational completeness proof forced our hand to add conditions or special cases.
on the respective fragments of higher-order logic (which in turn essentially coincide with Sup on first-order logic). Achieving these objectives is the main contribution of this paper. We made an effort to keep the calculus simple, but often the refutational completeness proof forced our hand to add conditions or special cases.
Like
 , our calculus
, our calculus
 operates on clauses that can contain Boolean subterms, and it interleaves clausification with other inferences. Like \(\lambda \)Sup,
operates on clauses that can contain Boolean subterms, and it interleaves clausification with other inferences. Like \(\lambda \)Sup,
 eagerly \(\beta \eta \)-normalizes terms, employs full higher-order unification, and relies on a fluid subterm superposition rule (FluidSup) to simulate superposition inferences below applied variables—i.e., terms of the form \(y\>t_1\dots t_n\) for \(n \ge 1\).
eagerly \(\beta \eta \)-normalizes terms, employs full higher-order unification, and relies on a fluid subterm superposition rule (FluidSup) to simulate superposition inferences below applied variables—i.e., terms of the form \(y\>t_1\dots t_n\) for \(n \ge 1\).
Because
 contains several superposition-like inference rules for Boolean subterms, our completeness proof requires dedicated fluid Boolean subterm hoisting rules (FluidBoolHoist, FluidLoobHoist), which simulate Boolean inferences below applied variables, in addition to FluidSup, which simulates superposition inferences.
contains several superposition-like inference rules for Boolean subterms, our completeness proof requires dedicated fluid Boolean subterm hoisting rules (FluidBoolHoist, FluidLoobHoist), which simulate Boolean inferences below applied variables, in addition to FluidSup, which simulates superposition inferences.
Due to restrictions related to the term order that parameterizes superposition, it is difficult to handle variables bound by unclausified quantifiers if these variables occur applied or in arguments of applied variables. We solve the issue by replacing such quantified terms \(\forall y.\>t\) by equivalent terms
 in a preprocessing step.
in a preprocessing step.
We implemented our calculus in the Zipperposition prover and evaluated it on TPTP and Sledgehammer benchmarks. The new Zipperposition outperforms all other higher-order provers and is on a par with an ad hoc implementation of Booleans in the same prover by Vukmirović and Nummelin [30]. We refer to the technical report [8] for the completeness proof and a more detailed account of the calculus and its evaluation.
2 Logic
Our logic is higher-order logic (simple type theory) with rank-1 polymorphism, Hilbert choice, and functional and Boolean extensionality. Its syntax mostly follows Gordon and Melham [17]. We use the notation \(\bar{a}_n\) or \(\bar{a}\) to stand for the tuple \((a_1,\dots ,a_n)\) where \(n \ge 0\). Deviating from Gordon and Melham, type arguments are explicit, written as \({\mathsf {c}}{\langle \bar{\tau }_m\rangle }\) for a symbol \({\mathsf {c}}:\mathsf {\Pi }\bar{\alpha }_m.\;\upsilon \) and types \(\bar{\tau }_m\). In the type signature \(\mathrm {\Sigma }_\mathsf {ty}\), we require the presence of a nullary Boolean type constructor
 and a binary function type constructor \(\rightarrow \). In the term signature \(\mathrm {\Sigma }\), we require the presence of the logical symbols
and a binary function type constructor \(\rightarrow \). In the term signature \(\mathrm {\Sigma }\), we require the presence of the logical symbols
 , and
, and
 . The logical symbols are shown in bold to distinguish them from the notation used for clauses below. Moreover, we require the presence of the Hilbert choice operator
. The logical symbols are shown in bold to distinguish them from the notation used for clauses below. Moreover, we require the presence of the Hilbert choice operator
 . Although
. Although
 is interpreted in our semantics, we do not consider it a logical symbol. Our calculus will enforce the semantics of
is interpreted in our semantics, we do not consider it a logical symbol. Our calculus will enforce the semantics of
 by an axiom, whereas the semantics of the logical symbols will be enforced by inference rules. We write
by an axiom, whereas the semantics of the logical symbols will be enforced by inference rules. We write  for the set of (term) variables. We use Henkin semantics, in the style of Fitting [15], with respect to which we can prove our calculus refutationally complete. In summary, our logic essentially coincides with the TPTP TH1 format [20].
for the set of (term) variables. We use Henkin semantics, in the style of Fitting [15], with respect to which we can prove our calculus refutationally complete. In summary, our logic essentially coincides with the TPTP TH1 format [20].
We generally view terms modulo \(\alpha \beta \eta \)-equivalence. When defining operations that need to analyze the structure of terms, however, we use a custom normal form as the default representative of a \(\beta \eta \)-equivalence class: The \(\beta \eta {\mathsf {Q}}_{\eta }\)-normal form \(t{\downarrow }_{\beta \eta {\mathsf {Q}}_{\eta }}\) of a term t is obtained by bringing the term into \(\eta \)-short \(\beta \)-normal form and finally applying the rewrite rule
 exhaustively whenever s is not a \(\lambda \)-expression. Here and elsewhere, \({\mathsf {Q}}\) stands for either
exhaustively whenever s is not a \(\lambda \)-expression. Here and elsewhere, \({\mathsf {Q}}\) stands for either
 or
or
 .
.
On top of the standard higher-order terms, we install a clausal structure that allows us to formulate calculus rules in the style of first-order superposition. A literal \(s \mathrel {\dot{\approx }}t\) is an equation \(s \approx t\) or disequation \(s \not \approx t\) of terms s and t; both equations and disequations are unordered pairs. A clause \(L_1 \vee \dots \vee L_n\) is a finite multiset of literals \(L_{\!j}\). The empty clause is written as \(\bot \). This clausal structure does not restrict the logic, because an arbitrary term t of Boolean type can be written as the clause
 .
.
We considered excluding negative literals by encoding them as
 , following
, following
 [16]. However, this approach would make the conclusion of the equality factoring rule (EFact) too large for our purposes. Regardless, the simplification machinery will allow us to reduce negative literals
[16]. However, this approach would make the conclusion of the equality factoring rule (EFact) too large for our purposes. Regardless, the simplification machinery will allow us to reduce negative literals
 and
and
 to
to
 and
and
 , respectively, thereby eliminating redundant representations of nonequational literals.
, respectively, thereby eliminating redundant representations of nonequational literals.
We let \({{\,\mathrm{CSU}\,}}(s,t)\) denote an arbitrary (preferably, minimal) complete set of unifiers for two terms s and t on the set of free variables of the clauses in which s and t occur. To compute such sets, Huet-style preunification [18] is not sufficient, and we must resort to a full unification procedure [19, 29]. To cope with the nontermination of such procedures, we use dovetailing as described by Vukmirović et al. [28, Sect. 5].
Some of the rules in our calculus introduce Skolem symbols, representing objects mandated by existential quantification. We assume that these symbols do not occur in the input problem. More formally, given a problem over a term signature \(\mathrm {\Sigma }\), our calculus operates on a Skolem-extended term signature \(\mathrm {\Sigma }_{\mathsf {sk}}\) that, in addition to all symbols from \(\mathrm {\Sigma }\), inductively contains symbols
 for all types \(\upsilon \), variables \(z:\upsilon \), and terms
for all types \(\upsilon \), variables \(z:\upsilon \), and terms
 over \(\mathrm {\Sigma }_{\mathsf {sk}}\), where \(\bar{\alpha }\) are the free type variables occurring in t and \(\bar{x}:\bar{\tau }\) are the free term variables occurring in t, both in order of first occurrence.
over \(\mathrm {\Sigma }_{\mathsf {sk}}\), where \(\bar{\alpha }\) are the free type variables occurring in t and \(\bar{x}:\bar{\tau }\) are the free term variables occurring in t, both in order of first occurrence.
3 The Calculus
The
 calculus closely resembles \(\lambda \)Sup, augmented with rules for Boolean reasoning that are inspired by
calculus closely resembles \(\lambda \)Sup, augmented with rules for Boolean reasoning that are inspired by
 . As in \(\lambda \)Sup, superposition-like inferences are restricted to certain first-order-like subterms, the green subterms, which we define inductively as follows: Every term t is a green subterm of t, and for all symbols
. As in \(\lambda \)Sup, superposition-like inferences are restricted to certain first-order-like subterms, the green subterms, which we define inductively as follows: Every term t is a green subterm of t, and for all symbols
 , if t is a green subterm of \(u_i\) for some i, then t is a green subterm of
, if t is a green subterm of \(u_i\) for some i, then t is a green subterm of
 . For example, the green subterms of
. For example, the green subterms of
 are the term itself,
are the term itself,
 ,
,
 , \({\mathsf {p}}\),
, \({\mathsf {p}}\),
 , and
, and
 . We write
. We write
 to denote a term s with a green subterm t and call the first-order-like context
to denote a term s with a green subterm t and call the first-order-like context
 a green context.
a green context.
Following \(\lambda \)Sup, we call a term t fluid if (1) \(t{\downarrow }_{\beta \eta {\mathsf {Q}}_{\eta }}\) is of the form \(y\>\bar{u}_n\) where \(n \ge 1\), or (2) \(t{\downarrow }_{\beta \eta {\mathsf {Q}}_{\eta }}\) is a \(\lambda \)-expression and there exists a substitution \(\sigma \) such that \(t\sigma {\downarrow }_{\beta \eta {\mathsf {Q}}_{\eta }}\) is not a \(\lambda \)-expression (due to \(\eta \)-reduction). Intuitively, fluid terms are terms whose normal form can change radically as a result of instantiation.
We define deeply occurring variables as in \(\lambda \)Sup, but exclude \(\lambda \)-expressions directly below quantifiers: A variable occurs deeply in a clause C if it occurs inside an argument of an applied variable or inside a \(\lambda \)-expression that is not directly below a quantifier.
Preprocessing. Our completeness theorem requires that quantified variables do not appear in certain higher-order contexts. We use preprocessing to eliminate problematic occurrences of quantifiers. The rewrite rules
 and
and
 , which we collectively denote by
, which we collectively denote by
 , are defined as
, are defined as
 and
and
 where the rewritten occurrence of \({\mathsf {Q}}{\langle \tau \rangle }\) is unapplied or has an argument of the form
where the rewritten occurrence of \({\mathsf {Q}}{\langle \tau \rangle }\) is unapplied or has an argument of the form
 such that x occurs as a nongreen subterm of v. If either of these rewrite rules can be applied to a given term, the term is
such that x occurs as a nongreen subterm of v. If either of these rewrite rules can be applied to a given term, the term is
 -reducible; otherwise, it is
-reducible; otherwise, it is
 -normal.
-normal.
For example, the term
 is
is
 -normal. A term may be
-normal. A term may be
 -reducible because a quantifier appears unapplied (e.g.,
-reducible because a quantifier appears unapplied (e.g.,
 ); a quantified variable occurs applied (e.g.,
); a quantified variable occurs applied (e.g.,
 ); a quantified variable occurs inside a nested \(\lambda \)-expression (e.g.,
); a quantified variable occurs inside a nested \(\lambda \)-expression (e.g.,
 ); or a quantified variable occurs in the argument of a variable, either a free variable (e.g.,
); or a quantified variable occurs in the argument of a variable, either a free variable (e.g.,
 ) or a variable bound above the quantifier (e.g.,
) or a variable bound above the quantifier (e.g.,
 ).
).
A preprocessor
 -normalizes the input problem. Although inferences may produce
-normalizes the input problem. Although inferences may produce
 -reducible clauses, we do not
-reducible clauses, we do not
 -normalize during the derivation process itself. Instead,
-normalize during the derivation process itself. Instead,
 -reducible ground instances of clauses will be considered redundant by the redundancy criterion. Thus, clauses whose ground instances are all
-reducible ground instances of clauses will be considered redundant by the redundancy criterion. Thus, clauses whose ground instances are all
 -reducible can be deleted. However, there are
-reducible can be deleted. However, there are
 -reducible clauses, such as
-reducible clauses, such as
 , that nevertheless have
, that nevertheless have
 -normal ground instances. Such clauses must be kept because the completeness proof relies on their
-normal ground instances. Such clauses must be kept because the completeness proof relies on their
 -normal ground instances.
-normal ground instances.
In principle, we could omit the side condition of the
 -rewrite rules and eliminate all quantifiers. However, the calculus (especially, the redundancy criterion) performs better with quantifiers than with \(\lambda \)-expressions, which is why we restrict
-rewrite rules and eliminate all quantifiers. However, the calculus (especially, the redundancy criterion) performs better with quantifiers than with \(\lambda \)-expressions, which is why we restrict
 -normalization as much as the completeness proof allows. Extending the preprocessing to eliminate all Boolean terms as in Kotelnikov et al. [21] does not work for higher-order logic because Boolean terms can contain variables bound by enclosing \(\lambda \)-expressions.
-normalization as much as the completeness proof allows. Extending the preprocessing to eliminate all Boolean terms as in Kotelnikov et al. [21] does not work for higher-order logic because Boolean terms can contain variables bound by enclosing \(\lambda \)-expressions.
Term Order. The calculus is parameterized by a well-founded strict total order \(\succ \) on ground terms satisfying these four criteria: (O1) compatibility with green contexts—i.e., \(s' \succ s\) implies
 ; (O2) green subterm property—i.e.
; (O2) green subterm property—i.e.
 where \(\succeq \) is the reflexive closure of \(\succ \); (O3)
where \(\succeq \) is the reflexive closure of \(\succ \); (O3)
 for all terms
for all terms
 ; (O4)
; (O4)
 for all types \(\tau \), terms t, and terms u such that
for all types \(\tau \), terms t, and terms u such that
 and u are
and u are
 -normal and the only Boolean green subterms of u are
-normal and the only Boolean green subterms of u are
 and
and
 . The restriction of (O4) to
. The restriction of (O4) to
 -normal terms ensures that term orders fulfilling the requirements exist, but it forces us to preprocess the input problem. We extend \(\succ \) to literals and clauses via the multiset extensions in the standard way [2, Sect. 2.4].
-normal terms ensures that term orders fulfilling the requirements exist, but it forces us to preprocess the input problem. We extend \(\succ \) to literals and clauses via the multiset extensions in the standard way [2, Sect. 2.4].
For nonground terms, \(\succ \) is required to be a strict partial order such that \(t \succ s\) implies \(t\theta \succ s\theta \) for all grounding substitutions \(\theta \). As in \(\lambda \)Sup, we also introduce a nonstrict variant \(\succsim \) for which we require that \(t\theta \succeq s\theta \) for all grounding substitutions \(\theta \) whenever \(t \succsim s\), and similarly for literals and clauses.
To construct a concrete order fulfilling these requirements, we define an encoding into untyped first-order terms, and compare these using a variant of the Knuth–Bendix order. In a first step, denoted
 , the encoding translates fluid terms t as fresh variables
, the encoding translates fluid terms t as fresh variables
 ; nonfluid \(\lambda \)-expressions
; nonfluid \(\lambda \)-expressions
 as
as
 ; applied quantifiers
; applied quantifiers
 as
as
 ; and other terms
; and other terms
 as
as
 . Bound variables are encoded as constants \({\mathsf {db}}^i\) corresponding to De Bruijn indices. In a second step, denoted
. Bound variables are encoded as constants \({\mathsf {db}}^i\) corresponding to De Bruijn indices. In a second step, denoted
 , the encoding replaces \({\mathsf {Q}}_1\) by \({\mathsf {Q}}_1'\) and variables z by \(z'\) whenever they occur below \({\mathsf {lam}}\). For example,
, the encoding replaces \({\mathsf {Q}}_1\) by \({\mathsf {Q}}_1'\) and variables z by \(z'\) whenever they occur below \({\mathsf {lam}}\). For example,
 is encoded as
is encoded as
 . The first-order terms can then be compared using a transfinite Knuth–Bendix order \(\succ _{{\mathsf {kb}}}\) [22]. Let the weight of
. The first-order terms can then be compared using a transfinite Knuth–Bendix order \(\succ _{{\mathsf {kb}}}\) [22]. Let the weight of
 and
and
 be \(\omega \), the weight of
be \(\omega \), the weight of
 and
and
 be 1, and the weights of all other symbols be less than \(\omega \). Let the precedence > be total and
be 1, and the weights of all other symbols be less than \(\omega \). Let the precedence > be total and
 be the symbols of lowest precedence, with
be the symbols of lowest precedence, with
 . Then let \(t \succ s\) if
. Then let \(t \succ s\) if
 and \(t \succsim s\) if
and \(t \succsim s\) if
 .
.
Selection Functions. The calculus is also parameterized by a literal selection function and a Boolean subterm selection function. We define an element x of a multiset M to be \(\unrhd \)-maximal for some relation \(\unrhd \) if for all \(y \in M\) with \(y \unrhd x\), we have \(y = x\). It is strictly \(\unrhd \)-maximal if it is \(\unrhd \)-maximal and occurs only once in M.
The literal selection function \( HLitSel \) maps each clause to a subset of selected literals. A literal may not be selected if it is positive and neither side is
 . Moreover, a literal
. Moreover, a literal
 may not be selected if \(y\>\bar{u}_n\), with \(n \ge 1\), is a \(\succeq \)-maximal term of the clause.
may not be selected if \(y\>\bar{u}_n\), with \(n \ge 1\), is a \(\succeq \)-maximal term of the clause.
The Boolean subterm selection function \( HBoolSel \) maps each clause C to a subset of selected subterms in C. Selected subterms must be green subterms of Boolean type. Moreover, a subterm s must not be selected if
 , if
, if
 , if s is a variable-headed term, if s is at the topmost position on either side of a positive literal, or if s contains a variable y as a green subterm, and
, if s is a variable-headed term, if s is at the topmost position on either side of a positive literal, or if s contains a variable y as a green subterm, and
 , with \(n \ge 1\), is a \(\succeq \)-maximal term of the clause.
, with \(n \ge 1\), is a \(\succeq \)-maximal term of the clause.
Eligibility. A literal L is (strictly) eligible w.r.t. a substitution \(\sigma \) in C if it is selected in C or there are no selected literals and no selected Boolean subterms in C and \(L\sigma \) is (strictly) \(\succsim \)-maximal in \(C\sigma .\)
The eligible subterms of a clause C w.r.t. a substitution \(\sigma \) are inductively defined as follows: Any selected subterm is eligible. If a literal
 with
with
 is either eligible and negative or strictly eligible and positive, then the subterm s is eligible. If a subterm t is eligible and the head of t is not
is either eligible and negative or strictly eligible and positive, then the subterm s is eligible. If a subterm t is eligible and the head of t is not
 or
or
 , all direct green subterms of t are eligible. If a subterm t is eligible and t is of the form
, all direct green subterms of t are eligible. If a subterm t is eligible and t is of the form
 or
or
 , then u is eligible if
, then u is eligible if
 and v is eligible if
and v is eligible if
 .
.
The Core Inference Rules. The calculus consists of the following core inference rules. The first five rules stem from \(\lambda \)Sup, with minor adaptions concerning Booleans:

-
Sup1. u is not fluid; 2. u is not a variable deeply occurring in C; 3. if u is a variable y, there must exist a grounding substitution \(\theta \) such that
 and \(C\sigma \theta \prec C''\sigma \theta \), where \(C'' = C\{y\mapsto t'\}\); 4. \(\sigma \in {{\,\mathrm{CSU}\,}}(t,u)\); 5. \(t\sigma \not \precsim t'\sigma \); 6. u is eligible in C w.r.t. \(\sigma \); 7. \(C\sigma \not \precsim D\sigma \); 8. \(t \approx t'\) is strictly eligible in D w.r.t. \(\sigma \); 9. \(t\sigma \) is not a fully applied logical symbol; 10. if
and \(C\sigma \theta \prec C''\sigma \theta \), where \(C'' = C\{y\mapsto t'\}\); 4. \(\sigma \in {{\,\mathrm{CSU}\,}}(t,u)\); 5. \(t\sigma \not \precsim t'\sigma \); 6. u is eligible in C w.r.t. \(\sigma \); 7. \(C\sigma \not \precsim D\sigma \); 8. \(t \approx t'\) is strictly eligible in D w.r.t. \(\sigma \); 9. \(t\sigma \) is not a fully applied logical symbol; 10. if
 , the subterm u is at the top level of a positive literal.
, the subterm u is at the top level of a positive literal. -
ERes1. \(\sigma \in {{\,\mathrm{CSU}\,}}(u,u')\); 2. \(u \not \approx u'\) is eligible in C w.r.t. \(\sigma \).
-
EFact1. \(\sigma \in {{\,\mathrm{CSU}\,}}(u,u')\); 2. \(u\sigma \not \precsim v\sigma \); 3. \((u \approx v)\sigma \) is \(\succsim \)-maximal in \(C\sigma \); 4. \(u\sigma \not \precsim v\sigma \); 5. nothing is selected in C.
-
FluidSup1. u is a variable deeply occurring in C or u is fluid; 2. z is a fresh variable; 3.
 ; 4. \((z\>t')\sigma \not = (z\>t)\sigma \); 5.–10. as for Sup.
; 4. \((z\>t')\sigma \not = (z\>t)\sigma \); 5.–10. as for Sup. -
ArgCong1. \(n > 0\); 2. \(\sigma \) is the most general type substitution that ensures well-typedness of the conclusion for a given n; 3. \(\bar{x}_n\) is a tuple of distinct fresh variables; 4. the literal \(s \approx s'\) is strictly eligible in C w.r.t. \(\sigma \).
The following rules are concerned with Boolean reasoning and originate from
 . They have been adapted to support polymorphism and applied variables.
. They have been adapted to support polymorphism and applied variables.

-
BoolHoist] 1. \(\sigma \) is a type unifier of the type of u with the Boolean type
 (i.e., the identity if u is Boolean or
(i.e., the identity if u is Boolean or
 if u is of type \(\alpha \) for some type variable \(\alpha \)); 2. the head of u is neither a variable nor a logical symbol; 3. u is eligible in C; 4. the occurrence of u is not at the top level of a positive literal.
if u is of type \(\alpha \) for some type variable \(\alpha \)); 2. the head of u is neither a variable nor a logical symbol; 3. u is eligible in C; 4. the occurrence of u is not at the top level of a positive literal. -
EqHoist, NeqHoist, ForallHoist, ExistsHoist 1.
 ,
,
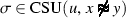 ,
,
 , or
, or
 , respectively; 2. x, y, and \(\alpha \) are fresh variables; 3. u is eligible in C w.r.t. \(\sigma \); 4. if the head of u is a variable, it must be applied and the affected literal must be of the form
, respectively; 2. x, y, and \(\alpha \) are fresh variables; 3. u is eligible in C w.r.t. \(\sigma \); 4. if the head of u is a variable, it must be applied and the affected literal must be of the form
 ,
,
 , or
, or
 where v is a variable-headed term.
where v is a variable-headed term. -
FalseElim1.
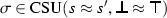 ; 2.
; 2.
 is strictly eligible in C w.r.t. \(\sigma \).
is strictly eligible in C w.r.t. \(\sigma \). -
BoolRw 1. \(\sigma \in {{\,\mathrm{CSU}\,}}(t,u)\) and \((t, t')\) is one of the following pairs, where y is a fresh variable:
 ,
,
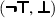 ,
,
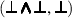 ,
,
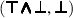 ,
,
 ,
,
 ,
,
 ,
,
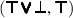 ,
,
 ,
,
 ,
,
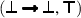 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ; 2. u is not a variable; 3. u is eligible in C w.r.t. \(\sigma \); 4. if the head of u is a variable, it must be applied and the affected literal must be of the form
; 2. u is not a variable; 3. u is eligible in C w.r.t. \(\sigma \); 4. if the head of u is a variable, it must be applied and the affected literal must be of the form
 ,
,
 , or \(u \approx v\) where v is a variable-headed term.
, or \(u \approx v\) where v is a variable-headed term. -
ForallRw, ExistsRw 1.
 and
and
 , respectively, where \(\beta \) is a fresh type variable, y is a fresh term variable, \(\bar{\alpha }\) are the free type variables and \(\bar{x}\) are the free term variables occurring in \(y\sigma \) in order of first occurrence; 2. u is not a variable; 3. u is eligible in C w.r.t. \(\sigma \); 4. if the head of u is a variable, it must be applied and the affected literal must be of the form
, respectively, where \(\beta \) is a fresh type variable, y is a fresh term variable, \(\bar{\alpha }\) are the free type variables and \(\bar{x}\) are the free term variables occurring in \(y\sigma \) in order of first occurrence; 2. u is not a variable; 3. u is eligible in C w.r.t. \(\sigma \); 4. if the head of u is a variable, it must be applied and the affected literal must be of the form
 , or \(u \approx v\) where v is a variable-headed term; 5. for ForallRw, the indicated occurrence of u is not in a literal
, or \(u \approx v\) where v is a variable-headed term; 5. for ForallRw, the indicated occurrence of u is not in a literal
 , and for ExistsRw, the indicated occurrence of u is not in a literal
, and for ExistsRw, the indicated occurrence of u is not in a literal
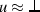 .
.
Like Sup, also the Boolean rules must be simulated in fluid terms. The following rules are Boolean counterparts of FluidSup:

-
FluidBoolHoist1. u is fluid; 2. z and x are fresh variables; 3. \(\sigma \in {{\,\mathrm{CSU}\,}}(z\>x{,}\;u)\); 4.
 ; 5.
; 5.
 and
and
 ; 6. u is eligible in C w.r.t. \(\sigma \).
; 6. u is eligible in C w.r.t. \(\sigma \). -
FluidLoobHoistLike the above but with
 replaced by
replaced by
 in condition 4.
in condition 4.
In addition to the inference rules, our calculus relies on two axioms, below. Axiom (Ext), from \(\lambda \)Sup, embodies functional extensionality; the expression
 abbreviates
abbreviates
 . Axiom (Choice) characterizes the Hilbert choice operator \(\varepsilon \).
. Axiom (Choice) characterizes the Hilbert choice operator \(\varepsilon \).

Rationale for the Rules. Most of the calculus’s rules are adapted from its precursors. Sup, ERes, and EFact are already present in Sup, with slightly different side conditions. Notably, as in \(\lambda \)fSup and \(\lambda \)Sup, Sup inferences are required only into green contexts. Other subterms are accessed indirectly via ArgCong and (Ext).
The rules BoolHoist, EqHoist, NeqHoist, ForallHoist, ExistsHoist, FalseElim, BoolRw, ForallRw, and ExistsRw, concerned with Boolean reasoning, stem from
 , which was inspired by
, which was inspired by
 . Except for BoolHoist and FalseElim, these rules have a condition stating that “if the head of u is a variable, it must be applied and the affected literal must be of the form
. Except for BoolHoist and FalseElim, these rules have a condition stating that “if the head of u is a variable, it must be applied and the affected literal must be of the form
 ,
,
 , or
, or
 where v is a variable-headed term.” The inferences at variable-headed terms permitted by this condition are our form of primitive substitution [1, 18], a mechanism that blindly substitutes logical connectives and quantifiers for variables z with a Boolean result type.
where v is a variable-headed term.” The inferences at variable-headed terms permitted by this condition are our form of primitive substitution [1, 18], a mechanism that blindly substitutes logical connectives and quantifiers for variables z with a Boolean result type.
Example 1
Our calculus can prove that Leibniz equality implies equality (i.e., if two values behave the same for all predicates, they are equal) as follows:

The EqHoist inference, applied on
 , illustrates how our calculus introduces logical symbols without a dedicated primitive substitution rule. Although
, illustrates how our calculus introduces logical symbols without a dedicated primitive substitution rule. Although
 does not appear in the premise, we still need to apply EqHoist on
does not appear in the premise, we still need to apply EqHoist on
 with
with
 . Other calculi [1, 9, 18, 26] would apply an explicit primitive substitution rule instead, yielding essentially
. Other calculi [1, 9, 18, 26] would apply an explicit primitive substitution rule instead, yielding essentially
 . However, in our approach this clause is subsumed and could be discarded immediately. By hoisting the equality to the clausal level, we bypass the redundancy criterion.
. However, in our approach this clause is subsumed and could be discarded immediately. By hoisting the equality to the clausal level, we bypass the redundancy criterion.
Next, BoolRw can be applied to
 with
with
 . The two FalseElim steps remove the
. The two FalseElim steps remove the
 literals. Then Sup is applicable with the unifier
literals. Then Sup is applicable with the unifier
 , and ERes derives the contradiction.
, and ERes derives the contradiction.
Like in \(\lambda \)Sup, the FluidSup rule is responsible for simulating superposition inferences below applied variables, other fluid terms, and deeply occurring variables. Complementarily, FluidBoolHoist and FluidLoobHoist simulate the various Boolean inference rules below fluid terms. Initially, we considered adding a fluid version of each rule that operates on Boolean subterms, but we discovered that FluidBoolHoist and FluidLoobHoist suffice to achieve refutational completeness.
Example 2
The clause set consisting of
 and
and
 highlights the need for FluidBoolHoist and its companion. The set is unsatisfiable because the instantiation
highlights the need for FluidBoolHoist and its companion. The set is unsatisfiable because the instantiation
 produces the clause
produces the clause
 , which is unsatisfiable in conjunction with
, which is unsatisfiable in conjunction with
 .
.
The literal selection function can select either literal in the first clause. ERes is applicable in either case, but the unifiers
 and
and
 do not lead to a contradiction. Instead, we need to apply FluidBoolHoist if the first literal is selected or FluidLoobHoist if the second literal is selected. In the first case, the derivation is as follows:
do not lead to a contradiction. Instead, we need to apply FluidBoolHoist if the first literal is selected or FluidLoobHoist if the second literal is selected. In the first case, the derivation is as follows:

The FluidBoolHoist inference uses the unifier
 . We apply ERes to the first literal of the resulting clause, with unifier
. We apply ERes to the first literal of the resulting clause, with unifier
 . Next, we apply EqHoist with the unifier
. Next, we apply EqHoist with the unifier
 to the literal created by FluidBoolHoist, effectively performing a primitive substitution. The resulting clause can superpose into
to the literal created by FluidBoolHoist, effectively performing a primitive substitution. The resulting clause can superpose into
 with the unifier
with the unifier
 . The two sides of the interpreted equality in the first literal can then be unified, allowing us to apply BoolRw with the unifier
. The two sides of the interpreted equality in the first literal can then be unified, allowing us to apply BoolRw with the unifier
 . Finally, applying ERes twice and FalseElim once yields the empty clause.
. Finally, applying ERes twice and FalseElim once yields the empty clause.
Remarkably, none of the provers that participated in the CASC-J10 competition can solve this two-clause problem within a minute. Satallax finds a proof after 72 s and LEO-II after over 7 minutes. Our new Zipperposition implementation solves it in 3 s.
The Redundancy Criterion. In first-order superposition, a clause is considered redundant if all its ground instances are entailed by \(\prec \)-smaller ground instances of other clauses. In essence, this will also be our definition, but we will use a different notion of ground instances and a different notion of entailment.
Given a clause C, let its ground instances
 be the set of all clauses of the form \(C\theta \) for some substitution \(\theta \) such that \(C\theta \) is ground and
be the set of all clauses of the form \(C\theta \) for some substitution \(\theta \) such that \(C\theta \) is ground and
 -normal, and for all variables x occurring in C, the only Boolean green subterms of \(x\theta \) are
-normal, and for all variables x occurring in C, the only Boolean green subterms of \(x\theta \) are
 and
and
 . The rationale of this definition is to ensure that ground instances of the conclusion of ForallHoist, ExistsHoist, ForallRw, and ExistsRw inferences are smaller than the corresponding instances of their premise by property (O4).
. The rationale of this definition is to ensure that ground instances of the conclusion of ForallHoist, ExistsHoist, ForallRw, and ExistsRw inferences are smaller than the corresponding instances of their premise by property (O4).
The redundancy criterion’s notion of entailment is defined via an encoding into a weaker logic, following \(\lambda \)fSup and \(\lambda \)Sup. In this paper, the weaker logic is ground first-order logic with interpreted Booleans—the ground fragment of the logic of
 . Its signature \((\mathrm {\Sigma }_\mathsf {ty},\mathrm {\Sigma }_{\mathrm {GF}})\) is derived from our higher-order signature \((\mathrm {\Sigma }_\mathsf {ty},\mathrm {\Sigma })\) as follows. The type constructors \(\mathrm {\Sigma }_\mathsf {ty}\) are the same in both signatures, but \({\rightarrow }\) is an uninterpreted type constructor in first-order logic. For each ground instance
. Its signature \((\mathrm {\Sigma }_\mathsf {ty},\mathrm {\Sigma }_{\mathrm {GF}})\) is derived from our higher-order signature \((\mathrm {\Sigma }_\mathsf {ty},\mathrm {\Sigma })\) as follows. The type constructors \(\mathrm {\Sigma }_\mathsf {ty}\) are the same in both signatures, but \({\rightarrow }\) is an uninterpreted type constructor in first-order logic. For each ground instance
 , we introduce a first-order symbol
, we introduce a first-order symbol
 with argument types \(\bar{\tau }_{\!j}\) and result type \(\tau _{\!j+1} \rightarrow \cdots \rightarrow \tau _n \rightarrow \tau \), for each j. Moreover, for each ground term \(\lambda x.\>t\), we introduce a symbol
with argument types \(\bar{\tau }_{\!j}\) and result type \(\tau _{\!j+1} \rightarrow \cdots \rightarrow \tau _n \rightarrow \tau \), for each j. Moreover, for each ground term \(\lambda x.\>t\), we introduce a symbol
 of the same type. The symbols
of the same type. The symbols
 , and
, and
 are identified with the corresponding first-order logical symbols.
are identified with the corresponding first-order logical symbols.
We define an encoding
 of
of
 -normal ground higher-order terms into this ground first-order logic recursively as follows:
-normal ground higher-order terms into this ground first-order logic recursively as follows:
 and
and
 for applied quantifiers;
for applied quantifiers;
 for \(\lambda \)-expressions; and
for \(\lambda \)-expressions; and
 for other terms. For quantified variables, we define
for other terms. For quantified variables, we define
 . Here,
. Here,
 -normality is crucial to ensure that bound variables do not occur applied or within \(\lambda \)-expressions. The definition of green subterms is devised such that green subterms correspond to first-order subterms via the encoding
-normality is crucial to ensure that bound variables do not occur applied or within \(\lambda \)-expressions. The definition of green subterms is devised such that green subterms correspond to first-order subterms via the encoding
 , with the exception of first-order subterms below quantifiers. The encoding
, with the exception of first-order subterms below quantifiers. The encoding
 is extended to clauses by mapping each literal and each side of a literal individually. From the entailment relation \(\models \) for the ground first-order logic, we derive an entailment relation
is extended to clauses by mapping each literal and each side of a literal individually. From the entailment relation \(\models \) for the ground first-order logic, we derive an entailment relation
 on
on
 -normal ground higher-order clauses by defining
-normal ground higher-order clauses by defining
 if
if
 . This relation is weaker than standard higher-order entailment; for example,
. This relation is weaker than standard higher-order entailment; for example,
 (because of the subscripts added by
(because of the subscripts added by
 ) and
) and
 (because of the \({\mathsf {lam}}\) symbols used by
(because of the \({\mathsf {lam}}\) symbols used by
 ).
).
Using
 , we define a clause C to be redundant w.r.t. a clause set N if for every
, we define a clause C to be redundant w.r.t. a clause set N if for every
 , we have
, we have
 or there exists a clause \(C' \in N\) such that \(C \sqsupset C'\) and
or there exists a clause \(C' \in N\) such that \(C \sqsupset C'\) and
 . The tiebreaker \(\sqsupset \) can be an arbitrary well-founded partial order on clauses; in practice, we use a well-founded restriction of the ill-founded strict subsumption relation [6, Sect. 3.4]. We denote the set of redundant clauses w.r.t. a clause set N by \({ Red _{\mathrm {C}}}(N)\). Note that
. The tiebreaker \(\sqsupset \) can be an arbitrary well-founded partial order on clauses; in practice, we use a well-founded restriction of the ill-founded strict subsumption relation [6, Sect. 3.4]. We denote the set of redundant clauses w.r.t. a clause set N by \({ Red _{\mathrm {C}}}(N)\). Note that
 is weak enough to ensure that the ArgCong inference rule and axiom (Ext) are not immediately redundant and can fulfill their purpose.
is weak enough to ensure that the ArgCong inference rule and axiom (Ext) are not immediately redundant and can fulfill their purpose.
For first-order superposition, an inference is considered redundant if for each of its ground instances, a premise is redundant or the conclusion is entailed by clauses smaller than the main premise. For most inference rules, our definition follows this idea, using
 for entailment; other rules need nonstandard notions of ground instances and redundancy. The definition of inference redundancy presented below is simpler than the more sophisticated notion in our technical report. Nonetheless, the redundant inferences below are a strict subset of the redundant inferences of our report and thus completeness also holds using the notion below. For the few prover optimizations based on inference redundancy that we know about (e.g., simultaneous superposition [4]), the following criterion suffices.
for entailment; other rules need nonstandard notions of ground instances and redundancy. The definition of inference redundancy presented below is simpler than the more sophisticated notion in our technical report. Nonetheless, the redundant inferences below are a strict subset of the redundant inferences of our report and thus completeness also holds using the notion below. For the few prover optimizations based on inference redundancy that we know about (e.g., simultaneous superposition [4]), the following criterion suffices.
For Sup, ERes, EFact, BoolHoist, FalseElim, EqHoist, NeqHoist, and BoolRw, we define ground instances as usual: Ground instances are all inferences obtained by applying a grounding substitution to premises and conclusion such that the result adheres to the conditions of the given rule w.r.t. selection functions that select literals and subterms as in the original premise. For FluidSup and FluidBoolHoist, we define ground instances in the same way except that we require that ground instances adhere to the conditions of Sup or BoolHoist, respectively. For ForallRw, ExistsRw, ForallHoist, ExistsHoist, which do not have ground instances in the sense above, we define a ground instance as any inference that is obtained by applying the unifier \(\sigma \) to the premise and then applying a grounding substitution to premise and conclusion, regardless of whether the resulting inference is an inference of our calculus.
For all rules except FluidLoobHoist and ArgCong, we define an inference to be redundant w.r.t. a clause set N if for each ground instance \(\iota \), a premise of
 is redundant w.r.t.
is redundant w.r.t.
 or the conclusion of
or the conclusion of
 is entailed w.r.t.
is entailed w.r.t.
 by clauses from
by clauses from
 that are smaller than the main (i.e., rightmost) premise of \(\iota \). For the rules FluidLoobHoist and ArgCong, as well as axioms (Ext) and (Choice)—viewed as premiseless inferences—we define an inference to be redundant w.r.t. a clause set N if all ground instances of its conclusion are contained in
that are smaller than the main (i.e., rightmost) premise of \(\iota \). For the rules FluidLoobHoist and ArgCong, as well as axioms (Ext) and (Choice)—viewed as premiseless inferences—we define an inference to be redundant w.r.t. a clause set N if all ground instances of its conclusion are contained in
 or redundant w.r.t.
or redundant w.r.t.
 . We denote the set of redundant inferences w.r.t. N by \({ Red _{\mathrm {I}}}(N)\).
. We denote the set of redundant inferences w.r.t. N by \({ Red _{\mathrm {I}}}(N)\).
Simplification Rules. Our redundancy criterion is strong enough to support counterparts of most simplification rules implemented in Schulz’s first-order E [25, Sect. 2.3.1 and 2.3.2]. Deletion of duplicated literals, deletion of resolved literals, syntactic tautology deletion, negative simplify-reflect, and clause subsumption adhere to our redundancy criterion. Positive simplify-reflect, equality subsumption, and rewriting (demodulation) of positive and negative literals are supported if they are applied on green subterms or on other subterms that are encoded into first-order subterms by
 and
and
 . Semantic tautology deletion can be applied as well, using
. Semantic tautology deletion can be applied as well, using
 ; moreover, for positive literals, the rewriting clause must be smaller than the rewritten clause.
; moreover, for positive literals, the rewriting clause must be smaller than the rewritten clause.
Under some circumstances, inference rules can be applied as simplifications. The FalseElim and BoolRw rules can be applied as a simplification if \(\sigma \) is the identity. If the head of u is
 , ForallHoist and ForallRw can both be applied and, together, serve as one simplification rule. The same holds for ExistsHoist and ExistsRw if the head of u is
, ForallHoist and ForallRw can both be applied and, together, serve as one simplification rule. The same holds for ExistsHoist and ExistsRw if the head of u is
 . For all of these rules, the eligibility conditions can be ignored.
. For all of these rules, the eligibility conditions can be ignored.
Clausification. Like
 , our calculus does not require the input problem to be clausified during the preprocessing, and it supports higher-order analogues of the three inprocessing clausification methods introduced by Nummelin et al. Inner delayed clausification relies on our core calculus rules to destruct logical symbols. Outer delayed clausification adds the following clausification rules to the calculus:
, our calculus does not require the input problem to be clausified during the preprocessing, and it supports higher-order analogues of the three inprocessing clausification methods introduced by Nummelin et al. Inner delayed clausification relies on our core calculus rules to destruct logical symbols. Outer delayed clausification adds the following clausification rules to the calculus:

The double bars identify simplification rules (i.e., the conclusions make the premise redundant and can replace it). The first two rules require that s has a logical symbol as its head, whereas the last two require that s and t are Boolean terms other than
 and
and
 . The function \(oc\) distributes the logical symbols over the clause C—e.g.,
. The function \(oc\) distributes the logical symbols over the clause C—e.g.,
 , and
, and
 . It is easy to check that our redundancy criterion allows us to replace the premise of the OuterClaus rules with their conclusion. Nonetheless, we apply EqOuterClaus and NeqOuterClaus as inferences because the premises might be useful in their original form.
. It is easy to check that our redundancy criterion allows us to replace the premise of the OuterClaus rules with their conclusion. Nonetheless, we apply EqOuterClaus and NeqOuterClaus as inferences because the premises might be useful in their original form.
Besides the two delayed clausification methods, a third inprocessing clausification method is immediate clausification. This clausifies the input problem’s outer Boolean structure in one swoop, resulting in a set of higher-order clauses. If unclausified Boolean terms rise to the top during saturation, the same algorithm is run to clausify them.
Unlike delayed clausification, immediate clausification is a black box and is unaware of the proof state other than the Boolean term it is applied to. Delayed clausification, on the other hand, clausifies the term step by step, allowing us to interleave clausification with the strong simplification machinery of superposition provers. It is especially powerful in higher-order contexts: Examples such as
 can be refuted directly by equality resolution, rather than via more explosive rules on the clausified form.
can be refuted directly by equality resolution, rather than via more explosive rules on the clausified form.
4 Refutational Completeness
Our calculus is dynamically refutationally complete for problems in
 -normal form. The full proof can be found in our technical report [8].
-normal form. The full proof can be found in our technical report [8].
Theorem 3
(Dynamic refutational completeness). Let \((N_i)_i\) be a derivation—i.e., \(N_i \setminus N_{i+1} \subseteq { Red _{\mathrm {C}}}(N_{i+1})\) for all i. Let \(N_0\) be
 -normal and such that \(N_0 \models \bot \). Moreover, assume that \((N_i)_i\) is fair—i.e., all inferences from clauses in the limit inferior \(\bigcup _i \bigcap _{\!j \ge i} N_{\!j}\) are contained in \(\bigcup _i { Red _{\mathrm {I}}}(N_i)\). Then we have \(\bot \in N_i\) for some i.
-normal and such that \(N_0 \models \bot \). Moreover, assume that \((N_i)_i\) is fair—i.e., all inferences from clauses in the limit inferior \(\bigcup _i \bigcap _{\!j \ge i} N_{\!j}\) are contained in \(\bigcup _i { Red _{\mathrm {I}}}(N_i)\). Then we have \(\bot \in N_i\) for some i.
Following the completeness proof of \(\lambda \)Sup, our proof is structured in three levels of logics. For each, we define a calculus and show that it is refutationally complete: ground monomorphic first-order logic with an interpreted Boolean type (\({\mathrm {GF}}\)); the
 -normal ground fragment of higher-order logic (\({\mathrm {GH}}\)); and higher-order logic (\({\mathrm {H}}\)).
-normal ground fragment of higher-order logic (\({\mathrm {GH}}\)); and higher-order logic (\({\mathrm {H}}\)).
The logic of the \({\mathrm {GF}}\) level is the ground fragment of
 ’s logic. The \({\mathrm {GF}}\) calculus is a ground version of
’s logic. The \({\mathrm {GF}}\) calculus is a ground version of
 , which Nummelin et al. showed refutationally complete. It consists of ground first-order equivalents of our rules, excluding ArgCong, FluidBoolHoist, and FluidLoobHoist, which are specific to higher-order logic. The counterparts to ForallHoist and ExistsHoist enumerate ground terms instead of producing free variables, to stay within the ground fragment. For compatibility with the nonground level, the conclusions of ForallRw and ExistsRw cannot contain concrete Skolem functions. Instead, the \({\mathrm {GF}}\) calculus is parameterized by a witness function that can assign an arbitrary term to each occurrence of a quantifier in a clause. This witness function is used to retrieve the Skolem terms in the \({\mathrm {GF}}\) equivalents of \(\textsc {ForallRw}\) and \(\textsc {ExistsRw}\).
, which Nummelin et al. showed refutationally complete. It consists of ground first-order equivalents of our rules, excluding ArgCong, FluidBoolHoist, and FluidLoobHoist, which are specific to higher-order logic. The counterparts to ForallHoist and ExistsHoist enumerate ground terms instead of producing free variables, to stay within the ground fragment. For compatibility with the nonground level, the conclusions of ForallRw and ExistsRw cannot contain concrete Skolem functions. Instead, the \({\mathrm {GF}}\) calculus is parameterized by a witness function that can assign an arbitrary term to each occurrence of a quantifier in a clause. This witness function is used to retrieve the Skolem terms in the \({\mathrm {GF}}\) equivalents of \(\textsc {ForallRw}\) and \(\textsc {ExistsRw}\).
On the next level, the \({\mathrm {GH}}\) calculus includes inference rules isomorphic to the \({\mathrm {GF}}\) rules, transferred to higher-order logic via
 . Moreover, it contains an ArgCong variant that enumerates ground terms instead of introducing fresh variables, as well as rules enumerating ground instances of axioms (Ext) and (Choice). We prove refutational completeness of the \({\mathrm {GH}}\) calculus by constructing a higher-order interpretation based on the model constructed for the completeness proof of the \({\mathrm {GF}}\) level. This proof step is analogous to the corresponding step in \(\lambda \)Sup’s proof, but we must also consider
. Moreover, it contains an ArgCong variant that enumerates ground terms instead of introducing fresh variables, as well as rules enumerating ground instances of axioms (Ext) and (Choice). We prove refutational completeness of the \({\mathrm {GH}}\) calculus by constructing a higher-order interpretation based on the model constructed for the completeness proof of the \({\mathrm {GF}}\) level. This proof step is analogous to the corresponding step in \(\lambda \)Sup’s proof, but we must also consider
 -normality and the logical symbols.
-normality and the logical symbols.
To lift completeness to the \({\mathrm {H}}\) level, we use the saturation framework of Waldmann et al. [31]. The main proof obligation it leaves us to show is that nonredundant \({\mathrm {GH}}\) inferences can be lifted to corresponding nonground \({\mathrm {H}}\) inferences. For this lifting, we must choose a suitable \({\mathrm {GH}}\) witness function and appropriate \({\mathrm {GH}}\) selection functions for literals and Boolean subterms, given a saturated clause set at the \({\mathrm {H}}\) level and the \({\mathrm {H}}\) selection functions. Then the saturation framework guarantees static refutational completeness w.r.t. Herbrand entailment, which is the entailment relation induced by the grounding function
 . We then show that this implies dynamic refutational completeness w.r.t. \(\models \) for
. We then show that this implies dynamic refutational completeness w.r.t. \(\models \) for
 -normal initial clause sets.
-normal initial clause sets.
5 Implementation
We implemented our calculus in the Zipperposition prover [14] , whose OCaml source code makes it convenient to prototype calculus extensions. Except for the presence of axioms (Ext) and (Choice), the new code gracefully extends Zipperposition’s implementation of
 in the sense that
in the sense that
 coincides with
coincides with
 on first-order problems. The same cannot be said w.r.t. \(\lambda \)Sup on Boolean-free problems because of the FluidBoolHoist and FluidLoobHoist rules, which are triggered by any applied variable. From the implementation of \(\lambda \)Sup, we inherit the given clause procedure, which supports infinitely branching inferences, as well as calculus extensions and heuristics [28]. From the implementation of
on first-order problems. The same cannot be said w.r.t. \(\lambda \)Sup on Boolean-free problems because of the FluidBoolHoist and FluidLoobHoist rules, which are triggered by any applied variable. From the implementation of \(\lambda \)Sup, we inherit the given clause procedure, which supports infinitely branching inferences, as well as calculus extensions and heuristics [28]. From the implementation of
 , we inherit the simplification rule BoolSimp, a mainstay of our Boolean simplification machinery.
, we inherit the simplification rule BoolSimp, a mainstay of our Boolean simplification machinery.
As in the implementation of \(\lambda \)Sup, we approximate fluid terms as terms that are either nonground \(\lambda \)-expressions or terms of the form \(x\, \bar{s}_n\) with \(n>0\). Two slight, accidental discrepancies are that we also count variable occurrences below quantifiers as deep and perform EFact inferences even if the maximal literal is selected. Since we expect FluidBoolHoist and FluidLoobHoist to be highly explosive, we penalize them and all of their offspring. In addition to various \(\lambda \)Sup extensions [6, Sect. 5], we also use all the rules for Boolean reasoning described by Vukmirović and Nummelin [30] except for the BoolEF rules.
6 Evaluation
We evaluate the calculus implementation in Zipperposition and compare it with other higher-order provers. Our experiments were performed on StarExec Miami servers equipped with Intel Xeon E5-2620 v4 CPUs clocked at 2.10 GHz. We used all 2606 TH0 theorems from the TPTP 7.3.0 library [27] and 1253 “Judgment Day” problems [12] generated using Sledgehammer (SH) [24] as our benchmark set. An archive containing the benchmarks and the raw evaluation results is publicly available [5].
Calculus Evaluation. In this first part, we evaluate selected parameters of Zipperposition by varying only the studied parameter in a fixed well-performing configuration. This base configuration disables axioms (Choice) and (Ext) and the Fluid- rules. It uses the unification procedure of Vukmirović et al. [29] in its complete variant—i.e., the variant that produces a complete set of unifiers. It uses none of the early Boolean rules described by Vukmirović and Nummelin [30]. The preprocessor
 is disabled as well. All of the completeness-preserving simplification rules listed in Sect. 3 are enabled. The configuration uses immediate clausification. We set the CPU time limit to 30 s in all three experiments.
is disabled as well. All of the completeness-preserving simplification rules listed in Sect. 3 are enabled. The configuration uses immediate clausification. We set the CPU time limit to 30 s in all three experiments.
In the first experiment, we assess the overhead incurred by the Fluid- rules. These rules unify with a term whose head is a fresh variable. Thus, we expected that they needed to be tightly controlled to achieve good performance. To test our hypothesis, we simultaneously modified the parameters of these three rules. In Figure 1, the off mode simply disables the rules, the pragmatic mode uses a terminating incomplete unification algorithm (the pragmatic variant of Vukmirović et al. [29]), and the complete mode uses a complete unification algorithm. The results show that disabling Fluid- rules altogether achieves the best performance. However, on TPTP problems, complete finds 35 proofs not found by off, and pragmatic finds 22 proofs not found by off. On Sledgehammer benchmarks, this effect is much weaker, likely because the Sledgehammer benchmarks require less higher-order reasoning: complete finds only one new proof over off, and pragmatic finds only four.
In the second experiment, we explore the clausification methods introduced at the end of Sect. 3: inner delayed clausification, outer delayed clausification, and immediate clausification. The modes inner and outer employ
 ’s Rename rule, which renames Boolean terms headed by logical symbols using a Tseitin-like transformation if they occur at least four times in the proof state. Vukmirović and Nummelin [30] observed that outer clausification can greatly help prove higher-order problems, and we expected it to perform well for our calculus, too. The results are shown in Figure 2. The results confirm our hypothesis: The outer mode outperforms immediate on both TPTP and Sledgehammer benchmarks. The inner mode performs worst, but on Sledgehammer benchmarks, it proves 17 problems beyond the reach of the other two. Interestingly, several of these problems contain axioms of the form
’s Rename rule, which renames Boolean terms headed by logical symbols using a Tseitin-like transformation if they occur at least four times in the proof state. Vukmirović and Nummelin [30] observed that outer clausification can greatly help prove higher-order problems, and we expected it to perform well for our calculus, too. The results are shown in Figure 2. The results confirm our hypothesis: The outer mode outperforms immediate on both TPTP and Sledgehammer benchmarks. The inner mode performs worst, but on Sledgehammer benchmarks, it proves 17 problems beyond the reach of the other two. Interestingly, several of these problems contain axioms of the form
 , and applying superposition and demodulation to these axioms is preferable to clausifying them.
, and applying superposition and demodulation to these axioms is preferable to clausifying them.
In the third experiment, we investigate the effect of axiom (Choice), which is necessary to achieve refutational completeness. To evaluate (Choice), we either disabled it in a configuration labeled off or set the axiom’s penalty p to different values. In Zipperposition, penalties are propagated through inference and simplification rules and are used to increase the heuristic weight of clauses, postponing the selection of penalized clauses. The results are shown in Figure 3. As expected, disabling (Choice), or at least penalizing it heavily, improves performance. Yet enabling (Choice) can be crucial: For 19 TPTP problems, the proofs are found when (Choice) is enabled and \(p=4\), but not when the rule is disabled. On Sledgehammer problems, this effect is weaker, with only two new problems proved for \(p=4\).
Prover Comparison. In this second part, we compare Zipperposition’s performance with other higher-order provers. Like at CASC-J10, the wall-clock time limit was 120 s, the CPU time limit was 960 s, and the provers were run on StarExec Miami. We used the following versions of all systems that took part in the THF division: CVC4 1.8[3], Leo-III 1.5.2[26], Satallax 3.5[13], and Vampire 4.5 [11]. The developers of Vampire have informed us that its higher-order schedule is optimized for running on a single core. As a result, the prover suffers some degradation of performance when running on multiple cores. We evaluate both the version of Zipperposition that took part in CASC-J10 (Zip) and the updated version of Zipperposition that supports our new calculus (New Zip). Zip’s portfolio of prover configurations is based on \(\lambda \)Sup and techniques described by Vukmirović and Nummelin [30]. New Zip’s portfolio is specially designed for our new calculus and optimized for TPTP problems. To assess the performance of Boolean reasoning, we used Sledgehammer benchmarks generated both with native Booleans (SH) and with an encoding into Boolean-free higher-order logic (
 ). For technical reasons, the encoding also performs \(\lambda \)-lifting, but this minor transformation should have little impact on results [6, Sect. 7].
). For technical reasons, the encoding also performs \(\lambda \)-lifting, but this minor transformation should have little impact on results [6, Sect. 7].
The results are shown in Figure 4. The two versions of Zipperposition are ahead of all other provers on both benchmark sets. This shows that, with thorough parameter tuning, higher-order superposition outperforms tableaux, which had been the state of the art in higher-order reasoning for a decade. The updated version of New Zip beats Zip on TPTP problems but lags behind Zip on Sledgehammer benchmarks as we have yet to further explore more general heuristics that work well with our new calculus. The Sledgehammer benchmarks fail to demonstrate the superiority of native Booleans reasoning compared with an encoding, and in fact CVC4 and Leo-III perform dramatically better on the encoded Boolean problems, suggesting that there is room for tuning.
7 Conclusion
We have created a superposition calculus for higher-order logic that is refutationally complete . Most of the key ideas have been developed in previous work by us and colleagues, but combining them in the right way has been challenging. A key idea was to
 -normalize away inconvenient terms.
-normalize away inconvenient terms.
Unlike earlier refutationally complete calculi for full higher-order logic based on resolution or paramodulation, our calculus employs a term order, which restricts the proof search, and a redundancy criterion, which can be used to add various simplification rules while keeping refutational completeness. These two mechanisms are undoubtedly major factors in the success of first-order superposition, and it is very fortunate that we could incorporate both in a higher-order calculus. An alternative calculus with the same two mechanisms could be achieved by combining
 with Bhayat and Reger’s combinatory superposition [10]. The article on \(\lambda \)Sup [6, Sect. 8] discusses related work in more detail.
with Bhayat and Reger’s combinatory superposition [10]. The article on \(\lambda \)Sup [6, Sect. 8] discusses related work in more detail.
The evaluation results show that our calculus is an excellent basis for higher-order theorem proving. In future work, we want to experiment further with the different parameters of the calculus (for example, with Boolean subterm selection heuristics) and implement it in a state-of-the-art prover such as E.
References
Andrews, P.B.: On connections and higher-order logic. J. Autom. Reason. 5(3), 257–291 (1989)
Bachmair, L., Ganzinger, H.: Rewrite-based equational theorem proving with selection and simplification. J. Log. Comput. 4(3), 217–247 (1994)
Barrett, C.W., Conway, C.L., Deters, M., Hadarean, L., Jovanovic, D., King, T., Reynolds, A., Tinelli, C.: CVC4. In: CAV. LNCS, vol. 6806, pp. 171–177. Springer (2011)
Benanav, D.: Simultaneous paramodulation. In: Stickel, M.E. (ed.) CADE-10. LNCS, vol. 449, pp. 442–455. Springer (1990)
Bentkamp, A., Blanchette, J., Tourret, S., Vukmirović, P.: Superposition for full higher-order logic (supplementary material), https://doi.org/10.5281/zenodo.4534759
Bentkamp, A., Blanchette, J., Tourret, S., Vukmirović, P., Waldmann, U.: Superposition with lambdas, accepted in J. Autom. Reason. Preprint at https://arxiv.org/abs/2102.00453v1 (2021)
Bentkamp, A., Blanchette, J.C., Cruanes, S., Waldmann, U.: Superposition for lambda-free higher-order logic. In: Galmiche, D., Schulz, S., Sebastiani, R. (eds.) IJCAR 2018. LNCS, vol. 10900, pp. 28–46. Springer (2018)
Bentkamp, A., Blanchette, J.C., Tourret, S., Vukmirović, P.: Superposition for full higher-order logic (technical report). Technical report (2021), https://matryoshka-project.github.io/pubs/hosup_report.pdf
Benzmüller, C., Paulson, L.C., Theiss, F., Fietzke, A.: LEO-II—A cooperative automatic theorem prover for higher-order logic. In: Armando, A., Baumgartner, P., Dowek, G. (eds.) IJCAR 2008. LNCS, vol. 5195, pp. 162–170. Springer (2008)
Bhayat, A., Reger, G.: Set of support for higher-order reasoning. In: Konev, B., Urban, J., Rümmer, P. (eds.) PAAR-2018. CEUR Workshop Proceedings, vol. 2162, pp. 2–16. CEUR-WS.org (2018)
Bhayat, A., Reger, G.: A combinator-based superposition calculus for higher-order logic. In: Peltier, N., Sofronie-Stokkermans, V. (eds.) IJCAR 2020, Part I. LNCS, vol. 12166, pp. 278–296. Springer (2020)
Böhme, S., Nipkow, T.: Sledgehammer: Judgement Day. In: Giesl, J., Hähnle, R. (eds.) IJCAR 2010. LNCS, vol. 6173, pp. 107–121. Springer (2010)
Brown, C.E.: Satallax: An automatic higher-order prover. In: Gramlich, B., Miller, D., Sattler, U. (eds.) IJCAR 2012. LNCS, vol. 7364, pp. 111–117. Springer (2012)
Cruanes, S.: Extending Superposition with Integer Arithmetic, Structural Induction, and Beyond. Ph.D. thesis, École polytechnique (2015)
Fitting, M.: Types, Tableaus, and Gödel’s God. Kluwer (2002)
Ganzinger, H., Stuber, J.: Superposition with equivalence reasoning and delayed clause normal form transformation. Information and Computation 199(1–2), 3–23 (2005)
Gordon, M.J.C., Melham, T.F. (eds.): Introduction to HOL: A Theorem Proving Environment for Higher Order Logic. Cambridge University Press (1993)
Huet, G.P.: A mechanization of type theory. In: Nilsson, N.J. (ed.) IJCAI-73. pp. 139–146. William Kaufmann (1973)
Jensen, D.C., Pietrzykowski, T.: Mechanizing \(\omega \)-order type theory through unification. Theor. Comput. Sci. 3(2), 123–171 (1976)
Kaliszyk, C., Sutcliffe, G., Rabe, F.: TH1: The TPTP typed higher-order form with rank-1 polymorphism. In: Fontaine, P., Schulz, S., Urban, J. (eds.) PAAR-2016. CEUR Workshop Proceedings, vol. 1635, pp. 41–55. CEUR-WS.org (2016)
Kotelnikov, E., Kovács, L., Suda, M., Voronkov, A.: A clausal normal form translation for FOOL. In: Benzmüller, C., Sutcliffe, G., Rojas, R. (eds.) GCAI 2016. EPiC, vol. 41, pp. 53–71. EasyChair (2016)
Ludwig, M., Waldmann, U.: An extension of the Knuth-Bendix ordering with LPO-like properties. In: Dershowitz, N., Voronkov, A. (eds.) LPAR-14. LNCS, vol. 4790, pp. 348–362. Springer (2007)
Nummelin, V., Bentkamp, A., Tourret, S., Vukmirović, P.: Superposition with first-class Booleans and inprocessing clausification. In: Platzer, A., Sutcliffe, G. (eds.) CADE-28. LNCS, Springer (2021)
Paulson, L.C., Blanchette, J.C.: Three years of experience with Sledgehammer, a practical link between automatic and interactive theorem provers. In: Sutcliffe, G., Schulz, S., Ternovska, E. (eds.) IWIL-2010. EPiC, vol. 2, pp. 1–11. EasyChair (2012)
Schulz, S.: E - a brainiac theorem prover. AI Commun. 15(2-3), 111–126 (2002)
Steen, A., Benzmüller, C.: The higher-order prover Leo-III. In: Galmiche, D., Schulz, S., Sebastiani, R. (eds.) IJCAR 2018. LNCS, vol. 10900, pp. 108–116. Springer (2018)
Sutcliffe, G.: The TPTP problem library and associated infrastructure—from CNF to TH0, TPTP v6.4.0. J. Autom. Reason. 59(4), 483–502 (2017)
Vukmirović, P., Bentkamp, A., Blanchette, J., Cruanes, S., Nummelin, V., Tourret, S.: Making higher-order superposition work. In: Platzer, A., Sutcliffe, G. (eds.) CADE-28. LNCS, Springer (2021)
Vukmirović, P., Bentkamp, A., Nummelin, V.: Efficient full higher-order unification. In: Ariola, Z.M. (ed.) FSCD 2020. LIPIcs, vol. 167, pp. 5:1–5:17. Schloss Dagstuhl—Leibniz-Zentrum für Informatik (2020)
Vukmirović, P., Nummelin, V.: Boolean reasoning in a higher-order superposition prover. In: PAAR-2020. CEUR Workshop Proceedings, vol. 2752, pp. 148–166. CEUR-WS.org (2020)
Waldmann, U., Tourret, S., Robillard, S., Blanchette, J.: A comprehensive framework for saturation theorem proving. In: Peltier, N., Sofronie-Stokkermans, V. (eds.) IJCAR 2020, Part I. LNCS, vol. 12166, pp. 316–334. Springer (2020)
Acknowledgment
Uwe Waldmann provided advice and carefully checked the completeness proof. Visa Nummelin led the design of the
 calculus. Simon Cruanes helped us with the implementation. Martin Desharnais generated the Sledgehammer benchmarks. Christoph Benzmüller, Ahmed Bhayat, Mathias Fleury, Herman Geuvers, Giles Reger, Alexander Steen, Mark Summerfield, Geoff Sutcliffe, and the anonymous reviewers helped us in various ways. We thank them all.
calculus. Simon Cruanes helped us with the implementation. Martin Desharnais generated the Sledgehammer benchmarks. Christoph Benzmüller, Ahmed Bhayat, Mathias Fleury, Herman Geuvers, Giles Reger, Alexander Steen, Mark Summerfield, Geoff Sutcliffe, and the anonymous reviewers helped us in various ways. We thank them all.
Bentkamp, Blanchette, and Vukmirović’s research has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program (grant agreement No. 713999, Matryoshka). Blanchette’s research has received funding from the Netherlands Organization for Scientific Research (NWO) under the Vidi program (project No. 016.Vidi.189.037, Lean Forward).
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2021 The Author(s)
About this paper
Cite this paper
Bentkamp, A., Blanchette, J., Tourret, S., Vukmirović, P. (2021). Superposition for Full Higher-order Logic. In: Platzer, A., Sutcliffe, G. (eds) Automated Deduction – CADE 28. CADE 2021. Lecture Notes in Computer Science(), vol 12699. Springer, Cham. https://doi.org/10.1007/978-3-030-79876-5_23
Download citation
DOI: https://doi.org/10.1007/978-3-030-79876-5_23
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-79875-8
Online ISBN: 978-3-030-79876-5
eBook Packages: Computer ScienceComputer Science (R0)




 and
and  , the subterm u is at the top level of a positive literal.
, the subterm u is at the top level of a positive literal. ; 4.
; 4.  (i.e., the identity if u is Boolean or
(i.e., the identity if u is Boolean or
 if u is of type
if u is of type  ,
,
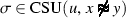 ,
,
 , or
, or
 , respectively; 2. x, y, and
, respectively; 2. x, y, and  ,
,
 , or
, or
 where v is a variable-headed term.
where v is a variable-headed term.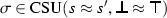 ; 2.
; 2.
 is strictly eligible in C w.r.t.
is strictly eligible in C w.r.t.  ,
,
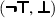 ,
,
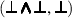 ,
,
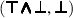 ,
,
 ,
,
 ,
,
 ,
,
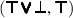 ,
,
 ,
,
 ,
,
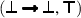 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ; 2. u is not a variable; 3. u is eligible in C w.r.t.
; 2. u is not a variable; 3. u is eligible in C w.r.t.  ,
,
 , or
, or  and
and
 , respectively, where
, respectively, where  , or
, or  , and for
, and for 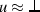 .
. ; 5.
; 5.
 and
and
 ; 6. u is eligible in C w.r.t.
; 6. u is eligible in C w.r.t.  replaced by
replaced by
 in condition 4.
in condition 4.


