Abstract
We present a complete superposition calculus for first-order logic with an interpreted Boolean type. Our motivation is to lay the foundation for refutationally complete calculi in more expressive logics with Booleans, such as higher-order logic, and to make superposition work efficiently on problems that would be obfuscated when using clausification as preprocessing. Working directly on formulas, our calculus avoids the costly axiomatic encoding of the theory of Booleans into first-order logic and offers various ways to interleave clausification with other derivation steps. We evaluate our calculus using the Zipperposition theorem prover, and observe that, with no tuning of parameters, our approach is on a par with the state-of-the-art approach.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
Superposition is a calculus for equational first-order logic that works on problems given in clausal normal form. Its immense success made preprocessing clausification a predominant mechanism in modern automatic theorem proving. However, this preprocessing is not without drawbacks. Clausification can transform simple problems, such as \(s \rightarrow s\) where s is a large formula, in a way that hides its original simplicity from the superposition calculus. Ganzinger and Stuber’s superposition-like calculus [13] operates on clauses that contain formulas as well as terms and replaces preprocessing clausification by inprocessing—meaning processing during the operation of the calculus itself. Inprocessing clausification allows superposition’s powerful simplification engine to work on formulas. For example, unit equalities can rewrite formulas s and t in \(s\leftrightarrow t\) before clausification duplicates the occurrences into \(s\rightarrow t\) and \(t\rightarrow s\). Whole formulas rather than simple literals can be removed by rules such as subsumption resolution [4].
Another issue with Boolean reasoning in the standard superposition calculus is that, in first-order logic, formulas cannot appear inside terms although this is often desirable for problems coming from software verifiers or proof assistants. Instead, authors of such tools need to resort to translations. Kotelnikov et al. studied effects of these translations in detail. They showed that simple axioms such as the domain cardinality axiom for Booleans ( ) can severely slow down superposition provers. To support more efficient reasoning on problems with first-class Booleans, they describe the FOOL logic, which admits functions that take arguments of Boolean type and quantification over Booleans. They further describe two approaches to reason in FOOL: The first one [17] requires an additional rule in the superposition calculus, whereas the second one [16] is completely based on preprocessing.
) can severely slow down superposition provers. To support more efficient reasoning on problems with first-class Booleans, they describe the FOOL logic, which admits functions that take arguments of Boolean type and quantification over Booleans. They further describe two approaches to reason in FOOL: The first one [17] requires an additional rule in the superposition calculus, whereas the second one [16] is completely based on preprocessing.
Our calculus combines complementary advantages of Ganzinger and Stuber’s and of Kotelnikov et al.’s work. Following Kotelnikov et al., our logic (Sect. 2) is similar to FOOL and supports nesting formulas inside terms, as well as quantifying over Booleans. Following Ganzinger and Stuber, our calculus (Sect. 3) reasons with formulas and supports inprocessing clausification.
Our calculus also extends the two approaches. To reduce the number of possible inferences, we generalize Ganzinger and Stuber’s Boolean selection functions, which allow us to restrict the Boolean subterms in a clause on which inferences can be performed. The term order requirements of our calculus are less restrictive than Ganzinger and Stuber’s. In addition to the lexicographic path order (LPO), we also support the Knuth-Bendix order (KBO) [15], which is known to work better with superposition in practice.
Our proof of refutational completeness (Sect. 4) lays the foundation for complete calculi in more complex logics with Booleans. Indeed, Bentkamp et al. [8] devised a refutationally complete calculus for higher-order logic based on our completeness theorem. Our theorem incorporates a powerful redundancy criterion that allows for a variety of inprocessing clausification methods (Sect. 5).
We implemented our approach in the Zipperposition theorem prover (Sect. 6) and evaluated it on thousands of problems that target our logic ranging from TPTP to SMT-LIB to Sledgehammer-generated benchmarks (Sect. 7). Without fine-tuning, our new calculus performs as well as known techniques. Exploring the strategic choices that our calculus opens should lead to further performance improvements. In addition, we corroborate the claims of Ganzinger and Stuber concerning applicability of formula-based superposition reasoning: We find a set of 17 TPTP problems (out of 1000 randomly selected) that Zipperposition can solve only using the techniques described in this paper. We refer to our technical report [25] for more details on our calculus and the complete completeness proof.
2 Logic
Our logic is a first-order logic with an interpreted Boolean type. It is essentially identical to the UF logic of SMT-LIB [5], including the Core theory, but without if-then-else and let expressions, which can be supported through simple translations. It also closely resembles Kotelnikov et al.’s FOOL [17], which additionally supports if-then-else and let expressions.
Our logic requires an interpreted Boolean type \(o\) and allows for an arbitrary number of uninterpreted types. The set of symbols must contain the logical symbols  ;
;  ;
;  ; and the overloaded symbols
; and the overloaded symbols  for each type \(\tau \). The logical symbols are printed in bold to distinguish them from the notation used for clauses below. Throughout the paper, we write tuples \((a_1, \dots , a_n)\) as \(\bar{a}_n\) or \(\bar{a}\).
for each type \(\tau \). The logical symbols are printed in bold to distinguish them from the notation used for clauses below. Throughout the paper, we write tuples \((a_1, \dots , a_n)\) as \(\bar{a}_n\) or \(\bar{a}\).
The set of terms is defined inductively as follows. Every variable is a term. If \({\mathsf {f}}:\bar{\tau }_n\rightarrow \upsilon \) is a symbol and \(\bar{t}_n:\bar{\tau }_n\) is a tuple of terms, then the application \({\mathsf {f}}(\bar{t}_n)\) (or simply \({\mathsf {f}}\) if \(n = 0\)) is a term of type \(\upsilon \). If x is a variable and \(t:o\) a Boolean term, then the quantified terms \(\forall x.\> t\) and \(\exists x.\> t\) are terms of Boolean type. We view quantified terms modulo \(\alpha \)-renaming. A formula is a term of Boolean type.
The root of a term is \({\mathsf {f}}\) if the term is an application \({\mathsf {f}}(\bar{t}_n)\); it is x if the term is a variable x; and it is \(\forall \) or \(\exists \) if the term is a quantified term \(\forall x.\> t\) or \(\exists x.\> t\). A variable occurrence is free in a term if it is not bound by \(\forall \) or \(\exists \). A term is ground if it contains no free variables. Substitutions are defined as usual in first-order logic and they rename quantified variables to avoid capture.
A literal \(s \mathrel {\dot{\approx }}t\) is an equation \(s \approx t\) or a disequation \(s \not \approx t\). Unlike terms constructed using the function symbols  and
and  , literals are unoriented. A clause \(L_1 \vee \dots \vee L_n\) is a finite multiset of literals \(L_{\!j}\). The empty clause is written as \(\bot \). Terms t of Boolean type are not literals. They must be encoded as
, literals are unoriented. A clause \(L_1 \vee \dots \vee L_n\) is a finite multiset of literals \(L_{\!j}\). The empty clause is written as \(\bot \). Terms t of Boolean type are not literals. They must be encoded as  and
and  , which we call predicate literals. Both are considered positive literals because they are equations, not disequations.
, which we call predicate literals. Both are considered positive literals because they are equations, not disequations.
We have considered excluding negative literals \(s \not \approx t\) by encoding them as  , following Ganzinger and Stuber. However, this approach requires an additional term order condition to make the conclusion of equality factoring small enough, excluding KBO. To support both KBO and LPO, we allow negative literals. Regardless, our simplification mechanism will allow us to simplify negative literals of the form
, following Ganzinger and Stuber. However, this approach requires an additional term order condition to make the conclusion of equality factoring small enough, excluding KBO. To support both KBO and LPO, we allow negative literals. Regardless, our simplification mechanism will allow us to simplify negative literals of the form  and
and  into
into  and
and  , respectively, thereby eliminating redundant representations of predicate literals.
, respectively, thereby eliminating redundant representations of predicate literals.
The semantics is a straightforward extension of standard first-order logic only adding the interpretation of the Boolean type as a two element domain, as in Kotelnikov et al.’s FOOL logic.
Some of our calculus rules introduce Skolem symbols, which are intended to be interpreted as witnesses for existentially quantified terms. Still, our semantics treats them as uninterpreted symbols. To achieve a satisfiability-preserving calculus, we assume that these symbols do not occur in the input problem. More precisely, we inductively extend the signature of the input problem by a symbol \({\mathsf {sk}}_{\forall \bar{y}.\exists z.t} :\bar{\tau } \rightarrow \upsilon \) for each term of the form \(\exists z.\>t\) over the extended signature, where \(\upsilon \) is the type of z and \(\bar{y}:\bar{\tau }\) are the free variables occurring in \(\exists z.\>t\), in order of first appearance.
3 The Calculus
Following standard superposition, our calculus employs a term order and a literal selection function to restrict the search space. To accommodate for quantified Boolean terms, we impose additional requirements on the term order. To support flexible reasoning with Boolean subterms, in addition to the literal selection function, we introduce a Boolean subterm selection function.
Term Order The calculus is parameterized by a strict well-founded order \(\succ \) on ground terms that fulfills: (O1)  for any term u that is not
for any term u that is not  or
or  ; (O2) \(\forall x.\,t\succ \{x\mapsto u\}t\) and \(\exists x.\,t\succ \{x\mapsto u\}t\) for any term u whose only Boolean subterms are
; (O2) \(\forall x.\,t\succ \{x\mapsto u\}t\) and \(\exists x.\,t\succ \{x\mapsto u\}t\) for any term u whose only Boolean subterms are  and
and  ; (O3) subterm property; (O4) compatibility with contexts (not necessarily below \(\forall \) and \(\exists \)); (O5) totality. The order is extended to literals, clauses, and nonground terms as usual [2]. The nonground order then also enjoys (O6) stability under grounding substitutions.
; (O3) subterm property; (O4) compatibility with contexts (not necessarily below \(\forall \) and \(\exists \)); (O5) totality. The order is extended to literals, clauses, and nonground terms as usual [2]. The nonground order then also enjoys (O6) stability under grounding substitutions.
Ganzinger and Stuber’s term order restrictions are similar but incompatible with KBO. Using an encoding of our terms into untyped first-order logic we describe how both LPO and the transfinite variant of KBO [19] can satisfy conditions (O1)–(O6).
Our encoding represents bound variables by De Bruijn indices, which become new constant symbols \({\mathsf {db}}_{n}\) for \(n\in \mathbb {N}\). Quantifiers are represented by two new unary function symbols, also denoted by \(\forall \) and \(\exists \). All other symbols are simply identified with their untyped counterpart. Regardless of symbol precedence or symbol weights, KBO and LPO enjoy properties (O3)–(O6) when applied to the encoded terms. They are even compatible with contexts below quantifiers.
To satisfy (O1) and (O2), let the precedence for LPO be  where \({\mathsf {f}}\) is any other symbol. For KBO, we can use the same symbol precedence and a symbol weight function \(\mathcal {W}\) that assigns each symbol ordinal weights (of the form \(\omega a+b\) with \(a,b\in \mathbb {N}\)), where
where \({\mathsf {f}}\) is any other symbol. For KBO, we can use the same symbol precedence and a symbol weight function \(\mathcal {W}\) that assigns each symbol ordinal weights (of the form \(\omega a+b\) with \(a,b\in \mathbb {N}\)), where  , and \(\mathcal {W}({\mathsf {f}})\in \mathbb {N}\setminus \{0\}\) for any other symbol \({\mathsf {f}}\).
, and \(\mathcal {W}({\mathsf {f}})\in \mathbb {N}\setminus \{0\}\) for any other symbol \({\mathsf {f}}\).
Selection and Eligibility
Following an idea of Ganzinger and Stuber, we parameterize our calculus with two selection functions: one selecting literals and one selecting Boolean subterms.
Definition 1
(Selection functions). The calculus is parameterized by a literal selection function \( FLSel \) and a Boolean subterm selection function \( FBSel \). The function \( FLSel \) maps each clause to a subset of its literals. The selection function \( FBSel \) maps each clause to a subset of its Boolean subterms. The literals \( FLSel (C)\) and the subterms \( FBSel (C)\) are selected in C. The following restrictions apply: (S1) A literal can only be selected if it is negative or of the form  . (S2) A Boolean subterm can only be selected if it is not
. (S2) A Boolean subterm can only be selected if it is not  ,
,  , or a variable. (S3) A Boolean subterm can only be selected if its occurrence is not below a quantifier. (S4) The topmost terms on either side of a positive literal cannot be selected.
, or a variable. (S3) A Boolean subterm can only be selected if its occurrence is not below a quantifier. (S4) The topmost terms on either side of a positive literal cannot be selected.
The interplay of maximality w.r.t. term order, literal and Boolean selection functions gives rise to a new notion of eligibility:
Definition 2
(Eligibility). A literal L is (strictly) eligible w.r.t. a substitution \(\sigma \) in C if it is selected in C or there are no selected literals and no selected Boolean subterms in C and \(\sigma L\) is (strictly) maximal in \(\sigma C.\) The eligible subterms of a clause C w.r.t. a substitution \(\sigma \) are inductively defined as follows: (E1) Any selected subterm is eligible. (E2) If a literal \(s \mathrel {\dot{\approx }}t\) with \(\sigma s\not \preceq \sigma t\) is either eligible and negative or strictly eligible and positive, then s is eligible. (E3) If a subterm is eligible and its root is not  ,
,  ,
,  , or
, or  , all of its direct subterms are also eligible. (E4) If a subterm is eligible and of the form
, all of its direct subterms are also eligible. (E4) If a subterm is eligible and of the form  or
or  , then s is eligible if \(\sigma s\not \preceq \sigma t\) and t is eligible if \(\sigma s\not \succeq \sigma t\). The substitution \(\sigma \) is left implicit if it is the identity substitution.
, then s is eligible if \(\sigma s\not \preceq \sigma t\) and t is eligible if \(\sigma s\not \succeq \sigma t\). The substitution \(\sigma \) is left implicit if it is the identity substitution.
The Core Inference Rules The following inference rules form our calculus:

The rules are subject to the following side conditions:
-
Sup (1) \(\sigma = \mathrm {mgu}(t, u)\); (2) u is not a variable; (3) \(\sigma t\not \preceq \sigma t'\); (4) \(D\prec C[u]\); (5) u is eligible in C w.r.t. \(\sigma \); (6) \(t \approx t'\) is strictly eligible in D w.r.t. \(\sigma \); (7) the root of t is not a logical symbol; (8) if
 , the subterm u is at the top level of a positive literal.
, the subterm u is at the top level of a positive literal. -
Factor (1) \(\sigma = \mathrm {mgu}(u, u')\); (2) \(\sigma u\not \approx t\not \in \sigma C\) for any term t; (3) no Boolean subterm and no literal is selected in C; (4) \(\sigma u\) is a maximal term in \(\sigma C\); (5) \(\sigma v\) is maximal in \(\left\{ t\mid \sigma u\approx t\in \sigma C\right\} \).
-
Irrefl (1) \(\sigma = \mathrm {mgu}(u, u')\); (2) \(u \not \approx u'\) is eligible in C w.r.t. \(\sigma \).
-
 (1)
(1)  ; (2) \(s \approx t\) is strictly eligible in C w.r.t. \(\sigma \).
; (2) \(s \approx t\) is strictly eligible in C w.r.t. \(\sigma \). -
BoolRw (1) \((t , t')\) is one of the following pairs, where x is a fresh variable:
 ,
, 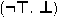 ,
,  ,
, 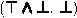 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ; (2) \(\sigma = \mathrm {mgu}(t,u)\); (3) u is not a variable; (4) u is eligible in C w.r.t. \(\sigma \).
; (2) \(\sigma = \mathrm {mgu}(t,u)\); (3) u is not a variable; (4) u is eligible in C w.r.t. \(\sigma \). -
\(\star \) Rw (where \(\star \in \{\forall , \exists \}\)) (1) v is a term that may refer to z; (2) \(\bar{y}\) are the free variables occurring in \(\forall z.\>v\) and \(\exists z.\>v\), respectively, in order of first appearance; (3) the indicated subterm is eligible in C; (4) for \(\forall \) Rw,
 is not a tautology; (5) for \(\exists \) Rw,
is not a tautology; (5) for \(\exists \) Rw,  is not a tautology. (In an implementation, the tautology check can be approximated by checking if the affected literal is of the form
is not a tautology. (In an implementation, the tautology check can be approximated by checking if the affected literal is of the form  or
or  .)
.) -
BoolHoist (1) u is a Boolean term whose root is an uninterpreted predicate; (2) u is eligible in C; (3) u is not a variable; (4) u is not at the top level of a positive literal.
-
\(\star \) Hoist (where
 ) (1) the indicated subterm is eligible in C; (2) y is a fresh variable.
) (1) the indicated subterm is eligible in C; (2) y is a fresh variable.
Rationale for the Rules Our calculus is a graceful generalization of superposition: if the input clauses do not contain any Boolean terms, it coincides with standard superposition. In addition to the standard superposition rules Sup, Factor, and Irrefl, our calculus contains various rules to deal with Booleans. For each logical symbol and quantifier, we must consider the case where it is true and the case where it is false. Whenever possible, we prefer rules that rewrite the Boolean subterm in place (with names ending in Rw). When this cannot be done in a satisfiability-preserving way, we resort to rules hoisting the Boolean subterm into a dedicated literal (with names ending in Hoist). For terms rooted by an uninterpreted predicate, the rule BoolHoist only deals with the case that the term is false. If it is true, we rely on Sup to rewrite it to  eventually.
eventually.
Example 3
The clause  can be refuted by the core inferences as follows. First we derive
can be refuted by the core inferences as follows. First we derive  (displayed on the left) and then we use it to derive \(\bot \) (displayed on the right). In this and the following example, we assume eager selection of literals whenever the selection restrictions allow it.
(displayed on the left) and then we use it to derive \(\bot \) (displayed on the right). In this and the following example, we assume eager selection of literals whenever the selection restrictions allow it.

The derivation illustrates how BoolHoist and Sup replace uninterpreted predicates by  and
and  to allow BoolRw to eliminate the surrounding logical symbols.
to allow BoolRw to eliminate the surrounding logical symbols.
Example 4
The clause  can be refuted as follows:
can be refuted as follows:

Redundancy Criterion In standard superposition, a clause is defined as redundant if all of its ground instances follow from smaller ground instances of other clauses. We keep this definition, but use a nonstandard notion of ground instances, inspired by constraint superposition [23]. In our completeness proof, this new notion of ground instances ensures that ground instances of the conclusion of \(\forall \) Rw, \(\exists \) Rw, \(\forall \) Hoist, and \(\exists \) Hoist inferences are smaller than the corresponding instances of their premise by property (O2).
Definition 5
(Redundancy of clauses). The ground instances of a clause C are all ground clauses of the form \(\gamma C\) where \(\gamma \) is a substitution such that for all variables x, the only Boolean subterms of \(\gamma x\) are  and
and  . A ground clause C is redundant w.r.t. a ground clause set N if there exist clauses \(C_1, \ldots , C_k \in N\) such that \(C_1, \dots , C_k \models C\) and \(C \succ C_i\) for all \(1\le i\le k\). A nonground clause C is redundant w.r.t. clauses N if C is strictly subsumed by a clause in N or every ground instance of C is redundant w.r.t. ground instances of N.
. A ground clause C is redundant w.r.t. a ground clause set N if there exist clauses \(C_1, \ldots , C_k \in N\) such that \(C_1, \dots , C_k \models C\) and \(C \succ C_i\) for all \(1\le i\le k\). A nonground clause C is redundant w.r.t. clauses N if C is strictly subsumed by a clause in N or every ground instance of C is redundant w.r.t. ground instances of N.
In standard superposition, an inference is defined as redundant if all its ground instances are, and a ground inference is defined as redundant if its conclusion follows from other clauses smaller than the main premise. We keep this definition as well, but we use a nonstandard notion of ground instances for some of the Boolean rules. In our report, we define a slightly stronger variant of inference redundancy via an explicit ground calculus, but the following notion is also strong enough to justify the few prover optimizations based on inference redundancy we know from the literature (e.g., simultaneous superposition [7]).
Definition 6
(Redundancy of inferences). A ground instance of a \(\forall \textsc {Rw}\), \(\exists \textsc {Rw}\), \(\forall \textsc {Hoist}\), or \(\exists \textsc {Hoist}\) inference is an inference obtained by applying a grounding substitution to premise and conclusion, regardless of whether the result is a valid \(\forall \textsc {Rw}\), \(\exists \textsc {Rw}\), \(\forall \textsc {Hoist}\), or \(\exists \textsc {Hoist}\) inference. A ground instance of an inference \(\iota \) of other rules is an inference \(\iota '\) of the same rule such that premises and conclusion of \(\iota '\) are ground instances of the respective premises and conclusion of \(\iota \). For \(\iota '\), we use selection functions that select the ground literals and Boolean subterms corresponding to the ones selected in the nonground premises. A ground inference with main premise C, side premises \(C_1, \ldots , C_n\), and conclusion D is redundant w.r.t. N if there exist clauses \(D_1,\dots ,D_k \prec C\) in N such that \(D_1, \ldots , D_k,C_1,\ldots ,C_n\models D\). A nonground inference is redundant if all its ground instances are redundant.
A clause set N is saturated if every inference from N is redundant w.r.t. N.
Simplification Rules The redundancy criterion is a graceful generalization of the criterion of standard superposition. Thus, the standard simplification and deletion rules, such as deletion of trivial literals and clauses, subsumption, and demodulation, can be justified. Demodulation below quantifiers is justified if the term order is compatible with contexts below quantifiers.
Some calculus rules can act as simplifications.  Elim can always be a simplification. Given a clause on which both \(\star \) Rw and \(\star \) Hoist apply, where \(\star \in \{\forall ,\exists \}\), the clause can be replaced by the conclusions of these rules. If \(\star \) Rw does not apply because of condition 4 or 5, \(\star \) Hoist alone can be a simplification. Also justified by redundancy, the rules BoolHoist and \(\star \) Hoist can simultaneously replace all occurrences of the eligible subterm they act on. For example, applying
Elim can always be a simplification. Given a clause on which both \(\star \) Rw and \(\star \) Hoist apply, where \(\star \in \{\forall ,\exists \}\), the clause can be replaced by the conclusions of these rules. If \(\star \) Rw does not apply because of condition 4 or 5, \(\star \) Hoist alone can be a simplification. Also justified by redundancy, the rules BoolHoist and \(\star \) Hoist can simultaneously replace all occurrences of the eligible subterm they act on. For example, applying  Hoist to
Hoist to  yields
yields  .
.
While experimenting with our implementation, we have observed that the following simplification rule from Vampire [18] can substantially shorten proofs:

In this rule, we require \(s \succ t\).
Interpreting literals of the form  as
as  and
and  as
as  we can apply the rule even to these positive literals. This especially convenient with rules such as BoolHoist. Consider the clause
we can apply the rule even to these positive literals. This especially convenient with rules such as BoolHoist. Consider the clause  , assume no literal is selected and the Boolean selection function always selects a subterm
, assume no literal is selected and the Boolean selection function always selects a subterm  . Applying BoolHoist to C we get
. Applying BoolHoist to C we get  . This can then be simplified to a tautological clause
. This can then be simplified to a tautological clause  using \(i-2\) LocalRw steps. If we did not use LocalRw, BoolHoist would produce \(i-2\) intermediary clauses starting from C, none of which would be recognized as a tautology.
using \(i-2\) LocalRw steps. If we did not use LocalRw, BoolHoist would produce \(i-2\) intermediary clauses starting from C, none of which would be recognized as a tautology.
Many rules of our calculus replace subterms with  or
or  . After this replacement, resulting terms can be simplified using Boolean equivalences that specify the behavior of logical operations on
. After this replacement, resulting terms can be simplified using Boolean equivalences that specify the behavior of logical operations on  and
and  . To this end, we use the rule BoolSimp [33], similar to simp of Leo-III [27, Sect. 4.2.1]:
. To this end, we use the rule BoolSimp [33], similar to simp of Leo-III [27, Sect. 4.2.1]:

This rule replaces s with t whenever  is contained in a predefined set of tautological equations. In addition to all equations that Leo-III uses for simp, we also include more complex ones, such as
is contained in a predefined set of tautological equations. In addition to all equations that Leo-III uses for simp, we also include more complex ones, such as  and
and  where \(u_i = v_j\) for some i and j. The exhaustive list is given in our technical report. Using BoolSimp and
where \(u_i = v_j\) for some i and j. The exhaustive list is given in our technical report. Using BoolSimp and  Elim, the twelve steps of Example 3 can be replaced by just two simplification steps.
Elim, the twelve steps of Example 3 can be replaced by just two simplification steps.
BoolSimp simplifies terms with logical symbol roots if one argument is either  or
or  or if two arguments are identical. Thus, after simplification, BoolRw applies only in two remaining cases: if all arguments of a logical symbol are distinct variables and if the sides of a (dis)equation are different and unifiable. This observation can be used to streamline the implementation of BoolRw.
or if two arguments are identical. Thus, after simplification, BoolRw applies only in two remaining cases: if all arguments of a logical symbol are distinct variables and if the sides of a (dis)equation are different and unifiable. This observation can be used to streamline the implementation of BoolRw.
4 Refutational Completeness
Our calculus is dynamically refutationally complete. All the rules that do not introduce Skolem symbols are also sound.
Completeness Theorem 7
Let \(S_0\) be an unsatisfiable set of clauses. Let \((S_i)_{i=0}^\infty \) be a fair derivation—i.e., a derivation where \(\bigcup _{i=0}^{\infty }\bigcap _{j=i}^{\infty }S_{j}\) is saturated. Then \(\bot \in S_i\) for some i.
We outline some key parts of the proof here and refer to our technical report [25] for the details. We first define a ground version of our calculus with standardly inherited redundancy criterion and prove it complete. Devising suitable ground analogues of the rules \(\forall \)Rw and \(\exists \)Rw was difficult because the arguments of the Skolems depend on the variables occurring in the premise. Therefore, we parameterize the ground calculus by a function that provides ground Skolem terms in the ground versions of these rules. When lifting the completeness result to the nonground level, we instantiate the parameter with a specific function that allows us to lift the \(\forall \) Rw and \(\exists \) Rw inferences.
To prove the ground calculus complete, we employ the framework for reduction of counterexamples [3]. It requires us to construct an interpretation \(\mathcal {I}\) given a saturated unsatisfiable clause set that does not contain \(\bot \). Then we must show that any counterexample—i.e., a clause that does not hold in \(\mathcal {I}\)—can be reduced to a smaller (\(\prec \)) counterexample by some inference.
The interpretation \(\mathcal {I}\) is defined by a normalizing rewrite system as in the standard completeness proof of superposition. To ensure a correct interpretation of Booleans, we incrementally add Boolean rewrite rules along with the rules produced by clauses as usual. If a counterexample can be rewritten by a Boolean rule, we reduce it by a \(\star \) Rw or \(\star \) Hoist inference. If it can be rewritten by a rule produced by a clause, we reduce it by a Sup inference.
We derive the dynamic completeness of our nonground calculus using the saturation framework [35]. It gives us a nonground clause set N to work with. We then have to choose the parameters of our ground calculus such that all of its inferences from the grounding of N are redundant or liftable. We show that inferences rewriting below variables are redundant. Other inferences we show to be liftable—i.e., they are a ground instance of some inference from N.
5 Inprocessing Clausification Methods
Our calculus makes preprocessing clausification unnecessary: A problem specified by a formula f can be represented as a clause  . Our redundancy criterion allows us to add various sets of rules to steer the inprocessing clausification.
. Our redundancy criterion allows us to add various sets of rules to steer the inprocessing clausification.
Without any additional rules, our core calculus rules perform all the necessary reasoning about formulas. We call this method inner delayed clausification because the calculus rules tend to operate on the inner Boolean subterms first.
The outer delayed clausification method adds the following rules to the calculus, which are guided by the outermost logical symbols. Let s and t be Boolean terms. Below, we let \(s^+\) range over literals of the form  and
and  , and \(s^-\) over literals of the form
, and \(s^-\) over literals of the form  and
and  .
.

The rules \(+\) OuterClaus and −OuterClaus are applicable to any term s whose root is a logical symbol, whereas the rules \(\approx \) OuterClaus and \({\not \approx }\) OuterClaus are only applicable if neither s nor t is  or
or  . Clearly, our redundancy criterion allows us to replace the premise of all OuterClaus-rules with their conclusions. Nonetheless, the rules \({\approx }\) OuterClaus and \({\not \approx }\) OuterClaus are not used as simplification rules since destructing equivalences disturbs the syntactic structure of the formulas, as noted by Ganzinger and Stuber [13]. The function \( oc (s,C)\) analyzes the shape of the formula s and distributes it over the clause C. For example,
. Clearly, our redundancy criterion allows us to replace the premise of all OuterClaus-rules with their conclusions. Nonetheless, the rules \({\approx }\) OuterClaus and \({\not \approx }\) OuterClaus are not used as simplification rules since destructing equivalences disturbs the syntactic structure of the formulas, as noted by Ganzinger and Stuber [13]. The function \( oc (s,C)\) analyzes the shape of the formula s and distributes it over the clause C. For example,  , and
, and  . This function also replaces quantified terms by either a fresh free variable or a Skolem in the body of the quantified term, depending on the polarity. The full definition of \( oc (s,C)\) is specified in our technical report.
. This function also replaces quantified terms by either a fresh free variable or a Skolem in the body of the quantified term, depending on the polarity. The full definition of \( oc (s,C)\) is specified in our technical report.
A third inprocessing clausification method is immediate clausification. It first preprocesses the input problem using a standard first-order clausification procedure such as Nonnengart and Weidenbach’s [24]. Then, during the proof search, when a clause C appears on which OuterClaus rules could be applied, we apply the standard clausification procedure on the formula \(\forall \bar{x}. \, C\) instead (where \(\bar{x}\) are the free variables of C), and replace C with the clausification results. With this method, the formulas are clausified in one step, making intermediate clausification results inaccessible to the simplification machinery.
Renaming Common Formulas Following Tseitin [31], clausification procedures usually rename common formulas to prevent a possible combinatorial explosion caused by naive clausification. In our two delayed clausification methods, we realize this idea using the following rule:

Here, the formula f has a logical root, \(\bar{x}\) are the distinct free variables in f, \({\mathsf {p}}\) is a fresh symbol, \(\sigma _i\) is a substitution, and the clauses \(R_1, \ldots , R_m\) are the result of simplifying a definition clause \(R = {\mathsf {p}}(\bar{x}) \approx f\) as described below. The rule avoids exponential explosion by replacing n positions in which results of f’s clausification will appear into a single position in R. Optimizations such as polarity-aware renaming [24, Sect. 4] also apply to Rename.
Several issues arise with Rename as an inprocessing rule. We need to ensure that in R, \(f \succ {\mathsf {p}}(\bar{x})\), since otherwise demodulation might reintroduce a formula f in the simplified clauses. This can be achieved by giving the fresh symbol \({\mathsf {p}}\) a precedence smaller than that of all symbols initially present in the problem (other than  and
and  ). To ensure the precedence is well founded, the precedence of \({\mathsf {p}}\) must be greater than that of symbols previously introduced by the calculus. For KBO, we additionally set the weight of \({\mathsf {p}}\) to the minimal possible weight.
). To ensure the precedence is well founded, the precedence of \({\mathsf {p}}\) must be greater than that of symbols previously introduced by the calculus. For KBO, we additionally set the weight of \({\mathsf {p}}\) to the minimal possible weight.
For Rename to be used as a simplification rule, we need to ensure that the conclusions are smaller than the premises. This is trivially true for all clauses other than the clause R. For example, let  (\(\sigma _i\) is the identity). Clearly, R is larger than \(C_i\). However, we can view the definition clause R as two clauses
(\(\sigma _i\) is the identity). Clearly, R is larger than \(C_i\). However, we can view the definition clause R as two clauses  and
and  . Then, we can apply a single step of the \(\textsc {OuterClaus}\) rules to \(R^+\) and \(R^-\) (on their subformula f), which further results in clauses \(R_1, \ldots , R_m\). Inspecting the \(\textsc {OuterClaus}\) rules, it is clear that \(m \le 4\), which makes enforcing this simplification tolerable. Furthermore, as f is simplified in each of \(R_1, \ldots , R_m\), they are smaller than any premise \(C_i\).
. Then, we can apply a single step of the \(\textsc {OuterClaus}\) rules to \(R^+\) and \(R^-\) (on their subformula f), which further results in clauses \(R_1, \ldots , R_m\). Inspecting the \(\textsc {OuterClaus}\) rules, it is clear that \(m \le 4\), which makes enforcing this simplification tolerable. Furthermore, as f is simplified in each of \(R_1, \ldots , R_m\), they are smaller than any premise \(C_i\).
Another potential source of a combinatorial explosion in our calculus are formulas that occur deep in the arguments of uninterpreted predicates. Consider the clause  where \(i,j>2\). If the first and the second literal are eligible in C, any clause
where \(i,j>2\). If the first and the second literal are eligible in C, any clause  (where \(i_1 + \cdots + i_k = i\) and \(j_1 + \cdots + j_l = j\)) , resulting from multiple BoolHoist applications, can be obtained in many different ways. This explosion can be avoided using the following rule:
(where \(i_1 + \cdots + i_k = i\) and \(j_1 + \cdots + j_l = j\)) , resulting from multiple BoolHoist applications, can be obtained in many different ways. This explosion can be avoided using the following rule:

where \({\mathsf {p}}\) is a fresh symbol, \(\bar{x}\) are all free variables occurring in \(s \approx t\), the clauses \(R_1, \ldots , R_4\) result from simplifying  as described above, and we impose the same precedence and weight restrictions on \({\mathsf {p}}\) as for Rename. Finally, we require that both \(s \approx t\) and C contain deep Booleans where a Boolean subterm \(u|_p\) of a term u is a deep Boolean if there are at least two distinct proper prefixes q of the position p such that the root of \(u|_q\) is an uninterpreted predicate.
as described above, and we impose the same precedence and weight restrictions on \({\mathsf {p}}\) as for Rename. Finally, we require that both \(s \approx t\) and C contain deep Booleans where a Boolean subterm \(u|_p\) of a term u is a deep Boolean if there are at least two distinct proper prefixes q of the position p such that the root of \(u|_q\) is an uninterpreted predicate.
Similarly to Rename, the definition clause R can be larger than the premise. As OuterClaus-rules might not apply to  , we need a different solution:
, we need a different solution:

In this rule u is a non-variable Boolean subterm, different from  and
and  , whose indicated occurrence is not in a literal \(u\approx b\) where b is
, whose indicated occurrence is not in a literal \(u\approx b\) where b is  ,
,  or a variable. Clearly, both conclusions of BoolHoistSimp are smaller than the premise. As before, observing that R is equivalent to two clauses
or a variable. Clearly, both conclusions of BoolHoistSimp are smaller than the premise. As before, observing that R is equivalent to two clauses  and
and  , we simplify \(R^+\) and \(R^-\) into clauses that are guaranteed to be smaller than the premise. This is achieved by applying BoolHoistSimp to one of the deep Boolean occurrences in both \(R^+\) and \(R^-\), which produces \(R_1, \ldots , R_4\) and reduces the size of resulting clauses enough for them to be smaller than the premise of RenameDeep. The RenameDeep rule can be applied analogously to negative literals \(s \not \approx t\).
, we simplify \(R^+\) and \(R^-\) into clauses that are guaranteed to be smaller than the premise. This is achieved by applying BoolHoistSimp to one of the deep Boolean occurrences in both \(R^+\) and \(R^-\), which produces \(R_1, \ldots , R_4\) and reduces the size of resulting clauses enough for them to be smaller than the premise of RenameDeep. The RenameDeep rule can be applied analogously to negative literals \(s \not \approx t\).
6 Implementation
Zipperposition [11] is an automatic theorem prover designed for easy prototyping of various extensions of superposition. So far, it has been extended to support induction, arithmetic, and various fragments of higher-order logic. We have implemented our calculus and its extensions described above in Zipperposition.
Zipperposition has long supported \(\lambda \) as the only binder. Because introducing new binders would significantly complicate the implementation, we decided to represent the terms \(\forall x.\, t\) and \(\exists x. \, t\) as \(\forall (\lambda x. \, t)\) and \(\exists (\lambda x. \, t)\), respectively.
We introduced a normalized presentation of predicate literals as either  or
or  . As Zipperposition previously encoded them as
. As Zipperposition previously encoded them as  or
or  , enforcing the new encoding was a source of tedious implementation effort.
, enforcing the new encoding was a source of tedious implementation effort.
Factor inferences happen even when the maximal literal is selected since the discovery of condition (3) as described in Sect. 3 came after the evaluation.
Zipperposition’s existing selection functions were not designed with Boolean subterm selection in mind. For instance, a function that selects a literal L with a selectable Boolean subterm s can make s eligible, even if the Boolean selection function did not select s. To mitigate this issue, we can optionally block selection of literals that contain selectable Boolean subterms.
We implemented four Boolean selection functions: selecting the leftmost innermost, leftmost outermost, syntactically largest or syntactically smallest selectable subterm. Ties are broken by selecting the leftmost term. Additionally, we implemented a Boolean selection function that does not select any subterm.
Vukmirović and Nummelin [33, Sect. 3.4] explored inprocessing clausification as part of their pragmatic approach to higher-order Boolean reasoning. They describe in detail how the formula renaming mechanism is implemented. We reuse their mechanism, and simplify definition clauses as described in Sect. 5.
7 Evaluation
The goal of our evaluation was to answer the following questions:
-
1.
How does our approach compare to preprocessing?
-
2.
How do the different inprocessing clausification methods compare?
-
3.
Is there an overhead of our calculus on problems without first-class Booleans?
-
4.
What effect do Boolean selection, LocalRw, and BoolHoistSimp have?
We filtered TPTP [29] and SMT-LIB [5] to get first-order benchmarks that actually do use the Boolean type. In TPTP THF we found 145 such problems (TPTP Bool) and in the UF section of SMT-LIB 5507 such problems. Martin Desharnais and Jasmin Blanchette generated 1253 Sledgehammer problems that target our logic. To measure the overhead of our calculus, we randomly chose 1000 FOF and CNF problems from the TPTP (TPTP FO). Even with this sample the experiment could take up to (145+5507+1253+1000) \(\times \) #modes \(\times \) 300 s \(\approx \) 9 CPU months. On StarExec servers, evaluation roughly took three days under low load. Otherwise evaluating on all 13 000 FOF and CNF problems could have taken 2.5 times longer.
SMT-LIB interprets the symbol \({\mathsf {ite}}\) as the standard if-then-else function [5, Sect. 3.7.1]. Whenever a term \(s = {\mathsf {ite}}(t_1,t_2,t_3)\) of type \(\tau \) occurs in a problem, we replace s with \({\mathsf {f}}_\tau (t_1,t_2,t_3)\), where \({\mathsf {f}}_\tau \) is a fresh symbol denoting the \({\mathsf {ite}}\) function of a particular return type. To comply with SMT-LIB, we add the following axioms:  and
and  . SMT-LIB allows the use of let variable bindings [5, Sect. 3.6.1]. We simply replace each variable with its definition in the body of the let bindings.
. SMT-LIB allows the use of let variable bindings [5, Sect. 3.6.1]. We simply replace each variable with its definition in the body of the let bindings.
Currently, among competing superposition-based provers only E and Vampire support first-order logic with interpreted Booleans, and they do so through preprocessing. We could not evaluate Vampire in the first-order mode with FOOL preprocessing because it yielded unsound results on TPTP Bool benchmarks. We were able to run E on all benchmarks, except for the ones in SMT syntax.
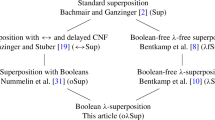
We used Zipperposition’s first-order portfolio, which invokes the prover sequentially with up to 13 configurations in different time slices. To compare different features, we ran different modes that enable a given feature in all of the portfolio configurations. All experiments were performed on the StarExec Iowa servers [28], equipped with Intel Xeon E5-2609 0 CPUs clocked at 2.40 GHz. We set the CPU time limit to 300 s. Figure 1 displays the results. An empty cell indicates that a mode is not evaluated on that benchmark set. An archive with the raw evaluation data is publicly available.Footnote 1
A preprocessing transformation that removes all Boolean subterms occurring as arguments of symbols [34, Sect. 8], similar to Kotelnikov et al.’s FOOL clausification approach [16], is implemented in Zipperposition. To answer question 1, we enabled preprocessing and compared it to our new calculus parameterized with the Boolean selection function that selects the smallest selectable subterm. The mode using our new calculus performs immediate inprocessing clausification, and we call it base, while the mode that preprocesses Boolean subterms is denoted by preprocess in Figure 1.
The obtained results do not give a conclusive answer to question 1. On both TPTP Bool and Sledgehammer problems, some configuration of our new calculus manages to prove one problem more than preprocessing. On SMT-LIB benchmarks, the best configuration of our calculus matches preprocessing. This shows that our calculus already performs roughly as well as previously known techniques and suggests that it will be able to outperform preprocessing techniques after tuning of its parameters.
For context, we provide the evaluation of E on supported benchmarks. On TPTP FO benchmarks it solves 643 problems, on TPTP Bool benchmarks 144 problems, and on Sledgehammer benchmarks 674 problems. Note that there is no straightforward way to compare these results with Zipperposition.
Our base mode uses immediate inprocessing clausification. To answer question 2, we compared base with a variant of base with outer delayed clausification (base+outer) and with a variant with inner delayed clausification (base+inner). In the delayed modes, we invoke the Rename rule on formulas that are discovered to occur more than four times in the proof state.
The results show that inner delayed clausification, which performs the laziest form of clausification, gives the worst results on most benchmark sets. Outer delayed clausification performs roughly as well as immediate clausification on problems targeting our logic. On purely first-order problems, it performs slightly worse than immediate clausification. However, outer delayed clausification solves 17 problems not solved by immediate clausification on these problems. This suggests that it opens new possibilities for first-order reasoning that need to be explored further with specialized strategies and additional rules.
We found a problem with a conjecture of the form  that only the delayed clausification modes can prove: the TPTP problem SWV122+1. The subformula renaming mechanism of immediate clausification obfuscates this problem, whereas delayed clausification allows BoolSimp to convert the negated conjecture to \(\bot \) directly, completing the proof in half a second.
that only the delayed clausification modes can prove: the TPTP problem SWV122+1. The subformula renaming mechanism of immediate clausification obfuscates this problem, whereas delayed clausification allows BoolSimp to convert the negated conjecture to \(\bot \) directly, completing the proof in half a second.
To answer question 3, we compared the mode of Zipperposition in which all rules introduced by our calculus are disabled (off) with base on purely first-order problems. Our results show that both modes perform roughly the same.
To answer question 4, we evaluated the Boolean selection functions we have implemented: syntactically smallest selectable term (used in base), syntactically largest selectable term (sel\(_\mathrm {max}\)), leftmost innermost selectable term (sel\(_\mathrm {li}\)), leftmost outermost selectable term (sel\(_\mathrm {lo}\)), and no Boolean selection (sel\(_\varnothing \)). We also evaluated two modes in which the rules LocalRw and BoolHoistSimp (BHS) are enabled. None of the selection functions influences the performance greatly. Similarly, we observe no substantial difference regardless of whether the rules LocalRw and BoolHoistSimp are enabled.
8 Related Work and Conclusion
The research presented in this paper extends superposition in two directions: with inprocessing clausification and with first-class Booleans. The first direction has been explored before by Ganzinger and Stuber [13], and others have investigated it in the context of other superposition-related calculi [1, 4, 9, 20, 21].
The other direction has been explored before by Kotelnikov et al., who developed two approaches to cope with first-class Booleans [16, 17]. For the quantified Boolean formula fragment of our logic, Seidl et al. developed a translation into effectively propositional logic [26]. More general approaches to incorporate theories into superposition include superposition for finite domains [14], hierarchic superposition [6], and superposition with (co)datatypes [10].
For SMT solvers [22], supporting first-class Booleans is a widely accepted standard [5]. In contrast, the TPTP TFX format [30], intended to promote first-class Booleans in the rest of the automated reasoning community, has yet to gain traction. Software verification tools could clearly benefit from its popularization, as some of them identify terms and formulas in their logic, e.g., Why3 [12].
In conclusion, we devised a refutationally complete superposition calculus for first-order logic with interpreted Booleans. Its redundancy criterion allows us to flexibly add inprocessing clausification and other simplification rules. We believe our calculus is an excellent choice for the basis of new superposition provers: it offers the full power of standard superposition, while supporting rich input languages such as SMT-LIB and TPTP TFX. Even with unoptimized implementation and basic strategies, our calculus matches the performance of earlier approaches. In addition, the freedom it offers in term order, literal and Boolean subterm selection opens possibilities that are yet to be explored. Overall, our calculus appears as a solid foundation for richer logics in which the Boolean type cannot be efficiently preprocessed, such as higher-order logic [8]. In future work, we plan to tune the parameters and would find it interesting to combine our calculus with clause splitting techniques, such as AVATAR [32].
References
Leo Bachmair and Harald Ganzinger. Non-clausal resolution and superposition with selection and redundancy criteria. In Andrei Voronkov, editor, Logic Programming and Automated Reasoning (LPAR’92), volume 624 of LNCS, pages 273–284. Springer, 1992.
Leo Bachmair and Harald Ganzinger. Rewrite-based equational theorem proving with selection and simplification. J. Log. Comput., 4(3):217–247, 1994.
Leo Bachmair and Harald Ganzinger. Resolution theorem proving. In John Alan Robinson and Andrei Voronkov, editors, Handbook of Automated Reasoning, volume I, pages 19–99. Elsevier and MIT Press, 2001.
Leo Bachmair, Harald Ganzinger, David A. McAllester, and Christopher Lynch. Resolution theorem proving. In Handbook of Automated Reasoning, pages 19–99. Elsevier and MIT Press, 2001.
Clark Barrett, Pascal Fontaine, and Cesare Tinelli. The SMT-LIB Standard: Version 2.6. Technical report, Department of Computer Science, The University of Iowa, 2017. Available at www.SMT-LIB.org.
Peter Baumgartner and Uwe Waldmann. Hierarchic superposition with weak abstraction. In Maria Paola Bonacina, editor, CADE-24, volume 7898 of LNCS, pages 39–57. Springer, 2013.
Dan Benanav. Simultaneous paramodulation. In Mark E. Stickel, editor, CADE-10, volume 449 of LNCS, pages 442–455. Springer, 1990.
Alexander Bentkamp, Jasmin Blanchette, Sophie Tourret, and Petar Vukmirović. Superposition for full higher-order logic. In André Platzer and Geoff Sutcliffe, editors, CADE-28, LNCS. Springer, 2021.
Christoph Benzmüller. Extensional higher-order paramodulation and RUE-resolution. In Harald Ganzinger, editor, CADE-16, volume 1632 of LNCS, pages 399–413. Springer, 1999.
Jasmin Christian Blanchette, Nicolas Peltier, and Simon Robillard. Superposition with datatypes and codatatypes. In Didier Galmiche, Stephan Schulz, and Roberto Sebastiani, editors, IJCAR 2018, volume 10900 of LNCS, pages 370–387. Springer, 2018.
Simon Cruanes. Extending Superposition with Integer Arithmetic, Structural Induction, and Beyond. Ph.D. thesis, École polytechnique, 2015.
Jean-Christophe Filliâtre and Andrei Paskevich. Why3—where programs meet provers. In Matthias Felleisen and Philippa Gardner, editors, European Symposium on Programming (ESOP 2013), volume 7792 of LNCS, pages 125–128. Springer, 2013.
Harald Ganzinger and Jürgen Stuber. Superposition with equivalence reasoning and delayed clause normal form transformation. Inf. Comput., 199(1-2):3–23, 2005.
Thomas Hillenbrand and Christoph Weidenbach. Superposition for bounded domains. In Maria Paola Bonacina and Mark E. Stickel, editors, Automated Reasoning and Mathematics, volume 7788 of LNCS, pages 68–100. Springer, 2013.
D. E. Knuth and P. B. Bendix. Simple word problems in universal algebras. In J. Leech, editor, Computational Problems in Abstract Algebra, pages 263–297. Pergamon Press, 1970.
Evgenii Kotelnikov, Laura Kovács, Martin Suda, and Andrei Voronkov. A clausal normal form translation for FOOL. In Christoph Benzmüller, Geoff Sutcliffe, and Raúl Rojas, editors, Global Conference on Artificial Intelligence (GCAI 2016), volume 41 of EPiC, pages 53–71. EasyChair, 2016.
Evgenii Kotelnikov, Laura Kovács, and Andrei Voronkov. A first class Boolean sort in first-order theorem proving and TPTP. In Manfred Kerber, Jacques Carette, Cezary Kaliszyk, Florian Rabe, and Volker Sorge, editors, Intelligent Computer Mathematics (CICM 2015), volume 9150 of LNCS, pages 71–86. Springer, 2015.
Laura Kovács and Andrei Voronkov. First-order theorem proving and Vampire. In Natasha Sharygina and Helmut Veith, editors, Computer Aided Verification (CAV 2013), volume 8044 of LNCS, pages 1–35. Springer, 2013.
Michel Ludwig and Uwe Waldmann. An extension of the Knuth-Bendix ordering with LPO-like properties. In Nachum Dershowitz and Andrei Voronkov, editors, Logic Programming and Automated Reasoning (LPAR 2007), volume 4790 of LNCS, pages 348–362. Springer, 2007.
Zohar Manna and Richard J. Waldinger. A deductive approach to program synthesis. ACM Trans. Program. Lang. Syst., 2(1):90–121, 1980.
Neil V. Murray. Completely non-clausal theorem proving. Artif. Intell., 18(1):67–85, 1982.
Robert Nieuwenhuis, Albert Oliveras, and Cesare Tinelli. Solving SAT and SAT modulo theories: From an abstract Davis–Putnam–Logemann–Loveland procedure to DPLL(T). J. ACM, 53(6):937–977, 2006.
Robert Nieuwenhuis and Albert Rubio. Basic superposition is complete. In Bernd Krieg-Brückner, editor, European Symposium on Programming (ESOP ’92), volume 582 of LNCS, pages 371–389. Springer, 1992.
Andreas Nonnengart and Christoph Weidenbach. Computing small clause normal forms. In Handbook of Automated Reasoning, pages 335–367. Elsevier and MIT Press, 2001.
Visa Nummelin, Alexander Bentkamp, Sophie Tourret, and Petar Vukmirović. Superposition with first-class Booleans and inprocessing clausification (technical report). Technical report, 2021. https://matryoshka-project.github.io/pubs/boolsup_report.pdf.
Martina Seidl, Florian Lonsing, and Armin Biere. qbf2epr: A tool for generating EPR formulas from QBF. In Pascal Fontaine, Renate A. Schmidt, and Stephan Schulz, editors, Practical Aspects of Automated Reasoning (PAAR-2012), volume 21 of EPiC Series in Computing, pages 139–148. EasyChair, 2012.
Alexander Steen. Extensional Paramodulation for Higher-order Logic and Its Effective Implementation Leo-III. Dissertationen zur künstlichen Intelligenz. Akademische Verlagsgesellschaft AKA GmbH, 2018.
Aaron Stump, Geoff Sutcliffe, and Cesare Tinelli. Starexec: A cross-community infrastructure for logic solving. In IJCAR 2014, volume 8562 of LNCS, pages 367–373. Springer, 2014.
Geoff Sutcliffe. The TPTP problem library and associated infrastructure—from CNF to TH0, TPTP v6.4.0. J. Autom. Reason., 59(4):483–502, 2017.
Geoff Sutcliffe and Evgenii Kotelnikov. TFX: the TPTP extended typed first-order form. In Boris Konev, Josef Urban, and Philipp Rümmer, editors, Practical Aspects of Automated Reasoning (PAAR-2018), volume 2162 of CEUR Workshop Proceedings, pages 72–87. CEUR-WS.org, 2018.
Grigori Tseitin. On the complexity of derivation in propositional calculus. In Automation of reasoning: Classical Papers on Computational Logic, volume 2, pages 466–483. Springer, 1983.
Andrei Voronkov. AVATAR: the architecture for first-order theorem provers. In CAV 2014, volume 8559 of LNCS, pages 696–710. Springer, 2014.
Petar Vukmirović and Visa Nummelin. Boolean reasoning in a higher-order superposition prover. In Pascal Fontaine, Konstantin Korovin, Ilias S. Kotsireas, Philipp Rümmer, and Sophie Tourret, editors, Practical Aspects of Automated Reasoning (PAAR-2020), volume 2752 of CEUR Workshop Proceedings, pages 148–166. CEUR-WS.org, 2020.
Petar Vukmirović, Jasmin Blanchette, Simon Cruanes, and Stephan Schulz. Extending a brainiac prover to lambda-free higher-order logic. Accepted in International Journal on Software Tools for Technology Transfer.
Uwe Waldmann, Sophie Tourret, Simon Robillard, and Jasmin Blanchette. A comprehensive framework for saturation theorem proving. In Nicolas Peltier and Viorica Sofronie-Stokkermans, editors, IJCAR 2020, LNCS. Springer, 2020.
Acknowledgment
Martin Desharnais and Jasmin Blanchette generated the Sledgehammer benchmarks. Simon Cruanes helped us with the implementation. The anonymous reviewers, Ahmed Bhayat, Jasmin Blanchette, and Uwe Waldmann suggested textual improvements. The maintainers of StarExec Iowa let us use their service. We thank them all. Nummelin’s research has received funding from the Netherlands Organization for Scientific Research (NWO) under the Vidi program (project No. 016.Vidi.189.037, Lean Forward). Bentkamp and Vukmirović’s research has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program (grant agreement No. 713999, Matryoshka).
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2021 The Author(s)
About this paper
Cite this paper
Nummelin, V., Bentkamp, A., Tourret, S., Vukmirović, P. (2021). Superposition with First-class Booleans and Inprocessing Clausification. In: Platzer, A., Sutcliffe, G. (eds) Automated Deduction – CADE 28. CADE 2021. Lecture Notes in Computer Science(), vol 12699. Springer, Cham. https://doi.org/10.1007/978-3-030-79876-5_22
Download citation
DOI: https://doi.org/10.1007/978-3-030-79876-5_22
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-79875-8
Online ISBN: 978-3-030-79876-5
eBook Packages: Computer ScienceComputer Science (R0)




 , the subterm u is at the top level of a positive literal.
, the subterm u is at the top level of a positive literal. (1)
(1)  ; (2)
; (2)  ,
, 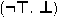 ,
,  ,
, 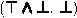 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ; (2)
; (2)  is not a tautology; (5) for
is not a tautology; (5) for  is not a tautology. (In an implementation, the tautology check can be approximated by checking if the affected literal is of the form
is not a tautology. (In an implementation, the tautology check can be approximated by checking if the affected literal is of the form  or
or  .)
.) ) (1) the indicated subterm is eligible in C; (2) y is a fresh variable.
) (1) the indicated subterm is eligible in C; (2) y is a fresh variable.