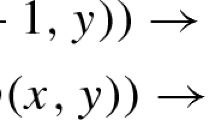Integer Induction in Saturation

Abstract

Integers are ubiquitous in programming and therefore also in applications of program analysis and verification. Such applications often require some sort of inductive reasoning. In this paper we analyze the challenge of automating inductive reasoning with integers. We introduce inference rules for integer induction within the saturation framework of first-order theorem proving. We implemented these rules in the theorem prover Vampire and evaluated our work against other state-of-the-art theorem provers. Our results demonstrate the strength of our approach by solving new problems coming from program analysis and mathematical properties of integers.

1 Introduction

One of the most commonly used data types in imperative/functional programs are integers. For example, iterating over arrays in imperative programs or recursively computing sums in functional programs include integer-valued program variables, as illustrated in Figure 1. While for many uses of integers in programming we only need to consider non-negative integers, there are also applications where integers are essential, for example, reasoning about memory. To formally prove functional correctness of such and similar programs, reasoning about integers is indispensable but so is handling some sort of induction over integers. In this paper we address these two reasoning challenges and fully automate inductive reasoning with integers within saturation-based theorem proving.

Induction in saturation-based theorem proving is a new exciting direction in the automation of induction, recently introduced in [5, 10, 16]. This work focused on induction on inductively defined data types, also called algebraic data types [12], such as natural numbers or lists. However, automating integer induction, that is, induction on integers, has not yet been addressed sufficiently.

While natural numbers have a well-founded order and induction over this order is very useful in automated inductive theorem proving, the standard order on integers is not well-founded, so it cannot be directly used as the induction ordering. In this paper we will use the observation that the standard ordering < is well-founded on every set of integers having a lower bound b and likewise, the inverse > of this ordering is well-founded on every set of integers having an upper bound b. This gives us two induction rules on such integer subsets: induction (with the base case b) using < and induction (with the base case b) using >, respectively, to prove that a property holds for all integers $\ge b$ and, respectively, $\le b$. We define these induction rules as upward, respectively, downward induction rules with symbolic bounds. We also consider two variations of these rules over integer intervals and refer to such rules as interval upward, respectively, downward induction rules with symbolic bounds.

For natural numbers, 0 is an obvious base case candidate, which also turns out to be successful in the theorem proving practice. It is also a natural base case candidate for induction. In this paper we will give some natural problems for which neither 0 nor any concrete integer is a good base case. Our paper focuses on the following three issues:

• 1. proofs of properties of integers by induction on bounded sets of integers in saturation theorem proving, using (interval) downward/upward induction rules with symbolic bounds;

• 2. techniques for discovering a suitable base case;

• 3. implementation techniques.

This paper is organized as follows. In Section 2 we illustrate our approach by considering properties of the functional and imperative programs of Figure 1. Then in Section 3 we define four induction rules over integers, called (interval) downward, respectively upward, induction rules with symbolic bounds, and prove their soundness. Section 4 introduces an extension of superposition calculus by our new integer induction rules. We demonstrate that, using this extension, superposition provers can prove integer properties similarly to how humans would do. This extension is especially successful when used together with the AVATAR architecture [19], since AVATAR helps in reasoning efficiently using constraints coming out of the integer induction rules.

We implemented our work in the Vampire theorem prover [13] and compare our implementation with other relevant provers, including Vampire without integer induction (Section 5). Our experiments show that integer induction can solve many new problems that could not so far be solved by any prover. For example, 75 problems coming from program analysis and/or mathematical integer properties could be solved only by Vampire with the new induction rules.

Contributions. This paper makes the following contributions:

• We introduce four new inference rules for automating integer induction: (interval) downward, respectively upward, induction rules with symbolic bounds (Section 3).

• Based on these rules, we introduce corresponding inference rules for integer induction in the superposition calculus (Section 4). These rules are formulated in the context of saturation-based theorem proving in a way that avoids an immediate combinatorial explosion of the search space.

• We implement and evaluate the new rules in the theorem prover Vampire. Our experimental results show that our implementation can solve a number of problems previously unsolved by any prover (Section 5).

• We introduce a large collection of new inductive benchmarks, publicly available at https://github.com/vprover/inductive_benchmarks.

2 Motivating Examples

2.1 Preliminaries

We assume familiarity with standard many-sorted first-order logic with equality. For details we refer to [13]. Throughout this paper we denote variables by x, y, e, j, n, m, constants by $c, c'$, Skolem constants by $\sigma$, all possibly with indices. We denote terms by t, literals by L, formulas by F and clauses by C. We denote the equality predicate by $=$ and write $t_1 \ne t_2$ for the literal $\lnot (t_1=t_2)$.

We will focus on integer induction. To this end, we assume a distinguished integer sort, denoted by $\mathbb Z$. When we use standard integer predicates <, $\le$, >, $\ge$, functions $+, -, \dots$ and constants $0, 1, 2, \dots$, we assume that they denote the corresponding interpreted integer predicates and functions with their standard interpretations. All other symbols are uninterpreted. We will write quantifiers like $\forall x\in \mathbb Z$ to denote that x has the integer sort.

In what follows, we will sometimes write “this problem requires integer induction”. This should not be regarded as a formal statement: this property is not easy to formalize in general and it is possible that some of these problems can be proved by certain combinations of decision procedures, first-order theorem proving with uninterpreted functions, and axiomatization of interpreted functions on integers. However, when we make such statements, one can see that these problems have relatively simple proofs involving induction and cannot be proved by existing provers without induction.

2.2 Examples

To illustrate problems arising in automating integer induction, let us consider the programs of Figure 1. Properties of both programs are specified using assertions expressed in first-order logic, with pre- and post-conditions specified by the keywords assume and assert, respectively.

Fig. 1.

Motivating examples for inductive reasoning with integers.

Functional programs. The ML-style functional program of Figure 1(a) computes the sum $\mathtt {sum}(n,m)$ of integers in the interval [n, m], that is $\sum _{i=n}^m i$, where $m \ge n$. The function definition uses the following axioms of $\mathtt {sum}$:

$$\begin{aligned} \forall n\in \mathbb Z. (\mathtt {sum}(n, n) = n); \end{aligned}$$

(1)

$$\begin{aligned} \forall n, m\in \mathbb Z. (n \ne m \rightarrow \mathtt {sum}(n, m) = n + \mathtt {sum}(n+1, m) ). \end{aligned}$$

(2)

We should prove the assertion

$$\begin{aligned} \forall n, m\in \mathbb Z.(n\le m\rightarrow 2\cdot \mathtt {sum}(n, m) = m\cdot (m+1) - n\cdot (n-1)). \end{aligned}$$

(3)

Formally proving (3) requires inductive reasoning with both integers and quantifiers. Let F[x] be a formula with one or more occurrences of an integer variable x and b an integer term not containing x. Consider the following formula:

$$\begin{aligned} F[b]\wedge \forall x\in \mathbb Z. (x\le b \wedge F[x] \rightarrow F[x-1]) \rightarrow \forall x\in \mathbb Z.(x\le b \rightarrow F[x]). \end{aligned}$$

(4)

This formula is valid. It is similar to the standard induction on natural numbers, yet with two essential differences. First, we use $x - 1$ instead of $x + 1$ and second, we use the term b where for the standard induction we would use 0. Note that b does not have to be a concrete integer, it can be any term. In the sequel we will refer to such terms b used in induction rules as symbolic bounds.

For proving (3) using a theorem prover, we first negate and skolemize (3), obtaining the following formula, where $\sigma _n, \sigma _m$ are fresh skolem constants:

$$\begin{aligned} \sigma _n\le \sigma _m\wedge 2 \cdot \mathtt {sum}(\sigma _n, \sigma _m) \not = \sigma _m\cdot (\sigma _m+1) - \sigma _n\cdot (\sigma _n-1) \end{aligned}$$

(5)

Modern theorem provers implementing linear integer arithmetic and quantifiers can prove unsatisfiability of (1), (2) and (5) in a relatively straightforward way if we also add an instance of induction rule (4) with

$$ \begin{array}{rcl} F[x] &{} {\mathop {=}\limits ^{\mathrm {def}}}&{} 2 \cdot \mathtt {sum}(x,\sigma _m) = \sigma _m\cdot (\sigma _m+1) - x\cdot (x-1); \\ b &{} {\mathop {=}\limits ^{\mathrm {def}}}&{} \sigma _m. \end{array} $$

Here and in the sequel ${\mathop {=}\limits ^{\mathrm {def}}}$ means “equal by definition” or “defined as”. If we want to automate this kind of reasoning, the main question is finding the corresponding instance of induction rule (4), that is, finding the induction formula F[x] and the (symbolic) bound b.

Imperative programs. The C-style imperative program of Figure 1(b) initializes an integer-valued array $\mathrm {A}$ starting at the index $pos$. We should prove the assertion stating that all array elements at indices greater than or equal to $pos$ are equal to each other. Proving such assertions typically requires loop invariants “summarizing” the loop behavior. One such invariant I is shown in the loop after the keyword inv. This invariant I could be derived by existing approaches to invariant generation [8, 9].

The assertion of Figure 1(b) is then proved using I, by establishing that the post-condition

$$\begin{aligned} \forall j \in \mathbb Z. ( pos \le j<\mathrm {A.size}\rightarrow \mathtt {val}_\mathrm {A}(j) = \mathtt {val}_\mathrm {A}( pos )) \end{aligned}$$

(6)

is a logical consequence of the invariant I and the negation of the loop condition:

$$\begin{aligned} \begin{array}{l} \forall j \in \mathbb Z. ( pos \le j< i \rightarrow \mathtt {val}_\mathrm {A}(j+1)=\mathtt {val}_\mathrm {A}(j));\\ \lnot (i+1 < \mathrm {A.size}). \end{array} \end{aligned}$$

(7)

Interestingly, modern theorem provers cannot perform such proofs. Similar to the first example, we can use an induction rule for integers formulated as follows:

$$\begin{aligned} \begin{array}{l} \big (F[b_1]\wedge \forall x\in \mathbb Z. (b_1\le x < b_2 \wedge F[x] \rightarrow F[x+1]) \big ) \\ \quad \quad \rightarrow \forall x\in \mathbb Z.(b_1\le x \le b_2 \rightarrow F[x]). \end{array} \end{aligned}$$

(8)

If we add an instance of this rule defined as follows:

$$ \begin{array}{rcl} F[x] &{} {\mathop {=}\limits ^{\mathrm {def}}}&{} \mathtt {val}_\mathrm {A}(x) = \mathtt {val}_\mathrm {A}( pos ); \\ b_1 &{} {\mathop {=}\limits ^{\mathrm {def}}}&{} pos ; \\ b_2 &{} {\mathop {=}\limits ^{\mathrm {def}}}&{} \mathrm {A.size}- 1, \end{array} $$

then state-of-the-art theorem provers can easily prove that (6) is a logical consequence of (7) and the corresponding instance of (8). For example, Cvc4  [1], Z3  [6] and Vampire prove such an instance in essentially no time. However, similarly to the example of Figure 1(a), in order to find such proofs automatically using the induction rule of (8), we need to be able to discover, during the proof search, the induction formula F[x] and the symbolic bounds $b_1,b_2$. In what follows, we describe our solution to automating this discovery by integrating integer induction within saturation-based theorem proving.

3 Integer Induction

In this section we define four induction rules, or induction schemas, on integers. Two of them were already considered in Section 2 – namely (4) and (8).

Definition 1 (Downward/Upward Induction)

A downward, respectively upward, induction axiom with symbolic bounds is any formula of the form

respectively, where F[x] is a formula with one or more occurrences of an integer variable x and b is an integer term not containing x.   $\square$

Note that (4) is a downward induction axiom with symbolic bounds.

Definition 2 (Interval Downward/Upward Induction)

An interval downward, respectively upward, induction axiom with symbolic bounds is any formula of the form

respectively, where F[x] is a formula with one or more occurrences of an integer variable x and $b_1,b_2$ are integer terms not containing x.   $\square$

Note that (8) is an interval upward induction axiom with symbolic bounds. The main motivation for interval induction rules is their utility in reasoning about loops, as illustrated by the example of Figure 1(a). While interval induction can be captured by induction with one bound, it would require additional case analysis, which is not efficient in saturation-based proving practice.

In the sequel, we will refer to the integer terms of $b,b_1,b_2$ from Definitions 1-2 as symbolic bounds and the formulas F[x] from the induction axioms of Definitions 1-2 as induction formulas.

Definition 3 (Downward/Upward Induction Rules)

The downward (respectively, upward) induction rule with symbolic bounds, or simply downward (respectively, upward) induction rule is the inference rule whose instances are all downward (respectively, upward) induction axioms with symbolic bounds.

Likewise, the interval downward (respectively, upward) induction rule with symbolic bounds, or simply interval downward (respectively, upward) induction rule is the inference rule whose instances are all interval downward (respectively, upward) induction axioms with symbolic bounds.    $\square$

It is easy to see that the following theorem holds.

Theorem 1 (Soundness)

The (interval) downward/upward induction rules of Definition 3 are sound, that is, all corresponding induction axioms from Definitions 1-2 are valid.   $\square$

4 Integer Induction in Saturation-Based Proof Search

Our next aim is to define analogues of the induction rules introduced in Section 3 that can be used in superposition theorem provers and their saturation algorithms. For a general discussion of superposition and saturation we refer to [13]. In this section we use $\square$ to denote the empty clause and write $\text {CNF}(F)$ to mean (any) clausal normal form of a formula F. We refer to the set of clauses on which a saturation algorithm operates as the search space.

The most general way to introduce our new induction rules at the calculus level is to add clausal forms of our new induction axioms to the search space. That is, for every induction axiom F from Section 3, we add the rule

However, we cannot efficiently implement such a calculus, as any formula with one variable can be used as an induction formula. We will therefore introduce different, more specialized, rules, which still correspond to the previously defined induction rules. The new rules use variations of the following three ideas:

• 1. Use only simple induction formulas, for example literals;

• 2. To find an induction formula, generalize a subgoal occurring in the search space. Then the derived induction formula can be immediately used to prove this subgoal;

• 3. Use (symbolic) bounds that correspond to bounds already occurring in the search space.

The first two ideas were already used in the first papers underlying our approach to induction in saturation theorem proving [10, 16]. For example, they can be implemented by using only induction formulas that are obtained from ground literals L[t] in the search space, where t is a ground term. The corresponding induction formula will be $\lnot L[x]$. The idea is that, when we prove the induction formula, $\lnot L[x]$ will be resolved against L[t].

The third idea is new. Note that, if we use the first two ideas and the upward induction rule, instead of $\lnot L[x]$ we will derive $b \le x \rightarrow \lnot L[x]$. When we resolve this against L[t], we obtain the clause $\lnot (b \le t)$. However, if we already previously derived $b \le t$, we can also resolve away $\lnot (b \le t)$. This gives us the idea to only apply the upward induction rules when we have $b \le t$.¹

Based on the three ideas above, we introduce the following four induction rules on clauses. In these rules t is a ground term, b is a constant and L[x] is a literal containing at least one occurrence of a variable x and no other variables. The rules depend on which comparisons among $t\ge b$, $t>b$, $t\le b$ and $t<b$ already occur in the current search space:

Note that $\texttt {IntInd}_{\ge }$ and $\texttt {IntInd}_{>}$ are upward induction rules, whereas $\texttt {IntInd}_{\le }$ and $\texttt {IntInd}_{<}$ are downward induction rules. One can also introduce non-ground analogues of these rules but we do not consider them in this paper.

Similarly to the above rules on the clausal level, we also introduce the interval upward/downward induction rules on clauses to be used in saturation algorithms for the superposition calculus. Since these rules are similar to each other, here we only define one rule $\texttt {IntInd}_{[\ge ]}$ for interval upward induction. For a ground term t, constants $b_1, b_2$, and L[x] a literal containing at least one occurrence of a variable x and no other variables, an interval upward induction rule on clauses:

In view of Theorem 1, all induction rules of Section 3 are sound. Assuming that our CNF function preserves satisfiability, we conclude that all our induction rules $\texttt {IntInd}_{\ge }$, $\texttt {IntInd}_{>}$, $\texttt {IntInd}_{\le }$, $\texttt {IntInd}_{<}$ and $\texttt {IntInd}_{[\ge ]}$ on the clausal level are sound.

Theorem 2 (Soundness)

For every satisfiability preserving CNF function, the induction rules from Definition 3 are sound.    $\square$

Example 1

To illustrate again how the choice of induction formulas allows us to have shorter clauses, consider $\texttt {IntInd}_{\le }$. The CNF in its conclusion consists of three clauses:

$$\begin{aligned} \begin{array}{l} \lnot L[b] \vee \sigma \le b \vee \lnot y \le b \vee L[y] \\ \lnot L[b] \vee L[\sigma ] \vee \lnot y \le b \vee L[y] \\ \lnot L[b] \vee \lnot L[\sigma - 1] \vee \lnot y \le b \vee L[y] \end{array} \end{aligned}$$

(9)

These clauses can be resolved against premises of $\texttt {IntInd}_{\le }$, yielding the following clauses:

$$\begin{aligned} \begin{array}{l} \lnot L[b] \vee \sigma \le b \vee C \\ \lnot L[b] \vee L[\sigma ] \vee C \\ \lnot L[b] \vee \lnot L[\sigma - 1] \vee C \end{array} \end{aligned}$$

(10)

They have an especially simple form when C is the empty clause $\square$. In this case we have three clauses:

$$\begin{aligned} \begin{array}{l} \lnot L[b] \vee \sigma \le b \\ \lnot L[b] \vee L[\sigma ] \\ \lnot L[b] \vee \lnot L[\sigma - 1] \end{array} \end{aligned}$$

(11)

which subsume the original three longer clauses and are ground. Since they are ground, they can be handled efficiently by AVATAR.   $\square$

Example 2

Let us now demonstrate how the downward induction rule $\texttt {IntInd}_{\le }$ works for refuting the inductive property (3) from our motivating example of Figure 1(a). We use literals from (5) as the premises of the $\texttt {IntInd}_{\le }$ rule. The corresponding instance of the downward induction rule is defined by

$$ \begin{array}{rcl} b &{} {\mathop {=}\limits ^{\mathrm {def}}}&{} \sigma _m; \\ t &{} {\mathop {=}\limits ^{\mathrm {def}}}&{} \sigma _n; \\ L[x] &{} {\mathop {=}\limits ^{\mathrm {def}}}&{} 2 \cdot \mathtt {sum}(x,\sigma _m) = \sigma _m\cdot (\sigma _m+1) - x\cdot (x-1). \end{array} $$

This instance of $\texttt {IntInd}_{\le }$ is:

This single instance of the induction rule does the magic. By adding its conclusion to the search space we can obtain a contradiction in a few steps by applying a few superposition rules and using ground reasoning in linear integer arithmetic with uninterpreted functions (as evidenced by the results for the first problem subset, x_all of sum, in Table 3).

We finally note that functional correctness of Figure 1(b) is proved by the interval upward induction rule $\texttt {IntInd}_{[\ge ]}$, in a similar way as above (and as evidenced by the results of Table 3 for declared_unint_ax-fin_conj-fin in val).    $\square$

What we find especially interesting in Example 2 is that the induction axiom used in it (and discovered by our implementation of induction in Vampire) uses the induction argument that would probably be used by a majority of humans who would try to argue why the program property holds.

5 Implementation and Experiments

5.1 Implementation

We implemented our integer induction rules $\texttt {IntInd}_{\ge }$, $\texttt {IntInd}_{>}$, $\texttt {IntInd}_{\le }$, $\texttt {IntInd}_{<}$ as well as $\texttt {IntInd}_{[\ge ]}$ and the other corresponding interval induction rules in Vampire. Further, we also implemented a more general induction rule IntInd that does not require bounds to be in the search space and uses 0 as the lower or the upper bound. Our implementation in Vampire, consisting of approximately 1,200 lines of new C++ code, is available at https://github.com/vprover/vampire. The size of this additional code is relatively small because Vampire has libraries for indexing and chaining inference rules that could be used off the shelf.

Our (interval) downward/upward induction rules described in Section 4 can be applied when either (i) the comparison literal (e.g., $t\ge b$ for the $\texttt {IntInd}_\ge$ rule) is selected and the corresponding clause $\lnot L[t] \vee C$ was already selected as an induction candidate before, or (ii) if $\lnot L[t] \vee C$ is selected as an induction candidate and the corresponding comparison literal was already selected before. To implement these rules efficiently, we should be able to efficiently retrieve comparison literals and literals selected for induction. To do so, we extended the indexing mechanism of Vampire to index such literals. We do not apply induction when the induction formula L[x] is a comparison having x as a top level argument, for example, $x \le t$, and allow to apply it to all other induction formulas deemed to be suitable by other user-specified options.

Our (interval) downward/upward induction rules in Vampire are enabled by the new option --induction int. The options --int_induction_interval infinite and --int_induction_interval finite limit the enabled rules to downward/upward only, and interval downward/upward only, respectively. Further, --int_induction_default_bound on enables the more general rule which does not require bounds to be in the search space. Our new induction rules can also be controlled by other Vampire options for well-founded/structural induction, such as --induction_on_complex_terms on, which enables applying induction on any ground complex term. To improve Vampire ’s performance for integer induction, we combined our new induction rules with --induction_on_complex_terms on and also other options not specific for induction. We extended Vampire with a new mode scheduling various option configurations for integer induction, switched on by the option --mode portfolio --schedule integer_induction. Additionally, we introduced the option --schedule induction which uses either the integer induction configurations as for --schedule integer_induction, or structural induction configurations, or both, depending on the data types used in the problem/property to be proved.

Fig. 2.

ML-like functional program computing integer powers for positive exponents.

5.2 Benchmarks

We used two sets of examples: (i) benchmark sets LIA and UFLIA from the SMT-LIB collection [2], consisting of, respectively, 607 and 10,137 examples, and (ii) 120 new benchmarks similar to our motivating examples from Section 2.

To the best of our knowledge, the state-of-the-art systems implementing inductive reasoning have so far not yet considered inductive reasoning over integers, with two exceptions: [17], which mainly focuses on induction over inductively defined data types but mentions induction on non-negative integers and [11], which supports inductive reasoning using recursive function definitions without any special treatment for integers.

Since integer induction has not yet attracted enough attention in theorem proving, there is no significant collection of benchmarks for integer induction. To properly carry out experiments, we therefore created a set of 120 new benchmarks based on variations of our motivating examples from Section 2 and on properties of computing integer powers. One example is the function correctness of the program of Figure 2, which is formalized as follows:

$$\begin{aligned} \begin{aligned} \text {axioms: }\quad&\forall x \in \mathbb Z. (\mathtt {power}(x, 1) = x)\\ \quad&\forall x, e \in \mathbb Z. (2\le e \rightarrow \mathtt {power}(x, e) = x\cdot \mathtt {power}(x, e-1)) \\ \text {conjecture: }\quad&\forall x, y, e.(1 \le e \rightarrow \mathtt {power}(x\cdot y, e) = \mathtt {power}(x, e)\cdot \mathtt {power}(y, e)) \end{aligned} \end{aligned}$$

(12)

Our set of 120 new benchmarks is described in Table 1 and available online at:

https://github.com/vprover/inductive_benchmarks

Table 1. Description of our benchmark set of 120 new examples.

To confirm that our new benchmarks require the use of inductive reasoning, we tested them on the SMT solver Z3  [6] that does not support induction. Z3 could not solve any of the 120 problems from our benchmark set. Names of subsets of our new benchmarks are constructed by joining variant tags described in Table 1. For example, problem (6) belongs to the category declared_unint_ax-fin_conj-fin of the set val. The following benchmark:

$$\begin{aligned} \begin{aligned} \text {axiom: }\quad&\forall x\in \mathbb Z. (\mathtt {val}(x) = \mathtt {val}(x+1)) \\ \text {conjecture: }\quad&\forall x, y \in \mathbb Z. (\mathtt {val}(x) = \mathtt {val}(y)) \end{aligned} \end{aligned}$$

(13)

belongs to declared_unint_ax-all_conj-all of val and the below example is from defined_inter_ax-geq_conj-geq of val:

$$\begin{aligned} \begin{aligned} \text {axioms: }\quad&\forall x\in \mathbb Z. (x \le 0 \rightarrow \mathtt {val}(x) = 0) \\ \quad&\forall x\in \mathbb Z. (0 < x \rightarrow \mathtt {val}(x) = \mathtt {val}(x-1)) \\ \text {conjecture: }\quad&\forall x \in \mathbb Z. ( 0\le x \rightarrow \mathtt {val}(x) = \mathtt {val}(0)) \end{aligned} \end{aligned}$$

(14)

While 9 of the benchmarks (all in val) use finite intervals in both the assertion and the invariant (ax-fin_conj-fin), the remaining 111 benchmarks require inductive reasoning over infinite intervals.

5.3 Experimental Setup

We ran our experiments on computers with 32 cores (AMD Epyc 7502, 2.5 GHz) and 1 TB RAM. In all experiments we used the memory limit of 16 GB per problem. For the new benchmarks we used a 300 seconds time limit. For the experiments on the larger LIA and UFLIA sets we used a 10 seconds time limit.

In what follows, Vampire refers to the (default) version of Vampire, as in [10, 16]. By Vampire-I we denote our new version of Vampire, using integer induction rules (--induction int). Vampire-I * refers to the portfolio mode of Vampire-I, scheduling various option configurations for integer induction (--mode portfolio --schedule induction).

For experiments with the new benchmarks, we note that Vampire without integer induction cannot solve any of the problems. In this set of experiments, we therefore compared Vampire-I to the provers Cvc4  [17] and Acl2  [11], which are, to the best of our knowledge, the only two automated solvers supporting inductive reasoning with integers in addition to reasoning with theories and quantifiers. For Cvc4, we used the ig configuration from [17]: --quant-ind --quant-cf --conjecture-gen --conjecture-gen-per-round=3 --full-saturate-quant. For Acl2, we used its default configuration and translated our new problem set into the functional program encoding syntax of Acl2. In the experiments with the LIA and UFLIA benchmark sets of SMT-LIB, we also used Z3  [6] in the default configuration.

We ran Cvc4, Z3, Vampire and Vampire-I on problems encoded in the SMT-LIB2 syntax [2]. For running Acl2 on the new benchmarks, we translated problems into the functional program encoding syntax of Acl2.

Table 2. Comparison of solvers on SMT-LIB benchmarks.

5.4 Experimental Results

SMT-LIB Benchmarks. First, we evaluated the improvements of integer induction in Vampire-I when compared to Vampire, Cvc4 and Z3 on the LIA and UFLIA sets of SMT-LIB [2]. We aimed to verify that Vampire-I ’s performance does not deteriorate due to adding integer induction, check whether Vampire-I can solve problems that could not be solved automatically before, and to identify the best values for options related to integer induction. To this end, we picked five different strategies (e.g. using different saturation algorithms and selection functions) and used different combinations of induction options. Table 2 summarizes our results, showcasing that integer induction enabled Vampire-I to solve over 100 new problems that Vampire could not solve before (last but one column of Table 2). Moreover, 45 of these problems were also new compared to Cvc4 and Z3 (last column of Table 2), which most likely means that no theorem prover was able to prove them before.

In problems solved using integer induction, the integer induction rules were applied often: at least one of the interval induction rules was used in nearly 99% of problems, while one of the induction rules with one bound was used in nearly all problems. The interval induction and induction rules were used on average 4559 and 1191 times, respectively. 89% of the proofs employed interval induction (67% upward, 29% downward), while 27% of the proofs used induction with one bound (22% upward, 8% downward). Additionally, over 64% of proofs only required one application of any induction rule.

Table 3. Experiments with our new benchmarks from Table 1.

Experiments with 120 New Benchmarks. Comparison results for Vampire-I, Acl2 and Cvc4 on our new benchmarks are displayed in Table 3, aggregated by benchmark subsets, as described in Table 1. We do not show Vampire in the table, since without integer induction it cannot solve any of the problems.

The results show that in some cases Acl2 can perform upward and downward induction on integers, but only when using interpreted constants as a base case (that is, it cannot handle symbolic bounds). However, it can only do so if it also proves termination of the recursively defined function. It also has issues with reasoning about multiplication.

Cvc4 has limited support for integer induction: it can apply upward induction but only when the base case is an interpreted constant. Since some problems seem to require induction with symbolic bounds, Cvc4 is mostly able to either solve all problems in a subset, or none of them. The only exception is the subset declared_mixed_ax-fin_conj-fin, in which Cvc4 solves one problem, which can be solved using upward induction with an interpreted constant as the base case.

Vampire-I * does not have any conceptual problems with solving the benchmarks. However, since it uses axioms and inference rules rather than dedicated decision procedures for handling integers, it sometime has issues with solving problems with large integer values. For example, for the infinite interval subset of the val benchmark set, the only problems Vampire-I * did not solve were those containing the interpreted constant 100 or -100. Similarly, in the power benchmark set, the unsolved problems contained large numbers. Finally, in the declared_mixed_ax-fin_conj-fin subset, the two problems Vampire-I * did not solve also required more sophisticated arithmetic reasoning. However, inability of efficiently dealing with large numbers is not an intrinsic problem of superposition theorem provers. Reasoning with quantifiers and theories is still in its infancy and major improvements are underway. For example, there are recent parallel developments in superposition and linear arithmetic [15] that should improve this kind of reasoning in Vampire.

6 Related Work

Previous works on automating induction mainly focused on inductive reasoning for inductively defined data types, for example in inductive theorem provers Acl2  [11], IsaPlanner [7], HipSpec [4], Zeno [18] and Imandra [14]; superposition theorem provers Zipperposition [5] and Vampire  [16]; and the SMT solver Cvc4  [17]. While most of these solvers support reasoning with integers, only Acl2 and Cvc4 implement some form of induction over integers.

The Acl2 approach [11] generates induction schemas based on recursive function calls in the property to be proved. Hence, it can only use induction to solve problems properties of recursively defined functions. On the other hand, the SMT-based setting of Cvc4  [17] applies induction by inductive strengthening of SMT properties in combination with subgoal discovery. As noted in Section 5, Cvc4 is limited to induction with concrete base cases and upward induction.

While downward integer induction can be considered a straightforward generalization of upward integer induction and does not solve many more problems in our benchmark sets, symbolic bounds provide a very powerful generalization, as witnessed by experimental results. In automated reasoning, the power provided by more general rules comes with the price of uncontrollable blowup of the search space. To harness this power we came up with defining (interval) upward/downward induction rules with symbolic bounds in the superposition calculus in such a way that they result in most cases in the addition of very simple clauses, which can be efficiently handled within the AVATAR architecture.

We believe that variants of our induction rules defined in Section 4 can also be successfully used by SMT solvers. The idea is to apply them, like we do, only when there is a suitable bound in the current candidate model. One can also combine this with the observation made in Example 1: one can resolve added induction formulas against literals already occurring in the search space to add only ground formulas.

The benchmark suite we propose and use in this paper is new and can be used to complement existing benchmarks: the TIP library [3] and the examples of [17]. Our 120 new examples are however more focused on integer properties, whereas [3, 17] contain a variety of problems mostly requiring induction over inductively defined types. Specifically, out of more than 500 inductive problems in TIP [3], only 3 use integers and no inductive data types. The examples from [17] contain 311 inductive benchmarks translated into three encodings, (i) using only inductive data types, (ii) using integers instead of natural numbers, but also other inductive data types (such as lists or trees), and (iii) using both integers and natural numbers to express the same properties, alongside other inductive data types. Problems from (iii) are also included in SMT-LIB [2]. Note that there is a substantial difference between our benchmarks and benchmarks from (ii). The latter mostly require inductive reasoning only for inductive data types (or no induction at all): they contain integers but only a few of them require inductive reasoning over integers, while most of our benchmarks require proper integer induction. For example, Vampire can solve 131 of 306 benchmarks in (ii) without using integer induction.

7 Conclusions

We introduced new inference rules for automating inductive reasoning with integers within saturation-based theorem proving. Many problems in program analysis and mathematical problems of integers previously unsolvable by any theorem prover can now be solved completely automatically. We believe our results can progress automated program analysis and automation of mathematics, where integers are universally used.