Abstract
Multiobjective optimization plays an increasingly important role in modern applications, where several objectives are often of equal importance. The task in multiobjective optimization and multiobjective optimal control is therefore to compute the set of optimal compromises (the Pareto set) between the conflicting objectives. Since the Pareto set generally consists of an infinite number of solutions, the computational effort can quickly become challenging which is particularly problematic when the objectives are costly to evaluate as is the case for models governed by partial differential equations (PDEs). To decrease the numerical effort to an affordable amount, surrogate models can be used to replace the expensive PDE evaluations. Existing multiobjective optimization methods using model reduction are limited either to low parameter dimensions or to few (ideally two) objectives. In this chapter, we present a combination of the reduced basis model reduction method with a continuation approach using inexact gradients. The resulting approach can handle an arbitrary number of objectives while yielding a significant reduction in computing time.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
References
S. Banholzer, D. Beermann, and S. Volkwein. POD-Based Bicriterial Optimal Control by the Reference Point Method. IFAC-PapersOnLine, 49(8):210–215, 2016.
S. Banholzer, D. Beermann, and S. Volkwein. POD-Based Error Control for Reduced-Order Bicriterial PDE-Constrained Optimization. Annual Reviews in Control, 44:226–237, 2017.
D. Beermann, M. Dellnitz, S. Peitz, and S. Volkwein. POD-based multiobjective optimal control of PDEs with non-smooth objectives. In Proceedings in Applied Mathematics and Mechanics (PAMM), pages 51–54, 2017.
D. Beermann, M. Dellnitz, S. Peitz, and S. Volkwein. Set-Oriented Multiobjective Optimal Control of PDEs using Proper Orthogonal Decomposition. In Reduced-Order Modeling (ROM) for Simulation and Optimization, pages 47–72. Springer, 2018.
A. Buffa, Y. Maday, A. T. Patera, C. Prudhomme, and G. Turinici. A priori convergence of the greedy algorithm for the parametrized reduced basis method. ESAIM: Mathematical Modelling and Numerical Analysis, 46(3):595–603, 2012.
T. Chugh, K. Sindhya, J. Hakanen, and K. Miettinen. A survey on handling computationally expensive multiobjective optimization problems with evolutionary algorithms. Soft Computing, pages 1–30, 2017.
C. A. Coello Coello, G. B. Lamont, and D. A. Van Veldhuizen. Evolutionary Algorithms for Solving Multi-Objective Problems, volume 2. Springer Science & Business Media, 2007.
M. Dellnitz, O. Schütze, and T. Hestermeyer. Covering Pareto Sets by Multilevel Subdivision Techniques. Journal of Optimization Theory and Applications, 124(1):113–136, Jan 2005.
M. Ehrgott. Multicriteria optimization. Springer Berlin Heidelberg New York, 2 edition, 2005.
B. Gebken, S. Peitz, and M. Dellnitz. On the hierarchical structure of Pareto critical sets. Journal of Global Optimization, 73(4):891–913, 2019.
M. A. Grepl and A. T. Patera. A posteriori error bounds for reduced-basis approximations of parametrized parabolic partial differential equations. ESAIM: Mathematical Modelling and Numerical Analysis, 39(1):157–181, 2005.
B. Haasdonk, J. Salomon, and B. Wohlmuth. A reduced basis method for the simulation of American options. In Numerical Mathematics and Advanced Applications 2011, pages 821–829, Berlin, Heidelberg, 2013. Springer Berlin Heidelberg.
J. Hesthaven, G. Rozza, and B. Stamm. Certified reduced basis methods for parametrized partial differential equations. SpringerBriefs in Mathematics, 2016.
C. Hillermeier. Nonlinear Multiobjective Optimization: A Generalized Homotopy Approach. Birkhäuser Basel, 2001.
M. Hinze, R. Pinnau, M. Ulbrich, and S. Ulbrich. Optimization with PDE Constraints. Springer, 2009.
L. Iapichino, S. Trenz, and S. Volkwein. Multiobjective optimal control of semilinear parabolic problems using POD. In B. Karasözen, M. Manguoglu, M. Tezer-Sezgin, S. Goktepe, and Ö. Ugur, editors, Numerical Mathematics and Advanced Applications (ENUMATH 2015), pages 389–397. Springer, 2016.
L. Iapichino, S. Ulbrich, and S. Volkwein. Multiobjective PDE-Constrained Optimization Using the Reduced-Basis Method. Advances in Computational Mathematics, 43(5):945–972, 2017.
K. Kunisch and S. Volkwein. Galerkin proper orthogonal decomposition methods for parabolic problems. Numerische Mathematik, 90(1):117–148, 2001.
J. Lee. Introduction to Smooth Manifolds. Springer-Verlag New York, 2012.
M. Ohlberger and F. Schindler. Non-conforming localized model reduction with online enrichment: Towards optimal complexity in PDE constrained optimization. In Finite Volumes for Complex Applications VIII - Hyperbolic, Elliptic and Parabolic Problems, pages 357–365. Springer International Publishing, 2017.
S. Peitz and M. Dellnitz. Gradient-Based Multiobjective Optimization with Uncertainties, pages 159–182. Springer International Publishing, 2017.
S. Peitz and M. Dellnitz. A Survey of Recent Trends in Multiobjective Optimal Control Surrogate Models, Feedback Control and Objective Reduction. Mathematical and Computational Applications, 23(2), 2018.
S. Peitz, S. Ober-Blöbaum, and M. Dellnitz. Multiobjective Optimal Control Methods for the Navier-Stokes Equations Using Reduced Order Modeling. Acta Applicandae Mathematicae, 161(1):171–199, 2019.
S. Peitz, K. Schäfer, S. Ober-Blöbaum, J. Eckstein, U. Köhler, and M. Dellnitz. A Multiobjective MPC Approach for Autonomously Driven Electric Vehicles. IFAC PapersOnLine, 50(1):8674–8679, 2017.
A. Quarteroni, A. Manoni, and F. Negri. Reduced Basis Methods for Partial Differential Equations. Springer, 2016.
G. Rozza, D. B. P. Huynh, and A. T. Patera. Reduced basis approximation and a posteriori error estimation for affinely parametrized elliptic coercive partial differential equations. Archives of Computational Methods in Engineering, 15(3):1, 2007.
O. Schütze, A. Dell’Aere, and M. Dellnitz. On Continuation Methods for the Numerical Treatment of Multi-Objective Optimization Problems. In Practical Approaches to Multi-Objective Optimization, number 04461 in Dagstuhl Seminar Proceedings, Dagstuhl, Germany, 2005. Internationales Begegnungs- und Forschungszentrum für Informatik (IBFI), Schloss Dagstuhl, Germany.
O. Schtze, O. Cuate, A. Martn, S. Peitz, and M. Dellnitz. Pareto explorer: a global/local exploration tool for many-objective optimization problems. Engineering Optimization, pages 1–24, 05 2019.
L. Sirovich. Turbulence and the dynamics of coherent structures part I: coherent structures. Quarterly of Applied Mathematics, XLV(3):561–571, 1987.
M. Tabatabaei, J. Hakanen, M. Hartikainen, K. Miettinen, and K. Sindhya. A survey on handling computationally expensive multiobjective optimization problems using surrogates: non-nature inspired methods. Structural and Multidisciplinary Optimization, 52(1):1–25, 2015.
Acknowledgements
This research was funded by the DFG Priority Programme 1962 “Non-smooth and Complementarity-based Distributed Parameter Systems”.
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Appendix A: Proof of Theorem 2.10
Appendix A: Proof of Theorem 2.10
To prove Theorem 2.10, we first have to investigate some of the properties of the optimization problem (2.6). This problem is quadratic with linear equality and inequality constraints. We will first investigate the uniqueness of the solution in the following lemma.
Lemma A.1
Let u ∈ φ−1(0) and let α1 and α2 be two solutions of (2.6) with α1 ≠ α2 . Then ω(α) = 0 for all α ∈ span({α1, α2}) and
Proof
For \(c_1, c_2 \in \mathbb {R} \setminus \{ 0 \}\) we have
From ω(α1) = ω(α2) = 0 it follows that 𝜖⊤ α1 = ∥DJr(u)⊤ α1∥ and 𝜖⊤ α2 = ∥DJr(u)⊤ α2∥. Let \(\sphericalangle \) be the angle between DJr(u)⊤ α1 and DJr(u)⊤ α2. Then
Assume \(cos(\sphericalangle ) \neq 1\) (i.e., \(cos(\sphericalangle ) - 1 < 0\)), ∥DJr(u)⊤
α1∥≠ 0, and ∥DJr(u)⊤
α2∥≠ 0. If we choose c
1 = t and c
2 = 1 − t for t ∈ (0, 1), then tα1 + (1 − t)α2 ∈ Δk and ω(tα1 + (1 − t)α2) < 0, which contradicts u ∈ φ−1(0). If ∥DJr(u)⊤
α1∥ = 0 or ∥DJr(u)⊤
α2∥ = 0, then (A.1) holds for  or
or  , respectively. If \(cos(\sphericalangle ) - 1 = 0\), then DJr(u)⊤
α1 and DJr(u)⊤
α2 are linearly dependent, so there are
, respectively. If \(cos(\sphericalangle ) - 1 = 0\), then DJr(u)⊤
α1 and DJr(u)⊤
α2 are linearly dependent, so there are  ,
,  such that
such that  for
for  . In particular, in any case we must have ω(α) = 0 for all α ∈ span({α1, α2}). □
. In particular, in any case we must have ω(α) = 0 for all α ∈ span({α1, α2}). □
The previous lemma implies that for k = 2, the solution of (2.6) for u ∈ φ−1(0) is non-unique iff DJr(u)DJr(u)⊤− 𝜖𝜖⊤ = 0. For k > 2, we can only have non-uniqueness if (A.1) holds. If we consider the dimensions of the spaces in (A.1), we see that in the generic case, it can only hold if
i.e., if all gradients of the objectives are linearly dependent in u. This motivates us to assume that in general, the solution of (2.6) is unique for almost all u ∈ φ−1(0).
We will now investigate the differentiability of φ. Our strategy is to apply the implicit function theorem to the KKT conditions of (2.6) to obtain a differentiable function ϕ that maps a point \(u \in \mathbb {R}^n\) onto the solution of (2.6) in u. This would imply the differentiability of φ via concatenation with ω. An obvious problem here is the fact that (2.6) has inequality constraints which, when activated or deactivated under variation of u, lead to non-differentiabilities in ϕ. Note that an inequality constraint being active means that one component of α is zero, i.e., one of the objective functions has no impact on the current problem. Thus, for our theoretical purposes, if there is an active inequality constraint in (2.6) we will just ignore the corresponding objective function. This approach is strongly related to the hierarchical decomposition of the Pareto critical set (cf. [10]).
For the reasons mentioned above, we will now consider the case where the solution of (2.6) is strictly positive in each component. The following lemma shows a technical result that will be used in a later proof.
Lemma A.2
Let u ∈ φ−1(0) and let  be a solution of (2.6) with α
i > 0 ∀i ∈{1, …, k}. Then
be a solution of (2.6) with α
i > 0 ∀i ∈{1, …, k}. Then  is unique if and only if there is no \(\beta \in \mathbb {R}^k \setminus \{ 0 \}\) with ω(β) = 0 and \(\sum _{i = 1}^k \beta _i = 0\).
is unique if and only if there is no \(\beta \in \mathbb {R}^k \setminus \{ 0 \}\) with ω(β) = 0 and \(\sum _{i = 1}^k \beta _i = 0\).
Proof
We will show that α is non-unique if and only if there is some \(\beta \in \mathbb {R}^k\) with ω(β) = 0 and \(\sum _{i = 1}^k \beta _i = 0\).
 : Let \(\tilde {\alpha }\) be another solution of (2.6). Then, as in the proof of Lemma A.1, we must have
: Let \(\tilde {\alpha }\) be another solution of (2.6). Then, as in the proof of Lemma A.1, we must have  for all \(c_1, c_2 \in \mathbb {R}\). This means we can choose
for all \(c_1, c_2 \in \mathbb {R}\). This means we can choose  .
.
⇐: Let \(\beta \in \mathbb {R}^k\) with ω(β) = 0 and \(\sum _{i = 1}^k \beta _i = 0\). Let s > 0 be small enough such that  . Then, as in (A.2), we have
. Then, as in (A.2), we have

Since by assumption φ(u) = 0 we must have  , so
, so  is another solution of (2.6). □
is another solution of (2.6). □
To be able to use the KKT conditions of (2.6) to obtain its solution, we have to make sure that these conditions are sufficient. Since (2.6) is a quadratic problem, this means we have to show that the matrix in the objective ω is positive semidefinite.
Lemma A.3
Let u ∈ φ−1(0) and let  be the unique solution of (2.6) with
be the unique solution of (2.6) with  ∀i ∈{1, …, k}. Then ω(β) ≥ 0 for all \(\beta \in \mathbb {R}^k\)
. In particular, DJ(u)DJ(u)⊤− 𝜖𝜖⊤ is positive semidefinite.
∀i ∈{1, …, k}. Then ω(β) ≥ 0 for all \(\beta \in \mathbb {R}^k\)
. In particular, DJ(u)DJ(u)⊤− 𝜖𝜖⊤ is positive semidefinite.
Proof
Assume there is some \(\beta \in \mathbb {R}^k\) with ω(β) < 0, i.e., 𝜖⊤ β > ∥DJr(u)⊤ β∥. We distinguish between two cases:
- Case 1::
-
\(\sum _{i = 1}^k \beta _i = 0\): Similar to the proof of Lemma A.1 we get

for all s > 0. In particular, since
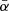 is positive, there is some
is positive, there is some  such that
such that  with
with  , which is a contradiction.
, which is a contradiction. - Case 2::
-
\(\sum _{i = 1}^k \beta _i \neq 0\). W.l.o.g. assume that \(\sum _{i = 1}^k \beta _i = 1\). Consider

Then  and
and  . By assumption, we must have
. By assumption, we must have  for all s such that
for all s such that  . By continuity of
. By continuity of  there must be some s∗ with
there must be some s∗ with  . Let
. Let  . Using (A.2) we get
. Using (A.2) we get

for all t ∈ (0, 1), which is a contradiction. □
The previous results now allow us to prove Theorem 2.10.
Theorem 2.10
Let  such that (2.6) has a unique solution
such that (2.6) has a unique solution  with
with  for all i ∈{1, …, k}. Let (2.6) be uniquely solvable in a neighborhood of
for all i ∈{1, …, k}. Let (2.6) be uniquely solvable in a neighborhood of  . Then there is an open set \(U \subseteq \mathbb {R}^n\) with
. Then there is an open set \(U \subseteq \mathbb {R}^n\) with  such that φ|U is continuously differentiable.
such that φ|U is continuously differentiable.
Proof
The KKT conditions for (2.6) are
for \(\lambda \in \mathbb {R}\) and \(\mu \in \mathbb {R}^k\). By Lemma A.3 these conditions are sufficient for optimality. By our assumption there is an open set U′ with  such that the solution of (2.6) is unique and positive. Thus, on U′, (A.3) is equivalent to
such that the solution of (2.6) is unique and positive. Thus, on U′, (A.3) is equivalent to
for some \(\lambda \in \mathbb {R}\). This system can be rewritten as G(u, (α, λ)) = 0 for

Derivating G with respect to (α, λ) yields
Let  such that
such that  . (Note that uniqueness of
. (Note that uniqueness of  implies uniqueness of
implies uniqueness of  here.) For
here.) For  to be singular, there would have to be some \(v = (v^1,v^2) \in \mathbb {R}^{k+1}\) with
to be singular, there would have to be some \(v = (v^1,v^2) \in \mathbb {R}^{k+1}\) with

and thus

By Lemma A.2, this is a contradiction to the assumption that  is a unique solution of (2.6). So
is a unique solution of (2.6). So  has to be regular. This means we can apply the implicit function theorem to obtain open sets \(U \subseteq U' \subseteq \mathbb {R}^n\), \(V \subseteq \mathbb {R}^{k+1}\) with
has to be regular. This means we can apply the implicit function theorem to obtain open sets \(U \subseteq U' \subseteq \mathbb {R}^n\), \(V \subseteq \mathbb {R}^{k+1}\) with  ,
,  and a continuously differentiable function ϕ = (ϕ
α, ϕ
λ) : U → V with
and a continuously differentiable function ϕ = (ϕ
α, ϕ
λ) : U → V with
In particular,

so φ|U is continuously differentiable. □
Remark A.4
From the proof of Theorem 2.10 we can even derive an explicit formula for the derivative of φ|U in  : First of all, the derivative of the implicit function ϕ is given by
: First of all, the derivative of the implicit function ϕ is given by

By applying the chain rule to (A.4), we obtain

\(\blacksquare \)
Rights and permissions
Copyright information
© 2022 Springer Nature Switzerland AG
About this chapter
Cite this chapter
Banholzer, S., Gebken, B., Dellnitz, M., Peitz, S., Volkwein, S. (2022). ROM-Based Multiobjective Optimization of Elliptic PDEs via Numerical Continuation. In: Hintermüller, M., Herzog, R., Kanzow, C., Ulbrich, M., Ulbrich, S. (eds) Non-Smooth and Complementarity-Based Distributed Parameter Systems. International Series of Numerical Mathematics, vol 172. Birkhäuser, Cham. https://doi.org/10.1007/978-3-030-79393-7_3
Download citation
DOI: https://doi.org/10.1007/978-3-030-79393-7_3
Published:
Publisher Name: Birkhäuser, Cham
Print ISBN: 978-3-030-79392-0
Online ISBN: 978-3-030-79393-7
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)



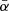 is positive, there is some
is positive, there is some  such that
such that  with
with  , which is a contradiction.
, which is a contradiction.