Abstract
Uncertainty affects all phases of the product life cycle of technical systems, from design and production to their usage, even beyond the phase boundaries. Its identification, analysis and representation are discussed in the previous chapter. Based on the gained knowledge, our specific approach on mastering uncertainty can be applied. These approaches follow common strategies that are described in the subsequent chapter, but require individual methods and technologies. In this chapter, first legal and technical aspects for mastering uncertainty are discussed. Then, techniques for product design of technical systems under uncertainty are presented. The propagation of uncertainty is analysed for particular examples of process chains. Finally, semi-active and active technical systems and their relation to uncertainty are discussed.
You have full access to this open access chapter, Download chapter PDF
Similar content being viewed by others
The first Chapters of this book provide the conceptual basis for mastering uncertainty in design, production and usage of load-bearing structures in mechanical engineering. This forms the fundamental floor of our house, presented in Chap. 1. Besides the presentation of our motivation, Chap. 1 reflects on the source and quality of models, as well as on data and the term “structures”. Chapter 2 provides a consistent classification and definition of uncertainty. This is essential for our specific approach on mastering uncertainty, which is described in Chap. 3, making use of three exemplary technical systems, which are introduced in Sect. 3.6. On the middle floor of the framework of mastering uncertainty, presented in Fig. 1.12, we discuss methods for analysis, quantification and evaluation of uncertainty in Chap. 4 and now introduce methods and technologies to apply our approach to technical systems.
Therefore, we first cover the technical and legal requirements for mastering uncertainty with a focus on product safety and liability in Sect. 5.1. Although legal uncertainty usually expresses itself during product usage, it has to be considered from the very beginning of the product life cycle during design and production. The technical specification of products, which has to define the technical requirements on the product, effects the uncertainty in an early stage of the development process. From a legal perspective, two points are important: firstly, to meet product safety requirements, sufficient knowledge of the legal framework regarding the specific application must be available; this might be challenging, especially for new developments; secondly, liability risks have to be minimised during the design and production phase.
In Sect. 5.2, we propose several methods to uncover and master uncertainty during the design phase. Therefore, we first introduce a method for the estimation of uncertainty occurring during the whole product life cycle, and a generic process model used to uncover uncertainty in production or application processes. Furthermore, uncertainty arising from models which are indispensable for product design, is discussed, and different ways to deal with it are presented. Our specific approach to master uncertainty in the product development process is presented using our our three demonstrator systems Modular Active Spring-Damper System, see Sect. 3.6.1, Active Air Spring, see Sect. 3.6.2, and 3D Servo Press, see Sect. 3.6.3.
The production phase usually takes place in the form of a process chain. Each single process, as well as the material passing through the process chain, is subject to uncertainty. The uncertainty is propagated through the process chain, see Sect. 3.2. In Sect. 5.3 we give examples on how to master this propagation of uncertainty in process chains.
Section 5.4 deals with methods and technologies to manipulate single processes and their application on both the production and usage phase. Based on the definition of semi-active and active processes, which is given in Sect. 3.3, we cover the manipulation of production processes using innovative components. Furthermore, we present several semi-active and active technologies to master uncertainty within the usage phase.
5.1 Technical and Legal Requirements for Mastering Uncertainty
Defining requirements in order to master uncertainty is the main goal of the following section. Both, technical and legal requirements may be established. Regarding the product phases design (A), production (B) and usage (C) presented in Fig. 1.3 legal uncertainty usually manifests itself during the usage phase, if the product causes damage. Ideally, legal requirements influence technical requirements and are already considered during the design and production phase of the product in order to achieve the highest possible certainty regarding legal liability of producers. The economic impact of legal requirements can be derived from the legal framework. We will focus on product safety and product liability. In the following, we understand product development as the totality of all steps leading to a marketable product, including design and production.
In Sect. 1.6 product design was discussed as a constrained optimisation problem, where the objective function has three challenging aspects, namely (i) minimal effort, (ii) maximal availability and (iii) maximal acceptability. Conformity with product liability is the formal aspect of acceptance.
The process of defining specifications in engineering design can be understood as a socio-technical system, whereby the functionality and quality of a product are the result of a complex and dynamic interaction of different stakeholder groups. In Sect. 5.1.1, we examine this process of how specifications are formulated. Furthermore, we consider the way specifications are used in product development. Therefore, a classification of specifications into objectives and constraints is introduced.
From the technical perspective, defining a precise and complete technical specification is the basis for the subsequent development process of any new product. In classical engineering design, uncertainty in the use of the product can derive from the misinterpretation of product requirements during product development. This uncertainty can potentially be addressed at a very early stage of the development process. We will discuss the general problem of specification uncertainty, as well as the impact technical specifications may have on the overall uncertainty of a complex load-bearing system in Sect. 5.1.2.
In order to clarify product requirements from a legal perspective, we need to apply the abstract knowledge of the legal framework to specific applications. Combining legal expertise with the fields of engineering and mathematics allows a more user-oriented approach to discuss the problem of legal uncertainty where it occurs.
Therefore, product safety requirements and the importance of technical standards will be addressed in order to prevent cost-intensive product recalls. For innovative products in particular, the problem arises that producers may not rely on technical standards in their development process, as such standards do not yet exist. The question, how producers should cope with this uncertainty is also part of our discussion in Sect. 5.1.3.
From a product liability perspective, many liability-causing legal risks can be avoided in the design of the product and during the organisation of the production process. We take an application-oriented approach to answer the question, which measures the producer needs to implement in order to minimise liability risks. The specific requirements for producers using algorithmic optimisation techniques in product development (Sect. 5.1.5) are of a different nature than the requirements for producers implementing an autonomous production process (Sect. 5.1.4). In both cases, the difficult question arises, how liability risks can be minimised, when using innovative development techniques or production methods.
Technical standards, although not always legally binding, are often the basis of contracts when selling products. Compliance with standards is therefore a requirement for products. However, technical standards must apply to many different occasions, and the language used is therefore ambiguous. In Sect. 5.1.6, an information system is proposed that detects semantic uncertainty in standards and provides suggestions to the users of standards to resolve the uncertainty.
Uncertainty does not only affect product development, but planning processes in general. In the scientific discipline of project management, concepts, methods and practices for dealing with uncertainty have been developed during the last decades. In Sect. 5.1.7, we reflect on these approaches from a historical perspective in order to provide a better understanding of current tools for planning processes.
In addition to the general technical methods for mastering uncertainty, we hope to provide another dimension to the tools which are discussed in Sect. 3.3.
5.1.1 ‘Just Good Enough’ Versus ‘as Good as It Gets’: Negotiating Specifications in a Conflict of Interest of the Stakeholders
Technical specifications provide requirements of the product or services that are considered in the design process and are discussed, quantified and checked by the stakeholders involved. In classical engineering design, they are supposed to be defined at the beginning of the product lifecycle. This classic approach dating back to Pahl and Beitz [215] and being the fundament of the guideline VDI 2221 [271] is related to uncertainty for two reasons. Firstly, at the beginning of the engineering design process, various ways of using and misusing the product have to be anticipated. Secondly, in retrospect of every engineering design process, the product functionality and quality can be seen as a result of a complex and dynamic interaction of the three stakeholders (1) supplier, (2) customer, (3) society. For us the supplier is in most cases identical with the manufacturer. There are several strategies known for mastering this uncertainty, such as user-centred design, requirement management and agile project management. A review of these methods exceeds the scope of this section. Instead, the following pages embody a reflection on how specifications are used as a design method in the context of Sustainable Systems Design (SSD) and of mathematical optimisation. Moreover, it outlines the process of how specifications are formulated by the three stakeholders mentioned above.
Classification of specifications into objectives and constraints
In SSD, see Sect. 1.6, Figs. 1.9 and 1.10, a constrained optimisation problem in the form of “maximise quality subject to functionality” is solved in the design process. Quality corresponds to the objectives and the functionality to the constraints of the optimisation problem.
The tree diagram in Fig. 5.1 provides a classification into two branches, objectives and constraints, which have four specification types in the leaves of the tree. There is one objective (a) and three different types of constraints (b), (c), (d):
-
(a)
quality objective,
-
(b)
quality constraints,
-
(c)
functional constraints,
-
(d)
restricted design space.
The assignment to constraints and sub-objectives is done by each stakeholder individually even though the same system is addressed as we will see in the following. The term “constraints” originates from the field of mathematical optimisation and describes the restricted solution space of the optimisation problem. In the context of technical specifications, it describes possible restrictions and limitations, but also demands and requirements.
-
(a)
Quality objectives are specified by weighted sub-objectives. Weights are impact-specific weighting factors often known as cost factors (e.g. pricing the environmental impact by \(CO_2\) taxation). Also, impact-specific incentives (e.g. financial subsidies for improvement) can be used as weights. The sub-objectives are the three quality directions minimal effort, maximal availability, maximal acceptability, Sect. 1.6. The three quality directions are in agreement with Taguchi’s quality engineering methodology [258]. Taguchi demands that manufacturers also consider the effort, i.e. the economic costs and the costs to society, as a quality measure. The weighted sub-objectives are approximated by agents (humans and/or machines) in an incremental Continuous Improvement Process (CIP) controlled by the target and impact-specific weighting factors. Hence, a quality objective defines a direction and not the required quality level.
-
(b)
Quality constraints ensure such required quality level. The advantage of quality constraints versus quality objectives is the clear commitment. The disadvantage is that constraints are fixed and not optimised. Hence, optimal quality and hence sustainability will never be reached by quality constraints. A typical quality specification is a cost limit to be reached in a design-to-cost engineering process or the setting of a pollution limit.
-
(c)
Functional constraints are specified on the basis of expressed or anticipated customer needs.
-
(d)
Restricted design space is given by available technologies, resources, operating modes, services. The design space may be extended by innovations or restricted by banning technologies, such as demanding carbon-free energy supply.
The tree diagram (solid line) classifies system specifications in the context of SSD as presented in Sect. 1.6 into objectives and constraints. There are a quality objectives, b quality constraints and c functional constraints specified on the basis of named or anticipated customer needs. A restriction of the design space d is the third and last constraint
Section 1.6 classifies acceptability into informal and formal acceptability. Formal acceptability is achieved by ensuring legal conformity or compliance with a contract between stakeholders. Hence, formal acceptability is assigned to quality specifications in the first place. Informal acceptability is fostered through positive user experience or positively perceived functional performance. The quality objective in Robust Design is a prominent example as presented in the third case study of Sect. 3.5. But how does the process of specifying objectives and constraints work? How are quality directions given and assigned to the different stakeholder groups?
Product functionality and quality is negotiated in a cybernetic system of the three external stakeholder groups (1) supplier, (2) customer, (3) society. Internal stakeholders, i.e. the employees of a company, are not the primary focus here. To understand the basic dynamics and outcome of this negotiating process, the external stakeholders can be modelled as agents in a cybernetic control system. The purpose of this section is not to provide and evaluate a detailed model, but to illustrate how the boundaries of SSD can be extended from an techno-economic system to a socio-technical system, see Fig. 5.2.
Cybernetic stakeholder system
The values of various parameters relevant in the process of negotiating and formulating the specifications (quality objectives, quality constraints, ...) in SSD are subject to processes that transcend the purely technical system. In order to understand how specifications are determined, we suggest that the socio-technical system can be modelled as a cybernetic system, see Fig. 5.2. We begin by identifying three stakeholders that are coupled in a control loop: (1) supplier, (2) customer of products and services like owners and operators and (3) society represented by one or several governments and non-governmental organisations.
This concept is now applied to analyse the dynamics of specifications using the example of the so called “energy ship”, cf. 1st case study in Sect. 3.3. Here, the supplier (2) is the ship manufacturer. The customer (1) is the owner and operator of the energy ships. The customer follows the Friedman doctrine, “the social responsibility of business is to increase profit” [109]. This is reflected in the customer’s quality objective: minimising the levelised costs of hydrogen (LCOH).
Tolerated functional and quality constraints are usually communicated to the supplier in a feedforward control. For example, quality constraints such as tolerated efficiency limits or service life guarantees can be required at the lowest possible price, which is a quality objective assigned to the supplier by the customer. However, formulating the quality constraints by the customer does not give the supplier any incentive to deliver the best possible product, but only to act according to the precept “just good enough”. On the one hand, this attitude is welcome in order to avoid overachievement. On the other hand, this attitude limits sustainability. Another possibility would be to map the quality constraint to a quality objective, i.e. to accept a higher price if the component efficiency is higher. This leads to the principle “as good as it gets”, which is essential for the development of sustainable products: quality objectives are followed in an incremental feed back control strategy as Fig. 5.3 implies. As discussed in Chap. 1, feed back control is robust with respect to uncertainty in the controlled systems. In contrast, feed forward control demands models of the controlled systems.
Society has many options for intervening as shown in Figs. 5.2 and 5.3. It may manipulate weighting factors in the quality objectives resulting in (i) incentivisation, i.e. certain technologies or solutions can become incentivised like discounted loans for fuel cell technology; (ii) penalisation, i.e. certain technologies or impacts are penalised for example by fiscal policies like \(C\!O_2\) tax; setting limits in the quality constraints by (iii) regulation, i.e. legal constraints are introduced to limit impact like minimum efficiency levels for fuel cells; or reduce the design space leading to (iv) restriction, i.e. the use of a certain technology is restricted like banning Diesel engines, which leads to an increased use of hydrogen and more profitability for the customer. This concerns both the customer and the supplier. As there is constant interaction, the respective specifications are negotiated in the market and they influence all stakeholders.
This classification is not strict and absolute. For example, companies can voluntarily overfulfil the normative requirements of the government, which is done in the context of Corporate Social Responsibility (CSR), and thus deviate from the Friedman doctrine [212]. However, this unnecessary over-fulfilment of quality constraints can lead to an increased reputation in turn, increased profit and thus improve the quality objective—maximise profit – of the company [212]. Companies of the Value Balancing Alliance [267], founded by BASF SE, Deutsche Bank, SAP and other companies in 2019, go one step further by defining the impact specific cost and the positive impact of their actions themselves. The high level of uncertainty provides scope for interpretation and raises the suspicion of greenwashing [251]. In the perspective of the presented model, the responsibilities of the stakeholders are mixed up, which can cause unintended dynamics. This is why transparent and measurable Key Performance Indicators for the impact are necessary.
Summary
It has been shown that specifications can be grouped into four categories: quality objectives, quality constraints, functional constraints and restrictions of the design space. To understand the process of establishing specifications in socio-technical systems, we interpreted the system from a cybernetic point of view. The analysis shows that the wide range of stakeholders generates further sources of uncertainty in the specification, which are located outside of the product design itself. This must be taken into account and adequately modelled, especially when anticipating future developments as done in feed forward control. Compliance with the Friedman doctrine, which has been dominant in the past two decades, has failed with regard to the development of sustainable socio-technical systems. Both suppliers and customers have to adopt the functional constraints of the other stakeholders as quality objectives. Only the clear commitment to this and making the design process transparent do enable sustainable socio-technical systems in the future. To shift the paradigm from “just good enough” to “as good as it gets”, the CIP, a well-known tool in business management, can be used.
5.1.2 Technical Specification
Uncertainty occurs in load-bearing systems in all phases of their virtual and real product life cycle, cf. Chap. 1. Especially, the development of new products is associated with particularly high uncertainty [216]. One important source for uncertainty is the technical specification of products, which is discussed in the following.
Uncertainty in product development can only be mastered in the long term, if it is given equal consideration to technical, economic and ecological requirements from the very first beginning. Correspondingly, reliable information from the technical specification supports decisions with far-reaching consequences in the development process.
New product ideas are often described by prospective users based on the intended application process or their contribution to the functionality of an overall system. However, the description of new product ideas is usually very imprecise. Thus, at the beginning of the development process, developers have to define the product properties in such a way that the resulting products are equipped with the desired properties in the use phase, cf. [224, 225].
The development task is analysed and detailed with regard to functionality and quality, effort, availability and acceptance, cf. Sect. 1.6. Usually, the development task is formally described in the form of requirements; and it is summarised in a document for the entire development team. The formal documentation is called technical specification. The document is frequently referred to as a requirements list, specification sheet, product concept catalogue or similar [69].
Although the technical solution is still largely unknown in the design phase, e.g. load assumptions must be made, product functions and basic dimensions have to be defined, as well as restrictions, e.g. with respect to costs and dimensions. Product development teams then use the technical specification during the entire development process as an information storage and decision basis.
The technical specification contributes to mastering of uncertainty in the development process by (i) defining requirements which are subject to uncertainty and (ii) directly specifying the requirements of the system in later use including foreseen uncertainties. Both contributions lead to a reduced modelling uncertainty.
The complete and detailed specification of the functional requirements helps product developers to reduce uncertainty during the creation of technical solutions. The completeness of the technical specification avoids that important functionalities are overlooked, whereas the sufficient level of detail prevents misinterpretations during product development. Both reduce model uncertainty, see Sect. 2.2, and structural uncertainty, see Sect. 2.3, in the development process, as well as uncertainty regarding the expectations of product use.
The models we have developed for the identification, classification and evaluation of uncertainty help designers to foresee influences relevant to uncertainty and to quantify an acceptable level of uncertainty, especially in product use. These can be formulated and documented as requirements in the technical specification. With the methods we have developed to master uncertainty in product development, uncertainty in life cycle processes can be predicted and the specified uncertainty requirements are met during product development.
Mastering uncertainty due to modelling
The development of new products is characterised by gradually more detailed models, such as functional structures, effect relationships, embodiment designs and geometry representations. The developers create these models based on assumptions, e.g. for loads, performance and available assembly space. These assumptions are based on information that is documented in the technical specification. Thus, the guidelines we developed to reduce modelling uncertainty [283] also serve as a guide to reduce uncertainty through the technical specification.
We exemplify the role of technical specifications by the development of a new bearing concept, presented in Sect. 5.4.2. The bearing is used as a key element in the challenging development of the 3D Servo Press, enabling a force of 1600 kN, see Sect. 3.6.3. It consists of a combination of roller and plain bearings. The use of bearings in such a special application leads to uncertainty in the development process, due to the complex load and installation conditions.
The choice of an appropriate and meaningful generic model for a development step is supported in particular by the most detailed possible documentation of critical system states and load cases.
For the description of the bearing function we use the model according to Holland [158], described in Sect. 5.4.2, which was adapted to the mode of operation of the combined bearing concept [247]. The model assumes a force equilibrium between the operating force \(F_{\text {op}}\), the plain bearing force \(F_{\text {pb}}\) and the roller bearing forces \(F_{\text {rb}}\). The plain bearing force \(F_{\text {pb}}\) is based on a pressure build-up in the lubricant, which depends on the dynamic viscosity \(\eta \) of the lubricant, which is supplied with pressure \(p_{\text {in}}\) and volume flow \(Q_{\text {in}}\), as well as the speeds of the shaft, \(\omega _{\text {shaft}}\), and bearing shell, \(\omega _{\text {shell}}\), and the position of the shaft inside the bearing shell.
For common plain bearing designs, a quasi-static load condition of the rotating shaft by a constant load is assumed. In this case, the rotation speeds of shaft and bearing shell cause a non-constant pressure distribution \(p_{\text {rot}}\) in the circumferential direction due to the radial shaft displacement e. However, the detailed specification of the force curve over the angle of rotation, which occurs in mechanical presses, indicates that a significant temporal change of the shaft displacement occurs due to a force peak at the operating point. This leads to an additional pressure build-up \(p_{\text {sq}}\) in the area of the minimal bearing gap \(h_\mathrm {min}\), which is not covered by the lubrication model for steady operation. The resulting forces on the shaft can be expressed by the Sommerfeld numbers for rotation, \(\text {So}_{\text {rot}}\), and squeezing, \(\text {So}_{\text {sq}}\),
Here, \(\delta \) describes the position of the minimal bearing gap in polar coordinates while \(\dot{\varepsilon }\) is the squeezing rate. The consideration of these two forces in the model is of decisive importance for the specific application. In Sect. 4.3.5 we have seen how large the effects of model uncertainty on the results can be when a model is applied inappropriately because of ignorance. Initiated by the specification of the force curve over the shaft’s angle of rotation, which varies considerably over time, the development of the combined roller and plain bearing system of the 3D Servo Press was based on the assumption that, in addition to the hydrodynamic effect, a displacement of the oil must be taken into account when designing the plain bearing. Since the relevant load conditions are thus recorded much more accurately, the uncertainty of the press development could be significantly reduced by the choice of the model.
In general, when specialising a generic model for the current development task, e.g. a functional structure, the developers define an appropriate system boundary and granularity of the model. The system boundary represents the part of reality that is considered as relevant. The granularity results from the scope and thus the number of components for modelling the system, see Sect. 1.3.
The technical specification influences uncertainty in modelling the system by information that acts as a basis for assumptions and decisions of the developers. In particular, detailed requirements regarding load assumptions, disturbance variables, resources and boundary conditions enable the developer to choose a model horizon that takes into account essential uncertainty-critical influencing parameters. The identification of critical uncertainty in the technical specification supports the definition of relevant components with adequate complexity. This ensures the conciseness of the model as a very important model feature and a prerequisite for successful product design.
We use the specification of the viscosity range of the system element lubricant which is a part of the roller and plain bearing as an example. The combined roller and plain bearing system is exposed to high loads. Due to its significant influence the temperature dependence of the dynamic lubricant viscosity \(\eta \) must be taken into account.
Another example concerning the adequate mapping of the combined roller plain bearing system in a model is the deviation of the assumed loading situation. A possible deviation from assumed conditions is given by an inclination of the operating load caused by uncertainty outside the system boundary of the combined bearing. The behaviour of the combined bearing under such disturbing influences is investigated in [132].
The force conduction through the roller bearings is calculated by means of \({F_{\text {rb}}=c_{\text {rb}}\, e}\) with \(c_{\text {rb}}\) representing the stiffness of the rolling elements, neglecting elastic deformations of the shaft and the plain bearing shell.
This example shows that neglecting insignificant influences contributes to simplifying models and improving their conciseness. The differentiation and detailing of critical requirements urges developers to decide explicitly on the admissibility of simplifying assumptions that affect particularly critical system properties, see Sect. 4.3.
In the example of the combined bearing system, the dependencies of viscosity on pressure and temperature were recognised by references in the technical specification, but the uncertainty by neglecting these dependencies was assumed to be acceptable.
In summary, it can be stated that the modelling of the system is based on the information of the technical specification. The technical specification supports the developers in making relevant assumptions and to work out appropriate system models by specific documentation of critical functional requirements. Thus, it can reduce the influence of uncertainty. Model uncertainty can be effectively controlled by incorporating all relevant system areas and system properties into the development process to optimally meet customer expectations, despite the simplification of reality.
Mastering uncertainty due to requirements
As shown in Sect. 1.6, informal acceptance can represent the fulfilment of customer expectations, which has a significant influence on the success of the product. As described there, a high level of acceptance is achieved by reducing effort and increasing availability. In order to ensure a high level of availability in product development, product developers detail this objective right from the start in the form of requirements that are as precise as possible or even quantified. They document these requirements in the technical specification as a basis for decision-making during product development.
However, the quantification of availability depends strongly on product usage and is not always possible, as already stated in Sect. 1.6. The models and methods we have developed for the identification, evaluation and quantification of uncertainty and uncertainty influences allow in these cases the indirect specification of availability requirements without the technical solutions being known.
The type of the product to be developed and its conditions of use determine the scope and description of the uncertainty that must be taken into account in the development. Depending on the degree of uncertainty these are documented in the technical specification in the form of requirements regarding reliability or robustness properties.
Systems and machines for stationary use in production are usually operated in factory buildings with largely determined environmental and process conditions. The reliability specification defines “the probability that the required function of a product will not fail during a defined period of time and under given working conditions” [143]. Reliability is indicated in the technical specification by performance indicators such as Mean Time Between Failure (MTBF), Mean Time To Repair (MTTR), Uptime or Production Yield. Reliability is therefore based on the assumption that the causes of uncertainty are largely known and vary only slightly. The specification must therefore ensure that disturbance influences are defined or eliminated during the operation of the systems.
When developing robust systems, information regarding uncertainty causes in the specification are a prerequisite to guarantee a high availability in use, cf. [192].
In our case of highly loaded roller bearings, lubrication must be ensured so that the calculated service life and frictional torques (and thus power loss) are achieved during operation. Regarding the combined roller and plain bearing presented in Sect. 5.4.2, the volume flow \(Q_{\text {pb}}\) of the lubricant exiting the plain bearing in the axial direction serves to lubricate the roller bearings. However, this coupling of the lubricant flows of the plain bearing and the rolling bearings has a considerable influence on the system behaviour and must therefore be taken into account in the development. However, on the one hand, the lubricant properties are predetermined by the design of the plain bearing and, on the other hand, the lubricant temperature and the lubricant flow vary depending on the operating conditions of the plain bearing. The developer can only master the undefined lubrication conditions by a robust design of the rolling bearing. A prerequisite for mastering the uncertainty in the robust design of roller bearings is therefore comprehensive information on the properties of the lubricant and the lubricant flow in the technical specification.
Conclusion
In a nutshell, during the development of new products, developers may significantly influence the uncertainty of the product to be developed with the technical specification. The specified properties of the system can have an indirect or direct influence.
Mainly the complete coverage of causes of uncertainty contributes to mastering uncertainty in the product development process. A mostly complete specification of functionality and uncertainty influences can reduce model uncertainty and indirectly enhance correct predictions and availability of the system and thus the informal acceptance.
Uncertainty can be directly reduced if uncertainty effects from and on the system environment are captured and specified comprehensively and as detailed as possible, preferably quantitatively. The checklists of the robust design methods of the early phases of product development can be particularly helpful in this respect.
Elaborating the technical specification, it is purposeful to anticipate development steps and to support the developers in making assumptions by specific information structured according to model characteristics, cf. [283].
5.1.3 Product Safety Requirements for Innovative Products
Product recalls, as discussed in Sect. 1.1, are expensive and harmful to the producer’s image and therefore should be avoided. Although product recalls become relevant in the usage phase of a product, the root cause often traces back to the design and production phase. Figure 1.3 presents an overview of the three product phases and how they are linked. But product recalls are only necessary for products that can be dangerous, i.e. they present potential risks to the body, health or life of consumers, users or third parties in general. Reasons for recalls can be manifold. For example, in certain sectors, the product quality decreases due to economic factors and strong competition [278, p. 62].
But another reason for product quality not complying with product safety requirements can be, that the requirements are becoming more and more diverse and complex, Sect. 1.1. Or even the fact that no technical standards are applicable to new and innovative products.
If a product is in use and it turns out that it poses a safety issue, it needs to be taken off the market. Legal product safety is this strict due to its preventive character. Its aim is to ensure that only safe products are in use and on the market. Together with product liability, product safety requirements provide full protection of the consumers’ legally protected rights. In this subsection we aim at clarifying what is required for the producer to prove the safety of his product.
Product safety
The Product Safety Act is the main legal framework for product safety in Germany. It is accompanied by numerous technical standards, which specify requirements for the practical application [173, marg. 2]. Furthermore, it is subject to European regulation, which is why many of the technical standards are developed by European Standardisation Organisations. Basically, two groups of products need to be distinguished. Those which fall into the category of harmonised products and those which do not. In the case of harmonised products, the producer compulsorily needs to comply with the provisions, applicable for the specific case. These provisions are mostly based on European Standards. If the product complies with said provisions, it is assumed to be safe and can therefore be placed on the market [195, marg. 3]. National provisions for harmonised products often only regulate a minimum of safety which the product has to achieve. They are often accompanied by industry standards which are more detailed but not obligatory since they lack legal quality [66, p. 42]; [117, p. 1492]. In the case of non-harmonised products, the producer can exclusively follow national standards. Similarly to harmonised products, the compliance with these standards implies their safety. But, the application of these technical standards is not mandatory. Nevertheless, producers need to prove the compliance of the product with safety standards set by the national provision and technical standards, as well as state-of-the-art technology. On the contrary, the non-compliance with said standards does not automatically imply that the product is unsafe. Unsafe products are rather those which pose a potential risk to the legal rights the Product Safety Act aims to protect namely a person’s health, body and life.
The Product Safety Act is the hurdle which anyone placing a non-food product on the market for the first time needs to clear. At the same time the product needs to be made available on the market for commercial use. Further, the Product Safety Act is not only applicable to products, but also to facilities which are deemed hazardous and thus require monitoring and inspection. For this discussion, we will solely focus on products.
Market surveillance
In cases of non-compliance with the safety requirements set by provisions and technical standards, Market Surveillance Authorities can direct producers to different behaviour in order to avert danger for consumers, due to the respective product. These measures may consist of requesting the producer to take action in order to end the risk accompanied with the product. They can also prohibit the further distribution of the product, or, in particularly risky cases, even demand the product to be recalled. Any of the mentioned measures are likely to have a negative impact on the producer’s reputation and are certain to cost money. Therefore, the objective is to avoid authority intervention at all times.
RAPEX
The so-called RAPEX-System (Rapid exchange of Information) enables both member states and the European Commission to exchange information on dangerous products which are on the European market, but are being taken off the market, or are part of a product recall.
In addition, the RAPEX-System determines the level of risk of a product [174, p. 38]. Producers need to apply this assessment system to their product. The level of risk also determines possible measures taken by the market surveillance authorities.
Technical standards and the proof of safety
Technical standards are developed by private institutions, which collect knowledge from industry standards and compile it into one comprehensive document. These standards are more user-friendly than the requirements set by legal provisions, since they can have a very specific scope of application. Furthermore, legal provisions are vaguer in order to be applicable to a wide variety of use cases. As mentioned before, technical standards concerning non-harmonised products have no legally binding character, as they do not undergo a legislative procedure. Nevertheless, they represent the state-of-the-art technology. Therefore, when the producer designs a product following the technical standards, it implies that the product complies with the current minimum safety standard existing in the industry. As a result, the product is deemed to be safe and can be distributed on the market.
Non-compliance with existing technical standards
If producers do not comply with existing and applicable technical standards, this does not per se indicate that the product is unsafe [165, p. 722]. The reasons for this non-compliance can vary. The producer could just have overlooked the existence of the technical standard or he could have consciously neglected it. The reason behind this could be that the producer found a better, easier or cheaper option to provide the same level of safety of the product with a different construction than recommended by the technical standard. Therefore, it is necessary for the producer to prove that the minimum safety, set by the technical standards applicable, is met otherwise.
Missing technical standards
Another problem arises, if no technical standards are available to the producer when designing the product. This can be the case for innovative products, when no clear industry standard has been developed, yet. Without technical standards, there is no implication for the safety of the product in terms of the Product Safety Act [117, p. 1493]. So, how can the safety of the product be determined? This question is particularly important for the producer, as the product cannot be marketed without the positive safety implication.
In most cases, it is neither practical nor possible to apply technical standards developed for a different scope of application to another product, even if the products are similar [213].
It becomes apparent that the effort for providing proof of the safety of the product is much higher than in the case of existing technical standards. The producer must apply some kind of risk analysis to prove the safety of the product. But no official guidelines exist for how this analysis should be executed and what information needs to be taken into account. This uncertainty increases the efforts of the producer to provide the necessary proof of safety even more.
Practical guidelines would help the producer to do what is expected. This would equally make products safer compared to the case where a producer sets his or her own standards to prove the safety of any innovative product. German jurisdiction only offers guidance, as it was decided that sampling inspections are not a permissible basis for providing proof of the product series as a whole [213].
Machinery directive
The Machinery Directive [97] also demands a risk analysis and gives guidance as to which aspects the producer needs to consider during the analysis. For example, the producer needs to consider the intended use in addition to the foreseeable misuse of the product and determine the limits of the product. In the case of the Machinery Directive, the product is a machine and the Directive only applicable to such. Additionally, the producer needs to identify potential hazards and dangerous situations caused by the machine. Just by mentioning these requirements, it becomes clear that the risk analysis described by the Machinery Directive is not very specific and does not include specifications on how the information to evaluate said aspects should be gained.
Product safety and market surveillance package
The requirements stated in Article 8 of the Proposal for a Product Safety and Market Surveillance Package [96] are similarly vague. In this proposal, technical documentation for the product is required and should contain, amongst others, an analysis of the possible risks related to the product. But again, it contains no guidance as to which information is relevant for the analysis.
Non-legislative guidelines
The decision of the European Commission concerning the RAPEX-Guidelines [95] is a non-legislative and therefore non-binding document. But other than the mentioned legislative acts, this guideline provides useful information on how to perform a risk analysis for products and recommends a three-part assessment.
The foundation of this assessment is to describe the product and the inherent danger as well as identifying the group of potential users. Regarding this, intended, as well as unintended users need to be considered. Potential users should also be categorised according to their vulnerability. For instance, children and elderly people are vulnerable users in most cases. But depending on the use case or type of product usually not particularly vulnerable users might become vulnerable, for example, if warnings and instructions on the product are written in a foreign language. If different types of users can be identified, the risk assessment might have to be performed for different scenarios considering the different users in order to identify the highest risk combination. For the actual risk analysis, the producer should first anticipate a situation in which the product inherent risk manifests itself by injuring a person. This scenario will mostly revolve around the potential defect the product can have during its lifetime. This defect then causes the injury of a user or person, who comes into contact with the product.
Furthermore, it is significant for the assessment of how severe the anticipated injury would be. According to the RAPEX-Guideline, factors for the evaluation can be the duration the hazard of the product has on the potential victim, the body part which would potentially be injured and the impact on the respective body part. For example, losing a finger is a much more severe injury than lightly burning the skin on one finger. The severity of the injury can then be used as an indicator for the level of danger the product poses and vice-versa. In case different scenarios are possible, the one causing the severest injury should be considered first, as preventing this scenario provides the greatest safety for potential users. The second step would be to determine the probability of the scenario and therefore the probability of the person getting injured due to the hazardousness of the product. The RAPEX-Guideline recommends separating the anticipated scenario into smaller steps, identifying the probability of each individual step and then multiplying the individual probabilities to receive the overall probability of the scenario.
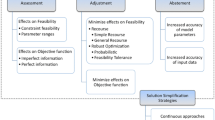
Lastly the RAPEX-Guideline recommends that the producer should combine the two steps, joining hazardousness and probability to obtain the risk of the product. Four risk categories are intended: serious, high, medium and low. Figure 5.4 demonstrates the combination of the probability of the injury, the severity of the expected injury, as well as the impact on the risk classification. Depending on the risk category, it is expected of the producer to apply a suitable effort to prevent the calculated risk. The higher the risk, the more important it is to mention that the whole process behind the described risk analysis should be documented, in particular in the case market surveillance authorities request this information. Figure 5.5 provides a simplified overview of the recommended procedure.
Risk level from the combination of the severity of injury and probability derived from RAPEX-Guideline [95], Table 4
Risk analysis derived from RAPEX-Guideline [95]
Finally, the recommended sources of information for all the consideration above are accident statistics, knowledge gained from previous and similar products, as well as experts’ opinions. As the problem discussed regards the question of how producers of innovative products can provide proof for the safety of their product in case no technical standards exist, it is highly likely that neither knowledge nor accident statistics exist that would be applicable to the product in question. Therefore, producers should base their assessments on information gained from experts’ opinions but not without checking the obtained information for plausibility.
Conclusion
We conclude that technical standards are a useful tool for mastering uncertainty. Compliance with these standards implies that the minimum safety requirements are met and that the product is safe enough to be distributed on the market. In some cases of new technology, technical standards do not exist and therefore no guidance is available to the producer. As a result, the producer must provide proof of the safety of his product in other ways. As no legally binding documents exist, we found that following the risk assessment described in the RAPEX-Guideline is currently the safest way for the producer to demonstrate the safety of his product.
5.1.4 Legal Uncertainty and Autonomous Manufacturing Processes
In the future of manufacturing more and more autonomous systems will be implemented to raise product quality and product safety. But first and foremost, they are implemented to make production processes more cost- and material-efficient. Although fully autonomously acting manufacturing processes are still to come, the discussion of relevant legal issues is very present. Without autonomous manufacturing processes on the market, there can be no jurisdiction to base legal requirements on. Uncertainty regarding legal requirements and legal risks can be one reason for the stagnation of innovation. The general issue and characterisation of uncertainty is discussed in Chap. 2. If the legal requirements that manufacturers must comply with could be specified today, innovation could be promoted and guided in the right direction. This tool for mastering legal uncertainty accompanies the methods for mastering uncertainty in a general technical sense as discussed in Sect. 3.3.
Legal literature often discusses, whether or not our existing liability regime is applicable to new and innovative technology [285]. This question arises because the current legal liability framework was established during a time way before automated processes were thinkable. Without going into more detail, it can be stated, that the current liability regime has such a broad spectrum that even autonomous systems generally fall into its scope. It goes without saying that some alterations will have to be made to the way we interpret regulations. Without these alterations, liability gaps can occur.
For the sake of a liability regime that is well suited for the innovative technology to come, and provides guidance as to what is legally expected from innovators and producers, this interpretation needs to take a practical approach. What are the specific problems that occur, when using, e.g. autonomous production processes, and how do we interpret the existing liability regime accordingly? Regarding liability risks in manufacturing processes, both conventional and autonomous, we are concerned with two main rules: Sect. 1 paragraph 1 of the Product Liability Act and Sect. 823 paragraph 1 of the German Civil Code. Contracts between the parties can also result in compensation, if they are violated. In the context of this discussion, however, we will exclusively focus on the aforementioned rules. Firstly, this is so because contracts are only binding between the parties resulting in the risk of uncertainty being much lower. Secondly, because the real legal uncertainty lies in the liability for damages inflicted on users and third parties.
Section 823 paragraph 1 of the german civil code
Section 823 paragraph 1 of the German Civil Code applies to damages done to life, body, health and property of a person. It is the key rule of German tort law. Manufacturers’ liability is only one facet of this rule, for a historical account see [36]. Its broad scope applies to many different actions causing the damages mentioned above. The first requirement of this rule to be applicable is that damage is done to one of the protected rights. Secondly, the damage must be caused by an intentional or negligent action. Finally, this action needs to be unlawful, meaning, not complying with the general principles of the law. Assuming that, in most cases, the manufacturer does not intend to harm another person’s rights, which is considered to be an intentional action, the large number of cases will evolve around the question of how to determine negligence. A negligent action is based on the violation of a security obligation. Generally, anyone who uses or creates a source of danger to others, needs to ensure that no harm is done [37, marg. 10]; [33, marg. 21 f.]. The security requirements that derive from this obligation depend on different factors: Potential users, whether they are consumers or professionals, intended and unintended but foreseeable use cases, which are limited by intentional misuse. All of these criteria need to be taken into consideration by the manufacturer. Users’ safety expectations must also be taken into account as far as they are reasonable.
In addition, the product has to comply with the current state-of-the-art safety standards. In this context, current refers to the point in time in which the product is marketed. German legislation has developed specifications for the safety obligations, the manufacturer has to comply with. They can be categorised in the areas of design, construction, instruction and monitoring of the product during its use phase. During the design phase, the producer is expected to choose the final product design with the required safety in mind. At the same time, he needs to document his decisions in this respect. In the event of liability claims, the producer needs to prove that no other design alternative would have been better suited to prevent the occurred damage [32, marg. 16].
Product liability act
For damages done to body, health or property of a person, Sect. 1 paragraph 1 of the Product Liability Act is applicable besides the general provisions of tort law. The Product Liability Act explicitly addresses producers of defective products. A product is defective, if it does not meet the expected safety standard. Safety requirements can be established similarly to Sect. 823 paragraph 1 of the German Civil Code. The same categorisation applies, except there is no obligation to monitor the product during its use phase. This is due to the fact that the aim of the Product Liability Act is to ensure that only safe products are placed on the market. Therefore, its relevance ends with the first placement of the product onto the market. Everything past this moment can only be regulated by Sect. 823 paragraph 1 of the German Civil Code. The main difference between the two provisions is the fact that the liability stated by the Product Liability Act is not based on fault, making it more consumer-friendly.
Automated deep drawing
For discussion purposes, we are going to evaluate the product liability issues concerning autonomous production processes referencing an autonomous deep drawing process. In order to get a better understanding of the problem, it is necessary to evaluate current state-of-the-art closed-loop controlled processes.
The demands on geometry and ever new materials pose a challenge for conventional deep drawing processes. The wall thickness of the final part has to be further reduced in order to make better use of the material, which increases the risk of wrinkling and cracking [7]. The use of more robust and thinner materials contributes to this effect as well. In addition, there are the fluctuations inherent in the process or the fluctuations in the material. All of this narrows the process window [168]. The deep drawing process consists of different steps, starting with the production of a blank cut from supplier coil material, followed by the actual deep drawing step and the quality control. The highly automated process has the ability to take data into account, which is provided by the supplier of the coil material. Also, the process can forward information from each production step to the next. Fluctuations and uncertainty in materials and between the individual steps of the process can therefore be taken into consideration. Information on the quality of the final product can then be fed back to adapt blank holder forces in the deep drawing process. Achieving the maximum drawing ratio, as displayed in Fig. 5.6, enables better material utilisation and the deep drawing of more complex geometries. Drawing ratio in general refers to the ratio of the blank diameter to the punch diameter. In conventional deep drawing processes, the maximum drawing ratio is linked to a higher risk of wrinkling or tearing, and therefore, to potential failure of the final product. With highly automated processes, the desired maximum drawing ratio becomes more achievable without taking higher risks.
Process window for deep drawing following [111]
Quality control checks random samples for compliance with specified product requirements. This is achieved by both optical measurements for the geometrical properties and destructive testing for robustness. Further, it is possible to measure blank holder forces, draw-in ratio of the blank, as well as wrinkling and tearing with real-time sensors in the tools. However, it is not possible to detect thinning of sheet metal or microscopic cracks without destructive testing. Thus, although the process can adapt to material fluctuations so that the geometry produced stays constant, other material properties that have never been problematic before can fluctuate. These undiscovered property fluctuations can have a great impact on the safety of a product, e.g. for load-bearing car components, such as car doors. Therefore, products can pass optical quality control and still fail during their use.
State-of-the-art deep drawing processes are based on the control of blank holder force in order to prevent wrinkling and tearing. Still, these offline closed-loop processes do not feedback information from the quality control or crash test data. As a consequence, the next step in the evolution of the deep drawing process must include such a feedback-loop, as well as the ability to adapt to an online closed-loop process. This will also involve processes to be able to learn. But while learning from geometry, data alone will prevent wrinkling and tearing, necking for example might be left unseen. In addition, the learning process needs to consider strength parameters. Since measuring strength has not yet been feasible inline, the measuring effort would be high. For the process to learn according to given strength parameters, measurements have to be taken frequently, for example every 100 parts.
Outlook on future autonomous processes
The autonomous production process will be able to make many relevant decisions by itself without human interaction, assuming that there is enough data from the use phase and failure of the previous product available. Even decisions concerning the design will be made by the process itself, for example choosing the coil material for deep drawing. According to the desire to produce more light-weight products, the process might decide to use a material that has not been used before, by applying the knowledge it has achieved from previous iterations with other materials. Errors might occur, if the new material behaves differently, due to the fact that it is more brittle, for example. Therefore, microscopic cracks may occur in the final product that cannot be detected 100 % by optical quality control, yet. Consequently, the process could not adapt its production parameters as there is no data base to learn from. The process might have to be limited to materials that have already been tested before. In this sense, the process could not act fully autonomous. Nevertheless, the ability to learn and adapt production parameters for every product counteracts material fluctuations as well as fluctuations in tolerances from upstream processes, and therefore copes better with many of the uncertainties equally occurring in current production processes.
Discussion
If products, manufactured by an autonomous production chain, cause harm to a person’s rights, the question arises who will take responsibility for the damages done. In most cases both Sect. 823 paragraph 1 of the German Civil Code and Sect. 1 paragraph 1 of the Product Liability Act apply. The Manufacturer of the product is held liable. Section 823 paragraph 1 of the German Civil Code requires a breach of duty of care, whereas liability under the Product Liability Act requires a defective product. Therefore, different categories of defects have been established: errors in the design, the fabrication, instruction or product monitoring. Errors in fabrication refer to deviations between the designed product and the final product after manufacturing. But, a 100 % error-free production is not expected of the producer. Therefore, he is not held liable for so called outliers in production [35, marg. 12]. For autonomous production processes, this category is no longer useful. Therefore, we focus on the other categories.
The interesting, and from a legal perspective, important feature of the autonomous production process is its ability to learn. During the deep drawing process, the parameters can be adapted to produce a product with a defined geometry. The process decides on the used material, the applied blank holder force and the duration of the deep drawing process. All these choices influence not only the geometry of the final product, but also its safety, for instance in the event of a crash. Conventionally, these choices would be made by the manufacturer, but in autonomous production processes, decisions are transferred to the process itself. Consequently, legal obligations concerning the safe product design can no longer be ascribed to a specific choice of the manufacturer. In order to identify legal obligations for the use of an autonomous production process, we have to consider the production process in its entirety, rather than the individual product, for a deeper discussion, also see [163].
Use of autonomous production processes
The first question to answer is whether autonomous production processes should be used at all, which is a crucial question for all new technologies that pose new risks. In order to give an answer, the interests at stake need to be considered. In an autonomous production process, parameters are set automatically during the process itself, rather than manually as in conventional production processes after a product inspection. Ideally, autonomous production processes minimise the risks of human misbehaviour and thus the risk of product failure.
In reality, there is still a lot of uncertainty, when trying to identify the actual risk of a product failure. Along the example of the automated deep drawing process, manufacturing close to the process limit also poses the risk of material thinning, which cannot be detected in a non- destructive way, yet. At the same time, completely new failures could occur, which have not been relevant for conventional production processes yet. The manufacturer needs to ensure that the products manufactured by such a process are as safe as the current state-of-the-art products [32]. The learning phase during the development of the production process needs to produce a steady product quality complying with the current state-of-the-art safety standards. Even then, a residual risk cannot be eradicated completely. Therefore, manufacturers have to find a way to quantify the risks as well as the safety-gain inherent to the autonomous production process. At which level of residual risk the autonomous production process may be used is not clear yet. This depends on the acceptance of such processes in the public and political opinion. Nevertheless, setting a standard for the permissible risk should not be left to the industry. Instead, clear guidelines should be developed by political institutions.
Obligations during the use of autonomous production processes
When applying the currently applicable legal framework to the technological innovation of the autonomous production process, two problems become apparent. Firstly, the learning character of the process is based on failure. Learning can only come from failure, whereas the legal obligation is based on avoiding such failure. Secondly, the functionality of the process is based on software. It is acknowledged that software cannot be produced 100 % free of errors. Knowing this, the manufacturer needs to take particular care in monitoring the functionality of the production process [253, p. 3147]. This obligation is conventionally not prioritised from a legal perspective, but serves as a compensation for the fact that all relevant design choices are made by the process, not the manufacturer. The producer’s obligation to design a safe product is therefore less demanding.
The question then is, how this obligation to monitor the process should be implemented. It is also worth mentioning that one cannot always conclude the safety of the product from the fact that the process functions correctly. As a result, the manufacturer should also identify safety relevant properties of the product and monitor them as well. The effort, the manufacturer needs to put into monitoring the process and the product depend on how the process learns and adapts. Particularly the frequency of a learning impulse is relevant, since the process only changes and adapts the process parameters after such impulses. If the process is based on the data of every single product, parameters can change after each product. Thus, the manufacturer would also have to monitor the safety relevant properties of each product. Whereas, if the data of only every hundredth product is used as a learning impulse, a change in the process parameters only occurs at this frequency. Then, it would be sufficient to check the properties of every hundredth product, i.e. the product after the learning impulse.
Obligations concerning the products of autonomous production processes
Lastly, the manufacturer has an obligation to monitor the product during its use phase. This way, defects that occur after a certain time in combination with other products or in general “in the field” can be detected. The information derived from this monitoring process is valuable and must be used to either prevent damage to protected legal rights or simply as input for future product development processes. The measures that need to be taken to monitor the product are manifold and depend on the specific product. But in general, it can be stated that the manufacturer needs to implement a complaint management system [103, marg. 379]. In addition to managing this passively achieved information, the manufacturer needs to actively inform himself about possible defects and errors concerning his product by checking newspapers, relevant journals [34, marg. 34], test reports or internet forums [146, p. 2729]. With the advancing technological innovation, it could also be possible to monitor products in real time. This would pose new legal questions which have to be discussed in the future.
Conclusions
In summary, autonomous production processes enable different and more efficient production ways. The current legal framework adapts to the new production technology. Manufacturers need to “train” the autonomous process until reliable results are achieved. The residual risks and the safety gained are to be quantified in some way. Guidelines to what level of residual risk is permissible should be developed by political institutions. When using an autonomous production process, the focus must be on monitoring the process and the resulting products during the production process, as well as on monitoring the products during the use phase.
5.1.5 Optimisation Methods and Legal Obligations
Computer software and hardware have improved so far that using simulation and optimisation tools in product development processes has become a common feature. These tools allow for more complex designs and larger systems, as well as improvement of development time, accuracy and safety. At the same time, optimisation methods are becoming more and more popular in developing product parts or a system topology. A new trend in mathematical optimisation is the treatment of resilient systems. Methods for developing resilient systems explicitly take failures of components into consideration, trying to guarantee at least a predefined limited function of the system itself. Although these methods are highly promising, the implementation is very complex and is usually done in the context of data, model and structural uncertainty, see Chap. 2. This uncertainty can then result in legal liability, if a person’s rights are harmed. In order to minimise legal uncertainty in the development process using optimisation methods as well as resilience optimisation methods, we need to understand the way these methods work and how their implementation affects the legal product development requirements we know. The concept and use of resilience for mastering uncertainty is described in Sects. 3.5 and 6.3.1.
Legal literature usually takes a more abstract approach to discussing the impact new technologies and new algorithmic design methods have on the existing legal framework. This is why we take a rather technical approach in order to gain a more specific and concrete idea as to how our current liability regime adapts to new algorithmic design methods. We also want to discuss which legal requirements can be derived for producers to comply with, and if and how the current legal framework might have to be adapted.
Legal liability
As seen in Sect. 5.1.4, Sect. 823 paragraph 1 of the German Civil Code is the key liability rule. In addition to producer liability, the provision generally covers cases in which a person is injured, killed, or the person’s property is impaired by a source of danger in circulation. The basis of this liability is the violation of a duty of care. Anyone who benefits from a dangerous product has to ensure that this product does not harm others [28]. In this sense, dangerous products are those, which are potentially dangerous for others, simply because of their nature, for example cars. The determination of necessary precautions depends on a number of factors. On the one hand, it depends on who the potential users are and therefore who is potentially at risk. On the other hand, it depends on which dangers can potentially occur. All this has to be considered by the manufacturer of a product or the operator of a system.
It should be emphasised, however, that only what is reasonable can be expected. The manufacturer or operator does not have to eliminate every residual risk at every price in order to be spared from liability. What can reasonably be expected varies from case to case. In principle, however, it can be said that the safety standard set by state-of-the-art technology has to be satisfied. On the one hand, the state-of-the-art is represented by norms and standards, but on the other hand by the solutions available on the market. Still, compliance with the current norms and standards alone does not necessarily protect against liability. In some cases, it will rather be necessary to take safety measures beyond norms and standards that are available according to the state-of-the-art technology. Norms and standards thus form a kind of minimum safety that should not be undercut. Although they are not legally binding, non-compliance with them has an indicative effect for non-compliance with safety requirements, which would have been possible according to state-of-the-art technology [31, with further references, marg. 16].
Resilience
The anticipation of several possible failures of the system or a product is a promising step into trying to make products safer. The idea is to ensure a pre-determined minimum functionality that the system or the product will still be able to achieve in case of disturbance or the malfunctioning of a specific amount of product components. Resilience can be implemented in the product development process, for instance by only considering design options that achieve the minimum functionality in the event of k component failures [9]. The product or system then has a so-called buffering capacity of k. For more than k component failures, no reliable outcome can be predicted. This is, in a way, a restriction when designing a product using resilience optimisation methods. Nevertheless, it is possible to concentrate on a defined number of component failures, rather than what causes a failure of the product or system at large. Furthermore, it is worth mentioning that the number of possible failure scenarios increases with the number of components and design options. Hence, the enumeration of all possible failure scenarios becomes practically impossible. More details on resilient system design can be found in Sect. 6.3.
Review of legal obligations
In order to identify the manufacturer’s duty of care when using optimisation methods, we take a closer look at the selection of the model on which algorithmic design methods are based on and differentiate between optimisation methods in general and resilience optimisation methods.
Selection of the model
All algorithmic design methods are based on a model of the system. In order to specify the legal obligations when using algorithmic design methods, considering the selection of the model of the system should be the starting point. These models always represent reality in a simplified way, see Sect. 1.3. Therefore, one model only applies to the specific application for which it is designed. If a model is used for the development of an application for which it does not provide reliable information, considerable deviations between the modelled system behaviour and the actual behaviour can occur during the usage phase.
It is important to note that in most cases many models are available, while some represent reality better than others. This results in the important restriction of the most reliable models often being too complex and thus too time-consuming for computation. In this respect, the developer needs to find a balance between an accurate model and the appropriate computation time.
When discussing legal obligations, the level of risk to third parties’ protected rights has to be determined and should be foreseen by the developer of a product [26, marg. 6]. First of all, the developer would have to ensure that the model he uses can generally provide reliable information about the product. The developer also needs to take the boundaries of the model into consideration, cf. Sect. 2.2. Furthermore, he has to have some kind of proof that the approximations made on the basis of the underlying model transfer into reality. This is usually achieved by model validation and verification. With the help of either experimental data or simulation results, it can be shown that the predicted behaviour is in accordance with the actual behaviour of the product. This procedure can be expected from the developer. Validating the model can imply that the producer of the product has fulfilled the safety obligations in the development phase. But in order to fully protect the developer from liability claims, safety aspects must be reproduced by the model as well.
Use of optimisation methods
Optimisation methods allow the development of more complex systems or products, as they simplify the design choices for the development process. These methods are based on mathematical models of the system and its environment. As already mentioned, one of the causes for uncertainty in using such methods arises from the fact that models can never be an exact representation of reality, as the latter is too complex to be computed. The outcome of the design with optimisation methods depends on the chosen model and on the chosen input parameters. These parameters are mostly economical and structural factors set by the developer. Moreover, the number of input parameters is finite. Safety of the product as such cannot be an input parameter. In fact, an optimal solution for the given optimisation problem can be structurally unsafe. This becomes clear, when considering optimisation problems that are used to minimise the material usage of a product.
As the producer cannot rely on the optimisation method to choose a particularly safe product design, he still needs to ensure that safety standards are met. So far, this process does not deviate from a development process which does not rely on optimisation methods. In a conventional development process, the developer would consider different design alternatives which solve the problem defined. These are the alternatives the developer would then have to choose from [274, marg. 972]. The decision would be made considering functionality and economic factors. Simultaneously, safety requirements can and should be considered when choosing the final product design.
In using optimisation methods for product development, the numerous possible design alternatives are not considered by the producer himself. The algorithm decides on one single product design that fits the defined problem the best, given the predefined input parameters. Output is therefore only one optimal design option. This one design alternative can of course be tested by the producer considering safety aspects. Conventionally, this does not suffice legal standards as they are developed by jurisdiction. The act of choosing the design and the consideration accompanying that process represents an important step that is ascribed to the producer. But imagining the producer would have to trace back every possible design alternative the algorithm considered during the optimisation process, all facilitation gained by using the algorithm would be lost. Apart from that, the time, cost and computational efforts would be great. Only measures are legally expectable, that are reasonable. These legal standards need to be adapted. Otherwise, innovations might be hindered. Therefore, to demonstrate the safety of a product in a way that exonerates the producer from liability claims, it needs to be possible to check only the design alternative the algorithm provides as an optimal output. Then again, it has to be taken into account that complex products or large systems, such as a bridge, cannot be tested in ‘real life’. Prototypes have their limits, where the size of the system or the number of components exceeds the feasible. Consequently, producers need to check and prove the safety of a product or system by using simulation methods. Then, the problem we discussed at the beginning becomes relevant again. Simulation algorithms are based on models of the product and its environment. Hence, the producer has to be certain about the boundaries of the simulation and the underlying model.
Use of resilience optimisation methods
Resilience optimisation enables the development of systems and products that can withstand a defined number of failures of an undetermined cause. For a defined number of failures within the system, functionality can be guaranteed. It is not possible to foresee every possible damage scenario in the development. The resilience optimisation method can therefore make this uncertainty more manageable. If the identification of potential users and dangers to them and third parties has been an essential part of a developer’s duty of care up to the current moment, this is no longer considered when using resilience optimisation methods. The system developed in this way guarantees a minimal functionality despite unknown failure scenarios. As long as the functionality of the system is guaranteed, no one will be harmed. At least in theory, resilience optimisation promises safer products. In reality, however, it is uncertain how these systems react to failures or damage events. Furthermore, the model and data uncertainty within the design stage might be significant. Nevertheless, resilience optimisation can be used to support engineers in the early design stage as for instance shown in Sect. 6.3.5.
As with the development of any new technology, the question is whether the product can be brought to market at all. If the risks of the product cannot be weighed against the supposed safety gain, marketing cannot be recommended [35, marg. 17]. It should also be noted, however, that currently neither standards nor practical experience can be used to develop products using resilience optimisation methods. In order to answer the question of marketing, appropriate methods for assessing the risk of the systems would have to be developed first. If the comparison with conventionally optimised systems turns out to be in favour of the safety gain, the product can be marketed.
Once this fundamental question has been clarified, the question still remains how the current legal framework can be transferred to the systems developed in this way. So far, the starting point has been, among other things, the obligation of the manufacturer to correctly assess the danger of the product for potential users, as well as third parties. This assessment should then be used as the basis for selecting an appropriate design. As already discussed regarding the conventional optimisation methods, the selection of a design alternative is now left to mathematical optimisation. Furthermore, due to resilience optimisation methods, the preceding step of assessing potential danger and user is omitted.
In the end, all that remains is the legal premise that the manufacturer must do everything reasonable to ensure the necessary safety of the product. What the manufacturer can reasonably be expected to do must be determined by weighing up the interests of the parties involved [29, marg. 10]; [27, marg. 7]. First and foremost, it will be a matter of comparing the expected safety gain from resilience optimised products and the remaining residual risk. Moreover, it must also be considered which legal interests are potentially at risk. The higher the significance of these legal interests is classified, the more resource-intensive security measures can be expected [30]; [35, marg. 8]. For example, if a person’s life is at risk, the producer is expected to take more costly precautions to avoid this danger compared to a case in which a person’s property is endangered. Nonetheless, the economic interests of the manufacturer can also be taken into account [35, marg. 18]. The development process becomes faster and ideally safer by implementing resilience optimisation methods. An obligation to simulate all possible failure scenarios would take a great amount of time, effort and resources. The entire reason why resilience optimisation methods are used in the development process of new products would be counteracted. One can therefore not expect the manufacturer to simulate all imaginable failure scenarios of the product for each design alternative. Otherwise, legal requirements would hinder innovation in product development which should not be the aim of technology-friendly development of the law.
The priority of all obligations concerning the development of a safe product is currently the duty of care in construction. Primarily, the producer has to ensure that the design of the product is safe [103, marg. 71 ff.]. Further obligations, such as instructing the user of the product to limit the use to a specific application or monitoring the product during the phase of usage, are only secondary. But considering the aforementioned points, it is relevant to see a shift in prioritisation of the producer’s obligations towards an increased importance of monitoring the product in its usage phase. First of all, it is important to limit the risks that still accompany the use of resilience optimisation techniques, secondly, to learn from products’ behaviour “in the field”.
Conclusions
Considering the information gathered, we can establish the following key findings from our work on legal requirements for the use of optimisation methods. The developer must be aware of the boundaries of implemented and used models. At the same time, the developer is also expected to validate the used models. When using optimisation methods for development, the developer can check only one optimal solution provided by the algorithm for compliance with safety requirements. Checking can also take place by using simulation methods. Before using resilience optimisation methods, the developer needs to prove that the gain of safety outweighs the remaining risks that are unknown. But the necessary methods need to be developed first. If this consideration turns out in favour of the use of resilience optimisation, new priorities in legal standards still need to be set. How to set these priorities will have to depend on the methods developed in the future. The main focus of the developer is to lie on monitoring the product during the usage phase to ensure the safety of users and third parties.
5.1.6 Linguistic Analysis of Technical Standards to Identify Uncertain Language Use
Technical standards play a major role in the entire product life cycle by standardising rules for the exchange of information, ensuring compatibility and reducing the variety of products, services, interfaces and terms. Technical standards are developed by international, national, and regional associations and are not to be confused with legal standards [102]. As we get to know in Sect. 5.1.3, the application of technical standards is voluntary in principle, but may as well be legally binding by law or contract. In both cases, technical standards should reduce the uncertainty of the product under development by defining formal quality requirements for product development (cf. Sect. 5.1.1 and 1.6). Consequently, unclear language use in technical standards leads to uncertainty during the product development process. In this section, we therefore focus on the linguistic analysis of technical standards to identify uncertain language in technical standards.
Since we do not know the impact of “semantic uncertainty” in standards on the product, its use and on its acceptance, we have to speak of “ignorance” (see Chap. 2). The aim of this study is an annotation method to avoid this ignorance with the help of an information system. The user of the information system can master uncertain language with the help of annotations, that give him or her hints that there is uncertainty and how to proceed.
A general requirement for technical standards, apart from the use of plain language, is the use of clear and concise expressions [76]. In contrast to that, Drechsler found that among users of technical standards, there is a considerable lack of knowledge of how technical standards are to be interpreted [82]. This discrepancy is not a coincidence but rather a consequence of the need to generalise technical standards in certain parts to make them applicable in a variety of contexts. However, underspecification inevitably leads to uncertainty as to how to correctly interpret the technical standard’s intent. Two conditions must be met to bridge the gap between deliberate and necessary underspecification and all the additional information needed for correct interpretation and, hence, full compliance with the intent of the technical standard. Firstly, the user of the technical standard must be aware of this gap and, secondly, the user needs to know where to find the missing information.
If we consider sentences with “should” for example: While “should” conveys a certain intent, it can also be interpreted as a mere suggestion. The uncertain parts of technical standards are not as easy to spot as the occurrence or the meaning of “should” illustrates in the following examples: Example 1: ‚‚Dies gilt insbesondere für Apparate, die einer regelmäßigen Inspektion und Wartung bedürfen ‘‘. [In particular, this applies to devices that are in need of scheduled inspection and maintenance.] [71, p. 38]. Example 2: ‚‚Die mit Trinkwasser in Kontakt kommenden Werkstoffe [...] dürfen Stoffe nicht in solchen Konzentrationen an das Trinkwasser abgeben, die höher sind als nach den allgemein anerkannten Regeln der Technik unvermeidbar [...] ‘‘. [The materials that come into contact with drinking water are not to release substances into the drinking water in concentrations higher than unavoidable according to the generally recognised rules of technology.] [71, p. 15].
In Example 1, there is no list of concrete devices, which makes this passage uncertain for as long as the maintenance needs of all devices used in a project are not checked and documented. While the solution—looking up technical specifications provided by the manufacturer—to the uncertainty in Example 1 is straightforward, Example 2 presents the user with a less clear-cut issue. There is no single manual or document that records the generally recognised rules of technology. To obtain the necessary information, engineers have to either rely on experience by utilising solutions from earlier projects, or they must find examples of solutions which clearly follow the generally recognised rules of technology.
The practice of how technical standards enter the process of product development also comes into play. There are various possibilities, all of which to be found on a scale between the following scenarios. Scenario 1: The users study all standards pertinent to a specific project. Scenario 2: The users study a subset of the pertinent standards whenever the need arises. Scenario 1 is unlikely due to the sheer number of pertinent standards; Scenario 2 inevitably leads to a number of uncertain statements in pertinent standards being overlooked. In any case, due to the uncertainty inherent in standards, none of the scenarios addressed leads necessarily to a standard-compliant product development without further steps.
In each of these cases, an information system which shows all (potentially) uncertain parts of pertinent norms can assist the user in dealing with uncertainty not only by alerting him to its presence but by informing him of its nature, and by providing hints, as to where further pertinent information can be found. The primary goals of this study are therefore twofold: (i) creating a taxonomy of uncertainty in technical standards, and (ii) developing an information system which displays uncertain parts and their classification to the end user. For a detailed account of the latter, see [254].
The technical standards chosen for analysis in this study are from the DIN 1988 series “Codes of practice for drinking water” due to their relevance for Sect. 6.3.5.
Basic notions and methodology
Standard-compliant product development requires knowledge of the pertinent technical standards and of anything needed to resolve any uncertainty inherent in the standards. Uncertainty can arise from ambiguous language as well as from lack of (specialised) knowledge. From a linguistic perspective, the meaning of a word is a cognitive entity (\(=\) concept) evoked by perceivable linguistic entities, such as strings of characters or sounds (\(=\) word forms). The concept is both an abstract representation of an entity in the world (\(=\) object, phenomenon) and a reference to this entity.
The relationship between words, concepts, and objects in the world can be characterised as triangular, and is commonly described as the Semiotic Triangle [211, p. 11]. Special knowledge often needs specialised language, which can be accomplished in several ways: New words like “Covid-19” may be created and spread with the express purpose of evoking a specific concept referring to a concrete object or phenomenon in the world. Also, existing words can be re-purposed by expressly restricting the concepts they evoke (\(=\) defining their meaning) or by using them in a specific way or in a specific context, such as “mouse” in the sense of “peripheral computer device”.
We understand uncertainty to mean a condition in which further steps of knowledge acquisition need to be taken to ensure standard compliance. Standards are not data in the sense of numbers, but more or less vague instructions for action that must be interpreted and supplemented by knowledge acquisition. Thus semantic uncertainty does not fit directly into the uncertainty classification from Chap. 2. Knowledge acquisition, in turn, is a process of understanding by interpreting information according to previous knowledge and applicable rules. We draw on the DIKW model (data, information, knowledge, wisdom) [4, 24, 230] in order to differentiate between knowledge, information, and data: data is a record of knowledge disassociated from the human mind, information is the result of cognitively processed data, and knowledge is the result of understanding the information by way of interpretation.
Annotating has a long-standing tradition in humanities and can be regarded as both, a part of knowledge acquisition and a scholarly primitive approach [193, 265]. We used the web service Weblicht [157], provided by CLARIAH DE [169], to automatically assign the base form (\(=\) lemma) to each word. This facilitates searches, for instances of word types, even if those word types have differing surface forms. For the manual annotation of uncertain words and phrases, we used the software INCEpTION [172] which can access multiple annotation layers (like part-of-speech and lemma) and allows for bottom-up development of annotation schemes.
Taxonomy design needs to incorporate a clear “differentiation between instances and classes” [287, p. 377], which in our case has been accomplished by a simple rule: Any concrete segment of text that demands further steps of knowledge acquisition is an instance of the super-class uncertainty and needs to be classified further. We employed a mixed development process, combining top-down and bottom-up approaches [208]: Previous knowledge of technical standards led us to distinguish evident from hidden uncertainty (top-down approach). Evident uncertainty means any uncertainty that remains after studying the norm text while hidden uncertainty arises from a conflict between individual knowledge and the specifications presented in standards. Prototypically, hidden uncertainty is individual and cannot be annotated which is why we concentrated on the branch of evident uncertainty. The subcategories of hidden uncertainty were developed in a bottom-up process.
Results
Evident uncertainty, a result of linguistic ambiguity, is divided into the semantic uncertainty and referential uncertainty, see Fig. 5.7. With regard to knowledge acquisition, semantic uncertainty is situated between information and knowledge and hinders the process of understanding while referential uncertainty is situated between data and information, and expands the pool of information, which needs to be part of the knowledge acquisition. The sub-classes of semantic uncertainty account for different forms of meaning related uncertainty. Modality covers any instances where uncertainty arises from modal expressions, such as “can” or “should”, while underspecification covers anything else. The sub-classes of referential uncertainty cover all instances of references in the technical standards. Known targets are all instances of named sources like “Diese Norm gilt in Verbindung mit DIN EN 806-2 [...] ” [This standard applies in conjunction with DIN EN 806-2] [71, p. 6] while unknown targets are references to unspecified sources like ‚‚Es sind die technischen Anweisungen der Hersteller zu beachten. ‘‘ [The technical specifications of the manufacturer are to be observed.] [71, p. 19].
Towards automated annotation using machine-learning
The next steps focus on automation with regard to both, document import and annotation. The first steps towards a cooperation with Beuth to provide XML files instead of PDFs have been taken. The annotation process is improved by making use of Inception’s in-built machine-learning (ML) and string matching capabilities. For the sake of proper ML work, a larger number of standards are annotated. For the string matching, the instances of the class semantic uncertainty and, to a lesser extent, of the class unknown target will be used to automatically retrieve synonyms from resources made available by lexicographic projects. Possible resources are the [Digital Dictionary of German] [148], the project openthesaurus.de [204], which is also the basis for the information provided in DWDS. Further services are DeReKoVecs [100], which analyses the relationships between words occurring in the Deutsches Referenzkorpus (DeReKo) [German reference corpus] and GermaNet [140, 154], a lexical-semantic net [153]. These measures are going to enable us to annotate both, technical standards which are directly pertinent to a given project, and technical standards which are referenced by these. Thus, users of the information system are going to profit two-fold, namely gain insight into uncertain parts and their classifications to then follow and master uncertainty spanning multiple documents.
5.1.7 From Risk to Uncertainty–New Logics of Project Management
This book analyses how “to ensure product safety in a world of products with ever increasing complexity”. Thereby “mastering uncertainty is central”, and, as emphasised in the introduction, it “requires contributions from engineering, mathematics and law”, cf. Chap. 1.
This section broadens the view in two respects. First, it examines how uncertainty is conceptualised and handled in the scientific discipline of project management. Second, it does so from a historical perspective by describing a historical shift in concepts in terms of dealing with uncertainty in the 1990s. The historical analysis of the changing term of uncertainty and the changing concepts developed by the discipline of project management leads to a better understanding and classification of current tools for planning processes in general.
In the second half of the 20th century, project management developed into a scientific discipline in order to ensure that projects are managed, controlled, and secured to run according to plan. Uncertainty is regarded as an “obstacle and a threat” [42, p. 5] to project success. Uncertainty should be minimised and made controllable. That does not come as a surprise, since challenges and problems that arise from unknown, unplanned or unexpected events and developments are obvious. In a recent study, Heidling stated that, of 318 projects “in the area of industrial, global large-scale projects 64 % (failed) to achieve the planned project goals” [150, p. 17].
The capacity of managing uncertainty is of great importance for the success of projects, especially in the context of increasing complexity and rapid change. In the relevant publications and journals of professional project management, this has been a topic of debate for many decades. The question of how uncertainty can be mastered led to many publications that questioned existing concepts and discussed new concepts for dealing with uncertainty. It is striking that the problems of dealing with uncertainty are addressed far more frequently than success factors that make uncertainty manageable.
This section asks (i) how uncertainty has been conceptualised in the discipline of project management over the last decades, and (ii) which methods have been developed for mastering uncertainty. In particular, the goal is to reveal the theoretical foundations and premises of project management, thus contributing to a fundamental understanding of the changing logic of project management. This section is based on programmatic publications within project management as a discipline. A study by Heidling, summarising and evaluating journal articles from the 2010s, should be highlighted, since it provides important insights for what follows in this section [150].
It is important to note that project management as a scientific discipline develops rather general and abstract models that do not focus on the specifics of various technological disciplines. Although project management emerged in the context of large technological projects, such as the development of the atomic bomb and space travel, models of project planning are being developed for various areas, from large technical projects to the planning of technological innovations to business projects and events. Therefore, this section does not deal with uncertainty in the process of product design, nor primarily with the control of technically induced uncertainty, but with uncertainty during the entire process of planning a project in general.
The thesis that will be developed is that, in the second half of the 20th century, we can observe a change in the concepts of uncertainty within project management, which led to the recognition of ignorance as a fundamental premise of all projects. In the theoretical foundations of project management, a paradigm shift happened: Uncertainty was redefined. The primary goal here is to analyse this change in concepts within the discipline of project management in the 1990s.
Before we can elaborate on that, it is necessary to take a closer look at the terminology used in project management and relate it to the terms used in this book. The terms of project management are strongly influenced by societal and sociological discourses. To make this clear: That which Chap. 2 of this book labels stochastic uncertainty, project management calls risk. In the models of project management, risk refers to possible, but not foreseeable events in the future that are known in principle and whose probability of occurrence can be calculated. However, further questions are asked, particularly in sociological discourse. It is asked how risks are produced by whom, how they are perceived by different actors and what significance is ascribed to them in each case. Thus, risk is a quantitative and qualitative category.
The technical term incertitude, cf. Chap. 2, is not used in the debates and models of project management at all. And while this volume differentiates further by distinguishing ignorance from incertitude, as defined in the introduction, within project management the term uncertainty is much less differentiated. While a paradigm shift in project management is clearly evident, the terms remain more vague than in the engineering disciplines. Models in project management only distinguish between risk and uncertainty. The interdisciplinary research field of Science Studies, which situates scientific knowledge in historical, philosophical and social context, in turn speak of the latter as unknown-unknowns, while this book uses the term ignorance.
Even before that distinction between risk and uncertainty has been drawn and a redefinition of the term uncertainty was discussed in the discipline of project management in the 1980s and 1990s, uncertainty has already been a category of project management, for example as technical uncertainty.
While in the first decades of project management the focus actually was on technical uncertainty, it has become obvious, from the 1970s and 1980s onwards, that not only the complexity of projects but also the complexity of uncertainty has increased. Societal processes became factors of uncertainty, such as civic protests against large-scale projects or the emergence of societal resistance to new technologies, for example. The pluralisation of the stakeholders involved, accelerated change processes, and changing market conditions, these developments all contributed to redefining the concept of uncertainty.
Thus, in a first step, the focus shifted from technical uncertainty to risks, thereby including technical, social and economic factors. In project management the concept of risk became central, e.g. [203]. At that very time the concept of risk also shaped social debates and the social science literature, e.g. [19, 227].
As early as the 1990s, however, the concept of risk was heavily criticised since it still aimed at controllability and mastering. In contrast, a redefined concept of uncertainty (here, exclusively meaning “ignorance”), which stressed the basically incalculable part of planning, was brought to the fore. This was accompanied by demands for new ways of dealing with such fundamental uncertainty in project planning. It is remarkable that this development can also be observed simultaneously in Science Studies and decision theory.
Similar strategies for dealing with uncertainty have been addressed within scientific project management as a discipline, as they are presented in Chap. 6 of this book, as will be shown in the following.
Risk versus uncertainty
The range of possible, unforeseen events that get in the way of project planning is wide. It ranges from technical problems, changes in the market, political or legal framework conditions to changes in the composition of the team, to name just a few factors. In an essay from 2013, Thamhain lists additional, concrete examples of uncertainty: “the failure of a certified component with proven liability in similar applications, a sudden bankruptcy of a customer organisation, or a competitor’s breakthrough invention/innovation that undermines the value of your current project or threats a major line of business. By definition, unknown-unknowns are not foreseeable and therefore cannot be dealt with proactively” [260, p. 23]. If the types of uncertainty enumerated here are neither new nor surprising, the decisive point is the reference to the unknown-unknowns (ignorance), which began to shape the discourse within project management starting in the 1990s. Uncertainty, in contrast to risk, thus refers to something that is incalculable; thus it evades planning.
Since the 1990s, this has been emphasised as a new challenge in project management and can be observed analogously in Science Studies, which have dealt with the concept of the unknown-unknown. As Peter Wehling summarised, conflicts about the risks of genetic engineering and nuclear technology in the 1970s and 1980s had already made it clear that societies were confronted with a new form of the unknown, namely “the unknown as an unknown threat” [276, p. 485]. The discovery of a fundamental, unpredictable ignorance went hand in hand not only with the new technologies already mentioned, such as genetic engineering and nuclear energy, but also with the perception of living in times of accelerated scientific and social change [10, 276].
However, while this was initially addressed under the term risk, this description proved to be inadequate, since risk was associated with the possibility of calculating and thus mastering it. As already indicated, the newly perceived challenge lay precisely in the fact that phenomena exist, which are “events that are known and predictable in principle”, as the term risk suggested, but that “the consequences of scientific and technological innovations [...] are simply unknown and incalculable” [277, p. 100].
Since the 1990s, project management has been asked to accept the unpredictable as an unavoidable dimension of every project and to find a different way of dealing with it. Exactly as was the case in the Science Studies, in project management, too, this was formulated as a criticism of the risk concept. Within project management, the concept of risk had also been used to refer to “events that are not completely predictable and controllable”. However, the assumption still was that “the probability of their occurrence could be calculated”. According to this logic, risks were transferred to the mode of predictability – thus becoming controllable. “Despite the recognition of uncertainty, certainty is nevertheless sought”, summarised Böhle [42, p. 5].
However, in contrast to assuming that uncertainty is a calculable unknown, beginning in the 1990s, the concept of uncertainty has been redefined in a fundamental way within the field of project management. A newly emerging debate within project management suggested abandoning the ideas that certainty is possible at all and that uncertainty can be calculated, which were associated with detailed planning.
This was a provocation at odds with many modern ways of thinking taken for granted. For example, in the mid-1990s, J. Davidson Davidson Frame, had tied the concept of risk to the question of available information. He held the view—also common in decision theory—that little or incomplete information itself was a risk [105]. Therefore, the solution was to have as much information available as possible. This corresponded to a modern view of science in general: the assumption was that the accumulation of knowledge would eliminate ignorance [276, p. 485].
However, by the 1970s and 1980s at the latest, it became clear that as projects became more complex, ignorance in the sense of the unavailable and uncontrollable also increased, see [226, p. 423]; [189, p. 1106]. Unknown-unknowns—which, in terms of project management, constituted uncertainty—are therefore not the result of incomplete information or of something that is not yet known, but rather something that at a certain point in time is, as a matter of principle, not knowable, and thus not calculable.
According to this logic, a distinction between risk and uncertainty (as in ignorance) has been introduced to project management [203] in order to make uncertainty—understood as ignorance or unknown-unknowns—a topic of project management and to develop new methods for dealing with and ultimately mastering it. In a nutshell: In the 1990s, uncertainty was discovered as something unpredictable and recognised as an unavoidable problem. This conclusion was accompanied by the demand to accept it and therefore to “develop capacity to act with uncertainty” in the sense of ignorance [42, p. 7].
But what did this mean for dealing with uncertainty in project management? What does it mean for the methods developed within the discipline of project management?
Criticism of quantitative and standardised methods
The conceptual shifts from the concept of risk to a stronger emphasis on incalculable uncertainty were, unsurprisingly, accompanied by criticism of quantitative methods. Starting in the 1970s, methods were being developed to quantify risks and to make probabilities of occurrence controllable by using mathematical-statistical methods [203]; [150, p. 19]. As Heidling emphasises, the concept of risk was inseparably linked to predictability and calculability [150, p. 18]; [279], see also DIN EC 62198 [73]. But doing so in this context was considered inappropriate for the novel focus of challenges posed by uncertainty in the sense of ignorance.
In the field of Science Studies, quantitative, probabilistic methods of risk analysis have been criticised and described as the expression of a “reductionist, analytical worldview” and as such regarded as necessary to overcome [110, p. 739].
The aforementioned assumption that more information and more knowledge lead to mastering planning processes, was also questioned. For example, the pursuit of completeness of information as the basis for project management was criticised as not leading to the expected results. This was accompanied by the critical reflection of very detailed, sequential planning processes [260, p. 20f]. Archibald pointed out that the traditional approach of using large amounts of information as basis for detailed planning would not lead to solutions, especially when dealing with uncertainty [10]. It was important to not consider as many factors as possible, but rather the “most important” ones. However, these are “often those with the greatest uncertainty, and the new logic requires giving them priority over the easy, material, more certain ones” [10].
Furthermore, using concepts like controlling and monitoring to predict future events correctly and in a systematic way was not considered helpful in meeting the challenges of uncertainty [150, p. 17]).
Closely connected with such criticism of reductionist, analytical methods were the questioning of project management methods which dealt primarily with unambiguousness, which by now was regarded as inappropriate. In the 1990s, an interesting attempt was made within project management to use fuzzy logic to break up an orientation towards unambiguity in order to calculate uncertainty [10].
Summarising the criticism of dealing with ignorance, it can be said, in a nutshell, that the previous methods, based on calculation, quantification and detailed, sequential planning, were considered obsolete. They were criticised as ineffective when the problem of uncertainty was addressed in terms of dealing with the unplannable.
In essence, this constitutes a fundamental criticism that these methods were characterised precisely by the fact that they were a means of planning the plannable, i.e., calculating the calculable and the knowable, and therefore did not even consider the unplannable and ambiguous. That which could not be planned was, according to the criticism, simply ignored. However, it was precisely this systematic omission that led to problems during the execution of projects. Thus, a fundamental critique was formulated, which posited that the limits of the methods had not been reflected upon. Thus, the model entailed only that which could be controlled within the confines of the model (quantifiability), see similarly [42, p. 8].
This criticism, often voiced within the project management community, resulted in the demand that dealing with uncertainty required a new logic and new procedures, especially in times of “accelerating rate of changes” [10].
Paradigm shift: a new logic in project management?
If we now look at what was supposed to characterise this new logic and new methods, it quickly becomes clear that the criticism of the so-called traditional concepts was much more incisive than what was asked of the new models and procedures. Defining the problem proved to be easier (until today) than finding a solution. In the same way, this applies to Science Studies or decision theories. Here, the answers to the question of how to deal with uncertainty looked strikingly similar.
Firstly, ways of thinking and approaches based on competences considered innately human were said to be, by their “nature”, counter to quantitative, standardised and rationalised procedures. It is especially the unpredictable that requires human experiential knowledge, intuition, heuristics and fuzzy thinking by real humans, as was often emphasised. As the horizon was to be extended beyond the measurable and quantifiable and diagnosed reductionisms were to be overcome, other heuristic, intuitive methods were now seen as appropriate solutions for dealing with uncertainty [10].
This was accompanied by an emphasis on the role of humans, who were no longer perceived as disruptive factors or in need of containment due to their subjectivity and assumed irrationality, but were discovered as potential. Using human skills was now considered the best way to react quickly and flexibly, which is very important when dealing with uncertainty.
Furthermore, demands were made for a holistic and synthesising approach, which would make interrelatedness and processual thinking the basis of planning, and eventually replace linear-causal thinking [10].
The calls for a new way of dealing with ignorance culminated in the demand to not only to accept uncertainty as inevitable but to see it as an opportunity: “Instead of considering uncertainty as a necessary evil, it should be considered as an extremely important, inspiring and useful factor given its inherent opportunities for making improvements and taking measures against risk. In the author’s opinion, uncertainty is likely to hold some of the greatest potential for improving management skills and efficiency today” [186, p. 21].
Uncertainty was thus even interpreted as an opportunity to improve things in ongoing projects, to react flexibly with the goal of ultimately becoming more efficient. Contrary to the idea of creating robust, nearly rigid project plans, a clear plea was made for flexible, incremental, almost improvising action.
If one compares the strategies for handling ignorance, which were discussed in project management in the 1990s, to the strategies for mastering uncertainty described in this book, fundamental similarities can be stated. The strategies to manage uncertainty in technical systems, described in Chap. 6, are robustness, flexibility and resilience. Even if the term resilience did not play a role in the models of project management, the efforts to permanently adapt and flexibly ensure the success of the planning process when faced with unforeseen challenges clearly correspond to the concepts described in Sect. 6.3. That holds particularly true for the role of humans in mastering uncertainty, which has proved to be the core concept of the new logic of project management since the 1990s.
However, a remarkable difference also needs to be noted. Most of the concepts presented in this book refer to technical systems, thus having to ensure that technology itself proves robust, flexible and resilient. Therefore, both quantitative-mathematical models as well the interplay of humans and technology provide a solution for mastering uncertainty.
In contrast, project management focuses on the planning process of projects of various kinds, which inevitably implies ignorance in terms of social, economic and political developments. Thus, since the 1990s, concepts have been developed that emphasise human capabilities, thereby constructing a strong contrast between humans acting with uncertainty (ignorance) on the one hand and quantitative-mathematical models to master ignorance on the other hand.
This constitutes a move away from a paradigm of steering, controlling, measuring, calculating and detailed and sequential planning of projects; it can be summarised with a picture used by Perminova et al.: Projects should be conducted as an exploration or an open-ended journey rather, and not as a precisely planned sequence of steps [221, p. 74]; [150, p. 24]. However, this almost poetic description often clashes with the efficient culture of controlling in many organisations as well as with the design of techno-economic systems.
Summary and outlook
When looking at the premises and theoretical foundations of project management with regard to dealing with uncertainty, there is no doubt that a fundamental paradigm shift has taken place since the 1990s. The description of uncertainty as a risk, which implies the assumption that planning processes are manageable and controllable by quantification and probabilistic methods has been questioned fundamentally. This has been accompanied by a shift in terminology from risk to uncertainty in the sense of ignorance. Dealing with uncertainty, i.e., with phenomena that one does not even know one does not know, required new methods, which, in simple terms, focused on intrinsically human characteristics, such as experiential knowledge, intuition, as well as heuristics and holistic thinking
The debate within project management, which boasts many analogies to debates within science studies and decision theory in the 1990s, reflects social and technological challenges. These include not only genetic engineering and nuclear energy, which are always mentioned, especially in science studies, but also disillusionment in the context of artificial intelligence (AI) research. It was precisely here that the limits of quantitative, so-called “brute force” methods and the “Good Old-Fashioned AI” methods became very clear in the 1980s.
Putting the demand for a new logic of project management into historical context, the turn towards so-called human competencies becomes apparent, as a result of the limitations of technological methods, as well as of challenges arising from new technologies. This brought about a new dimension of ignorance. Disillusionment and the experience of the limits of mathematical-statistical-technical planning methods led to an emphasis on human-based planning procedures, and it also brought previously underestimated and unnoticed factors into focus.
The question of how to deal with uncertainty and, above all, unforeseen events in projects of all kinds remains a core question for their success. There is a lack of systematic and empirical, and above all historically comparative, studies focusing on this question, which, on the one hand, analyse concrete planning practices, and on the other hand, describe the empirical level chronologically up to the present. After all, concepts, methods and practices of project management are always time-bound. They do not only react to changing challenges by developing new approaches. The answers to new challenges also reflect contemporarily dominant approaches, as the strong focus in the 1990s on experiential knowledge, intuition and heuristics shows. This does not mean that the answers are not accurate. However, looking at things from a historical perspective makes it clear that one mainstream might chase the next. That means that we also have to critically reflect current trends: Construing a contrast between human behaviour, capabilities and technical (quantitative-mathematical) solutions, which was typical for the 1990s, is now being replaced by a stronger emphasis on the interaction and close cooperation between humans and machines.
However, no universal solution for this unpredictable uncertainty has been developed, nor are project management practices actually being driven by this insight (yet).
5.2 Product Design Under Uncertainty
The entire life cycle of a product is predetermined by the product design. Since all three phases of the product life cycle design, production and usage are accompanied by uncertainty, see Sect. 1.2, an adequate anticipation of this uncertainty is the key for a successful product design. This anticipation is very demanding, because normally neither the involved stakeholders nor the events that occur in a product life are known a priori. We propose to tackle this challenge with several methods that uncover and help to reduce uncertainty in all stages of the design process in a systematic way.
The newly introduced “Uncertainty Mode and Effects Analysis” (UMEA), described in Sect. 5.2.1, allows for analysis and evaluation of occurring uncertainty in all phases of the product life cycle. One approach to reduce uncertainty in the design phase is the systematic involvement of stakeholders. This involvement can be used to reduce the fluctuation of requirements during the development and increase of the knowledge about the product to be developed by extending the designers’ model horizon, see Sect. 1.3. A systematic approach for this involvement is given in Sect. 5.2.2.
Uncertainty influences the execution of all kinds of technical processes along the product life cycle, e.g. production processes or application processes. One possibility to uncover uncertainty is therefore to analyse processes with the aid of a generalised process model. Possible deviations can be attributed to system components in a standardised way and by this, uncertainty is disclosed reliably to a large extent. Such a generic process model and its application is depicted in Sect. 5.2.3.
As discussed in Sect. 1.3, models can be useful, but at the same time have their limits. Reliable information sources can help to overcome these limits. But in many cases, relevant information cannot be gained directly in experiments. A conflict between accessibility and reliability has to be solved. In Sect. 5.2.4 this challenge and possible solutions are presented for the domain metal forming processes.
Mathematical models can also be used to uncover uncertainty during the design phase. The models can be based purely on physical laws (white box models) or on data (black and grey box models), cf. Sect. 1.3. Often, a large number of uncertain design variables has to be considered. In the case of stochastic uncertainty or incertitude, information about the relevant domain of uncertainty is given, cf. Chap. 2. Due to time consuming calculations, white box models are difficult to compute for a representative number of possible combinations. Instead, fast models modelling based on surrogate models in Sect. 5.2.5 and demonstrate their usefulness for density and quantile estimation in Sect. 5.2.6.
Product design does not only comprise the initial design but also design changes that become necessary later. This applies in particular to special purpose machines, which are built to fulfil customer specific requirements. With regard to these, it is indispensable to master uncertainty, if ignorance, see Chap. 2, ultimately leads to clearly visible deviations from customer requirements. We propose a change procedure in Sect. 5.2.7, which helps to master uncertainty in these situations without jeopardising customer satisfaction.
5.2.1 The Method of Uncertainty Analysis and Evaluation: UMEA
In this section, the Uncertainty Mode and Effects Analysis methodology UMEA is presented, which we have developed for a comprehensive, consistent and uniform uncertainty analysis in the entire development process, cf. [86, 89]. Uncertainty occurs in all phases of the virtual and real product life cycle. In the virtual product life cycle mainly uncertainty in the specification as shown in Sect. 5.1.2, and model uncertainty, discussed in Sect. 2.2, cause deviations of the planned product properties from expected properties. Products then do not fulfil the customer expectations regarding functionality, effort and availability. In addition, real products sometimes do not meet the planned properties due to uncertainty that occurs in all phases of the real product life cycle and is propagated in the process chains. In both cases, the acceptance of the products decreases due to uncertainty and endangers the market success of the products, cf. [90, 142, 143].
Especially in the case of new developments, the virtual product life cycle is characterised by a lack of secure information. Especially the early phases therefore represent a typical situation of high uncertainty. The complexity, importance and criticality of the situation is explained in Sect. 5.2.2. There, in addition to the solution of the technical task, the innovation and time pressure as well as the interconnectedness are emphasised. Misjudgements by developers regarding available resources, material properties or disturbance parameters contribute to uncertainty and can lead to critical system states in the later use phase, cf. [89].
The detailed analysis of uncertainty that can occur in the entire product life cycle is therefore a prerequisite for mastering uncertainty in the development of new systems. The uncertainty analysis has to be carried out from the beginning and throughout the entire development process. The results of the analysis act as a basis for system synthesis, e.g. by the robust design method [90]. However, previous methods of uncertainty analysis only consider a narrow range of the life cycle of a product [142]. The diverse influences in the individual life cycle processes and the propagation of uncertainty in the process chains as shown in Sect. 3.2 make it necessary to include identification and evaluation of uncertainty over the entire life cycle into the uncertainty analysis.
Analysing uncertainty in development processes
The term UMEA is an extension of ‘Failure Mode and Effects Analysis—FMEA’ [74]. However, the scope, consideration horizon and application range go far beyond FMEA. The UMEA is based on a procedure consisting of four phases. In addition to the identification of uncertainty and sources of uncertainty, e.g. by the method of technical process analysis that will be described in Sect. 5.2.3 in detail, the stepwise procedure for UMEA is oriented towards the main challenges of the mastering of uncertainty during the entire product development process: (i) uniform procedure for uncertainty analysis across all concretisation stages in the product development process, (ii) focus on critical product properties and uncertainty influences, (iii) consideration of the propagation of uncertainty in the product life cycle with regard to its effects in the usage phase.
Procedure at UMEA; process steps with associated models and methods following [90]
The stepwise procedure at UMEA comprises four phases shown in Fig. 5.8: (i) environmental and goal analysis, (ii) identification of uncertainty and its causes, (iii) determination of uncertainty effects, (iv) evaluation and decision.
Product properties are characterised by an extreme amount, a high versatility and cross-linked uncertainty. The ‘environmental and goal analysis’ contributes to a purposeful focus on properties which are particularly critical with regard to uncertainty. The system is delimited from its environment and a system boundary is defined as depicted in Sect. 1.3. This is the prerequisite for distinguishing between external and internal influences and supports the determination of the causes of uncertainty. Furthermore, the evaluating parties (e.g. users, stakeholders, requirement groups) are identified and their value concepts are specified. This can be used to describe the expectations of the basic system properties (e.g. maximising the benefits and quality of the system usage, minimal life cycle costs). The tolerated uncertainty can also be documented in the technical specification as explained in Sect. 5.1.2.
In the second phase, an identification of uncertainty and its sources will be carried out. For this purpose, the processes of the life cycle identified as relevant are analysed in detail and significant influences to uncertainty are identified, e.g. by a technical process analysis, as already mentioned above.
In the third phase, uncertainty effects will be analysed. The existing relationships between external influences, the process parameters and the properties of the result of the process are specified and accumulated over the process chains of the entire product life cycle as comprehensively as possible. The deviations in the result of the process are mainly assessed based on the sensitivity of the individual processes with regard to the identified causes of uncertainty, see below in this section.
In the fourth phase, the existing uncertainty is mostly assessed with regard to the usage processes. Depending on the level and probability of the accumulated uncertainty, a risk can be determined taking into account possible deviations from the expected system properties and the resulting consequences in the specific context of use. Based on this evaluation, a decision is made on adequate measures to master uncertainty in the system adaptation. The steps ‘evaluation of uncertainty and risk’ and ‘decision making’ can be combined into one phase for simplification as shown in Fig. 5.8.
The uncertainty mode and effects analysis methodology
In order to meet the requirement of a comprehensive, continuous and uniform uncertainty analysis in the development process, the UMEA must be applicable at all levels of abstraction and depict the propagation of uncertainty in the product life cycle. UMEA therefore goes beyond the description of a single method and is oriented towards a modular concept.
Models and numerous methods for mastering uncertainty have existed for some time, cf. [142]. So far, however, these have only been used isolated, referred to individual problems and not under the integrating aspect of mastering uncertainty. The UMEA methodology mainly combines these methods in a systematic procedure for a comprehensive uncertainty analysis during the entire development process. UMEA thus takes advantage of existing methods, but goes far beyond existing methods in terms of uncertainty analysis.
UMEA’s analysis activities are supported by a collection of methods that can be combined according to the underlying procedure. The systematic mastering of uncertainty includes methods for identifying and describing uncertainty, for evaluating the criticality of uncertainty, and approaches to reduce uncertainty in the system design, cf. [89].
Of particular note is the combination of process models and matrix-based analyses to identify the sources of uncertainty and determine the consequences of uncertainty, cf. [86]. The detailed modelling of the single processes provides qualitative information about the relevant properties of the process’s initial states and the uncertainty-relevant influencing parameters during the process execution. Based on a sensitivity matrix, the interrelationship between uncertainty in the initial state and the uncertainty-relevant influences of the process parameters can often be described quantitatively, cf. [89].
For this purpose, the expected level and deviation of the influencing parameters on the process (e.g. disturbance parameters) and the operator (e.g. work equipment in a manufacturing process) are estimated. Depending on the information available, this is made quantitatively or qualitatively according to the uncertainty model. Furthermore, the deviations in the properties of the operand (e.g. partially manufactured component, initial state) caused by previous processes are estimated. The effect of the individual influencing parameters and the uncertainty of the process execution on the properties of the operand in the final state (e.g. dimensions and shape of the manufactured component, process result) are determined by means of sensitivities. The consideration of interdependencies between the influencing parameters and effects requires a complex structure of the sensitivity matrices. The uncertainty of the process result are calculated quantitatively or at least qualitatively by adding up the partial deviations, cf. [86].
The modelling of process chains consisting of multiple processes forms the basis for quantifying the propagation and accumulation of uncertainty over the entire product life cycle. The properties including their uncertainty in the final state of a process form the initial state of the subsequent process. The uncertainty of the follow-up process can be calculated or estimated in the same way using a further sensitivity matrix. Thus, the uncertainty of production processes is accumulated up to the usage processes. The accumulation of uncertainty does not necessarily lead to an increase of uncertainty. By defining the processes and their sequence, uncertainty can also be reduced by assigning optimised processes regarding uncertainty. These processes often show a low sensitivity to critical product properties. Uncertainty from previous processes can also be mitigated or even compensated for. Examples are the process sequences of drilling and reaming discussed in detail in Sect. 4.1.3.
Applying the UMEA methodology
For evaluation we have applied UMEA exemplary to design optimisation of a very simple tripod demonstrator representing a system for uniform load distribution. In this tripod demonstrator, three legs are symmetrically and parallel attached to a load distribution ring. The device is loaded by a mass. The load is to be evenly distributed on the three legs of the demonstrator, cf. [223]. The application of the UMEA is described in detail and discussed in depth in [87] and in [86].
In the first phase ‘environmental and goal analysis’ of the UMEA the even load distribution on the legs and the analysis of the influence of the tripod production is recognised as a goal. In order to exclude influences by eccentric tripod load and uneven or inclined ground contact area, these are included within the system boundary.
In the second and third phase the ‘identification of uncertainty and their causes’ as well as the ‘determination of uncertainty effects’ are performed. The uneven load distribution in the legs is identified as the uncertainty to be optimised during use. In the example, different vertical distances between the load distribution ring and the contact area at the three legs, here referred to as ‘total leg length’, can be identified as the source of uncertainty. The further analysis shows that the ‘total leg length’ depends on the length dimensions of the leg components, which are influenced by the manufacturing process. Furthermore, a non-parallel and non-positional mounting of the legs during assembly influences the ‘total leg length’.
In the ‘evaluation and decision’ of the fourth phase it is a recognised calculation that in the present system the length and the axial position of the leg components influence the uncertainty more than the angular deviation from the vertical attachment. Therefore, it was decided to develop different fastening designs. In the end, the design was selected that offers the highest manufacturing and assembly accuracy with respect to the leg length and position.
By applying UMEA to a current conducting plug connector in the engine compartment of an automobile, we have demonstrated that UMEA is in principle also applicable to more complex systems, cf. [86]. However, the disturbance influences by dirt, corrosion, vibration and temperature are a great challenge.The UMEA has contributed to mastering the uncertainty, especially by systematically incorporating the experience of the specialists.
Conclusion
The UMEA methodology developed represents a cross-process uncertainty analysis that covers the entire life cycle of the physical product with a focus on production and usage. It enables uncertainty of the entire product life cycle to be comprehensively and specifically analysed and evaluated in the entire system development process, cf. [89]:
-
Methods are provided that can be used from the beginning in all phases of the development process with increasing degree of more detailed description.
-
It is intended for use at a high level of abstraction as well as for very specific design phases.
-
In the analysis, the planned processes of the entire physical product life cycle are included and the propagation of uncertainty in the process chains is also considered.
-
A focus on relevant influences and deviations is made several times in order to master the extend and variety of uncertainty in the system development.
-
Finally, UMEA goes beyond an uncertainty analysis and provides prioritised information for mastering uncertainty in system design.
In the modular concept of UMEA, well-known methods were adapted and complemented by special methods. UMEA links the different models and methods, each adapted to increasing degrees of concretisation, in a uniform procedure for the uncertainty analysis.
A fully quantified analysis of uncertainty in all steps of the UMEA is usually neither possible nor reasonable. For a methodical analysis of an entire process chain during development, qualitative approaches need to be complemented by suitable quantitative analysis methods to an appropriate extent. If, for example, significant uncertainty in the production processes are quantitatively known, the uncertainty calculation can be done without a detailed analysis.
5.2.2 Mastering Uncertainty in Product Development
For the sake of improving product development, we present a method that takes user requirements into account while being independent of the product or personal experience. The methodology extends and improves existing approaches by taking comprehensively into account the roles for the design unit and the design process.
Design engineers have to master numerous and distinct challenges in the modern industrial environment. For this purpose, engineers work in close cooperation with specialists from various disciplines and with different skills [219]. In addition to conventional development methods, design engineers are increasingly working with agile development methods. In comparison to classical development methods, the agile methods rely on a reduced set of planning and product specifications, while at the same time strongly integrating customer feedback. Thereby, the skills and approaches of the designers must also be suitable for working in international teams. Due to increasing international division of labour, a reduction of in-house developments and a high effort for project management can be observed. In addition to these tasks, design engineers interact with customers, suppliers and various departments of the company and have to accomplish communication and strategy tasks [81]. Furthermore, they bear a huge responsibility for society, customers and the company [21]. To fulfil these responsibilities, designers are supported by a wide range of methodologies. Despite the evolution of responsibilities, the primary task for designers remains to design functional, innovative, safe and sustainable products, cf. Chap. 2. However, professional experience so far has been an essential factor in managing the daily tasks [219]. The aim of the design tasks is to ensure that the products generate economic added value for the company.
In addition to the expanded roles of responsibility, the product life cycle has changed due to the “frontloading” [164] and the shortened development times [250]. The frontloading approach shifts development decisions and activities to early stages of development, allowing challenges to be identified and saving development time. The frontloading and the shortened development times can partly lead to premature products and impact the customer satisfaction in an unfortunate way. This form of acceptance (cf. Sect. 1.7) can result in high losses and cause damages which are extended especially by merging mechanical, electrical and data processing solutions to the brand [13, 139]. Uncertainty is even more pronounced due to the simultaneously increasing complexity of products.
Thus, the application of suitable design methods is becoming increasingly important. However, current design methods focus on the design process and neglect the working environment. The working environment is determined by standardised CAD and PDM systems. Standardised CAD and PDM lead to a higher amount of available information. The use and usability of the available information depends strongly on the experience of the design engineer [47].
The economic and social changes introduced by industrial rationalisation and automation have led to the development of various methods and approaches which help to structure and simplify the design process. The step-by-step approach according to VDI guideline 2221 [269] is a universal but somewhat unpractical approach for the design of technical systems. In addition to VDI 2221, Birkhofer [40] gives a detailed overview of the design development that has taken place so far. However, the existing methods with their sequential structure do not represent real design processes [242], because they do not explicitly capture the iterative steps of product development.
The method developed by Schmitt [241] is based on known problem-solving strategies and expands these by including the working environment. The primary objectives of product development remain the realisation of customer demands and the compliance with market requirements. In order to achieve these goals, the task of product development is to generate suitable product data [217]. For this purpose, three axioms are defined as basis for the following product development method [241]. The axioms are to be regarded as equally important for successful product development and thus for the success of a company [241]. The three axioms are as follows:
-
(i)
Products are always developed under sustainable aspects.
-
(ii)
Decision-making and its comprehensible documentation in product development require the distinct definition of evaluation criteria.
-
(iii)
The development process is an iterative procedure that must be individually adapted to each task and is highly dependent on the involved stakeholders.
A design unit as an organisational unit closely collaborates with marketing, sales, purchasing and production [85]. This strong integration into the corporate environment results in complex influences on the product development process. In order to take these influences into account, the involved roles of operation are considered. According to [106], stakeholder groups represent groups or individuals who influence corporate goals or may be affected by them. A differentiation is made between external and internal stakeholders. The specific roles of internal stakeholders, who are located within the company boundaries together with the design unit, are presented in more detail below.
With regard to their contributions to the overall product development process, the internal stakeholder can be divided into two groups: (i) the first internal stakeholder group is responsible for the product definition. This includes employees from sales, distribution and marketing. They have in common that they develop and define the desired properties of a product in customer contact or on the basis of market data [41]. The second internal stakeholder group is involved in the product realisation department and in the product development process. This group includes all persons in the company who are involved in the implementation of the real product. This includes production, testing and purchasing. The management can be found in both internal stakeholder groups described above. This means that there is no separation with respect to technological and economic influences.
In the general overview of the method by Schmitt [241] shown in Fig. 5.9, the core tasks of the two stakeholder groups are divided into three roles: classification, decision and design. All roles benefit from the generated product data.
As described in [241], the aim of the shown roles is to define all relevant goals resulting from the complex interaction between product components, stakeholders, expectation and the environment before the development process begins. Typical goals for the product development are, for example, functionality, time and cost requirements, cf. Sect. 1.1. The task of the internal stakeholder group “Product Definition” is to transfer the requirements and desires of the customer into dependent product properties and to communicate the goals during the process. The customer only recognises the dependent properties, whereas the design unit defines the independent properties and on the basis of this definition influences the dependent properties.
The design unit is responsible for the actual product development (Fig. 5.9 “create”). The design unit has to identify the independent properties relevant for achieving the objectives. In consultation with the internal stakeholder group product realisation, the properties must be compared with customer requirements and wishes. Based on the solutions developed in the Product Realisation department, the design unit prepares the decision-making process for the Product Realisation stakeholder group [241].
Decisions with great consequences for product development are decided, implemented and documented in the role “decide”. It should be noted that a distinction is made between the decisions of the design unit and those of the internal Product Realisation stakeholder group. The comparison between the dependent properties with regard to the fulfilment of customer wishes and requirements is carried out during development activities. The product data compiled by the development unit represents the result of the method and serves as the basis for evaluation in the respective iterations [241].
Depending on the results of the described comparison, a further iteration of the process might be necessary. If conflicting goals cannot be resolved the internal project group, the stakeholder group responsible for the product definition contacts the customer again. However, further iterations may result from a seemingly successful completion of product development. This is the case, for example, if the customer’s requirements are formulated in a misleading way or if they have been transferred to incorrect dependent properties. In this case, a closed loop is created which can be run through in an iterative manner during product development [241].
Through the iterative process and under consideration of the customer influence, the previous method can be extended to Fig. 5.10. This results in a closed product development cycle, which represents the interactions between the individual stakeholders. Stakeholders outside the company’s boundaries can open up new opportunities for the development unit.
Potential examples are new or adapted solutions from suppliers. The government and the society, as well as competitors and external stakeholders are special because of their influences. The influence of all external stakeholders can lead to new goals as well as new opportunities for the design unit. On the one hand, the government certification of operating materials or the rejection of patent applications by competitors can create new opportunities for the design unit. On the other hand, new goals and requirements can be generated for the design unit due to laws, public interest in technologies, as well as pioneering products of the competitors. The depth of the technological horizon describes the technical and methodological knowledge of the development unit acquired over the years of professional activities. Examples are design specifications for components, detailed knowledge of machine elements and their possible applications. In order to obtain or generate the information required for the design, the development unit has two communication partners at its disposal. On the one hand, the internal and on the other hand the external stakeholders can be consulted for the absolutely necessary exchange of information. In case of high uncertainty due to limited information, it may be necessary to define new goals by communicating with the internal stakeholder group Product Definition. This influences the requirements and thus reduces the needed effort [241].
Research on design methodology has been conducted for decades, resulting in different approaches and methods to support designers. Due to the changing conditions and requirements of products and markets, new approaches have been developed and existing ones adapted. Nevertheless, there is a gap between the promises of academic methodological approaches and industrial reality. One reason for this is that methodological approaches in industry are so far perceived as inefficient. Developing a method that extends the system boundaries of the design process to internal and external influences seems promising to update established approaches and move towards a dynamic, closed-loop system [242]. Therefore, the discussed method is based on specific participants in the product development process and their activities and responsibilities. The approach extends and improves existing ones by extending the system boundary to take into account influences on the design unit and the design process. Thus, the approach represents a possible solution to transfer industrial reality into a universal methodological approach. Preliminary analyses of the industrial application show that the method simplifies the task of the designers [241]. This shows how important it is to create a basis for a new generation of design methods [241]. By involving stakeholders in the development process, product expectations can be improved.
5.2.3 Methodical Uncertainty Consideration in Technical Process Modelling
In this subsection, the generic model of technical processes is presented, which we developed for the comprehensive identification of uncertainty in all phases of the product life cycle. A special feature of this universal model is the purposeful localisation of uncertainty and the sources of uncertainty. Thus, the model has the character of a reasonably structured checklist and provides basic advice on effective approaches to reduce uncertainty.
As presented in Chap. 1, acceptance describes the fulfilment of expectations of a product or component in terms of functionality, availability and effort. However, acceptance is not a characteristic of the product in the narrow sense, but matters only in connection with the process steps. This applies to the process steps of all life cycle phases, e.g. in product development with regard to the planned properties, in production with regard to manufacturing tolerances, or in usage with regard to performance and efficiency.
Additionally, the term uncertainty covers both, the measurable or perceptible uncertainty of a product, and the causes why uncertainty arises in the entire life cycle of a product, cf. [143]. Consequently, the analysis of process steps has to identify and locate the sources of uncertainty, the emergence of uncertainty, and the propagation of uncertainty. Therefore, modelling the technical process steps in the product life cycle in detail has a key role in mastering uncertainty.
Mastering uncertainty in life cycle processes
A process step, here called process in simplified terms, can be considered in the context of technical systems in principle as a time dependent transformation of an operand from an initial state to a usually changed final state, cf. [72, 272]. The model of technical processes developed by Heidemann has proven convincingly to be the most suitable model for describing processes from a large number of different models, cf. [149]. In the following, the generic model and the specified models of technical processes derived from it will be referred to as process model for simplicity reasons.
It can be stated as common sense that the properties of products cannot or cannot completely be determined in both, the virtual and the real product life cycle, cf. [143]. The sources of uncertainty can be located in all life cycle phases. However, previous approaches to manage uncertainty are mostly based on an isolated consideration of uncertainty. The robust design approach of Taguchi, see Sect. 3.5, for example, primarily refers to the production of products, cf. [257, 258]. Taguchi implicitly assumes that the properties of the manufactured product, which have been planned during the development phase, correspond to the current expectations of the customer and that the product is used as intended. Further, he concentrates on the quantification of deviations in the final state of the process steps without analysing the causal influences in a well-founded structured model of the system.
In contrast, our comprehensive approach to the analysis of uncertainty is based on the modelling of processes that can be linked to process chains (or networks). In addition to the analysis of the result of a process step, the overall mastering of uncertainty in product development requires the identification of all possible sources of uncertainty in this process step. Therefore, in addition to the uncertainty of the system elements themselves, various external influences on the system that can cause uncertainty must be considered. Only two typical examples out of a huge number are thermal deformation of machine tools during production and pollution during the system’s usage.
In order to be able to consider the sources of uncertainty, we have further developed the Heidemann process model for a comprehensive uncertainty analysis. Therefore, we have integrated all elements and the linking influences into the process model, which are relevant for the analysis of uncertainty in processes, cf. [175]. The generic process model is shown in Fig. 5.11.
Process model for the detailed analysis of uncertainty in processes following [175]
In this process model systems are basically represented by the process itself, the initial and final state of the operand, the work equipment and the relationships between them. The modelling is particularly illustrative in production processes in which, for example, a more or less finished part is produced from a semi-finished material (operand, initial state) by a forming process. If, for example, a servo press is used for forming, it is modelled as a work equipment that starts the process by means of working factors e.g. the ram force and ram motion, cf. Sect. 3.6.3. Additionally, the system environment (e.g. buildings, adjoining systems, nature), necessary resources (e.g. power supply, coolant) and user (e.g. operator) as well as their relations to the system are represented. Uncertainty regarding the result of a process step is modelled by the deviations of the properties and state variables of the operand in the final state.
In the example of a forming process these are e.g. dimensional and form deviations of the manufactured part. Uncertainty of the process result can be caused by influences of all other elements of the process model and their interdependence. To support the mostly complete identification of the sources of uncertainty, the process model can be used as a kind of checklist. The process model is mainly used in the early phases of system development. It initially serves developers to identify essential design parameters and to describe uncertainty qualitatively, when assessing robustness of working concepts based on physical effects. This is discussed later in Sect. 6.1.5.
Identification and location of uncertainty using the process model
The main purpose of process modelling for the mastering of uncertainty is (i) the largely complete identification of uncertainty and sources of uncertainty and (ii) the reasonable and sense-attributing location of the sources of uncertainty. According to their localisation in the process model, groups of typical sources of uncertainty can be identified. We recognised three groups having characteristic properties with respect to mastering of uncertainty: (i) all elements inside and outside the system boundary, (ii) planned functional interaction inside and outside the system boundary, (iii) unintended influences between all elements inside and outside the system boundary. Additionally, the effective direction of the interactions and influences have to be considered, e.g. disturbance parameters of the environment on the work equipment and emissions of the work equipment on the environment.
In the following, an overview of the utilisation of the process model is given. Taking the example of the Modular Active Spring-Damper System (MAFDS) described in Sect. 3.6.1 the identification of potential uncertainty is illustrated only very briefly and exemplarily. If necessary, reference is made to the aircraft landing gear or vehicle running gear approximated by the demonstrator. First, the usage process is considered. The special features regarding other life cycle processes are added afterwards. The description is focused on the groups of typical sources of uncertainty.
Process elements (operand, initial state, final state, process, work equipment)
The MAFDS simulates the support of the aircraft on ground contact during landing by decelerating a falling mass by a supporting load bearing system, when it hits the foundation. The forces to be transmitted are comparable to driving over a road unevenness. In the example of the MAFDS test setup the loading mass is modelled as an operand, which represents, for example, the partial mass of a vehicle or aircraft. The initial state is described by the properties and state variables of the operand. In case of the demonstrator, these are mainly the properties mass and weight and the state variables direction and speed of the movement of the mass. The process represents the deceleration of the mass on contact with the ground, which can be described as a time-dependent course of movement. The final state defines the result of the process. When planning usage processes, the final state usually represents the expected result of the process. In the demonstrator, the final state is essentially described by the position of the mass. In case of a running gear, the deceleration values of the operand are mainly decisive for the user. Acceleration values that are not or not fully accepted by the user, e.g. for reasons of comfort or safety, represent the uncertainty of the process result.
This differentiated consideration highlights the fact that, in contrast to the work equipment, the developer can only influence the properties of the operand, the process, the initial state, and as a consequence, the final state, all of which depend on the usage of the system to a limited extent. Since they cannot be determined, they represent a high degree of uncertainty. In the case of usage processes, the corresponding uncertainty can be mastered more or less only in the development process by a carefully and detailed technical specification, cf. Sect. 5.1.2. Since the initial state is significantly influenced by the preceding process step, cross-process analysis is very important in production processes. In Sect. 4.1.3 and later also in Sect. 6.1.8, this is illustrated by the example of drilling and reaming, where the uncertainty of the initial state during reaming can be influenced to a certain extent by the preceding drilling process.
Resources and inputs of work equipment
After ground contact, the MAFDS is supported on the foundation of the test setup. The supporting forces, or in a broader sense the foundation including the impact surface, are modelled as resource in the process model. Thus, it represents, for example, the condition of the road surface when looking at a chassis. Time-dependent deviations of the contact area in displacement, position, and especially in direction represent the uncertainty of the resource. For the simulation of uncertainty in the test setup, impact surfaces with different angles are provided. This allows analysing effects of an uneven road surface on running gears.
In many cases, as for example here with the running gear, the resources can practically not be influenced by the developer. The corresponding uncertainty can only be mastered by elaborating the technical specification and designing the work equipment accordingly, see Sect. 5.1.2. In the case of stationary production processes, there is usually a much smaller uncertainty regarding the supply of energy. It can be mastered either by choosing an energy source with low uncertainty or by additional measures, such as buffer storage.
Operator inputs mainly represent the operation of the work equipment. Operating errors often represent a considerable uncertainty, which is sometimes extremely difficult to master, especially in active systems. In a similar way to other resources, input uncertainty can be managed by reducing the volume and complexity of the inputs required. For example, a high degree of automation of work equipment usually reduces the uncertainty of operating errors. In case of the MAFDS, operator influences are limited to the triggering of the drop test. Thus, uncertainty of the operator is negligible here.
Unintended influences between all elements of the process model
The work equipment unintendedly interacts with the system environment, the operator and the resources. The modelling of the corresponding relationships represents on the one hand disturbance parameters on the work equipment, on the other hand side effects, which are caused by the work equipment, cf. [192]. For the MAFDS, disturbances and side effects are of minor importance, since it is shielded and operated in a low disturbance laboratory environment. In the case of represented landing gears or vehicle chassis, temperature and radiation influences, chemical and mechanical influences, as well as pollution can occur from the environment as disturbance parameters that can impair the function of the work equipment.
Conversely, the work equipment also generates side effects, which usually have a negative impact on other system elements in form of emissions, e.g. neighbouring systems or components. In the case of represented landing gears or vehicle chassis, for example, abrasion, noise and vibrations can have an environmental impact, a loss of comfort for the passengers (users) and a friction value-reducing effect on the road surface (resource). The side effects are often not acceptable and are perceived as uncertainty, cf. [175]. The process model thus indicates that disturbance parameters can be mastered by eliminating them or taking measures to reduce their influence, cf. [192]. Corresponding design strategies are discussed in detail later in Sect. 6.1.5.
Interactions between work equipment and process are, in principle, comparable to disturbances and side effects, and can be identified in a similar way; but they have a different quality. Corresponding sources of uncertainty are usually more difficult to master due to the close interlinkage of process and work equipment within the system boundary. Typical and critical cases are, e.g. soiling or contamination of food processing systems, cf. [22].
Conclusion
The process model is apparently a very simple generic model. The described analysis with the help of the process model impressively shows the complexity in scope and diversity of the resources of uncertainty. By classification and meaningful localisation in the process model, useful advice for the identification and design of robust and resilient solutions can be derived.
The findings and results of a process model analysis can be documented in the technical specification that serves as a basis for the subsequent system synthesis, cf. Sect. 5.1.2. Thus, the process model analysis is indirectly a purposeful basis for the later mathematical modelling and simulation of the systems.
When looking at production processes, the process model assist engineers to identify and locate uncertainty equally. It is very important to realise that in contradiction to usage processes in production processes the parts and components of the load-bearing systems are modelled as operands and the machine tools as work equipment.
5.2.4 Conflicting Objectives in the Determination of Process and Component Control
The quality of products is one of the most important requirements in production technology. Fluctuations in semi-finished products and the forming process can influence the quality of products in a wide range, cf. Sect. 1.7. In addition to known and unknown uncertainties (Sect. 2.2) in production processes, the influence of ecological and economic effects on production technology is increasing. Furthermore, the forming processes are influenced by known uncertainties, such as temperature, tools, machines and lubricants. Especially in the last three phases (cf. Sect. 6.1.5) of the design process (cf. Sect. 1.2), sensors can be integrated cost-effectively at optimal measuring positions in tools as well as machines. The subsequent integration of sensors proves to be cost-intensive and difficult, depending on the required measurement quality. In order to consider the correlation between sensor position, costs, measuring uncertainty and product quality in the phase of the design process, a model for evaluation is presented and discussed using the example of the 3D Servo Press (Sect. 3.6.3) and conventional forming processes.
The most important semi-finished product properties in sheet metal forming are usually sheet thickness, yield strength, anisotropy and surface properties, as these influence the process and recovery behaviour [191]. In order to reduce product uncertainty, narrow tolerances for semi-finished product properties are therefore required. As a result, the testing effort, energy consumption and manufacturing costs increase during the production of semi-finished products. Another approach is the closed-loop control of product properties to make the process insensitive to process fluctuations (Sect. 1.3). This requires all the components of a closed-loop control (see also Sect. 5.3.2), which consist of sensors, state observers, controllers and actuators [243]. Thereby the position of the sensors is important for the closed-loop quality control [126]. We refer to [56] for a literature review on special measurement and control approaches which are relevant for this topic. Due to the high relevance of the measuring position, it is important to consider the sensor position in the product development process to quantify uncertainty, as it has been done with the example of the 3D Servo Press (Sect. 3.6.3) in the change process (Sect. 5.2.7). Therefore, a method for the representation of the spatially opposite degree of interest in knowledge of a measurand and its measurability in the form of the target diagram in Fig. 5.12 was presented [56, 59, 122].
The target diagram, given by [56], using the example of the measurement positions of the 3D Servo Press
The target diagram of Calmano [56] shows possible measuring positions for the determination of machine, process and component parameters. For the example of a forming machine, the system is subdivided into the frame, drives, fixture, guides and clamps. A further subdivision is made for the tool, which is not directly a part of the forming machine. The innermost circle is further divided into the areas tool, product and the forming zone. By a symbolic evaluation from low (–) to high (++) (compare Fig. 5.12), an estimation of the measurability and the possible interest of the respective measuring position is possible. In the direction of the centre of the target diagram (Fig. 5.12), the knowledge gain of the measured technical/physical quantity increases, which reduces sensor uncertainty. The measurability, however, decreases for most physical quantities towards the centre of the target and proves to be most technologically challenging in the component. Compared to the forming zone, measuring positions, such as the frame and drives, are already equipped with conventional measuring equipment by default or can be realised with only minor technical and financial hurdles [59].
With regard to the time sequence of the forming process it can be seen that many product properties are still changing during the recovery phase after the forming process and therefore cannot be measured directly in the process. These relations increase the uncertainty for control systems. For this reason, Fig. 5.12 can be extended by the time-dependency (Fig. 5.13).
Challenges of sensor integration with time consideration [59]
An example of the time dependence of product properties is the resulting angle in a bending process. As long as the forming tool is in workpiece contact, the final bending angle cannot be measured. Only after the tool is no longer in contact with the workpiece, the stored elastic energy is released until a stress equilibrium is reached. Afterwards, the final bending angle can be measured. The recovery phase leads to the problem that even with successful sensor integration in the forming zone, the final product properties cannot be measured during the process. For this reason, control engineering uses condition monitors which, for example, instead of the bending angle provide indirect information about machine and tool variables, such as positions, speeds and reaction forces [59, 122].
In conventional press development, it is common practice to determine the press force by the frame elongation. In the target diagram (Fig. 5.12), the measuring position is at the outer ring. The geometry of the frame has a significant influence on the elongation, so that a calibration of the sensors is necessary. Calibration is carried out by applying known forces to the ram. Subsequently, mathematical models can be used to derive the desired measured variable (Sect. 1.3). During process operation it is possible that eccentric forces act on the ram by combining different forming processes, which were unknown in product development. Uneven process forces lead to unwanted ram tilting due to machine stiffness. This is accompanied by the possibility of a secondary force flow. This means that during process operation, there is a possibility that the occurring forces are not measured with sufficient accuracy and therefore the process has a high unknown uncertainty.
For this reason, the force measurement on the 3D Servo Press was shifted towards the centre of the target diagram (Fig. 5.12). In addition, the 3D Servo Press has a large number of sensors compared to conventional presses. The measurement of the force is realised by strain sensors similar to conventional presses. To reduce the unknown uncertainty, the strain is measured in the direct force flow of the kinematics at the drive rods (see Sect. 5.2.7). Due to the rotationally symmetrical drive rods, three strain sensors are installed per drive rod. This ensures that the most accurate force measurement possible is obtained even if the actuator stem is deflected. In order to realise a displacement control in addition to the force monitoring or force control of the press, displacement sensors with a minimum resolution of 2 \(\upmu \)m are also integrated in the press, making it possible to reduce the uncertainty. These are located on the so-called “bearing frame”, which is responsible for the force guidance and displacement of the slide in the frame. The selected positioning reduces the influence of bearing play and friction losses caused by the main gears. In addition to the sensors close to the process, the sensors of the eight servo motors are available for control. The motor torque and the angle of rotation can be determined in the motors. Due to the different measuring positions, it is possible to draw conclusions on the machine status, for example, in addition to control engineering applications, Sect. 4.2. Due to the additional degrees of freedom and the integrated sensors of the 3D Servo Press, the number of additional actuators and sensors required for flexible forming tools can be minimised, which is associated with a reduction in tool costs. The integration of the sensors and the selected measuring position affect the control quality [56] and thus the uncertainty. Therefore, the selection of a suitable control concept is important. Calmano [56] has developed a method for this purpose using different forming processes, which can be used to select suitable control concepts under consideration of economic aspects.
There is a conflict of aims between quality and productivity in a production system of forming technology under the premise of improving the economic efficiency through cost reduction and revenue increase. The methodology shown above reduces the uncertainty for the selection of the control system. The approach is a control of component properties in the process, whereby the expenditure for their implementation is set in relation to the contribution margin increase by means of investment cost calculation. The concept variants of the control approaches are created by synthesis of different measuring, determining and influencing the defined target variables. The analysis of the concept variants with regard to quality is done by an uncertainty analysis of the designed overall system. Process sequences and reject rates are taken into consideration for the analysis of productivity. The expenditure for the implementation of the concept variants is estimated on the basis of development and failure costs as well as purchased components. The economic evaluation correlates these variables by means of investment cost accounting and identifies the most economically advantageous concept variant [56].
Especially with small quantities and frequent product changes, the cost of tool-integrated actuators and sensors is a significant factor in tool costs, which is why they must be taken into account in product development. This results in a conflict of objectives between accurate measurement of the target value with a low uncertainty for closed-loop control and economic efficiency. When integrating sensors, the use of the shown methods plays an important role in the economic implementation of new measuring systems. The example of the 3D Servo Press shows that the transfer of the tool actuators and sensors to the forming machines enables an improved measuring strategy with simultaneous economic advantages. As shown, the selection of suitable measured variables, influencing variables and control concepts for the control of product properties, however, is still dependent on the process used, taking into account the economic and technological advantages and disadvantages. Therefore, these process-specific parameters have to be analysed depending on the process and evaluated under the mentioned influencing variables. The shown methods open up new possibilities for digitalised production.
5.2.5 Estimation of Surrogate Models
Introduction to surrogate models
Experiments with technical systems are often described by mathematical models. Such models, implemented as computer code, enable the use of so-called computer experiments, i.e. the experiment is simulated via a computer program using the underlying mathematical model. Thus, the technical system can be analysed by using computer experiments instead of real experiments. The mathematical model is given by a function \( m :\mathbb {R}^d\rightarrow \mathbb {R}\), which models the functional relation between the d -dimensional input of the experiment and its real valued output. An overview on the design and analysis of such computer experiments can be found in Santner et al. [232] and Fang et al. [99]. Often these computer programs are complex and thus computational expensive to evaluate, but to properly analyse the experiment it is necessary to generate a large sample of computer experiments. To circumvent this problem, surrogate models can be used, cf. e.g. [15, 119, 166, 281]. A surrogate model is an estimator of the computer experiment m , which usually is much faster to evaluate. Thus, they can generate a large sample of computer experiments. A rather general method to estimate a surrogate model based on a max-min approach is described in this section. Finally, we illustrate its usefulness on the digital twin of the MAFDS, Sect. 3.6.1, as described in [15].
Mathematical setting
The method described in the following is based on the following mathematical setting:
Let X, \(X_{1}\), \(X_2\), \( \ldots \) be independent and identically distributed random variables with values in \(\mathbb {R}^d\), and let \(m:\mathbb {R}^d\rightarrow \mathbb {R}\) be a measurable function. Here, X is the input variable of an experiment with the technical system and m is a computer experiment associated with the experiment with the technical system, where m(X) describes the outcome of the computer experiment. Given the data set
of size \( n \in \mathbb {N}\), the aim is construct an estimator \( \hat{m}_{n} \), the surrogate model of m. Typically the data uncertainty in this case can be classified as stochastic data uncertainty as described in Sect. 2.1.1, but the method can also be applied in the other classes of data uncertainty described in Sect. 2.1.1.
Estimate a surrogate model based on a max-min approach
In most cases computer experiments are deterministic, i.e. for a given input X the result is always the same. Thus, instead of using the typical least squares approach, the surrogate model is defined as the minimiser of the maximal absolute deviation, i.e. it is defined by
where \( {\mathcal {F}}_{n} \) is a set of functions. In other words, to construct the surrogate model a class of functions \( {\mathcal {F}}_{n} \) is chosen and then a function \( f :\mathbb {R}^d\rightarrow \mathbb {R}\) is selected from this set, such that the empirical maximal deviation is minimised. A possibility to compute this estimate is to use nonlinear programming, e.g. gradient descent [231] or Levenberg–Marquard [201]. Here, one has to neglect the fact that the gradient of (5.2) does not exist and use a numerical approximation of the gradient instead.
Which class of functions to use depends on the particular setting and the dimension d . Usually, if the dimension is not too big, B-splines can be applied as shown in [14]. If furthermore the input X is deterministic and the input dimension is small, a quasi-spline approximation should be used as discussed in [92].
In case of a large input dimension one possibility is to use neural networks, since they are usually able to achieve good results by circumventing the so-called curse of dimensionality as discussed in [176]. Below we will introduce a special class of sparsely connected neural networks, especially designed for computer simulations built in a modular way. We use them to estimate a surrogate model of the MAFDS, Sect. 3.6.1 and finally discuss the usefulness of this approach.
In a first step the so-called spaces of hierarchical neural networks with parameters K , M , \( d^* \), d and level l are defined as follows, see [14]. Let \(\sigma :\mathbb {R}\rightarrow \mathbb {R}\) be the so-called logistic squasher \(\sigma (x)=1/(1+\exp (-x))\) \((x \in \mathbb {R})\).
For \( M \in \mathbb {N}\), \( d \in \mathbb {N}\) and \( d^* \in \{0, \ldots ,d\} \), we denote the set of all functions \( f:\mathbb {R}^d\rightarrow \mathbb {R}\) that satisfy
for some \( \mu _{i},\lambda _{i,j},\theta _{i,j,v} \in \mathbb {R}\), by \( {\mathcal {F}}_{M,d,d^*}^{(\text {NN})}\), where \( x^{(v)} \) denotes the v-th component of the vector x.
For \( \ell = 0 \), the space of hierarchical neural networks is defined by
For \( \ell > 0 \), define recursively
Kohler and Krzyżak [176] introduced these classes of hierarchical neural networks as an approximation for so-called hierarchical interaction models. We do not explain the advantages of hierarchical interaction models at this point, but we want to remark that this class of functions is a realistic assumption on technical systems built in a modular way.
Application to data of the MAFDS
We apply the surrogate estimator based on neural networks to a computer simulation of the MAFDS (cf. Sect. 3.6.1). In the computer experiment a Modular Active Spring-Damper System is guided on a frame and falls down on the base of the frame. Virtual sensors allow the measurement of different parameters, such as acceleration, absolute position of the Modular Active Spring-Damper System, or the forces at the point of impact. In the simulation, the correlation of the nine normally distributed input variables presented in Table 5.1 on the computed output variable, the maximum force at the point of impact, is analysed.
The computation of a single output value, during which a differential-algebraic equation system must be solved by the procedure RecurDyn of the software Siemens NX, takes about three minutes in this setup. Based on \( n = 250 \) generated realisations of the nine-dimensional input distribution and the corresponding observed outputs, we estimate the neural network surrogate model defined by (5.3).
The estimate is computed by using nonlinear programming, to be exact the Levenberg-Marquard method, where the parameters K , M , \( d^* \) and \( \ell \) will be selected data dependent from fixed sets. The neural network parameters are chosen by a splitting of the sample, where we use \( n_{t} = \lceil {2}/{3} \cdot n\rceil \) training data and the remaining \( n - n_{t} \) data points as testing data. We use the fixed sets \( K \in \{1,\ldots ,5\} \), \( M \in \{0,\ldots ,12\} \), \( d^* \in \{1,\ldots ,d\} \) and \( \ell \in \{0,1,2\} \). Since (5.2) is not differentiable, we generate a starting point by the approximation of a least squares approach first, and then use the Levenberg-Marquard method with a numerical approximations of the Jacobian matrix.
This surrogate model is able to compute 10 000 output values in less than one second. Using this surrogate model it hence becomes possible to generate a large sample of computer simulated values, which will be used in the application of the methods in Sect. 5.2.6.
5.2.6 Density and Quantile Estimation in Simulation Models
In an early stage of the development, usually no prototype of the technical system is available, and thus computer simulations of the experiment with the technical system are used to analyse properties of this technical system. Often quantifying the distribution of the outcome of an experiment is the focus of the method, since the outcome often determines properties of the system, which can be used in the design. To quantify the distribution of the outcome of the experiment we describe a method to estimate its density, and a method to estimate quantiles of the distribution. In Fig. 3.2 of Sect. 3.1 the method is assigned to the product or system design phase (A).
Introduction
Constructing prototypes of technical systems is often expensive and time consuming. Thus to reduce the effort, one can use physical knowledge of the system to implement a computer simulation \( m :\mathbb {R}^d\rightarrow \mathbb {R}\) based on a mathematical model. This model describes the functional relationship between the d-dimensional input X of an experiment and the real valued outcome of an experiment Y. For example, if the technical system is a spring damper, then the input could be the drop height, payload and the spring stiffness and the outcome could be the maximal compression of the spring damper. Usually these computer models do not perfectly describe reality, but in an early stage, if no or only a small sample of real experiments are on hand, it is usually beneficial to assume that the underlying computer model fits reality perfectly, i.e.
holds. To construct an estimator of the above mentioned characteristics of the distribution of Y, a large quantity of computer simulations is needed. In this context, surrogate models as described in Sect. 5.2.5 are playing a crucial role to generate these samples. In the following, we will present two methods to quantify uncertainty, more precisely, we will describe a method to estimate the density of Y and a method to estimate quantiles of Y.
Both methods assume that either the underlying distribution of X is known, or that a large sample of input values is available. In reality this is often not the case. But often the distribution of the input variable is easily estimated since the randomness in the inputs is often induced by measurement errors or production tolerances. To apply the methods below it becomes then necessary to estimate the underlying distribution and generate a sample of input values based on this estimated distribution. For a multivariate normal distributed input variable, one can use the method described as in Sect. 4.3.8. An overview of methods to generate a data set based on a specific class of distribution can be found in Devroye [77].
Mathematical setting
All of the methods discussed below use the following setting: Let \( m:\mathbb {R}^d\rightarrow \mathbb {R}\) be a measurable function with \( m(X) = Y \) and assume that the data set
where \( n,N_{n} \in \mathbb {N}\) is available. According to Sect. 2.1 the uncertainty in the data can be classified as stochastic data uncertainty. Let \( g :\mathbb {R}\rightarrow \mathbb {R}\) be the unknown density of Y w.r.t. the Lebesgue measure which we assume to exist.
Adaptive estimation of a density based on surrogate models
In this and the next section, two methods of uncertainty quantification based on surrogate models are presented. A detailed overview of estimating surrogate models can be found in Sect. 5.2.5, hence we will neglect how to estimate surrogate models in the presentation below.
We assume that a surrogate model \( m_{n} \) of m estimated on \( (X_{1},m(X_{1}))\),\(\ldots \), \((X_{n},m(X_{n}))\) is already constructed. Based on this surrogate estimate we will present a method proposed in [101]. Firstly, choose \( N_{l} \in \{1,\ldots ,N_{n}-1 \} \), and denote \( N_{t} = N_{n} - N_{l} \). Next, define the density estimator based on the learning data \( N_{l} \) and depending on a bandwidth \( h > 0 \) and a kernel function \( K:\mathbb {R}\rightarrow \mathbb {R}\) by
and define the corresponding empirical measure on the test data by
where \( I_{A} :\mathbb {R}\rightarrow \{0,1\} \) is the indicator function which takes value 1 on A and is 0 elsewhere.
Finally choose a finite bandwidth set \( \mathcal {P}_{N_{n}} \subseteq (0,\infty ) \) and define the data-driven bandwidth choice by
where
and define the estimator of the density g by \( \hat{g}_{N_{l},\hat{h}_{N_{n}}} \).
Monte Carlo quantile estimator based on surrogate models
As before it is assumed that a surrogate model \( m_{n} \) of m estimated on \( (X_{1},m(X_{1}))\), \(\ldots \),\((X_{n},m(X_{n})) \) is already constructed. Then the most simple way to construct an estimator \( \hat{q}_{m_{n}(X),N_{n},\alpha } \) of the \( \alpha \in (0,1) \) quantile \( q_{Y,\alpha } \) of Y defined by
where G is the cumulative distribution function of Y given by
is a Monte Carlo estimator. As in Enss et al. [92] or Kohler and Krzyżak [177] the estimator is defined by
where
Note that this is equivalent to choosing the \( \lceil N_{n} \cdot \alpha \rceil \) biggest values of \( m_{n}(X_{n+1}) \), \( \ldots \), \( m_{n}(X_{n+N_{n}}) \).
This method is a straight-forward Monte Carlo approach. A more complicated and thus in many cases more exact method can be found in Kohler and Tent [178].
Application to data of the MAFDS
As an application to illustrate the two methods described above we use the computer simulation of the MAFDS as described in Sect. 5.2.5 and use the same method to estimate a surrogate model as described in this section. To estimate the density by the above described adaptive approach we use \( N_{n} = 10^4 \) realisations evaluated with the surrogate model. The finite parameter set \( \mathcal {P}_{N_{n}} \) is set as \( \{2^l: l \in \{-5,-4,\ldots ,10\}\} \) and as kernel we use the Epanechnikov kernel defined by \( K(y) = (3/4) \cdot \max \{1-y^2,0\} \), where \( (x)_{+} \) equals x for \( x > 0 \) and 0 otherwise. The result is displayed in Fig. 5.14.
The estimated density and quantiles can now be used for further development and to analyse properties of the technical system.
Adaptive surrogate density estimator, defined as in (5.6), based on a sample of \( 10^4\) realisations
Since the calculation of the quantile estimate is much faster we use \( N_{n} = 10^6 \) realisations in this case. We use these realisations to calculate the 0.5, 0.95, 0.98 and 0.99-quantiles as described in Sect. 5.2.6. The result is summarised in Table 5.2.
5.2.7 Mastering Uncertainty in Customer-Integrated Change Management
Long-term competitiveness of companies that manufacture individual products can only be ensured by a continuing increase in efficiency, an accelerated process chain and company-wide learning [252]. Efficient processing involves a low use of enterprise resources with the best possible product quality. The customer-integrated approach of the metalworking industry is already helpful, but customer integration would be necessary to be even more competitive [171].
A section within project management where integration is a very promising approach is engineering change management, since this currently requires large resources. These processes often involve unforeseeable changes. Dealing with these changes leads to uncertainty regarding the impact in terms of time, cost and quality of the product.
The avoidance and efficient handling of change processes are important factors to mastering uncertainty. Baumberger points out that customer-specific developments of capital goods, such as the 3D Servo Press, in many cases have company structures that are strongly oriented towards individual development and production, which offer further potential for optimisation during the development process [17]. If a change is detected at a late stage of the product development process, this not only affects the product, but also has a significant impact on the costs of implementing the change. In this context the Rule-of-Ten approach is used in numerous studies (see [63, 141, 229]). The Rule-of-Ten describes the disproportionate increase of the change effort depending on the change time [16, 64, 107]. Here, the change-costs increase exponentially with each phase of the life cycle by a “factor ten” [108].
The temporal distribution of the changes that actually occurred additionally increases the cost share of the changes in relation to the total project costs. According to a literature-based analysis by Bauer [16], three quarters of all changes occur at a time when a simple change to the product data is no longer sufficient. If changes in the planning and development phase can often be implemented by short iterations and adaptation of the product data, the lack of manufacturability and assemblability in the production phase, in particular, cause a large part of the change expenditure [84, 116].
Therefore, one of the most important tasks of change management is to avoid late changes and to shift changes into early phases by determining and recording product requirement as completely as possible [18, 62, 190]. In addition to DIN 199-4 [67], other change management approaches such as the “Generic Engineering Change Process” according to Jarratt [162], the “Strategic Automotive Product Data Standards Industry Group” (SASIG) [233], the “Implementation of a milestone-supported Customer Change Management” according to Sauer [234], the “Decentralised Change Management” according to Kleedoerfer [170], the “Design Change” process according to Yu [284], the “advanced CMII-based ECM framework” according to Wu [282], “engineering change process framework” according to Stekolschik [255] and the “Generic Engineering Change Process” according to Riviere [229] exist.
A large number of scientific approaches include a structured representation of the change process, which implies the need for clear, formalised process steps. Currently, none of the scientific publications fully meets the requirements described for the integration of a cause and effect analysis in the early phases of process flow.
Strategies for the avoidance and control of technical changes are frequent approaches of the scientific literature to make change processes more efficient, to increase quality and to reduce costs. However, the applicability of the strategies to change processes in individual production must be examined.
Many of the models presented were derived from series production processes. Since none of the work adapts the models to individual production, it can be assumed that direct transferability is not possible. Furthermore, the deficit of missing integration of customers into the change process becomes apparent. The method’s orientation towards customer-related changes is only postulated in the work of Sauer, which focuses on customer changes during the change process execution. In the following, the structure of the adapted change process (see Fig. 5.15) is described.
The model aims to support companies in the implementation and execution of customer-integrated change management. In addition, the procedure model serves as a planning instrument to make the phase-specific activities transparently available to the involved stakeholders. The relevance of the customer is taken into account to the extent that the customer is the core element at the centre of the model. The change procedure itself is represented in nine steps. In addition to the customer and the phases of the change procedure, the outer layer, consisting of the three areas “Management & Organisation”, “Human Resources” and “Methods & Aids”, completes the basic structure.
In the following, the individual phases of the change procedure are described. The first phase of the procedure is defined as the phase of deviation analysis. This phase includes an examination of the target and actual values and can therefore be seen as a trigger for a change process. It is of high relevance that the underlying causes are identified in the case of a detected deviation. The deviations are the basis for a change request. In addition to a deviation analysis, further preliminary calculations are necessary. In the following phase of the procedure “write request”, the information for the rate request is summarised. The preceding phase of write request, rate request and application decision excludes changes at an early stage which do not promise success. If the change request is approved, from a macroscopic point of view, the planning phase begins, which consists of the phases, finding solutions and detailing.
In the phase of finding solutions, classical methods support the operator in the generation of possible solutions as well as in the subsequent phase of solution evaluation, which includes a risk and impact analysis. The involvement of the customer is an important component to benefit from his extended application experience. In addition, active involvement takes place in the change decision phase in order to record all customer requirements. For this purpose, communication channels, such as meetings or e-mail exchanges, or software-assisted tools can be used. In a transparent and comprehensible decision-making process misunderstandings due to the “communication barrier” between companies and customers but also between departments can be eliminated. Once a satisfactory solution has been found, evaluated and approved by the change control board taking into account all economic and technological criteria, the change implementation phase begins.
Depending on the scope of the change and the point in time when the need for change is discovered, the implementation phase is in the simplest case a simple document change; however, for complex processes the change process can extend over different departments and over a longer period of time. As in general project management, it is important that the change status, cost and schedule are continuously monitored. In addition to the technological implementation, the change procedure is concluded with a conscientious and detailed change review. In addition to the documentation of all changed data, this also includes a preparation of the data in the sense of a “change review” for individual production (Fig. 5.15). The individual phases differ in the scope and depth of the description. This is accompanied by the fact that methodological aspects are of particular importance in the analysis, evaluation and decision phases as well as in the change review phase. Special expertise and procedures predominate in the phases close to implementation. This expertise is not generally valid and can therefore only be described insufficiently [156].
Procedure model on the example of the 3D servo press
The presented modification procedure is applied to the case of sensor integration for the control optimisation of the 3D Servo Press, Sect. 3.6.3. The change was initiated by the requirement to integrate an additional monitoring and closed-loop control of the process force by means of integrated force sensors. This change was motivated by a technical innovation, with the aim of implementing the changed requirements with regard to the closed-loop control of the machine. Accordingly, an adjustment of the target property is carried out.The idea for the modification came from the Research and Development Department (R&D) at a time when large parts of the gear unit (Sect. 3.6.3) had already been manufactured but not yet assembled. Similarly, production of the lower part has not yet begun. Since the internal customer, in this case the R&D department, has initiated the change, the customer is fully involved in all processes of the change process. The change request is justified by the fact, which Groche et al. [126] have determined, that a closed-loop control of presses via the engine parameters and kinematics model is not sufficient due to friction. A first solution suggested by the customer is the integration of the sensors in the direct force flow, which is carried out for each individual gear. Thus, the integration of the sensor technology focuses on the components located in the direct force flow between bearing frame and gearbox. The drive rod, which is located in the direct force flow between the bearing frame and the gearbox, turns out to be the most promising component to be changed. The cost of the change can be identified as the procurement of the sensors and the integration into the production process. It should be noted, however, that the drive rod was already finished but not yet assembled. Furthermore, the need for action, effort and costs for the modification were estimated. To find a solution, a conventional procedure is used whereby creative methods such as brainstorming were used to develop the design solutions shown in Fig. 5.16.
The technical feasibility, costs and effort of the respective solutions were evaluated by the core team and in coordination with sensor vendors and manufacturers. The uncertainty of the respective solution regarding robustness in operation, sensor failure, overload and reduction of gear stiffness was to be evaluated. At the same time, production costs and effort must be included in the analysis. The first solution with direct force measurement using a piezoelectric-force measuring ring between the drive rod and the bearing frame proved to be the simplest solution in terms of feasibility and costs. However, this solution has the greatest influence on the strength of the gear. The second variant can be described by indirect force measurement using a force measuring ring in the force shunt. A part of the force is transmitted directly via the structure into the bearing frame, another part is transmitted via an adapter plate and the force washer in order to measure the process force. The advantages are higher rigidity and low stress on the sensor. Production, on the other hand, is more complex, because it is necessary to achieve a uniform height of the bearing surface and the drive rod on the bearing frame. The third variant involves the integration of a surface strain sensor, which also operates according to the piezoelectric effect. This approach is already used in the prototype of the 3D Servo Press and proved successful. However, three sensors each are required on the drive rod in order to obtain high-quality force measurements in the event of a possible deflection of the drive rod. A calibration of the installed sensors is necessary for all three variants and does not represent an advantage or disadvantage for any variant.
All three variants are subsequently evaluated by the internal customer and the project core team. In the questioning of the customer after the fulfilment degree of the respective variant, based on the classification of the change request the third change variant is evaluated most positively. The decision is then documented and made available transparently to all parties involved. The change variant is released and orders are issued to carry out all necessary change tasks. The responsible change manager is commissioned to take over change controlling and to regularly inform the customer and the Change Control Board about the status of implementation. The last step of the change review completes the change procedure. Further change processes follow the same procedure, as shown in the example of the 3D Servo Press.
The procedure model presented shows that the formulation of the question has a considerable influence on the classification of the customer needs. With regard to the requirements, there is a clear difference in the product to be developed. The transferability to serial production is possible, however, associated with clearly larger expenditure in the organisation.
5.3 Mastering Propagated Uncertainty in Process Chains
The production phase in the life cycle of products or systems, linking the design phase with the usage phase, see Sect. 1.2, is usually structured as a process chain. This section describes methods to master uncertainty along process chains. Following the representation shown in Fig. 3.3 in Sect. 3.2, a process chain consists of subsequent single processes, each of which is subject to disturbances. Furthermore, the material fed into the process to produce the product contributes to uncertainty, e.g. by semi-finished product variations.
Uncertainty during the production process propagates into the product and can make it infeasible to carry out subsequent steps in a production chain or to guarantee product quality. To manage this challenge, standardisation methods have been used for several hundred years. If the effect of uncertainty is particularly known, i.e. incertitude, it can be mastered by the definition of tolerances, cf. Chap. 2. However, since the influence of the uncertainty along the process chain is often unknown, it is possible that relevant product properties being subject to uncertainty and being important for quality are not considered; or the definition of tolerances for the considered properties is not appropriate. To cope with uncertainty in process chains, two processes have emerged in the last decades: firstly, robust single processes make the process chain less sensitive to quantified uncertainty, as they fulfil their function, even if the system is disturbed in a limited and predictable way, cf. Sect. 3.5; secondly, modern resilient processes, as introduced in Sect. 3.5, do not only allow to react to disturbances but also to learn from them in order to master unknown effects of uncertainty, i.e. ignorance (see Chap. 2). In the following subsections, examples are given on how to react to disturbances in order to ensure function and quality (see Chap. 1) of the system, which is in this case represented by the process chain itself. Furthermore, we illustrate how product property defects can be fed back in such a way that the process chain acquires the resilience functions of learning and anticipating, which are described in detail in Sect. 6.3. Using the example of a combined process chain which consists of forming and cutting processes, it is shown how uncertainty can be reduced (Sect. 5.3.1). In Sect. 5.3.2, the regulation of product specific requirements and the effects on the uncertainty are discussed. With this knowledge, it is shown how the propagation of uncertainty can be quantified and how the process chain can be adapted at an early stage of the production process. Section 5.3.3 provides an example for a flexible process chain using the 3D Servo Press in order to adapt product properties during the production process. One approach to master uncertainty by reducing process-related fluctuations in product quality are smart structures. Integrated in load-bearing structures and machine elements, as shown in Sect. 5.3.4, they can be used to monitor and control the production process (Sect. 5.3.5). Section 5.3.6 shows a new process-integrated calibration method to increase efficiency in the manufacture of smart structures.
5.3.1 Uncertainty Propagation in a Forming and Machining Process Chain
In production, the interlinking of forming and machining processes represents a classic value chain. Process chains, as described in Sect. 3.2, are characterised by uncertainty, such as batch-related uncertainty in the material properties or positioning uncertainty of the machine tool. Furthermore, the open-loop or closed-loop control of the machine tool affects uncertainty (Sect. 5.3.2).
In the context of process chains the concept of the Austauschbau, as described in Chap. 2, plays a decisive role. One way to master uncertainty in form of incertitude in the Austauschbau is by defining tolerance limits, within which the component has to be positioned during the transition between the process steps. The definition of tolerance limits is usually done opposite to the direction of the value chain starting with the finished part. The required tolerances of the preceding process steps are usually determined according to the experience of the employees. As a result, the accuracy requirements of early process steps are often based on a subjective view. In particular tolerances that are too tightly selected allow little room to compensate fluctuations in raw material quality, for example, although the continuous optimisation of production steps enables the development of controlled processes or robust tools that are able to master larger uncertainty in component specifications.
Since process simulation and optimisation are often focused on one single process, predictions of component quality over the entire process chain are currently difficult to assess and heavily depend on experience and knowledge [46]. However, little attention is paid to the interfaces between the processes that are critical for linking the different process steps. One reason for this lack is that there are hardly any compatible interfaces between different simulation tools [46]. With the current production approaches, variable products with application-specific requirements, such as required by the MAFDS (Sect. 3.6.1), cannot be realised taking uncertainty into account. Therefore, we investigate a possible combined process chain consisting of cutting, forming, heat treatment and machining (see Fig. 5.17), with the main focus on the forming and cutting processes. We chose orbital forming, an incremental forming process, in which only a partial contact surface is created between the punch and the workpiece, as an exemplary forming process. Relative to a point on the workpiece-tool contact surface, the stress builds up accumulatively due to the intermittent tool contact. At the same time, the lower rolling friction between the workpiece and the punch enables a radial material flow, also known as the mushroom effect [187]. This effect can be controlled by varying the tool angle, the feed rate and the rotational speed in order to counteract fluctuations in the semi-finished product [58]. The forming machine we use is a 3D Servo Press (as described in Sect. 3.6.3) with three independently controllable degrees of freedom in the slide [126]. Since we control the material flow by adjusting the process parameters due to previous semi-finished product uncertainties, it is necessary to predict the effects on the subsequent steps, such as reaming. By coupling the forming prediction with the reaming prediction, a closed-loop process control can be achieved, which reduces the uncertainty due to semi-finished product variations.
Process chain consisting of forming and machining as well as feedback of the final component properties [46]
As a first step we implement the forming process in a 3D finite element simulation using the simulation tool Simufact Forming to map the relevant forming step [46]. In the simulation a tube with an nominal outside diameter of 48 mm and a nominal initial height of 34 mm is formed to a bevel gear with a nominal height of 17.7 mm. During the forming process a perforation with a nominal diameter of 7.5 mm is added to the centre of the bevel gear. The influence of the parameters tool angle, infeed speed and form of motion on the resulting material flow is investigated and variables for process control are identified [58]. At the same time, variations in the angle at a constant tool angle lead to a deviation of the height profile. This requires compensation by calibrating the workpiece towards the end of the orbital forming process by levelling the surface with a constant angle.
While we use the material flow as a variable in further work to control the component geometry with regard to mould filling and height, quantitative evaluation of the effect on perforation requires coupling to a reaming simulation. Furthermore, this enables the optimisation of the reaming strategy based on formed components.
Reaming is often used towards the end of the value chain. It serves the purpose of producing functional bores with shapes and of positioning within a required tolerance range. For productivity reasons, multi-bladed reaming tools that combine the functions “cutting” and “guiding” in one tool element are often used. These tools have been the subject of scientific investigations. The influence of disturbance variables on the quality of the reamed bore is investigated with regard to diameter, circularity and cylindrical shape on the one hand [38, 179] and the deflection of the tool on the other [45, 145]. Tool deflection leads to an increased diameter of the envelope cylinder of all bore centres of the reamed bore. Adapting the cutting edge geometry by increasing the setting angle results in a reduction of tool deflection in the transient entry phase into the workpiece. An upstream pilot process achieves a significant reduction of the deflection, especially with long cantilevered tools with a length-to-diameter ratio of \(L/D \approx 10\). The model we used to simulate the reaming process is the mechanistic model described in Sect. 4.1.3. It is based on a geometric intersection model to calculate the undeformed chip cross-section [1], an empirical cutting force model [3] and a multi-body model to represent the dynamic tool behaviour based on the Jefcott rotor theory [44].
A central point for the representation of the process chain is the linking of the individual models of the forming and machining processes. Figure 5.18 illustrates the interface to transfer the geometry between simulations. One output variable of the forming simulation is the surface of the part after forming. The component surface is represented in standard tessellation language file format (STL) by numerous triangular faces and their respective three vertex points. We then generated a new cylindrical grid using the vertices to remesh the wall of the punch hole in steps of 1°. The polygons of the 2D element model, which represent the workpiece in the reaming simulation, are then generated from the nodes of the newly meshed grid.
The perforation in the centre of the component, which is produced during the forming process, is machined using reamers in order to generate a high quality cylindrical surface. To investigate the influence of the process and geometry parameters on the displacement of the reaming tool, a tool with a diameter of \(D = 8.3\,{\text {mm}}\) and a cantilever length of \(L = 30\,{\text {mm}}\) is simulated. We vary the process parameters with regard to achieving a constant feed rate of  during the entire machining process. In addition, we determine a suitable running-in strategy, using a reduced feed rate of
during the entire machining process. In addition, we determine a suitable running-in strategy, using a reduced feed rate of  until a reaming depth of \(4\,{\text {mm}}\), followed by an abrupt increase to achieve the final feed rate. In the case of machining valve guides in the cylinder head of a combustion engine, we demonstrate the positive influence of an upstream pilot process using a short cantilevered reaming tool [45]. The diameter and cantilever length of the pilot reamer are reduced by 0.1 mm and 10 mm respectively. The depth of the pilot bore is \(2\,{\text {mm}}\). For all simulations we chose a cutting speed of
until a reaming depth of \(4\,{\text {mm}}\), followed by an abrupt increase to achieve the final feed rate. In the case of machining valve guides in the cylinder head of a combustion engine, we demonstrate the positive influence of an upstream pilot process using a short cantilevered reaming tool [45]. The diameter and cantilever length of the pilot reamer are reduced by 0.1 mm and 10 mm respectively. The depth of the pilot bore is \(2\,{\text {mm}}\). For all simulations we chose a cutting speed of  .
.
Typically, reaming tools with a setting angle of \(\kappa = 45^{\circ }{}\) are used in industrial practice for standard applications. In theory, increasing the setting angle to \(\kappa = 75^{\circ }{}\) leads to a reduction in the passive force Fp at the individual cutting edges, reducing tool deflection especially in the face of disturbance variables. In the case of upsetting, using a reaming tool with a setting angle of \(\kappa = 75^{\circ }{}\) can reduce the tool deflection by 25% compared to a tool with a setting angle of \(\kappa = 45^{\circ }{}\). Considering orbital forming, the use of a reaming tool with a setting angle of \(\kappa = 75^{\circ }{}\) can reduce the tool deflection by 45%. In both cases, however, the tool deflection, even with adapted cutting geometry, is still about 20 \(\upmu \)m, based on a machining depth of 17 mm (Fig. 5.19a). For functional bores, which serve to guide other components, it is often necessary to minimise the tool deflection and the associated reduction of the radial deviation of the reamed bore even further in order to fulfil the functions and reduce the wear symptoms.
Therefore, in a second step, we investigate various machining strategies for the reaming process of the formed components (Fig. 5.19b). Based on the previous results, we select \(\kappa = 75^{\circ }{}\) as the setting angle of the tool. The results of the simulation indicate the positive effect of an adapted running-in strategy (Fig. 5.19b). By reducing the feed rate during the entry phase into the workpiece, we could reduce the process forces significantly and thus minimise tool deflection. In the case of upsetting, we can reduce the tool deflection by 65% from 20 \(\upmu \)m to 7 \(\upmu \)m. With orbital forming, a 45% reduction in deflection from 21 \(\upmu \)m to 11.5 \(\upmu \)m can be achieved. Thus an improvement of the reaming quality can be obtained without the employment of further tools and with an increase of the main time from 0.5 s to 1 s. The introduction of a pilot process upstream of the actual reaming process enables a further significant reduction in tool deflection. Due to the increased stiffness of the pilot reamer, it is hardly deflected despite the occurrence of disturbance variables. In theory the following reaming process has a reduced radial allowance of \(a_\text {p} = 0.05\,{\text {mm}}\) up to a depth of 2 mm due to the preceding process in the transient entry phase. In addition, the influence of disturbance variables within these 2 mm can be largely eliminated by the pilot process. Therefore, the deflection of the tool can be limited to values around 1 \(\upmu \)m.
The presented results illustrate the possibilities of a coherent consideration of forming and machining process step within the process chain. By using the simulation tools, we could show that different process parameters during the forming of the workpiece have a significant influence on the component geometry. An unfavourable selection of forming parameters leads to imperfections in the perforation after forming. Without an adapted reaming process this would cause an interrupted cut during the reaming operation and impaired bore quality. By using the knowledge from the combined models along the process chain, however, the uncertainty in the reaming process can be mastered. With the selection of a suitable cutting geometry and an adapted machining strategy, a significant reduction in tool deflection is possible. Furthermore, the results from the analysis of the process chain can be fed back into the forming process in order to establish a closed loop for the control of uncertainty in the process chain and thus master the chained uncertainty.
5.3.2 Closed-Loop Control of Product Stiffness and Geometry
Uncertainty in manufacturing processes affects the properties of a product and as a consequence affects the product’s usage behaviour. Currently, product properties are ensured in an open-loop approach by skilled workers and process planners. Product quality therefore depends mainly on the experience and qualification of these people. At the same time, changing and increasingly complex process chains present a growing challenge. Changes in the process chain and uncertainty in ambient conditions as well as properties of the raw materials affect both, product and process. Therefore, methods are needed to master uncertainty in the production phase (Sect. 1.2) and along the complete process chain.
The automatic closed-loop control of forming processes experiences a constantly growing attention, focussing on the control of individual geometric product properties [8]. The automation of production processes, however, is accompanied by the fact that several product properties need to be controlled simultaneously and boundary conditions have to be met. Sometimes, the properties to be controlled are conflicting with each other. The requirements for automated driving proposed by the German Association of the Automotive Industry (German abbreviation: VDA) can serve as an analogy where a fully automated car is in charge of all the driving and does not require any human intervention [268]. When transferred to manufacturing, a fully automated process requires that all relevant product properties are controlled and that boundary conditions are not only met but also extended if necessary [125].
To differentiate the degree of automation of process chains, the VDA introduced different levels as shown in Fig. 5.20, which are determined by the autonomous abilities of the system, in the style of the levelling scheme used for autonomous driving cars.
The objective in increasing the automation level is the reduction and compensation of disturbances, i.e. to increase the robustness of the process, compare Chaps. 3 and 6. By breaking this objective down into sub-objectives, subtasks can be defined and automated piece by piece. For example, tasks that are carried out by the staff at lower levels can be replaced by automated quality inspection systems and closed-loop control at higher levels.
Both, control methods and equipment for measuring and manipulating product properties, are required to climb the automation levels. But we already face a conflict of objectives when measuring product properties, which is between good measurability and information content (Sect. 5.2.4). With increasing spatial distance between the machine drives and the product being manufactured, the manipulability of the product properties decreases. Furthermore, the uncertainty increases with increasing measuring distance to the product [56]. Moreover, the use of adjustment mechanisms leads to a high effort in process design if tools have to be equipped with additional actuators. Solutions to this problem are offered by presses with several degrees of freedom in the ram, such as the 3D Servo Press presented in Sect. 3.6.3. By having the complexity of the actuators in the machine, new processes can easily be developed [58, 160], and passive standard processes, such as deep drawing, can be enhanced [51].
Under the assumption that the product properties, i.e. the controlled variables, can be determined, their optimal manipulation represents a new challenge. The manipulating variables are drive motions but also, among other properties, the tool design, lubrication, temperature. These influence the product properties in a non-linear way. Finding optimal process variables is an iterative process and supported by simulations. Once the desired product properties are achieved, the manipulating variables are kept constant and process fluctuations are kept to a minimum using open-loop control. However, if disturbances occur, such as deviating material properties in a new batch or fluctuating semi-finished product properties, an open-loop control cannot compensate for this [57].
On the other hand, closed-loop control of individual product properties allows to adjust the process to deviant product properties by feeding back the actual product property. Incremental forming processes are particularly suitable, since they can be controlled from one increment to the next. In free bending, for example, the springback of the material is a decisive influence of the final component geometry. The latter depends strongly on the material properties of the current workpiece. By measuring the geometry after springback while still clamped, the bending operation can be adjusted and iterated to the desired geometry, as we demonstrated in [58].
Although the product’s geometry is its most evident property, it is only one of many relevant properties. This is demonstrated in the Modular Active Spring-Damper System (German acronym: MAFDS), see Sect. 3.6.1, which contains, among other components, active support with spring membranes. In addition to the geometry, these must rely, above all, on the stiffness of the spring membranes. While the geometry ensures the mountability, the stiffness is decisive for the function of the shunt-damping, as well as the active buckling stabilisation. The stiffness of the membranes is mainly determined by the material properties and their geometry. Single-Point-Incremental-Forming (SPIF), a process in which a sheet metal component is incrementally formed with a tool tip, is therefore particularly suitable for production. The process makes it possible to produce almost any geometry, as long as the load-bearing capacity of the material is maintained. If variations in the material occur, the stiffness can be corrected by making minimal adjustments to the geometry within the tolerable limits [155].
Whereas open-loop control acts, closed-loop control reacts, i.e. it only takes action when a deviation is detected. This is acceptable for disturbances with slow dynamics. However, if the disturbances occur with high dynamics from part to part, as is usual in production, the controller is unable to handle them well. Examples for such disturbances are fluctuations in the lubrication and the semi-finished product properties. Nevertheless, sometimes information about the material properties of the semi-finished product can be aggregated from process data of upstream processes. With the aid of disturbance models \(G_\mathrm {v}(z)\) we anticipate the effect of measurable disturbances v on the final product properties and compensate it using a disturbance feedforward control [124]. For example, shear-cutting processes are typically carried out prior to the actual forming operation. Disturbances are already visible in the force measurements of the cutting data. However, it remains challenging to select data features containing enough information to predict the product properties. Methods from the field of machine learning offer the possibility to identify relevant features from a data set and to create prediction models [159].
The effect of such measurable disturbances v can then be compensated for before they become noticeable in the product. However, we typically face disturbances \(\varepsilon \) that cannot be measured, or whose effects on the product properties are not known. Based on a known process transfer function \(G_\mathrm {s}(z)\), we combine the disturbance feed-forward \(G_\mathrm {s}^{-1} G_\mathrm {v}(z)\) with a closed-loop control \(G_\mathrm {c}(z)\) to a resilient process chain shown in Fig. 5.21. Such a control structure compensates for abrupt fluctuations caused by batch changes, as well as long-term disturbances, such as wear and temperature drifts. While the tool can also be equipped with additional temperature sensors, measuring the wear online is still a research issue.
Resilient process chain by means of closed-loop process control with disturbance feed-forward [124]
The coupling of different product properties challenges their simultaneous control. When correcting one product property, additional control measures are necessary to keep the other product properties constant. Boundary conditions further intensify this problem. To decouple product properties when implementing a closed-loop control, models are required that describe the effect of the manipulated variables and the coupling of the product properties. Since these models usually can only be evaluated by simulations, extended control approaches are necessary. The model-predictive control is a suitable approach, which is based on the recurrent solution of an optimal control problem. By means of an optimisation algorithm new optimal control variables are obtained after each forming step. Uncertainty, which becomes visible in the deviation of the predicted and measured product property, is taken into account after each step. This results in a closed control loop [160].
Future highly automated manufacturing process chains require cross-process control loops that predict and compensate for deviations. Current developments show that an online closed-loop still presents major challenges. Its realisation requires both, observers that estimate the final product properties during the process, and control devices that enable real-time control actions. We presented methods to control product properties beyond its geometry while complying with predefined boundary conditions. This requires the real-time manipulation of actuators involved in the process. Especially the real-time interface to a forming machine is crucial for future process control. While the research press presented in Sect. 3.6.3 already allows for online control, industrial forming machines do not offer such interfaces, yet.
5.3.3 Controlled Partial Post-compaction of Sintered Bevel Gears
Powder metallurgy serves as a manufacturing technology for a wide range of applications, one example of which is the manufacture of gear wheels. Powder metallurgical production offers economical and ecological advantages, such as profitable cycle times, good automation possibilities [238] and an optimal use of raw materials, due to the possibility of producing near-net-shape components [78]. Furthermore, the sintering of components from powder materials offers the possibility to realise different material combinations which cannot be produced by melting metallurgy at all, or only with increased effort [238]. However, the use of gears for power transmission in safety-relevant systems places high demands on process reliability and the final component quality [83].
Sintered components are porous bodies whose mechanical properties depend on porosity and pore density [238]. The porosity P describes the volume fraction of pores present in the component, while the pore density is the ratio of the number of pores to the length of the body. Pores lead to material weakening due to notch effects under load and are therefore a possible source of component failure, especially in areas of stress concentrations [55, 137]. A local reduction of the porosity can increase the fatigue strength of sintered components [209, 259]. For this reason, a targeted post-compaction of the most heavily loaded component areas is used to minimise the local pore content. In this way the quality of the product can be improved in terms of an increased availability, cf. Sect. 1.7.
Since both process stages, i.e. sintering and post-compaction, place different demands on the functionality of the machines used, conventional post-compaction takes place in a separate process step downstream of the actual sintering process. This means that the process is associated with additional costs for machines and tools, as well as a higher logistical effort [23, 197]. In order to better exploit the potential of powder metallurgical production for safety-relevant components of load-bearing structures, we developed a process concept that enables the combination of both process steps, the sintering process and the post-compaction, in one process sequence. For this purpose, the additional degrees of freedom in the ram motion of the 3D Servo Press presented in Sect. 3.6.3 are used to realise an integrated partial post-compaction process at the example of bevel gear manufacturing.
A measure for the quality of the post-compaction process is the relative density D, defined as
In the following we present a simulation model which serves to predict the relative density distribution in sintered components. This model is validated by experiments for an uniaxial load case and then extended for three-dimensional load conditions. The resulting model will be used to develop a process strategy for the partial post-compaction of sintered bevel gears using the 3D Servo Press.
Development of a simulation model for the uniaxial load case
A continuum-mechanical simulation model was developed. The governing equations were solved by a Finite Element (FE) solver, which was extended by an adequate material model for the process design. This model was adapted to the requirements of the specific application and validated by means of real tests to ensure that the model predicts the process behaviour in the best possible way and thus minimises model uncertainty as described in Sect. 2.2.
According to Parteder [220], the relative density D is used to assess the residual porosity at the end of the manufacturing process. The used material model must therefore primarily ensure the mapping of density development during the process. The Gurson model [136], based on the material behaviour according to Levy-Mises and described by a yield criterion, is able to predict the behaviour of porous media [220].
The development of the relative density can be calculated from the flow potential \(\Phi \) as described by Parteder [220]. In order to take individual material properties into account, this model has been extended by further model parameters \(q_i\) (\(i=1,2,3\)) according to Tvergaard [264], which includes the dependence of the yield stress on the density [98].
The change in pore shape during the process has a significant influence on the density development [54, 182, 220]. Therefore, instead of constant Tvergaard parameters, condition-dependent parameters are used, which are adapted to the temporal deviatoric deformation \(\varepsilon _{\text {e}}\) during the simulation on the basis of experimentally determined material parameters. The necessary material data were generated in uniaxial compression tests with cylindrical specimens made of porous pure iron.
Results from the real uniaxial tests are compared with the simulation results. The evaluation of the model uncertainty is based on the components’ densities in different stages of the compression tests. Experimental data of the porosity are derived from optically recorded microsection samples of the test components. A comparison of results from simulation and experiment is shown in Fig. 5.22. The data correspond to the relative density D after one to four post-compaction stages. The different stages represent specific values of the absolute density \(\rho \) reached in the experiment after a defined punch travel or process force. The density in the initial state is set to \(6.4~{\text {g}}/{{\text {cm}}^3}\). The input parameters for the simulation are either defined process forces (F) or punch displacements (P). Values of both types of parameters correspond to the measured ones in test stages with defined values of density. The black bars in the middle represent the experimentally determined values (E).
Comparison between a constant Tvergaard parameters and b state dependent parameters after 4 consecutive post-compaction stages for an initial absolute density \(\rho =6.4\,{\text {g}}/{{\text {cm}}^3}\) according to Brenner [50]; the current absolute densities after each stage are \(6.6\,{\text {g}}/{{\text {cm}}^3}\) (stage 1), \(6.8\,{\text {g}}/{{\text {cm}}^3}\) (stage 2), \(7.0\,{\text {g}}/{{\text {cm}}^3}\) (stage 3) and \(7.2\,{\text {g}}/{{\text {cm}}^3}\) (stage 4); the values in the tables show the percentage deviation between experiment (E) and simulations with defined process forces (F) and defined punch displacements (P)
The displayed results exhibit an overall good agreement between the simulation with state-dependent model parameters (Fig. 5.22b) and the experimental results for this uniaxial load case. The deviations between simulation and experiment are small. This is especially true for the simulation with predefined punch displacements. In comparison, a larger deviation can be determined using constant Tvergaard parameters as displayed in Fig. 5.22a. This shows that the model uncertainty can be significantly reduced by using state-dependent model parameters.
Adaptation of the model for multiaxial loading
The prevailing stress conditions in forming processes are usually multiaxial. The compaction of an isotropic material is based on the mechanism of pore closure within the material, which is decisively influenced by the prevailing stress state [220]. For this reason, a suitable comparison variable is required to investigate the density development as a function of different stress states. Therefore, a modification of the Gurson-Tvergaard model including the multiaxiality X in the determination of the Tvergaard parameters \(q_i\) was performed. The multiaxiality X is defined as the ratio of the hydrostatic stress component \(\sigma _{\text {h}}\) to the deviatoric stress \(\sigma _{\text {e}}\) [220]. These can be calculated from the stress components \(\sigma _i\) in the three principal directions:
In order to improve the prediction accuracy of the simulation model for the multiaxial load case, the parameters \(q_i(\varepsilon _\text {e},X)\) depending on the deviatoric deformation \(\varepsilon _\text {e}\) and the multiaxiality X can be determined with the help of a cell model calculation according to Needleman [205] and Tvergaard [264]. The cell model calculation establishes a relationship between the microscopic properties of the material and its macroscopic damage behaviour [220].
After the successful implementation of the cell model calculation into the FE simulation using subroutines to determine the state-dependent model parameters, we performed a validation of the advanced model using ball indentation tests. A hardened (55–65 HRC) spherical tool component, which is assumed as rigid in the simulation model, with a ball radius \(r_\text {s}\) is pressed into a sample body with a press force increasing linearly over the penetration depth up to a maximum of 70 kN. The investigations were performed with sphere radii of 5 and 10 mm. The load cases of the simulation are given by the course of the press force.
Comparison of the spatial distribution of relative density D between a experiment and b FE simulation for a ball indentation test (\(r_\text {s}=10\,\text {mm}\)) according to Strauß [256]
The spatial distribution of the relative density at the end of the indentation process serves as a comparative quantity. The penetration depth achieved is 4.75 mm. In Fig. 5.23 the optically evaluated relative density distribution of the experiment (left) for \(r_\text {s}=10\,\text {mm}\) is compared to the simulation result. The comparison shows a good qualitative agreement, especially in the contact area, where fully compacted material is present. The largest deviations occur in the upper edge area, since the ejection process necessary in the experiment leads to an increase in density of the surface area due to the ejection force. In addition, the course of the density in the centre deviates noticeably in the axial direction. This is probably due to uncertain test conditions that cannot be taken into account in the simulation, such as the existence of backlash between the test specimen and the die, which leads to radial displacements of the test specimen. As a result of the validation, however, a sufficient accuracy of the simulation model for the application in multiaxial load cases can be determined.
Process strategy for partial post-compaction
In addition to the vertical degree of freedom in conventional presses, the 3D Servo Press described in Sect. 3.6.3 has the additional option of tilting the ram. This allows the press ram to be deflected by an angle of up to approximately \(3^{\circ }\). In this way, the vertical ram movement can be superimposed by, for example, tumbling or swivelling movements in two planes [128]. Based on the developed simulation model, an FE-supported design of optimised post-compaction processes was carried out. The aim is to investigate the potential of process integration of post-compaction processes for the property adjustment of porous sintered components. The multiaxis post-compaction process takes place by utilising the additional ram degrees of freedom of the 3D Servo Press in the form of a tumbling tool movement. Figure 5.24 schematically sketches the process concept for the tumbling post-compaction compared to a conventional unidirectional compaction. The three independently controllable and adjustable eccentric drives enable the realisation of a tumbling die movement by phase shifted translational movements of the three ram drives, see Sect. 3.6.3.
Schematic illustration of a a conventional purely vertical ram movement compared to b the ram movement in a tumbling compaction process as possible on the 3D Servo Press according to Strauß [256]: the arrows symbolise the degrees of freedom
In this way, the degree of compaction can be specifically influenced in the post-compaction process. The aim is to partially increase the relative density D of the end product in the critical stress zones in order to avoid component failure caused by residual porosity. In the case of gear manufacturing, these are located in the marginal zones, such as the tooth flanks and the tooth root [137]. The edge zones of the tooth tip are also the goal of further optimisation with regard to the possible degree of compaction.
To estimate the achievable local degree of compaction by means of a specific ram inclination, the post-compaction of a single tooth is simulated. The modified tool paths alter the material flow, the influence of which on the result of the compaction process is investigated. The sample to be compacted consists of a simplified tooth geometry, which is derived from an involute gearing. Exploiting the symmetry only half of the geometry is modelled.
In Fig. 5.25, the spatial distribution of the relative density after the post-compaction process is compared to the density distribution of the uniaxially compacted tooth. Here, the density values in the area of the tooth flank and the tooth root are significantly lower than in the tumbling process. It is only in the area of the tooth tip where a fully compacted material area is visible. The density distribution in the remaining areas, however, is more homogeneous than in the tumbling process.
Simulation results for the density distribution a after the conventional uniaxial process compared to b the optimised compaction process according to Strauß [256]
On the basis of the simulations carried out, a clear influence of the friction in the contact area between workpiece and die can be observed. Furthermore, large deformations are visible at the edge areas close to the contact zone between workpiece and die. It can be expected that the higher density in highly loaded product areas will lead to an improvement of the product’s durability and strength.
The results show that extended tool kinematics can be used to positively influence compaction processes. Especially if locally high densities are required, tumbling motions can have a positive influence on the density development in critical component areas.
With the presented application, we have optimised the manufacturing process of a machine element in such a way that the properties of the end product can be specifically influenced without a subsequent separate processing step. The use of the 3D Servo Press enables a flexibilisation of the process chain. Thus, a consistent product quality can be achieved by adapting the manufacturing process to product requirements that arise in the usage phase and are not yet known during the design phase.
5.3.4 Forming Integration of Functional Materials in Load-Bearing Structures and Machine Elements
The classic approach to deal with uncertainty in mechanical load-bearing structures is to oversize the structure by taking into account a safety factor, see Sect. 1.2. Uncertainty in load-bearing structures can occur for a wide range of reasons. Typical causes are material imperfections, geometric inaccuracies or inaccurate assembly. Sources of uncertainty in mechanical engineering prevail preferentially at joints. Here, discontinuities in material behaviour or discontinuous force flow occur and lead to uncertain load scenarios. Therefore, the design and manufacturing of joints has to be carried out carefully. Bolted connections require special attention since the loads acting on the fastener can be multidimensional [121]. Smart load-bearing structures and machine elements contribute significantly to reducing the existing uncertainty. With the possibility of monitoring the actual load conditions and reacting accordingly, see Sect. 6.3 , oversizing can be avoided, resources be conserved and economic efficiency be increased [263]. Furthermore, the acquisition of process variables, e.g. process forces and torques, at the machine structure enables to verify the models of technical processes.
Smart structures comprise structures with built-in sensors and/or actuators linked via a controller [43]. So far, load-bearing structures and sensors or actuators are separately manufactured and assembled in a further process [48]. In this section, we present a novel approach for the production of smart tubular metal structures through joining by forming. The approach allows for the production of different designs of smart structures and machine elements. The sensory bending dumbbells, drive shaft and fastening element in Fig. 5.26 are some examples of possible smart structures created by this approach.
These structures can be used in a growing range of applications due to ongoing digitalisation. Exemplary applications such as structure condition monitoring, load path analysis or lifetime estimation can be realised. Furthermore, smart structures can be used for process monitoring, allowing control approaches which boost efficiency and improve product quality. This approach offers many advantages. On the one hand, the manufacturing process is highly economical, since the functional material is integrated into the load-bearing structure during its shaping. Thus no further process steps are required. On the other hand, this integral joining ensures that the sensitive functional materials are protected from external influences, thus enhancing the lifespan of these materials.
The joining process
The novel manufacturing process for the creation of smart structures is based on joining by forming. The load-bearing structure is plastically deformed, resulting in a form and force-fit joint between the structure and the integrated functional materials [135]. For this joining operation, rotary swaging appears to be particularly suitable, as it is an established process for joining metal wires and bushings [263]. In this process, the cross-section of the workpiece is incrementally reduced by the forming dies, allowing the functional element to be integrated into the metallic structure. In order to prevent any damage of the functional element during integration, metallic end caps are used [134]. The integration of a piezo ring in a metallic tube by the recess swaging process is shown in Fig. 5.27.
a Swaging unit [49], b motion sequence of the dies and c aluminium tube with integrated piezo ring
Figure 5.27 shows three of the four dies of the rotary swaging unit, which oscillate simultaneously at \(30\,{\text {Hz}}\) in the radial direction. While the workpiece rotates, the dies move closer to each other in the radial direction, see Fig. 5.27b, leading to an incremental reduction in the tube cross-section [123]. The piezo ring is guided and placed through the groove on the inner surfaces of the dies. During forming, the tube material flows to the end caps on the left and right and pretensions to the piezo ring [134]. This pretension defines the working range of sensory structures, as it will be reduced under tensile loads on the structure. It also ensures the functionality of piezoelectric actuators since they require a certain preload for the operation.
An adaptation of the process for the production of smart structures with homogeneous outer diameters is presented in [121]. Figure 5.28 shows a spring element with four strain gauges SG1–4 applied to measure temperature, force and bending moments integrated into a screw-shaped structure. Due to the preform of the structure and the geometrical design of the spring element, the radial motion of the dies leads to the integration of the transducer in pretension, see Fig. 5.27. In a downstream process, the fastening head and the threads can be machined [121].
a Process design for the manufacture of sensory fasteners, b finished sensory fastener with positions of the strain gauges on the spring element [121]
Unlike the process presented in Fig. 5.27, the final structure here has a uniform radius over the whole length after the integration process. For more flexibility in adjusting the pretension on the integrated functional materials, the integration process was extended to be based on in-feed rotary swaging. Through this extension, a better control of the pretension at the integrated functional material is achieved and an elongation of the joining zone is avoided [135].
At the first step of this integration process, the inner and outer preform is created in the structure using mandrels as well as the die geometry. In the second step, the functional material is inserted into the tube and pressed by the mandrel. As soon as the dies leave the integration zone, the mandrel is removed and the rest of the tube is further formed, as shown in Fig. 5.29.
Extended integration process for the production of smart structures based on in-feed rotary swaging [127]
Summary
It can be summarised that the introduced approach for the creation of smart structures and smart machine elements has many advantages, e.g. economic efficiency in production and the protection of integrated functional materials against environmental influences. The main characteristic of the presented integration process is the pretension of integrated functional materials. This pretension ensures the functionality of both integrated sensors and actuators. While integrated piezo actuators, e.g. need this pretension for the operation, the force measurement range of the tensile load of the sensor structures depends directly on the value of the pretension. As has been shown in the integration process based on in-feed rotary swaging, smart structures can be produced in various designs and with a flexibly adjustable pretension. They can also be produced as semi-finished products for further processing or individualisation stages [180]. In this way, sensory structures can be used for strategies to reduce uncertainty in many applications in mechanical engineering, e.g. structural condition monitoring.
5.3.5 Process Controlling During the Production of Smart Structures
The approach presented in Sect. 5.3.4 for the production of smart structures by means of forming technology allows the simultaneous joining of functional materials, as well as the forming of load-bearing structures and machine elements by rotary swaging [121, 134]. The functional elements are integrated into metallic hollow tubes by preload, which is created by a form- and force-fit joint. As a characteristic of the applied process, the functionality of the integrated functional elements, e.g. a force transducer, depends directly on the level of preload. A too high preload can damage the functional element, too low ones can prevent reliable operation. Considering the process design in Fig. 5.29, deviations in the integration process, as generally discussed in Sect. 3.2 for process chains, can be expected. Stochastic data uncertainty in the properties of semi-finished metallic tubes as well as in the process model (see Sect. 1.6) lead to a deviation in the adjusted preload, as this preload largely depends on the material flow at the end caps of the integrated functional element [180]. In order to master the described uncertainty in the production of smart structures, an approach for process monitoring and process control is necessary and is described in the following. For this purpose, the force transducer to be integrated is calibrated and then integrated into the tube. In this way, the inline measurement of the actual preload can be achieved.
Figure 5.30 shows the force signal curve measured by the integrated axial force transducer during the integration process
As can be seen in Fig. 5.30, a certain preload of about \(1.5\,{\text {kN}}\) is adjusted at the beginning of the integration process. Subsequently, the dies start the forming process. With each stroke of the oscillating dies of the rotary swaging machine, the tensile force in the tube and the integrated transducer increases. Due to uncertainty in the integration process caused by thermal shrinking, fluctuation in the coefficient of friction, misalignment of components as well as geometrical deviations of the tube, a control approach to adjust a specific preload based on the measured signals of the integrated force transducer must be implemented [180].
The control approach
Since the preload changes during the integration process and the remaining preload are only set after thermal equalisation, the control of the preload must be performed before the required information is fully provided [181]. A prediction model of the integration process seems to be suitable for this purpose. For the investigation of the preload evolution over the integration process, the time \(t_1\) with the maximum remaining preload force was determined. Besides this reference point, three further time points with fixed time shift were also considered: \(t_2 = t_1 +0.75\,{\text {s}}\), and \(t_3 = t_1 + 1.25\,{\text {s}}\) and \(t_4 = t_1 + 1.5\,{\text {s}}\). For all these discrete points, a correlation coefficient r according to Bravais/Pearson is determined to describe the degree of correlation of the preload between 12 specimens in their time values and the remaining preload at the end of the process [181].
Measured force during the integration process and correlation analyses of preload evolution of 12 specimens [181]
It can be seen in Fig. 5.31 that the correlation increases towards the end of the process. The later the preload force is evaluated, the better the quality of the predicted remaining preload \(F_\text {rem,end}\). From time \(t_2\) on, the correlation factor r is at least 79%. For the three discrete points during the forming process \(F_\text {rem}\) (\(t_\text {2}\)), \(F_\text {rem}\)(\(t_\text {3}\)), \(F_\text {rem}\) (\(t_\text {4}\)), a continuously improved correlation with the remaining preload \(F_\text {rem,end}\) is observed [181].
Two process parameters exist on the experimental machine (rotary swaging), the process parameters of which can be manipulated during the forming process, and they also have a major influence on the preload force: the mandrel force\(F_\text {mand}\) and the in-feed speed v . On the one hand, it has been shown that the short contact effect of the mandrel, with the progress of the process, reduces the ability to affect the resulting preload. On the other hand, the in-feed speed has a better effect on the resulting preload, since it directly affects the forming forces and therefore the material flow at the end caps of the integrated force transducer [181]. For this reason, the in-feed speed is used as a manipulation parameter for the controller approach.
Based on the trials conducted in [181], the following conclusion can be drawn: in order to obtain the widest possible range of achievable preload forces, the in-feed speed must already be adjusted at \(t = 2\,{\text {s}}\). At this time, the process can be influenced most effectively (Fig. 5.32). However, the highest possible accuracy of the predicted preload is only given in the time range between \(t = 2.5\,{\text {s}}\) and \(t = 3\,{\text {s}}\) (see the correlation value in Fig. 5.31). In order to meet both, the requirement for high accuracy and the requirement for a wide control range, the selected control approach consists of three stages: An open-loop control, an early preload pre-control between \(t = 2\,{\text {s}}\) and \(t = 2.5\,{\text {s}}\) with the aid of the prediction model and a subsequent adaptive control for fine adjustment starting from \(t = 2.5\,{\text {s}}\). The in-feed speed is manipulated with the aid of a feed-forward parameter from \(t = 2\,{\text {s}}\) according to the target preload value. The adjustability of the preload at this point is the highest (see Fig. 5.31). At \(t = 2.5\,{\text {s}}\) the signal can be fedback to the controller. The predictability at this point is high enough to fine-tune the process while still providing good adjustability. The control approach therefore consists of the three phases: Open-loop control, preload pre-control and feedback control (see Fig. 5.32).
Control approach to adjust the preload using the in-feed speed [181]
After designing the controller and the prediction model based on the correlation analysis in Fig. 5.31, sensory structures with controlled preload can be produced. Once the integration process has begun, the prediction model starts analysing the force peaks and valleys of each die stroke, with referencing the measured data to the reference point \(t_1\). The controller works in open-loop mode until time \(t_2\). The in-feed speed in this mode has a constant value \(v_1\). From time \(t_2\), the in-feed speed is adjusted to \(v_2\) according to the preload control parameter. In the last step, at point \(t_3\), the feedback control is activated and the in-feed speed is set to \(v_3\). The results of this control strategy were evaluated at two different force levels to investigate the flexibility of this approach. A significant increase can be observed in the achievement of the target preload force (Fig. 5.33). The repeatability is also increased in comparison to the uncontrolled processes. The accuracy and repeatability of the controlled process are increased at higher preload forces. These results prove that the inline measured signals can be used to control the preload of the integrated transducer of smart structures, resulting in a higher accuracy and a smaller deviation.
Result of the controller approach compared to the uncontrolled process [181]
Summary
Utilising the force signal of the transducer to be integrated for process monitoring and process control in the production of smart structures can significantly reduce the process-related fluctuations in the produced parts. Through correlation analysis, the resulting preload, which is directly measurable only after the process, could already be predicted in the second part of the forming process. In addition, it could be shown that it is possible to change the preload without affecting the resulting form of the smart load-bearing structure. Using the developed control approach, the fluctuation of the achieved preload force could be reduced by up to 60%.
5.3.6 Process-Integrated Calibration of Smart Structures
Smart structure and machine elements contribute to reduce uncertainties in mechanical engineering. With their abilities to monitor and react to the current load state, approaches for active process manipulation can be implemented. In Sect. 5.3.4, we discussed the efficiency in the production of smart structures by means of forming technologies. Process design for the integration of functional material into metallic tubular structure by rotary swaging is presented in [121, 127, 133]. An approach to deal with stochastic data uncertainty in the properties of semi-finished metallic tubes by controlling the joining process is presented in Sect. 5.3.5. Despite the efficiency achieved in the manufacturing process, the required time consuming downstream calibration process is still a limiting factor for a broad industrial implementation of sensory structures. Defined test sequences are carried out on a testing machine, for example, according to the standard DIN EN ISO 376 for force sensors in [70].
In this section, we present an approach to increase the efficiency in the production of sensory structures. By means of a suitable setup and process-adapted signal processing, it is possible to replace standard time-consuming downstream calibration processes with process-integrated calibration [6]. Once the sensory functional element is firmly integrated into the structure and the forming dies leave the joining zone (see Sect. 5.3.4), the process forces required for the subsequent forming of the structure can be used to implement a dynamic calibration of the sensory structure. For this purpose, a special sensory clamping was designed as a machine-side reference point. By measuring the forming forces in both modes, namely in the integrated sensor element and at the machine-side reference point, a calibration is realised as shown in [6]. For the sensory clamping, strain gauge sensors are applied to measure the axial force on the clamping surface. Due to the rotation of the clamping, signal amplifiers with wireless signal transmission are used (measuring nodes). The measurement setup in Fig. 5.34 contains the integrated strain gauge based axial force sensor within the tube and the two other machine-side axial force sensors on the clamping rotated 90° to each other for higher accuracy.
Measurement setup for the process-integrated calibration of smart structure produced by rotary swaging [6]
Signal processing
By looking at the force signals \(F_\text {ax,tube}\) and \(F_\text {ax,clamping}\) in Fig. 5.35, the manufacturing process can be divided into three phases. In the first phase, a certain compressive force is applied to the integrated force transducer by the mandrel to adjust the required pretension. The mandrel force remains until the forming dies leave the joining zone and the transducer is firmly joined into the structure. Once the transducer is fully integrated into the structure, the mandrel is removed and the rest of the tube is pulled out of the swaging unit and formed by in-feed rotary swaging, see Sect. 5.3.4. As a result, the load direction changes and a high tensile force peak is induced with every stroke of the oscillating dies. At the beginning of the forming process (\(18\,{\text {s}} \leqslant t \leqslant 40\,{\text {s}}\)), a high forming frequency (approx. \(30\,{\text {Hz}}\)) leads to a high density of these force peaks. After the cooling-down of the joining zone in the tube, the adjusted pretension almost reaches a constant value (see also Fig. 5.34) and the dynamics of the forming dies are reduced to avoid resonance effects of the clamping [6]. The calibration phase can begin accordingly.
Progression of the axial forces both in the integrated force transducer and in the sensory clamping during the manufacturing process (normed to the max values) and the beginning of the calibration phase [6]
Even after the identified time to start the calibration, both force signals \(F_\text {ax,tube}\) and \(F_\text {ax,clamping}\) are affected by two significant interferences: On the one hand, the high temperature at the integrated transducer caused by the plastic deformation of the tube leads to a drift in the force signal \(F_\text {ax,tube}\). On the other hand, the eccentricity of the clamping during rotation causes a sinusoidal zero-point drift in both signals. Once forming starts, the sinusoidal zero-point drift becomes greater as a result of bending the tube by the oscillating dies, and it becomes less uniform as a result of the high forming moments causing the workpiece to slip, see also [6, 180]. Since neither the amplitude nor the angular frequency of the sinusoidal zero-point drift can be modulated, as the deformation behaviour is not precisely predictable, it is necessary to elaborate suitable approaches for the signal processing prior to calibration [6]. Based on the main characteristics of the incremental forming processes, i.e. that a release state occurs after each load state, an approach to correct the signals is introduced in [6]. The actual position of the zero-point in each signal is determined and then forced to the nominal position [6, 180]. Firstly, the lower envelope in each signal is determined. Secondly, the lower envelope is filtered by using a Gaussian smoothing filter to get a clear zero-point drift curve. Finally, the raw signal is corrected with the determined zero-point drift curve. Figure 5.36 illustrates this procedure.
Signal processing and correction: a raw signal, b the lower envelope (grey) and the filtered lower envelope (black), c force signal after correction the zero-point drift [6]
Figure 5.36a shows that the initial signal has a constant zero offset, as long as the clamping fixture does not rotate (\(t < 2\,{\text {s}}\)). Once the rotation starts (\(t > 2\,{\text {s}}\)), small sinusoidal zero shifts with relative constant amplitude and angular frequency occur (\(t < 10\,{\text {s}}\)). This drift is caused by the gravitational force of the mass of the structure. When the deformation begins (at \(t = 10\,{\text {s}}\)), the amplitude of the sinusoidal drift becomes higher with non-uniform angular frequency, which can be observed clearly in Fig. 5.36b. Once the signals are corrected, an accurate zero-point position can be observed, see Fig. 5.36c and the calibration can be carried out by correlating both signals from the integrated force sensor and the sensory clamping.
Results
To determine the achievable accuracy of the in-process calibration, the generated sensory structures were re-calibrated according to the standard calibration (DIN EN ISO 376) on a tensile testing machine (Zwick Roell 100). A comparison between the two types of the calibration shows a good correlation. In Fig. 5.37, both calibration methods are shown for an exemplary sensory structure. While the nominal force rises gradually in a standard calibration, it usually reaches the nominal value in less than one second with one stroke of the forming dies. Both calibrations, however, show good linearity, allowing the calibration coefficient to be calculated as the slope of the linear fit of the measured points. By evaluating the deviation of the process-integrated calibrations from the reference in several samples, a maximum nominal value-related deviation of 2% was observed.
Comparison of process-integrated and standardised calibration of a sensory structure with integrated axial force sensor and the calibration value-related deviation [6]
Summary
The novel approach, introduced in Sect. 5.3.4, for the creation of smart structures through integration of functional materials in load-bearing structures using incremental forming processes provides numerous economic and functional advantages. By means of the possibility of process monitoring (see Sect. 5.3.5) during the integration of the functional materials and, therefore, the realisation of control approaches, this manufacturing process gains the flexibility to adjust the pretension of integrated functional materials as a further advantage.
A further benefit of incremental forming for the production of smart structures could thus be demonstrated. Since the incremental process implies that every loading state is followed by a release, the acquired data can be easily processed and process-related interference effects can be corrected.
In a nutshell, smart structures with integrated functional elements help to master uncertainty in mechanical structures in their usage phase. By inline process monitoring and process-integrated calibration of smart structures, uncertainty in their manufacturing is reduced. Faulty integration processes can be detected, e.g. by evaluating the standard deviation of the process-integrated calibration [6].
5.4 Semi-active and Active Process Manipulation
In the preceding Sects. 5.1, 5.2 and 5.3, we presented both, methods and technologies, to master uncertainty in the design and production phase of mechanical engineering structures; such methods and technologies are motivated by the cross-phase treatment of uncertainty, see Sect. 3.1. This section is focused on the application of methods and technologies to semi-actively or actively manipulate processes and thus master uncertainty within the production and usage phase. In this context, we adhere to the definition of semi-active and active processes given in Sects. 3.2 and 3.4, according to which additional energy for actuators is introduced into a structure to either change or control mechanical properties, such as stiffness or damping (semi-active), or to directly influence a process, e.g. by force generating actuators to reduce vibrations or stabilise equilibrium conditions (active). The first half of this section covers the semi-active and active process manipulation of production processes by innovative tools and controllers to master uncertainty within the production phase. We present the active control of press stiffness, see Sect. 5.4.1, state control with semi-active roller and plain bearings, see Sect. 5.4.2, and a sensor-integrated compensation chuck control for tapping, see Sect. 5.4.3. In the second half of this section, uncertainty within the usage phase of mechanical load-bearing structures is mastered by semi-active and active technologies. We present technologies for vibration attenuation, such as a shock absorber with integrated hydraulic vibration absorber, see Sect. 5.4.4, an Active Air Spring, see Sect. 5.4.5, and piezo-elastic supports in beam truss structures, see Sect. 5.4.6. Furthermore, we introduce approaches for active buckling control, see Sect. 5.4.7, and semi-active load redistribution, see Sect. 5.4.8.
5.4.1 Control of Press Stiffness
The functionally quality, cf. Chap. 1, of metal-formed products highly depends on the ability of the production machine to guide the tool accurately along a path. Since presses are subject to high loads, the exact positioning of the tool is challenging. Due to the elastic response of press components, variable loads lead to deviations in the tool path and thus in the product properties. Therefore, the press stiffness is one of the most important design parameters [79].
The press stiffness is defined as the ratio between a static load applied on the press ram and its deflection [68]. A common approach to modify the press stiffness is to adjust its design [80]. Numerous frame and gear designs that enhance stiffness have been established [79]. However, these also limit the accessibility of the working area [129]. Their focus is mainly on the stiffness in stroke direction, the torsional stiffness [68]. However, presses provide a degree of freedom exactly in stroke direction by means of their main drives. Especially multi-point servo presses as the 3D Servo Press presented in Sect. 3.6.3 come with the advantage of providing multiple main drives. We present an alternative method of adjusting the stiffness by means of active process compensation. This method requires additional sensors and novel observer models to detect the ram deflection and makes use of the machine’s servo drives.
Furthermore, methods to identify the stiffness have to be extended. Although the complete press stiffness matrix in all six spatial directions of the ram has already been investigated in science for hydraulic [12] as well as for mechanical [61] presses, so far the stiffness has only been considered in one operating point. This is based on DIN 55189-1 [68], which prescribes that the stiffness must be determined in the bottom dead centre. Numerical press models, e.g. finite element models, are often used in press design to evaluate the press behaviour, but can only be used offline due to their high calculation effort. However, elastic models are required for the exact determination of the ram position and its control. The extent to which reduced-order models are applicable for this task still needs to be investigated. This is addressed in the following.
We evaluate the method at hand of the 10 kN Version of the 3D Servo Press, a servo press that is able to move the three eccentric drives independently. The transmission ratio of all three eccentric drives can additionally be adjusted via the common spindle drives [239]. This also affects the force transmission, which is why the gear position must be taken into account when modelling the press stiffness [126]. Due to the variable force transmission, the load on the elastic machine elements changes. An additional shift in the joint positions due to the deflection and a progressive bearing stiffness result in a nonlinear stiffness model as described in Sect. 4.3.2.
The compliance of the ram as represented by Chodnikiewicz [61] and Arentoft [11] can be described as a \(6\times 6\) press compliance matrix \(\Lambda \). The deflection of the ram position at its tool centre point (TCP) under a given load vector l can be described by
with the translatory and angular displacements of the TCP \(\Delta x_\mathrm {tcp}\), \(\Delta y_\mathrm {tcp}\), \(\Delta z_\mathrm {tcp}\) and \(\Delta \theta _x\), \(\Delta \theta _y\), \(\Delta \theta _z\), respectively. Since process forces occur mainly in the vertical z -direction, i.e. the stroke direction, the \(\lambda _{i3}\) compliance must be reduced. Off-centre loads result in additional tilting moments that affect the ram tilting by means of the compliance parameters \(\lambda _{i4}\) and \(\lambda _{i5}\).
The press compliance can be modelled by considering relevant machine components as trusses and beams [126]. Calculating \(\Lambda (q)\) at the current drive positions q allows to estimate the machine behaviour for control algorithms. The position vector q consists of the three eccentric drive angles \(\varphi _{\mathrm {ecc},i}\), \(i \in \{1, 2, 3\}\) and the upper and lower vertical spindle positions \(z_\mathrm {su}\), \(z_\mathrm {sl}\). Since the compliance model is highly non-linear, we evaluated the model for different q . The compliance of \(\lambda _{33}\) as a function of the upper and lower spindle positions \(z_\mathrm {su}, z_\mathrm {sl}\) is shown in Fig. 5.38 for constant eccentric angles \(\varphi _{\mathrm {ecc},i} = 270^\circ \). The operating area of the spindles is limited by the installation space and the singularities of the spindle kinematics. Figure 5.38 shows that the compliance strongly depends on the position of the spindles. The respective position of the spindles is visualised exemplarily by the corresponding kinematics. To investigate the dependence of press compliance \(\lambda _{33}\) on the eccentric position, three spindle positions 1, 2, 3 with significantly different compliance were chosen.
Simulated compliance map of the 3D Servo Press prototype depending on the spindle configuration \(z_\mathrm {su}, z_\mathrm {sl}\) at constant \(\varphi _{\mathrm {ecc},i}=270^\circ \) [126]
Figure 5.39 shows a comparison between simulated and experimentally determined compliance \(\lambda _{33}\) as a function of the eccentric angles \(\varphi _{\mathrm {ecc},i}\) for the spindle configurations 1, 2, 3. Apparently, the compliance also strongly depends on the eccentric position and therefore cannot be assumed to be constant. The deviation between simulation and experiment indicates uncertainty. Stiffness parameters are based on the nominal values of geometric parameters, such as cross-sections and lengths, as well as material parameters. These parameters are subject to manufacturing tolerances which are propagated into the model as data uncertainty. Furthermore, the model order reduction simplifies the model and hence increases model uncertainty. How this uncertainty can be evaluated and reduced is described in Sect. 4.3.2. Nevertheless, the reduced-order model is already able to represent the variability of the compliance and is valuable for the online control.
Comparison of simulated (lines) and experimentally (cross markers) determined compliance of \(\lambda _{33}\), depending on the eccentric positions \(\varphi _{\mathrm {ecc},i}\) [126]
In [126] we designed an experimental setup to identify compliance matrices of both, the passive and the active system, \(\Lambda _\mathrm {p}, \Lambda _\mathrm {a}\) respectively. The test setup allows a variable load vector l to be applied at the ram TCP and the ram displacement \(\Delta p\) to be determined at the operating point \(q_\mathrm {ref}\) (Fig. 5.38). In \(n=18\) measurements, we applied 30% of the nominal force with a pneumatic cylinder and measured the displacements and rotations of the ram TCP with dial gauges.
In comparison to the model-based estimated compliance matrix \(\hat{\Lambda }_\mathrm {p}\), the measured passive compliance
results. The bold highlighted entries correspond to the degrees of freedom of the control \(z_\mathrm {tcp}, \theta _x, \theta _y\).
The control of the machine requires, on the one hand, a kinematic model f (q) for the control law [161] and, on the other hand, a model of the ram \(f_\mathrm {ram}(D_y)\) in order to estimate the ram position by means of the integrated displacement sensors \(D_y\) [126]. By extending the rigid-body model of the press to the elastic model, the estimation accuracy of the ram position p can be enhanced. As a position feedback in the press is used, it is helpful to split the press compliance models at the measuring position into the gear and the ram
Thus, the control structure shown in Fig. 5.40 results. Using the extended ram observer
the measured deflection in the press gear \(\hat{D}_y\) is used to estimate the actual ram position \(\hat{p}\). All model assumptions and measured variables are indicated by \(\hat{(\cdot )}\), as they are subject to uncertainty. Section 6.1.7 investigates how data and measurement uncertainty affects this closed-loop control and how to design a robust control.
The active press system compensates deviations detected in \(D_y\), which are caused, among other things, by the gear compliance \(\Lambda _\mathrm {gear}\). In addition, the observer also takes into account the ram compliance \(\Lambda _\mathrm {ram}\), which cannot be measured in the process.
For the active system, we measured the press compliance matrix as
Since only the degrees of freedom \(z_\mathrm {tcp}\), \(\theta _x\), \(\theta _y\) are controllable, only the corresponding lines \(\lambda _{3,i}\), \(\lambda _{4,i}\), \(\lambda _{5,i}\) can be modified. While especially \(\lambda _{33}\), \(\lambda _{44}\), \(\lambda _{55}\) have been reduced significantly compared to Eq. (5.17), other entries remain almost unchanged. However, it is noteworthy that \(\lambda _{33}\) has a negative value, which means a displacement against the load direction. A negative stiffness is physically uncommon at first, but it is a characteristic of active systems, such as active suspensions (Sect. 3.6.2). In this case, the compliance model overestimates the actual compliance at this operating point and thus overcompensates it.
In order to increase the mechanical stiffness of presses, so far the press design has been adjusted. In contrast, an active process manipulation method has been presented to increase the stiffness by means of closed-loop control. This method requires control capabilities which multi-point presses already provide by using their main drives. Therefore, no additional force generating actuators are required. The precise measurement of the ram position is the main challenge. As direct tactile measurement is infeasible, a robust sensor positioning must be carried out at a distant position. This results in the need for observers that can determine the ram position from spatially distant measurements. For this purpose, we developed a reduced-order elastic model and included it in an observer. Comparing active and passive systems we have shown that the use of control loops and reduced compliance models allows an exact ram positioning and thus a significant reduction of the compliance.
5.4.2 State Control of Combined Roller and Plain Bearings
The development of industrial production plants is characterised by the demand for high productivity and optimal material utilisation. Especially in forming technology, which is characterised by high investment requirements for machines, the trend therefore goes towards flexible machine technologies with a wide range of applications and high adaptability to multiple production conditions, which makes it possible to master uncertainty occurring in the production process (see Sect. 1.2) and the resulting fluctuations in product quality.
Pioneers of such a machine technology are servo presses with an almost freely adjustable motion kinematics of the ram, thus rendering optimised motion and speed sequences of the tools possible. Due to the almost speed-independent nominal torque of servo motors, servo presses can be used to achieve high accelerations, as well as standstills under high loads [245]. This allows both, the application limits of presses to be significantly extended [214], and the cycle time to be reduced [130]. The 3D Servo Press presented in Sect. 3.6.3 is a prototype of this press technology, which is able to combine the flexibility of hydraulic presses and the economics of mechanical presses [202]. However, the increase in machine flexibility and the extension of the application limits also result in new, challenging load scenarios for the machine elements. Since these requirements can no longer be met by pure plain or roller bearings, motor acceleration in servo presses is usually limited and, therefore the potentials of servo technology in presses cannot be fully exploited [245].
An existing problem in industrial practice is the lack of knowledge of the current condition of bearings and machines. Without this knowledge, the optimum time for maintenance or servicing cannot be determined exactly, which is why fixed maintenance intervals are common in practise. This can lead to two different worst case scenarios: In the first case, maintenance is carried out at a time when it is not yet necessary, thus leading to rising costs. In the other extreme case, damage to a machine element occurs shortly after maintenance, whereby it is not immediately noticed and can therefore lead to consequential damage. Both cases can be avoided by continuous condition monitoring, which enables early damage detection. Sensor-based condition monitoring also provides the basis for preventing possible bearing or machine damage by implementing semi-active or active components. Thus, the operating limits of the machine can be extended and an extension of the service life may be achieved.
Conventional, pure roller or plain bearings are usually only suitable for a part of the application spectrum of servo presses. Roller bearings offer a lower starting torque, but have poorer damping properties, and are generally not economically feasible for high operating loads [131]. Plain bearings, on the other hand, are subject to play, which increases the cost of control [131]. Furthermore, at low speeds, mixed friction occurs in plain bearings due to local deficient lubrication, which causes increased wear, especially in the oscillating stroke due to the constant changes in direction of motion. In order to meet the increased requirements for the bearings of the 3D Servo Press, we designed a combined roller and plain bearing combining the advantages of different conventional bearing types. Monitoring of the bearings’ behaviour is used to determine not only the bearings’ condition but also to draw conclusions on the current machine condition. Based on these findings, it is possible to actively control relevant bearing characteristics.
The approach of combining both types of bearings in order to unite their specific advantages has been principally known for a long time [167, 207, 210, 222]. In the approach we present here, a plain bearing is complemented by two roller bearings arranged on both sides, which can be designed as cylindrical roller bearings or angular contact ball bearings. These hold the bearing shaft centrally in the plain bearing shell and reduce wear in the plain bearing during start-up [131]. This allows high loads to be transmitted and at the same time prevents backlash during start-up. Therefore, combined roller bearings offer great potential to meet the increasing requirements in the field of bearing supports for servo presses [245].
The structure of the combined bearing is shown in Fig. 5.41. The bore diameter of the roller bearings is smaller than the one of the plain bearing. This results in a shaft shoulder on which the inner rings of the roller bearings abut axially. Radial play in the cylindrical roller bearing is eliminated by an interference fit between its inner ring and the shaft shoulder. If angular contact ball bearings are used, a variable preload of the roller bearings can be achieved by means of additional bearing caps. The plain bearing, which is supplied with lubricant via a bore in the bearing shell, can be preloaded by increasing the supply pressure [245].
The combination of the three bearings creates a statically over-determined system, which makes a robust design necessary for industrial use. After the basic feasibility of combined roller and plain bearing arrangements was demonstrated in [240], we developed a design methodology that takes into account the distribution of the operating force \(F_{\text {op}}\) between the roller bearing force \(F_{\text {rb}}\) and the plain bearing force \(F_{\text {pb}}\) as a function of the operating conditions.
Distribution of force flow in combined roller and plain bearing, according to Sinz [247]
Simulation model and design methodology
For the design and dimensioning of the presented bearing combination and for the estimate of operational safety, the force-path curve of the shaft is used to describe the dynamical behaviour of the bearing, resulting in the shaft displacement e (t). To determine e (t), we developed a simulation model according to [5, 270], which is grounded on the theory of hydrodynamic lubrication. The validity of this model, based on Reynolds [228], which is discussed in Sect. 1.3, is given for the investigated speed range of up to 400 \(\mathrm {rpm}\) because of the small relative bearing clearance \(\psi \) of the developed bearing configuration in combination with high-viscosity oils. The shaft displacement e can be calculated by solving a differential equation based on the equilibrium of forces at the shaft according to Holland [158], which is extended by the effect of the rolling bearing forces [247] and allows to determine the load distribution on the various bearing components [130]. The force that a roller bearing exerts on the shaft is determined by means of the roller bearing stiffness \(c_{\text {rb}}\) via \(F_{\text {rb}} = c_{\text {rb}} e\). The overall stiffness \(c_{\text {cb}}\) of the combined bearing serves as an indicator to assess the functional capability of the bearing combination.
The resulting simulation model enables not only the calculation of the shaft displacement path e (t) but also the determination of other relevant parameters, such as dynamic viscosity \(\mu \), relative bearing clearance \(\psi \), eccentricity \(\varepsilon \), lubricant temperature \(\vartheta \) and volume flow \(Q_{\text {in}}\). The results are validated using an example plain bearing from [75] and experimentally determined force- and speed-dependent displacement of the bearing shaft in the plain bearing shell of the combined bearing. The validated model forms the basis of the design methodology, which is presented in the following.
With the help of the developed simulation, a sensitivity analysis was performed in [247] to identify the relevant influencing parameters in the design of the combined bearing. The load ratio, which describes the distribution of the operating force between rolling and plain bearings, is of particular interest. Roller bearings are suitable for operating at lower load and speed, since they have smaller load capacities than plain bearings of the same dimensions. For this reason, a load ratio \({F_{\text {pb}}}/{F_{\text {rb}}} > 1\) is favourable at higher speeds and loads in the interest of operational safety. As a result of the performed sensitivity analysis, the stiffness of the roller bearings \(c_\text {rb}\), the relative bearing clearance \(\psi \) and the lubricant viscosity \(\eta \) can be identified as the main influencing variables. The total stiffness \(c_\text {cb}\) of the bearings increases linearly with increasing speed. Based on these findings, a design methodology for combined bearings can be developed. This is divided into the three steps pre-dimensioning, calculation and verification, which are carried out in an iterative process [247].
Sensor-based condition monitoring
In order to quantify the industrial benefit of the presented bearing combination, we developed a test rig in [247], which enables the condition monitoring of a sensor-equipped bearing during operation. This allows continuous testing and evaluation with regard to defined technological and economic criteria and comparison with conventional bearings. The application and load limits of the combined bearings and their emergency running characteristics are determined.
Figure 5.42 shows the developed sensor-monitored bearing. To detect the shaft displacement path e (t) in the plain bearing, the test bearing is equipped with two eddy current sensors arranged at 90° to each other, which serve to detect the position of the shaft. Three temperature sensors measure the temperature on the outside of the roller bearing outer rings and the outside temperature of the plain bearing shell. In order not to influence the lubricant film in the plain bearing, the lubricant film temperature is not measured directly in the plain bearing, but only the temperature of the lubricant escaping from the bearing in the oil tank of the test rig. The operating force, which is applied by a hydraulic actuator via the housing on the opposite of the pressure inlet, is recorded by means of a piezoelectric force transducer. The oil supply pressure is recorded via a pressure gauge attached to the inlet. The accelerations that occur during operation are measured by a triaxial acceleration sensor mounted on the outside of the bearing bracket.
The radial displacement of the shaft in the plain bearing is assumed to be equal to the displacement in the roller bearings, neglecting any elastic deformation of the bearing housing or shaft in contact with the rolling elements. The stiffness of the rolling elements \(c_\text {rb}\) is assumed to be constant in the circumferential direction. The force \(F_\text {pb}\), which is discharged via the plain bearing, results from the difference between the measured operating force \(F_\text {op}\) and the roller bearing forces. With knowledge of the individual bearing forces, the operating behaviour and service life of the bearings can be estimated [247].
Sensor-equipped combined roller and plain bearing, according to Sinz [247]
For this purpose, tests are carried out in full rotation and in pivoting operation mode to investigate the influence of the speed and radial displacement of the shaft on the overall stiffness of the bearing combination developed. The roller bearings are designed both as cylindrical roller bearings and angular contact ball bearings. During the test runs with various operating forces, it has been shown that in full rotation an increasing rotational speed leads to a continuously increasing load ratio. Above a certain speed, the plain bearing takes over the major part of the load and presses the shaft into the centre of the plain bearings, resulting in a higher resistance to load shocks at high speeds [247]. For the movement sequence in pivoting mode, a characteristic forward and backward stroke movement is used. The assumption of a constant roller bearing stiffness leads to a constant load ratio, so that the maxima of the forces of both bearing types are superimposed [247].
Semi-active manipulation of the bearing behaviour
On the basis of the knowledge gained on the behaviour and design of combined roller and plain bearings, the following section considers possibilities for semi-active process manipulation (cf. Secti. 3.4) during operation to react specifically to disturbing influences during operation. Two approaches are possible for this purpose: Firstly, a control of the feed pressure \(p_\text {in}\) of the lubricant can be used to influence the bearing behaviour; Secondly, additional actuators can be integrated and used for an adaptive adjustment of the roller bearing preload.
The lubricating oil supply pressure \(p_\text {in}\) can be used to preload the combined bearing via the plain bearing. The resulting preload can be interpreted as an increase in the effective operating force \(F_\text {op}\), which leads to an increased radial displacement of the shaft. However, the effect on the overall stiffness of the combined bearing is small. It should be mentioned that in the calculation model described above, the outer rings of the roller bearings and the plain bearing shell are assumed to be concentric. Due to occurring inaccuracy during manufacturing and assemblage of the combined bearing, the centres of roller bearings and plain bearing do not match exactly in the conducted experimental investigations leading to an initial displacement of the shaft in the plain bearing.
In Fig. 5.43 the stiffness \(c_\text {cb}\) of the combined bearing is shown as a function of the rotational speed in full rotation operation for both angular contact ball and cylindrical roller bearings. The non-linear stiffness behaviour of the roller bearings leads to a non-linearity in the stiffness curves, especially at low speeds. If the speed is increased, the pressure build-up in the lubricant in the plain bearing gap centres the shaft in the plain bearing shell, which leads to an increase in the bearing stiffness. As the shaft displacement e in the bearing converges towards a very small value, the stiffness, determined by \(c_\text {cb}={F_\text {op}}/{e}\), reacts extremely sensitive to changes of e , resulting in an oscillation in the stiffness curves at high speeds. However, due to the better damping properties of the plain bearing, when increasing \(p_\text {in}\) from 1 bar to 10 bar, the preload via the lubricant pressure causes both a smoothing of the stiffness curves and a lower standard deviation, which increases operational reliability [246].
Stiffness of combined bearings determined by carrying out experiments in full rotation mode, according to Sinz [246]: a roller bearings design as angular contact ball bearings, b roller bearings design as cylindrical roller bearings
The preload of the roller bearings has a decisive influence on the behaviour of the combined bearing in different load and operating conditions. As already described, the influence of the plain bearing increases continuously with increasing speed. In the case of a radial external load perpendicular to the shaft axis, this curve flattens out when a preload is applied to one or both roller bearings, so that the load ratio with increasing preload is below that of the non-preloaded condition. Conversely, this means that, depending on the external load, the load ratio \({F_{\text {pb}}}/{F_{\text {rb}}}\) can be increased in a targeted manner by reducing the roller bearing preload, i.e. the main load can be shifted to the plain bearing.
The overall stiffness of the bearing, i.e. the resistance against a displacement of the shaft centre due to an applied operating force, grows with increasing speed, especially in full rotation mode, due to the higher load carrying capacity of the plain bearings. The stiffness can be additionally increased by preloading the roller bearings. To make use of this knowledge, it is conceivable to equip the bearing with active components that can change the preload of the roller bearings during operation. The described effects could be validated in special tests. To change the preload, paraffin wax actuators were used. They were mounted between the bearing pedestal and the bearing covers. Through the supply of heat, a force is exerted on the outer rings of the angular contact ball bearings and thus reduces the preload [132].
Conclusion
The combination of roller and plain bearings offers high potentials for the application in servo presses. Designed properly, the roller bearings bear the largest share of the load at low circumferential speeds and operating forces, while the plain bearings carry a larger ratio of the force with increasing speeds and loads. This load transfer has already been proven experimentally [131, 245].
In-depth investigations of the operational behaviour of the combined bearing and the evaluation of its industrial applicability have been carried out on a special test rig. Due to the resulting reduction of the roller bearing load in the combined bearing compared to pure roller bearings, the nominal lifetime of the roller bearings increases significantly despite a reduction of the required inner diameter. The use of combined roller and plain bearings is currently limited to prototypes, since the maturity for widespread industrial use is not yet given [131]. However, the potential resulting from the combination have already been proven [247].
Monitoring the operation state of bearings offers new potentials for the application in modern production machines. Examining a newly developed combined roller and plain bearing, we showed the possibility to use the bearings as both a sensor and actor in the drive train of the 3D Servo Press. Sensor-based condition monitoring of bearings allows conclusions on the current operation conditions of the press system, while the implementation of active components in the bearing makes it possible to influence the system’s behaviour depending on the particular load scenario.
Condition monitoring makes it possible to detect detuned load conditions in the process, such as asymmetrical process forces, which can lead to ram tilting, as was shown in [132]. With the knowledge about their influence on the bearing stiffness, damping as well as the bearing clearance and load ratio of combined bearings, the controllability of the machine as well as the operating limits of the bearing can be extended by active bearing components, which leads to a reduction of tool wear, whereby a reduction of process uncertainty as well as an increase in component quality can be expected as well.
5.4.3 Development of a Sensor-Integrated Compensation Chuck for Semi-active Control of the Tapping Process
The tapping process is a widely used machining process for internal thread making and usually takes place at the end of the value chain, so that non-compliance of required thread quality, or even the destruction of the thread due to uncertainty, is therefore associated with high economic costs [273]. Possible uncertainty during thread cutting are axis offset, concentricity error, synchronisation error, sloped pre-drill bore, faulty pre-drill bore diameter and tool wear [2, 185]. Here, we are facing two types of uncertainty both classified as incertitude. As introduced in Sect. 2.1 there is data uncertainty hidden in state variables, e.g. feed rate or motor spindle speed. Structural uncertainty as described in Sect. 2.3 results from the upstream process of machining the pre-drilling, since the tapping process is a combined process. In addition to the methods and technologies to master uncertainty during the design and production phase presented in Chap. 5 an alternative strategy is the semi-active process manipulation described in Sect. 5.4. for mastering uncertainty during the production phase, Sect. 1.2. One of the core components of such a semi-active system for process manipulation are appropriate sensors to detect uncertainty. For the detecting of uncertainty within the tapping process, various approaches are being developed. In [185] and [266] the motor spindle currents were used as a data source to detect uncertainty while tapping by a two-stage pair-wise feature selection and classification algorithm based on wavelet transformations [185] and statistical process control [266]. The detection of progressive wear of an M12 tap by examining the frequency spectrum of vibration measurements of the workpiece and the motor spindle during tapping is shown in [200]. The authors in [60] and [188] used dynamometers as data source for diagnosis of the tapping process by using an information and multiple probability voting scheme [60] and artificial neural networks [188].
The company Bilz Werkzeugfabrik has developed a sensor-integrated tapping chuck which detects the occurrence of length compensation [39], thus resulting in a binary information only, which is not appropriate for semi-active control. In this subsection, we introduce the concept for a semi-active control of the tapping process on the basis of the length compensation chuck (LCC) Softsynchro 3 from the tool manufacturer Emuge Franken [88] shown in Fig. 5.44a. This is a purely mechanical system for handling synchronisation errors only. The Softsynchro 3 consists of a hollow shank taper with an attached hollow cylindrical part in which a piston clamping the tapping tool can move maximum 1.5 mm in both z -axis directions. Two pairs of axial ball bearings offset by \(180^{\circ }{}\) are guiding the piston and transmitting the process torque from the hollow shaft taper to the tapping tool. The axial system stiffness in z -axis direction is determined by two polymer spring elements offset by \(180^{\circ }\). Further, we present three sensor concepts to measure the close-to-tool vibrations, the process torque and the axial length compensation for uncertainty detection during the tapping process, as well as the integration of these sensors into the LCC. Compared to [185, 266], the process torque is measured directly on the LCC and not indirectly via the motor spindle currents. In comparison to [200], the vibration sensor introduced in this work measures the vibrations close to the tapping tool. The concept we present here to measure the axial length compensation is unique and allows to quantify the synchronisation error. The use of a dynamometer as in the approaches [60, 188] is deliberately avoided, since dynamometers have a number of disadvantages, such as high costs and a smaller workspace. The three sensor concepts measure the corresponding measurement quantities close to the process and therefore provide an appropriate data source for semi-active control to master the uncertainty of the tapping process.
a Sectional view of Softsynchro 3 [88] and b modelling of stiffness
Concept of semi-active control of the tapping process
Within a semi-active control approach, the production process of tapping is not directly influenced by actuators but by the machine tool. In Fig. 5.45 we present a schematic diagram of the setup and the functional principle for semi-active control during the tapping process. To detect uncertainty while tapping, the LCC Softsynchro 3 is equipped with the three sensor concepts mentioned above. For signal pre-processing, data acquisition (A/D converter) and data processing we developed a rotating telemetry unit. The data acquisition of the sensor data while tapping as well as the communication with the machine tool for semi-active control is made via the wireless radio standard WiFi. For mastering uncertainty while tapping by semi-active control, it is necessary to define appropriate control variables within the machining process containing process parameters, e.g. motor spindle speed and feed rate. Beside definition of such control variables by process parameters, it is necessary to influence them within the numerical control (NC) of the machine tool. As mentioned in Fig. 5.45, the NC of the selected machine tool contains a OPC-UA (Open Platform Communications—Unified Architecture) server, which makes a communication of the machine tool with other production machines possible. By linking this ability with synchronised actions [244] within the NC program makes process manipulation during machining processes possible, since synchronised actions can influence process parameters synchronously to the NC program execution.
Sensor integration
A sensor concept has been developed to measure lateral vibrations close to the tapping tool shown in Fig. 5.46a. The vibration sensor is screwed onto a sleeve which is glued onto the tapping tool, allowing a non-destructive use of the vibration sensor in case of tool breakage. Two accelerometers based on Microelectromechanical system (MEMS) measure the acceleration in x - and y -axis direction. The process torque is determined with a strain gauge full bridge, which for design reasons can only be applied to the outer surface of the cylindrical part (Fig. 5.44a) of the LCC. By means of a Finite Element Method calculation we localised the position of the maximum mechanical shear stress illustrated in Fig. 5.46b, and thus the appropriate application positions of the strain gauges. The measured strain \(\varepsilon _{45}\ \)is converted into the process torque \(M_{T}\) by assuming a linear-elastic behaviour by Eq. (5.22)
where \(d_{a}\) is the outer and \(d_{i}\) the inner diameter of the cylindrical part (Fig. 5.44a), the modulus of elasticity is represented by E and the Poisson\('\)s ratio by \(\nu \).
To measure the axial length compensation a sensor based on strain gauges has been developed shown in Fig. 5.46c. This sensor consists of an outer ring and an inner ring, which are connected by two webs. Due to this design, the sensor behaves like a spring element, whereby the spring stiffness is largely determined by the lower side of the two webs forming a full bridge configuration allowing a sensitive measuring of the strain due to displacement of the inner ring in the z -axis direction. By integrating the axial length compensation sensor into the LCC (Fig. 5.44a) and connecting the outer ring with the bottom side of the cylindrical part (Fig. 5.44a) and the inner ring with the bottom side of the piston (Fig. 5.44a), the axial length compensation can be quantified indirectly. The original axial system stiffness mainly determined by the two polymer spring rings \(c_{P}\) in Fig. 5.44b is increased by the sensor stiffness \(c_{S}\) in Fig. 5.44b resulting in a new axial system stiffness which is given by
Therefore, the geometry of the sensor was designed in a way that the sensor stiffness \(c_{S}\) is less than ten percent of original axial system stiffness \(c_{S}<0.2 c_{P}\).
Evaluation of the close-to-tool vibration sensor
For evaluation of the vibration sensor, we carried out thread cutting tests with thread dimension M8\(\times \)1.25 mm on a GROB G350 machine tool. The thread has the dimension M8\(\times \)1.25 mm and the material type 42CrMo4. The spindle speed was 9.7 Hz and the cutting speed 148.8 m/min. The vibration signals of both MEMS accelerometers while cutting a single thread are shown in Fig. 5.47. It can be seen that each signal contains a constant acceleration component, on which a low-frequency harmonic oscillation of 9.7 Hz is superimposed. The constant acceleration corresponds to the centripetal acceleration, which is included in the vibration signals due to the measuring direction of the MEMS accelerometers in x - and y -axis, thus radial direction. In this case, the low-frequency harmonic oscillation corresponds to the spindle speed signal, because the machine tool used to perform the experiments is a horizontally mounted motor spindle. In this arrangement, the acceleration due to gravity is no longer perpendicular to the plane of rotation (x -y plane), so that the gravity is also measured by the MEMS accelerometers depending on the angle of rotation of the motor spindle. Since the two measuring directions of the MEMS accelerometers are orthogonal to each other, the harmonic components of both MEMS accelerometers caused by gravity are phase-shifted by \(90^{\circ }{}\) to each other. Furthermore, the reversal point of the tapping cycle can be seen in both vibration signals and is also marked in Fig. 5.47.
Conclusion and outlook
The evaluation of the developed vibration sensor provides plausible results, so that the measurement data of the vibration sensor can be used to detect uncertainty during tapping process. Next, the sensors for measuring the process torque as well as the axial length compensation must also be validated for plausibility and calibrated within thread cutting tests. Within the scope of further thread cutting tests, uncertainty during the tapping process, e.g. exceeding threshold values of corresponding process quantities measured by the integrated sensors have to be detected. Subsequently, appropriate control variables are to be derived for the semi-active control of the tapping process and the control algorithm is to be implemented in the micro-controller of the telemetry unit. The presented technology enables the mastering of uncertainty of the tapping process within the production phase of mechanical components used in structural dynamic systems such as the MAFDS presented in Sect. 3.6.1.
5.4.4 Shock Absorber with Integrated Hydraulic Vibration Absorber to Improve Driving Dynamics
A car driving on an uneven road is subject to vibrations that are handled by suspension struts similar to the MAFDS, see Sect. 3.6.1. Their main task is to reduce vibrations. This can be done by (i) passive elements like spring, damper and dynamic vibration absorber, (ii) semi-active systems like adjustable damper, and (iii) active systems, such as the Active Air Spring, see Sect. 3.6.2. In the following, we focus on the usage of a passive dynamic vibration absorber, see Sect. 1.3, and discuss a semi-active option.
The essential requirements for the suspension strut of modern vehicles are to ensure high driving safety and high driving comfort at the same time. The driving safety is affected by data uncertainty of the wheel mass and tire stiffness, which can be classified as incertitude, Sect. 2.1. A higher wheel mass, for example a tire covered with mud, leads to a loss of driving safety. The driver’s control of the vehicle can only be ensured, if there is wheel-ground contact. The suspension strut links the car’s body to the wheel. The vertical suspension strut force, therefore, has to be sufficient to ensure the best transmission behaviour of horizontal manoeuvres. According to Mitschke [198], the driving dynamics are measured by the dynamic wheel load fluctuation. If the fluctuation is higher than the static load, the tire loses contact to the ground. Driving comfort is measured by accelerations on the occupants. The suspension strut as a link between body and wheel affects both, driving dynamics and driving safety.
However, when tuning the system, these two objectives are in conflict. As an example, we consider a quarter-car simulation of a reference car with adjustable damper and a constant body spring stiffness using an excitation according to a federal highway at 100 km/h. The quarter car has the parameters of a middle class car also used in Sect. 3.6.2. As a reference for following investigations, the grey line in the conflict diagram in Fig. 5.48 depicts the corresponding Pareto-front for varying damping coefficient, where the standard deviations are extracted from a time signal of wheel load and body acceleration. By increasing the damping coefficient, the body accelerations are also increased, whereas the wheel-load fluctuation decreases.
Fluid dynamic vibration absorber
To improve upon this boundary, a structural expansion, a dynamic vibration absorber with a hydraulic translated fluid mass, the Fluid Dynamic Vibration Absorber (FDVA) has been developed [52]. Its advantages can be seen in Fig. 5.48. The black solid line shows the Pareto-front of the FDVA with damper. The dashed black line refers to the FDVA without damper. It can be seen that this more simple configuration is only useful when the comfort is neglectable, e.g. for sport cars. In combination with a damper the FDVA is able to reduce wheel load fluctuations with the same comfort compared to the reference. In the following, we present the design and operation principle of the FDVA, as well as the validation of the used models and the discussion of simulations leading to Fig. 5.48.
A classic dynamic vibration absorber consists of a capacity and a heavy mass, which contradicts the goal of lightweight construction. In comparison to a classic dynamic vibration absorber, the Fluid Dynamic Vibration Absorber (FDVA) [52], reduces the dynamic mass by means of hydraulic transmission. By using the continuity equation, Bernoulli’s equation and principle of linear momentum, the possible reduction of mass can be derived from the axiomatic model of the FDVA
with the piston mass \(m_\mathrm {P}\), the ratio \(\alpha =A/a\) between the surface of the piston A and the ducts a , the relation of duct length to cylinder length \(\beta \), the duct fluid mass \(m_\mathrm {F}\) the absorber motion z , the excitation motion \(z_0\), the vibration absorber spring stiffness k , and the pressure loss \(p_\mathrm {L}\).
Figure 5.49 shows the principle of lightweight design at the hydraulic transmission. The duct fluid mass \(m_\mathrm {F}\) is transmitted by \(\alpha ^2\), which we see at the deviation between inertia and mass, if the piston mass \(m_\mathrm {P}\) moves towards zero. The ratio \(\alpha =A/a\) is determined by the geometry. The duct fluid mass \(m_\mathrm {F}\) is negligible in terms of weight, but translated it has the largest contribution to inertia.
We built a prototype of the FDVA to validate the axiomatic model, Eq. (5.24), see Fig. 5.50. It consists of a double-acting hydraulic cylinder where the chambers are connected via twelve ducts on the outside. The ducts can be closed by mechanical valves in order to change the ratio \(\alpha \). A spring connects the piston rod of the hydraulic cylinder with the wheel axle. The body spring is connected parallel to the FDVA and links the wheel axle to the housing of the FDVA, which in turn is attached to the chassis.
Sectional view of the FDVA functional demonstrator [52]
FDVA model validation
The characteristics of a dynamic vibration absorber are used to validate the axiomatic model. Therefore, we evaluate the transmissibility V and the phase shift \(\psi \) of foot excitation \(z_\mathrm {S}\) to piston motion \(z_\mathrm {FDVA}\) at a frequency band with frequencies from 0.1 to 25 Hz, since the quarter car, the basis of our investigations, is usually applied in this range [198]. We mounted the functional demonstrator into the Hardware-in-the-Loop test rig, see Sect. 4.3.4 and open-loop-tests were conducted. The model, Eq. (5.24), was evaluated in [53]. Figure 5.51 shows the results for the exemplary configuration of two opened ducts. Both, experiment and model, show a phase shift \(\psi =\pi /2\) at 8 Hz. The spring stiffness is 57.400 N/m and the fluid mass \(m_\mathrm {F}\) is 1.6 kg. The eigenfrequency \(\omega =2\pi \sqrt{k/m_\mathrm {A}}\) at 8 Hz provides evidence that the inertia is translated.
Improvement by use of the FDVA
We use the validated model to estimate the improved driving dynamics. The quarter car, a simple dual mass oscillator, is equipped with the model of the FDVA. The three equations of motion for body (index B), wheel (index W) and FDVA according to Fig. 5.50 are then
with mass m, motion z, damping coefficient b, stiffness k, tire stiffness \(k_\mathrm {T}\) and road excitation \(z_0\). The body stiffness \(k_{\mathrm {B}}\) contains the secondary stiffness of the suspension strut for a realistic simulation. These equations can be used to calculate the driving dynamics and comfort. For the FDVA with duct fluid mass of \(m_F=72\) g translated by a translation factor of \(\alpha =59.45\) the results are given in Fig. 5.48.
For the FDVA with damper in the design point an increase to the reference car of 5% in driving dynamic at a constant driving comfort is possible. The peak of wheel load fluctuation in the frequency response reduces by 15%.
Now, we discuss the possibility to master uncertainty using the passive FDVA. The passive FDVA is designed to absorb the eigenfrequency of the unsprung mass, which is formed by the mass of break, wheel carrier, upper and lower control arm and wheel. The wheel mass depends on the brand and the wear condition and therefore is uncertain.
The tire is another uncertain factor. While driving, the tire is able to heat up and the stiffness increases. Thus, the eigenfrequency of the wheel increases, too. Investigations show that in realistic changes of wheel mass, tire stiffness and road conditions the improvement through the FDVA in comparison to a standard shock absorber is independent of a change of eigenfrequency.
Semi-active FDVA
Compared to a passive FDVA, a semi-active FDVA is able to adopt its eigenfrequency to a change of the system’s eigenfrequency. A system’s eigenfrequency can variate by a change of inductance or compliance. In the case of a high system eigenfrequency change, e.g. for a sprung foundation, where the change of mass depends on the assembly of the test bench and thus can be in the range of several hertz, the semi-active FDVA is useful. For the adaptation to the system eigenfrequency the transmission factor \(\alpha \) or the length of the duct and the damping of the FDVA has to be changed.
The wheel of a car has only a small change of unsprung mass and tire stiffness, thus showing a neglectable system eigenfrequency change. The extra effort to design a semi-active FDVA for a car on the one hand is not necessary, and on the other hand is too expensive.
Conclusion
A standard shock absorber equipped with the passive FDVA is able to maintain the driving dynamics. This is equivalent to the driving safety in a larger area of application, when the road, tire or loading conditions of the vehicle are unknown. If we know the boundary of the parameter changes and can classify them with tolerances, passive systems can be sufficient. Semi-active and active systems require a higher effort, but they are able to adopt a wider range of parameter changes.
5.4.5 Active Air Spring for Vibration Reduction in Vehicle Chassis
In autonomously driven cars, passengers are able to spend time on activities other than driving [151, 248]. The highest possible level of driving comfort is increasingly important, as it is the case with today’s luxury class vehicles. The suspension system of the vehicle has the greatest influence on driving comfort [147]. When designing the spring and damper system, driving comfort and driving safety are two conflicting objectives [198]. It is not possible to optimise both at the same time, however, a compromise between the two is feasible.
The simplest model for the vertical dynamics of a car is the quarter car introduced in Sect. 3.6.2 [198]. With this two-mass oscillator, driving comfort can be evaluated by the standard deviation of body acceleration \(\sigma _{\ddot{z}_\mathrm {b}}\). The standard deviation of the force between wheel and road \(\sigma _{F_\mathrm {w}}\) describes the driving safety. As shown in Sect. 3.6.2 there are boundary lines, so-called Pareto lines, for passive suspensions consisting of springs and dampers which cannot be improved upon by any passive system. To further increase the driving comfort, active systems must be applied. The active system increases the function “driving comfort” of the vehicle. This gain in function can be used to master uncertainty that occurs during the usage phase of the entire system. The active suspension is able to compensate varying parameters (data uncertainty Sect. 2.1), e.g. a changed wheel mass. Since the distribution of the variation is not known, this is an incertitude. The active module is also able to master uncertainty in excitation as we show later in this section. Since the excitation is unknown in the design phase, this is ignorance. We have developed an Active Air Spring (cf. Sect. 3.6.2) to demonstrate the capabilities of an active suspension system [20, 147]. This subsection gives a short review on experimental results of the Active Air Spring which actively increases driving comfort compared to the passive system.
All investigations are carried out on a hardware-in-the-loop (HiL) test rig (cf. Sect. 4.3.4). Figure 5.52 shows the layout of the test rig, which consists of a uniaxial test rig that deflects the air spring and measures its reaction force. The dynamics of the quarter car and the controller of the active system are simulated in a real-time simulation (for parameters see Sect. 3.6.2). Hardware and simulation are connected via the deflection \(\Delta z=z_\mathrm {b}-z_\mathrm {w}\) and the force measurement signal F .
In principle, the quarter car can be excited by any base excitation \(z_\mathrm {r}\). In the following, the rides over (i) a single obstacle and (ii) on a road are examined. The ride over a single obstacle (i) demonstrates the active manipulation of the quarter car. The quarter car rides at a speed of \(v=10\,\mathrm {km/h}\) over an obstacle created as a cosine shaped bump with a height of \(h=5\,\mathrm {cm}\) and a total width of \(l=100\,\mathrm {cm}\). Maximum driving comfort is reached, if the body is at rest \((\ddot{z}_\mathrm {b}=0)\). It is to be taken into account that the controller has been designed for the stochastic excitations of a road and is not optimised for the crossing of a single obstacle. The excitation therefore is uncertain. This data uncertainty occurs in the use phase of the Active Air Spring. Figure 5.53 shows the result of the HiL test for a passive and an active system. The time sequences of the excitation \(z_\mathrm {r}\), the body movement \(z_\mathrm {b}\) and acceleration \(\ddot{z}_\mathrm {b}\), the wheel force fluctuation \(\Delta F_\mathrm {w}\), the force between wheel and road and the deflection \(\Delta z\) are shown. The results for the passive system were also determined with the HiL test rig, by deactivating the actuator.
The active suspension system comes much closer to the target of keeping the body at rest than the passive system, since the body movements \(z_\mathrm {b}\) are smaller. The lower body acceleration \(\ddot{z}_\mathrm {b}\) results in increasing driving comfort and the smaller wheel force fluctuation \(\Delta F_\mathrm {w}\) increases driving safety. It is possible to reduce the body accelerations by 53%. The active system requires more suspension stroke than the passive system, since the deflection \(\Delta z\) increases. The deflection of the Active Air Spring is almost equal to the excitation, which is obvious, since the body is almost at rest. Hence, increasing driving comfort is only possible with larger suspension stroke. Furthermore, these results demonstrate that the designed controller is robust against ignorance in the excitation of the system.
The ride on a road (ii) is examined by excitation with a stochastically generated signal. For this purpose, white noise n is filtered so that the contained spectrum corresponds to riding on a highway with 100 km/h [147]. Figure 5.54 shows the frequency response of the performance indicators driving safety \(F_\mathrm {w}\) and driving comfort \(\ddot{z}_\mathrm {b}\) during such excitation. Frequencies above 25 Hz are not considered, since they are negligible for chassis applications [198]. As before, the response of the passive chassis is used as a reference.
It can be seen that the active system causes a significant vibration reduction in terms of driving safety and driving comfort in the range up to 5 Hz. In the range above 5 Hz no significant improvements are achieved. However, no deterioration can be seen either. The reason is the speed of the actuator which has a transfer function that corresponds approximately to a 1st order low pass filter with a cut-off frequency of 5 Hz [183]. At frequencies above 5 Hz, the influence of the actuator is therefore limited. However, it should be noted that the possible comfort margin above 5 Hz is also small.
The conflict diagram, cf. Fig. 5.55, shows the performance indicators, standard deviation of body acceleration \(\sigma _{\ddot{z}_\mathrm {b}}\) and wheel load \(\sigma _{F_\mathrm {w}}/F_\mathrm {w,0}\) in relation to the static wheel load can be shown in a comparative manner. Figure 5.55 shows the Pareto line for the passive and active system and the results for the passive and active chassis. The Pareto lines are the results of the H2 optimisation as shown in Sect. 3.6.2.
The active system will increase comfort by 28% with loosing 4.7% of driving safety. The active system comes much closer to the active Pareto front. We have to consider that the results for both, the passive and the active system, are influenced by the HiL test rig (see Sect. 4.3.4). This degrades the test results in comparison to the limit lines which can be determined by simulating the influence of the HiL test rig.
In summary, the active system is suitable for increasing driving comfort by up to 28% while nearly maintaining the level of driving safety. The active system increases the function of the suspension system, which is not possible with a passive or semi-active system. Even when driving over a single obstacle, the actuator system isolates the chassis from the excitation. The active system is therefore able to compensate the uncertainty in excitation, which is limited in the case of a passive chassis.
5.4.6 Vibration Attenuation in Beam Truss Structures Via (Semi-)active Piezoelectric Shunt-Damping
Piezoelectric shunt-damping as a (semi-)active process manipulation, see Sects. 3.2 and 3.4, is an alternative to tuned mass dampers or mechanical vibration absorbers and has been extensively researched by the scientific community in the past decades [104, 118, 138, 199]. In piezoelectric shunt-damping, a piezoelectric transducer converts mechanical energy due to a system’s vibration into electrical energy that is dissipated in an electrical resistance shunted to the transducer. There are various possible shunts, which can be used for piezoelectric shunt-damping to attenuate vibrations in a narrow frequency band [199]. Therefore, they are to be tuned precisely to a system’s resonance frequency to achieve an optimal vibration attenuation [118, 199, 206]. If the shunt comprises an electrical resistance (R) and inductance (L), it is called an RL-shunt. It functions and is tuned analogously to a mechanical vibration absorber [206], but requires less space and additional weight. Adding a negative capacitance (C) to the RL-shunt results in an RLC-shunt [206]. A mathematical model of the system with shunted piezoelectric transducers, that adequately predicts the system’s outputs is required to tune the shunt parameters within a model-based approach. However, if data uncertainty occurs, see Sect. 2.1, e.g. due to a variation of model parameters or boundary conditions, the model output varies, which leads to detuned shunt parameters as well as to a decrease in the achievable vibration attenuation [118, 184]. In this section, we therefore discuss the effects of aleatoric and epistemic data uncertainty from different sources on the vibration attenuation of a single beam and a beam truss structure in the usage phase via piezoelectric shunt-damping, see Sect. 1.2.
Uncertainty in vibration attenuation in a single beam test setup
In [118], Götz conducted an extensive numerical and experimental study on the attenuation of lateral vibrations of a single beam at the first resonance frequency via piezoelectric shunt-damping. Figure 5.56a shows the corresponding single beam test setup with the slender aluminum beam 1 that is of the same design as the beams comprising the MAFDS described in Sect. 3.6.1. It is connected to a slide bearing 2 and a fixed bearing 3 via the novel piezo-elastic supports A and B. A static axial load \(F_\mathrm {ax}\) can be applied to the beam using the spindle type lifting gear 4, which is measured with the force sensor 5. Support A is used to excite the beam in the y - and z -direction, while support B is shunted to an RL- or RLC-shunt to attenuate the lateral vibrations, which are measured by two accelerometers 6. Figure 5.56b shows the sectional view of the piezo-elastic support in Fig. 5.56c, with the membrane spring B1 that restricts lateral and axial displacement but allows rotation of the beam’s end. Two piezoelectric stack transducers B2 are positioned opposite two helical disc springs B3 mechanically prestressing the stack transducers. Both are connected to the beam via the axial extension B4, which connects both springs to the beam, and transforms the beam’s lateral vibration into axial deflections of the stack transducers. The concept of the piezo-elastic support was patented in [91] and, apart from piezoelectric shunt-damping, is also used for active buckling control, see Sect. 5.4.7 [235].
a Single beam test setup, b sectional view and c photo of the piezo-elastic support [118]
The single beam test setup in Fig. 5.56a was designed to investigate uncertainty in the attenuation of lateral vibrations at the beam’s first resonance frequency via piezoelectric shunt-damping. An epistemic data uncertainty, see Sect. 2.1, is the variation of static axial loads that results in a decrease of the first resonance frequency for compressive loads as well as an increase for tensile loads, [118, 120]. For the vibration attenuation via piezoelectric shunt-damping, the RL- and RLC-shunts were used. For that, the shunts were tuned to the unloaded beam. Figure 5.56a shows the experimental amplitude response \(|G_\mathrm {y}|\) from the beam’s excitation force at support A in y -direction to the measured acceleration in y -direction at accelerometer 6, see Fig. 5.56a, for axial tensile load \(F_\mathrm {ax} = -1200\,\mathrm {N}\), axially unloaded beam \(F_\mathrm {ax} = 0\,\mathrm {N}\) and axial compressive load \(F_\mathrm {ax} = 1200\,\mathrm {N}\). Thereby, \(\hat{G}_\mathrm {y}\) denotes the maximum amplitude without shunt-damping, \(\hat{G}^\mathrm {RL}_\mathrm {y}\) the maximum amplitude with the RL-shunt and \(\hat{G}^\mathrm {RLC}_\mathrm {y}\) the maximum amplitude with the RLC-shunt in Fig. 5.57a. Vibration attenuation is achieved with RL- and RLC-shunts, but is reduced for the uncertain axial loads compared to the unloaded beam. However, the attenuation with the RLC-shunt is always higher than with the RL-shunt with the maximum amplitude of the RL-shunt \(\hat{G}^\mathrm {RL}_\mathrm {y} = 29.26\,\mathrm {m/s^2/V}\) being higher than the maximum amplitude of the RLC-shunt \(\hat{G}^\mathrm {RLC}_\mathrm {y} = 4.68\,\mathrm {m/s^2/V}\). Furthermore, the attenuation deviates less for the RLC-shunt, suggesting that the RLC-shunt is less sensitive to uncertainty in the axial load compared to the RL-shunt [118, 120].
a Experimental amplitude response \(|G_\mathrm {y}|\) for axial tensile load \(F_\mathrm {ax} = -1200\,\mathrm {N}\)  , axial compressive load \(F_\mathrm {ax} = 1200\,\mathrm {N}\)
, axial compressive load \(F_\mathrm {ax} = 1200\,\mathrm {N}\)  and axially unloaded beam \(F_\mathrm {ax} = 0\,\mathrm {N}\)
and axially unloaded beam \(F_\mathrm {ax} = 0\,\mathrm {N}\) 
 a shunt as well as with
a shunt as well as with  and
and  shunt and b normalised histogram of the numerically simulated maximum amplitudes \(\hat{G}_\mathrm {y}\) for
shunt and b normalised histogram of the numerically simulated maximum amplitudes \(\hat{G}_\mathrm {y}\) for  and
and  shunt, according to [118]
shunt, according to [118]
Figure 5.57b shows the histogram of the numerically simulated maximum amplitudes \(\hat{G}_\mathrm {y}\) with epistemic uncertainty from the axial load, aleatoric uncertainty from the manufacturing and assembly of the piezo-elastic support as well as from the variation of shunt components and transducer parameters for RL- and RLC-shunts, according to [118]. The 95% quantile of the maximum amplitude \(Q^{95}\) and the most likely maximum amplitude \(\sum \) are used to compare the uncertainty in vibration attenuation when using the RL- and RLC-shunts. The most likely maximum amplitude \(\sum _\mathrm {RL} = 26.77\,\mathrm {m/s^2/V}\) as well as the 95% quantile of the maximum amplitude \(Q^{95}_\mathrm {RL} = 35.81\,\mathrm {m/s^2/V}\) of the RL-shunt are higher than the RLC-shunt’s most likely maximum amplitude \(\sum _\mathrm {RLC} = 5.42\,\mathrm {m/s^2/V}\) and \(95\%\) quantile of the maximum amplitude \(Q^{95}_\mathrm {RL} = 35.81\,\mathrm {m/s^2/V}\).
Numerical investigation of piezoelectric shunt-damping in a beam truss structure
After the extensive investigation of piezoelectric shunt-damping in a single beam test setup subject to data uncertainty, piezoelectric shunt-damping with the piezo-elastic support is investigated in the two-dimensional beam truss structure shown in Fig. 5.58. It is derived from the upper truss structure of the MAFDS in Sect. 3.6.1. The beam truss structure comprises seven beams 1 to 7 connected to each other via five spheres A to E with connector elements. Additional masses m can be attached at spheres D and E to introduce epistemic uncertainty in the static load of the beam truss structure. This results in a variation of the axial loads of the individual beams shifting the structural eigenfrequencies of the two-dimensional beam truss structure, see Fig. 5.56a. The piezo-elastic support F connects beam 2 with sphere B, where an electrodynamic shaker G is attached that dynamically excites the beam truss structure. Seven accelerometers are each positioned slightly off-centred at beams 1 to 7 to determine the local lateral vibrational behaviour.
Here, we numerically investigate the vibration attenuation of the two-dimensional beam truss structure with the piezo-elastic support shunted to an RL- and RLC-shunt without additional masses \(m_\mathrm {-} = 0\,\mathrm {kg}\) as well as with an additional mass \(m_\mathrm {0} = 50\,\mathrm {kg}\) and \(m_\mathrm {+} = 100\,\mathrm {kg}\) at each sphere D and E using a finite-element model derived in [184]. Figure 5.59 shows the numerically simulated amplitude response \(|G_\mathrm {w}|\) with maximum amplitude \(\hat{G}_\mathrm {w} = 29.06\,\mathrm {dB}\) from the excitation with the electrodynamic shaker to the accelerometer at beam 2, Fig. 5.58. The RL- and RLC-shunts are tuned to the two-dimensional beam truss structure’s first eigenfrequency at additional mass \(m_\mathrm {0}\) and used for all three uncertain load cases. Analogous to the single beam test setup, the maximum amplitude with RL-shunt \(\hat{G}^\mathrm {RL}_\mathrm {w} = 19.08\,\mathrm {dB}\) is higher than the RLC-shunt’s maximum amplitude \(\hat{G}^\mathrm {RL}_\mathrm {w} = 0.81\,\mathrm {dB}\). Furthermore, the vibration attenuation with the RLC-shunt is less sensitive to the uncertain loads than with the RL-shunt.
Numerically simulated amplitude responses \(|G_\mathrm {w}|\) of the two-dimensional beam truss structure a shunt and additional mass \(m_\mathrm {0} = 50\,\mathrm {kg}\)  and with (a)
and with (a)  shunt and (b)
shunt and (b)  shunt for various additional masses \(m_\mathrm {-} = 0\,\mathrm {kg}\)
shunt for various additional masses \(m_\mathrm {-} = 0\,\mathrm {kg}\)  , \(m_\mathrm {0} = 50\,\mathrm {kg}\)
, \(m_\mathrm {0} = 50\,\mathrm {kg}\)  and \(m_\mathrm {+} = 100\,\mathrm {kg}\)
and \(m_\mathrm {+} = 100\,\mathrm {kg}\)  at spheres D and E, Fig. 5.58
at spheres D and E, Fig. 5.58
Conclusion
In this section, we presented piezoelectric shunt-dampings with the piezo-elastic support as a possible (semi-)active process manipulation for vibration attenuation in the single beam shown in Fig. 5.56a, if non-stochastic and stochastic data uncertainty are present [118]. For a two-dimensional beam truss structure, numerical investigations show a successful vibration attenuation with piezoelectric shunt-damping, if data uncertainty is present. In general, we are able to demonstrate that a higher and less sensitive vibration attenuation of a single beam and a beam truss structure are achieved with the RLC-shunt in comparison to the RL-shunt. The numerical results for the beam truss structure will be experimentally validated in the future at the test setup of the two-dimensional beam truss structure, see Fig. 5.58. Furthermore, piezoelectric shunt-damping will be further investigated in the complex structural dynamic system of the MAFDS, Sect. 3.6.1.
5.4.7 Active Buckling Control of Compressively Loaded Beam-Columns and Trusses
Lightweight mechanical truss structures that comprise slender beam-columns and stiff nodes are commonly used in mechanical engineering applications to distribute both (quasi-)static and dynamic loads within the usage phase, see Sect. 3.1, e.g. in aircraft landing gears or vehicle suspension struts [280]. However, the slender beam-columns are sensitive to failure by buckling when loaded by compressive axial loads \(F_x\) and their maximum bearable axial loads \(F_{x,\mathrm {max}}\) are considerably reduced by data uncertainty in the material, geometry, loading or support properties [262], see Sect. 2.1. In order to increase the maximum bearable axial load, active buckling control of rather academic beam-column systems with rectangular cross-sections has been investigated numerically and experimentally [25, 93, 94, 196, 261, 275, 286]. In contrast, we apply active buckling control to a practical beam-column system with a circular cross-section in order to demonstrate the mastering of uncertainty in beam-column buckling by active process manipulation, which was motivated in Sect. 3.2 and Sect. 3.4. The beam-column system is later integrated into the Modular Active Spring-Damper System (MAFDS) presented in Sect. 3.6.1. In the following, first the concept of active buckling control and the application to a single beam-column system is presented. Then, the application to a three-dimensional tetrahedron truss structure is discussed.
Active buckling control in a single beam-column system
The concept of active buckling control was experimentally investigated first for the single beam-column system shown in Fig. 5.60a [235, 236]. The beam-column used for active buckling control is a slender beam-column with length \(l_\mathrm {b}=400\,\mathrm {mm}\) and a circular solid cross-section with constant radius \(r_\mathrm {b}=4\,\mathrm {mm}\). It is made from high-strength aluminium alloy EN AW-7075 with Young’s modulus \(E_\mathrm {b}=71\,\mathrm {GPa}\) and density \(\varrho _\mathrm {b}=2850\,\mathrm {kg/m^3}\) to avoid plastic deformation due to beam-column buckling [262]. Four strain gauge sensors in the beam-column centre are used to measure the surface strains due to bending to calculate the deflection of the beam-column in the local y - and z -directions.
a Single beam-column system for active buckling control, b sectional view of piezo-elastic support with local x -, y - and z -directions [235]
The lower and upper beam-column ends are connected to piezo-elastic supports with integrated piezoelectric stack actuators depicted in Fig. 5.60b; these are fixed to a baseplate and a parallel guidance to allow the introduction of compressive axial loads \(F_x\), respectively. The novel concept of the piezo-elastic support was patented in [91] and, other than for active buckling control, is also used for vibration attenuation with shunted piezoelectric transducers, as discussed in Sect. 5.4.6 and [118, 120]. The piezo-elastic supports provide elastic boundary conditions for the beam-column and include the piezoelectric stack actuators, which are mechanically prestressed by allocated helical disk springs. The piezoelectric stack actuators are integrated in the lateral load path via axial extensions at a distance \(l_\mathrm {ext}\) from the beam-column ends and exert active lateral forces in the local y - and z -directions, so that they may influence the lateral beam-column deflections. The central element of the piezo-elastic supports are two differently shaped membrane spring elements that are manufactured by a single point incremental forming process with the 3D Servo Press presented in Sects. 3.6.3 and 5.4.1 and [155]. The membrane spring elements bear the axial and lateral loads and allow rotations in any plane perpendicular to the beam-column’s local x -axis.
The piezo-elastic supports with integrated piezoelectric stack actuators stabilise the beam-column in arbitrary lateral direction by active bending moments at each end of the beam-column. A linear parameter-varying (LPV) controller, in particular a gain-scheduled \(\mathcal {H}_\infty \) controller, which guarantees stability and performance for arbitrary trajectories of dynamic axial loads \(F_x(t)\), is used for the active buckling control. For controller design, the beam-column including the piezo-elastic supports is modelled by an axial load-dependent finite element (FE) model for the FE degrees of freedom r(t) with equation of motion and output equation
where M is the mass matrix, D is the damping matrix, \(K \big ( F_x(t) \big )\) is the axial load-dependent stiffness matrix, B is the voltage input matrix and C is the output matrix. The actuator voltages of the piezoelectric stack actuators \(V_{\mathrm {pz}}\) and the beam-column bending strains \(\varepsilon _{\mathrm {s}}\) are combined in the beam-column input and output vectors
After Laplace transformation, the \(2 \times 2\) matrix of transfer functions
describes the transfer behaviour from the actuator voltages u to the beam-column strains y (5.28) [249].
The most sensitive parameters of the axial load-dependent FE model (5.26) and (5.27) of the beam-column system, which is augmented by the dynamic transfer behaviour of electrical components used for signal conditioning, are calibrated with experimental data and then used to design the LPV controller. Subsequently, the passive (without controller) and active (with controller) beam-column systems are loaded by quasi-static and dynamic axial loads \(F_x(t)\) and the absolute lateral modal displacement \(q_1(t)\) is measured. Figure 5.61a shows the experimental load-displacement curves of passive buckling and active buckling control for the single beam-column system in Fig. 5.60a subjected to a slowly increasing quasi-static axial load \(F_x(t)\). We conducted the experiments with a representative sample of 30 nominally identical passive and active beam-column systems in order to quantify stochastic data uncertainty in the maximum bearable axial loads according to the classification of uncertainty presented in Chap. 2.
Passive  and active
and active  beam-column systems with quasi-static axial load \(F_x(t)\), a absolute modal displacement \(q_{1}\) versus axial load \(F_x\) with maximum admissible displacement \(q_{1,\mathrm {max}}\)
beam-column systems with quasi-static axial load \(F_x(t)\), a absolute modal displacement \(q_{1}\) versus axial load \(F_x\) with maximum admissible displacement \(q_{1,\mathrm {max}}\)  , b normalised histograms and fitted three-parameter Weibull distributions \(p_\mathrm {W}(F_{x,\mathrm {max}})\) of maximum bearable axial loads \(F_{x,\mathrm {max}}\) with most likely value \(\Sigma _{F_{x,\mathrm {max}}}\) and interpercentile range \(R_{F_{x,\mathrm {max}}}\) [235]
, b normalised histograms and fitted three-parameter Weibull distributions \(p_\mathrm {W}(F_{x,\mathrm {max}})\) of maximum bearable axial loads \(F_{x,\mathrm {max}}\) with most likely value \(\Sigma _{F_{x,\mathrm {max}}}\) and interpercentile range \(R_{F_{x,\mathrm {max}}}\) [235]
Normalised histograms and three-parameter Weibull distribution fits \(p_\mathrm {W}(F_{x,\mathrm {max}})\) for the maximum bearable loads \(F_{x,\mathrm {max}}\) of the passive and active beam-column systems are shown in Fig. 5.61b. For the active beam-column system, the most likely maximum bearable axial load \(\Sigma _{F_{x,\mathrm {max}}}\) increases by 29% and the variability expressed by the interpercentile range \(R_{F_{x,\mathrm {max}}}\) reduces by 70% in comparison to the passive beam-column system. Thus, stochastic uncertainty in the maximum bearable axial loads is mastered by active process manipulation using active buckling control for the single beam-column system.
Active buckling control in a tetrahedron truss structure
As an intermediate step to the integration of active buckling control in the MAFDS, which represents a realistic load-bearing structure, Sect. 3.6.1, we investigate active buckling control in an experimental three-dimensional tetrahedron truss structure. Figure 5.62 shows the experimental tetrahedron truss structure that comprises three beam-columns b1–b3 with piezo-elastic supports, in the following called active beam-columns, and three passive beams b4–b6. They are connected to each other via the spheres S1–S4, where the spheres S1–S3 are clamped and sphere S4 is free and may be used to introduce vertical compressive loads \(F_{z^{\prime }}\) into the tetrahedron truss structure in global \(z^{\prime }\)-direction.
The lateral dynamic behaviour of the three active beam-columns, which is essential for the model-based controller synthesis for active buckling control, was investigated in [237]. Here, we used the experimental beam-column transfer functions (5.29) of the unloaded active beam-columns b1–b3 in the tetrahedron truss structure in Fig. 5.62 to calibrate the FE model of the single beam-column (5.26) and (5.27). The lateral dynamic behaviour of all active beam-columns b1–b3 are very similar and their boundary conditions in the tetrahedron truss structure are adequately described by the numerical beam-column transfer function (5.29) originating from the single beam-column test setup in Fig. 5.60a. Thus, no additional model of the tetrahedron truss structure is necessary and the calibrated FE beam-column models will be used for the model-based controller synthesis as well as active buckling control of the tetrahedron truss structure in future investigations.
In conclusion, active buckling control may be used to master uncertainty in the maximum bearable load of mechanical load-bearing structures prone to buckling. The effectiveness of this form of active process manipulation was shown for a single beam-column system subject to quasi-static and dynamic axial loads. Furthermore, it is currently tested for a tetrahedron truss structure and prepared for the integration in the MAFDS.
5.4.8 Load Redistribution Via Semi-active Guidance Elements in a Kinematic Structure
In many mechanical engineering applications, withstanding external loads is one of the key tasks within the usage phase, see Sect. 3.1. In most cases, the load is transmitted from one or more points of load application via a predetermined load path to the structural supports. Additionally, defined kinematics are often an important part of the functional performance in a load-bearing structure to enable a specified relative displacement of structural components. An example is the compression stroke of a landing gear or a suspension strut in airplanes or vehicles. A spring-damper often determines the main kinetic properties [183]. The compression stroke, in turn, is enabled by guidance elements, such as torque-links or other suspension links [65, 152]. In general, the guidance elements kinematically connect two or more parts of a load-bearing structure in order to achieve defined relative displacements. In most cases, the load path going through the load-bearing structure is predetermined in the design phase and, mostly, is not subject to any changes during the structure’s lifetime [218]. However, if parts of the load-bearing structure become weak or suffer damage, e.g. due to deterioration or overload, the load capacity may become lower than designed leading to uncertainty [112]. In this case, semi-active process manipulation, as introduced in Sects. 3.2 and 3.4, in form of load redistribution can be an option to master this uncertainty by adjusting the load path and, thus, reducing the effects of damage or prevent further damage, compare Sect. 3.6.1. Also, a desired support reaction force ratio achieved by load redistribution during operation might be useful if the predetermined load path is not suitable anymore [115]. In the following, first the concept of load redistribution and the investigated test setup are presented. Then, semi-active guidance elements for load redistribution are introduced. Finally, numerical and experimental results are discussed.
Concept of load redistribution
Figure 5.63 depicts a schematic representation of an exemplary load-bearing structure to demonstrate load redistribution, compare Sect. 4.1.2. It represents a simplified surrogate version of the MAFDS, Sect. 3.6.1. A spring-damper and two semi-active guidance elements connect a mass and a beam forming a load-bearing structure. The beam distributes the load to two supports at its ends. Varying support stiffness simulates varying load capacity in an academic and reproducible way and is a manifestation of data uncertainty, see Sect. 2.1. Load redistribution according to [114, 115] entails the redistribution of loads between the left and right support in case of present or anticipated damage. The loads previously passed through the spring-damper solely (grey line in Fig. 5.63) are partly redistributed via the controlled semi-active guidance elements. If, for example, the left support is assumed to be damaged or weak, it can be relieved via the right semi-active guidance element providing a load path in addition to the spring-damper. Hence, parts of the loading are bypassed through the right semi-active guidance element towards the undamaged right support. The additional load path is depicted in Fig. 5.63 by a dashed black line passing through the right semi-active guidance element compared to a thin black line indicating the corresponding weaker load path through the spring-damper. Load redistribution during operation can be attributed as semi-active process manipulation and is part of Structural Health Control SHC [194]. SHC combines structural health monitoring, assessing the structural health condition, e.g. the load-bearing capacity, and an adequate semi-active or active process manipulation in order to load or unload load-bearing components, compare Sect. 3.4.
Semi-active load redistribution test setup with original and additional load path via the right semi-active guidance element [113]
Semi-active guidance elements
Figure 5.64a depicts a close-up view of the right semi-active guidance element mounted to the test setup, compare Sect. 4.1.2. The already existing components of the load-bearing structure, i.e. the guidance elements, are augmented with electromagnetic friction brakes for semi-active process manipulation to adapt the structure’s load path via an induced friction moment. Figure 5.64b depicts a CAD illustration of the semi-active guidance element. It consists of two kinematic links connected by a middle joint, which is equipped with an electromagnetic friction brake. Within the friction brake, the electromagnetically induced normal force \(F_\mathrm {a}\) acts on the friction lining in negative x -direction and is controlled via a controlled input voltage applied to the brake’s electromagnet. The normal force \(F_\mathrm {a}\), in turn, causes a friction moment \(M_\mathrm {f}\) and changes the load transmitting properties of the semi-active guidance element by increasing or decreasing the possible amount of the loading passing through the joint. The mathematical relation between the electromagnetic normal force \(F_\mathrm {a}\) and the related friction moment \(M_\mathrm {f}\) is presented in [112, 113] applying the LuGre friction model.
Semi-active guidance element, a realisation and b CAD illustration according to [113]
Numerical and experimental results of load redistribution
The uncertainty within the load path, assumed to be a support with reduced stiffness, is supposed to be mastered by means of semi-active load redistribution. The supports’ stiffness is adjustable for the experiments in order to introduce uncertainty in a repeatable and measurable way. Thereby, we can numerically and experimentally investigate and evaluate the load redistribution capability within the exemplary load-bearing structure from Sect. 4.1.2. The stiffness reduction, which is achieved via the adjustable supports in Fig. 5.63 according to [144], causes uncertain dynamic behaviour and uncertain load capacity. In our example, this is misalignment of the beam and undesired support reaction force ratio among the two supports, for details see [112]. Here, we exemplarily present the resulting load path when trying to reduce the undesired misalignment caused by a damaged support with reduced stiffness. The load path is evaluated by means of the left and right support reaction forces \(F_\mathrm {L}\) and \(F_\mathrm {R}\). A comprehensive case study comprising different control strategies and different levels of damage is presented in [112].
Figure 5.65 depicts the simulated and measured load path of the load-bearing structure due to an external force excitation by the dropped load mass resulting in a step load applied to the mass, compare Fig. 5.63. A time series of two seconds is simulated and measured to analyse the load path and load redistribution capability with and without semi-active control. For the numerical results, we consider the remaining model prediction uncertainty by conducting Monte Carlo (MC) simulations with the calibrated parameter ranges, compare Sect. 4.1.2. Instead of ignoring the uncertainty by stating only one deterministic curve, the uncertainty in the model prediction caused by the remaining parameter uncertainty is indicated by shaded areas in Fig. 5.65. Solid lines represent the measured load paths, averaged for 10 measurements [112].
Measured support reaction force \(F_\mathrm {L}\) ( ) and \(F_\mathrm {R}\) (
) and \(F_\mathrm {R}\) ( ) versus time t and the predicted uncertainty ranges with the calibrated math. model
) versus time t and the predicted uncertainty ranges with the calibrated math. model  due to model parameter uncertainty for the passive and semi-active load-bearing structure [112], cf. Fig. 4.7 in Sect. 4.1.2 for model calibration results
due to model parameter uncertainty for the passive and semi-active load-bearing structure [112], cf. Fig. 4.7 in Sect. 4.1.2 for model calibration results
For the experimental results in Fig. 5.65, the excitation load is equally distributed to both supports in case of no semi-active load redistribution. This leads to almost identical measured support reaction forces. In case of a support with reduced stiffness and, hence, load-bearing capacity, the load redistribution results from the semi-active guidance elements. The excitation load is no longer equally distributed to the supports, but depends on the support stiffness. The steady state load reduction of the assumed to be damaged right support is about 24%. The shaded area of the MC simulation results show similar dynamic behaviour for the entire time scale. Thus, the numerical results widely encompass the experimental results for both support reaction forces with and without semi-active load redistribution. The measured steady state left and right support reaction forces \(F_\mathrm {L}\) and \(F_\mathrm {R}\) are within the range of the model predictions. Taking into account the overall time scale, the load paths and the load redistribution capability is predicted sufficiently accurate using the calibrated parameter ranges from Sect. 4.1.2 and considering the remaining parameter uncertainty.
The load is partly redistributed towards the undamaged support and the damaged support is relieved. Since we cannot redistribute loads unlimitedly, there remains a steady state control deviation for the numerical and experimental results. This is most probably bot not exclusively due to the limitations of the semi-active approach, which cannot introduce energy into the structure via the electromagnetic friction brakes to completely eliminate the control deviation, compare Sect. 3.4. Overall, a successful semi-active process manipulation with significant load redistribution is numerically and experimentally proved [112, 114, 115].
For a more practical application of load redistribution, the concept of semi-active guidance elements as shown in Fig. 5.64 is transferred into up-scaled semi-active guidance elements for the MAFDS in future work, see Sect. 3.6.1. Thus, the planar load redistribution problem transforms into a spatial load redistribution problem. The load path of the MAFDS will become adaptable in order to master uncertainty in the spatial structure application.
Change history
05 January 2022
.
References
Abele E, Bölling C (2014) Modellierung der geometrischen Eingriffsbedingungen bei der Ventilsitzbearbeitung am Zylinderkopf. wt Werkstattstechnik online 104(H. 11/12):735–740
Abele E, Geßner F (2018) Spanungsquerschnittmodell zum Gewindebohren. wt Werkstattstechnik. Online 108(1–2):2–6
Abele E, Hauer T, Haydn M (2011) Modellierung der Prozesskräfte beim Reiben mit Mehrschneidenreibahlen—Implementierung eines Kraftmodells für die Simulation der Reibbearbeitung. wt Werkstattstechnik online 101(6):407–412
Ackoff RL (1989) From data to wisdom. J Appl Syst Anal 16(1):3–9
Affenzeller J, Gläser H (1996) Lagerung und Schmierung von Verbrennungsmotoren, Die Verbrennungskraftmaschine Neue Folge, vol 8. Springer, Vienna. https://doi.org/10.1007/978-3-7091-6568-3
Al-Baradoni N, Krech M, Groche P (2020) In-process calibration of smart structures produced by incremental forming. In: Production engineering, pp 1–9. https://doi.org/10.1007/s11740-020-01002-6
Ali S, Hinduja S, Atkinson J, Bolt P, Werkhoven R (2008) The effect of ultra-low frequency pulsations on tearing during deep drawing of cylindrical cups. Int J Mach Tools Manuf 48(5):558–564. https://doi.org/10.1016/j.ijmachtools.2007.06.013
Allwood JM, Duncan SR, Cao J, Groche P, Hirt G, Kinsey BL, Kuboki T, Liewald M, Sterzing A, Tekkaya AE (2016) Closed-loop control of product properties in metal forming. CIRP Ann 65(2):573–596. https://doi.org/10.1016/j.cirp.2016.06.002
Altherr LC, Joggerst L, Leise P, Pfetsch ME, Schmitt A, Wendt J (2019) On obligations in the development process of resilient systems with algorithmic design methods. In: Pelz PF, Groche P (eds) Uncertainty in mechanical engineering III, applied mechanics and materials, vol 885. Trans Tech Publications, pp 240–252. https://doi.org/10.4028/www.scientific.net/AMM.885.240
Archibald RD (1994) Uncertainty and change require a new management model. PM Netw. 8(5):6–10
Arentoft M, Eriksen M, Wanheim T (2000) Determination of six stiffnesses for a press. J Mater Process Technol 105(3):246–252. https://doi.org/10.1016/s0924-0136(00)00559-8
Arentoft M, Wanheim T (2005) A new approach to determine press stiffness. CIRP Ann 54(1):265–268. https://doi.org/10.1016/s0007-8506(07)60099-7
Bates H, Holweg M, Lewis M, Oliver N (2007) Motor vehicle recalls: Trends, patterns and emerging issues. Omega 35(2):202–210
Bauer B, Devroye L, Kohler M, Krzyżak A, Walk H (2017) Nonparametric estimation of a function from noiseless observations at random points. J Multivar Anal 160:93–104. https://doi.org/10.1016/j.jmva.2017.05.010
Bauer B, Heimrich F, Kohler M, Krzyżak A (2019) On estimation of surrogate models for multivariate computer experiments. Ann Inst Stat Math 71(1):107–136. https://doi.org/10.1007/s10463-017-0627-8
Bauer W (2016) Planung und Entwicklung änderungsrobuster Plattformarchitekturen. Dissertation, TU München
Baumberger GC (2007) Methoden zur kundenspezifischen Produktdefinition bei individualisierten Produkten. Produktentwicklung. Verl. Dr. Hut, München
Becerril L, Sauer M, Lindemann U (2016) Estimating the effects of engineering changes in early stage product development. In: DSM 2016: sustainability in modern project management—proceedings of the 18th international DSM conference, pp 125–135. https://doi.org/10.19255/JMPM-DSM2016
Beck U (1986) Risikogesellschaft: Auf dem Weg in eine andere Moderne. Suhrkamp, Frankfurt a. M
Bedarff T, Hedrich P, Pelz PF (2014) Design of an active air spring damper. In: Murrenhoff H (ed) 9th international fluid power conference (9th IFK). HP - Fördervereinigung Fluidtechnik, Aachen, pp 356–365
Beder S (1998) The new engineer: management and professional responsibility in a changing world. Macmillan Education
Beetz JP (2018) Modelle und Methoden zur systematischen Entwicklung hygienegerechter Produkte. Dissertation, TU Darmstadt
Behrens BA, Yilkiran T, Vahed N, Frischkorn C (2014) Einfluss des Materialflusses auf die Verdichtung beim Sinterschmieden: Pulvermetallurgie und Umformtechnik. Whitepaper, Umformtechnik.net. https://umformtechnik.net/content/location/72775
Bender M (2016) Forschungsumgebungen in den Digital Humanities: Nutzerbedarf, Wissenstransfer, Textualität, Sprache und Wissen, vol 22. De Gruyter, Berlin
Berlin AA, Chase JG, Yim MH, Maclean JB, Olivier M, Jacobsen SC (1998) MEMS-based control of structural dynamic instability. J Intell Mater Syst Struct 9(7):574–586. https://doi.org/10.1177/1045389X9800900709
BGH: Urteil vom 02. März 2010—VI ZR 223/09
BGH: Urteil vom 02. Oktober 2012—VI ZR 311/11
BGH: Urteil vom 07. Oktober 1975—VI ZR 43/74
BGH: Urteil vom 08. November 2005—VI ZR 332/04
BGH: Urteil vom 09. Dezember 1986—VI ZR 65/86
BGH: Urteil vom 09. September 2008—VI ZR 279/06
BGH: Urteil vom 16. Juni 2009—VI ZR 107/08
BGH: Urteil vom 17. Juni 1997—VI ZR 156/96
BGH: Urteil vom 17. März 1981—VI ZR 286/78
BGH: Urteil vom 17. März 2009—VI ZR 176/08
BGH: Urteil vom 26. November 1968—VI ZR 212/66
BGH: Urteil vom 28. April 1952—III ZR 118/51
Bhattacharyya O, Kapoor SG, DeVor RE (2006) Mechanistic model for the reaming process with emphasis on process faults. Int J Mach Tools Manuf 46(7–8):836–846. https://doi.org/10.1016/j.ijmachtools.2005.07.022
Bilz Werkzeugfabrik GmbH and Co. KG: HFP—wireless monitoring for multispindle tapping (2020). https://www.bilz.de/produkte/messtechnik-smarttools/prozessueberwachung-fuer-gewindebearbeitung. (Visited 12/2020)
Birkhofer H (2011) The future of design methodology. Springer, Berlin
Birkhofer H, Waeldele M (2008) Properties and characteristics and attributes and...—an approach on structuring the description of technical systems. In: DS 57: proceedings of AEDS 2008 workshop
Böhle F, Heidling E, Neumer J, Kuhlmey A, Winnig M, Trobisch N, Kraft D, Denisow K (2016) Umgang mit Ungewissheit in Projekten. Technical Report, GPM Deutsche Gesellschaft für Projektmanagement e. V., Nuremberg
Boller C (2001) Composites for sensors and actuators. In: Buschow KJ, Cahn RW, Flemings MC, Ilschner B, Kramer EJ, Mahajan S, Veyssière P (eds) Encyclopedia of materials: science and technology. Elsevier, Oxford, pp 1376–1382. https://doi.org/10.1016/B0-08-043152-6/00256-4
Bölling C (2019) Simulationsbasierte Auslegung mehrstufiger Werkzeugsysteme zur Bohrungsfeinbearbeitung am Beispiel der Ventilführungs- und Ventilsitzbearbeitung. Dissertation, TU Darmstadt. http://tubiblio.ulb.tu-darmstadt.de/111353/
Bölling C, Güth S, Abele E (2015) Control of uncertainty in high precision cutting processes: reaming of valve guides in a cylinder head of a combustion engine. In: Pelz PF, Groche P (eds) Uncertainty in mechanical engineering II, applied mechanics and materials, vol 807. Trans Tech Publications, pp 153–161
Bölling C, Hoppe F, Geßner F, Knoll M, Abele E, Groche P (2018) Fortpflanzung von Unsicherheit in Prozessketten. wt Werkstattstechnik Online 108(1–2):82–88
Bonnardel N, Marmèche E (2005) Towards supporting evocation processes in creative design: A cognitive approach. Int J Hum Comput Stud 63(4–5):422–435
Brenneis M, Groche P (2012) Smart components through rotary swaging. In: Material forming ESAFORM 2012, key engineering materials, vol 504. Trans Tech Publications, pp 723–728.https://doi.org/10.4028/www.scientific.net/KEM.504-506.723
Brenneis M, Ibis M, Duschka A, Groche P (2014) Towards mass production of smart products by forming technologies. In: WGP congress 2012, advanced materials research, vol 907. Trans Tech Publications, pp 113–125. https://doi.org/10.4028/www.scientific.net/AMR.907.113
Brenner DP (2014) Einsatzmöglichkeiten der zusätzlichen Stößelfreiheitsgrade der 3D-Servo-Presse in Prozessen der Pulvermetallurgie: Potential applications using the additional degrees of freedom of the 3d-servo-press in powder metallurgy processes. Diplomarbeit, TU Darmstadt
Breunig A, Hoppe F, Groche P (2019) Localized blank-holder pressure control in cup drawing through tilting of the ram. In: Proceedings of NUMIFORM, pp 583–586
Brötz N, Hedrich P, Pelz PF (2018) Integrated fluid dynamic vibration absorber for mobile applications. In: 11th international fluid power conference, vol 1, pp 14–24
Brötz N, Pelz PF (2020) Bayesian uncertainty quantification in the development of a new vibration absorber technology. In: IMAC XXXVIII, vol 1
Budiansky B, Hutchinson JW, Slutsky S (1982) Void growth and collapse in viscous solids. In: Hopkins HG (ed) Mechanics of solid. Pergamon Press, Oxford, pp 13–45. https://doi.org/10.1016/B978-0-08-025443-2.50009-4
Bührig-Polaczek A (ed) (2013) Handbuch Urformen: Handbuch der Fertigungstechnik, second edn. Hanser, München. https://doi.org/10.3139/9783446434066
Calmano S (2017) Methodik zur Regelung von Bauteileigenschaften in Umformprozessen. Dissertation, TU Darmstadt
Calmano S, Hesse D, Hoppe F, Groche P (2015) Evaluation of control strategies in forming processes. In: Qin Y, Dean TA, Lin J, Yuan SJ, Vollertsen F (eds) Proceedings of the 4th international conference on new forming technology (ICNFT), Article 04002. https://doi.org/10.1051/matecconf/20152104002
Calmano S, Hesse D, Hoppe F, Traidl P, Sinz J, Groche P (2015) Orbital forming of flange parts under uncertainty. In: Pelz PF, Groche P (eds) Uncertainty in mechanical engineering II, applied mechanics and materials, vol 807. Trans Tech Publications, pp 121–129. https://doi.org/10.4028/www.scientific.net/AMM.807.121
Calmano S, Schmitt S, Groche P (2013) Prevention of over-dimensioning in light-weight structures by control of uncertainties during production. In: International conference on “New Developments in Forging Technology”. MAT INFO Werkstoff-Informationsgesellschaft mbH, Fellbach, pp 313–317
Chen YB, Sha JL, Wu SM (1990) Diagnosis of the tapping process by information measure and probability voting approach. J Eng Ind 112(4):319–325. https://doi.org/10.1115/1.2899594
Chodnikiewicz K, Balendra R (2000) The calibration of metal-forming presses. J Mater Process Technol 106(1–3):28–33. https://doi.org/10.1016/s0924-0136(00)00633-6
Chucholowski N, Langer S, Ferreira M, Forcellini F, Maier A (2012) Engineering change management report 2012: Survey results on causes and effects, current practice, problems, and strategies in Brazil. Universidade Federal de Santa Catarina
Clark KB, Fujimoto T (1991) Product development performance: Strategy, organization, and management in the world auto industry. Harvard Business School Press
Conrat Niemerg JI (1997) Änderungskosten in der Produktentwicklung. Dissertation, TU München
Currey NS (1988) Aircraft landing gear design: Principles and practices, 4th edn. AIAA education series. American Institute of Aeronautics and Astronautics, Washington, DC
Deutscher Bundestag: Drucksache 17/6276 (2001)
Deutsches Institut für Normung (1979) DIN 199–4. Begriffe im Zeichnungs- und Stücklistenwesen - Zeichnungen. Beuth, Berlin
Deutsches Institut für Normung (1988) DIN 55189-1:1988-12. Werkzeugmaschinen; Ermittlung von Kennwerten für Pressen der Blechverarbeitung bei statischer Belastung; Mechanische Pressen [Machine tools; determination of the ratings of presses for sheet metal working under static load; mechanical presses]. Beuth, Berlin
Deutsches Institut für Normung (2009) DIN 69901-5:2009-01. Projektmanagement – Projektmanagementsysteme – Teil 5: Begriffe. Beuth, Berlin. https://doi.org/10.31030/1498911
Deutsches Institut für Normung (2011) DIN EN ISO 376:2011–09 Metallische Werkstoffe - Kalibrierung der Kraftmessgeräte für die Prüfung von Prüfmaschinen mit einachsiger Beanspruchung [Metallic materials—Calibration of force-proving instruments used for the verification of uniaxial testing machines]. Beuth, Berlin
Deutsches Institut für Normung (2012) DIN 1988-200:2012-05. Technische Regeln für Trinkwasser-Installationen – Teil 200: Installation Typ A (Geschlossenes System) – Planung, Bauteile, Apparate, Werkstoffe; Technische Regel des DVGW. Beuth, Berlin. https://doi.org/10.31030/1887421
Deutsches Institut für Normung (2014) DIN IEC 60050–351:2014–09 Internationales Elektrotechnisches Wörterbuch: Teil 351: Leittechnik [International electrotechnical vocabulary - Part 351: Control technology]. Beuth, Berlin
Deutsches Institut für Normung: DIN EN 62198, VDE 0050-6. Managing risk in projects – Application guidelines. Beuth, Berlin (2014-08)
Deutsches Institut für Normung (2015) DIN 60812. Fehlzustandsart- und -auswirkungsanalyse (FMEA): (IEC 56/1579/CD:2014), vol. 03.120.01, 21.020, 29.020. Beuth, Berlin. https://doi.org/10.31030/2328411
Deutsches Institut für Normung (2017) DIN 31652-1. Gleitlager – Hydrodynamische Radial-Gleitlager im stationären Betrieb: Teil 2: Funktionen für die Berechnung von Kreiszylinderlagern. https://doi.org/10.31030/2588236
Deutsches Institut für Normung (2020) DIN 820-2. Standardization – Part 2: Presentation of documents (ISO/IEC Directives – Part 2:2018, modified). 820-2. Beuth, Berlin
Devroye L (1986) Non-uniform random variate generation. Springer, New York
Doege E, Behrens BA (2010) Handbuch Umformtechnik: Grundlagen, Technologien, Maschinen, 2nd edn. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-04249-2
Doege E, Lange K (1980) Static and dynamic stiffness of presses and some effects on the accuracy of workpieces. CIRP Ann 29(1):167–171. https://doi.org/10.1016/s0007-8506(07)61316-x
Doege E, Silberbach G (1990) Influence of various machine tool components on workpiece quality. CIRP Ann 39(1):209–213. https://doi.org/10.1016/s0007-8506(07)61037-3
Dowlatshahi S (2000) Designer-buyer-supplier interface: Theory versus practice. Int J Prod Econ 63(2):111–130
Drechsler S (2016) Kompetenzbedarfe von Maschinenbauingenieuren in Bezug auf Richtlinien, Normen und Standards zur Ausübung ihrer beruflichen Tätigkeit. Dissertation, Karlsruher Institut für Technologie (KIT). https://doi.org/10.5445/IR/1000059347
Dsuban, A., Lohn, J., Brüggemann, J.P., Kullmer, G.: Ein Qualitätssicherungskonzept für die additive Fertigung. In: H.A. Richard, B. Schramm, T. Zipsner (eds.) Additive Fertigung von Bauteilen und Strukturen, pp. 23–34. Springer, Wiesbaden and Cham (2019). DOI https://doi.org/10.1007/978-3-658-27412-2_2
Eckert C, Clarkson PJ, Zanker W (2004) Change and customisation in complex engineering domains. Res Eng Des 15(1):1–21
Ehrlenspiel K, Meerkamm H (2013) Integrierte Produktentwicklung: Denkabläufe, Methodeneinsatz. Hanser, Zusammenarbeit
Eifler T (2014) Modellgestützte Methodik zur systematischen Analyse von Unsicherheit im Lebenslauf technischer Systeme. Dissertation, TU Darmstadt
Eifler T, Enss GC, Haydn M, Mosch L, Platz R, Hanselka H (2012) Approach for a consistent description of uncertainty in process chains of load carrying mechanical systems. In: Hanselka H, Groche P, Platz R (eds) Uncertainty in mechanical engineering, applied mechanics and materials, vol 104. Trans Tech Publications, pp 133–144. https://doi.org/10.4028/www.scientific.net/AMM.104.133
EMUGE-Werk Richard Glimpel GmbH & Co. KG (2019) Softsynchro 3. https://www.emuge.com/sites/default/files/literature/Emuge-Catalog-520.pdf
Engelhardt R (2012) Uncertainty mode and effects analysis—Heuristische Methodik zur Analyse und Beurteilung von Unsicherheiten in technischen Systemen des Maschinenbaus. Dissertation, TU Darmstadt (2012)
Engelhardt R, Birkhofer H, Kloberdanz H, Mathias J (2009) Uncertainty-mode-and effects-analysis—an approach to analyze and estimate uncertainty in the product life cycle. In: Norell Bergendahl M (ed) Design theory and research methodology. Design Society, Glasgow, pp 191–202. https://www.designsociety.org/publication/28585/Uncertainty-Mode-+and+Effects-Analysis+ Visited 12/2020
Enss GC, Gehb CM, Götz B, Melz T, Ondoua S, Platz R, Schaeffner M (2015) Device for bearing design elements in lightweight structures (Festkörperlager). Patent DE 10 2015 101 084 A1
Enss GC, Kohler M, Krzyżak A, Platz R (2016) Nonparametric quantile estimation based on surrogate models. IEEE Trans Inform Theory 62(10):5727–5739. https://doi.org/10.1109/TIT.2016.2586080
Enss GC, Platz R (2016) Evaluation of uncertainty in experimental active buckling control of a slender beam-column with disturbance forces using Weibull analysis. Mech Syst Signal Process 79:123–131. https://doi.org/10.1016/j.ymssp.2016.02.066
Enss GC, Platz R, Hanselka H (2012) Uncertainty in loading and control of an active column critical to buckling. Shock Vib 19(5):929–937. https://doi.org/10.3233/SAV-2012-0700
European Commission: Commission Implementing Decision (EU) 2019/417 of 8 November 2018 laying down guidelines for the management of the European Union Rapid Information System ‘RAPEX’ established under Article 12 of Directive 2001/95/EC on general product safety and its notification system – C(2018) 7334
European Commission: Proposal for a Regulation of the European Parliament and of the Council on consumer product safety and repealing Council Directive 87/357/EEC and Directive 2001/95/EC: COM(2013) – 78 final (Feb. 13, 2013)
European Parliament, Council of the European Union: Directive 2006/42/EC of the European Parliament and of the council of 17 may 2006 on machinery, and amending directive 95/16/EC. Official Journal of the European Union (2006). URL https://eur-lex.europa.eu/eli/dir/2006/42/oj
Faleskog J, Gao X, Shih CF (1998) Cell model for nonlinear fracture analysis - I. Micromechanics calibration. Int J Fracture 89(4):355–373. https://doi.org/10.1023/A:1007421420901
Fang KT, Li R, Sudjianto A (2006) Design and modeling for computer experiments. Chapman & Hall/CRC, Boca Raton, FL
Fankhauser P, Kupietz M (2017) DeReKoVecs. http://corpora.ids-mannheim.de/openlab/derekovecs/. (Visited 12/2020)
Felber T, Kohler M, Krzyżak A (2015) Adaptive density estimation from data with small measurement errors. IEEE Trans Inform Theory 61(6):3446–3456. https://doi.org/10.1109/TIT.2015.2421297
Feldhusen J, Grote KH (eds) (2013) Pahl/Beitz Konstruktionslehre: Methoden und Anwendung erfolgreicher Produktentwicklung, eighth edn. Springer Vieweg, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-29569-0
Foerste U (2012) §24. In: Foerste U, Westphalen F (eds) Produkthaftungshandbuch. Beck, München
Forward RL (1979) Electronic damping of vibrations in optical structures. Appl Opt 18(5):690–697
Frame JD (1994) The new project management: tools for an age of rapid change, complexity, and other business realities. Jossey-Bass, Chichester
Freeman RE, McVea J (2001) A stakeholder approach to strategic management. The Blackwell Handbook of Strategic Management pp. 189–207 (2001)
Fricke E (1998) Der Änderungsprozeß als Grundlage einer nutzerzentrierten Systementwicklung. Dissertation, TU München, München
Fricke E, Gebhard B, Negele H, Igenbergs E (2000) Coping with changes: causes, findings, and strategies. Syst Eng 3(4):169–179
Friedman M (2007) The social responsibility of business is to increase its profits. In: W.C. Zimmerli, M. Holzinger, K. Richter (eds.) Corporate Ethics and Corporate Governance. Springer, Berlin, Heidelberg, pp 173–178. https://doi.org/10.1007/978-3-540-70818-6_14
Funtowicz SO, Ravetz JR (1993) Science for the post-normal age. Futures 25(7):739–755
Gantar G, Kuzman K, Filipič B (2005) Increasing the stability of the deep drawing process by simulation-based optimization. J Mater Process Technol 164–165:1343–1350. https://doi.org/10.1016/j.jmatprotec.2005.02.099
Gehb CM (2019) Uncertainty evaluation of semi-active load redistribution in a mechanical load-bearing structure. Dissertation, TU Darmstadt
Gehb CM, Atamturktur S, Platz R, Melz T (2020) Bayesian inference based parameter calibration of the LuGre-friction model. Exp Tech 44:369–382. https://doi.org/10.1007/s40799-019-00355-7
Gehb CM, Platz R, Melz T (2017) Global load path adaption in a simple kinematic load-bearing structure to compensate uncertainty of misalignment due to changing stiffness conditions of the structure’s supports. In: Barthorpe RJ, Platz R, Lopez I, Moaveni B, Papadimitriou C (eds) Model validation and uncertainty quantification, Volume 3, conference proceedings of the society for experimental mechanics series. Springer, Cham, pp 133–144. https://doi.org/10.1007/978-3-319-54858-6_14
Gehb CM, Platz R, Melz T (2019) Two control strategies for semi-active load path redistribution in a load-bearing structure. Mech Syst Signal Process 118:195–208. https://doi.org/10.1016/j.ymssp.2018.08.044
Gemmerich M (1995) Technische Produktänderungen. Betriebswirtschaftliche und empirische Modellanalyse. https://doi.org/10.1007/978-3-663-09030-4
Giesberts L, Gayger M (2019) Sichere Produkte ohne technische Normen: Anforderungen an neuartige Produkte wie autonome Systeme. Neue Zeitschrift für Verwaltungsrecht 38(20):1491–1495
Götz B (2019) Evaluation of uncertainty in the vibration attenuation with shunted piezoelectric transducers integrated in a beam-column support. Dissertation, TU Darmstadt. https://tuprints.ulb.tu-darmstadt.de/8608
Götz B, Kersting S, Kohler M (2018) Estimation of an improved surrogate model in uncertainty quantification by neural networks. Submitted for publication
Götz B, Platz R, Melz T (2018) Effect of static axial loads on the lateral vibration attenuation of a beam with piezo-elastic supports. Smart Mater Struct 27(3). https://doi.org/10.1088/1361-665X/aaa937
Groche P, Brenneis M (2014) Manufacturing and use of novel sensoric fasteners for monitoring forming processes. Measurement 53:136–144. https://doi.org/10.1016/j.measurement.2014.03.042
Groche P, Calmano S, Felber T, Schmitt S (2015) Statistical analysis of a model based product property control for sheet bending. Prod Eng 9(1):25–34
Groche P, Fritsche D, Tekkaya E, Allwood J, Hirt G, Neugebauer R (2007) Incremental bulk metal forming. CIRP Ann 56(2):635–656. https://doi.org/10.1016/j.cirp.2007.10.006
Groche P, Hoppe F, Hesse D, Calmano S (2016) Blanking-bending process chain with disturbance feed-forward and closed-loop control. J Manuf Process 24:62–70. https://doi.org/10.1016/j.jmapro.2016.07.005
Groche P, Hoppe F, Kessler T, Kleemann A (2018) Industrial working environment 2025. In: Liewald M (ed) New Developments in Sheet Metal Forming. institute for metal forming technology. Stuttgart, pp 125–136
Groche P, Hoppe F, Sinz J (2017) Stiffness of multipoint servo presses: Mechanics versus control. CIRP Ann 66(1):373–376. https://doi.org/10.1016/j.cirp.2017.04.053
Groche P, Krech M (2017) Efficient production of sensory machine elements by a two-stage rotary swaging process - relevant phenomena and numerical modelling. J Mater Process Technol 242:205–217. https://doi.org/10.1016/j.jmatprotec.2016.11.034
Groche P, Scheitza M, Kraft M, Schmitt S (2010) Increased total flexibility by 3D servo presses. CIRP Ann 59(1):267–270. https://doi.org/10.1016/j.cirp.2010.03.013
Groche P, Schneider R (2004) Method for the optimization of forming presses for the manufacturing of micro parts. CIRP Ann 53(1):281–284. https://doi.org/10.1016/s0007-8506(07)60698-2
Groche P, Sinz J (2016) Innovation durch Kombination: Wälz-Gleit-Lagerung für Servopressen. MM Maschinenmarkt 41
Groche P, Sinz J, Felber P (2018) Kombinierte Wälz-Gleitlager: Anforderungsgerechter Funktionsübergang. Konstruktionspraxis. Sonderheft SH1/2018
Groche P, Sinz J, Germann T (2020) Efficient validation of novel machine elements for capital goods. CIRP Ann 69(1):125–128. https://doi.org/10.1016/j.cirp.2020.03.004
Groche P, Türk M (2010) Integration of adaptive components by incremental forming processes. In: SPIE Smart Structures/NDE—For the Latest Research on Smart Sensors, NDE, Aerospace Systems, Energy Harvesting, San Diego, USA (2010)
Groche P, Türk M (2011) Smart structures assembly through incremental forming. CIRP Ann 60(1):21–24. https://doi.org/10.1016/j.cirp.2011.03.003
Groche P, Wohletz S, Brenneis M, Pabst C, Resch F (2014) Joining by forming - a review on joint mechanisms, applications and future trends. J Mater Process Technol 214(10):1972–1994. https://doi.org/10.1016/j.jmatprotec.2013.12.022
Gurson AL (1977) Continuum theory of ductile rupture by void nucleation and growth: Part I - yield criteria and flow rules for porous ductile media. J Eng Mater Technol 99(1):2–15. https://doi.org/10.1115/1.3443401
Haberhauer H, Bodenstein F (2011) Maschinenelemente: Gestaltung, Berechnung, Anwendung, sixteenth edn. Springer, Berlin. https://doi.org/10.1007/978-3-642-14290-1
Hagood NW, Crawley EF (1991) Experimental investigation into passive damping enhancement for space structures. J Guidance, Control, Dyn 14(6):1100–1109
Hales C, Gooch S (2004) Managing engineering design. Springer, Berlin
Hamp B, Feldweg H (1997) GermaNet—a lexical-semantic net for German. In: Proceedings of ACL workshop automatic information extraction and building of lexical semantic resources for NLP applications, pp 9–15
Hamraz B, Caldwell NH, Clarkson PJ (2013) A holistic categorization framework for literature on engineering change management. Syst Eng 16(4):473–505
Hanselka H, Engelhardt R, Koenen JF, Enss GC, Sichau A, Platz R, Kloberdanz H, Birkhofer H (2010) A model to categorise uncertainty in load-carrying systems. In: Heisig P (ed) Proceedings of the 1st international conference on modelling and management engineering processes. University of Cambridge, pp 53–64
Hanselka H, Platz R (2010) Ansätze und Maßnahmen zur Beherrschung von Unsicherheit in lasttragenden Systemen des Maschinenbaus. Konstruktion 2010(11–12):55–62
Hansmann J, Kaal W, Seipel B, Melz T (2012) Einstellbares Federelement für Adaptierbaren Schwingungstilger. ATZ - Automobiltechnische Zeitschrift 114(3):242–247. https://doi.org/10.1365/s35148-012-0295-1
Hauer T (2012) Modellierung der Werkzeugabdrängung beim Reiben – Ableitung von Empfehlungen für die Gestaltung von Mehrschneidenreibahlen. Schriftenreihe des PTW. Shaker, Aachen. TU Darmstadt, Dissertation
Hauschka C, Klindt T (2007) Eine Rechtspflicht zur Compliance im Reklamationsmanagement. Neue Juristische Wochenschrift 60(38):2726–2729
Hedrich P (2018) Konzeptvalidierung einer aktiven Luftfederung im Kontext autonomer Fahrzeuge, Forschungsberichte zur Fluidsystemtechnik, vol 20. Shaker, Aachen
Heid U, Schierholz S, Schweickard W, Wiegand HE, Gouws RH, Wolski W (eds) (2010) Das Digitale Wörterbuch der Deutschen Sprache (DWDS). Lexicographica. de Gruyter, Berlin, New York
Heidemann B (2001) Trennende Verknüpfung: Ein Prozessmodell als Quelle für Produktideen, Fortschritt-Berichte VDI Reihe 1, Konstruktionstechnik, Maschinenelemente, vol 351. VDI Verlag, Düsseldorf (2001). TU Darmstadt, Dissertation
Heidling E (2016) Erscheinungsformen und Typen von Ungewissheit in Projekten. Technical Report, GPM Deutsche Gesellschaft für Projektmanagement e. V., Nuremberg. Chapter in Böhle. Umgang mit Ungewissheit, Fritz et al. in Projekten
Heinrichs D (2015) Autonomes Fahren und Stadtstruktur. In: Maurer M, Gerdes, JC, Lenz B, Winner H (eds) Autonomes Fahren: Technische, rechtliche und gesellschaftliche Aspekte. Springer, Berlin, Heidelberg, pp 219–239. https://doi.org/10.1007/978-3-662-45854-9_11
Heißing B, Ersoy M (eds) (2007) Fahrwerkhandbuch: Grundlagen, Fahrdynamik, Komponenten, Systeme, Mechatronik, Perspektiven. Vieweg & Sohn, GWV Fachverlage, Wiesbaden. https://doi.org/10.1007/978-3-8348-9151-8
Henrich V (2015) Word sense disambiguation with GermaNet. Dissertation, Universität Tübingen. https://doi.org/10.15496/publikation-4706
Henrich V, Hinrichs E (2010) GernEdiT—the Germanet editing tool. In: Proceedings of the seventh international conference on language resources and evaluation (LREC’10). European Language Resources Association (ELRA), Valletta, Malta
Hesse D, Hoppe F, Groche P (2017) Controlling product stiffness by an incremental sheet metal forming process. Procedia Manuf 10:276–285. https://doi.org/10.1016/j.promfg.2017.07.058
Hiller F (1997) Ein Konzept zur Gestaltung von Änderungsprozessen in der Produktentwicklung. Dissertation, TU Kaiserslautern
Hinrichs EW, Hinrichs M, Zastrow T (2010) WebLicht: Web-based LRT services for German. In: Proceedings of the ACL 2010 system demonstrations, pp 25–29
Holland J (1996) Beitrag zur Erfassung der Schmierungsverhältnisse in Verbrennungskraftmaschinen, VDI-Forschungsheft, vol 475. VDI Verlag, Düsseldorf
Hoppe F, Hohmann J, Knoll M, Kubik C, Groche P (2019) Feature-based supervision of shear cutting processes on the basis of force measurements: Evaluation of feature engineering and feature extraction. Procedia Manuf 34:847–856. https://doi.org/10.1016/j.promfg.2019.06.164
Hoppe F, Knoll M, Götz B, Schaeffner M, Groche P (2018) Reducing uncertainty in shunt damping by model-predictive product stiffness control in a single point incremental forming process. In: Pelz PF, Groche P (eds) Uncertainty in mechanical engineering iii, applied mechanics and materials, vol 885. Trans Tech Publications, pp 35–47. https://doi.org/10.4028/www.scientific.net/AMM.885.35
Hoppe F, Pihan C, Groche P (2019) Closed-loop control of eccentric presses based on inverse kinematic models. Procedia Manuf 29:240–247. https://doi.org/10.1016/j.promfg.2019.02.132
Jarratt T, Clarkson J, Eckert C (2005) Engineering change. In: Design process improvement. Springer, Berlin, pp 262–285
Joggerst L, Knoll M, Hoppe F, Wendt J, Groche P (2018) Autonomous manufacturing processes under legal uncertainty. In: Pelz PF, Groche P (eds) Uncertainty in mechanical engineering III, applied mechanics and materials, vol 885. Trans Tech Publications, pp 227–239. https://doi.org/10.4028/www.scientific.net/AMM.885.227
Jürgens U (2000) New product development and production networks: global industrial experience. Springer, Berlin
Kapoor A, Klindt T (2012) Das neue deutsche Produktsicherheitsgesetz (ProdSG). Neue Zeitschrift für Verwaltungsrecht 31(12):719–724
Kennedy MC, O’Hagan A (2001) Bayesian calibration of computer models (with discussion). J R Stat Soc: Ser B (Statistical Methodology) 63(3):425–464. https://doi.org/10.1111/1467-9868.00294
Kier M, Wegner S, Bey R (2011) Neuartige Lagerungstechnik des Kurbeltriebs von Verbrennungsmotoren zur Verbesserung der Effizienz und Minderung der Emissionen: Abschlussbericht. Technical Report. 25518-24/0, Deutsche Bundesstiftung Umwelt AZ, Herzogenrath
Kitayama S, Natsume S, Yamazaki K, Han J, Uchida H (2016) Numerical investigation and optimization of pulsating and variable blank holder force for identification of formability window for deep drawing of cylindrical cup. Int J Adv Manuf Technol 82:583–593. https://doi.org/10.1007/s00170-015-7385-7
Klammt A (2019) Erfolgreicher Start von neuem Verbundprojekt CLARIAH-DE. https://dhd-blog.org/?p=11593. (Visited 12/2020)
Kleedörfer RW (1998) Prozess-und Änderungsmanagement der integrierten Produktentwicklung. Dissertation, TU München
Kleinaltenkamp M (1996) Customer integration - Kundenintegration als Leitbild für das Business-to-Business Marketing. In: Kleinaltenkamp M, Fließ S, Jacob F (eds) Customer integration. Gabler Verlag, Wiesbaden, pp 13–24
Klie JC, Bugert M, Boullosa B, de Castilho RE, Gurevych I (2018) The INCEpTION Platform: Machine-assisted and knowledge-oriented interactive annotation. In: Proceedings of the 27th international conference on computational linguistics: system demonstrations. Association for Computational Linguistics, pp 5–9
Klindt T (2014) § 8 Produktsicherheitsrecht – Marktüberwachungsrecht. In: Lenz T (ed) Produkthaftung. C. H. Beck, München, pp I–III
Klindt T (2015) Produktsicherheitsrecht, quo vadis? Zeitschrift für Innovations und Technikrecht, pp 37–38
Kloberdanz H, Engelhardt R, Mathias J, Birkhofer H (2009) Process based uncertainty analysis—an approach to analyze uncertainties using a process model. In: Norell Bergendahl M (ed) Design theory and research methodology, ds/design society. Design Society, Glasgow, pp 465–474. https://www.designsociety.org/publication/28608/Process+Based+Uncertainty+Analysis+
Kohler M, Krzyżak A (2017) Nonparametric regression based on hierarchical interaction models. IEEE Trans Inform Theory 63(3):1620–1630. https://doi.org/10.1109/TIT.2016.2634401
Kohler M, Krzyżak A (2018) Adaptive estimation of quantiles in a simulation model. IEEE Trans Inform Theory 64(1):501–512. https://doi.org/10.1109/TIT.2017.2743177
Kohler M, Tent R (2019) Nonparametric quantile estimation using surrogate models and importance sampling. Metrika. https://doi.org/10.1007/s00184-019-00736-3
Koppka F (2008) A contribution to the maximization of productivity and workpiece quality of the reaming process by analyzing its static and dynamic behavior: An analysis with focus on automotive powertrain production. Schriftenreihe des PTW. Shaker, Aachen (2009). TU Darmstadt, Dissertation
Krech M (2020) Adaptiver Umformprozess zur Herstellung und simultanen Kalibrierung von metallischen Strukturen mit bauteilintegrierten Kraft- und Drehmomentsensoren [Adaptive forming process for the production and simultaneous calibration of metallic structures with component-integrated force and torque sensors]. Dissertation, TU Darmstadt
Krech M, Trunk A, Groche P (2017) Controlling the sensor properties of smart structures produced by metal forming. Procedia Eng 207:1415–1420. https://doi.org/10.1016/j.proeng.2017.10.906. International Conference on the Technology of Plasticity, ICTP 2017
Lee BJ, Mear ME (1994) Studies of the growth and collapse of voids in viscous solids. J Eng Mater Technol 116(3):348–358. https://doi.org/10.1115/1.2904298
Lenz E, Hedrich P, Pelz PF (2018) Aktive Luftfederung - Modellierung, Regelung und Hardware-in-the-Loop-Experimente. Forschung im Ingenieurwesen 82(3):171–185. https://doi.org/10.1007/s10010-018-0272-2
Lenz J, Holzmann H, Platz R, Melz T (2019) Vibration attenuation of a truss structure with piezoelectric shunt-damping for varying static axial loads in the truss members. In: Proceedings of international conference on structural engineering dynamics (ICEDyn), pp 1–11
Li W, Li D, Ni J (2003) Diagnosis of tapping process using spindle motor current. Int J Mach Tools Manuf 43(1):73–79. https://doi.org/10.1016/S0890-6955(02)00142-6
Lichtenberg S (2000) Proactive management of uncertainty using the successive principle: a practical way to manage opportunities and risks. Polyteknisk Press
Liu G, Yuan SJ, Wang ZR, Zhou DC (2004) Explanation of the mushroom effect in the rotary forging of a cylinder. J Mater Process Technol 151(1–3):178–182. https://doi.org/10.1016/j.jmatprotec.2004.04.035
Liu T, Ko E, Sha S (1991) Diagnosis of tapping operations using an AI approach. In: Proceedings. 1991 IEEE international conference on robotics and automation. IEEE Comput. Soc. Press, pp 1556–1561. https://doi.org/10.1109/ROBOT.1991.131838
Luhmann N (1997) Die Gesellschaft der Gesellschaft, vol 2. Suhrkamp, Frankfurt a. M
Mahlamäki K, Ström M, Eisto T, Hölttä V (2009) Lean product development point of view to current challenges of engineering change management in traditional manufacturing industries. In: 2009 IEEE international technology management conference (ICE). IEEE, pp 1–8
Marciniak Z, Duncan J, Hu J (2002) Mechanics of sheet metal forming. Elsevier
Mathias J (2016) Auf dem Weg zu robusten Lösungen. Dissertation, TU Darmstadt
Meister JC (forthcoming) From TACT to CATMA or a mindful approach to text annotation and analysis. In: Rockwell G, Sinclair S (eds) Festschrift for John Bradley
Melz T, Hanselka H, Matthias M (2006) Adaptronische Systeme für automotive Anwendungen am Beispiel eines modularen, aktiven Strukturinterfaces [Smart Structures for Automotive Applications with the Example of a Modular Active Interface]. at – Automatisierungstechnik 54(6). https://doi.org/10.1524/auto.2006.54.6.284
Menz S (2015) §4. In: Klindt T (ed) Produktsicherheitsgesetz ProdSG. C. H. Beck, München
Meressi T, Paden B (1993) Buckling control of a flexible beam using piezoelectric actuators. J Guidance, Control, Dyn 16(5):977–980. https://doi.org/10.2514/3.21113
Merkel J (2008) Untersuchungen zum Einfluss von Kugelstrahl- und Festwalzbehandlungen auf den Randschichtzustand und die Schwingfestigkeit von Sintereisenwerkstoffen, Schriftenreihe Werkstoffwissenschaft und Werkstofftechnik, vol 45. Shaker, Aachen. Karlsruhe University, Dissertation
Mitschke M, Wallentowitz H (2014) Dynamik der Kraftfahrzeuge. Springer Vieweg, Wiesbaden. https://doi.org/10.1007/978-3-658-05068-9
Moheimani SOR, Fleming AJ (2006) Piezoelectric transducers for vibration control and damping. Advances in industrial control. Springer, London. https://doi.org/10.1007/1-84628-332-9
Monka P, Monkova K, Uban M, Hruzik L, Vasina M (2018) Vibrodiagnostics as the tool of a tap wear monitoring. Procedia Struct Integrity 13:959–964. https://doi.org/10.1016/j.prostr.2018.12.179
Moré JJ (1978) The Levenberg–Marquardt algorithm: implementation and theory. In: Numerical analysis. Springer, Berlin, pp 105–116
Mori K (2011) Application of servo presses to sheet metal forming. Key Eng Mater 473:27–36. https://doi.org/10.4028/www.scientific.net/KEM.473.27
Morris PWG (1997) The management of projects. T. Telford, London
Naber D (2005) OpenThesaurus: Ein offenes deutsches Wortnetz. In: Fisseni B, Schmitz HC, Schroeder B, Wagner P (eds) Sprachtechnologie, mobile Kommunikation und linguistische Ressourcen: Beiträge zur GLDV-Tagung 2005 in Bonn, no. 8 in Sprache, Sprechen und Computer; Computer studies in language and speech. Peter Lang, Frankfurt am Main, New York
Needleman A (1972) A numerical study of necking in circular cylindrical bar. J Mech Phys Solids 20(2):111–127. https://doi.org/10.1016/0022-5096(72)90035-X
Neubauer M, Oleskiewicz R, Popp K, Krzyzynski T (2006) Optimization of damping and absorbing performance of shunted piezo elements utilizing negative capacitance. J Sound Vib 298(1–2):84–107. https://doi.org/10.1016/j.jsv.2006.04.043
Niwa K, Matsumura H (1993) Gleit-wälz-lager. Patent DE4327543 C2
Noy NF, McGuinness DL (2000) Ontology development 101: A guide to reating your first ontology
Nusskern P, Hoffmeister J, Schulze V (2014) Powder metallurgical components: Improvement of surface integrity by deep rolling and case hardening. Procedia CIRP 13:192–197. https://doi.org/10.1016/j.procir.2014.04.033
Obara RM (1998) Kombiniertes Lager. Patent DE69927078 T2
Ogden CK, Richards IA (1923) The meaning of meaning. K. Paul, Trench, Trubner and Company, New York
Okereke C (2015) Business. In: Bäckstrand K, Lövbrand E (eds) Research handbook on climate governance. Edward Elgar Publishing, pp 262–272. https://doi.org/10.4337/9781783470600.00034
OLG Frankfurt: Urteil vom 05. Juli 2018—6 U 28/18
Osakada K, Mori K, Altan T, Groche P (2011) Mechanical servo press technology for metal forming. CIRP Ann 60(2):651–672. https://doi.org/10.1016/j.cirp.2011.05.007
Pahl G, Beitz W (1977) Konstruktionslehre: Handbuch für Studium und Praxis. Springer, Berlin
Pahl G, Beitz W (1997) Konstruktionslehre: Methoden und Anwendung, 4th edn. Springer, Berlin, Heidelberg, New York
Pahl G, Beitz W (2013) Konstruktionslehre: Methoden und Anwendung. Springer, Berlin
Pahl G, Beitz W, Feldhusen J, Grote KH (2005) Konstruktionslehre: Grundlagen erfolgreicher Produktentwicklung Methoden und Anwendung, 6th edn. Springer, Berlin, Heidelberg. https://doi.org/10.1007/b137606
Pahl G, Beitz W, Feldhusen J, Grote KH (2007) Engineering design: a systematic approach, 3rd edn. Springer, London, Cham. https://doi.org/10.1007/978-1-84628-319-2
Parteder E (2000) Ein Modell zur Simulation von Umformprozessen pulvermetallurgisch hergestellter hochschmelzender Metalle, Umformtechnische Schriften, vol 94. Shaker, Aachen (2000). RWTH Aachen, Dissertation
Perminova O, Gustafsson M, Wikström K (2008) Defining uncertainty in projects - a new perspective. Int J Project Manag 26(1):73–79
Peterson RA (1964) Combination bearing. Patent US3305280 A
Platz R, Ondoua S, Habermehl K, Bedarff T, Hauer T, Schmitt SO, Hanselka H (2010) Approach to validate the influences of uncertainties in manufacturing on using load-carrying structures. In: ISMA2010 international conference on noise and vibration engineering, pp 5319–5334
Pohl K (2010) Requirements engineering: fundamentals. Principles and Techniques. Springer, Heidelberg
Pohl K, Rupp C (2015) Basiswissen Requirements Engineering: Aus- und Weiterbildung zum Certified Professsional for Requirements Engineering, fourth edn. dpunkt.verlag, Heidelberg
Ravetz JR (1986) Usable knowledge, usable ignorance: Incomplete science with policy implications. In: Clark C, Munn RE (eds) Sustainable development of the biosphere. Cambridge University Press, Cambridge, pp 415–432
Renn O (1981) Wahrnehmung und Akzeptanz technischer Risiken. Dissertation, University of Köln. https://doi.org/10.18419/opus-7503
Reynolds O (1886) IV. On the theory of lubrication and its application to Mr. Beauchamp tower’s experiments, including an experimental determination of the viscosity of olive oil. Philoso Trans R Soc Lond 177:157–234. https://doi.org/10.1098/rstl.1886.0005
Riviere A, Féru F, Tollenaere M (2003) Controlling product related engineering changes in the aircraft industry. In: DS 31: Proceedings of ICED 03, the 14th international conference on engineering design. Stockholm
Rowley J (2007) The wisdom hierarchy: Representations of the DIKW hierarchy. J Inform Sci 2(33):163–180. https://doi.org/10.1177/0165551506070706
Ruder S (2016) An overview of gradient descent optimization algorithms. arXiv:1609.04747
Santner TJ, Williams BJ, Notz WI (2018) The design and analysis of computer experiments, 2nd edn. Springer series in statistics. Springer, New York
SASIG (2009) ECM Recommendation Part 0. Verband der Automobilindustrie
Sauer M (2013) Vorgehensmodell zur Implementierung eines meilensteingestützten Kundenänderungsmanagements. No. 21 in Stuttgarter Beiträge zur Produktionsforschung. Fraunhofer-Verlag, Stuttgart
Schaeffner M (2019) Quantification and evaluation of uncertainty in active buckling control of a beam-column subject to dynamic axial loads. Dissertation, TU Darmstadt. https://tuprints.ulb.tu-darmstadt.de/8652
Schaeffner M, Platz R (2018) Gain-scheduled \(H_\infty \) buckling control of a circular beam-column subject to time-varying axial loads. Smart Mater Struct 27(6). https://doi.org/10.1088/1361-665X/aab63a
Schaeffner M, Platz R, Melz T (2020) Adequate mathematical beam-column model for active buckling control in a tetrahedron truss structure. In: Proceedings of the 38th IMAC, conference proceedings of the society for experimental mechanics. Springer, Berlin, pp 323–332. https://doi.org/10.1007/978-3-030-47638-0_35
Schatt W, Wieters KP, Kieback B (eds) (2007) Pulvermetallurgie: Technologien und Werkstoffe, second edn. VDI-Buch. Springer, Berlin. https://doi.org/10.1007/978-3-540-68112-0
Scheitza M (2010) Konzeption eines flexiblen 3D-Servo-Pressensystems und repräsentative Basisanwendungen: Matthias Scheitza. Berichte aus Produktion und Umformtechnik. Shaker, Aaachen
Scheitza M, Schmitt SO, Emde S (2013) Potential and challenges of combined roller and plain bearings for servo presses. Adv Mater Res 769:285–292. https://doi.org/10.4028/www.scientific.net/AMR.769.285
Schmitt SO (2015) Vorgehensmodell der realen iterativen Produktentwicklung. Shaker, Aachen
Schmitt SO, Scheitza M, Groche P (2015) A model for improving the applicability of design methodologies to mechanical engineering design routines. J Eng Des 26(10–12):302–320
Schneider W, Heinrich B (2008) Praktische Regelungstechnik, vol 3. Vieweg+Teubner, Wiesbaden
Siemens AG: SINUMERIK 840D sl/828D Synchronaktionen. Funktionshandbuch (2015). https://cache.industry.siemens.com/dl/files/521/109481521/att_862872/v1/FBSYsl_1015_de_de-DE.pdf
Sinz J, Groche P (2019) Effekte der Größenskalierung auf die Funktionsfähigkeit kombinierter Wälz-Gleitlager. In: 13. VDI-Fachtagung Gleit- und Wälzlagerungen 2019: Gestaltung – Berechnung – Einsatz, VDI-Berichte Band 2348. VDI Verlag
Sinz J, Knoll M, Groche P (2019) Operational effects on the stiffness of combined roller and plain bearings. Procedia Manuf 41:650–657. https://doi.org/10.1016/j.promfg.2019.09.054
Sinz J, Niessen B, Groche P (2018) Combined roller and plain bearings for forming machines: Design methodology and validation. In: Schmitt R, Schuh G (eds) Advances in production research: proceedings of the 8th congress of the german academic association for production technology (WGP). Springer, Berlin, pp 126–135
Sivak M, Schoettle B (2015) Motion sickness in self-driving vehicles. Technical Report. UMTRI-2015-12, Transportation Research Institute, University of Michigan
Skogestad S, Postlethwaite I (2001) Multivariable feedback control. Wiley, New York
Smith PG, Reinertsen DG (1992) Shortening the product development cycle. Res Technol Manag 35(3):44–49
Sommer S (2020) Wertberichtigung. Brand eins 10:94
Spath D, Koch S (2009) Grundlagen der Organisationsgestaltung. In: Handbuch Unternehmensorganisation. Springer, Berlin, pp 3–24
Spindler G (2004) IT-Sicherheit und Produkthaftung - Sicherheitslücken, Pflichten der Hersteller und der Softwarenutzer. Neue Juristische Wochenschrift 57(44):3145–3150
Stegmeier J, Hartig J, Bartsch S, Leštáková M, Logan K, Rapp A, Pelz PF (2021) Semantic uncertainty in norms. In: Groche P, Pelz PF (eds) Uncertainty in mechanical engineering: selected, peer reviewed papers from the 4th international conference on uncertainty in mechanical engineering (ICUME 2021). Springer, Berlin
Stekolschik A (2016) Engineering change management method framework in mechanical engineering. In: IOP conference series: materials science and engineering, vol 157. https://doi.org/10.1088/1757-899x/157/1/012008
Strauß D (2015) Examination regarding the redensification of porous sintering parts respecting the additional movement capabilities of the 3D servo press. Master-thesis, TU Darmstadt
Taguchi G, Chowdhury S, Taguchi S (2000) Robust engineering: learn how to boost quality while reducing costs and time to market. McGraw-Hill, New York. http://www.loc.gov/catdir/bios/mh041/99041786.html
Taguchi G, Yano H, Chowdhury S, Taguchi S (2005) Taguchi’s quality engineering handbook. Wiley, Hoboken, N.J and Livonia, Mich. https://doi.org/10.1002/9780470258354
Takemasu T, Koide T, Shinbutsu T, Sasaki H, Takeda Y, Nishida S (2014) Effect of surface rolling on load bearing capacity of pre-alloyed sintered steel gears with different densities. Procedia Eng 81:334–339. https://doi.org/10.1016/j.proeng.2014.10.002
Thamhain H (2013) Managing risks in complex projects. Project Manag J 44(2):20–35
Thompson SP, Loughlan J (1995) The active buckling control of some composite column strips using piezoceramic actuators. Compos Struct 32:59–67. https://doi.org/10.1016/0263-8223(95)00048-8
Timoshenko SP, Gere JM (1961) Theory of elastic stability. McGraw-Hill
Türk M, Groche P (2010) Integration of adaptive components by incremental forming processes. In: Ghasemi-Nejhad MN (ed) Active and passive smart structures and integrated systems 2010, vol 7643. International Society for Optics and Photonics, SPIEM, pp 447–455. https://doi.org/10.1117/12.847280
Tvergaard V (1981) Influence of voids on shear band instabilities under plane strain conditions. Int J Fracture 17(4):389–407. https://doi.org/10.1007/BF00036191
Unsworth J (2000) Scholarly primitives: What methods do humanities researchers have in common, and how might our tools reflect this? In: Symposium on humanities computing: formal methods, experimental practice, vol 13. London. https://johnunsworth.name/Kings.5-00/primitives.html (Visited 12/2020)
Val AGD, Fernández J, Arizmendi M, Veiga F, Urízar J, Berriozábal A, Axpe A, Diéguez P (2013) On line diagnosis strategy of thread quality in tapping. Procedia Engineering 63:208–217. https://doi.org/10.1016/j.proeng.2013.08.196. The Manufacturing Engineering Society International Conference, MESIC 2013
Value Balancing Alliance e. V (2020). https://www.value-balancing.com
Verband der Automobilindustrie (VDA) (2015) Automatisierung von Fahrerassistenzsystemen zum automatisierten Fahren. VDA Magazin – Automatisierung
Verein Deutscher Ingenieure (1986) VDI 2221:1986–11 Methodik zum Entwickeln und Konstruieren technischer Systeme und Produkte [Systematic approach to the development and design of technical systems and products]. Beuth, Berlin
Verein Deutscher Ingenieure (1992) VDI 2204 Blatt 2:1992–09 Auslegung von Gleitlagerungen; Berechnung [Design of plain bearings; calculation]. Beuth, Berlin
Verein Deutscher Ingenieure (1993) VDI 2221:1993–05 Methodik zum Entwickeln und Konstruieren technischer Systeme und Produkte [Systematic approach to the development and design of technical systems and products]. Beuth, Berlin
Verein Deutscher Ingenieure (2005) VDI/VDE 3682:2005–09 Formalisierte Prozessbeschreibungen [Formalised process descriptions]. Beuth, Berlin
Verein Deutscher Ingenieure (2015) VDI 3334:2015–03 Maschinelle Innengewindefertigung [Machining of internal threads]. Beuth, Berlin
Wagner G (2020) § 823. In: F.J. Säcker, R. Rixecker, H. Oetker, B. Limperg (eds.) Münchener Kommentar zum Bürgerlichen Gesetzbuch, vol 7, eighth edn. C. H. Beck, München
Wang QS (2010) Active buckling control of beams using piezoelectric actuators and strain gauge sensors. Smart Mater Struct 19(6):1–8. https://doi.org/10.1088/0964-1726/19/6/065022
Wehling P (2007) Wissen und Nichtwissen. In: Schützeichel R (ed) Handbuch Wissenssoziologie und Wissensforschung. UVK, Konstanz, pp 485–494
Wehling P (2012) Gibt es Grenzen der Erkenntnis? Von der Fiktion grenzenlosen Wissens zur Politisierung des Nichtwissens. In: Wengenroth U (ed) Grenzen des Wissens - Wissen um Grenzen. Velbrück, Weilerswist, pp 90–117
Wendt J, Oberländer M (2016) Product compliance: Neue Anforderungen an sichere Produkte. Zeitschrift für Energie- und Technikrecht, pp 62–70
Wideman R (1986) Risk management. Project Manag J17(8):20–26
Wiedemann J (2007) Leichtbau. Springer, Elemente und Konstruktion
Wong RKW, Storlie CB, Lee TCM (2017) A frequentist approach to computer model calibration. J R Stat Soc Ser B Stat Methodol 79(2):635–648. https://doi.org/10.1111/rssb.12182
Wu WH, Fang LC, Wang WY, Yu MC, Kao HY (2014) An advanced CMII-based engineering change management framework: the integration of PLM and ERP perspectives. Int J Prod Res 52(20):6092–6109
Würtenberger J (2018) Ein Beitrag zur Identifikation und Beherrschung von Unsicherheit bei der Modellierung technischer Systeme. Dissertation, TU Darmstadt
Yu X, Yang Z, Wang G, Lu J (2013) Study on design change review for small and medium-sized enterprises. In: 2013 IEEE international conference on industrial engineering and engineering management. IEEE, pp 556–560
Zech H (2019) Künstliche Intelligenz und Haftungsfragen. Zeitschrift für die Privatrechtswissenschaft 5(2):198–219
Zenz G, Humer A (2015) Stability enhancement of beam-type structures by piezoelectric transducers. Acta Mechanica 226(12):3961–3976. https://doi.org/10.1007/s00707-015-1445-9
Zirn C, Nastase V, Strube M (2008) Distinguishing between instances and classes in the Wikipedia taxonomy. In: Bechhofer S, Hauswirth M, Hoffmann J, Koubarakis M (eds) The semantic web: research and applications, vol 5021. Springer, Berlin, Heidelberg, pp 376–387. https://doi.org/10.1007/978-3-540-68234-9_29
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2021 The Author(s)
About this chapter
Cite this chapter
Groche, P. et al. (2021). Methods and Technologies for Mastering Uncertainty. In: Pelz, P.F., Groche, P., Pfetsch, M.E., Schaeffner, M. (eds) Mastering Uncertainty in Mechanical Engineering. Springer Tracts in Mechanical Engineering. Springer, Cham. https://doi.org/10.1007/978-3-030-78354-9_5
Download citation
DOI: https://doi.org/10.1007/978-3-030-78354-9_5
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-78353-2
Online ISBN: 978-3-030-78354-9
eBook Packages: EngineeringEngineering (R0)