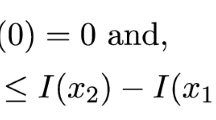Risk-Sharing and Contingent Premia in the Presence of Systematic Risk: The Case Study of the UK COVID-19 Economic Losses

Abstract

Motivated by macroeconomic risks, such as the COVID-19 pandemic, we consider different risk management setups and study efficient insurance schemes in the presence of low probability shock events that trigger losses for all participants. More precisely, we consider three platforms: the risk-sharing, insurance and market platform. First, we show that under a non-discriminatory insurance assumption, it is optimal for everybody to equally share all risk in the market. This gives rise to a new concept of a contingent premium which collects the premia ex-post after the losses are realised. Insurance is then a mechanism to redistribute wealth, and we call this a risk-sharing solution. Second, we show that in an insurance platform, where the insurance is regulated, the tail events are not shared, but borne by the government. Third, in a competitive market we see how a classical solution can raise the risk of insolvency. Moreover, in a decentralised market, the equilibrium cannot be reached if there is adequate sensitivity to the common shock events. In addition, we have applied our theory to a case where the losses are calibrated based on the UK Coronavirus Job Retention Scheme.

6.1 Introduction

The recent COVID-19 crisis increased the collective need for risk management tools for financial institutions, and such tools require the management of systematic losses, illiquidity, default, and the need for financial aid by the government. Most of the credit by borrowing became uncertain, and there is an imminent demand by the clients and the regulator to manage and mitigate the credit risk.

Motivated by the large economic loss due to the recent COVID-19 pandemic, the management of the macroeconomic risk has become the subject of new research. The economic impact of COVID-19 not only emphasises the need for risk management tools to deal with the economic losses for each single country, but it has also shown the need for the global measures to overcome the economic impact. In this paper we look at this problem from an insurance perspective. We consider three risk management platforms, namely, risk-sharing, insurance and the market platform.

In the risk-sharing platform we consider a machinery that redistributes the wealth of the policyholders. We will see that among the three platforms, the risk-sharing platform is the only one that can give the perfect pooling solution, which is the most optimal solution. This means that everybody’s wealth is the average of the society’s (or insurance cohort’s) wealth. Furthermore, this solution gives rise to the concept of a contingent premium, which means that the premium cannot be collected ex-ante but ex-post. As a wealth distribution mechanism, this platform is to some extent resembling the state fiscal and monetary policies, which will be discussed in the next section.

In the second platform we consider a regulated insurance company that offers insurance policies. The optimal solution in this platform is a partial pooling that shares the wealth in the non-extreme events. In this platform, the policyholders do not pay for the extreme events which necessitates the existence of a protection to the policyholder by providing a bail-out plan.

In the third platform, we consider two different markets: a competitive and a decentralised market. In the competitive market, the optimal premium is the mean of the losses that is identical to classical solutions. However, as we will discuss, this platform significantly increases the insolvency risk. In the decentralised market, the main objective is to reach the market equilibrium. We will see that if the systematic event is not a tail event,¹ which means that large losses occur with sufficiently large probability, then the market equilibrium does not exist despite avoiding the risk of insolvency. On the contrary, if the systematic event is a tail event, despite of rising the insolvency risk, there exists an equilibrium in the market.

To study the implications of our paper, we have constructed an example based on the economic impact of COVID-19 in the UK and particularly we use a calibration arising from the Coronavirus Job Retention Scheme (UK furlough scheme during the COVID-19 pandemic). In this way we can measure several things, for instance the magnitude of the insolvency risk in a competitive market or the magnitude of the pricing gaps in a decentralised market due to a difference in the market demand and supply prices. We have made some observations; given the magnitude of the economic risk generated during the COVID-19 pandemic in the UK, traditional insurance products with ex-ante premia are not sufficient to cope with such huge financial losses. Therefore, a new paradigm needs to be adopted where a contingent premium can readily be incorporated to deal with substantial systematic events.

This paper is organised as follows. In Sect. 6.2 we discuss five risk levels in insurance and introduce the concept of systematic risk. In Sect. 6.3 we introduce the mathematical setup, the preliminaries, and a classical insurance platform. In Sect. 6.4 we define three platforms: the risk-sharing, insurance, and market platform. In this section we obtain the optimal solution in each platform and discuss some policy implications. In Sect. 6.5 we study the three platforms in the presence of three common shock models and study the results of particular examples. Especially, we construct our examples for a case that is calibrated based on the UK Coronavirus Job Retention Scheme. In Sect. 6.6 we conclude.

6.2 Risk Levels and Systematic Risk in Insurance

The general idea in risk management is to dilute the risk by splitting it into smaller risks, sharing, and spanning it over time. This can be called ‘smoothing’ and risk management ‘tools’ help to do this. We can identify two approaches to risk management: diversification and risk-sharing. Diversification means that the risk of a portfolio of assets is less than the sum of the risks of the single assets. In mathematical terms this can be formulated as follows: any convex combination of two assets carries lower risk than single ones. Despite all the controversies about the definition of diversification, and that it always can reduce the risk, the majority has widely accepted this approach. On the aggregate risk, financial institutions need to hold capital to be allowed to bear any remaining risk.

On the other hand, the underlying idea of risk-sharing is to exchange risk with counterparties such as an insurer, reinsurer, or via market securitisation. Risk-sharing with expected utility by maximising the agents preferences has been studied extensively in actuarial science and economics, see for instance Borch (1962) and Wilson (1968). The most popular concept of efficiency is Pareto optimality. A risk-sharing contract is called Pareto optimal if there does not exist another feasible contract that is better for all agents and strictly better for at least one agent. For instance, if agents are endowed with exponential utilities, then it is Pareto optimal to share the aggregate risk in the market in a proportional way. On the other hand, if coherent distortion risk measures, such as the well-known Expected Shortfall, are used, it is Pareto optimal to share the aggregate risk in the market via tranches (Boonen 2015). Risk-sharing can be related to the concept of hedging or reinsurance. This is closely related to market principles, like Arrow-Debreu equilibria, no-arbitrage, and no-good-deal principles (Assa and Karai 2012). This also has been discussed by Albrecht (1991), and practical considerations as pricing principle are discussed by Wang et al. (1997), where an axiomatic characterisation of the insurance prices is shown.

To see how the two approaches can be used in the real application we need to know about the risk levels. We have identified different levels of risks by the risk trading markets as we assume the existence of a market is the main indication of the willingness to introduce a risk management product. As such we can identify five different levels.

• The retail-level: At this level individuals usually share their risk with another entity; for example, they can buy insurance policies for sharing the risk (a risk transfer). The insurance retail market is where the risk is managed.

• The corporate level: At this level companies use a combination of diversification and risk-sharing approaches to manage the risk e.g., an insurance company pools the risk of its client while at the same time buys reinsurance. The (re)insurance market is where the risk is managed.

• The catastrophic level: The main characteristic of catastrophic risk is that their impact is in most cases independent of the pool size, and therefore cannot be managed easily in insurance markets. Natural disasters or cyber risks are among the most known examples of catastrophic risks. The usual ways of managing such risks include introducing a risk transfer platform to share the risk with the financial markets, through for example CAT bonds; or in general to introduce Alternative Risk Transfers (ART) (Banks 2004; Olivieri and Pitacco 2011). These arrangements can transfer the risk of systematic events and can help the managing of the catastrophe risk by lowering the cost of reinsurance, and or the need for capital allocation. Cyber risk includes the costs involved in the event of a data breach or ransomware (Eling 2020).

• The systemic level: The risk of system failure is endogenous, and a result of system failure due to the connectedness of insurers’ or banks’ lending relations. At the theoretical level there have been some discussions how to manage the systemic risk by Merton (1990) and Shiller (2007).

• The macro-level: The examples can include world wars and pandemics where no market for trading risk can be considered even at the theoretical level. The underlying probability distribution and the corresponding losses are exogenous and hard to accurately predict. In a macro-level risk, the challenge is that since the insurance market is not feasible even at a theoretical level, it seems there is no efficient way for risk management. From the insurance perspective, we need to have a deeper understanding of insurance principles as well as the time direction of an insurance’s risk management.

At all five levels, systematic risk may exist, which can be interpreted as a market risk factor that affects the risk variables in the same direction. Systematic risk is usually attributed to a common shock. Examples of systematic risk include financial market indices, but also the aging population, and epidemics. Given the magnitude and the systematic nature, there are lots of discussions on how and in which market to manage the risk of systematic events.

• Bilateral GDP income swaps by Merton (1990) or GDP linked securities by Shiller (2007) are among the major “theoretical” solutions. The idea here is to introduce some securities that can share the risk among the countries in the world. These solutions without a doubt need international collaboration to run markets that trade such instruments.

• Another way of managing the systematic risks is risk-sharing, which is claimed to be happening by globalisation (Flood et al. 2012) and peer-to-peer insurance (Denuit 2020; Feng et al. 2020).

• Another option is to run a deficit and essentially transfer the systematic risk to the same society that needs to bear the risk. This is an example of market failure as society would not be willing to take a rather expensive and uncertain product. But the state, including the government and the central banks, have the authority and tools to sell the risk by running state policies such as monetary and fiscal policies.

It seems that with the current risk management tools a systematic risk has been considered manageable, at the practical or theoretical level, as long as it does not belong to the category of macro risks. That also includes any insurance solution. So, it is necessary to have a closer look into the insurance risk management mechanisms and approaches to see the problem.

In insurance, a stronger approach than diversification is risk pooling, which under the assumption of independence of losses implies the “insurance principle”. The insurance principle is explained as follows by Albrecht (1991):

for a growing collective the relative (i.e. divided by the number of risks) safety loading and the relative security capital required to maintain a certain security level of the insurance company is decreasing.

Pooling means sharing losses by aggregating the accident costs and then split this equally. However, if there is a risk of common shocks, it is no longer clear that pooling can imply the principle of insurance. Common shock is modelled to include systematic risk, and heavy losses on the common shock lead to heavy losses of the insurers. Any ex-ante risk management approach needs to render a present value that represents the risk. This is necessary to make a correct risk assessment. This brings us to the concept of risk valuation. Pooling can help to make such an assessment under the independence assumption of losses. However, as we relax the independence assumption, which means there is a risk of common shocks, pooling no longer will be able to easily render a deterministic value. The (wide) dependency relation can properly be related to the concept of systematic risk. The meaning of this is that under a systematic risk circumstance, pooling would not mitigate all randomness and the remaining randomness needs to be measured for valuation.

In a historical context there have been two major risk management institutions i.e., the insurance and the banking industry, with more than 300 years of modern history. While insurance leverages against insurable risk by collecting premia ex-ante, banking leverages against the credit risk by collecting interest ex-post. In the past 300 years, the world has witnessed a handful number of macro risks, including pandemics, world wars, etc. However, insurance never was part of the solution whereas (central) banking always has played a crucial role. By far, the most well-known ways to encounter macro risk is to introduce fiscal and monetary policies, that can be regarded as ex-post policies.

It seems at a macro level risk, insurance may not be sustainable solution. For insurance, we are often using a future extreme loss as a benchmark (say “once in 100 years”), which makes us rely on the modelling aspect of a quantitative risk assessment. The modelling of rare systematic events usually result in a lack of robustness and huge risk assessment errors. However, even with reliable models, the aggregate nature of common shocks, that is one of the major characteristics of systematic events, is a major challenge for introducing sound insurance solutions. The alternative solutions include the monetary and fiscal policies that are implemented by the state institutions like central banks and the governments. Given that in a macro-level event the whole system will be impacted, the governments will need to borrow the risk capital from the future generations and the contributions from the past (the buffer) are generally insufficient. So, an important point here is to distinguish the differences in the time direction of a sound risk management solution for macro risks. This will be more discussed in the following which constitutes part of the main contribution of this paper by introducing insurances with contingent premia as an ex-post rather than ex-ante policies.

In this paper we model systematic events that have an impact on a large part of the pool of policyholders. The closest concept in the literature to this is probably the concept of common shocks. The idea is to introduce an independent random variable (independent from losses), that represents the losses with a common cause. This variable can either be summed up or multiplied to the other random variables or it can change the severity and frequency of losses. Lindskog and McNeil (2003) use the common Poisson shock processes to model dependent event frequencies and examine these models in the context of insurance loss modelling. Meyers (2007) discusses an approach where the common shock variable is a multiplier of a pool of independent losses. In this paper, the author describes some more general models involving common shocks to both the claim count and claim severity distributions. Avanzi et al. (2018) consider a model where the common shock is additive with the loss variables. For the estimation of diversification benefits, they develop a methodology for the construction of large correlation matrices to any dimension.

The concepts of macroeconomic risk and systematic risk have been thoroughly studied in the literature. However, to the best of the authors knowledge they are not covering the type of risk we discuss in this paper. In the literature, macroeconomic risk is usually referred to as the risk generated by macroeconomic factors and political decisions which can include GDP, inflation, unemployment and central bank interest rate. The main objective is to manage the risk of the macroeconomic factors on financial stock returns or global investment. For instance, Majumder and Majumder (2002) consider the volatility of GDP as the most common problem worldwide whose risk can be shared through the trading of GDP growth rate-related bond, to obtain a mutually preferable allocation of aggregate income.

On the other hand, systematic risk in the literature is usually known as a cause of insurance failure, that is associated with many losses that are positively correlated. Beyond the common shock model that we study in this paper, other popular ways to model systematic risk is via vine copulas (Aas et al. 2009) or positive dependence constraints (Bignozzi et al. 2015).

The focus in this paper is on systematic risk rather than on systemic risk. Systemic risk involves the modelling of the potential collapse of a system and the corresponding default events and is typically modelled via interbank lending networks (see, e.g., Eisenberg and Noe 2001). Our focus is the modelling of common shocks in (insurance) loss variables.

6.3 Mathematical Setup

6.3.1 Probability Space

Let us consider a non-atomic probability space $(\Omega ,\mathcal {F},P)$, where $\Omega$ is the states of the world, $\mathcal F$ is a sigma algebra and P is a probability measure. All random variables are measurable with respect to $\mathcal F$. We assume our probability space is rich enough to introduce any sequence of i.i.d. random variables with a given distribution. Consider a set of bounded losses $X_{1},X_{2},\ldots$ and assume that the losses are identically distributed with a shared distribution $X_{i}\sim X$. Let us assume that $X_{i}$ is non-negative and satisfies $\text {esssup}(X_{i})=M$. We also denote the cumulative distribution function of random variable X by $F_{X}$ and the expectation is denoted by E. We consider a framework with two time steps 0, 1.

Consider a set of policyholders $\left\{ 1,2,\ldots ,n\right\}$. We assume that the policyholders are homogeneous in that they have the same initial wealth $w_{0}$ at time 0 and have loss variable $X_{1},X_{2},\ldots ,X_{n}$ that are identically distributed at time 1. The final wealth of policyholder i at time 1 is given by $W_i$ and is a measurable random variable. In absence of purchasing insurance, the final wealth of each single policyholder i is $W_i=w_{0}-X_{i}$. The policyholders are endowed with Von Neumann-Morgenstern expected utility (see Varian 2019) functions denoted by $u_{i}$, $1=1,2,\ldots ,n$, which are assumed to be increasing and concave.

In the following, we consider a risk tolerance parameter $\eta \in (0,1)$, that is usually very close to 0. This parameter will be used to measure the sensitivity against the tail (usually unfavourable) events. This parameter specifies the tail events as events $A\in \mathcal {F}$ such that $P(A)\le \eta$. This definition is motivated by Liu and Wang (2021).²

6.3.2 Insurance Preliminaries

We assume two major types of economic agents in our setup: policyholders (also called insureds) and an insurer. The policyholders and the insurer have different attitudes towards risk and insurance.

Policyholders. Policyholders are endowed with risk-averse preferences. To model the behaviour of such agents we could consider suitable utility functions that are applied to the agents’ final wealth, which is random. Alternatively, one can also consider the policyholders as risk-neutral (expected profit maximising) agents; this is often assumed in reinsurance where the reinsurance buyer is a firm itself or when the insurance is traded as part of business risk management, for instance in a supply chain (Assa et al. 2021). Risk aversion for expected utility maximising agents implies that the utility function is concave. All policyholders maximise their own utility. A choice is objective if all agents agree on the same choice regardless of the utility functions they have. It is well known that a policy is objectively chosen i.e., it is the best choice for all utility functions if and only if it is second-order stochastic dominant. Considering two random variables X and Y, we say that X dominates Y in second stochastic dominance if $E(u(Y))\le E(u(X))$ for all increasing and convex utility functions u, and this is denoted by

$$Y\preceq _{SSD}X.$$

In some cases, one also assumes that all policyholders have the same utility function. In this case, one also can appeal to the well-known concept of a representative agent.

The demand for insurance with alternative (not expected utility) preferences has been extensively studied in the literature, see for instance Schlesinger (2000) for an overview. An interesting type of utility that is very useful for investigating the insurance demand is the one that is promoted by prospect theory of Kahneman and Tversky (1979) or rank-dependent utility theory of Quiggin (1993). In our work we consider insuring against low probability events, like events that are expected to happen only once in 100 years, but that have a very large impact in the insurable losses in the market. To better understand the aspects of the problem, note that from the demand side we are dealing with policyholders. For a policyholder, 1% is an ultra-low probability. It is known in the literature that prospect theory and rank-dependent utility theory provide better assessment of the demand for this situation compared with other measures, as the policyholder is expected to overweight the probability of 1% in their mental assessment of the risk. A good study about this subject is Schmidt (2016), who explains empirical evidence that show that people are unwilling to insure rare losses at subsidised premia. There is also a discussion around the importance of risk aversion and loss aversion for assessing small-probability losses (Eeckhoudt et al. 2018).

Insurer. The insurer is an entity that offers the risk management tool to the policyholders. The insurer can be a firm (e.g., an insurance company), government or a (guarantee) fund. The insurer’s concern is either to maximise the expected profit or to reach a particular business objective; for instance, to reach a targeted loss ratio. If the insurer is a government, the objective of the insurer is given by a social welfare function, and the insurer can bail-out the pool of policyholders with taxpayers’ money in case of high aggregate losses. The insurer is here modelled as a mutual insurer or a stock insurer, and we assume that the insurers are concerned with the welfare of the policyholders or with a non-negative expected profit condition per policy. Moreover, we assume that the insurer does not “over-insure” a risky position. In fact, a special case of over-insuring is double insurance, and this is generally not legally allowed. There are different objectives for the insurer in our platforms that can be seen later in (6.1), (6.2), (6.5) and (6.11).

Risk management platforms. In this paper we use three risk platforms: (a) risk-sharing, (b) insurance and (c) market platforms. In the risk-sharing platform the policyholders share the risk by introducing a fund. There is no other entity like government or the insurance company. In insurance platform we consider there is an insurance company that issues the insurances for the policyholders. The policyholders are making their decision by maximising their preferences and the insurance company is concerned with the welfare of all policyholders. Finally, we consider two market platforms, one that sets for a competitive market solution and another one where in a decentralised market the equilibrium needs to be reached.

In all our platforms, we assume that the following assumption holds, which we denote by NDI (non-discriminatory insurance).

Assumption NDI The insurance will treat all the policyholders equally so that their final wealth has the same distribution.

NDI explicitly tells us that there are no claim hierarchies or priority claims, and all policyholders are treated the same. Any re-labelling (also called permutation) of the policyholder set $\left\{ 1,2,\ldots ,n\right\}$ leads to the same insurance contract. Under NDI, if all policyholders use the same utility function, then the utility after purchasing insurance is the same for every policyholder. This utility can then be interpreted as the utility of a representative policyholder. However, as we will see we do not need to assume that the policyholders have the same utility. In the literature, optimal insurance contracts often satisfy NDI (see, e.g., Albrecht and Huggenberger 2017; Boonen 2019), but we are the first to impose NDI ex-ante as a property for “desirable” insurance contracts. In addition, from a technical point of view and unlike most of the literature, NDI is not concerned about the joint distribution of the policyholders’ final wealth i.e., the final wealth joint distributions of the same number of policyholders do not need to be identical. In addition, we do not need to assume that the policyholders have the same utility functions.

As an immediate implication of NDI, we have the following useful lemma.

Lemma 6.1

Consider a set of individual identically distributed wealth, $W_{1},\ldots ,W_{n}$ then for all $j=1,\ldots ,n$, $W_{j}\preceq _{SSD}\frac{\sum _{_{1\le i\le n}}W_{i}}{n}$.

Proof

Let u be an increasing, concave function that is twice differentiable and let $W=\sum _{1\le i\le n}W_{i}$. We prove this for $W_{j}$, for a given $j\in \{1,\ldots ,n\}$. Using Taylor’s theorem, we get for some $\zeta _{i}\in \left[ \text {min}\left\{ W_{i},W/n\right\} ,\text {max}\left\{ W_{i},W/n\right\} \right]$:

$$\begin{aligned}&E(u(W_{j})) =n\times \frac{1}{n}\times E(u(W_{j}))=\frac{1}{n}\sum _{i}E\left( u(W_{i})\right) \\&\quad =\frac{1}{n}\sum _{i}\left( E\left( u\left( \frac{W}{n}\right) +u'\left( \frac{W}{n}\right) \left( W_{i}-\frac{W}{n}\right) \right) +\frac{1}{2}u''(\zeta _{i})\left( W_{i}-\frac{W}{n}\right) ^{2}\right) \\&\quad =E\left( u\left( \frac{W}{n}\right) \right) +\frac{1}{n}E\left( u'\left( \frac{W}{n}\right) \sum _{i}\left( W_{i}-\frac{W}{n}\right) \right) \\&\quad +\frac{1}{2n}E\left( \sum _{i}u''(\zeta _{i})\left( W_{i}-\frac{W}{n}\right) ^{2}\right) \\&\quad \le E\left( u\left( \frac{W}{n}\right) \right) +\frac{1}{n}E\left( u'\left( \frac{W}{n}\right) \left( \sum _{i}\left( W_{i}-\frac{W}{n}\right) \right) \right) =E\left( u\left( \frac{W}{n}\right) \right) . \end{aligned}$$

By a simple approximation, the same is true if we consider that the function u is concave and not necessarily two times differentiable. Since the function u has been chosen arbitrarily it follows that $W_{j}\preceq _{SSD}\frac{W}{n}$.

Definition 6.1

An insurance scheme s is a set of non-negative random variables,

$$ s=(\lambda _{1},\lambda _{2},\ldots ,\lambda _{n},f_{1},f_{2},\ldots ,f_{n}), $$

where $\lambda _{i}$ is policyholder i’s liability to the insurer known as the premium and $f_{i}$ is the insurer’s liability to policyholder i known as the insurance indemnity.

According to this definition, under the scheme s, the policyholder i final wealth is given by

$$W_i=w_{0}-\lambda _{i}-X_{i}+f_{i}.$$

If the premia are deterministic, then it is an ex-ante policy. However, in this paper we also consider the case where both the insurance indemnity and the premium to be random variables. For that reason, we may also use the term contingent premium instead of premium.

An interesting example is the perfect pooling insurance scheme: we call the insurance scheme $s=(\lambda _{1},\lambda _{2},\ldots ,\lambda _{n},f_{1},f_{2},\ldots ,f_{n})$ a perfect pooling scheme if $\lambda _{1}=\lambda _{2}=\cdots =\lambda _{n}=\frac{\sum _{i}X_{i}}{n}$ and $f_{i}=X_{i}$ for all $i=1,2,\ldots ,n$. In that case, all risk variables in the market are aggregated, and all policyholders bear an equal share of the aggregated risk. Here, the premium is stochastic. We will show that if there is infinitely many policyholders, then deterministic premia appear when the policyholders are endowed with i.i.d. loss variables.

6.4 Risk Management Platforms

In this section, we study three different risk platforms. First, in Sect. 6.4.1, we propose a pure risk-sharing platform. In Sect. 6.4.2, we propose an insurance platform, in which there is a mutual insurer that can opt to default and is protected by a government. Finally, in Sect. 6.4.3, we propose a market platform and consider a competitive and a decentralised model.

6.4.1 Risk-Sharing Platform

In this part, we consider a risk-sharing platform where there is no role for the insurer, but individuals share their risk directly with each other (for instance, via a peer-to-peer network). Lemma 6.1 can be used to show that under NDI the best allocation is the perfect pooling. As we have mentioned before, based on the individual’s final wealth we can consider that the total wealth is given by $W=nw_{0}-\sum _{i}X_{i}$. Suppose the risk-sharing platform is designed to solve³

$$\begin{aligned} {\left\{ \begin{array}{ll} \text {max}&{} \sum _{i}E\left( u_{i}(w_{0}-\lambda _{i}-X_{i}+f_{i})\right) ,\\ \text {s.t.}&{} \forall j, 0\le f_{j}\le X_{j},\sum _{i}\lambda _{i}=\sum _{i}f_{i},\\ &{} \text {NDI holds}, \end{array}\right. } \end{aligned}$$

(6.1)

where $\sum _{i}\lambda _{i}=\sum _{i}f_{i}$ is a budget constraint that guarantees that the aggregate premia are equal to the aggregate insurance indemnities. From Lemma 6.1 it follows that the optimal allocation of total wealth is given by $\frac{W}{n}=w_{0}-\frac{\sum _{i}X_{i}}{n}$. Then, the final wealth of individual j after risk-sharing is given by $w_{0}-\lambda _{j}-X_{j}+f_{j}=w_{0}-\frac{\sum _{i}X_{i}}{n}, j=1,\ldots ,n,$ where $\lambda _{j}$ is the premium and $f_{j}$ is the coverage for policyholder j. This risk exposure after risk-sharing is obtained by choosing full coverage of the losses, $f_{j}=X_{j}$, and $\lambda _{j}=\lambda =\frac{\sum _{i}X_{i}}{n}$. This is a general rule for the premium of insurance with full risk coverage. So we have the following theorem.

Theorem 6.1

Consider a set of identically distributed risk variables, $X_{1},X_{2},\ldots ,X_{n}$, then the perfect pooling insurance scheme is a solution to the problem (6.1).

Note that with infinite number of policyholders if the losses are i.i.d then the premium will converge to the mean, but in the case that we do not have the i.i.d assumption this may no longer hold.

6.4.2 Insurance Platform

Another way of risk management is to introduce an insurance platform. We first take the perspective of a mutual insurer. In mutual insurance, all policyholders share the insurable risk with each other, and the insurer itself has no profit objective. For a typical insurer, the major consideration is the risk of insolvency. This to some extent hints for a different answer than the risk-sharing which is characterised in the following theorem. But before that let us introduce the partial pooling insurance scheme as an insurance scheme $s=(\lambda _{1},\lambda _{2},\ldots ,\lambda _{n},f_{1},f_{2},\ldots ,f_{n})$ where

$$\lambda _{1}=\cdots =\lambda _{n}=\frac{\sum _{i}X_{i}}{n}1_{\left\{ \frac{\sum _{i}X_{i}}{n}\le \mathrm {VaR}_{1-\eta }\left( \frac{\sum _{i}X_{i}}{n}\right) \right\} },$$

for some $\eta \in (0,1)$, and $f_{j}=X_{j}$, $j=1,2,\ldots ,n$, where $1_A$ is defined as the indicator function of the event $A\in \mathcal F$.

Theorem 6.2

Consider a set of identically distributed risk variables, $X_{1},X_{2},\ldots ,X_{n}$, then the partial pooling insurance scheme is a solution to the following problem⁴:

$$\begin{aligned} {\left\{ \begin{array}{ll} \mathrm {max}&{} \sum _{i}E\left( u_{i}(w_{0}-\lambda _{i}-X_{i}+f_{i})\right) ,\\ \mathrm {s.t.}&{} \forall j, 0\le f_{j}\le X_{j},P\left( \sum _{i}f_{i}\le \sum _{i}\lambda _{i}\right) \ge 1-\eta ,\\ &{} \text {NDI holds}. \end{array}\right. } \end{aligned}$$

(6.2)

Proof

Consider an insurance scheme $s=(\lambda _{1},\lambda _{2},\ldots ,\lambda _{n},f_{1},f_{2},\ldots ,f_{n})$, where $\forall j, 0\le f_{j}\le X_{j}$, $P\left( \sum _{i}f_{i}\le \sum _{i}\lambda _{i}\right) \ge 1-\eta$ and NDI holds i.e., $(w_{0}-\lambda _{j}-X_{j}+f_{j})_{(j=1,2,\ldots ,n)}$ are identically distributed. Let $\lambda _{j}^{'}=\lambda _{j}+(X_{j}-f_{j})$. Observe that

$$\begin{aligned} w_{0}-\lambda _{j}-X_{j}+f_{j}&=w_{0}-\left( \lambda _{j}+(X_{j}-f_{j})\right) -X_{j}+\left( f_{j}+(X_{j}-f_{j})\right) \\&=w_{0}-\lambda _{j}^{'}-X_{j}+X_{j}=w_{0}-\lambda _{j}^{'}. \end{aligned}$$

First, by NDI this shows that $\lambda _{j}^{'},j=1,2,\ldots ,n$ have the same distribution. Second, we have

$$ \sum _{i}\lambda _{i}\ge \sum _{i}f_{i}\Leftrightarrow \sum _{i}\left( \lambda _{i}+(X_{i}-f_{i})\right) \ge \sum _{i}X_{i}\Leftrightarrow \sum _{i}\lambda _{i}^{'}\ge \sum _{i}X_{i}. $$

Given the two points above, the insurance scheme $s^{'}=(\lambda _{1}^{'},\ldots ,\lambda _{n}^{'},X_{1},\ldots ,X_{n})$ respects the NDI assumption that has the same objective value as (6.2). So, we can replace $f_{j}$ by $X_{j}$ and $\lambda _{j}$ by $\lambda _{j}^{'}$, and rewrite the problem as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} \text {max}&{} \sum _{i}E\left( u_{i}\left( w_{0}-\lambda _{i}^{'}\right) \right) ,\\ \text {s.t.}&{} P\left( \sum _{i}X_{i}\le \sum _{i}\lambda _{i}^{'}\right) \ge 1-\eta ,\\ &{} \text {NDI holds}. \end{array}\right. } \end{aligned}$$

(6.3)

Now let $\lambda =\frac{\sum _{i}\lambda _{i}^{'}}{n}$. Consider the insurance scheme $s^{''}=(\lambda ,\lambda ,\ldots ,\lambda ,X_{1},X_{2},\ldots ,X_{n})$. It is clear that $s^{''}$ satisfies NDI. On the other hand, based on Lemma 6.1, it holds that $\sum _{i}E(u_{i}(w_{0}-\lambda _{i}^{'}))\le \sum _{i}E(u_{i}(w_{0}-\lambda ))$. Given the last two points and given that $\sum _{i}X_{i}\le \sum _{i}\lambda _{i}^{'}=\sum _{i}\lambda$ we get that the solution must satisfy:

$$\begin{aligned} {\left\{ \begin{array}{ll} \text {max} E\left( u(w_{0}-\lambda )\right) ,\\ P\left( X\le \lambda \right) \ge 1-\eta ,\\ \end{array}\right. } \end{aligned}$$

(6.4)

where $u=u_1+\cdots +u_n$ and $X=\frac{\sum _{i}X_{i}}{n}$.

Let us introduce $A=\left\{ X=\frac{\sum _{i}X_{i}}{n}\le \lambda ^{*}\right\}$ where $\lambda ^{*}$ is a solution to (6.4). As all utility functions are increasing, the maximum on A happens at $\lambda ^{*}=\frac{\sum _{i}X_{i}}{n}$ and on $A^{C}$ at 0. This means $\lambda ^{*}=\frac{\sum _{i}X_{i}}{n}1_{A}$. Now, let us look at $A^{C}$. Since a utility function is increasing then the values of $\frac{\sum _{i}X_{i}}{n}$ on A must be smaller than the values of $\frac{\sum _{i}X_{i}}{n}$ on $A^{C}$. This implies that $A=\left\{ \frac{\sum _{i}X_{i}}{n}\le \mathrm {VaR}_{1-\eta }\left( \frac{\sum _{i}X_{i}}{n}\right) \right\}$. So, the solution is given by, $\lambda ^{*}=\frac{\sum _{i}X_{i}}{n}1_{\left\{ \frac{\sum _{i}X_{i}}{n}\le \mathrm {VaR}_{1-\eta }\left( \frac{\sum _{i}X_{i}}{n}\right) \right\} }$. This proves the theorem.

There are a few points that need to be discussed. First, by NDI, the risk exposure after purchasing the optimal insurance scheme does not depend on the individual policyholders. Second, by setting $\eta =0$, meaning a perfect solvency condition $\sum _{i}f_{i}\le \sum _{i}\lambda _{i}$, we get the perfect pooling solution, which is also optimal for the risk-sharing platform. Third, if we moreover assume that the random losses are independent, then for both the risk-sharing and the insurance platform, we get the same solution in the limit: $\lambda ^{*}\rightarrow E(X)$, as $n\rightarrow \infty$. However, the most important point is the difference between the optimal value of the risk-sharing and the insurance platform. In the insurance platform, part of the risk can be forgiven. More precisely, the average risk above the value $\mathrm {VaR}_{1-\eta }\left( \frac{\sum _{i}X_{i}}{n}\right)$ is not covered by the policyholders, and the government provides protection to the policyholders. Note that such a so-called bail-out happens with probability $\eta$, that is usually small. This is to some extent a huge difference and is not at all desirable for the system. This is an important point to observe that the existence of the government will shelter the agents against the part of the risk that is the most harmful. However, at a large scale it seems the government needs to borrow enough funds to manage the risk which indicates the necessity of sponsorship. The sponsorship can either be in the form of a guarantee fund or can be a social reinsurance.

Remark 6.1

With a similar proof, we get that if we assume that $\lambda$ is deterministic (an ex-ante policy), then a solution is given by $\lambda _1=\cdots =\lambda _n=\mathrm {VaR}_{1-\eta }\left( \frac{\sum _i X_i}{n}\right)$.

Remark 6.2

In light of Theorem 6.2 one may consider the insurance scheme given by $s=(\lambda _{1},\lambda _{2},\ldots ,\lambda _{n},f_{1},f_{2},\ldots ,f_{n})$ where

$$\lambda _{1}=\cdots =\lambda _{n}=\min \left\{ \frac{\sum _{i}X_{i}}{n},\mathrm {VaR}_{1-\eta }\left( \frac{\sum _{i}X_{i}}{n}\right) \right\} $$

and $f_{i}=X_{i},i=1,2,\ldots ,n$. This insurance scheme satisfies the following condition:

If $\sum _{i}f_{i}>\sum _{i}\lambda _{i}$ , then $\sum _{i}\lambda _{i}=\mathrm {VaR}_{1-\eta }\left( \sum _{i}f_{i}\right)$. This condition states that the government only covers losses beyond the deductible threshold, which is the threshold for a bail-out.

Remark 6.3

In this paper, the insurance policies rely on the credit worthiness of the policyholders. Doherty and Schlesinger (1990) and Cummins and Mahul (2004) study insurance policies under conditions of default risk. In addition, Boonen (2019) considers a limited liability framework where the multivariate risk of the policyholders is exchangeable and focuses on the optimal allocation of losses in default. An interesting finding of this work is that a protection fund can be welfare-improving. A protection fund charges levies to policyholders with low realised losses, and this is used to compensate policyholders with high losses in case of a default of the insurer. While limited liability in the existing literature is considered when the insurers can default on their obligations, in this paper our focus is on a mutual insurer that can opt to default only with a sufficiently small probability. In case of default, the insurance claims will be covered by a government.

6.4.3 Market Platform

So far, we have discussed the risk-sharing and the insurance platforms. However, let us look at the problem from a market perspective. We have chosen two different market platforms; one where we consider a competitive market and another one where we consider a decentralised market.

6.4.3.1 Competitive Market

In this part, we present a model in which a “classical” solution appears, and the premium is deterministic. There is a competitive insurance market, in which the policyholders seek optimal insurance contracts with a (stock) insurer that is faced with the participation constraint to make a non-negative expected profit on each insurance policy.

Theorem 6.3

Consider a set of identically distributed risk variables, $X_{1},X_{2},\ldots ,X_{n}$ then the insurance scheme $s=(\lambda _{1},\lambda _{2},\ldots ,\lambda _{n},f_{1},f_{2},\ldots ,f_{n})$ where $\lambda _{1}=\cdots =\lambda _{n}=E(X_{i})$, and $f_{j}=X_{j},j=1,2,\ldots ,n$ solves

$$\begin{aligned} {\left\{ \begin{array}{ll} \mathrm {max}&{} \sum _{i}E\left( u_{i}(w_{0}-\lambda _{i}-X_{i}+f_{i})\right) ,\\ \mathrm {s.t.}&{} \forall j,0\le f_{j}\le X_{j},E(\lambda _{j})\ge E(f_{j}),\\ &{} \text {NDI holds}. \end{array}\right. } \end{aligned}$$

(6.5)

Proof

From NDI, it follows that $(w_{0}-\lambda _{j}-X_{j}+f_{j})_{j=1,2,\ldots ,n}$ are identically distributed, and thus we have $w_{0}-\lambda _{j}-X_{j}+f_{j}=w_{0}-\lambda _{j}^{'}$ for $\lambda _{j}^{'}=\lambda _{j}+(X_{j}-f_{j})$. By NDI, it follows that $\lambda _{j}^{'},j=1,2,\ldots ,n$ have the same distribution. Moreover, we have

$$ E(\lambda _{j})\ge E(f_{j})\Leftrightarrow E(\lambda _{j}+(X_{j}-f_{j}))\ge E(X_{j})\Leftrightarrow E(\lambda _{j}^{'})\ge E(X_{j}). $$

Given the two points above, the insurance scheme $s^{'}=(\lambda _{1}^{'},\lambda _{2}^{'},\ldots ,\lambda _{n}^{'},X_{1},X_{2},\ldots ,X_{n})$ respects the NDI assumption and thus we have the same objective value as (6.5). So, we can replace $f_{j}$ by $X_{j}$ and $\lambda _{j}$ by $\lambda _{j}^{'}$, and rewrite the problem as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} \text {max}&{} \sum _{i}E\left( u_{i}\left( w_{0}-\lambda _{i}^{'}\right) \right) ,\\ \text {s.t.}&{} E(\lambda _{j}^{'})\ge E(f_{j}),\\ &{} \text {NDI holds}. \end{array}\right. } \end{aligned}$$

(6.6)

Now let $\lambda _{j}^{''}=\tilde{\lambda }=\frac{\sum _{i}\lambda _{i}^{'}}{n},j=1,2,\ldots ,n$. Consider the insurance scheme $s^{''}=(\lambda _{1}^{''},\lambda _{2}^{''},\ldots ,\lambda _{n}^{''},X_{1},X_{2},\ldots ,X_{n})$. It is clear that $s^{''}$ satisfies NDI. On the other hand, from Lemma 6.1 we get $\sum _{i}E\left( u_{i}\left( w_{0}-\lambda _{i}^{'}\right) \right) \le \sum _{i}E\left( u_{i}\left( w_{0}-\lambda _{i}^{''}\right) \right)$. Given the last two points and given that $\sum _{i}X_{i}\le \sum _{i}\lambda _{i}^{'}=\sum _{i}\lambda _{i}^{''}$ we get that the solution must solve:

$$\begin{aligned} {\left\{ \begin{array}{ll} \text {max}&{} \sum _{i}E\left( u_{i}\left( w_{0}-\lambda _{i}\right) \right) ,\\ \text {s.t.}&{} \forall j, E(\lambda _{j})\ge E(f_{j}). \end{array}\right. } \end{aligned}$$

(6.7)

Since the utility function is concave, it holds by Jensen’s inequality that $E(u_{i}(w_{0}-E(\tilde{\lambda })))\ge E(u_{i}(w_{0}-\tilde{\lambda }))$. From this and the fact that the utility function is increasing, (6.7) is solved by $\lambda _j=\tilde{\lambda }=E(X_{i})$. This proves the theorem.

Theorem 6.3 describes a classic situation where deterministic premia are optimal. The key assumption here is that the insurer is a separate firm that is able to pool and manage risk in absence of a regulator. In absence of such an unregulated firm, the policyholders can still decide to share risk via a variety of platforms, and then stochastic premia may become optimal.

Since there is no regulator it is important to understand the risk associated with such policies. We look at the probability of insolvency: $P(\sum _i X_i>n\tilde{\lambda })$. So, in the limit for an infinite number of policyholders, we look at the following quantity:

$$\begin{aligned} P\left( \lim _n\frac{\sum _i X_i}{n}>\tilde{\lambda }\right) . \end{aligned}$$

(6.8)

Moreover, we can also measure the average relative magnitude of the losses in default, i.e.,

$$\begin{aligned} \frac{E\left( \lim _n \frac{\sum X_i}{n}-\tilde{\lambda }\Big |\lim _n \frac{\sum X_i}{n}>\tilde{\lambda }\right) }{\tilde{\lambda }}. \end{aligned}$$

(6.9)

This also can be interpreted as the average violation from solvency:

$$\begin{aligned} {E\left( \lim _n \frac{\sum X_i}{n\tilde{\lambda }}-1\Big |\lim _n \frac{\sum X_i}{n\tilde{\lambda }}>1\right) }. \end{aligned}$$

(6.10)

Now, let us compare the solutions of (6.1) and (6.5) in light of the criteria in (6.8)–(6.10). Note that if we consider the case when the losses are independent, then the contingent premium and the deterministic premium are equal if there is an infinite number of policyholders, and the criteria in (6.8)–(6.10) will suggest the use of the deterministic premium. The important issue is that in the presence of a common shock or systematic risk the expected contingent premium $\tilde{\lambda }= E(\lambda )$ cannot truly be representative of the real macro-level impact. We will show examples of this with common shock models in Sect. 6.5.

6.4.3.2 Decentralised Market

In the decentralised market, our focus is on deterministic (ex-ante) premia, and we solve the supply and the demand problem separately. Our main concern is to observe if an equilibrium exists.

Let us first consider the supply side of the market. We use a very popular method in the industry, by keeping the loss ratio below a targeted loss ratio. So, let consider the insurance company, which is the supply side of the market, wants to keep the loss ratio at a given level $\beta \in (0,1]$. Based on Assa and Wang (2020) this value is around 65 per cent for the industry. In the case that the only aim of the insurer is the insurance solvency, we can consider $\beta =1$. For instance, in the case that the insurance is run as a state back scheme or when it is run based on a fund, we can assume that $\beta =1$. In this case the insurance is not supposed to make profit.

In what follows, we need to do the valuation of insurance products. We have adopted a very simple approach by finding the premium $\lambda$ as follows:

$$\begin{aligned} \lambda ^S = \inf \left\{ \tilde{\lambda }:P\left( \frac{\sum _i X_i}{n\tilde{\lambda }}\ge \beta \right) \le \eta \right\} , \end{aligned}$$

(6.11)

where the fraction $\frac{\sum _i X_i}{n\tilde{\lambda }}$ is called the loss ratio.

Note that here we have considered the full coverage $f_j=X_j$ to follow the results of the previous sections. It is not very difficult to see that this can be done through the following assessment:

$$\begin{aligned} \lambda ^S=\frac{1}{\beta } \mathrm {VaR}_{1-\eta }\left( \frac{\sum _iX_i}{n}\right) . \end{aligned}$$

On the other hand, we need to explore the market demand price. So, let us consider a representative agent with a utility u. Using a utility indifference approach for losses with identically distributes as X, we know that the premium for an insurance contract with full coverage is given as follows:

$$\begin{aligned} u(w_0-\lambda ^D )=E(u(w_0-X)), \end{aligned}$$

or,

$$\begin{aligned} \lambda ^D=w_0-u^{-1} (E(u(w_0-X))), \end{aligned}$$

where the inverse utility function $u^{-1}$ exists because u is increasing.

We say that an equilibrium exists if $\lambda ^D\ge \lambda ^S$, and an equilibrium price is given by $\lambda \in [\lambda ^S,\lambda ^D ]$. In the case that we have linear utility (i.e. risk-neutral agents) we have that $\lambda _{Lin}^D=E(X)$. On the other hand, by Jensen’s inequality we have:

$$\begin{aligned} \lambda ^D=w_0-u^{-1} (E(u(w_0-X)))\ge E(X)=\lambda _{Lin}^D. \end{aligned}$$

So as a sufficient condition for the existence of an equilibrium we can check the following condition:

$$\begin{aligned} E(X)=\lambda _{Lin}^D\ge \lambda ^S. \end{aligned}$$

We also can find the following demand price for the random variable $\tfrac{\sum _iX_i}{n}$:

$$\begin{aligned} \lambda _{Ave}^D=w_0-u^{-1} \left( E\left( u\left( w_0-\frac{\sum _i X_i}{n}\right) \right) \right) . \end{aligned}$$

We claim that $\lambda ^D\ge \lambda _{Ave}^D$. To see this note that by using the Lemma 6.1 we have that

$$ u(w_0-\lambda ^D )=E(u(w_0-X))\le E\left( u\left( w_0-\frac{\sum _iX_i}{n}\right) \right) =u(w_0-\lambda _{Ave}^D ),$$

and so $\lambda ^D\ge \lambda _{Ave}^D$. So, this can also be used to introduce the following sufficient condition for the existence of an equilibrium:

$$\begin{aligned} \lambda _{Ave}^D\ge \lambda ^S. \end{aligned}$$

For instance, in the case that we are only concerned with the insurance solvency i.e., $\beta =1$, then in the limit we can see that for i.i.d losses we get:

$$\begin{aligned}&\lambda _{Ave}^D\rightarrow E(X), \text { and }\\&\lambda ^S\rightarrow E(X),\text { as }n\rightarrow \infty .\end{aligned}$$

This readily justifies the existence of the insurance market for the assumptions above.

Remark 6.4

As one can see in all three platforms we studied above the independence assumption with an infinite number of policyholders will result in the classical solution. This explains why in many standard models when we are not facing the risk of common shock a (non-contingent) actuarial premium can be the optimal answer. This can be regarded from the so-called “principle of insurance” perspective, as it was discussed in the introduction. It is not very difficult to see that by using the central limit theorem we have that

$$\begin{aligned}&\zeta =P(S_n>n(E(X_i)+z_n ))=P\left( \frac{\frac{S_n}{n}-E(X_i)}{\frac{\sigma }{\sqrt{n}}} >\frac{z_n}{\frac{\sigma }{\sqrt{n}}}\right) \approx 1-\Phi \left( \frac{z_n}{\frac{\sigma }{\sqrt{n}}}\right) \\&\Rightarrow z_n\approx \frac{\sigma }{\sqrt{n}} \Phi ^{-1}(1-\zeta )\rightarrow 0,\end{aligned}$$

for any $\zeta \in (0,1)$, where $z_n$ is the relative risk loading $S_n=\sum _{i=1}^n X_i$, $\sigma$ the standard deviation of $X_i$, and $\Phi$ is the CDF of a standard normal distribution.

6.5 Systematic Risk Model and Common Shocks

In this section we focus on the common shock models and will study different risk management framework in the presence of a common shock. For each framework, we also consider specific examples to better understand the impact of the common shocks on the risk management frameworks.

For simplicity, we have chosen the Bernoulli distribution for losses and the constant absolute risk aversion (CARA, or exponential) utility function, i.e.,

$$\begin{aligned} u(x)=\frac{1-e^{-ax}}{a},\text { for } a>0 \text { and }u(x)=x \text { for }a=0. \end{aligned}$$

Here, a is the risk aversion parameter. Advantages of using CARA utility are the possibility of using negative wealth, the price invariance to the initial wealth and also additivity w.r.t independent losses. A disadvantage of using the CARA utility is that the risk aversion parameter a depends on the currency (a scaling problem), which makes the calibration of the parameter a challenging. In the literature the risk aversion parameter a is a number very close to 0. However, in very particular cases it can even reach values close to $a=1$ (see, e.g., Babcock et al. 1993). In our numerical assessment we consider $a\in [0,1]$.

With the CARA utility we readily derive that

$$\begin{aligned} \lambda ^D=\frac{\log (E(e^{aX}))}{a}. \end{aligned}$$

In the market platform, we must essentially make sure that $\lambda ^S\le \lambda ^D.$ With CARA utility when the losses are i.i.d, based on what have been discussed with infinite number of policyholders, we can verify this relation by the Jensen inequality for $a\ne 0$ as follows:

$$\begin{aligned} \lambda ^S=E(X)=\frac{E(aX)}{a}=\frac{\log (e^{E(aX)})}{a}\le \frac{\log (E(e^{aX}))}{a}=\lambda ^D. \end{aligned}$$

The case $a=0$ is obvious.

However, if the above condition does hold, we also want to see the degree of violation of this condition. In a market setup, as mainly the demand is the driving force of the market, we scale everything with the market demand prices and assess the relative pricing gap, i.e.,

$$\begin{aligned} RPG=\frac{\lambda ^S-\lambda ^D}{\lambda ^D}=\frac{\lambda ^S}{\lambda ^D}-1. \end{aligned}$$

This value shows how large the gap is between the supply and demand sides of the market. Another benefit of using this quantity is that it is dimension free, so we do not have problem with scales.

In terms of the tolerance probability of the insurance company, i.e., the parameter $\eta$, we generally consider two cases, one where the probability of the common shock event is greater and one where the common shock is less than the VaR-parameter. In our case study, since we assume a probability of common shock $\gamma$ to be equal to 0.01, we consider $\eta =0.005$ and $\eta =0.015$. In this way we can see the impact of the risk management by checking if the insurance risk tolerance parameter is sensitive to common shock or not. We also consider the effect of the probability of the non-systematic (alternatively called idiosyncratic) event which we denote by p.

In the following, in three sections we consider three different common shock examples, including the additive, multiplicative and risk rate common shock models. Then in each section we consider the risk-sharing, insurance, and market platforms. We use the examples of the Bernoulli loss variables along with the CARA utility and $n\rightarrow \infty$. One of the benefits of using a Bernoulli distribution is that we can easily associate the common shock to the systematic event. In the following, we will specify the systematic event in each case. It is very important to realise if the systematic event is regarded as a tail event. More precisely, if the systematic event probability is less than the parameter $\eta$, then it is also a tail event.

For the common shocks, we focus on an example of a wide-spread pandemic event like the Spanish flu and the recent COVID-19, which we assume to be a macro event of roughly 1 per cent of probability (“once every 100 years”). We also follow the example of the UK Coronavirus Job Retention Scheme presented by Assa (2020) as a case-study with systematic risk. The calibration in this paper helps us to set suitable values for the parameters. For instance, for the idiosyncratic event we can consider $p=0.06$; so for completeness in this paper we can consider a wider range of $0.05\le p\le 0.1$. We also consider $\gamma = 0.01$.

6.5.1 Additive Common Shock Model

Let us consider an i.i.d. sequence of risk variables $Y_j,j=1,2,\ldots ,n$ and another non-negative random variable Z, independent from all $Y_j,j=1,2,\ldots ,n$. Let us introduce the loss variables as $X_j=Y_j+Z$. We assume all random variables $Y_i$ have the same distribution as Y. This additive common shock model is proposed by Avanzi et al. (2018) and Boonen (2019) for the modelling of insurable losses. In this setup the common shock is represented by the random loss Z. The systematic event needs to be introduced for each case. However, in this framework a natural suggestion is an event $S\in \sigma (Z)$, where $\sigma (Z)$ is the sigma-field generated by Z. In our examples we consider Bernoulli distributions for Y and Z. Let us consider an idiosyncratic loss variable $Y=1_{\mathcal L_Y}$ and a systematic loss variable $Z=1_{S}$, where $P(\mathcal L_Y )=p$ and $P(S )=\gamma$. So, naturally the systematic event that we consider is S.

• 1. Risk-sharing platform. As we have seen in Sect. 6.4.1, for risk-sharing we need to be knowledgeable about the average. This is given by:

  $$\begin{aligned} \frac{\sum _i(Y_i+Z)}{n} = \frac{\sum _i Y_i}{n}+Z\rightarrow E(Y)+Z. \end{aligned}$$

  This is the best allocation for a risk-sharing platform because of Lemma 6.1. As one can see the average still includes the common shocks.

  If we consider our example we can see the contingent premium to be given as $p+1_{S}$. It is very interesting to compare this solution to the classical problem we considered in (6.5), where the solution is just the average of the loss variable which here is given by $p+\gamma$. So, there is a trade-off in the contingent premium, while in the non-systematic event the contingent premium is less i.e., $p<p+\gamma$, but once the systemic event happens the contingent premium is much higher i.e., $p+\gamma <p+1$. One can see that there is a chance of $\gamma =0.01$ that a big loss would hit all. This is generally not sufficient for any insurance scheme to be considered sustainable.

• 2. Insurance platform. As we have seen in Sect. 6.4.1, for mutual insurance we need to understand the event $\left\{ \frac{\sum _i X_i}{n}\le \mathrm {VaR}_{1-\eta }\left( \frac{\sum _iX_i}{n}\right) \right\}$ for $n\rightarrow \infty$. This limit is given by:

  $$\begin{aligned}\left\{ \frac{\sum _i X_i}{n}\le \mathrm {VaR}_{1-\eta }\left( \frac{\sum _iX_i}{n}\right) \right\}&\rightarrow \{E(Y)+Z\le E(Y)+\mathrm {VaR}_{1-\eta }(Z)\}\\ {}&=\{Z\le \mathrm {VaR}_{1-\eta }(Z)\},\end{aligned}$$

  and as a result, we get in limit that

  $$\begin{aligned} \lambda _i=\lambda ^*\rightarrow (E(Y)+Z) 1_{\{Z\le \mathrm {VaR}_{1-\eta }(Z)\}}, \end{aligned}$$

  for the solution $\{\lambda _1,\lambda _2,\ldots ,\lambda _n\}$ of Problem (6.2).

  Now let us consider our special case of Bernoulli distributions. Here we have two cases. First let us consider $\eta =0.005<0.01=\gamma$. In this case we have $\mathrm {VaR}_{1-\eta }(Z)=1$, and as a result we get $\{Z\le \mathrm {VaR}_{1-\eta }(Z)\}=\Omega ,$ and $\lambda ^*=E(Y)+Z$. This essentially means that in the case that the risk tolerance parameter is set at a value that is smaller than the probability of the systematic event, which means that the systematic event is not perceived as a tail event, then, the solution is identical to the one from the risk sharing platform. Second, let us consider $\eta =0.015>0.01=\gamma$. In this case we have $\mathrm {VaR}_{1-\eta }(Z)=0$, and then we get $\{Z\le \mathrm {VaR}_{1-\eta }(Z)\}=S^C$ and $\lambda ^*=E(Y)1_{S^C}$. Thus, if the risk tolerance parameter is larger than the probability of the systematic event, then we may end up with a solution that will put a large burden on the government due to tail risk.

• 3. Market platform. In the market platform we consider the competitive and decentralised markets.

  Competitive market. It is very easy to see that $\tilde{\lambda }= E(Y+Z)$. For the Bernoulli example this is easily given by $p+\gamma$. In order to see the risk impact of the policy we need to find out about the probability of default generated by (6.5), as in (6.8) which is $P\left( Z>E(Z) \right)$. For the Bernoulli model this value is equal to $P(S)=\gamma$. The average relative magnitude of the losses in default is given by:

  $$E\left( \frac{1_S+p}{\gamma +p}-1\Big |S\right) =\frac{1-\gamma }{\gamma +p}.$$

  If we consider the parameter values of our calibration based on the UK Coronavirus Job Retention Scheme, the average relative magnitude of the losses in default is at least $\frac{1-0.01}{0.01+0.1}=9= 900\%$, which is quite high.

  Decentralised market. We need to find $\mathrm {VaR}_{1-\eta }\left( \frac{\sum _i X_i}{n}\right)$ in the limit to find the supply price as follows:

  $$\begin{aligned} \lambda ^S=\frac{1}{\beta } \mathrm {VaR}_{1-\eta }\left( \frac{\sum _i X_i}{n}\right) \rightarrow \frac{1}{\beta } \mathrm {VaR}_{1-\eta }(E(Y)+Z)=\frac{1}{\beta }(E(Y)+\mathrm {VaR}_{1-\eta }(Z)), \end{aligned}$$

  which holds true by continuity of the VaR risk measure (see Proposition 4.11 in Marinacci and Montrucchio 2004). We also need the demand price

  $$\begin{aligned} \lambda ^D=w_0-u^{-1}(E(u(w_0-Y-Z))). \end{aligned}$$

  Our aim is to see when we can verify the market condition $\lambda ^S\le \lambda ^D$. By considering the CARA utility we have that,

  $$\begin{aligned} \lambda ^D=\frac{\log (E(e^{aX}))}{a}=\frac{\log (E(e^{aY}))}{a}+\frac{\log (E(e^{aZ}))}{a}, \qquad a>0, \end{aligned}$$

  and,

  $$\begin{aligned} \lambda ^D=E(Y)+E(Z),\qquad a=0. \end{aligned}$$

  Now, let us look at the pricing gaps:

  $$ \lambda ^S-\lambda ^D=\left\{ \begin{array}{ll}E(Y)+\mathrm {VaR}_{1-\eta }(Z)-\left( \frac{\log (E(e^{aY}))}{a}+ \frac{\log (E(e^{aZ} ))}{a}\right) , &{} a>0,\\ \mathrm {VaR}_{1-\eta }(Z)-E(Z), &{} a=0.\end{array}\right. $$

  Computing this gap is not an easy job in general. When we use the Bernoulli loss distribution, we derive with our assumptions the following:

  $$ \lambda ^S-\lambda ^D=\left\{ \begin{array}{ll}p+1_{\gamma>\eta }-\left( \frac{ \log (1-p+pe^a)}{a}+ \frac{\log (1-\gamma +\gamma e^a)}{a}\right) , &{} a>0,\\ \mathrm {VaR}_{1-\eta }(Z)-E(Z), &{} a=0.\end{array}\right. $$

  As explained in the beginning of this section motivated by the COVID-19 case study, we use $\gamma =0.01$. Next, we study the pricing gaps. In Fig. 6.1 we show the relative pricing gaps for two cases, one when the risk assessment is sensitive to the systematic risk ($\eta <\gamma$), and one otherwise. As one can see that if the systematic risk probability parameter $\gamma$ is “captured” by the risk confidence parameter $\eta$ ($\eta <\gamma$), then the relative price gaps in Fig. 6.1(left) are always positive and greater than 5.5 (meaning 550%) and can become as large as 16 times (1600%) the demand price. On the other hand, one can see that if the risk confidence parameter $\eta$ is larger than the systematic risk parameter $\gamma$, then the prices gap is negative which means that an equilibrium price exists. The VaR may however not be an adequate measure to determine the riskiness of the loss variable as the common shock is not measured. The main problem is the common shock that has a great impact on the valuation. Some side-observation includes the reduction of the gap with the increase of the risk aversion parameter which makes economic sense. However, the behaviour of the pricing gap is different with respect to the changes in the non-systematic risk parameter p.

Fig. 6.1

Relative pricing gap for additive common shocks

6.5.2 Multiplicative Common Shock Model

We consider a model, where the common shock is multiplicative, and the individual risks are given by: $X_j=ZY_j$, where $Z\ge 0,E(Z)>0$, and the risk variables $Y_j,j=1,2,\ldots ,n,$ are i.i.d. and independent of Z. Similar to Sect. 6.5.1 we consider Bernoulli losses. Let us consider loss $Y=1_{\mathcal {L}_Y}$ and $Z= 1+z1_{S}$, where $P(\mathcal {L}_Y )=p$ and $P(S )=\gamma$ and $z>0$ is the magnitude of the systematic losses. For simplicity we assume $z=2$ and 4 for two different values of the common shock effect. We again consider S as the systematic event.

Similar to Sect. 6.5.1, one can get that for the risk-sharing platform it holds that:

• 1. Risk-sharing platform. Based on discussions in Sect. 6.4.1, we need to find the average in limit:

  $$\begin{aligned} \lambda = \frac{\sum _i(ZY_i)}{n}=Z\frac{\sum _i Y_i}{n}\rightarrow Z E(Y). \end{aligned}$$

  This is the best allocation for a risk-sharing platform because of Lemma 6.1. As one can see the average still includes the common shock Z.

  Now let us again consider Bernoulli distributions for the losses. We then get that $\lambda = Z E(Y)=p+ pz1_{S}$. Similar to the comparison we made in Sect. 6.5.1 with the solution $\tilde{\lambda }=E(Z)E(Y)=p+p\gamma z$ in (6.5), one can realise the trade-off between the two solutions. It is again important to note that the solution in (6.5) cannot be truly representative of the real macro-level impact due to the systematic risk.

• 2. Insurance platform. As we have seen in Sect. 6.4.2, for mutual insurance we need to understand the event $\left\{ \frac{\sum _i X_i}{n}\le \mathrm {VaR}_{1-\eta }\left( \frac{\sum _iX_i}{n}\right) \right\}$ for $n\rightarrow \infty$. This limit is given by:

  $$\begin{aligned} \left\{ \frac{\sum _i X_i}{n}\le \mathrm {VaR}_{1-\eta }\left( \frac{\sum _iX_i}{n}\right) \right\}&\rightarrow \{ZE(Y)\le \mathrm {VaR}_{1-\eta }(Z) E(Y)\}\\ {}&=\{Z\le \mathrm {VaR}_{1-\eta }(Z)\},\end{aligned}$$

  and as a result, we get in the limit that

  $$\begin{aligned} \lambda _i=\lambda ^*\rightarrow E(Y)Z 1_{\{Z\le \mathrm {VaR}_{1-\eta }(Z)\}}, \end{aligned}$$

  for the solution $\{\lambda _1,\lambda _2,\ldots ,\lambda _n\}$ of Problem (6.2).

  Now let us consider the Bernoulli losses. Similarly to Sect. 6.5.1 we distinguish two cases. One where the risk tolerance parameter is sensitive to the common shock (i.e., systematic event does not belongs to the tail), in which case the solution is identical to the risk-sharing solution; and one where the solution is much less impactful for the policyholders and given by $\lambda ^*=E(Y)z1_{S^C}$.

• 3. Market platform. Like before, here we need to look at the following two models.

  Competitive market. Very similar to the previous case we can see that the probability of insolvency in (6.5) is equal to P(S), and the average relative magnitude of the losses in default is given as

  $$E\left( \frac{p(1+z1_S)}{p(1+z\gamma )}-1\Big |S\right) =\frac{z(1-\gamma )}{1+z\gamma }=\frac{1-\gamma }{\frac{1}{z}+\gamma }.$$

  For our case study on the UK Coronavirus Job Retention Scheme we see that for $\gamma =0.01$, we get $\frac{99}{\frac{100}{z}+1}\ge 1.94=\%194$. This is very high value. Decentralised market. Now we want to see if we can verify the market condition $\lambda ^S\le \lambda ^D$. In this case we have that

  $$\begin{aligned}\lambda ^D&=\frac{\log (E(e^{aX}))}{a}=\frac{\log (E(e^{aZY}))}{a}, \qquad a>0,\text { and }\\ \lambda ^D&=E(Y)E(Z), \qquad a=0.\end{aligned}$$

  Let us consider the example with Bernoulli-distributed factors. With our assumptions we can see that for $\beta =1$

  $$\begin{aligned} \lambda ^S=E(Y) \mathrm {VaR}_{1-\eta }(Z)=p1_{\{\gamma >\eta \}}. \end{aligned}$$

  In addition, it holds that

  $$e^{aYZ}=e^{a1_{\mathcal {L}_Y} + az 1_{\mathcal {L}_Y\cap S}}=\left\{ \begin{array}{ll} e^{a(1+z)} &{}\text { on }S\cap \mathcal {L}_Y, \\ e^a &{}\text { on }\mathcal {L}_Y\backslash S,\\ 1 &{}\text { on }\mathcal {L}_Y^C,\end{array}\right. $$

  which is equal to

  $$\left\{ \begin{array}{ll} e^{a(1+z)} &{}\text { with prob. } \gamma p, \\ e^a &{}\text { with prob. }(1-\gamma )p,\\ 1 &{}\text { with prob. } 1-p.\end{array}\right. $$

  This implies that

  $$\begin{aligned} \lambda ^D=\frac{\log (E(e^{aYZ}))}{a}=\frac{\log (p\gamma e^{a(1+z)} +p(1-\gamma )e^a+(1-p))}{a}, \end{aligned}$$

  and

  $$ \lambda ^S-\lambda ^D=\left\{ \begin{array}{ll} p(1+z 1_{\gamma>\eta })-\frac{\log \left( p\gamma e^{a(1+z)} +p(1-\gamma ) e^a+(1-p)\right) }{a}, &{}a>0,\\ p((1+z 1_{\gamma >\eta })-\alpha ), &{} a=0.\end{array}\right. $$

  Like before, motivated by the UK COVID-19 case study we use the calibration $\gamma =0.01$. We next examine the pricing gaps.

  The results in Fig. 6.2 are very similar to what we have observed in Fig. 6.1, which means there is a trade-off between correctly covering the risk via a VaR and the existence of the market equilibrium. This observation holds true almost regardless of the values of the risk aversion parameter, the non-systematic risk and even the value of z.

Fig. 6.2

Relative pricing gap for multiplicative common shocks

6.5.3 Risk Rate Common Shock Model

In this example we discuss different levels of the systematic risk in the market. As it has been discussed in the beginning of the paper, risk management solutions emerge to take care of different level of risk. Markets that deal with less risky aggregate losses are more likely to form and the risk would more perfectly be managed. On the opposite side we have the markets that are dealing with larger aggregate losses, which are much harder to create. Here, we use a very simple setup to demonstrate the different levels of systematic risk while still focussing on identically distributed individual loss variables. The major difference is the aggregate risk rather than the individual risk. This differentiates this example from the other two examples where the aggregate risk is not the essential differentiator.

Let us consider a partition $\Omega _1,\ldots ,\Omega _m$ of $\Omega$ where $p_k:=P(\Omega _k)$ for all $k=1,\ldots ,m$. The elements of the partition represent different layers of the risk management market. We assume that $p_1>p_2>\cdots>p_m>0$, associating smaller probabilities with events with larger impact. Let us consider a sequence of loss variables $\{X_n\}_{n\in \mathbb {N}}$ so that $\{X_n|\Omega _k\}_{n\in \mathbb {N}}$ is i.i.d. in the probability space $(\Omega _k,P_{\Omega _k})$, where $P_{\Omega _k}$ is the conditional probability on $\Omega _k$ for any $k=1,\ldots ,m$. Let us assume that $E(X_i|\Omega _1)\le \cdots \le E(X_i|\Omega _m)$. This assumption can reflect the fact that more harmful events cause larger expected losses. By assumption it is clear that $E_k=E(X_1|\Omega _k)=\cdots =E(X_n|\Omega _k)$, for $k=1,\ldots ,m$. It is also clear that the loss distribution is given as follows:

$$\begin{aligned} F_X=\sum _k p_k F_{X|\Omega _k}. \end{aligned}$$

To better understand the example, we also discuss a special case of this model by assuming only a systematic and a non-systematic event. This means in a probabilistic setup the probability space $\Omega$ can be partitioned into S and $S^C$, for systematic and non-systematic events, respectively. Let $\gamma =P(S)$ be a positive number that is the probability of the macro event (e.g., every 100 years). We assume in the systematic event the probability of the loss distribution will change. The same is assumed for the complement set $S^C$. Let $Sys=\{\emptyset ,S,S^C,\Omega \}$, be the sigma-field generated by systematic event. Let us assume $E(X_j |S)=\delta M$ and $E(X_j |S^C )=\alpha M$. We assume that $\alpha >\delta$ which is reflecting the fact that the magnitude of the losses during the systematic event is larger than non-systematic event.

Using the calibration by Assa (2020) on the UK Coronavirus Job Retention Scheme, we set $\alpha =0.27$ and $\delta =0.06$ and $\gamma =0.01$. However, for completeness we consider a range for $\delta \in [0.05,0.1]$.

Now let us see what will happen to the optimal strategies given by the propositions we have discussed.

• 1. Risk-sharing platform. By using the law of large numbers on each conditional space we need to specifically look at the following quantities:

  $$\begin{aligned} \lambda =\frac{\sum _i X_i}{n}=\frac{\sum _i X_i}{n}1_{\Omega _1}+\cdots +\frac{\sum _i X_i}{n}1_{\Omega _m}\rightarrow \sum _k E(X|\Omega _k)1_{\Omega _k}. \end{aligned}$$

  Considering the special case of $m=2$, we have that,

  $$\begin{aligned} \lambda =E(X|S^C)1_{S^C}+E(X|S)1_{S}=\delta M1_{S^C}+\alpha M1_{S}=\delta M +(\alpha -\delta )M1_S. \end{aligned}$$

• 2. Insurance platform. As we have seen we need to find the following quantity

  $$\begin{aligned}\lambda ^*&=\frac{\sum _i X_i}{n} 1_{\left\{ \frac{\sum _i X_i}{n}\le \mathrm {VaR}_{1-\eta }\left( \frac{\sum _i X_i}{n}\right) \right\} }\\ {}&\rightarrow \left( \sum _k E(X|\Omega _k)1_{\Omega _k}\right) 1_{\left\{ \sum _k E(X|\Omega _k)1_{\Omega _k}\le \mathrm {VaR}_{1-\eta }\left( \sum _k E(X|\Omega _k)1_{\Omega _k}\right) \right\} }.\end{aligned}$$

  Let $m^*=\min \{k:\sum _{k'\le k} P(\Omega _{k'})\ge 1-\eta \}$. Then it is clear that

  $$\begin{aligned} \mathrm {VaR}_{1-\eta }\left( \sum _{k} E(X|\Omega _{k})1_{\Omega _{k}}\right) =E(X|\Omega _{m^*}), \end{aligned}$$

  and that

  $$\begin{aligned}\lambda ^*&=\frac{\sum _i X_i}{n} 1_{\left\{ \frac{\sum _i X_i}{n}\le \mathrm {VaR}_{1-\eta }\left( \frac{\sum _i X_i}{n}\right) \right\} }\rightarrow \left( \sum _k E(X|\Omega _k)1_{\Omega _k}\right) 1_{\Omega _1\cup \cdots \cup \Omega _{m^*}}\\ {}&=\sum _{k\le m^*}E(X|\Omega _k) 1_{\Omega _k}.\end{aligned}$$

  Now using the example of $m=2$, we easily derive that if $\eta =0.005<0.01=\gamma$ then

  $$\begin{aligned} \lambda ^*=E(X|S^C)1_{S^C}+E(X|S)1_{S}=\delta M1_{S^C}+\alpha M1_{S}, \end{aligned}$$

  and if $\eta =0.015>0.01=\gamma$ we have

  $$\begin{aligned} \lambda ^*=E(X|S^C)1_{S^C}=\delta M1_{S^C}. \end{aligned}$$

  Hence, if the systematic risk is not a tail event then the solution is identical to the risk-sharing solution. Otherwise, the systematic risk is fully borne by the government, and the policyholders only pay a premium if the non-systematic (idiosyncratic) risk is realized.

• 3. Market platform. Here we need to look at the following models.

  Competitive market. One can realise the following trade-off between the model (6.5) and (6.1) premium and the contingent premium:

  $$\delta M \le \tilde{\lambda }= (1-\gamma )\delta M+\gamma \alpha M\le \alpha M. $$

  The probability of the insolvency is equal to $p=P(S)$. We also find that the average relative magnitude of the losses in default is given by:

  $$\begin{aligned} {E\left( \frac{\delta 1_{S^C}+\alpha 1_{S}}{\delta (1-p)+\alpha p}-1\Big |S\right) =\frac{(1-p)(\alpha -\delta )}{\delta (1-p)+\alpha p}\approx \frac{\alpha }{\delta }-1\ge 1.7}. \end{aligned}$$

  Decentralised market. We need to consider the following values.

  $$\begin{aligned}\lambda ^S&\rightarrow =\frac{1}{\beta } \mathrm {VaR}_{1-\eta }\left( \sum _kE(X|\Omega _k)1_{\Omega _k}\right) =\frac{1}{\beta }E(X|\Omega _{m^*}),\\ \lambda ^D&=w_0-u^{-1}(E(u(w_0-X))).\end{aligned}$$

  Using the Bernoulli distributions for the conditional losses we can also find the loss distribution. Let us consider the following model: for any j let $X_j |\Omega _k=1_{\mathcal L_{jk}}$, where $\mathcal L_{jk}\subseteq \Omega _k$, and the sequence of the sets $\{\mathcal L_{jk}\}_j$ are independent in $(\Omega _k,P_{\Omega _k})$ and $P_{\Omega _k} (\mathcal L_{jk})=E_k$. So, if we consider a loss variable X with the same joint distribution as the losses $X_j$, it itself has a Bernoulli distribution given by $X=1_{\mathcal L}$, where $P(\mathcal L)=\sum _k p_k E_k$. Using the exponential utility, we can find the demand price as follows:

  $$\begin{aligned} \lambda ^D=\frac{\log (E(e^{aX}))}{a}=\frac{\log (1-\sum _k p_k E_k + e^a \sum _k p_k E_k)}{a}, \qquad a>0, \end{aligned}$$

  and

  $$\begin{aligned} \lambda ^D=E(1_{\mathcal L})=\sum _k p_k E_k, \qquad a=0. \end{aligned}$$

  We display the relative pricing gap in Fig. 6.3. Now let us consider our example of the UK Coronavirus Job Retention Scheme for $\beta =1$. Interestingly, we can see the same results as in Figs. 6.1 and 6.2, which means regardless of all other parameters there is a trade-off between the existence of the market equilibrium and correct risk coverage.

Fig. 6.3

Relative pricing gap for risk rate common shocks and $\gamma =0.01$

Remark 6.5

In all examples, we can observe an interesting fact that is that the optimal risk-sharing approach in the limit for $n\rightarrow \infty$ will result in the following

$$\begin{aligned} \lambda =E(X|Sys), \end{aligned}$$

where Sys is the sigma-field representing the systematic events. More precisely, for the examples with the risk-sharing and insurance platforms, it is $Sys=\sigma (Z)$, and in the example with the market platform, it is $Sys=\sigma (\Omega _1,\ldots ,\Omega _n)$. The observation that the average of infinitely many exchangeable random variables reduce to a conditional expectation is not surprising to us, as it is related to De Finetti’s theorem with exchangeable risk (see Kingman 1978, for more details on De Finetti’s theorem).

6.6 Conclusion

In this paper, we considered an insurance cohort with identically distributed loss variables, and this insurance cohort sought an insurance scheme that keeps everybody’s final wealth distributionally the same. This was called the non-discriminatory insurance (NDI) assumption. We have considered a very general setting where there is no need for any dependency structure of the wealth variables; this essentially means that we did not assume that losses, or the wealth distributions, are i.i.d or exchangeable. This general setup is motivated by systematic loss events such as a widespread pandemic (e.g., Spanish flu or COVID-19) with large macroeconomic loss impact. The idea is to provide a platform where we can properly study the risk management of macro-level losses.

We considered three different platforms: a risk-sharing, an insurance and a market platform. There are some general observations from studying these platforms. First, we showed that under NDI the most efficient final wealth is nothing but the average wealth; regardless of the dependency structure. Second, from the first observation we realised that there are benefits of introducing a contingent, ex-post premium. This essentially means that ex-post policies are shown to be more efficient than the current ex-ante insurance policies.

For any specific platform we also have made very interesting observations based on three common shock models, which include the additive, multiplicative and the risk rating common shock model. First, the risk-sharing platform is an efficient platform and any insurance scheme only acts as a wealth re-distributor ex-post. Second, in the insurance platform as the insurance companies are regulated and need to be solvent the optimal answer is a partial risk-sharing scheme. As a result, we observe that in this platform the risk-sharing platform the policyholders do not bear the risk of the tail events which necessitated the existence of a social scheme run by the state or government to bear the tail event risk. Third, we studied the market platform. In a competitive market, we see that we will come up with a deterministic premium, which gives an ex-ante policy. However, we observe that this platform dramatically increases the risk of insolvency. In the decentralised market platform, we realised that there is a trade-off between the tail risk of the insurer (supply side) and the market equilibrium. On one hand, if the common shock is not a tail event then we have no market equilibrium. On the other hand, if the common shock is tail event, even though a market equilibrium exists, there is substantial tail risk. Apparently if there is no common shock then both absence of tail risk and insurance market equilibrium can happen at the same time.

We have calibrated our models to the Coronavirus Job Retention Scheme (the UK furlough scheme during the COVID-19 pandemic), and all the observations are made on that basis. The results of the paper suggest new policy implications; the most important of which is the consideration of ex-post (contingent) premia, where the insurance premium is collected after the observation of the realised losses. Our observation is that in the presence of common shock, the major issue would not be the sophistication of the loss modelling or contracting, but it is the paradigm that may need to be changed. The insurance market needs be sustainable for systematic shock events, which for our case study means that unemployment insurance premia becomes contingent to the occurrence of the systematic risks such as COVID-19. This means that to reach the optimal allocation one adjusts the premium by directing wealth from people who did not lose to the people who have lost. In short, such insurance plans serve as a mechanism to diversify idiosyncratic risk and to share systematic risk. The systematic risk caused by COVID-19 is hard to insure as discussed by Richter and Wilson (2020).

The observation from the real world to a good extent confirms our conclusions. First, there has been a dispute⁵ over the insurance coverage of the pandemic losses in the UK which has emphasised the unwillingness (or inability) of the supply-side (insurers) of the insurance market to settle the claims. Second, the government in the UK has introduced a generous furlough scheme⁶ that ran for a few months to cover a large portion of the workforce in the UK. This has been executed in different means but the necessary capital will increase the government deficit and need to be paid back either by direct taxes or inflation. That can be regarded as some kind of contingent premia. Third, the UK government has supported businesses through the Trade Credit Insurance (TCI) guarantee, which again seems to be more like a contingency measure.⁷ However, none of these solutions are carefully planned, and they are all based on the short-term assessments. Finding an insurance solution consistent to what we discuss in this paper seems to be a suitable direction to consider for further research.